4.1 Definiciones y propiedades básicas. f (x) = f (x) =lim h 0. ln(x+h) ln x. h 0 =lim. x h x = 1+ h x. sin(x+h) sin x. a b. sin.
|
|
|
- Francisca Maestre Hidalgo
- hace 5 años
- Vistas:
Transcripción
1 Tema 4 Derivación 4. Definiciones y propiedades básicas Definición 4.. Dada una función f : D R R, diremosquef es derivable en un punto x 0 D, si existe el límite siguiente, que denotaremos f 0 (x 0 ) o df dx x 0 : f 0 f(x) f(x 0 ) (x 0 ) := lim x x0 x x 0 lim x 0 f(x 0 + x) f(x 0 ) x f(x 0 + ) f(x 0 ) = lim 0 f (x) = lim = lim 0 x 0 = f (x) x. El límite f 0 (x 0 ) se denomina derivada, respecto de x, de la función f en el punto x 0. Ejemplo 4.. Dada la función f (x) =lnx, suderivadaenunpuntox será: f 0 f(x+) f(x) ln(x+) ln x ln (x) = lim 0 = lim 0 = lim x+ x 0 = ln(+ lim x) 0 =lim 0 ln + x =lim 0 ln + x x x = lim 0 ln + x = ln x i lim x x x 0 + = ln e = x x x Ejemplo 4.. En el caso de f (x) =sinx: f 0 f(x+) f(x) (x) = lim 0 = lim 0 sin(x+) sin x Y, recordando que sin a sin b =cos a+b lim 0 sin(x+) sin x lim 0 cos x+ sin =lim 0 cos x+ sin = sin a b =lim 0 cos x+ sin lim 0 =cosx sin x Ya que, según se vió en el tema (Ejercicios resueltos):lim x 0 x =.
2 TEMA 4 Dado que la derivada es un límite, igual que existen límites laterales existen derivadas laterales: Definición 4.. Dada una función f : D R R,diremosqueenx 0 D admite: derivada lateral por la dereca, que denotamos f 0 (x) ó f 0 x + x + 0 : 0 f 0 (x + f(x 0 + ) f(x 0 ) 0 ) := lim 0 >0 derivada lateral por la izquierda, que denotamos f 0 (x 0 ) ó f 0 (x) : x 0 f 0 (x f(x 0 ) f(x 0 ) 0 ):=lim 0 >0 Como en el caso de los límites laterales, la existencia de derivada implica la existencia, e igualdad, de las derivadas laterales. Recíprocamente si existen y coinciden las derivadas laterales, existe la derivada y coincide con ellas. En caso de que alguna de las derivadas laterales no exista, o en caso de que sean distintas, no existe la derivada. Igual que no existe el límite, si los límites laterales son distintos o alguno de ellos no existe. Teorema 4.. Dada la función f : D R R, tenemos: f derivable en x D f continua en x. Nota 4.. El recíproco del teorema precedente es falso, como puede verse, por ejemplo, con la función f (x) := x, enelpuntox =0: 4 3 y -4-0 x 4 lim x 0 + f (x) = lim x 0 + x = lim 0 0+ = 0 = lim 0 0 = lim x 0 x =lim x 0 f (x) Límites que coinciden con f (0), es decir f es continua en 0, pero:
3 4.3 3 f 0 (0 + ) = lim 0 >0 f 0 (0 ) = lim 0 >0 f(0+) f(0) f(0 ) f(0) = lim 0 >0 = lim 0 >0 0 0 =lim 0 >0 = lim 0 >0 = = Las derivadas laterales son diferentes, por lo que f no es derivable en Interpretación geométrica de la derivada Supuesto que la curva representada en la figura corresponde a la función de ecuación y = f (x), consideremos los puntos: P =(x, f (x)), A =(x + x, f (x)+ f (x)) Como podemos ver, considerando el triángulo AP B: f(x) = AB =tanα, x PB pero, cuando x 0, elpuntoa tiende a coincidir con el punto P,demanera que la cuerda AP pasa a ser la tangente a la curva en P y, en el límite, el ángulo α pasa a coincidir con el ángulo β, así f 0 f (x) = lim x 0 x = lim tan α =tanβ x 0 Por tanto la derivada de una función en un punto es, numéricamente, igual al valor de la tangente trigonométrica del ángulo formado, con el sentido positivo del eje OX, porlatangentegeométrica alacurvacorrespondiente, en el punto dado. En los puntos en que la curva admite dos tangentes distintas, la derivada no existe, pues tendría dos derivadas distintas, una por cada tangente. A ëf{x} P β α ëx B 4.3 Derivadas de las operaciones con funciones Teorema 4.3. Dadas dos funciones f,g : X R R, derivablesenun punto x X, con derivadas respectivas f 0 (x),g 0 (x) en tal punto, se verifica:
4 4 TEMA 4 i. f + g es derivable en x, siendo(f + g) 0 (x) =f 0 (x)+g 0 (x). ii. Dada una constante λ R, λf es derivable en x y (λf) 0 (x) =λf 0 (x). iii. f g es derivable en x, siendo(f g) 0 (x) ³ =f 0 (x) g (x)+f (x) g 0 (x). iv. f 0 es derivable en x si g(x) 6= 0,siendo f g g (x) = f 0 (x)g(x) f(x)g 0 (x). (g(x)) 4.4 Derivadas de funciones elementales Veremos algunas, las derivadas de las funciones cos x, tan x, cot x, sec x, csc x, se deducen de la derivada de la función sin x. Teorema 4.4. Se verifica: i. f (x) =cte f 0 (x) =0 ii. f (x) =x n f 0 (x) =nx n iii. f (x) =sinx f 0 (x) =cosx iv. f (x) =lnx f 0 (x) = x. 4.5 Regla de la cadena (Derivada de la función de función) Dada una función g (f), enlaquef a su vez es función de otra variable x, se trata de dar una regla que permita derivar g respecto de x. Por ejemplo si queremos derivar la función y =ln x +, con respecto a x, x podemos considerar las funciones f = f (x) = x + x siguiente teorema da una regla para calcular dy dx : Teorema 4.5. (Regla de la cadena)dadaslasfunciones: f : A R R, derivableenx A, conf (A) B g : B R R, derivable en y = f (x) B La función compuesta g f, es derivable en x; siendo: dg(f(x)) dx En el ejemplo precedente será: f =(g f) 0 (x) =g 0 (f (x)) f 0 (x) = dg df df dx dy dg (f (x)) = = dg dx dx df df dx = d ln f df x x x (x +) = x x 4 x + x x 4 =,yg = g (f) =lnf, el d x + x dx = x (x +) Como consecuencia inmediata de este teorema, resultan las reglas usuales de derivación:
5 4.6 5 f (x) =cosx =sin π x f 0 (x) = cos π x π x 0 = cos π x = sin x f (x) =u n (x) f 0 (x) =nu n (x) u 0 (x) f (x) =lnu (x) f 0 (x) = u0 (x) u(x) f (x) =a u(x),siendoa constante: ln f (x) =u (x) ln a f 0 (x) f(x) = u 0 (x)lna f 0 (x) =a u(x) ln a u 0 (x) f (x) =sinu (x) f 0 (x) =cosu (x) u 0 (x). 4.6 Derivadadelafuncióninversa Recordemos que, tal como se definió en el tema relativo a funciones y continuidad, dada una función f : A R R con f (A) :=B R, diremos que f admite una inversa f : B A, sif f (y) =y, y B es decir f f = B,yf f (x) =x, x A, of f = A, donde A,y B, representan las funciones identidad de A y B respectivamente, es decir A (x) =x, x A, y B (y) =y, y B. A f f El siguiente teorema da una regla de derivación de la función inversa de una dada: Teorema 4.6. Dada una función monótona f :[a, b] [c, d] =f ([a, b]), verificando: i. Es derivable en [a, b] ii. Admite inversa g Entonces g es derivable en [c, d], siendo: g 0 (y) = = y = f 0 (x) f 0 (g(y)) f (x) [c, d]. Debe tenerse cuidado con las variables que utilizan f y g: Ejemplo 4.6. Calcular la derivada de y =arcsinx Sea g (x) =arcsinx, eslainversadef (y) =siny, así aplicando el resultado anterior será: B
6 6 TEMA 4 g 0 (x) = obien: f 0 (y) g0 (x) = cos y Pero la derivada g 0 (x), debe darse en función de x, así que: g 0 (x) = = cos y sin = y x En casos como el precedente, puede utilizarse otro método: Dada y =arccosx, tenemos: cos y = x, derivando, de acuerdo con la regla de la cadena: sin y y 0 =,portanto: y 0 = = sin y cos = y x De todo lo anterior podemos deducir una tabla de derivadas: función f (x) u n (x) ln u (x) a u(x) sin u (x) cos u (x) tan u (x) cot u (x) sec u (x) csc u (x) arcsin u (x) arccos u (x) arctan u (x) función derivada f 0 (x) nu n (x) u 0 (x) u 0 (x) u(x) a u(x) ln a u 0 (x) cos u (x) u 0 (x) sin u (x) u 0 (x) [ + tan u (x)] u 0 (x) =sec u (x) u 0 (x) [ + cot u (x)] u 0 (x) = csc u (x) u 0 (x) sec u (x) tan u (x) u 0 (x) csc u (x) cot u (x) u 0 (x) u0 (x) u (x) u0 (x) u (x) u 0 (x) +u (x) 4.7 Teoremas de valor medio. Aplicaciones 4.7. Teoremas de valor medio Definición 4.7. Dada una función f : X R R diremos que x 0 X es un punto crítico (a veces estacionario) silafunciónf es derivable en x 0 y f 0 (x 0 )=0. Teorema 4.7. Dada una función f :[a, b] R R, verificando: i. f continua en [a, b] ii. f derivable en (a, b) En estas condiciones si f tiene un extremo (máximo o mínimo), local en x 0 (a, b) entonces x 0 es un punto crítico de f, esdecirf 0 (x 0 )=0.
7 4.7 7 Advertencia 4.7. El recíproco del anterior no es cierto, como podemos ver con la función: f (x) := x5 0 4x +x, suderivadaf 0 (x) = x4 8x + 4 se anula para x =donde f no tiene extremo y x Teorema 4.7. (De Rolle): Dada una función f :[a, b] R R, talque i. f continua en [a, b] ii. f derivable en (a, b) iii. f (a) =f (b) En estas condiciones existe al menos un c (a, b), talquef 0 (c) =0. Gráficamente este teorema asegura, de acuerdo con la interpretación geométrica de la derivada, que la curva representativa de la función dada, tiene al menos un punto en el que la tangente es paralela a OX : a c b Teorema (Del valor medio, odelosincrementos finitos de Lagrange): Dada una función f :[a, b] R R, talque i. f continua en [a, b] ii. f derivable en (a, b)
8 8 TEMA 4 En estas condiciones existe un c (a, b), talque f 0 (c) = f (b) f (a). b a Así en las ipótesis del teorema, podemos escribir: f (b) f (a) =f 0 (c)(b a), o bien poniendo a = x, b = x +, c = x + θ con θ (0, ):x f (x + ) f (x) =f 0 (x + θ) o f = x f 0 (x + θ x) Queeslafórmula de los incrementos finitos de Lagrange. Esta propiedad tiene una interpretación gráfica: existe un c (a, b), tal que la tangente a la curva, representada por f (x), enelpunto(c, f (c)), es paralela a la cuerda que une (a, f (a)), con(b, f (b)) {c,f{c}õ f{x+}_f{x} a c b Teorema (Del valor medio generalizado de Caucy) Dadas dos funciones f,g :[a, b] R R, tales que: i. f,g continuas en [a, b] ii. f,g derivables en (a, b), cong 0 (x) 6= 0 x (a, b) En estas condiciones existe un c (a, b), talque f 0 (c) g 0 (c) = f (b) f (a) g (b) g (a). 4.8 Aplicación al estudio de límites indeterminados Teorema 4.8. (regla de L Hôpital-Bernoulli): Dadas dos funciones f,g :(a, b) R R, tales que: i. f,g derivables en (a, b), cong 0 (x) 6= 0 x (a, b)
9 4.8 9 ½. limx a + f (x) =lim x a + g (x) =0 ii. Se verifica una de las condiciones:. lim x a + f (x) = lim x a + g (x) = En tal caso será lim f(x) x a + = lim g(x) x a f 0 (x) + g 0 (x) lim x a + f 0 (x) g 0 (x) = L. El resultado sigue siendo válido si se reemplaza lim x a + = L, siempre que exista el por lim x a El resultado anterior permite resolver directamente las indeterminaciones de tipo,o 0. Otras formas de indeterminación se estudiaron en la sección 0.4, de entre las resolubles usando la regla de l Hôpital-Bernoulli, tenemos: -Caso0 : lim x a f (x) =0, lim x a g (x) =, Podemos poner: f(x) lim x a f (x) g (x) = lim x a, que denotando G (x) =,resulta: g(x) g(x) f(x) lim x a f (x) g (x) = lim x a, y estamos en la forma 0: G(x) 0 En los casos sìguientes utilizamos la transformación, vista ya en.4: lim x a f (x) g(x) = lim x a e ln f(x)g(x) = lim x a e g(x)lnf(x) limx a g(x)lnf(x) = e -Caso0 0 : lim x a f (x) = 0, lim x a g (x) = 0, la transformación mencionada la transforma en e 0,dadoque: lim x a f (x) g(x) = e limx a g(x)lnf(x) = e 0 ( ) Con lo que estamos en el caso anterior -Caso 0 : lim x a f (x) =, lim x a g (x) =0, esta forma queda: lim x a f (x) g(x) = e lim x a g(x)lnf(x) = e 0 -Caso : lim x a f (x) =, lim x a g (x) =, esta forma puede resolverse como la anterior: lim x a f (x) g(x) = e lim x a g(x)lnf(x) = e 0 O bien tal como se indicó en.4, con la transformación lim x a f (x) g(x) = lim x a e g(x)[f(x) ] Ejemplo 4.8. Calcular lim x (x 4) ln (x ) Es del caso 0 : lim x (x ln(x ) 4) ln (x ) = lim x x 4 Aplicando la regla de L Hôpital: lim x (x 4) x(x ) = lim x =lim x x x (x 4)x (x ) x = lim x 0 4 =0 (x 4) =lim x (x 4) x(x )
10 0 TEMA 4 Ejemplo 4.8. Calcular lim x [ln (x )] ( x 4) Es del caso 0 : lim x [ln (x )] 4) (x = limx e 4) (x ln[ln(x )] =lim x e Aplicando la regla de L Hôpital: x ln[ln(x )] ln(x ) (x ) ln(x ) lim x =lim x x x =lim x 4 (x 4) x = (x 4) ln[ln(x )] x 4 (x lim 4) x = lim (x ) (x+) x(x ) ln(x ) x = lim x(x ) ln(x ) x (x )(x+) Por tanto lim x ln[ln(x )] x 4 x ln(x ) =0 =0. Esimportanterecordar,queellímite pedido no es este, sino lim x [ln (x )] ( x 4) =limx e lim x [ln (x )] ( x 4) = e 0 =. Ejemplo Calcular lim x (x 3) ln(x ) Es del caso : lim x e 3 ) [ln(x )](x = limx e 4) (x ln(x ) = lim x e Aplicando la regla de L Hôpital: ln(x ) x 4 x x 4 ) ln[ln(x )] x 4, así que: ln(x ) x 4 (x lim x e =lim x e 4) =lim x e (x x(x ) = limx e (x ) (x+) lim x e (x )(x+) x = e 0 =. x(x ) = 4.9 Determinación de extremos locales Vimos que si una función derivable en un punto x, tieneunextremoenx, su derivada en tal punto x es nula, es decir x es un punto crítico. Una función puede tener extremo en un punto x 0, y no ser derivable en él, por ejemplo y = x en el punto x = Criterio de la primera derivada Teorema 4.9. Dada una función f :[x 0, x 0 + ] R R, continua en [x 0, x 0 + ] yderivableen(x 0, x 0 ) (x 0,x 0 + ). En tal caso: i. Si x<x 0 f 0 (x) > 0 y x>x 0 f 0 (x) < 0: f tiene máximo local en x 0. ii. Si x<x 0 f 0 (x) < 0 y x>x 0 f 0 (x) > 0:f tiene mínimo local en x 0.
11 4.9 Definición 4.9. Diremos que una función f : I R R, es de clase C k en I, lo que se denota f C k (I), si la función y sus derivadas de orden menor o igual que k, soncontinuaseni Criterio de la segunda derivada Teorema 4.9. Dada una función f :[x 0, x 0 + ] R R, tal que: i. f C ([x 0, x 0 + ]). ii. f 0 (x 0 )=0 En estas condiciones:. f 00 (x 0 ) > 0 f tiene mínimo local en x 0.. f 00 (x 0 ) < 0 f tiene máximo local en x Caso de la segunda derivada nula Considerando una función f de clase C n, caso de tener extremo en un punto x 0, deberá ser f 0 (x 0 ) = 0, supongamos además que f 00 (x 0 ) = 0, o más generalmente que f (k (x 0 )=0, k<n, con lo que el criterio precedente no decide sobre la existencia de extremo. El siguiente teorema da un criterio basado en el orden de la primera derivada no nula en x 0 : Teorema Dada una función f : D R R, verificando: i f es de clase C n en un entorno [x 0, x 0 + ] de un punto x 0 D ii. f (k (x 0 )=0, k<n iii. f (n (x 0 ) 6= 0 En estas condiciones: ½ a. f. si n es par y (n (x 0 ) > 0 tiene mínimo local en x 0 b. f (n (x) < 0 tiene máximo local en x 0. si n es impar y ½ a. f (n (x 0 ) > 0 f es creciente en x 0 b. f (n (x) < 0 f es decreciente en x 0 En realidad este criterio incluye los dos anteriores. Ejemplo 4.9. Determianr los extremos de y = x4 x3 + 3x 5 3 y 0 = x3 3 x +3x, que se anula para x =0y x =3 y 00 = x 4x +3,parax =0vale 3, por lo que ay un mínimo en (0, 5) Pero para x =3,seanula. y 000 =x 4, que para x =3,vale+, por lo que al ser la primera derivada no nula (para x =3), de orden impar, y positiva, la función crece en x =3.
12 TEMA x Asíntotas Definición 4.0. Diremos que una recta es una asíntota de una curva de ecuación y = f (x) si la distancia entre un punto de la curva, y la recta tiende a cero, cuando la distancia entre tal punto de la curva y (0, 0), tiende ainfinito. Hay tres tipos de asíntotas: a. asíntotas orizontales: f tiene una asíntota orizontal y = b si lim x ± f (x) =b 6= b. asíntotas verticales: f tiene una asíntota vertical x = a 6= si lim x a f (x) = c. asíntotas oblícuas: f tiene una asíntota oblícua y = mx + n si la distancia entre esta recta y (x, f (x)) tiendeaceroaltenderx a ± Teorema 4.0. (Determinación de las asíntotas oblícuas): Si y := mx + n (0 6= m 6=,n6= ) es una asíntota oblícua de la curva representada por f (x) entonces: f (x) m = lim x x, n =lim f (x) mx x
13 4. 3 f(x) y=mx+n n x Advertencia 4.0. Suele decirse, que una curva que admite asíntota orizontal no admite asíntota oblícua, esto es cierto con matices: si ay asíntota orizontal con x + no ay asíntota oblícua con x +, pero puede aberla con x, lo mismo puede decirse si ay asíntota orizontal con x. Ver por ejemplo el ejercicio resuelto n o Concavidad Definición 4.. Diremos que una curva es cóncava acia arriba, (o convexa acia abajo), entorno de un punto x 0 si, entorno de x 0 la curva está situada por encima de la tangente a la curva en x 0. De manera análoga se define la concavidad acia abajo. Cuando, por el contrario, en un semientorno de x 0 la curva está por encima, y en otro por debajo de la tangente, diremos que en x 0 ay un punto de inflexión. Ejemplo 4.. En la figura adjunta, la curva tiene una concavidad de tipo en x 0 :
14 4 TEMA 4 B P f(x) y=f(xü)+f»(xü)(x-xü) xü x Teorema 4.. Dada la ecuación y = f (x), de una curva. Si entorno de un punto x 0 la función f es de clase C,y: i. f 00 (x) > 0 en tal entorno la curva es cóncava acia las YY positivas. ii. f 00 (x) < 0 en tal entorno la curva es cóncava acia las YY negativas. iii. f 00 (x) cambia de signo al pasar de valores menores que x 0 avalores mayores que x 0,enx 0 la curva tiene un punto de inflexión. 4.. Caso de la segunda derivada nula Teorema 4.. Dada la ecuación de una curva y = f (x). Sientornode un punto x 0, se verifica que f es de clase C n en tal entorno, con f 00 (x 0 )= f 000 (x 0 )=... = f (n (x 0 )=0, f (n (x 0 ) 6= 0: i. caso de ser n par:. si f (n (x) > 0 la curva es cóncava acia las YY positivas entorno de x 0.. si f (n (x) < 0 la curva es cóncava acia las YY negativas entorno de x 0. ii. caso de ser n impar, la curva tiene un punto de inflexión en x 0 siendo:. creciente si f (n (x 0 ) > 0. decreciente si f (n (x 0 ) < 0. Ejemplo 4.. En el ejemplo anterior (4.9.), lafuncióny = x4 x x 5 y 0 = x3 3 x +3x, y 00 = x 4x +3=(x ) (x 3), esnegativaen(, 3), porloquees cóncavaaciaabajo, y cóncava acia arriba,en (, ) (3, ), y 00 se anula x =y x =3. y 000 =x 4, que para x =3,vale+, por lo que al ser la primera derivada no nula (para x =3), de orden impar, y positiva, la función crece en x =3,
15 4. 5 alainversaenx =, es negativa por lo que decrece, abiendo punto de inflexión en ambos casos, como se aprecia en la figura. - x
Tema 3 Continuidad Definición de Continuidad Operaciones y Composición de Funciones Continuas
 Tema 3 Continuidad 3..- Definición de Continuidad Una función se dice continua en un punto de su dominio, si existe el límite de la función y coincide con el valor de la función en dicho punto. Es decir:
Tema 3 Continuidad 3..- Definición de Continuidad Una función se dice continua en un punto de su dominio, si existe el límite de la función y coincide con el valor de la función en dicho punto. Es decir:
Derivación de funciones reales de una variable
 Derivación de funciones reales de una variable Derivada de una función en un punto. Interpretación física y geométrica Aproximación de raíces: Método de Newton Raphson Derivabilidad Cálculo de derivadas
Derivación de funciones reales de una variable Derivada de una función en un punto. Interpretación física y geométrica Aproximación de raíces: Método de Newton Raphson Derivabilidad Cálculo de derivadas
Nociones básicas. Febrero, 2005
 Febrero, 2005 Índice general Funciones es de variable Derivación de funciones es de variable Funciones es de variable Derivación de funciones es de variable Conjuntos de números IN Z Q IR C Densidad de
Febrero, 2005 Índice general Funciones es de variable Derivación de funciones es de variable Funciones es de variable Derivación de funciones es de variable Conjuntos de números IN Z Q IR C Densidad de
Cálculo Diferencial de una Variable
 Departamento de Matemática Aplicada Universitat Politècnica de València, España Fundamentos Matemáticos para la Ingenieria Civil Esquema Esquema de la exposición Definición. Interpretación geométrica de
Departamento de Matemática Aplicada Universitat Politècnica de València, España Fundamentos Matemáticos para la Ingenieria Civil Esquema Esquema de la exposición Definición. Interpretación geométrica de
C alculo Octubre 2010
 Cálculo Octubre 2010 Derivada. Introducción Recordemos la definición de pendiente de una recta: α y 1 y0 x 0 x 1 Pendiente= m = tanα = y 1 y 0 x 1 x 0 Y ahora consideremos las pendientes de las rectas
Cálculo Octubre 2010 Derivada. Introducción Recordemos la definición de pendiente de una recta: α y 1 y0 x 0 x 1 Pendiente= m = tanα = y 1 y 0 x 1 x 0 Y ahora consideremos las pendientes de las rectas
Cálculo Diferencial en una variable
 Tema 2 Cálculo Diferencial en una variable 2.1. Derivadas La derivada nos proporciona una manera de calcular la tasa de cambio de una función Calculamos la velocidad media como la razón entre la distancia
Tema 2 Cálculo Diferencial en una variable 2.1. Derivadas La derivada nos proporciona una manera de calcular la tasa de cambio de una función Calculamos la velocidad media como la razón entre la distancia
CÁLCULO DIFERENCIAL. b) Al darle a x valores suficientemente grandes, los valores de f(x) crecen cada vez más
 1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO: CÁLCULO DIFERENCIAL Una función f(x) tiene por límite L en el número real x = c, si para toda sucesión de valores x n c del dominio que tenga por límite c, la sucesión
1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO: CÁLCULO DIFERENCIAL Una función f(x) tiene por límite L en el número real x = c, si para toda sucesión de valores x n c del dominio que tenga por límite c, la sucesión
= f (a) R. f(x) f(a) x a. recta por (a, f(a)) de pendiente f(a+h2) f(a) recta tangente por (a, f(a)) de pendiente f (a)
 1 1. DERIVACIÓN 1.1. DEFINICIONES Y RESULTADOS PRINCIPALES Definición 1.1. Derivada. Sea f una función definida en un intervalo abierto I con a I. Decimos que f es derivable en a si existe y es real el
1 1. DERIVACIÓN 1.1. DEFINICIONES Y RESULTADOS PRINCIPALES Definición 1.1. Derivada. Sea f una función definida en un intervalo abierto I con a I. Decimos que f es derivable en a si existe y es real el
Derivación. Aproximaciones por polinomios.
 Derivación... 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Matemáticas (Grado en Químicas) Contenidos Derivada 1 Derivada 2 3 4 5 6 Outline Derivada 1 Derivada 2 3 4 5 6 Definición
Derivación... 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Matemáticas (Grado en Químicas) Contenidos Derivada 1 Derivada 2 3 4 5 6 Outline Derivada 1 Derivada 2 3 4 5 6 Definición
Teoremas del valor medio
 Teoremas del valor medio Teorema de Rolle Teorema de Cauchy Teorema de Lagrange Teorema de Rolle Sea f x una función contínua en a; b, derivable en a; b y f a = f(b) entonces existe al menos un cε a; b
Teoremas del valor medio Teorema de Rolle Teorema de Cauchy Teorema de Lagrange Teorema de Rolle Sea f x una función contínua en a; b, derivable en a; b y f a = f(b) entonces existe al menos un cε a; b
Derivadas e integrales
 Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es ÍNDICE Matemáticas Cero Índice. Definiciones 3. Herramientas 4.. Reglas de derivación.......................
Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es ÍNDICE Matemáticas Cero Índice. Definiciones 3. Herramientas 4.. Reglas de derivación.......................
Derivadas e integrales
 Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 5 2.1. Reglas de derivación............................
Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 5 2.1. Reglas de derivación............................
TEMA 3: CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES REALES DE UNA VARIABLE REAL. f : R R
 TEMA 3: CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES REALES DE UNA VARIABLE REAL. Concepto de función. Definición Se llama función (real de variable real) a toda aplicación f : R R f() que a cada número le
TEMA 3: CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES REALES DE UNA VARIABLE REAL. Concepto de función. Definición Se llama función (real de variable real) a toda aplicación f : R R f() que a cada número le
1. Nociones básicas. Oct, 2008
 Cálculo 1. Nociones básicas Oct, 2008 Nociones básicas Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial y logarítmica Funciones
Cálculo 1. Nociones básicas Oct, 2008 Nociones básicas Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial y logarítmica Funciones
Derivabilidad de funciones de una
 Tema 3 Derivabilidad de funciones de una variable El objetivo del presente tema es la derivación de funciones reales de variable real, así como sus diversas aplicaciones entre las que destacamos la representación
Tema 3 Derivabilidad de funciones de una variable El objetivo del presente tema es la derivación de funciones reales de variable real, así como sus diversas aplicaciones entre las que destacamos la representación
Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García. UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior
 INGENIERÍAS TÉCNICAS INDUSTRIALES TEORIA DE CÁLCULO I Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento
INGENIERÍAS TÉCNICAS INDUSTRIALES TEORIA DE CÁLCULO I Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento
Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización.
 TEMA 1 Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización. Límite finito en un punto: Consideremos una función f definida en las proimidades
TEMA 1 Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización. Límite finito en un punto: Consideremos una función f definida en las proimidades
Función Real de variable Real. Definiciones
 Función Real de variable Real Definiciones Función Sean A y B dos conjuntos cualesquiera. Una aplicación de A en B es una relación que asocia a cada elemento (x=variable independiente) de A un único valor
Función Real de variable Real Definiciones Función Sean A y B dos conjuntos cualesquiera. Una aplicación de A en B es una relación que asocia a cada elemento (x=variable independiente) de A un único valor
Teorema de los extremos absolutos (del supremo y el ínfimo), de Weiestrass.
 CALCULO DIFERENCIAL TEMA 1 : PROPIEDADES DE LAS FUNCIONES CONTINUAS Teorema del signo. Sea f:[a,b] >R una función continua en (a,b) entonces si f(x0)"0, existe un entorno E(x0,) en que f tiene el mismo
CALCULO DIFERENCIAL TEMA 1 : PROPIEDADES DE LAS FUNCIONES CONTINUAS Teorema del signo. Sea f:[a,b] >R una función continua en (a,b) entonces si f(x0)"0, existe un entorno E(x0,) en que f tiene el mismo
Capítulo 2: Cálculo diferencial de una y varias variables
 Capítulo 2: Cálculo diferencial de una y varias variables (Fundamentos Matemáticos de la Biotecnología) Departamento de Matemáticas Universidad de Murcia Contenidos Límites y continuidad Límites laterales
Capítulo 2: Cálculo diferencial de una y varias variables (Fundamentos Matemáticos de la Biotecnología) Departamento de Matemáticas Universidad de Murcia Contenidos Límites y continuidad Límites laterales
Nombre y Apellidos: x e 1 x 1 x f(x) = ln(x) x
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Nombre y Apellidos: Cálculo I Convocatoria de Diciembre de Diciembre de 008 DNI: (6.5 p.) ) Se considera la función f : R R definida
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Nombre y Apellidos: Cálculo I Convocatoria de Diciembre de Diciembre de 008 DNI: (6.5 p.) ) Se considera la función f : R R definida
Cociente incremental. Mide la variación media de f(x) en (x 0, x 0 + x)
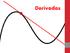 Derivadas Cociente incremental Sea y= f(x) continua en x=x 0 x: incremento de la variable independiente y: incremento de la variable dependiente Se llama cociente incremental al cociente y f ( x x f xo
Derivadas Cociente incremental Sea y= f(x) continua en x=x 0 x: incremento de la variable independiente y: incremento de la variable dependiente Se llama cociente incremental al cociente y f ( x x f xo
CONCEPTOS QUE DEBES DOMINAR
 INTERVALOS CONCEPTOS QUE DEBES DOMINAR Un intervalo es un conjunto infinito de números reales comprendidos entre dos extremos, que pueden estar incluidos en él o no. 1. Intervalo abierto (a, b): Comprende
INTERVALOS CONCEPTOS QUE DEBES DOMINAR Un intervalo es un conjunto infinito de números reales comprendidos entre dos extremos, que pueden estar incluidos en él o no. 1. Intervalo abierto (a, b): Comprende
TEMA 5. FUNCIONES DERIVABLES. TEOREMA DE TAYLOR
 TEMA 5. FUNCIONES DERIVABLES. TEOREMA DE TAYLOR 5.1 DERIVADA DE UNA FUNCIÓN 5.1.1 Definición de derivada Definición: Sea I in intervalo abierto, f : I y a I. Diremos que f es derivable en a si existe y
TEMA 5. FUNCIONES DERIVABLES. TEOREMA DE TAYLOR 5.1 DERIVADA DE UNA FUNCIÓN 5.1.1 Definición de derivada Definición: Sea I in intervalo abierto, f : I y a I. Diremos que f es derivable en a si existe y
Introducción a las derivadas
 Introducción a las derivadas Esquema Tasa de variación media en un intervalo Para una función f(x) se define la tasa de variación media de f en un intervalo [a, b], contenido en el dominio f(x), mediante
Introducción a las derivadas Esquema Tasa de variación media en un intervalo Para una función f(x) se define la tasa de variación media de f en un intervalo [a, b], contenido en el dominio f(x), mediante
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid Resueltos Isaac Musat Hervás 22 de mayo de 203 Capítulo 7 Año 2006 7.. Modelo 2006 - Opción A Problema 7.. 2 puntos Un punto de luz situado
Problemas de Selectividad de Matemáticas II Comunidad de Madrid Resueltos Isaac Musat Hervás 22 de mayo de 203 Capítulo 7 Año 2006 7.. Modelo 2006 - Opción A Problema 7.. 2 puntos Un punto de luz situado
TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN 9.1 DERIVADA DE UNA FUNCIÓN EN UN PUNTO
 TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN MATEMÁTICAS II º Bach TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN 9. DERIVADA DE UNA FUNCIÓN EN UN PUNTO TASA DE VARIACIÓN MEDIA Definición Se llama tasa de variación
TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN MATEMÁTICAS II º Bach TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN 9. DERIVADA DE UNA FUNCIÓN EN UN PUNTO TASA DE VARIACIÓN MEDIA Definición Se llama tasa de variación
RESUMEN DE DERIVADAS. TVM = f(x) = lim 1+2h+h 2-1. = lim 1+h) lim. = 0 = lim h2+h)
 RESUMEN DE DERIVADAS Tasa de variación Media. Definición: se llama tasa de variación media (TVM) de una función f(x) entre los valores x 1 y x 2 al cociente entre el incremento que experimenta la variable
RESUMEN DE DERIVADAS Tasa de variación Media. Definición: se llama tasa de variación media (TVM) de una función f(x) entre los valores x 1 y x 2 al cociente entre el incremento que experimenta la variable
Derivada de una función en un punto. Función derivada. Diferencial de una función en un punto. dy = f (x) dx. Derivada de la función inversa
 Derivada de una función en un punto Las tres expresiones son equivalentes. En definitiva, la derivada de una función en un punto se obtiene como el límite del cociente incremental: el incremento del valor
Derivada de una función en un punto Las tres expresiones son equivalentes. En definitiva, la derivada de una función en un punto se obtiene como el límite del cociente incremental: el incremento del valor
TEMA 11: ESTUDIO LOCAL Y GLOBAL DE FUNCIONES. OPTIMIZACIÓN
 TEMA 11: ESTUDIO LOCAL Y GLOBAL DE FUNCIONES. OPTIMIZACIÓN ESTUDIO DE LA MONOTONÍA DEF.- Una función es CRECIENTE en un intervalo I del dominio de la función si: x1 < x2 I f ( x1 ) f ( x2). Si se cumple
TEMA 11: ESTUDIO LOCAL Y GLOBAL DE FUNCIONES. OPTIMIZACIÓN ESTUDIO DE LA MONOTONÍA DEF.- Una función es CRECIENTE en un intervalo I del dominio de la función si: x1 < x2 I f ( x1 ) f ( x2). Si se cumple
AYUDA MEMORIA PARA EL ESTUDIO DE MATEMÁTICAS II - SISTEMAS
 AYUDA MEMORIA PARA EL ESTUDIO DE MATEMÁTICAS II - SISTEMAS Potencias de la unidad imaginaria i 0 = 1 i 1 = i i 2 = 1 i 3 = i i 4 = 1 Los valores se repiten de cuatro en cuatro, por eso, para saber cuánto
AYUDA MEMORIA PARA EL ESTUDIO DE MATEMÁTICAS II - SISTEMAS Potencias de la unidad imaginaria i 0 = 1 i 1 = i i 2 = 1 i 3 = i i 4 = 1 Los valores se repiten de cuatro en cuatro, por eso, para saber cuánto
Cálculo diferencial de funciones reales de variable real
 Cálculo diferencial de funciones reales de variable real María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I (1 o Ingeniería Electrónica Automática e Industrial) M. Muñoz (U.P.C.T.) Cálculo diferencial
Cálculo diferencial de funciones reales de variable real María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I (1 o Ingeniería Electrónica Automática e Industrial) M. Muñoz (U.P.C.T.) Cálculo diferencial
1. Nociones básicas. Oct, 2007
 Cálculo 1. Nociones básicas Oct, 2007 Nociones básicas Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial y logarítmica Funciones
Cálculo 1. Nociones básicas Oct, 2007 Nociones básicas Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial y logarítmica Funciones
TEORÍA DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 2: Cálculo diferencial de una variable. Domingo Pestana Galván José Manuel Rodríguez García
 TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 2: Cálculo diferencial de una variable Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 TEMA
TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 2: Cálculo diferencial de una variable Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 TEMA
Criterio 1: Sea f una función derivable en (a,b). f es estrictamente creciente en el intervalo abierto (a, b) si f es positiva en dicho intervalo.
 UNIDAD. APLICACIONES DE LAS DERIVADAS.. Información etraída de la primera derivada.. Información etraída de la segunda derivada.. Derivabilidad en intervalos: Teorema de Rolle, del valor medio y Caucy..4
UNIDAD. APLICACIONES DE LAS DERIVADAS.. Información etraída de la primera derivada.. Información etraída de la segunda derivada.. Derivabilidad en intervalos: Teorema de Rolle, del valor medio y Caucy..4
Aplicaciones de las derivadas
 Aplicaciones de las derivadas. Recta tangente a una curva en un punto La pendiente de la recta tangente a la gráfica de la función f() en el punto ( 0, f( 0 )) viene dada por f ( 0 ) siempre que la función
Aplicaciones de las derivadas. Recta tangente a una curva en un punto La pendiente de la recta tangente a la gráfica de la función f() en el punto ( 0, f( 0 )) viene dada por f ( 0 ) siempre que la función
(Límites y continuidad, derivadas, estudio y representación de funciones)
 ANÁLISIS I: CÁLCULO DIFERENCIAL (Límites y continuidad, derivadas, estudio y representación de funciones) Curso 009-010 -Enunciados: pg -Soluciones: pg 3 Curso 010-011 -Enunciados: pg 5 -Soluciones: pg
ANÁLISIS I: CÁLCULO DIFERENCIAL (Límites y continuidad, derivadas, estudio y representación de funciones) Curso 009-010 -Enunciados: pg -Soluciones: pg 3 Curso 010-011 -Enunciados: pg 5 -Soluciones: pg
DERIVABILIDAD DE FUNCIONES REALES DE VARIABLE REAL
 DERIVABILIDAD DE FUNCIONES REALES DE VARIABLE REAL Definición. Sea f :]a, b[ R y x 0 ]a, b[. Sedicequef es derivable en x 0 si existe f(x lim 0 +h) f(x 0 ) h 0 h yesfinito. En ese caso denotaremos por
DERIVABILIDAD DE FUNCIONES REALES DE VARIABLE REAL Definición. Sea f :]a, b[ R y x 0 ]a, b[. Sedicequef es derivable en x 0 si existe f(x lim 0 +h) f(x 0 ) h 0 h yesfinito. En ese caso denotaremos por
TEMA 7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES 7.1 CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO
 TEMA 7 DERIVADAS Y APLICACIONES MATEMÁTICAS CCSSI º Bac TEMA 7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES 7. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Definición : Se llama
TEMA 7 DERIVADAS Y APLICACIONES MATEMÁTICAS CCSSI º Bac TEMA 7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES 7. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Definición : Se llama
DERIVADAS 1.- TASA DE VARIACIÓN MEDIA DE UNA FUNCIÓN. Antes de dar la definición veamos unos ejemplos:
 DERIVADAS 1.- TASA DE VARIACIÓN MEDIA DE UNA FUNCIÓN. Antes de dar la definición veamos unos ejemplos: Definición: 2.- TASA DE VARIACIÓN INSTANTÁNEA. DEFINICIÓN DE DERIVADA DE UNA FUNCIÓN EN UN PUNTO.
DERIVADAS 1.- TASA DE VARIACIÓN MEDIA DE UNA FUNCIÓN. Antes de dar la definición veamos unos ejemplos: Definición: 2.- TASA DE VARIACIÓN INSTANTÁNEA. DEFINICIÓN DE DERIVADA DE UNA FUNCIÓN EN UN PUNTO.
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática ( )
 Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 3 (DERIVADAS) Profesora: Yulimar Matute Febrero 2012 DERIVADAS POR DEFINICIÓN
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 3 (DERIVADAS) Profesora: Yulimar Matute Febrero 2012 DERIVADAS POR DEFINICIÓN
en un punto determinado. Esto es, qué le pasa a f (x) cuando varía x en los alrededores de un punto a. , su derivada en el punto x = 3 es
 UAH Actualización de Conocimientos de Matemáticas para Tema 08 DERIVADAS Derivada de una función en un punto Una función f () es derivable en el punto a si f ( a + ) f ( a) eiste el límite: lím Este límite
UAH Actualización de Conocimientos de Matemáticas para Tema 08 DERIVADAS Derivada de una función en un punto Una función f () es derivable en el punto a si f ( a + ) f ( a) eiste el límite: lím Este límite
Derivada y diferencial
 Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Aplicaciones de la DERIVADA
 Teorema (criterio de la segunda derivada para extremos relativos) Sea c un número crítico de una función f en el que f ( c ) = 0, suponiendo que existe f (x) para todos los valores de x en un intervalo
Teorema (criterio de la segunda derivada para extremos relativos) Sea c un número crítico de una función f en el que f ( c ) = 0, suponiendo que existe f (x) para todos los valores de x en un intervalo
Apéndice 8: La recta real y el espacio métrico R n. Funciones de una variable: límites, continuidad y cálculo diferencial
 Apéndice 8: La recta real y el espacio métrico R n. Funciones de una variable: límites, continuidad y cálculo diferencial Operaciones simbólicas En este apartado tratamos de resolver algunos problemas
Apéndice 8: La recta real y el espacio métrico R n. Funciones de una variable: límites, continuidad y cálculo diferencial Operaciones simbólicas En este apartado tratamos de resolver algunos problemas
1. Función de primer grado. La recta.
 Cálculo 1. Función de primer grado. La recta. Consideremos una función definida mediante una línea recta: Y X(x,y) y y 0 P (x 0,y 0) B(0,b) x x 0 O X Sea P (x 0, y 0 ) un punto de la recta que suponemos
Cálculo 1. Función de primer grado. La recta. Consideremos una función definida mediante una línea recta: Y X(x,y) y y 0 P (x 0,y 0) B(0,b) x x 0 O X Sea P (x 0, y 0 ) un punto de la recta que suponemos
Cálculo: Notas sobre diferenciabilidad en una variable
 Cálculo: Notas sobre diferenciabilidad en una variable Antonio Garvín Curso 04/05 1 Derivabilidad en una variable 1.1 La derivada de una función en un punto Para una función f: R R tal que todo un intervalo
Cálculo: Notas sobre diferenciabilidad en una variable Antonio Garvín Curso 04/05 1 Derivabilidad en una variable 1.1 La derivada de una función en un punto Para una función f: R R tal que todo un intervalo
Capítulo 2. Derivación de funciones.
 Capítulo 2. Derivación de funciones. Objetivos del tema Concepto matemático de derivada. Interpretaciones del concepto de derivada. Cálculo de derivadas de funciones y funciones definidas a trozos. Propiedades
Capítulo 2. Derivación de funciones. Objetivos del tema Concepto matemático de derivada. Interpretaciones del concepto de derivada. Cálculo de derivadas de funciones y funciones definidas a trozos. Propiedades
Funciones. Objetivos Definición. Repasar las funciones elementales. Recordar los conceptos de continuidad y límite.
 Capítulo 6 Funciones Objetivos Repasar las funciones elementales. Recordar los conceptos de continuidad y límite. Revisar el concepto de derivada y su aplicación. Representar funciones. 6.1. Definición
Capítulo 6 Funciones Objetivos Repasar las funciones elementales. Recordar los conceptos de continuidad y límite. Revisar el concepto de derivada y su aplicación. Representar funciones. 6.1. Definición
2 x
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08-2 Importante: Visita regularmente ttp://www.dim.ucile.cl/~calculo. Aí encontrarás las guías de ejercicios
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08-2 Importante: Visita regularmente ttp://www.dim.ucile.cl/~calculo. Aí encontrarás las guías de ejercicios
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 5 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 5 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
DERIVADA DE UNA FUNCIÓN
 DERIVADA DE UNA FUNCIÓN 3URI/XLV~xH] Se estudia aquí uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. Además de la definición y su interpretación, se allarán las
DERIVADA DE UNA FUNCIÓN 3URI/XLV~xH] Se estudia aquí uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. Además de la definición y su interpretación, se allarán las
Funciones de Una Variable Real I. Derivadas
 Contents : Derivadas Universidad de Murcia Curso 2010-2011 Contents 1 Funciones derivables Contents 1 Funciones derivables 2 Contents 1 Funciones derivables 2 3 Objetivos Funciones derivables Definir,
Contents : Derivadas Universidad de Murcia Curso 2010-2011 Contents 1 Funciones derivables Contents 1 Funciones derivables 2 Contents 1 Funciones derivables 2 3 Objetivos Funciones derivables Definir,
a) p = ½. b) p = 0. c) Ninguna de las anteriores. Solución: Para que sea continua en x = 0 debe cumplirse que lím
 Matemáticas Empresariales I PREGUNTAS DE TIPO TEST DERIVADAS Y APLICACIONES si 0. La función f ( ) sen es continua en = 0 si: p si 0 a) p = ½. b) p = 0. Para que sea continua en = 0 debe cumplirse que
Matemáticas Empresariales I PREGUNTAS DE TIPO TEST DERIVADAS Y APLICACIONES si 0. La función f ( ) sen es continua en = 0 si: p si 0 a) p = ½. b) p = 0. Para que sea continua en = 0 debe cumplirse que
FUNCIONES DE UNA VARIABLE
 FUNCIONES DE UNA VARIABLE Una función es una regla que a cada número x R le asigna un único valor f x) R El dominio de f son los puntos en los que está definida Dom f ) = {x R/ f x)} La gráfica de f es
FUNCIONES DE UNA VARIABLE Una función es una regla que a cada número x R le asigna un único valor f x) R El dominio de f son los puntos en los que está definida Dom f ) = {x R/ f x)} La gráfica de f es
BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE
 BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE El concepto de derivada. Relación entre continuidad y derivabilidad. Función derivada. Operaciones con derivadas. Derivación de las funciones
BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE El concepto de derivada. Relación entre continuidad y derivabilidad. Función derivada. Operaciones con derivadas. Derivación de las funciones
Fundamentos matemáticos. Tema 5 Derivación de funciones de una y varias variables
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 5 Derivación de funciones de una y varias variables José Barrios García Departamento de Análisis Matemático Universidad de La
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 5 Derivación de funciones de una y varias variables José Barrios García Departamento de Análisis Matemático Universidad de La
RESUMEN DE ANÁLISIS MATEMÁTICAS II
 RESUMEN DE ANÁLISIS MATEMÁTICAS II 1. DOMINIO DE DEFINICIÓN Y CONTINUIDAD 1.1. FUNCIONES ELEMENTALES (No tienen puntos angulosos) Tipo de función f (x) Dom (f) Continuidad Polinómicas P(x) R Racional P(x)/Q(x)
RESUMEN DE ANÁLISIS MATEMÁTICAS II 1. DOMINIO DE DEFINICIÓN Y CONTINUIDAD 1.1. FUNCIONES ELEMENTALES (No tienen puntos angulosos) Tipo de función f (x) Dom (f) Continuidad Polinómicas P(x) R Racional P(x)/Q(x)
2. Continuidad y derivabilidad. Aplicaciones
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Derivadas. Jesús García de Jalón de la Fuente. IES Ramiro de Maeztu Madrid
 Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta
Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta
Fundamentos de Matemáticas - Grado en Ingeniería Agrícola - Profª. Mónica Esquivel
 Fundamentos de Matemáticas - Grado en Ingeniería Agrícola - Profª. Mónica squivel Tema 1 FUNCION RAL D VARIABL RAL. CONTINUIDAD. DRIVABILIDAD 1.1. Funciones reales de variable real: generalidades I V R
Fundamentos de Matemáticas - Grado en Ingeniería Agrícola - Profª. Mónica squivel Tema 1 FUNCION RAL D VARIABL RAL. CONTINUIDAD. DRIVABILIDAD 1.1. Funciones reales de variable real: generalidades I V R
PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : (0,+ ) R la función definida por f(x) = 3x + 1 x. (a) [1 5 puntos] Determina los intervalos de crecimiento y de decrecimiento y los extremos relativos de f (puntos donde
Opción A Ejercicio 1.- Sea f : (0,+ ) R la función definida por f(x) = 3x + 1 x. (a) [1 5 puntos] Determina los intervalos de crecimiento y de decrecimiento y los extremos relativos de f (puntos donde
Derivadas 1 1. FUNCIÓN DERIVABLE EN UN PUNTO, DERIVADA DE UNA FUNCIÓN EN UN PUNTO. CONCEPTO DE FUNCIÓN DERIVADA, DERIVADA SEGUNDA DE UNA FUNCIÓN.
 Derivadas. FUNCIÓN DERIVABLE EN UN PUNTO, DERIVADA DE UNA FUNCIÓN EN UN PUNTO. CONCEPTO DE FUNCIÓN DERIVADA, DERIVADA SEGUNDA DE UNA FUNCIÓN.. Función derivable en un punto, derivada de una función en
Derivadas. FUNCIÓN DERIVABLE EN UN PUNTO, DERIVADA DE UNA FUNCIÓN EN UN PUNTO. CONCEPTO DE FUNCIÓN DERIVADA, DERIVADA SEGUNDA DE UNA FUNCIÓN.. Función derivable en un punto, derivada de una función en
Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto:
 1 LA DERIVADA EN EL TRAZADO DE CURVAS Significados de los signos de la Primera y Segunda derivada. Plantearemos a través del estudio del signo de la primera derivada, las condiciones que debe cumplir una
1 LA DERIVADA EN EL TRAZADO DE CURVAS Significados de los signos de la Primera y Segunda derivada. Plantearemos a través del estudio del signo de la primera derivada, las condiciones que debe cumplir una
Examen de Matemáticas 2 o de Bachillerato Mayo 2003
 Examen de Matemáticas o de Bachillerato Mayo 1. (a) Dibuja el recinto limitado por las curvas y = e x+, y = e x y x =. (b) Halla el área del recinto considerado en el apartado anterior. (a) El dominio
Examen de Matemáticas o de Bachillerato Mayo 1. (a) Dibuja el recinto limitado por las curvas y = e x+, y = e x y x =. (b) Halla el área del recinto considerado en el apartado anterior. (a) El dominio
M a t e m á t i c a s I I 1
 Matemáticas II Matemáticas II CASTILLA Y LEÓN CONVOCATORIA SEPTIEMBRE 9 SOLUCIÓN DE LA PRUEBA DE ACCESO AUTOR: José Luis Pérez Sanz Prueba A Problemas a) f(x) x El denominador de f(x) nunca se anula; por
Matemáticas II Matemáticas II CASTILLA Y LEÓN CONVOCATORIA SEPTIEMBRE 9 SOLUCIÓN DE LA PRUEBA DE ACCESO AUTOR: José Luis Pérez Sanz Prueba A Problemas a) f(x) x El denominador de f(x) nunca se anula; por
Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o
![Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o](/thumbs/74/71098358.jpg) DERIVADAS Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-, 3] hallar x o El teorema de Lagrange dice que: f(3) - f(-) = f
DERIVADAS Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-, 3] hallar x o El teorema de Lagrange dice que: f(3) - f(-) = f
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
Ejercicios resueltos de cálculo Febrero de 2016
 Ejercicios resueltos de cálculo Febrero de 016 Ejercicio 1. Calcula los siguientes ites: x 5x 1. x + x + 1 x 1 x. x x. x + x + 1 x x 4. x 0 x cos x sen x x Solución: 1. Indeterminación del tipo. Tenemos:
Ejercicios resueltos de cálculo Febrero de 016 Ejercicio 1. Calcula los siguientes ites: x 5x 1. x + x + 1 x 1 x. x x. x + x + 1 x x 4. x 0 x cos x sen x x Solución: 1. Indeterminación del tipo. Tenemos:
Cálculo 1 _Comisión 1 Año Extremos absolutos
 Extremos absolutos Def: f ( es un máximo absoluto de f x Df: f( f( Def: f ( es un mínimo absoluto de f x Df: f( f( Procedimiento: 1) hallar los puntos críticos de f 2) Evaluar esos puntos en la función
Extremos absolutos Def: f ( es un máximo absoluto de f x Df: f( f( Def: f ( es un mínimo absoluto de f x Df: f( f( Procedimiento: 1) hallar los puntos críticos de f 2) Evaluar esos puntos en la función
Práctica 3: Diferenciación
 Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) Primer Cuatrimestre - 03 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable. Vericar que se
Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) Primer Cuatrimestre - 03 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable. Vericar que se
Problemas de Cálculo Matemático E.U.A.T. CURSO Primer cuatrimestre
 1 Problemas de Cálculo Matemático EUAT CURSO 00-003 Primer cuatrimestre Problemas del Tema 5 Teoremas relativos a funciones derivables y aplicaciones 1 La función f(x) = 1 3 x se anula para x 1 = 1 y para
1 Problemas de Cálculo Matemático EUAT CURSO 00-003 Primer cuatrimestre Problemas del Tema 5 Teoremas relativos a funciones derivables y aplicaciones 1 La función f(x) = 1 3 x se anula para x 1 = 1 y para
Universidad Simón Bolıvar. Departamento de Matemáticas puras y aplicadas. MA1111. Tercer Parcial. Sept-Dic 2009 (30 pts).
 Universidad Simón Bolıvar. Departamento de Matemáticas puras y aplicadas. MA1111. Tercer Parcial. Sept-Dic 2009 (30 pts). Nombre: Carnét: 1. Responda con verdadero o falso, cada una de las siguientes proposiciones,
Universidad Simón Bolıvar. Departamento de Matemáticas puras y aplicadas. MA1111. Tercer Parcial. Sept-Dic 2009 (30 pts). Nombre: Carnét: 1. Responda con verdadero o falso, cada una de las siguientes proposiciones,
Tema 8: Derivación. José M. Salazar. Noviembre de 2016
 Tema 8: Derivación. José M. Salazar Noviembre de 2016 Tema 8: Derivación. Lección 9. Derivación: teoría fundamental. Lección 10. Aplicaciones de la derivación. Índice 1 Extremos de funciones y clasificación
Tema 8: Derivación. José M. Salazar Noviembre de 2016 Tema 8: Derivación. Lección 9. Derivación: teoría fundamental. Lección 10. Aplicaciones de la derivación. Índice 1 Extremos de funciones y clasificación
DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA APELLIDOS:
 DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA Análisis Matemático I EXAMEN FINAL APELLIDOS: NOMBRE: D.N.I. CUESTIONARIO DE RESPUESTA MÚLTIPLE (5%) (Cada respuesta incorrecta resta, puntos)
DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA Análisis Matemático I EXAMEN FINAL APELLIDOS: NOMBRE: D.N.I. CUESTIONARIO DE RESPUESTA MÚLTIPLE (5%) (Cada respuesta incorrecta resta, puntos)
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid Resueltos Isaac Musat Hervás 22 de mayo de 201 Capítulo 4 Año 200 4.1. Modelo 200 - Opción A Problema 4.1.1 2 puntos Determinar los valores
Problemas de Selectividad de Matemáticas II Comunidad de Madrid Resueltos Isaac Musat Hervás 22 de mayo de 201 Capítulo 4 Año 200 4.1. Modelo 200 - Opción A Problema 4.1.1 2 puntos Determinar los valores
C alculo Septiembre 2010
 Cálculo Septiembre 2010 Funciones reales de variable real Conjuntos de números Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial
Cálculo Septiembre 2010 Funciones reales de variable real Conjuntos de números Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial
el blog de mate de aida CS II: Representación de funciones y optimización.
 Pág.1 CRECIMIENTO Y DECRECIMIENTO. En la figura se observa la recta tangente a una función creciente. La recta tangente es siempre creciente también para cualquier punto, por lo que su pendiente será positiva
Pág.1 CRECIMIENTO Y DECRECIMIENTO. En la figura se observa la recta tangente a una función creciente. La recta tangente es siempre creciente también para cualquier punto, por lo que su pendiente será positiva
Funciones reales de variable real
 Tema Funciones reales de variable real Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real.. Conceptos Generales Definición.
Tema Funciones reales de variable real Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real.. Conceptos Generales Definición.
x y +az +bt = 20 (a) Realizamos transformaciones elementales sobre la matriz ampliada del sistema a b a 1 b 2 10
 UC3M Matemáticas para la Economía Examen Final, 26/6/24 RESUELTO Dados los parámetros a, b 2 R, se considera el sistema lineal 8 < x 2y +z +2t = 2x 3y +4z 2t = 2 : x y +az +bt = 2 (a) (6 puntos) Discutir
UC3M Matemáticas para la Economía Examen Final, 26/6/24 RESUELTO Dados los parámetros a, b 2 R, se considera el sistema lineal 8 < x 2y +z +2t = 2x 3y +4z 2t = 2 : x y +az +bt = 2 (a) (6 puntos) Discutir
Apuntes Matemáticas 2º de bachillerato. Tema 5. Estudio de funciones
 Apuntes Tema 5 Estudio de funciones 5.1 Dominio Hay que determinar para qué intervalos de números reales, o puntos aislados, la función existe o está definida. Para ello tenemos que prestar atención a
Apuntes Tema 5 Estudio de funciones 5.1 Dominio Hay que determinar para qué intervalos de números reales, o puntos aislados, la función existe o está definida. Para ello tenemos que prestar atención a
=lim h 0. )=lim h 0 h. (2+h 2)2 2+h 4 ( 4)
 Tema 4 Derivación Ejercicios resueltos Derivación Ejercicio Estudiar la continuidad y derivabilidad de la función: ½ f () = si ( ) en el punto =. 4 si > Estudiemos primero los límites laterales en =: f
Tema 4 Derivación Ejercicios resueltos Derivación Ejercicio Estudiar la continuidad y derivabilidad de la función: ½ f () = si ( ) en el punto =. 4 si > Estudiemos primero los límites laterales en =: f
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid Resueltos) Isaac Musat Hervás 22 de mayo de 2013 Capítulo 5 Año 2004 5.1. Modelo 2004 - Opción A Problema 5.1.1 2 puntos) a) 1 punto) Calcular
Problemas de Selectividad de Matemáticas II Comunidad de Madrid Resueltos) Isaac Musat Hervás 22 de mayo de 2013 Capítulo 5 Año 2004 5.1. Modelo 2004 - Opción A Problema 5.1.1 2 puntos) a) 1 punto) Calcular
Problemas tipo examen
 Problemas tipo examen La división en temas no es exhaustiva. Las referencias (H n- m) indican el problema m de la hoja n y las referencias (A- cd), con A en números romanos indican un examen del mes A
Problemas tipo examen La división en temas no es exhaustiva. Las referencias (H n- m) indican el problema m de la hoja n y las referencias (A- cd), con A en números romanos indican un examen del mes A
Apuntes de cálculo diferencial en una y varias variables reales. Eduardo Liz Marzán
 Apuntes de cálculo diferencial en una y varias variables reales Eduardo Liz Marzán Febrero de 2016 Índice general 1. Preliminares 1 1.1. Introducción....................................... 1 1.2. La relación
Apuntes de cálculo diferencial en una y varias variables reales Eduardo Liz Marzán Febrero de 2016 Índice general 1. Preliminares 1 1.1. Introducción....................................... 1 1.2. La relación
Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León
 Selectividad Septiembre 01 Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES: 1.- OPTATIVIDAD: El alumno deberá escoger
Selectividad Septiembre 01 Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES: 1.- OPTATIVIDAD: El alumno deberá escoger
entonces las derivadas laterales existen y son iguales. y vale lo mismo. Si existen las derivadas laterales y son iguales, entonces existe f (a)
 DERIVADAS. TEMA 2. BLOQUE 1 1.- DERIVADA DE UNA FUNCIÓN EN UN PUNTO Se llama derivada de la función y = f ( en el punto de abscisa x = a al límite f ( f ( a f ( a = lím x a x a Si existe f (a entonces
DERIVADAS. TEMA 2. BLOQUE 1 1.- DERIVADA DE UNA FUNCIÓN EN UN PUNTO Se llama derivada de la función y = f ( en el punto de abscisa x = a al límite f ( f ( a f ( a = lím x a x a Si existe f (a entonces
c) Calcular las asíntotas horizontales y verticales de f y representar de forma aproximada
 Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas Cálculo I Curso 2011/2012 2 de julio de 2012 (75 p) 1) Se considera la función f : R R definida por f(x) = ex 2 e x + 1 a) Determinar
Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas Cálculo I Curso 2011/2012 2 de julio de 2012 (75 p) 1) Se considera la función f : R R definida por f(x) = ex 2 e x + 1 a) Determinar
MATEMÁTICA - 6 A C y D - Prof. Sandra M. Corti
 TEMA: Derivada La derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente Sea f(x) una función continua
TEMA: Derivada La derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente Sea f(x) una función continua
DERIV. DE UNA FUNC. EN UN PUNTO
 DERIVADA DE UNA FUNCIÓN Se abre aquí el estudio de uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. En este tema, además de definir tal concepto, se mostrará su significado
DERIVADA DE UNA FUNCIÓN Se abre aquí el estudio de uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. En este tema, además de definir tal concepto, se mostrará su significado
CÁLCULO DIFERENCIAL E INTEGRAL I APLICACIONES DE LA DERIVADA. 1. Derivabilidad y monotonía. creciente para x en cierto intervalo f es < 0
 CÁLCULO DIFERENCIAL E INTEGRAL I APLICACIONES DE LA DERIVADA 1. Derivabilidad y monotonía Tenemos también el resultado: f (x) > 0 creciente para x en cierto intervalo f es Lo cual es claro, pues: Si la
CÁLCULO DIFERENCIAL E INTEGRAL I APLICACIONES DE LA DERIVADA 1. Derivabilidad y monotonía Tenemos también el resultado: f (x) > 0 creciente para x en cierto intervalo f es Lo cual es claro, pues: Si la
5. ANÁLISIS MATEMÁTICO // 5.2. DERIVADA DE
 5. ANÁLISIS MATEMÁTICO // 5.2. DERIVADA DE UNA FUNCIÓN EN UN PUNTO Y APLICACIONES. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2010-2011 5.2.1. El problema de la tangente. Derivada.
5. ANÁLISIS MATEMÁTICO // 5.2. DERIVADA DE UNA FUNCIÓN EN UN PUNTO Y APLICACIONES. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2010-2011 5.2.1. El problema de la tangente. Derivada.
Si la variable independiente x con un valor inicial a que le da un valor final b a la diferencia b-a se le llama incremento de la variable y se
 Si la variable independiente x con un valor inicial a que le da un valor final b a la diferencia b-a se le llama incremento de la variable y se simboliza con la letra delta. La derivada de la función con
Si la variable independiente x con un valor inicial a que le da un valor final b a la diferencia b-a se le llama incremento de la variable y se simboliza con la letra delta. La derivada de la función con
Curso Propedéutico de Cálculo Sesión 3: Derivadas
 Curso Propedéutico de Cálculo Sesión 3: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 3 4 5 6 7 Esquema 1 2 3 4 5 6 7 Introducción La derivada
Curso Propedéutico de Cálculo Sesión 3: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 3 4 5 6 7 Esquema 1 2 3 4 5 6 7 Introducción La derivada
CRECIMIENTO Y DECRECIMIENTO. MÁXIMOS Y MÍNIMOS.
 pág.1 CRECIMIENTO Y DECRECIMIENTO. MÁXIMOS Y MÍNIMOS. En la figura se observa la recta tangente a una función creciente. La recta tangente es siempre creciente también para cualquier punto, por lo que
pág.1 CRECIMIENTO Y DECRECIMIENTO. MÁXIMOS Y MÍNIMOS. En la figura se observa la recta tangente a una función creciente. La recta tangente es siempre creciente también para cualquier punto, por lo que
Tasa de variación. Tasa de variación media
 Tasa de variación Consideremos una función y = f(x) y consideremos dos puntos próximos sobre el eje de abscisas "a" y "a+h", siendo "h" un número real que corresponde al incremento de x (Δx). Se llama
Tasa de variación Consideremos una función y = f(x) y consideremos dos puntos próximos sobre el eje de abscisas "a" y "a+h", siendo "h" un número real que corresponde al incremento de x (Δx). Se llama
Lección 3: Aproximación de funciones. por polinomios. Fórmula de Taylor para
 Lección 3: Aproximación de funciones por polinomios. Fórmula de Taylor para funciones escalares 3.1 Introducción Cuando es difícil trabajar con una función complicada, tratamos a veces de hallar una función
Lección 3: Aproximación de funciones por polinomios. Fórmula de Taylor para funciones escalares 3.1 Introducción Cuando es difícil trabajar con una función complicada, tratamos a veces de hallar una función
