Capítulo 2. Derivación de funciones.
|
|
|
- Vanesa Piñeiro Cortés
- hace 5 años
- Vistas:
Transcripción
1 Capítulo 2. Derivación de funciones.
2 Objetivos del tema Concepto matemático de derivada. Interpretaciones del concepto de derivada. Cálculo de derivadas de funciones y funciones definidas a trozos. Propiedades de forma de una función y su análisis mediante derivadas sucesivas. Cálculo de límites mediante el teorema de L Hôpital. 1
3 1 Concepto de derivada Supongamos que nos desplazamos desde la ciudad A hasta la B utilizando un automóvil. Si nuestro viaje viaje dura b horas, tenemos la función e : [0, b] R. t e(t) = Kilómetros recorridos hasta la hora t Pretendemos calcular la velocidad a la que circulábamos justo en ese instante t 0. Si realizamos el calculo e(b) e(t 0 ) b t 0 obtendremos la velocidad media en el intervalo de tiempo [t 0, b]. En general, e(t) e(t 0 ) t t 0 no será más que la media de las velocidades en el intervalo (t 0, t)para estudiar la velocidad justo en t 0 calculamos e(t) e(t 0 ) lim. t t 0 t t 0 Este límite nos proporciona la velocidad instantánea justo en el instante t 0 que queríamos encontrar. Dicho límite es lo que llamaremos derivada de la función e en el punto t 0. 2
4 e 100 e(t) t 3
5 Definición 1. Dada f : D R: i) Diremos que f es derivable en x 0 Ac(D) y que su derivada en tal punto es L R si se verifica que f(x) f(x 0 ) lim = L. x x 0 x x 0 En tal caso escribiremos f (x 0 ) = L ó df dx (x 0) = L. Si el límite anterior no existe o es ±, diremos que la función f no es derivable en el punto x 0. ii) Dado un subconjunto H D, decimos que f es derivable en H si es derivable en todos los puntos de H. Si f es derivable en D (en todo su dominio) diremos que f es una función derivable. iii) Sea f : D R una función real y sea D 1 = {x D : f es derivable en x}. Si D 1, llamaremos función derivada de la función f a la función f : D 1 R x f (x). 4
6 Pudiera ser que el límite de la derivada no existiera pero que sí dispusiéramos de los límites laterales. Entonces hablaremos de derivadas laterales de la función. Definición 2. i) Decimos que la función f es derivable por la izquierda en x 0 y que el valor de la derivada por la izquierda de f en x 0 es L R, si tiene sentido y existe el límite lim x x 0 f(x) f(x 0 ) x x 0 = L. ii) Decimos que la función f es derivable por la derecha en x 0 y que el valor de la derivada por la derecha de f en x 0 es L R, si tiene sentido y existe el límite lim x x + 0 f(x) f(x 0 ) x x 0 = L. Al igual que sucede para la continuidad, una función podrá ser derivable solo en aquellos puntos en los que esté definida. 5
7 Ejemplo 3. Sabemos que, dados los números reales a y b, una función del tipo f(x) = ax + b es un polinomio de grado 1 que se representa siempre como una recta. Tomemos un punto cualquiera x 0 R. Según la definición tenemos que f (x 0 ) = lim x x0 f(x) f(x 0 ) x x 0 = lim x x0 ax + b (ax 0 + b) x x 0 a(x x 0 ) = lim = lim a = a. x x0 x x 0 x x0 Por tanto, una recta es siempre una función derivable en todos los puntos. La función derivada será f (x) = a. Por ejemplo da la recta f(x) = 10x 7 es la función constante f (x) = 10. 6
8 Dada una función f : D R, si admitimos que es derivable en x 0 D tendremos que Pero entonces, f(x) f(x 0 ) lim = L R. x x 0 x x 0 lim x x 0 f(x) f(x 0 ) = lim x x0 (x x 0 ) f(x) f(x 0) x x 0 f(x) f(x 0 ) = lim (x x 0 ) lim = 0 L = 0 x x0 x x }{{} 0 x x 0 =0 De donde lim f(x) = f(x 0 ). x x 0 En otras palabras, tenemos la siguiente: Propiedad 4. Toda función derivable en un punto es también continua en ese punto. 7
9 1.1 Interpretaciones de la derivada La derivada como velocidad de variación: Ejemplos 5. 1) La cantidad de empleados de cierta empresa viene dada, en función del número de días pasados desde el comienzo del año, por la función: f : [0, 365] R f(x) = cos ( ) 2πx. 365 La gráfica correspondiente es, Sabemos que la derivada de la función f es la velocidad de variación de f(x) con respecto a x. Tenemos: } f(x) = número de empleados f (x) = empleados. x = días día 8
10 Por tanto, f (x) es la variación de empleados (contratos o despidos) por día en el día x. La función derivada de f es Entonces, por ejemplo: f (x) = πsen ( ) 2πx. 365 f (50) = En el día x = 50, la velocidad de contratación fue de empleados/día. Por tanto en el día 50 se contrataron aproximadamente empleados. f (182) = En el día x = 182, la velocidad de contratación fue de empleados/día. Por tanto el día 182 se contrataron aproximadamente empleados. f (260) = En el día x = 260, la velocidad de contratación fue de empleados/día. Por tanto el día 260 se produjeron aproximadamente despidos
11
12 2) Al realizar el estudio de la actividad de un negocio es habitual estudiar lo que se denomina función de costos que mide el coste necesario para producir una cierta cantidad de unidades. Supongamos que en una empresa que produce componentes electrónicos se tiene la siguiente función de costos (medida en euros): ( ) x + 10 C(x) = x + 10 log. 10 En tal caso: Para producir x = 10 unidades el costo será de C(10) = euros. Para producir x = 20 unidades el costo será de C(20) = euros. La gráfica de la función de costos es
13 Si calculamos la derivada de la función C(x) obtendremos la velocidad de variación del coste con respecto a la cantidad de unidades producidas: C(x) = coste de producción en euros x = unidades C coste en euros (x) = = euros unidad unidad. Es decir, C (x) es el coste por unidad (lo que cuesta fabricar una unidad) cuando llevamos producidas x unidades. así que: C (x) = x + 20 x + 10, El coste por unidad cuando hemos producido 10 unidades es C (10) = 1.5 euros/unidad. El coste por unidad cuando hemos producido 20 unidades es C (20) = 1.33 euros/unidad. } 12
14 La derivada C (x) se denomina coste marginal. En nuestro caso la gráfica de costes marginales es: Se observa que el precio por unidad cuando la producción es muy baja se aproxima a 2 euros y a medida que aumenta la producción se reduce hasta 1 euro. 13
15 Interpretación geométrica de la derivada: Habitualmente un ángulo se mide en grados sexagesimales o en radianes. Así por ejemplo, α = 45 o grados = π 4 radianes Sin embargo en diferentes ocasiones se emplea el concepto de pendiente para indicar o medir el valor de una ángulo. Definición 6. Dado el ángulo α, llamamos pendiente de α al número m = tan(α). De este modo, la pendiente del ángulo de la gráfica será m = tan(45 o ) = tan( π 4 ) = 1. 14
16 De forma más intuitiva, la pendiente de un ángulo nos indica las unidades que ascendemos por cada unidad que avanzamos si seguimos la dirección de ese ángulo. m = 1 m = 2 m =
17 Si consideramos una recta, por ejemplo la función r(x) = x+1, podemos también calcular el ángulo que forma esa recta con la horizontal y su pendiente. Además es evidente que ese ángulo será el mismo en cualquier punto de la recta: r(x) α = π 4 m = tan(π 4 ) 0.6 α = π 4 m = tan(π 4 ) = α = π 4 m = tan(π 4 ) =
18 Si en lugar de una recta consideramos una función cualquiera, por ejemplo f(x) = x , tendremos: m = 8 5 = f(x) m = 1 m = 2 5 = Un razonamiento similar al que hemos realizado al inicio del tema permite demostrar que si f es derivable en x 0 tendremos, 17
19 Si en lugar de una recta consideramos una función cualquiera, por ejemplo f(x) = x , tendremos: m = 8 5 = f(x) m = 1 m = 2 5 = pendiente de f en x 0 = f (x 0 ). 18
20 Si en lugar de una recta consideramos una función cualquiera, por ejemplo f(x) = x , tendremos: m = 8 5 = f(x) m = 1 m = 2 5 = f (x) = 2x 19
21 Si en lugar de una recta consideramos una función cualquiera, por ejemplo f(x) = x , tendremos: m = 8 5 = f(x) m = 1 m = 2 5 = f (x) = 2x x 0 = 0.2 f (0.2) = =
22 Si en lugar de una recta consideramos una función cualquiera, por ejemplo f(x) = x , tendremos: m = 8 5 = f(x) m = 1 m = 2 5 = 0.4 = f (0.2) f (x) = 2x x 0 = 0.2 f (0.2) = =
23 Si en lugar de una recta consideramos una función cualquiera, por ejemplo f(x) = x , tendremos: m = 8 5 = f(x) m = 1 m = 2 5 = 0.4 = f (0.2) f (x) = 2x x 0 = 0.5 f (0.5) = = 1 22
24 Si en lugar de una recta consideramos una función cualquiera, por ejemplo f(x) = x , tendremos: m = 8 5 = f(x) m = 1 = f (1) m = 2 5 = 0.4 = f (0.2) f (x) = 2x x 0 = 0.5 f (0.5) = = 1 23
25 Si en lugar de una recta consideramos una función cualquiera, por ejemplo f(x) = x , tendremos: m = 8 5 = f(x) m = 1 = f (1) m = 2 5 = 0.4 = f (0.2) f (x) = 2x x 0 = 0.8 f (0.5) = =
26 Si en lugar de una recta consideramos una función cualquiera, por ejemplo f(x) = x , tendremos: m = 8 5 = 1.6 = f (0.8) f(x) m = 1 = f (1) m = 2 5 = 0.4 = f (0.2) f (x) = 2x x 0 = 0.8 f (0.8) = =
27 Si consideramos una recta cualquiera, f(x) = ax + b, sabemos que tiene la misma pendiente en todos los puntos y de hecho, si calculamos su derivada, observamos que tiene siempre el mismo valor, f (x) = a que es la pendiente de la recta. De este modo, observamos directamente que la pendiente de cualquier recta es el coeficiente, a que acompaña a la variable x en la fórmula de la recta. Ejemplo 7. La pendiente de la recta f(x) = 3x 10 es m = 3 ya que el coeficiente que acompaña a la variable, x, es precisamente 3. De otro modo tenemos también que f (x) = 3. 26
28 Se llama recta tangente a una función f en el punto x 0 a la recta que en el punto x 0 toma el mismo valor y tiene la misma pendiente que f. Es decir, pasa por (x 0, f(x 0 )) con la misma pendiente que f en x 0. Es fácil comprobar que: r(x) = f(x 0 ) + f (x 0 )(x x 0 ). Por ejemplo, la recta tangente a la función f(x) = x en x 0 = 0.5 será r(x) = f(0.5) + f (0.5)(x 0.5) r(x) = (x 0.5) r(x) = x f(x) r(x)
29
30
31 2 Calculo de derivadas De la misma manera que hicimos en el caso de los límites, utilizaremos las propiedades de la derivada respecto de las operaciones algebraicas para poder realizar cálculos sin tener que acudir a la evaluación del límite de la definición de derivada. Propiedades 8. Sean f y g funciones reales de variable real. Entonces Si f y g son derivables en x R se verifica que 1. f + g es derivable en x y (f + g) (x) = f (x) + g (x). 2. k f es derivable en x para cualquier k R y 3. f g es derivable en x y (k f) (x) = k f (x). (f g) (x) = f (x) g(x) + f(x) g (x). 4. Si g(x) 0 entonces f g es derivable en x y ( ) f (x) = f (x) g(x) f(x) g (x). g (g(x)) 2 30
32 (Regla de la cadena) Si f es derivable en x y g es derivable en f(x) entonces g f es derivable en x y se verifica que: (g f) (x) = g (f(x)) f (x). A la fórmula anterior se la conoce como regla de la cadena. (Teorema de la función inversa) Si f es derivable en x, biyectiva sobre su imagen y verifica que f (x) 0 entonces la función inversa de f, f 1, es derivable en y = f(x) y se verifica que ( f 1 ) (y) = 1 f (x). Toda función que se obtenga por composición u operación de funciones derivables será una función derivable. 31
33 La siguiente lista nos proporciona un repertorio inicial de funciones derivables: 1. Dado k R y f(x) = k (función constante), f (x) = 0, x R. 2. Dado α R, f(x) = x α es derivable en todos los puntos en los que está definida su función derivada, 3. (e x ) (x) = e x, x R. f (x) = αx α Para a > 0, (a x ) (x) = log(a) a x, x R. 5. (log) (x) = 1 x, x R+. 6. Para a 1, (log a ) (x) = 1 log(a) 1 x, x R+. 7. (cos) (x) = sen(x), x R. 8. (sen) (x) = cos(x), x R. 9. (tan) (x) = 1 cos 2 (x), x R {π (arccos) (x) = 1, x ( 1, 1). 1 x 2 + k π/k Z}. 32
34 11. (arcsen) (x) = 1, x ( 1, 1). 1 x (arctg) (x) = x2, x R. 33
35 2.1 Derivación de funciones definidas a trozos Dada f(x) = f 1 (x) si a 1 < x < a 2, < f 2 (x) si a 2 x < a 3,.. f k 1 (x) si a k 1 < x < a k, 34
36 1) En el interior de los intervalos de definición: Si las funciones f 1 (x), f 2 (x),..., f k 1 (x) son respectivamente derivables en los intervalos (a 1, a 2 ), (a 2, a 3 ),..., (a k 1, a k ), entonces f(x) será derivable en esos intervalos y su derivada será f (x) = f 1(x) si a 1 < x < a 2, f 2(x). si a 2 < x < a 3,. f k 1 (x) si a k 1 < x < a k. 35
37 2) En los puntos de cambio de definición: Derivable en a i si: a) f(x) es continua en a i, b) existe el límite lim x ai f (x) y es un número real. Si se cumplen ambas condiciones entonces, además, f (a i ) = lim x ai f (x). Si tal límite no existe o toma valor ±, o si f(x) no es continua en a i, entonces f(x) no es derivable en a i. 36
38 3 Derivación y propiedades de forma de una función Definición 9. Sea f : D R una función real de variable real y sea H D. Entonces: Decimos que f es creciente (respec. estrictamente creciente, decreciente, estrictamente decreciente, constante) en H si f H es creciente (respec. estrictamente creciente, decreciente, estrictamente decreciente, constante). Decimos que f tiene un máximo absoluto en el punto x 0 D si f(x 0 ) f(x), x D. Decimos que f tiene un mínimo absoluto en el punto x 0 D si f(x 0 ) f(x), x D. 37
39 Decimos que f tiene un máximo local en el punto x 0 D si a, b R, a < x 0 < b, tales que f(x 0 ) f(x), x D (a, b). Si la desigualdad de la definición tiene lugar de forma estricta salvo en el punto x 0 (la desigualdad se verifica no sólo para sino también para >), diremos que f tiene un máximo local estricto en x 0. Decimos que f tiene un mínimo local en el punto x 0 D si a, b R, a < x 0 < b, tales que f(x 0 ) f(x), x D (a, b). Si la desigualdad de la definición tiene lugar de forma estricta salvo en el punto x 0 (la desigualdad se verifica no sólo para sino también para <), diremos que f tiene un mínimo local estricto en x 0. 38
40
41
42 Decimos que f es convexa en H si a, b H, tales que a < b, se verifica que f(x) f(a) + x a (f(b) f(a)), x H (a, b), b a es decir, si se tiene que dentro del conjunto H, f está por debajo del segmento que une los puntos (a, f(a)) y (b, f(b)). Si la desigualdad de la definición se verifica de forma estricta (la desigualdad se verifica no sólo con sino además con <) entonces diremos que f es estrictamente convexa en H. 41
43 f r 1 2 a 3 4 b 42
44 f r 1 2 a 3 4b 43
45 r f 1 2 a 3 4 b 44
46 Decimos que f es cóncava en H si a, b H, tales que a < b, se verifica que f(x) f(a) + x a (f(b) f(a)), x H (a, b), b a es decir, si se tiene que dentro del conjunto H, f está por encima del segmento que une los puntos (a, f(a)) y (b, f(b)). Si la desigualdad de la definición se verifica de forma estricta (la desigualdad se verifica no sólo con sino además con >) entonces diremos que f es estrictamente cóncava en H. 45
47 a r b f 46
48 1 2 a 3 b 4 r f 47
49 1 2 a 3 4 r b f 48
50 Decimos que f tiene un punto de inflexión en x 0 D si a, b R, a < x 0 < b tales que se cumple alguna de las siguientes condiciones: a) f es estrictamente cóncava en (a, x 0 ] D y es estrictamente convexa en [x 0, b) D. b) f es estrictamente convexa en (a, x 0 ] D y es estrictamente cóncava en [x 0, b) D. 49
51 Ejemplo
52 Ejemplo
53 Ejemplo Los máximos y mínimos separan los intervalos de crecimiento y decrecimiento Los puntos de inflexión separan los intervalos de concavidad y convexidad. 52
54 La propiedades de forma que verifica una función en cada intervalo dependerán de los signos de sus derivadas sucesivas. Definición 11. Sea una función real, f : D R. Entonces: a) Definimos la función derivada primera de f como la función derivada de f. b) Dado n N, si la función derivada n-ésima de f está definida y es derivable en algún punto, definimos la función derivada (n + 1)-ésima de f como su derivada. Notaremos a la función derivada n-ésima de f como f n) ó d n f dx n. Si, para n N, la función f n) está definida en el punto x 0 D, diremos que la función f es n veces derivable en x 0 y notamos al valor de la derivada n-ésima en tal punto como f n) (x 0 ), d n f dx n(x 0) ó d n f dx n x 0. Las funciones derivada primera, segunda y tercera se suelen designar mediante f, f y f, en lugar de f 1), f 2) y f 3). 53
55 Definición 12. Dado un conjunto D R y f : D R, diremos que f es de clase C n en D si se cumple las dos condiciones siguientes: 1. La función f n) está definida en todo D. 2. La función f n) es continua en D. El conjunto de todas las funciones de clase C n en D se denota mediante C n (D). Así mismo, una función que es de clase C n en D para cualquier n N, se dice que es una función de clase C en D. El conjunto de todas las funciones de clase C en D se denota mediante C (D). 54
56 Propiedades 13. Sea f : D R una función real, sea un intervalo I = (a, b) D y x 0 (a, b). Se verifica que: i) Si f es derivable en I se tiene que: 1. Si f (x) > 0, x I, entonces f es estrictamente creciente en I. 2. Si f (x) < 0, x I, entonces f es estrictamente decreciente en I. 3. Si f (x) = 0, x I, entonces f es una función constante en I. 55
57 ii) Si f es derivable en x 0 y f tiene un máximo o un mínimo local en x 0 entonces f (x 0 ) = 0. iii) Si f es de clase C 2 en I y f (x 0 ) = 0 entonces: 1. Si f (x 0 ) > 0 entonces f tiene un mínimo local estricto en x Si f (x 0 ) < 0 entonces f tiene un máximo local estricto en x 0. iv) Si dado n N, f es de clase C n y se cumple que y que f (x 0 ) = f (x 0 ) = = f n 2) (x 0 ) = f n 1) (x 0 ) = 0 entonces: f n) (x 0 ) 0, 1. Si f n) (x 0 ) > 0 y n es par entonces x 0 es un mínimo local estricto de f. 2. Si f n) (x 0 ) < 0 y n es par entonces x 0 es un máximo local estricto de f. 3. Si n es impar entonces f no tiene máximo ni mínimo local en x 0. 56
58 v) Si f es de clase C 2 en I entonces: 1. Si f (x) 0, x I entonces f es convexa en I. 2. Si f (x) > 0, x I entonces f es estrictamente convexa en I. 3. Si f (x) 0, x I entonces f es cóncava en I. 4. Si f (x) < 0, x I entonces f es estrictamente cóncava en I. vi) Si f es de clase C 2 en I y x 0 es un punto de inflexión de f entonces f (x 0 ) = 0. vii) Si f es de clase C 3 en I y se verifica que f (x 0 ) = 0 y f (x 0 ) 0 entonces x 0 es un punto de inflexión de f. 57
59 Ejemplo
60 Ejemplo
61 Ejemplo
62 Ejemplo
63 Ejemplo
64 Ejemplo
65 Ejemplo
66 Ejemplo
67 Ejemplo
68 Ejemplo
69 Ejemplo
70 Durante los primeros seis meses del año, se prevé que las cotizaciones en bolsa de una empresa varíen según la función C : [0, 6] R C(t) = t 3 6t 2 + 3t + 25, donde t indica el mes y C(t) el valor en euros de una acción en ese mes. Determinar entre qué valores oscilarán las cotizaciones de las acciones durante los seis primeros meses. Realizar el mismo estudio para los cinco primeros meses y para los dos primeros meses. 69
71 Durante los primeros seis meses del año, se prevé que las cotizaciones en bolsa de una empresa varíen según la función C : [0, 6] R C(t) = t 3 6t 2 + 3t + 25, donde t indica el mes y C(t) el valor en euros de una acción en ese mes. Determinar entre qué valores oscilarán las cotizaciones de las acciones durante los seis primeros meses. Realizar el mismo estudio para los cinco primeros meses y para los dos primeros meses
72 4 La regla de l Hôpital Dadas dos funciones, f, g : D R, si f(x 0 ) = g(x 0 ) = 0 ó f(x 0 ) = g(x 0 ) =, el límite f(x) lim x x 0 g(x) conduce a una indeterminación del tipo 0 0 o del tipo. Si f(x 0 ) = g(x 0 ) = 0, f(x) lim x x 0 g(x) = lim x x 0 f(x) f(x 0 ) x x 0 g(x) g(x 0 ) x x 0 = f(x) f(x 0 ) lim x x0 x x 0 g(x) g(x 0 ) lim x x 0 x x 0 = f (x 0 ) g (x 0 ). 71
73 Teorema 15 (Reglas de l Hôpital). Sean dos funciones reales f y g, sea x 0 R y un intervalo I = (a, b) R tal que x 0 I de manera que se verifican las siguientes condiciones 1. f y g son derivables en I {x 0 }. 2. g (x) 0, x I {x 0 }. 3. Se cumple alguna de las dos siguientes condiciones: a) lim f(x) = lim g(x) = 0. x x0 x x0 b) lim g(x) = +. x x0 Entonces se verifica que: f (x) lim x x 0 g (x) = L lim f(x) x x 0 g(x) = L, donde L puede ser un número real, + ó. La propiedad también es correcta para el límite por la izquierda o por la derecha. 72
74 Ejemplos 16. 1) Si calculamos el límite lim x 0 sen(x) x de forma directa, sen(x) lim x 0 x pero aplicando L Hôpital tenemos, lim x 0 sen(x) x = lim x 0 sen (x) (x) = 0 0, = lim x 0 cos(x) 1 = 1. 73
75 2) Calculemos el límite lim x 0 x x. De entrada tenemos que lim x 0 xx = 0 0. Utilizando las propiedades del logaritmo sabemos que en cuyo caso, x x = e x log(x), lim x 0 xx = lim e x log(x) = e lim x 0 x log(x). x 0 Ahora, en lugar del límite inicial, debemos calcular lim x 0 x log(x). Pero escribiendo ese producto en forma de cociente y aplicando la regla de l Hôpital, lim x log(x) = lim x 0 x 0 Finalmente, log(x) x 1 = lim x 0 log (x) (x 1 ) = lim x 0 lim x 0 xx = e lim x 0 x log(x) = e 0 = 1. 1 x = lim x 2 x 0 x = 0. 74
76 5 Material Adicional 5.1 Teoremas clásicos de derivación Dada una función f : [a, b] R, si f(a) = f(b), su gráfica será algo del tipo f a c b La intuición nos indica que, forzosamente, en algún punto intermedio entre a y b la tangente a la función debe ser horizontal. El Teorema de Rolle afirma que esto efectivamente es así. Teorema 17 (Teorema de Rolle). Sea f una función continua en un intervalo [a, b] y derivable en (a, b) entonces si f(a) = f(b) se verifica que existe c (a, b) tal que f (c) = 0. 75
77 Cuando f(a) f(b) el razonamiento anterior no es válido pero es fácil formular una versión del Teorema de Rolle para esta situación. Teorema 18 (Teorema del valor medio). Sea f una función continua en un intervalo [a, b] y derivable en (a, b) entonces existe c (a, b) tal que f(b) f(a) = f (c)(b a). f a c b 76
78 5.2 Desarrollo de Taylor y McLaurin Supongamos que queremos encontrar una función de forma que en cierto punto x 0 sus derivadas tomen sucesivamente los valores f 0, f 1,..., f k, es decir, f(x 0 ) = f 0, f (x 0 ) = f 1, f (x 0 ) = f 2,..., f n) (x 0 ) = f n. Hay muchas maneras de resolver este problema pero la forma más sencilla consiste en considerar el siguiente polinomio: p n (x) = f 0 + f 1 1! (x x 0) + f 2 2! (x x 0) f n n! (x x 0) n (1) es una solución a este problema, donde n! = (n 1) n es lo que se denomina número factorial. Es fácil comprobar que p(x 0 ) = f 0, p (x 0 ) = f 1, p (x 0 ) = f 2,..., p n) (x 0 ) = f n. 77
79 Tomemos ahora una función f : D R, n veces derivable en cierto punto x 0. Supongamos que únicamente tenemos información de la función en el punto x 0 f(x 0 ), f (x 0 ), f (x 0 ),..., f n) (x 0 ). Será posible reconstruir la función f a partir de esta información? Definición 19. Sea f : D R una función de clase C n en D y sea x 0 D. Llamamos polinomio de Taylor de grado n de f en x 0 al polinomio p n (x) = f(x 0 )+ f (x 0 ) (x x 0 )+ f (x 0 ) (x x 0 ) f n) (x 0 ) (x x 0 ) n. 1! 2! n! El polinomio de Taylor de grado n en x 0 = 0 se denomina también polinomio de McLaurin de grado n. El polinomio de Taylor de una función constituye una aproximación de dicha función que presenta la ventaja de un más fácil manejo. 78
80
81
82
83
84
85 Propiedad 20. Sea un intervalo I = (a, b), sea f : I R una función de clase C n+1 en I y sea x 0 I. Entonces para cualquier x I existe un punto real ξ situado entre x 0 y x tal que f(x) = f(x 0 ) + f (x 0 ) 1! (x x 0 ) + + f n) (x 0 ) (x x 0 ) n n! + f n+1) (ξ) (n + 1)! (x x 0) n+1. A la fórmula anterior se la conoce como fórmula de Taylor de grado n de la función f en el punto x 0. 84
86 La formula de Taylor nos proporciona el error cometido al tomar el polinomio de Taylor en lugar de la función. f(x) = f(x 0 ) + f (x 0 ) (x x 0 ) + + f n) (x 0 ) (x x 0 ) n } 1! {{ n! } p n (x) + f n+1) (ξ) (n + 1)! (x x 0) n+1. f(x) p n (x) = f n+1) (ξ) (n + 1)! (x x 0) n+1 y por lo tanto el error cometido será E n (x) = f n+1) (ξ) (n + 1)! (x x 0) n+1. 85
Derivación de Funciones
 Capítulo 2 Derivación de Funciones La derivada es la formalización matemática del concepto de velocidad Puesto que utilizamos funciones para representar fenómenos que evolucionan con respecto al tiempo,
Capítulo 2 Derivación de Funciones La derivada es la formalización matemática del concepto de velocidad Puesto que utilizamos funciones para representar fenómenos que evolucionan con respecto al tiempo,
Derivación de Funciones
 Capítulo 8 Derivación de Funciones La derivada es la formalización matemática del concepto de velocidad. Puesto que utilizamos funciones para representar fenómenos que evolucionan con respecto al tiempo,
Capítulo 8 Derivación de Funciones La derivada es la formalización matemática del concepto de velocidad. Puesto que utilizamos funciones para representar fenómenos que evolucionan con respecto al tiempo,
= f (a) R. f(x) f(a) x a. recta por (a, f(a)) de pendiente f(a+h2) f(a) recta tangente por (a, f(a)) de pendiente f (a)
 1 1. DERIVACIÓN 1.1. DEFINICIONES Y RESULTADOS PRINCIPALES Definición 1.1. Derivada. Sea f una función definida en un intervalo abierto I con a I. Decimos que f es derivable en a si existe y es real el
1 1. DERIVACIÓN 1.1. DEFINICIONES Y RESULTADOS PRINCIPALES Definición 1.1. Derivada. Sea f una función definida en un intervalo abierto I con a I. Decimos que f es derivable en a si existe y es real el
Derivación. Aproximaciones por polinomios.
 Derivación... 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Matemáticas (Grado en Químicas) Contenidos Derivada 1 Derivada 2 3 4 5 6 Outline Derivada 1 Derivada 2 3 4 5 6 Definición
Derivación... 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Matemáticas (Grado en Químicas) Contenidos Derivada 1 Derivada 2 3 4 5 6 Outline Derivada 1 Derivada 2 3 4 5 6 Definición
Cálculo Diferencial en una variable
 Tema 2 Cálculo Diferencial en una variable 2.1. Derivadas La derivada nos proporciona una manera de calcular la tasa de cambio de una función Calculamos la velocidad media como la razón entre la distancia
Tema 2 Cálculo Diferencial en una variable 2.1. Derivadas La derivada nos proporciona una manera de calcular la tasa de cambio de una función Calculamos la velocidad media como la razón entre la distancia
Nociones básicas. Febrero, 2005
 Febrero, 2005 Índice general Funciones es de variable Derivación de funciones es de variable Funciones es de variable Derivación de funciones es de variable Conjuntos de números IN Z Q IR C Densidad de
Febrero, 2005 Índice general Funciones es de variable Derivación de funciones es de variable Funciones es de variable Derivación de funciones es de variable Conjuntos de números IN Z Q IR C Densidad de
Cálculo Diferencial de una Variable
 Departamento de Matemática Aplicada Universitat Politècnica de València, España Fundamentos Matemáticos para la Ingenieria Civil Esquema Esquema de la exposición Definición. Interpretación geométrica de
Departamento de Matemática Aplicada Universitat Politècnica de València, España Fundamentos Matemáticos para la Ingenieria Civil Esquema Esquema de la exposición Definición. Interpretación geométrica de
Derivación de funciones reales de una variable
 Derivación de funciones reales de una variable Derivada de una función en un punto. Interpretación física y geométrica Aproximación de raíces: Método de Newton Raphson Derivabilidad Cálculo de derivadas
Derivación de funciones reales de una variable Derivada de una función en un punto. Interpretación física y geométrica Aproximación de raíces: Método de Newton Raphson Derivabilidad Cálculo de derivadas
Derivada y diferencial
 Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Funciones de Una Variable Real I. Derivadas
 Contents : Derivadas Universidad de Murcia Curso 2010-2011 Contents 1 Funciones derivables Contents 1 Funciones derivables 2 Contents 1 Funciones derivables 2 3 Objetivos Funciones derivables Definir,
Contents : Derivadas Universidad de Murcia Curso 2010-2011 Contents 1 Funciones derivables Contents 1 Funciones derivables 2 Contents 1 Funciones derivables 2 3 Objetivos Funciones derivables Definir,
Capítulo 2: Cálculo diferencial de una y varias variables
 Capítulo 2: Cálculo diferencial de una y varias variables (Fundamentos Matemáticos de la Biotecnología) Departamento de Matemáticas Universidad de Murcia Contenidos Límites y continuidad Límites laterales
Capítulo 2: Cálculo diferencial de una y varias variables (Fundamentos Matemáticos de la Biotecnología) Departamento de Matemáticas Universidad de Murcia Contenidos Límites y continuidad Límites laterales
TEORÍA DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 2: Cálculo diferencial de una variable. Domingo Pestana Galván José Manuel Rodríguez García
 TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 2: Cálculo diferencial de una variable Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 TEMA
TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 2: Cálculo diferencial de una variable Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 TEMA
Cálculo diferencial de funciones reales de variable real
 Cálculo diferencial de funciones reales de variable real María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I (1 o Ingeniería Electrónica Automática e Industrial) M. Muñoz (U.P.C.T.) Cálculo diferencial
Cálculo diferencial de funciones reales de variable real María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I (1 o Ingeniería Electrónica Automática e Industrial) M. Muñoz (U.P.C.T.) Cálculo diferencial
C alculo Octubre 2010
 Cálculo Octubre 2010 Derivada. Introducción Recordemos la definición de pendiente de una recta: α y 1 y0 x 0 x 1 Pendiente= m = tanα = y 1 y 0 x 1 x 0 Y ahora consideremos las pendientes de las rectas
Cálculo Octubre 2010 Derivada. Introducción Recordemos la definición de pendiente de una recta: α y 1 y0 x 0 x 1 Pendiente= m = tanα = y 1 y 0 x 1 x 0 Y ahora consideremos las pendientes de las rectas
Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García. UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior
 INGENIERÍAS TÉCNICAS INDUSTRIALES TEORIA DE CÁLCULO I Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento
INGENIERÍAS TÉCNICAS INDUSTRIALES TEORIA DE CÁLCULO I Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
CÁLCULO DIFERENCIAL. b) Al darle a x valores suficientemente grandes, los valores de f(x) crecen cada vez más
 1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO: CÁLCULO DIFERENCIAL Una función f(x) tiene por límite L en el número real x = c, si para toda sucesión de valores x n c del dominio que tenga por límite c, la sucesión
1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO: CÁLCULO DIFERENCIAL Una función f(x) tiene por límite L en el número real x = c, si para toda sucesión de valores x n c del dominio que tenga por límite c, la sucesión
Función Real de variable Real. Definiciones
 Función Real de variable Real Definiciones Función Sean A y B dos conjuntos cualesquiera. Una aplicación de A en B es una relación que asocia a cada elemento (x=variable independiente) de A un único valor
Función Real de variable Real Definiciones Función Sean A y B dos conjuntos cualesquiera. Una aplicación de A en B es una relación que asocia a cada elemento (x=variable independiente) de A un único valor
DERIVABILIDAD DE FUNCIONES REALES DE VARIABLE REAL
 DERIVABILIDAD DE FUNCIONES REALES DE VARIABLE REAL Definición. Sea f :]a, b[ R y x 0 ]a, b[. Sedicequef es derivable en x 0 si existe f(x lim 0 +h) f(x 0 ) h 0 h yesfinito. En ese caso denotaremos por
DERIVABILIDAD DE FUNCIONES REALES DE VARIABLE REAL Definición. Sea f :]a, b[ R y x 0 ]a, b[. Sedicequef es derivable en x 0 si existe f(x lim 0 +h) f(x 0 ) h 0 h yesfinito. En ese caso denotaremos por
Derivadas. 1. Tasa de variación media La tasa de variación media de una función f(t) en un intervalo [a, b] se define como:
![Derivadas. 1. Tasa de variación media La tasa de variación media de una función f(t) en un intervalo [a, b] se define como: Derivadas. 1. Tasa de variación media La tasa de variación media de una función f(t) en un intervalo [a, b] se define como:](/thumbs/71/66199093.jpg) Derivadas Antes de dar la definición de derivada de una función en un punto, vamos a introducir el concepto de tasa de variación media y dos ejemplos o motivaciones iniciales que nos van a dar la medida
Derivadas Antes de dar la definición de derivada de una función en un punto, vamos a introducir el concepto de tasa de variación media y dos ejemplos o motivaciones iniciales que nos van a dar la medida
TEMA 5. FUNCIONES DERIVABLES. TEOREMA DE TAYLOR
 TEMA 5. FUNCIONES DERIVABLES. TEOREMA DE TAYLOR 5.1 DERIVADA DE UNA FUNCIÓN 5.1.1 Definición de derivada Definición: Sea I in intervalo abierto, f : I y a I. Diremos que f es derivable en a si existe y
TEMA 5. FUNCIONES DERIVABLES. TEOREMA DE TAYLOR 5.1 DERIVADA DE UNA FUNCIÓN 5.1.1 Definición de derivada Definición: Sea I in intervalo abierto, f : I y a I. Diremos que f es derivable en a si existe y
Nombre y Apellidos: x e 1 x 1 x f(x) = ln(x) x
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Nombre y Apellidos: Cálculo I Convocatoria de Diciembre de Diciembre de 008 DNI: (6.5 p.) ) Se considera la función f : R R definida
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Nombre y Apellidos: Cálculo I Convocatoria de Diciembre de Diciembre de 008 DNI: (6.5 p.) ) Se considera la función f : R R definida
Derivadas. Jesús García de Jalón de la Fuente. IES Ramiro de Maeztu Madrid
 Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta
Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta
Examen de Cálculo infinitesimal PROBLEMAS. 1 + a + a a n a n+1
 Examen de Cálculo infinitesimal. 4-2-203. PROBLEMAS. Calcular el límite de la sucesión definida por donde a >. + a + a 2 + + a n a n+ Solución. Sea x n = + a + a 2 + + a n, y n = a n+. Es claro que y n
Examen de Cálculo infinitesimal. 4-2-203. PROBLEMAS. Calcular el límite de la sucesión definida por donde a >. + a + a 2 + + a n a n+ Solución. Sea x n = + a + a 2 + + a n, y n = a n+. Es claro que y n
Derivabilidad de funciones de una
 Tema 3 Derivabilidad de funciones de una variable El objetivo del presente tema es la derivación de funciones reales de variable real, así como sus diversas aplicaciones entre las que destacamos la representación
Tema 3 Derivabilidad de funciones de una variable El objetivo del presente tema es la derivación de funciones reales de variable real, así como sus diversas aplicaciones entre las que destacamos la representación
2. Continuidad y derivabilidad. Aplicaciones
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Tema 7: Aplicaciones de la derivada
 Tema 7: Aplicaciones de la derivada 1. Introducción En la unidad anterior hemos establecido el concepto de derivada de una función f(x) en un punto x 0 de su dominio y la hemos interpretado geométricamente
Tema 7: Aplicaciones de la derivada 1. Introducción En la unidad anterior hemos establecido el concepto de derivada de una función f(x) en un punto x 0 de su dominio y la hemos interpretado geométricamente
CONCEPTOS QUE DEBES DOMINAR
 INTERVALOS CONCEPTOS QUE DEBES DOMINAR Un intervalo es un conjunto infinito de números reales comprendidos entre dos extremos, que pueden estar incluidos en él o no. 1. Intervalo abierto (a, b): Comprende
INTERVALOS CONCEPTOS QUE DEBES DOMINAR Un intervalo es un conjunto infinito de números reales comprendidos entre dos extremos, que pueden estar incluidos en él o no. 1. Intervalo abierto (a, b): Comprende
1. Nociones básicas. Oct, 2008
 Cálculo 1. Nociones básicas Oct, 2008 Nociones básicas Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial y logarítmica Funciones
Cálculo 1. Nociones básicas Oct, 2008 Nociones básicas Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial y logarítmica Funciones
Apuntes de Funciones
 Apuntes de Funciones El concepto de función es un elemento fundamental dentro del análisis matemático, así como en sus aplicaciones. Esta idea se introdujo con el objetivo de matematizar la transformación
Apuntes de Funciones El concepto de función es un elemento fundamental dentro del análisis matemático, así como en sus aplicaciones. Esta idea se introdujo con el objetivo de matematizar la transformación
Nombre y Apellidos: e f(x) dx. Estudiar si converge la integral impropia
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Febrero 27 de Enero de 26 Nombre y Apellidos: DNI: 6.25 p.) ) Se considera la función f : [, ) R definida
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Febrero 27 de Enero de 26 Nombre y Apellidos: DNI: 6.25 p.) ) Se considera la función f : [, ) R definida
Tema 8: Derivación. José M. Salazar. Noviembre de 2016
 Tema 8: Derivación. José M. Salazar Noviembre de 2016 Tema 8: Derivación. Lección 9. Derivación: teoría fundamental. Lección 10. Aplicaciones de la derivación. Índice 1 Extremos de funciones y clasificación
Tema 8: Derivación. José M. Salazar Noviembre de 2016 Tema 8: Derivación. Lección 9. Derivación: teoría fundamental. Lección 10. Aplicaciones de la derivación. Índice 1 Extremos de funciones y clasificación
Tema 1. Cálculo diferencial
 Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES
 ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES I ) DOMINIO DE DEFINICIÓN DE UNA FUNCIÓN: Es el conjunto de puntos donde tiene sentido realizar las operaciones indicadas en el criterio de definición de la
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES I ) DOMINIO DE DEFINICIÓN DE UNA FUNCIÓN: Es el conjunto de puntos donde tiene sentido realizar las operaciones indicadas en el criterio de definición de la
5. ANÁLISIS MATEMÁTICO // 5.1. DERIVADAS Y
 5. ANÁLISIS MATEMÁTICO // 5.1. DERIVADAS Y APLICACIONES. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2017-2018 5.1.1. El problema de la tangente. Derivada. Pierre de Fermat tenía una
5. ANÁLISIS MATEMÁTICO // 5.1. DERIVADAS Y APLICACIONES. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2017-2018 5.1.1. El problema de la tangente. Derivada. Pierre de Fermat tenía una
Universidad Carlos III de Madrid
 Universidad Carlos III de Madrid Ejercicio 1 2 3 4 5 6 Total Puntos Departmento de Economía Matematicas I Examen Final 16 enero 2019 APELLIDOS: Duración: 2 horas. NOMBRE: ID: GRADO: GRUPO: (1) Sea la función
Universidad Carlos III de Madrid Ejercicio 1 2 3 4 5 6 Total Puntos Departmento de Economía Matematicas I Examen Final 16 enero 2019 APELLIDOS: Duración: 2 horas. NOMBRE: ID: GRADO: GRUPO: (1) Sea la función
5. ANÁLISIS MATEMÁTICO // 5.2. DERIVADA DE
 5. ANÁLISIS MATEMÁTICO // 5.2. DERIVADA DE UNA FUNCIÓN EN UN PUNTO Y APLICACIONES. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2010-2011 5.2.1. El problema de la tangente. Derivada.
5. ANÁLISIS MATEMÁTICO // 5.2. DERIVADA DE UNA FUNCIÓN EN UN PUNTO Y APLICACIONES. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2010-2011 5.2.1. El problema de la tangente. Derivada.
CÁLCULO ELEMENTAL PROBLEMAS. Valor absoluto. Funciones y sus gráficas
 CÁLCULO ELEMENTAL PROBLEMAS Valor absoluto - Resolver las ecuaciones siguientes: (i) 2x 6 = x (ii) x + 8 = 3x 4 2- Resolver la inecuación 2x 3 4 Funciones y sus gráficas 3- Dada f(x) = 2x 2 x, hallar f(
CÁLCULO ELEMENTAL PROBLEMAS Valor absoluto - Resolver las ecuaciones siguientes: (i) 2x 6 = x (ii) x + 8 = 3x 4 2- Resolver la inecuación 2x 3 4 Funciones y sus gráficas 3- Dada f(x) = 2x 2 x, hallar f(
Teoremas del valor medio
 Teoremas del valor medio Teorema de Rolle Teorema de Cauchy Teorema de Lagrange Teorema de Rolle Sea f x una función contínua en a; b, derivable en a; b y f a = f(b) entonces existe al menos un cε a; b
Teoremas del valor medio Teorema de Rolle Teorema de Cauchy Teorema de Lagrange Teorema de Rolle Sea f x una función contínua en a; b, derivable en a; b y f a = f(b) entonces existe al menos un cε a; b
1. Lección 6 - Derivabilidad
 1. Lección 6 - Derivabilidad Apuntes: Matemáticas Empresariales I Si el concepto de continuidad era importante para la aplicación de las matemáticas a la economía, el concepto fundamental del cálculo infinitesimal,
1. Lección 6 - Derivabilidad Apuntes: Matemáticas Empresariales I Si el concepto de continuidad era importante para la aplicación de las matemáticas a la economía, el concepto fundamental del cálculo infinitesimal,
TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN 9.1 DERIVADA DE UNA FUNCIÓN EN UN PUNTO
 TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN MATEMÁTICAS II º Bach TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN 9. DERIVADA DE UNA FUNCIÓN EN UN PUNTO TASA DE VARIACIÓN MEDIA Definición Se llama tasa de variación
TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN MATEMÁTICAS II º Bach TEMA 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN 9. DERIVADA DE UNA FUNCIÓN EN UN PUNTO TASA DE VARIACIÓN MEDIA Definición Se llama tasa de variación
Derivación de funciones de una variable real
 Capítulo 4 Derivación e funciones e una variable real 4.1. Derivaa e una función 4.1.1. Introucción Definición 4.1.1. Sea f : (a, b) R R y x 0 (a, b). Se ice que la función f es erivable en el punto x
Capítulo 4 Derivación e funciones e una variable real 4.1. Derivaa e una función 4.1.1. Introucción Definición 4.1.1. Sea f : (a, b) R R y x 0 (a, b). Se ice que la función f es erivable en el punto x
Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización.
 TEMA 1 Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización. Límite finito en un punto: Consideremos una función f definida en las proimidades
TEMA 1 Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización. Límite finito en un punto: Consideremos una función f definida en las proimidades
Universidad Carlos III de Madrid
 Universidad Carlos III de Madrid Departamento de Economía Examen final de Matemáticas I 3 de febrero de 4 APELLIDOS: NOMBRE: DNI: Titulación: Grupo: MODELO :. Sea A!!x,y"! R : x" y " ; x # " y si " x ;
Universidad Carlos III de Madrid Departamento de Economía Examen final de Matemáticas I 3 de febrero de 4 APELLIDOS: NOMBRE: DNI: Titulación: Grupo: MODELO :. Sea A!!x,y"! R : x" y " ; x # " y si " x ;
RESUMEN DE DERIVADAS. TVM = f(x) = lim 1+2h+h 2-1. = lim 1+h) lim. = 0 = lim h2+h)
 RESUMEN DE DERIVADAS Tasa de variación Media. Definición: se llama tasa de variación media (TVM) de una función f(x) entre los valores x 1 y x 2 al cociente entre el incremento que experimenta la variable
RESUMEN DE DERIVADAS Tasa de variación Media. Definición: se llama tasa de variación media (TVM) de una función f(x) entre los valores x 1 y x 2 al cociente entre el incremento que experimenta la variable
MATEMÁTICAS I BOLETÍN DE PROBLEMAS 3.DIFERENCIABILIDAD DE FUNCIONES REALES DE VARIABLE REAL. Moebius
 2018-19 MATEMÁTICAS I BOLETÍN DE PROBLEMAS 3.DIFERENCIABILIDAD DE FUNCIONES REALES DE VARIABLE REAL. 1. Halle la derivada de las siguientes funciones: a) f(x) = 3x 4 + 2 x 5 + 5 x 2 b) f(x) = 2x 1 2x+1
2018-19 MATEMÁTICAS I BOLETÍN DE PROBLEMAS 3.DIFERENCIABILIDAD DE FUNCIONES REALES DE VARIABLE REAL. 1. Halle la derivada de las siguientes funciones: a) f(x) = 3x 4 + 2 x 5 + 5 x 2 b) f(x) = 2x 1 2x+1
Universidad Carlos III de Madrid
 Universidad Carlos III de Madrid Ejercicio 1 3 4 5 6 Total Puntos Departamento de Economía Examen Final de Matemáticas I 0 de Enero de 015 APELLIDOS: Duración del Examen: horas NOMBRE: DNI: Titulación:
Universidad Carlos III de Madrid Ejercicio 1 3 4 5 6 Total Puntos Departamento de Economía Examen Final de Matemáticas I 0 de Enero de 015 APELLIDOS: Duración del Examen: horas NOMBRE: DNI: Titulación:
UNIDAD 10. DERIVADAS. APLICACIONES DE LAS DERIVADAS
 Unidad 0. Derivadas. Aplicaciones de las derivadas UNIDAD 0. DERIVADAS. APLICACIONES DE LAS DERIVADAS. TASA DE VARIACIÓN MEDIA. Se llama TASA DE VARIACIÓN MEDIA (TVM) de una función () f en un intervalo
Unidad 0. Derivadas. Aplicaciones de las derivadas UNIDAD 0. DERIVADAS. APLICACIONES DE LAS DERIVADAS. TASA DE VARIACIÓN MEDIA. Se llama TASA DE VARIACIÓN MEDIA (TVM) de una función () f en un intervalo
TEMA 2. FUNCIONES REALES DE VARIABLE REAL 2.4. APLICACIONES DE LA DERIVABILIDAD
 TEMA. FUNCIONES REALES DE VARIABLE REAL.4. APLICACIONES DE LA DERIVABILIDAD .4. APLICACIONES DE LA DERIVABILIDAD.4.1. Intervalos de crecimiento y decrecimiento.4.. Etremos locales de una función.4.3. Intervalos
TEMA. FUNCIONES REALES DE VARIABLE REAL.4. APLICACIONES DE LA DERIVABILIDAD .4. APLICACIONES DE LA DERIVABILIDAD.4.1. Intervalos de crecimiento y decrecimiento.4.. Etremos locales de una función.4.3. Intervalos
Funciones reales de variable real
 Tema Funciones reales de variable real Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real.. Conceptos Generales Definición.
Tema Funciones reales de variable real Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real.. Conceptos Generales Definición.
Unidad 8: Derivadas. Técnicas de derivación. Aplicación al estudio y representación de funciones. Primitiva de una función (integración).
 representación de funciones Primitiva de una función (integración) 1 Unidad 8: Derivadas Técnicas de derivación Aplicación al estudio y representación de funciones Primitiva de una función (integración)
representación de funciones Primitiva de una función (integración) 1 Unidad 8: Derivadas Técnicas de derivación Aplicación al estudio y representación de funciones Primitiva de una función (integración)
MATEMÁTICAS II. Apuntes
 MATEMÁTICAS II. Apuntes Curso preparatorio para el acceso a la universidad para mayores de 5 años Tema 1 Arturo de Pablo Elena Romera Open Course Ware, UC3M http://ocw.uc3m.es/matematicas Índice general
MATEMÁTICAS II. Apuntes Curso preparatorio para el acceso a la universidad para mayores de 5 años Tema 1 Arturo de Pablo Elena Romera Open Course Ware, UC3M http://ocw.uc3m.es/matematicas Índice general
Criterio 1: Sea f una función derivable en (a,b). f es estrictamente creciente en el intervalo abierto (a, b) si f es positiva en dicho intervalo.
 UNIDAD. APLICACIONES DE LAS DERIVADAS.. Información etraída de la primera derivada.. Información etraída de la segunda derivada.. Derivabilidad en intervalos: Teorema de Rolle, del valor medio y Caucy..4
UNIDAD. APLICACIONES DE LAS DERIVADAS.. Información etraída de la primera derivada.. Información etraída de la segunda derivada.. Derivabilidad en intervalos: Teorema de Rolle, del valor medio y Caucy..4
Control 1, MA-1A2 Cálculo Diferencial e Integral Escuela de Ingeniería, FCFM, U. de Chile Semestre 2008/2 (30 de Agosto)
 Control 1, MA-1A Cálculo Diferencial e Integral Escuela de Ingeniería, FCFM, U. de Chile Semestre 008/ (30 de Agosto) P1) Considere la función definida mediante la siguiente ley: x si x < a f(x) = x +
Control 1, MA-1A Cálculo Diferencial e Integral Escuela de Ingeniería, FCFM, U. de Chile Semestre 008/ (30 de Agosto) P1) Considere la función definida mediante la siguiente ley: x si x < a f(x) = x +
Cálculo: Notas sobre diferenciabilidad en una variable
 Cálculo: Notas sobre diferenciabilidad en una variable Antonio Garvín Curso 04/05 1 Derivabilidad en una variable 1.1 La derivada de una función en un punto Para una función f: R R tal que todo un intervalo
Cálculo: Notas sobre diferenciabilidad en una variable Antonio Garvín Curso 04/05 1 Derivabilidad en una variable 1.1 La derivada de una función en un punto Para una función f: R R tal que todo un intervalo
Tema 6: Derivada de una función
 Tema 6: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Tema 6: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Tema 7: Derivada de una función
 Tema 7: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Tema 7: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
CÁLCULO. Ingeniería Industrial. Curso Departamento de Matemática Aplicada II. Universidad de Sevilla.
 CÁLCULO Ingeniería Industrial. Curso 2009-2010. Departamento de Matemática Aplicada II. Universidad de Sevilla. Lección 1. Derivadas. Polinomios de Taylor. Resumen de la lección. 1.1. La derivada y la
CÁLCULO Ingeniería Industrial. Curso 2009-2010. Departamento de Matemática Aplicada II. Universidad de Sevilla. Lección 1. Derivadas. Polinomios de Taylor. Resumen de la lección. 1.1. La derivada y la
UNIVERSIDAD CARLOS III DE MADRID. Departamento de Matemáticas CAPÍTULO 3 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO
 UNIVERSIDAD CARLOS III DE MADRID Departamento de Matemáticas MATEMÁTICAS CAPÍTULO 3 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 2010 2011 Elaborado por Elena Romera Índice general
UNIVERSIDAD CARLOS III DE MADRID Departamento de Matemáticas MATEMÁTICAS CAPÍTULO 3 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 2010 2011 Elaborado por Elena Romera Índice general
TEMA 3: CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES REALES DE UNA VARIABLE REAL. f : R R
 TEMA 3: CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES REALES DE UNA VARIABLE REAL. Concepto de función. Definición Se llama función (real de variable real) a toda aplicación f : R R f() que a cada número le
TEMA 3: CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES REALES DE UNA VARIABLE REAL. Concepto de función. Definición Se llama función (real de variable real) a toda aplicación f : R R f() que a cada número le
Tema 5 Aplicaciones del cálculo diferencial
 Tema 5 Aplicaciones del cálculo diferencial 1. APLICACIONES EN UNA VARIABLE 1.1. Extremos relativos. Proposición 1.1: Monotonía Sea f : [a, b] R continua en [a, b] y derivable en (a, b), entonces: (1)
Tema 5 Aplicaciones del cálculo diferencial 1. APLICACIONES EN UNA VARIABLE 1.1. Extremos relativos. Proposición 1.1: Monotonía Sea f : [a, b] R continua en [a, b] y derivable en (a, b), entonces: (1)
CONTINUIDAD Y DERIVADA CONCEPTO DE DERIVADA DE UNA FUNCIÓN. REGLAS DE DERIVACIÓN
 Índice Presentación... 3 Concepto de derivada de una función en un punto... 4 La derivada como un límite... 5 Derivada y continuidad. Funciones no derivables... 6 Función derivada. Reglas para derivar...
Índice Presentación... 3 Concepto de derivada de una función en un punto... 4 La derivada como un límite... 5 Derivada y continuidad. Funciones no derivables... 6 Función derivada. Reglas para derivar...
DERIVADAS Y APLICACIONES MANUEL BALLESTEROS HONRADO
 DERIVADAS Y APLICACIONES MANUEL BALLESTEROS HONRADO . TASA DE VARIACIÓN MEDIA. Imaginemos la siguiente tabla que relaciona los kilómetros recorridos por un ciclista en las siete horas que dura una etapa
DERIVADAS Y APLICACIONES MANUEL BALLESTEROS HONRADO . TASA DE VARIACIÓN MEDIA. Imaginemos la siguiente tabla que relaciona los kilómetros recorridos por un ciclista en las siete horas que dura una etapa
1. Nociones básicas. Oct, 2007
 Cálculo 1. Nociones básicas Oct, 2007 Nociones básicas Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial y logarítmica Funciones
Cálculo 1. Nociones básicas Oct, 2007 Nociones básicas Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial y logarítmica Funciones
Universidad Carlos III de Madrid
 Universidad Carlos III de Madrid Departamento de Economía Examen final de Matemáticas I 9 de septiembre de 004 APELLIDOS: NOMBRE: DNI: Titulación: Grupo: MODELO :. Sea A x,y R : x ; e x y e x. Se pide:
Universidad Carlos III de Madrid Departamento de Economía Examen final de Matemáticas I 9 de septiembre de 004 APELLIDOS: NOMBRE: DNI: Titulación: Grupo: MODELO :. Sea A x,y R : x ; e x y e x. Se pide:
FUNCIONES REALES DE VARIABLE REAL
 FUNCIONES REALES DE VARIABLE REAL Función: Es toda aplicación definida entre conjuntos numéricos. Cuando el conjunto inicial y final son los números Reales, se llaman funciones reales de variable real.
FUNCIONES REALES DE VARIABLE REAL Función: Es toda aplicación definida entre conjuntos numéricos. Cuando el conjunto inicial y final son los números Reales, se llaman funciones reales de variable real.
RESUMEN DE ANÁLISIS MATEMÁTICAS II
 RESUMEN DE ANÁLISIS MATEMÁTICAS II 1. DOMINIO DE DEFINICIÓN Y CONTINUIDAD 1.1. FUNCIONES ELEMENTALES (No tienen puntos angulosos) Tipo de función f (x) Dom (f) Continuidad Polinómicas P(x) R Racional P(x)/Q(x)
RESUMEN DE ANÁLISIS MATEMÁTICAS II 1. DOMINIO DE DEFINICIÓN Y CONTINUIDAD 1.1. FUNCIONES ELEMENTALES (No tienen puntos angulosos) Tipo de función f (x) Dom (f) Continuidad Polinómicas P(x) R Racional P(x)/Q(x)
Cálculo I Aplicaciones de la Derivada: El Teorema del Valor Medio, Crecimiento y Decrecimiento. Julio C. Carrillo E. * 1.
 4.3. Aplicaciones de la Derivada: El Teorema del Valor Medio, Crecimiento y Decrecimiento Julio C. Carrillo E. * Índice 1. Introducción 1 2. Teoremas de Rolle y del valor medio 1 3. Criterio para el crecimiento
4.3. Aplicaciones de la Derivada: El Teorema del Valor Medio, Crecimiento y Decrecimiento Julio C. Carrillo E. * Índice 1. Introducción 1 2. Teoremas de Rolle y del valor medio 1 3. Criterio para el crecimiento
Aplicaciones de la derivada
 Instituto Tecnológico Autónomo de México Departamento de Matemáticas Cálculo Diferencial e Integral I (MAT14100) Lista de Ejercicios Aplicaciones de la derivada Cálculo Diferencial e Integral I. Aplicaciones
Instituto Tecnológico Autónomo de México Departamento de Matemáticas Cálculo Diferencial e Integral I (MAT14100) Lista de Ejercicios Aplicaciones de la derivada Cálculo Diferencial e Integral I. Aplicaciones
Problemas tipo examen
 Problemas tipo examen La división en temas no es exhaustiva. Las referencias (H n- m) indican el problema m de la hoja n y las referencias (A- cd), con A en números romanos indican un examen del mes A
Problemas tipo examen La división en temas no es exhaustiva. Las referencias (H n- m) indican el problema m de la hoja n y las referencias (A- cd), con A en números romanos indican un examen del mes A
REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL
 REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL CORRESPONDENCIA. Se llama CORRESPONDENCIA entre dos conjuntos A y B a toda ley que asocia elementos del conjunto A con elementos del conjunto B. Se
REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL CORRESPONDENCIA. Se llama CORRESPONDENCIA entre dos conjuntos A y B a toda ley que asocia elementos del conjunto A con elementos del conjunto B. Se
C alculo Septiembre 2010
 Cálculo Septiembre 2010 Funciones reales de variable real Conjuntos de números Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial
Cálculo Septiembre 2010 Funciones reales de variable real Conjuntos de números Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial
Aplicaciones de las derivadas
 Aplicaciones de las derivadas. Recta tangente a una curva en un punto La pendiente de la recta tangente a la gráfica de la función f() en el punto ( 0, f( 0 )) viene dada por f ( 0 ) siempre que la función
Aplicaciones de las derivadas. Recta tangente a una curva en un punto La pendiente de la recta tangente a la gráfica de la función f() en el punto ( 0, f( 0 )) viene dada por f ( 0 ) siempre que la función
Teorema de los extremos absolutos (del supremo y el ínfimo), de Weiestrass.
 CALCULO DIFERENCIAL TEMA 1 : PROPIEDADES DE LAS FUNCIONES CONTINUAS Teorema del signo. Sea f:[a,b] >R una función continua en (a,b) entonces si f(x0)"0, existe un entorno E(x0,) en que f tiene el mismo
CALCULO DIFERENCIAL TEMA 1 : PROPIEDADES DE LAS FUNCIONES CONTINUAS Teorema del signo. Sea f:[a,b] >R una función continua en (a,b) entonces si f(x0)"0, existe un entorno E(x0,) en que f tiene el mismo
Curso Propedéutico de Cálculo Sesión 3: Derivadas
 Curso Propedéutico de Cálculo Sesión 3: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 3 4 5 6 7 Esquema 1 2 3 4 5 6 7 Introducción La derivada
Curso Propedéutico de Cálculo Sesión 3: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 3 4 5 6 7 Esquema 1 2 3 4 5 6 7 Introducción La derivada
Boletín II. Cálculo diferencial de funciones de una variable
 CÁLCULO Boletín II. Cálculo diferencial de funciones de una variable Ejercicios básicos 1. Sea f la función dada por 5x 2. a) Utiliza la definición de derivada para demostrar que f (x) = 10x. b) Calcula
CÁLCULO Boletín II. Cálculo diferencial de funciones de una variable Ejercicios básicos 1. Sea f la función dada por 5x 2. a) Utiliza la definición de derivada para demostrar que f (x) = 10x. b) Calcula
(3 p.) 3) Se considera la superficie z = z(x, y) definida implícitamente por la ecuación. 3x 2 z x 2 y 2 + 2z 3 3yz = 15.
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 2012/2013 21 de junio de 2013 4 p.) 1) Se considera la función fx) = x 4 e 1 x 2. a) Calcular los intervalos de
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 2012/2013 21 de junio de 2013 4 p.) 1) Se considera la función fx) = x 4 e 1 x 2. a) Calcular los intervalos de
Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto:
 1 LA DERIVADA EN EL TRAZADO DE CURVAS Significados de los signos de la Primera y Segunda derivada. Plantearemos a través del estudio del signo de la primera derivada, las condiciones que debe cumplir una
1 LA DERIVADA EN EL TRAZADO DE CURVAS Significados de los signos de la Primera y Segunda derivada. Plantearemos a través del estudio del signo de la primera derivada, las condiciones que debe cumplir una
MATEMÁTICA - 6 A C y D - Prof. Sandra M. Corti
 TEMA: Derivada La derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente Sea f(x) una función continua
TEMA: Derivada La derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente Sea f(x) una función continua
Nombre y Apellidos: x (1 + ln(x)) si x > 0 f(x) = 0 si x = 0.
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Septiembre de Septiembre de 008 Nombre y Apellidos: DNI: (6.5 p.) ) Se considera la función f : [0,
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Septiembre de Septiembre de 008 Nombre y Apellidos: DNI: (6.5 p.) ) Se considera la función f : [0,
Matemática Aplicada - Licenciatura de Farmacia - Curso 2005/ HOJA 1 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 1. x = x + 5 si x < 0.
 Matemática Aplicada - Licenciatura de Farmacia - Curso 005/006 - HOJA 1 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 1 1) Estudiemos cada caso: x = x+5 a) El único número que verifica la condición es x =
Matemática Aplicada - Licenciatura de Farmacia - Curso 005/006 - HOJA 1 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 1 1) Estudiemos cada caso: x = x+5 a) El único número que verifica la condición es x =
Fundamentos de Matemáticas - Grado en Ingeniería Agrícola - Profª. Mónica Esquivel
 Fundamentos de Matemáticas - Grado en Ingeniería Agrícola - Profª. Mónica squivel Tema 1 FUNCION RAL D VARIABL RAL. CONTINUIDAD. DRIVABILIDAD 1.1. Funciones reales de variable real: generalidades I V R
Fundamentos de Matemáticas - Grado en Ingeniería Agrícola - Profª. Mónica squivel Tema 1 FUNCION RAL D VARIABL RAL. CONTINUIDAD. DRIVABILIDAD 1.1. Funciones reales de variable real: generalidades I V R
Ejercicios resueltos de cálculo Febrero de 2016
 Ejercicios resueltos de cálculo Febrero de 016 Ejercicio 1. Calcula los siguientes ites: x 5x 1. x + x + 1 x 1 x. x x. x + x + 1 x x 4. x 0 x cos x sen x x Solución: 1. Indeterminación del tipo. Tenemos:
Ejercicios resueltos de cálculo Febrero de 016 Ejercicio 1. Calcula los siguientes ites: x 5x 1. x + x + 1 x 1 x. x x. x + x + 1 x x 4. x 0 x cos x sen x x Solución: 1. Indeterminación del tipo. Tenemos:
1. El Teorema de Rolle Generalizado.
 Proyecto III: Los Teoremas de Rolle y del valor Medio Objetivos: Profundizar el estudio de algunos teoremas del cálculo diferencial 1 El Teorema de Rolle Generalizado La formulación más común del Teorema
Proyecto III: Los Teoremas de Rolle y del valor Medio Objetivos: Profundizar el estudio de algunos teoremas del cálculo diferencial 1 El Teorema de Rolle Generalizado La formulación más común del Teorema
AYUDA MEMORIA PARA EL ESTUDIO DE MATEMÁTICAS II - SISTEMAS
 AYUDA MEMORIA PARA EL ESTUDIO DE MATEMÁTICAS II - SISTEMAS Potencias de la unidad imaginaria i 0 = 1 i 1 = i i 2 = 1 i 3 = i i 4 = 1 Los valores se repiten de cuatro en cuatro, por eso, para saber cuánto
AYUDA MEMORIA PARA EL ESTUDIO DE MATEMÁTICAS II - SISTEMAS Potencias de la unidad imaginaria i 0 = 1 i 1 = i i 2 = 1 i 3 = i i 4 = 1 Los valores se repiten de cuatro en cuatro, por eso, para saber cuánto
2º BACHILLERATO. EJERCICIOS DE REPASO 1ª EVALUACIÓN
 2º BACHILLERATO. EJERCICIOS DE REPASO 1ª EVALUACIÓN 1.) Resuelve las siguientes derivadas: a) b) c) d) e) f) g) h) i) j) k) l) m) n) o) p) q) r) f(x) = arcsen 2.) Resuelve la siguiente derivada, simplificando
2º BACHILLERATO. EJERCICIOS DE REPASO 1ª EVALUACIÓN 1.) Resuelve las siguientes derivadas: a) b) c) d) e) f) g) h) i) j) k) l) m) n) o) p) q) r) f(x) = arcsen 2.) Resuelve la siguiente derivada, simplificando
Funciones de una variable real II Fórmula de Taylor y aplicaciones
 Universidad de Murcia Departamento Matemáticas Funciones de una variable real II Fórmula de Taylor y aplicaciones B. Cascales J. M. Mira L. Oncina Departamento de Matemáticas Universidad de Murcia Grado
Universidad de Murcia Departamento Matemáticas Funciones de una variable real II Fórmula de Taylor y aplicaciones B. Cascales J. M. Mira L. Oncina Departamento de Matemáticas Universidad de Murcia Grado
Tema 8: Aplicaciones de la derivada
 1. Introducción Tema 8: Aplicaciones de la derivada En la unidad anterior hemos establecido el concepto de derivada de una función f(x) en un punto x 0 de su dominio y la hemos interpretado geométricamente
1. Introducción Tema 8: Aplicaciones de la derivada En la unidad anterior hemos establecido el concepto de derivada de una función f(x) en un punto x 0 de su dominio y la hemos interpretado geométricamente
Límites y Continuidad
 Tema 2 Límites y Continuidad Introducción En este tema se trata el concepto de límite de una función real de variable real y sus propiedades, así como algunas de las técnicas fundamentales para el cálculo
Tema 2 Límites y Continuidad Introducción En este tema se trata el concepto de límite de una función real de variable real y sus propiedades, así como algunas de las técnicas fundamentales para el cálculo
Lección 3: Aproximación de funciones. por polinomios. Fórmula de Taylor para
 Lección 3: Aproximación de funciones por polinomios. Fórmula de Taylor para funciones escalares 3.1 Introducción Cuando es difícil trabajar con una función complicada, tratamos a veces de hallar una función
Lección 3: Aproximación de funciones por polinomios. Fórmula de Taylor para funciones escalares 3.1 Introducción Cuando es difícil trabajar con una función complicada, tratamos a veces de hallar una función
Cociente incremental. Mide la variación media de f(x) en (x 0, x 0 + x)
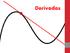 Derivadas Cociente incremental Sea y= f(x) continua en x=x 0 x: incremento de la variable independiente y: incremento de la variable dependiente Se llama cociente incremental al cociente y f ( x x f xo
Derivadas Cociente incremental Sea y= f(x) continua en x=x 0 x: incremento de la variable independiente y: incremento de la variable dependiente Se llama cociente incremental al cociente y f ( x x f xo
c) Calcular las asíntotas horizontales y verticales de f y representar de forma aproximada
 Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas Cálculo I Curso 2011/2012 2 de julio de 2012 (75 p) 1) Se considera la función f : R R definida por f(x) = ex 2 e x + 1 a) Determinar
Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas Cálculo I Curso 2011/2012 2 de julio de 2012 (75 p) 1) Se considera la función f : R R definida por f(x) = ex 2 e x + 1 a) Determinar
Funciones convexas Definición de función convexa. Tema 7
 Tema 7 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Tema 7 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
LA FUNCIÓN f VISTA A TRAVÉS DE f Y f.
 ANÁLISIS MATEMÁTICO BÁSICO. LA FUNCIÓN f VISTA A TRAVÉS DE f Y f. Dada una función f : R R derivable, podemos considerar su función derivada f : R R. Esta función a su vez puede ser derivable, y tendremos
ANÁLISIS MATEMÁTICO BÁSICO. LA FUNCIÓN f VISTA A TRAVÉS DE f Y f. Dada una función f : R R derivable, podemos considerar su función derivada f : R R. Esta función a su vez puede ser derivable, y tendremos
Material de uso exclusivamente didáctico 1
 TEMA 1 Ejercicio 1 ( puntos) Sea f(x) = 10 + 4. Hallar a R tal que f(a) = 9. Para el valor encontrado, hallar la ecuación de la recta tangente x 4 al gráfico de f en (a; f(a)) f(a) = 9 10 a 4 + 4 = 9 10
TEMA 1 Ejercicio 1 ( puntos) Sea f(x) = 10 + 4. Hallar a R tal que f(a) = 9. Para el valor encontrado, hallar la ecuación de la recta tangente x 4 al gráfico de f en (a; f(a)) f(a) = 9 10 a 4 + 4 = 9 10
Análisis Matemático I
 Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
Ejercicios resueltos. 4 continua en R luego continua en cualquier. , [ 1,1] = 0 que equivale a decir 1,1
![Ejercicios resueltos. 4 continua en R luego continua en cualquier. , [ 1,1] = 0 que equivale a decir 1,1 Ejercicios resueltos. 4 continua en R luego continua en cualquier. , [ 1,1] = 0 que equivale a decir 1,1](/thumbs/54/33117646.jpg) Teoremas de continuidad y derivabilidad Ejercicios resueltos.- Demostrar que la siguiente ecuación tiene una solución en el intervalo, : 4 º. Se considera la función 4 continua en R luego continua en cualquier
Teoremas de continuidad y derivabilidad Ejercicios resueltos.- Demostrar que la siguiente ecuación tiene una solución en el intervalo, : 4 º. Se considera la función 4 continua en R luego continua en cualquier
BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE
 BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE El concepto de derivada. Relación entre continuidad y derivabilidad. Función derivada. Operaciones con derivadas. Derivación de las funciones
BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE El concepto de derivada. Relación entre continuidad y derivabilidad. Función derivada. Operaciones con derivadas. Derivación de las funciones
