RESOLVIENDO PROBLEMAS DE MATEMÁTICA

Transcripción

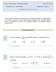
1 RESOLVIENDO PROBLEMAS DE MATEMÁTICA RESOLUCIÓN DE LOS PROBLEMAS PROPUESTOS PROBLEMA 14 (16115) Probar que, 3, 5 no pueden ser términos de una misma progresión aritmética. Sean a m, a n 3, a p 5, siendo m< n < p. Se tiene: Es decir: a n a m + (n m).d a p a n + (p n).d n m ( 3 )( 5 3) p n (n m).d (p n).d n m p n pero tal igualdad es imposible, pues siendo m, n, p N, ha de ser n m Q, y sin embargo, p n es irracional.

2 PROBLEMA 13 (181115) Sea el conjunto X a, b,c, d,e T X X,φ, { a}, { a, b}, { a, c, d}, { a, b, c, d}, a, b,e Dado el subconjunto A a, b,c { } y una topología T X definida en X por { { }} { } de X, se pide: a) Encontrar los puntos interiores de A. b) Encontrar los puntos exteriores de A. c) Encontrar los puntos fronteras de A. a) El interior de A es la unión de todos los abiertos contenidos en A, o bien el mayor de tales abiertos. Del enunciado, los únicos abiertos contenidos en A son: luego: { } y { a, b} φ, a int(a) φ { a} { a, b} { a,b} b) El exterior de A es el interior de su complementario CA respecto al espacio X, soporte de la topología CA d, e { } el único abierto contenido en CA es φ, luego int(ca) φ. Ext(A) int(ca) φ b) La frontera de A podemos calcularla de un par de maneras: - Como es la intersección de las clausuras de A y de su complementario: Front(A) A CA Para determinar ambas clausuras, veamos la familia de cerrados: F X,φ, { b, c, d, e}, { c, d,e}, { b, e}, { e}, c, d el único cerrado que contiene a A a, b,c contienen a CA d, e { { }} { } es X. Los cerrados que { } son X y { c, d,e}, por lo que - Como Front(A) A int(a), será: A X y CA X { c, d,e} { c, d,e} Front(A) A CA X { c, d,e} { c, d,e} Front(A) A int(a) { a, b, c, d, e} { a, b} { c, d,e}

3 PROBLEMA 1 (11015) Demostrar que la integral general de la ecuación diferencial puede expresarse por llamando dy dx p: d y dx log x. dy dx y(x) d y dx log x. dy dx dp dx log dp dx x.p 0 p 0 dx x 1 log x ( )+ C 0 d dy dy log x. dx dx dx 0 log x d 1 log x dx p 1 x(log x 1) + C p Integral general: dy p x(1 log x)+ C dx 1 y(x) x( 1 log x)+ C ( ) 1 y(x) dx x 1 log x ( )+ C

4 PROBLEMA 11 (30915) En una batalla en la que participan entre y soldados, han resultado muertos 3/165 del total. Y han resultado heridos 35/143 del total. Cuántos soldados resultaron ilesos en esta batalla?. Puesto que tanto el número de muertos total, (M), como el número total de heridos (H), han de ser números naturales, el número total de soldados en la batalla (T) ha de ser múltiplo de 165 y también múltiplo de 143. Veamos cuál de estos múltiplos está comprendido entre y Hallamos en primer lugar el MCM(143,165): M(143,165) MCM (11.13,3.5.11) El múltiplo que buscamos es un múltiplo de 145 que sea menor que y mayor que Como es el único múltiplo de 145 comprendido entre y es 145x51075, ya que 145x48580 es menor que por tanto el total de soldados en la batalla es T 1075 Muertos: M Heridos: H Ilesos: I T (M + H ) 6605

5 PROBLEMA 10 (60815) En una reunión hay varias personas. Se incorpora Alicia y la media de la edad aumenta en 4 años. Posteriormente se incorpora Beatriz, que es gemela de Alicia, y la media de edad vuelve a aumentar, pero en este caso solo en 3 años. Cuántas personas había en la reunión antes de entrar Alicia? Si es n el número de personas de la reunión antes de que entre Alicia, y las edades de todas ellas son e 1,...,e n, se tiene que la edad media es M 1 n n e i i1 Y una vez entre Alicia, de edad e n+1, la edad media será M n+1 Y al entrar posteriormente Beatriz, de edad e n+1 : n+1 e i i1 M n+ n+ e i i1 O sea, se tiene que Es decir: o bien: e e n n.m e e n + e n+1 (n+1).(m + 4) e e n + e n+1 + e n+1 (n+ ).(M + 7) nm + e n+1 (n+1).(m + 4) (n+1).(m + 4)+ e n+1 (n+ ).(M + 7) (n+1).(m + 4) n.m (n+ ).(M + 7) Mn+ M +8n+8 Mn+ M + 7n+14 8n+8 7n+14 n 6 Habían 6 personas cuando entró Alicia.

6 PROBLEMA 119 (90715) a) Qué es una diferencial exacta?. b) Es diferencial exacta la ecuación P(x,y).dx+Q(x,y).dy, si son P(x,y)3y+10x y Q(x,y)3x+y?. Si es así, integrarla. a) La ecuación diferencial P(x,y).dx+Q(x,y).dy es diferencial exacta sii existe una función U(x,y) tal que o sea, tal que U P(x, y) x U Q(x, y) y U y x U y x U x y U x y P(x, y) y Q(x, y) x Por tanto, la condición necesaria y suficiente para que tal ecuación sea diferencial exacta es que: b) Como es: La integración: De ser entonces: P(x, y) y Q(x, y) x 3 3 P(x, y) y P(x, y) y P(x, y) U x U 3y+10x U x (3y+10x)dx Q(x, y) x Q(x, y) x dif. exacta 3xy+ 5x +ϕ(y) Q(x, y) U 3x+ y 3x+ y 3x+ϕ '(y) ϕ '(y) y ϕ(y) y y En definitiva: U(x, y) 3xy + 5x + y ± C, Ccte arbitraria

7 PROBLEMA 118 (010715) ( ) 3 a) Hallar un vector normal a la superficie z+ x + y + x + y genérico (x, y, z) (0,0,0). en un punto b) Hallar el coseno del ángulo θ formado por el vector normal anterior y el eje z, y. determinar lim cosθ ( x,y)(0,0) a) Hacemos: S z x + y ( x + y ) 3, con lo que obtenemos: S x x+ 3x(x + y ), x + y de lo cual, el vector normal es: b) cosθ S. k, y como es S S y y+ 3y(x + y ), x + y S x+ 3x(x + y ) x + y, S y 1 y+ 3y(x + y ), 1 x + y S x + 6x (x + y )+ 9x (x + y ) + y + 6y (x + y )+ 9y (x + y ) + (x + y ) x + y se tiene: Finalmente: + 6(x + y )+ 9(x + y ) cosθ S. k S 1 + 6(x + y )+ 9(x + y ) lim cosθ 1 ( x,y)(0,0) PROBLEMA 117 (030615) Hallar las dos dimensiones de un rectángulo sabiendo que se expresan en decímetros por dos números enteros, y en metros por dos números decimales no enteros. Se sabe

8 también que el perímetro se expresa en metros y la superficie en metros cuadrados por el mismo número decimal. Sean x,y las dos dimensiones expresadas en decímetros. Si las queremos expresar en metros serán: x/10 y y/10. Como las medidas en metros son números decimales no enteros, se deduce que ni x ni y son múltiplos de 10: x 10, y 10 Como la superficie y el perímetro se expresan, en metros, por el mismo número, se cumplirá que: x 10. y 10 x 10 + y 10 de donde resulta x y 0 para que x sea entero y distinto de múltiplo de 10 ha de ser distinto de múltiplo de 10 el sumando de la expresión anterior 400 y 0 10 y también y Como es , se deduce que para que y 0 igual a 4 o bien a 5 : 400 Si y 0 4 y 0 5 y 45 x 36 Si 400 y 0 5 y 0 4 y 36 x 45 Dimensiones del rectángulo: 36 decímetros de ancho por 45 decímetros de alto (o al revés) Comprobamos: Superficie en metros: 3 6x m, Perímetro en metros:.( )16 0 m sea entero con la condición antedicha, ha de ser

9 PROBLEMA 116 (060515) Resolver la ecuación z 3 (8+ i).z + (4+ 4i).z (4 6i) 0, sabiendo que el afijo de una de las raíces está en la bisectriz del primer cuadrante. Sea z 1 la raiz que tiene su afijo en la bisectriz del primer cuadrante. Será, entonces, z 1 x+ xi x(1+ i). Vamos a sustituir en la ecuación dada: z 1 x (1+i) x i, z 3 1 x ix(1+ i) x 3 + x 3 i x 3 ( 1+ i) al sustituir, se tiene: x 3 ( 1+i) (8 + i)x i + (4 + 4i)x(1+ i) (4 6i) 0 ordenamos partes reales e imaginarias: ( x 3 + x + 0x 4)+ (x 3 16x + 8x+ 6)i 0 O sea: x 3 + x + 0x 4 0 x 3 16x + 8x+ 6 0 Sumamos para reducir a una ecuación de º: 7x 4x+ 9 0 Al resolver, se tiene: x 4 ± ( 4) ±18 14 Si x 3, z 1 3(1+ i) 3+ 3i, y si x 37,z 1 (3+ 3i) 7 Veamos la primera solución, z i. Dividamos el polinomio de tercer grado para obtener una ecuación de º en la variable z, usando la Regla de Ruffini: 1 (8+i) 4+ 4i (4 6i) 3+ 3i 1 9i 4 6i 3+ 3i 1 5+ i 3 5i Se obtiene como cociente z + ( 5+ i)z+ (3 5i). Resolvemos la ecuación de º: z + ( 5+ i)z+ (3 5i) 0 z ( 5+ i)± ( 5+ i) 4(3 5i) Las tres raíces pedidas son z i, z 4 i, z 3 1 i 4 i 1 i La segunda solución posible, z 1 (3+ 3i) 7, no es válida, ya que al dividir el polinomio de tercer grado para obtener la ecuación de º en z, usando, como antes, la Regla de Ruffini, no se obtiene resto cero. z i, z 4 i, z 3 1 i

10 PROBLEMA 115 (080415) Determinar el lugar geométrico de los puntos de contacto de las tangentes trazadas por (-6,0) a las elipses que tienen por semiejes b3 y a (es decir, de ecuación reducida dada por x / a + y /91). Representar gráficamente dicho lugar geométrico. a) Ecuación de las tangentes en un punto (x 0, y 0 ):.x De ser 0 + y y ' 0 0 ' 0 y a a Se tiene: ' y y 0 y 0 (x x 0 ) y y 0 3 a x 0 y 0 y.y x.x 0 x 0 a a + y y.y x.x 0 1 a b) Determinando el semieje a: Puesto que las tangentes pasan por el punto (-6,0): 0.y ( 6).x 0 a 1 a 6x 0 c) Lugar geométrico de los puntos de contacto: x 0 (x x 0 ) a yy 0 a y 0 9x.x 0 + 9x 0 y 0 x 0 /( 6x 0 )+ y 0 /91 x 0 3 y 0 6 d) Representación:

11 PROBLEMA 114 (110315) Al quitar un número de una lista de diez enteros consecutivos resulta que la suma de los nueve restantes es 014. Qué número hemos quitado? (Olimpiada Matemática Española 014) RESOLUCION (de Jerónimo Basa, 13 marzo 015): Pinche en este link: RESOLUCIÓN (de casanchi): Sean los números enteros x, x + 1, x +, x + 3, x + 4, x + 5, x + 6, x + 7, x + 8, x + 9. Quitemos el entero x + k, 0 k 9 : Se tiene: o sea: x + ( x + 1) + ( x + ) ( x + 9) ( x + k) 014 9x + 45 k x k 1969 Probamos valores de k, de 0 a 9: Si k0: 9 x x 1969 / 9 Z Si k1: 9 x x 1970 / 9 Z Si k: 9 x 1969 x 1971/ 9 19 Z Los numeros enteros sucesivos son 19, 0, 1,, 3, 4, 5, 6, 7, 8. El número que hay que quitar es el x + k La suma de los 9 restantes numeros enteros es 014. Comprobamos:

12 PROBLEMA 113 (11015) Dada la cónica de ecuación general dada por 4x y +8xy x+ 5 0, se pide: a) Clasificarla. b) Obtener su ecuación reducida. Para una ecuación general de la forma a 11 x + a y + a 1 + a 01 x+ a 0 y+ a 00 0, la matriz de la cónica es y sus invariantes métricos son en nuestro caso: A A 5 1/ 0 1/ A a 00 a 01 a 0 a 10 a 11 a 1 a 00 a 01 a 0 a 10 a 11 a 1 a 0 a 1 a a 0 a 1 a, A 00 A 5 1/ 0 1/ a) Clasificación: - Por ser A 0 : es cónica irreducible. - Por ser A 00 0 : es cónica irreducible con centro. - Por ser A 00 < 0 : es hipérbola. - Por ser a 11 + a 0: hipérbola no equilátera. b) Ecuación reducida: La ecuación reducida es a 11 " x + a " y " " + a 00 0, siendo a 00 soluciones de la ecuación de º z (a 11 + a )z+ A 00 0 : " a / 4 a 11 a 1 a 1 a, a 11 + a -39/, A , a 11 + a 4 + ( ) A / A 00, y a " " 11, a son las dos 39 48, a 11 " 6, a " 4. Por tanto, la ecuación reducida es 3x y 39 / 96

13 PROBLEMA 11 (140115) a) Demostrar el Teorema de Milne-Thomsom para funciones de una variable compleja: f (z) u(x, y)+iv(x, y) f '(z) u x (z,0) iu y (z,0), x, y R x b) Dada la función u(x, y), hallar otra función v(x, y) tal que la función x + y w(x+ iy) u(x, y)+ iv(x, y) sea función holomorfa de la variable z x+ iy. c) Calcular w(z) en el ejemplo anterior ulilizando el Teorema de Milne-Thomson. a) Si en z x+ iy hacemos zx, entonces y0. Con lo que: f (z) u(z,0)+ iv(z,0), y al diferenciar: f '(z) u x (z,0)+ iv x (z,0). Aplicamos las ecuaciones de Cauchy-Riemann ( u x v y, u y v x ), con lo que resulta la expresión buscada: f '(z) u x (z,0) iu y (z,0). b) De ser u(x, y) Cauchy-Riemann: v y y x x x + y, se tienen sus derivadas: u x y x x + y, u y xy x + y, y aplicando x + y, v x dv v x dx + v y dy v x dx + v y dy y la función holomorfa pedida es: x x 0 w(z) xy x. Por tanto es: + y y y 0 x y xy x + y dx y x + x + y dy y x + y x 0 x x + y iy x + y x iy x + y c) f '(z) u x (z,0)+ iu y (z,0) 0 x i.0 (x z + 0) z 1 f (z) 1/z 4 z Si hacemos w(z) f (z): w(z) f (z) 1 z 1 x+ iy x iy x + y y 0