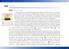
x = A(t)x + b(t), (10.1)

Transcripción

1 Lección 0 Sistemas no homogéneos y Aplicaciones 0.. Introducción Los sistemas de ecuaciones diferenciales lineales no homogéneos son de la forma x = Atx + bt, 0. donde, para cada t, At es una matriz n n, x es un vector columna de funciones incógnita y bt es un vector columna de funciones conocidas. La forma de proceder para resolver este tipo de sistemas es la misma que ya estudiamos para las ecuaciones diferenciales lineales no homogéneas Lección 2. Primero demostraremos que la solución general del sistema 0. es la suma de la solución general del sistema homogéneo x = Atx y de una solución particular del no homogéneo. A continuación diseñaremos un método para encontrar una solución particular del sistema no homogéneo. Finalmente aplicaremos todo esto a los sistemas de coeficientes constantes. En la última parte de la lección veremos algunas aplicaciones de la resolución de sistemas lineales a problemas en Ingeniería Química. 73

2 74 Sistemas no homogéneos y aplicaciones 0.2. Solución general de los sistemas no homogéneos El siguiente resultado es la base para encontrar todas las soluciones del sistema 0.: Teorema 0..- Sea x h t la solución general del sistema homogéneo x = Atx y sea x p t una solución particular del sistema no homogéneo 0.. Entonces la solución general del sistema 0. es de la forma xt = x h t + x p t. Demostración.- Desde luego si xt = x p t + x h t entonces xt es solución de 0.. En efecto, x t = x pt + x h t = Atx pt + bt + Atx h t = = Atx p t + x h t + bt = Atxt + bt. Así pues todas las funciones vectoriales de la forma xt = x p t + x h t son solución del sistema no homogéneo. Veamos que no hay más; es decir, que cualquier solución es de esta forma. Sea xt una solución cualquiera del sistema 0. y x p t una solución particular del mismo. Entonces x t x pt = Atxt + bt Atx p t bt = Atxt x p t, de modo que xt x p t es una solución del sistema homogéneo x = Atx. Sea, ahora, Xt = x t x 2 t x n t una matriz fundamental de soluciones del sistema homogéneo x = Atx; es decir, x t, x 2 t,..., x n t forman un sistema fundamental de soluciones de x = Atx. Como xt x p t es una solución del sistema homogéneo x t = Atxt, debe poder escribirse como una combinación lineal de las columnas de Xt: xt x p t = c x t + c 2 x 2 t + + c n x n t para algunas constantes c, c 2,..., c n. Por lo tanto xt = x p t + c x t + c 2 x 2 t. Esto significa que cualquier solución del sistema no homogéneo es suma de una solución particular de éste y de una solución del sistema homogéneo. Y esto es lo que se quería demostrar.

3 0.3 Método de variación de las constantes Método de variación de las constantes Al igual que para las ecuaciones lineales utilizaremos el método de variación de las constantes para obtener una solución particular de los sistemas no homogéneos. Una vez sepamos cómo hacerlo, estaremos en condiciones de hallar las soluciones de los sistemas no homogéneos de coeficientes constantes porque para estos sistemas sabemos obtener sistemas fundamentales de soluciones del sistema homogéneo correspondiente. Recordemos que la solución general del sistema homogéneo x = Atx se puede escribir de la siguiente forma xt = Xtc, donde Xt es una matriz fundamental de soluciones y c un vector arbitrario de números reales constantes. El método de variación de las constantes consiste en buscar una solución particular del sistema no homogéneo x = Atx + bt de la forma x p t = Xtct, 0.2 donde se ha sustituído el vector de constantes c por un vector de funciones ct que se trata de determinar para que x p t sea solución del sistema no homogéneo. En lo que sigue haremos las operaciones necesarias para dar una expresión lo más explícita posible de ct y, a partir de ella, de xt. Antes de proceder debemos recordar que, como Xt es una matriz fundamental de soluciones, es invertible para todo t en el que At es continua y X t = AtXt. Ahora, lo que queremos es que el vector x p t = c tx t + c 2 tx 2 t + + c n x n t = Xtct 0.3 sea una solución del sistema 0.; i.e. del sistema x t = Atxt + bt. Ahora bien, para que el vector x p t sea una solución de 0. debe suceder que x pt = Atx p t + bt. 0.4 Pero para derivar un producto de matrices de funciones se procede como para derivar un producto de funciones respetando el orden de multiplicación. Como por 0.3 x p t = Xtct: x pt = X tct + Xtc t. Y como X t = AtXt, se tiene que Sustituyendo en 0.4 obtenemos x pt = AtXtct + Xtc t AtXtct + Xtc t = Atx p t + bt = AtXtct + bt

4 76 Sistemas no homogéneos y aplicaciones Por lo tanto, para que x p t dado por 0.3 sea una solución particular del sistema no homogéneo 0. basta que Xtc t = bt 0.5 Este es un sistema lineal de ecuaciones cuyos coeficientes e incógnitas son funciones, pero como la matriz de los coeficientes Xt es una matriz invertible siempre tiene solución: c t = Xt bt. Ahora basta integrar para calcular ct: ct = Xt bt dt. Esta expresión es análoga a la que obtuvimos para las ecuaciones lineales no homogéneas véase la ecuación 2.8 de la Lección 2. Ahora sólo tenemos que sustituir en 0.2 para encontrar una expresión de una solución particular de la ecuación no homogénea: x p t = Xtct = Xt Xt bt dt. 0.6 Obsérvese la anología, de nuevo, con la ecuación 2.9 de la Lección 2 para la solución particular de la ecuación lineal no homogénea. Una vez obtenida la expresión para x p t, de acuerdo con el Teorema 0., la solución general del sistema no homogéneo será xt = x h t + x p t = Xtc + Xt Xt bt dt 0.7 = Xt c + Xt bt dt. Nótese que Xt bt es un vector, y Xt bt dt es otro vector: aquel cuyas componentes se obtienen al integrar las componentes de Xt bt. Observaciones La expresión 0.7 es una fórmula cerrada para expresar la solución general de un sistema no homogéneo de ecuaciones diferenciales lineales. Desde un punto de vista teórico es muy interesante poder hacerlo de esta forma, pero no es muy práctico a la hora de calcular de forma explícita las soluciones. Ello es debido a la presencia de Xt, la inversa de la matriz fundamental de soluciones. El cálculo de esta inversa puede ser terriblemente costoso. Lo que se hace en la práctica es resolver el sistema 0.5 para calcular c t; y a continuación integrar esta expresión. Esta es la forma práctica de calcular Xt bt dt que, en realidad, es ct. El siguiente ejemplo puede servir para aclarar todo este proceso.

5 0.3 Método de variación de las constantes 77 Ejemplo Hallar la solución general del sistema x = 2x + 4x 2 + x 3 + e t x 2 = x + 3x 2 + x 3 + te t x 3 = x + e t Hallamos primero la solución general del sistema homogéneo, cuya matriz de coeficientes es y su polinomio característico det λ λ 3 0 λ A = Los valores propios son λ =, doble, y λ 2 =., = λ 3 λ 2 λ + = λ 2 λ +. Planteamos y resolvemos el sistema característico correspondiente al valor propio λ = : 3 4 v 3v 4v 2 v 3 = 0 I 3 Av = 0 2 v 2 = 0 v 2v 2 v 3 = 0 0 v 3 v + v 3 = 0 Siempre hay que comprobar que el determinante de la matriz λi A es cero con λ el valor propio que se esté considerando. En este caso puede no parecer inmediato que así es. 4 Un momento de observación nos permite ver que la segunda columna 2 de la matriz 0 I 3 A se obtiene al restar la primera a la tercera. Esto siginfica que la segunda columna es una combinación lineal de las otras dos y que, por lo tanto, deti 3 A = 0. Además hay varias submatrices de tamaño 2 2 que son no singulares. Una sencilla es la formada por las filas y columnas segunda y tercera: 2 0 Entonces rangi 3 A = 2 y podemos despejar v 2 y v 3 en función de v : v 3 = v y 2v 2 + v 3 = v v 3 = v, v 2 = v.

6 78 Sistemas no homogéneos y aplicaciones Conseguimos un vector propio asociado al valor propio λ = dando a v el valor, por ejemplo: v =. Una solución será x t = e λt v = e t. Como la dimesión del subespacio de soluciones es = 3 2 = n rangi 3 A y λ = es valor porpio de multiplicidad algebraica q = 2, debemos encontrar un vector propio generalizado. Para ello calculamos I 3 A 2 : I 3 A 2 = que obviamente tiene rango = n q = 3 2. Podemos encontrar una solución del sistema I 3 A 2 v = 0 que sea linealmente independiente de v. Es fácil ver que la solución general de este sistema es: v v. v 3 Debemos escoger un vector de esta forma que sea linealmente independiente con Una posible elección es 0 v 2 = 0. Con este vector conseguimos una segunda solución del sistema homogéneo:, x 2 t = e ta v 2 = = e t v 2 + ta Iv 2 = = e t 0 + t 2 0 = 0 t = e t t t.

7 0.3 Método de variación de las constantes 79 Finalmente, debemos calcular un vector propio asociado a λ 2 = : 4 v v 4v 2 v 3 = 0 I 3 Av = 0 4 v 2 = 0 v 4v 2 v 3 = 0 0 v 3 v v 3 = 0. Claramente rang I 3 A = 2 y una submatriz cuadrada de orden 2 con determinante distinto de cero es, de nuevo, la fomada por las dos últimas filas y columnas. Despejando v 2 y v 3 en función de v obtenemos que v 3 = v y v 2 = 0. Poniendo v = tenemos que el vector v 3 = 0 es un vector propio asociado a λ 2 =. La terecera solución será x 3 t = e t 0. Y una matriz fundamental de soluciones será Xt = e t te t e t x x 2 x 3 = e t te t 0. e t te t e t La solución general del sistema homogéneo será: x h t = Xtc = e t [c + c 2 t] + c 3 e t e t [c + c 2 t] e t [ c + c 2 t] + c 3 e t. Ya tenemos la solución general del sistema homogéneo y una matriz fundamental de soluciones. Una solución particular del sistema no homogéneo se puede obtener por el método de variación de las constantes: x p t = Xtct siendo ct la integral de la solución del sistema Xtc t = bt. Debemos resolver el siguiente sistema y luego integrar la solución: e t c t + te t c 2t + e t c 3t = e t Xtc t = bt e t c t + te t c 2t = te t e t c t + te t c 2t + e t c 3t = e t Restando a la primera ecuación la segunda obtenemos e t c 3t = e t te t c 3t = te 2t c 3 t = te 2t dt

8 80 Sistemas no homogéneos y aplicaciones Integrando por partes c 3 t = t e 2t. 4 Sumando las ecuaciones primera y tercera: e t c 2t + 2e t c 3t = 2e t c 2t + 2 t = 2 c 2t = 2t c 2 t = t 2. Sustituyendo las expresiones obtenidas en la segunda ecuación: e t c t + 2t 2 e t = te t c t = t 2t 2 c t = 2 3 t3 + 2 t2. Entonces la solución particular del sistema no homogéneo es e t [c t + c 2 tt] + c 3 te t x p t = Xtct = e t [c t + c 2 tt] = e t [ c t + c 2 t t] + c 3 te t Y la solución general: xt = x h t + x p t = t 3 + t2 t t3 3 + t2 2 e t 5t t2 2 t c + c 2 t + 3 t + t2 + t3 e t + c e t c + c 2 t + t2 + t3 e t 2 3 c + c 2 t + 3 t + 3t2 + 5t e t + c 3 e t Volvamos a escribir la expresión de la solución general del sistema no homogéneo de ecuaciones diferenciales lineales 0.7: xt = Xt c + Xt bt dt. En el caso particular en que el sistema sea de coeficientes constantes: x = Ax + bt sabemos que una matriz fundamental de soluciones es Xt = e ta. Además sabemos también que la inversa de e ta es e ta ver 9.4 en la Lección 9. Así pues, en este caso, podemos escribir la solución como sigue: xt = e c ta + e ta bt dt. 0.8 Esta expresión es útil en aquellas situaciones en las que, por un medio u otro, podamos calcular de forma explícita la exponencial de ta. Por ejemplo, cuando A tiene un único valor propio, la Proposición 9.7 de la Lección 9 nos proporciona una forma explícita de calcular e ta. No obstante, en los ejercicios, procederemos siempre como en el ejemplo de más arriba.. e t e t.

9 0.3 Método de variación de las constantes El Problema de condiciones iniciales Tal y como vimos en la Lección 8, el Problema de condiciones iniciales para un sistema lineal de dimensión n, que escribiremos, { x = Ax + bt xt 0 = x 0 se resuelve de forma similar a como hacíamos para las ecuaciones lineales. Tenemos dos opciones: a Hallar la constante de la solución general mediante sustitución de la condición inicial en la misma, o b Usar una expresión cerrada para la solución de dicho problema. La primera opción ya la hemos utilizado en numerosas ocasiones: una vez obtenida la solución general xt, que depende de un vector de constantes arbitrarias c, se sustituye la condición inicial xt 0 = x 0 y se resuelve el sistema algebraico lineal correspondiente. Una vez obtenida la constante, se sustituye en la solución general obteniendo la solución particular que satisface la condición inicial dada. Este es el método habitual para sistemas y el que usaremos en el ejemplo de más abajo. Existe, no obstante, una forma de expresar la solución del problema de condiciones iniciales similar a la que obtuvimos para las ecuaciones lineales ver la Sección 2.4, Lección 2: t xt = e t t 0A x 0 + e t0 sa bs ds 0.9 t 0 Desde luego una función vectorial como la de 0.9 es solución de la ecuación x = Ax + bt porque es una forma particular de la solución general 0.8. Además es inmediato que xt 0 = e 0 x 0 = I n x 0 = x 0, por lo que también se cumple la condición inicial. Como siempre, en el caso de los sistemas, las expresiones cerradas tienen un mayor interés teórico que práctico, salvo que se disponga de un procedimiento rápido para hallar la exponencial de una matriz. a Nótese que si el sistema es homogéneo bs = 0 entonces la expresión 0.9 se reduce xt = e t t 0A x 0, que es la expresión que encontramos en la Propiosición 9.3 en la Lección 9.

10 82 Sistemas no homogéneos y aplicaciones Ejemplo Hallar la solución del siguiente problema de condiciones iniciales: 4 4 x = 0 8 x0 = 2 Calculamos, en primer lugar, el polinomio característico de A = λ det 0 λ 8 = λ 2 4λ Las raíces de este polinomio son λ = 2 + 2i y λ 2 = 2 2i. Por lo tanto los valores propios de A son números complejos conjugados. Buscamos un vector propio para el valor propio 2 + 2i: 2+2iI 2 Av = i i v v 2 = 0 0 { 6 + 2iv 4v 2 = 0 0v iv 2 = 0. 0 Multiplicamos la primera ecuación por y se la sumamos a la segunda. Con esto 6 + 2i anulamos la segunda ecuación, lo que demuestra que la segunda ecuación es combinación lineal de la primera y que rang2 + 2iI 2 A =. Además el nuevo sistema, equivalente, se reduce a una ecuación 6 + 2iv 4v 2 = 0 la otra es 0=0. Por lo tanto v 2 = 3 + 2i v. 2 Un vector propio de A asociado al valor propio 2+2i se obtiene dando cualquier valor distinto de cero a v. En particular poniendo v = 2 tenemos que v = = + i 3 + i 3 es un vector propio de A asociado al valor propio 2 + 2i. Una solución compleja del sistema será: 2 0 xt = e 2+2it v = e 2t cos2t + i sen2t + i 3 Dos soluciones reales linealmente independientes son la parte real y la parte imaginaria de esta solución. Las calculamos. Ponemos v = v + iv 2. Así xt = e 2t cos2t + i sen2tv + iv 2 = = e 2t [cos2tv sen2tv 2 + icos2tv 2 + sen2tv ].

11 0.3 Método de variación de las constantes 83 Por lo tanto y x t = e 2t cos2tv sen2tv 2 = e 2t 2 cos2t, 3 cos2t sen2t x 2 t = e 2t cos2tv 2 + sen2tv = e 2t 2 sen2t. 3 sen2t + cos2t Una matriz fundamental de soluciones en este caso es Xt = e 2t 2 cos2t 2 sen2t 3 cos2t sen2t 3 sen2t + cos2t Y la solución general del sistema: xt = Xtc = e 2t 2 cos2t 2 sen2t c. 3 cos2t sen2t 3 sen2t + cos2t c 2 Para calcular la solución que verifica la condición inicial x0 = planteamos el sistema: 2 X0c = x0 e cos2 0 2 sen2 0 c = 3 cos2 0 sen2 0 3 sen2 0 + cos2 0 2 Es decir, c c 2 = 2 { 2c = 3c + c 2 = 2. Por lo tanto, c = /2 y c 2 = /2. La solución del problema de condiciones iniciales será: xt = e 2t 2 cos2t 2 sen2t /2 cos2t + sen2t = e 2t 3 cos2t sen2t 3 sen2t + cos2t /2 2 cos2t + sen2t Escrito en función de las componentes: x t = e 2t cos2t + sen2t x 2 t = e 2t 2 cos2t + sen2t.. c 2. Para finalizar, utilizamos la expresión 0.9 para escribir la solución del siguiente tipo especial de sistema lineales no homogéneos: { x = Ax + But x0 = x 0. donde B es una matriz de tamaño n m y ut es una función vectorial de m componentes. A este tipo de sistemas se les llama sistemas dinámicos lineales o sistemas lineales de control.

12 84 Sistemas no homogéneos y aplicaciones El significado de este terminología se explicará en un curso posterior. En este caso el término no homogéneo es el vector bt = But cuyas componentes son combinaciones lineales de las funciones que componen el vector ut, que se conoce con el nombre de vector de controles o entradas. De acuerdo con 0.9 la solución general de este problema de condiciones iniciales será nótese que t 0 = 0 t xt = e x ta 0 + e sa Bus ds = = e ta x 0 + t 0 0 e t sa Bus ds. Este tipo de sistemas aparece en numerosas aplicaciones y su estudio constituye toda una rama de las matemáticas y la ingeniería Aplicaciones de los Sistemas de Ecuaciones Diferenciales Cinética Química Comenzamos la Lección 8 de introducción alos sistemas de ecuaciones con un problema de cinética química que daba lugar a un sistema de ecuaciones diferenciales en las concentraciones de los reactantes y productos que no era lineal. No le podemos aplicar, en consecuencia, las técnicas que hemos desarrollado en este capítulo. En una próxima lección estudiaremos un poco los sistemas no lineales. Sin embargo hay reacciones químicas que sí se pueden modelizar mediante sistemas lineales. Tal es el caso de la siguiente ecuación estequiométrica: A + B k k 2 En estas ecuaciones k es la constante de velocidad de la reacción A+B C, k 2 la constante de velocidad de reacción A + B C y k 3 la de C D. De acuerdo con lo que ya vimos en la Lección 4, la variación de las concentraciones de las sustancias presentes en estas reacciones responde al siguiente sistema de ecuaciones diferenciales: { d[a] = k [A] α [B] β + k 2 [C] γ dt d[c] dt = d[b] dt C k 3 D = k [A] α [B] β k 2 [C] γ k 3 [C] δ donde α, β y γ son los órdenes de reacción de las sustancias A, B y C, respectivamente en la primera reacción A + B C y δ es el orden de reacción respecto de C en la segunda C D.

13 0.4 Aplicaciones de los Sistemas de Ecuaciones Diferenciales 85 En particular para una reacción simple, de primer orden respecto de todas las sustancias, del tipo A k B k 2 el sistema de ecuaciones diferenciales que lo rige sería: C { d[a] dt d[b] dt = k [A] = k [A] k 2 [B] Supongamos además que las concentraciones iniciales, para t = 0, de las sustancias son [A] 0 = a y, lógicamente, [B] 0 = [C] 0 = 0. Entonces si xt e yt representan las concentración de las sustancias A y B que han reaccionado después de t minutos, tenemos que [A] = a xt, [B] = yt. Además, como no hay ni entradas ni salidas, la suma de las concentraciones de las tres sustancias se mantiene constantemente igual a a. Así [C] = xt yt, y el sistema de ecuaciones queda: { da x dt = k a x dy dt = k a x k 2 y { z = k z y = k z k 2 y donde hemos hecho la sustitución zt = a xt. De hecho zt es la concentración de la sustancia A después de t minutos. Además, las condiciones iniciales son a = [A] 0 = a x0 = z0 y y0 = 0. En realidad no es necesraio emplear las técnicas para la resolución de sistemas. Podríamos resolver la primera de estas dos ecuaciones que es en variables separables para calcular zt. Y una vez obtenida esta función sustituir su valor en la segunda ecuación. La ecuación resultante sería una ecuación lineal no homogénea de primer orden, que se integraría por el método habitual. Sin embargo, como práctica de lo estudiado en este capítulo resolveremos el sistema utilizando las técnicas expuestas en el mismo. La matriz del sistema es k 0 A = k k 2 y su polinomio característico pλ = λ + k λ + k 2, cuyas raíces son λ = k y λ 2 = k 2. Estas raíces pueden ser repetidas o no según que k = k 2 o k k 2, respectivamente. Si k = k 2 entonces un vector propio de A asociado a la raíz doble k es 0 v =, y un vector propio generalizado sería v 2 = k 0

14 86 Sistemas no homogéneos y aplicaciones Así un vector solución del sistema de ecuaciones diferenciales es 0 x t = e kt v = k e k t. Y el otro e k t x 2 t = e ta v 2 = = e kt v 2 + ta + k I 2 v 2 = = e k t 0 + t = 0 k t k t La solución general del sistema es: zt = yt a 2 e k t a + a 2 tk e k t Imponemos ahora las condiciones iniciales: z0 = a, y0 = 0: a 0 = a2 Entonces a 2 = a y a = 0, y la solución del Problema de Condiciones iniciales es: a zt = ae k t yt = ak te k t Si k k 2 debemos encontrar vectores propios asociados a los valores propios λ = k y λ 2 = k 2. Para el primero debemos resolver el sistema 0 0 v 0 = k k 2 k v 2 0 Una solución es k2 k v = k Resolviendo el sistema k k 2 0 k 0 obtenemos el vector v 2 = v 0 v 2 = 0 0

15 0.4 Aplicaciones de los Sistemas de Ecuaciones Diferenciales 87 que es un vector propio asociado a λ 2 = k 2. La solución general del sistema en este caso será: zt = a yt e kt v + a 2 e kt v 2 = = a k 2 k e k t a k e k t + a 2 e k 2t Imponemos las condiciones iniciales z0 = a, y0 = 0: a a k = 2 k 0 a k + a 2 de donde obtenemos: a a = a 2 = ak k 2 k k k 2 por lo que la solución del Problema de condiciones iniales es: zt = ae k t yt = ak k 2 k e k t e k 2t Y la solución del problema; es decir, la concentración de cada sustancia presente después de t minutos es: [A] = [A] 0 e k t [B] = [A] 0 k k 2 k e k t e k 2t si k k 2 [A] 0 k te k t si k = k 2 [C] = [A] 0 [A] [B] La Figura 0. ilustra los tres tipos de comportamientos exhibidos por el sistema. En todos los casos se ha tomado [A] 0 = y k = en unidades apropiadas. La primera figura, con k 2 = 0, muestra el comportamineto del sistema para valores de k muy pequeños en comparación con los de k 2. En este caso la cantidad de la sustancia intermedia B es, a lo largo de todo el tiempo de reacción, pequeña respecto de A y C. En efecto, al ser la constante de velocidad de la segunda reacción mucho mayor que la primera, la sustancia B se convierte rápidamente en la sustancia C, mientras que la formación de B a partir de A es lenta. Por el contrario, la figura c muestra el comportamineto cuando k es 0 veces mayor que k 2. Se observa que la cantidad de B es grande relativamente a la de C debido a que el proceso B C es lento. En este caso B sólo comienza a decrecer cuando se empieza a agotar la cantidad de sustancia A.

16 88 Sistemas no homogéneos y aplicaciones C A C A B B A B C a k =, k = 0 b k = k = c k =, k = Figura 0.: Comparativa de la evolución de las sustancias en A B C Balance de materia Al igual que para ecuaciones también se pueden presentar problemas sobre balances de materia que dan lugar a sistemas de ecuaciones lineales. El siguiente es un ejemplo típico. Ejemplo Dos tanques están conectados como se muestra en la Figura 0.2. Inicialmente en el depósito B hay Kgr. de sal disuelto y en el tanque A sólo hay agua. En ese mismo instante se comienza a bombear una disolución de agua y sal con un caudal de 4 l./min. y una concentración de 30 gr./l. al tanque A. La disolución circula entre los tanques y hacia el exterior de acuerdo a los datos de la Figura 0.2, y se supone que se encuentra uniformemente distribuída. a Halla la concentración de sal en cada tanque en cualquier instante. b Cuándo será máxima y mínima la concentración en el tanque A? Y en el tanque B? c Prueba que la concentración de los dos tanques tiende a equilibrarse. Es decir, la concentración límite, cuando t +, en ambos tanques es la misma. Solución.- La forma de solucionar este tipo de problemas consiste en realizar un balance de materia Acumulación = Entradas-Salidas+Generación para cada depósito. En este caso no hay generación de materia; así que si designemos con los símbolos c A t y c B t las funciones que nos proporcionan las concentraciones en los tanques A y B a lo largo del tiempo:

17 0.4 Aplicaciones de los Sistemas de Ecuaciones Diferenciales 89 4 l./min. 3 l./min. 30 gr./l. A 00 l. B 00 l. 2 l./min. 2 l./min. l./min. Figura 0.2: Entrada en A: ṁ ea = 30 gr./l. 4 l./min. +c B gr./l. l./min. = 20 + c B gr./min. Salida del tanque A: ṁ sa = 5 l./min.c A gr./l. = 5c A gr./min. Acumulación en el tanque A= dc AV = V c dt A = 00c A Entrada en el tanque B: ṁ eb = 3 l./min. c A gr./l. = 3c A gr./min. Salida del tanque B: ṁ sb = 3 l./min. c B gr./l. = 3c B gr./min. Acumulación en el tanque B= dc BV = V c dt B = 00c B Concentración inicial en A: c A 0 = 0 gr./l. Concentración inicial en B: c B 0 = 000 gr./00 l.= 0 gr./l. El balance de materia en cada tanque da lugar a un sistema lineal de ecuaciones diferenciales de primer orden: { dca V dt dc B V dt = ṁ ea ṁ sa = ṁ eb ṁ sb En este caso concreto el sistema es: { 00c A = 20 + c B 5c A 00c B = 3c A 3c B c A = 5 00 c A + 00 c B c B = 3 00 c A 3 00 c B con una condición inicial: c A 0 = 0, c B 0 = 0. Se trata de un sistema no homogéneo. Buscamos primero la solución general del sistema homogéneo La matriz del sistema es A = 3 3. Ponemos B = 00A. Si λ es valor propio λ de B con v como vector propio, entonces es el correspondiente valor propio de A con el 00 mismo vector propio v. Calculamos, entonces, los valores propios de B: λ + 5 det = λ 2 + 8λ + 2 = λ + 6λ λ + 3

18 90 Sistemas no homogéneos y aplicaciones Así pues, los valores propios de B son λ = 2 y λ 2 = 6, y los de A: λ = 2 00 y λ 2 = Calculamos un vector propio para cada valor propio. Empezamos con λ = 2. Debemos resolver el sistema λ I 2 Bv = 0 3 v 0 = 3v v 2 = 0 3 v 2 0 3v + v 2 = 0 v 2 = 3v. Escogiendo v =, un vector propio asociado al valor propio λ = 2 es q =. Y la 3 solución correspondiente recordemos que los vectores propios de A y B son los mismos : x t = e 2 00 t 3 = e 2 00 t 3e 2 00 t. Procedemos de la misma forma con λ 2 = 6: v 0 = v v 2 = v 3v 2 = 0 v 2 = v. v 2 Escogiendo v =, un vector propio asociado al valor propio λ = 6 es q 2 = solución correspondiente: x 2 t = e 6 00 e t 6 00 = t. e 6 00 t. Y la La solución general del sistema homogéneo será: c e x h t = 2 00 t + c 2 e 6 00 t 3c e 2 00 t c 2 e 6 00 t con c y c 2 constantes arbitrarias. Calculamos una solución del sistema no homogéneo por el método de variación de las constantes: x p t = c tx t + c 2 tx 2 t, siendo c t y c 2 t las funciones que se obtienen integrando las soluciones del siguiente sistema: Sumando a la segunda ecuación la primera: c te 2 00 t + c 2te 6 00 t = c te 2 00 t c 2te 6 00 t = 0 4c te 2 00 t = c t = e 2 00 t c t = 5e 2 00 t.

19 0.4 Aplicaciones de los Sistemas de Ecuaciones Diferenciales 9 Y multiplicando la segunda ecuación por y sumando al resultado 3 veces la primera ecuación: 4c 2te 6 00 t = c 2t = e 6 00 t c 2 t = 5e 6 00 t Así que x p t = c tx t + c 2 tx 2 t = 5e 2 00 e t 2 00 t + 5e 6 3e 2 00 t 00 e t 6 00 t 30 =. e 6 00 t 30 La solución general del sistema no homogéneo será c e xt = 2 00 t + c 2 e 6 00 t c e 2 00 t c 2 e 6 00 t + 30 Imponemos ahora la condición inicial c A = 0, c B = 0: 0 c + c = x0 = c + c 2 = c c c c 2 = 20 c = 2 5, c 2 = 7 5. La concentración en cada tanque en cada instante será c A t = 2 5e 2 00 t 7 5e 6 00 t + 30 c B t = 37 5e 2 00 t + 7 5e 6 00 t + 30 b Tanto e 2 00 t como e 6 00 t son funciones decrecientes para todo t, por lo que c A t = 2 5e 2 00 t 7 5e 6 00 t + 30 es una función creciente siempre. En consecuencia la concentración en el tanque A será mínima en el instante inicial y nunca será máxima, aunque se acerca asintóticamente a 30 gr./l.. Esto es exactamente lo que nos dice el planteamiento del problema: inicialmente en A no hay sal y en cuanto se abren los grifos empieza a haberla. Y cada vez hay más sal, proviniente del exterior y de B. Así que la concentración mínima es en el instante inicial que es c A 0 = 0 y nunca hay un valor máximo de sal aunque siempre c A t < 30. Para el tanque B la situación es muy diferente. Podemos pensar de dos maneras. La primera formalmente. Para calcular el mínimo de una función derivable, hallamos su primera derivada, la igualamos a cero y sustituímos el valor en la segunda para comprobar que ésta es positiva: c 75 B t = 00 t t = 0 e 4 00 t = 75 Y 4 00 c Bt = e 2 00 e 6 75 t = ln 05 t = 25 ln 7505 = e 00 t e t c B8 48 = > 0.

20 92 Sistemas no homogéneos y aplicaciones Por lo tanto, la concentración en el tanque B es mínima en el instante t = 8 48 min., y no tiene máximo porque c B t sólo se anula en un punto. A partir de t = 8 48 la concentración de B crece indefinidamente acercándose cada vez más a 30 gr./l.. La segunda forma de pensar es más intuitiva: inicialmente en B hay sal y en A no. Cuando comienza el intercambio entre los depósitos de A y B, y dependiendo de los caudales de intercambio y la concentración de sal que entra en A desde el exterior, puede suceder que la concentración de sal en B disminuya. Si lo hace, lo hará hasta que las concentraciones de A y B coincidan, y a partir de ese intante ambas concentraciones aumentarán de la misma manera. Es decir, la concentración en B será mínima cuando c A = c B. Teniendo en cuenta que la segunda ecuación del sistema es c B = 3c A 3c B, esto significa exactamente que c B t = 0. De ahí que imponiendo la condición c At = c B t obtenemos también que en t = 8 48 min. se alcanza la mínima concentración en B. c De las expresiones de c A t y c B t sale que lím c At = lím c Bt = 30, t + t + límite que ya se ha utilizado en el apartado anterior. La Figura 0.3 muestra las gráficas de la evolución de la concentración en cada depósito. En ellas se aprecian las propiedades que hemos venido estudiando en los apartados anteriores c A t c B t Figura 0.3: Gráficas de las soluciones del sistema que modeliza la evolución de las concentraciones en los dos tanques