LAS NOCIONES DE VECINDAD Y DE ENTORNO EN LA COMPRENSIÓN DE LOS NÚMEROS REALES
|
|
|
- Sergio Álvarez Ojeda
- hace 7 años
- Vistas:
Transcripción
1 LAS NOCIONES DE VECINDAD Y DE ENTORNO EN LA COMPRENSIÓN DE LOS NÚMEROS REALES RESUMEN. Maribel Anacona. Universidad del Valle, Colombia Luis Carlos Arboleda. Universidad del Valle, Colombia Javier Pérez Fernández. Universidad de Cádiz, España La problemática alrededor de la enseñanza de los números reales es un tema de gran sensibilidad en la comunidad educativa a nivel internacional. Las presentaciones axiomáticas, frecuentes en los textos de cálculo y análisis, generalmente ocultan la intervención de conceptos de naturaleza topológica esenciales en la construcción de los reales. El propósito de esta comunicación es mostrar, a partir de la construcción de los reales del grupo Bourbaki, que las nociones de vecindad y entorno proveen a través de las estructuras topológicas y uniformes, condiciones abstractas que favorecen la intuición y dotan de sentido los conceptos de continuidad, convergencia y completez, claves en la constitución de los reales. Nivel educativo: Bachillerato, Universidad. 1. INTRODUCCIÓN. Es indudable la importancia que tiene en la formación matemática de los estudiantes de Matemáticas y de Licenciatura en Matemáticas, la comprensión de las propiedades fundamentales de los números reales (R). Sin embargo, R se presenta generalmente, como un conjunto de números que satisface los axiomas de una estructura de cuerpo más el axioma de completitud. Este último axioma contiene la esencia del continuo numérico, pero su presentación axiomática no deja ver fácilmente cuáles son las propiedades topológicas que diferencian a R del conjunto Q de los números racionales. De ahí la importancia de estudiar algunas de las construcciones y tratar de identificar en el proceso mismo de elaboración, algunos de los conceptos esenciales que caracterizan a R. Por esta razón, consideramos de utilidad que el docente reconozca el grado de complejidad que se sintetiza y se oculta detrás de las presentaciones axiomáticas, y pueda identificar en el marco de una reflexión histórico-epistemológica algunas de las dificultades inherentes a su enseñanza. La construcción de los reales realizada por el grupo Bourbaki, ofrece algunos elementos conceptuales que sirven de sustento para una reflexión educativa a nivel de la formación secundaria y universitaria. Intentamos mostrar que desde el nivel de abstracción y generalidad, característico de la práctica matemática de Bourbaki, es posible identificar el papel que desempeñan ciertos conceptos en la constitución de R; lo cual es difícil de observar desde espacios muy particulares. Iniciamos con una presentación muy esquemática de la construcción de los reales por el grupo Bourbaki, en la que no nos interesan los detalles técnicos, sino el proceso lógico de construcción; de tal manera que podamos identificar los pasos y conceptos esenciales que lo conforman. Luego, haremos un análisis 1 de 7
2 epistemológico del rol que juegan en dicha construcción las nociones de vecindad y entorno. 2. LOS REALES DE BOURBAKI La construcción de los números reales por Bourbaki es una generalización de la construcción de los reales por Cantor. Mientras Cantor completa el cuerpo Q de los racionales, Bourbaki completa el grupo topológico Q dotado de una estructura uniforme. En ambos procesos se requiere del concepto de convergencia. Mientras en Cantor se trata de la convergencia de sucesiones de Cauchy de números racionales, en Bourbaki se trata de la convergencia de filtros de Cauchy. 2.1 LOS PASOS EN LA CONSTRUCCIÓN Bourbaki parte de la consideración de Q como grupo aditivo, en el cual se define una relación de orden compatible con la estructura de grupo. Es decir, una relación que verifique la siguiente condición: x y x + z y + z, z Q. Esto significa que el orden es invariante bajo traslación. Tenemos entonces los racionales con las estructuras de grupo y de orden compatibles entre sí. En símbolos: Q, +,. Con esta relación de orden, Bourbaki define sobre Q una topología compatible con su estructura de grupo aditivo, a través de un sistema fundamental de vecindades alrededor del origen, que identificamos por τ = {(-a, a): a Q + }. Con la introducción de la topología Bourbaki está garantizando el tratamiento matemático de todos los conceptos relacionados con la noción de proximidad a un punto fijo, tales como continuidad puntual, filtro y convergencia, claves en la construcción de los reales. Que esta topología sea compatible con la estructura de grupo aditivo significa que la función suma f: Q Q Q definida como f (x, y)=x + y es continua en Q Q; y que la función opuesto g: Q Q definida como g(x)=-x es también continua en Q. De esta forma Q, +,, τ se constituye en el espacio topológico de la recta racional. Posteriormente, Bourbaki define una estructura uniforme sobre el grupo topológico Q, a través del sistema fundamental de entornos: U = {Ua: a Q + }, donde Ua = {(x, y) Q Q: x y <a, a Q + }. Estos entornos formalizan la noción de cercanía entre dos puntos cualesquiera del espacio. Con ellos podemos expresar formalmente la idea de que x 1 está tan cerca de x 2 como y 1 lo está de y 2. Con la introducción de las estructuras uniformes Bourbaki garantiza el tratamiento de los conceptos relacionados con la cercanía entre puntos dos a dos, tales como continuidad uniforme, filtros de Cauchy y convergencia de filtros de Cauchy; conceptos esenciales en la construcción de los reales. Las estructuras uniformes son una generalización de la noción de distancia y dotan de una especie de seudométrica a los espacios topológicos. Un espacio uniforme tiene por tanto una estructura más débil que una estructura métrica, pero más rica que una estructura topológica. En símbolos, se tiene el espacio topológico uniforme Q, +,, τ, U. Una vez Q está dotado de estas dos estructuras, Bourbaki completa el conjunto Q, a través de los filtros minimales de Cauchy; y finalmente extiende 2 de 7
3 las propiedades algebraicas de grupo a cuerpo, para obtener el cuerpo completo R. El esquema de la construcción se presenta en la siguiente figura. Figura 1. Esquema de la construcción de los reales por Bourbaki Bourbaki cuando define una topología sobre Q compatible con su estructura de grupo aditivo, establece como punto de partida un dominio de magnitudes topológicas (la topología al mismo nivel del álgebra y el orden), que posteriormente completa a través de la estructura uniforme; sólo al final hace la extensión algebraica de grupo a cuerpo. De esta forma, la topología se constituye en un requisito epistemológico para la construcción, a diferencia de las construcciones clásicas, en las que la topología se agrega sólo al final. Otro momento clave lo constituye el ingreso de las estructuras uniformes, que permiten dotar al espacio topológico Q de una especie de seudométrica, clave en el proceso de completación. Este aspecto también es novedoso en la propuesta de Bourbaki, puesto que en las construcciones clásicas, se parte de Q como espacio métrico, lo cual hace innecesario la presencia de las estructuras uniformes. A continuación presentamos los conceptos que Bourbaki requiere en la construcción de los reales y que permite comprender el ingreso de las estructuras topológicas y uniformes. 2.2 LOS CONCEPTOS CLAVES EN LA CONSTRUCCIÓN Recordemos que la noción de vecindad captura la noción de cercanía en un espacio abstracto. En un espacio topológico, podemos hablar legítimamente de los puntos de un espacio que están cercanos a un punto dado, o que son vecinos de un punto fijo. Esta noción es clave para establecer, por ejemplo, la continuidad puntual de una función definida entre espacios topológicos. Sabemos que en este tipo de funciones, las imágenes de los puntos cercanos a un punto dado, están cerca a la imagen del punto. Una noción de suma importancia que introduce Bourbaki es la de filtro, la cual fue definida por Henri Cartan (Cartan 1937) en las tempranas épocas del grupo. Los filtros constituyen una generalización de la noción de sucesión. Ellos son 3 de 7
4 empleados en espacios en los que no se verifica ningún axioma de numerabilidad y dónde la topología del espacio no hace referencia a ninguna métrica. Junto con la noción de filtro está la definición de límite de un filtro: un filtro F converge a un punto x, si cualquier vecindad (por pequeña que sea) que se tome alrededor del punto x pertenece al filtro F. Los conceptos de filtro y límite de filtro, equivalen a los conceptos de sucesión y convergencia de una sucesión, en espacios completamente abstractos. Un papel análogo al que desempeña la noción de vecindad en los espacios topológicos, lo desempeña la noción de entorno en los espacios uniformes. Fue André Weil quien en 1936 introdujo la noción de espacio uniforme, a través de la formalización de los entornos (Dugac 1984). Los entornos capturan la noción de cercanía dos a dos, permiten formalizar la idea de que x 1 está tan cerca de x 2 como y 1 lo está de y 2. Esto no es posible en un espacio topológico, pues la noción de vecindad sólo permite establecer que x 1 está tan cerca de x como x 2 lo está de x. Un entorno sobre los números racionales está dado por el siguiente conjunto: U a = {(x, y) Q Q: x y <a}, donde a Q +. Q a U a Q Figura 2. Un entorno sobre los racionales El conjunto B = {U a ; a Q + } constituye un sistema fundamental de entornos de la estructura uniforme del grupo aditivo Q de la recta racional. Con el ingreso de las estructuras uniformes, Bourbaki puede definir otros conceptos que son sustanciales en la construcción de los reales, tales como filtros de Cauchy y convergencia de filtros de Cauchy. Un filtro de Cauchy es un filtro que contiene puntos muy cercanos dos a dos. Los elementos minimales (por la relación de inclusión) del conjunto de filtros de Cauchy sobre un espacio uniforme son llamados filtros minimales de Cauchy. Ellos desempeñan el rol de representantes de la clase de equivalencia de los filtros de Cauchy que convergen a un punto dado. Así como en los espacios métricos se tiene que toda sucesión convergente es de Cauchy, en los espacios uniformes se tiene que todo filtro convergente es un filtro de Cauchy. Pero la recíproca sólo se verifica en los espacios completos. Un espacio completo es un espacio uniforme en el que todo filtro de Cauchy converge. Bourbaki finalmente muestra que el conjunto Q * formado por todos los filtros minimales de Cauchy sobre Q, es completo. Se trata de la misma construcción de Cantor, pero a un nivel más alto de abstracción y generalidad. Si bien para Cantor, los reales son clases de 4 de 7
5 equivalencia de sucesiones de racionales de Cauchy, para Bourbaki los números reales son para Bourbaki filtros minimales de Cauchy. Una vez hemos esbozado algunos aspectos centrales de la construcción de Bourbaki, nos detenemos a analizar el papel que juegan las nociones de vecindad y de entorno en el proceso mismo de comprensión de los reales. 3. LAS NOCIONES DE VECINDAD Y DE ENTORNO EN LA CONSTRUCCIÓN DE LOS REALES En primer lugar, nos referimos a la noción de vecindad formalizada a través de las estructuras topológicas y al papel que juega en la definición de las propiedades abstractas de continuidad puntual de una función y de convergencia de filtros, ambos esenciales en la construcción de R. La definición formal de continuidad puntual de una función definida en espacios topológicos es la siguiente (Bourbaki 1965, p. 24): Se dice que una aplicación f de un espacio topológico X en un espacio topológico X es continua es un punto x o X si, cualquiera que sea la vecindad V de f(x o ) en X, existe una vecindad V de x o en X tal que la relación x V implica que f(x) V. V X f X. x o. f(x o ) V Figura 3. Continuidad puntual de una función definida entre espacios topológicos Intuitivamente decimos que una función es continua en un punto x o, si f(x) está tan cerca como se quiera de f(x o ), siempre que x esté muy cerca de x o. Es decir, si las imágenes de los puntos cercanos a x o están cerca de f(x o ). Esta definición muestra que la noción de vecindad está en la base de la noción de continuidad. Es importante resaltar aquí que, el hecho de pasar a un nivel más alto de abstracción y generalidad no significa necesariamente mayor dificultad de comprensión. Por el contrario, consideramos que la definición de continuidad en espacios topológicos resulta incluso más intuitiva que la expresada en términos de ε y δ, cuando se define tradicionalmente la continuidad puntual en una función de R en R. La noción vecindad también es clave en la definición de límite de un filtro. Recordemos que un filtro F converge a un punto x, si cualquier vecindad (por pequeña que sea) que se tome alrededor del punto x pertenece al filtro F. En esta definición se ve claramente que el asunto de la convergencia está relacionado con la cercanía a un punto dado. Sin embargo, la noción de vecindad no es suficiente para definir otros conceptos fundamentales como continuidad uniforme, filtros de Cauchy y convergencia de filtros de Cauchy. 5 de 7
6 La definición formal de continuidad uniforme de una función definida en espacios uniformes es la siguiente (Bourbaki 1965, p.187): Una aplicación f de un espacio uniforme X en un espacio uniforme X, es uniformemente continua si, para cada entorno V de X, existe un entorno V de X tal que la relación (x, y) V implica (f (x), f (y)) V. X f V X V (x, y) (f(x), f (y)) X X Figura 4. Continuidad uniforme de una función definida entre espacios uniformes Intuitivamente decimos que una función f es uniformemente continua si f(x) y f(y) están tan cerca como se quiera, siempre que x y y estén muy cerca. Obsérvese que la noción de cercanía que se requiere es distinta a la ofrecida por una vecindad. En la continuidad uniforme no se mira la función en torno a un punto fijo, sino que los puntos se comparan dos a dos. De ahí la necesidad de definir, las estructuras uniformes, que dan legitimidad conceptual a la noción de entorno, la cual captura la cercanía dos a dos. De igual forma la noción de entorno está en la base de la definición de filtro de Cauchy. Tal como habíamos mencionado, un filtro de Cauchy es un filtro que contiene conjuntos muy pequeños ; es decir, un filtro que contiene puntos muy cercanos dos a dos. Los filtros de Cauchy para Bourbaki, al igual que las sucesiones de Cauchy para Cantor, desempeñan un papel fundamental en la construcción de los reales. Recordemos que los reales son finalmente para Bourbaki, filtros minimales de Cauchy. 4. CONCLUSIONES Las nociones de vecindad y de entorno juegan un papel fundamental en la definición de conceptos claves en la construcción de los reales por Bourbaki, tales como continuidad, continuidad uniforme, filtros, filtros de Cauchy, convergencia de filtros y convergencia de filtros de Cauchy. Ellas brindan legitimidad matemática a la noción de cercanía. Si bien la noción de vecindad nos habla de los puntos vecinos o cercanos a un punto dado; la noción de entorno hace lo propio con puntos comparados dos a dos. A pesar de su importancia en la construcción de los reales, ellas no aparecen frecuentemente y de manera explícita en las construcciones de R. La razón fundamental es que no es fácil evidenciar su necesidad conceptual en espacios particulares como Q o el mismo R. En estos espacios la cercanía está garantizada por la noción de distancia, y en los espacios métricos no se requiere de las nociones de vecindad y de entorno. Precisamente ellos surgen como respuesta matemática al problema de dotar de una noción de cercanía a los espacios más abstractos y generales (Arboleda 1980). 6 de 7
7 Es así como la construcción de los reales por Bourbaki, ofrece un escenario muy interesante de explorar puesto que los conceptos se presentan en un alto nivel de generalidad; y desde allí podemos ver algunas nociones básicas que se mimetizan en las particularidades de los espacios más familiares. Para Bourbaki entre más abstractos se presentan los conceptos, más se fortalece la intuición de los mismos, porque la abstracción elimina todo esto que es contingente en una teoría (Bourbaki 1962). Esto significa que entre más abstracto sea el concepto, hay menos factores adicionales que pueden confundir la intuición del mismo. En un nivel más alto de abstracción, la intuición es más apropiada pues existen menos posibilidades de equivocación. Es una razón más para entender en un sentido amplio la propuesta de Bourbaki, en la que se llevan y se presentan los conceptos en su más alto grado de abstracción y generalidad. En el programa de axiomatización estructural de los Bourbaki, simplicidad en la presentación formal de las teorías se identifica con economía de pensamiento. Las estructuras y sistemas axiomáticos expresan de la manera más general propiedades simples de distintas teorías particulares. Las formas de pensamiento asociadas con estructuras matemáticas constituyen un avance significativo con respecto a anteriores formas de trabajo centradas en particularidades y sobrecargadas de hipótesis restrictivas y específicas. La reflexión epistemológica sobre el significado de la simplicidad en la ciencia puede permitirle a quien enseña a tomar conciencia de que lo simple de la definición formal de un objeto se aprende, no tanto mediante la exhibición de ejemplares concretos, sino recreando la actividad matemática que condujo a lo simple a partir de problemas complejos. En este sentido, el ideal de simplicidad se constituye en un propósito central de la educación matemática como disciplina centrada en la formación de pensamiento matemático. REFERENCIAS. ANACONA, M. & ORTIZ, G. (2011) La noción de vecindad en la apropiación de los números reales: Arbeláez, G., Recalde, L. (Eds). Los números reales como objeto matemático. Una perspectiva histórico-epistemológica (pp ). Cali: Programa editorial, Universidad del Valle. ARBOLEDA, L.C (1980). Las primeras investigaciones sobre los espacios topológicos. X Coloquio colombiano de Matemáticas. Sociedad colombiana de matemáticas. Paipa. BOURBAKI, N. (1962). La arquitectura de las matemáticas. En F. Le Lionnais (Ed). Las grandes corrientes del pensamiento matemático (pp ). Buenos Aires: Eudeba. BOURBAKI, N. (1965). Topologie générale. Éléments de Mathématique. Livre III. Hermann. Paris. CARTAN, H (1937). Théorie des filtres. Comptes-rendus de l Académie des Sciences de Paris. No. 205, pp DUGAC, P. (1984). Histoire des espaces complets. Revue d histoire des sciences. Tome 37, No. 1, pp de 7
Continuidad. 5.1 Continuidad en un punto
 Capítulo 5 Continuidad 5.1 Continuidad en un punto Definición 5.1.1 (Aplicación continua en un punto). Sean (X, τ) e (Y, τ ) dos espacios topológicos, y sea f : X Y una aplicación entre ellos. Diremos
Capítulo 5 Continuidad 5.1 Continuidad en un punto Definición 5.1.1 (Aplicación continua en un punto). Sean (X, τ) e (Y, τ ) dos espacios topológicos, y sea f : X Y una aplicación entre ellos. Diremos
Convergencia de sucesiones
 TEMA 4. CONVERGENCIA DE SUCESIONES 65 Tema 4. Convergencia de sucesiones Definición 5.4.1. Sea X un conjunto: una sucesión en X es una aplicación s : N X; denotaremos x n := s(n) y por S := {x n } n N
TEMA 4. CONVERGENCIA DE SUCESIONES 65 Tema 4. Convergencia de sucesiones Definición 5.4.1. Sea X un conjunto: una sucesión en X es una aplicación s : N X; denotaremos x n := s(n) y por S := {x n } n N
Espacios topológicos. 3.1 Espacio topológico
 Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Caracterización de los números reales
 Grado 11 Matematicas - Unidad 1 Operando en el conjunto de los números reales Tema Caracterización de los números reales Nombre: Curso: Breve historia de los reales A continuación se da una brevísima historia
Grado 11 Matematicas - Unidad 1 Operando en el conjunto de los números reales Tema Caracterización de los números reales Nombre: Curso: Breve historia de los reales A continuación se da una brevísima historia
Reconocer y utilizar las propiedades sencillas de la topología métrica.
 3 Funciones continuas De entre todas las aplicaciones que pueden definirse entre dos espacios métrico, las aplicaciones continuas ocupan un papel preponderante. Su estudio es fundamental no sólo en topología,
3 Funciones continuas De entre todas las aplicaciones que pueden definirse entre dos espacios métrico, las aplicaciones continuas ocupan un papel preponderante. Su estudio es fundamental no sólo en topología,
Espacios completos. 8.1 Sucesiones de Cauchy
 Capítulo 8 Espacios completos 8.1 Sucesiones de Cauchy Definición 8.1.1 (Sucesión de Cauchy). Diremos que una sucesión (x n ) n=1 en un espacio métrico (X, d) es de Cauchy si para todo ε > 0 existe un
Capítulo 8 Espacios completos 8.1 Sucesiones de Cauchy Definición 8.1.1 (Sucesión de Cauchy). Diremos que una sucesión (x n ) n=1 en un espacio métrico (X, d) es de Cauchy si para todo ε > 0 existe un
Ideas Matemáticas en situaciones del Tablet. M. Soledad Montoya González
 T / / / Ideas Matemáticas en situaciones del Tablet M. Soledad Montoya González soledad.montoya@ucv.cl Intuitivamente podemos señalar que el razonamiento lógico matemático tiene que ver con el pensar.
T / / / Ideas Matemáticas en situaciones del Tablet M. Soledad Montoya González soledad.montoya@ucv.cl Intuitivamente podemos señalar que el razonamiento lógico matemático tiene que ver con el pensar.
Por ser f continua y R compacto, existen x 0, y 0 en R tales que f(x 0 ) = sup{f(t) : t R} y f(y 0 ) = inf{f(t) : t R}
 Proposición. Sea un rectángulo en R n, y sea f : R una función continua. Entonces f es integrable en. Conjuntos de Demostración: Como f es continua en, y es compacto, f es acotada en, y uniformemente continua.
Proposición. Sea un rectángulo en R n, y sea f : R una función continua. Entonces f es integrable en. Conjuntos de Demostración: Como f es continua en, y es compacto, f es acotada en, y uniformemente continua.
Subconjuntos notables de un Espacio Topológico
 34 Capítulo 4 Subconjuntos notables de un Espacio Topológico 4.1 Adherencia Definición 4.1.1 (Punto adherente). Sea (X, τ) un espacio topológico, y sea S un subconjunto de X. Diremos que x X es un punto
34 Capítulo 4 Subconjuntos notables de un Espacio Topológico 4.1 Adherencia Definición 4.1.1 (Punto adherente). Sea (X, τ) un espacio topológico, y sea S un subconjunto de X. Diremos que x X es un punto
Cálculo Diferencial: Enero 2016
 Cálculo Diferencial: Enero 2016 Selim Gómez Ávila División de Ciencias e Ingenierías Universidad de Guanajuato 9 de febrero de 2016 / Conjuntos y espacios 1 / 21 Conjuntos, espacios y sistemas numéricos
Cálculo Diferencial: Enero 2016 Selim Gómez Ávila División de Ciencias e Ingenierías Universidad de Guanajuato 9 de febrero de 2016 / Conjuntos y espacios 1 / 21 Conjuntos, espacios y sistemas numéricos
CONSTRUCCIÓN DIDÁCTICA DE LOS NÚMEROS ENTEROS DESDE LA TEORÍA LOS MODOS DE PENSAMIENTO.
 CONSTRUCCIÓN DIDÁCTICA DE LOS NÚMEROS ENTEROS DESDE LA TEORÍA LOS MODOS DE PENSAMIENTO. Bonilla Barraza,D. Parraguez González,M. Pontificia Universidad Católica de Valparaíso (Chile) danielabonillab@gmail.com,
CONSTRUCCIÓN DIDÁCTICA DE LOS NÚMEROS ENTEROS DESDE LA TEORÍA LOS MODOS DE PENSAMIENTO. Bonilla Barraza,D. Parraguez González,M. Pontificia Universidad Católica de Valparaíso (Chile) danielabonillab@gmail.com,
1. Sucesiones y redes.
 1. Sucesiones y redes. PRACTICO 7. REDES. Se ha visto que el concepto de sucesión no permite caracterizar algunas nociones topológicas, salvo en espacios métricos. Esto empieza con algunas definiciones
1. Sucesiones y redes. PRACTICO 7. REDES. Se ha visto que el concepto de sucesión no permite caracterizar algunas nociones topológicas, salvo en espacios métricos. Esto empieza con algunas definiciones
Matemáticas UNIDAD 3 CONSIDERACIONES METODOLÓGICAS. Material de apoyo para el docente. Preparado por: Héctor Muñoz
 CONSIDERACIONES METODOLÓGICAS Material de apoyo para el docente UNIDAD 3 Preparado por: Héctor Muñoz Diseño Gráfico por: www.genesisgrafica.cl MÚLTIPLOS Y DIVISORES DE NÚMEROS NATURALES 1. DESCRIPCIÓN
CONSIDERACIONES METODOLÓGICAS Material de apoyo para el docente UNIDAD 3 Preparado por: Héctor Muñoz Diseño Gráfico por: www.genesisgrafica.cl MÚLTIPLOS Y DIVISORES DE NÚMEROS NATURALES 1. DESCRIPCIÓN
A continuación se presenta la información de la altura promedio para el año de 1998 en Holanda de hombres y mujeres jóvenes.
 M150: Creciendo A) Presentación del problema LOS JOVENES CRECEN MAS ALTO A continuación se presenta la altura promedio para el año de 1998 en Holanda de hombres y mujeres jóvenes. B) Preguntas del problema
M150: Creciendo A) Presentación del problema LOS JOVENES CRECEN MAS ALTO A continuación se presenta la altura promedio para el año de 1998 en Holanda de hombres y mujeres jóvenes. B) Preguntas del problema
Funciones y Cardinalidad
 Funciones y Cardinalidad Definición 1 Llamaremos función f entre dos conjuntos A y B a una relación que verifica las siguientes propiedades: i) Dom(f) = A ii) Si (a, b), (a, c) f entonces b = c Dicho de
Funciones y Cardinalidad Definición 1 Llamaremos función f entre dos conjuntos A y B a una relación que verifica las siguientes propiedades: i) Dom(f) = A ii) Si (a, b), (a, c) f entonces b = c Dicho de
Estructuras Algebraicas
 Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
Matemáticas II. Carrera: IFM Participantes. Representantes de la academia de sistemas y computación de los Institutos Tecnológicos.
 1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos Matemáticas II Licenciatura en Informática IFM - 0424 3-2-8 2.- HISTORIA DEL PROGRAMA
1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos Matemáticas II Licenciatura en Informática IFM - 0424 3-2-8 2.- HISTORIA DEL PROGRAMA
COLEGIO HELVETIA PROGRAMA DE MATEMÁTICAS GRADO ONCE
 COLEGIO HELVETIA PROGRAMA DE MATEMÁTICAS GRADO ONCE 201-2015 OBJETIVO GENERAL: Entender las bases conceptuales de función, el problema del infinito, así como sus aplicaciones a otras áreas del conocimiento
COLEGIO HELVETIA PROGRAMA DE MATEMÁTICAS GRADO ONCE 201-2015 OBJETIVO GENERAL: Entender las bases conceptuales de función, el problema del infinito, así como sus aplicaciones a otras áreas del conocimiento
IVÁN DARÍO JARAMILLO MAGAÑA
 LA CONSTRUCCIÓN DE LOS NÚMEROS REALES POR FRED RICHMAN Y SUS APORTES PARA LA COMPRESIÓN DE LOS NÚMEROS REALES EN EL CONTEXTO DE FORMACIÓN DE PROFESORES IVÁN DARÍO JARAMILLO MAGAÑA FABIÁN SÁNCHEZ VILLAFAÑE
LA CONSTRUCCIÓN DE LOS NÚMEROS REALES POR FRED RICHMAN Y SUS APORTES PARA LA COMPRESIÓN DE LOS NÚMEROS REALES EN EL CONTEXTO DE FORMACIÓN DE PROFESORES IVÁN DARÍO JARAMILLO MAGAÑA FABIÁN SÁNCHEZ VILLAFAÑE
Axiomas de separación
 CAPíTULO 6 Axiomas de separación Tema 1. Axiomas de separación: conceptos básicos El objetivo de este capítulo es considerar ciertas propiedades topológicas que comparten algunos espacios topológicos y
CAPíTULO 6 Axiomas de separación Tema 1. Axiomas de separación: conceptos básicos El objetivo de este capítulo es considerar ciertas propiedades topológicas que comparten algunos espacios topológicos y
Álgebra de Boole. Retículos.
 CAPÍTULO 4. Álgebra de Boole. Retículos. Este capítulo introduce dos estructuras algebraicas muy importantes : la estructura de álgebra de Boole y la de retículo. Estas estructuras constituyen una parte
CAPÍTULO 4. Álgebra de Boole. Retículos. Este capítulo introduce dos estructuras algebraicas muy importantes : la estructura de álgebra de Boole y la de retículo. Estas estructuras constituyen una parte
1. Convergencia en medida
 FACULTAD CS. FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA3801 Teoría de la Medida. Semestre 2009-02 Profesor: Jaime San Martín Auxiliares: Andrés Fielbaum y Cristóbal Guzmán Clase auxiliar 7 21 de Septiembre
FACULTAD CS. FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA3801 Teoría de la Medida. Semestre 2009-02 Profesor: Jaime San Martín Auxiliares: Andrés Fielbaum y Cristóbal Guzmán Clase auxiliar 7 21 de Septiembre
TEMA N 1 LÓGICA Y CONJUNTOS
 TEMA N 1 LÓGICA Y CONJUNTOS DEFINICIÓN Y NOTACIÓN DE CONJUNTOS OBJETIVOS Comprenderás, o repasarás, la idea intuitiva de conjunto. Definirás conjuntos por enumeración y por comprensión, así como su forma
TEMA N 1 LÓGICA Y CONJUNTOS DEFINICIÓN Y NOTACIÓN DE CONJUNTOS OBJETIVOS Comprenderás, o repasarás, la idea intuitiva de conjunto. Definirás conjuntos por enumeración y por comprensión, así como su forma
UNIVERSIDAD AUTÓNOMA DE ZACATECAS UNIDAD DE MATEMÁTICAS MAESTRÍA EN MATEMÁTICA EDUCATIVA
 UNIVERSIDAD AUTÓNOMA DE ZACATECAS UNIDAD DE MATEMÁTICAS MAESTRÍA EN MATEMÁTICA EDUCATIVA EL APRENDIZAJE Y ENSEÑANZA DEL CONCEPTO DE ECUACIÓN DE PRIMER GRADO AVANCES DE INVESTIGACIÓN LES MARCO AURELIO TORRES
UNIVERSIDAD AUTÓNOMA DE ZACATECAS UNIDAD DE MATEMÁTICAS MAESTRÍA EN MATEMÁTICA EDUCATIVA EL APRENDIZAJE Y ENSEÑANZA DEL CONCEPTO DE ECUACIÓN DE PRIMER GRADO AVANCES DE INVESTIGACIÓN LES MARCO AURELIO TORRES
Derivada de la función compuesta. Regla de la cadena
 Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones
![Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones](/thumbs/49/25360651.jpg) Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Dirección de Desarrollo Curricular Secretaría Académica
 PLAN DE ESTUDIOS DE EDUCACIÓN MEDIA SUPERIOR CAMPO DISCIPLINAR Matemáticas PROGRAMA DE ASIGNATURA (UNIDADES DE APRENDIZAJE CURRICULAR) Cálculo Diferencial PERIODO IV CLAVE BCMA.04.04-08 HORAS/SEMANA 4
PLAN DE ESTUDIOS DE EDUCACIÓN MEDIA SUPERIOR CAMPO DISCIPLINAR Matemáticas PROGRAMA DE ASIGNATURA (UNIDADES DE APRENDIZAJE CURRICULAR) Cálculo Diferencial PERIODO IV CLAVE BCMA.04.04-08 HORAS/SEMANA 4
INSTITUCION EDUCATIVA LA PRESENTACION
 INSTITUCION EDUCATIVA LA PRESENTACION Nombre de la alumna: Área: MATEMATICAS Asignatura: Matemáticas Docente: Luis López Zuleta Tipo de Guía: Conceptual PERIODO GRADO FECHA DURACION DOS 7º 25 de abril
INSTITUCION EDUCATIVA LA PRESENTACION Nombre de la alumna: Área: MATEMATICAS Asignatura: Matemáticas Docente: Luis López Zuleta Tipo de Guía: Conceptual PERIODO GRADO FECHA DURACION DOS 7º 25 de abril
GUIA DE CATEDRA Matemática Empresarial Guía N.3 F. Elaboración 09 abril /11 F. 1 Revisión 09/04/11 Pagina 1 de 8
 Plan de Estudios: Semestre 1 Área: Matemática 1 Nº Créditos: Intensidad horaria semanal: 3 Hrs T Hrs P Total horas: 6 Tema: Desigualdades 1. OBJETIVO Apropiar los conceptos de desigualdades y establecer
Plan de Estudios: Semestre 1 Área: Matemática 1 Nº Créditos: Intensidad horaria semanal: 3 Hrs T Hrs P Total horas: 6 Tema: Desigualdades 1. OBJETIVO Apropiar los conceptos de desigualdades y establecer
RESPUESTAS REPARTIDO 3 PARA ESCRITO TEORICO Diego Danieli 2IA UTU BUCEO AXIOMAS - TEOREMAS CÓMO SE CONSTRUYE LA GEOMETRIA MODERNA?
 AXIOMAS - TEOREMAS CÓMO SE CONSTRUYE LA GEOMETRIA MODERNA? FUNDAMENTOS 1 Comenzó siendo un conjunto de reglas y conocimientos obtenidos por la experiencia, usados por los constructores y medidores de terrenos.
AXIOMAS - TEOREMAS CÓMO SE CONSTRUYE LA GEOMETRIA MODERNA? FUNDAMENTOS 1 Comenzó siendo un conjunto de reglas y conocimientos obtenidos por la experiencia, usados por los constructores y medidores de terrenos.
1 Números reales. Funciones y continuidad.
 1 Números reales. Funciones y continuidad. En este tema nos centraremos en el estudio de la continuidad de funciones reales, es decir, funciones de variable real y valor real. Por ello es esencial en primer
1 Números reales. Funciones y continuidad. En este tema nos centraremos en el estudio de la continuidad de funciones reales, es decir, funciones de variable real y valor real. Por ello es esencial en primer
Construcción axiomática del conjunto de los números naturales a partir de una condición sobre su cardinalidad
 Recibido: 8 de febrero 2016 Aceptado: 27 de febrero 2016 Construcción axiomática del conjunto de los números naturales a partir de una condición sobre su cardinalidad Axiomatic construction of the set
Recibido: 8 de febrero 2016 Aceptado: 27 de febrero 2016 Construcción axiomática del conjunto de los números naturales a partir de una condición sobre su cardinalidad Axiomatic construction of the set
Para desarrollar esta actividad evaluativa, revisaremos y recordaremos tres (3) conceptos básicos:
 Para desarrollar esta actividad evaluativa, revisaremos y recordaremos tres (3) conceptos básicos: Álgebra. Trigonometría. Geometría Analítica. 1. Conceptos fundamentales de Álgebra: La palabra álgebra
Para desarrollar esta actividad evaluativa, revisaremos y recordaremos tres (3) conceptos básicos: Álgebra. Trigonometría. Geometría Analítica. 1. Conceptos fundamentales de Álgebra: La palabra álgebra
Definición 1. Dado un conjunto C una aplicación definida por : C C C
 ESTRUCTURAS ALGEBRAICAS. En matemáticas aparecen distintos conjuntos cuyos elementos podemos operar de alguna manera. Los conjuntos de números usuales: N, Z, Q, y R son unos ejemplos claros. Otros ejemplos
ESTRUCTURAS ALGEBRAICAS. En matemáticas aparecen distintos conjuntos cuyos elementos podemos operar de alguna manera. Los conjuntos de números usuales: N, Z, Q, y R son unos ejemplos claros. Otros ejemplos
Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 1: Aplicaciones Lineales EPN, verano 2012
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 1: Aplicaciones Lineales EPN, verano 212 Introducción Algunas fechas: 197: Noción de Operador lineal
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 1: Aplicaciones Lineales EPN, verano 212 Introducción Algunas fechas: 197: Noción de Operador lineal
b) Sea una relación de equivalencia en A y una operación en A. Decimos que y son compatibles si a b a c b c y c a c b para todo a, b, c A
 APENDICE Relaciones y Operaciones Compatibles 1 Definición: a) Sea A un conjunto y una relación entre elementos de A. Decimos que es una relación de equivalencia si es: i Reflexiva: a A, a a. ii Simétrica:
APENDICE Relaciones y Operaciones Compatibles 1 Definición: a) Sea A un conjunto y una relación entre elementos de A. Decimos que es una relación de equivalencia si es: i Reflexiva: a A, a a. ii Simétrica:
Por qué expresar de manera algebraica?
 Álgebra 1 Sesión No. 2 Nombre: Fundamentos de álgebra. Parte II. Objetivo: al finalizar la sesión, el estudiante conocerá e identificará las expresiones racionales, las diferentes formas de representar
Álgebra 1 Sesión No. 2 Nombre: Fundamentos de álgebra. Parte II. Objetivo: al finalizar la sesión, el estudiante conocerá e identificará las expresiones racionales, las diferentes formas de representar
Sesión No. 1. Contextualización. Nombre: Fundamentos del Álgebra MATEMÁTICAS
 Matemáticas 1 Sesión No. 1 Nombre: Fundamentos del Álgebra Contextualización Esta sesión está diseñada para ofrecer una breve explicación de los principios aritméticos y algebraicos que se requieren para
Matemáticas 1 Sesión No. 1 Nombre: Fundamentos del Álgebra Contextualización Esta sesión está diseñada para ofrecer una breve explicación de los principios aritméticos y algebraicos que se requieren para
Matemáticas UNIDAD 5 CONSIDERACIONES METODOLÓGICAS. Material de apoyo para el docente. Preparado por: Héctor Muñoz
 CONSIDERACIONES METODOLÓGICAS Material de apoyo para el docente UNIDAD 5 Preparado por: Héctor Muñoz Diseño Gráfico por: www.genesisgrafica.cl LA RELACIÓN DE PROPORCIONALIDAD 1. DESCRIPCIÓN GENERAL DE
CONSIDERACIONES METODOLÓGICAS Material de apoyo para el docente UNIDAD 5 Preparado por: Héctor Muñoz Diseño Gráfico por: www.genesisgrafica.cl LA RELACIÓN DE PROPORCIONALIDAD 1. DESCRIPCIÓN GENERAL DE
Teoremas de Convergencia
 Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
TEMA 2. ESPACIOS VECTORIALES
 TEMA 2. ESPACIOS VECTORIALES CÉSAR ROSALES GEOMETRÍA I En este tema comenzaremos el estudio de los objetos que nos interesarán en esta asignatura: los espacios vectoriales. Estos son estructuras básicas
TEMA 2. ESPACIOS VECTORIALES CÉSAR ROSALES GEOMETRÍA I En este tema comenzaremos el estudio de los objetos que nos interesarán en esta asignatura: los espacios vectoriales. Estos son estructuras básicas
UNIDAD III LÍMITES Y DERIVADAS
 OBJETIVO: Que el alumno comprenda la definición de límite de una función y derivada de la misma, para su posterior análisis y aplicación en el área de agronomía. Introducción El análisis matemático es
OBJETIVO: Que el alumno comprenda la definición de límite de una función y derivada de la misma, para su posterior análisis y aplicación en el área de agronomía. Introducción El análisis matemático es
Límites y continuidad
 Límites y continuidad Podríamos empezar diciendo que los límites son importantes en el cálculo, pero afirmar tal cosa sería infravalorar largamente su auténtica importancia. Sin límites el cálculo sencillamente
Límites y continuidad Podríamos empezar diciendo que los límites son importantes en el cálculo, pero afirmar tal cosa sería infravalorar largamente su auténtica importancia. Sin límites el cálculo sencillamente
Pablo Cobreros Tema 6. El tamaño del infinito
 Lógica II Pablo Cobreros pcobreros@unav.es Tema 6. El tamaño del infinito Introducción Introducción La noción de cardinal Afirmaciones acerca del tamaño La noción de cardinal El tamaño del infinito Introducción
Lógica II Pablo Cobreros pcobreros@unav.es Tema 6. El tamaño del infinito Introducción Introducción La noción de cardinal Afirmaciones acerca del tamaño La noción de cardinal El tamaño del infinito Introducción
PRINCIPIOS DE LA DINÁMICA
 Capítulo 3 PRINCIPIOS DE LA DINÁMICA CLÁSICA 3.1 Introducción En el desarrollo de este tema, cuyo objeto de estudio son los principios de la dinámica, comenzaremos describiendo las causas del movimiento
Capítulo 3 PRINCIPIOS DE LA DINÁMICA CLÁSICA 3.1 Introducción En el desarrollo de este tema, cuyo objeto de estudio son los principios de la dinámica, comenzaremos describiendo las causas del movimiento
MAESTRÍA EN EDUCACIÓN SNIES:
 MAESTRÍA EN EDUCACIÓN SNIES: 105148 PRESENTACIÓN DEL PROGRAMA La Maestría en Educación es un programa de profundización que ofrece una sólida formación teórica y metodológica que permita desarrollar competencias
MAESTRÍA EN EDUCACIÓN SNIES: 105148 PRESENTACIÓN DEL PROGRAMA La Maestría en Educación es un programa de profundización que ofrece una sólida formación teórica y metodológica que permita desarrollar competencias
Unidad II. Conjuntos. 2.1 Características de los conjuntos.
 Unidad II Conjuntos 2.1 Características de los conjuntos. Es la agrupación en un todo de objetos bien diferenciados en el la mente o en la intuición, por lo tanto, estos objetos son bien determinados y
Unidad II Conjuntos 2.1 Características de los conjuntos. Es la agrupación en un todo de objetos bien diferenciados en el la mente o en la intuición, por lo tanto, estos objetos son bien determinados y
UNIDAD II: TEORÍA DE CONJUNTOS 2.1. INTRODUCCIÓN
 UNDD : TEORÍ DE CONJUNTOS 2.1. NTRODUCCÓN Según Georg Cantor un conjunto es la reunión, agrupación o colección de elementos bien definidos que tienen una propiedad en común, concepto que ha penetrado y
UNDD : TEORÍ DE CONJUNTOS 2.1. NTRODUCCÓN Según Georg Cantor un conjunto es la reunión, agrupación o colección de elementos bien definidos que tienen una propiedad en común, concepto que ha penetrado y
Integrales múltiples
 ntegrales múltiples Cálculo (2003) El objetivo de este capítulo es definir y aprender a calcular integrales de funciones reales de varias variables, que llamamos integrales múltiples. Las motivación más
ntegrales múltiples Cálculo (2003) El objetivo de este capítulo es definir y aprender a calcular integrales de funciones reales de varias variables, que llamamos integrales múltiples. Las motivación más
Teoría de la Probabilidad Tema 2: Teorema de Extensión
 Teoría de la Probabilidad Tema 2: Teorema de Extensión Alberto Rodríguez Casal 25 de septiembre de 2015 Definición Una clase (no vacía) A de subconjuntos de Ω se dice que es un álgebra si A es cerrada
Teoría de la Probabilidad Tema 2: Teorema de Extensión Alberto Rodríguez Casal 25 de septiembre de 2015 Definición Una clase (no vacía) A de subconjuntos de Ω se dice que es un álgebra si A es cerrada
Guía para maestro. Fracciones algebraicas. Compartir Saberes.
 Guía para maestro Guía realizada por Yenny Marcela Naranjo Máster en Educación Matemática yennymarce3@gmail.com Las fracciones algebraicas son generalmente explicadas mediante la simbología matemática,
Guía para maestro Guía realizada por Yenny Marcela Naranjo Máster en Educación Matemática yennymarce3@gmail.com Las fracciones algebraicas son generalmente explicadas mediante la simbología matemática,
Asignatura: Matemática Fundamental [405036M-02] Taller 1 Lenguaje Simbólico y lógica proposicional
![Asignatura: Matemática Fundamental [405036M-02] Taller 1 Lenguaje Simbólico y lógica proposicional Asignatura: Matemática Fundamental [405036M-02] Taller 1 Lenguaje Simbólico y lógica proposicional](/thumbs/49/25492005.jpg) Asignatura: Matemática Fundamental [405036M-02] Taller 1 Lenguaje Simbólico y lógica proposicional 1. Responda las siguientes preguntas: a) Qué es un lenguaje formal? b) Qué es lenguaje matemático? c)
Asignatura: Matemática Fundamental [405036M-02] Taller 1 Lenguaje Simbólico y lógica proposicional 1. Responda las siguientes preguntas: a) Qué es un lenguaje formal? b) Qué es lenguaje matemático? c)
CONJUNTOS Y SISTEMAS NUMÉRICOS
 1. CONJUNTOS. 1.1 Conceptos básicos Medir y contar fueron las primeras actividades matemáticas del hombre y ambas nos conducen a los números. Haciendo marcas, medían el tiempo y el conteo de bienes que
1. CONJUNTOS. 1.1 Conceptos básicos Medir y contar fueron las primeras actividades matemáticas del hombre y ambas nos conducen a los números. Haciendo marcas, medían el tiempo y el conteo de bienes que
ENFOQUE PARA LA DE LA HISTORIA
 HISTORIA ENFOQUE PARA LA ENSEÑANZA DE LA HISTORIA FORMATIVO consideran la diversidad de los sujetos históricos y el estudio de la sociedad en sus diversas dimensiones: sociales, culturales, políticas y
HISTORIA ENFOQUE PARA LA ENSEÑANZA DE LA HISTORIA FORMATIVO consideran la diversidad de los sujetos históricos y el estudio de la sociedad en sus diversas dimensiones: sociales, culturales, políticas y
EL PENSAMIENTO CRÍTICO Y CREATIVO A LA HORA DE ELABORAR
 EL PENSAMIENTO CRÍTICO Y CREATIVO A LA HORA DE ELABORAR EL CURRICULUM BUAP DHPC ELABORADO POR: FLORES ZAMORA ALEJANDRA FABIOLA Introducción Sin duda alguna, hablar de los tipos de pensamiento que existen
EL PENSAMIENTO CRÍTICO Y CREATIVO A LA HORA DE ELABORAR EL CURRICULUM BUAP DHPC ELABORADO POR: FLORES ZAMORA ALEJANDRA FABIOLA Introducción Sin duda alguna, hablar de los tipos de pensamiento que existen
Recordemos que utilizaremos, como es habitual, la siguiente notación para algunos conjuntos de números que son básicos.
 Capítulo 1 Preliminares Vamos a ver en este primer capítulo de preliminares algunos conceptos, ideas y propiedades que serán muy útiles para el desarrollo de la asignatura. Se trata de resultados sobre
Capítulo 1 Preliminares Vamos a ver en este primer capítulo de preliminares algunos conceptos, ideas y propiedades que serán muy útiles para el desarrollo de la asignatura. Se trata de resultados sobre
SESIÓN 10 DERIVACIÓN DE FUNCIONES TRIGONOMÉTRICAS DIRECTAS
 SESIÓN 0 DERIVACIÓN DE FUNCIONES TRIGONOMÉTRICAS DIRECTAS I. CONTENIDOS:. Derivadas de funciones trigonométricas directas. Ejercicios resueltos. Estrategias Centradas en el Aprendizaje: Ejercicios propuestos
SESIÓN 0 DERIVACIÓN DE FUNCIONES TRIGONOMÉTRICAS DIRECTAS I. CONTENIDOS:. Derivadas de funciones trigonométricas directas. Ejercicios resueltos. Estrategias Centradas en el Aprendizaje: Ejercicios propuestos
13. Utilizar la fórmula del término general y de la suma de n términos consecutivos
 Contenidos mínimos 3º ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Utilizar las reglas de jerarquía de paréntesis y operaciones, para efectuar cálculos con números racionales, expresados en forma
Contenidos mínimos 3º ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Utilizar las reglas de jerarquía de paréntesis y operaciones, para efectuar cálculos con números racionales, expresados en forma
Matemáticas Universitarias
 Matemáticas Universitarias 1 Sesión No. 1 Nombre: Introducción al algebra Objetivo de la asignatura: El estudiante aplicará los conceptos fundamentales del álgebra como números reales, exponentes, radicales
Matemáticas Universitarias 1 Sesión No. 1 Nombre: Introducción al algebra Objetivo de la asignatura: El estudiante aplicará los conceptos fundamentales del álgebra como números reales, exponentes, radicales
Se desea estudiar el comportamiento de una función a medida independiente x se aproxima a un valor específico.
 Tema: Límites de las funciones Objetivos: Comprender el concepto de límite de una función y las propiedades de los límites. Calcular el límite de una función algebraica utilizando las propiedades de los
Tema: Límites de las funciones Objetivos: Comprender el concepto de límite de una función y las propiedades de los límites. Calcular el límite de una función algebraica utilizando las propiedades de los
Medios y Enseñanza de las Matemáticas en el Bachillerato Tecnológico: Álgebra y Programa de Cómputo Derive en el Aula
 Educación y Nuevas Tecnologías. Tareas de Indagación Medios y Enseñanza de las Matemáticas en el Bachillerato Tecnológico: Álgebra y Programa de Cómputo Derive en el Aula Dirección: Ignacio Garnica Dovala
Educación y Nuevas Tecnologías. Tareas de Indagación Medios y Enseñanza de las Matemáticas en el Bachillerato Tecnológico: Álgebra y Programa de Cómputo Derive en el Aula Dirección: Ignacio Garnica Dovala
SUMILLAS DE ASIGNATURAS
 PROGRAMA DE ESTUDIOS GENERALES SUMILLAS DE ASIGNATURAS PLAN CURRICULAR 2014-1 I. OBLIGATORIAS COMUNES PSICOLOGÍA Es una asignatura de naturaleza teórico práctica, cuyo propósito es comprender los procesos
PROGRAMA DE ESTUDIOS GENERALES SUMILLAS DE ASIGNATURAS PLAN CURRICULAR 2014-1 I. OBLIGATORIAS COMUNES PSICOLOGÍA Es una asignatura de naturaleza teórico práctica, cuyo propósito es comprender los procesos
Diferenciabilidad en un intervalo
 Diferenciabilidad en un intervalo Ahora que conocemos cómo calcular la derivada de una función en un punto conviene hacer la pregunta más general: «Cómo podemos saber si una derivada se puede derivar en
Diferenciabilidad en un intervalo Ahora que conocemos cómo calcular la derivada de una función en un punto conviene hacer la pregunta más general: «Cómo podemos saber si una derivada se puede derivar en
Observa la imagen y luego realiza el ejercicio
 La recta numérica, un camino al estudio de los números Identificación del conjunto de números irracionales Observa la imagen y luego realiza el ejercicio Figura 1. Caricatura de los números irracionales
La recta numérica, un camino al estudio de los números Identificación del conjunto de números irracionales Observa la imagen y luego realiza el ejercicio Figura 1. Caricatura de los números irracionales
Identificación de inecuaciones lineales en los números reales
 Grado Matematicas - Unidad Operando en el conjunto de Tema Identificación de inecuaciones lineales en los números reales Nombre: Curso: A través de la historia han surgido diversos problemas que han implicado
Grado Matematicas - Unidad Operando en el conjunto de Tema Identificación de inecuaciones lineales en los números reales Nombre: Curso: A través de la historia han surgido diversos problemas que han implicado
Sucesiones Introducción
 Temas Límites de sucesiones. convergentes. Sucesiones divergentes. Sucesiones Capacidades Conocer y manejar conceptos de sucesiones convergentes y divergentes. Conocer las principales propiedades de las
Temas Límites de sucesiones. convergentes. Sucesiones divergentes. Sucesiones Capacidades Conocer y manejar conceptos de sucesiones convergentes y divergentes. Conocer las principales propiedades de las
Espacios conexos. Capítulo Conexidad
 Capítulo 5 Espacios conexos 1. Conexidad En este capítulo exploraremos el concepto de conexidad en un espacio métrico, y estudiaremos algunas de sus aplicaciones. Definición 5.1. Decimos que el espacio
Capítulo 5 Espacios conexos 1. Conexidad En este capítulo exploraremos el concepto de conexidad en un espacio métrico, y estudiaremos algunas de sus aplicaciones. Definición 5.1. Decimos que el espacio
Es importante recordar el concepto de intervalo abierto notado. (a, b)={x R/a x bt} donde a y b no pertenecen al intervalo abierto
 INICIACION AL CALCULO LIMITE DE UNA FUNCION EN UN PUNTO Cuando se inicia un trabajo de cálculo, es importante aclarar,que históricamente a partir del siglo xviii y con los trabajos de Newton en Inglaterra
INICIACION AL CALCULO LIMITE DE UNA FUNCION EN UN PUNTO Cuando se inicia un trabajo de cálculo, es importante aclarar,que históricamente a partir del siglo xviii y con los trabajos de Newton en Inglaterra
MATEMÁTICAS TEMA 50. Polinomios. Operaciones. Fórmula de Newton. Divisibilidad de polinomios. Fracciones algebraicas
 MATEMÁTICAS TEMA 50 Polinomios. Operaciones. Fórmula de Newton. Divisibilidad de polinomios. Fracciones algebraicas ÍNDICE. 1. Introducción. 2. El anillo de los polinomios. 3. Potencia de un polinomio.
MATEMÁTICAS TEMA 50 Polinomios. Operaciones. Fórmula de Newton. Divisibilidad de polinomios. Fracciones algebraicas ÍNDICE. 1. Introducción. 2. El anillo de los polinomios. 3. Potencia de un polinomio.
Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos
![Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos](/thumbs/53/31721818.jpg) Semana02[1/23] 9 de marzo de 2007 Introducción Semana02[2/23] La teoría de conjuntos gira en torno a la función proposicional x A. Los valores que hacen verdadera la función proposicional x A son aquellos
Semana02[1/23] 9 de marzo de 2007 Introducción Semana02[2/23] La teoría de conjuntos gira en torno a la función proposicional x A. Los valores que hacen verdadera la función proposicional x A son aquellos
Matemática. 00 de Mes de 0000
 Matemática 00 de Mes de 0000 Organización de Subniveles Subnivel Elemental de la Educación General Básica - Segundo, Tercero y Cuarto año de EGB Subnivel Media de la Educación General Básica - Quinto,
Matemática 00 de Mes de 0000 Organización de Subniveles Subnivel Elemental de la Educación General Básica - Segundo, Tercero y Cuarto año de EGB Subnivel Media de la Educación General Básica - Quinto,
Qué debo saber para realizar la prueba de Lectura?
 Guía para resolver la prueba de Graduandos 2016 Qué debo saber para realizar la prueba de Lectura? En este documento encontrará información importante acerca de las destrezas cognitivas de comprensión
Guía para resolver la prueba de Graduandos 2016 Qué debo saber para realizar la prueba de Lectura? En este documento encontrará información importante acerca de las destrezas cognitivas de comprensión
LENGUAJE. Lengua, habla y norma
 LENGUAJE Lengua, habla y norma CONTENIDO El signo y la palabra La palabra Lenguaje: en su acepción restringida El lenguaje El código: la lengua y el habla La lengua El habla La norma En conclusión Lic.
LENGUAJE Lengua, habla y norma CONTENIDO El signo y la palabra La palabra Lenguaje: en su acepción restringida El lenguaje El código: la lengua y el habla La lengua El habla La norma En conclusión Lic.
UNIDAD DE APRENDIZAJE I
 UNIDAD DE APRENDIZAJE I Saberes procedimentales 1. Define en forma correcta el concepto de desigualdad y el de valor absoluto. 2. Explica la diferencia entre constante, parámetro y variable. 3. Define
UNIDAD DE APRENDIZAJE I Saberes procedimentales 1. Define en forma correcta el concepto de desigualdad y el de valor absoluto. 2. Explica la diferencia entre constante, parámetro y variable. 3. Define
Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 7: Lunes 22 - Viernes 27 de Abril. Contenidos
 Coordinación de Matemática I (MAT01) 1 er Semestre de 013 Semana 7: Lunes - Viernes 7 de Abril Cálculo Contenidos Clase 1: Álgebra de límites. Teorema del Sandwich. Cálculo de límites. Límites trigonométricos.
Coordinación de Matemática I (MAT01) 1 er Semestre de 013 Semana 7: Lunes - Viernes 7 de Abril Cálculo Contenidos Clase 1: Álgebra de límites. Teorema del Sandwich. Cálculo de límites. Límites trigonométricos.
PROGRAMA DE MATEMÁTICA DIVERSIFICACIÓN CIENTÍFICA SEGUNDO AÑO DE BA CHILLERATO REFORMULACIÓN 2006 AJUSTE 2010 INTRODUCCIÓN
 PROGRAMA DE MATEMÁTICA DIVERSIFICACIÓN CIENTÍFICA SEGUNDO AÑO DE BA CHILLERATO REFORMULACIÓN 2006 AJUSTE 2010 INTRODUCCIÓN El programa se estructura en tres Bloques Temáticos: NÚMERO, ANÁLISIS MATEMÁTICO
PROGRAMA DE MATEMÁTICA DIVERSIFICACIÓN CIENTÍFICA SEGUNDO AÑO DE BA CHILLERATO REFORMULACIÓN 2006 AJUSTE 2010 INTRODUCCIÓN El programa se estructura en tres Bloques Temáticos: NÚMERO, ANÁLISIS MATEMÁTICO
Seminario Avance de Proyectos de Investigación
 http://www.matedu.cinvestav.mx/~cognicion/ Programa de Maestría en Ciencias del Departamento de Matemática Educativa Seminario Avance de Proyectos de Investigación El seminario Avance de proyectos de investigación
http://www.matedu.cinvestav.mx/~cognicion/ Programa de Maestría en Ciencias del Departamento de Matemática Educativa Seminario Avance de Proyectos de Investigación El seminario Avance de proyectos de investigación
35 Están en capacidad de resolver problemas que
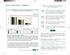 Meta: Matemática Grado 9 8 7 6 ES DE LOGRO EN MATEMÁTICA 8 8 8 8 8 55 5 52 49 52 7 6 7 4 6 ES DE LOGRO Sólo 6 de cada estudiantes de grado º en el Meta alcanzan el nivel esperado de calidad en la matemática
Meta: Matemática Grado 9 8 7 6 ES DE LOGRO EN MATEMÁTICA 8 8 8 8 8 55 5 52 49 52 7 6 7 4 6 ES DE LOGRO Sólo 6 de cada estudiantes de grado º en el Meta alcanzan el nivel esperado de calidad en la matemática
CONSTRUCCIÓN DE LOS NÚMEROS REALES: COMPLETACIÓN DE LA ESTRUCTURA TOPOLÓGICA
 CONSTRUCCIÓN DE LOS NÚMEROS REALES: COMPLETACIÓN DE LA ESTRUCTURA TOPOLÓGICA VIVIANA ANDREA PATIÑO MUÑOZ UNIVERSIDAD DEL VALLE INSTITUTO DE EDUCACIÓN Y PEDAGOGÍA LICENCIATURA EN MATEMÁTICA Y FÍSICA (3487)
CONSTRUCCIÓN DE LOS NÚMEROS REALES: COMPLETACIÓN DE LA ESTRUCTURA TOPOLÓGICA VIVIANA ANDREA PATIÑO MUÑOZ UNIVERSIDAD DEL VALLE INSTITUTO DE EDUCACIÓN Y PEDAGOGÍA LICENCIATURA EN MATEMÁTICA Y FÍSICA (3487)
Unidad Temática 3: Probabilidad y Variables Aleatorias
 Unidad Temática 3: Probabilidad y Variables Aleatorias 1) Qué entiende por probabilidad? Cómo lo relaciona con los Sistemas de Comunicaciones? Probabilidad - Definiciones Experimento aleatorio: Un experimento
Unidad Temática 3: Probabilidad y Variables Aleatorias 1) Qué entiende por probabilidad? Cómo lo relaciona con los Sistemas de Comunicaciones? Probabilidad - Definiciones Experimento aleatorio: Un experimento
Las particiones y el Teorema de Bolzano
 Miscelánea Matemática 41 (005) 1 7 SMM Las particiones y el Teorema de Bolzano Carlos Bosch Giral Departamento de Matemáticas ITAM Río Hondo # 1 Tizapán San Angel 01000 México D.F. México bosch@itam.mx
Miscelánea Matemática 41 (005) 1 7 SMM Las particiones y el Teorema de Bolzano Carlos Bosch Giral Departamento de Matemáticas ITAM Río Hondo # 1 Tizapán San Angel 01000 México D.F. México bosch@itam.mx
TEMA. Resolución de problemas. [2.1] Cómo estudiar este tema? [2.2] Definición de problema. [2.3] Tipología de problema
![TEMA. Resolución de problemas. [2.1] Cómo estudiar este tema? [2.2] Definición de problema. [2.3] Tipología de problema TEMA. Resolución de problemas. [2.1] Cómo estudiar este tema? [2.2] Definición de problema. [2.3] Tipología de problema](/thumbs/53/31448552.jpg) Resolución de problemas [2.1] Cómo estudiar este tema? [2.2] Definición de problema [2.3] Tipología de problema [2.4] Pensamiento formal y pensamiento concreto [2.5] Cómo mejorar el planteamiento de los
Resolución de problemas [2.1] Cómo estudiar este tema? [2.2] Definición de problema [2.3] Tipología de problema [2.4] Pensamiento formal y pensamiento concreto [2.5] Cómo mejorar el planteamiento de los
Capitulo 4. DECISIONES BAJO RIESGO TEORIA DE JUEGOS
 Capitulo 4. DECISIONES BAJO RIESGO TEORIA DE JUEGOS INTRODUCCIÓN En el mundo real, tanto en las relaciones económicas como en las políticas o sociales, son muy frecuentes las situaciones en las que, al
Capitulo 4. DECISIONES BAJO RIESGO TEORIA DE JUEGOS INTRODUCCIÓN En el mundo real, tanto en las relaciones económicas como en las políticas o sociales, son muy frecuentes las situaciones en las que, al
Tema 6: Teoría Semántica
 Tema 6: Teoría Semántica Sintáxis Lenguaje de de las las proposiciones Lenguaje de de los los predicados Semántica Valores Valores de de verdad verdad Tablas Tablas de de verdad verdad Tautologías Satisfacibilidad
Tema 6: Teoría Semántica Sintáxis Lenguaje de de las las proposiciones Lenguaje de de los los predicados Semántica Valores Valores de de verdad verdad Tablas Tablas de de verdad verdad Tautologías Satisfacibilidad
Física MEMOFICHAS_CAMINOS_FISICA.indd 1 27/06/14 9:28
 Física Estructura de la serie El proyecto Los Caminos del Saber Física para media es un programa de educación con soluciones tecnológicas que apoyan el libro de texto para que docentes y estudiantes enriquezcan
Física Estructura de la serie El proyecto Los Caminos del Saber Física para media es un programa de educación con soluciones tecnológicas que apoyan el libro de texto para que docentes y estudiantes enriquezcan
AMPLIACIÓN DE MATEMÁTICAS
 AMPLIACIÓN DE MATEMÁTICAS SUCESIONES DE FUNCIONES En primer curso estudiamos el concepto de convergencia de una sucesión de números. Decíamos que dada una sucesión de números reales (x n ) n=1 R, ésta
AMPLIACIÓN DE MATEMÁTICAS SUCESIONES DE FUNCIONES En primer curso estudiamos el concepto de convergencia de una sucesión de números. Decíamos que dada una sucesión de números reales (x n ) n=1 R, ésta
Departamento de Educación Gobierno de Navarra Plan institucional de mejora de la lectura.
 EJEMPLOS DE PREGUNTAS PARA LA EVALUACIÓN DE LA COMPRENSIÓN LECTORA 21 Proceso En qué consiste este proceso Ejemplos de tipos de preguntas Búsqueda de información A veces, leemos para identificar y recuperar
EJEMPLOS DE PREGUNTAS PARA LA EVALUACIÓN DE LA COMPRENSIÓN LECTORA 21 Proceso En qué consiste este proceso Ejemplos de tipos de preguntas Búsqueda de información A veces, leemos para identificar y recuperar
Es claro que es una relación de equivalencia. Para ver que tener la misma cardinalidad y la cardinalidad están bien definidas queremos ver que
 Capítulo II Cardinalidad Finita II.1. Cardinalidad Definimos I n para n N como I n = {k N : 1 k n}. En particular I 0 =, puesto que 0 < 1. Esto es equivalente a la definición recursiva { si n = 0 I n =
Capítulo II Cardinalidad Finita II.1. Cardinalidad Definimos I n para n N como I n = {k N : 1 k n}. En particular I 0 =, puesto que 0 < 1. Esto es equivalente a la definición recursiva { si n = 0 I n =
HOJAS DE TRABAJO SECTOR. Matemáticas. Material de apoyo para el docente UNIDAD 1. Preparado por: Héctor Muñoz
 HOJAS DE TRABAJO SECTOR Material de apoyo para el docente UNIDAD 1 Preparado por: Héctor Muñoz Diseño Gráfico por: www.genesisgrafica.cl 1. BREVE PRESENTACIÓN DE LA UNIDAD INTRODUCCIÓN A LOS NÚMEROS ENTEROS
HOJAS DE TRABAJO SECTOR Material de apoyo para el docente UNIDAD 1 Preparado por: Héctor Muñoz Diseño Gráfico por: www.genesisgrafica.cl 1. BREVE PRESENTACIÓN DE LA UNIDAD INTRODUCCIÓN A LOS NÚMEROS ENTEROS
Conjuntos Los conjuntos se emplean en muchas áreas de las matemáticas, de modo que es importante una comprensión de los conjuntos y de su notación.
 NÚMEROS REALES Conjuntos Los conjuntos se emplean en muchas áreas de las matemáticas, de modo que es importante una comprensión de los conjuntos y de su notación. Un conjunto es una colección bien definida
NÚMEROS REALES Conjuntos Los conjuntos se emplean en muchas áreas de las matemáticas, de modo que es importante una comprensión de los conjuntos y de su notación. Un conjunto es una colección bien definida
ALGEBRA DE BOOLE George Boole C. E. Shannon E. V. Hungtington [6]
![ALGEBRA DE BOOLE George Boole C. E. Shannon E. V. Hungtington [6] ALGEBRA DE BOOLE George Boole C. E. Shannon E. V. Hungtington [6]](/thumbs/51/28877791.jpg) ALGEBRA DE BOOLE El álgebra booleana, como cualquier otro sistema matemático deductivo, puede definirse con un conjunto de elementos, un conjunto de operadores y un número de axiomas no probados o postulados.
ALGEBRA DE BOOLE El álgebra booleana, como cualquier otro sistema matemático deductivo, puede definirse con un conjunto de elementos, un conjunto de operadores y un número de axiomas no probados o postulados.
Bloque 3. El propósito central de este bloque es el estudio de las fracciones. Fracciones comunes
 Bloque Fracciones comunes El propósito central de este bloque es el estudio de las fracciones comunes, sus operaciones propiedades. En las actividades que aquí se incluen se trata la construcción de las
Bloque Fracciones comunes El propósito central de este bloque es el estudio de las fracciones comunes, sus operaciones propiedades. En las actividades que aquí se incluen se trata la construcción de las
TEMARIO DE PROFESORES DE ENSEÑANZA SECUNDARIA MATEMÁTICAS
 HOJA INFORMATIVA A.5.2.33 TEMARIO DE PROFESORES DE ENSEÑANZA SECUNDARIA MATEMÁTICAS Publicado en el B.O.E. de 21 de Septiembre de 1.993 MARZO 1998 MATEMÁTICAS 1. Números naturales. Sistemas de numeración.
HOJA INFORMATIVA A.5.2.33 TEMARIO DE PROFESORES DE ENSEÑANZA SECUNDARIA MATEMÁTICAS Publicado en el B.O.E. de 21 de Septiembre de 1.993 MARZO 1998 MATEMÁTICAS 1. Números naturales. Sistemas de numeración.
BLOQUE 5. SUCESIONES Y SERIES DE NÚMEROS REALES
 BLOQUE 5 SUCESIONES Y SERIES DE NÚMEROS REALES Sucesiones de números reales - Límite de una sucesión - Cálculo de límites Series de números reales Progresiones aritméticas y geométricas Series geométricas
BLOQUE 5 SUCESIONES Y SERIES DE NÚMEROS REALES Sucesiones de números reales - Límite de una sucesión - Cálculo de límites Series de números reales Progresiones aritméticas y geométricas Series geométricas
Límite de funciones. Por otra parte se dice que una función es discontínua si para algún (os) valor (es) de x no existe valor de y.
 Límite de funciones El concepto de límite se explica y define desde diferentes perspectivas en los libros de cálculo. Se habla por ejemplo del límite de una sucesión (como ya se explicó), o bien del límite
Límite de funciones El concepto de límite se explica y define desde diferentes perspectivas en los libros de cálculo. Se habla por ejemplo del límite de una sucesión (como ya se explicó), o bien del límite
Semana 5: La composición como una operación
 Semana 5: La composición como una operación 1. Tipos de funciones De manera intuitiva, nos referimos por inversa de una función a otra función que deshace los cambios hechos por la función original, a
Semana 5: La composición como una operación 1. Tipos de funciones De manera intuitiva, nos referimos por inversa de una función a otra función que deshace los cambios hechos por la función original, a
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS
 UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS FACULTAD DE LETRAS Y CIENCIAS HUMANAS E.A.P. DE COMUNICACIÓN SOCIAL Labor realizada en la facultad de derecho y ciencia política de la Universidad Nacional Mayor
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS FACULTAD DE LETRAS Y CIENCIAS HUMANAS E.A.P. DE COMUNICACIÓN SOCIAL Labor realizada en la facultad de derecho y ciencia política de la Universidad Nacional Mayor
Definición 1 Un semigrupo es un conjunto E provisto de una operación binaria asociativa sobre E, se denota por (E, ).
 ALGEBRA La primera parte del presente libro está dedicada a las estructuras algebraicas. En esta parte vamos a iniciar agregándole a los conjuntos operaciones. Cuando las operaciones tienen determinadas
ALGEBRA La primera parte del presente libro está dedicada a las estructuras algebraicas. En esta parte vamos a iniciar agregándole a los conjuntos operaciones. Cuando las operaciones tienen determinadas
Indagación en diversas fuentes de información acerca de la existencia de los números irracionales. Análisis de situaciones
 NÚMEROS REALES OBJETIVOS CONTENIDOS 1.Analizar situaciones Existencia de que números irra- hacen evidente cionales. la existencia de números PROCEDIMIENTOS Indagación en diversas fuentes de información
NÚMEROS REALES OBJETIVOS CONTENIDOS 1.Analizar situaciones Existencia de que números irra- hacen evidente cionales. la existencia de números PROCEDIMIENTOS Indagación en diversas fuentes de información
INSTITUCIÓN EDUCATIVA SAN VICENTE DE PAÚL ANÁLISIS RESULTADOS PRUEBAS SABER 3, 5 Y
 INSTITUCIÓN EDUCATIVA SAN VICENTE DE PAÚL ANÁLISIS RESULTADOS PRUEBAS SABER 3, 5 Y 9 2015 RESULTADOS DE TERCER GRADO EN EL ÁREA DE LENGUAJE Comparación de porcentajes según niveles de desempeño por año
INSTITUCIÓN EDUCATIVA SAN VICENTE DE PAÚL ANÁLISIS RESULTADOS PRUEBAS SABER 3, 5 Y 9 2015 RESULTADOS DE TERCER GRADO EN EL ÁREA DE LENGUAJE Comparación de porcentajes según niveles de desempeño por año
