Límites de funciones de varias variables.
|
|
|
- Monica Espejo San Segundo
- hace 9 años
- Vistas:
Transcripción
1 Límites continuidad de funciones de varias variables Límites de funciones de varias variables. En este apartado se estudia el concepto de límite de una función de varias variables algunas de las técnicas utilizadas en su cálculo. Después, basándose en este concepto, se establece la definición de función continua cómo estudiar la continuidad de una función de varias variables. En principio se comienza con campos escalares después se etiende la definición a los campos vectoriales. Límite de un campo escalar. Antes de comenzar con los campos escalares conviene recordar la definición de límite en un punto de una función real de variable real = f () de la forma: donde D=(a,b) es un intervalo abierto. f :D En este conteto se dice que dado D {a,b} el límite de la función = f (), cuando tiende a, es L si ε > eiste δ > tal que D con tal que < δ se tenga que f ( ) L < ε. NOTAS: 1ª. Se destaca que esta definición de límite está basada en la idea topológica de proimidad, entre los valores de la variable con los de la función f () con L. ª. También es valioso darse cuenta de que esta definición no proporciona ningún método para calcular el límite de una función en un punto. La definición sirve, no obstante, para verificar si dicho límite tiene un valor de terminado. 3ª. También se debe destacar que en el límite de una función en un punto no influe el valor f ( ) de la función en dicho punto. Para etender este concepto a un campo escalar es necesario ampliar la idea de proimidad n en el conjunto al espacio. Para ello se introduce la definición de bola abierta en n (que equivale al concepto de entrono de un punto en ). Definición: Se denomina bola abierta de centro radio r > al conjunto de todos los puntos n tales que < r. Esto es: B(,r) = { n / < r } NOTAS: 1ª. Obsérvese que en este caso los elementos de representan como tales (esto es con una flechita encima). n son vectores por eso se ª. En el caso de la bola abierta B(,r) corresponde a los puntos interiores al círculo (esto es sin contar la circunferencia) de centro 3 radio r. En el caso de se trataría de los puntos interiores a una esfera. Una vez introducido el concepto de bola abierta aparece, de forma natural, el de conjunto n abierto como aquel subconjunto de que se ajusta a la siguiente definición. Definición: Se dice que el conjunto D r > tal que la bola B(,r) D. n es un conjunto abierto en NOTA: También se puede decir que D es abierto si para todo una bola abierta de centro que esté totalmente contenida en D. n si D eiste D es posible encontrar 1
2 Límites continuidad de funciones de varias variables Asimismo es necesario introducir el concepto de frontera de un conjunto D definición en este caso es: n. La Definición: Se dice que un punto n es un punto frontera de D n si para cualquier bola abierta B(,r) se tiene que B(,r) D φ B( n,r) ( -D) φ. NOTA. La frontera de un conjunto D n, simbolizada por D, es el conjunto de todos sus puntos frontera. En este momento, con todas las definiciones anteriores establecidas, se puede introducir el concepto de límite de un campo escalar en un punto. Definición: Sea el campo escalar de n variables, n > de la forma: f :D n siendo D abierto, sea un punto (D D). Se dice que L es el límite de f () cuando si ε > eiste δ > tal que D con < δ se cumple que f ( ) L < ε. Este hecho se simboliza por la epresión: lim f ( ) = L NOTAS: 1ª. Una definición análoga a esta puede ser la siguiente: En las condiciones anteriores se dice que lim f ( ) = L si ε > eiste δ > tal que con B(,δ ) D se tiene que f () B(,ε ). ª.- Se conservan todas las propiedades sobre la suma, producto cociente de límites que tenían los límites de las funciones reales de variable real. 3ª.- En condiciones normales el cálculo de límites de campos escalares se hace sustituendo el valor en la función f (). Cuando se producen indeterminaciones es necesario estudiar el límite con más detalle para determinar su naturaleza. 4ª.- En un campo escalar de dos variables, cuando ( tiende a (, ) se definen los límites iterados como: lim (lim f ( ) lim (lim f ( ) Entonces, si la función f ( tiene límite L, cuando ( tiende a (, ), ambos límites iterados eisten también toman el valor L. Sin embargo, la eistencia e igualdad de límites iterados no conduce a la eistencia de límite. Este hecho es útil para determinar cual puede ser el límite en casos conflictivos. EJEMPLO: Calcular el límite de la función z = en los puntos (1,) (,). En primer lugar, el cálculo del límite cuando (, tiende a (1,) se efectúa, de forma sencilla, como: 5 1 (1,) = = 1+ 4 En cambio, al calcular el límite en el origen de coordenadas, de la misma forma, se
3 Límites continuidad de funciones de varias variables obtiene una indeterminación: (,) = + (indeterminación). Utilizando los límites iterados se puede ver que, en el caso de eistir, el límite debería ser L=: lim (lim ) = lim =, e igualmente, lim (lim ) = + Para poder demostrar que es el valor del límite cuando (, (,) ha que poder encontrar un valorδ > de tal forma que cuando se tenga la acotación (, (,) < δ se esté seguro de que también se satisface la acotación f ( < ε, siendo ε > un valor cualquiera (en general el valor δ dependerá del valor ε, esto es δ = δ (ε ) ). como En este caso + + (, (,) < δ se considera como < δ f ( < ε < ε. En este conteto, el proceso de demostración se basa en establecer una cadena de desigualdades que acoten el valor de, con ello, la acotación de por alguna epresión que dependa de también supondrá una acotación de. Encontrar esta sucesión de acotaciones no siempre es posible ni fácil. Tampoco eisten reglas fijas para hallarla. En muchas ocasiones depende de la pericia del usuario En este caso una posibilidad es: = Esto es, se ha encontrado la acotación 5. Entonces dado cualquier valor de ε > se toma un valor < δ < ε / 5 (ha infinitos). Con este valor δ > se tiene asegurado que cuando (, (,) = < δ el valor de f ( = tanto: ε < 5δ = 5 = ε. 5 está acotado por 5 Todo lo anterior confirma que (,) = que a su vez esta acotado por 5 δ por 3
4 Límites continuidad de funciones de varias variables NOTA: La demostración de que el límite de una función en un punto eiste, además, calcularlo no siempre es una tarea fácil. Por otro lado, utilizar la definición para determinar la validez de un límite puede ser, muchas veces, difícil engorroso. A veces es posible encontrar algún método alternativo que permita calcular el límite de forma directa. En cualquier caso, el problema más importante que se encuentra en este cálculo es la necesidad de asegurar la eistencia de límite en un punto sea cual sea la forma de aproimarse al mismo. Muchas veces se utiliza este hecho para verificar la no eistencia de límite en un punto. Esto se suele hacer viendo que el valor del límite depende de la forma de acercamiento al mismo. Este particular se ilustra en el siguiente ejemplo. EJEMPLO: Estudiar: (,) En esta ocasión, no es posible obtener el valor del límite sustituendo directamente los valores = e = en la epresión de la función, pues se obtiene una indeterminación. El estudio de los límites iterados conduce a lim (lim ) = lim = ; lim (lim ) = + Pero en este caso, en vez de recurrir a la definición, es conveniente estudiar el límite cuando el acercamiento a (,) se hace de otra forma, por ejemplo a través de la recta =. Esto es, por puntos de la forma (, ) con. En este caso el límite se calcula así: (,) 1 = ) (,) = + Es decir, se obtiene un valor del límite que no coincide con los límites iterados. Por tanto el límite anterior no eiste. A veces es posible calcular el límite de una función de dos variables, cuando (, (,), mediante el cambio a coordenadas polares. En ese caso se hace la sustitución: = r cos( θ ), = r sen( θ ) la tendencia (, (,) por r. Entonces, en algunas ocasiones, cuando el límite es independiente del valor de θ se puede obtener su valor. Cuando el límite depende de θ resulta obvio que no eiste. EJEMPLO: En el límite anterior: (,) se puede aplicar la técnica del paso a polares para determinar el límite: 4
5 Límites continuidad de funciones de varias variables En este caso se obtiene: (,) = lim 3 5r cos ( θ ) sen( θ ) r r (cos ( θ ) + sen ( θ )) = lim r 5r cos ( θ ) sen( θ ) Teniendo en cuenta que cos ( θ ) sen( θ ) está acotado se desprende que este límite es. (,) = lim r 5r cos ( θ ) sen( θ ) = Si se estudia el otro ejemplo por este método se obtiene: EJEMPLO: Estudiar el límite (,) mediante su cambio a polares. (,) r cos( θ ) sen( θ ) = lim r r (cos ( θ ) + sen ( θ )) = lim θ θ r cos( ) sen( ) En este caso, al haber desaparecido la variable r, el valor del límite depende únicamente del valor de θ (esto es, de la dirección de aproimación), por lo tanto, este límite no eiste. Límite de un campo vectorial. En el caso de un campo vectorial de la forma f :D n m Eistirá el límite de f () = ( f1( ), f( ),..., fm( )) cuando si eiste el límite de cada una de sus componentes (cada componente es un campo escalar). Esto es, si f () = ( f1( ), f( ),..., fm( )) entonces: lim f ( ) = ( L, L,..., Lm ) lim f ( ) = L, lim f ( ) = L,...,lim 1 1 fm1( ) = Lm 1 NOTA: Se conservan todas las propiedades de la suma, producto cociente de límites de los límites de los campos escalares. 5
6 Límites continuidad de funciones de varias variables Continuidad de funciones de varias variables. En este apartado se introduce la definición de función de varias variables continua en un punto. La forma de definir la continuidad en este conteto es análoga a la utilizada para funciones reales de variable real. Se comienza con la continuidad de campos escalares se etiende, de forma natural, para campos vectoriales. Continuidad de campos escalares. La definición de campo escalar continuo en un punto es la siguiente. Definición: Sea el campo escalar de n variables, n > de la forma: f :D n siendo D abierto, sea un punto D. Se dice que f () es continua en si: lim f ( ) = f ( ) Si la función no es continua se denomina discontinua. NOTAS: 1ª. Tipos de discontinuidad: En esta definición se determina que para establecer la continuidad de f () en el punto son necesarias tres cosas: a) La eistencia de lim f ( ) =L. b) Que la función f () esté definida en D. c) Que ambos valores sean iguales. Si alguna de las tres condiciones no se cumple la función f () es discontinua en D. De todas estas condiciones la más importante es la eistencia del límite. Si el límite no eiste no ha nada que hacer, pero si la continuidad falla por alguna de las otras razones es posible hacer un apaño para que la función sea continua. Este apaño consiste en redefinir la función en ese punto. Por esta razón la discontinuidad de una función en un punto puede ser de dos tipos: 1.- Discontinuidad esencial. Cuando no eiste el límite no ha nada que hacer..- Discontinuidad evitable. Cuando eistiendo el límite la función no está definida o su valor no coincide con dicho límite ( Hombre!... Pero se puede arreglar). ª. Se conservan todas las propiedades de continuidad de la suma, producto cociente de funciones continuas que tenían las funciones reales de variable real continuas. 3ª. Se dice que un campo escalar en continuo en un conjunto abierto D n si es continuo en cada uno de los puntos de D. EJEMPLO: La función f ( = es continua en todo punto ( tal que (, (,). En el punto (,) la función no está definida pues la epresión anterior no tiene sentido cuando (, = (,). Sin embargo, la función sí tiene límite cuando (, (,). Esto es: 6
7 Límites continuidad de funciones de varias variables (,) = Se trata, por tanto, de una discontinuidad evitable. Esta circunstancia permite hacer que la función sea continua añadiendo a su definición el valor f (,) =. De esta manera también será continua en (, = (,). La función redefinida tendrá por epresión: f ( = si ( (,) si ( = (,) EJEMPLO: La función: f ( = también es continua en todos los puntos ( tales que (, (,). Sin embargo, en el punto (, = (,) no sólo no está definida, sino que no eiste su límite cuando (, (,). En este caso se trata de una discontinuidad esencial n es posible, de ninguna manera, redefinir la función encontrar un valor para f (,) que remedie esta situación de discontinuidad. Continuidad de campos vectoriales. En el caso de un campo vectorial de la forma f :D n m La función f () = ( f1( ), f( ),..., fm( )) será continua en D si lo es cada una de sus componentes. Esto, es si todas las funciones f1( ), f( ),..., fm( ) son continuas en. NOTA: Se conservan todas las propiedades de la suma, producto cociente de funciones continuas en campos escalares. Composición de funciones. La composición de funciones es una operación entre funciones que permite obtener una función nueva, a partir de otras dos o más funciones, cuando se cumplen unas determinadas condiciones. En el caso de funciones reales de variable real se realizaba de la siguiente forma: Dadas dos funciones: g :I f :J tales que g (I) J, se podía construir la función f g :I definida por la epresión ( f g )() = f (g ()). En el caso de las funciones reales de variable real, la función compuesta es continua en un punto I si la función g() es continua en I, además, f( es continua en el punto = g( ) J. 7
8 Límites continuidad de funciones de varias variables Las funciones de varias variables también se pueden componer entre si. En este caso, es necesario tener en cuenta las dimensiones de los espacios inicial final de las funciones a que deben coincidir adecuadamente. Así, dada la función f :D podrá componerse con otra función de la forma g :H n tal que g ( H) D. Entonces, se podrá construir la función compuesta: n f g : H siendo ( f g ) ( 1,..., n) = f ( g1( 1,..., n), g( 1,..., n )) EJEMPLO: Sean las funciones f ( = + sen( ), g ( = ( u + w,uv en este caso la función compuesta es f g : que tiene por epresión ( f g ) ( u, = f ( g1(, g( ), esto es: ( f g ) ( u, = g 1 ( g( +sen ( g 1( + g( ) = ( u + w ) + (uv sen( u + w + uv + 3 NOTA: También es posible establecer la composición de dos campos vectoriales de la forma: f :D m p g :H n m con g (H) D La continuidad de las funciones compuestas se asienta en la continuidad de las funciones que las componen. Así, en este mismo caso, la función f g : H n p será continua en H, si la función g es continua en H la función f es continua en g ( ) D. 8
Tema 7. Límites y continuidad. 7.1 Definición de límite de una función
 Tema 7 Límites y continuidad 7.1 Definición de límite de una función Sea f : I R, I R yseaa I un punto de acumulación de I, decimos que f() tiene límite l R en el punto a f() =l si ε > 0, η > 0: a < η
Tema 7 Límites y continuidad 7.1 Definición de límite de una función Sea f : I R, I R yseaa I un punto de acumulación de I, decimos que f() tiene límite l R en el punto a f() =l si ε > 0, η > 0: a < η
S11: Funciones continuas. Limites con dos variables.
 S11: Funciones continuas. Limites con dos variables. Una función f() es continua en un punto interior a X si: 1) f = a B 2) f = A A = B = f(a) a + Discontinuidad de 1ª especie: A y B Si A = B f(a) (Discontinuidad
S11: Funciones continuas. Limites con dos variables. Una función f() es continua en un punto interior a X si: 1) f = a B 2) f = A A = B = f(a) a + Discontinuidad de 1ª especie: A y B Si A = B f(a) (Discontinuidad
Funciones de varias variables. Continuidad
 Capítulo 1 Funciones de varias variables. Continuidad 1. Topología en R n Definición (Norma, espacio vectorial normado). Una norma sobre R n es una aplicación: : R n [0,+ [ x x, que satisface las siguientes
Capítulo 1 Funciones de varias variables. Continuidad 1. Topología en R n Definición (Norma, espacio vectorial normado). Una norma sobre R n es una aplicación: : R n [0,+ [ x x, que satisface las siguientes
x 1 3 f) x e lim x lim + 2 lim lim log x lim x 1 (x 1)(x 4) lim x 1 (x 2)(x 5) (x 2)(x 3) 1. Calcular los siguientes límites no indeterminados 1 :
 + ln 4 + f + 5 EJERCICIOS de LÍMITES DE FUNCIONES y CONTINUIDAD. Calcular los siguientes límites no indeterminados : 4 + + 4 f) e log g) 0, + 4 i) 0+ + 4 e) j) 4. Dada la gráfica de la figura, indicar
+ ln 4 + f + 5 EJERCICIOS de LÍMITES DE FUNCIONES y CONTINUIDAD. Calcular los siguientes límites no indeterminados : 4 + + 4 f) e log g) 0, + 4 i) 0+ + 4 e) j) 4. Dada la gráfica de la figura, indicar
Derivación de funciones de varias variables.
 Derivación de funciones de varias variables. En este apartado se presentan los conceptos básicos que aparecen en la derivación de funciones de varias variables. La idea es establecer un método para estudiar
Derivación de funciones de varias variables. En este apartado se presentan los conceptos básicos que aparecen en la derivación de funciones de varias variables. La idea es establecer un método para estudiar
Límites y Continuidad de funciones de varias variables
 1- Se construe un depósito de propano adosando dos hemisferios a los etremos de un cilindro circular recto Epresar el volumen V de ese depósito en función del radio r del cilindro de su altura h - Determinar
1- Se construe un depósito de propano adosando dos hemisferios a los etremos de un cilindro circular recto Epresar el volumen V de ese depósito en función del radio r del cilindro de su altura h - Determinar
Un i d a d 2. Co n t i n U i da d. Objetivos. Al inalizar la unidad, el alumno:
 Un i d a d Co n t i n U i da d Objetivos Al inalizar la unidad, el alumno: Identificará cuándo una función es continua en un punto y en un intervalo. Aplicará las operaciones de las funciones continuas
Un i d a d Co n t i n U i da d Objetivos Al inalizar la unidad, el alumno: Identificará cuándo una función es continua en un punto y en un intervalo. Aplicará las operaciones de las funciones continuas
Límite de una función Funciones continuas
 Límite de una función Funciones continuas Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid 2014-2015 1 LÍMITE CUANDO LA VARIABLE TIENDE A INFINITO. 3 1. Límite cuando la variable tiende
Límite de una función Funciones continuas Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid 2014-2015 1 LÍMITE CUANDO LA VARIABLE TIENDE A INFINITO. 3 1. Límite cuando la variable tiende
SOLUCIONES Límites y continuidad de funciones de varias variables 06-07
 SOLUCIONES Límites continuidad de funciones de varias variables 6-7 Determinar las guientes funciones son acotadas: a z sen ( + ) cos( - e ), sen ( + ) cos( - e ), luego, es acotada: b z sen + sen Es acotada,
SOLUCIONES Límites continuidad de funciones de varias variables 6-7 Determinar las guientes funciones son acotadas: a z sen ( + ) cos( - e ), sen ( + ) cos( - e ), luego, es acotada: b z sen + sen Es acotada,
Límites y Continuidad de funciones de varias variables
 1- Se construe un depósito de propano adosando dos hemisferios a los etremos de un cilindro circular recto Epresar el volumen V de ese depósito en función del radio r del cilindro de su altura h - Determinar
1- Se construe un depósito de propano adosando dos hemisferios a los etremos de un cilindro circular recto Epresar el volumen V de ese depósito en función del radio r del cilindro de su altura h - Determinar
Funciones: Límites y continuidad.
 Límites finitos de sucesiones. Funciones: límites y continuidad Matemáticas I Funciones: Límites y continuidad. + Decimos que una sucesión numérica ( ) n= tiene por límite r R y se escribe =r o de forma
Límites finitos de sucesiones. Funciones: límites y continuidad Matemáticas I Funciones: Límites y continuidad. + Decimos que una sucesión numérica ( ) n= tiene por límite r R y se escribe =r o de forma
(Soluc: a) ; b)- ; c)± ; d)± ; e)± ; f) 0; g)± ; h) ; i)± ; x 1. 3 f) x e. lim x 2 x 1. lim x. lim. lim log x. lim. lim. x 1 (x 1)(x 4) lim x 1.
 + ln 4 + f + 5 EJERCICIOS de LÍMITES de FUNCIONES y CONTINUIDAD. Calcular los siguientes límites no indeterminados : 4 + + 4 f) e log g) 0, + 4 d) i) 0+ + 4 e) j) 4. Dada la gráfica de la figura, indicar
+ ln 4 + f + 5 EJERCICIOS de LÍMITES de FUNCIONES y CONTINUIDAD. Calcular los siguientes límites no indeterminados : 4 + + 4 f) e log g) 0, + 4 d) i) 0+ + 4 e) j) 4. Dada la gráfica de la figura, indicar
LÍMITES Y CONTINUIDAD
 LÍMITES Y CONTINUIDAD Tema 4: LÍMITES Y CONTINUIDAD. Índice:. Límite de una función en un punto. Límites laterales.. Límites en el infinito.. Cálculo de límites... Propiedades de los límites... Límites
LÍMITES Y CONTINUIDAD Tema 4: LÍMITES Y CONTINUIDAD. Índice:. Límite de una función en un punto. Límites laterales.. Límites en el infinito.. Cálculo de límites... Propiedades de los límites... Límites
Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización.
 TEMA 1 Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización. Límite finito en un punto: Consideremos una función f definida en las proimidades
TEMA 1 Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización. Límite finito en un punto: Consideremos una función f definida en las proimidades
TEORÍA DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 1: Funciones de una variable real. Domingo Pestana Galván José Manuel Rodríguez García
 TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 1: Funciones de una variable real Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 CAPÍTULO 1.
TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 1: Funciones de una variable real Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 CAPÍTULO 1.
TEMA 10.-LÍMITES DE FUNCIONES Y CONTINUIDAD
 TEMA.-Límites de funciones y continuidad.- Matemáticas I. SUCESIONES DE NÚMEROS REALES TEMA.-LÍMITES DE FUNCIONES Y CONTINUIDAD Una sucesión de números reales es un conjunto de números (a, a, a 3,...,
TEMA.-Límites de funciones y continuidad.- Matemáticas I. SUCESIONES DE NÚMEROS REALES TEMA.-LÍMITES DE FUNCIONES Y CONTINUIDAD Una sucesión de números reales es un conjunto de números (a, a, a 3,...,
Unidad 9. Límites, continuidad y asíntotas
 Unidad 9. Límites, continuidad y asíntotas. Límite de una función en un punto Piensa y calcula Halla mentalmente y completa la tabla siguiente:,9,99,,00,0, f () =,9,99,,00,0, f () =,9,99 3, 3 3,00 3,0
Unidad 9. Límites, continuidad y asíntotas. Límite de una función en un punto Piensa y calcula Halla mentalmente y completa la tabla siguiente:,9,99,,00,0, f () =,9,99,,00,0, f () =,9,99 3, 3 3,00 3,0
Topología en R n. Continuidad de funciones de varias variables
 . Continuidad de funciones de varias variables María Muñoz Guillermo [email protected] U.P.C.T. Matemáticas I (1 o Grado en Ingeniería Electrónica Industrial y Automática) M. Muñoz (U.P.C.T.) Continuidad
. Continuidad de funciones de varias variables María Muñoz Guillermo [email protected] U.P.C.T. Matemáticas I (1 o Grado en Ingeniería Electrónica Industrial y Automática) M. Muñoz (U.P.C.T.) Continuidad
Capítulo 1 LÍMITES Y CONTINUIDAD Versión Beta 1.1
 Capítulo 1 LÍMITES Y CONTINUIDAD Versión Beta 1.1 www.mathspace.jimdo.com Tabla de contenido Capítulo 1...1 LÍMITES Y CONTINUIDAD...1 1.1. LÍMITES...2 1.1.1 Definición formal...2 1.1.2. Cálculo de límites...2
Capítulo 1 LÍMITES Y CONTINUIDAD Versión Beta 1.1 www.mathspace.jimdo.com Tabla de contenido Capítulo 1...1 LÍMITES Y CONTINUIDAD...1 1.1. LÍMITES...2 1.1.1 Definición formal...2 1.1.2. Cálculo de límites...2
Cálculo Diferencial e Integral - Límite y continuidad. Farith J. Briceño N.
 Cálculo Diferencial e Integral - Límite y continuidad. Farith J. Briceño N. Objetivos a cubrir Código : MAT-CDI.5 Límites laterales. Cálculo de límites. Límites en el infinito. Límites infinitos Límites
Cálculo Diferencial e Integral - Límite y continuidad. Farith J. Briceño N. Objetivos a cubrir Código : MAT-CDI.5 Límites laterales. Cálculo de límites. Límites en el infinito. Límites infinitos Límites
LÍMITE DE UNA FUNCIÓN EN UN PUNTO
 pág. LÍMITE DE UNA FUNCIÓN EN UN PUNTO c significa que toma valores cada vez más próimos a c. Se lee tiende a c. Por ejemplo: ; `9; `; `; `; `; `9; `; `999; Es una secuencia de números cada vez más próimos
pág. LÍMITE DE UNA FUNCIÓN EN UN PUNTO c significa que toma valores cada vez más próimos a c. Se lee tiende a c. Por ejemplo: ; `9; `; `; `; `; `9; `; `999; Es una secuencia de números cada vez más próimos
Facultad de Ciencias Naturales y Museo Trabajo Práctico Nº Cátedra de Matemática
 Facultad de Ciencias Naturales y Museo Trabajo Práctico Nº 6-0- TRABAJO PRÁCTICO Nº 6 Parte I Intervalos. Límite de una función: definición, teoremas, límites laterales, límites infinitos, límites al infinito.
Facultad de Ciencias Naturales y Museo Trabajo Práctico Nº 6-0- TRABAJO PRÁCTICO Nº 6 Parte I Intervalos. Límite de una función: definición, teoremas, límites laterales, límites infinitos, límites al infinito.
= 1. x = 3: Lím = Asíntota vertical en x = 3: = 0 ; No se anula nunca. Punto de corte con OY es (0, 3) 3 x
 Modelo 4. Problema A.- (Calificación máima: puntos) 4 si Se considera la función real de variable real f ( ) si > a) Determínense las asíntotas de la función y los puntos de corte con los ejes. a. Asíntotas
Modelo 4. Problema A.- (Calificación máima: puntos) 4 si Se considera la función real de variable real f ( ) si > a) Determínense las asíntotas de la función y los puntos de corte con los ejes. a. Asíntotas
(Soluc: a) ; b)- ; c)± ; d)± ; e)± ; f) 0; g)± ; h) ; i)± ; x 1. 3 f) x e. lim x 2 x 1. lim x. lim. lim log x. lim. lim. x 1 (x 1)(x 4) lim x 1.
 + ln 4 + f + 5 EJERCICIOS de LÍMITES DE FUNCIONES y CONTINUIDAD. Calcular los siguientes límites no indeterminados : 4 + + 4 f) e log 0, + 4 i) 0+ + 4 4. Dada la gráfica de la figura, indicar si eiste
+ ln 4 + f + 5 EJERCICIOS de LÍMITES DE FUNCIONES y CONTINUIDAD. Calcular los siguientes límites no indeterminados : 4 + + 4 f) e log 0, + 4 i) 0+ + 4 4. Dada la gráfica de la figura, indicar si eiste
1. Halla el dominio, el recorrido, las asíntotas y los límites e imágenes que se indican para cada gráfica. y asíntota vertical de:
 Identificación gráfica de funciones, límites asíntotas Al observar la gráfica de una función es posible determinar gran cantidad de parámetros características de dicha función aunque no conozcamos su epresión,
Identificación gráfica de funciones, límites asíntotas Al observar la gráfica de una función es posible determinar gran cantidad de parámetros características de dicha función aunque no conozcamos su epresión,
INTRODUCCIÓN. FUNCIONES. LÍMITES.
 INTRODUCCIÓN. FUNCIONES. LÍMITES. Este capítulo puede considerarse como una prolongación y extensión del anterior, límite de sucesiones, al campo de las funciones. Se inicia recordando el concepto de función
INTRODUCCIÓN. FUNCIONES. LÍMITES. Este capítulo puede considerarse como una prolongación y extensión del anterior, límite de sucesiones, al campo de las funciones. Se inicia recordando el concepto de función
Universidad Abierta y a Distancia de México. 2 cuatrimestre. Cálculo diferencial. Unidad 2. Límites y continuidad
 Unidad Límites y continuidad Universidad Abierta y a Distancia de Méico cuatrimestre Cálculo diferencial Unidad Límites y continuidad Educación Abierta y a Distancia * Ciencias Eactas, Ingenierías y Tecnologías
Unidad Límites y continuidad Universidad Abierta y a Distancia de Méico cuatrimestre Cálculo diferencial Unidad Límites y continuidad Educación Abierta y a Distancia * Ciencias Eactas, Ingenierías y Tecnologías
f, y el Funciones de varias variables Función de dos variables Definición. Es una función f que asigna a cada pareja ordenada ( xy, ) de D un
 Funciones de varias variables Función de dos variables Definición. Es una función f que asigna a cada pareja ordenada (, ) de D un único número real f (, ). El conjunto D es el dominio de f, el correspondiente
Funciones de varias variables Función de dos variables Definición. Es una función f que asigna a cada pareja ordenada (, ) de D un único número real f (, ). El conjunto D es el dominio de f, el correspondiente
Límites y continuidad
 9 Matemáticas I : Cálculo diferencial en IR Tema 9 Límites y continuidad 9. Límite y continuidad de una función en un punto Definición 9.- Un punto IR se dice punto de acumulación de un conjunto A si,
9 Matemáticas I : Cálculo diferencial en IR Tema 9 Límites y continuidad 9. Límite y continuidad de una función en un punto Definición 9.- Un punto IR se dice punto de acumulación de un conjunto A si,
Razonar si son ciertas o falsas las siguientes igualdades: Asociar cada función con su gráfica. (19) Si x 2 > 0, entonces x > 0.
 Razonar si son ciertas o falsas las siguientes igualdades: ) a + b) = a + b ) ) a + b = a + b e = e 4) a + ab b + a = a 5) 8 + = 6) a ) = a 5 7) 8) a = a 4 = 4 9) 9 = 0) ) e ) = e + = ) e ln = ) ln 0 =
Razonar si son ciertas o falsas las siguientes igualdades: ) a + b) = a + b ) ) a + b = a + b e = e 4) a + ab b + a = a 5) 8 + = 6) a ) = a 5 7) 8) a = a 4 = 4 9) 9 = 0) ) e ) = e + = ) e ln = ) ln 0 =
Problemas de limites, continuidad y derivabilidad. Calcula los siguientes límites de funciones racionales, irracionales y exponenciales
 Problemas de limites, continuidad y derivabilidad Calcula los siguientes límites de funciones racionales, irracionales y eponenciales - ) = [ = = = = = = = . ) = [0. ] = = = = = = = = = 0 = [ = p=
Problemas de limites, continuidad y derivabilidad Calcula los siguientes límites de funciones racionales, irracionales y eponenciales - ) = [ = = = = = = = . ) = [0. ] = = = = = = = = = 0 = [ = p=
Continuidad de funciones reales y vectoriales de variable vectorial
 Capítulo 6 Continuidad de funciones reales y vectoriales de variable vectorial 6.1. Introducción Hasta el momento hemos estudiado funciones reales de variable real, es decir, funciones de la forma f :
Capítulo 6 Continuidad de funciones reales y vectoriales de variable vectorial 6.1. Introducción Hasta el momento hemos estudiado funciones reales de variable real, es decir, funciones de la forma f :
Mostrará la convergencia o divergencia de funciones mediante el criterio de límite de una función en un punto.
 Un i d a d Lí m i t e s Objetivos Al inalizar la unidad, el alumno: Mostrará la convergencia o divergencia de funciones mediante el criterio de límite de una función en un punto. Calculará límites de funciones
Un i d a d Lí m i t e s Objetivos Al inalizar la unidad, el alumno: Mostrará la convergencia o divergencia de funciones mediante el criterio de límite de una función en un punto. Calculará límites de funciones
UNIDAD 9 LÍMITES DE FUNCIONES. CONTINUIDAD.
 IES Padre Poveda (Guadi) UNIDAD 9 LÍMITES DE FUNCIONES. CONTINUIDAD.. Límite de una función en un punto... Límites laterales... Límite de una función en un punto.. Límites en el infinito... Comportamiento
IES Padre Poveda (Guadi) UNIDAD 9 LÍMITES DE FUNCIONES. CONTINUIDAD.. Límite de una función en un punto... Límites laterales... Límite de una función en un punto.. Límites en el infinito... Comportamiento
Límite y Continuidad de funciones de una variable
 Introducción Límite y de funciones de una variable Departamento de Matemática Aplicada Universitat Politècnica de València, España Fundamentos Matemáticos para la Ingenieria Civil Límite y de funciones
Introducción Límite y de funciones de una variable Departamento de Matemática Aplicada Universitat Politècnica de València, España Fundamentos Matemáticos para la Ingenieria Civil Límite y de funciones
f : R R Definición 2. Se llama dominio de una función f (lo denotaremos por Dom f) al conjunto de valores para los que está bien definida f(x) :
 Resumen Tema 2: Funciones Concepto de función. Gráficas Definición. Se llama función (real de variable real) a toda aplicación f : R R que a cada número le hace corresponder otro valor f(). f() Definición
Resumen Tema 2: Funciones Concepto de función. Gráficas Definición. Se llama función (real de variable real) a toda aplicación f : R R que a cada número le hace corresponder otro valor f(). f() Definición
Tema 3. LÍMITES Y CONTINUIDAD DE FUNCIONES
 Tema LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g ( ) ENT[ ] h ( ) i ( ) 4 en el punto Para ello, damos a valores próimos
Tema LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g ( ) ENT[ ] h ( ) i ( ) 4 en el punto Para ello, damos a valores próimos
Funciones en R n Conceptos métricos y topológicos Límites y continuidad en R 2. Funciones en R n : nociones topológicas
 Funciones en R n : nociones topológicas 1 Funciones en R n 2 Conceptos métricos y topológicos 3 Límites y continuidad en R 2 Definición Definición Llamaremos función escalar real de n variables reales,
Funciones en R n : nociones topológicas 1 Funciones en R n 2 Conceptos métricos y topológicos 3 Límites y continuidad en R 2 Definición Definición Llamaremos función escalar real de n variables reales,
SOLUCIONES DE LAS ACTIVIDADES Págs. 239 a 257
 TEMA. LÍMITES Y CONTINUIDAD SOLUCIONES DE LAS ACTIVIDADES Págs. 9 a 7 Página 9 Página. a) f() 0. a) f() 0, 0,0 0,00 0,000 f(),,9,99,999,9,99,999,9999 f() 00 0.000 0 6 0 8 b) f() 0 0, 0,0 0,00 0,000 f(),,0,00,000
TEMA. LÍMITES Y CONTINUIDAD SOLUCIONES DE LAS ACTIVIDADES Págs. 9 a 7 Página 9 Página. a) f() 0. a) f() 0, 0,0 0,00 0,000 f(),,9,99,999,9,99,999,9999 f() 00 0.000 0 6 0 8 b) f() 0 0, 0,0 0,00 0,000 f(),,0,00,000
TEMA 2. FUNCIONES REALES DE VARIABLE REAL 2.2. LÍMITES Y CONTINUIDAD
 TEMA. FUNCIONES REALES DE VARIABLE REAL.. LÍMITES Y CONTINUIDAD . FUNCIONES REALES DE VARIABLE REAL.. LÍMITES Y CONTINUIDAD... LÍMITE DE UNA FUNCIÓN EN UN PUNTO... LÍMITES INFINITOS... LÍMITES EN EL INFINITO..4.
TEMA. FUNCIONES REALES DE VARIABLE REAL.. LÍMITES Y CONTINUIDAD . FUNCIONES REALES DE VARIABLE REAL.. LÍMITES Y CONTINUIDAD... LÍMITE DE UNA FUNCIÓN EN UN PUNTO... LÍMITES INFINITOS... LÍMITES EN EL INFINITO..4.
Función de dos variables
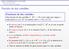 Funciones escalares de dos variables Función de dos variables Funciones de dos variables Una función de dos variables F : R 2 R es una regla que asigna a cada punto (x, y) R 2 un número real z = F (x,
Funciones escalares de dos variables Función de dos variables Funciones de dos variables Una función de dos variables F : R 2 R es una regla que asigna a cada punto (x, y) R 2 un número real z = F (x,
Normas Equivalentes. Espacios Normados de Dimensión Finita
 Capítulo 2 Normas Equivalentes. Espacios Normados de Dimensión Finita Dos son los resultados más importantes que, sobre la equivalencia de normas, veremos en este capítulo. El primero de ellos establece
Capítulo 2 Normas Equivalentes. Espacios Normados de Dimensión Finita Dos son los resultados más importantes que, sobre la equivalencia de normas, veremos en este capítulo. El primero de ellos establece
1. LÍMITE DE UNA FUNCIÓN REAL
 INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resolución Nº 88 de noviembre.8/ Secretaria De Educación Distrital REGISTRO DANE Nº-99 Teléfono 6 Barrio Bastidas Santa Marta DEPARTAMENTO DE MATEMATICAS
INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resolución Nº 88 de noviembre.8/ Secretaria De Educación Distrital REGISTRO DANE Nº-99 Teléfono 6 Barrio Bastidas Santa Marta DEPARTAMENTO DE MATEMATICAS
32 EJERCICIOS de CONTINUIDAD 2º BACH.
 3 EJERCICIOS de CONTINUIDAD º BACH. RECORDAR: f() continua en = a lim f(a) Es decir: Una función es continua en un punto si el límite a coincide con la imagen en dicho punto. A efectos prácticos, para
3 EJERCICIOS de CONTINUIDAD º BACH. RECORDAR: f() continua en = a lim f(a) Es decir: Una función es continua en un punto si el límite a coincide con la imagen en dicho punto. A efectos prácticos, para
TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS
 Estudios J.Concha ( fundado en 00) ESO, BACHILLERATO y UNIVERSIDAD Departamento Bachillerato MATEMATICAS º BACHILLERATO Profesores Javier Concha y Ramiro Froilán Tema 8 Límites de funciones, continuidad
Estudios J.Concha ( fundado en 00) ESO, BACHILLERATO y UNIVERSIDAD Departamento Bachillerato MATEMATICAS º BACHILLERATO Profesores Javier Concha y Ramiro Froilán Tema 8 Límites de funciones, continuidad
9 Continuidad. Solucionario ACTIVIDADES INICIALES EJERCICIOS PROPUESTOS. 9.I. Dibuja la gráfica de las siguientes funciones.
 Solucionario 9 Continuidad 9.I. Dibuja la gráfica de las guientes funciones. ACTIVIDADES INICIALES a) < f( ) > b) f ( ) a) Si (, ). El segmento de recta pasa por el punto (, ) y se acerca al (, ). Si [,
Solucionario 9 Continuidad 9.I. Dibuja la gráfica de las guientes funciones. ACTIVIDADES INICIALES a) < f( ) > b) f ( ) a) Si (, ). El segmento de recta pasa por el punto (, ) y se acerca al (, ). Si [,
TEMA 9 : LÍMITES DE FUNCIONES. CONTINUIDAD
 MATEMÁTICAS I LÍMITES-CONTINUIDAD TEMA 9 : LÍMITES DE FUNCIONES. CONTINUIDAD 1. LÍMITES EN EL INFINITO En ocasiones interesa estudiar el comportamiento de una función (la tendencia) cuando los valores
MATEMÁTICAS I LÍMITES-CONTINUIDAD TEMA 9 : LÍMITES DE FUNCIONES. CONTINUIDAD 1. LÍMITES EN EL INFINITO En ocasiones interesa estudiar el comportamiento de una función (la tendencia) cuando los valores
Tema 3. LÍMITES Y CONTINUIDAD DE FUNCIONES
 1 Tema LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g( ) ENT[ ] h ( ) i ( ) 4 en el punto = Para ello, damos a valores
1 Tema LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g( ) ENT[ ] h ( ) i ( ) 4 en el punto = Para ello, damos a valores
******* Enunciados de Problemas *******
 ******* Enunciados de Problemas ******* CÁLCULO ESCUELA SUPERIOR DE LA MARINA CIVIL DIPLOMADO EN MÁQUINAS NAVALES DIPLOMADO EN NAVEGACIÓN MARÍTIMA ISIDORO PONTE ESMC EL NÚMERO REAL Sea o un número racional
******* Enunciados de Problemas ******* CÁLCULO ESCUELA SUPERIOR DE LA MARINA CIVIL DIPLOMADO EN MÁQUINAS NAVALES DIPLOMADO EN NAVEGACIÓN MARÍTIMA ISIDORO PONTE ESMC EL NÚMERO REAL Sea o un número racional
- Fernando Sánchez - Departamento de Matemáticas - Universidad de Extremadura. Cálculo II. Funciones. Límites y continuidad
 - Fernando Sánchez - - 6 Funciones Cálculo II de Rn en Rm Límites y continuidad En este capítulo se van a estudiar funciones f : A R n m donde A es un conjunto en R n, f = (f 1,..., f m ), x = (x 1,...,
- Fernando Sánchez - - 6 Funciones Cálculo II de Rn en Rm Límites y continuidad En este capítulo se van a estudiar funciones f : A R n m donde A es un conjunto en R n, f = (f 1,..., f m ), x = (x 1,...,
TEMA 9- LÍMITES Y CONTINUIDAD MATEMÁTICAS I 1º BACHILLERATO 1 TEMA 9 LÍMITES DE FUNCIONES, CONTINUIDAD Y RAMAS INFINITAS
 TEMA 9- LÍMITES Y CONTINUIDAD MATEMÁTICAS I 1º BACHILLERATO 1 TEMA 9 LÍMITES DE FUNCIONES, CONTINUIDAD Y RAMAS INFINITAS TEMA 9- LÍMITES Y CONTINUIDAD MATEMÁTICAS I 1º BACHILLERATO 9.1. LÍMITE DE UNA FUNCIÓN
TEMA 9- LÍMITES Y CONTINUIDAD MATEMÁTICAS I 1º BACHILLERATO 1 TEMA 9 LÍMITES DE FUNCIONES, CONTINUIDAD Y RAMAS INFINITAS TEMA 9- LÍMITES Y CONTINUIDAD MATEMÁTICAS I 1º BACHILLERATO 9.1. LÍMITE DE UNA FUNCIÓN
LIMITES Y CONTINUIDAD
 Contenidos LIMITES Y CONTINUIDAD. Limite de una función en un punto.. Limite en el infinito. Asíntotas de una curva.. Calculo de límites..4 Función continua en un punto y en un intervalo..5 Operaciones
Contenidos LIMITES Y CONTINUIDAD. Limite de una función en un punto.. Limite en el infinito. Asíntotas de una curva.. Calculo de límites..4 Función continua en un punto y en un intervalo..5 Operaciones
De los tres conceptos que se estudian es este tema, funciones, límites y continuidad, el primero y el último son muy sencillos de comprender.
 INTRODUCCIÓN. FUNCIONES. LÍMITES. Este tema lo iniciamos recordando el concepto de función y dando algunas nociones básicas sobre funciones, para dar paso al estudio del límite de una función, cálculo
INTRODUCCIÓN. FUNCIONES. LÍMITES. Este tema lo iniciamos recordando el concepto de función y dando algunas nociones básicas sobre funciones, para dar paso al estudio del límite de una función, cálculo
FUNCIONES VECTORIALES DE VARIABLE ESCALAR
 CAPITULO II CALCULO II 2.1 CONCEPTOS BÁSICOS FUNCIONES VECTORIALES DE VARIABLE ESCALAR Una función vectorial (o a valores vectoriales) de una variable real (escalar), es una función del en la cual, a cada
CAPITULO II CALCULO II 2.1 CONCEPTOS BÁSICOS FUNCIONES VECTORIALES DE VARIABLE ESCALAR Una función vectorial (o a valores vectoriales) de una variable real (escalar), es una función del en la cual, a cada
Tema 1: Cálculo diferencial en varias variables ENUNCIADO Y RESPUESTA AL EJERCICIO: ENUNCIADO
 Tema : Cálculo diferencial en varias variables FECHA: 3/3/ TIEMPO RECOMENDADO: / Hora Puntuación/TOTAL:,5/ Sea la función f(,) definida de la siguiente forma en todo (,) de IR : Y RESPUESTA AL EJERCICIO:
Tema : Cálculo diferencial en varias variables FECHA: 3/3/ TIEMPO RECOMENDADO: / Hora Puntuación/TOTAL:,5/ Sea la función f(,) definida de la siguiente forma en todo (,) de IR : Y RESPUESTA AL EJERCICIO:
8. FUNCIONES DE VARIAS VARIABLES.
 8. FUNCIONES DE VARIAS VARIABLES. En este tema comenzamos el análisis de funciones de varias variables reales. Comenzaremos estudiando el espacio euclídeo n-dimensional para continuar el estudio (sencillo)
8. FUNCIONES DE VARIAS VARIABLES. En este tema comenzamos el análisis de funciones de varias variables reales. Comenzaremos estudiando el espacio euclídeo n-dimensional para continuar el estudio (sencillo)
Longitud, áreas y volúmenes. Trigonometría. Circunferencia de radio R Círculo de radio R. 1 Triángulo de base B y altura H A = (BH ) 2
 Longitud, áreas y volúmenes Circunferencia de radio R Círculo de radio R A πr L πr Triángulo de base B y altura H A (BH ) Cuadrado de lado L A L Rectángulo de base B y altura H Superficie esférica A 4πR
Longitud, áreas y volúmenes Circunferencia de radio R Círculo de radio R A πr L πr Triángulo de base B y altura H A (BH ) Cuadrado de lado L A L Rectángulo de base B y altura H Superficie esférica A 4πR
TEMA 6 : LÍMITES DE FUNCIONES. CONTINUIDAD
 TEMA 6 : DE FUNCIONES. CONTINUIDAD. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. Ejercicio: Observa la gráfica siguiente: a) Estudia el dominio, el recorrido y la continuidad de f(). b) Indica si eisten los límites
TEMA 6 : DE FUNCIONES. CONTINUIDAD. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. Ejercicio: Observa la gráfica siguiente: a) Estudia el dominio, el recorrido y la continuidad de f(). b) Indica si eisten los límites
Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) x u + f
 1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
Existencia y unicidad de soluciones
 48 Análisis matemático para Ingeniería. M. MOLERO; A. SALVADOR; T. MENARGUEZ; L. GARMENDIA CAPÍTULO 8 Eistencia y unicidad de soluciones En el capítulo anterior se han introducido las ecuaciones diferenciales
48 Análisis matemático para Ingeniería. M. MOLERO; A. SALVADOR; T. MENARGUEZ; L. GARMENDIA CAPÍTULO 8 Eistencia y unicidad de soluciones En el capítulo anterior se han introducido las ecuaciones diferenciales
José Vicente Ugarte Susaeta. Profesor de la Universidad Comercial de Deusto
 MATEMÁTICAS PARA ECONOMÍA Y EMPRESA CÁLCULO DE UNA VARIABLE José Vicente Ugarte Susaeta Profesor de la Universidad Comercial de Deusto Con la colaboración de Miguel Ángel Larrinaga Ojanguren Profesor de
MATEMÁTICAS PARA ECONOMÍA Y EMPRESA CÁLCULO DE UNA VARIABLE José Vicente Ugarte Susaeta Profesor de la Universidad Comercial de Deusto Con la colaboración de Miguel Ángel Larrinaga Ojanguren Profesor de
el blog de mate de aida CSI: Límites y continuidad. . Se lee x tiende a x por la derecha. , se expresa así: , se expresa así: por la derecha)
 pág. LÍMITE DE UNA FUNCIÓN EN UN PUNTO gnifica que toma valores cada vez más próimos a. Se lee tiende a. Ejemplo: ;,9;,;,;,8;,;,9;,;,999; Es una secuencia de números cada vez más próimos a. Escribimos.
pág. LÍMITE DE UNA FUNCIÓN EN UN PUNTO gnifica que toma valores cada vez más próimos a. Se lee tiende a. Ejemplo: ;,9;,;,;,8;,;,9;,;,999; Es una secuencia de números cada vez más próimos a. Escribimos.
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a
Cálculo II. Tijani Pakhrou
 Cálculo II Tijani Pakhrou Índice general 1. Nociones topológicas en R n 1 1.1. Distancia y norma euclídea en R n.................... 1 1.2. Bolas abiertas y cerradas en R n..................... 3 1.3.
Cálculo II Tijani Pakhrou Índice general 1. Nociones topológicas en R n 1 1.1. Distancia y norma euclídea en R n.................... 1 1.2. Bolas abiertas y cerradas en R n..................... 3 1.3.
LÍMITES Y CONTINUIDAD
 LÍMITES Y CONTINUIDAD. LÍMITE DE UNA FUNCIÓN EN UN PUNTO Dada una función f(), diremos que el ite de f() cuando tiende a a es el número real L y lo escribiremos f() = L, si al tomar cada vez valores más
LÍMITES Y CONTINUIDAD. LÍMITE DE UNA FUNCIÓN EN UN PUNTO Dada una función f(), diremos que el ite de f() cuando tiende a a es el número real L y lo escribiremos f() = L, si al tomar cada vez valores más
Se dice que la variable L se hace infinita cuando llega a ser mayor, en valor absoluto, que cualquier número dado por grande que sea.
 DEFINICIÓN DE LIMITE: Se dice que una constante A es el Límite de una variable cuando ésta se aproima a aquélla, de modo que la diferencia! A, en valor absoluto, puede hacerse tan pequeña como se quiera.
DEFINICIÓN DE LIMITE: Se dice que una constante A es el Límite de una variable cuando ésta se aproima a aquélla, de modo que la diferencia! A, en valor absoluto, puede hacerse tan pequeña como se quiera.
FUNCIONES DE UNA VARIABLE
 FUNCIONES DE UNA VARIABLE 1- Definiciones 2- Algunas funciones reales 3- Ecuaciones de curvas planas en coordenadas cartesianas 4- Coordenadas polares 5- Coordenadas paramétricas 6- Funciones hiperbólicas
FUNCIONES DE UNA VARIABLE 1- Definiciones 2- Algunas funciones reales 3- Ecuaciones de curvas planas en coordenadas cartesianas 4- Coordenadas polares 5- Coordenadas paramétricas 6- Funciones hiperbólicas
FUNCIONES DE DOS VARIABLES
 FUNCIONES DE DOS VARIABLES - Funciones de dos variables reales - Límites 3- Continuidad de funciones de dos variables 4- Derivabilidad de funciones de dos variables 5- Diferenciabilidad de funciones de
FUNCIONES DE DOS VARIABLES - Funciones de dos variables reales - Límites 3- Continuidad de funciones de dos variables 4- Derivabilidad de funciones de dos variables 5- Diferenciabilidad de funciones de
Tema 5. Límites y continuidad de funciones
 Matemáticas Aplicadas a las Ciencias Sociales II Análisis: Límites y continuidad 97 Tema 5 Límites y continuidad de funciones Límite de una función en un punto Idea inicial Si una función f está definida
Matemáticas Aplicadas a las Ciencias Sociales II Análisis: Límites y continuidad 97 Tema 5 Límites y continuidad de funciones Límite de una función en un punto Idea inicial Si una función f está definida
Límites y Derivadas 2d. Matemáticas para Ingeniería I Otono 2016 Lilia Meza Montes IFUAP
 Límites y Derivadas d Matemáticas para Ingeniería I Otono 016 Lilia Meza Montes IFUAP Función de una variable Función : regla que asocia un único valor a cada elemento de un conjunto. R y() R 0 Dominio:
Límites y Derivadas d Matemáticas para Ingeniería I Otono 016 Lilia Meza Montes IFUAP Función de una variable Función : regla que asocia un único valor a cada elemento de un conjunto. R y() R 0 Dominio:
2-LÍMITES Y CONTINUIDAD
 -Distancia entre dos números: d(a,b)= -LÍMITES Y CONTINUIDAD Sea f una función a y L R 0 Propiedad- =L Ejemplos: -f()= + = = = ( = = =5 ( ) - = = = ( ) - = M > > para suficientemente próimos a a =a es
-Distancia entre dos números: d(a,b)= -LÍMITES Y CONTINUIDAD Sea f una función a y L R 0 Propiedad- =L Ejemplos: -f()= + = = = ( = = =5 ( ) - = = = ( ) - = M > > para suficientemente próimos a a =a es
- Fernando Sánchez - Departamento de Matemáticas - Universidad de Extremadura. Cálculo II. Funciones. Límites y continuidad
 - Fernando Sánchez - - 6 Funciones Cálculo II de Rn en Rm Límites y continuidad En este capítulo se van a estudiar funciones f : A R n R m donde A es un conjunto en R n, f = (f 1,..., f m ), x = (x 1,...,
- Fernando Sánchez - - 6 Funciones Cálculo II de Rn en Rm Límites y continuidad En este capítulo se van a estudiar funciones f : A R n R m donde A es un conjunto en R n, f = (f 1,..., f m ), x = (x 1,...,
CÁLCULO II Funciones de varias variables
 CÁLCULO II Funciones de varias variables Facultad de Informática (UPM) Facultad de Informática (UPM) () CÁLCULO II Funciones de varias variables 1 / 36 Funciones de varias variables Función vectorial de
CÁLCULO II Funciones de varias variables Facultad de Informática (UPM) Facultad de Informática (UPM) () CÁLCULO II Funciones de varias variables 1 / 36 Funciones de varias variables Función vectorial de
GUIA DE MATEMATICAS I, CAPITULO III
 UNIVERSIDAD NACIONAL EXPERIMENTAL DE GUAYANA VICE-RECTORADO ACADEMICO DEPARTAMENTO DE CIENCIA Y TECNOLOGIA AREA DE MATEMATICAS GUIA DE MATEMATICAS I, CAPITULO III Prof. Orlando Baisdem Pérez Puerto Ordaz,
UNIVERSIDAD NACIONAL EXPERIMENTAL DE GUAYANA VICE-RECTORADO ACADEMICO DEPARTAMENTO DE CIENCIA Y TECNOLOGIA AREA DE MATEMATICAS GUIA DE MATEMATICAS I, CAPITULO III Prof. Orlando Baisdem Pérez Puerto Ordaz,
1. Medida Exterior. Medida de Lebesgue en R n
 1. La integral de Lebesgue surge del desarrollo de la integral de Riemann, ante las dificultades encontradas en las propiedades de paso al ĺımite para calcular la integral de una función definida como
1. La integral de Lebesgue surge del desarrollo de la integral de Riemann, ante las dificultades encontradas en las propiedades de paso al ĺımite para calcular la integral de una función definida como
