Taller Trigonometría
|
|
|
- Sandra Salazar Morales
- hace 10 años
- Vistas:
Transcripción
1 Taller Trigonometría 1. Verificar si los siguientes ejercicios son o no identidades trigonométricas: ( 1 cos )( 1 cos ) sen b. Csc sec cos sen Cotan c. sec - Csc tan - Cotan sen cos sen d. 1 1 cos cos sec 6 - tan sec tan f. sen 1- tan cos 1- cotan sen cos. La gran Pirámide de Egipto es regular y de base cuadrad El ángulo de inclinación de las caras respecto a la base es de 5º, desde una distancia de 100m perpendicular al punto medio de un lado de la base, se ve la punta de la Pirámide con un ángulo de elevación de 34º, cuál es la altura de este monumento de la humanidad? 3. Un golfista golpea la pelota desde el punto de saque (te) y la envía hasta le punto P de la figura; a qué distancia se encuentra la pelota del hoyo? 4. Determine el valor de la recta BC de la figura, teniendo en cuenta la información suministrada en el dibujo. 5. Encuentre el valor exacto de cada una de las seis razones trigonométricas del ángulo teta para cada figur
2 6. un aeroplano se encuentra volando a una altura de 7600 m cuando los motores fallan repentinament Determinar el ángulo de deslizamiento ϴ, necesario para que el aeroplano pueda llegar a un terreno plano que se encuentra a 5000 m del lugar donde sucede la falla de los motores. (vea la figura adjunta) 7. Un vigilante se encuentra en la ventana de un faro como el dela figura, a una altura de 3 m sobre el nivel del océano. El ángulo de depresión del barco es de 7. a qué distancia se encuentra el barco del faro? 8. Determine el área del trapezoide isósceles de la figura 9. Obtenga el área del paralelogramo de la figura b. 10. Encuentre la distancia desde A hasta C cruzando el estanque de la figura b. Encuentre la distancia desde A hasta B 11. La torre Eiffel, la mas alta construida antes de la era de las antenas de television, fue terminada el 31 de marzo de Encuentre la altura de esta torre, (sin contar la antena de television instalada en la punta), usando la informacion dada en la figur
3 1. Un barco frente a la consta de la ciudad de Nueva York, toma una observacion de la estacion de la libertad, que es de casi 305 pies de altur Si el angulo de elevacion a la parte superior de la estatua es de 0º, a qué distancia se encuetnra el barco de la base de la estatua? 1. Haga la gráfica de cada función. Muestre al menos un periodo. y 3 sen x b. y sen x - 1 c. y - sen x d.. y cos x 4. y cos x f. y 3 sen - x g. y 3 Cos x 3 h. y 3 Cos (x 3) 14. Demuestre cada identidad trigonométrica, siguiendo el debido proceso. sec - Csc sen - cos b. sec - cos sen tan sec Csc c. sen - tan Tan cos Cotan 3 sen Cos sen Cos 3 1- sen cos 1 sen 1 sen d.. 4tan sec 1 sen 1 sen f.. 1- Cos tan - cotan sen Cos g.. 1 cos sen 1 cos - sen sec tan h. ( a sen bcos ) ( a cos - b sen ) a b i. Csc 4 Csc cot an 4 cotan j. sen (cot an tan ) sec k. (Sen Cos ) ( sen cos ) l. (tan tan )(1 - cotan cotan ) (cotan cotan )(1 - tan tan ) 0 Utilizando los teoremas del seno, coseno o pitaghoras, soluciones con el debido proceso los siguientes ejrcicios. Tome como guia las imágenes correspondientes. 15. Un granjero planea construir una cerca al rededor del campo triangular mostrado en la figur Determine la longitud de la cerca necesaria con aproximación de un hectómetro. Si desea dar tres vueltas de alambre por cada lado.
4 16. La casa de la figura interfiere con la trayectoria de la línea recta A- D, por lo que es necesario trazar una nueva trayectoria de A a B y de ahí al punto E. determine la longitud EC y el ángulo DCE, de modo que A, B, C y D se encuentren en línea rect 17. En la figura se muestra una montaña a través de la cual se desea construir un túnel. Un topógrafo ha realizado las mediciones,mostradas en la figura, para determinar la longitud de dicho túnel. Determine esa longitud (AB). 18. En el diseño de un puerto se ubica un arrecife en la carta geográfica, dirigiendo una visual desde los puntos A, B y C en el puerto. Obtenga los valores de AD y BD, si el ángulo CAD =10,5º. 19. Un granjero tiene una banda trasportadora de 10 m de longitud, como lo muestra la figura, se puede apreciar que la puerta del deposito de grano se encuentra a una altura de 6, m sobre el nivel del terreno. El granjero desea que la banda trasportadora se introduzca 1m dentro del depósito. En esta situación determine los valores de α y d. 0. Obtenga el área y el perímetro del trapezoide con una decima de aproximación. 1. Determine el area y periometro del paralelogramo ABCD de la figura de acuerdo con los datos especificados a continaucion. AD=9; CD = 1 ; <A = 76º
5 Para profundizar. Probar o refutar cada una de las siguientes identidades trigonométricas
6 Ejercicios sobre secciones cónicas. 1. Determine los vértices, el foco y la directriz de las siguientes parábolas: y 4x b. x 8y 0 c. ( x 1) 8( y ) 0 d. ( x 3 ) ( y ) 0 x x 8y 9 0 f. x 4x 4y 4 0. Con los datos dados a continuación halle la ecuación de las correspondientes parábolas: a. Vértice :(0,0); foco (,0) b. Vértice :(3,); foco (1,) c. Vértice :(0,4); directriz y d. f. g. 3. En los siguientes ejercicios halle el centro, focos, vértices y la excentricidad de cada elips c. 9x 1x 4y 36x 8y 31 0 b. 0y 1x 40y 37 0 d. 16x x y y 3x 50y 31 0 (x - 1) 9 ( y 5 ) 15 1 f. (x ) 4( y 4 ) 1 g. 4x y 1 4.En los siguientes ejercicios halle el centro, focos, vértices de las correspondientes hipérbolas. Con la ayuda de las asíntotas, represente los gráficos de cada un d. y 9x x 1 4 y ( x 1) ( y 4 ) f x 6y x y b. 1 c. 5y 4x y x x 64y 63 0
7 Referencias: Stewart, J. Cálculo. Trascendentes tempranas.cengage Learning. Sexta edición Texto guía del curso. Stewart. Weisstein, E.W: CRC Concise Encyclopedia of Mathematics. Chapman & Hall 1999 Heath, Sir Thomas (191) (en inglés). A history of Greek Mathematics vol. 1. Londres, Inglaterra: Oxford University Press. OCLC «Esquema del desarrollo histórico de la matemática» págs. pág. 6. Universidad Nacional del Nordest J J O'Connor y E F Robertson. «Abu Abdallah Mohammad ibn Jabir Al-Battani» (en inglés) (html). Consultado el «La trigonometria àrab, Al-Battani, Abu l-wafa, Ibn Yunus, Nasir al-tusi» (en catalán) (html). Consultado el «Al-Kashi, Gamshid ibn Messaoud» (en francés). Viète, François (1579). Canon mathematicus seu ad triangul Lutetia Mettayer. OCLC Boyer, Carl B.; Uta C. Merzbach (1968). A History of Mathematics. New York: Estados Unidos: John Wiley & Sons. pp ISBN
Identidades Trigonométricas
 Identidades Trigonométricas Una identidad trigonométrica es una igualdad entre expresiones que contienen funciones trigonométricas y es válida para todos los valores del ángulo en los que están definidas
Identidades Trigonométricas Una identidad trigonométrica es una igualdad entre expresiones que contienen funciones trigonométricas y es válida para todos los valores del ángulo en los que están definidas
Geometria Analítica Laboratorio #1 Sistemas de Coordenadas
 1. Verificar las identidades siguientes: 1) P (3, 3), Q( 1, 3), R(4, 0) Laboratorio #1 Sistemas de Coordenadas 2) O( 10, 2), P ( 6, 3), Q( 5, 1) 2. Demuestre que los puntos dados forman un triángulo isósceles.
1. Verificar las identidades siguientes: 1) P (3, 3), Q( 1, 3), R(4, 0) Laboratorio #1 Sistemas de Coordenadas 2) O( 10, 2), P ( 6, 3), Q( 5, 1) 2. Demuestre que los puntos dados forman un triángulo isósceles.
Universidad de la Frontera. Geometría Anaĺıtica: Departamento de Matemática y Estadística. Cĺınica de Matemática. J. Labrin - G.
 Universidad de la Frontera Departamento de Matemática y Estadística Cĺınica de Matemática 1 Geometría Anaĺıtica: J. Labrin - G.Riquelme 1. Los puntos extremos de un segmento son P 1 (2,4) y P 2 (8, 4).
Universidad de la Frontera Departamento de Matemática y Estadística Cĺınica de Matemática 1 Geometría Anaĺıtica: J. Labrin - G.Riquelme 1. Los puntos extremos de un segmento son P 1 (2,4) y P 2 (8, 4).
TÉCNICAS GRÁFICAS FUNDAMENTALES.- EJERCICIOS PROPUESTOS
 TÉCNICAS GRÁFICAS FUNDAMENTALES.- EJERCICIOS PROPUESTOS Los siguientes ejercicios tienen el propósito de hacer que el estudiante use las construcciones geométricas fundamentales y además adquiera práctica
TÉCNICAS GRÁFICAS FUNDAMENTALES.- EJERCICIOS PROPUESTOS Los siguientes ejercicios tienen el propósito de hacer que el estudiante use las construcciones geométricas fundamentales y además adquiera práctica
TEMA 6 SEMEJANZA DE TRIÁNGULOS
 Tema 6 Semejanza de triángulos Matemáticas - 4º ESO 1 TEMA 6 SEMEJANZA DE TRIÁNGULOS ESCALAS EJERCICIO 1 : En una fotografía, María y Fernando miden,5 cm y,7 cm, respectivamente; en la realidad, María
Tema 6 Semejanza de triángulos Matemáticas - 4º ESO 1 TEMA 6 SEMEJANZA DE TRIÁNGULOS ESCALAS EJERCICIO 1 : En una fotografía, María y Fernando miden,5 cm y,7 cm, respectivamente; en la realidad, María
MATERIA:_Matemáticas V 5010 CICLO ESCOLAR_ PROFESOR:
 MATERIA:_Matemáticas V 5010 CICLO ESCOLAR_2014-2015 PROFESOR: Relaciones y funciones. Para las siguientes funciones encuentra el dominio por medio de su regla de correspondencia e intervalo correspondiente
MATERIA:_Matemáticas V 5010 CICLO ESCOLAR_2014-2015 PROFESOR: Relaciones y funciones. Para las siguientes funciones encuentra el dominio por medio de su regla de correspondencia e intervalo correspondiente
UNIVERSIDAD NACIONAL DE ASUNCIÓN FACULTAD DE INGENIERÍA CURSO PREPARATORIO DE INGENIERÍA (CPI) EJERCITARIO TEÓRICO DE GEOMETRÍA ANALÍTICA
 UNIVERSIDAD NACIONAL DE ASUNCIÓN FACULTAD DE INGENIERÍA CURSO PREPARATORIO DE INGENIERÍA (CPI) EJERCITARIO TEÓRICO DE GEOMETRÍA ANALÍTICA AÑO 2014 RECTAS - EJERCICIOS TEÓRICOS 1- Demostrar que la ecuación
UNIVERSIDAD NACIONAL DE ASUNCIÓN FACULTAD DE INGENIERÍA CURSO PREPARATORIO DE INGENIERÍA (CPI) EJERCITARIO TEÓRICO DE GEOMETRÍA ANALÍTICA AÑO 2014 RECTAS - EJERCICIOS TEÓRICOS 1- Demostrar que la ecuación
VERSIÓN 31 1, 1. 12y 24 0 es: MATEMÁTICAS V. 1.- La gráfica de la ecuación. 3.- El dominio de la función f x. es: A) B) B), 1 A) 1, E) 1, C) D)
 1.- La gráfica de la ecuación MATEMÁTICAS V B) 1y 4 0 es:.- El dominio de la función f 1, B), 1 4 es: 1 1, 1 VERSIÓN 1 C), 1 1, C) 4.- Determina el rango de la función y. y B) y C) 1 y y y 0, 0.- Para
1.- La gráfica de la ecuación MATEMÁTICAS V B) 1y 4 0 es:.- El dominio de la función f 1, B), 1 4 es: 1 1, 1 VERSIÓN 1 C), 1 1, C) 4.- Determina el rango de la función y. y B) y C) 1 y y y 0, 0.- Para
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGINA 180 EJERCICIOS Semejanza de figuras 1 Sobre un papel cuadriculado, haz un dibujo semejante a este ampliado al triple de su tamaño: 2 En un mapa a escala 1 :50 000 la distancia entre dos pueblos,
Pág. 1 PÁGINA 180 EJERCICIOS Semejanza de figuras 1 Sobre un papel cuadriculado, haz un dibujo semejante a este ampliado al triple de su tamaño: 2 En un mapa a escala 1 :50 000 la distancia entre dos pueblos,
DEPARTAMENTO DE GEOMETRIA ANALITICA SEMESTRE 2016-1 SERIE ÁLGEBRA VECTORIAL
 1.-Sea C(2, -3, 5) el punto medio del segmento dirigido AB. Empleando álgebra vectorial, determinar las coordenadas de los puntos A y B, si las componentes escalares de AB sobre los ejes coordenados X,
1.-Sea C(2, -3, 5) el punto medio del segmento dirigido AB. Empleando álgebra vectorial, determinar las coordenadas de los puntos A y B, si las componentes escalares de AB sobre los ejes coordenados X,
Tema 6: Trigonometría.
 Matemáticas Ejercicios Tema 6 4º ESO OPCIÓN B Bloque III: Trigonometría Tema 6: Trigonometría. 1.- Un carpintero quiere construir una escalera de tijera cuyos brazos, una vez abiertos, formen un ángulo
Matemáticas Ejercicios Tema 6 4º ESO OPCIÓN B Bloque III: Trigonometría Tema 6: Trigonometría. 1.- Un carpintero quiere construir una escalera de tijera cuyos brazos, una vez abiertos, formen un ángulo
Preparación para la XLVII Olimpiada Matemática Española (II) Soluciones
 Preparación para la XLVII Olimpiada Matemática Española (II) Soluciones Eva Elduque Laburta y Adrián Rodrigo Escudero 5 de noviembre de 010 Problema 1. Construir un triángulo conocidos 1. un lado, su ángulo
Preparación para la XLVII Olimpiada Matemática Española (II) Soluciones Eva Elduque Laburta y Adrián Rodrigo Escudero 5 de noviembre de 010 Problema 1. Construir un triángulo conocidos 1. un lado, su ángulo
8º Grado Matemática. Teorema de Pitágoras Distancia y Punto Medio. Slide 1 / 86. Slide 2 / 86. Slide 4 / 86. Slide 3 / 86. Slide 6 / 86.
 Slide 1 / 86 New Jersey Center for Teaching and Learning Iniciativa de Matemática Progresiva Este material está disponible gratuitamente en www.njctl.org y está pensado para el uso no comercial de estudiantes
Slide 1 / 86 New Jersey Center for Teaching and Learning Iniciativa de Matemática Progresiva Este material está disponible gratuitamente en www.njctl.org y está pensado para el uso no comercial de estudiantes
4. Resolver eliminando signos de agrupación: -3, * ( ) + - 5. Demostrar la propiedad conmutativa de la suma con:
 GUIA DE EJERCICIOS DE MATEMÁTICA PRIMER AÑO APELLIDOS NOMBRES 1-La suma de dos números consecutivos es 61. cuáles son los números? 2. La suma de dos números pares consecutivos es 146. cuáles son los números?
GUIA DE EJERCICIOS DE MATEMÁTICA PRIMER AÑO APELLIDOS NOMBRES 1-La suma de dos números consecutivos es 61. cuáles son los números? 2. La suma de dos números pares consecutivos es 146. cuáles son los números?
Departamento de Matemáticas Página 1 I.E.S. Antonio Gala
 PRIMERA EVALUACIÓN ATENCIÓN: No olvides poner tu nombre y apellidos Cuidado con las faltas de No tengas prisa en acabar Revisa todo antes de entregar Suerte Ejercicio nº 1.- Racionaliza: a) + 6, b) 1 +
PRIMERA EVALUACIÓN ATENCIÓN: No olvides poner tu nombre y apellidos Cuidado con las faltas de No tengas prisa en acabar Revisa todo antes de entregar Suerte Ejercicio nº 1.- Racionaliza: a) + 6, b) 1 +
Sistemas de representación: Planos Acotados. Ejercicios.
 Sistemas de representación: Planos Acotados. Ejercicios. Las proyecciones de los puntos A'(3) y C'(8) son los extremos de uno de los diámetros de una circunferencia de 60 mm. de φ. La pendiente de
Sistemas de representación: Planos Acotados. Ejercicios. Las proyecciones de los puntos A'(3) y C'(8) son los extremos de uno de los diámetros de una circunferencia de 60 mm. de φ. La pendiente de
CENAFE MATEMÁTICAS POLÍGONOS
 POLÍGONOS Es la porción del plano comprendida dentro de una línea poligonal cerrada. Es la superficie del plano limitada por una línea poligonal. La medida de un polígono es su área. Criterios de clasificación:
POLÍGONOS Es la porción del plano comprendida dentro de una línea poligonal cerrada. Es la superficie del plano limitada por una línea poligonal. La medida de un polígono es su área. Criterios de clasificación:
Departamento de Matematicas UNIVERSIDAD DE LOS ANDES. Precálculo. (2Cos(2w) 1)(2Sen(3w) 2) = 0. hallar β en el intervalo [0, 2π]
![Departamento de Matematicas UNIVERSIDAD DE LOS ANDES. Precálculo. (2Cos(2w) 1)(2Sen(3w) 2) = 0. hallar β en el intervalo [0, 2π] Departamento de Matematicas UNIVERSIDAD DE LOS ANDES. Precálculo. (2Cos(2w) 1)(2Sen(3w) 2) = 0. hallar β en el intervalo [0, 2π]](/thumbs/24/4399971.jpg) Departamento de Matematicas UNIVERSIDAD DE LOS ANDES. Precálculo Parcial III 15 % Estudiante: Tiempo: 1 h. Fecha: 1 Resolver la ecuación para w en 0 w 2π. (2Cos(2w) 1)(2Sen(3w) 2) = 0 2 Hallar los ceros
Departamento de Matematicas UNIVERSIDAD DE LOS ANDES. Precálculo Parcial III 15 % Estudiante: Tiempo: 1 h. Fecha: 1 Resolver la ecuación para w en 0 w 2π. (2Cos(2w) 1)(2Sen(3w) 2) = 0 2 Hallar los ceros
6. VECTORES Y COORDENADAS
 6. VECTORES Y COORDENADAS Página 1 Traslaciones. Vectores Sistema de referencia. Coordenadas. Punto medio de un segmento Ecuaciones de rectas. Paralelismo. Distancias Página 2 1. TRASLACIONES. VECTORES
6. VECTORES Y COORDENADAS Página 1 Traslaciones. Vectores Sistema de referencia. Coordenadas. Punto medio de un segmento Ecuaciones de rectas. Paralelismo. Distancias Página 2 1. TRASLACIONES. VECTORES
GUIA PARA EL EXAMEN EXTRAORDINARIO DE MATEMATICAS V
 GUIA PARA EL EXAMEN EXTRAORDINARIO DE MATEMATICAS V 1) Determinar el dominio de las siguientes funciones dando el resultado en parentesis para:. y = x + 4. y = 3x c). y = x 3 x+ ) Obtener el rango para
GUIA PARA EL EXAMEN EXTRAORDINARIO DE MATEMATICAS V 1) Determinar el dominio de las siguientes funciones dando el resultado en parentesis para:. y = x + 4. y = 3x c). y = x 3 x+ ) Obtener el rango para
UNIVERSIDAD TECNOLÓGICA EQUINOCCIAL SISTEMA DE EDUCACIÓN A DISTANCIA CARRERA DE CIENCIAS DE EDUCACIÓN AREA DE MATEMÁTICAS. Módulo
 UNIVERSIDAD TECNOLÓGICA EQUINOCCIAL SISTEMA DE EDUCACIÓN A DISTANCIA CARRERA DE CIENCIAS DE EDUCACIÓN AREA DE MATEMÁTICAS Módulo TRIGONOMETRÍA Y DIBUJO TÉCNICO Msc. Sexto Nivel Tercera Edición Quito, marzo
UNIVERSIDAD TECNOLÓGICA EQUINOCCIAL SISTEMA DE EDUCACIÓN A DISTANCIA CARRERA DE CIENCIAS DE EDUCACIÓN AREA DE MATEMÁTICAS Módulo TRIGONOMETRÍA Y DIBUJO TÉCNICO Msc. Sexto Nivel Tercera Edición Quito, marzo
Tema 1: Cuerpos geométricos. Aplicaciones
 Tema 1: Cuerpos geométricos. Aplicaciones 1.- los polígonos. Un polígono es un trozo de plano limitado por una línea poligonal (sin curvas) cerrada. Es un polígono No son polígonos Hay dos clases de polígonos:
Tema 1: Cuerpos geométricos. Aplicaciones 1.- los polígonos. Un polígono es un trozo de plano limitado por una línea poligonal (sin curvas) cerrada. Es un polígono No son polígonos Hay dos clases de polígonos:
Guía para el examen de clasificación de matemáticas para las carreras de: actuaría, economía, ingenierías y matemáticas aplicadas.
 Guía para el eamen de clasificación de matemáticas para las carreras de: actuaría, economía, ingenierías matemáticas aplicadas. Septiembre 23 Índice. Instrucciones.. Objetivo....2. Requisitos....3. Característicasdeleamen...
Guía para el eamen de clasificación de matemáticas para las carreras de: actuaría, economía, ingenierías matemáticas aplicadas. Septiembre 23 Índice. Instrucciones.. Objetivo....2. Requisitos....3. Característicasdeleamen...
GEOMETRIA ANALITICA PROBLEMARIO. M. en C. JOSÉ CORREA BUCIO ELABORADO POR:
 GEOMETRIA ANALITICA PROBLEMARIO ELABORADO POR: SEMESTRE AGOSTO 13 - ENERO 1 GEOMETRIA ANALITICA CBTis No. 1 SISTEMA UNIDIMENSIONAL 1.- Localizaremos en un eje de coordenadas los puntos que tienen por coordenadas
GEOMETRIA ANALITICA PROBLEMARIO ELABORADO POR: SEMESTRE AGOSTO 13 - ENERO 1 GEOMETRIA ANALITICA CBTis No. 1 SISTEMA UNIDIMENSIONAL 1.- Localizaremos en un eje de coordenadas los puntos que tienen por coordenadas
RELACIÓN DE TRIGONOMETRÍA
 RELACIÓN DE TRIGONOMETRÍA ) Resuelve el triángulo ABC rectángulo en A del que se sabe que: a cm y ˆB 7º0' La hipotenusa mide 7 m y un cateto 8 m. Un cateto mide 0 cm, y su ángulo opuesto 0º. ) De un triángulo
RELACIÓN DE TRIGONOMETRÍA ) Resuelve el triángulo ABC rectángulo en A del que se sabe que: a cm y ˆB 7º0' La hipotenusa mide 7 m y un cateto 8 m. Un cateto mide 0 cm, y su ángulo opuesto 0º. ) De un triángulo
1. Vectores 1.1. Definición de un vector en R2, R3 (Interpretación geométrica), y su generalización en Rn.
 1. VECTORES INDICE 1.1. Definición de un vector en R 2, R 3 (Interpretación geométrica), y su generalización en R n...2 1.2. Operaciones con vectores y sus propiedades...6 1.3. Producto escalar y vectorial
1. VECTORES INDICE 1.1. Definición de un vector en R 2, R 3 (Interpretación geométrica), y su generalización en R n...2 1.2. Operaciones con vectores y sus propiedades...6 1.3. Producto escalar y vectorial
Primer Simposio Latinoamericano para la integración de la tecnología en el aula de ciencias y matemáticas
 Primer Simposio Latinoamericano para la integración de la tecnología en el aula de ciencias y matemáticas PROBLEMAS DE OPTIMIZACIÓN 1.-Entre todos los rectángulos de perímetro 10 cm. encontrar el de mayor
Primer Simposio Latinoamericano para la integración de la tecnología en el aula de ciencias y matemáticas PROBLEMAS DE OPTIMIZACIÓN 1.-Entre todos los rectángulos de perímetro 10 cm. encontrar el de mayor
UNIDAD 7 FUNCIONES TRIGONOMÉTRICAS
 UNIDAD 7 FUNCIONES TRIGONOMÉTRICAS Uso de la calculadora. Calcula, usando calculadora: a) sen 0 b) cos 70 e) cos 89 0 f) tan c) tan 0 0 g) sen 80 7 d) sen 7 0 h) cos 6 8. Encuentra el valor del ángulo
UNIDAD 7 FUNCIONES TRIGONOMÉTRICAS Uso de la calculadora. Calcula, usando calculadora: a) sen 0 b) cos 70 e) cos 89 0 f) tan c) tan 0 0 g) sen 80 7 d) sen 7 0 h) cos 6 8. Encuentra el valor del ángulo
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Junio 2010 DIBUJO TÉCNICO II. CÓDIGO
 PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Junio 2010 DIBUJO TÉCNICO II. CÓDIGO CRITERIOS PARA LA REALIZACIÓN DE LA PRUEBA 1.- Se establecen dos opciones A- y B- de tres problemas
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Junio 2010 DIBUJO TÉCNICO II. CÓDIGO CRITERIOS PARA LA REALIZACIÓN DE LA PRUEBA 1.- Se establecen dos opciones A- y B- de tres problemas
Movimientos en el plano
 7 Movimientos en el plano Objetivos En esta quincena aprenderás a: Manejar el concepto de vector como elemento direccional del plano. Reconocer los movimientos principales en el plano: traslaciones, giros
7 Movimientos en el plano Objetivos En esta quincena aprenderás a: Manejar el concepto de vector como elemento direccional del plano. Reconocer los movimientos principales en el plano: traslaciones, giros
Practica No. 02 LEVANTAMIENTO TOPOGRÁFICO DE UN TERRENO CON WINCHA Y JALÓNES AGRIMENSURA
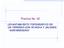 Practica No. 02 LEVANTAMIENTO TOPOGRÁFICO DE UN TERRENO CON WINCHA Y JALÓNES AGRIMENSURA C D B A Canal de riego Parcela de Cultivo Objetivo: Realizar el levantamiento de una pequeña parcela usando instrumentos
Practica No. 02 LEVANTAMIENTO TOPOGRÁFICO DE UN TERRENO CON WINCHA Y JALÓNES AGRIMENSURA C D B A Canal de riego Parcela de Cultivo Objetivo: Realizar el levantamiento de una pequeña parcela usando instrumentos
CRITERIOS DE VALORACIÓN
 PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Junio 2010 DIBUJO TÉCNICO II. CÓDIGO Ejercicio nº 1 CRITERIOS DE VALORACIÓN OPCIÓN A 1. Construcción del heptágono conocido el lado...
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Junio 2010 DIBUJO TÉCNICO II. CÓDIGO Ejercicio nº 1 CRITERIOS DE VALORACIÓN OPCIÓN A 1. Construcción del heptágono conocido el lado...
GUIA ADICIONAL CÁLCULO 1 GEOMETRÍA ANALÍTICA. 1.- Grafique los siguientes puntos y encuentre la distancia entre ellos:
 GUIA ADICIONAL CÁLCULO GEOMETRÍA ANALÍTICA ELEMENTOS DE GEOMETRÍA ANALÍTICA.- Grafique los siguientes puntos y encuentre la distancia entre ellos: a ) A(, 3) B( 5,3) b ) A( 4, 5) B(5, 3) c ) A(4, ) B(6,
GUIA ADICIONAL CÁLCULO GEOMETRÍA ANALÍTICA ELEMENTOS DE GEOMETRÍA ANALÍTICA.- Grafique los siguientes puntos y encuentre la distancia entre ellos: a ) A(, 3) B( 5,3) b ) A( 4, 5) B(5, 3) c ) A(4, ) B(6,
PLAN DE MEJORAMIENTO GRADO DÉCIMO. Solución de triángulos rectángulos, en diferentes contextos, aplicando la trigonometría y el teorema de Pitágoras.
 PLAN DE MEJORAMIENTO GRADO DÉCIMO INSTITUCIÓN EDUCATIVA LOMA HERMOSA DOCENTE: WÍLMAR ALONSO RAMÍREZ G. Refuerzo matemáticas 2011, grado 10 o Fecha: 25/07/2011 PRIMER PERÍODO Competencias: Solución de triángulos
PLAN DE MEJORAMIENTO GRADO DÉCIMO INSTITUCIÓN EDUCATIVA LOMA HERMOSA DOCENTE: WÍLMAR ALONSO RAMÍREZ G. Refuerzo matemáticas 2011, grado 10 o Fecha: 25/07/2011 PRIMER PERÍODO Competencias: Solución de triángulos
3.1 DEFINICIÓN. Figura Nº 1. Vector
 3.1 DEFINICIÓN Un vector (A) una magnitud física caracterizable mediante un módulo y una dirección (u orientación) en el espacio. Todo vector debe tener un origen marcado (M) con un punto y un final marcado
3.1 DEFINICIÓN Un vector (A) una magnitud física caracterizable mediante un módulo y una dirección (u orientación) en el espacio. Todo vector debe tener un origen marcado (M) con un punto y un final marcado
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- [2 5 puntos] Una ventana normanda consiste en un rectángulo coronado con un semicírculo. De entre todas las ventanas normandas de perímetro 10 m, halla las dimensiones del marco
Opción A Ejercicio 1.- [2 5 puntos] Una ventana normanda consiste en un rectángulo coronado con un semicírculo. De entre todas las ventanas normandas de perímetro 10 m, halla las dimensiones del marco
Traslación de puntos
 LECCIÓN CONDENSADA 9.1 Traslación de puntos En esta lección trasladarás figuras en el plano de coordenadas definirás una traslación al describir cómo afecta un punto general (, ) Una regla matemática que
LECCIÓN CONDENSADA 9.1 Traslación de puntos En esta lección trasladarás figuras en el plano de coordenadas definirás una traslación al describir cómo afecta un punto general (, ) Una regla matemática que
PROBLEMAS MÉTRICOS. Página 183 REFLEXIONA Y RESUELVE. Diagonal de un ortoedro. Distancia entre dos puntos. Distancia de un punto a una recta
 PROBLEMAS MÉTRICOS Página 3 REFLEXIONA Y RESUELVE Diagonal de un ortoedro Halla la diagonal de los ortoedros cuyas dimensiones son las siguientes: I) a =, b =, c = II) a = 4, b =, c = 3 III) a =, b = 4,
PROBLEMAS MÉTRICOS Página 3 REFLEXIONA Y RESUELVE Diagonal de un ortoedro Halla la diagonal de los ortoedros cuyas dimensiones son las siguientes: I) a =, b =, c = II) a = 4, b =, c = 3 III) a =, b = 4,
1.4. Ejercicios Finales. Figura 1.26: Descomposición de un vector a en suma de un vector paralelo a b y otro perpendicular a b. 10.
 Figura 1.26: Descomposición de un vector a en suma de un vector paralelo a b y otro perpendicular a b. 10. a b = a bˆx 11. a b = a bẑ 12. a b = a bẑ 13. a a = 1 14. a a = 0 1.4. Ejercicios Finales 1. Un
Figura 1.26: Descomposición de un vector a en suma de un vector paralelo a b y otro perpendicular a b. 10. a b = a bˆx 11. a b = a bẑ 12. a b = a bẑ 13. a a = 1 14. a a = 0 1.4. Ejercicios Finales 1. Un
Estudiando Trigonometría
 La idea es relacionar los segmentos de un triángulo rectángulo cualquiera con sus respectivos ángulos interiores de modo que tras un tiempo se generalice a cualquier situación def.: Teorema de Pitágoras
La idea es relacionar los segmentos de un triángulo rectángulo cualquiera con sus respectivos ángulos interiores de modo que tras un tiempo se generalice a cualquier situación def.: Teorema de Pitágoras
Módulo 4-Diapositiva 24 Ley de Senos y Cosenos. Universidad de Antioquia
 Módulo 4-Diapositiva 24 Ley de Senos y Cosenos Facultad de Ciencias Exactas y Naturales Temas Ley del Seno Ley del Seno Solución de Triángulos y Aplicaciones Ángulos de Elavación y de Depresión La siguiente
Módulo 4-Diapositiva 24 Ley de Senos y Cosenos Facultad de Ciencias Exactas y Naturales Temas Ley del Seno Ley del Seno Solución de Triángulos y Aplicaciones Ángulos de Elavación y de Depresión La siguiente
OLIMPÍADA JUVENIL DE MATEMÁTICA 2009 CANGURO MATEMÁTICO PRUEBA PRELIMINAR SÉPTIMO GRADO
 OLIMPÍADA JUVENIL DE MATEMÁTICA 2009 CANGURO MATEMÁTICO PRUEBA PRELIMINAR SÉPTIMO GRADO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. Cuál de los siguientes números es par? A 2009 B 2 + 0 + 0 + 9
OLIMPÍADA JUVENIL DE MATEMÁTICA 2009 CANGURO MATEMÁTICO PRUEBA PRELIMINAR SÉPTIMO GRADO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. Cuál de los siguientes números es par? A 2009 B 2 + 0 + 0 + 9
Cómo construir un reloj de Sol
 Cómo construir un reloj de Sol Historia de los Relojes de Sol: Desde tiempos inmemoriales la humanidad ha sabido que la forma en la que cambia la sombra de un objeto indica la hora del día, que la sombra
Cómo construir un reloj de Sol Historia de los Relojes de Sol: Desde tiempos inmemoriales la humanidad ha sabido que la forma en la que cambia la sombra de un objeto indica la hora del día, que la sombra
Ejercicios de Trigonometría
 Ejercicios de Trigonometría 1) Indica la medida de estos ángulos en radianes: a) 0º b) 45º c) 60º d) 120º Recuerda que 360º son 2π radianes, con lo que para hacer la conversión realizaremos una simple
Ejercicios de Trigonometría 1) Indica la medida de estos ángulos en radianes: a) 0º b) 45º c) 60º d) 120º Recuerda que 360º son 2π radianes, con lo que para hacer la conversión realizaremos una simple
INSTITUTO FRANCISCO POSSENTI, A.C. Per crucem ad lucem. Preparatoria (1085)
 INSTITUTO FRANCISCO POSSENTI, A.C. Per crucem ad lucem Preparatoria (1085) GUÍA DE MATEMÁTICAS V CLAVE: 1500 Unidad I: RELACIONES Y FUNCIONES Considera las gráficas de las siguientes funciones y determina
INSTITUTO FRANCISCO POSSENTI, A.C. Per crucem ad lucem Preparatoria (1085) GUÍA DE MATEMÁTICAS V CLAVE: 1500 Unidad I: RELACIONES Y FUNCIONES Considera las gráficas de las siguientes funciones y determina
Vectores: Producto escalar y vectorial
 Nivelación de Matemática MTHA UNLP 1 Vectores: Producto escalar y vectorial Versores fundamentales Dado un sistema de coordenadas ortogonales, se considera sobre cada uno de los ejes y coincidiendo con
Nivelación de Matemática MTHA UNLP 1 Vectores: Producto escalar y vectorial Versores fundamentales Dado un sistema de coordenadas ortogonales, se considera sobre cada uno de los ejes y coincidiendo con
UNIVERSIDAD COMPLUTENSE DE MADRID
 TIEMPO: INSTRUCCIONES GENERALES Y VALORACIÓN 120 minutos. INSTRUCCIONES: La prueba consiste en la realización de cinco ejercicios, a elegir entre dos opciones, denominadas A y B. El alumno realizará una
TIEMPO: INSTRUCCIONES GENERALES Y VALORACIÓN 120 minutos. INSTRUCCIONES: La prueba consiste en la realización de cinco ejercicios, a elegir entre dos opciones, denominadas A y B. El alumno realizará una
EJERCICIOS DE MATEMÁTICAS B, 4º ESO. (Septiembre 2011)
 EJERCICIOS DE MATEMÁTICAS B, º ESO. (Septiembre ) ARITMÉTICA. Realiza las siguientes operaciones, simplificando cuando sea posible 9 e). Realiza los siguientes ejercicios con potencias 9 e) 9 8.- Realiza
EJERCICIOS DE MATEMÁTICAS B, º ESO. (Septiembre ) ARITMÉTICA. Realiza las siguientes operaciones, simplificando cuando sea posible 9 e). Realiza los siguientes ejercicios con potencias 9 e) 9 8.- Realiza
UNIDAD N 4: TRIGONOMETRÍA
 Matemática Unidad 4 - UNIDD N 4: TRIGONOMETRÍ ÍNDICE GENERL DE L UNIDD Trigonometría....... 3 Sistema de medición angular... 3 Sistema seagesimal...... 3 Sistema Radial....... 3 Tabla de conversión entre
Matemática Unidad 4 - UNIDD N 4: TRIGONOMETRÍ ÍNDICE GENERL DE L UNIDD Trigonometría....... 3 Sistema de medición angular... 3 Sistema seagesimal...... 3 Sistema Radial....... 3 Tabla de conversión entre
1.- Encontrar los intervalos de crecimiento y decrecimiento de las funciones:
 F. EJERCICIOS PROPUESTOS. 1.- Encontrar los intervalos de crecimiento y decrecimiento de las funciones: (a) f(x) =x 3 /3+3x 2 /2 10x. Resp.: Crece en (, 5) y en (2, ); decrece en ( 5, 2). (b) f(x) =x 3
F. EJERCICIOS PROPUESTOS. 1.- Encontrar los intervalos de crecimiento y decrecimiento de las funciones: (a) f(x) =x 3 /3+3x 2 /2 10x. Resp.: Crece en (, 5) y en (2, ); decrece en ( 5, 2). (b) f(x) =x 3
Muchas veces hemos visto un juego de billar y no nos percatamos de los movimientos de las bolas (ver gráfico 8). Gráfico 8
 Esta semana estudiaremos la definición de vectores y su aplicabilidad a muchas situaciones, particularmente a las relacionadas con el movimiento. Por otro lado, se podrán establecer las características
Esta semana estudiaremos la definición de vectores y su aplicabilidad a muchas situaciones, particularmente a las relacionadas con el movimiento. Por otro lado, se podrán establecer las características
8 GEOMETRÍA ANALÍTICA
 8 GEOMETRÍA ANALÍTICA EJERCICIOS PROPUESTOS 8. Las coordenadas de los vértices de un rectángulo son A(, ); B(, 5); C(6, 5), y D(6, ). Halla las coordenadas y representa los vectores AB, BC, CD y DA. Qué
8 GEOMETRÍA ANALÍTICA EJERCICIOS PROPUESTOS 8. Las coordenadas de los vértices de un rectángulo son A(, ); B(, 5); C(6, 5), y D(6, ). Halla las coordenadas y representa los vectores AB, BC, CD y DA. Qué
Definición de vectores
 Definición de vectores Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son: Origen: O también denominado Punto de aplicación. Es el punto exacto sobre
Definición de vectores Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son: Origen: O también denominado Punto de aplicación. Es el punto exacto sobre
INECUACIONES Y VALOR ABSOLUTO
 INECUACIONES Y VALOR ABSOLUTO U.C.V. F.I.U.C.V. CÁLCULO I (051) - TEMA 1 Pág.: 1 de 3 1. Resuelva las siguientes ecuaciones: a. 4 3x = 5 b. x + 1x + = 3 c. x + 1x + 4 = 10 d. x 1 + = 4 e. x + 3 = 4 f.
INECUACIONES Y VALOR ABSOLUTO U.C.V. F.I.U.C.V. CÁLCULO I (051) - TEMA 1 Pág.: 1 de 3 1. Resuelva las siguientes ecuaciones: a. 4 3x = 5 b. x + 1x + = 3 c. x + 1x + 4 = 10 d. x 1 + = 4 e. x + 3 = 4 f.
DIBUJO TÉCNICO. UNIDAD DIDÁCTICA 9: Geometría 2D (V)
 UNIDAD DIDÁCTICA 9: Geometría 2D (V) ÍNDICE Página: 1 CURVAS CÓNICAS. ELEMENTOS CARACTERÍSTICOS.. 2 2 TRAZADO MEDIANTE RADIOS VECTORES 4 3 RECTAS TANGENTES A CÓNICAS 5 3.1 CIRCUNFERENCIAS FOCALES 6 3.2
UNIDAD DIDÁCTICA 9: Geometría 2D (V) ÍNDICE Página: 1 CURVAS CÓNICAS. ELEMENTOS CARACTERÍSTICOS.. 2 2 TRAZADO MEDIANTE RADIOS VECTORES 4 3 RECTAS TANGENTES A CÓNICAS 5 3.1 CIRCUNFERENCIAS FOCALES 6 3.2
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/2010. Solución al primer examen parcial. x - x 3 1
 UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
17π. 10π. π B) 5 π C) π D) 3 π E) 2π. 225 en radianes es: = radianes, su equivalencia en grados es: 3 π. = es: B. Sesión 3
 Sesión Unidad II Funciones trigonométricas. A. Grados y radianes..- l equivalente de O en radianes es:.- La equivalencia en radianes de es: rad rad 9 rad rad rad.- l equivalente de en radianes es: rad
Sesión Unidad II Funciones trigonométricas. A. Grados y radianes..- l equivalente de O en radianes es:.- La equivalencia en radianes de es: rad rad 9 rad rad rad.- l equivalente de en radianes es: rad
Cuadernillo de actividades
 Construyendo con Geogebra II Jornadas sobre Geogebra en Andalucía Abril 2011 Actividades para el Taller: Construyendo con EVA COSTA GAVILÁN Mª TRINIDAD CASTILLO CARA Mª ÁNGELES MARTÍN TAPIAS Cuadernillo
Construyendo con Geogebra II Jornadas sobre Geogebra en Andalucía Abril 2011 Actividades para el Taller: Construyendo con EVA COSTA GAVILÁN Mª TRINIDAD CASTILLO CARA Mª ÁNGELES MARTÍN TAPIAS Cuadernillo
Movimientos en el plano
 Movimientos en el plano TEORIA Vectores Concepto de vector. Coordenadas Un vector AB está determinado por dos puntos del plano, A(x1, y1) que es su origen y B(x 2,y 2 ) que es su extremo. Las coordenadas
Movimientos en el plano TEORIA Vectores Concepto de vector. Coordenadas Un vector AB está determinado por dos puntos del plano, A(x1, y1) que es su origen y B(x 2,y 2 ) que es su extremo. Las coordenadas
UNIVERSIDAD COMPLUTENSE DE MADRID
 TIEMPO: INSTRUCCIONES GENERALES Y VALORACIÓN 120 minutos INSTRUCCIONES: La prueba consiste en la realización de cinco ejercicios, a elegir entre dos opciones, denominadas A y B. El alumno realizará una
TIEMPO: INSTRUCCIONES GENERALES Y VALORACIÓN 120 minutos INSTRUCCIONES: La prueba consiste en la realización de cinco ejercicios, a elegir entre dos opciones, denominadas A y B. El alumno realizará una
EXAMEN DE POLINOMIOS, ECUACIONES Y SISTEMAS 6-3-7
 I.E.S. Humanes Junio de 007 EXAMEN DE POLINOMIOS, ECUACIONES Y SISTEMAS 6-3-7 1º) Resuelve: 3 x ( x 3) = 7x 3 ( x + 4) x x + 4 º) Resuelve: = 3 1 3º) Resuelve: ( x 1) = ( x 1 ) ( x + ) x 4º) Resuelve:
I.E.S. Humanes Junio de 007 EXAMEN DE POLINOMIOS, ECUACIONES Y SISTEMAS 6-3-7 1º) Resuelve: 3 x ( x 3) = 7x 3 ( x + 4) x x + 4 º) Resuelve: = 3 1 3º) Resuelve: ( x 1) = ( x 1 ) ( x + ) x 4º) Resuelve:
TEMA 1: REPRESENTACIÓN GRÁFICA. 0.- MANEJO DE ESCUADRA Y CARTABON (Repaso 1º ESO)
 TEMA 1: REPRESENTACIÓN GRÁFICA 0.- MANEJO DE ESCUADRA Y CARTABON (Repaso 1º ESO) Son dos instrumentos de plástico transparente que se suelen usar de forma conjunta. La escuadra tiene forma de triángulo
TEMA 1: REPRESENTACIÓN GRÁFICA 0.- MANEJO DE ESCUADRA Y CARTABON (Repaso 1º ESO) Son dos instrumentos de plástico transparente que se suelen usar de forma conjunta. La escuadra tiene forma de triángulo
Como el ángulo es mayor que 360º lo tratamos del siguiente modo:
 MATEMÁTICAS 4º ESO EXAMEN DE TRIGONOMETRÍA RESUELTO EXAMEN RESUELTO Halla las razones trigonométricas de los siguientes ángulos: a) 740º Como el ángulo es maor que lo tratamos del siguiente modo: 740 60
MATEMÁTICAS 4º ESO EXAMEN DE TRIGONOMETRÍA RESUELTO EXAMEN RESUELTO Halla las razones trigonométricas de los siguientes ángulos: a) 740º Como el ángulo es maor que lo tratamos del siguiente modo: 740 60
Ecomundo Centro de Estudios. Taller para la segunda unidad del mes de Mayo del presente año 2010.
 Taller para la segunda unidad del mes de Mayo del presente año 2010. Instrucciones: Realizar el taller en hoja papel milimetrado. Utilice el número necesario de hojas, no olvide engrapar su trabajo. Utilice
Taller para la segunda unidad del mes de Mayo del presente año 2010. Instrucciones: Realizar el taller en hoja papel milimetrado. Utilice el número necesario de hojas, no olvide engrapar su trabajo. Utilice
Guía - 2 de Funciones: Trigonometría
 Centro Educacional San Carlos de Aragón. Coordinación Académica Enseñanza Media. Sector: Matemática. Nivel: NM 4 Prof.: Ximena Gallegos H. Guía - de Funciones: Trigonometría Nombre(s): Curso: Fecha. Contenido:
Centro Educacional San Carlos de Aragón. Coordinación Académica Enseñanza Media. Sector: Matemática. Nivel: NM 4 Prof.: Ximena Gallegos H. Guía - de Funciones: Trigonometría Nombre(s): Curso: Fecha. Contenido:
 EXAMEN A: Ejercicio nº 1.- Página 1 de 25 Indica el valor de los ángulos señalados en cada figura: Ejercicio nº 2.- La siguiente figura es una esfera de centro C y radio 3 unidades. Cómo definirías dicha
EXAMEN A: Ejercicio nº 1.- Página 1 de 25 Indica el valor de los ángulos señalados en cada figura: Ejercicio nº 2.- La siguiente figura es una esfera de centro C y radio 3 unidades. Cómo definirías dicha
MATEMATICAS V PRIMER SEMESTRE. 1.- Hallar el dominio de una función (UNIDAD 1 Relaciones y funciones)
 PRIMER SEMESTRE MATEMATICAS V 1.- Hallar el dominio de una función (UNIDAD 1 Relaciones y funciones) a) Y 3x 2 4x b) y 3 x c) y x 10 d) y x 4x 2 4 2.- Trigonometría Dado un triángulo determinar el valor
PRIMER SEMESTRE MATEMATICAS V 1.- Hallar el dominio de una función (UNIDAD 1 Relaciones y funciones) a) Y 3x 2 4x b) y 3 x c) y x 10 d) y x 4x 2 4 2.- Trigonometría Dado un triángulo determinar el valor
TRIGONOMETRIA. 1. Sabiendo que. y que es del 2º cuadrante y. del 4º,calcular el valor exacto de cos( )
 TRIGONOMETRIA 1. Sabiendo que 17 cos ec y sec 8 del 4º,calcular el valor exacto de cos() 5 4 y que es del º cuadrante y a 1. Obtener el valor de cos,sabiendo que cotg a= siendo a un ángulo 5 del tercer
TRIGONOMETRIA 1. Sabiendo que 17 cos ec y sec 8 del 4º,calcular el valor exacto de cos() 5 4 y que es del º cuadrante y a 1. Obtener el valor de cos,sabiendo que cotg a= siendo a un ángulo 5 del tercer
GUIAS DE ESTUDIO FINALES (PRIMERO Y SEGUNDO SEMESTRES) CICLO ESCOLAR QUINTO GRADO
 MATEMÁTICAS PRIMER SEMESTRE 1. Hallar el dominio de una función 4x a) y 3 x b) y x 10 4x c) y x 2 4 2. Graficar funciones exponenciales a) graficar y = 3 x+2 para x en (-2,-1,0,1,2,3) b) graficar y = 2
MATEMÁTICAS PRIMER SEMESTRE 1. Hallar el dominio de una función 4x a) y 3 x b) y x 10 4x c) y x 2 4 2. Graficar funciones exponenciales a) graficar y = 3 x+2 para x en (-2,-1,0,1,2,3) b) graficar y = 2
DEPARTAMENTO DE CIENCIAS BÁSICAS TALLER 2009_II PRECALCULO. PRIMERA PARTE: Preguntas Tipo Ecaes.
 DEPARTAMENTO DE CIENCIAS BÁSICAS TALLER 009_II PRECALCULO PRIMERA PARTE: Preguntas Tipo Ecaes. 1. La ecuación de la circunferencia con radio r= 7 y centro C(4, -10) es: a) (X - 4) + (Y 10) = 49 b) (X +
DEPARTAMENTO DE CIENCIAS BÁSICAS TALLER 009_II PRECALCULO PRIMERA PARTE: Preguntas Tipo Ecaes. 1. La ecuación de la circunferencia con radio r= 7 y centro C(4, -10) es: a) (X - 4) + (Y 10) = 49 b) (X +
KIG: LA GEOMETRÍA A GOLPE DE RATÓN. Asesor de Tecnologías de la Información y de las Comunicaciones
 KIG: LA GEOMETRÍA A GOLPE DE RATÓN Asesor de Tecnologías de la Información y de las Comunicaciones GNU/LINEX Mariano Real Pérez KIG KDE Interactive geometry (Geometría interactiva de KDE) es una aplicación
KIG: LA GEOMETRÍA A GOLPE DE RATÓN Asesor de Tecnologías de la Información y de las Comunicaciones GNU/LINEX Mariano Real Pérez KIG KDE Interactive geometry (Geometría interactiva de KDE) es una aplicación
Apoyo para la preparación de los estudios de Ingeniería y Arquitectura Física (Preparación a la Universidad) Unidad 4: Vectores
 Apoyo para la preparación de los estudios de Ingeniería y Arquitectura Física (Preparación a la Universidad) Unidad 4: Vectores Universidad Politécnica de Madrid 5 de marzo de 2010 2 4.1. Planificación
Apoyo para la preparación de los estudios de Ingeniería y Arquitectura Física (Preparación a la Universidad) Unidad 4: Vectores Universidad Politécnica de Madrid 5 de marzo de 2010 2 4.1. Planificación
XIII Concurso Intercentros de Matemáticas de la Comunidad de Madrid
 PRU POR QUIPOS 1º y 2º de.s.o. (45 minutos) 1. n el triángulo dibujamos tres paralelas a la base que dividen a la altura sobre dicho lado en cuatro partes iguales. Si el área del trapecio rayado es 35
PRU POR QUIPOS 1º y 2º de.s.o. (45 minutos) 1. n el triángulo dibujamos tres paralelas a la base que dividen a la altura sobre dicho lado en cuatro partes iguales. Si el área del trapecio rayado es 35
4.1 EL SISTEMA POLAR 4.2 ECUACIONES EN COORDENADAS POLARES 4.3 GRÁFICAS DE ECUACIONES EN COORDENADAS
 4 4.1 EL SISTEMA POLAR 4. ECUACIONES EN COORDENADAS POLARES 4.3 GRÁFICAS DE ECUACIONES EN COORDENADAS POLARES: RECTAS, CIRCUNFERENCIAS, PARÁBOLAS, ELIPSES, HIPÉRBOLAS, LIMACONS, ROSAS, LEMNISCATAS, ESPIRALES.
4 4.1 EL SISTEMA POLAR 4. ECUACIONES EN COORDENADAS POLARES 4.3 GRÁFICAS DE ECUACIONES EN COORDENADAS POLARES: RECTAS, CIRCUNFERENCIAS, PARÁBOLAS, ELIPSES, HIPÉRBOLAS, LIMACONS, ROSAS, LEMNISCATAS, ESPIRALES.
MATEMÁTICAS 1º BACHILLERATO INTERNACIONAL NIVEL MEDIO Serie: Trigonometría
 MATEMÁTICAS 1º BACHILLERATO INTERNACIONAL NIVEL MEDIO Serie: Trigonometría Salvo indicación contraria, las soluciones se redondearán con tres cifras significativas 1. El diagrama muestra un círculo de
MATEMÁTICAS 1º BACHILLERATO INTERNACIONAL NIVEL MEDIO Serie: Trigonometría Salvo indicación contraria, las soluciones se redondearán con tres cifras significativas 1. El diagrama muestra un círculo de
( 2x) Guía de Trigonometría. 1. Determine si las siguientes igualdades determinan identidades trigonométricas. + =. (a) x =. = 2. (b) cos. 2cos.
 Guía de Trigonometría Determine si las siguientes igualdades determinan identidades trigonométricas (a) (b) (c) (d) cos + cos + sen + sen = tg sen cos x = tg cos cos π sen xsec π csc cot x tg π x + 6 =
Guía de Trigonometría Determine si las siguientes igualdades determinan identidades trigonométricas (a) (b) (c) (d) cos + cos + sen + sen = tg sen cos x = tg cos cos π sen xsec π csc cot x tg π x + 6 =
Rectas y Cónicas. Sistema de Coordenadas Cartesianas. Guía de Ejercicios # Encuentre las coordenadas de los puntos mostrados en la figura.
 Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a la recta x + 7y + 1 = 0
 Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
COLEGIO NACIONAL NICOLÁS ESGUERRA
 COLEGIO NACIONAL NICOLÁS ESGUERRA Jornada Mañana EDIFICAMOS FUTURO TALLER DE TRIGONOMETRIA FECHA / 11/2015 GRADO DECIMO NOMBRE Código Curso PROFESORES: GLORIA VALBUENA ADRIANA PACHON TODO LO QUE LA MENTE
COLEGIO NACIONAL NICOLÁS ESGUERRA Jornada Mañana EDIFICAMOS FUTURO TALLER DE TRIGONOMETRIA FECHA / 11/2015 GRADO DECIMO NOMBRE Código Curso PROFESORES: GLORIA VALBUENA ADRIANA PACHON TODO LO QUE LA MENTE
UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERÍA INSTITUTO DE CIENCIAS BASICAS
 UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERÍA INSTITUTO DE CIENCIAS BASICAS Álgebra Guía de Ejercicios º Elementos Elementos de Geometría Analítica Plana ELEME TOS DE GEOMETRÍA A ALÍTICA Distancia
UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERÍA INSTITUTO DE CIENCIAS BASICAS Álgebra Guía de Ejercicios º Elementos Elementos de Geometría Analítica Plana ELEME TOS DE GEOMETRÍA A ALÍTICA Distancia
6.- En un puerto de montaña aparece una señal de tráfico que señala una pendiente del 12 %. Cuál sería ese desnivel en grados?
 TRIGONOMETRÍA 1.- En un triángulo rectángulo, la hipotenusa mide 8 dm y tgα 1' 43, siendo α uno de los ángulos agudos. Halla la medida de los catetos..- Si cos α 0' 46 y 180º α 70º, calcula las restantes
TRIGONOMETRÍA 1.- En un triángulo rectángulo, la hipotenusa mide 8 dm y tgα 1' 43, siendo α uno de los ángulos agudos. Halla la medida de los catetos..- Si cos α 0' 46 y 180º α 70º, calcula las restantes
1. Trigonometría 4º ESO-B. Cuaderno de ejercicios. Matemáticas JRM. Nombre y apellidos... INTRODUCCIÓN A LA TRIGONOMETRÍA Página 1
 1. Trigonometría 4º ESO-B Cuaderno de ejercicios Matemáticas JRM Nombre y apellidos... INTRODUCCIÓN A LA TRIGONOMETRÍA Página 1 RESUMEN DE OBJETIVOS 1. Razones trigonométricas de un ángulo agudo. OBJETIVO
1. Trigonometría 4º ESO-B Cuaderno de ejercicios Matemáticas JRM Nombre y apellidos... INTRODUCCIÓN A LA TRIGONOMETRÍA Página 1 RESUMEN DE OBJETIVOS 1. Razones trigonométricas de un ángulo agudo. OBJETIVO
APLICACIONES DEL CÁLCULO DIFERENCIAL-II
 APLICACIONES DEL CÁLCULO DIFERENCIAL-II. Estudia si crecen o decrecen las siguientes funciones en los puntos indicados: π a) f() cos en 0 b) f() ln ( arc tg ) en 0 π c) f() arc sen en 0 d) f() ln en 0
APLICACIONES DEL CÁLCULO DIFERENCIAL-II. Estudia si crecen o decrecen las siguientes funciones en los puntos indicados: π a) f() cos en 0 b) f() ln ( arc tg ) en 0 π c) f() arc sen en 0 d) f() ln en 0
b1ct Propuesta Actividades Recuperación Matemáticas
 b1ct Propuesta Actividades Recuperación Matemáticas Bloque Números 1 Resuelve: a. Si tomas como valor de 11. 1 la aproximación. 1, qué errores absoluto y relativo has cometido?. Solución: 0. 000; 0. 0%
b1ct Propuesta Actividades Recuperación Matemáticas Bloque Números 1 Resuelve: a. Si tomas como valor de 11. 1 la aproximación. 1, qué errores absoluto y relativo has cometido?. Solución: 0. 000; 0. 0%
13 LONGITUDES Y ÁREAS
 1 LONGITUDES Y ÁREAS EJERCICIOS PROPUESTOS 1.1 Calcula el perímetro de las siguientes figuras. a),5 cm b) cm cm cm cm a) p,5 8 5 1 cm b) p 9 cm 1. Halla el perímetro de estas figuras. a) Un cuadrado de
1 LONGITUDES Y ÁREAS EJERCICIOS PROPUESTOS 1.1 Calcula el perímetro de las siguientes figuras. a),5 cm b) cm cm cm cm a) p,5 8 5 1 cm b) p 9 cm 1. Halla el perímetro de estas figuras. a) Un cuadrado de
5 Geometría analítica plana
 Solucionario Geometría analítica plana ACTIVIDADES INICIALES.I. Halla las coordenadas del punto medio del segmento de extremos A(, ) y B(8, ). El punto medio es M(, 8)..II. Dibuja un triángulo isósceles
Solucionario Geometría analítica plana ACTIVIDADES INICIALES.I. Halla las coordenadas del punto medio del segmento de extremos A(, ) y B(8, ). El punto medio es M(, 8)..II. Dibuja un triángulo isósceles
b) Calcula el valor de x, aplicando las propiedades de los logaritmos: b) Obtén el criterio de formación de la siguiente sucesión recurrente:
 Ejercicio nº.- a) Calcula, utilizando la definición de logaritmo: log log log 9 b) Calcula el valor de, aplicando las propiedades de los logaritmos: 8 log log log4 Ejercicio nº.- a) Halla el término general
Ejercicio nº.- a) Calcula, utilizando la definición de logaritmo: log log log 9 b) Calcula el valor de, aplicando las propiedades de los logaritmos: 8 log log log4 Ejercicio nº.- a) Halla el término general
1. Aplicar el teorema de Pitágoras para responder a las siguientes cuestiones (y hacer un dibujo aproximado,
 FICHA 1: Teorema de Pitágoras 1. Aplicar el teorema de Pitágoras para responder a las siguientes cuestiones (y hacer un dibujo aproximado, cuando proceda): a) Hallar la hipotenusa de un triángulo rectángulo
FICHA 1: Teorema de Pitágoras 1. Aplicar el teorema de Pitágoras para responder a las siguientes cuestiones (y hacer un dibujo aproximado, cuando proceda): a) Hallar la hipotenusa de un triángulo rectángulo
_ Antología de Física I. Unidad II Vectores. Elaboró: Ing. Víctor H. Alcalá-Octaviano
 24 Unidad II Vectores 2.1 Magnitudes escalares y vectoriales Unidad II. VECTORES Para muchas magnitudes físicas basta con indicar su valor para que estén perfectamente definidas y estas son las denominadas
24 Unidad II Vectores 2.1 Magnitudes escalares y vectoriales Unidad II. VECTORES Para muchas magnitudes físicas basta con indicar su valor para que estén perfectamente definidas y estas son las denominadas
x y y x 2x y x y x 2y 2 5 x 2y 2 5 EJERCICIOS PROPUESTOS
 Solucionario 6 CÓNICAS 6.I. Calcula las ecuaciones de los siguientes lugares geométricos e identifícalos. a) Puntos que equidistan de A(3, 3) y de B(, 5). b) Puntos que equidistan de r: y 0 y s: y 0. c)
Solucionario 6 CÓNICAS 6.I. Calcula las ecuaciones de los siguientes lugares geométricos e identifícalos. a) Puntos que equidistan de A(3, 3) y de B(, 5). b) Puntos que equidistan de r: y 0 y s: y 0. c)
EL TRIÁNGULO. Recordemos algunas propiedades elementales de los triángulos
 EL TRIÁNGULO 1. EL TRIÁNGULO. PRIMERAS PROPIEDADES El triángulo es un polígono que tiene tres lados y tres ángulos. Es, por tanto, el polígono más simple y el conocimiento de sus características y propiedades
EL TRIÁNGULO 1. EL TRIÁNGULO. PRIMERAS PROPIEDADES El triángulo es un polígono que tiene tres lados y tres ángulos. Es, por tanto, el polígono más simple y el conocimiento de sus características y propiedades
LA MATEMÁTICA DEL TELEVISOR
 LA MATEMÁTICA DEL TELEVISOR ADRIANA RABINO Y PATRICIA CUELLO 1. Las publicidades, por lo general, describen el tamaño de las pantallas de TV dando la longitud de su diagonal en pulgadas (1 = 2,47 cm).
LA MATEMÁTICA DEL TELEVISOR ADRIANA RABINO Y PATRICIA CUELLO 1. Las publicidades, por lo general, describen el tamaño de las pantallas de TV dando la longitud de su diagonal en pulgadas (1 = 2,47 cm).
INSTITUTO POLITÉCNICO NACIONAL CECYT LÁZARO CÁRDENAS DEL RÍO ÁREA BÁSICA ACADÉMIA DE MATEMÁTICAS TURNO MATUTINO
 PRIMER EXAMEN PARCIAL INSTITUTO POLITÉCNICO NACIONAL CECYT LÁZARO CÁRDENAS DEL RÍO ÁREA BÁSICA ACADÉMIA DE MATEMÁTICAS TURNO MATUTINO GUÍA DE GEOMETRÍA ANALÍTICA 2016-2017A SISTEMA DE COORDENADAS, LUGARES
PRIMER EXAMEN PARCIAL INSTITUTO POLITÉCNICO NACIONAL CECYT LÁZARO CÁRDENAS DEL RÍO ÁREA BÁSICA ACADÉMIA DE MATEMÁTICAS TURNO MATUTINO GUÍA DE GEOMETRÍA ANALÍTICA 2016-2017A SISTEMA DE COORDENADAS, LUGARES
INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (1085) GUÍA DE MATEMÁTICAS V (1500)
 INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (1085) GUÍA DE MATEMÁTICAS V (1500) UNIDAD I: RELACIONES Y FUNCIONES. Considera las siguientes funciones y gráficas para determinar en
INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (1085) GUÍA DE MATEMÁTICAS V (1500) UNIDAD I: RELACIONES Y FUNCIONES. Considera las siguientes funciones y gráficas para determinar en
MINISTERIO DE EDUCACIÓN Concurso Nacional de Matemática Educación Preuniversitaria Curso 2009 2010 Temario por Grados
 MINISTERIO DE EDUCACIÓN Concurso Nacional de Matemática Educación Preuniversitaria Curso 009 010 Temario por Grados Nombre: Grado: Escuela: Provincia: Municipio: Número C.I.: Calif: La distribución de
MINISTERIO DE EDUCACIÓN Concurso Nacional de Matemática Educación Preuniversitaria Curso 009 010 Temario por Grados Nombre: Grado: Escuela: Provincia: Municipio: Número C.I.: Calif: La distribución de
Estalmat - Andalucía Oriental Más triángulos
 Estalmat - Andalucía Oriental Más triángulos Pascual Jara y Ceferino Ruiz 20 de octubre de 2007. 1.- La Recta de Euler 1 En un triángulo cualquiera ABC, dibuja el Baricentro G, el Ortocentro H y el Circuncentro
Estalmat - Andalucía Oriental Más triángulos Pascual Jara y Ceferino Ruiz 20 de octubre de 2007. 1.- La Recta de Euler 1 En un triángulo cualquiera ABC, dibuja el Baricentro G, el Ortocentro H y el Circuncentro
UNIVERSIDAD NACIONAL DE ASUNCIÓN FACULTAD DE INGENIERÍA CURSO PREPARATORIO DE INGENIERÍA (CPI) PROGRAMA DE ASIGNATURA GEOMETRÍA ANALÍTICA
 UNIVERSIDAD NACIONAL DE ASUNCIÓN FACULTAD DE INGENIERÍA CURSO PREPARATORIO DE INGENIERÍA (CPI) PROGRAMA DE ASIGNATURA GEOMETRÍA ANALÍTICA AÑO 2014 I. FUNDAMENTACIÓN En esta disciplina se estudian las operaciones
UNIVERSIDAD NACIONAL DE ASUNCIÓN FACULTAD DE INGENIERÍA CURSO PREPARATORIO DE INGENIERÍA (CPI) PROGRAMA DE ASIGNATURA GEOMETRÍA ANALÍTICA AÑO 2014 I. FUNDAMENTACIÓN En esta disciplina se estudian las operaciones
GEOMETRIA 8 AÑO 2011 1. Nombre:.Curso:
 GEOMETRIA 8 AÑO 2011 1 GUÍA DE APOYO AL TEMA : GEOMETRÍA Prof. Juan Schuchhardt E. Nombre:.Curso: UNIDAD #4 GEOMETRIA Tema # 2: Cuerpos geométricos En esta unidad aprenderás a: Identificar cuerpos poliédricos,
GEOMETRIA 8 AÑO 2011 1 GUÍA DE APOYO AL TEMA : GEOMETRÍA Prof. Juan Schuchhardt E. Nombre:.Curso: UNIDAD #4 GEOMETRIA Tema # 2: Cuerpos geométricos En esta unidad aprenderás a: Identificar cuerpos poliédricos,
