Control óptimo estocástico en la enseñanza de la economía matemática
|
|
|
- Esteban Cordero Padilla
- hace 5 años
- Vistas:
Transcripción
1 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez Resme: E ese docmeo expoemos de maera ddácca el plaeameo del problema de corol ópmo esocásco e empo coo, e el cal las resrccoes so procesos de dfsó observables codcdos por el movmeo geomérco browao. Asmsmo, co el propóso de lsrar el so del corol ópmo esocásco e la ecoomía maemáca, preseamos de maera ddácca dos ejemplos. El prmero es modelo de agee ecoómco racoal qe dspoe de a rqeza cal y efrea la decsó de cómo dsrbr s rqeza ere cosmo y porafolo de acvos e horzoe de plaeacó fo, de maera al qe maxmce s ldad oal esperada por el cosmo. El segdo ejemplo correspode al caso de horzoe emporal fo cya dracó es esocásca. Palabras clave: opmzacó dámca esocásca, corol ópmo esocásco e empo coo, ecacó dferecal parcal de Hamlo-Jacob-Bellma, eorema de verfcacó del cálclo esocásco, lema -dmesoal de Iô. Sochasc opmal corol he eachg of mahemacal ecoomcs Absrac: I hs paper we prese a ddacc way he saeme of he sochasc opmal corol problem coos me where cosras are observable dffso processes drve by he geomerc Browa moo. Frhermore, order o llsrae he se of sochasc opmal corol Mahemacal Ecoomcs, we prese a edcaoal way wo examples. The frs s a model of a raoal ecoomc age ha has a al wealh ad faces he decso of how o dsrbe hs wealh cosmpo ad a porfolo of asses a fe plag horzo, so as o maxmze hs oal expeced ly for cosmpo. The secod example cocers he case of a fe me horzo of sochasc drao. Keywords: sochasc dyamc opmzao, sochasc opmal corol coos me, paral dffereal eqao of Hamlo-Jacob-Bellma, verfcao heorem of sochasc calcls, - dmesoal Iô s lema. Fe cha de re cep có: 10 de abrl de 011. Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011, pp EM3-3_pp dd 147 1/4/11 10:34:0 PM
2 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca Irodccó La ecesdad de aplcar el corol ópmo esocásco e empo coo como herramea de modelacó e las cecas ecoómcas se ha cremeado oablemee e las úlmas décadas. Las respesas de vesgacó a ales ecesdades se ha hecho paees e dversos exos, por ejemplo, Veegas-Maríez (008), Herádez-Lerma (1994), Björk (004), Hyê (009), ere oros. Así pes, Veegas-Maríez (008) presea dversas aplcacoes ecoómcas del corol ópmo, deermsa y esocásco, e empo coo. Por s pare, Herádez-Lerma (1994) desarrolla aplcacoes ecoómco-faceras de procesos de dfsó markovaos corolados e horzoe de empo fo. Asmsmo, Björk (004) presea la eoría de corol ópmo esocásco para la modelacó del problema de seleccó de carera y cosmo ópmos. A pesar del éxo e ss aplcacoes, es be coocdo qe el corol ópmo esocásco e empo coo o es fácl de compreder por el rgor maemáco qe lo ssea y mcho meos es fácl de aplcar, a para aqellos qe so maemácos o especalsas e el área. Por lo aes referdo, el objevo de ese docmeo es presear de maera accesble y ddácca el modelo de corol ópmo esocásco e empo coo y algas de ss aplcacoes e Ecoomía para aqellos qe o so ecesaramee experos e corol ópmo esocásco, pero qe lo reqere como herramea e ss acvdades profesoales o de vesgacó. Co ese objevo e mee, de maera ddácca, se formlará el problema de corol ópmo esocásco y se preseará la écca de programacó dámca para obeer la ecacó dferecal parcal (edp) o leal de Hamlo- Jacob-Bellma (hjb), cya solcó os lleva a ecorar el corol ópmo y, co ello, las rayecoras ópmas de las varables qe opmza la fcó objevo. 1 Asmsmo, como lsracó, se presea dos ejemplos de aplcacó. El prmero de ellos correspode a modelo de agee ecoómco qe desea maxmzar s ldad oal esperada y descoada de cosmo e horzoe emporal fo y el segdo ejemplo versa sobre agee ecoómco qe desea maxmzar s ldad e horzoe emporal fo y esocásco. Ese rabajo esá orgazado de la sgee maera. E la seccó, se hace el plaeameo del problema geeral de corol ópmo esocásco e empo 1 Para a rgrosa formalzacó de problemas de corol ópmo esocásco e empo dscreo y coo léase Herádez-Lerma (1994). Para a ampla refereca de problemas de corol ópmo esocásco e empo dscreo y coo, aplcados e Cecas Ecoómcas, reférase a Veegas-Maríez (008). 148 Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011 EM3-3_pp dd 148 1/4/11 10:34:0 PM
3 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez coo cado las resrccoes so dfsoes codcdas por movmeos browaos. E la seccó 3, se plaea de maera geeral la meodología de programacó dámca (recrsvdad) e la qe se basa la solcó del problema de corol ópmo plaeado, obeedo como reslados cerales: prmero, la ecacó dferecal parcal o leal de Hamlo-Jacob-Bellmam y, segdo, las codcoes de prmer orde qe lleva a ecorar de maera geeral la expresó de la varable ópma de corol. E la seccó 4, se eca el eorema de verfcacó del corol ópmo esocásco y s demosracó se presea e el apédce A. de ese docmeo. E la seccó 5, se realza a prmera aplcacó del modelo de corol ópmo esocásco y se presea s solcó. E la seccó 6, se descrbe evamee, medae oro ejemplo, la aplcacó del problema de corol ópmo esocásco y s solcó co la verfcacó correspodee. La seccó 7 presea las coclsoes de ese rabajo y la úlma seccó coee apédce e el qe se desarrolla dealladamee el lema de Iô para movmeos browaos y la demosracó del eorema de verfcacó del cálclo esocásco, co la ecó de proporcoarle al lecor las pares del aálss qe o aparece e el cerpo prcpal del rabajo. Plaeameo del problema de corol ópmo esocásco La opmzacó dámca esocásca es el esdo de ssemas dámcos sjeos a perrbacoes aleaoras qe pede ser coroladas co el objevo de opmzar algú crero de desempeño. Srge e problemas de oma de decsoes bajo cerdmbre y ecera campo my férl para s aplcacó e ecoomía y fazas. E co, se lzaba los prcpos de opmzacó de Poryag y Bellma, pero e los úlmos años la eoría de corol se ha desarrollado oablemee movada por los problemas qe srge e la ecoomía maemáca y las maemácas faceras (Hyê, 009). El corol ópmo esocásco es a écca maemáca sada para resolver problemas de opmzacó de ssemas qe evolcoa e el empo e ambee de cerdmbre. El problema maemáco geeral de opmzacó eremporal esocásca, e empo coo o dscreo, se compoe de a fcó objevo, defda sobre varos perodos (fos o fos) sjea a resrccoes, de las cales, al meos a de ellas es dámca, así como a codcoes de froera (Wckes, 008), lzado varables de corol qe perme opmzar la Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 149 1/4/11 10:34:0 PM
4 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca fcó objevo, a f de ecorar las sedas ópmas y obeer así la rayecora ópma de las varables de esado a parr de la ecacó de movmeo qe las e (Cerda, 001). Ese problema eremporal comúmee se cooce como problema de corol ópmo esocásco e opmzacó dámca. Para esablecer el modelo maemáco geeral del problema de corol ópmo esocásco e opmzacó dámca e empo coo, resla ecesaro dspoer del plaeameo geeral del problema maemáco. Para ello, se cosdera ssema dámco formlado e empo coo e el horzoe emporal [0, T], y se defe las fcoes μ, x,, dadas por, μ : R + R R k R, σ : R + R R k R d. y σ, x, Para po x 0 R cosdere la sgee ecacó dferecal esocásca de esado d μ (,, )d σ (,, )dw (1) 0 = x 0, () e dode se cosdera el proceso -dmesoal como el proceso de varables de esado qe se reqere corolar, el proceso k-dmesoal como el proceso de corol, cya correca eleccó corolará a, y W es proceso de Weer o movmeo browao d-dmesoal, defdo sobre espaco fjo de probabldad co a flracó ( Ω,F, (F W) 0,T,P ). Se defe a coacó a regla de corol admsble; para al efeco, se cosdera la clase de procesos de corol admsble como proceso de corol cyo valor e el empo se adapa al proceso de esado, y el cal se obee medae la fcó (, x). defda por : R R R k, = (, ), así defda, se llama regla de corol de reroalmeacó. Spógase ahora qe se elge la regla de corol de reroalmeacó fja (, x) y se ssye e 1, de dode se obee la ecacó dferecal esocásca 150 Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011 EM3-3_pp dd 150 1/4/11 10:34:1 PM
5 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez d σ (,,(, ))dw. (3) d μ,,(, ) Además, se mpoe a la resrccó de qe, para cada, U R k, dode U es la clase de coroles admsbles. Defcó 1. Ua regla de corol (, x) es admsble s (Björk, 004); 3 ) (, x) U, R y x R ) Para calqer po cal (, x) dado, la ecacó dferecal esocásca ( ) ds σ ( s, s,( s, s )) dw s d s μ s, s, s, s = x ee a úca solcó. Peso qe el problema de corol ópmo por defr se ecera e el marco esocásco y oda vez qe el proceso de esado es -dmesoal, será ecesaro defr las sgees fcoes y esablecer el eorema fdameal del cálclo esocásco, llamado lema de Iô para el caso de varables. Defcó ) Para calqer vecor fjo R k, las fcoes m y s esá defdas por μ σ (, x) μ (, x,) (, x) σ, x, y se spoe co segdas dervadas coas. ) Para calqer regla de corol las fcoes m y s esá defdas por μ σ ( ) ( ) (, x) μ, x,, x (, x) σ, x,, x y se spoe co segdas dervadas coas. 3 Varos de los cocepos eórcos fdameales lzados, así como alga de la oacó adopada e ese docmeo, provee del exo de Björk (004). Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 151 1/4/11 10:34:3 PM
6 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca Lema de Iô 4 para varables ) Cosdere la fcó y = f (x, ), x = (x 1, x,, x ), la ecacó dferecal esocásca dx = μ, )d + σ, ) dw y calqer vecor fjo R k, e dode, como ya se dcó, W es movmeo browao defdo sobre espaco fjo de probabldad co a flracó W ameada 1Ω,F, (F ) [0,T ],. Eoces, medae a aplcacó esádar de expasó e sere de Taylor y el so de las reglas del cálclo de Iô, se obee el eorema fdameal del cálclo esocásco (véase el apédce A, seccó A.1), f x, dy = + =1 f x, + 1 j =1 =1 μ f x, j σ, )σ j, )ρ j, ) d + f x, σ, )dw. =1 ) Aálogamee, para calqer regla de corol, se ee (véase el apédce A, seccó A.1) f x, dy = + =1 f x, + 1 j =1 =1 μ f x, j σ, )σ j, )ρ j, ) d + f x, σ, )dw. =1 Dada a regla de corol co s correspodee proceso corolado, algas veces saremos la oacó dode, d = μ d + σ dw (4) 4 Varos de los cocepos eórcos fdameales lzados, así como alga de la oacó empleada e ese docmeo se adopa del lbro de Veegas-Maríez (008). 15 Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011 EM3-3_pp dd 15 1/4/11 10:34:4 PM
7 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez (, ) Para defr la fcó objevo del problema de corol se cosdera las fcoes (Cerda, 001): y F : R R R k R dada por,, F (,, ) Φ : R R dada por Φ dode F valúa el desempeño del ssema a ravés del empo y F es el esado e el qe qeda el ssema e el horzoe emporal del problema. Se spoe qe ao F como F so de clase C. Se defe la fcoal objevo de esro problema como la fcó J 0 : U R defda por, J 0 T ( ) E F (,, )dφ T 0 F 0, dode es la solcó de 3, co codcó cal 0 = x 0, y dode F 0 represea la formacó dspoble hasa el empo = 0. El problema de corol pede ser escro como o de maxmzacó de la fcoal J 0 1, sobre odo U, de dode se defe la fcoal ópma por Ĵ 0 max U J 0 ( ). S exse la regla de corol admsble û al qe J û Ĵ0 0 eoces û se defe como a regla de corol ópmo para el problema dado. Defcó 3. Se spoe a pareja 1, x fja, dode 0, T y x R. El problema de corol P 1, x se defe como: Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 153 1/4/11 10:34:5 PM
8 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca sjeo a las ecacoes dámcas y a la resrccó T Maxmzar E F ( s, s, s )d s Φ T F d s μ ( s, s,( s, s )) ds σ s, (, s, s ( s )) dw (5) s ( s, y ) U, para odo ( s, y ),T = x (6) R. (7) Ecacó de Hamlo-Jacob-Bellma E esa seccó os efocamos e la regla de corol ópmo para el problema de corol dado, para lo cal, lzaremos la programacó dámca. Defcó 4 ) La fcó de valor esá defda por J, x, J : R R U R T E F s, s, s dsφ T F jo co las ecacoes dámcas 5 y 6. ) La fcó de valor ópmo es y esá defda por Ĵ : R R R Ĵ (, ) max J (, x,). U 154 Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011 EM3-3_pp dd 154 1/4/11 10:34:7 PM
9 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez El objevo, ahora, es caracerzar la fcó de valor e el corol ópmo y hacer a dervacó de s ecacó dferecal parcal, mejor coocda como la edp de hjb, 5 por lo cal se hace los sgees spesos. Spesos 1. Se spoe qe: 1) Exse a regla de corol ópmo. ) La fcó de valor ópmo Jˆ es de clase C. ( 0,T ) R Cosdere el par, x fjo pero arbraro y spoga cremeo my peqeño, de hecho, dferecal d R, al qe < + d < T. També elegmos a regla de corol fja pero arbrara. Por ao, dada la defcó de la fcó de valor ópmo y el cremeo d, se ee la relacó recrsva emporal (Veegas-Maríez, 008), T Ĵ (, ) = max J (, x,) = maxe F ( s, U U s, s )ds +Φ ( T ) F + d T = maxe F ( s, U s, s )ds + F ( s, s, s )ds +Φ ( T ) F +d + d = maxe F ( s, U s, s )ds +Ĵ ( + d, + d ) F, a esa expresó se le aplca e el prmer smado el eorema del valor medo de cálclo egral y, e el segdo smado se aplca expasó e sere de Taylor, de lo qe resla = max Ĵ, E F, U, smplfcado, se ee 0 = max U d + o d E F (,, )d + o d + Ĵ, ( ) + dĵ, ( ) + o ( d ) F F + dĵ, E la expresó aeror aplcamos el lema de Iô para obeer la dferecal esocásca de Jˆ, así 5 La ecacó de hjb es el reslado ceral e la eoría de corol ópmo. La ecacó correspodee e empo dscreo se cooce como la ecacó de Bellma.., Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 155 1/4/11 10:34:8 PM
10 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca 0 max U 1 j 1 1 Ĵ, ( ) EF (,, )d o d Ĵ (, ) Ĵ σ j, )σ j, )ρ j d 1 1 Ĵ,, μ σ, ), )dw F. Peso qe dw N 1d, al omar valores esperados a los érmos aleaoros de la ecacó aeror, se sge qe: 0 max U 1 j 1 1 Ĵ, ( ) F (,, )d o d Ĵ (, ) σ j, )σ j, )ρ j d. Ĵ, Ahora, se dvde ere d y se oma el líme cado d 0 0 lm max F (, d 0 U,) d o ( d ) Ĵ, d d Ĵ, ( ) 1 σ j, )σ j, d )ρ j j 1 1 d y así se obee falmee la edp de hjb: 0 max U 1 Ĵ, ( ) F,, j 1 1 Ĵ, j σ 156 Edcacó Maemáca, vol. 3, úm. 3, dcembre de Ĵ, μ Ĵ, μ, ), ) μ, ), )σ j, )ρ j. (8) EM3-3_pp dd 156 1/4/11 10:34:9 PM
11 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez Peso qe el aálss ha sdo realzado sobre po fjo pero arbraro, la ecacó se sosee para odo po 1, x 10, T R, y podemos esablecer ahora el sgee eorema. Teorema 1. Ecacó de Hamlo-Jacob-Bellma Bajo los spesos 1 se afrma lo sgee: a) Jˆ sasface la ecacó Hamlo-Jacob-Bellma + Ĵ, ( ) 0 = maxf, U, + Ĵ (, ) + 1 σ j j =1 =1 Ĵ(, T ) = Φ( T ) para oda 0,T =1, )σ j Ĵ, R. μ, )ρ j, ) para oda pareja (x, ) ( 0,T ) R b) Para cada 1, x 10, T R, el máxmo e la ecacó hjb es alcazado por = û 1,x. Codcoes de prmer orde A parr de la ecacó de hjb, se sge qe es la úca varable, ya qe x y so fjos y las fcoes F, Jˆ, μ,σ y σ j se cosdera como dadas. S se ee qe U es máxmo, eoces se obee la sgee ecacó dferecal parcal de segdo orde e Jˆ, + Ĵ, ( ) 0 = F,, + =1 Ĵ, μ + 1 Ĵ, σ j, )σ j, )ρ j. j =1 =1, ) Al dervar dcha ecacó co respeco de la varable de corol se ee la codcó de prmer orde Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 157 1/4/11 10:34:30 PM
12 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca 0 F (,, ) 1 j 1 1 Ĵ (, ) Ĵ, j σ 1, )σ j Ĵ, μ, ), )ρ j. (9) La ecacó 9, codcoada por las fcoes F, Jˆ (jo co ss dervadas parcales) μ,σ y σ j, caracerza al corol ópmo e fcó de x y y Jˆ; es decr, û = û 1, x, Jˆ. Para resolver la ecacó de hjb y ecorar la rayecora ópma del corol, eórcamee se procede a resolver por el méodo de fcoes e varables separables (e prodco), ya qe se raa de a ecacó dferecal parcal o leal; aqe es ecesaro recordar qe, e geeral, es dfícl obeer a solcó explíca de la ecacó de hjb. S embargo, para el po de aplcacoes qe se reqere e las cecas ecoómcas, exse algos casos e los qe, a pesar de ser o rvales, la ecacó de hjb ee a solcó aalíca; véase, al respeco, Mero (1990), Lehoczky (1983) y Hakasso (1970). Teorema de verfcacó Obsérvese qe el eorema 1 ee la forma de a codcó ecesara, pero aforadamee la ecacó de hjb ambé acúa como codcó sfcee para el problema de corol ópmo. El reslado qe ssea esa codcó, el cal se eca a coacó, se cooce como el eorema de verfcacó para la programacó dámca (reférase al apédce A seccó A. para ver la demosracó del eorema de verfcacó). Teorema. Teorema de verfcacó Spoga qe se ee las fcoes H(, ) y g(, x), ales qe ) H sasface la egral de Iô y es solcó de la edp hjb, es decr, 0 max U H, ( ) F,, 1 H, μ, ) 158 Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011 EM3-3_pp dd 158 1/4/11 10:34:31 PM
13 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez Ï Ì Ó 1 j 1 1 H, j σ, )σ j H(, T ) Φ( T ) para odo R, )ρ j para odo par (x, ) ( 0,T )R ) La fcó g es a regla de corol admsble. ) Para cada 1, x 10, T R, 1, x, fjo pero arbraro, el máxmo e la ecacó de hjb es alcazado por la eleccó = g 1, x. Por lo ao se sosee lo sgee: 1) La fcó de valor ópmo Jˆ del problema de corol, esa dada por Ĵ(, ) H(, ). ) Exse a regla de corol ópma û al qe û 1, x = g 1, x. U problema de cosmo ópmo Cosdere agee ecoómco racoal de vda fa, lo qe se erprea como qe s descedeca heredará s rqeza y s fcó de ldad por el cosmo. E el empo = 0, el agee es doado co a rqeza cal x 0 y efrea el problema de cómo dsrbr s rqeza ere versó y cosmo e horzoe fo de al modo qe maxmce s fcó de ldad por el cosmo. Así pes, spoemos qe la ldad oal del agee esá dada por E F ( c s,s)ds F 0 0 dode F es la fcó de sasfaccó por el cosmo y F 0 es la formacó dspoble e el empo 0. Spoemos qe el agee pede verr a pare de s dero como ahorro e baco qe le oorga a asa de erés r > 0, lbre de resgo de cmplmeo. Así, el saldo de la versó e el empo es B = B 0 e r, el cal pede ser expresado medae la ecacó dferecal Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 159 1/4/11 10:34:3 PM
14 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca db rb d, co B 0 dado, lo cal mplca qe R B db B rd. (10) També pede verr e acvo co resgo cyo proceso de precos es codcdo por la sgee ecacó dferecal esocásca: Lo cal codce a ds = ms d + ss dw, dr S ds μd + σdw S, (11) dode W es proceso de Weer, ambé llamado movmeo browao, qe esá defdo sobre espaco fjo de probabldad co s flracó ameada Ω,F, (F W) 0,T,P. Las proporcoes de la rqeza qe se desará a los acvos s resgo y co resgo e el porafolo de versó e el empo las deoaremos por 1 - q y q. Asmsmo, deoaremos por c la asa de cosmo, a la qe se le pde qe c 0, 0. Adcoalmee, resrgmos las esraegas de cosmoversó a qe sea aofacables y spoemos, además, qe vvmos e mdo e el qe las egocacoes so posbles de maera coa s crrr e gú momeo e cosos por comsoes a agees de bolsa pagos de mpesos a aordades fscales. Spoemos ambé qe las veas e coro (pedr accoes presadas) so permdas e lmadas. De esa maera, s represea la rqeza del cosmdor e el empo, eoces la dámca del proceso de la rqeza esá dada por: d ( 1 θ )dr B θ dr S c d ( 1 θ )rd θ ( μd σdw ) c d rd θ rd θ μd θ σdw c d θ ( μ r )d ( r c )d θ σdw r θ ( μ r ) c d θ σdw, (1) 160 Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011 EM3-3_pp dd 160 1/4/11 10:34:33 PM
15 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez eqvaleemee, dode d μ d + σ dw (13) μ r θ ( μ r ) c y σ θ σ. (14) E la ecacó 1 se erprea θ μd como el redmeo esperado de la versó co resgo de q pesos drae el perodo de a + d ; θ σdw represea el resgo mplcado e verr los q pesos e el acvo resgoso; el érmo 11 - q rd es el erés gaado por el ahorro de 11 - q pesos y, falmee, c d represea el cosmo e el ervalo de empo de a + d (Seh y Thompso, 000). E resme, y esablecedo formalmee el problema de maxmzacó de ldad del cosmdor como problema de corol ópmo esocásco, se ee: Maxmzar E F ( c θ,c s,s)ds s F 0 dx r θ ( μ r ) c d θ σdw (15) 0 x 0 c 0, 0 Para dar solcó a esro problema, defmos la fcó de valor de la sgee maera: E F ( c θ R,0 c s,s)ds F s d max E F ( c θ R,0 c s,s)ds s F ( c s,s)ds d J (, ) max x F (16) Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 161 1/4/11 10:46:57 PM
16 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca Al aplcar el eorema del valor medo del cálclo egral al prmer smado y recrsvdad al segdo smado, se obee qe max J, θ R,c, +d { F ( c, )d o ( d ) J ( d, d ) F }. S se lza la expasó e sere de Taylor al segdo smado, se obee max J, θ R,c, d coseceemee, 0 max θ R,c { F ( c, )d o ( d ) J (, ) dj (, ) o ( d ) F }, d { F ( c, )d o ( d ) dj (, ) F }. Al aplcar a dj 1, el lema de Iô y smplfcar, se obee 0 max F ( c, )d o d θ R,c, +d J (, ) J (, ) J (, ) μ 1 J (, ) σ dw σ d F. Ahora se oma el valor esperado de la úlma ecacó, peso qe dw se dsrbye N 10, d, se elma el érmo co el movmeo browao, de lo qe resla 0 max θ R,c, d J, F ( c, )d o d d J, 1 μ d F. J, σ d A coacó se dvde la expresó aeror ere d y se oma el líme de ésa cado d 0, para obeer la edp de hjb 16 Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011 EM3-3_pp dd 16 1/4/11 10:46:58 PM
17 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez 0 max F c θ R,c, J (, ) J (, ) μ 1 J (, ) σ. (17) Ahora spoemos qe la fcó de ldad es de la forma F 1c, = e -r V 1c, dode V 1c es membro de la famla de fcoes de ldad hara (Mero, 1990 y Hakasso, 1970) 6 y r es parámero qe represea la asedad por cosmr del agee. Para esro problema elegmos, e parclar, la fcó de cosmo F ( c, ) e ρ c γ, co 0 γ 1, Noe qe V 1c ee la propedad de qe V ʹ( 0) γc γ dado qe 0 γ 1, c c 0 lo qe forzará a qe el cosmo sea posvo a ravés del horzoe emporal. Al spoer máxmo eror y hacer las sscoes correspodees, de la edp de hjb se obee 0 e ρ c γ J, 1 J, J (, ) ( θ σ). r θ μ r c Lo qe ahora se reqere es opmzar para c y q. Las codcoes de prmer orde so: 0 e ρ γc γ 1 J (, ) γc γ 1 J, e ρ (18) 6 S la fcó de ldad es al qe s medda de aversó absola o relava al resgo es posva e hperbólca e el cosmo y peso qe se ha speso qe los precos de los acvos so geerados por el movmeo browao, será posble obeer solcoes explícas para el cosmo y porafolo ópmos. Para amplo aálss de fcoes de ldad de po hara, véase por ejemplo Mero (1990) y Hakasso (1970). Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 163 1/4/11 10:46:59 PM
18 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca 0 J (, ) ( μ r ) J (, ) J, ( μ r ) θ σ θ. J, σ Ahora, para elegr la fcó J 1, qe sasfaga la edp de hjb y oda vez qe se raa de a ecacó dferecal parcal o leal, s fcó solcó es prodco de fcoes e varables separables (e prodco) de la forma J (, ) V ( x )h( )e ρ, es decr, J (, ) h( )e ρ x γ. (19) Ua vez elegdo el caddao de solcó para J, se calcla ss dervadas parcales J (, ) γx γ1 h( )e ρ, J, J, γ( γ 1) x γ h( )e ρ, ρx γ h( )e ρ x γ hʹ( )e ρ. (0) Ssmos los valores aerores e las codcoes de prmer orde de al maera qe θ γc γ1 J x, J x, ĉ xh ( μ r ) x σ J x, e ρ 1 γ1 γx γ1 h( )e ρ e ρ c γ1 x γ1 h( ) ( ), μ r x σ γ γ 1 (1) γx γ1 e ρ ( ˆθ x γ e ρ μ r ) σ ( γ 1). () 164 Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011 EM3-3_pp dd 164 1/4/11 10:47:00 PM
19 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez Observamos qe la proporcó ópma qe se asga a la eeca del acvo resgoso es cosae y la regla ópma de cosmo es leal e la rqeza. Para sar el eorema de verfcacó, se reqere mosrar qe J 1, reselve la ecacó de hjb, por lo qe ssmos las ecacoes 0, 1 y e la ecacó 18, de al modo qe: 0 x γ hʹ ( h( ) ( ρ) γ r μ r ) σ ( γ 1) ( 1 γ)h γ γ1 ( ). 1 γ( μ r ) σ γ 1 (3) Al deoar las cosaes k 1 ρ ( γ r μ r ) σ ( γ 1) 1 γ( μ r ) σ γ 1 y k ( 1 γ), (4) se ee la ecacó dferecal ordara γ 0 x γ γ1 hʹ ( ) k 1 h( ) k h ( ). (5) S esa ecacó se sosee para oda x y, eoces h1 debe de resolver la ecacó hʹ ( ) k 1 h k h γ γ1 ( ), (6) la cal es a ecacó de Beroll co p 1x = k 1, q 1x = -k y γ γ 1. Para rasformar la ecacó de Beroll e a ecacó dferecal leal de a fcó (descoocda), ssmos z h 1 h 1 γ1 ( ), de dode se ee qe h z 1 γ y hʹ( ) ( 1 γ)z γ z ʹ, al ssr e 6 y mlplcar ambos lados de la ecacó por z γ, se obee, ( 1 γ) Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 165 1/4/11 10:47:01 PM
20 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca zʹ k 1 1 γ z k ( 1 γ) o zʹ k 11 z k. (7) Para resolver esa ecacó leal, se ee qe el facor egrae esá dado por e k 11, de dode se obee qe z 1 es z μ q ( )d k 5 μ k k 11 k 5 e k11, μ ( ) e k d 11 k e k11 d k 5 e k 11 k e d k k 5 11 e k 11 (8) y, por ao, h k k k 5 e k γ. (9) Hemos mosrado qe, s J esá defda por 19 co h1 dada por 9 y defda como la solcó de 5 y s defmos qˆ y ĉ por 1 y, eoces J sasface la ecacó de hjb y qˆ y ĉ cosge opmzar el problema de corol ópmo. U problema de cosmo-versó ópmos Cosderemos agee ecoómco y ervalo de empo fjo [0, T ], e el empo = 0; el agee es doado co a rqeza cal 0 y el problema qe efrea es cómo dsrbr s rqeza ere versó y cosmo de al modo qe s rqeza o sea egava e horzoe de empo fo y al qe maxmce s ldad oal esperada y descoada por el cosmo. Spogamos qe la ldad del agee esá dada por: T E F (,c )d Φ ( T ) F Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011 EM3-3_pp dd 166 1/4/11 10:47:0 PM
21 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez dode F es la fcó de ldad para cosmo y F es la fcó de legado o hereca (o fcó de rero e el empo T ), la cal mde la ldad de eer algo de dero al fal del perodo. Spoemos qe el agee pede verr a pare de s dero como ahorro e baco qe le oorga a asa de erés r > 0 (coamee capalzable). Así, el moo acmlado e el empo es B = B 0 e r, el cal pede ser expresado medae la ecacó dferecal dr B = db = rd. (30) B També pede verr e acvo co resgo cyo proceso de precos es modelado por la ecacó dferecal esocásca dr S = ds S = αd + σdw, (31) dode W es proceso de Weer, o movmeo browao, defdo sobre espaco fjo de probabldad 1Ω,F, (F W) 0,T,P co s flracó ameada. Como aes, las proporcoes relavas al porafolo e el empo las deoamos por 1 - q y q para los acvos lbre de resgo y co resgo, respecvamee, c deoa la asa de cosmo y se resrge a las esraegas de cosmo-versó qe sea aofacables. Además, se spoe qe el agee vve e mdo e el qe las egocacoes so posbles de maera coa s crrr e gú momeo e cosos por comsoes a agees de bolsa pagos de mpesos a aordades fscales, y qe las veas e coro so permdas e lmadas. De esa maera, s represea la rqeza del cosmdor e el empo, eoces la dámca del proceso de la rqeza esá dada por, d = r + θ α - r eqvaleemee, - c d + θ σdw, (3) d = α d + σ dw (33) Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 167 1/4/11 10:47:03 PM
22 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca dode α r θ ( α r ) c y σ θ σ. (34) Dados los spesos del problema, obsérvese qe el agee pede pedr presada a cadad lmada e verrla e accoes, por lo qe, e algú momeo, s rqeza podría llegar a ser cero e clso egava. De esa maera, T es a varable aleaora, la cal se llama empo de paro. Para lbrar ese problema, se resrge el domo a D 0,T x x 0, y se defe la fcó { } τ m f { 0 0 },T, y la erpreacó correspodee es qe, cado el proceso de rqeza pege e la froera del domo, es decr, sea cero, eoces la acvdad se erma y ya o hay hereca, de esa maera lo aral es qe f sea cero. E resme, y esablecedo formalmee el problema de maxmzacó de ldad del cosmdor como problema de corol ópmo esocásco, se ee τ Maxmzar E F (,c θ,c )d F 0, 0 d θ ( α r )d ( r c )d θ σdw, 0 x 0, c 0, 0. (35) Para dar solcó a esro problema y ecorar las proporcoes ópmas e el porafolo de versó y el cosmó ópmo del agee maxmzador, defmos la fcó de valor de esro problema de la sgee maera: J (, ) max θ R,0 c s, τ max θ R,0 c s, τ τ E F ( c s,s)ds F d τ E F ( c s,s)ds + F ( c s,s)ds d F. (36) Despés de aplcar el eorema del valor medo del cálclo egral al prmer smado y recrsvdad al segdo smado, se obee qe 168 Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011 EM3-3_pp dd 168 1/4/11 10:47:04 PM
23 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez max J, θ R,0 c, d { F ( c, )d o ( d ) J ( d, d ) F }. Al aplcar la expasó e sere de Taylor al segdo smado, se ee por cosgee, J (, ) max θ R,0 c, d { F ( c, )d o ( d ) J (, ) dj (, ) o ( d ) F } 0 max θ R,0 c s, d { F ( c, )d o ( d ) dj (, ) F }. Al aplcar a dj 1, el lema de Iô y smplfcar, se obee 0 max F ( c, )d o d θ R,0 c, d J (, ) J (, ) J (, ) α 1 J (, ) σ dw σ d F. A coacó, se obee el valor esperado de esa úlma ecacó y, peso qe dw se dsrbye N 10, d, se elma el érmo co browao, de lo qe resla 0 max θ R,0 c, d J, F ( c, )d o d d J, 1 α d F. J, σ d Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 169 1/4/11 10:47:05 PM
24 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca Ahora se dvde esa expresó ere d y se oma s líme cado d 0 0 max F c θ R,0 c, J (, ) J (, ) α 1 J (, ) σ. A esa ecacó le aexamos las codcoes de froera correspodees para obeer la edp de hjb Ï Ì Ó 0 max θ R,0 c, d J (, ) F c, J (, ) α 1 J (, ) J T, x σ, 0, 0. (37) J,0 Las codcoes de froera corpora el empo de paro. Spoemos ahora qe la fcó de ldad es de la forma F c, e ρ V c, dode V 1c es membro de la famla de fcoes de ldad hara (Mero, 1990; Hakasso, 1970); para esro problema e parclar, elegmos la fcó de cosmo e ρ c γ F c,, 0 γ 1. γ Observe qe V 1c ee la propedad de qe V ʹ0 c γ, c c 0 lo qe forzará a qe el cosmo sea posvo a ravés del horzoe emporal. Al spoer máxmo eror y hacer las sscoes correspodees e la edp de hjb, se ee 0 e ρ c γ 1 γ J, J, J (, ) r θ α r c ( θ σ). (38) 170 Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011 EM3-3_pp dd 170 1/4/11 10:47:06 PM
25 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez Ahora, lo qe se reqere es opmzar para c y q, de dode se obee las codcoes de prmer orde, γ1 c J x, e ρ y θ J ( x, ) x ( α r ) J x, x σ, (39) Ahora be, para elegr la fcó J 1, qe sasfaga la edp de hjb y ya qe se raa de a ecacó dferecal parcal o leal, s solcó es prodco de fcoes separables de al maera qe: J (, ) e ρ h( ) x γ γ, (40) jo co h 1T = 0 debdo a las codcoes de froera de la ecacó de hjb. Dado J, se ee qe J ( x, ) x γ J x, γ e ρ hʹ1 ρ x γ γ e ρ h1 x γ1 e ρ h1 J x, ( γ 1) x γ e ρ h1. S ssmos los valores de 41 e 39, se obee: 1 (41) c γ 1 x γ1 e ρ h1 e ρ c x γ1 h1 γ1 γ1 ĉ xh 1, (4) x γ e ρ h1 x σ ˆθ x γ1 e ρ h1 x α r α r γ 1 σ γ 1, (43) obsérvese qe ĉ es leal e la rqeza y la proporcó de porafolo ópmo qˆ es cosae. Para hacer la verfcacó medae el eorema ecado, se reqere mosrar qe J 1, reselve la ecacó de hjb, para lo qe ssmos las ecacoes 41, 4 y 43 e la ecacó 38, de dode se obee la ecacó, 1 Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 171 1/4/11 10:47:07 PM
26 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca 0 x γ hʹ 1 h γ ρ ( r α r ) γ σ ( γ 1 ) 1 ( α r ) σ γ 1 ( 1 γ γ ) γ1 h. γ Despés de mlplcar por g, se ee qe 0 x γ hʹ h ρ γ γ1 ( 1 γ)h. rγ γ ( α r ) σ ( γ 1) S se ssye los érmos cosaes por ρ rγ γ ( α r ) σ ( γ 1) 1 γ( α r ) σ γ 1 1 γ( α r ) σ γ 1 k 3 y k 4 ( 1 γ) se obee la ecacó dferecal ordara γ 0 x γ γ1 hʹ k 3 h k 4 h. (44) S esa ecacó se sosee para oda x y, eoces h 1 debe de resolver la ecacó γ hʹ k h k h γ1, h(t ) 0, (45) 3 4 qe es a ecacó de Beroll co p(x) k 3, q(x) k 4 y γ γ 1. Aálogamee al ejercco aeror, se hace la sscó z h 1 γ1 h, de dode se ee qe h z 1 γ y hʹ 1 γz γ z ʹ, al ssr e 45 y mlplcar ambos lados de la ecacó por ( 1 γ, se obee, ) z γ 1 17 Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011 EM3-3_pp dd 17 1/4/11 10:47:09 PM
27 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez zʹ k 3 1 γ z k 4 ( 1 γ) o zʹ k 33 z k 44, (46) para resolver esa ecacó leal, se ee qe el facor egrae esá dado por: de dode se obee qe z 1 es y, por ao, μ e k d 33 z μ q d k 6 μ k 44 e d k k 6 33 e k 33 e k 33, h k 44 k k 6 e k33 33 k e k33 d k 44 6 e k 33 k 44 k k 6 e k33, (47) 33 1 γ. (48) Ahora be, para sasfacer la codcó de froera se debe de cmplr: h( T ) k 1 γ 44 k k 6 e Tk33 0 k 44 k 33 k 6 e Tk por cosgee, la solcó de 45 esá dada por, h k 44 k 44 ( e T )k 33 k 33 k 33 k 44 k 33 e Tk33 k 6 1 γ. (49) Hemos así mosrado qe s J esá dada por 40, co 49 defda como la solcó de 45 y s defmos qˆ y ĉ por 43 y 4, eoces J sasface la ecacó de hjb y qˆ y ĉ cosge opmzar el problema de corol ópmo co horzoe emporal esocásco. Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 173 1/4/11 10:47:10 PM
28 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca Coclsoes Es de recoocerse el mporae papel qe ha desempeñado la maemáca e la ecoomía. Específcamee, la eoría de corol ópmo esocásco e empo coo se ha revelado como srmeo fdameal e la ecoomía maemáca cado se reqere modelar alga acvdad ecoómca qe se desarrolla de maera dámca. Por lo aeror, ese docmeo vo como propóso hacer accesbles la eseñaza y el apredzaje de la modelacó e problemas de opmzacó dámca e ecoomía maemáca. Por lo qe, de maera ddácca, se preseó de maera geeral el modelo maemáco del problema de corol ópmo esocásco e empo coo. Además, de modo ameo y secllo, se dedjo la ecacó dferecal parcal de segdo orde y leal, ecacó de hjb (codcó ecesara de ópmo) del problema e cesó, cya solcó lleva a ecorar las rayecoras ópmas qe da solcó al problema plaeado, lo cal asegra el eorema de verfcacó (demosrado e el apédce). Asmsmo, se presearo dos ejemplos de aplcacó e ecoomía maemáca, el prmero de ellos correspode a modelo de cosmdor racoal qe dspoe de a rqeza cal y efrea la decsó de dsrbr s rqeza ere cosmo y porafolo de acvos e horzoe de plaeacó fo de al modo qe maxmce s ldad oal esperada por el cosmo. El segdo ejemplo es aálogo al prmero, co la salvedad de qe ahora se esablece horzoe emporal fo cya dracó es esocásca. Ua parclardad e ambos ejemplos es el speso de qe la dámca de los precos esá modelada por proceso de dfsó, lo cal corpora mayor realsmo al modelado. La prcpal dfclad de los problemas de corol ópmo esocásco es resolver la ecacó de hjb, ya qe o hay a eoría geeral dspoble para eso. No obsae, para el caso de las aplcacoes qe os ocpa e ese aríclo, es posble ecorar solcoes aalícas y cerradas de dcha ecacó sempre qe se corpore e los spesos qe la dámca de los precos sge el movmeo geomérco browao y la fcó de ldad es del po Uc, e ρ V c,dode V es membro de la famla de fcoes de po hara (Hyperbolc Absole Rsk Averso). 7 7 Para a ampla clasfcacó de las fcoes po hara, véase por ejemplo Mero (1990) y Hakaso(1970). 174 Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011 EM3-3_pp dd 174 1/4/11 10:47:11 PM
29 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez Apédce A A.1. Le m a de Iô para el caso de m o v m e o s browaos geomércos e forma dferecal Cosdere la fcó f x,, x (x 1, x,, x ), y la sgee ecacó dferecal esocásca: dx μ, )d σ, )dw, (A.1) dode dw N 10, d es movmeo browao o proceso de Weer. Cosdere ambé la sgee abla de mlplcacó para la dferecacó esocásca, d dw dw j d dw 0 d r j d dw j 0 r j d d Obsérvese qe, e la abla aeror, el coefcee de correlacó r = 1, para odo = 1,,. Para obeer el lema de Iô, prmeramee se hace a expasó e sere de Taylor hasa los érmos de segdo orde, ya qe los érmos de orde mayor se alaría segú la abla arrba ecada. Por lo qe se ee f x, df ( x, ) j 1 d f x, 1 f x, j f x, dx dx j dx dx j f x, j f x, dx dx j dx d (A.) Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 175 1/4/11 10:47:1 PM
30 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca 1 f x, ddx f ( x, ) d. (A.) Ahora, se ssye e la ecacó el movmeo geomérco browao e s forma dferecal y se hace so de las reglas de mlplcacó para la dferecacó esocásca, f x, df ( x, ) 1 1 j j 1 d f x, f x, 1 j f x, j f x, μ, )d σ, )dw ( μ, )d σ, )dw ) dx dx j dx j dx, al ssr dx μ, )d μ, )σ, )ddw σ, )dw. dx dx j μ, )μ j ( x j, )d μ, )σ j ( x j, )ddw j μ j ( x j, )σ, )ddw σ, )σ j ( x j, )dw dw j σ, )σ j ( x j, )ρ j d. y smplfcar, se ee qe f ( x, ) df ( x, ) 1 1 f x, d μ, ) d 1 1 μ, ) f ( x, ) d f x, 1 μ x, x f ( x, ) σ, ) dw 176 Edcacó Maemáca, vol. 3, úm. 3, dcembre de σ, ) ddw EM3-3_pp dd 176 1/4/11 10:47:14 PM
31 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez j 1 1 f x, σ, ) dw σ j x, f x, de dode, falmee, se obee 1 1 j 1 f x, f x, d j 1 σ j, )ρ j dw dw j σ j σ ρ j dw j dw μ x, f x, 1 f x, σ, )d j 1 j σ j x, f x, d j f x, σ, )ρ j d, f ( x, ) σ, )dw j σ x, σ j, )ρ j d df x, f x, 1 j f x, f ( x, ) μ, ) j σ x, f x, σ, )dw. 1 σ j, )ρ j d (A.3) A.. Demosracó del eorema de verfcacó para programacó dámca Demosracó del eorema. Spógase qe H y g so dadas como se ecó aerormee. Se elje a regla de corol arbrara Œ U y po fjo 1x,. Se defe el proceso e el ervalo de empo 3, T 4 como la solcó de la ecacó Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 177 1/4/11 10:48:53 PM
32 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca d μ s, s ( s )ds σ ( s, s )dw s, (A.4) = x. Obsérvese prmero qe H ( T, T ) H ( ( T ), + ( T ) ) H, T H ( s, H (, ) s ) 1 1 H s, s μ dh, j 1 1 H s, s j σ, )σ j T H s,, ) s ds σ, ) dw s. 1 Ahora be, como H es solcó de la edp hjb, se ee qe H (, x) H (, x) F (, x,) μ, ) 1 1 H (, x ) σ j, )σ j, )ρ j ds 0, U, j 1 1 (A.5), )ρ j eoces, para cada s, se cmple qe H, ( ) H ( s, s ) μ, ) 1 1 H s, ( s ) σ j, )σ j, )ρ j ds F s, j 1 1 ( s ) (A.7) dada la codcó de froera de la edp hjb y las ecacoes A.6 y A.7, se sge qe T H (, s ) F ( s, s,)ds Φ( T ) T 1 σ, ) H s, s dw s (A.6) 178 Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011 EM3-3_pp dd 178 1/4/11 10:48:54 PM
33 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez al omar valor esperado se ee T H (, s ) E F ( s, s,)ds Φ( T ) J, x, de dode se coclye qe, H, ( s ) max J (, x,) Ĵ, ( ), (A.8) eso oda vez qe la regla de corol fe elegda arbraramee. Ahora, spoga qe se elge a regla de corol 1, x = g 1, x, dado por speso el cso del eorema, de maera aáloga se obee, H, x 1 j 1 1 F g (, x) H, x j g σ 1 H, x g, )σ j g μ, ), )ρ j ds 0, lo qe codce a la sgee galdad T H (, s ) E F g g g ( s, s )ds Φ( T ) J (, x, g). (A.9) Dado qe Ĵ, es la fcó de valor ópma, se ee qe J (, x, g), (A.10) Ĵ, pero al r las ecacoes A.8, A.9 y A.10, se sge es decr, H(, ) Ĵ, s ( ) J (, x, g) H(, s ), H(, ) Ĵ, s ( ) J (, x, g) por ao, H = Ĵ y g es la regla de corol ópma. Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 179 1/4/11 10:48:55 PM
34 Corol ópmo esocásco e la eseñaza de la ecoomía maemáca Referecas bblográfcas Bersekas, D. (005), Dyamc programmg ad opmal corol, 3a. ed., Belmo, Massachses, Ahea Scefc. Björk, T. (004), Arbrage Theory Coos Tme, a. ed., Oxford Uversy Press. Björk, T., J. Myhrma y M. Persso (1987), Opmal cosmpo wh sochasc prces coos me, Joral of Appled Probably, vol. 4, úm. 1, pp Cerda, E. (001), Opmzacó dámca, Madrd, Prece-Hall. Hakasso, N. (1970), Opmal Ivesme ad Cosmpo Sraeges der Rsk for a Class of Uly Fcos, Ecoomerca, vol. 38, úm. 5, pp Herádez-Lerma, O. (1994), Lecres o Coos-Tme Markov Corol Processes, Aporacoes Maemácas 3, Socedad Maemáca Mexcaa. Hyê, P. (009), Coos-me Sochasc Corol ad Opmzao wh Facal Applcaos, Berl y Hedelberg, Sprger. Lehoczky, J., S. Seh y S. Shreve (1983), Opmal Cosmpo ad Ivesme Polces Allowg Cosmpo Cosras ad Bakrpcy, Mahemacs of Operaos Research, vol. 8, úm. 4, pp Mero, R. (1990), Coos-Tme Face, Cambrdge, Massachses, Basl Blackwell. Schmdl, H (008), Sochasc Corol Israce, Lodres, Sprger. Seh, S. y G. Thompso (000), Opmal Corol Theory, Neva York, Sprger. Veegas-Maríez, F. (008), Resgos faceros y ecoómcos, prodcos dervados y decsoes ecoómcas bajo cerdmbre, a. ed., Méxco, Cegage. Wckes, M. (008), Macroecoomc Theory: A Dyamc Geeral Eqlbrm Approach, Prceo ad Oxford Uversy Press. 180 Edcacó Maemáca, vol. 3, úm. 3, dcembre de 011 EM3-3_pp dd 180 1/4/11 10:48:56 PM
35 Ma. Teresa V. Maríez Palacos y Fracsco Veegas-Maríez Daos de los aores Ma. Teresa V. Maríez Palacos Escela Speror de Ecoomía del Iso Polécco Nacoal (ese-p). erevolea@homal.com Fracsco Veegas-Maríez Escela Speror de Ecoomía del Iso Polécco Nacoal (ese-p). fveegas1111@yahoo.com.mx Edcacó Maemáca, vol. 3, úm. 3, dcembre de EM3-3_pp dd 181 1/4/11 10:48:56 PM
{ a 1, a 2,..., a } n. Cualquier vector n
 Deparameo de Aálss Ecoómco UNIVERSIDAD DE ZARAGOZA Tema 3: Formas cuadrácas reales Para odo el ema, se cosdera e R u ssema de refereca (o base) dado { a 1, a 2,..., a }. Cualquer vecor x R se escrbe de
Deparameo de Aálss Ecoómco UNIVERSIDAD DE ZARAGOZA Tema 3: Formas cuadrácas reales Para odo el ema, se cosdera e R u ssema de refereca (o base) dado { a 1, a 2,..., a }. Cualquer vecor x R se escrbe de
Álgebra Manuel Hervás Curso
 Álgebra Mauel Hervás Curso 0-0 FORMAS LINEALES Defcó Sea E u espaco vecoral sobre referdo a ua base B e e e,,, Se deoma Forma Leal sobre a la aplcacó leal f : E al que x E f ( x) b De modo que elegdo u
Álgebra Mauel Hervás Curso 0-0 FORMAS LINEALES Defcó Sea E u espaco vecoral sobre referdo a ua base B e e e,,, Se deoma Forma Leal sobre a la aplcacó leal f : E al que x E f ( x) b De modo que elegdo u
Estimación de parámetros en ecuaciones diferenciales estocásticas aplicadas a finanzas
 Esmacó de parámeros e ecuacoes dferecales esocáscas aplcadas a fazas Joh Freddy Moreo Trujllo * jho.moreo@uexerado.edu.co * Docee vesgador. Faculad de Fazas, Gobero y Relacoes Ieracoales. Uversdad Exerado
Esmacó de parámeros e ecuacoes dferecales esocáscas aplcadas a fazas Joh Freddy Moreo Trujllo * jho.moreo@uexerado.edu.co * Docee vesgador. Faculad de Fazas, Gobero y Relacoes Ieracoales. Uversdad Exerado
2. Movimiento Browniano.
 Movmeo Browao Defcó y Propedade Báca Defcó : EL proceo de Weer (ó movmeo Browao e u proceo eocáco (Ver ZDZ co valore e R defdo para [, al que: W = co probabldad gual a uo La rayecora o coua Para cualquer
Movmeo Browao Defcó y Propedade Báca Defcó : EL proceo de Weer (ó movmeo Browao e u proceo eocáco (Ver ZDZ co valore e R defdo para [, al que: W = co probabldad gual a uo La rayecora o coua Para cualquer
Curvas Sistemas Gráficos Ing. Horacio Abbate 1
 Crvas Ssemas Gráfcos Ig. Horaco Abbae Polomos de erse Para y cosderar Para y cosderar - - Forma a base ara los olomos de grado. Calqer olomo de grado se ede descrbr como a combacó leal de olomos de erse
Crvas Ssemas Gráfcos Ig. Horaco Abbae Polomos de erse Para y cosderar Para y cosderar - - Forma a base ara los olomos de grado. Calqer olomo de grado se ede descrbr como a combacó leal de olomos de erse
1.1 MEDIA Y VARIANZA. Demostración: NOTAS: 1 n
 . TORÍA ASINTÓTICA Jore duardo Orz Trvño rofesor Asocado eparameo de Ieería de Ssemas e Idusral Uversdad Nacoal de Colomba jeorz@ual.edu.co (a) Se euca (s demosracó) varos resulados mporaes de esadísca.
. TORÍA ASINTÓTICA Jore duardo Orz Trvño rofesor Asocado eparameo de Ieería de Ssemas e Idusral Uversdad Nacoal de Colomba jeorz@ual.edu.co (a) Se euca (s demosracó) varos resulados mporaes de esadísca.
Introducción a la Econometría Curso 2009/ Serie de Problemas 21
 Iroduccó a la Ecoomería Curso 9/78 Sere de Problemas. Supoga que u vesgador dspoe de ua muesra de grupos (clases) de educacó prmara y ulza daos del úmero de alumos e cada clase (CS) y de la oa meda obeda
Iroduccó a la Ecoomería Curso 9/78 Sere de Problemas. Supoga que u vesgador dspoe de ua muesra de grupos (clases) de educacó prmara y ulza daos del úmero de alumos e cada clase (CS) y de la oa meda obeda
Educación Matemática ISSN: Grupo Santillana México México
 Edcació Maemáica ISSN: 1665-586 revedma@yahoo.com.mx Grpo Saillaa México México Maríez Palacios, Ma. Teresa V.; Veegas-Maríez, Fracisco Corol ópimo esocásico e la eseñaza de la ecoomía maemáica Edcació
Edcació Maemáica ISSN: 1665-586 revedma@yahoo.com.mx Grpo Saillaa México México Maríez Palacios, Ma. Teresa V.; Veegas-Maríez, Fracisco Corol ópimo esocásico e la eseñaza de la ecoomía maemáica Edcació
PLAN DE TRABAJO 11 Período 23/10/06 al 3/11/06. Durante estas dos semanas estudiarás los modelos de regresiones lineales.
 Pla de Trabajo 0- Año 006 Curso Lbre Assdo de Esadísca II Docees resposables: Lercy Barros - María Sague PLAN DE TRABAJO Período 3/0/06 al 3//06 TEMAS A ESTUDIAR Durae esas dos semaas esudarás los modelos
Pla de Trabajo 0- Año 006 Curso Lbre Assdo de Esadísca II Docees resposables: Lercy Barros - María Sague PLAN DE TRABAJO Período 3/0/06 al 3//06 TEMAS A ESTUDIAR Durae esas dos semaas esudarás los modelos
VOLUMEN IV CAPITULO 3 METODOLOGÍA PARA LA ACTULIZACIÓN DE LAS CURVA DE COSTOS ÓPTIMOS DE RACIONAMIENTO DE ELECTRICIDAD Y GAS NATURAL
 ESTUDO DE OSTOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL Volume V apulo 3 forme Fal Revsó. VOLUMEN V APTULO 3 METODOLOGÍA PARA LA ATULZAÓN DE LAS URVA DE OSTOS ÓPTMOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL
ESTUDO DE OSTOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL Volume V apulo 3 forme Fal Revsó. VOLUMEN V APTULO 3 METODOLOGÍA PARA LA ATULZAÓN DE LAS URVA DE OSTOS ÓPTMOS DE RAONAMENTO DE ELETRDAD Y GAS NATURAL
Flujo en acuífero libre
 SESIÓN PRÁCTICA 5 EDP PARABÓLICA CON ÉTODO CN VARIABLE Fljo e acíero lbre E esa sesó se aalza medae el méodo Cra-Ncolso de derecas as la evolcó emporal del vel reáco sobre a geomería de acíero lbre alerada
SESIÓN PRÁCTICA 5 EDP PARABÓLICA CON ÉTODO CN VARIABLE Fljo e acíero lbre E esa sesó se aalza medae el méodo Cra-Ncolso de derecas as la evolcó emporal del vel reáco sobre a geomería de acíero lbre alerada
74 Elena J. Martínez 1º cuat. 2015
 7 Elea J. Maríez º ca. 5 Score geerale: El e de lcoo e baa e lo rago de lo valore abolo de la obervacoe. Geeralzaremo el e, lzado o lo rago o coe de lo rago de lo valore abolo, deomada core. Decó: Sea
7 Elea J. Maríez º ca. 5 Score geerale: El e de lcoo e baa e lo rago de lo valore abolo de la obervacoe. Geeralzaremo el e, lzado o lo rago o coe de lo rago de lo valore abolo, deomada core. Decó: Sea
MODELO CIR. Nota Técnica RESUMEN EJECUTIVO
 Noa Técca Eero 28, 2014 MODELO CIR RESUMEN EJECUTIVO Al modelar asas de erés se debe omar e cuea que esas so posvas, que hsórcamee ha mosrado u comporameo esable, eedo cambos sgfcavos úcamee como reflejo
Noa Técca Eero 28, 2014 MODELO CIR RESUMEN EJECUTIVO Al modelar asas de erés se debe omar e cuea que esas so posvas, que hsórcamee ha mosrado u comporameo esable, eedo cambos sgfcavos úcamee como reflejo
1.1.- Concepto Definición de cono Definición de función homogénea Interpretación económica de la función homogénea
 Fucoes homogéeas FUNCIONES HOMOGÉNEAS (ESQUEMA).- Cocepo y propedades...- Cocepo Defcó de coo Defcó de fucó homogéea Ierpreacó ecoómca de la fucó homogéea..- Propedades (Operacoes co fucoes homogéeas)
Fucoes homogéeas FUNCIONES HOMOGÉNEAS (ESQUEMA).- Cocepo y propedades...- Cocepo Defcó de coo Defcó de fucó homogéea Ierpreacó ecoómca de la fucó homogéea..- Propedades (Operacoes co fucoes homogéeas)
Vida media residual de mixturas finitas y aplicaciones a sistemas coherentes
 Vda meda resdual de mxuras fas y aplcacoes a ssemas coherees Vda meda resdual de mxuras fas y aplcacoes a ssemas coherees Navarro Camacho, Jorge jorgeav@umes Deparameo de Esadísca e Ivesgacó Operava Uversdad
Vda meda resdual de mxuras fas y aplcacoes a ssemas coherees Vda meda resdual de mxuras fas y aplcacoes a ssemas coherees Navarro Camacho, Jorge jorgeav@umes Deparameo de Esadísca e Ivesgacó Operava Uversdad
4.4. La ciudad circular El Modelo de Salop
 4.4. La cudad crcular El Malde Machado Ecoomía Idusral - Malde Machado La Cudad Crcular El modelo de Salop 4.4. La cudad crcular El E el modelo de Hoellg habamos supueso que solo hay dos empresas. Ahora
4.4. La cudad crcular El Malde Machado Ecoomía Idusral - Malde Machado La Cudad Crcular El modelo de Salop 4.4. La cudad crcular El E el modelo de Hoellg habamos supueso que solo hay dos empresas. Ahora
La Docencia y la importancia de la investigación en Ingeniería
 a Doceca y la mporaca de la esgacó e Igeería J.M. CARBAO JIMÉNEZ. Profesor Iesgador de ESCOM IPN. carballomeez@gmal.com J. GARCÍA MARTINEZ. Iesgador de la ESM-IPN. bucefalo@yahoo.com.m J.A.JÁREZ RAMÍREZ.
a Doceca y la mporaca de la esgacó e Igeería J.M. CARBAO JIMÉNEZ. Profesor Iesgador de ESCOM IPN. carballomeez@gmal.com J. GARCÍA MARTINEZ. Iesgador de la ESM-IPN. bucefalo@yahoo.com.m J.A.JÁREZ RAMÍREZ.
MATLAB: MATRIX LABORATORY
 Uversdad de Ce Facad de Cecas Físcas Maemácas Deparameo de Igeería Qímca Boecoogía IQ46B Operacoes de raserecas I MALAB: MARIX LABORAORY Igor Gzmá Ovares . ESRUCURA DE LA PRESENACIÓN.- Méodo Nmérco para
Uversdad de Ce Facad de Cecas Físcas Maemácas Deparameo de Igeería Qímca Boecoogía IQ46B Operacoes de raserecas I MALAB: MARIX LABORAORY Igor Gzmá Ovares . ESRUCURA DE LA PRESENACIÓN.- Méodo Nmérco para
x independiente y dependiente 0301a) Concepto de Cambio Fenómenos F( t + t Generalidades Cambio Ejemplo: crecimiento exponencial Cambio de F Positivo
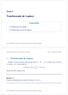
 = ( + ( Cabo de ( + ( ( + > ( > 0 Posvo + ( + = ( = 0 ( ( + Nulo + Tpos ( + ( Cabo + Geeraldades Nauraleza El cabo puede ser Carácer Varable Cabo Cosae Aueo o creeo Dsucó o decreeo = Varacó cero ( = (
= ( + ( Cabo de ( + ( ( + > ( > 0 Posvo + ( + = ( = 0 ( ( + Nulo + Tpos ( + ( Cabo + Geeraldades Nauraleza El cabo puede ser Carácer Varable Cabo Cosae Aueo o creeo Dsucó o decreeo = Varacó cero ( = (
MÉTODOS MATEMÁTICOS EN TEORÍA FINANCIERA
 MÉTODOS MATEMÁTICOS EN TEORÍA FINANCIERA José Rgobero Parada Daza Uversdad de Cocepcó, Chle Regsro Propedad Ielecual Nº.798 I.S.B.N. 956-89-9- Auor: José Rgobero Parada Daza ÍNDICE CAPÍTULO I OPTIMIZACIÓN
MÉTODOS MATEMÁTICOS EN TEORÍA FINANCIERA José Rgobero Parada Daza Uversdad de Cocepcó, Chle Regsro Propedad Ielecual Nº.798 I.S.B.N. 956-89-9- Auor: José Rgobero Parada Daza ÍNDICE CAPÍTULO I OPTIMIZACIÓN
UNIDAD 7.- Matrices (tema 1 del libro) = MATRICES
 UNIDD.- Marces (ema del lbro). MTRICES Ua mar se puede eeder como ua abla de úmeros ordeados e flas columas Defcó.- Se llama mar de dmesó m a u cojuo de úmeros reales dspuesos e m flas columas de la sguee
UNIDD.- Marces (ema del lbro). MTRICES Ua mar se puede eeder como ua abla de úmeros ordeados e flas columas Defcó.- Se llama mar de dmesó m a u cojuo de úmeros reales dspuesos e m flas columas de la sguee
Figura 1. Figura 2. Para realizar este análisis asumiremos las siguientes condiciones:
 Coverdor PUH PU El coverdor Push Pull es u coverdor que hace uso de u rasformador para eer aslameo ere la esó de erada y la esó de salda. Posee además ua ducaca magezae propa del rasformador que como al
Coverdor PUH PU El coverdor Push Pull es u coverdor que hace uso de u rasformador para eer aslameo ere la esó de erada y la esó de salda. Posee además ua ducaca magezae propa del rasformador que como al
INGENIERÍA DE CONFIABILIDAD.. PORQUE UNA DE LAS FORMAS MÁS IMPORTANTES DE AGREGAR VALOR, ES EVITAR QUE SE DESTRUYA
 Lecura 6 PRONÓSTICOS EN ACTIVOS REPARABLES INGENIERÍA DE CONFIABILIDAD.. PORQUE UNA DE LAS FORMAS MÁS IMPORTANTES DE AGREGAR VALOR, ES EVITAR QUE SE DESTRUYA Medardo Yañez Yañez Meda, Medardo - Gómez de
Lecura 6 PRONÓSTICOS EN ACTIVOS REPARABLES INGENIERÍA DE CONFIABILIDAD.. PORQUE UNA DE LAS FORMAS MÁS IMPORTANTES DE AGREGAR VALOR, ES EVITAR QUE SE DESTRUYA Medardo Yañez Yañez Meda, Medardo - Gómez de
TRANSMISIÓN DE CALOR MULTIDIRECCIONAL Y TRANSITORIA
 Daposva ema6: rasmsó de calor muldreccoal rasora RANSMISIÓN DE CALOR MULIDIRECCIONAL Y RANSIORIA J.M.Corberá, R. Roo (UPV Daposva ema6: rasmsó de calor muldreccoal rasora ÍNDICE. RANSMISIÓN DE CALOR MULIDIRECCIONAL.
Daposva ema6: rasmsó de calor muldreccoal rasora RANSMISIÓN DE CALOR MULIDIRECCIONAL Y RANSIORIA J.M.Corberá, R. Roo (UPV Daposva ema6: rasmsó de calor muldreccoal rasora ÍNDICE. RANSMISIÓN DE CALOR MULIDIRECCIONAL.
Duración y Convexidad I
 Marí Herádez errao Modelo Aleravo Duracó y Covexdad I E ese maeral se presea de forma accesble, mas co u grado resposable de rgor maemáco, los cocepos de duracó y covexdad. e asume que el lecor cuea co
Marí Herádez errao Modelo Aleravo Duracó y Covexdad I E ese maeral se presea de forma accesble, mas co u grado resposable de rgor maemáco, los cocepos de duracó y covexdad. e asume que el lecor cuea co
Taller de Preparación para el examen Models Life Contingencies (MLC) de la SOA.
 Taller de Preparacó para el eame Models Lfe Cogeces MLC de la SO. Trdad Gozález Bolla El presee es u forme del rabajo desarrollado durae el aller de preparacó para el eame MLC de SO ue uo lugar e la Faculad
Taller de Preparacó para el eame Models Lfe Cogeces MLC de la SO. Trdad Gozález Bolla El presee es u forme del rabajo desarrollado durae el aller de preparacó para el eame MLC de SO ue uo lugar e la Faculad
( ) = 1 ; f k. u v. uk v. vk u. Diferenciacion e Interpolacion 1/8. Diferenciacion e Interpolacion numerica. Diferencias finitas
 Derecaco e Iterpolaco /8 Derecaco e Iterpolaco merca. Derecas tas Dadas las abscsas X ormemete espacadas X X h, a las qe correspode alores de co (): (X) se dee las prmeras derecas tas ( Haca delate ) como:
Derecaco e Iterpolaco /8 Derecaco e Iterpolaco merca. Derecas tas Dadas las abscsas X ormemete espacadas X X h, a las qe correspode alores de co (): (X) se dee las prmeras derecas tas ( Haca delate ) como:
Modelos de Regresión análisis de regresión diagrama de dispersión coeficientes de regresión
 Modelos de Regresó E muchos problemas este ua relacó herete etre dos o más varables, resulta ecesaro eplorar la aturaleza de esta relacó. El aálss de regresó es ua técca estadístca para el modelado la
Modelos de Regresó E muchos problemas este ua relacó herete etre dos o más varables, resulta ecesaro eplorar la aturaleza de esta relacó. El aálss de regresó es ua técca estadístca para el modelado la
Tema 1: Transformada de Laplace. Contenidos Transformada de Laplace
 Tema Traformada de aplace Traformada de aplace Traformada vera de aplace Coedo Grupo EDUMATICUS. Deparameo de Maemáca Aplcada. Uverdad de Málaga Amplacó de Cálculo 2/. Ecuela Polécca Superor Tema : Traformada
Tema Traformada de aplace Traformada de aplace Traformada vera de aplace Coedo Grupo EDUMATICUS. Deparameo de Maemáca Aplcada. Uverdad de Málaga Amplacó de Cálculo 2/. Ecuela Polécca Superor Tema : Traformada
TEMAS DE MATEMÁTICAS (Oposiciones de Secundaria)
 TEMAS DE MATEMÁTICAS (Oposcoes de Secudara TEMA 8 MATRICES. ALGEBRA DE MATRICES. APLICACIONES AL CAMPO DE LAS CIENCIAS SOCIALES Y DE LA NATURALEZA.. Iroduccó.. Cocepo báscos... Tpos de marces. 3. M mx
TEMAS DE MATEMÁTICAS (Oposcoes de Secudara TEMA 8 MATRICES. ALGEBRA DE MATRICES. APLICACIONES AL CAMPO DE LAS CIENCIAS SOCIALES Y DE LA NATURALEZA.. Iroduccó.. Cocepo báscos... Tpos de marces. 3. M mx
Reglas para el manejo de los índices de deuda de la BNV. Bolsa Nacional de Valores Version 4.4 13/07/2005
 Reglas para el maejo de los ídces de deuda de la BV Bolsa acoal de Valores Verso 4.4 3/07/005 ága de 6 COTEIDO ITRODUCCIÓ... 4. erspecva geeral... 4 MAEJO DE LOS ÍDICES... 6. Comé de Ídces de íulos de
Reglas para el maejo de los ídces de deuda de la BV Bolsa acoal de Valores Verso 4.4 3/07/005 ága de 6 COTEIDO ITRODUCCIÓ... 4. erspecva geeral... 4 MAEJO DE LOS ÍDICES... 6. Comé de Ídces de íulos de
VALOR EN RIESGO PARA UN PORTAFOLIO CON OPCIONES FINANCIERAS *
 Revsa Igeerías Uversdad de Medellí VALOR EN RIESGO PARA UN PORTAFOLIO CON OPCIONES FINANCIERAS * Carlos Alexáder Grajales Correa ** Fredy Ocars Pérez Ramírez *** Recbdo: 6//009 Acepado: 08/0/00 RESUMEN
Revsa Igeerías Uversdad de Medellí VALOR EN RIESGO PARA UN PORTAFOLIO CON OPCIONES FINANCIERAS * Carlos Alexáder Grajales Correa ** Fredy Ocars Pérez Ramírez *** Recbdo: 6//009 Acepado: 08/0/00 RESUMEN
MATEMÁTICA DE LAS OPERACIONES FINANCIERAS I
 FAUTAD DE. EONÓMAS Y EMPRESARAES MATEMÁTA DE AS OPERAONES FNANERAS URSO / DÍA de febrero de ONOATORA FEBRERO Prcal HORA 6 MATERA AUXAR alcladora facera DURAÓN horas. a eyes faceras Descrbr razoadamee las
FAUTAD DE. EONÓMAS Y EMPRESARAES MATEMÁTA DE AS OPERAONES FNANERAS URSO / DÍA de febrero de ONOATORA FEBRERO Prcal HORA 6 MATERA AUXAR alcladora facera DURAÓN horas. a eyes faceras Descrbr razoadamee las
TEMA 5: CAPITALIZACIÓN COMPUESTA ÍNDICE
 Maemácas Faceras Prof. Mª Mercedes Rojas de Graca TEMA 5: APITALIZAIÓN OMPUESTA ÍNDIE. APITALIZAIÓN OMPUESTA..... ONEPTO..... DESRIPIÓN DE LA OPERAIÓN....3. ARATERÍSTIAS DE LA OPERAIÓN....4. DESARROLLO
Maemácas Faceras Prof. Mª Mercedes Rojas de Graca TEMA 5: APITALIZAIÓN OMPUESTA ÍNDIE. APITALIZAIÓN OMPUESTA..... ONEPTO..... DESRIPIÓN DE LA OPERAIÓN....3. ARATERÍSTIAS DE LA OPERAIÓN....4. DESARROLLO
Una Estrategia de Acumulación de Reservas Mediante Opciones de Venta de Dólares. El Caso de Banco de México
 Ua Esraega de Acumulacó de Reservas Medae Opcoes de Vea de Dólares. El Caso de Baco de Méxco INDICE I. REUMEN... II. INTRODUCCIÓN...3 III. IV. OPCIONE DE VENTA DE DÓLARE...4 III.. PRINCIPALE CARACTERÍTICA...4
Ua Esraega de Acumulacó de Reservas Medae Opcoes de Vea de Dólares. El Caso de Baco de Méxco INDICE I. REUMEN... II. INTRODUCCIÓN...3 III. IV. OPCIONE DE VENTA DE DÓLARE...4 III.. PRINCIPALE CARACTERÍTICA...4
INSTITUTO POLITÉCNICO NACIONAL
 INTITUTO POLITÉCNICO NACIONAL ECUELA UPERIOR DE FÍICA Y MATEMÁTICA APLICACIONE EN FINANZA DE MODELO AUTORREGREIVO TEI QUE, PARA OBTENER EL TITULO DE INGENIERO MATEMÁTICO, PREENTA. CLAUDIA VIRIDIANA VÁZQUEZ
INTITUTO POLITÉCNICO NACIONAL ECUELA UPERIOR DE FÍICA Y MATEMÁTICA APLICACIONE EN FINANZA DE MODELO AUTORREGREIVO TEI QUE, PARA OBTENER EL TITULO DE INGENIERO MATEMÁTICO, PREENTA. CLAUDIA VIRIDIANA VÁZQUEZ
Redes Neuronales con Base Radial (Poggio y Girosi,1990)
 Redes euroales co Base Radal Poggo y ros,990 Iroduccó a las Redes euroales Arfcales Esquema de rabajo: Esrucura de ua RBF Problema de clasfcacó ora vez Ejemplo XOR Teorema de Cover úmero de euroas Problema
Redes euroales co Base Radal Poggo y ros,990 Iroduccó a las Redes euroales Arfcales Esquema de rabajo: Esrucura de ua RBF Problema de clasfcacó ora vez Ejemplo XOR Teorema de Cover úmero de euroas Problema
Tema 2: El modelo básico de regresión lineal múltiple (I)
 Tema : l modelo básco de regresó leal múltple I Casaldad la ocó de cetrs parbs e el aálss ecoométrco Repaso del cocepto de regresó smple: Recta de regresó poblacoal p verss recta de regresó estmada Motvacó
Tema : l modelo básco de regresó leal múltple I Casaldad la ocó de cetrs parbs e el aálss ecoométrco Repaso del cocepto de regresó smple: Recta de regresó poblacoal p verss recta de regresó estmada Motvacó
Para el caso τ = 20 [min], la función se puede representar de las siguientes formas: a) Función Matemática: b) Tabla de Valores
![Para el caso τ = 20 [min], la función se puede representar de las siguientes formas: a) Función Matemática: b) Tabla de Valores Para el caso τ = 20 [min], la función se puede representar de las siguientes formas: a) Función Matemática: b) Tabla de Valores](/thumbs/63/49997694.jpg) 1 RAPIDEZ DE CAMBIO Semaa 05 1 Varables depedees y o depedees Defr los cocepos: varable, cosae, cremeo, varacó. Defr los cocepos: varable depedee, varable depedee. Recoocer varables depedees e depedees.
1 RAPIDEZ DE CAMBIO Semaa 05 1 Varables depedees y o depedees Defr los cocepos: varable, cosae, cremeo, varacó. Defr los cocepos: varable depedee, varable depedee. Recoocer varables depedees e depedees.
Cálculo Estocástico Variación Cuadrática para Martingalas Continuas y Acotadas
 1 Cálculo Esocásco Varacón Cuadráca para Marngalas Connuas y Acoadas Gullermo Garro Defncón Varacón fna. Un proceso X es de varacón fna o acoada s sus rayecoras son de varacón fna, c.s. Es decr, s exse
1 Cálculo Esocásco Varacón Cuadráca para Marngalas Connuas y Acoadas Gullermo Garro Defncón Varacón fna. Un proceso X es de varacón fna o acoada s sus rayecoras son de varacón fna, c.s. Es decr, s exse
ECUACIÓN DE DIFUSIÓN PARA FLUJO DE FLUIDOS EN MEDIOS POROSOS.
 09- ECUACIÓN DE DIFUSIÓN PARA FLUJO DE FLUIDOS EN MEDIOS POROSOS. Iroduccó. Para obeer la ecuacó geeral que descrbe el comorameo del flujo de fludos a ravés de medos orosos, se hace uso de dferees rcos
09- ECUACIÓN DE DIFUSIÓN PARA FLUJO DE FLUIDOS EN MEDIOS POROSOS. Iroduccó. Para obeer la ecuacó geeral que descrbe el comorameo del flujo de fludos a ravés de medos orosos, se hace uso de dferees rcos
Tarificación de bonos sobre catástrofes (cat bonds) con desencadenantes de índices de pérdidas. Modelación mediante un proceso de Ornstein-Uhlenbeck
 REVISTA DE MÉTODOS CUANTITATIVOS PARA LA ECONOMÍA Y LA EMPRESA (24). Págas 340 361. Dcembre de 2017. ISSN: 1886-516X. D.L: SE-2927-06. www.upo.es/revsas/dex.php/revmecua/arcle/vew/2891 Tarfcacó de boos
REVISTA DE MÉTODOS CUANTITATIVOS PARA LA ECONOMÍA Y LA EMPRESA (24). Págas 340 361. Dcembre de 2017. ISSN: 1886-516X. D.L: SE-2927-06. www.upo.es/revsas/dex.php/revmecua/arcle/vew/2891 Tarfcacó de boos
Flujo en acuífero libre
 SESIÓN PRÁCTICA EDP PARABÓLICA CON MÉTODO FTCS Flujo e acuíero lbre E esa sesó se aalza medae el méodo eplíco de derecas as la evolucó emporal del vel reáco sobre ua geomería de acuíero lbre alerada por
SESIÓN PRÁCTICA EDP PARABÓLICA CON MÉTODO FTCS Flujo e acuíero lbre E esa sesó se aalza medae el méodo eplíco de derecas as la evolucó emporal del vel reáco sobre ua geomería de acuíero lbre alerada por
REDES DE BASE RADIAL. 1. Funciones de Base Radial.
 Tema 5: Redes de Base Radal Sstemas Coexostas 1 REDES DE BASE RADIAL 1. Fcoes de Base Radal. 2. Dervacó del Modelo Neroal. 2.1. Arqtectra de a RBFN 2.2. Fcoaldad. 2.3. Carácter Local de a RBFN. 3. Etreameto.
Tema 5: Redes de Base Radal Sstemas Coexostas 1 REDES DE BASE RADIAL 1. Fcoes de Base Radal. 2. Dervacó del Modelo Neroal. 2.1. Arqtectra de a RBFN 2.2. Fcoaldad. 2.3. Carácter Local de a RBFN. 3. Etreameto.
F = = 0. 64, que es la eficiencia del test de signo relativa al
 Méodos No Paramércos I 5 Elea J. Maríez do cua. 004 Efceca: La efceca del es de Fredma relava al es F es ( f ( x dx e(, F σ + e observa que o hereda la efceca de los ess de Wlcoxo y Ma-Whey relavas al
Méodos No Paramércos I 5 Elea J. Maríez do cua. 004 Efceca: La efceca del es de Fredma relava al es F es ( f ( x dx e(, F σ + e observa que o hereda la efceca de los ess de Wlcoxo y Ma-Whey relavas al
TEMA 5: ANÁLISIS CONJUNTO DE VARIABLES ALEATORIAS Y DISTRIBUCIÓN DE AGREGADOS
 MÉTODOS ESTADÍSTICOS PARA LA EMPRESA TEMA 5: ANÁLISIS CONJUNTO DE VARIABLES ALEATORIAS DISTRIBUCIÓN DE AGREGADOS 5..- Dstrbucoes -dmesoales. Aálss margal y codcoado 5..- Varables aleatoras depedetes. Propedades
MÉTODOS ESTADÍSTICOS PARA LA EMPRESA TEMA 5: ANÁLISIS CONJUNTO DE VARIABLES ALEATORIAS DISTRIBUCIÓN DE AGREGADOS 5..- Dstrbucoes -dmesoales. Aálss margal y codcoado 5..- Varables aleatoras depedetes. Propedades
REVISTA INVESTIGACION OPERACIONAL Vol. 22, No. 2, 2001
 REVISA INVESIGACION OPERACIONAL Vol., No., SOLUCIONES A DIFERENES PROBLEMAS DENRO DEL CAMPO DE LA COMUNICACION ESADISICA J. Navarro Moreo, J.C. Ruz Mola y R.M. Ferádez Alcalá, Deparameo de Esadísca e Ivesgacó
REVISA INVESIGACION OPERACIONAL Vol., No., SOLUCIONES A DIFERENES PROBLEMAS DENRO DEL CAMPO DE LA COMUNICACION ESADISICA J. Navarro Moreo, J.C. Ruz Mola y R.M. Ferádez Alcalá, Deparameo de Esadísca e Ivesgacó
Supongamos que hemos aplicado el test F y hemos rechazado la H0.
 Comparacó de medas tomadas de a pares CONDICION Meda s --------- ---------- ------ ---------- 0.00 3.0000 0.00 3.73 3 97.00 3.0000 4 93.00.44 TOTAL 98.73.6036 Supogamos que hemos aplcado el test F y hemos
Comparacó de medas tomadas de a pares CONDICION Meda s --------- ---------- ------ ---------- 0.00 3.0000 0.00 3.73 3 97.00 3.0000 4 93.00.44 TOTAL 98.73.6036 Supogamos que hemos aplcado el test F y hemos
NOMBRE Apellido Paterno Apellido Materno Nombre(s)
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE CIENCIAS BÁSICAS COORDINACIÓN DE CIENCIAS APLICADAS DEPARTAMENTO DE PROBABILIDAD ESTADÍSTICA SEGUNDO EXAMEN FINAL RESOLUCIÓN SEMESTRE
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE CIENCIAS BÁSICAS COORDINACIÓN DE CIENCIAS APLICADAS DEPARTAMENTO DE PROBABILIDAD ESTADÍSTICA SEGUNDO EXAMEN FINAL RESOLUCIÓN SEMESTRE
7. Contrastes de Hipótesis
 7. Corases de póess Curso - Esadísca Corase de póess Se ha realzado ua ecuesa a 4 persoas elegdas al azar Llamado p a la proporcó de voaes del pardo políco A. Podemos afrmar que p >.5. p? Resulado Ecuesa
7. Corases de póess Curso - Esadísca Corase de póess Se ha realzado ua ecuesa a 4 persoas elegdas al azar Llamado p a la proporcó de voaes del pardo políco A. Podemos afrmar que p >.5. p? Resulado Ecuesa
Capítulo 3. Consideraciones sobre métodos numéricos
 3.. Iroduccó 5 Capíulo 3. Cosderacoes sobre méodos umércos 3.. Iroduccó E ese capíulo se presea la eoría y alguos cocepos sobre los que se susea los esquemas umércos de ala resolucó. Su aplcacó a las ecuacoes
3.. Iroduccó 5 Capíulo 3. Cosderacoes sobre méodos umércos 3.. Iroduccó E ese capíulo se presea la eoría y alguos cocepos sobre los que se susea los esquemas umércos de ala resolucó. Su aplcacó a las ecuacoes
Introducción a la Estadística Descriptiva
 Iroduccó a la Esadísca Descrpva ª Edcó Carla Re Graña María Raml Díaz ITRODUCCIÓ A LA ESTADÍSTICA DESCRIPTIVA. ª Edcó o esá permda la reproduccó oal o parcal de ese lbro, su raameo formáco, la rasmsódeguaformaoporcualquermedo,aseaelecróco,mecáco,porfoocopa,por
Iroduccó a la Esadísca Descrpva ª Edcó Carla Re Graña María Raml Díaz ITRODUCCIÓ A LA ESTADÍSTICA DESCRIPTIVA. ª Edcó o esá permda la reproduccó oal o parcal de ese lbro, su raameo formáco, la rasmsódeguaformaoporcualquermedo,aseaelecróco,mecáco,porfoocopa,por
Años I0 t (base 1992 = 100)
 Esadísca y Meodología de la vesgacó Dada cualquer varable de la que coocemos los valores referdos a dsos perodos emporales, eedemos por úmero ídce de esa varable e dchos perodos el resulado de dvdr los
Esadísca y Meodología de la vesgacó Dada cualquer varable de la que coocemos los valores referdos a dsos perodos emporales, eedemos por úmero ídce de esa varable e dchos perodos el resulado de dvdr los
Estimación de parámetros Tema 2. Propiedades de los buenos estimadores. 2. Estimación por intervalos
 Uverdad Auóoma de Madrd Emacó de parámero Tema. Emacó puual Propedade de lo bueo emadore. Emacó por ervalo.. Coruccó del ervalo de cofaza. íme cofdecale. Nvel de cofaza y vel de rego... Iervalo de cofaza
Uverdad Auóoma de Madrd Emacó de parámero Tema. Emacó puual Propedade de lo bueo emadore. Emacó por ervalo.. Coruccó del ervalo de cofaza. íme cofdecale. Nvel de cofaza y vel de rego... Iervalo de cofaza
1. Los postulados de la Mecánica Cuántica. 2. Estados Estacionarios. 3. Relación de Incertidumbre de Heisenberg. 4. Teorema de compatibilidad.
 Parte : MECÁNICA CUÁNTICA 1. Los postulados de la Mecáca Cuátca.. Estados Estacoaros. 3. Relacó de Icertdumbre de Heseberg. 4. Teorema de compatbldad. 1 U breve repaso de Mecáca Clásca 1. Partícula clásca:
Parte : MECÁNICA CUÁNTICA 1. Los postulados de la Mecáca Cuátca.. Estados Estacoaros. 3. Relacó de Icertdumbre de Heseberg. 4. Teorema de compatbldad. 1 U breve repaso de Mecáca Clásca 1. Partícula clásca:
Hallar la media y varianza. Obtener la F.G.M y obtenerlas de nuevo.
 FGM-MARKOV 7.-Una varable aleaora ene de funcón de cuanía x Px ( ),3,3, 3, Hallar la meda y varanza. Obener la F.G.M y obenerlas de nuevo. En base a la funcón de cuanía µ α Ex P ( ),3 +,3 +, + 3,,3 σ α
FGM-MARKOV 7.-Una varable aleaora ene de funcón de cuanía x Px ( ),3,3, 3, Hallar la meda y varanza. Obener la F.G.M y obenerlas de nuevo. En base a la funcón de cuanía µ α Ex P ( ),3 +,3 +, + 3,,3 σ α
La inferencia estadística es primordialmente de naturaleza
 VI. Ifereca estadístca Ifereca Estadístca La fereca estadístca es prmordalmete de aturaleza ductva y llega a geeralzar respecto de las característcas de ua poblacó valédose de observacoes empírcas de la
VI. Ifereca estadístca Ifereca Estadístca La fereca estadístca es prmordalmete de aturaleza ductva y llega a geeralzar respecto de las característcas de ua poblacó valédose de observacoes empírcas de la
TEMA 3. Medidas de variabilidad y asimetría. - X mín. X máx
 TEMA 3 Meddas de varabldad y asmetría 1. MEDIDAS DE VARIABILIDAD La varabldad o dspersó hace refereca al grado de varacó que hay e u cojuto de putuacoes. Por ejemplo: etre dos dstrbucoes que preseta la
TEMA 3 Meddas de varabldad y asmetría 1. MEDIDAS DE VARIABILIDAD La varabldad o dspersó hace refereca al grado de varacó que hay e u cojuto de putuacoes. Por ejemplo: etre dos dstrbucoes que preseta la
PROGRAMACIÓN MATEMÁTICA Y TEORIA DE LA CARTERA: UNA APLICACIÓN CON MAPLE. Eva Mª del Pozo García Mª Jesús Segovia Vargas Zuleyka Díaz Martínez
 PROGRAMACIÓN MATEMÁTICA Y TEORIA DE LA CARTERA: UNA APLICACIÓN CON MAPLE Eva Mª del Pozo García Mª Jesús Segova Vargas Zuleyka Díaz Martíez Departameto de Ecoomía Facera y Cotabldad I Uversdad Complutese
PROGRAMACIÓN MATEMÁTICA Y TEORIA DE LA CARTERA: UNA APLICACIÓN CON MAPLE Eva Mª del Pozo García Mª Jesús Segova Vargas Zuleyka Díaz Martíez Departameto de Ecoomía Facera y Cotabldad I Uversdad Complutese
Inferencia Estadística
 Ifereca Estadístca Poblacó y muestra Coceptos y defcoes Muestra Aleatora Smple (MAS) Cosderemos ua poblacó, cuya fucó de dstrbucó esta dada por F(), la cual está costtuda por u úmero fto de posbles valores,
Ifereca Estadístca Poblacó y muestra Coceptos y defcoes Muestra Aleatora Smple (MAS) Cosderemos ua poblacó, cuya fucó de dstrbucó esta dada por F(), la cual está costtuda por u úmero fto de posbles valores,
Orden de la tirada. Figura 1: Frecuencia relativa de cara para una sucesión de 400 tiradas.
 Estadístca (Q) Dra. Daa M. Kelmasky 99. Teoremas límte Frecueca Relatva 0.5 0.6 0.7 0.8 0.9.0 0 00 00 300 400 Orde de la trada Fgura : Frecueca relatva de cara para ua sucesó de 400 tradas. La fgura muestra
Estadístca (Q) Dra. Daa M. Kelmasky 99. Teoremas límte Frecueca Relatva 0.5 0.6 0.7 0.8 0.9.0 0 00 00 300 400 Orde de la trada Fgura : Frecueca relatva de cara para ua sucesó de 400 tradas. La fgura muestra
Ejercicios T9c- VARIABLE ALEATORIA, MODELOS DE PROBABILIDAD UNIVARIANTES C
 Ejerccos T9c- VARIABLE ALEATORIA, MODELOS DE PROBABILIDAD UNIVARIANTES C FGM-MARKOV 7.-Una varable aleaora ene de funcón de cuanía x Px ( ),3,3, 3, Hallar la meda y varanza. Obener la F.G.M y obenerlas
Ejerccos T9c- VARIABLE ALEATORIA, MODELOS DE PROBABILIDAD UNIVARIANTES C FGM-MARKOV 7.-Una varable aleaora ene de funcón de cuanía x Px ( ),3,3, 3, Hallar la meda y varanza. Obener la F.G.M y obenerlas
Respuesta. Si 100 manzanas es una muestra suficientemente grande podemos ocupar el TCL. Por lo tanto:
 Curso: Estadístca Iferecal (ICO 8306) Profesores: Esteba Calvo, Pablo Huechapa y Omar Ramos Ayudates: José T. Meda, Fabo Salas y Daela Vlches PROBLEMA Cosdere que Ud. es dueño de u campo que produce mazaas,
Curso: Estadístca Iferecal (ICO 8306) Profesores: Esteba Calvo, Pablo Huechapa y Omar Ramos Ayudates: José T. Meda, Fabo Salas y Daela Vlches PROBLEMA Cosdere que Ud. es dueño de u campo que produce mazaas,
LA MEDIANA ROBUSTA SOBRE UN ÁRBOL CUANDO LA DEMANDA ES INCIERTA
 LA MEDIANA ROBUSTA SOBRE UN ÁRBOL CUANDO LA DEMANDA ES INCIERTA M.J. Caós M. Maríez 2 M. Mocholí V. Navarro 3 U. de Valeca Florda Uversara U. de Valeca U. de Valeca mara..caos@uv.es marsam@florda-u.es
LA MEDIANA ROBUSTA SOBRE UN ÁRBOL CUANDO LA DEMANDA ES INCIERTA M.J. Caós M. Maríez 2 M. Mocholí V. Navarro 3 U. de Valeca Florda Uversara U. de Valeca U. de Valeca mara..caos@uv.es marsam@florda-u.es
Cuatro medidas de inflación subyacente para Uruguay
 Cuaro meddas de flacó subyacee para Uruguay Rosaa Ferádez 002-2005 688-7565 CUATRO MEDIDAS DE INFLACIÓN SUBYACENTE PARA URUGUAY Rosaa Ferádez Casro Área de Ivesgacoes Ecoómcas Baco Ceral del Uruguay Julo
Cuaro meddas de flacó subyacee para Uruguay Rosaa Ferádez 002-2005 688-7565 CUATRO MEDIDAS DE INFLACIÓN SUBYACENTE PARA URUGUAY Rosaa Ferádez Casro Área de Ivesgacoes Ecoómcas Baco Ceral del Uruguay Julo
1.3. Longitud de arco.
 .. Logtud de arco. Defcó. Sea C ua curva suave defda paramétrcamete por la fucó vectoral f : R R / f () t = ( f() t, f() t,, f ( t) ) e el espaco R, co t [ a, b], que se recorre exactamete ua vez cuado
.. Logtud de arco. Defcó. Sea C ua curva suave defda paramétrcamete por la fucó vectoral f : R R / f () t = ( f() t, f() t,, f ( t) ) e el espaco R, co t [ a, b], que se recorre exactamete ua vez cuado
Introducción a la simulación de fluidos Animación Avanzada
 Itrodccó a la smlacó de fldos Amacó Avazada Ivá Aldá Íñgez 5 de Marzo de 04 Ídce Motvacó Mecáca comptacoal de fldos Método de dferecas ftas Ecacó de coveccó Ecacó de dfsó Motvacó FX Motvacó FX Motvacó
Itrodccó a la smlacó de fldos Amacó Avazada Ivá Aldá Íñgez 5 de Marzo de 04 Ídce Motvacó Mecáca comptacoal de fldos Método de dferecas ftas Ecacó de coveccó Ecacó de dfsó Motvacó FX Motvacó FX Motvacó
TEMA 5.- LA DECISIÓN DE INVERTIR EN UN CONTEXTO DE RIESGO Introducción.
 TEMA 5.- LA DECISIÓN DE INVERTIR EN UN CONTEXTO DE RIESGO 5..- Itroduccó. Stuacoes segú el vel de formacó: Certeza. Icertdumbre parcal o resgo: (Iversoes co resgo) Icertdumbre total: (Iversoes co certdumbre)
TEMA 5.- LA DECISIÓN DE INVERTIR EN UN CONTEXTO DE RIESGO 5..- Itroduccó. Stuacoes segú el vel de formacó: Certeza. Icertdumbre parcal o resgo: (Iversoes co resgo) Icertdumbre total: (Iversoes co certdumbre)
02 ) 2 0 en el resto. Tiempo (meses) Ventilador adicional No No Si No Si Si Si Si No Si Tipo carcasa A C B A B A B C B C
 Ua empresa motadora de equpos electrócos está realzado u estudo sobre aluos de los compoetes que utlza. E partcular mde el tempo de vda e meses reales de los procesadores que mota, dode a aluos de ellos
Ua empresa motadora de equpos electrócos está realzado u estudo sobre aluos de los compoetes que utlza. E partcular mde el tempo de vda e meses reales de los procesadores que mota, dode a aluos de ellos
Ingeniería de Confiabilidad - Equipos
 SECCION 4. Igeería de Cofabldad-Equpos Igeería de Cofabldad - Equpos Seccó 4 Medardo Yañez Herado Gómez de la Vega Kara Semeco Soo Nayrh Meda Esa seccó esa dedcada al esudo de los aspecos físcos y aleaoros
SECCION 4. Igeería de Cofabldad-Equpos Igeería de Cofabldad - Equpos Seccó 4 Medardo Yañez Herado Gómez de la Vega Kara Semeco Soo Nayrh Meda Esa seccó esa dedcada al esudo de los aspecos físcos y aleaoros
Fórmulas de de Derivación Numérica: Aproximación de de la la derivada de de orden k de de una función
 Uversdad Poltécca de Madrd Igeería de Mas Fórmulas de de Dervacó Numérca: Aproxmacó de de la la dervada de de orde k de de ua ucó Pro. Arturo Hdalgo LópezL Pro. Alredo López L Beto Pro. Carlos Code LázaroL
Uversdad Poltécca de Madrd Igeería de Mas Fórmulas de de Dervacó Numérca: Aproxmacó de de la la dervada de de orde k de de ua ucó Pro. Arturo Hdalgo LópezL Pro. Alredo López L Beto Pro. Carlos Code LázaroL
Intensificación en Estadística
 GRADO EN VETERINARIA DEPARTAMENTO DE ESTADÍSTICA E IO 0-0 IV Curso Cero Itesfcacó e Estadístca Itroduccó a la fucó Sumatoro Itroduccó Cocepto de fucó sumatoro Aplcacoes Itroduccó Cocepto de fucó sumatoro
GRADO EN VETERINARIA DEPARTAMENTO DE ESTADÍSTICA E IO 0-0 IV Curso Cero Itesfcacó e Estadístca Itroduccó a la fucó Sumatoro Itroduccó Cocepto de fucó sumatoro Aplcacoes Itroduccó Cocepto de fucó sumatoro
1.2. Medidas de Concentración
 .. Meddas de Cocetracó Matlde Machado.. Meddas de Cocetracó La gra mayora de los mercados se ecuetra etre los extremos de competeca perfecta (cocetracó mma) y moopolo (cocetracó máxma). Las meddas de cocetracó
.. Meddas de Cocetracó Matlde Machado.. Meddas de Cocetracó La gra mayora de los mercados se ecuetra etre los extremos de competeca perfecta (cocetracó mma) y moopolo (cocetracó máxma). Las meddas de cocetracó
parciales de segundo orden.
 MMII_L_c: Irodcció a las ecacioes e derivadas parciales de segdo orde. Gió: E esa lecció esableceremos las propiedades geerales de las ecacioes e derivadas parciales de segdo orde, qe lego va a ser esdiadas
MMII_L_c: Irodcció a las ecacioes e derivadas parciales de segdo orde. Gió: E esa lecció esableceremos las propiedades geerales de las ecacioes e derivadas parciales de segdo orde, qe lego va a ser esdiadas
FEM-OF: EDP Elíptica de 2 Orden
 9/02/2008 Capítulo 5: FM-OF: D líptca de 2 Orde Idce: 5..- Operador Dferecal líptco 5.2.- roblema Básco 5.3.- Fucoes Óptmas 5.4.- FM-OF Steklov-ocaré 5.5.- FM-OF Trefftz-Herrera 5.6.- FM-OF etrov-galerk
9/02/2008 Capítulo 5: FM-OF: D líptca de 2 Orde Idce: 5..- Operador Dferecal líptco 5.2.- roblema Básco 5.3.- Fucoes Óptmas 5.4.- FM-OF Steklov-ocaré 5.5.- FM-OF Trefftz-Herrera 5.6.- FM-OF etrov-galerk
Introducción al Algebra Lineal en Contexto Autor José Arturo Barreto M.A. Web:
 Itroduccó al Algebra Leal e Cotexto Autor José Arturo Barreto M.A. Web: www.abaco.com.e www.mprofe.com.e josearturobarreto@yahoo.com Descomposcó e Valor Sgular (SVD: Sgular Value Decomposto) El sguete
Itroduccó al Algebra Leal e Cotexto Autor José Arturo Barreto M.A. Web: www.abaco.com.e www.mprofe.com.e josearturobarreto@yahoo.com Descomposcó e Valor Sgular (SVD: Sgular Value Decomposto) El sguete
1 3 i + + A = 0, B = ½, C = 1, D = -½, dx dx de donde, :
 Hoj de Prolem Aál IV /. d L ríce de l eccó o,,,, í qe el polomo e decompoe de l form: Decompoemo e frccoe mple: D B A defcdo coefcee, e oee lo vlore: A, B ½,, D -½, Por lo qe: d d d / lclemo por eprdo
Hoj de Prolem Aál IV /. d L ríce de l eccó o,,,, í qe el polomo e decompoe de l form: Decompoemo e frccoe mple: D B A defcdo coefcee, e oee lo vlore: A, B ½,, D -½, Por lo qe: d d d / lclemo por eprdo
TEMA 3: EQUIVALENCIA FINANCIERA DE CAPITALES
 Maemácas Faceras Prof. Mª Mercees Rojas e Graca TEMA 3: EQUIVALENIA FINANIERA DE APITALE ÍNDIE. PRINIPIO DE EQUIVALENIA DE APITALE: ONEPTO. APLIAIONE DEL PRINIPIO DE EQUIVALENIA: UTITUIÓN DE APITALE....
Maemácas Faceras Prof. Mª Mercees Rojas e Graca TEMA 3: EQUIVALENIA FINANIERA DE APITALE ÍNDIE. PRINIPIO DE EQUIVALENIA DE APITALE: ONEPTO. APLIAIONE DEL PRINIPIO DE EQUIVALENIA: UTITUIÓN DE APITALE....
Qué es ESTADISTICA? OBJETIVO. Variabilidad de las respuestas. Las mismas condiciones no conducen a resultados exactamente similares PROBLEMA SOLUCIÓN
 Qué es ESADISICA? Es u couto de la rama de las Matemátcas Es algo aburrdo que mplca u motó de cuetas 3 Es u couto de téccas que se puede usar para probar cualquer cosa 4 Es u couto de coocmetos téccas
Qué es ESADISICA? Es u couto de la rama de las Matemátcas Es algo aburrdo que mplca u motó de cuetas 3 Es u couto de téccas que se puede usar para probar cualquer cosa 4 Es u couto de coocmetos téccas
Sistemas Productivos
 Ssemas Producvos º Elemeos de dseño del proceso producvo A la hora de dseñar ua udad producva, hay que realzar ua sere de decsoes esraégcas que cluye ecesaramee:. Localzacó de la plaa: lugar dode físcamee
Ssemas Producvos º Elemeos de dseño del proceso producvo A la hora de dseñar ua udad producva, hay que realzar ua sere de decsoes esraégcas que cluye ecesaramee:. Localzacó de la plaa: lugar dode físcamee
4 METODOLOGIA ADAPTADA AL PROBLEMA
 4 MEODOLOGA ADAPADA AL PROBLEMA 4.1 troduccó Báscamete el problema que se quere resolver es ecotrar la actuacó óptma sobre las tesoes de los geeradores, la relacó de tomas de los trasformadores y el valor
4 MEODOLOGA ADAPADA AL PROBLEMA 4.1 troduccó Báscamete el problema que se quere resolver es ecotrar la actuacó óptma sobre las tesoes de los geeradores, la relacó de tomas de los trasformadores y el valor
x θ es conocida pero se desconoce θ total o ˆθ ) debe ser función de los datos de la muestra
 Estmacó putual de parámetros. Parámetro( : Característca de la poblacó. E estadístca la forma fucoal de f ( ; es coocda pero se descooce total o parcalmete. La estmacó del parámetro ( debe ser fucó de
Estmacó putual de parámetros. Parámetro( : Característca de la poblacó. E estadístca la forma fucoal de f ( ; es coocda pero se descooce total o parcalmete. La estmacó del parámetro ( debe ser fucó de
SISTEMAS DE ECUACIONES NO LINEALES
 SISTEMAS DE ECUACIONES NO INEAES Capítulo 7 Sstemas de ecuacoes o leales c Elzabeth Vargas 7 INTRODUCCIÓN os métodos teratvos para resolver ua ecuacó o leal se puede eteder para ecotrar la solucó de u
SISTEMAS DE ECUACIONES NO INEAES Capítulo 7 Sstemas de ecuacoes o leales c Elzabeth Vargas 7 INTRODUCCIÓN os métodos teratvos para resolver ua ecuacó o leal se puede eteder para ecotrar la solucó de u
ÁLGEBRA II (LSI PI) TRANSFORMACIONES LINEALES UNIDAD Nº 5. Facultad de Ciencias Exactas y Tecnologías UNIVERSIDAD NACIONAL DE SANTIAGO DEL ESTERO
 2017 ÁLGEBRA II (LSI PI) UNIDAD Nº 5 RANSFORMACIONES LINEALES Facultad de Cecas Exactas y ecologías UNIERSIDAD NACIONAL DE SANIAGO DEL ESERO aa Error! No hay texto co el estlo especfcado e el documeto
2017 ÁLGEBRA II (LSI PI) UNIDAD Nº 5 RANSFORMACIONES LINEALES Facultad de Cecas Exactas y ecologías UNIERSIDAD NACIONAL DE SANIAGO DEL ESERO aa Error! No hay texto co el estlo especfcado e el documeto
TEMA 2.- LA CAPITALIZACIÓN COMPUESTA.
 TEMA.- LA APITALIZAIÓN OMPUESTA. Objevo: Foralzar la ley de capalzacó copuesa y esudar sus agudes dervadas.. EXPRESIÓN ANALÍTIA Y REPRESENTAIÓN GRÁFIA. La ley facera de capalzacó copuesa ee la sguee expresó
TEMA.- LA APITALIZAIÓN OMPUESTA. Objevo: Foralzar la ley de capalzacó copuesa y esudar sus agudes dervadas.. EXPRESIÓN ANALÍTIA Y REPRESENTAIÓN GRÁFIA. La ley facera de capalzacó copuesa ee la sguee expresó
MODELOS DE REGRESIÓN LINEALES Y NO LINEALES: SU
 MODELOS DE REGRESIÓN LINEALES Y NO LINEALES: SU APLICACIÓN EN PROBLEMAS DE INGENIERÍA Clauda Maard Facultad de Igeería. Uversdad Nacoal de Lomas de Zamora Uversdad CAECE Bueos Ares. Argeta. maard@uolsects.com.ar
MODELOS DE REGRESIÓN LINEALES Y NO LINEALES: SU APLICACIÓN EN PROBLEMAS DE INGENIERÍA Clauda Maard Facultad de Igeería. Uversdad Nacoal de Lomas de Zamora Uversdad CAECE Bueos Ares. Argeta. maard@uolsects.com.ar
Expectativas del Mercado y Creación de Valor en la Empresa
 2d teratoal Coferece o dustral Egeerg ad dustral Maagemet X Cogreso de geería de Orgazacó September 3-5, 28, Burgos, Spa Expectatvas del Mercado y Creacó de Valor e la Empresa elpe Ruz López 1, Cáddo Barrea
2d teratoal Coferece o dustral Egeerg ad dustral Maagemet X Cogreso de geería de Orgazacó September 3-5, 28, Burgos, Spa Expectatvas del Mercado y Creacó de Valor e la Empresa elpe Ruz López 1, Cáddo Barrea
VARIABLE ALEATORIA Y FUNCIÓN DE DISTRIBUCIÓN
 VARIABLE ALEATORIA Y FUNCIÓN DE DISTRIBUCIÓN - INTRODUCCIÓN E este tema se tratará de formalzar umércamete los resultados de u feómeo aleatoro Por tato, ua varable aleatora es u valor umérco que correspode
VARIABLE ALEATORIA Y FUNCIÓN DE DISTRIBUCIÓN - INTRODUCCIÓN E este tema se tratará de formalzar umércamete los resultados de u feómeo aleatoro Por tato, ua varable aleatora es u valor umérco que correspode
3 = =. Pero si queremos calcular P (B) 2, ya que si A ocurrió, entonces en la urna
 arte robabldad codcoal rof. María. tarell - robabldad codcoal.- Defcó Supogamos el expermeto aleatoro de extraer al azar s reemplazo dos bolllas de ua ura que cotee 7 bolllas rojas y blacas. summos que
arte robabldad codcoal rof. María. tarell - robabldad codcoal.- Defcó Supogamos el expermeto aleatoro de extraer al azar s reemplazo dos bolllas de ua ura que cotee 7 bolllas rojas y blacas. summos que
Análisis amortizado. Técnicas Avanzadas de Programación - Javier Campos 205
 Aálss amortzado Téccas Avazadas de Programacó - Javer Campos 205 Aálss amortzado El pla: Coceptos báscos: Método agregado Método cotable Método potecal Prmer ejemplo: aálss de tablas hash dámcas Motículos
Aálss amortzado Téccas Avazadas de Programacó - Javer Campos 205 Aálss amortzado El pla: Coceptos báscos: Método agregado Método cotable Método potecal Prmer ejemplo: aálss de tablas hash dámcas Motículos
Tema 5: Equilibrio General Parte III OWC Economía para Matemáticos. Fernando Perera Tallo ttp://bit.ly/8l8ddu
 y Tea 5: Equlbro Geeral Parte III OWC Ecooía para Mateátcos Ferado Perera Tallo ttp://bt.ly/8l8ddu Esteca de Equlbro Ferado Perera-Tallo A lo largo de esta presetacó os vaos a cocetrar e espacos Eucldos,
y Tea 5: Equlbro Geeral Parte III OWC Ecooía para Mateátcos Ferado Perera Tallo ttp://bt.ly/8l8ddu Esteca de Equlbro Ferado Perera-Tallo A lo largo de esta presetacó os vaos a cocetrar e espacos Eucldos,
CAPÍTULO 6. CINEMÁTICA DIFERENCIAL DEL ROBOT PARALELO
 CAÍUO. CNMÁCA DFRNCA D ROBO ARAO es seccó se descrbe el álss de elocddes y celercoes del robo prlelo, el cul puede llerse cbo mede ls ecucoes pr momeo geerl debdo que o ese deslzmeo e ls coeoes. ss ecucoes
CAÍUO. CNMÁCA DFRNCA D ROBO ARAO es seccó se descrbe el álss de elocddes y celercoes del robo prlelo, el cul puede llerse cbo mede ls ecucoes pr momeo geerl debdo que o ese deslzmeo e ls coeoes. ss ecucoes
Modelación hidrológica empleando isoyetas de relieve, una aproximación geoestadística
 lmae Varably ad hage Hydrologcal Impacs Proceedgs of he Ffh FRIND World oferece held a Havaa uba November 006 IAHS Publ. 308 006. 6 odelacó hdrológca empleado soyeas de releve ua aproxmacó geoesadísca
lmae Varably ad hage Hydrologcal Impacs Proceedgs of he Ffh FRIND World oferece held a Havaa uba November 006 IAHS Publ. 308 006. 6 odelacó hdrológca empleado soyeas de releve ua aproxmacó geoesadísca
TIPOS DE TENDENCIAS Y SUS CONSEQUENCIAS. Tendencias estocásticas versus deterministas.
 TIPOS D TNDNCIAS Y SUS CONSQUNCIAS. Tendencas esocáscas versus deermnsas. Concepos báscos. Parmos de la base que una sere emporal es la realzacón de un proceso esocásco. Tal y como vmos en los modelos
TIPOS D TNDNCIAS Y SUS CONSQUNCIAS. Tendencas esocáscas versus deermnsas. Concepos báscos. Parmos de la base que una sere emporal es la realzacón de un proceso esocásco. Tal y como vmos en los modelos
INSTITUTO POLITECNICO NACIONAL CENTRO DE INVESTIGACIÓN Y DESARROLLO DE TECNOLOGÍA DIGITAL MAESTRIA EN CIENCIAS CON ESPECIALIDAD EN SISTEMAS DIGITALES
 INSTITUTO POLITCNICO NACIONAL CNTRO D INVSTIGACIÓN Y DSARROLLO D TCNOLOGÍA DIGITAL MASTRIA N CINCIAS CON SPCIALIDAD N SISTMAS DIGITALS MODLADO D ANTNAS MPLANDO DIFRNCIAS FINITAS N L DOMINIO DL TIMPO TSIS
INSTITUTO POLITCNICO NACIONAL CNTRO D INVSTIGACIÓN Y DSARROLLO D TCNOLOGÍA DIGITAL MASTRIA N CINCIAS CON SPCIALIDAD N SISTMAS DIGITALS MODLADO D ANTNAS MPLANDO DIFRNCIAS FINITAS N L DOMINIO DL TIMPO TSIS
División de Estadísticas y Proyecciones Económicas (DEPE) Centro de Proyecciones Económicas (CPE)
 Comsó Ecoómca para Amérca Lata y el Carbe (CEPAL Dvsó de Estadístcas y Proyeccoes Ecoómcas (DEPE Cetro de Proyeccoes Ecoómcas (CPE Estmacó Putual de Parámetros Chrsta A. Hurtado Navarro Mayo, 006 Estmacó
Comsó Ecoómca para Amérca Lata y el Carbe (CEPAL Dvsó de Estadístcas y Proyeccoes Ecoómcas (DEPE Cetro de Proyeccoes Ecoómcas (CPE Estmacó Putual de Parámetros Chrsta A. Hurtado Navarro Mayo, 006 Estmacó
TEMA 6 MUESTREO POR CONGLOMERADOS MONOETÁPICO
 TEA 6 UESTREO POR COGLOERADOS OOETÁPICO Cotedo 1- Defcó. Aplcacó. Seleccó de ua muestra por Coglomerados. Etapas. otacó. - uestreo mooetápco co coglomerados de gual tamaño. Estmacó de la meda, el total
TEA 6 UESTREO POR COGLOERADOS OOETÁPICO Cotedo 1- Defcó. Aplcacó. Seleccó de ua muestra por Coglomerados. Etapas. otacó. - uestreo mooetápco co coglomerados de gual tamaño. Estmacó de la meda, el total
TEMA 3.- OPERACIONES DE AMORTIZACION : PRESTAMOS A INTERES VARIABLE 3.1.-CLASIFICACIÓN DE LOS PRÉSTAMOS A INTERÉS VARIABLE :
 Dpto. Ecoomía Facera y otabldad Pla de Estudos 994 urso 008-09. TEMA 3 Prof. María Jesús Herádez García. TEMA 3.- OPERAIONES DE AMORTIZAION : PRESTAMOS A INTERES VARIABLE 3..-LASIFIAIÓN DE LOS PRÉSTAMOS
Dpto. Ecoomía Facera y otabldad Pla de Estudos 994 urso 008-09. TEMA 3 Prof. María Jesús Herádez García. TEMA 3.- OPERAIONES DE AMORTIZAION : PRESTAMOS A INTERES VARIABLE 3..-LASIFIAIÓN DE LOS PRÉSTAMOS
6. ESTIMACIÓN PUNTUAL
 Defcoes 6 ESTIMACIÓN PUNTUAL E la práctca, los parámetros de ua dstrbucó de probabldad se estma a partr de la muestra La fereca estadístca cosste e estmar los parámetros de ua dstrbucó; y e evaluar ua
Defcoes 6 ESTIMACIÓN PUNTUAL E la práctca, los parámetros de ua dstrbucó de probabldad se estma a partr de la muestra La fereca estadístca cosste e estmar los parámetros de ua dstrbucó; y e evaluar ua
Gestión de operaciones
 Gestó de operacoes Modelado de restrccoes co varables baras Modelado de programacó o leal Pedro Sáchez pedro.sachez@upcomllas.es Cotedo Restrccoes especales Restrccoes lógcas Productos de varables Modelos
Gestó de operacoes Modelado de restrccoes co varables baras Modelado de programacó o leal Pedro Sáchez pedro.sachez@upcomllas.es Cotedo Restrccoes especales Restrccoes lógcas Productos de varables Modelos
