(Polinomio de Taylor en R n )
|
|
|
- Jesús Naranjo Álvarez
- hace 6 años
- Vistas:
Transcripción
1 APROXIMACIÓN POR POLINOMIOS (Polinomio de Taylor en R n ) MARíA DEL CARMEN CALVO En este trabajo nos ocuparemos de extender a funciones de varias variables los resultados obtenidos para funciones de una variable. I. Introducción Antes de ocuparnos del tema específico necesitamos tratar algunos asuntos esencialmente algebraicos que facilitarán luego la comprensión de los conceptos principales. A partir de una función f : R n R y de un punto a R n vamos a encontrar la forma en que se puede escribir un polinomio de grado y otro de grado que cumplen la condición P(a) = f (a) Nos interesan especialmente porque el polinomio de Taylor, al tener que aproximar a la función cerca de a, deberá comenzar por coincidir con ella en ese punto. FORMA GENERAL DE UN POLINOMIO DE GRADO EN R n Sea P : R n R un polinomio de grado menor o igual que tal que P(a) = f (a). La condición sobre su grado obliga a que sólo contenga monomios de grado o cero. Por lo tanto, P(x) = b x + + b n x n + c donde b,..., b n, c R están fijos. Llamando b = (b,..., b n )
2 MARIA DEL CARMEN CALVO se puede escribir en la forma P(x) = b x + c La condición P(a) = f (a) dice que b a + c = f (a) O sea, c = f (a) b a Llegamos finalmente a nuestro objetivo donde b R n. P(x) = b (x a) + f (a) (.) Ejemplo Consideremos la función f (x, y, z) = 3 cos(x+y) xyz, el punto a = (0, π, ) y P el polinomio de grado P(x, y, z) = 3x y + 4z + π que satisface P(0, π, ) = f (0, π, ) = 3 Es inmediato ver que se puede escribir en la forma P(x, y, z) = (3,, 4) (x, y, z) + π Siguiendo el procedimiento del desarrollo anterior, reemplazamos (x, y, z) por y obtenemos (x, y π, z ) + (0, π, ) P(x, y, z) = (3,, 4) [(x, y π, z ) + (0, π, )] + π = (3,, 4) (x, y π, z ) + (3,, 4) (0, π, ) + π = (3,, 4) (x, y π, z ) π π = (3,, 4) (x, y π, z ) 3 Lo hemos escrito entonces en la forma (.) con b = (3,, 4)
3 FACULTAD DE CIENCIAS FISICOMATEMATICAS E INGENIERIA UCA CALCULO AVANZADO PRIMER CUATRIMESTRE FORMA GENERAL DE UN POLINOMIO DE GRADO EN R n Sea P : R n R un polinomio de grado menor o igual que tal que P(a) = f (a). La condición sobre su grado obliga a que sólo contenga monomios de grado, o cero. Por lo tanto, n P(x) = a i j x i x j + d x + + d n x n + c i, j= donde a i j, d k y c son números reales fijos y la matriz (a i j ) simétrica. Recordando que los polinomios de grado con todos sus monomios de grado representan formas cuadráticas, podemos escribir a este polinomio en la forma P(x) = x A x t + d x + c siendo A = (a i j ) R n n simétrica, d R n y c R. Nos proponemos aquí hacer algo similar al caso anterior; i.e., expresarlo en términos de las diferencias x a. Con ese propósito, en la ecuación anterior escribimos x = x a + a con lo cual, recordando las propiedades del producto de matrices y del producto escalar, obtenemos P(x) = (x a + a) A (x a + a) t + d (x a + a) + c = (x a) A (x a) t + a A (x a) t + (x a) A a t + a A a t + d (x a) + d a + c = (x a) A (x a) t + (aa) (x a) + d (x a) + a A a t + d a + c = (x a) A (x a) t + [(aa) + d] (x a) + [a A a t + d a + c] Llamando y teniendo en cuenta que b = d + aa f (a) = P(a) = a A a t + d a + c Llegamos finalmente a la forma en que queríamos escribir a P, donde A R n n es simétrica y b R n. P(x) = (x a) A (x a) t + b (x a) + f (a) (.) Ejemplo Sean f (x, y, z) = xy +xz e yz, a = (, 0, ) y P(x, y, z) = 4x 3y +z +xy yz+3x y+z 4 que satisface P(, 0, ) = 5 = f (, 0, ) y además que: y A y t = (y A y t ) t = ((y) t ) t (ya) t = y(ya) t = y (Ay)
4 4 MARIA DEL CARMEN CALVO Este polinomio se puede escribir en la forma, P(x, y, z) = ( x y z ) 4 0 x y + (3,, ) (x, y, z) 4 0 z Reemplazamos (x, y, z) = (x, y, z + ) + (, 0, ) P(x, y, z) = [( x y z + ) + ( 0 )] 4 0 x y z + + (3,, ) [(x, y, z + ) + (, 0, )] 4 = ( x y z + ) 4 0 x y ( x y z + ) z + 0 ( 0 ) 4 0 x y + ( 0 ) z (3,, ) (x, y, z + ) + (3,, ) (, 0, ) 4 = ( x y z + ) 4 0 x y ( x y z + ) 4 0 z + ( 4 ) x y + ( 4 ) 0 z + + (3,, ) (x, y, z + ) + 4 = ( x y z + ) 4 0 x y (4,, ) (x, y, z + ) z + + (3,, ) (x, y, z + ) 3 = ( x y z + ) 4 0 x y 0 z + + [ (4,, ) + (3,, )] (x, y, z + ) 5 = ( x y z + ) 4 0 x y + (,, 5) (x, y, z + ) 5 0 z + Esto responde a la forma (.) con 4 0 A = 0 y b = (,, 5)
5 FACULTAD DE CIENCIAS FISICOMATEMATICAS E INGENIERIA UCA CALCULO AVANZADO PRIMER CUATRIMESTRE II. Polinonio de Taylor de orden en R n Vamos a probar que para cada función f : R n R diferenciable en el punto a existe un único polinomio P : R n R que satisface f (x) P (x) = 0 (.) Comencemos por notar que un polinomio que cumple esta condición, en particular satisface P (a) = f (a) dado que, siendo que el cociente en (.) tiende a cero y el demoninador también, no queda otra posibilidad que también lo haga el numerador; con lo cual, por ser ambas funciones continuas implica que f (a) P (a) = f (x) P (x) = 0 Lo que diferencia a P del resto de los polinomios que coinciden con f justo en a es que su gráfico es el que está más cerca del gráfico de f para los x suficiente cercanos a a. Recordando la forma que tienen todos los polinomios que coinciden con f en a podemos escribir P (x) = b (x a) + f (a) Se trata entonces de ver quién es ese vector b. Escribamos la condición (.) usando esta expresión de P, f (x) f (a) b (x a) = 0 Pero esto, por ser f diferenciable, sólo se cumple cuando Concluimos de esta forma que b = f (a) P (x) = f (a) (x a) + f (a) es el único polinomio de grado menor o igual que que cumple (.). Además, cuando n =, su gráfico es el plano tangente al gráfico de f en (a, f (a)). III. Expresión del término complementario de orden en R n El término complementario de Taylor de orden alrededor del punto a se define por cf. la ecuación (.) R (x) = f (x) P (x)
6 6 MARIA DEL CARMEN CALVO es decir, indica la diferencia entre la función y el polinomio de Taylor de orden y nos da por lo tanto el error que cometemos al aproximar a f por P en cada punto x. Teniendo en cuenta que R (x) x a = f (x) P (x) x a podemos lograr que el error que cometemos en esa aproximación sea tan chico como se quiera con tal de tomar a x suficientemente cerca de a. Nos proponemos ahora encontrar una forma de escribir a este resto que recuerde lo sabido para funciones de una variable. Como pretendemos utilizar la forma Hessiana de f, vamos a pedir que esta función sea de clase C en un entorno de a. Para facilitar los cálculos definiremos a partir de f una función de una variable para la cual ya sabemos escribir su fórmula de Taylor de orden. Más precisamente, supongamos que f es de clase C en el disco D : < r sabemos que el segmento [a, x] D para todo x D. Pero D también incluye al segmento [a x, a] 3 ; luego, el segmento [a x, x] D. Esto se aprecia en el siguiente esquema gráfico, = 0 D x a a-x Comenzamos parametrizando este segmento, α : [, ] D, α(t) = a + t(x a) cuyo vector tangente en todo instante es x a y a continuación definimos la función ϕ : [, ] R, ϕ(t) = f (α(t)) 3 simétrico de [a, x] respecto de a sobre la recta que pasa por a y x
7 FACULTAD DE CIENCIAS FISICOMATEMATICAS E INGENIERIA UCA CALCULO AVANZADO PRIMER CUATRIMESTRE que resulta de clase C y además satisface ϕ(0) = f (a), ϕ() = f (x), ϕ (t) = f (α(t)) (x a) La fórmula de Taylor de orden de ϕ alrededor de t = 0 es ϕ(t) = p (t) + r (t) = ϕ(0) + ϕ (0)t + ϕ (t 0 ) t para un cierto t 0 entre 0 y t. Escrito en términos de f, para t =, nos da f (x) = f (a) + f (a) (x a) + ϕ (t 0 ) (para un 0 < t 0 < ) Necesitamos encontrar la expresión del resto en términos de f para lo cual deberemos derivar ϕ (t) = f (α(t)) (x a) = f x (α(t))(x a ) + + f x n (α(t))(x n a n ) Aplicando la regla de la cadena en cada sumando obtenemos ϕ (t) = ( f x )(α(t)) (x a) (x a ) ( f x n )(α(t)) (x a) (x n a n ) = ( ( f x )(α(t)) (x a),..., ( f x n )(α(t)) (x a) ) (x a) = (x a) ( ( f x )(α(t)) (x a),..., ( f x n )(α(t)) (x a) ) Recordando que cada fila de la matriz Hessiana es el gradiente de cada derivada parcial primera de f vemos que ( f x )(α(t)) (x a). = MH f (α(t))(x a)t ( f x n )(α(t)) (x a) de donde resulta que ϕ (t) = (x a)mh f (α(t))(x a) t = H f (α(t))(x a) Tomando t = t 0 obtenemos ϕ (t 0 ) = H f (α(t 0 ))(x a) Si llamamos c = α(t 0 ), hemos probado que la fórmula de Taylor de orden de f alrededor de a se escribe donde c = α(t 0 ) [a, x] 4. 4 por ser 0 < t 0 < f (x) = P (x) + H f (c)(x a)
8 8 MARIA DEL CARMEN CALVO IV. Polinonio de Taylor de orden en R n Supongamos que la función f : R n R es de clase C en el punto a. Mostraremos que existe un único polinomio P : R n R de grado menor o igual que tal que f (x) P (x) = 0 (4.) Comencemos por notar que esta condición implica que, en particular, f (x) P (x) = 0 (4.) Esto se deduce inmediatamente de f (x) P (x) = f (x) P (x) Como observamos en una sección anterior, la condición (4.) obliga a que P (a) = f (a) y por lo tanto es posible escribirlo en la forma (.) P (x) = (x a)a(x a) t + b (x a) + f (a) Reescribimos la condición (4.) usando esta expresión de P f (x) b (x a) f (a) + x a A(x a)t = 0 Ahora bien, la expresión x a está acotada dado que tiene norma mientras que A(x a)t tiende a cero cuando x tiende a a. Esto nos dice que el segundo sumando tiende a cero cuando x a y en consecuencia dado que la suma también converge a cero lo propio debe suceder con el primer sumando; i.e., f (x) b (x a) f (a) = 0 Pero entonces b (x a) + f (a) tiene que ser el polinomio de Taylor de orden de f en a por lo cual b = f (a) Tenemos hasta ahora que el polinomio que buscamos debe tener la forma P (x) = f (a) + f (a) (x a) + (x a)a(x a) t sólo nos resta ver quiénes son los elementos de la matriz A. Para lograr este objetivo vamos a usar el hecho que la existencia del ite múltiple de la condición (4.) asegura que se obtiene el mismo resultado cuando uno se aproxima a a por cualquier camino en particular.
9 FACULTAD DE CIENCIAS FISICOMATEMATICAS E INGENIERIA UCA CALCULO AVANZADO PRIMER CUATRIMESTRE Consideremos en primera instancia c(t) = (a,..., a i, t, a i+,..., a n ) que tiende a a cuando t a i. Conviene notar además que y también que d(t) = c(t) a = (0,..., 0, t a i, 0,..., 0) y c(t) a = d(t) = t a i a i a i a ni d(t)a(d(t)) t = d(t) = ( 0 0 t a i 0 0 ) = (t a i ) a ii.. La condición (4.) nos permite afirmar entonces que a i a i a ni f (c(t)) f (a) f (a)(d(t)) (t a i ) a ii (t a i ) 0 cuando t a i. De aquí podemos concluir que a ii = t ai f (c(t)) f (a) f (a)(d(t)) (t a i ) es decir, a ii = t ai f (a,..., t,..., a n ) f (a,..., a n ) f x i (a)(t a i ) (t a i ) Siendo éste un ite de una variable en el que tanto numerador como denominador tienden a cero cuando t a i podemos aplicar l Hospital para concluir que a ii = t ai = t a i = f (a) xi f x i (a,..., t,..., a n ) f x i (a) (t a i ) f x i (a,..., t,..., a n ) f x i (a) t a i A esta altura podemos decir que la matriz A coincide con MH f (a), al menos, en su diagonal principal. Para calcular el resto de los elementos de A y comprobar finalmente que A = MH f (a) bastaría con reproducir lo hecho con los elementos de la diagonal pero esta vez usando el camino g(t) = (a,..., a i, a i + t, a i+,..., a j, a j + t, a j+,..., a n ) a
10 0 MARIA DEL CARMEN CALVO cuando t 0. Llegamos entonces a que hay a lo sumo un polinomio que puede cumplir la condición (4.) P (x) = f (a) + f (a) (x a) + H f (a)(x a) Sólo nos resta comprobar que este polinomio efectivamente satisface la condición que lo caracteriza. Para ello utilizaremos un argumento muy similar al empleado en la sección anterior para llegar a la expresión del resto de orden. Más precisamente, para cada x llamamos y definimos u = x a ϕ(t) = f (a + tu) Cuentas similares a las hechas en esa ocasión nos permiten ahora decir que ϕ(0) = f (a), ϕ() = f (x), ϕ (0) = f (a) (x a), ϕ (0) = H f (a)(x a) Como para ϕ sabemos que escribiéndolo en términos de f llegamos a que t 0 ϕ(t) ϕ(0) ϕ (0)t ϕ (0)t t = 0 x a f (x) f (a) f (a) (x a) H f (a)(x a) = x a ϕ() ϕ(0) ϕ (0) ϕ (0) = 0 dado que cuando x a, 0. Queda probado entonces que P (x) = f (a) + f (a) (x a) + H f (a)(x a) es el único polinomio de grado menor o igual que que satisface la condición (4.). Observaciones. El polinomio de Taylor de orden de f alrededor de a se puede expresar en la forma P (x) = P (x) + H f (a)(x a). El polinomio de Taylor de orden de f alrededor de a aproxima mejor a f cerca de a que el polinomio de orden. En efecto, P satisface f (x) P (x) = 0
11 FACULTAD DE CIENCIAS FISICOMATEMATICAS E INGENIERIA UCA CALCULO AVANZADO PRIMER CUATRIMESTRE 007 y como tiende a cero más rápido que, esto nos dice que para cada x suficientemente cercano a a, la diferencia f (x) P (x) es menor que la diferencia f (x) P (x) 3. Esta propiedad vale en general: cuanto más alto es el grado del polinomio de Taylor mayor es su aproximación a la función cerca del punto.
(tres ejemplos) 1. Sea f : R 2 R dada por f (x, y) = x 4 + y 4 2(x y) 2.
 EXTREMOS LIBRES: LOCALES Y ABSOLUTOS (tres ejemplos) 1. Sea f : R 2 R dada por f (x, y) = x 4 + y 4 2(x y) 2. a) Probar que (0, 0) es un punto crítico pero no extremo b) Probar que ± 2(1, 1) son mínimos
EXTREMOS LIBRES: LOCALES Y ABSOLUTOS (tres ejemplos) 1. Sea f : R 2 R dada por f (x, y) = x 4 + y 4 2(x y) 2. a) Probar que (0, 0) es un punto crítico pero no extremo b) Probar que ± 2(1, 1) son mínimos
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES ) HOJA 3: Derivadas parciales y diferenciación.
 UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS SOLUCIONES ) 3-1. Calcular, para las siguientes funciones. a) fx, y) x cos x sen y b) fx, y) e xy c) fx, y) x + y ) lnx + y )
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS SOLUCIONES ) 3-1. Calcular, para las siguientes funciones. a) fx, y) x cos x sen y b) fx, y) e xy c) fx, y) x + y ) lnx + y )
ANÁLISIS I MATEMÁTICA 1 ANÁLISIS II (Computación) Práctica 5 - Verano 2009
 ANÁLISIS I MATEMÁTICA ANÁLISIS II (Computación) Práctica 5 - Verano 2009 Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior. Calcular las derivadas
ANÁLISIS I MATEMÁTICA ANÁLISIS II (Computación) Práctica 5 - Verano 2009 Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior. Calcular las derivadas
Práctica 5: Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos
 Análisis I Matemática I Análisis II (C) Cuat II - 2009 Práctica 5: Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior 1. Calcular las derivadas
Análisis I Matemática I Análisis II (C) Cuat II - 2009 Práctica 5: Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior 1. Calcular las derivadas
Análisis Matemático 2
 Análisis Matemático 2 Una resolución de ejercicios con hipervínculos a videos on-line Autor: Martín Maulhardt Revisión: Fernando Acero y Ricardo Sirne Análisis Matemático II y II A Facultad de Ingeniería
Análisis Matemático 2 Una resolución de ejercicios con hipervínculos a videos on-line Autor: Martín Maulhardt Revisión: Fernando Acero y Ricardo Sirne Análisis Matemático II y II A Facultad de Ingeniería
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
Capítulo VI. Diferenciabilidad de funciones de varias variables
 Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Teoremas de Taylor. Capítulo 7
 Capítulo 7 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor. Por
Capítulo 7 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor. Por
todos los puntos de U, y las funciones df : U R m son continuas en x, entonces F es diferenciable en x.
 clase C 1 clase C p 1. clase C 1 Consideremos U un abierto de R n, y F : U R m. Si para cada x U existe df (x), podemos definir una función df : U R m df (x) = ( 1 (x),..., m (x)) y tiene sentido estudiar
clase C 1 clase C p 1. clase C 1 Consideremos U un abierto de R n, y F : U R m. Si para cada x U existe df (x), podemos definir una función df : U R m df (x) = ( 1 (x),..., m (x)) y tiene sentido estudiar
La derivada y la recta tangente a una curva
 En la primera mitad del siglo XVII no se conocían métodos generales para calcular la tangente a una curva en un punto de la misma. Este problema se presentaba con frecuencia en mecánica, en óptica y en
En la primera mitad del siglo XVII no se conocían métodos generales para calcular la tangente a una curva en un punto de la misma. Este problema se presentaba con frecuencia en mecánica, en óptica y en
Polinomio de Taylor. Extremos.
 CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
Capítulo 3. Funciones con valores vectoriales
 Capítulo 3. Funciones con valores vectoriales 3.1. Curvas: recta tangente y longitud de arco 3.2. Superficies parametrizadas 3.3. Campos vectoriales, campos conservativos Capítulo 3. Funciones con valores
Capítulo 3. Funciones con valores vectoriales 3.1. Curvas: recta tangente y longitud de arco 3.2. Superficies parametrizadas 3.3. Campos vectoriales, campos conservativos Capítulo 3. Funciones con valores
x 2 y si x 3y 2 si x = 3y Describir el conjunto de los puntos de discontinuidad de f en coordenadas polares.
 FIUBA 07-05-11 Análisis Matemático II Parcial - Tema 1 1. Sea f(x, y) = { x y si x 3y si x = 3y Describir el conjunto de los puntos de discontinuidad de f en coordenadas polares.. Sea G(x, y) = (u(x, y),
FIUBA 07-05-11 Análisis Matemático II Parcial - Tema 1 1. Sea f(x, y) = { x y si x 3y si x = 3y Describir el conjunto de los puntos de discontinuidad de f en coordenadas polares.. Sea G(x, y) = (u(x, y),
1. DIFERENCIABILIDAD EN VARIAS VARIABLES
 . DIFERENCIABILIDAD EN VARIAS VARIABLES. Calcular las derivadas direccionales de las siguientes funciones en el punto ā y la dirección definida por v... f(x, y = x + 2xy 3y 2, ā = (, 2, v = ( 3 5, 4 5.
. DIFERENCIABILIDAD EN VARIAS VARIABLES. Calcular las derivadas direccionales de las siguientes funciones en el punto ā y la dirección definida por v... f(x, y = x + 2xy 3y 2, ā = (, 2, v = ( 3 5, 4 5.
Tema 6: Funciones de varias variables
 Tema 6: Funciones de varias variables de febrero de 6 Preliminares: derivadas parciales. Sea F una función de dos variables, como por ejemplo la función definida por F(x; y) = x y 3 Podemos derivarla con
Tema 6: Funciones de varias variables de febrero de 6 Preliminares: derivadas parciales. Sea F una función de dos variables, como por ejemplo la función definida por F(x; y) = x y 3 Podemos derivarla con
Polinomio de Taylor. Extremos.
 CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
Ba s e, d i M e n s i ó n y Mat r i z
 Unidad 4 Ba s e, d i M e n s i ó n y Mat r i z de transición Objetivos: Al inalizar la unidad, el alumno: Conocerá la deinición de base de un espacio vectorial Identiicará bases canónicas para algunos
Unidad 4 Ba s e, d i M e n s i ó n y Mat r i z de transición Objetivos: Al inalizar la unidad, el alumno: Conocerá la deinición de base de un espacio vectorial Identiicará bases canónicas para algunos
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 01/02
 Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
(Variables separadas Homogéneas Diferenciales Exactas Ecuaciones Diferenciales Lineales de Primer Orden)
 ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN (Variables separadas Homogéneas Diferenciales Exactas Ecuaciones Diferenciales Lineales de Primer Orden) MARíA DEL CARMEN CALVO Comencemos repasando
ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN (Variables separadas Homogéneas Diferenciales Exactas Ecuaciones Diferenciales Lineales de Primer Orden) MARíA DEL CARMEN CALVO Comencemos repasando
10. Series de potencias
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 7-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 7-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
MATEMÁTICAS II Notas de clase
 MATEMÁTICAS II Notas de clase Ramón Espinosa Departamento de Matemáticas, ITAM Resumen El propósito de estas notas es presentar algunos temas que se ven en el curso de Matemáticas II en el ITAM. En particular
MATEMÁTICAS II Notas de clase Ramón Espinosa Departamento de Matemáticas, ITAM Resumen El propósito de estas notas es presentar algunos temas que se ven en el curso de Matemáticas II en el ITAM. En particular
c) Calcular las asíntotas horizontales y verticales de f y representar de forma aproximada
 Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas Cálculo I Curso 2011/2012 2 de julio de 2012 (75 p) 1) Se considera la función f : R R definida por f(x) = ex 2 e x + 1 a) Determinar
Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas Cálculo I Curso 2011/2012 2 de julio de 2012 (75 p) 1) Se considera la función f : R R definida por f(x) = ex 2 e x + 1 a) Determinar
Minimización de una forma cuadrática sobre una recta (ejercicios)
 Minimización de una forma cuadrática sobre una recta (ejercicios) Objetivos. Dada una forma cuadrática positiva definida, encontrar su mínimo sobre una recta dada. Mostrar que en el punto mínimo el gradiente
Minimización de una forma cuadrática sobre una recta (ejercicios) Objetivos. Dada una forma cuadrática positiva definida, encontrar su mínimo sobre una recta dada. Mostrar que en el punto mínimo el gradiente
Unidad 2 Polinomios PÁGINA 28 SOLUCIONES. Sacar factor común. a) b) Evaluar un polinomio en un punto.
 Unidad Polinomios PÁGINA 8 SOLUCIONES Sacar factor común. a) b) 3x 6 3 ( x ) 3 5x 10x 5x 5 x( x x1) Evaluar un polinomio en un punto. Dado el polinomio P(x) = x 4 x 3 x + 1, podemos asegurar que: a) P(1)
Unidad Polinomios PÁGINA 8 SOLUCIONES Sacar factor común. a) b) 3x 6 3 ( x ) 3 5x 10x 5x 5 x( x x1) Evaluar un polinomio en un punto. Dado el polinomio P(x) = x 4 x 3 x + 1, podemos asegurar que: a) P(1)
Clase 4: Diferenciación
 Clase 4: Diferenciación C.J Vanegas 27 de abril de 2008 1. Derivadas Parciales Recordemos que la definición de derivada parcial: sea fa R R, definida sobre un f(x) f(x 0 ) intervalo abierto A. f es derivable
Clase 4: Diferenciación C.J Vanegas 27 de abril de 2008 1. Derivadas Parciales Recordemos que la definición de derivada parcial: sea fa R R, definida sobre un f(x) f(x 0 ) intervalo abierto A. f es derivable
Teorema de la Función Implícita
 Teorema de la Función Implícita Sea F : U R p+1 R U abierto F (x 1, x 2,..., x q, y) y un punto a (a 1, a 2,..., a q, b) en U tal que i)f (a 1, a 2,..., a q, b) 0 ii) 0 y continua, existe entonces una
Teorema de la Función Implícita Sea F : U R p+1 R U abierto F (x 1, x 2,..., x q, y) y un punto a (a 1, a 2,..., a q, b) en U tal que i)f (a 1, a 2,..., a q, b) 0 ii) 0 y continua, existe entonces una
La trascendencia de e y π
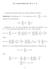 La trascendencia de e y π Comenzamos introduciendo unos convenios útiles de notación: Definición 1 Escribiremos h r = r!, de modo que si fz) = m c r z r C[z], entonces fh) representará fh) = m c r h r
La trascendencia de e y π Comenzamos introduciendo unos convenios útiles de notación: Definición 1 Escribiremos h r = r!, de modo que si fz) = m c r z r C[z], entonces fh) representará fh) = m c r h r
CAPÍTULO 4: DERIVADAS DE ORDEN SUPERIOR. En este capítulo D denota un subconjunto abierto de R n.
 April 15, 2009 En este capítulo D denota un subconjunto abierto de R n. 1. Introducción Definición 1.1. Dada una aplicación f : D R, definimos la derivada parcial segunda de f como D ij f = 2 f = ( ) x
April 15, 2009 En este capítulo D denota un subconjunto abierto de R n. 1. Introducción Definición 1.1. Dada una aplicación f : D R, definimos la derivada parcial segunda de f como D ij f = 2 f = ( ) x
Tema 3: Espacios eucĺıdeos
 Marisa Serrano, Zulima Fernández Universidad de Oviedo 25 de noviembre de 2009 email: mlserrano@uniovi.es Índice 1 2 3.1 V, R espacio vectorial, la aplicación : V V R ( v, u) v u a) v 1, v 2, u V α, β
Marisa Serrano, Zulima Fernández Universidad de Oviedo 25 de noviembre de 2009 email: mlserrano@uniovi.es Índice 1 2 3.1 V, R espacio vectorial, la aplicación : V V R ( v, u) v u a) v 1, v 2, u V α, β
Teóricas de Análisis Matemático (28) Práctica 6 L Hospital. x x. lim
 Teóricas de Análisis Matemático (8) Práctica 6 L Hospital Caso cero sobre cero Veamos tres problemas de límites conocidos: Práctica 6 Parte Regla de L Hospital 3 3 3 sen(3) Los límites y se resuelven mediante
Teóricas de Análisis Matemático (8) Práctica 6 L Hospital Caso cero sobre cero Veamos tres problemas de límites conocidos: Práctica 6 Parte Regla de L Hospital 3 3 3 sen(3) Los límites y se resuelven mediante
ÁLGEBRA II (LSI PI) UNIDAD Nº 2 GEOMETRÍA ANALÍTICA. Facultad de Ciencias Exactas y Tecnologías UNIVERSIDAD NACIONAL DE SANTIAGO DEL ESTERO
 17 ÁLGEBRA II (LSI PI) UNIDAD Nº GEOMETRÍA ANALÍTICA Facultad de Ciencias Exactas y Tecnologías aa Error! No hay texto con el estilo especificado en el documento. 1 UNIVERSIDAD NACIONAL DE SANTIAGO DEL
17 ÁLGEBRA II (LSI PI) UNIDAD Nº GEOMETRÍA ANALÍTICA Facultad de Ciencias Exactas y Tecnologías aa Error! No hay texto con el estilo especificado en el documento. 1 UNIVERSIDAD NACIONAL DE SANTIAGO DEL
si existe un entorno V de a contenido en A, tal que la diferencia f(x) f(a) no cambia de signo cuando x V :
 Capítulo 7 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor es el estudio de los extremos relativos de una función escalar. Aunque la analogía con el caso de una variable es total,
Capítulo 7 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor es el estudio de los extremos relativos de una función escalar. Aunque la analogía con el caso de una variable es total,
Definición 11.1 Sea f : A E F una aplicación r-veces diferenciable en un punto a A. o
 Capítulo 11 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor.
Capítulo 11 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor.
Soluciones a los ejercicios del examen final
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 201/14 20 de diciembre de 201 Soluciones a los ejercicios del examen final 1) Se considera la función f : R R
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 201/14 20 de diciembre de 201 Soluciones a los ejercicios del examen final 1) Se considera la función f : R R
Extremos de funciones de varias variables
 Capítulo 6 Extremos de funciones de varias variables En este capítulo vamos a considerar la teoría clásica de extremos para funciones diferenciables de varias variables, cuyos dos tópicos habituales son
Capítulo 6 Extremos de funciones de varias variables En este capítulo vamos a considerar la teoría clásica de extremos para funciones diferenciables de varias variables, cuyos dos tópicos habituales son
(x x 0 ) y 0. O bien z z 0 = x 0. y notamos a este límite ᾱ (t 0 ) = dᾱ dt (t 0).
 O bien z z 0 = x 0 z 0 (x x 0 ) y 0 z 0 (y y 0 ). Para obtener la ecuación cartesiana de este plano hacemos x 0 (x x 0 )+y 0 (y y 0 )+z 0 (z z 0 ) = 0, como x 0 + y0 + z0 = x 0 + y0 + r (x 0 + y0) = r
O bien z z 0 = x 0 z 0 (x x 0 ) y 0 z 0 (y y 0 ). Para obtener la ecuación cartesiana de este plano hacemos x 0 (x x 0 )+y 0 (y y 0 )+z 0 (z z 0 ) = 0, como x 0 + y0 + z0 = x 0 + y0 + r (x 0 + y0) = r
1. Para la función f(x) = x sen x, halle su polinomio de Taylor de orden 2 en a = 0. x x3 3! + x5
 Cálculo I (Grado en Ingeniería Informática Problemas resueltos, -, -4 y 4-5 (tercera parte Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić, Luis Guijarro (coordinadores,
Cálculo I (Grado en Ingeniería Informática Problemas resueltos, -, -4 y 4-5 (tercera parte Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić, Luis Guijarro (coordinadores,
f(x(t), y(t), z(t)) = k
 Plano tangente a cuádrica Cada una de las supercies cuádricas es el lugar geométrico de los punto del espacio que satisfacen una ecuación polinomial en tres variables, el problema de dar un método para
Plano tangente a cuádrica Cada una de las supercies cuádricas es el lugar geométrico de los punto del espacio que satisfacen una ecuación polinomial en tres variables, el problema de dar un método para
Mini-apunte teoría primer parcial de Análisis Matemático II
 Mini-apunte teoría primer parcial de Análisis Matemático II 1. Ecuaciones Diferenciales Definición 1.1 (ED). Una Ecuación Diferencial es una ecuación en la que intervienen una o más variables independientes,
Mini-apunte teoría primer parcial de Análisis Matemático II 1. Ecuaciones Diferenciales Definición 1.1 (ED). Una Ecuación Diferencial es una ecuación en la que intervienen una o más variables independientes,
Polinomios de Aproximación (Polinomios de Taylor P n )
 Polinomios de Aproximación ( P n ) Sabemos que la recta tangente a una función en un punto es la mejor aproximación lineal a la gráca de f en las cercanías del punto de tangencia (xo, f(xo)), es aquella
Polinomios de Aproximación ( P n ) Sabemos que la recta tangente a una función en un punto es la mejor aproximación lineal a la gráca de f en las cercanías del punto de tangencia (xo, f(xo)), es aquella
Álgebra Lineal. Ejercicios de evaluación. Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas
 Álgebra Lineal Ejercicios de evaluación Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas AUTORES: J. S ALAS, A. T ORRENTE Y E.J.S. V ILLASEÑOR Problema
Álgebra Lineal Ejercicios de evaluación Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas AUTORES: J. S ALAS, A. T ORRENTE Y E.J.S. V ILLASEÑOR Problema
Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) x u + f
 1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
Ejercicios Resueltos Tema 5
 Ejercicios Resueltos Tema 5 Ejercicio 1 Estudiar si la forma bilineal f : R n R n R definida por k f ((x 1,..., x n ), (y 1,..., y n )) = x i y i, siendo 1 k < n, es un producto escalar de R n i=1 Solución.
Ejercicios Resueltos Tema 5 Ejercicio 1 Estudiar si la forma bilineal f : R n R n R definida por k f ((x 1,..., x n ), (y 1,..., y n )) = x i y i, siendo 1 k < n, es un producto escalar de R n i=1 Solución.
Ecuaciones Diferenciales Ordinarias Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Matemática Semestre de Otoño, 2012
 Universidad de Chile Ecuaciones Diferenciales Ordinarias Facultad de Ciencias Físicas y Matemáticas Profesora Salomé Martínez Departamento de Ingeniería Matemática Semestre de Otoño, 2012 Pauta: Auxiliar
Universidad de Chile Ecuaciones Diferenciales Ordinarias Facultad de Ciencias Físicas y Matemáticas Profesora Salomé Martínez Departamento de Ingeniería Matemática Semestre de Otoño, 2012 Pauta: Auxiliar
TEORIA MATEMATICAS 5 PRIMER PARCIAL
 Def: Grafica de una función TEORIA MATEMATICAS 5 PRIMER PARCIAL Sea:. Definimos la grafica de f como el subconjunto de formado por los puntos, de en los que es un punto de U. Simbólicamente grafica es:
Def: Grafica de una función TEORIA MATEMATICAS 5 PRIMER PARCIAL Sea:. Definimos la grafica de f como el subconjunto de formado por los puntos, de en los que es un punto de U. Simbólicamente grafica es:
4to Concurso Unversitario de Matemáticas Galois-Noether 2014 Segunda Etapa
 4to Concurso Unversitario de Matemáticas Galois-Noether 2014 Segunda Etapa Sábado 9 de agosto 2014 Bienvenido a la Segunda Etapa del Concurso Universitario de Matemáticas Galois-Noether Instrucciones Lee
4to Concurso Unversitario de Matemáticas Galois-Noether 2014 Segunda Etapa Sábado 9 de agosto 2014 Bienvenido a la Segunda Etapa del Concurso Universitario de Matemáticas Galois-Noether Instrucciones Lee
Cálculo infinitesimal Grado en Matemáticas Curso 20014/15 Clave de soluciones n o 6. Derivadas de orden superior
 Cálculo infinitesimal Grado en Matemáticas Curso 2004/5 Clave de soluciones n o 6 Derivadas de orden superior 70. Hallar los polinomios de Taylor del grado indicado y en el punto indicado para las siguientes
Cálculo infinitesimal Grado en Matemáticas Curso 2004/5 Clave de soluciones n o 6 Derivadas de orden superior 70. Hallar los polinomios de Taylor del grado indicado y en el punto indicado para las siguientes
Práctica 3: Diferenciación
 Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) Primer Cuatrimestre - 03 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable. Vericar que se
Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) Primer Cuatrimestre - 03 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable. Vericar que se
Lección 2: Funciones vectoriales: límite y. continuidad. Diferenciabilidad de campos
 Lección 2: Funciones vectoriales: límite y continuidad. Diferenciabilidad de campos vectoriales 1.1 Introducción En economía, frecuentemente, nos interesa explicar la variación de unas magnitudes respecto
Lección 2: Funciones vectoriales: límite y continuidad. Diferenciabilidad de campos vectoriales 1.1 Introducción En economía, frecuentemente, nos interesa explicar la variación de unas magnitudes respecto
Curso 2010/ de julio de (2.75 p.) 1) Se considera la función f : (0, ) (0, ) definida por
 Cálculo I Curso 2010/2011 Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas 5 de julio de 2011 (275 p) 1) Se considera la función f : (0, ) (0, ) definida por f(x) = 1 + ex x e x a)
Cálculo I Curso 2010/2011 Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas 5 de julio de 2011 (275 p) 1) Se considera la función f : (0, ) (0, ) definida por f(x) = 1 + ex x e x a)
Distancia entre dos rectas que se cruzan Perpendicular común
 Perpendicular común En un espacio de tres dimensiones dos rectas se cruzan cuando no tienen ningún punto en común y no están contenidas en el mismo plano. Si no tienen ningún punto en común pero sí que
Perpendicular común En un espacio de tres dimensiones dos rectas se cruzan cuando no tienen ningún punto en común y no están contenidas en el mismo plano. Si no tienen ningún punto en común pero sí que
APUNTES DE MATEMÁTICAS UNIVERSIDAD DE SEVILLA GRADOS EN ECONOMÍA Y ADMINISTRACIÓN DE EMPRESAS PRIMER CURSO
 APUNTES E MATEMÁTICAS EXÁMENES RESUELTOS E MATEMÁTICAS I EPARTAMENTO E ECONOMÍA APLICAA I UNIVERSIA E SEVILLA GRAOS EN ECONOMÍA Y AMINISTRACIÓN E EMPRESAS PRIMER CURSO Jesús Muñoz San Miguel http://www.personal.us.es/jmiguel
APUNTES E MATEMÁTICAS EXÁMENES RESUELTOS E MATEMÁTICAS I EPARTAMENTO E ECONOMÍA APLICAA I UNIVERSIA E SEVILLA GRAOS EN ECONOMÍA Y AMINISTRACIÓN E EMPRESAS PRIMER CURSO Jesús Muñoz San Miguel http://www.personal.us.es/jmiguel
Espacios vectoriales
 CAPíTULO 2 Espacios vectoriales 1. Definición de espacio vectorial Es frecuente representar ciertas magnitudes físicas (velocidad, fuerza,...) mediante segmentos orientados o vectores. Dados dos de tales
CAPíTULO 2 Espacios vectoriales 1. Definición de espacio vectorial Es frecuente representar ciertas magnitudes físicas (velocidad, fuerza,...) mediante segmentos orientados o vectores. Dados dos de tales
SEGUNDO TURNO TEMA 1
 TEMA 1 Ejercicio 1 ( puntos) Dada la función polinómica f(x) = x + 2x 2 x 2, hallar los intervalos de positividad y negatividad de f sabiendo que el gráfico de dicha función corta al eje x en el punto
TEMA 1 Ejercicio 1 ( puntos) Dada la función polinómica f(x) = x + 2x 2 x 2, hallar los intervalos de positividad y negatividad de f sabiendo que el gráfico de dicha función corta al eje x en el punto
Soluciones de los ejercicios del primer examen parcial
 Matemáticas III (GIC, curso 2015 2016) Soluciones de los ejercicios del primer examen parcial EJERCICIO 1. Determina en qué ecuación se transforma la ecuación en derivadas parciales z yy + 3z xy + 2z xx
Matemáticas III (GIC, curso 2015 2016) Soluciones de los ejercicios del primer examen parcial EJERCICIO 1. Determina en qué ecuación se transforma la ecuación en derivadas parciales z yy + 3z xy + 2z xx
(3 p.) 3) Se considera la superficie z = z(x, y) definida implícitamente por la ecuación. 3x 2 z x 2 y 2 + 2z 3 3yz = 15.
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 2012/2013 21 de junio de 2013 4 p.) 1) Se considera la función fx) = x 4 e 1 x 2. a) Calcular los intervalos de
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 2012/2013 21 de junio de 2013 4 p.) 1) Se considera la función fx) = x 4 e 1 x 2. a) Calcular los intervalos de
La Diferencial. La Diferencial. Verónica Briceño V. Octubre 2013
 Octubre 2013 Linealización Recordar... f (a) = lím x a f (x) f (a) x a Linealización Recordar... f (a) = lím x a f (x) f (a) x a Linealización Recordar... f (a) = lím x a f (x) f (a) x a Notar que: Linealización
Octubre 2013 Linealización Recordar... f (a) = lím x a f (x) f (a) x a Linealización Recordar... f (a) = lím x a f (x) f (a) x a Linealización Recordar... f (a) = lím x a f (x) f (a) x a Notar que: Linealización
CÁLCULO II Funciones de varias variables
 CÁLCULO II Funciones de varias variables Facultad de Informática (UPM) Facultad de Informática (UPM) () CÁLCULO II Funciones de varias variables 1 / 36 Funciones de varias variables Función vectorial de
CÁLCULO II Funciones de varias variables Facultad de Informática (UPM) Facultad de Informática (UPM) () CÁLCULO II Funciones de varias variables 1 / 36 Funciones de varias variables Función vectorial de
Índice. 1 Extremos relativos. 2 Funciones convexas y extremos
 Índice Funciones de varias variables reales I Extremos y diferenciabilidad José Manuel Mira Ros 1 Extremos relativos Condiciones necesarias para las diferenciales primera y segunda Condiciones suficientes
Índice Funciones de varias variables reales I Extremos y diferenciabilidad José Manuel Mira Ros 1 Extremos relativos Condiciones necesarias para las diferenciales primera y segunda Condiciones suficientes
son dos elementos de Rⁿ, definimos su suma, denotada por
 1.1 Definición de un vector en R², R³ y su Interpretación geométrica. 1.2 Introducción a los campos escalares y vectoriales. 1.3 La geometría de las operaciones vectoriales. 1.4 Operaciones con vectores
1.1 Definición de un vector en R², R³ y su Interpretación geométrica. 1.2 Introducción a los campos escalares y vectoriales. 1.3 La geometría de las operaciones vectoriales. 1.4 Operaciones con vectores
Práctica 1. Continuidad Ejercicios resueltos
 Práctica 1. Continuidad Ejercicios resueltos 1. Estudiar la continuidad de los campos escalares definidos por f(x, y) = x y x 2 + y 2 g(x, y) = x2 y x 2 + y 4 h(x, y) = x y2 x 2 + y 4 para todo (x, y)
Práctica 1. Continuidad Ejercicios resueltos 1. Estudiar la continuidad de los campos escalares definidos por f(x, y) = x y x 2 + y 2 g(x, y) = x2 y x 2 + y 4 h(x, y) = x y2 x 2 + y 4 para todo (x, y)
MATEMÁTICAS 1º BACH. C. N. Y S. 25 de enero de 2010 Geometría y Logaritmos
 MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
May 4, 2012 CAPÍTULO 5: OPTIMIZACIÓN
 May 4, 2012 1. Optimización Sin Restricciones En toda esta sección D denota un subconjunto abierto de R n. 1.1. Condiciones Necesarias de Primer Orden. Proposición 1.1. Sea f : D R diferenciable. Si p
May 4, 2012 1. Optimización Sin Restricciones En toda esta sección D denota un subconjunto abierto de R n. 1.1. Condiciones Necesarias de Primer Orden. Proposición 1.1. Sea f : D R diferenciable. Si p
IES Fco Ayala de Granada Junio de 2016 (Modelo 2) Soluciones Germán-Jesús Rubio Luna. Opción A. a g(x)
 IES Fco Ayala de Granada Junio de 06 (Modelo ) Soluciones Germán-Jesús Rubio Luna germanjss@gmailcom Opción A Ejercicio opción A, modelo Junio 06 ln( + ) - a sen() + cos(3) ['5 puntos] Sabiendo que lim
IES Fco Ayala de Granada Junio de 06 (Modelo ) Soluciones Germán-Jesús Rubio Luna germanjss@gmailcom Opción A Ejercicio opción A, modelo Junio 06 ln( + ) - a sen() + cos(3) ['5 puntos] Sabiendo que lim
Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) x u + f
 1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
Para calcular las asíntotas, empezaremos por las verticales, precisamente en ese punto donde no está definida la función.
 1.- Dada la función: f(x) = x + 1 a) Calculad el dominio de f(x). Encontrar también sus asíntotas verticales, horizontales y oblicuas. b) Encontrad la recta tangente a f(x) en el punto x= 0. c) Calculad
1.- Dada la función: f(x) = x + 1 a) Calculad el dominio de f(x). Encontrar también sus asíntotas verticales, horizontales y oblicuas. b) Encontrad la recta tangente a f(x) en el punto x= 0. c) Calculad
Cálculo I (Grado en Ingeniería Informática) Problemas adicionales resueltos
 Cálculo I (Grado en Ingeniería Informática) - Problemas adicionales resueltos Calcula el ĺımite lím ( n + n + n + ) n Racionalizando el numerador, obtenemos L lím ( n + n + n (n + n + ) (n + ) + ) lím
Cálculo I (Grado en Ingeniería Informática) - Problemas adicionales resueltos Calcula el ĺımite lím ( n + n + n + ) n Racionalizando el numerador, obtenemos L lím ( n + n + n (n + n + ) (n + ) + ) lím
1. Funciones diferenciables
 1. diferenciables Volvamos sobre el significado de la derivada de una función real de una variable real, Como vimos en el capítulo anterior, f : (a, b) R derivable en x 0, equivale a que f(x) f(x 0 ) =
1. diferenciables Volvamos sobre el significado de la derivada de una función real de una variable real, Como vimos en el capítulo anterior, f : (a, b) R derivable en x 0, equivale a que f(x) f(x 0 ) =
1. Para la función f(x) = x sen x, halle su polinomio de Taylor de orden 2 en a = 0. x x3 3!, x x3
 Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
Powered by TCPDF (
 Powered by TCPDF (www.tcpdf.org) Análisis Matemático II - Curso 2018 Nota sobre formas cuadráticas y aplicación al análisis de extremos de una función Breve resumen acerca de las formas cuadráticas Necesitamos
Powered by TCPDF (www.tcpdf.org) Análisis Matemático II - Curso 2018 Nota sobre formas cuadráticas y aplicación al análisis de extremos de una función Breve resumen acerca de las formas cuadráticas Necesitamos
x 2 + ln(x + z) y = 0 yz + e xz 1 = 0 define una curva C regular en un entorno de (1, 1, 0) y halle el plano normal a C en dicho punto.
 1 Sea f : R R una función C 3 que satisface f(1, ) = (0, 0), y cuya matriz ( Hessiana ) en (1, ) es: 1 0 H = 0 Hallar todos los b ɛ R de manera que la función: g( = f( + 1 b b (y ) ) tenga extremo en (1,
1 Sea f : R R una función C 3 que satisface f(1, ) = (0, 0), y cuya matriz ( Hessiana ) en (1, ) es: 1 0 H = 0 Hallar todos los b ɛ R de manera que la función: g( = f( + 1 b b (y ) ) tenga extremo en (1,
CÁLCULO II Grados en Ingeniería
 CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
f(x) = x 2 Ejercicio 121 Para x = 1/2 formar los cocientes incrementales f/ x para los incrementos entre x = 1 y x = 1+ x de tres maneras diferentes:
 22 CAPÍTULO 3. INTEGRALES: CÁLCULO POR MEDIO DE PRIMITIVAS 3.2. La derivada En la sección 3. analizamos los incrementos y cocientes incrementales de varias funciones. En esta sección nos concentraremos
22 CAPÍTULO 3. INTEGRALES: CÁLCULO POR MEDIO DE PRIMITIVAS 3.2. La derivada En la sección 3. analizamos los incrementos y cocientes incrementales de varias funciones. En esta sección nos concentraremos
Práctica 3: Diferenciación
 Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) 1er. Cuatrimestre 2017 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable 1. Vericar que se
Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) 1er. Cuatrimestre 2017 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable 1. Vericar que se
Factorización de polinomios FACTORIZACIÓN DE POLINOMIOS
 FACTORIZACIÓN DE POLINOMIOS 1. Polinomios Un monomio es el producto de un número real por una o más letras que pueden estar elevadas a exponentes que sean números naturales. La suma de los exponentes de
FACTORIZACIÓN DE POLINOMIOS 1. Polinomios Un monomio es el producto de un número real por una o más letras que pueden estar elevadas a exponentes que sean números naturales. La suma de los exponentes de
Tema 5 Aplicaciones del cálculo diferencial
 Tema 5 Aplicaciones del cálculo diferencial 1. APLICACIONES EN UNA VARIABLE 1.1. Extremos relativos. Proposición 1.1: Monotonía Sea f : [a, b] R continua en [a, b] y derivable en (a, b), entonces: (1)
Tema 5 Aplicaciones del cálculo diferencial 1. APLICACIONES EN UNA VARIABLE 1.1. Extremos relativos. Proposición 1.1: Monotonía Sea f : [a, b] R continua en [a, b] y derivable en (a, b), entonces: (1)
Teorema de la Función Implícita
 Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
M a t e m á t i c a s I I 1
 Matemáticas II Matemáticas II CASTILLA Y LEÓN CONVOCATORIA SEPTIEMBRE 9 SOLUCIÓN DE LA PRUEBA DE ACCESO AUTOR: José Luis Pérez Sanz Prueba A Problemas a) f(x) x El denominador de f(x) nunca se anula; por
Matemáticas II Matemáticas II CASTILLA Y LEÓN CONVOCATORIA SEPTIEMBRE 9 SOLUCIÓN DE LA PRUEBA DE ACCESO AUTOR: José Luis Pérez Sanz Prueba A Problemas a) f(x) x El denominador de f(x) nunca se anula; por
Funciones convexas Definición de función convexa. Tema 7
 Tema 7 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Tema 7 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Campos escalares: gráficas, límites y continuidad
 Campos escalares: gráficas, ites y continuidad de febrero de 0 Gráficas de un campo escalar Dominio de un campo escalar Un campo escalar definido sobre un subconjunto U de R n, es una función f con dominio
Campos escalares: gráficas, ites y continuidad de febrero de 0 Gráficas de un campo escalar Dominio de un campo escalar Un campo escalar definido sobre un subconjunto U de R n, es una función f con dominio
Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. ) ( + ( ) ( )
 MATRICES Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. Ejemplo 1. Algunos ejemplos de matrices ( + ( ) ( + ( ) El tamaño o el orden de una
MATRICES Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. Ejemplo 1. Algunos ejemplos de matrices ( + ( ) ( + ( ) El tamaño o el orden de una
Reglas de derivación Sumas, productos y cocientes. Tema 4
 Tema 4 Reglas de derivación Aclarado el concepto de derivada, su significado analítico y sus interpretaciones geométrica y física, pasamos a desarrollar las reglas básicas para el cálculo de derivadas
Tema 4 Reglas de derivación Aclarado el concepto de derivada, su significado analítico y sus interpretaciones geométrica y física, pasamos a desarrollar las reglas básicas para el cálculo de derivadas
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES ) y = ex cos y. e x cos y e x sin y. y 2.
 UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES HOJA 4: Derivadas de orden superior 4-1. Sea u : R R definida por u(x, y e x sen y. Calcula las cuatro parciales segundas,
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES HOJA 4: Derivadas de orden superior 4-1. Sea u : R R definida por u(x, y e x sen y. Calcula las cuatro parciales segundas,
ANÁLISIS II Computación. Práctica 4. x 3. x 2 + y 2 si (x, y) (0, 0)
 facultad de ciencias exactas y naturales uba primer cuatrimestre 2007 ANÁLISIS II Computación Práctica 4 Derivadas parciales 1. Calcular a) f y (2, 1) para f(x, y) = xy + x y b) f z (1, 1, 1) para f(x,
facultad de ciencias exactas y naturales uba primer cuatrimestre 2007 ANÁLISIS II Computación Práctica 4 Derivadas parciales 1. Calcular a) f y (2, 1) para f(x, y) = xy + x y b) f z (1, 1, 1) para f(x,
Para saber si tiene asíntotas horizontales hacemos los límites en los infinitos.
 1.- Considerad las funciones: f(x) = x + 2 2x x + 2 g(x) = 2 x + 2 a) Determinar el dominio de la función f(x) y calcular sus asíntotas (horizontales, verticales y oblicuas) en caso de que existan. b)
1.- Considerad las funciones: f(x) = x + 2 2x x + 2 g(x) = 2 x + 2 a) Determinar el dominio de la función f(x) y calcular sus asíntotas (horizontales, verticales y oblicuas) en caso de que existan. b)
1.3.1 Fundamentos de cálculo vectorial
 131 Fundamentos de cálculo vectorial 1 Función escalar Una función se define como una representación escalar que está dada en términos de un vector Un ejemplo analítico puede darse por la función f(x)
131 Fundamentos de cálculo vectorial 1 Función escalar Una función se define como una representación escalar que está dada en términos de un vector Un ejemplo analítico puede darse por la función f(x)
Matemáticas III Tema 1 Funciones de varias variables. Diferenciabilidad
 Matemáticas III Tema 1 Funciones de varias variables. Diferenciabilidad Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino Córdoba, S. 2014. OCW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia Creative
Matemáticas III Tema 1 Funciones de varias variables. Diferenciabilidad Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino Córdoba, S. 2014. OCW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia Creative
Coordinación de Matemáticas III (MAT 023) x a. Además, diremos que f es continua en U si f es continua en cada punto de U.
 Coordinación de Matemáticas III (MAT 023) 1 er Semestre de 2013 Continuidad de Funciones en Varias Variables 1. Continuidad Definición 1.1. Sean U R n abierto, a U y f : U R una función real de varias
Coordinación de Matemáticas III (MAT 023) 1 er Semestre de 2013 Continuidad de Funciones en Varias Variables 1. Continuidad Definición 1.1. Sean U R n abierto, a U y f : U R una función real de varias
Diferenciciación en R n
 Diferenciciación en R n R. Álvarez-Nodarse Universidad de Sevilla Cómo definir la derivada? Definición Sea A un abierto de R n, a A y f : A R n R m. La derivada parcial i-ésima (1 i n) de f en a se define
Diferenciciación en R n R. Álvarez-Nodarse Universidad de Sevilla Cómo definir la derivada? Definición Sea A un abierto de R n, a A y f : A R n R m. La derivada parcial i-ésima (1 i n) de f en a se define
Integrales Curvilíneas.
 CAPÍTULO 7 Integrales Curvilíneas. Este capítulo abre la segunda parte de la materia : el cálculo integral vectorial. Las integrales de línea de campos escalares y vectoriales tienen aplicaciones a la
CAPÍTULO 7 Integrales Curvilíneas. Este capítulo abre la segunda parte de la materia : el cálculo integral vectorial. Las integrales de línea de campos escalares y vectoriales tienen aplicaciones a la
Matemáticas III Andalucía-Tech
 Matemáticas III Andalucía-Tech Tema Optimización en campos escalares Índice 1. Formas cuadráticas y matrices simétricas reales 1. Extremos relativos de un campo escalar 3.1. Polinomio de Taylor de un campo
Matemáticas III Andalucía-Tech Tema Optimización en campos escalares Índice 1. Formas cuadráticas y matrices simétricas reales 1. Extremos relativos de un campo escalar 3.1. Polinomio de Taylor de un campo
Tema 4 Diferenciación de funciones de una y varias
 Tema 4 Diferenciación de funciones de una y varias variables. CÁLCULO DIFERENCIAL DE FUNCIONES DE UNA VARIABLE Definición.: Función derivable Sea f : R R definida en un entorno de a R, se dice que f es
Tema 4 Diferenciación de funciones de una y varias variables. CÁLCULO DIFERENCIAL DE FUNCIONES DE UNA VARIABLE Definición.: Función derivable Sea f : R R definida en un entorno de a R, se dice que f es
Funciones Implícitas.
 CAPÍTULO 5 Funciones Implícitas. En este capítulo presentamos el concepto de función implícita. Esta idea nos ayuda a obtener derivadas de funciones que no podemos conocer explícitamente, pero su aplicación
CAPÍTULO 5 Funciones Implícitas. En este capítulo presentamos el concepto de función implícita. Esta idea nos ayuda a obtener derivadas de funciones que no podemos conocer explícitamente, pero su aplicación
Integrales Curvilíneas.
 CAPÍTULO 8 Integrales Curvilíneas. Este capítulo abre la segunda parte de la materia : el cálculo integral vectorial. Las integrales de línea de campos escalares y vectoriales tienen aplicaciones a la
CAPÍTULO 8 Integrales Curvilíneas. Este capítulo abre la segunda parte de la materia : el cálculo integral vectorial. Las integrales de línea de campos escalares y vectoriales tienen aplicaciones a la
Tarea 1 - Vectorial
 Tarea - Vectorial 2050. Part :. - 3.2.. Un cerro se queda en las montañas en la altura de 6 mil metros. El cerro tiene la forma del gráfico de la función z = f(x, y) = x 2 y 2. Observamos que plaquitas
Tarea - Vectorial 2050. Part :. - 3.2.. Un cerro se queda en las montañas en la altura de 6 mil metros. El cerro tiene la forma del gráfico de la función z = f(x, y) = x 2 y 2. Observamos que plaquitas
Funciones reales de varias variables.
 Tema 4 Funciones reales de varias variables. 4.1. El espacio euclídeo R n. Definición 4.1.1. Se define el producto escalar entre vectores de R n como la aplicación: ( ) : R n R n R : x y = (x 1, x 2,...,
Tema 4 Funciones reales de varias variables. 4.1. El espacio euclídeo R n. Definición 4.1.1. Se define el producto escalar entre vectores de R n como la aplicación: ( ) : R n R n R : x y = (x 1, x 2,...,
9. Diferenciación de funciones reales de varias variables reales Diferenciación DERIVADAS PARCIALES
 9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
PRACTICO: : LÍMITES DE FUNCIONES
 APUNTE TEORICO-PRACTICO PRACTICO: : LÍMITES DE FUNCIONES UNIVERSIDAD NACIONAL DE RIO NEGRO Asignatura: Matemática 1 Carreras: Lic. en Economía Profesor: Prof. Mabel Chrestia Semestre: 1ero Año: 16 Introducción
APUNTE TEORICO-PRACTICO PRACTICO: : LÍMITES DE FUNCIONES UNIVERSIDAD NACIONAL DE RIO NEGRO Asignatura: Matemática 1 Carreras: Lic. en Economía Profesor: Prof. Mabel Chrestia Semestre: 1ero Año: 16 Introducción
PRACTICO: : LÍMITES DE FUNCIONES
 APUNTE TEORICO-PRACTICO PRACTICO: : LÍMITES DE FUNCIONES UNIVERSIDAD NACIONAL DE RIO NEGRO Asignatura: Matemática 1 Carreras: Lic. en Economía Profesor: Prof. Mabel Chrestia Semestre: 1ero Año: 15 Introducción
APUNTE TEORICO-PRACTICO PRACTICO: : LÍMITES DE FUNCIONES UNIVERSIDAD NACIONAL DE RIO NEGRO Asignatura: Matemática 1 Carreras: Lic. en Economía Profesor: Prof. Mabel Chrestia Semestre: 1ero Año: 15 Introducción
