Diseño en espacio de estados
|
|
|
- Juan José San Segundo Maestre
- hace 6 años
- Vistas:
Transcripción
1 Diseño en espacio de estados Dr. Guillermo Valencia-Palomo Instituto Tecnológico de Hermosillo. División de estudios de posgrado e investigación. Junio, 2011.
2 1 Introducción Contenido 2 Controlabilidad y observabilidad Controlabilidad Observabilidad 3 Formas canónicas Forma canónica controlable Forma canónica observable Forma canónica de Jordan 4 Diseño de controladores Control por retroalimentación de estados Regulador lineal cuadrático (LQR) Seguimiento y acción integral 5 Diseño de observadores Observador de estados completo Observador de orden mínimo Controladores basados en observador 2 / 90
3 Introducción Un sistema moderno complejo posee muchas entradas y muchas salidas que se relacionan entre sí en una forma complicada. De esta forma, y especialmente cuando el nivel de acoplamiento del sistema es elevado, el análisis clásico se complica enormemente. Para analizar un sistema de este tipo, se requiere la complejidad de las expresiones matemáticas, además de recurrir a una computadora que realice gran parte de los cálculos necesarios en el análisis. El enfoque en el espacio de estados para los análisis de sistemas es el más conveniente desde este punto de vista. Mientras que la teoría de control convencional se basa en la relación entrada-salida, o función de transferencia, la teoría de control moderna 1 se basa en la descripción de las ecuaciones de un sistema en términos de n ecuaciones diferenciales de primer orden, que se combinan en una ecuación diferencial matricial de primer orden. 1 La teoría del control moderno se reconoce usualmente como el desarrollo teórico que se inició a comienzos de los años 60, a partir del trabajo pionero de R. Kalman. 3 / 90
4 Introducción La representación en variables de estado ha mostrado ser más útil, que la representación externa (entrada-salida), pues permite un análisis más profundo de las propiedades de un sistema dado. La representación en variables de estado permite la descripción completa del sistema, a diferencia al enfoque basado en funciones de transferencia, donde sólo se describe la parte completamente controlable y completamente observable. Esto último ha dejado de manifiesto algunas limitaciones de las funciones de transferencia para el análisis de sistemas, principalmente porque este tipo de modelos expresa sólo las propiedades de entradasalida de un sistema, tales como estabilidad, velocidad, respuesta en frecuencia, y otras propiedades y limitaciones fundamentales producto de la ubicación de los ceros y polos. 4 / 90
5 Introducción Por último, la descripción en variables de estado permite tratar de manera unificada tanto los sistemas escalares como los sistemas multivariables. El uso de la notación matricial simplifica enormemente la representación matemática de los sistemas de ecuaciones. El incremento en la cantidad de variables de estado, de entradas o de salidas no aumenta la complejidad de las ecuaciones. De hecho, el análisis de los sistemas complicados con entradas y salidas múltiples se realiza mediante procedimientos sólo ligeramente más complicados que los requeridos para el análisis de sistemas de ecuaciones diferenciales escalares de primer orden. 5 / 90
6 Controlabilidad Una propiedad muy importante que nos interesa en sistemas de control es saber cuándo es posible llevar, o no, el vector de estado a un punto específico del espacio de estado, a través de las señales de entrada al sistema. 6 / 90
7 Controlabilidad Una propiedad muy importante que nos interesa en sistemas de control es saber cuándo es posible llevar, o no, el vector de estado a un punto específico del espacio de estado, a través de las señales de entrada al sistema. Se debe recordar que el estado de un sistema por lo general está formado por algunas de sus variables físicas (o alguna función de sus variables físicas), como temperatura, presión o el nivel de algún tanque, que pueden ser críticas e interesa mantenerlas controladas entre algunos valores específicos. 6 / 90
8 Controlabilidad Una propiedad muy importante que nos interesa en sistemas de control es saber cuándo es posible llevar, o no, el vector de estado a un punto específico del espacio de estado, a través de las señales de entrada al sistema. Se debe recordar que el estado de un sistema por lo general está formado por algunas de sus variables físicas (o alguna función de sus variables físicas), como temperatura, presión o el nivel de algún tanque, que pueden ser críticas e interesa mantenerlas controladas entre algunos valores específicos. Esta noción de controlabilidad se puede formalizar con la siguiente definición: Controlabilidad Un estado x(t) = x i se dice controlable en t = t 0 si existe un intervalo de tiempo finito [t 0, t f ] y una entrada (no necesariamente acotada) u(t), t [t 0, t f ] tal que x(t f ) = x f. Si todos los estados son controlables, entonces se dice que el sistema es completamente controlable. 6 / 90
9 Considere el sistema descrito por, Controlabilidad ẋ(t) = Ax(t)+Bu(t); con x(t) R n, u(t) R m n, A R n n, B R n m. El sistema es completamente controlable en t = t 0 si es posible llevar al vector de estados x(t) con valor inicial x i utilizando una entrada (no necesariamente acotada) u(t) hasta un valor final x f en un tiempo finito. Sin pérdida de generalidad, se asume que x(t f ) = 0 y t 0 = 0. La solución general de este sistema es, x(t) = e At x(0)+ t 0 e A(t τ) Bu(τ)dτ; Para el tiempo t = t f, se puede calcular como x(t f ) = 0 = e At f x(0)+ tf 0 e A(t f τ) Bu(τ)dτ; 7 / 90
10 Controlabilidad Despejando x(0), tf x(0) = e Aτ Bu(τ)dτ; 0 Refiriéndonos a la fórmula de interpolación de Sylvester, e Aτ puede ser reescrito como, n 1 e Aτ = α j (τ)a j ; j=0 Sustituyendo en la ecuación, n 1 tf x(0) = A j B α j (τ)u(τ)dτ; j=0 0 } {{ } β j n 1 = A j Bβ j ; j=0 8 / 90
11 Controlabilidad Reescribiendo la ecuación en forma matricial, x(0) = [ B AB... A n 1 B ] β 0 β 1. β n 1 Con este resultado se pueden establecer las condiciones para la controlabilidad completa del sistema dado un estado inicial x(0).. 9 / 90
12 Controlabilidad Reescribiendo la ecuación en forma matricial, x(0) = [ B AB... A n 1 B ] β 0 β 1. β n 1 Con este resultado se pueden establecer las condiciones para la controlabilidad completa del sistema dado un estado inicial x(0).. Condición necesaria y suficiente para la controlabilidad El par (A,B) es completamente controlable dado un estado inicial x(0) si y sólo si la matriz de controlabilidad Γ c R n mn es de rango n, Γ c = [ B AB... A n 1 B ]. 9 / 90
13 Controlabilidad En el caso que un sistema no sea completamente controlable, este puede descomponerse un subsistema completamente controlable y uno completamente incontrolable. 10 / 90
14 Controlabilidad En el caso que un sistema no sea completamente controlable, este puede descomponerse un subsistema completamente controlable y uno completamente incontrolable. Considere un sistema para el cual rango{γ c } = k < n, entonces existe una matriz de transformación de similaridad T tal que x(t) = T 1 x(t), Ā = T 1 AT; B = T 1 B; donde las matrices tienen la siguiente forma: [ ] [ Āc Ā Ā = 12 Bc ; B = 0 Ā nc 0 con Āc R k k, Bc R k m, Ānc R n k n k y el par (Āc, B c ) es completamente controlable. La nueva representación del sistema es, [ ] [ x c Āc Ā = 12 x nc 0 Ā nc ][ xc x nc ] + [ Bc 0 ] ; ] u(t). 10 / 90
15 Controlabilidad El subespacio controlable del modelo en variables de estado está compuesto por todos los estados generados como combinación de los estados en x c (t). La estabilidad de este subespacio está determinada por la ubicación de los valores propios de la matriz Āc. 11 / 90
16 Controlabilidad El subespacio controlable del modelo en variables de estado está compuesto por todos los estados generados como combinación de los estados en x c (t). La estabilidad de este subespacio está determinada por la ubicación de los valores propios de la matriz Āc. Por otra parte, el subespacio no controlable está formado por todos los estados generados como combinación lineal de los estados en x nc (t). La estabilidad de este subespacio queda determinada por los valores propios de la matriz Ānc. De esta forma, u(t) no tiene efecto alguno sobre el subespacio no controlable; por lo que en el mejor de los casos, podríamos esperar que este subespacio fuera al menos estable, de manera que sus estados decaigan naturalmente al origen. 11 / 90
17 Controlabilidad El subespacio controlable del modelo en variables de estado está compuesto por todos los estados generados como combinación de los estados en x c (t). La estabilidad de este subespacio está determinada por la ubicación de los valores propios de la matriz Āc. Por otra parte, el subespacio no controlable está formado por todos los estados generados como combinación lineal de los estados en x nc (t). La estabilidad de este subespacio queda determinada por los valores propios de la matriz Ānc. De esta forma, u(t) no tiene efecto alguno sobre el subespacio no controlable; por lo que en el mejor de los casos, podríamos esperar que este subespacio fuera al menos estable, de manera que sus estados decaigan naturalmente al origen. Sistema estabilizable Se denomina sistema estabilizable al sistema cuyo subespacio no controlable es estable. Dicho de otra manera, al sistema cuyos estados inestables son controlables. 11 / 90
18 Controlabilidad Para cuestiones prácticas, no se requiere que el vector de estados sea completamente controlable. De hecho basta con que la combinación de estados que componen la salida sea controlable, por ello es necesario definir la propiedad de controlabilidad de la salida. 12 / 90
19 Controlabilidad Para cuestiones prácticas, no se requiere que el vector de estados sea completamente controlable. De hecho basta con que la combinación de estados que componen la salida sea controlable, por ello es necesario definir la propiedad de controlabilidad de la salida. Considere un sistema descrito por la siguiente representación en espacio de estados: ẋ(t) = Ax(t)+Bu(t); y(t) = Cx(t)+Du(t); con x(t) R n, u(t) R m n, y(t) R l, A R n n, B R n m, C R l n, D R l m. Para este caso, la matriz de controlabilidad Γ c R l (n+1)m ahora se escribe como Γ c = [ CB CAB... CA n 1 B D ]. Para que exista controlabilidad completa de la salida, Γ c debe de ser de rango l. Note que la presencia de D siempre ayuda a la controlabilidad. 12 / 90
20 Observabilidad Si se observa el modelo de estado de un sistema dado, se aprecia que la salida de éste depende directamente del estado, por tanto se podría suponer que si se observa esta salida durante un intervalo de tiempo, entonces se podría obtener información sobre el vector de estado. La propiedad asociada a esta idea se denomina observabilidad, y puede formalizarse con la siguiente definición: 13 / 90
21 Observabilidad Si se observa el modelo de estado de un sistema dado, se aprecia que la salida de éste depende directamente del estado, por tanto se podría suponer que si se observa esta salida durante un intervalo de tiempo, entonces se podría obtener información sobre el vector de estado. La propiedad asociada a esta idea se denomina observabilidad, y puede formalizarse con la siguiente definición: Observabilidad El estado x(t) se dice observable en t = t 0 si es posible determinar su valor a partir de los valores de y(t) y u(t) en un intervalo de tiempo finito [t 0, t f ]. El sistema se dice completamente observable si todos sus estados son observables. 13 / 90
22 Observabilidad Si se observa el modelo de estado de un sistema dado, se aprecia que la salida de éste depende directamente del estado, por tanto se podría suponer que si se observa esta salida durante un intervalo de tiempo, entonces se podría obtener información sobre el vector de estado. La propiedad asociada a esta idea se denomina observabilidad, y puede formalizarse con la siguiente definición: Observabilidad El estado x(t) se dice observable en t = t 0 si es posible determinar su valor a partir de los valores de y(t) y u(t) en un intervalo de tiempo finito [t 0, t f ]. El sistema se dice completamente observable si todos sus estados son observables. De la definición, se concluye que el sistema es completamente observable si para cada cambio del vector de estado existe un cambio en la salida. 13 / 90
23 Observabilidad Considere un sistema descrito por la siguiente representación en espacio de estados: ẋ(t) = Ax(t)+Bu(t); y(t) = Cx(t)+Du(t); con x(t) R n, u(t) R m n, y(t) R l, A R n n, B R n m, C R l n, D R l m. El valor de la salida se puede calcular de la siguiente manera: la solución general de este sistema es, x(t) = e At x(0)+ t y(t) = Ce At x(0)+c 0 e A(t τ) Bu(τ)dτ; t 0 e A(t τ) Bu(τ)dτ + Du(t); Ya que las matrices A, B, C, D son conocidas, así como la entrada u(t), los dos últimos términos de la ecuación de salida son conocidos y pueden ser restados del valor de y(t). 14 / 90
24 Observabilidad Por lo que para determinar las condiciones suficientes y necesarias para que la observabilidad completa se de, es suficiente trabajar con y(t) = Ce At x(0); De la misma forma que en el caso de controlabilidad la ecuación anterior se reescribe utilizando la fórmula de interpolación de Sylvester, n 1 y(t) = α j (t)ca j x(0); j=0 15 / 90
25 Observabilidad Por lo que para determinar las condiciones suficientes y necesarias para que la observabilidad completa se de, es suficiente trabajar con y(t) = Ce At x(0); De la misma forma que en el caso de controlabilidad la ecuación anterior se reescribe utilizando la fórmula de interpolación de Sylvester, n 1 y(t) = α j (t)ca j x(0); Condición necesaria y suficiente para la observabilidad j=0 El par (A,C) es completamente observable para estado inicial x(0) si y sólo si la matriz de observabilidad Γ o R n ln es de rango n, [ ( ] Γ o = C T A T C T... A T) n 1 C T. 15 / 90
26 Observabilidad En forma análoga a lo que sucede con la controlabilidad de los estados de un sistema, pueden existir algunos de ellos que sean observables y otros que no lo sean, es decir, la salida del sistema no aporta información sobre ellos. 16 / 90
27 Observabilidad En forma análoga a lo que sucede con la controlabilidad de los estados de un sistema, pueden existir algunos de ellos que sean observables y otros que no lo sean, es decir, la salida del sistema no aporta información sobre ellos. Considere un sistema para el cual rango{γ o } = k < n, entonces existe una matriz de transformación de similaridad T tal que x(t) = T 1 x(t), Ā = T 1 AT; C = CT, y toman la siguiente forma: [ ] Āo 0 [ Ā = ; C = Co 0 ] ; Ā 21 Ā no con Āo R k k, Co R l k, Ā no R n k n k y el par (Āo, C o ) es completamente observable. El estado (transformado) y la ecuaciones de salida se expresan como: [ x o x no ] = [ Āo 0 Ā 21 y(t) = [ Co Ā no ][ xo 0 ][ x o x no ] x no ] + [ Bo B no ] u(t); 16 / 90
28 Observabilidad La descripción anterior pone en evidencia el problema que puede surgir cuando se intenta controlar un sistema usando sólo su salida, pues en ésta no aparece información alguna sobre el estado x no (t). El subespacio observable de un modelo es el espacio formado por todos los estados que se generan como combinaciones lineales de los estados en x o (t). La estabilidad de este subespacio queda determinada por la ubicación de los valores propios de la matriz Āo. El subespacio no observable de un modelo, es el espacio formado por todos los estados generados como combinación lineal de los estados en x no. La estabilidad de este subespacio queda determinada por los valores propios de la matriz Āno. 17 / 90
29 Observabilidad La descripción anterior pone en evidencia el problema que puede surgir cuando se intenta controlar un sistema usando sólo su salida, pues en ésta no aparece información alguna sobre el estado x no (t). El subespacio observable de un modelo es el espacio formado por todos los estados que se generan como combinaciones lineales de los estados en x o (t). La estabilidad de este subespacio queda determinada por la ubicación de los valores propios de la matriz Āo. El subespacio no observable de un modelo, es el espacio formado por todos los estados generados como combinación lineal de los estados en x no. La estabilidad de este subespacio queda determinada por los valores propios de la matriz Āno. Sistema detectable Se denomina sistema detectable al sistema cuyo subespacio no observable es estable. Dicho de otra manera, al sistema cuyos estados inestables son observables. 17 / 90
30 Ejercicio 1 Para el sistema [ 1 1 ẋ(t) = 2 1 y(t) = [ 1 Ejercicios 0 ] x(t); ] [ 0 x(t)+ 1 ] u(t); Describa sus propiedades de (i) controlabilidad y (ii) observabilidad. 18 / 90
31 Ejercicio 1 Para el sistema [ 1 1 ẋ(t) = 2 1 y(t) = [ 1 Ejercicios 0 ] x(t); ] [ 0 x(t)+ 1 ] u(t); Describa sus propiedades de (i) controlabilidad y (ii) observabilidad. Solución: Para ambos casos, verificamos las condiciones necesarias y suficientes. Para la controlabilidad: Γ c = [ B AB ] [[ 0 = 1 ] [ ][ 0 1 ]] = [ ] ; 18 / 90
32 Ejercicio 1 Para el sistema [ 1 1 ẋ(t) = 2 1 y(t) = [ 1 Ejercicios 0 ] x(t); ] [ 0 x(t)+ 1 ] u(t); Describa sus propiedades de (i) controlabilidad y (ii) observabilidad. Solución: Para ambos casos, verificamos las condiciones necesarias y suficientes. Para la controlabilidad: Γ c = [ B AB ] [[ 0 = 1 ] [ ][ 0 1 ]] = [ La matriz de controlabilidad se encuentra de forma escalonada, se tienen dos filas linealmente independientes y por lo tanto su rango es dos, con lo que concluimos que el sistema es totalmente controlable. ] ; 18 / 90
33 Ejercicios Para el caso de controlabilidad de la salida: Γ c = [ CB CAB ] = [ 0 1 ] ; 19 / 90
34 Ejercicios Para el caso de controlabilidad de la salida: Γ c = [ CB CAB ] = [ 0 1 ] ; La matriz de controlabilidad se encuentra de forma escalonada, se tiene una fila linealmente independiente y por lo tanto su rango es uno, con lo que concluimos que la salida del sistema es totalmente controlable. 19 / 90
35 Ejercicios Para el caso de controlabilidad de la salida: Γ c = [ CB CAB ] = [ 0 1 ] ; La matriz de controlabilidad se encuentra de forma escalonada, se tiene una fila linealmente independiente y por lo tanto su rango es uno, con lo que concluimos que la salida del sistema es totalmente controlable. Para la observabilidad: [ ] Γ o = C T A T C T = [ ] ; 19 / 90
36 Ejercicios Para el caso de controlabilidad de la salida: Γ c = [ CB CAB ] = [ 0 1 ] ; La matriz de controlabilidad se encuentra de forma escalonada, se tiene una fila linealmente independiente y por lo tanto su rango es uno, con lo que concluimos que la salida del sistema es totalmente controlable. Para la observabilidad: [ ] Γ o = C T A T C T = [ La matriz de observabilidad se encuentra de forma escalonada, se tienen dos filas linealmente independientes y por lo tanto su rango es dos, con lo que concluimos que los estados del sistema son totalmente observables. ] ; 19 / 90
37 Ejercicios Ejercicio 2 Para el sistema [ 1 1 ẋ(t) = 0 1 ] [ 1 x(t)+ 0 ] u(t); y(t) = [ 0 1 ] x(t); Describa sus propiedades de (i) controlabilidad y (ii) observabilidad. 20 / 90
38 Ejercicios Ejercicio 2 Para el sistema [ 1 1 ẋ(t) = 0 1 ] [ 1 x(t)+ 0 ] u(t); y(t) = [ 0 1 ] x(t); Describa sus propiedades de (i) controlabilidad y (ii) observabilidad. Solución: Para ambos casos, verificamos las condiciones necesarias y suficientes. Para la controlabilidad: Γ c = [ B AB ] = [ ] ; 20 / 90
39 Ejercicios Ejercicio 2 Para el sistema [ 1 1 ẋ(t) = 0 1 ] [ 1 x(t)+ 0 ] u(t); y(t) = [ 0 1 ] x(t); Describa sus propiedades de (i) controlabilidad y (ii) observabilidad. Solución: Para ambos casos, verificamos las condiciones necesarias y suficientes. Para la controlabilidad: Γ c = [ B AB ] = [ La matriz de controlabilidad tiene rango uno, por lo que concluimos que el sistema no es completamente controlable al tener dos estados. Sin embargo, el sistema es estabilizable ya que su estado no controlable es estable. ] ; 20 / 90
40 Ejercicios Para el caso de controlabilidad de la salida: Γ c = [ CB CAB ] = [ 0 0 ] ; 21 / 90
41 Ejercicios Para el caso de controlabilidad de la salida: Γ c = [ CB CAB ] = [ 0 0 ] ; La matriz de controlabilidad es nula, y por lo tanto su rango es cero, con lo que concluimos que la salida del sistema es no es controlable controlable. 21 / 90
42 Ejercicios Para el caso de controlabilidad de la salida: Γ c = [ CB CAB ] = [ 0 0 ] ; La matriz de controlabilidad es nula, y por lo tanto su rango es cero, con lo que concluimos que la salida del sistema es no es controlable controlable. Para la observabilidad: [ Γ o = C T A T C T ] = [ ] ; 21 / 90
43 Ejercicios Para el caso de controlabilidad de la salida: Γ c = [ CB CAB ] = [ 0 0 ] ; La matriz de controlabilidad es nula, y por lo tanto su rango es cero, con lo que concluimos que la salida del sistema es no es controlable controlable. Para la observabilidad: [ Γ o = C T A T C T ] = [ ] ; La matriz de observabilidad es de rango uno, con lo que concluimos que el sistema no es totalmente observable. También se ve que el sistema tampoco es detectable ya que no es posible determinar el valor del estado inestable a partir de la salida. 21 / 90
44 Formas canónicas Como se ha mencionado anteriormente existen muchos métodos para la obtención de la representación en espacio de estados de un sistema. Para el caso de sistemas SISO se pueden construir formas preestablecidas en espacio de estados dependiendo de la elección de las variables de estado. 22 / 90
45 Formas canónicas Como se ha mencionado anteriormente existen muchos métodos para la obtención de la representación en espacio de estados de un sistema. Para el caso de sistemas SISO se pueden construir formas preestablecidas en espacio de estados dependiendo de la elección de las variables de estado. Esto es particularmente útil para obtener una representación que: garantice la controlabilidad completa de los estados; garantice la observabilidad compelta de los estados; garantice el desacoplo total o parcial de los estados. 22 / 90
46 Formas canónicas Como se ha mencionado anteriormente existen muchos métodos para la obtención de la representación en espacio de estados de un sistema. Para el caso de sistemas SISO se pueden construir formas preestablecidas en espacio de estados dependiendo de la elección de las variables de estado. Esto es particularmente útil para obtener una representación que: garantice la controlabilidad completa de los estados; garantice la observabilidad compelta de los estados; garantice el desacoplo total o parcial de los estados. Estas formas predeterminadas reciben el nombre de: forma canónica controlable; forma canónica observable; y forma canónica de Jordan, cuyo caso particular es la forma canónica diagonal. 22 / 90
47 Forma canónica controlable La forma canónica controlable es la forma típica de representar una ecuación diferencial de orden n puesto que las variables de estado se obtienen de una forma natural. Considere la siguiente ecuación diferencial d n y(t) dt n + a 0 d n 1 y(t) dt n a n 1 dy(t) dt b 0 d n u(t) dt n + a n = + b 1 d n 1 u(t) dt n b n 1 du(t) dt + b n por facilidad y correspondencia considere también su representación en función de transferencia, Y(s) U(s) = b 0s n + b 1 s n b n 1 s + b n s n + a 1 s n a n 1 s+a n. 23 / 90
48 Forma canónica controlable En la forma canónica controlable los bloques de los integradores están unidos uno detrás del otro, por lo que los estados se escogen integrándolos en serie. Esto es, x 1 = y; x 2 = ẋ 1 = ẏ; x 3 = ẋ 2 = ÿ;... x n = ẋ n 1 ; Lo cual en espacio de estados toma la siguiente forma: ẋ(t) = x(t) a n a n 1 a n 2... a u(t); y(t) = [ b n a n b 0 b n 1 a n 1 b 0... b 1 a 1 b 0 ] x(t)+b0 u(t). 24 / 90
49 Forma canónica observable La estructura interna de la forma canónica observable es diferente a la de la llamada forma canónica controlable. Se obtiene aplicando el método de la programación anidada (se empieza definiendo una variable de salida y recursivamente se obtienen relaciones en función de las demás variables de estado en función de las derivadas de la salida). Las ecuaciones de estado resultantes son: a n a n 1 ẋ(t) = x(t) a 1 y(t) = [ ] x(t)+b 0 u(t). b n a n b 0 b n 1 a n 1 b 0. b 1 a 1 b 0 u(t); 25 / 90
50 Forma canónica de Jordan La forma canónica de Jordan se puede obtener aplicando una expansión en fracciones parciales de la función de transferencia. Asumiendo que el sistema posee n raíces distintas: Y(s) U(s) = b 0 + c 1 s p 1 + c 2 s p c n s p n. Las ecuaciones de estado resultantes son: p p ẋ(t) = x(t) p n y(t) = [ c 1 c 2... c n ] x(t)+b0 u(t). u(t); 26 / 90
51 Forma canónica de Jordan Si el sistema tiene raíces repetidas es difícil saber a simple vista si el sistema tiene una forma diagonal o no. Lo que se hace es encontrar una representación de estados genérica ẋ(t) = Ax(t)+Bu(t); y(t) = Cx(t)+Du(t); y hacer un cambio de variable de estados x(t) = Pz(t) donde P es una matriz de transformación lineal construida con los vectores propios de A. Si no es posible encontrar los n vectores propios necesarios para encontrar P tal que diagonalize A; los vectores propios encontrados se completan con vectores propios generalizados, en cuyo caso el sistema será diagonal por bloques llamado forma de Jordan. Quedando el sistema redefinido como: ż(t) = P 1 APz(t)+P 1 Bu(t); y(t) = CPz(t)+Du(t). 27 / 90
52 Ejercicio Ejercicio 3 Determine la formas canónica controlable, observable y de Jordan del siguiente sistema G(s) = s + 3 s 2 + 3s + 2 ; 28 / 90
53 Ejercicio 3 Ejercicio Determine la formas canónica controlable, observable y de Jordan del siguiente sistema G(s) = s + 3 s 2 + 3s + 2 ; Solución: Para obtener la forma canónica controlable simplemente se sustituyen los valores en la forma general, por lo que la representación en espacio de estados queda, [ 0 1 ẋ(t) = 2 3 y(t) = [ 3 1 ] x(t). ] [ 0 x(t)+ 1 ] u(t); 28 / 90
54 Ejercicio De la misma forma, para obtener la forma canónica observable simplemente se sustituyen los valores en la forma general, por lo que la representación en espacio de estados queda, [ ] [ ] ẋ(t) = x(t)+ u(t); y(t) = [ 0 1 ] x(t). 29 / 90
55 Ejercicio De la misma forma, para obtener la forma canónica observable simplemente se sustituyen los valores en la forma general, por lo que la representación en espacio de estados queda, [ ] [ ] ẋ(t) = x(t)+ u(t); y(t) = [ 0 1 ] x(t). Para la forma de Jordan verificamos las raíces del numerador, que son p 1 = 1 y p 2 = 2; por lo que el sistema tiene una representación de forma diagonal. Expandiendo en fracciones parciales G(s) = s+3 s 2 + 3s+2 = 2 s+1 1 s+2 ; Quedando la representación en espacio de estados [ ] [ ] ẋ(t) = x(t)+ u(t); y(t) = [ ] x(t). 29 / 90
56 Diseño de controladores Muchas de las plantas industriales tienen diversas variables para ser controladas y diversas variables para ser manipuladas y, en general, las variables se encuentran acopladas. 30 / 90
57 Diseño de controladores Muchas de las plantas industriales tienen diversas variables para ser controladas y diversas variables para ser manipuladas y, en general, las variables se encuentran acopladas. En el enfoque de control clásico lo que se hace es diseñar compensadores que desacoplen las variables para suprimir las interacciones entre ellas y posteriormente diseñar múltiples controladores monovariables. Para esto, primero requiere de cómo relacionar las variables de entradas y salidas; esto es, determinar cuál variable de entrada estará asociada a cierta variable de salida y además de que la planta debe de tener el mismo número de entradas que de salidas. 30 / 90
58 Diseño de controladores Muchas de las plantas industriales tienen diversas variables para ser controladas y diversas variables para ser manipuladas y, en general, las variables se encuentran acopladas. En el enfoque de control clásico lo que se hace es diseñar compensadores que desacoplen las variables para suprimir las interacciones entre ellas y posteriormente diseñar múltiples controladores monovariables. Para esto, primero requiere de cómo relacionar las variables de entradas y salidas; esto es, determinar cuál variable de entrada estará asociada a cierta variable de salida y además de que la planta debe de tener el mismo número de entradas que de salidas. Una de las ventajas del enfoque en espacio de estados es que los procesos multivariables pueden ser tratados de forma natural, y el aumento de variables no cambia la forma de diseñar los controladores. 30 / 90
59 Control por retroalimentación de estados En esta sección nos enfocaremos al problema de regulación de la salida. En regulación, el objetivo radica en hacer que la(s) variable(s) a ser controlada(s) llegue(n) hasta un valor deseado y permanezcan en ese valor. 31 / 90
60 Control por retroalimentación de estados En esta sección nos enfocaremos al problema de regulación de la salida. En regulación, el objetivo radica en hacer que la(s) variable(s) a ser controlada(s) llegue(n) hasta un valor deseado y permanezcan en ese valor. El control clásico-convencional de regulación por retroalimentación con ganancia K se muestra en el siguiente esquema, r(t) + - u(t) Planta y(t) K 31 / 90
61 Control por retroalimentación de estados En esta sección nos enfocaremos al problema de regulación de la salida. En regulación, el objetivo radica en hacer que la(s) variable(s) a ser controlada(s) llegue(n) hasta un valor deseado y permanezcan en ese valor. El control clásico-convencional de regulación por retroalimentación con ganancia K se muestra en el siguiente esquema, r(t) + - u(t) Planta y(t) K Donde la ley de control es u(t) = r(t) Ky(t). Dado que la señal r(t) no cambia, es posible considerarla como referencia de todas las demás señales, esto es, consideraremos r(t) = 0; la ley de control se reduce a u(t) = Ky(t). 31 / 90
62 Control por retroalimentación de estados Usando variables de estados la referencia r(t) representa un punto en el espacio n-dimensional de estados y mediante alguna transformación se puede hacer un cambio de coordenadas poniendo a r(t) en el origen sin pérdida de generalidad. 32 / 90
63 Control por retroalimentación de estados Usando variables de estados la referencia r(t) representa un punto en el espacio n-dimensional de estados y mediante alguna transformación se puede hacer un cambio de coordenadas poniendo a r(t) en el origen sin pérdida de generalidad. El control por retroalimentación de estados es análogo a la regulación por retroalimentación convencional, con la excepción de que lo que se retroalimenta no es la salida y(t) propiamente, sino el estado x(t). 32 / 90
64 Control por retroalimentación de estados Usando variables de estados la referencia r(t) representa un punto en el espacio n-dimensional de estados y mediante alguna transformación se puede hacer un cambio de coordenadas poniendo a r(t) en el origen sin pérdida de generalidad. El control por retroalimentación de estados es análogo a la regulación por retroalimentación convencional, con la excepción de que lo que se retroalimenta no es la salida y(t) propiamente, sino el estado x(t). Ley de control para regulación por retroalimentación de estados Para el sistema ẋ(t) = Ax(t) + Bu(t), y(t) = Cx(t), x R n, u R m, y R l, la ley de control para regulación por retroalimentación de estados es, con K R m 1. u(t) = Kx(t), 32 / 90
65 Control por retroalimentación de estados El esquema para el control por retroalimentación de estados se muestra en la siguiente figura. r(t)=0 + - u(t) B + + x(t) dt x(t) C y(t) A K 33 / 90
66 Control por retroalimentación de estados El esquema para el control por retroalimentación de estados se muestra en la siguiente figura. r(t)=0 + - u(t) B + + x(t) dt x(t) C y(t) A K Note que se requiere de que el vector de estados esté completamente disponible, por lo que en el mejor de los casos la matriz de salida C será una matriz identidad y así se asumirá durante esta sección, por lo que y(t) = x(t). Sin embargo, lo más común es que la(s) salidas sea(n) una combinación lineal del(de los) estado(s). 33 / 90
67 Control por retroalimentación de estados Con esta nueva entrada u(t) = Kx(t) la nueva dinámica del sistema en espacio de estados es 34 / 90
68 Control por retroalimentación de estados Con esta nueva entrada u(t) = Kx(t) la nueva dinámica del sistema en espacio de estados es ẋ(t) = Ax(t)+Bu(t); ẋ(t) = Ax(t) BKx(t); ẋ(t) = (A BK) x(t); el sistema se vuelve un sistema autónomo cuya nueva matriz de transición de estados es (A BK). 34 / 90
69 Control por retroalimentación de estados Con esta nueva entrada u(t) = Kx(t) la nueva dinámica del sistema en espacio de estados es ẋ(t) = Ax(t)+Bu(t); ẋ(t) = Ax(t) BKx(t); ẋ(t) = (A BK) x(t); el sistema se vuelve un sistema autónomo cuya nueva matriz de transición de estados es (A BK). Si se elige la matriz K de manera adecuada, la matriz (A BK) se convierte en una matriz que producirá estabilidad de manera asintótica y será factible lograr que x(t) tienda al origen conforme aumenta el tiempo. Los valores propios de la matriz (A BK) determinarán la evolución en el tiempo del sistema. Si éstos tienen parte real negativa entonces x(t) tenderá al origen. 34 / 90
70 Control por retroalimentación de estados Observaciones Este esquema de control necesita que el vector de estados esté totalmente disponible a la salida o pueda ser reconstruido de alguna forma a través de la salida. 2 Utilizando alguna otra técnica, no con la de ubicación de polos. 35 / 90
71 Control por retroalimentación de estados Observaciones Este esquema de control necesita que el vector de estados esté totalmente disponible a la salida o pueda ser reconstruido de alguna forma a través de la salida. Los valores propios de la matriz (A BK) son los valores propios del sistema en lazo cerrado. 2 Utilizando alguna otra técnica, no con la de ubicación de polos. 35 / 90
72 Control por retroalimentación de estados Observaciones Este esquema de control necesita que el vector de estados esté totalmente disponible a la salida o pueda ser reconstruido de alguna forma a través de la salida. Los valores propios de la matriz (A BK) son los valores propios del sistema en lazo cerrado. La controlabilidad completa del sistema es una condición necesaria y suficiente para poder ubicar los valores propios de lazo cerrado del regulador de forma arbitraria. 2 Utilizando alguna otra técnica, no con la de ubicación de polos. 35 / 90
73 Control por retroalimentación de estados Observaciones Este esquema de control necesita que el vector de estados esté totalmente disponible a la salida o pueda ser reconstruido de alguna forma a través de la salida. Los valores propios de la matriz (A BK) son los valores propios del sistema en lazo cerrado. La controlabilidad completa del sistema es una condición necesaria y suficiente para poder ubicar los valores propios de lazo cerrado del regulador de forma arbitraria. Sin embargo, para poder regular al sistema 2 es suficiente con que el sistema sea estabilizable, puesto que esta propiedad garantiza que el subespacio no controlable es estable y los estados que no se pueden controlar convergerán al origen de manera natural. 2 Utilizando alguna otra técnica, no con la de ubicación de polos. 35 / 90
74 Control por retroalimentación de estados Es importante de hacer notar que en el control clásico se diseñan compensadores para que el sistema tenga un determinado factor de amortiguamiento ζ y una frecuencia natural no amortiguada ω n determinada asumiendo que los efectos de los polos no dominantes son despreciables. 36 / 90
75 Control por retroalimentación de estados Es importante de hacer notar que en el control clásico se diseñan compensadores para que el sistema tenga un determinado factor de amortiguamiento ζ y una frecuencia natural no amortiguada ω n determinada asumiendo que los efectos de los polos no dominantes son despreciables. Mientras que con el control por retroalimentación de estados utilizando la técnica llamada asignación de polos o posicionamiento de polos se especifican todos y cada uno de las raíces del lazo cerrado. 36 / 90
76 Control por retroalimentación de estados Antes de mencionar los pasos para el cálculo de la matriz K se hacen algunas definiciones. Sea T la matriz que de transformación que, mediante una nueva definición de los estados z(t) = Tx(t), convierte al sistema en su forma controlable, definida por T = Γ c W; donde Γ c es la matriz de controlabilidad del sistema y a n 1 a n 2... a 1 1 a n 2 a n W = ; a donde los coeficientes a i se obtienen del polinomio característico de la matriz A: det(λi A) = λ n + a 1 λ n a n 1 λ+a n. 37 / 90
77 Control por retroalimentación de estados Pasos para el cálculo de la matriz de retroalimentación K 1 Verificar la condición de controlabilidad del sistema. 38 / 90
78 Control por retroalimentación de estados Pasos para el cálculo de la matriz de retroalimentación K 1 Verificar la condición de controlabilidad del sistema. 2 Determinar el polinomio característico de A. 38 / 90
79 Control por retroalimentación de estados Pasos para el cálculo de la matriz de retroalimentación K 1 Verificar la condición de controlabilidad del sistema. 2 Determinar el polinomio característico de A. 3 Determinar la matriz de transformación T. 38 / 90
80 Control por retroalimentación de estados Pasos para el cálculo de la matriz de retroalimentación K 1 Verificar la condición de controlabilidad del sistema. 2 Determinar el polinomio característico de A. 3 Determinar la matriz de transformación T. 4 Usando los valores propios deseados, escribir el polinomio característico que se busca como λ n +α 1 λ n α n 1 λ+α n. 38 / 90
81 Control por retroalimentación de estados Pasos para el cálculo de la matriz de retroalimentación K 1 Verificar la condición de controlabilidad del sistema. 2 Determinar el polinomio característico de A. 3 Determinar la matriz de transformación T. 4 Usando los valores propios deseados, escribir el polinomio característico que se busca como λ n +α 1 λ n α n 1 λ+α n. 5 El valor de K se puede determinar a partir de la siguiente ecuación K = [ α n a n α n 1 a n 1... α 1 a 1 ] T / 90
82 Control por retroalimentación de estados Note que, cuando el orden del sistema no es muy grande, la sustitución directa de K en el polinomio característico deseado puede ser más simple det(λi A+BK) = (λ λ 1 )(λ λ 2 )...(λ λ n ), donde λ i son los i valores propios deseados del lazo cerrado. 39 / 90
83 Control por retroalimentación de estados Note que, cuando el orden del sistema no es muy grande, la sustitución directa de K en el polinomio característico deseado puede ser más simple det(λi A+BK) = (λ λ 1 )(λ λ 2 )...(λ λ n ), donde λ i son los i valores propios deseados del lazo cerrado. Dado que ambos miembros de esta ecuación característica son polinomios en λ, igualando los coeficientes de las potencias iguales de λ en ambos miembros, es posible determinar los valores de K. Este método no es muy conveniente para cuando el orden del sistema es grande ya que se vuelve muy pesado. 39 / 90
84 Control por retroalimentación de estados Note que, cuando el orden del sistema no es muy grande, la sustitución directa de K en el polinomio característico deseado puede ser más simple det(λi A+BK) = (λ λ 1 )(λ λ 2 )...(λ λ n ), donde λ i son los i valores propios deseados del lazo cerrado. Dado que ambos miembros de esta ecuación característica son polinomios en λ, igualando los coeficientes de las potencias iguales de λ en ambos miembros, es posible determinar los valores de K. Este método no es muy conveniente para cuando el orden del sistema es grande ya que se vuelve muy pesado. Es de hacer notar que existen otros métodos para la determinación de K, uno de los más difundidos es utilizando la fórmula de Ackerman. Sin embargo, este método no será tratado en este curso. 39 / 90
85 Control por retroalimentación de estados Comentarios Es importante señalar que K no es la única para el sistema determinado, sino que depende de las ubicaciones de los valores propios en lazo cerrado deseados (los cuales determinan la velocidad y el amortiguamiento de la respuesta) seleccionados. 40 / 90
86 Control por retroalimentación de estados Comentarios Es importante señalar que K no es la única para el sistema determinado, sino que depende de las ubicaciones de los valores propios en lazo cerrado deseados (los cuales determinan la velocidad y el amortiguamiento de la respuesta) seleccionados. En sistemas multivariables K no es única para un determinado conjunto de valores propios en lazo cerrado deseados. 40 / 90
87 Control por retroalimentación de estados Comentarios Es importante señalar que K no es la única para el sistema determinado, sino que depende de las ubicaciones de los valores propios en lazo cerrado deseados (los cuales determinan la velocidad y el amortiguamiento de la respuesta) seleccionados. En sistemas multivariables K no es única para un determinado conjunto de valores propios en lazo cerrado deseados. Observe que la selección de los valores propios en un lazo cerrado deseados, o de la ecuación característica deseada, es un compromiso entre la rapidez de la respuesta del vector de error y la sensibilidad ante perturbaciones y el ruido en la medición. Es decir, si incrementamos la velocidad de respuesta de error, por lo general se incrementan los procesos adversos de las perturbaciones y el ruido en la medición. 40 / 90
88 Ejercicios Ejercicio 4 Diseñe un controlador por retroalimentación de estados que estabilice en el origen al sistema definido por ẋ(t) = Ax(t)+Bu(t) con [ ] [ ] A = ; B = ; Ubique los valores propios del sistema en lazo cerrado en λ 1 = 4 y en λ 2 = 5. Asuma el vector de estados completamente medible. 41 / 90
89 Ejercicios Solución: En este caso, los valores propios del sistema en lazo abierto son λ 1 = 1 y λ 2 = 1 por lo que el sistema es inestable y requiere de estabilización. Como primer paso, se verifica la matriz de controlabilidad, [ ] 0 1 Γ o = ; 1 1 cuyo rango es 2 y por tanto completamente controlable. El polinomio característico deseado es p(λ) = (λ+4)(λ+5) = λ 2 + 9λ+20. Se requiere calcular una matriz de ganancias de retroalimentación K = [ k 1 k 2 ]. La matriz de transferencia de estados del lazo cerrado es (A BK) y su polinomio característico es det(λi A+BK) = λ 2 + k 2 λ+(k 2 + k 1 1). 42 / 90
90 Ejercicios Se pueden obtener los valores de k 1 y k 2 igualando los polinomios λ 2 + 9λ+20 = λ 2 + k 2 λ+(k 2 + k 1 1); de esta forma, k 1 = 12 y k 2 = 9. La ley de control que estabiliza al sistema es: u(t) = [ 12 9 ] x(t); Para efectos de comprobación la matriz de transición de estados en lazo cerrado (A BK) queda [ ] 1 1 A BK = ; 12 8 la cual tiene los valores propios en las ubicaciones deseadas. 43 / 90
91 Ejercicios Finalmente se simula la ley de control para ciertas condiciones iniciales del vector de estados. Respuesta a las condiciones iniciales del regulador por realimentación de estados 4 x 1 Amplitud 2 0 x Tiempo (s) 10 5 u(t) Tiempo (s) 44 / 90
92 Ejercicios Ejercicio 5 Diseñe un controlador por retroalimentación de estados que estabilice en el origen al sistema definido por ẋ(t) = Ax(t)+Bu(t) con A = ; B = 6 2 ; Ubique los valores propios del sistema en lazo cerrado en λ 1 = 6 y enλ 23 = 2±3j. Asuma el vector de estados completamente medible. 45 / 90
93 Ejercicios Ejercicio 5 Diseñe un controlador por retroalimentación de estados que estabilice en el origen al sistema definido por ẋ(t) = Ax(t)+Bu(t) con A = ; B = 6 2 ; Ubique los valores propios del sistema en lazo cerrado en λ 1 = 6 y enλ 23 = 2±3j. Asuma el vector de estados completamente medible. Solución: En este caso, los valores propios del sistema en lazo abierto son λ 12 = ±2 y λ 3 = 1 por lo que el sistema es inestable y requiere de estabilización. 45 / 90
94 Ejercicios Como primer paso, se verifica la propiedad de controlabilidad, Γ o = ; La matriz Γ o es de rango 3 (no se muestra la comprobación). Se calcula la ecuación característica, por lo que det(λi A) = λ 3 + a 1 λ 2 + a 2 λ+a 3 = λ 3 +λ 2 4λ 4; Se calcula la matriz de transformación T: T = Γ o W = = El polinomio característico deseado es p(λ) = (λ+2+3j)(λ+2 3j)(λ+6) = (λ 2 + 4λ+13)(λ+6); = λ 3 +α 1 λ 2 +α 2 λ+α 3 = λ λ λ+78; 46 / 90
95 Posteriormente se calcula K, Ejercicios K = [ α 3 a 3 α 2 a 2 α 1 a 1 ] T 1 ; = [ ] T 1 ; = [ ]. La ley de control que estabiliza al sistema es: u(t) = [ ] x(t); Para efectos de comprobación la matriz de transición de estados en lazo cerrado (A BK) queda A BK = ; la cual tiene los valores propios en las ubicaciones deseadas. 47 / 90
96 Ejercicios Finalmente se simula la ley de control para ciertas condiciones iniciales del vector de estados. Respuesta a las condiciones iniciales del regulador por realimentación de estado 5 Amplitud x 1 x 2 x Tiempo (s) 10 0 u(t) Tiempo (s) 48 / 90
97 Regulador lineal cuadrático (LQR) El regulador lineal cuadrático (LQR) es un tipo de controlador (regulador de retroalimentación de estados) que pertenece a la familia de los controladores óptimos y tiene la ventaja de que permite diseñar la matriz de retroalimentación K de una manera un poco más sistemática y no necesita la total controlabilidad del sistema, solamente que el sistema sea estabilizable. 49 / 90
98 Regulador lineal cuadrático (LQR) El regulador lineal cuadrático (LQR) es un tipo de controlador (regulador de retroalimentación de estados) que pertenece a la familia de los controladores óptimos y tiene la ventaja de que permite diseñar la matriz de retroalimentación K de una manera un poco más sistemática y no necesita la total controlabilidad del sistema, solamente que el sistema sea estabilizable. Regulador lineal cuadrático (LQR) El regulador lineal cuadrático está definido, para el sistema ẋ(t) = Ax(t) + Bu(t), como la ley de control u(t) = Kx(t) que minimiza el índice de desempeño (función de costo): J = 0 x(t) T Qx(t)+u(t) T Ru(t)dt; donde Q R n n, R R m m son las matrices de peso del estado y la entrada respectivamente, siendo ambas definidas positivas, n es el orden del sistema y m el número de entradas al sistema. 49 / 90
99 Regulador lineal cuadrático (LQR) Para resolver el problema de minimización, se asume que el sistema en lazo cerrado será estable. Sustituyendo la ley de control, ẋ(t) = Ax(t) BKx(t) = (A BK)x(t); J = = 0 0 x(t) T Qx(t)+x(t) T K T RKx(t)dt; x(t) T (Q+K T RK)x(t)dt; Haciendo x(t) T (Q + K T RK)x(t) = d dx (x(t)t Px(t)) con P = P T > 0 (para hacer J decreciente), x(t) T (Q+K T RK)x(t) = ẋ(t) T Px(t) x(t) T Pẋ(t); x(t) T (Q+K T RK)x(t) = x(t) T [ (A BK) T P+P(A BK) ] x(t); (Q+K T RK) = (A BK) T P+P(A BK); Por lo que si (A BK) es estable existe una matriz P = P T > 0 que satisfaga esta ecuación. 50 / 90
100 Regulador lineal cuadrático (LQR) El problema se convierte entonces, en determinar los valores de P para verificar que sea definida positiva y se cumpla la condición (existe más de una solución si y sólo si el sistema es estable). La función de costo puede ser evaluada como, J = x(t) T (Q+K T RK)x(t)dt = x(t) T Px(t) 0 = x( ) T Px( )+x(0) T Px(0); Como se está asumiendo que el sistema es estable x( ) 0, la función de costo puede ser obtenida en términos de las condiciones iniciales de los estados: J = x(0) T Px(0). Para obtener la solución del problema de control, se reescribe R = T T T con T no singular, esto es posible ya que R>0: (A T K T B T )P+P(A BK)+Q+K T T T TK = 0; 0 ; 51 / 90
101 Regulador lineal cuadrático (LQR) Manipulando algebraicamente, [ ( A T P+PA+ TK T T) ] 1 T [ B T P TK ( T T) ] 1 B T P PBR 1 B T P+Q = 0; 52 / 90
102 Regulador lineal cuadrático (LQR) Manipulando algebraicamente, [ ( A T P+PA+ TK T T) ] 1 T [ B T P TK ( T T) ] 1 B T P PBR 1 B T P+Q = 0; La minimización con respecto a K requiere la minimización de ( x(t) [TK T T T) ] 1 T [ ( B T P TK T T) ] 1 B T P x(t); 52 / 90
103 Regulador lineal cuadrático (LQR) Manipulando algebraicamente, [ ( A T P+PA+ TK T T) ] 1 T [ B T P TK ( T T) ] 1 B T P PBR 1 B T P+Q = 0; La minimización con respecto a K requiere la minimización de ( x(t) [TK T T T) ] 1 T [ ( B T P TK T T) ] 1 B T P x(t); Como la expresión es cuadrática, el mínimo ocurre en el origen, [ ( TK T T) ] 1 T [ ( B T P TK T T) ] 1 B T P = 0; ( TK = T T) 1 B T P; K =R 1 B T P; donde ( ) indica que el valor de ( ) es el óptimo. 52 / 90
104 Regulador lineal cuadrático (LQR) Ecuación de Riccati La ecuación que debe de satisfacer P = P T > 0, utilizando u (t) = K x(t) = R 1 B T Px(t) se reduce a Llamada ecuación de Riccati. A T P+ PA PBR 1 B T P+Q = 0; 53 / 90
105 Regulador lineal cuadrático (LQR) Ecuación de Riccati La ecuación que debe de satisfacer P = P T > 0, utilizando u (t) = K x(t) = R 1 B T Px(t) se reduce a Llamada ecuación de Riccati. A T P+ PA PBR 1 B T P+Q = 0; Pasos para el cálculo de la matriz de retroalimentación K (LQR) 53 / 90
106 Regulador lineal cuadrático (LQR) Ecuación de Riccati La ecuación que debe de satisfacer P = P T > 0, utilizando u (t) = K x(t) = R 1 B T Px(t) se reduce a Llamada ecuación de Riccati. A T P+ PA PBR 1 B T P+Q = 0; Pasos para el cálculo de la matriz de retroalimentación K (LQR) 1 Verifique que el sistema sea estabilizable. 53 / 90
107 Regulador lineal cuadrático (LQR) Ecuación de Riccati La ecuación que debe de satisfacer P = P T > 0, utilizando u (t) = K x(t) = R 1 B T Px(t) se reduce a Llamada ecuación de Riccati. A T P+ PA PBR 1 B T P+Q = 0; Pasos para el cálculo de la matriz de retroalimentación K (LQR) 1 Verifique que el sistema sea estabilizable. 2 Resuelva la ecuación de Riccati para P. Si existe P > 0 podrá ser posible encontrar K tal que u (t) = K x(t) estabilize al sistema. 53 / 90
108 Regulador lineal cuadrático (LQR) Ecuación de Riccati La ecuación que debe de satisfacer P = P T > 0, utilizando u (t) = K x(t) = R 1 B T Px(t) se reduce a Llamada ecuación de Riccati. A T P+ PA PBR 1 B T P+Q = 0; Pasos para el cálculo de la matriz de retroalimentación K (LQR) 1 Verifique que el sistema sea estabilizable. 2 Resuelva la ecuación de Riccati para P. Si existe P > 0 podrá ser posible encontrar K tal que u (t) = K x(t) estabilize al sistema. 3 Calcule la ley de control de u (t) = K x(t) = R 1 B T Px(t). 53 / 90
Diseño en espacio de estados
 Diseño en espacio de estados Dr. Guillermo Valencia-Palomo gvalencia@ith.mx Instituto Tecnológico de Hermosillo. División de estudios de posgrado e investigación. Octubre, 2011. 1 Introducción Contenido
Diseño en espacio de estados Dr. Guillermo Valencia-Palomo gvalencia@ith.mx Instituto Tecnológico de Hermosillo. División de estudios de posgrado e investigación. Octubre, 2011. 1 Introducción Contenido
Control Moderno. Ene.-Jun Diseño de controlador con referencia a la entrada, servosistemas. Dr. Rodolfo Salinas. mayo 2007
 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Diseño de controlador con referencia a la entrada, servosistemas Dr. Rodolfo Salinas mayo 2007
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Diseño de controlador con referencia a la entrada, servosistemas Dr. Rodolfo Salinas mayo 2007
Controlabilidad completa del estado para sistemas en tiempo continuo
 Capítulo 11: CONTROLABILIDAD Y OBSERVABILIDAD Se dice que un sistema es controlable en el instante t0 si es posible llevarlo de cualquier estado inicial x(t0) a cualquier otro estado, empleando un vector
Capítulo 11: CONTROLABILIDAD Y OBSERVABILIDAD Se dice que un sistema es controlable en el instante t0 si es posible llevarlo de cualquier estado inicial x(t0) a cualquier otro estado, empleando un vector
Sistemas de Control lineal óptimo con realimentación de estado
 Capítulo 5 Sistemas de Control lineal óptimo con realimentación de estado La principal restricción de este sistema de control es suponer que se puede medir en todo instante de tiempo el estado completo
Capítulo 5 Sistemas de Control lineal óptimo con realimentación de estado La principal restricción de este sistema de control es suponer que se puede medir en todo instante de tiempo el estado completo
1 Control Óptimo. 1.1 Introducción Problema típico de control óptimo
 1 Control Óptimo 1.1 Introducción El control óptimo es una rama del control moderno que se relaciona con el diseño de controladores para sistemas dinámicos tal que se minimice una función de medición que
1 Control Óptimo 1.1 Introducción El control óptimo es una rama del control moderno que se relaciona con el diseño de controladores para sistemas dinámicos tal que se minimice una función de medición que
Parte I. Diseño utilizando Variables de Estado
 Parte I. Diseño utilizando Variables de Estado El control de un proceso representado a través de variables de estado nos proporciona la ventaja de que se tendrán a todas las variables del proceso cumpliendo
Parte I. Diseño utilizando Variables de Estado El control de un proceso representado a través de variables de estado nos proporciona la ventaja de que se tendrán a todas las variables del proceso cumpliendo
Control Moderno. Ene.-Jun Observabilidad y Observadores de Estado. Dr. Rodolfo Salinas. mayo 2007
 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Observabilidad y Observadores de Estado Dr. Rodolfo Salinas mayo 2007 Control Moderno N1 mayo
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Observabilidad y Observadores de Estado Dr. Rodolfo Salinas mayo 2007 Control Moderno N1 mayo
2.1 Descripción en espacio de estado de sistemas dinámicos
 2 Análisis de sistemas lineales 2.1 Descripción en espacio de estado de sistemas dinámicos El objetivo de este capítulo es formular una teoría general de describir los sistemas dinámicos en funcion de
2 Análisis de sistemas lineales 2.1 Descripción en espacio de estado de sistemas dinámicos El objetivo de este capítulo es formular una teoría general de describir los sistemas dinámicos en funcion de
CAPÍTULO. Control Proporcional Integral Generalizado. II.1 Introducción. II. Control Proporcional Integral Generalizado
 CAPÍTULO II Control Proporcional Integral Generalizado II.1 Introducción El uso de observadores en electrónica de potencia no es una práctica común debido al incremento en el costo del circuito; es decir,
CAPÍTULO II Control Proporcional Integral Generalizado II.1 Introducción El uso de observadores en electrónica de potencia no es una práctica común debido al incremento en el costo del circuito; es decir,
Teoría de Control Moderna
 1! Modelos en Variables de Estado Juan Antonio Hernández Tamames, Susana Borromeo Curso 2014-2015 Teoría de Control Moderna 2! Teoría de control clásica basada en la relación entrada-salida o función de
1! Modelos en Variables de Estado Juan Antonio Hernández Tamames, Susana Borromeo Curso 2014-2015 Teoría de Control Moderna 2! Teoría de control clásica basada en la relación entrada-salida o función de
Descomposiciones Canónicas
 Observabilidad p. 1/12 Descomposiciones Canónicas Las descomposiciones canónicas de las ecuaciones de estado permiten establecer la relación entre Controlabilidad, Observabilidad, y una matriz de transferencia
Observabilidad p. 1/12 Descomposiciones Canónicas Las descomposiciones canónicas de las ecuaciones de estado permiten establecer la relación entre Controlabilidad, Observabilidad, y una matriz de transferencia
Control por realimentación del estado
 Control por realimentación del estado Introducción Realimentación del estado Control de sistemas monovariables Control de sistemas multivariables U.P.M.-DISAM P. Campoy Electrónica y Regulación Introducción:
Control por realimentación del estado Introducción Realimentación del estado Control de sistemas monovariables Control de sistemas multivariables U.P.M.-DISAM P. Campoy Electrónica y Regulación Introducción:
Muestreo de sistemas continuos
 Muestreo de sistemas continuos Dr. Guillermo Valencia-Palomo gvalencia@ith.mx Instituto Tecnológico de Hermosillo. División de estudios de posgrado e investigación. Septiembre, 2. Introducción Señal muestreada
Muestreo de sistemas continuos Dr. Guillermo Valencia-Palomo gvalencia@ith.mx Instituto Tecnológico de Hermosillo. División de estudios de posgrado e investigación. Septiembre, 2. Introducción Señal muestreada
Si u y v son vectores cualquiera en W, entonces u + v esta en W. Si c es cualquier numero real y u es cualquier vector en W, entonces cu esta en W.
 Unidad 4 Espacios vectoriales reales 4.1 Subespacios Si V es un espacio vectorial y W un subconjunto no vacío de V. Entonces W es un subespacio de V si se cumplen las siguientes condiciones Si u y v son
Unidad 4 Espacios vectoriales reales 4.1 Subespacios Si V es un espacio vectorial y W un subconjunto no vacío de V. Entonces W es un subespacio de V si se cumplen las siguientes condiciones Si u y v son
Control Moderno. Ene.-Jun Diseño de controlador por retroalimentación de estado. Dr. Rodolfo Salinas. mayo 2007
 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Diseño de controlador por retroalimentación de estado Dr. Rodolfo Salinas mayo 2007 Control
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Diseño de controlador por retroalimentación de estado Dr. Rodolfo Salinas mayo 2007 Control
Control Moderno. Ene.-Jun UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN. Facultad de Ingeniería Mecánica y Eléctrica. Dr. Rodolfo Salinas.
 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 27 Dr. Rodolfo Salinas abril 27 Control Moderno N abril 27 Dr. Rodolfo Salinas Respuesta en el tiempo
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 27 Dr. Rodolfo Salinas abril 27 Control Moderno N abril 27 Dr. Rodolfo Salinas Respuesta en el tiempo
Observadores del estado
 Observadores del estado Introducción Definición Dinámica del sistema con observador monovariables multivariables U.P.M.-DISAM P. Campoy Control en el espacio de estado 1 Introducción Concepto: el observador
Observadores del estado Introducción Definición Dinámica del sistema con observador monovariables multivariables U.P.M.-DISAM P. Campoy Control en el espacio de estado 1 Introducción Concepto: el observador
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada
 Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227C) Clase 5-2 Elizabeth Villota Cerna Semestre 29 II -
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227C) Clase 5-2 Elizabeth Villota Cerna Semestre 29 II -
UNIVERSIDAD NACIONAL DEL CALLAO
 UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERIA ELECTRICA Y ELECTRONICA INSTITUTO DE INVESTIGACION DE LA FACULTAD DE INGENIERIA ELECTRICA Y ELECTRONICA INFORME FINAL DEL TEXTO TEXTO: DISEÑO DE SISTEMAS
UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERIA ELECTRICA Y ELECTRONICA INSTITUTO DE INVESTIGACION DE LA FACULTAD DE INGENIERIA ELECTRICA Y ELECTRONICA INFORME FINAL DEL TEXTO TEXTO: DISEÑO DE SISTEMAS
Comportamiento dinámico: Estabilidad
 Lección 4 Comportamiento dinámico: Estabilidad 1 Estabilidad Dos tipos de estabilidad: ẋ(t) = f(t, x(t), u(t)) Estabilidad interna: ẋ(t) = f(t, x(t)) Estabilidad externa o estabilidad BIBO (bounded input-bounded
Lección 4 Comportamiento dinámico: Estabilidad 1 Estabilidad Dos tipos de estabilidad: ẋ(t) = f(t, x(t), u(t)) Estabilidad interna: ẋ(t) = f(t, x(t)) Estabilidad externa o estabilidad BIBO (bounded input-bounded
ÁLGEBRA LINEAL. EXAMEN FINAL 18 de Enero de b) (0, 5 puntos) Estudia si la siguiente afirmación es verdadera o falsa, justificando
 ÁLGEBRA LINEAL EXAMEN FINAL 8 de Enero de Apellidos y Nombre: Duración del examen: 3 horas Publicación de notas: enero Revisión de Examen: feb Ejercicio. ( puntos a (, puntos Estudia si la siguiente afirmación
ÁLGEBRA LINEAL EXAMEN FINAL 8 de Enero de Apellidos y Nombre: Duración del examen: 3 horas Publicación de notas: enero Revisión de Examen: feb Ejercicio. ( puntos a (, puntos Estudia si la siguiente afirmación
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS
 Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
donde,, es controlable si y solo si la matriz de controlabilidad tiene rango,
 TEORÍA DE CONTROL Tema 8. Controlabilidad y Observabilidad La controlabilidad y la observabilidad son dos conceptos desarrollados para la representación de sistemas en espacio de estado, estos permiten
TEORÍA DE CONTROL Tema 8. Controlabilidad y Observabilidad La controlabilidad y la observabilidad son dos conceptos desarrollados para la representación de sistemas en espacio de estado, estos permiten
EJERCICIOS RESUELTOS Y PROPUESTOS
 UNIVERSIDAD NACIONAL DE INGENIERÍA Facultad de Ingeniería Mecánica MT 227 Control Moderno y Óptimo EJERCICIOS RESUELTOS Y PROPUESTOS Estabilidad según Lyapunov (1) Un buen modelo de un niño impulsandose
UNIVERSIDAD NACIONAL DE INGENIERÍA Facultad de Ingeniería Mecánica MT 227 Control Moderno y Óptimo EJERCICIOS RESUELTOS Y PROPUESTOS Estabilidad según Lyapunov (1) Un buen modelo de un niño impulsandose
Representación en el espacio de estado. Sistemas Control Embebidos e Instrumentación Electrónica UNIVERSIDAD EAFIT
 Representación en el espacio de estado Representación en espacio de estado Control clásico El modelado y control de sistemas basado en la transformada de Laplace, es un enfoque muy sencillo y de fácil
Representación en el espacio de estado Representación en espacio de estado Control clásico El modelado y control de sistemas basado en la transformada de Laplace, es un enfoque muy sencillo y de fácil
Realimentación de Estado DSEÑO DE SSTEMAS DE Los polos del sistema en lazo cerrado se reubican mediante una matriz de ganancias K (dimensiones rxn) qu
 DSEÑO DE SSTEMAS DE Diseño en el Espacio de Estados Objetivo: Cambiar la situación de los "n" polos del sistema para cambiar su dinámica en bucle cerrado (sistema más rápido, con más o menos sobreoscilación,
DSEÑO DE SSTEMAS DE Diseño en el Espacio de Estados Objetivo: Cambiar la situación de los "n" polos del sistema para cambiar su dinámica en bucle cerrado (sistema más rápido, con más o menos sobreoscilación,
No usar por academias
 ECUACIONES DIFERENCIALES I Grupo D 1 de septiembre de 003 Apellidos: Nombre: D.N.I.: Firma: 1. Considérese la ecuación y = 1 + y x. i) Hallar su solución general. ii) Dibujar aproximadamente sus curvas
ECUACIONES DIFERENCIALES I Grupo D 1 de septiembre de 003 Apellidos: Nombre: D.N.I.: Firma: 1. Considérese la ecuación y = 1 + y x. i) Hallar su solución general. ii) Dibujar aproximadamente sus curvas
Automatización de Procesos/Sistemas de Control Ing. Biomédica e Ing. Electrónica Capitulo V Controladores PID
 Automatización de Procesos/Sistemas de Control Ing. Biomédica e Ing. Electrónica Capitulo V Controladores PID D.U. Campos-Delgado Facultad de Ciencias UASLP Enero-Junio/2014 1 CONTENIDO Motivación Estructura
Automatización de Procesos/Sistemas de Control Ing. Biomédica e Ing. Electrónica Capitulo V Controladores PID D.U. Campos-Delgado Facultad de Ciencias UASLP Enero-Junio/2014 1 CONTENIDO Motivación Estructura
Control Automático. Control con observadores de estado
 Control Automático Control con observadores de estado Contenido Observabilidad Observadores de estado sin entrada r Cálculo de la ganancia K del observador usando Ackermann Compensadores con entrada de
Control Automático Control con observadores de estado Contenido Observabilidad Observadores de estado sin entrada r Cálculo de la ganancia K del observador usando Ackermann Compensadores con entrada de
CONTROL POR REALIMENTACIÓN DE ESTADOS
 CONTROL POR REALIMENTACIÓN DE ESTADOS Fernando di Sciascio (2016) Control por Realimentación de Estados ì ï xt () = Axt () + But () í ï yt () = Cxt () ïî El par (A,B) es controlable. Y() s -1 Gol() s =
CONTROL POR REALIMENTACIÓN DE ESTADOS Fernando di Sciascio (2016) Control por Realimentación de Estados ì ï xt () = Axt () + But () í ï yt () = Cxt () ïî El par (A,B) es controlable. Y() s -1 Gol() s =
EXAMEN PARCIAL I
 UNIVERSIDAD NACIONAL DE INGENIERÍA - FIM MT 7 Control Moderno y Óptimo EXAMEN PARCIAL - 04I Problema : Un tanque vacio con masa m o es posicionado sobre g un resorte lineal con rigidez k. El tanque es
UNIVERSIDAD NACIONAL DE INGENIERÍA - FIM MT 7 Control Moderno y Óptimo EXAMEN PARCIAL - 04I Problema : Un tanque vacio con masa m o es posicionado sobre g un resorte lineal con rigidez k. El tanque es
Sistemas de control con realimentación de la salida
 Capítulo 7 Sistemas de control con realimentación de la salida 7.1. Introducción En el capítulo 5 se supuso que estaba disponible el vector de estado completamente. Relajando esta suposición y estudiando
Capítulo 7 Sistemas de control con realimentación de la salida 7.1. Introducción En el capítulo 5 se supuso que estaba disponible el vector de estado completamente. Relajando esta suposición y estudiando
Sistema neumático de control de nivel
 ULA. FACULTAD DE INGENIERIA. ESCUELA DE MECANICA. TEORIA DE CONTROL. EJERCICIOS FINAL Ejercicio 1. Primera parte: Modelado y de un tanque de agua, con su sistema de medición de nivel. La figura muestra
ULA. FACULTAD DE INGENIERIA. ESCUELA DE MECANICA. TEORIA DE CONTROL. EJERCICIOS FINAL Ejercicio 1. Primera parte: Modelado y de un tanque de agua, con su sistema de medición de nivel. La figura muestra
Diseño por ubicación de polos
 Control Automático Diseño por ubicación de polos Contenido Introducción Métodos para la ubicación de polos Realimentación de estado Modificación del lugar de las raíces Introducción Para diseñar un regulador
Control Automático Diseño por ubicación de polos Contenido Introducción Métodos para la ubicación de polos Realimentación de estado Modificación del lugar de las raíces Introducción Para diseñar un regulador
El modelo matemático tiende a ser lo más simple posible, con una representación. A la hora de desarrollar un modelo matemático:
 Modelo matemático de procesos 1. Modelo Matemático Un modelo matemático muy exacto implica un desarrollo matemático muy complejo. Por el contrario, un modelo matemático poco fino nos deparará un desarrollo
Modelo matemático de procesos 1. Modelo Matemático Un modelo matemático muy exacto implica un desarrollo matemático muy complejo. Por el contrario, un modelo matemático poco fino nos deparará un desarrollo
1. Análisis de Sistemas Discretos
 . Análisis de Sistemas Discretos. Análisis de Sistemas Discretos.. Introducción.. Estabilidad... Estabilidad de Sistemas Lineales 3... Estabilidad de Sistemas con Entrada y Salida Acotadas(BIBO) 4..3.
. Análisis de Sistemas Discretos. Análisis de Sistemas Discretos.. Introducción.. Estabilidad... Estabilidad de Sistemas Lineales 3... Estabilidad de Sistemas con Entrada y Salida Acotadas(BIBO) 4..3.
Modelos en el Espacio de Estado
 José Luis Rodríguez, PhD, Octubre del 00 Modelos en el Espacio de Estado Introducción: La tendencia moderna en la ingeniería de sistemas es hacia una complejidad cada vez mayor, debido principalmente a
José Luis Rodríguez, PhD, Octubre del 00 Modelos en el Espacio de Estado Introducción: La tendencia moderna en la ingeniería de sistemas es hacia una complejidad cada vez mayor, debido principalmente a
Diseño Básico de Controladores
 Diseño Básico de Controladores No existen reglas para el diseño de controladores. Para una planta y especificaciones dadas pueden existir dos o mas controladores que entreguen buen desempeño. En las siguientes
Diseño Básico de Controladores No existen reglas para el diseño de controladores. Para una planta y especificaciones dadas pueden existir dos o mas controladores que entreguen buen desempeño. En las siguientes
Control Automático I - Certamen 2 Pauta de Correción
 Control Automático I - Certamen 2 Pauta de Correción 7 de Septiembre 215 1. 1.1. Un sistema electro-mecánico tiene el modelo nominal G (s) = 1 (s+2), cuya salida es la velocidad angular de un eje. Los
Control Automático I - Certamen 2 Pauta de Correción 7 de Septiembre 215 1. 1.1. Un sistema electro-mecánico tiene el modelo nominal G (s) = 1 (s+2), cuya salida es la velocidad angular de un eje. Los
Estimación de Estados Observadores Reducidos o de Orden Mínimo. Fernando di Sciascio (2016)
 Estimación de Estados Observadores Reducidos o de Orden Mínimo Fernando di Sciascio (206) Observadores reducidos o de orden mínimo o El vector de estado x(t) es de dimensión n y la salida y(t) es un escalar
Estimación de Estados Observadores Reducidos o de Orden Mínimo Fernando di Sciascio (206) Observadores reducidos o de orden mínimo o El vector de estado x(t) es de dimensión n y la salida y(t) es un escalar
Control Moderno - Ing. Electrónica Ejercicio Resuelto 3: Teorema de Cayley-Hamilton
 Control Moderno - Ing. Electrónica Ejercicio Resuelto 3: Teorema de Cayley-Hamilton Introducción A continuación se presentan unos pocos y simples ejemplos que muestran como puede emplearse el Teorema de
Control Moderno - Ing. Electrónica Ejercicio Resuelto 3: Teorema de Cayley-Hamilton Introducción A continuación se presentan unos pocos y simples ejemplos que muestran como puede emplearse el Teorema de
Teoría Moderna de Control Lineal
 Teoría Moderna de Control Lineal 2 Índice general 1. Sistemas lineales determinísticos multivariables, invariantes, continuos 1 1.1. Introducción....................................... 1 1.1.1. Descripción
Teoría Moderna de Control Lineal 2 Índice general 1. Sistemas lineales determinísticos multivariables, invariantes, continuos 1 1.1. Introducción....................................... 1 1.1.1. Descripción
DIAGRAMAS DE ESTADO. Fernando di Sciascio (2017)
 DIAGRAMAS DE ESTADO Fernando di Sciascio (2017) Diagramas de Estado Los Diagramas de Estado son una extensión de los diagramas de flujo señal y permiten describir gráficamente ecuaciones diferenciales
DIAGRAMAS DE ESTADO Fernando di Sciascio (2017) Diagramas de Estado Los Diagramas de Estado son una extensión de los diagramas de flujo señal y permiten describir gráficamente ecuaciones diferenciales
Control Moderno: Paradigmas y Desafíos
 Control Moderno: Paradigmas y Desafíos Elizabeth Villota Cerna Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica 1 Paradigma del control por realimentación entradas exógenas salidas
Control Moderno: Paradigmas y Desafíos Elizabeth Villota Cerna Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica 1 Paradigma del control por realimentación entradas exógenas salidas
SOLUCIONARIO PROBLEMAS REALIMENTACION DE ESTADOS
 SOLUCIONARIO PROBLEMAS REALIMENTACION DE ESTADOS P1: Sea un servo descrito por la función de transferencia de estados digital. Deseamos diseñar un control por realimentación a) Escriba las ecuaciones de
SOLUCIONARIO PROBLEMAS REALIMENTACION DE ESTADOS P1: Sea un servo descrito por la función de transferencia de estados digital. Deseamos diseñar un control por realimentación a) Escriba las ecuaciones de
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones.
 Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
AUTOMATIZACION Y CONTROL DE PROCESOS FACEyT UNT ESTABILIDAD DE LOS SISTEMAS EN LAZO CERRADO
 Análisis Cualitativo de la Respuesta Temporal de un Sistema Si se conocen la función de transferencia G(s) de un dado sistema y la entrada x(t), se puede evaluar la salida y(t) a partir de: y(s) G (s )
Análisis Cualitativo de la Respuesta Temporal de un Sistema Si se conocen la función de transferencia G(s) de un dado sistema y la entrada x(t), se puede evaluar la salida y(t) a partir de: y(s) G (s )
MATEMÁTICAS ESPECIALES II PRÁCTICA 5 Parte I - Sistemas de ecuaciones diferenciales de primer orden.
 MATEMÁTICAS ESPECIALES II - 8 PRÁCTICA 5 Parte I - Sistemas de ecuaciones diferenciales de primer orden. Considere el sistema de ecuaciones diferenciales ordinarias (EDOs) de primer orden dx dt = f (t,
MATEMÁTICAS ESPECIALES II - 8 PRÁCTICA 5 Parte I - Sistemas de ecuaciones diferenciales de primer orden. Considere el sistema de ecuaciones diferenciales ordinarias (EDOs) de primer orden dx dt = f (t,
1. Problema clásico de EDO
 FACULTAD CS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA57C Control Óptimo Semestre 27-2 Profesor: Rafael Correa Auxiliar: Oscar Peredo Clase Auxiliar #1 31 de julio de 27 1 Problema clásico de EDO Problema
FACULTAD CS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA57C Control Óptimo Semestre 27-2 Profesor: Rafael Correa Auxiliar: Oscar Peredo Clase Auxiliar #1 31 de julio de 27 1 Problema clásico de EDO Problema
2 Espacios vectoriales
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 2 Espacios vectoriales 2.1 Espacio vectorial Un espacio vectorial sobre un cuerpo K (en general R o C) es un conjunto V sobre el que hay
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 2 Espacios vectoriales 2.1 Espacio vectorial Un espacio vectorial sobre un cuerpo K (en general R o C) es un conjunto V sobre el que hay
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones.
 Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
11 REPRESENTACIÓN EN EL ESPACIO DE ESTADO. 1.3 SOLUCIÓN DE ECUACIONES DE ESTADO EN TIEMPO
 Control Avanzado. Luis Edo García Jaimes 1 TABLA DE CONTENIDO 1. ANÁLISIS DE SISTEMAS DE CONTROL EN EL ESPACIO DE 5 ESTADO 1.1 FORMAS CANÓNICAS PARA ECUACIONES EN EL ESPACIO DE ESTADO EN TIEMPO DISCRETO
Control Avanzado. Luis Edo García Jaimes 1 TABLA DE CONTENIDO 1. ANÁLISIS DE SISTEMAS DE CONTROL EN EL ESPACIO DE 5 ESTADO 1.1 FORMAS CANÓNICAS PARA ECUACIONES EN EL ESPACIO DE ESTADO EN TIEMPO DISCRETO
Lugar Geométrico de las Raíces Herramienta para diseño de sistemas de control
 Lugar Geométrico de las Raíces Herramienta para diseño de sistemas de control Elizabeth Villota Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica UNI-FIM 1 Modelado Modelo: representación
Lugar Geométrico de las Raíces Herramienta para diseño de sistemas de control Elizabeth Villota Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica UNI-FIM 1 Modelado Modelo: representación
Departamento de Ingeniería Matemática - Universidad de Chile
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 9: Sistemas de EDOs lineales
 ETS Minas: Métodos Matemáticos Resumen y ejemplos Tema 9: Sistemas de EDOs lineales Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Noviembre
ETS Minas: Métodos Matemáticos Resumen y ejemplos Tema 9: Sistemas de EDOs lineales Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Noviembre
Ecuación algebraica de Riccati
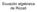 Ecuación algebraica de Riccati Definiciones básicas La ecuación de Riccati es a esta se le asocia una matriz de Hamilton de dimensión Definiciones básicas Lema: El espectro s(h) del conjunto de eigenvalores
Ecuación algebraica de Riccati Definiciones básicas La ecuación de Riccati es a esta se le asocia una matriz de Hamilton de dimensión Definiciones básicas Lema: El espectro s(h) del conjunto de eigenvalores
Diagonalización de matrices
 7 Diagonalización de matrices 7.1. Matrices diagonalizables Existen diversos procesos en los que el estado en cada uno de sus pasos se puede representar por un determinado vector y en los que, además,
7 Diagonalización de matrices 7.1. Matrices diagonalizables Existen diversos procesos en los que el estado en cada uno de sus pasos se puede representar por un determinado vector y en los que, además,
1. Problema de Generación de Trayectoria
 Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227C) Clase11-1 Elizabeth Villota Cerna Semestre 21I - UNI
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227C) Clase11-1 Elizabeth Villota Cerna Semestre 21I - UNI
Introducción al Control Óptimo
 Ingeniería en Control y Automatización Introducción al Control Óptimo Aplicación a sistemas de control moderno ERÍA DEL CNRL III de diciembre de 6 Autor: M. en C. Rubén Velázquez Cuevas Escuela Superior
Ingeniería en Control y Automatización Introducción al Control Óptimo Aplicación a sistemas de control moderno ERÍA DEL CNRL III de diciembre de 6 Autor: M. en C. Rubén Velázquez Cuevas Escuela Superior
MATRICES Y SISTEMAS DE ECUACIONES
 MATRICES Y SISTEMAS DE ECUACIONES Definición Una matriz real de orden m n es una tabla ordenada de m n números reales a 11 a 12 a 1n a A = 21 a 22 a 2n a m1 a m2 a mn en la cual las líneas horizontales
MATRICES Y SISTEMAS DE ECUACIONES Definición Una matriz real de orden m n es una tabla ordenada de m n números reales a 11 a 12 a 1n a A = 21 a 22 a 2n a m1 a m2 a mn en la cual las líneas horizontales
Planificaciones Teoría de Control II. Docente responsable: SACO ROBERTO. 1 de 5
 Planificaciones 6628 - Teoría de Control II Docente responsable: SACO ROBERTO 1 de 5 OBJETIVOS En este curso se introduce al estudiante de ingeniería electrónica a los problemas del control de sistemas
Planificaciones 6628 - Teoría de Control II Docente responsable: SACO ROBERTO 1 de 5 OBJETIVOS En este curso se introduce al estudiante de ingeniería electrónica a los problemas del control de sistemas
MATRICES Y SISTEMAS DE ECUACIONES
 MATRICES Y SISTEMAS DE ECUACIONES Definición Una matriz real de orden m n es una tabla ordenada de m n números reales a 11 a 12 a 1n A = a 21 a 22 a 2n a m1 a m2 a mn en la cual las líneas horizontales
MATRICES Y SISTEMAS DE ECUACIONES Definición Una matriz real de orden m n es una tabla ordenada de m n números reales a 11 a 12 a 1n A = a 21 a 22 a 2n a m1 a m2 a mn en la cual las líneas horizontales
Podemos pues formular los dos problemas anteriores en términos de matrices.
 Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
MODELACION EN VARIABLES DE ESTADO
 CAPÍTULO VIII INGENIERÍA DE SISTEMAS I MODELACION EN VARIABLES DE ESTADO 8.1. DEFINICIONES Estado: El estado de un sistema dinámico es el conjunto más pequeño de variables de modo que el conocimiento de
CAPÍTULO VIII INGENIERÍA DE SISTEMAS I MODELACION EN VARIABLES DE ESTADO 8.1. DEFINICIONES Estado: El estado de un sistema dinámico es el conjunto más pequeño de variables de modo que el conocimiento de
Controlabilidad y observabilidad
 Lección 5 Controlabilidad y observabilidad 1 Eventos alcanzables y controlables Σ = (T, U, U, X, Y, ψ, η) un sistema de control arbitrario T X= Espacio de eventos (t, x) T X= el estado del sistema en el
Lección 5 Controlabilidad y observabilidad 1 Eventos alcanzables y controlables Σ = (T, U, U, X, Y, ψ, η) un sistema de control arbitrario T X= Espacio de eventos (t, x) T X= el estado del sistema en el
Consideremos la función de transferencia de un sistema en lazo cerrado: 1 + KG(s)H(s) = 0 (2) K > 4 (4)
 LUGAR GEOMÉTRICO DE LAS RAICES INTRODUCCION Cuando un parámetro de un sistema cambia, las raíces de su ecuación característica se mueven en el plano s; estas variaciones es lo que define el Lugar Geométrico
LUGAR GEOMÉTRICO DE LAS RAICES INTRODUCCION Cuando un parámetro de un sistema cambia, las raíces de su ecuación característica se mueven en el plano s; estas variaciones es lo que define el Lugar Geométrico
SISTEMAS DE CONTROL AVANZADO
 SISTEMAS DE CONTROL AVANZADO LUIS EDO GARCÍA JAIMES POLITÉCNICO COLOMBIANO J.I.C PRIMERA PARTE ANÁLISIS DE SISTEMAS DE CONTROL EN EL ESPACIO DE ESTADO Este método tiene como objetivo la descripción de
SISTEMAS DE CONTROL AVANZADO LUIS EDO GARCÍA JAIMES POLITÉCNICO COLOMBIANO J.I.C PRIMERA PARTE ANÁLISIS DE SISTEMAS DE CONTROL EN EL ESPACIO DE ESTADO Este método tiene como objetivo la descripción de
Solución de Sistemas Dinámicos
 Sistemas Dinámicos Solución de Sistemas Dinámicos M.Sc. I.M. Manuel F. Mejía De Alba Maestría en Modelado y Simulación Universidad Central y Universidad Jorge Tadeo Lozano Agosto de 2014 1/14 Contenido
Sistemas Dinámicos Solución de Sistemas Dinámicos M.Sc. I.M. Manuel F. Mejía De Alba Maestría en Modelado y Simulación Universidad Central y Universidad Jorge Tadeo Lozano Agosto de 2014 1/14 Contenido
Sistemas de control Versión Estabilidad de Sistemas Método de Routh
 Sistemas de control 67- Versión Estabilidad de Sistemas Método de Routh Se analizarán temas relacionados con la estabilidad de los sistemas lineales; la misma es una propiedad inherente del sistema y no
Sistemas de control 67- Versión Estabilidad de Sistemas Método de Routh Se analizarán temas relacionados con la estabilidad de los sistemas lineales; la misma es una propiedad inherente del sistema y no
Sistemas de segundo orden: especificicaciones de diseño del régimen transitorio. Controladores P, PD y P-D
 Sistemas de segundo orden: especificicaciones de diseño del régimen transitorio. Controladores P, PD y P-D Félix Monasterio-Huelin de febrero de 6 Índice Índice Índice de Figuras Índice de Tablas. Respuesta
Sistemas de segundo orden: especificicaciones de diseño del régimen transitorio. Controladores P, PD y P-D Félix Monasterio-Huelin de febrero de 6 Índice Índice Índice de Figuras Índice de Tablas. Respuesta
Problemas de Espacios Vectoriales
 Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
Universidad Nacional de La Plata Facultad de Ingeniería Departamento de Electrotecnia Cátedra de Control Moderno. Cayley-Hamilton
 Universidad Nacional de La Plata Facultad de Ingeniería Departamento de Electrotecnia Cátedra de Control Moderno Cayley-Hamilton Año 26 1. Introducción A continuación se presentan unos pocos y simples
Universidad Nacional de La Plata Facultad de Ingeniería Departamento de Electrotecnia Cátedra de Control Moderno Cayley-Hamilton Año 26 1. Introducción A continuación se presentan unos pocos y simples
DIAGRAMAS DE ESTADO. Fernando di Sciascio (2016)
 DIAGRAMAS DE ESTADO Fernando di Sciascio (2016) Diagramas de Estado Los Diagramas de Estado son una extensión de los diagramas de flujo señal y permiten describir gráficamente ecuaciones diferenciales
DIAGRAMAS DE ESTADO Fernando di Sciascio (2016) Diagramas de Estado Los Diagramas de Estado son una extensión de los diagramas de flujo señal y permiten describir gráficamente ecuaciones diferenciales
CLAVE: MIS 206 PROFESOR: MTRO. ALEJANDRO SALAZAR GUERRERO
 MATEMÁTICAS AVANZADAS PARA LA INGENIERÍA EN SISTEMAS CLAVE: MIS 206 PROFESOR: MTRO. ALEJANDRO SALAZAR GUERRERO 1 1. SISTEMAS LINEALES DISCRETOS Y CONTINUOS 1.1. Modelos matemáticos 1.2. Sistemas 1.3. Entrada
MATEMÁTICAS AVANZADAS PARA LA INGENIERÍA EN SISTEMAS CLAVE: MIS 206 PROFESOR: MTRO. ALEJANDRO SALAZAR GUERRERO 1 1. SISTEMAS LINEALES DISCRETOS Y CONTINUOS 1.1. Modelos matemáticos 1.2. Sistemas 1.3. Entrada
A = [a 1 a 2 a 3. El sistema Ax = c tiene infinitas soluciones N. Existe un único vector x tal que T (x) = c X. T es suprayectiva
 Asignatura: ÁLGEBRA LINEAL Fecha: 6 de Julio de Fecha publicación notas: 6 de Julio de Fecha revisión examen: de Julio de Duración del examen: horas y media APELLIDOS Y NOMBRE: DNI: Titulación:. ( punto:,
Asignatura: ÁLGEBRA LINEAL Fecha: 6 de Julio de Fecha publicación notas: 6 de Julio de Fecha revisión examen: de Julio de Duración del examen: horas y media APELLIDOS Y NOMBRE: DNI: Titulación:. ( punto:,
DEPARTAMENTO DE INGENIERÍA MECÁNICA. Cátedra: Sistemas de Control TEO 03/2015
 FUNCIÓN TRANSFERENCIA 1 Función Transferencia Es una expresión matemática que caracteriza lasrelacionesde Entrada Salida de sistemas lineales invariantes en el tiempo. Se define como la relación de la
FUNCIÓN TRANSFERENCIA 1 Función Transferencia Es una expresión matemática que caracteriza lasrelacionesde Entrada Salida de sistemas lineales invariantes en el tiempo. Se define como la relación de la
AUTOMATIZACION Y CONTROL DE PROCESOS FACEyT UNT ESTABILIDAD DE LOS SISTEMAS EN LAZO CERRADO
 Análisis Cualitativo de la Respuesta Temporal de un Sistema Si se conocen la función de transferencia G(s) de un dado sistema y la entrada x(t), se puede evaluar la salida y(t) a partir de: y(s) G (s )
Análisis Cualitativo de la Respuesta Temporal de un Sistema Si se conocen la función de transferencia G(s) de un dado sistema y la entrada x(t), se puede evaluar la salida y(t) a partir de: y(s) G (s )
VALORES PROPIOS (AUTOVALORES) VECTORES PROPIOS (AUTOVECTORES)
 VALORES PROPIOS (AUTOVALORES) Y VECTORES PROPIOS (AUTOVECTORES) Autovalores y Autovectores Los vectores propios o autovectores de una matriz A son todos los vectores x i 0, a los que la transformación
VALORES PROPIOS (AUTOVALORES) Y VECTORES PROPIOS (AUTOVECTORES) Autovalores y Autovectores Los vectores propios o autovectores de una matriz A son todos los vectores x i 0, a los que la transformación
Preparaduría V. 1.- Sea A una matriz diagonal n n cuyo polinomio característico es
 Preparaduría V 1.- Sea A una matriz diagonal n n cuyo polinomio característico es (x c 1 ) d1 (x c 2 ) d2... (x c k ) d k donde los c 1,..., c k son distintos dos a dos. Sea V el espacio de matrices n
Preparaduría V 1.- Sea A una matriz diagonal n n cuyo polinomio característico es (x c 1 ) d1 (x c 2 ) d2... (x c k ) d k donde los c 1,..., c k son distintos dos a dos. Sea V el espacio de matrices n
Antecedentes de Control
 Apéndice A Antecedentes de Control Para cualquier tipo de análisis de sistemas de control, es importante establecer ciertos conceptos básicos. Sistemas de control retroalimentados Un sistema que mantiene
Apéndice A Antecedentes de Control Para cualquier tipo de análisis de sistemas de control, es importante establecer ciertos conceptos básicos. Sistemas de control retroalimentados Un sistema que mantiene
Álgebra Lineal. Departamento de Matemáticas Universidad de Los Andes. Primer Semestre de 2007
 Álgebra Lineal Departamento de Matemáticas Universidad de Los Andes Primer Semestre de 2007 Universidad de Los Andes () Álgebra Lineal Primer Semestre de 2007 1 / 50 Texto guía: Universidad de Los Andes
Álgebra Lineal Departamento de Matemáticas Universidad de Los Andes Primer Semestre de 2007 Universidad de Los Andes () Álgebra Lineal Primer Semestre de 2007 1 / 50 Texto guía: Universidad de Los Andes
Algebra Lineal XIX: Espacio Nulo y Rango de una Matriz y Matriz Inversa.
 Algebra Lineal XIX: Espacio Nulo y Rango de una Matriz y Matriz Inversa José María Rico Martínez Departamento de Ingeniería Mecánica Facultad de Ingeniería Mecánica Eléctrica y Electrónica Universidad
Algebra Lineal XIX: Espacio Nulo y Rango de una Matriz y Matriz Inversa José María Rico Martínez Departamento de Ingeniería Mecánica Facultad de Ingeniería Mecánica Eléctrica y Electrónica Universidad
Diagonalización de matrices
 Diagonalización de matrices María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Diagonalización de matrices Matemáticas I 1 / 22 Valores y vectores propios de una matriz Definición
Diagonalización de matrices María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Diagonalización de matrices Matemáticas I 1 / 22 Valores y vectores propios de una matriz Definición
MATRICES. Se denomina matriz de dimensión m n a todo conjunto cuyos elementos están dispuestos en m filas y n columnas. o simplemente A = (a.
 MATRICES Se denomina matriz de dimensión m n a todo conjunto cuyos elementos están dispuestos en m filas y n columnas A= 2 1 5 0 3 8 A es de dimensión 2 3. a a a En general una matriz de dimensión 2 3
MATRICES Se denomina matriz de dimensión m n a todo conjunto cuyos elementos están dispuestos en m filas y n columnas A= 2 1 5 0 3 8 A es de dimensión 2 3. a a a En general una matriz de dimensión 2 3
Clase 10 Diseño Óptimo Variables de Estado.doc 1
 . Diseño Óptimo en Variables de Estado. Diseño Óptimo en Variables de Estado.. Planteo del Problema... Criterio 3.. Regulador Lineal Óptimo (LQC) 5.3. Ecuación de Ricatti 9.4. Valor Medio de una Forma
. Diseño Óptimo en Variables de Estado. Diseño Óptimo en Variables de Estado.. Planteo del Problema... Criterio 3.. Regulador Lineal Óptimo (LQC) 5.3. Ecuación de Ricatti 9.4. Valor Medio de una Forma
Instituto Politécnico Nacional
 Instituto Politécnico Nacional Escuela Superior de Ingeniería Mecánica y Eléctrica, Zacatenco Ingeniería en Comunicaciones y Electrónica Academia de Matemáticas Fundamentos de Álgebra. Tarea 2 Julio César
Instituto Politécnico Nacional Escuela Superior de Ingeniería Mecánica y Eléctrica, Zacatenco Ingeniería en Comunicaciones y Electrónica Academia de Matemáticas Fundamentos de Álgebra. Tarea 2 Julio César
Matemáticas para la Empresa
 Matemáticas para la Empresa 1 o L. A. D. E. Curso 2008/09 Relación 1. Espacios Vectoriales 1. a) En IR 2 se consideran las operaciones habituales: (x, y) + (x, y ) = (x + x, y + y ) λ(x, y) = (λx, λy)
Matemáticas para la Empresa 1 o L. A. D. E. Curso 2008/09 Relación 1. Espacios Vectoriales 1. a) En IR 2 se consideran las operaciones habituales: (x, y) + (x, y ) = (x + x, y + y ) λ(x, y) = (λx, λy)
Álgebra Lineal. Tema 8. Valores y vectores propios. Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas
 Álgebra Lineal Tema 8. Valores y vectores propios Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas AUTORES: J. S ALAS, A. T ORRENTE Y E.J.S. V ILLASEÑOR
Álgebra Lineal Tema 8. Valores y vectores propios Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas AUTORES: J. S ALAS, A. T ORRENTE Y E.J.S. V ILLASEÑOR
Autovalores y autovectores Diagonalización y formas canónicas
 Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
ESPACIOS VECTORIALES Y APLICACIONES LINEALES
 Departamento de Matemática Aplicada II E.E.I. ÁLGEBRA Y ESTADÍSTICA Boletín n o (010-011 ESPACIOS VECTORIALES Y APLICACIONES LINEALES 1. En el espacio vectorial ordinario R 4 estudiar cuáles de los siguientes
Departamento de Matemática Aplicada II E.E.I. ÁLGEBRA Y ESTADÍSTICA Boletín n o (010-011 ESPACIOS VECTORIALES Y APLICACIONES LINEALES 1. En el espacio vectorial ordinario R 4 estudiar cuáles de los siguientes
0.1. Error en Estado Estacionario
 0. Error en Estado Estacionario 0.. Error en Estado Estacionario La respuesta permanente es aquella que se alcanza cuando el sistema se establece y es muy importante su estudio pues informa lo que sucede
0. Error en Estado Estacionario 0.. Error en Estado Estacionario La respuesta permanente es aquella que se alcanza cuando el sistema se establece y es muy importante su estudio pues informa lo que sucede
Línea de investigación o de trabajo: Electrónica de Potencia y Control Automático
 ASIGNATURA: TEORÍA DE SISTEMAS LINEALES Nombre de la asignatura: TEORÍA DE SISTEMAS LINEALES Línea de investigación o de trabajo: Electrónica de Potencia y Control Automático Tiempo de dedicación del estudiante
ASIGNATURA: TEORÍA DE SISTEMAS LINEALES Nombre de la asignatura: TEORÍA DE SISTEMAS LINEALES Línea de investigación o de trabajo: Electrónica de Potencia y Control Automático Tiempo de dedicación del estudiante
UNIDAD DIDÁCTICA I Teoría de Filtrado Óptimo 1
 Índice PRÓLOGO IX UNIDAD DIDÁCTICA I Teoría de Filtrado Óptimo 1 1 Representación de Estado de Sistemas Lineales 5 11 Representación de Estado en Tiempo Continuo 5 12 Matriz de Transición 1 121 Definición
Índice PRÓLOGO IX UNIDAD DIDÁCTICA I Teoría de Filtrado Óptimo 1 1 Representación de Estado de Sistemas Lineales 5 11 Representación de Estado en Tiempo Continuo 5 12 Matriz de Transición 1 121 Definición
Elementos de control en lazo cerrado 14 de diciembre de 2011
 . Introducción Elementos de control en lazo cerrado 4 de diciembre de 2 d i d o r C u G o y d m Figura : Lazo de control estándar. La Figura muestra un lazo de control elemental. En dicha figura, G o corresponde
. Introducción Elementos de control en lazo cerrado 4 de diciembre de 2 d i d o r C u G o y d m Figura : Lazo de control estándar. La Figura muestra un lazo de control elemental. En dicha figura, G o corresponde
