Sistemas de Control lineal óptimo con realimentación de estado
|
|
|
- Eva María Veronica Fidalgo Bustos
- hace 5 años
- Vistas:
Transcripción
1 Capítulo 5 Sistemas de Control lineal óptimo con realimentación de estado La principal restricción de este sistema de control es suponer que se puede medir en todo instante de tiempo el estado completo del sistema para realimentarlo Mejorar la estabilidad de sistemas de control realimentando el estado Control lineal con realimentación del estado Veamos como las propiedades de estabilidad de sistemas de control se pueden mejorar realimentando el estado. Consideremos el siguiente S.L.V.T: ẋ(t) = A(t) x(t) + B(t) u(t) (5.1) Si el estado se puede medir en todo instante, es posible construir una ley de control de la forma: u(t) = F (t) x(t) + u (t) (5.2) F (t): es una matriz de ganancia de realimentación variante en el tiempo. u (t): es una nueva entrada. Si esta ley de control se conecta al sistema (5.1), el sistema en lazo cerrado queda descrito por: ẋ(t) = [A(t) B(t) F (t)] x(t) + B(t) u (t) (5.3) La estabilidad de este sistema depende de A(t), B(t) y F (t). Introduzcamos la siguiente terminología: 49
2 Definición 5.1. La ley de control lineal: La denominaremos: Ley de control A.E para el sistema: Si el sistema en lazo cerrado: es asintóticamente estable. u(t) = F (t) x(t) + u (t) (5.4) ẋ(t) = A(t) x(t) + B(t) u(t) (5.5) ẋ(t) = [A(t) B(t) F (t)] x(t) + B(t) u (t) (5.6) Observación: Si el sistema (5.5) es I.T y se escoge una matriz F constante, la estabilidad del sistema (5.6) es determinada por los valores característicos de la matriz [A B F ] Condiciones para estabilización y asignación de polos En esta sección se establece: 1. Bajo que condiciones, los polos en el lazo cerrado de un S.L.I.T. se pueden ubicar en cualquier localización del plano complejo mediante realimentación lineal del estado. 2. Bajo que condiciones, el sistema se puede estabilizar. Teorema 5.1. Consideremos el S.L.I.T. ẋ(t) = A x(t) + B u(t) (5.7) con la ley de control I.T. u(t) = F x(t) + u (t) (5.8) Entonces los valores característicos del lazo cerrado, es decir, los valores característicos de [A B F ], se pueden colocar arbitrariamente en el plano complejo (con la restricción que los valores característicos complejos ocurran en pares complejos conjugados) escogiendo F adecuadamente si y sólo si el sistema (5.7) es completamente controlable. Observación: Este teorema no dice donde ubicar los polos en el semiplano izquierdo Regulador óptimo lineal determinístico Un S.L.I.T. se puede estabilizar con una ley lineal de realimentación cuando es C.C.. También se pueden escoger los polos del lazo cerrado para que la convergencia a cero del estado sea arbitrariamente rápida. Normalmente esto involucra entradas con grandes amplitudes, esto impone límite a la distancia en que se deben colocar los polos a la izquierda del eje imaginario. Luego hay que tomar en cuenta la velocidad de convergencia al estado cero y la magnitud de la entrada. Consideremos el S.L.I.T. ẋ(t) = A(t) x(t) + B(t) u(t) (5.9) 50
3 la idea es llevar el sistema desde un estado inicial arbitrario al estado cero tan rápido como sea posible. Un criterio útil es: x T (t) R 1 (t) x(t) dt (5.10) con R 1 (t) una matriz simétrica no-negativa definida. Este criterio ilustra la desviación acumulativa de x(t) desde el estado cero durante el intervalo [, t 1 ]. Usualmente disponemos de: z(t) = D(t) x(t) (5.11) luego el problema real es llevar z(t) a cero tan rápido como sea posible, luego (5.10) se reduce a: z T (t) R 3 (t) z(t) dt (5.12) con: R 1 (t) = D T (t) R 3 (t) D(t) (5.13) R 3 (t) matriz de ponderación simétrica positiva definida. Para prevenir grandes amplitudes en la entrada se incluye en el criterio a minimizar, quedando: [z T (t) R 3 (t) z(t) + u T (t) R 2 (t) u(t)] dt (5.14) con R 2 (t) una matriz de ponderación simétrica positiva definida. La importancia relativa de los dos términos, en el criterio, se determina por las matrices R 3 y R 2. También es muy importante que el estado terminal x(t 1 ) esté lo más cercano al estado cero, esto lleva a incluir un tercer término en el criterio. Luego resulta: [z T (t) R 3 (t) z(t) + u T (t) R 2 (t) u(t)] dt + x T (t 1 ) P 1 x(t 1 ) (5.15) donde P 1 es una matriz constante simétrica no-negativa definida. Definición 5.2. Considerar el S.L.V.T.: ẋ(t) = A(t) x(t) + B(t) u(t) (5.16) x( ) = x 0 (5.17) con la variable controlada: z(t) = D(t) x(t) (5.18) Considerar también el criterio: [z T (t) R 3 (t) z(t) + u T (t) R 2 (t) u(t)] dt + x T (t 1 ) P 1 x(t 1 ) (5.19) donde P 1 es una matriz simétrica no negativa definida, R 3 (t) y R 2 (t) son matrices simétricas positiva definidas para t t 1. Entonces el problema de determinar una entrada u o (t), t t 1, para que el criterio sea mínimo se llama: el problema del regulador óptimo lineal determinístico (P.R.O.L.D). 51
4 Definición 5.3. Si todas las matrices involucradas en la formulación del problema del regulador óptimo lineal determinístico son constantes, entonces nos referiremos al problema del regulador óptimo lineal determinístico invariante en el tiempo Solución del problema del regulador Es conveniente re-escribir el criterio (5.15) en la forma: [x T (t) R 1 (t) x(t) + u T (t) R 2 (t) u(t)] dt + x T (t 1 ) P 1 x(t 1 ) (5.20) donde R 1 (t) es una matriz simétrica no-negativa definida: R 1 (t) = D T (t) R 3 (t) D(t) (5.21) donde R 3 (t) y R 2 (t) son matrices simétricas positiva definidas. Supongamos que la entrada que minimiza este criterio existe y la denominaremos u o (t), t t 1. Sea x o (t) el estado óptimo para u o (t). Entonces el siguiente teorema nos define la solución: Teorema 5.2. Considerar el P.R.O.L.D.. Entonces la entrada óptima se puede generar desde una ley de control de la forma: u o (t) = F (t) x o (t) (5.22) La matriz P (t) está dada por: F (t) = R 1 2 (t) BT (t) P (t) (5.23) P (t) = [Φ 21 (t, t 1 ) + Φ 22 (t, t 1 ) P 1 ] [Φ 11 (t, t 1 ) + Φ 12 (t, t 1 ) P 1 ] 1 (5.24) donde Φ 11 (t, ), Φ 12 (t, ), Φ 21 (t, ) y Φ 22 (t, ) se obtienen particionando la matriz de transición Φ(t, ) de la ecuación diferencial de estado: ẋ(t) A(t) B(t) R 1 2 = (t) BT (t) x(t) (5.25) ṗ(t) R 1 (t) A T (t) p(t) R 1 (t) = D T (t) R 3 (t) D(t) (5.26) Se puede derivar la ecuación matricial diferencial que cumple la matriz P (t). Se consigue con el siguiente teorema: Teorema 5.3. La entrada óptima para el P.R.O.L.D. se genera con la ley de control lineal: u o (t) = F o (t) x o (t) (5.27) F o (t) = R 1 2 B T (t) P (t) (5.28) 52
5 en este caso, la matriz P (t) es simétrica y no-negativa definida que satisface la ecuación matricial de Riccati: P (t) = R 1 (t) P (t) B(t) R 1 2 (t) BT (t) P (t) + P (t) A(t) + A T (t) P (t) (5.29) con la condición terminal: y P (t 1 ) = P 1 (5.30) R 1 (t) = D T (t) R 3 (t) D(t) (5.31) Para la solución óptima tenemos: t [ ] x ot (τ) R 1 (τ) x o (τ) + u ot (τ) R 2 (τ) u o (τ) dτ + x ot (t 1 ) P 1 x o (t 1 ) = x ot (t) P (t) x o (t) (5.32) Vemos que la matriz P (t) no solamente da la ley de realimentación óptima sino que también permite evaluar el criterio para cualquier estado inicial y tiempo inicial. Del teorema 5.2 se puede extraer el siguiente resultado, que será útil cuando veamos el problema del observador óptimo: Lema 5.1. Considerar la ecuación diferencial matricial: P (t) = R1 (t) + F T (t) R 2 (t) F (t) + P (t)[a(t) B(t) F (t)] + [A(t) B(t) F (t)] T P (t) (5.33) con la condición terminal: P (t 1 ) = P 1 (5.34) donde R 1 (t), R 2 (t), A(t) y B(t) son matrices conocidas de dimensiones apropiadas, con R 1 (t) no-negativa definida y R 2 (t) positiva definida para t t 1, y P 1 no-negativa definida y constante. Tomando F (t) como una función matricial continua arbitraria para t t 1. Entonces para t t 1 : P (t) P (t) (5.35) donde P (t) es la solución de la ecuación de Riccati: P (t) = R 1 (t) P (t) B(t) R 1 2 (t) BT (t) P (t) + P (t) A(t) + A T (t) P (t) (5.36) P (t 1 ) = P 1 La desigualdad (5.35) se convierte en igualdad si: F (τ) = R 1 2 (τ) BT (τ) P (τ) t τ t 1 (5.37) Solución en estado estacionario del P.R.O.L.D. Desde un punto de vista práctico, es natural considerar períodos largos de control. A continuación se indicarán las propiedades asintóticas del regulador óptimo. Para el caso variante en el tiempo, tenemos el siguiente teorema: 53
6 Teorema 5.4. Considerar la ecuación matricial de Riccati: P (t) = D T (t) R 3 (t) D(t) P (t) B(t) R 1 2 (t) BT (t) P (t) + A T (t) P (t) + P (t) A(t) (5.38) Supongamos que A(t) es continua y acotada, que B(t), D(t), R 3 (t) y R 2 (t) son continuas y acotadas por tramos en [, ), y además que: donde α y β son constantes positivas. i.) Entonces si el sistema: R 3 (t) α I, R 2 (t) β I t (5.39) ẋ(t) = A(t) x(t) + B(t) u(t) (5.40) z(t) = D(t) x(t) es: a.) Completamente controlable o b.) Exponencialmente estable la solución P (t) de la ecuación de Riccati (5.38) con la condición terminal P (t 1 ) = 0 converge a una función matricial no-negativa definida P (t) cuando t 1. P (t) es una solución de la ecuación (5.38). ii.) Más aún, si el sistema (5.40) es: c.) Uniformemente completamente controlable y uniformemente completamente reconstruible o d.) Exponencialmente estable la solución P (t) de la ecuación de Riccati (5.38) con la condición terminal P (t 1 ) = P 1 converge a P (t) cuando t 1 para cualquier P 1 0. Considerando la estabilidad de la ley de control en estado estacionario, tenemos el siguiente resultado: Teorema 5.5. Considerando el P.R.O.L.D. y suponiendo que se satisfacen las suposiciones del Teorema 5.4 con respecto a A, B, C, D, R 3 y R 2. Entonces si el sistema (5.40) es: a.) U.C.C y U.C.R o b.) Exponencialmente estable los siguientes factores se mantienen: i.) La ley de control óptimo en estado estacionario: u(t) = R 1 2 (t) BT (t) P (t) x(t) (5.41) 54
7 es exponencialmente estable. ii.) La ley de control (5.41) minimiza: { [ lím z T (t) R 3 (t) z(t) + u T (t) R 2 (t) u(t) ] } dt + x T (t 1 ) P 1 x(t 1 ) t 1 (5.42) para todo P 1 0. El valor mínimo de (5.42) está dado por: x T ( ) P ( ) x( ) (5.43) Para el caso del regulador óptimo invariante en el tiempo, las propiedades en estado estacionario, se resumen en el siguiente teorema: Teorema 5.6. Considerando el problema del regulador invariante en el tiempo para el sistema: ẋ(t) = A x(t) + B u(t) (5.44) z(t) = D x(t) y el criterio [ z T (t) R 3 z(t) + u T (t) R 2 u(t) ] dt + x T (t 1 ) P 1 x(t 1 ) (5.45) con R 3 > 0, R 2 > 0, P 1 > 0. La ecuación de Riccati asociada está dada por: P (t) = D T R 3 D P (t) B R 1 2 B T P (t) + A T P (t) + P (t) A (5.46) con la condición terminal: P (t 1 ) = P 1 (5.47) a.) Suponga que P 1 = 0. Entonces cuando t 1 la ecuación de Riccati aproxima a una constante, en estado estacionario, de valor P si y sólo si el sistema no posee polos que son al mismo tiempo inestables, incontrolables y reconstruibles. b.) Si el sistema (5.44) es completamente controlable y completamente reconstruible, la solución de la ecuación de Riccati (5.46) se aproxima a un valor único P cuando t 1 para todo P 1 0. c.) Si P existe, es una solución matriz simétrica no-negativa definida de la ecuación algebraica de Riccati: 0 = D T R 3 D P B R 1 2 B T P + A T P + P A (5.48) Si el sistema (5.44) es C.C. y C.R., P es la única solución matriz simétrica positiva definida de la ecuación (5.48). d.) Si P existe, la ley de control en estado estacionario: es A.E si y sólo si el sistema (5.44) es C.C. y C.R. u(t) = F (t) x(t) (5.49) F (t) = R 1 2 B T P (5.50) 55
8 e.) Si el sistema (5.44) es C.C. y C.R., la ley de control en estado estacionario minimiza: { [ lím z T (t) R 3 z(t) + u T (t) R 2 u(t) ] } dt + x T (t 1 ) P 1 x(t 1 ) (5.51) t 1 para todo P 1 0. Para la ley de control en estado estacionario el criterio (5.44) toma el valor: x T ( ) P x( ) (5.52) Solución del problema del regulador invariante en el tiempo por diagonalización Se verá la solución en estado estacionario del problema del regulador invariante en el tiempo. Veremos como calcular computacionalmente la solución en estado estacionario, P, de la ecuación de Riccati, derivar información sobre los polos del regulador en lazo cerrado y su comportamiento. Teorema 5.7. Considerar el P.R.O.L.D.I.T. y suponer que el sistema: ẋ(t) = A x(t) + B u(t) (5.53) z(t) = D x(t) es C.C. y C.R.. Se define la matriz 2nx2n: A Z = D T R 3 D B R 1 2 B T A T (5.54) y se asume que Z tiene 2n valores característicos distintos. Entonces: a.) Si λ es un valor característico de Z, λ también es un valor característico. Z no tiene valores característicos con parte real cero. b.) Los valores característicos del regulador óptimo en lazo cerrado son aquellos valores característicos de Z que tiene parte real negativa. c.) Si Z es diagonalizable en la forma: Z = W [ Λ 0 0 Λ ] W 1 (5.55) donde la matriz diagonal Λ tiene como elementos de la diagonal los valores característicos de Z con parte real positiva, la solución en estado estacionario de la ecuación de Riccati: se puede escribir como: P (t) = D T R 3 D P (t) B R 1 2 B T P (t) + A T P (t) + P (t) A (5.56) P = W 22 W 1 12 = V 1 12 V 11 (5.57) donde el W ij y V ij con i, j = 1, 2, se obtienen particionando W y V = W 1, respectivamente. La matriz inversa en ambas expresiones existe. d.) La respuesta en estado estacionario del regulador óptimo en lazo cerrado se puede escribir como: x(t) = W 12 e Λ(t t0) W 1 12 x 0 (5.58) 56
9 5.3. Regulador y servo con referencia distinta de cero. Se supuso que el estado cero es el estado de equilibrio deseado del sistema. En la práctica no siempre es verdad. En este caso, se supone que el set-point es constante por largos periodos de tiempo pero que de tiempo en tiempo es modificado. Para el caso en que la entrada u(t) tiene la misma dimensión que la variable controlada z(t) se tiene el siguiente resultado: Teorema 5.8. Consideremos el S.L.I.T. : ẋ(t) = A x(t) + B u(t) (5.59) z(t) = D x(t) donde z y u tienen las mismas dimensiones. Consideremos alguna ley de control invariante en el tiempo A.E.: u(t) = F x(t) + u (t) (5.60) Tomemos H(s) la matriz de lazo abierto: y H c (s) como la matriz de lazo cerrado: H(s) = D [si A] 1 B (5.61) H c (s) = D [si A + B F ] 1 B (5.62) Entonces H c (0) es no singular y la variable controlada z(t) se puede, bajo condiciones de estado estacionario, mantener en algún valor constante z 0 escogiendo: u (t) = H 1 c (0) z 0 (5.63) si y sólo si H(s) tenga un polinomio numerador distinto de cero que no tenga ceros en el origen. 57
Sistemas de control con realimentación de la salida
 Capítulo 7 Sistemas de control con realimentación de la salida 7.1. Introducción En el capítulo 5 se supuso que estaba disponible el vector de estado completamente. Relajando esta suposición y estudiando
Capítulo 7 Sistemas de control con realimentación de la salida 7.1. Introducción En el capítulo 5 se supuso que estaba disponible el vector de estado completamente. Relajando esta suposición y estudiando
Teoría Moderna de Control Lineal
 Teoría Moderna de Control Lineal 2 Índice general 1. Sistemas lineales determinísticos multivariables, invariantes, continuos 1 1.1. Introducción....................................... 1 1.1.1. Descripción
Teoría Moderna de Control Lineal 2 Índice general 1. Sistemas lineales determinísticos multivariables, invariantes, continuos 1 1.1. Introducción....................................... 1 1.1.1. Descripción
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS
 Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
Control Moderno. Ene.-Jun Diseño de controlador con referencia a la entrada, servosistemas. Dr. Rodolfo Salinas. mayo 2007
 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Diseño de controlador con referencia a la entrada, servosistemas Dr. Rodolfo Salinas mayo 2007
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Diseño de controlador con referencia a la entrada, servosistemas Dr. Rodolfo Salinas mayo 2007
Sistemas de Control con entradas estocásticas
 Capítulo 4 Sistemas de Control con entradas estocásticas 4.1. Introducción Un sistema de control es un sistema dinámico que cuando evoluciona en el tiempo se comporta de una forma predescrita. Loa componentes
Capítulo 4 Sistemas de Control con entradas estocásticas 4.1. Introducción Un sistema de control es un sistema dinámico que cuando evoluciona en el tiempo se comporta de una forma predescrita. Loa componentes
MATEMÁTICAS ESPECIALES II PRÁCTICA 5 Parte I - Sistemas de ecuaciones diferenciales de primer orden.
 MATEMÁTICAS ESPECIALES II - 8 PRÁCTICA 5 Parte I - Sistemas de ecuaciones diferenciales de primer orden. Considere el sistema de ecuaciones diferenciales ordinarias (EDOs) de primer orden dx dt = f (t,
MATEMÁTICAS ESPECIALES II - 8 PRÁCTICA 5 Parte I - Sistemas de ecuaciones diferenciales de primer orden. Considere el sistema de ecuaciones diferenciales ordinarias (EDOs) de primer orden dx dt = f (t,
Apéndice sobre ecuaciones diferenciales lineales
 Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Comportamiento dinámico: Estabilidad
 Lección 4 Comportamiento dinámico: Estabilidad 1 Estabilidad Dos tipos de estabilidad: ẋ(t) = f(t, x(t), u(t)) Estabilidad interna: ẋ(t) = f(t, x(t)) Estabilidad externa o estabilidad BIBO (bounded input-bounded
Lección 4 Comportamiento dinámico: Estabilidad 1 Estabilidad Dos tipos de estabilidad: ẋ(t) = f(t, x(t), u(t)) Estabilidad interna: ẋ(t) = f(t, x(t)) Estabilidad externa o estabilidad BIBO (bounded input-bounded
TEMA 4.- SISTEMAS DE ECUACIONES DIFERENCIALES ORDINARIAS
 TEMA 4- SISTEMAS DE ECUACIONES DIFERENCIALES ORDINARIAS 41 - Introducción Denición: Un sistema de ecuaciones diferenciales de primer orden en el que sus derivadas estén dadas explícitamente se puede expresar
TEMA 4- SISTEMAS DE ECUACIONES DIFERENCIALES ORDINARIAS 41 - Introducción Denición: Un sistema de ecuaciones diferenciales de primer orden en el que sus derivadas estén dadas explícitamente se puede expresar
Comportamiento dinámico: Estabilidad
 Lección 5 Comportamiento dinámico: Estabilidad Estabilidad Dos tipos de estabilidad: ẋ(t) = f(t, x(t), u(t)) Estabilidad interna: ẋ(t) = f(t, x(t)) Estabilidad externa o Estabilidad Entrada-Salida : {
Lección 5 Comportamiento dinámico: Estabilidad Estabilidad Dos tipos de estabilidad: ẋ(t) = f(t, x(t), u(t)) Estabilidad interna: ẋ(t) = f(t, x(t)) Estabilidad externa o Estabilidad Entrada-Salida : {
1. Método del Lugar de las Raíces
 . Método del Lugar de las Raíces. MÉTODO DEL LUGAR DE LAS RAÍCES..... IDEA BÁSICA... 3.. LUGAR DE LAS RAÍCES DE SISTEMAS SIMPLES... 0.3. LUGAR DE GANANCIA CONSTANTE....4. REGLAS PARA LA CONSTRUCCIÓN DEL
. Método del Lugar de las Raíces. MÉTODO DEL LUGAR DE LAS RAÍCES..... IDEA BÁSICA... 3.. LUGAR DE LAS RAÍCES DE SISTEMAS SIMPLES... 0.3. LUGAR DE GANANCIA CONSTANTE....4. REGLAS PARA LA CONSTRUCCIÓN DEL
1. Método del Lugar de las Raíces
 . Método del Lugar de las Raíces. MÉTODO DEL LUGAR DE LAS RAÍCES..... IDEA BÁSICA...3.. LUGAR DE LAS RAÍCES DE SISTEMAS SIMPLES...0.3. LUGAR DE GANANCIA CONSTANTE....4. REGLAS PARA LA CONSTRUCCIÓN DEL
. Método del Lugar de las Raíces. MÉTODO DEL LUGAR DE LAS RAÍCES..... IDEA BÁSICA...3.. LUGAR DE LAS RAÍCES DE SISTEMAS SIMPLES...0.3. LUGAR DE GANANCIA CONSTANTE....4. REGLAS PARA LA CONSTRUCCIÓN DEL
2. El Segundo Método de Estabilidad de Liapunov. 2. El Segundo Método de Estabilidad de Liapunov
 2.1. Introducción. Funciones de Liapunov 2.1. Introducción. Funciones de Liapunov Consideremos el sistema no lineal autónomo (1.12) y = f (y) donde f : D R N R N, con f Lip loc (D) y f (0) = 0, D abierto
2.1. Introducción. Funciones de Liapunov 2.1. Introducción. Funciones de Liapunov Consideremos el sistema no lineal autónomo (1.12) y = f (y) donde f : D R N R N, con f Lip loc (D) y f (0) = 0, D abierto
CAPITULO 4 ESTABILIDAD. Ing. Diego Alejandro Patiño G. M. Sc., Ph. D.
 CAPITULO 4 ESTABILIDAD Ing. Diego Alejandro Patiño G. M. Sc., Ph. D. Estabilidad Cada punto donde la bola se puede detener es un punto de equilibrio. A y F: puntos inestables: un cambio infinitesimal en
CAPITULO 4 ESTABILIDAD Ing. Diego Alejandro Patiño G. M. Sc., Ph. D. Estabilidad Cada punto donde la bola se puede detener es un punto de equilibrio. A y F: puntos inestables: un cambio infinitesimal en
Universidad Nacional de La Plata Facultad de Ingeniería Departamento de Electrotecnia Cátedra de Control Moderno. Cayley-Hamilton
 Universidad Nacional de La Plata Facultad de Ingeniería Departamento de Electrotecnia Cátedra de Control Moderno Cayley-Hamilton Año 26 1. Introducción A continuación se presentan unos pocos y simples
Universidad Nacional de La Plata Facultad de Ingeniería Departamento de Electrotecnia Cátedra de Control Moderno Cayley-Hamilton Año 26 1. Introducción A continuación se presentan unos pocos y simples
4.- ANALISIS DE SISTEMAS EN TIEMPO CONTINUO
 ANALISIS DE SISTEMAS EN TIEMPO CONTINUO Dinámica de Sistemas 4. 4.- ANALISIS DE SISTEMAS EN TIEMPO CONTINUO 4..- Efecto de los polos en el comportamiento del sistema. 4..- Estabilidad. 4.3.- Análisis de
ANALISIS DE SISTEMAS EN TIEMPO CONTINUO Dinámica de Sistemas 4. 4.- ANALISIS DE SISTEMAS EN TIEMPO CONTINUO 4..- Efecto de los polos en el comportamiento del sistema. 4..- Estabilidad. 4.3.- Análisis de
1. Estabilidad de Sistemas Lineales y Sistemas Lineales Perturbados
 1. Estabilidad de Sistemas Lineales y Sistemas Lineales Perturbados 1.1. Introducción. Repaso de resultados conocidos AMPLIACIÓN DE ECUACIONES DIFERENCIALES GRADO EN MATEMÁTICAS, Universidad de Sevilla
1. Estabilidad de Sistemas Lineales y Sistemas Lineales Perturbados 1.1. Introducción. Repaso de resultados conocidos AMPLIACIÓN DE ECUACIONES DIFERENCIALES GRADO EN MATEMÁTICAS, Universidad de Sevilla
Control Moderno. Ene.-Jun Diseño de controlador por retroalimentación de estado. Dr. Rodolfo Salinas. mayo 2007
 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Diseño de controlador por retroalimentación de estado Dr. Rodolfo Salinas mayo 2007 Control
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Diseño de controlador por retroalimentación de estado Dr. Rodolfo Salinas mayo 2007 Control
Examen Ingeniería de Control 12/2014
 Examen Ingeniería de Control /04 Examen Ingeniería de Control /04 Examen Ingeniería de Control /04 Examen Ingeniería de Control /04 SOLUCIÓN EJERCICIO DE ESTADO:. (0.75 puntos) Proponer y justificar qué
Examen Ingeniería de Control /04 Examen Ingeniería de Control /04 Examen Ingeniería de Control /04 Examen Ingeniería de Control /04 SOLUCIÓN EJERCICIO DE ESTADO:. (0.75 puntos) Proponer y justificar qué
Teoría de Control, el ejemplo del péndulo *
 Teoría de Control, el ejemplo del péndulo * Eduardo Cerpa ** Índice Resumen A través del clásico ejemplo del péndulo introduciremos la Teoría de Control. Esta teoría estudia cómo modificar la conducta
Teoría de Control, el ejemplo del péndulo * Eduardo Cerpa ** Índice Resumen A través del clásico ejemplo del péndulo introduciremos la Teoría de Control. Esta teoría estudia cómo modificar la conducta
Sistemas lineales de ecuaciones diferenciales. Juan-Miguel Gracia
 Sistemas lineales de ecuaciones diferenciales Juan-Miguel Gracia Índice Sistemas lineales 2 Búsqueda de una solución especial 3 Aplicación a sistemas 4 Problema de condiciones iniciales 2 / 2 Sistemas
Sistemas lineales de ecuaciones diferenciales Juan-Miguel Gracia Índice Sistemas lineales 2 Búsqueda de una solución especial 3 Aplicación a sistemas 4 Problema de condiciones iniciales 2 / 2 Sistemas
Control Moderno. Ene.-Jun Observabilidad y Observadores de Estado. Dr. Rodolfo Salinas. mayo 2007
 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Observabilidad y Observadores de Estado Dr. Rodolfo Salinas mayo 2007 Control Moderno N1 mayo
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 2007 Observabilidad y Observadores de Estado Dr. Rodolfo Salinas mayo 2007 Control Moderno N1 mayo
Control Moderno. Ene.-Jun UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN. Facultad de Ingeniería Mecánica y Eléctrica. Dr. Rodolfo Salinas.
 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 27 Dr. Rodolfo Salinas abril 27 Control Moderno N abril 27 Dr. Rodolfo Salinas Respuesta en el tiempo
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN Facultad de Ingeniería Mecánica y Eléctrica Control Moderno Ene.-Jun. 27 Dr. Rodolfo Salinas abril 27 Control Moderno N abril 27 Dr. Rodolfo Salinas Respuesta en el tiempo
2. Estabilidad en Sistemas Lineales Invariantes en el Tiempo.
 Capítulo 3 2. Estabilidad en Sistemas Lineales Invariantes en el Tiempo. 3.1 Introducción Un sistema estable se define como aquel que tiene una respuesta limitada. Es decir, un sistema es estable si estando
Capítulo 3 2. Estabilidad en Sistemas Lineales Invariantes en el Tiempo. 3.1 Introducción Un sistema estable se define como aquel que tiene una respuesta limitada. Es decir, un sistema es estable si estando
b) Calcular sus cuatro puntos de equilibrio y estudiar la estabilidad en cada uno por el método de linealización.
 Examen Final de EDOs Fecha: 14 de enero de 2013 Problemas Tiempo total: 2 horas y 30 minutos 1. Es un problema largo, pero casi todos los apartados son de tipo estándar. La interdependencia entre apartados
Examen Final de EDOs Fecha: 14 de enero de 2013 Problemas Tiempo total: 2 horas y 30 minutos 1. Es un problema largo, pero casi todos los apartados son de tipo estándar. La interdependencia entre apartados
Estabilidad BIBO de Sistemas Lineales
 Estabilidad BIBO de Sistemas Lineales Notas para el curso del Sistemas Lineales 2 UNIVERSIDAD DE LA REPÚBLICA FACULTAD DE INGENIERÍA INSTITUTO DE INGENIERÍA ELÉCTRICA Montevideo, segundo semestre del 27
Estabilidad BIBO de Sistemas Lineales Notas para el curso del Sistemas Lineales 2 UNIVERSIDAD DE LA REPÚBLICA FACULTAD DE INGENIERÍA INSTITUTO DE INGENIERÍA ELÉCTRICA Montevideo, segundo semestre del 27
Análisis de Sistemas No Lineales
 Análisis de Sistemas No Lineales Análisis de Estabilidad: Caso No Autónomo Dr. Fernando Ornelas Tellez Universidad Michoacana de San Nicolas de Hidalgo Morelia, Michoacán Sistemas de Control Dr. Fernando
Análisis de Sistemas No Lineales Análisis de Estabilidad: Caso No Autónomo Dr. Fernando Ornelas Tellez Universidad Michoacana de San Nicolas de Hidalgo Morelia, Michoacán Sistemas de Control Dr. Fernando
1. Ecuaciones lineales con coeficientes constantes. Ecuaciones de primer orden. 2. Encontrar la solución de los siguientes problemas de valor inicial.
 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes problemas de valor inicial. ẋ =5x, x0) =.. ẋ + x =0, x) =.. ẋ + x = te t, x0) =. si
. Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes problemas de valor inicial. ẋ =5x, x0) =.. ẋ + x =0, x) =.. ẋ + x = te t, x0) =. si
EJERCICIOS RESUELTOS Y PROPUESTOS
 UNIVERSIDAD NACIONAL DE INGENIERÍA Facultad de Ingeniería Mecánica MT 227 Control Moderno y Óptimo EJERCICIOS RESUELTOS Y PROPUESTOS Estabilidad según Lyapunov (1) Un buen modelo de un niño impulsandose
UNIVERSIDAD NACIONAL DE INGENIERÍA Facultad de Ingeniería Mecánica MT 227 Control Moderno y Óptimo EJERCICIOS RESUELTOS Y PROPUESTOS Estabilidad según Lyapunov (1) Un buen modelo de un niño impulsandose
Práctica 5. Autovalores y autovectores. Diagonalización de matrices y de transformaciones lineales.
 Práctica 5 Autovalores y autovectores Diagonalización de matrices y de transformaciones lineales Nota: salvo indicación particular, se considera que todas las matrices pertenecen a C n n 1 Encuentre los
Práctica 5 Autovalores y autovectores Diagonalización de matrices y de transformaciones lineales Nota: salvo indicación particular, se considera que todas las matrices pertenecen a C n n 1 Encuentre los
El método de súper y sub soluciones en el espacio de funciones casi periódicas.
 El método de súper y sub soluciones en el espacio de funciones casi periódicas. Universidad de Buenos Aires - IMAS (CONICET) UMA - Bahía Blanca - 2016 Super y sub soluciones Problema periódico asociado
El método de súper y sub soluciones en el espacio de funciones casi periódicas. Universidad de Buenos Aires - IMAS (CONICET) UMA - Bahía Blanca - 2016 Super y sub soluciones Problema periódico asociado
ECUACIONES DIFERENCIALES ORDINARIAS. HOJA 7. Estabilidad
 ECUACIONES DIFERENCIALES ORDINARIAS. HOJA 7. ESTABILIDAD DE LOS SISTEMAS NO LINEALES. PRINCIPIO DE LINEALIZACIÓN. TEOREMA DE GROBMAN-HARTMAN Estabilidad 1. Definición. Sea f : Ω R n R n un campo C 1, y
ECUACIONES DIFERENCIALES ORDINARIAS. HOJA 7. ESTABILIDAD DE LOS SISTEMAS NO LINEALES. PRINCIPIO DE LINEALIZACIÓN. TEOREMA DE GROBMAN-HARTMAN Estabilidad 1. Definición. Sea f : Ω R n R n un campo C 1, y
Introducción al Control Óptimo
 Ingeniería en Control y Automatización Introducción al Control Óptimo Aplicación a sistemas de control moderno ERÍA DEL CNRL III de diciembre de 6 Autor: M. en C. Rubén Velázquez Cuevas Escuela Superior
Ingeniería en Control y Automatización Introducción al Control Óptimo Aplicación a sistemas de control moderno ERÍA DEL CNRL III de diciembre de 6 Autor: M. en C. Rubén Velázquez Cuevas Escuela Superior
MT227 Sistemas Lineales. Función de transferencia. Elizabeth Villota
 MT227 Sistemas Lineales. Función de transferencia Elizabeth Villota 1 Sistemas Lineales Sistema no lineal, forma espacio de estados: Sea la salida correspondiente a la condición inicial y entrada escrita
MT227 Sistemas Lineales. Función de transferencia Elizabeth Villota 1 Sistemas Lineales Sistema no lineal, forma espacio de estados: Sea la salida correspondiente a la condición inicial y entrada escrita
Breve revisión de estabilidad de sistemas dinámicos
 Breve revisión de estabilidad de sistemas dinámicos Estabilidad de Sistemas Eléctricos de Potencia Pablo Monzón Instituto de Ingeniería Eléctrica (IIE) Facultad de Ingeniería-Universidad de la República
Breve revisión de estabilidad de sistemas dinámicos Estabilidad de Sistemas Eléctricos de Potencia Pablo Monzón Instituto de Ingeniería Eléctrica (IIE) Facultad de Ingeniería-Universidad de la República
Parte I. Diseño utilizando Variables de Estado
 Parte I. Diseño utilizando Variables de Estado El control de un proceso representado a través de variables de estado nos proporciona la ventaja de que se tendrán a todas las variables del proceso cumpliendo
Parte I. Diseño utilizando Variables de Estado El control de un proceso representado a través de variables de estado nos proporciona la ventaja de que se tendrán a todas las variables del proceso cumpliendo
Ecuación algebraica de Riccati
 Ecuación algebraica de Riccati Definiciones básicas La ecuación de Riccati es a esta se le asocia una matriz de Hamilton de dimensión Definiciones básicas Lema: El espectro s(h) del conjunto de eigenvalores
Ecuación algebraica de Riccati Definiciones básicas La ecuación de Riccati es a esta se le asocia una matriz de Hamilton de dimensión Definiciones básicas Lema: El espectro s(h) del conjunto de eigenvalores
Introducción a la optimización con algoritmos. Ejercicios. 0 2 f(x + t(y x))(y x)dt. J(x + t(y x))(y x)dt siendo J la matriz Jacobiana de F.
 Introducción a la optimización con algoritmos Ejercicios Preliminares 1. Demostrar que si f C 2 (IR n ), f : IR n IR entonces f(y) f(x) = 1 0 2 f(x + t(y x))(y x)dt. 2. Demostrar que si F C 1 (IR n ),
Introducción a la optimización con algoritmos Ejercicios Preliminares 1. Demostrar que si f C 2 (IR n ), f : IR n IR entonces f(y) f(x) = 1 0 2 f(x + t(y x))(y x)dt. 2. Demostrar que si F C 1 (IR n ),
SOLUCIONARIO PROBLEMAS REALIMENTACION DE ESTADOS
 SOLUCIONARIO PROBLEMAS REALIMENTACION DE ESTADOS P1: Sea un servo descrito por la función de transferencia de estados digital. Deseamos diseñar un control por realimentación a) Escriba las ecuaciones de
SOLUCIONARIO PROBLEMAS REALIMENTACION DE ESTADOS P1: Sea un servo descrito por la función de transferencia de estados digital. Deseamos diseñar un control por realimentación a) Escriba las ecuaciones de
Formulación del problema de la ruta más corta en programación lineal
 Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Control Moderno - Ing. Electrónica Ejercicio Resuelto 3: Teorema de Cayley-Hamilton
 Control Moderno - Ing. Electrónica Ejercicio Resuelto 3: Teorema de Cayley-Hamilton Introducción A continuación se presentan unos pocos y simples ejemplos que muestran como puede emplearse el Teorema de
Control Moderno - Ing. Electrónica Ejercicio Resuelto 3: Teorema de Cayley-Hamilton Introducción A continuación se presentan unos pocos y simples ejemplos que muestran como puede emplearse el Teorema de
Ecuaciones diferenciales con retardo
 Ecuaciones diferenciales con retardo Clase 1, versión preliminar (las críticas son bienvenidas) 1 Introducción Con probabilidad 1, la primera clase de un primer curso sobre ecuaciones diferenciales comienza
Ecuaciones diferenciales con retardo Clase 1, versión preliminar (las críticas son bienvenidas) 1 Introducción Con probabilidad 1, la primera clase de un primer curso sobre ecuaciones diferenciales comienza
Estabilidad de ecuaciones diferenciales
 Capítulo 3 Estabilidad de ecuaciones diferenciales En este tema estudiaremos como resolver sistema de ecuaciones diferenciales lineales de coeficientes constantes utilizando la transformada de Laplace,
Capítulo 3 Estabilidad de ecuaciones diferenciales En este tema estudiaremos como resolver sistema de ecuaciones diferenciales lineales de coeficientes constantes utilizando la transformada de Laplace,
Lección 6: Ecuaciones diferenciales
 Lección 6: Ecuaciones diferenciales 61 Introducción La estática comparativa ha dominado el estudio de la economía durante mucho tiempo, y aún hoy se sigue utilizando para resolver muchos problemas económicos
Lección 6: Ecuaciones diferenciales 61 Introducción La estática comparativa ha dominado el estudio de la economía durante mucho tiempo, y aún hoy se sigue utilizando para resolver muchos problemas económicos
Sistemas dinámicos - Estabilidad
 Sistemas dinámicos - Estabilidad Por correcciones, dudas o sugerencias escribir a mijailapor@gmail.com 1. Caracterización general A diferencia de los análisis estático o estático-comparativo, donde se
Sistemas dinámicos - Estabilidad Por correcciones, dudas o sugerencias escribir a mijailapor@gmail.com 1. Caracterización general A diferencia de los análisis estático o estático-comparativo, donde se
3. Sistemas de n ecuaciones diferenciales lineales de primer orden
 Dpto Matemática Aplicada, Facultad de Informática, UPM EDO Sistemas Lineales 1 3 Sistemas de n ecuaciones diferenciales lineales de primer orden Se define un sistema de ecuaciones diferenciales lineales
Dpto Matemática Aplicada, Facultad de Informática, UPM EDO Sistemas Lineales 1 3 Sistemas de n ecuaciones diferenciales lineales de primer orden Se define un sistema de ecuaciones diferenciales lineales
Diagonalización de matrices
 7 Diagonalización de matrices 7.1. Matrices diagonalizables Existen diversos procesos en los que el estado en cada uno de sus pasos se puede representar por un determinado vector y en los que, además,
7 Diagonalización de matrices 7.1. Matrices diagonalizables Existen diversos procesos en los que el estado en cada uno de sus pasos se puede representar por un determinado vector y en los que, además,
VALORES PROPIOS (AUTOVALORES) VECTORES PROPIOS (AUTOVECTORES)
 VALORES PROPIOS (AUTOVALORES) Y VECTORES PROPIOS (AUTOVECTORES) Autovalores y Autovectores Los vectores propios o autovectores de una matriz A son todos los vectores x i 0, a los que la transformación
VALORES PROPIOS (AUTOVALORES) Y VECTORES PROPIOS (AUTOVECTORES) Autovalores y Autovectores Los vectores propios o autovectores de una matriz A son todos los vectores x i 0, a los que la transformación
Sistemas autónomos. Introducción a la teoría cualitativa.
 Lección 4 Sistemas autónomos. Introducción a la teoría cualitativa. 4.1 Sistemas autónomos. Mapas de fase. En esta lección nos centraremos en el estudio de sistemas autónomos, es decir, aquellos que pueden
Lección 4 Sistemas autónomos. Introducción a la teoría cualitativa. 4.1 Sistemas autónomos. Mapas de fase. En esta lección nos centraremos en el estudio de sistemas autónomos, es decir, aquellos que pueden
E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 9: Sistemas de EDOs lineales
 ETS Minas: Métodos Matemáticos Resumen y ejemplos Tema 9: Sistemas de EDOs lineales Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Noviembre
ETS Minas: Métodos Matemáticos Resumen y ejemplos Tema 9: Sistemas de EDOs lineales Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Noviembre
Carlos Mario Vélez S. Universidad EAFIT. Temas 1. Generalidades sobre estabilidad 2. Estabilidad de Lyapunov
 Objetivo específico Presentar la teoría de estabilidad de Lyapunov aplicada a sistema lineales y no lineales e ilustrar su uso en el análisis y diseño de sistemas no lineales Temas.. Método directo de
Objetivo específico Presentar la teoría de estabilidad de Lyapunov aplicada a sistema lineales y no lineales e ilustrar su uso en el análisis y diseño de sistemas no lineales Temas.. Método directo de
1. Es un problema largo, pero casi todos los apartados son de tipo estándar. Consideramos el sistema no lineal 2D cuadrático dado por
 Fecha: 7 de enero de 24 Problemas Tiempo total: 2 horas y 3 minutos Es un problema largo, pero casi todos los apartados son de tipo estándar Consideramos el sistema no lineal 2D cuadrático dado por { x
Fecha: 7 de enero de 24 Problemas Tiempo total: 2 horas y 3 minutos Es un problema largo, pero casi todos los apartados son de tipo estándar Consideramos el sistema no lineal 2D cuadrático dado por { x
Introducción. Por favor. No olvide bajar el tono a su. Franco E., Rosero E., Ramírez J.M. () SISTEMAS DE CONTROL II GICI / 42
 Introducción Por favor No olvide bajar el tono a su teléfono móvil!. Franco E., Rosero E., Ramírez J.M. () SISTEMAS DE CONTROL II GICI 2008 1 / 42 Introducción UNIDAD I ESTABILIDAD DE SISTEMAS DINÁMICOS
Introducción Por favor No olvide bajar el tono a su teléfono móvil!. Franco E., Rosero E., Ramírez J.M. () SISTEMAS DE CONTROL II GICI 2008 1 / 42 Introducción UNIDAD I ESTABILIDAD DE SISTEMAS DINÁMICOS
Apéndice sobre ecuaciones diferenciales lineales
 Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 1. Determinante wronskiano 2 1.1. Wronskiano de f 1 (t), f 2 (t),..., f n (t)............... 3 1.2. Derivada
Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 1. Determinante wronskiano 2 1.1. Wronskiano de f 1 (t), f 2 (t),..., f n (t)............... 3 1.2. Derivada
Solución de Sistemas de Ecuaciones Diferenciales Lineales
 Solución de Sistemas de Ecuaciones Diferenciales Lineales Departamento de Matemáticas, CCIR/ITESM 9 de febrero de Índice..Introducción.................................................Ejemplo.................................................3.Ejemplo................................................
Solución de Sistemas de Ecuaciones Diferenciales Lineales Departamento de Matemáticas, CCIR/ITESM 9 de febrero de Índice..Introducción.................................................Ejemplo.................................................3.Ejemplo................................................
14 Sistemas lineales de ecuaciones diferenciales con coeficientes
 Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 14 Sistemas lineales de ecuaciones diferenciales con coeficientes constantes 14.1 Definición Se llama sistema lineal con coeficientes constantes al
Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 14 Sistemas lineales de ecuaciones diferenciales con coeficientes constantes 14.1 Definición Se llama sistema lineal con coeficientes constantes al
Tema 8 Ecuaciones diferenciales
 Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
Raíz cuadrada. Superficies de Riemann
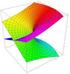 Raíz cuadrada Superficies de Riemann Aplicación: Circuito RLC (a) (b) Aplicación: Circuito RLC Para el circuito (a): De la ley de Ohm con Aplicación: Circuito RLC Es más conveniente utilizar un voltaje
Raíz cuadrada Superficies de Riemann Aplicación: Circuito RLC (a) (b) Aplicación: Circuito RLC Para el circuito (a): De la ley de Ohm con Aplicación: Circuito RLC Es más conveniente utilizar un voltaje
MODELOS DE SERIES DE TIEMPO 1. Modelos capaces de predecir, interpretar y evaluar hipótesis con datos económicos y financieros.
 MODELOS DE SERIES DE TIEMPO 1 Introducción Modelos capaces de predecir, interpretar y evaluar hipótesis con datos económicos y financieros. Originalmente tuvieron como objetivo hacer predicciones. Descomposición
MODELOS DE SERIES DE TIEMPO 1 Introducción Modelos capaces de predecir, interpretar y evaluar hipótesis con datos económicos y financieros. Originalmente tuvieron como objetivo hacer predicciones. Descomposición
Unidad V Respuesta de los sistemas de control
 Unidad V Respuesta de los sistemas de control MC Nicolás Quiroz Hernández Un controlador automático compara el valor real de la salida de una planta con la entrada de referencia (el valor deseado), determina
Unidad V Respuesta de los sistemas de control MC Nicolás Quiroz Hernández Un controlador automático compara el valor real de la salida de una planta con la entrada de referencia (el valor deseado), determina
UNIDAD DIDÁCTICA I Teoría de Filtrado Óptimo 1
 Índice PRÓLOGO IX UNIDAD DIDÁCTICA I Teoría de Filtrado Óptimo 1 1 Representación de Estado de Sistemas Lineales 5 11 Representación de Estado en Tiempo Continuo 5 12 Matriz de Transición 1 121 Definición
Índice PRÓLOGO IX UNIDAD DIDÁCTICA I Teoría de Filtrado Óptimo 1 1 Representación de Estado de Sistemas Lineales 5 11 Representación de Estado en Tiempo Continuo 5 12 Matriz de Transición 1 121 Definición
1 Control Óptimo. 1.1 Introducción Problema típico de control óptimo
 1 Control Óptimo 1.1 Introducción El control óptimo es una rama del control moderno que se relaciona con el diseño de controladores para sistemas dinámicos tal que se minimice una función de medición que
1 Control Óptimo 1.1 Introducción El control óptimo es una rama del control moderno que se relaciona con el diseño de controladores para sistemas dinámicos tal que se minimice una función de medición que
ECUACIONES DIFERENCIALES ORDINARIAS. HOJA 8. Conjuntos invariantes
 ECUACIONES DIFERENCIALES ORDINARIAS. HOJA 8. CONJUNTOS INVARIANTES Y CONJUNTOS LÍMITE. ESTABILIDAD POR EL MÉTODO DE LIAPUNOV. Conjuntos invariantes 1. Definición. Se dice que un conjunto D Ω es positivamente
ECUACIONES DIFERENCIALES ORDINARIAS. HOJA 8. CONJUNTOS INVARIANTES Y CONJUNTOS LÍMITE. ESTABILIDAD POR EL MÉTODO DE LIAPUNOV. Conjuntos invariantes 1. Definición. Se dice que un conjunto D Ω es positivamente
AUTOMATIZACION Y CONTROL DE PROCESOS FACEyT UNT ESTABILIDAD DE LOS SISTEMAS EN LAZO CERRADO
 Análisis Cualitativo de la Respuesta Temporal de un Sistema Si se conocen la función de transferencia G(s) de un dado sistema y la entrada x(t), se puede evaluar la salida y(t) a partir de: y(s) G (s )
Análisis Cualitativo de la Respuesta Temporal de un Sistema Si se conocen la función de transferencia G(s) de un dado sistema y la entrada x(t), se puede evaluar la salida y(t) a partir de: y(s) G (s )
Controlabilidad, Observabilidad y Detactabilidad
 Controlabilidad, Observabilidad y Detactabilidad Controlabilidad: Definición básica Considere el siguiente sistema lineal e invariante en el tiempo Controlabilidad: diremos que el par (A,B) es controlable
Controlabilidad, Observabilidad y Detactabilidad Controlabilidad: Definición básica Considere el siguiente sistema lineal e invariante en el tiempo Controlabilidad: diremos que el par (A,B) es controlable
Elementos de control en lazo cerrado 14 de diciembre de 2011
 . Introducción Elementos de control en lazo cerrado 4 de diciembre de 2 d i d o r C u G o y d m Figura : Lazo de control estándar. La Figura muestra un lazo de control elemental. En dicha figura, G o corresponde
. Introducción Elementos de control en lazo cerrado 4 de diciembre de 2 d i d o r C u G o y d m Figura : Lazo de control estándar. La Figura muestra un lazo de control elemental. En dicha figura, G o corresponde
Controlabilidad completa del estado para sistemas en tiempo continuo
 Capítulo 11: CONTROLABILIDAD Y OBSERVABILIDAD Se dice que un sistema es controlable en el instante t0 si es posible llevarlo de cualquier estado inicial x(t0) a cualquier otro estado, empleando un vector
Capítulo 11: CONTROLABILIDAD Y OBSERVABILIDAD Se dice que un sistema es controlable en el instante t0 si es posible llevarlo de cualquier estado inicial x(t0) a cualquier otro estado, empleando un vector
1. Problema de Generación de Trayectoria
 Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227C) Clase11-1 Elizabeth Villota Cerna Semestre 21I - UNI
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227C) Clase11-1 Elizabeth Villota Cerna Semestre 21I - UNI
= = Amplificador inversor. Considere el amplificador operacional de la figura Obtengamos el voltaje de salida
 Amplificadores operacionales. Los amplificadores operacionales, también conocidos como amp ops, se usan con frecuencia para amplificar las señales de los circuitos Los amp ops también se usan con frecuencia
Amplificadores operacionales. Los amplificadores operacionales, también conocidos como amp ops, se usan con frecuencia para amplificar las señales de los circuitos Los amp ops también se usan con frecuencia
Sistemas de control Versión Estabilidad de Sistemas Método de Routh
 Sistemas de control 67- Versión Estabilidad de Sistemas Método de Routh Se analizarán temas relacionados con la estabilidad de los sistemas lineales; la misma es una propiedad inherente del sistema y no
Sistemas de control 67- Versión Estabilidad de Sistemas Método de Routh Se analizarán temas relacionados con la estabilidad de los sistemas lineales; la misma es una propiedad inherente del sistema y no
Diferencia entre análisis y síntesis
 Diferencia entre análisis y síntesis ANÁLISIS Excitación conocida Respuesta? Circuito conocido xt () y()? t SÍNTESIS Y DISEÑO Excitación conocida Circuito? Respuesta deseada valores elementos? xt () yt
Diferencia entre análisis y síntesis ANÁLISIS Excitación conocida Respuesta? Circuito conocido xt () y()? t SÍNTESIS Y DISEÑO Excitación conocida Circuito? Respuesta deseada valores elementos? xt () yt
Prof. Virginia Mazzone - Mariana Suarez
 SISTEMAS NO LINEALES SISTEMAS DE SEGUNDO ORDEN Prof. Virginia Mazzone - Prof. Mariana Suarez 1 Introducción Método de isoclinas Ejemplos 3 Introducción Un sistema de segundo orden autónomo está representado
SISTEMAS NO LINEALES SISTEMAS DE SEGUNDO ORDEN Prof. Virginia Mazzone - Prof. Mariana Suarez 1 Introducción Método de isoclinas Ejemplos 3 Introducción Un sistema de segundo orden autónomo está representado
Control Moderno: Paradigmas y Desafíos
 Control Moderno: Paradigmas y Desafíos Elizabeth Villota Cerna Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica 1 Paradigma del control por realimentación entradas exógenas salidas
Control Moderno: Paradigmas y Desafíos Elizabeth Villota Cerna Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica 1 Paradigma del control por realimentación entradas exógenas salidas
Diagonalización de matrices
 Diagonalización de matrices María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Diagonalización de matrices Matemáticas I 1 / 22 Valores y vectores propios de una matriz Definición
Diagonalización de matrices María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Diagonalización de matrices Matemáticas I 1 / 22 Valores y vectores propios de una matriz Definición
MODELACION EN VARIABLES DE ESTADO
 CAPÍTULO VIII INGENIERÍA DE SISTEMAS I MODELACION EN VARIABLES DE ESTADO 8.1. DEFINICIONES Estado: El estado de un sistema dinámico es el conjunto más pequeño de variables de modo que el conocimiento de
CAPÍTULO VIII INGENIERÍA DE SISTEMAS I MODELACION EN VARIABLES DE ESTADO 8.1. DEFINICIONES Estado: El estado de un sistema dinámico es el conjunto más pequeño de variables de modo que el conocimiento de
ECUACIONES DIFERENCIALES ORDINARIAS, MAT1532 EXAMEN FINAL
 ECUACIONES DIFERENCIALES ORDINARIAS, MAT1532 EXAMEN FINAL PROFESORES ISABEL FLORES Y ROLANDO REBOLLEDO Ejercicio 1. [15 %] Resolver la ecuación 1) x + 5x + 6x = 25t 2 cos t Solución. Esta ecuación se puede
ECUACIONES DIFERENCIALES ORDINARIAS, MAT1532 EXAMEN FINAL PROFESORES ISABEL FLORES Y ROLANDO REBOLLEDO Ejercicio 1. [15 %] Resolver la ecuación 1) x + 5x + 6x = 25t 2 cos t Solución. Esta ecuación se puede
Automatización de Procesos/Sistemas de Control Ing. Biomédica e Ing. Electrónica Capitulo V Controladores PID
 Automatización de Procesos/Sistemas de Control Ing. Biomédica e Ing. Electrónica Capitulo V Controladores PID D.U. Campos-Delgado Facultad de Ciencias UASLP Enero-Junio/2014 1 CONTENIDO Motivación Estructura
Automatización de Procesos/Sistemas de Control Ing. Biomédica e Ing. Electrónica Capitulo V Controladores PID D.U. Campos-Delgado Facultad de Ciencias UASLP Enero-Junio/2014 1 CONTENIDO Motivación Estructura
0.1. Error en Estado Estacionario
 0. Error en Estado Estacionario 0.. Error en Estado Estacionario La respuesta permanente es aquella que se alcanza cuando el sistema se establece y es muy importante su estudio pues informa lo que sucede
0. Error en Estado Estacionario 0.. Error en Estado Estacionario La respuesta permanente es aquella que se alcanza cuando el sistema se establece y es muy importante su estudio pues informa lo que sucede
Lugar Geométrico de las Raíces Herramienta para diseño de sistemas de control
 Lugar Geométrico de las Raíces Herramienta para diseño de sistemas de control Elizabeth Villota Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica UNI-FIM 1 Modelado Modelo: representación
Lugar Geométrico de las Raíces Herramienta para diseño de sistemas de control Elizabeth Villota Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica UNI-FIM 1 Modelado Modelo: representación
Métodos de gradiente. Métodos de Krylov
 Métodos de gradiente. Métodos de Krylov Damián Ginestar Peiró Departamento de Matemática Aplicada Universidad Politécnica de Valencia Curso 2012-2013 (UPV) Métodos de gradiente. Métodos de Krylov Curso
Métodos de gradiente. Métodos de Krylov Damián Ginestar Peiró Departamento de Matemática Aplicada Universidad Politécnica de Valencia Curso 2012-2013 (UPV) Métodos de gradiente. Métodos de Krylov Curso
Automatización de Procesos/Sistemas de Control Ing. Biomédica e Ing. Electrónica Capitulo VI Lugar de las Raíces
 Automatización de Procesos/Sistemas de Control Ing. Biomédica e Ing. Electrónica Capitulo VI Lugar de las Raíces D.U. Campos-Delgado Facultad de Ciencias UASLP Enero-Junio/2014 1 CONTENIDO Motivación Pasos
Automatización de Procesos/Sistemas de Control Ing. Biomédica e Ing. Electrónica Capitulo VI Lugar de las Raíces D.U. Campos-Delgado Facultad de Ciencias UASLP Enero-Junio/2014 1 CONTENIDO Motivación Pasos
Consideremos la función de transferencia de un sistema en lazo cerrado: 1 + KG(s)H(s) = 0 (2) K > 4 (4)
 LUGAR GEOMÉTRICO DE LAS RAICES INTRODUCCION Cuando un parámetro de un sistema cambia, las raíces de su ecuación característica se mueven en el plano s; estas variaciones es lo que define el Lugar Geométrico
LUGAR GEOMÉTRICO DE LAS RAICES INTRODUCCION Cuando un parámetro de un sistema cambia, las raíces de su ecuación característica se mueven en el plano s; estas variaciones es lo que define el Lugar Geométrico
Sistemas de Control II Prof. Diego Mauricio Rivera Sistemas de control en tiempo discreto
 Sistemas de Control II Prof. Diego Mauricio Rivera diegomrivera@gmail.com Sistemas de control en tiempo discreto Actualizado Marzo 22 de 2017 Contenido Introducción al control digital Señales en un sistema
Sistemas de Control II Prof. Diego Mauricio Rivera diegomrivera@gmail.com Sistemas de control en tiempo discreto Actualizado Marzo 22 de 2017 Contenido Introducción al control digital Señales en un sistema
Respuesta temporal, Sistemas de orden 1
 Respuesta temporal, Sistemas de orden Transparencias Introducción a la Teoría de Control R. Canetti 203 RESPUESTA TEMPORAL Cómo responde un sistema dinámico lineal, de parámetros concentrados, invariante
Respuesta temporal, Sistemas de orden Transparencias Introducción a la Teoría de Control R. Canetti 203 RESPUESTA TEMPORAL Cómo responde un sistema dinámico lineal, de parámetros concentrados, invariante
A = α cuyos VAPs son λ = 2 y λ ± = α ± i. (No hace falta que comprobeis este dato.) a) Calcular la solución general real del sistema x = Ax.
 Examen Final de Ecuaciones Diferenciales Fecha: 7 de junio de 013 3 Problemas (7.5 puntos) Tiempo total: horas 30 minutos Problema 1 [.5 puntos]. Consideramos la matriz A = α 1 0 1 α 0, α R, 0 0 cuyos
Examen Final de Ecuaciones Diferenciales Fecha: 7 de junio de 013 3 Problemas (7.5 puntos) Tiempo total: horas 30 minutos Problema 1 [.5 puntos]. Consideramos la matriz A = α 1 0 1 α 0, α R, 0 0 cuyos
Antecedentes de Control
 Apéndice A Antecedentes de Control Para cualquier tipo de análisis de sistemas de control, es importante establecer ciertos conceptos básicos. Sistemas de control retroalimentados Un sistema que mantiene
Apéndice A Antecedentes de Control Para cualquier tipo de análisis de sistemas de control, es importante establecer ciertos conceptos básicos. Sistemas de control retroalimentados Un sistema que mantiene
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias.
 Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Por ej. la respuesta de un sistema de segundo orden a una entrada escalón unitaria es:
 ERROR EN ESTADO ESTABLE La respuesta en el dominio del tiempo de un sistema de control correspondiente a cierta entrada se puede dividir normalmente en dos partes: a) respuesta transitoria: es la que tiende
ERROR EN ESTADO ESTABLE La respuesta en el dominio del tiempo de un sistema de control correspondiente a cierta entrada se puede dividir normalmente en dos partes: a) respuesta transitoria: es la que tiende
Lista de ejercicios # 4
 UNIVERSIDAD DE COSTA RICA MA-5 FACULTAD DE CIENCIAS Ecuaciones Diferenciales para Ingeniería ESCUELA DE MATEMÁTICA Primer Ciclo del 5 Lista de ejercicios # 4 Sistemas de ecuaciones diferenciales. EPII-II-
UNIVERSIDAD DE COSTA RICA MA-5 FACULTAD DE CIENCIAS Ecuaciones Diferenciales para Ingeniería ESCUELA DE MATEMÁTICA Primer Ciclo del 5 Lista de ejercicios # 4 Sistemas de ecuaciones diferenciales. EPII-II-
VALORES Y VECTORES PROPIOS
 VALORES Y VECTORES PROPIOS En diversos campos de la ingeniería y las matemáticas surge el problema de calcular los valores escalares λ y los vectores x 0 tales que para la matriz cuadrada A se cumple Ax
VALORES Y VECTORES PROPIOS En diversos campos de la ingeniería y las matemáticas surge el problema de calcular los valores escalares λ y los vectores x 0 tales que para la matriz cuadrada A se cumple Ax
5 Estabilidad de soluciones de equilibrio
 Prácticas de Ecuaciones Diferenciales G. Aguilar, N. Boal, C. Clavero, F. Gaspar Estabilidad de soluciones de equilibrio Objetivos: Clasificar y analizar los puntos de equilibrio que aparecen en los sistemas
Prácticas de Ecuaciones Diferenciales G. Aguilar, N. Boal, C. Clavero, F. Gaspar Estabilidad de soluciones de equilibrio Objetivos: Clasificar y analizar los puntos de equilibrio que aparecen en los sistemas
Subespacios de espacios vectoriales
 Subespacios de espacios vectoriales Objetivos. Estudiar la definición, el criterio y algunos ejemplos de subespacios vectoriales. Muchos espacios vectoriales importantes (por ejemplo, espacio de soluciones
Subespacios de espacios vectoriales Objetivos. Estudiar la definición, el criterio y algunos ejemplos de subespacios vectoriales. Muchos espacios vectoriales importantes (por ejemplo, espacio de soluciones
1. El Teorema de Rolle Generalizado.
 Proyecto III: Los Teoremas de Rolle y del valor Medio Objetivos: Profundizar el estudio de algunos teoremas del cálculo diferencial 1 El Teorema de Rolle Generalizado La formulación más común del Teorema
Proyecto III: Los Teoremas de Rolle y del valor Medio Objetivos: Profundizar el estudio de algunos teoremas del cálculo diferencial 1 El Teorema de Rolle Generalizado La formulación más común del Teorema
SISTEMAS LINEALES DE ECUACIONES DIFERENCIALES HOMOGÉNEAS DE PRIMER ORDEN
 SISTEMAS LINEALES DE ECUACIONES DIFERENCIALES HOMOGÉNEAS DE PRIMER ORDEN Alejandro Lugon 26 de mayo de 2010 1. Ecuaciones planares: dos dimensiones El sistema homogéneo: ẋ a 11 x + a 12 y (1) ẏ a 21 x
SISTEMAS LINEALES DE ECUACIONES DIFERENCIALES HOMOGÉNEAS DE PRIMER ORDEN Alejandro Lugon 26 de mayo de 2010 1. Ecuaciones planares: dos dimensiones El sistema homogéneo: ẋ a 11 x + a 12 y (1) ẏ a 21 x
MAT1202: Algebra Lineal GUIA N 6 Otoño 2002 Valores y Vectores Propios
 Pontificia Universidad Católica de Chile Facultad de Matemáticas MAT1202: Algebra Lineal GUIA N 6 Otoño 2002 Valores y Vectores Propios 1. Determine los valores y vectores propios de 0 3 A + I = 1 3 A
Pontificia Universidad Católica de Chile Facultad de Matemáticas MAT1202: Algebra Lineal GUIA N 6 Otoño 2002 Valores y Vectores Propios 1. Determine los valores y vectores propios de 0 3 A + I = 1 3 A
Notas Sobre Estabilidad BIBO y Estabilidad Interna en Ciertas Clases de Sistemas
 F. Najson Sistemas Lineales 2 Octubre 28 Notas Sobre Estabilidad BIBO y Estabilidad Interna en Ciertas Clases de Sistemas Sobre Estabilidad BIBO Comencemos definiendo ciertas clases de funciones necesarias
F. Najson Sistemas Lineales 2 Octubre 28 Notas Sobre Estabilidad BIBO y Estabilidad Interna en Ciertas Clases de Sistemas Sobre Estabilidad BIBO Comencemos definiendo ciertas clases de funciones necesarias
