Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada
|
|
|
- Sebastián Guzmán Hernández
- hace 5 años
- Vistas:
Transcripción
1 Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 7C) Clase 3- Elizabeth Villota Cerna Semestre 9 I - UNI /4/9. Linealización El reemplazar un sistema no lineal por su aproximación lineal se denomina linealización. Una motivación para la linealización es que el comportamiento dinámico de muchos sistemas no lineales dentro de un rango de variables puede ser aproximado a modelos de sistemas lineales. Siendo ese el caso, podemos usar técnicas bien desarrolladas de análisis y síntesis de sistemas lineales para analizar un sistema no lineal. Cabe destacar que se debe tener mucho cuidado cuando se realiza el análisis de sistemas linealizados ya que la intención no es introducir errores al analizar sistemas no lineales. Consideremos el caso de un sistema (elemento no lineal) con una variable de estado x y una variable de salida y que están relacionadas por la siguiente ecuación: y = h(x), () donde la función h : R R es contínua y diferenciable; esto es h C. Consideremos x o como el punto de operación. Si expandemos h en la serie de Taylor alrededor del punto x o se obtiene: y = h(x), = h(x o ) + dh(x o) dx (x x o) + términos de alto orden. () La linealización de h(x) alrededor del punto x o consiste en reemplazar h por una aproximación lineal de la forma: y = h(x o ) + dh(x o) dx (x x o) y = y o + dh(x (3) o) dx (x x o), donde y o = h(x o ). Si ỹ = y y o y x = x x o. Luego, podemos reescribir (3) como: ỹ = dh(x o) x, (4) dx y sobre un rango pequeño de x, la linea (3) es una buena aproximación de la curva y = h(x) en la vecindad del punto de operación x o, ver Fig. para una ilustración de la aproximación. y dh(x y y ) (x x ) dx y h(x) y x x Figura : Aproximación lineal de la función y = h(x) Si h : R n R, esto es, y = h(x,x,,x n ), que significa que la variable dependiente depende de varias variables - se puede aplicar el mismo principio. Sea: x o = [ x o x o x no ] T (5)
2 el punto de operación. La expansión de la serie de Taylor de h alrededor del punto de operación x o resulta en: y h(x o ) = h(x o ) T (x x o ) + términos de alto orden, (6) donde: [ h h(x o ) T = x x=xo h x x=xo h ] x n. (7) x=xo Geométricamente, la linealización de h alrededor de x o se puede pensar como el localizar un plano tangente sobre una superficie no lineal en el punto de operación x o, como mostrado en la Fig.. y h(x) Tangent plane h(x ) x x x Figura : Plano tangente como aproximación lineal de una función de dos variables... Linealizando ecuaciones diferenciales Consideremos ahora un sistema dinámico modelado por un conjunto de ecuaciones diferenciales no lineales: dx = f (x,x,,x n,u,u,,u m ), dx = f (x,x,,x n,u,u,,u m ),. dx n. = f n (x,x,,x n,u,u,,u m ).. (8) Asumiendo que las funciones f i, i =,,,n, son contínuas y diferenciables. El conjunto de las ecuaciones arriba mostradas se puede representar en la forma vectorial por: dx = f(x,u). (9) Sea u e = [ u e u e u ne ] T una entrada constante que fuerza al sistema (9) a que se asiente en un estado de equilibrio x e = [ x e x e x ne ] T; esto es, ue y x e satisfacen: f(x e,u e ) =. () Los estados de equilibrio son llamados también puntos estacionarios, puntos constantes o puntos de reposo, ya que si el sistema se ubica inicialmente en x = x e, luego permanecerá en x(t) = x e para todo tiempo t. Por lo general cuando hablamos de la existencia de un u e nos referimos a condiciones de operación puesto que el sistema necesitaría de esa inyección ya sea de fuerza (torque, etc.) para mantenerse en el punto de equilibrio. Cuando analizamos la dinámica de un sistema no forzado, hacemos u e = y luego buscamos el punto de equilibrio x e para el sistema dinámico dx = f(x), es decir la solución de f(x e) =. En el caso de un sistema dinámico no forzado, éste puede presentar cero, uno o más puntos de equilibrio. Para estudiar y analizar el comportamiento local del sistema alrededor del punto de equilibrio (x e,u e ), se supone que tanto x x e como u u e son pequeños, tal que perturbaciones no lineales pueden ser Sin pérdida de generalidad se puede asumir que x e = y u e =. Ver Notas de clase Clase3-.pdf Clase 3-, pág.
3 ignoradas en comparación a los términos lineales (de orden bajo). Este argumento es similar a cuando usamos aproximaciones de ángulos pequeños, reemplazando sinθ con θ y cosθ con para θ cerca a cero. Si ahora perturbamos el estado de equilibrio haciendo: La expansión de la serie de Taylor resulta en: x = x e + x, u = u e + ũ. () donde: d x f f x (x x e,u e ) =. f n x = f(x e + x,u e + ũ), = f(x e,u e ) + f x (x e,u e ) x + f u (x e,u e ) x + términos de alto orden, f x n. f n x n x = xe, u = u e y f f u (x u e,u e ) =. f n u f u m. f n u m x = xe, u = u e () (3) son las matrices Jacobianas de f con respecto a x y u, evaluadas en el punto de equilibrio, (x e,u e ). Nótese que: d x = d x e + d x = d x, (4) porque x e es una constante. Adicionalmente, f(x e,u e ) =, luego definiendo A R n n y B R n m de la siguiente forma: A = f x (x e,u e ) y B = f u (x e,u e ). (5) Finalmente, eliminando los términos de orden alto, se llega a la siguiente aproximación lineal: d x = A x + Bũ. (6) De forma similar, si las salidas del modelo del sistema no lineal son de la forma: o en notación vectorial: y = h (x,x,,x n,u,u,,u m ), y = h (x,x,,x n,u,u,,u m ),. (7). y p = h p (x,x,,x n,u,u,,u m ). y = h(x,u), (8) entonces la expansión de la serie de Taylor puede ser usada nuevamente para llevar a la aproximación lineal de la ecuación de salida del sistema. Sea: y = y e + ỹ, (9) luego obtenemos: donde: h C = h x (x x e,u e ) =. h p x ỹ = C x + Dũ, () h x n. h p x n x = xe, u = u e R p n, () Clase 3-, pág. 3
4 y, h D = h u (x u e,u e ) =. h p u h u m. h p u m x = xe, u = u e R p m () son las matrices Jacobianas de h con respecto a x y u, evaluadas en el punto de operación (x e,u e ). El hecho de que modelos lineales puedan ser usados para estudiar el comportamiento de un sistema no lineal cerca a los puntos de operación es bien importante. De hecho, lo que haremos en las próximas secciones es aprovechar esta aproximación local lineal de un sistema no lineal para diseñar leyes de control por realimentación que mantengan al sistema cerca al punto de equilibrio (diseño de dinámica). Entonces la realimentación se usará para hacer que las soluciones del sistema controlado permanezcan cerca al punto de operación, ver Fig. 3. x z π/ π 3π/ π x π π/ π/ π z Figura 3: Comparación entre los planos de fase de un sistema no lineal (a) y su aproximación lineal alrededor del origen (b). Nótese que cerca al punto de equilibrio en el centro de las gráficas, los planos de fase (y como consecuencia la dinámica) es practicamente idéntica.. Ejemplo: Vehículo aéreo con impulsadores Considere el movimiento de el vehículo aéreo, tal como el Harrier jump jet mostrado en la Fig. 4. El Harrier es capaz de despegar verticalmente al redireccionar los impulsadores principales hacia abajo y a través del uso de impulsadores pequeños de maniobra que están localizados en sus alas. Un modelo simplificado es mostrado en la Fig. 4(b) donde el enfoque del movimiento del vehículo es en un plano vertical que corta las alas del vehículo. Las ecuaciones de movimiento serán calculadas representando las fuerzas generadas por el impulsador principal y los impulsadores de maniobra como F y F (actuando a una distancia r por debajo del vehículo). Sea (x,y,θ) la posición y la orientación del centro de masa del vehículo. Sea m la masa del vehículo, J el momento de inercia, g la constante graviatacional y c el coeficiente de amortiguamiento. Luego las ecuaciones de movimiento son: mẍ = F cosθ F sinθ cẋ, mÿ = F sinθ + F cosθ cẏ, (3) T θ = rf. Se cree conveniente redefinir las entradas tal que el origen sea considerado el punto de equilibrio del sistema con entrada cero. Haciendo u = F y u = F mg, las ecuaciones resultan: mẍ = mgsinθ cẋ + u cosθ u sinθ, mÿ = mg(cosθ ) cẏ + u sinθ + u cosθ, T θ = ru. (4) Estas ecuaciones definen el movimiento del vehículo como un conjunto de tres ecuaciones diferenciales acopladas. Clase 3-, pág. 4
5 θ y r F (a) Harrier jump jet x (b) Simplified model F Figura 4: (a) Vehículo aéreo con impulsadores y su (b) modelo simplificado donde el impulso neto ha sido descompuesto entre la fuerza horizontal F y la fuerza vertical F actuando a una distancia r del centro de masa. Describiendo la dinámica del vehículo en la forma de espacio de estados: z 4 z 5 dz z 6 = gsinz 3 c m z 4 + u m cosz 3 u m sinz 3, (5) g(cosz 3 ) c m z 5 + u m sinz 3 + u m cosz 3 u J r donde z = [ x y θ ẋ ẏ θ] T... Modelo lineal del vehículo aéreo con impulsadores Suponiendo que u = y u =, la dinámica del sistema se simplica a: z 4 z 5 dz = z 6 gsinz 3 c m z. (6) 4 g(cosz 3 ) c m z 5 Los puntos de equilibrio del sistema están dados cuando se hacen cero las velocidades ẋ, ẏ y θ y escogiendo las siguientes variables que satisfagan la siguiente ecuación: [ ] [ ] gsinz = 3e, z g(cosz 3e ) 3e = θ e =. (7) Entonces, el punto de equilibrio corresponde a la posición vertical del vehículo. Nótese que x e y y e no están especificados. Esto ocurre porque nosotros podriamos trasladar el sistema a una nueva posición (más arriba) y todavia obtener un punto de equilibrio. Calculando la matriz de estados A y la matriz de entrada B: A = f z = ze g c/m, (8) c/m Clase 3-, pág. 5
6 B = f u = ze /m. (9) /m r/j Luego el sistema linealizado del vehículo aéreo con impulsores puede ser escrito como: d x = g c/m x + /m ũ (3) c/m /m r/j 3. Ejemplo: Manipulador Robótico (El siguiente problema ha sido adaptado de Snyder, W.E., Industrial Robots: Computer interfacing and control) En la Fig. 7 se muestra el manipulador robótico θ r. Un representación esquemática del robot es presentada en la Fig. 8 donde se asume una configuración de masas concentradas. La masa m = kg representa la masa del cilindro exterior y se ubica en el centro de masa del mismo. La constante r = m designa la distancia fija entre el centro de masa del cilindro exterior y el centro de rotación. La masa de la carga es representada por m = 3kg y se asume que está localizada al final de un pistón de un brazo telescópico cuya distancia radial r es medida a partir del centro de rotación. El ángulo de rotación del brazo manipulador es θ. Se asume que las entradas al sistema son el torque T θ aplicado en el centro de rotación en la dirección del ángulo θ y la fuerza traslacional (radial) F r aplicada en la dirección r. Despreciar la masa del cilindro interior. Usar g = m/sec como aceleración de la gravedad. Figura 5: Manipulador robótico θ r y r r m g m x Figura 6: Representación esquemática del manipulador robótico θ r Clase 3-, pág. 6
7 Construiremos las ecuaciones de movimiento del sistema en base a las ecuaciones de Lagrange y luego las representaremos en la forma espacio de estados. 3.. Ecuaciones de movimiento usando Lagrange 3 Energía Cinética (T) Primero encontramos la energia cinética total del sistema. Para esto definimos las posiciones de la masa m : x = r cosθ, y = r sinθ. Nótese que r es una constante y que las posiciones de la masa m hacen referencia al movimiento traslacional que experimenta el centro de masa del cilindro externo (masa concentrada). Diferenciando x y y con respecto al tiempo se obtiene: ẋ = r θsinθ, ẏ = r θcosθ. La magnitud del cuadrado del vector velocidad de la masa m es: v = x + y = r θ sin θ + r θ cos θ = r θ. Entonces, la energia cinética de la masa m es: T = m v = m r θ. Ahora derivaremos una expresión para la energia cinética de la segunda masa. La posición de la masa m es: x = rcosθ, y = rsinθ. Nótese que r no es una constante y que la posiciones de la masa m hacen referencia al movimiento traslacional que experimenta la masa de carga (masa concentrada). Diferenciando x y y con respecto al tiempo se obtiene: ẋ = ṙcosθ r θsinθ, ẏ = ṙsinθ + r θcosθ. La magnitud del cuadrado del vector velocidad de la masa m es: v = x + y = (ṙcosθ r θsinθ) + (ṙsinθ + r θcosθ) = ṙ + r θ. Entonces, la energía cinética de la masa m es: T = m v = m (ṙ + r θ ). 3 Energía Potencial (V ) Ahora encontraremos la energía potencial del sistema. La energía potencial de la masa m es: V = m gr sinθ. La energía potencial de la masa m es: V = m grsinθ Ecuaciones de movimiento La función Lagrangiana (o Lagrangiano) para el sistema es: L = T V = m r θ + m (ṙ + r θ ) m gr sinθ m grsinθ. El manipulador posee dos grados de libertad (r y θ). Luego, tenemos dos ecuaciones de movimiento para el sistema: Clase 3-, pág. 7
8 ( ) d L ( θ d L ṙ La primera ecuación de movimiento resulta en: L θ = T θ ) L r = F r m r θ + m r θ + m rṙ θ + gcosθ(m r + m r) = T θ. La segunda ecuación de movimiento viene a ser: m r m r θ + m gsinθ = F r. 3.. Representación espacio de estados Definiendo las siguientes variables: Luego podemos escribir: d z z z 3 z 4 }{{} dz = z = θ, z = θ, z 3 = r, z 4 = ṙ. z m z z 3 z 4 gcosz (m r + m z 3 ) + u m r + m z3 z 4 zz 3 gsinz + u m }{{ } f(z,u), (3) donde u = T θ y u = F r. Asumiendo que la salida está dada por la posición de la masa de carga, v = x = rcosθ y v = y = rsinθ se tiene: [ ] [ ] v z3 cosz =, (3) v z 3 sinz }{{}}{{} v h(z, u) 3.3. Linealización Para encontrar el modelo linealizado del manipulador robótico debemos calcular primero los puntos (estados) de equilibrio Puntos de equilibrio para entradas nulas Considerando entradas nulas (u = y u = ), el modelo del sistema resulta en: dz = z gcosz (m r + m z 3 ) m r + m z 3 z 4 gsinz, (33) e igualando las derivadas a cero, la ecuación que debemos resolver es la siguiente: [ ] gcosz (m r + m z 3 ) = m r + m z3, (34) gsinz Clase 3-, pág. 8
9 como no existe un z tal que cosz = y sinz = simultáneamente, esto significa que el modelo no forzado que hemos considerado para el manipulador robótico no presenta puntos de equilibrio z e ; es decir, el sistema dinámico analizado no presenta condiciones iniciales z() que tal que el sistema permanecerá en ese punto z() indefinidamente ( coincide esto con lo que te dice tu intuición?) Punto de operación (entradas constantes) Considerando entradas constantes (u = u e y u = u e ) e igualando las derivadas a cero resulta: z e gcosz e (m r + m z 3e ) + u e = m r + m z3, (35) z 4e gsinz e + u e m Luego, el modelo del sistema será linealizado alrededor del punto de equilibrio: z e = [ z e z 3e ] T, donde z e y z 3e satisfacen las siguientes ecuaciones: u e cosz e = g(m r + m z 3e ) sinz e = u e. gm Calculando los elementos de las matrices Jacobianas del sistema no lineal definido en (48) tenemos: f f = = z z f f = = z 3 z 4 f gsinz(mr + mz3) f = z m r + = mz3z4 mz 3 z m r + mz 3 f = m(zz4 + gcosz)(mr + m z3) ( m z z 3z 4 gcosz (m r + m z 3) + u )(m z 3) f z 3 (m r + = mzz3 mz 3 ) z 4 m r + mz 3 f 3 f 3 = = z z f 3 f 3 = = z 3 z 4 f 4 f = gcosz 4 z z = z 3 f 4 = z f 4 = z 3 z 4 y, f = u f = u m r + m z3 f 3 = u f 4 = u Adicionalmente, para la matriz de salida (49): f = u f = u f 3 = u f 4 = u m (36) (37) y, h h = z 3 sinz = z z h h = z 3 cosz = z z h = u h = u h h = cosz = z 3 z 4 h h, (38) = sinz = z 3 z 4 h = u h, (39) = u Clase 3-, pág. 9
10 y Evaluando las matrices Jacobianas en (z e,u e ) tenemos: u f e (m r + m z 3e ) m u e x (z e,u e ) = m (m r + m z3e ) (m r + m z3e )(m r + m z 3e ) u e z 3e m r + m z 3e h x (z e,u e ) = f u (z e,u e ) = z 3e m r + m z3e u e z 3 gm u e g(m r + m z 3e ) [ h u (z e,u e ) = m u e (4), (4) g(m r + m z 3e ) u e gm, (4) ]. (43) Modelo lineal en la forma espacio de estados Usando las matrices Jacobianas arriba mencionadas y definiedo: f z (z e,u e ) = A y f u (z e,u e ) = B h z (z e,u e ) = C y h u (z e,u e ) = D Luego las matrices correspondientes para la representación espacio de estados lineal alrededor del punto de operación (z e,u e ) son: u e (m r + m z 3e ) m u e A = m (m r + m z3e ) (m r + m z3e )(m r + m z 3e ), B = u e z 3e m r + m z 3e y: C = z 3e u e z 3 gm u e g(m r + m z 3e ) u e g(m r + m z 3e ) u e gm, D = La represenatción espacio de estados lineal queda de la siguiente forma: 3 u e(m r + m z 3e) m u e d z = m (m r 6 + mz 3e ) (m r + mz 3e )(mr + mz3e) z u e 5 4 z 3e m r + m z 3e ṽ = 6 4 z 3e u e z 3 gm u e g(m r + m z 3e) u e g(m r + m z 3e) u e gm z + m r + m z3e m, (44) [ ], (45) m r + mz 3e m 3 ũ (46) 7 5» ũ. (47) Clase 3-, pág.
11 3.4. Ideas adicionales acerca del modelo Si asumimos que r = cte = r y que el objetivo es mantener θ = π/, entonces el problema del manipulador robótico se puede interpretar como un péndulo invertido con masa m + m. Qué pasa cuando θ = π/ y r = cte > r, qué sistema tenemos?. Otra simplificación del modelo se puede dar cuando se considera θ = y r variable, en ese caso podemos hablar de traslación de la masa de carga en la dirección horizontal. 4. Manipulador Robótico - incluyendo la dinámica del cuerpo rígido (El siguiente problema ha sido adaptado de Snyder, W.E., Industrial Robots: Computer interfacing and control) En la Fig. 7 se muestra el manipulador robótico θ r. Un representación esquemática del robot es presentada en la Fig. 8. La masa m o = kg representa la masa del cilindro exterior y se ubica en el centro de masa del cilindro exterior, I o representa el momento de inercia del cilindro exterior con respecto a su centro de masa. La constante ro = m designa la distancia fija entre el centro de masa del cilindro exterior y el centro de rotación. La masa de la carga es representada por m l = 3kg y se asume que está localizada al final de un pistón de un brazo telescopico cuya distancia radial r es media a partir del centro de rotación. El ángulo de rotación del brazo manipulador es θ. El cilindro interno del brazo telescópico tiene masa m i = kg y momento de inercia igual a I i. Asuma que las entradas al sistema son el torque T θ aplicado en el centro de rotación en la dirección del ángulo θ y la fuerza traslacional (radial) F r aplicada en la dirección r. Despreciar la masa del cilindro interior. Usar g = 9,8m/sec como aceleración de la gravedad. Figura 7: Manipulador robótico θ r I i, m i, r o m l I o, m o, r o Figura 8: Representación esquemática del manipulador robótico θ r Construiremos las ecuaciones de movimiento del sistema en base a las ecuaciones de Lagrange y luego las representaremos en la forma espacio de estados. Clase 3-, pág.
12 4.. Ecuaciones de movimiento usando Lagrange 4 Energía Cinética Primero encontramos la energia cinética total del sistema. La energia cinética traslacional es obtenida definiendo las posiciones de los centros de masa de los cilindros externo e interno con masas m o y m i, y la posición de la masa de carga m l : x o = r ocosθ, y o = r osinθ. x i = (r r o)cosθ, y i = (r r o)sinθ. x l = rcosθ, y l = rsinθ. Nótese que r o es una constante, mientras que r no lo es. Diferenciando x e y con respecto al tiempo se obtiene: ẋ o = r θsinθ, o ẏ o = r θcosθ. o ẋ i = ṙcosθ r θsinθ + r o θsinθ, ẏ i = ṙsinθ + r θcosθ r o θcosθ. ẋ l = ṙcosθ r θsinθ, ẏ l = ṙsinθ + r θcosθ. La magnitud del cuadrado del vector velocidad de los centros de masa de los cilindros exterior e interior, y de la masa de la carga es: vo = x o + y o = r o 4 θ sin θ + r o 4 θ cos θ = ro 4 θ. v i = ẋ i + ẏ i = 4 (ṙcosθ + (r o r) θsinθ) + 4 (ṙsinθ (r o r) θcosθ) = 4ṙ + 4 (r o r) θ. vl = x l + y l = (ṙcosθ r θsinθ) + (ṙsinθ + r θcosθ) = ṙ + r θ. Entonces, la energia cinética traslacional de los cilindros y masa de carga respectivamente es: T to = m ovo = 4 m o(ro θ ). T ti = m ivi = 4 m i(ṙ + (r o r) θ ). T tl = m lv l = m l(ṙ + r θ ). Considerando que los cilindros son cuerpos rígidos, debemos adicionar su energía cinética rotacional a la energia cinética total del sistema. Este no es el caso para la masa de carga, que es considerada como una masa concentrada (partícula). La energia cinética rotacional de los cilindros se obtiene usando: T ro = I oω T ri = I iω Asumiendo que el cilindro interno es una varilla, su momento de inercia con respecto al centro de gravedad es I i = m ir. Para el caso del cilindro externo hueco se puede considerar que I o = m o(3t + ro), donde t depende de los radios internos y externos del cilindro hueco. Sabiendo que ω = θ, se obtiene: T ro = m o(3t + ro) θ Clase 3-, pág.
13 T ri = m iro θ Sumando las energías cinéticas resulta: T = T t + T r T = ( 4 m o(ro θ ) + 4 m i(ṙ + (r o r) θ ) + m l (ṙ + r θ ) + m iro θ + ) m o(3t + ro) θ T = ( m o ( 3 r θ o + 4 t ) + m i ( 4ṙ + 3 r θ + 4 r θ o ) r or θ ) + m l (ṙ + r θ ). 4 Energía Potencial Ahora encontraremos la energía potencial del sistema. La energía potencial de los centros de masa de los cilindros (m o y m i ) y la masa de carga m l : V o = m ogr o sinθ. Luego la energia potencial total es: V = V i = m ig(r r o)sinθ. V l = m l grsinθ. ( (m or o + m i (r ) r o)) + m l gsinθ Ecuaciones de movimiento La función Lagrangiana (o Lagrangiano) para el sistema es: ( L = T V = m o ( 3 r θ o + 4 t ) + m i ( 4ṙ + 3 r θ + 4 r θ o r or θ ) + m l (ṙ + r θ ) ) ( (m or o + m i (r r o)) + m l r ) gsinθ. El manipulador posee dos grados de libertad (r y θ). Luego, tenemos dos ecuaciones de movimiento para el sistema: ( ) d L ( θ d L ṙ La primera ecuación de movimiento resulta en: L θ = T θ ) L r = F r 3 m or o θ + 3 m ir θ + 4 m ir o θ m irr o θ m ir o ṙ θ + 3 m irṙ θ + m l r θ + m l rṙ θ +gcosθ ( (m or o + m i (r r o)) + m l r ) = T θ. La segunda ecuación de movimiento viene a ser: 4 m i r + m l r 3 m ir θ + 4 m ir o θ m l r θ + ( m i + m l )gsinθ = F r. Clase 3-, pág. 3
14 4.. Representación espacio de estados Definiendo las siguientes variables: se puede escribir: d z z z 3 z 4 }{{} dz = z = θ, z = θ, z 3 = r, z 4 = ṙ, z 3 m iz z 3 z 4 m l z z 3 z 4 + m ir o z z 4 gcosz ( m or o + m i(z 3 ro ) + m lz 3 ) + u 3 m oro + 3 m iz3 + 4 m iro m iz 3 r o + m l z3 z 4 3 m izz 3 + m l zz 3 ( m i + m l )gsinz + u m l + 4 m i } {{ } f(z,u), (48) donde u = T θ y u = F r. Asumiendo que la salida está dada por la posición de la masa de carga, v = x l = rcosθ y v = y l = rsinθ se tiene: [ ] [ ] v z3 sinz =, (49) v z 3 cosz }{{}}{{} v h(z, u) Fuente: Capítulos del libro Systems and Control de Stanislaw H. Zak (). Fuente: Capítulos y 3 del libro Feedback Systems: An Introduction for Scientists and Engineers, de Karl J. Åström y Richard M. Murray. Clase 3-, pág. 4
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada
 Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 7C) Clase-b Elizabeth Villota Cerna Semestre II - UNI 8/9/.3.
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 7C) Clase-b Elizabeth Villota Cerna Semestre II - UNI 8/9/.3.
1. Problema de Generación de Trayectoria
 Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227C) Clase11-1 Elizabeth Villota Cerna Semestre 21I - UNI
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227C) Clase11-1 Elizabeth Villota Cerna Semestre 21I - UNI
Control Clásico y Moderno
 Elizabeth Villota Control Clásico y Moderno Notas de Clase MT22 27 de septiembre de 22 Springer Índice general. Modelado de sistemas..........................................................................
Elizabeth Villota Control Clásico y Moderno Notas de Clase MT22 27 de septiembre de 22 Springer Índice general. Modelado de sistemas..........................................................................
Elizabeth Villota. Teoría de Control II. Notas de Clase S de mayo de Springer
 Elizabeth Villota Teoría de Control II Notas de Clase S235 3 de mayo de 22 Springer Índice general Modelado de sistemas Conceptos en modelado Contribución al modelado de la mecánica y de la ingeniería
Elizabeth Villota Teoría de Control II Notas de Clase S235 3 de mayo de 22 Springer Índice general Modelado de sistemas Conceptos en modelado Contribución al modelado de la mecánica y de la ingeniería
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada
 Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227C) Clase 5-2 Elizabeth Villota Cerna Semestre 29 II -
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227C) Clase 5-2 Elizabeth Villota Cerna Semestre 29 II -
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada
 Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 7C) Clase - Elizabeth Villota Cerna Semestre 9 I - UNI 3/7/9
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 7C) Clase - Elizabeth Villota Cerna Semestre 9 I - UNI 3/7/9
Examen de Física I ( ). Solución test de teoría: código Solución test de problemas: código
 Examen de Física I (17-01-12). Solución test de teoría: código 73-3600 211212222112222122212221111111211222 Solución test de problemas: código 89-3800 121423 Problema 1 Una pequeña cuenta de collar puede
Examen de Física I (17-01-12). Solución test de teoría: código 73-3600 211212222112222122212221111111211222 Solución test de problemas: código 89-3800 121423 Problema 1 Una pequeña cuenta de collar puede
6 DINAMICA DEL CUERPO RIGIDO
 6 DINAMICA DEL CUERPO RIGIDO 6. CINEMATICA 6.. Configuracion de un Cuerpo Rígido: Angulos de Euler Un cuerpo rígido se puede entender como una distribución continua de materia que se subdivide en pequeños
6 DINAMICA DEL CUERPO RIGIDO 6. CINEMATICA 6.. Configuracion de un Cuerpo Rígido: Angulos de Euler Un cuerpo rígido se puede entender como una distribución continua de materia que se subdivide en pequeños
Momento angular de una partícula. Momento angular de un sólido rígido
 Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
( ) 2 = 0,3125 kg m 2.
 Examen de Física-1, 1 Ingeniería Química Examen final Enero de 2014 Problemas (Dos puntos por problema) Problema 1: Un bloque de masa m 1 2 kg y un bloque de masa m 2 6 kg están conectados por una cuerda
Examen de Física-1, 1 Ingeniería Química Examen final Enero de 2014 Problemas (Dos puntos por problema) Problema 1: Un bloque de masa m 1 2 kg y un bloque de masa m 2 6 kg están conectados por una cuerda
Capítulo 10. Rotación de un Cuerpo Rígido
 Capítulo 10 Rotación de un Cuerpo Rígido Contenido Velocidad angular y aceleración angular Cinemática rotacional Relaciones angulares y lineales Energía rotacional Cálculo de los momentos de inercia Teorema
Capítulo 10 Rotación de un Cuerpo Rígido Contenido Velocidad angular y aceleración angular Cinemática rotacional Relaciones angulares y lineales Energía rotacional Cálculo de los momentos de inercia Teorema
DINÁMICA DE LA ROTACIÓN
 DINÁMICA DE LA ROTACIÓN 1. La polea de la figura tiene radio R y momento de inercia, respecto a un eje que pasa por su centro de masa perpendicular al plano del papel. La cuerda no resbala sobre la polea
DINÁMICA DE LA ROTACIÓN 1. La polea de la figura tiene radio R y momento de inercia, respecto a un eje que pasa por su centro de masa perpendicular al plano del papel. La cuerda no resbala sobre la polea
TUTORIAL DE LINEALIZACIÓN. Utilizar otro sistema aproximante:
 TUTORIAL DE LINEALIZACIÓN ANDRÉS GARCÍA, OSVALDO AGAMENNONI Y JOSÉ FIGUEROA Resumen. En este tutorial encontará una guía rápida a cerca de la linealización de sistemas de control no-lineales o lo que es
TUTORIAL DE LINEALIZACIÓN ANDRÉS GARCÍA, OSVALDO AGAMENNONI Y JOSÉ FIGUEROA Resumen. En este tutorial encontará una guía rápida a cerca de la linealización de sistemas de control no-lineales o lo que es
Mecánica Teórica Curso Boletín de problemas 2 Grupo 2
 Mecánica Teórica Curso 2017-18 Boletín de problemas 2 Grupo 2 Física Teórica, Universidad de Sevilla 6 de octubre de 2017 1- Dar un conjunto de coordenadas generalizadas necesarias para especificar completamente
Mecánica Teórica Curso 2017-18 Boletín de problemas 2 Grupo 2 Física Teórica, Universidad de Sevilla 6 de octubre de 2017 1- Dar un conjunto de coordenadas generalizadas necesarias para especificar completamente
Facultad de Física, P. Universidad Católica de Chile. FIS-1513: Estática y Dinámica. Interrogación 2. Viernes 14 de Septiembre de 2011
 Facultad de Física, P. Universidad Católica de Chile FIS-1513: Estática y Dinámica Secciones 01 02 03, Profesores: Rafael Benguria, Samuel Hevia y Roberto Rodríguez Interrogación 2 Viernes 14 de Septiembre
Facultad de Física, P. Universidad Católica de Chile FIS-1513: Estática y Dinámica Secciones 01 02 03, Profesores: Rafael Benguria, Samuel Hevia y Roberto Rodríguez Interrogación 2 Viernes 14 de Septiembre
Física General 1 Proyecto PMME - Curso 2007 Instituto de Física Facultad de Ingeniería UdelaR
 Física General 1 Proecto PMME - Curso 007 Instituto de Física Facultad de Ingeniería UdelaR TITULO DINAMICA DEL CARRETEL AUTORES Santiago Duarte, Nicolás Puppo Juan Manuel Del Barrio INTRODUCCIÓN En este
Física General 1 Proecto PMME - Curso 007 Instituto de Física Facultad de Ingeniería UdelaR TITULO DINAMICA DEL CARRETEL AUTORES Santiago Duarte, Nicolás Puppo Juan Manuel Del Barrio INTRODUCCIÓN En este
Estática y Dinámica Analítica
 Estática y Dinámica Analítica p. 1/25 Estática y Dinámica Analítica Mecánica II Temas 6 y 7 Manuel Ruiz Delgado Escuela Técnica Superior de Ingenieros Aeronáuticos Universidad Politécnica de Madrid Mecánica
Estática y Dinámica Analítica p. 1/25 Estática y Dinámica Analítica Mecánica II Temas 6 y 7 Manuel Ruiz Delgado Escuela Técnica Superior de Ingenieros Aeronáuticos Universidad Politécnica de Madrid Mecánica
Esta relación se obtiene mediante el denominado modelo dinámico, que relaciona matemáticamente:
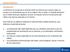 Introducción La dinámica se ocupa de la relación entre las fuerzas que actúan sobre un cuerpo y el movimiento que en el se origina. Por lo tanto, el modelo dinámico de un robot tiene por objetivo conocer
Introducción La dinámica se ocupa de la relación entre las fuerzas que actúan sobre un cuerpo y el movimiento que en el se origina. Por lo tanto, el modelo dinámico de un robot tiene por objetivo conocer
Estática. M = r F. donde r = OA.
 Estática. Momento de un vector respecto de un punto: Momento de una fuerza Sea un vector genérico a = AB en un espacio vectorial V. Sea un punto cualesquiera O. Se define el vector momento M del vector
Estática. Momento de un vector respecto de un punto: Momento de una fuerza Sea un vector genérico a = AB en un espacio vectorial V. Sea un punto cualesquiera O. Se define el vector momento M del vector
Dinámica del Sólido Rígido
 Dinámica del Sólido Rígido El presente documento de clase sobre dinámica del solido rígido está basado en los contenidos volcados en la excelente página web del curso de Física I del Prof. Javier Junquera
Dinámica del Sólido Rígido El presente documento de clase sobre dinámica del solido rígido está basado en los contenidos volcados en la excelente página web del curso de Física I del Prof. Javier Junquera
Facultad de Física, P. Universidad Católica de Chile. FIS-1513: Estática y Dinámica
 Facultad de Física, P. Universidad Católica de Chile FIS-1513: Estática y Dinámica Secciones 01 02 03, Profesores: Rafael Benguria, Samuel Hevia y Roberto Rodríguez SOLUCIÓN: Interrogación 1 Viernes 9
Facultad de Física, P. Universidad Católica de Chile FIS-1513: Estática y Dinámica Secciones 01 02 03, Profesores: Rafael Benguria, Samuel Hevia y Roberto Rodríguez SOLUCIÓN: Interrogación 1 Viernes 9
ECUACION DINÁMICA DE ROTACIÓN PURA DE UN CUERPO RIGIDO ALREDEDOR DE UN EJE ω
 ECUACION DINÁMICA DE ROTACIÓN PURA DE UN CUERPO RIGIDO ALREDEDOR DE UN EJE ω Suponiendo un cuerpo rígido que gira con velocidad angular ω alrededor del eje Z que permanece fijo al cuerpo. dl = ( dm R 2
ECUACION DINÁMICA DE ROTACIÓN PURA DE UN CUERPO RIGIDO ALREDEDOR DE UN EJE ω Suponiendo un cuerpo rígido que gira con velocidad angular ω alrededor del eje Z que permanece fijo al cuerpo. dl = ( dm R 2
 Relación entre Torque y Aceleración Angular. En los ejemplos de aplicación de un torque, el efecto observable es un movimiento de rotación que parte del reposo, o también puede ser un movimiento que pase
Relación entre Torque y Aceleración Angular. En los ejemplos de aplicación de un torque, el efecto observable es un movimiento de rotación que parte del reposo, o también puede ser un movimiento que pase
Dinámica del movimiento rotacional
 Dinámica del movimiento rotacional Torca, momento angular, momento cinético o momento de torsión: La habilidad de una fuerza para rotar o girar un cuerpo alrededor de un eje. τ = r F r= es la posición
Dinámica del movimiento rotacional Torca, momento angular, momento cinético o momento de torsión: La habilidad de una fuerza para rotar o girar un cuerpo alrededor de un eje. τ = r F r= es la posición
27 de octubre de 2010
 Pontificia Universidad Católica de Chile Facultad de Física FIZ 11 Mecánica Clásica Profesor: Andrés Jordán Ayudantes: Eduardo Bañados T. eebanado@uc.cl Ariel Norambuena ainoramb@uc.cl Torque, Momento
Pontificia Universidad Católica de Chile Facultad de Física FIZ 11 Mecánica Clásica Profesor: Andrés Jordán Ayudantes: Eduardo Bañados T. eebanado@uc.cl Ariel Norambuena ainoramb@uc.cl Torque, Momento
Análisis y Control de Sistemas Lineales. Modelado de Sistemas mecánicos
 Análisis y Control de Sistemas Lineales Modelado de Sistemas mecánicos Contenido Modelos de elementos mecánicos de traslación Ejemplos Modelos de elementos mecánicos de rotación Ejemplos Ejercicios Modelos
Análisis y Control de Sistemas Lineales Modelado de Sistemas mecánicos Contenido Modelos de elementos mecánicos de traslación Ejemplos Modelos de elementos mecánicos de rotación Ejemplos Ejercicios Modelos
Guia 2 - Ecuaciones de Lagrange - Mecánica Clasica - Cátedra G.Mindlin
 Guia 2 - Ecuaciones de Lagrange - Mecánica Clasica - Cátedra G.Mindlin 1er Cuatrimestre 2018 a. Ejemplos de ecuaciones de Lagrange 1. En la figura se muestra un esquema de un yoyo cilíndrico de masa m
Guia 2 - Ecuaciones de Lagrange - Mecánica Clasica - Cátedra G.Mindlin 1er Cuatrimestre 2018 a. Ejemplos de ecuaciones de Lagrange 1. En la figura se muestra un esquema de un yoyo cilíndrico de masa m
Guía de ejercicios N o 10. Cinemática y Dinámica rotacional
 FIS1503 - Física general - Ingeniería 1er. Semestre 2010 Guía de ejercicios N o 10 Cinemática y Dinámica rotacional 1. Una rueda giratoria requiere 3 s para hacer 37 revoluciones. Su rapidez angular al
FIS1503 - Física general - Ingeniería 1er. Semestre 2010 Guía de ejercicios N o 10 Cinemática y Dinámica rotacional 1. Una rueda giratoria requiere 3 s para hacer 37 revoluciones. Su rapidez angular al
Cuestionario sobre las Leyes de Newton
 Cuestionario sobre las Leyes de Newton 1. Enuncie las leyes de Newton y represente gráficamente o por medio de una ilustración Primera Ley: La primera ley de Newton, conocida también como Ley de inercia,
Cuestionario sobre las Leyes de Newton 1. Enuncie las leyes de Newton y represente gráficamente o por medio de una ilustración Primera Ley: La primera ley de Newton, conocida también como Ley de inercia,
MECÁNICA CLÁSICA CINEMATICA. FAyA Licenciatura en Química Física III año 2006
 Física III año 26 CINEMATICA MECÁNICA CLÁSICA La cinemática estudia el movimiento de los cuerpos, sin tener en cuenta las causas que lo producen. Antes de continuar establezcamos la diferencia entre un
Física III año 26 CINEMATICA MECÁNICA CLÁSICA La cinemática estudia el movimiento de los cuerpos, sin tener en cuenta las causas que lo producen. Antes de continuar establezcamos la diferencia entre un
Control Moderno: El espacio de estados
 Lección 3 Control Moderno: El espacio de estados 1 Estados: Definición y ejemplo Estados: variables internas que describen la evolución del sistema. El conocimiento de estas variables en t = t 0 junto
Lección 3 Control Moderno: El espacio de estados 1 Estados: Definición y ejemplo Estados: variables internas que describen la evolución del sistema. El conocimiento de estas variables en t = t 0 junto
Momento angular o cinético
 Momento angular o cinético Definición de momento angular o cinético Consideremos una partícula de masa m, con un vector de posición r y que se mueve con una cantidad de movimiento p = mv z L p O r y x
Momento angular o cinético Definición de momento angular o cinético Consideremos una partícula de masa m, con un vector de posición r y que se mueve con una cantidad de movimiento p = mv z L p O r y x
MECANICA CLASICA Coordenadas generalizadas. Grados de libertad. Lagrange.
 MECANICA CLASICA Coordenadas generalizadas. Grados de libertad. Lagrange. 1. Se tiene el sistema de la figura, donde x 1, x 2 se miden a partir de las posiciones de equilibrio. Sea q 1 = x 1 + x 2 y q
MECANICA CLASICA Coordenadas generalizadas. Grados de libertad. Lagrange. 1. Se tiene el sistema de la figura, donde x 1, x 2 se miden a partir de las posiciones de equilibrio. Sea q 1 = x 1 + x 2 y q
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada
 Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227C) Clase5-2 Elizabeth Villota Cerna Semestre 2I - UNI
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227C) Clase5-2 Elizabeth Villota Cerna Semestre 2I - UNI
Dinámica del Sólido Rígido
 Dinámica del Sólido Rígido El presente documento de clase sobre dinámica del solido rígido está basado en los contenidos volcados en la excelente página web del curso de Física I del Prof. Javier Junquera
Dinámica del Sólido Rígido El presente documento de clase sobre dinámica del solido rígido está basado en los contenidos volcados en la excelente página web del curso de Física I del Prof. Javier Junquera
Examen de Física-1, 1 Ingeniería Química Examen final. Enero de 2013 Problemas (Dos puntos por problema).
 Examen de Física-1, 1 Ingeniería Química Examen final. Enero de 013 Problemas Dos puntos por problema. Problema 1 Primer parcial: El radio de una noria de feria mide 5 m y da una vuelta en 10 s. a Hállese
Examen de Física-1, 1 Ingeniería Química Examen final. Enero de 013 Problemas Dos puntos por problema. Problema 1 Primer parcial: El radio de una noria de feria mide 5 m y da una vuelta en 10 s. a Hállese
Javier Junquera. Movimiento de rotación
 Javier Junquera Movimiento de rotación Bibliografía Física, Volumen 1, 3 edición Raymod A. Serway y John W. Jewett, Jr. Ed. Thomson ISBN: 84-9732-168-5 Capítulo 10 Física, Volumen 1 R. P. Feynman, R. B.
Javier Junquera Movimiento de rotación Bibliografía Física, Volumen 1, 3 edición Raymod A. Serway y John W. Jewett, Jr. Ed. Thomson ISBN: 84-9732-168-5 Capítulo 10 Física, Volumen 1 R. P. Feynman, R. B.
Examen de Física I ( ). Solución test de teoría: código Solución test de problemas: código
 Examen de Física I (19-06-12). test de teoría: código 31-4702 221212222211221111121211111211222211 test de problemas: código 10-4811 222355 Problema 1 Un jugador de fútbol lanza la pelota en un tiro libre
Examen de Física I (19-06-12). test de teoría: código 31-4702 221212222211221111121211111211222211 test de problemas: código 10-4811 222355 Problema 1 Un jugador de fútbol lanza la pelota en un tiro libre
APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 12 CONSERVACIÓN DE LA CANTIDAD DE MOVIMIENTO ANGULAR
 APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 12 CONSERVACIÓN DE A CANTIDAD DE MOVIMIENTO ANGUAR Cantidad de movimiento angular de una partícula. Así como en el movimiento de traslación
APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 12 CONSERVACIÓN DE A CANTIDAD DE MOVIMIENTO ANGUAR Cantidad de movimiento angular de una partícula. Así como en el movimiento de traslación
DINAMICA DEL PUNTO. Es el momento con respecto a un punto O de la cantidad de movimiento de una partícula móvil.
 DINMIC DEL PUNTO Leyes de Newton Primera ley o ley de inercia: si sobre un sistema material no actúa fuerza alguna sigue en reposo o movimiento rectilíneo uniforme si inicialmente lo estaba. Segunda ley
DINMIC DEL PUNTO Leyes de Newton Primera ley o ley de inercia: si sobre un sistema material no actúa fuerza alguna sigue en reposo o movimiento rectilíneo uniforme si inicialmente lo estaba. Segunda ley
1. RODADURA SOBRE UN PLANO INCLINADO: MONTAJE EXPERIMENTAL
 UNIVERSIDAD DEL VALLE Departamento de Física Laboratorio de Física Fundamental I Profesor: Otto Vergara. Diciembre 2 de 2012 NOTAS CLASE 4 1. RODADURA SOBRE UN PLANO INCLINADO: MONTAJE EXPERIMENTAL Figura
UNIVERSIDAD DEL VALLE Departamento de Física Laboratorio de Física Fundamental I Profesor: Otto Vergara. Diciembre 2 de 2012 NOTAS CLASE 4 1. RODADURA SOBRE UN PLANO INCLINADO: MONTAJE EXPERIMENTAL Figura
Prof. Virginia Mazzone - Mariana Suarez
 SISTEMAS NO LINEALES SISTEMAS DE SEGUNDO ORDEN Prof. Virginia Mazzone - Prof. Mariana Suarez 1 Introducción Método de isoclinas Ejemplos 3 Introducción Un sistema de segundo orden autónomo está representado
SISTEMAS NO LINEALES SISTEMAS DE SEGUNDO ORDEN Prof. Virginia Mazzone - Prof. Mariana Suarez 1 Introducción Método de isoclinas Ejemplos 3 Introducción Un sistema de segundo orden autónomo está representado
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada
 Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227B) Clase09-03 Elizabeth Villota En esta parte presentaremos
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227B) Clase09-03 Elizabeth Villota En esta parte presentaremos
Programa de Doctorado en Física Pontificia Universidad Católica de Valparaíso Universidad Técnica Federico Santa María
 1 Mecánica Clásica - II Semestre 2014 Programa de Doctorado en Física Pontificia Universidad Católica de Valparaíso Universidad Técnica Federico Santa María Problema 1. Una barra rígida (de altura despreciable)
1 Mecánica Clásica - II Semestre 2014 Programa de Doctorado en Física Pontificia Universidad Católica de Valparaíso Universidad Técnica Federico Santa María Problema 1. Una barra rígida (de altura despreciable)
Física: Torque y Momento de Torsión
 Física: Torque y Momento de Torsión Dictado por: Profesor Aldo Valcarce 2 do semestre 2014 Relación entre cantidades angulares y traslacionales. En un cuerpo que rota alrededor de un origen O, el punto
Física: Torque y Momento de Torsión Dictado por: Profesor Aldo Valcarce 2 do semestre 2014 Relación entre cantidades angulares y traslacionales. En un cuerpo que rota alrededor de un origen O, el punto
LABORATORIO Nº 2 PRIMERA Y SEGUNDA CONDICIÓN DE EQUILIBRIO
 LABORATORIO Nº 2 PRIMERA Y SEGUNDA CONDICIÓN DE EQUILIBRIO I. LOGRO Comprobar experimental, gráfica y analíticamente la primera y segunda condición de equilibrio a través de diagramas de cuerpo libre.
LABORATORIO Nº 2 PRIMERA Y SEGUNDA CONDICIÓN DE EQUILIBRIO I. LOGRO Comprobar experimental, gráfica y analíticamente la primera y segunda condición de equilibrio a través de diagramas de cuerpo libre.
2xy 3x 2 y 2 y(0) = 1
 ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA DEPARTAMENTO DE MATEMÁTICA APLICADA II Ingeniería Técnica Industrial. Especialidad en Mecánica Soluciones al Primer Parcial de Ampliación de Matemáticas. Curso
ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA DEPARTAMENTO DE MATEMÁTICA APLICADA II Ingeniería Técnica Industrial. Especialidad en Mecánica Soluciones al Primer Parcial de Ampliación de Matemáticas. Curso
Momento angular o cinético
 Momento angular o cinético Definición de momento angular o cinético Consideremos una partícula de masa m, con un vector de posición r y que se mueve con una cantidad de movimiento p = mv z L p O r y x
Momento angular o cinético Definición de momento angular o cinético Consideremos una partícula de masa m, con un vector de posición r y que se mueve con una cantidad de movimiento p = mv z L p O r y x
4. Problema del Regulador Cuadrático Lineal - Horizonte Infinito
 Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 7C) Clase - Elizabeth Villota Cerna Semestre 9 II - UNI 3//9
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 7C) Clase - Elizabeth Villota Cerna Semestre 9 II - UNI 3//9
MDOF. Dinámica Estructural Aplicada II C 2012 UCA
 MDOF Dinámica Estructural Aplicada II C 2012 UCA Desde el punto de vista dinámico, interesan los grados de libertad en los que se generan fuerzas generalizadas de inercia significativas; es decir, fuerzas
MDOF Dinámica Estructural Aplicada II C 2012 UCA Desde el punto de vista dinámico, interesan los grados de libertad en los que se generan fuerzas generalizadas de inercia significativas; es decir, fuerzas
4. Fuerzas centrales. Comprobación de la segunda Ley de Kepler
 4. Fuerzas centrales. Comprobación de la segunda Ley de Kepler Fuerza central Momento de torsión respecto un punto Momento angular de una partícula Relación Momento angular y Momento de torsión Conservación
4. Fuerzas centrales. Comprobación de la segunda Ley de Kepler Fuerza central Momento de torsión respecto un punto Momento angular de una partícula Relación Momento angular y Momento de torsión Conservación
Objetos en equilibrio - Ejemplo
 Objetos en equilibrio - Ejemplo Una escalera de 5 m que pesa 60 N está apoyada sobre una pared sin roce. El extremo de la escalera que apoya en el piso está a 3 m de la pared, ver figura. Cuál es el mínimo
Objetos en equilibrio - Ejemplo Una escalera de 5 m que pesa 60 N está apoyada sobre una pared sin roce. El extremo de la escalera que apoya en el piso está a 3 m de la pared, ver figura. Cuál es el mínimo
2DA PRÁCTICA CALIFICADA
 2DA PRÁCTICA CALIFICADA DINÁMICA (IC 244) ALUMNOS : CARITAS BARRIENTOS, Ronald ROBLES ROCHA, Hamilton TORRES PÉREZ, Walter A. TORO VELARDE, William DOCENTE : Ing. CASTRO PÉREZ, Cristian CINÉTICA DE UNA
2DA PRÁCTICA CALIFICADA DINÁMICA (IC 244) ALUMNOS : CARITAS BARRIENTOS, Ronald ROBLES ROCHA, Hamilton TORRES PÉREZ, Walter A. TORO VELARDE, William DOCENTE : Ing. CASTRO PÉREZ, Cristian CINÉTICA DE UNA
MT 221 Modelado. Elizabeth Villota
 MT 221 Modelado Elizabeth Villota Objetivos Definir que es un modelo y su uso para responder preguntas relacionadas a un sistema. Introducir los conceptos de estado, dinámica, entradas y salidas. Proveer
MT 221 Modelado Elizabeth Villota Objetivos Definir que es un modelo y su uso para responder preguntas relacionadas a un sistema. Introducir los conceptos de estado, dinámica, entradas y salidas. Proveer
Respuesta en la Frecuencia
 Respuesta en la Frecuencia Elizabeth Villota Cerna Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica UNI-FIM 08 Junio 2012 1 Desempeño en el dominio de la frecuencia SLIT 2do orden (masa-resorte-amortiguador)
Respuesta en la Frecuencia Elizabeth Villota Cerna Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica UNI-FIM 08 Junio 2012 1 Desempeño en el dominio de la frecuencia SLIT 2do orden (masa-resorte-amortiguador)
En general un cuerpo puede tener dos tipos distintos de movimiento simultáneamente.
 TORQUE Y EQUILIBRIO DE CUERPO RÍGIDO. En general un cuerpo puede tener dos tipos distintos de movimiento simultáneamente. De traslación a lo largo de una trayectoria, de rotación mientras se está trasladando,
TORQUE Y EQUILIBRIO DE CUERPO RÍGIDO. En general un cuerpo puede tener dos tipos distintos de movimiento simultáneamente. De traslación a lo largo de una trayectoria, de rotación mientras se está trasladando,
Módulo 1: Mecánica Sólido rígido. Rotación (II)
 Módulo 1: Mecánica Sólido rígido. Rotación (II) 1 Segunda ley de Newton en la rotación Se puede hacer girar un disco por ejemplo aplicando un par de fuerzas. Pero es necesario tener en cuenta el punto
Módulo 1: Mecánica Sólido rígido. Rotación (II) 1 Segunda ley de Newton en la rotación Se puede hacer girar un disco por ejemplo aplicando un par de fuerzas. Pero es necesario tener en cuenta el punto
APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 10 CINEMÁTICA DE ROTACIÓN
 APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 10 CINEMÁTICA DE ROTACIÓN Movimiento de rotación Qué tienen en común los movimientos de un disco compacto, las sillas voladoras, un esmeril,
APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 10 CINEMÁTICA DE ROTACIÓN Movimiento de rotación Qué tienen en común los movimientos de un disco compacto, las sillas voladoras, un esmeril,
Acústica y vibraciones mecánicas
 Sistemas de un grado de libertar libre Ecuación de movimiento de un sistema masa-resorte Considerando el sistema de la figura y por la aplicación dela segunda ley de Newton o principio de conservación
Sistemas de un grado de libertar libre Ecuación de movimiento de un sistema masa-resorte Considerando el sistema de la figura y por la aplicación dela segunda ley de Newton o principio de conservación
Bajo estas hipótesis la ley de Newton permite escribir las ecuaciones del cohete (ver Figura 1.1) como. = m(t) g + T (t), = g + dx dt (0) = v 0.
 CAPÍTULO 1 INTRODUCCIÓN Ejercicios resueltos Problema 1. Desarrolle un modelo simplificado de un coete como un cuerpo sujeto a la gravedad que se mueve en vertical por el empuje de una fuerza de propulsión
CAPÍTULO 1 INTRODUCCIÓN Ejercicios resueltos Problema 1. Desarrolle un modelo simplificado de un coete como un cuerpo sujeto a la gravedad que se mueve en vertical por el empuje de una fuerza de propulsión
10 cm longitud 30 m. Calcular: (a) la velocidad en el pie del plano inclinado si
 Las pesas de la figura ruedan sin deslizar y sin 6 cm rozamiento por un plano inclinado 30 y de 10 cm longitud 30 m. Calcular: (a) la velocidad en el pie del plano inclinado si 100 cm las pesas parten
Las pesas de la figura ruedan sin deslizar y sin 6 cm rozamiento por un plano inclinado 30 y de 10 cm longitud 30 m. Calcular: (a) la velocidad en el pie del plano inclinado si 100 cm las pesas parten
No usar por academias
 ECUACIONES DIFERENCIALES I Grupo D 1 de septiembre de 003 Apellidos: Nombre: D.N.I.: Firma: 1. Considérese la ecuación y = 1 + y x. i) Hallar su solución general. ii) Dibujar aproximadamente sus curvas
ECUACIONES DIFERENCIALES I Grupo D 1 de septiembre de 003 Apellidos: Nombre: D.N.I.: Firma: 1. Considérese la ecuación y = 1 + y x. i) Hallar su solución general. ii) Dibujar aproximadamente sus curvas
03 de noviembre de 2010
 Pontificia Universidad Católica de Chile Facultad de Física FIZ 11 Mecánica Clásica Profesor: Andrés Jordán Ayudantes: Eduardo Bañados T. eebanado@uc.cl Ariel Norambuena ainoramb@uc.cl Momento Angular
Pontificia Universidad Católica de Chile Facultad de Física FIZ 11 Mecánica Clásica Profesor: Andrés Jordán Ayudantes: Eduardo Bañados T. eebanado@uc.cl Ariel Norambuena ainoramb@uc.cl Momento Angular
TEORÍA DE CONTROL SISTEMAS NO LINEALES
 TEORÍA DE CONTROL SISTEMAS NO LINEALES Ecuaciones en el espacio de estados. Considere un sistema representado por un sistema de ecuaciones diferenciales ordinaras con alinealidades continuas. Las fi son
TEORÍA DE CONTROL SISTEMAS NO LINEALES Ecuaciones en el espacio de estados. Considere un sistema representado por un sistema de ecuaciones diferenciales ordinaras con alinealidades continuas. Las fi son
Programa de Acceso Inclusivo, Equidad y Permanencia PAIEP U. de Santiago
 Estática A Fuerzas Si sobre un cuerpo actúan solo dos fuerzas en la misma línea, y el cuerpo está en reposo o moviéndose con velocidad constante, las fuerzas son iguales pero de sentidos contrarios. Si
Estática A Fuerzas Si sobre un cuerpo actúan solo dos fuerzas en la misma línea, y el cuerpo está en reposo o moviéndose con velocidad constante, las fuerzas son iguales pero de sentidos contrarios. Si
La cantidad de movimiento angular obedece una ley de conservación muy similar a la que obedece el momentum lineal.
 En vista de la gran analogía que se han presentado entre la mecánica lineal y la mecánica rotacional, no debe ser ninguna sorpresa que la cantidad de movimiento o momento lineal tenga un similar rotacional.
En vista de la gran analogía que se han presentado entre la mecánica lineal y la mecánica rotacional, no debe ser ninguna sorpresa que la cantidad de movimiento o momento lineal tenga un similar rotacional.
Estabilidad. Ecuaciones generales. Referencia Básica [Pad96] Helicópteros () Estabilidad Ecuaciones generales 1 / 22
![Estabilidad. Ecuaciones generales. Referencia Básica [Pad96] Helicópteros () Estabilidad Ecuaciones generales 1 / 22 Estabilidad. Ecuaciones generales. Referencia Básica [Pad96] Helicópteros () Estabilidad Ecuaciones generales 1 / 22](/thumbs/89/97754750.jpg) Estabilidad Ecuaciones generales Referencia Básica [Pad96] Helicópteros () Estabilidad Ecuaciones generales 1 / 22 Mecánica del vuelo del helicóptero I Las ecuaciones que rigen la dinámica del helicóptero
Estabilidad Ecuaciones generales Referencia Básica [Pad96] Helicópteros () Estabilidad Ecuaciones generales 1 / 22 Mecánica del vuelo del helicóptero I Las ecuaciones que rigen la dinámica del helicóptero
AAD (HE) Estabilidad Conceptos generales 1 / 21. Hipótesis
 Mecánica del vuelo del helicóptero II 7. Estabilidad 7.1 Conceptos generales Debido a los movimientos de batimiento y arrastre de las palas el centro de gravedad cambiará su situación. Las fuerzas exteriores
Mecánica del vuelo del helicóptero II 7. Estabilidad 7.1 Conceptos generales Debido a los movimientos de batimiento y arrastre de las palas el centro de gravedad cambiará su situación. Las fuerzas exteriores
Dinámica en dos o tres dimensiones
 7.0.2. Dinámica en dos o tres dimensiones Ejercicio 7.27 Un cuerpo de masa 8kg, describe una trayectoria cuyas ecuaciones paramétrica son: x =2+5t 2t 2 m e y = t 2 m.determinela fuerza aplicada sobre el
7.0.2. Dinámica en dos o tres dimensiones Ejercicio 7.27 Un cuerpo de masa 8kg, describe una trayectoria cuyas ecuaciones paramétrica son: x =2+5t 2t 2 m e y = t 2 m.determinela fuerza aplicada sobre el
Problemas de Física I
 Problemas de Física I DINÁMICA DEL SÓLIDO RÍGIDO (1 er Q.:prob impares, 2 ndo Q.:prob pares) 1. (T) Dos partículas de masas m 1 y m 2 están unidas por una varilla de longitud r y masa despreciable. Demostrar
Problemas de Física I DINÁMICA DEL SÓLIDO RÍGIDO (1 er Q.:prob impares, 2 ndo Q.:prob pares) 1. (T) Dos partículas de masas m 1 y m 2 están unidas por una varilla de longitud r y masa despreciable. Demostrar
Problemas. Laboratorio. Física moderna 09/11/07 DEPARTAMENTO DE FÍSICA E QUÍMICA. Nombre:
 Física moderna 9/11/7 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: 1. Un muelle de constante k =, 1 3 N/m está apoyado en una superficie horizontal sin rozamiento. A 1, m hay un bucle vertical de
Física moderna 9/11/7 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: 1. Un muelle de constante k =, 1 3 N/m está apoyado en una superficie horizontal sin rozamiento. A 1, m hay un bucle vertical de
EJERCICIOS RESUELTOS Y PROPUESTOS
 UNIVERSIDAD NACIONAL DE INGENIERÍA Facultad de Ingeniería Mecánica MT 227 Control Moderno y Óptimo EJERCICIOS RESUELTOS Y PROPUESTOS Estabilidad según Lyapunov (1) Un buen modelo de un niño impulsandose
UNIVERSIDAD NACIONAL DE INGENIERÍA Facultad de Ingeniería Mecánica MT 227 Control Moderno y Óptimo EJERCICIOS RESUELTOS Y PROPUESTOS Estabilidad según Lyapunov (1) Un buen modelo de un niño impulsandose
Mecánica Clásica 1er. Cuat. 2017
 Mecánica Clásica 1er. Cuat. 2017 Guía 6: Cinemática y dinámica del cuerpo rígido, ángulos de Euler, ecuaciones de Euler. Problema 1: Analizar los siguientes puntos. a) Mostrar que la velocidad angular
Mecánica Clásica 1er. Cuat. 2017 Guía 6: Cinemática y dinámica del cuerpo rígido, ángulos de Euler, ecuaciones de Euler. Problema 1: Analizar los siguientes puntos. a) Mostrar que la velocidad angular
Mecánica Clásica (B) 2do. cuatrimestre de 2017 AD Primer parcial (con soluciones) 12/10
 Mecánica Clásica B) do. cuatrimestre de 017 AD Primer parcial con soluciones) 1/10 Problema 1. El marco exterior de un giróscopo rota con velocidad angular constante ω = ωẑ, como muestra la figura, donde
Mecánica Clásica B) do. cuatrimestre de 017 AD Primer parcial con soluciones) 1/10 Problema 1. El marco exterior de un giróscopo rota con velocidad angular constante ω = ωẑ, como muestra la figura, donde
Segundo curso del Grado en Matemáticas. Representamos el espacio físico como un espacio vectorial de dimensión 3, x R 3. 3 x i e i = x i e i, (1) i=1
 MECÁNICA Segundo curso del Grado en Matemáticas Introcción Representación matemática del espacio físico Representamos el espacio físico como un espacio vectorial de dimensión 3, x R 3 x = x 1 e 1 +x 2
MECÁNICA Segundo curso del Grado en Matemáticas Introcción Representación matemática del espacio físico Representamos el espacio físico como un espacio vectorial de dimensión 3, x R 3 x = x 1 e 1 +x 2
Cinemática del sólido rígido
 Cinemática del sólido rígido Teoría básica para el curso Cinemática del sólido rígido, ejercicios comentados α δ ω B B A A P r B AB A ω α O Ramírez López-Para, Pilar Loizaga Garmendia, Maider López Soto,
Cinemática del sólido rígido Teoría básica para el curso Cinemática del sólido rígido, ejercicios comentados α δ ω B B A A P r B AB A ω α O Ramírez López-Para, Pilar Loizaga Garmendia, Maider López Soto,
Dinámica del billar. F. Javier Gil Chica
 Dinámica del billar F. Javier Gil Chica Resumen La dinámica del choque entre dos bolas de billar es un problema clásico que se encuentra al menos citado en multitud de textos elementales de física. En
Dinámica del billar F. Javier Gil Chica Resumen La dinámica del choque entre dos bolas de billar es un problema clásico que se encuentra al menos citado en multitud de textos elementales de física. En
FUNDAMENTOS Y MODELOS MATEMÁTICOS DE LOS SISTEMAS DE CONTROL UNIDAD 1
 FUNDAMENTOS Y MODELOS MATEMÁTICOS DE LOS SISTEMAS DE CONTROL UNIDAD 1 Contenido El concepto de realimentación. Establecimiento de las ecuaciones diferenciales que rigen a un sistema. Función de transferencia.
FUNDAMENTOS Y MODELOS MATEMÁTICOS DE LOS SISTEMAS DE CONTROL UNIDAD 1 Contenido El concepto de realimentación. Establecimiento de las ecuaciones diferenciales que rigen a un sistema. Función de transferencia.
Unidad 4C: Torque y momento angular Preparada por Rodrigo Soto
 FI1A2 - SISTEMAS NEWTONIANOS Semestre 2008-1 Profesores: Hugo Arellano, Diego Mardones y Nicolás Mujica Departamento de Física Facultad de Ciencias Físicas y Matemáticas Universidad de Chile Unidad 4C:
FI1A2 - SISTEMAS NEWTONIANOS Semestre 2008-1 Profesores: Hugo Arellano, Diego Mardones y Nicolás Mujica Departamento de Física Facultad de Ciencias Físicas y Matemáticas Universidad de Chile Unidad 4C:
Cátedra Matemática del PIT. Gradiente y Derivada Direccional
 Cátedra Matemática del PIT Gradiente y Derivada Direccional Propósito de la Unidad Hallar y usar las derivadas direccionales de una función de dos variables. Hallar el gradiente de una función de dos variables.
Cátedra Matemática del PIT Gradiente y Derivada Direccional Propósito de la Unidad Hallar y usar las derivadas direccionales de una función de dos variables. Hallar el gradiente de una función de dos variables.
Ayudantía 17. Figura 1: (R h) 2 + d 2 = R 2 (1) h = R R
 Pontificia Universidad Católica de Chile Facultad de Física FIS1533 - Electricidad y Magnetismo Profesor: Máximo Bañados Ayudante: Alonso Ruiz (airuiz@uc.cl) Problema 1 Ayudantía 17 Considere una partícula
Pontificia Universidad Católica de Chile Facultad de Física FIS1533 - Electricidad y Magnetismo Profesor: Máximo Bañados Ayudante: Alonso Ruiz (airuiz@uc.cl) Problema 1 Ayudantía 17 Considere una partícula
2.004 MODELISMO, DINÁMICA Y CONTROL II Primavera Soluciones del boletín de problemas 6
 2.004 MODELISMO, DINÁMICA Y CONTROL II Primavera 2003 Soluciones del boletín de problemas 6 Problema 1. Varilla deslizándose por una pared. Dado que los extremos de la varilla están forzados a permanecer
2.004 MODELISMO, DINÁMICA Y CONTROL II Primavera 2003 Soluciones del boletín de problemas 6 Problema 1. Varilla deslizándose por una pared. Dado que los extremos de la varilla están forzados a permanecer
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA TERCERA EVALUACIÓN DE FÍSICA A MARZO 4 DE 015 SOLUCIÓN Analice las siguientes siete preguntas,
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA TERCERA EVALUACIÓN DE FÍSICA A MARZO 4 DE 015 SOLUCIÓN Analice las siguientes siete preguntas,
PROGRAMA. Introducción a la Dinámica Clásica
 UNIVERSIDAD CENTROCCIDENTAL LISANDRO ALVARADO DECANATO DE CIENCIAS Y TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA PROGRAMA LICENCIATURA EN CIENCIAS MATEMATICAS. ÁREA DE FISICA PROGRAMA Introducción a la Dinámica
UNIVERSIDAD CENTROCCIDENTAL LISANDRO ALVARADO DECANATO DE CIENCIAS Y TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA PROGRAMA LICENCIATURA EN CIENCIAS MATEMATICAS. ÁREA DE FISICA PROGRAMA Introducción a la Dinámica
Para verificar que el sistema converge se deberán cumplir con las siguientes condiciones en las formulas con derivadas parciales: + 1
 MAT 5 B Sistemas de ecuaciones no lineales EJERCICIOS RESUELTOS. Resuelva el siguiente sistema de ecuaciones no lineales, utilizando el método de punto fijo multivariable: x cos x x SOLUCIÓN x 8 x +. +
MAT 5 B Sistemas de ecuaciones no lineales EJERCICIOS RESUELTOS. Resuelva el siguiente sistema de ecuaciones no lineales, utilizando el método de punto fijo multivariable: x cos x x SOLUCIÓN x 8 x +. +
Vibraciones Linealización de ecuaciones diferenciales
 Vibraciones Linealización de ecuaciones diferenciales MScAA Marcos Knoblauch Departamento de Aeronáutica Universidad Nacional de La Plata Introducción Este documento contiene las ecuaciones y conceptos
Vibraciones Linealización de ecuaciones diferenciales MScAA Marcos Knoblauch Departamento de Aeronáutica Universidad Nacional de La Plata Introducción Este documento contiene las ecuaciones y conceptos
PROBLEMAS PROPUESTOS
 PROBLEMAS PROPUESTOS En los problemas que a continuación se proponen, el campo gravitacional de intensidad g actúa verticalmente en el plano que coincide con la hoja de papel. 1.- La esfera A de radio
PROBLEMAS PROPUESTOS En los problemas que a continuación se proponen, el campo gravitacional de intensidad g actúa verticalmente en el plano que coincide con la hoja de papel. 1.- La esfera A de radio
Capítulo 5. Integrales sobre curvas y superficies
 Capítulo 5. Integrales sobre curvas y superficies 5.1. Integrales de funciones escalares sobre curvas 5.2. Integrales de campos vectoriales sobre curvas 5.3. Teorema de Green 5.4. Integrales sobre superficies
Capítulo 5. Integrales sobre curvas y superficies 5.1. Integrales de funciones escalares sobre curvas 5.2. Integrales de campos vectoriales sobre curvas 5.3. Teorema de Green 5.4. Integrales sobre superficies
4.2. FUERZAS Y MOMENTOS EN DINÁMICA DE ROTACIÓN.
 4.2. FUERZAS Y MOMENTOS EN DINÁMICA DE ROTACIÓN. 4.2.1. El momento de inercia de un cilindro respecto del eje que pasa por el centro de sus bases es mr 2 /2, siendo m su masa y R el radio. Si se aplica
4.2. FUERZAS Y MOMENTOS EN DINÁMICA DE ROTACIÓN. 4.2.1. El momento de inercia de un cilindro respecto del eje que pasa por el centro de sus bases es mr 2 /2, siendo m su masa y R el radio. Si se aplica
Diego Luis Aristizábal R., Roberto Restrepo A., Tatiana Muñoz H. Profesores, Escuela de Física de la Universidad Nacional de Colombia Sede Medellín
 NIVERSIDD NCIONL DE COLOMI SEDE MEDELLÍN FCLTD DE CIENCIS-ESCEL DE FÍSIC FÍSIC MECÁNIC MÓDLO # : SISTEM DE PRTÍCLS DINÁMIC DEL CERPO RÍGIDO (II)- Diego Luis ristizábal R., Roberto Restrepo., Tatiana Muñoz
NIVERSIDD NCIONL DE COLOMI SEDE MEDELLÍN FCLTD DE CIENCIS-ESCEL DE FÍSIC FÍSIC MECÁNIC MÓDLO # : SISTEM DE PRTÍCLS DINÁMIC DEL CERPO RÍGIDO (II)- Diego Luis ristizábal R., Roberto Restrepo., Tatiana Muñoz
ANÁLISIS II Computación. Práctica 4. x 3. x 2 + y 2 si (x, y) (0, 0)
 facultad de ciencias exactas y naturales uba primer cuatrimestre 2007 ANÁLISIS II Computación Práctica 4 Derivadas parciales 1. Calcular a) f y (2, 1) para f(x, y) = xy + x y b) f z (1, 1, 1) para f(x,
facultad de ciencias exactas y naturales uba primer cuatrimestre 2007 ANÁLISIS II Computación Práctica 4 Derivadas parciales 1. Calcular a) f y (2, 1) para f(x, y) = xy + x y b) f z (1, 1, 1) para f(x,
Tema 2: Representación y modelado de sistemas dinámicos
 Fundamentos de Control Automático 2º G. Ing. Tecn. Industrial Tema 2: Representación y modelado de sistemas dinámicos Índice del tema Tema 2: Representación y modelado de sistemas dinámicos 2. Señales
Fundamentos de Control Automático 2º G. Ing. Tecn. Industrial Tema 2: Representación y modelado de sistemas dinámicos Índice del tema Tema 2: Representación y modelado de sistemas dinámicos 2. Señales
ECUACIONES DIFERENCIALES LINEALES DE SEGUNDO ORDEN
 ECUACIONES DIFERENCIALES LINEALES DE SEGUNDO ORDEN Movimiento Libre No Amortiguado Una de las aplicaciones de las ecuaciones diferenciales de segundo orden es la resolución de problemas de movimiento armónico
ECUACIONES DIFERENCIALES LINEALES DE SEGUNDO ORDEN Movimiento Libre No Amortiguado Una de las aplicaciones de las ecuaciones diferenciales de segundo orden es la resolución de problemas de movimiento armónico
Campo Eléctrico. Es el portador de la fuerza eléctrica. q 2. q 1
 Campo Eléctrico Es el portador de la fuerza eléctrica. q 1 q 2 E1 E2 Por qué se usa el campo eléctrico? Porque es útil simplificar el problema separándolo en partes. Porque nos permite pensar en una situación
Campo Eléctrico Es el portador de la fuerza eléctrica. q 1 q 2 E1 E2 Por qué se usa el campo eléctrico? Porque es útil simplificar el problema separándolo en partes. Porque nos permite pensar en una situación
; (4ptos) U r 4r cuál debe ser radio de orbita circular (3ptos). y la energía
 PROBLEMAS PARA III-er PREIO MECANICA TEORICA I 1) Dos partículas con las masas m A 1 y m B (aquí y en adelante se utilizan las unidades adimensionales) inicialmente están localizadas en el plano XOY en
PROBLEMAS PARA III-er PREIO MECANICA TEORICA I 1) Dos partículas con las masas m A 1 y m B (aquí y en adelante se utilizan las unidades adimensionales) inicialmente están localizadas en el plano XOY en
Sistemas autónomos. Introducción a la teoría cualitativa.
 Lección 4 Sistemas autónomos. Introducción a la teoría cualitativa. 4.1 Sistemas autónomos. Mapas de fase. En esta lección nos centraremos en el estudio de sistemas autónomos, es decir, aquellos que pueden
Lección 4 Sistemas autónomos. Introducción a la teoría cualitativa. 4.1 Sistemas autónomos. Mapas de fase. En esta lección nos centraremos en el estudio de sistemas autónomos, es decir, aquellos que pueden
Examen de Física-1, 1 Ingeniería Química Examen final. Enero de 2011 Problemas (Dos puntos por problema).
 Examen de Física-1, 1 Ingeniería Química Examen final Enero de 2011 Problemas (Dos puntos por problema) Problema 1 (Primer parcial): Un muelle de constante k =10 4 N/m está comprimido 20 cm Al liberarlo
Examen de Física-1, 1 Ingeniería Química Examen final Enero de 2011 Problemas (Dos puntos por problema) Problema 1 (Primer parcial): Un muelle de constante k =10 4 N/m está comprimido 20 cm Al liberarlo
Práctico 2: Mecánica lagrangeana
 Mecánica Anaĺıtica Curso 2016 Práctico 2: Mecánica lagrangeana 1. La polea y la cuerda de la figura son ideales y los bloques deslizan sin roce. Obtenga las aceleraciones de los bloques a partir de las
Mecánica Anaĺıtica Curso 2016 Práctico 2: Mecánica lagrangeana 1. La polea y la cuerda de la figura son ideales y los bloques deslizan sin roce. Obtenga las aceleraciones de los bloques a partir de las
