Tema 5. Modelos multivariantes no estacionarios
|
|
|
- María Nieves Carmona Ayala
- hace 5 años
- Vistas:
Transcripción
1 Tem 5. Modelos mulivrines no escionrios. Modelos VAR con vribles no escionris. Coinegrción 3. Modelos vecoriles con mecnismo de corrección del equilibrio 4. Meodologí pr l consrucción de modelos VEqCM 5. Ejemplos de modelos VEqCM 6. Regresiones espuris.
2 . Modelos VAR con vribles no escionris Vmos considerr el siguiene modelo VAR() Si iene un ríz uniri sbemos que el modelo no es escionrio. Vmos considerr que, en ese cso, ods ls vribles del sisem ienen el mismo orden de inegrción. 0 Φ I
3 Ejemplo: Ls dos series ienen un ríz uniri ± Φ ) )( 0.5 ( I
4 Ejemplo: En ese cso, un serie no es escionri pero l or sí ± Φ ) )( 0.5 ( I
5 En el cso de un sisem no escionrio en el que ls dos vribles ienen el mismo orden de inegrción, podemos ener dos siuciones diferenes: ) b) Φ Φ I I
6 Esos dos csos son olmene diferenes. En el primer cso, podemos considerr el modelo donde cd vrible del sisem prece en primers diferencis
7 En el cso más generl,, seguirí un modelo VAR(p): Ese modelo esá represenndo ls relciones coro plzo enre mbs vribles. W p p p p p p ) ( ) ( ) ( ) ( () () () ()... p p p p ) ( ) ( () ()...
8 6. Coinegrción Vmos considerr hor que el modelo VAR() no es escionrio pero que Φ I En ese cso, l diferencición de cd un de ls vribles no serí decud ddo que se inroducirí un medi móvil no inverible en el modelo (esrímos sobrediferencindo). L diferenci enre el cso nerior ese es debid que en ese úlimo eise lo que se conoce como coinegrción enre ls vribles.
9 Pr ilusrr el concepo de coinegrción, vmos considerr dos series cuos niveles evolucionn lo lrgo del iempo sin endenci, es decir, son vribles I() sin consne. En ese cso, un represención posible de ess series es: Cundo coinciden, eise coinegrción. En ese cso, ls series esán relcionds lrgo plzo (de form permnene). η µ µ ε µ η δ δ ε δ η η
10 Vmos considerr ls siguienes vribles: Y Y.5 η ε σ η µ µ σ ε µ 0 ), ( Corr ε ε σ η δ δ ε δ ε
11 Vmos considerr hor ls siguienes vribles δ δ σ η δ ε Corr( η, η η ) Y Y4
12 Cundo los niveles subcenes esán relciondos enre sí, enonces ls series esán relcionds en el lrgo plzo mnendrán un relción de equilibrio enre ells.
13 Definición forml de coinegrción pr dos vribles I(): Dos vribles esán coinegrds si cd un de ells es I() pero eise un combinción linel de mbs vribles que es escionri. ε η η µ µ ε µ η δ δ ε δ η βη ε βη βη δ βη δ δ βε ε β
14 Ls vribles mnendrán un relción de equilibrio lrgo plzo que viene dd por β (, -β) es lo que se conoce como vecor de coinegrción Si plnemos l regresión β u Ls perurbciones son ls desviciones de l relción de equilibrio lrgo plzo.
15 3. Modelos vecoriles con mecnismo de corrección del error Pr modelizr ls relciones enre vribles no escionris coinegrds enemos que plner un modelo que eng en cuen que dichs vribles mnienen no relciones coro plzo como lrgo plzo. Dicho modelo es el modelo VAR con Mecnismo de corrección del error (MCE): VEqCM
16 El modelo VAR-MCE pr dos vribles viene ddo por: es el mecnismo de corrección del error de, iene signo negivo. p p p p p p ) ( ) ( ) ( ) ( () () () ()... ) ( β α α α
17 4. Meodologí pr l consrucción de modelos VEqCM Se puede esimr conrsr l coinegrción uilizndo el méodo de Máim Verosimiliud de Johnsen. Sin embrgo, eise un méodo en dos eps más sencillo: i) Esimr primero l relción de equilibrio lrgo plzo: u β Si ls vribles esán coinegrds, ls perurbciones deben ser escionris.
18 Por lo no, un vez esimdos los prámeros por MCO, se hce un conrse de ríces uniris en los residuos. Si se rechz l hipóesis nul de no-escionriedd, ls vribles esán coinegrds.
19 Vmos considerr, por ejemplo, ls series: Y Y
20 Y Residuls
21 Oro ejemplo: Y Y4
22 Y Residuls
23 ii) Se esim el modelo VAR-MCE susiuendo ls desviciones del equilibrio l lrgo plzo por los residuos del modelo nerior. p p p p p p u ) ( ) ( ) ( ) ( () () () ()... ˆ α α
24
25 Alernivmene, el modelo se puede esimr por MV en un únic ep
26 5. Ejemplo: Relciones dinámics enre precios del vcuno El objeivo es conrsr empíricmene l inegrción espcil enre los dos circuios en los que rdicionlmene h esdo frgmendo el mercdo inerncionl de crne de vcuno. Pr ello, se v conrsr si eise un relción de equilibrio lrgo plzo enre dos precios represenivos de cd uno de los dos circuios.
27 El precio elegido como represenivo del circuio de fiebre fos es el precio mensul de eporción FOB de crne de vcuno en Argenin como represenivo del circuio libre de fiebre fos, el precio de imporción CIF de crne usrlin en Esdos Unidos. Los precios, medidos en dólres por oneld, hn sido observdos mensulmene durne el periodo comprendido enre enero de 977 diciembre de 997.
28 L rnsformción logrímic de mbs series de precios prece represend en el siguiene gráfico en el que puede precirse que su nivel prece evolucionr lo lrgo del iempo LARG LUSA
29 LUSA(4) Esdísico -.83 Vlores críicos (%, 5%, 0%) -4.00, -3.43, -3.4 DLUSA(4) , -.87, -.57 LARG(4) , -3.43, -3.4 DLARG(4) , -.87, -.57
30 El gráfico de ls series nos señl mbién ls siguienes crcerísics: Hs proimdmene el fin del ño 990, l evolución lrgo plzo de mbos precios es mu similr, con un diferencil proimdmene consne enre ellos. A prir de 99 prece hber un cmbio en el ipo de relción lrgo plzo que mnienen mbos precios. A prir de proimdmene 994, mbs series convergen en su evolución.
31 El primer cmbio en l relción de equilibrio lrgo plzo puede jusificrse porque el 4 de mo de 989, el Prido Jusicilis gn ls elecciones presidenciles: Nuev oriención en l políic económic con medids de esbilizción El secor del vcuno mbién eperimen un fuere liberlizción
32 El segundo cmbio puede esr jusificdo por cmbios en el propio mercdo inerncionl del vcuno. A medidos de 989, los Gobiernos de Argenin, Brsil Urugu, juno con el cenro Pnmericno de Fiebre Afos, firmron un convenio pr el conrol l errdicción de l enfermedd en l Cuenc de l Pl. Urugu fue declrdo en 993, pís libre de fos con vcunción mienrs que Argenin recibió dich declrción en mo de 997.
33 Pr inroducir el efeco de esos dos cmbio, se inroducen en el modelo VAR-MCE, dos vribles ficicis: que om vlor cero hs diciembre de 990. A prir de ese momeno, om vlores,, 3, hs diciembre de 994, volviendo omr vlor cero prir de ese momeno. D que es un vrible esclón que om vlor cero hs diciembre de 994 uno prir de ese momeno. D
34 Resuldos de l esimción: 4 LUSA * (0,4) 0,6 3 LUSA * (0,) 0,5 LUSA * (0,) 0,05 LUSA * (0,) 0,0 4 LARG * (0,06) 0,09 3 LARG * (0,06) 0,8 LARG * (0,06) 0,0 LARG * (0,06) 0,9 ) - * D (0,) 0,5 - - * D (0,00) 0,008 - LUSA LARG (0,03) 0,5 * ( (0,03) 0,3 LARG 4 LUSA * (0,06) 0,06 3 LUSA * (0,07) 0,04 LUSA * (0,05) 0, LUSA * (0,06) 0,46 4 LARG * (0,04) 0,06 3 LARG * (0,04) 0,03 LARG * (0,04) 0,09 LARG * (0,04) 0,0004 ) - * D (0,) 0,5 - - * D (0,00) 0,008 - LUSA LARG (0,03) 0,5 * ( (0,0) 0,008 LUSA
35 Los esdísicos Bo-Ljung correspondienes los residuos de ls ecuciones de los precios LARG LUSA omn vlores de respecivmene, no deecndo problems de ml especificción en el modelo.
36 L relción de equilibrio lrgo plzo enre mbos precios viene dd por: LARG LUSA.008 D 0.5 D (0.00) (0.) (0.03) Enre enero de 99 diciembre de 994, los precios rgeninos crecen un rimo del 0.8%. A prir de enero de 995, los dos precios se inegrn olmene l diferenci enre ellos desprece l cncelrse l consne de l consne de l relción de equilibrio lrgo plzo con el coeficiene del esclón.
37 En cuno l relción dinámic coro plzo, los precios rgeninos relizn el juse ne ls desviciones respeco l equilibrio de lrgo plzo. Además, ls vriciones en el precio de ese pís, responden su propio psdo (son significivos los coeficienes con 3 rerdos) sí como ls vriciones de los precios en Esdos Unidos.
38 Finlmene, ls vriciones de los precios de Esdos Unidos responden su propio psdo (son significivos los coeficienes de los rerdos ). Además, ls vriciones en esos precios no responden ls desviciones del equilibrio lrgo plzo.
39 Un ejercicio eórico (omdo de ls nos del profesor A. Esps) Considere el siguiene modelo VAR(): Tiene esrucur ringulr, es decir, el psdo de no influe en, pero el de és sí que fec. Como Cov(, )0.5, ls vribles e ienen un covrinz conemporáne de 0.5. Ω
40 L ecución crcerísic del modelo es: cus ríces son.49. Por lo no, el sisem no es escionrio. Vmos ver cuáles son los modelos univrines que se derivn pr cd un de ls vribles: ( L)( 0.7L) 0.4 ( L)
41 Ambs vribles ienen un ríz uniri sus primers diferencis ienen medi cero. Por lo no, mbs ienen oscilciones locles de nivel. Vmos reformulr el modelo VAR nerior como un modelo vecoril con mriz de covrinzs digonl, sbiendo que l cuslidd conemporáne v desde. Pr ello vmos considerr que b b Corr( ε, σ σ σ 0.5 ε ) ε 0.5 ε
42 Por lo no, enemos el siguiene sisem de dos ecuciones: ε En ese cso, ls vribles esán coinegrds ddo que l perurbción del modelo que relcion con es escionri. En consecuenci, el modelo propido pr represenr ls relciones dinámics enre mbs vribles es un modelo VAR-MCE. Vmos derivr dicho modelo.
43 Vmos considerr ls epresiones neriores de ls vribles: ε De donde, Escionrio 0.4 ε Escionrio ε Escionrio
44 L relción de equilibrio lrgo plzo enre mbs vribles viene dd por: L velocidd de juse de desviciones con respeco l equilibrio lrgo plzo es L correlción conemporáne enre e es 0.5. L vrible sigue mermene un modelo de pseo leorio
45 Finlmene si susiuimos en ls epresiones neriores ls perurbciones incorrelds por ls originles conemporánemene correlcionds, obenemos el modelo VAR-MCE ε ε
46 En ese ejemplo, ls vribles no esán correlcionds coro plzo. Tod l relción dinámic enre mbs vribles viene recogid por su relción de equilibrio lrgo plzo. Además, l vrible es fueremene eógen porque no responde ls desviciones del equilibrio lrgo plzo no depende coro plzo de ls vriciones de l vrible
47 6. Regresiones espuris Como en el cso de los modelos VAR escionrios, si se sisfcen ls condiciones de eogeneidd, es posible reducir el número de ecuciones del modelo. En el cso de que ods ls vribles sen eógens menos un, obendrímos un modelo uniecucionl.
48 El modelo uniecucionl que se obiene cundo ls vribles son no-coinegrds es un modelo en el que ods ls vribles precen en primers diferencis. Por or pre, cundo ls vribles esán coinegrds, el modelo uniecucionl recoge el mecnismo de corrección del equilibrio o del error.
49 El modelo de l función de rnsferenci pr vribles no coinegrds h que especificrlo en érminos de ls vribles diferencids, ddo que enre ls vribles en niveles no eisen relciones lrgo plzo. Si se inenr regresr ls vribles en niveles, se obiene lo que se conoce como el problem de ls regresiones espuris: regresiones donde el esdísico es lmene significivo con coeficienes de deerminción mu grndes unque, en relidd, l esimción es inconsisene. L form de deecr un regresión espuri es medine l observción de que los residuos del modelo no son escionrios.
Tema 4. Modelos multivariantes recursivos. Variables exógenas. Modelos uniecuacionales. Causalidad en sentido de Granger.
 Tem 4. Modelos mulivrines recursivos. Vribles exógens. Modelos uniecucionles.. El Modelo VARp escionrio. Cuslidd en senido de Grnger.. Esimción de modelos VAR 3. Modelos VAR con vribles exógens. Modelo
Tem 4. Modelos mulivrines recursivos. Vribles exógens. Modelos uniecucionles.. El Modelo VARp escionrio. Cuslidd en senido de Grnger.. Esimción de modelos VAR 3. Modelos VAR con vribles exógens. Modelo
4. Modelos AR(1) y ARI(1,1).
 4. Modelos AR( ARI(,. Los modelos uorregresivos son quellos modelos ARMA(p,q en los que q0. En generl, vmos denorlos por AR(p. En un modelo AR(p en vlor en el momeno de l serie se expres como un combinción
4. Modelos AR( ARI(,. Los modelos uorregresivos son quellos modelos ARMA(p,q en los que q0. En generl, vmos denorlos por AR(p. En un modelo AR(p en vlor en el momeno de l serie se expres como un combinción
Tema 2. Modelos univariantes lineales: MA e IMA
 Tem. Modelos univrines lineles: MA e IMA. Procesos esocásicos escionrios. L función de uocorrelción el correlogrm.. El proceso ruido blnco. 3. Modelos MA( e IMA(,. Generlizción modelos MA(q e IMA(,q 4.
Tem. Modelos univrines lineles: MA e IMA. Procesos esocásicos escionrios. L función de uocorrelción el correlogrm.. El proceso ruido blnco. 3. Modelos MA( e IMA(,. Generlizción modelos MA(q e IMA(,q 4.
respectivamente. son series estacionarias. primera diferencia regular y no la estacional por lo que (b) es falsa. Como
 NOMBRE Y APELLIDO: ECONOMETRÍA II CURSO 009/00 Primer evlución prcil NOTA: En ls preguns 3 4 debe rzonr jusificr correcmene odos los punos de su respues Ls respuess sin jusificr se punurán con un cero
NOMBRE Y APELLIDO: ECONOMETRÍA II CURSO 009/00 Primer evlución prcil NOTA: En ls preguns 3 4 debe rzonr jusificr correcmene odos los punos de su respues Ls respuess sin jusificr se punurán con un cero
SOSTENIBILIDAD DE UNA POLÍTICA FISCAL
 1 SOSTENIBILIDAD DE UNA POLÍTICA FISCAL Definición de un políic fiscl sosenible El concepo de políic fiscl sosenible no cep un definición precis. Sin embrgo, un definición generl (unque lgo rivil) es que
1 SOSTENIBILIDAD DE UNA POLÍTICA FISCAL Definición de un políic fiscl sosenible El concepo de políic fiscl sosenible no cep un definición precis. Sin embrgo, un definición generl (unque lgo rivil) es que
Unidad Nº 1 Sistemas de ecuaciones. Método de Gauss 1
 Unidd Nº Sisems de ecuciones. Méodo de Guss Memáics plicds ls Ciencis Sociles II. ANAYA JRCICIOS PROPUSTOS (págin Sin resolverlos, son equivlenes esos sisems? b, d c ---oooo--- Se r de prir de uno de los
Unidd Nº Sisems de ecuciones. Méodo de Guss Memáics plicds ls Ciencis Sociles II. ANAYA JRCICIOS PROPUSTOS (págin Sin resolverlos, son equivlenes esos sisems? b, d c ---oooo--- Se r de prir de uno de los
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE VALENCIA SEPTIEMBRE (RESUELTOS por Antonio Menguiano)
 I.E.S. CASTELAR BADAJOZ PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE VALENCIA SEPTIEBRE (RESUELTOS por Anonio enguino) ATEÁTICAS II Tiempo máimo: hors Se elegirá el Ejercicio A o el B, del que sólo se hrán
I.E.S. CASTELAR BADAJOZ PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE VALENCIA SEPTIEBRE (RESUELTOS por Anonio enguino) ATEÁTICAS II Tiempo máimo: hors Se elegirá el Ejercicio A o el B, del que sólo se hrán
, verificar que x. vectores propios. Determinar los valores propios correspondientes. Solución: λ
 re 7 Sen : definido por (, y ) ( + y, ) y f ( ) + Hllr f ( )(, y) f ( )(, y) ( y, + y) Pr l mriz A, verificr que (,,) y (,, ) son vecores propios Deerminr los vlores propios correspondienes λ, λ, respecivmene
re 7 Sen : definido por (, y ) ( + y, ) y f ( ) + Hllr f ( )(, y) f ( )(, y) ( y, + y) Pr l mriz A, verificr que (,,) y (,, ) son vecores propios Deerminr los vlores propios correspondienes λ, λ, respecivmene
Examen 1: Vectores, Cinemática y Dinámica. 26 de Noviembre de º Bachillerato B
 6 de Noviembre de 010 Nombre: º Bchillero B Elegir res problems y dos cuesiones, el problem P1 es obligorio. Cd problem se vlorrá con hs,5 punos, mienrs que ls cuesiones vldrán hs 1,5 punos cd un. C1.-
6 de Noviembre de 010 Nombre: º Bchillero B Elegir res problems y dos cuesiones, el problem P1 es obligorio. Cd problem se vlorrá con hs,5 punos, mienrs que ls cuesiones vldrán hs 1,5 punos cd un. C1.-
Análisis de Series de Tiempo
 CURSO REGIONAL SORE HOJA DE ALANCE DE ALIMENTOS, SERIES DE TIEMPO Y ANÁLISIS DE POLÍTICA MSc. Sndr Hernández sndr.hernndezro@gmil.com Sede Subregionl de l CEPAL en México Ciudd de México, del 9 l 3 de
CURSO REGIONAL SORE HOJA DE ALANCE DE ALIMENTOS, SERIES DE TIEMPO Y ANÁLISIS DE POLÍTICA MSc. Sndr Hernández sndr.hernndezro@gmil.com Sede Subregionl de l CEPAL en México Ciudd de México, del 9 l 3 de
Relaciones dinámicas entre precios del vacuno. Ejemplo preperado por la Profa.Esther Ruíz
 Relaciones dinámicas enre precios del vacuno Ejemplo preperado por la Profa.Esher Ruíz Relaciones dinámicas enre precios del vacuno El objeivo de esa sección es conrasar empíricamene la inegración espacial
Relaciones dinámicas enre precios del vacuno Ejemplo preperado por la Profa.Esher Ruíz Relaciones dinámicas enre precios del vacuno El objeivo de esa sección es conrasar empíricamene la inegración espacial
MODELOS ARIMA Mayo 2001
 MODELOS ARIMA Mo Prof. Rfel de Arce Prof. Rmón Mhí Dpo. Economí Aplicd U.D.I. Economerí e Informáic ADE Economerí II. Modelos de Series emporles Págin INRODUCCIÓN En 97, Box Jenkins desrrollron un cuerpo
MODELOS ARIMA Mo Prof. Rfel de Arce Prof. Rmón Mhí Dpo. Economí Aplicd U.D.I. Economerí e Informáic ADE Economerí II. Modelos de Series emporles Págin INRODUCCIÓN En 97, Box Jenkins desrrollron un cuerpo
Solución: Las transformaciones y el resultado de hacer el determinante en cada caso son:
 Memáics II Deerminnes PVJ7. Se l mriz 8 9 7 Se B l mriz que resul l relizr en ls siguienes rnsformciones: primero se muliplic por sí mism, después se cmbin de lugr l fil segund y l ercer y finlmene se
Memáics II Deerminnes PVJ7. Se l mriz 8 9 7 Se B l mriz que resul l relizr en ls siguienes rnsformciones: primero se muliplic por sí mism, después se cmbin de lugr l fil segund y l ercer y finlmene se
CAPÍTULO 9. INTEGRALES IMPROPIAS 9.1. Límites de integración infinitos 9.2. Integrales con integrando que tiende a infinito 9.3. Observaciones a las
 CAPÍTULO 9. INTEGRALES IMPROPIAS 9.. Límies de inegrción infinios 9.. Inegrles con inegrndo que iende infinio 9.. Oservciones ls inegrles impropis Cpíulo 9 Inegrles impropis f ( ) f ( ) f f ( ) () f()
CAPÍTULO 9. INTEGRALES IMPROPIAS 9.. Límies de inegrción infinios 9.. Inegrles con inegrndo que iende infinio 9.. Oservciones ls inegrles impropis Cpíulo 9 Inegrles impropis f ( ) f ( ) f f ( ) () f()
4.5 Filtros analógicos: respuesta al escalón
 Universidd rlos III de Mdrid 4.5 Filros nlógicos: respues l esclón Respues l esclón de un filro nlógico de primer orden. dy () + y() =, x() = u() y () d y() = Y º) Polinomio crcerísico Ps () = s+ riz s
Universidd rlos III de Mdrid 4.5 Filros nlógicos: respues l esclón Respues l esclón de un filro nlógico de primer orden. dy () + y() =, x() = u() y () d y() = Y º) Polinomio crcerísico Ps () = s+ riz s
MATEMÁTICAS II PRUEBAS DE ACCESO A LA UNIVERSIDAD DE OVIEDO
 MTEMÁTCS RUEBS DE CCESO L UNVERSDD DE OVEDO.- MTRCES Y DETERMNNTES.- MODELO DE RUEB roduco de mrices: concepo. Condiciones pr su relición. Es posible que pr dos mrices B no cudrds puedn eisir B B?. b Si
MTEMÁTCS RUEBS DE CCESO L UNVERSDD DE OVEDO.- MTRCES Y DETERMNNTES.- MODELO DE RUEB roduco de mrices: concepo. Condiciones pr su relición. Es posible que pr dos mrices B no cudrds puedn eisir B B?. b Si
Determinantes y matrices
 Deerminnes mrices. Dds ls mrices:, Hll l invers de, l mriz l que. ; ; djun de De. lcul l mriz invers de l mriz L mriz invers viene dd por, siendo l mriz de los djunos de. El deerminne de vle L mriz de
Deerminnes mrices. Dds ls mrices:, Hll l invers de, l mriz l que. ; ; djun de De. lcul l mriz invers de l mriz L mriz invers viene dd por, siendo l mriz de los djunos de. El deerminne de vle L mriz de
MATRICES Y DETERMINANTES.
 punes de. Cbñó MTRICES Y DETERMINNTES. CONTENIDOS: Definición y erminologí básic. Operciones con mrices: sum y produco. Produco de un mriz por un esclr. Mriz opues. Mriz invers. Epresión mricil de un sisem
punes de. Cbñó MTRICES Y DETERMINNTES. CONTENIDOS: Definición y erminologí básic. Operciones con mrices: sum y produco. Produco de un mriz por un esclr. Mriz opues. Mriz invers. Epresión mricil de un sisem
TÉCNICAS AVANZADAS DE SERIES TEMPORALES PARA LA PREDICCIÓN ECONÓMICA Y EL ANÁLISIS DE COYUNTURA
 Dpo. de Esdísic,Esr.Ec.y O.E.I. TÉCNICAS AVANZADAS DE SERIES TEMPORAES PARA A PREDICCIÓN ECONÓMICA Y E ANÁISIS DE COYUNTURA Técnics vnzds de series emporles Dpo. de Esdísic,Esr.Ec.y O.E.I. PREDICCIÓN ECONÓMICA
Dpo. de Esdísic,Esr.Ec.y O.E.I. TÉCNICAS AVANZADAS DE SERIES TEMPORAES PARA A PREDICCIÓN ECONÓMICA Y E ANÁISIS DE COYUNTURA Técnics vnzds de series emporles Dpo. de Esdísic,Esr.Ec.y O.E.I. PREDICCIÓN ECONÓMICA
EJERCICIOS UNIDADES 1 y 2: MATRICES Y DETERMINANTES = = A donde ( ) ( ) 2. B calcule la matriz X que verifique.
 IES Pdre Poved (Gudi) Memáics plicds ls SS II Deprmeno de Memáics loque I: Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJERIIOS UNIDDES : MTRIES Y DETERMINNTES (Jun-96) Encuenre
IES Pdre Poved (Gudi) Memáics plicds ls SS II Deprmeno de Memáics loque I: Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJERIIOS UNIDDES : MTRIES Y DETERMINNTES (Jun-96) Encuenre
EJERCICIOS UNIDADES 1 y 2: MATRICES Y DETERMINANTES = = A donde ( ) ( ) 2. B calcule la matriz X que verifique.
 ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
Determinantes y matrices
 emáics SS Deerminnes José rí rínez edino Deerminnes mrices. Dds ls mrices:, Hll l invers de, l mriz l que. ; ; djun de De. lcul l mriz invers de l mriz L mriz invers viene dd por, siendo l mriz de los
emáics SS Deerminnes José rí rínez edino Deerminnes mrices. Dds ls mrices:, Hll l invers de, l mriz l que. ; ; djun de De. lcul l mriz invers de l mriz L mriz invers viene dd por, siendo l mriz de los
CAPÍTULO 6 UNA ALTERNATIVA A LA APLICACIÓN EMPÍRICA DE LOS MODELOS FELTHAM-OHLSON
 Un lerniv l plicción empíric de los modelos Felhm-Ohlson CAPÍTULO 6 CAPÍTULO 6 UNA ALTERNATIVA A LA APLICACIÓN EMPÍRICA DE LOS MODELOS FELTHAM-OHLSON Hemos observdo un serie de resuldos en el cpíulo quino
Un lerniv l plicción empíric de los modelos Felhm-Ohlson CAPÍTULO 6 CAPÍTULO 6 UNA ALTERNATIVA A LA APLICACIÓN EMPÍRICA DE LOS MODELOS FELTHAM-OHLSON Hemos observdo un serie de resuldos en el cpíulo quino
L[u] = ( pu ) + qu. u(t) =
![L[u] = ( pu ) + qu. u(t) = L[u] = ( pu ) + qu. u(t) =](/thumbs/81/83618912.jpg) Función de Green Asumiremos que el operdor diferencil esá en form de divergenci: L[u] = ( pu ) + qu con p C [, b], p > y q C[, b], q. El problem es, dd un ϕ C[, b] enconr u l que: { L[u]() = ϕ() (, b)
Función de Green Asumiremos que el operdor diferencil esá en form de divergenci: L[u] = ( pu ) + qu con p C [, b], p > y q C[, b], q. El problem es, dd un ϕ C[, b] enconr u l que: { L[u]() = ϕ() (, b)
EJERCICIOS UNIDADES 1 y 2: MATRICES Y DETERMINANTES = = A donde ( ) ( ) 2. B calcule la matriz X que verifique.
 ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
Integración y Derivación Fraccionaria
 Cpíulo 2 Inegrción y Derivción Frccionri Anes de denrrnos en los operdores de inegrción y derivción generlizdos recordremos lgunos resuldos y nociones del cálculo elemenl que servirán como puno de prid
Cpíulo 2 Inegrción y Derivción Frccionri Anes de denrrnos en los operdores de inegrción y derivción generlizdos recordremos lgunos resuldos y nociones del cálculo elemenl que servirán como puno de prid
α el sistema es compatible indeterminado y la solución es α el sistema es incompatible; Si 1 α y 1
 ÁLGEBRA Preguns de Selecividd de l Comunidd Vlencin Resuelos en vídeo hp://www.prendermemics.org/bmeccnnlgebr_pu.hml Pág.. (PAU junio A Clculr los vlores que sisfcen ls siguienes ecuciones: C AY AX B AX
ÁLGEBRA Preguns de Selecividd de l Comunidd Vlencin Resuelos en vídeo hp://www.prendermemics.org/bmeccnnlgebr_pu.hml Pág.. (PAU junio A Clculr los vlores que sisfcen ls siguienes ecuciones: C AY AX B AX
EJERCICIOS PROPUESTOS
 Deerminnes y. Ejercicios resuelos. EJERCICIOS PROPUESTOS. Clcul el vlor de los siguienes deerminnes. 4 6 e) 4 5 7 4 d) 0 4 f) + 4 ( ) 4 6 4 8 6 = = = 5 0 4 6 7 4 = + = = = = 5 0 4 = + 4 + 0 0 4 = 4+ 0+
Deerminnes y. Ejercicios resuelos. EJERCICIOS PROPUESTOS. Clcul el vlor de los siguienes deerminnes. 4 6 e) 4 5 7 4 d) 0 4 f) + 4 ( ) 4 6 4 8 6 = = = 5 0 4 6 7 4 = + = = = = 5 0 4 = + 4 + 0 0 4 = 4+ 0+
SISTEMAS DE ECUACIONES LINEALES: MÉTODO DE GAUSS
 SISTEMAS DE ECUACIONES LINEALES: MÉTODO DE GAUSS Ejercicio nº.- Pon un ejemplo, cundo se posible, de un sisem de dos ecuciones con res incógnis que se: ) Compible deermindo Compible indeermindo c) Incompible
SISTEMAS DE ECUACIONES LINEALES: MÉTODO DE GAUSS Ejercicio nº.- Pon un ejemplo, cundo se posible, de un sisem de dos ecuciones con res incógnis que se: ) Compible deermindo Compible indeermindo c) Incompible
SISTEMAS DE ECUACIONES LINEALES amn
 Apunes de A. Cbñó Memáics plicds cc.ss. SISTEMAS DE ECUACIONES LINEALES. CONTENIDOS: Plnemienos de problems lineles. Soluciones de un sisem de ecuciones lineles. Sisems lineles equivlenes. Méodo de reducción
Apunes de A. Cbñó Memáics plicds cc.ss. SISTEMAS DE ECUACIONES LINEALES. CONTENIDOS: Plnemienos de problems lineles. Soluciones de un sisem de ecuciones lineles. Sisems lineles equivlenes. Méodo de reducción
Observabilidad del estado: necesidad
 Conrol en el Espcio de Esdo 5. Observbilidd por Pscul Cmpoy pscul.cmpoy@upm.es Universidd Poliécnic Mdrid U.P.M.-DISAM P. Cmpoy Conrol en el Espcio de Esdo 1 Observbilidd del esdo: necesidd r() u() B x
Conrol en el Espcio de Esdo 5. Observbilidd por Pscul Cmpoy pscul.cmpoy@upm.es Universidd Poliécnic Mdrid U.P.M.-DISAM P. Cmpoy Conrol en el Espcio de Esdo 1 Observbilidd del esdo: necesidd r() u() B x
Método de Gauss. Pon un ejemplo, cuando sea posible, de un sistema de dos ecuaciones con tres incógnitas que sea:
 Méodo de Guss Ejercicio nº.- Pon un ejemplo, cundo se posible, de un sisem de dos ecuciones con res incógnis que se: ) compible deermindo compible indeermindo c) incompible Jusific en cd cso us respuess.
Méodo de Guss Ejercicio nº.- Pon un ejemplo, cundo se posible, de un sisem de dos ecuciones con res incógnis que se: ) compible deermindo compible indeermindo c) incompible Jusific en cd cso us respuess.
ACTIVIDADES INICIALES
 Solucionrio Deerminnes CTIVIDDES INICILES.I. usc ls relciones de dependenci linel enre ls fils columns de ls siguienes mrices e indic el vlor de su rngo. rg() F F Como C C C rg().ii. Comprue que ls siguienes
Solucionrio Deerminnes CTIVIDDES INICILES.I. usc ls relciones de dependenci linel enre ls fils columns de ls siguienes mrices e indic el vlor de su rngo. rg() F F Como C C C rg().ii. Comprue que ls siguienes
Clasificación y resolución de sistemas por métodos elementales. 1. Resuelve utilizando el método de de reducción de Gauss Jordan, los sistemas:
 Álgebr: Sisems José Mrí Mríne Medino MATEMÁTICAS II TEMA Sisems de ecuciones lineles: Problems propuesos Clsificción resolución de sisems por méodos elemenles Resuelve uilindo el méodo de de reducción
Álgebr: Sisems José Mrí Mríne Medino MATEMÁTICAS II TEMA Sisems de ecuciones lineles: Problems propuesos Clsificción resolución de sisems por méodos elemenles Resuelve uilindo el méodo de de reducción
funciones primitivas se le llama integral indefinida y se representa por dx = F(x) + C F'(x) = f(x) ( ) '( ) '( ) '( ) f x f x dx C f'( x)
 INTEGRALES INDEFINIDAS Un función F() se dice que es primiiv de or función f() cundo F'() = f() Por ejemplo F() = es primiiv de f() = Or primiiv de f() = podrí ser F() = + 5, o en generl, F() = + C, donde
INTEGRALES INDEFINIDAS Un función F() se dice que es primiiv de or función f() cundo F'() = f() Por ejemplo F() = es primiiv de f() = Or primiiv de f() = podrí ser F() = + 5, o en generl, F() = + C, donde
165. Clasificar la cónica: y hallar su ecuación reducida. Demostración. Formaremos el discriminante: = = Hallaremos los invariantes de la cónica:
 Hoj de Problems Geomerí V 6. lsificr l cónic: f hllr su ecución reducid. Demosrción. Formremos el discriminne: / ; / como se r de un prábol rel. Hllremos los invrines de l cónic: l ecución reducid será
Hoj de Problems Geomerí V 6. lsificr l cónic: f hllr su ecución reducid. Demosrción. Formremos el discriminne: / ; / como se r de un prábol rel. Hllremos los invrines de l cónic: l ecución reducid será
PRÁCTICA 3 LEYES DE NEWTON
 Fundmenos Físicos de l Inenierí Inenierí Indusril Prácics de Lbororio PRÁCTIC 3 LEYES DE NEWTON 3 OJETIVO- Deerminr ls leyes que rien l relciones espcio-iempo y velocidd-iempo en movimienos uniformemene
Fundmenos Físicos de l Inenierí Inenierí Indusril Prácics de Lbororio PRÁCTIC 3 LEYES DE NEWTON 3 OJETIVO- Deerminr ls leyes que rien l relciones espcio-iempo y velocidd-iempo en movimienos uniformemene
A EXAMEN RESUELTO Fecha: junio 2008 (primera semana) Código asignatura:
 Fech: junio 8 (primer semn) Códio sinur: 54137 1. El enerdor, G, de l fiur cons de curo uniddes de 555 MVA cd un, que funcionn un ensión enre fses de 4 kv y 6 Hz, suminisrndo poenci un nudo de poenci infini,
Fech: junio 8 (primer semn) Códio sinur: 54137 1. El enerdor, G, de l fiur cons de curo uniddes de 555 MVA cd un, que funcionn un ensión enre fses de 4 kv y 6 Hz, suminisrndo poenci un nudo de poenci infini,
Definición de un árbol Rojinegro
 Definición de un árol Rojinegro Árol inrio esrico (los nodos nulos se ienen en cuen en l definición de ls operciones odo nodo oj es nulo) Cd nodo iene esdo rojo o negro Nodos oj (nulos) son negros L rí
Definición de un árol Rojinegro Árol inrio esrico (los nodos nulos se ienen en cuen en l definición de ls operciones odo nodo oj es nulo) Cd nodo iene esdo rojo o negro Nodos oj (nulos) son negros L rí
I.E.S. Ciudad de Arjona Departamento de Matemáticas. 1º BAC
 I.E.S. Ciudd de Arjon Deprmeno de Memáics. º BAC UNIDAD Nº : ECUACIONES, SISTEMAS E INECUACIONES. A. ECUACIONES. ECUACIONES DE PRIMER GRADO. Ls ecuciones de primer grdo son quells en l que inerviene polinomios
I.E.S. Ciudd de Arjon Deprmeno de Memáics. º BAC UNIDAD Nº : ECUACIONES, SISTEMAS E INECUACIONES. A. ECUACIONES. ECUACIONES DE PRIMER GRADO. Ls ecuciones de primer grdo son quells en l que inerviene polinomios
Observabilidad. U.P.M.-DISAM P. Campoy Control en el Espacio de Estado 2
 Observbilidd Inroducción Definiciones Observbilidd en sisems lineles Observbilidd en sisems lineles e invrines. Subespcio no-observble Subsisem observble Seprción del subsisem conrolble y observble U.P.M.-DISAM
Observbilidd Inroducción Definiciones Observbilidd en sisems lineles Observbilidd en sisems lineles e invrines. Subespcio no-observble Subsisem observble Seprción del subsisem conrolble y observble U.P.M.-DISAM
Cálculo Integral. dt, entonces: a) f no es integrable en 11. , pues no es continua. c) f es integrable en Dada f integrable en ab
 .- Se F () ( ) d, enonces: cos Cálculo Inegrl ) F'() -(cos ) sen b) F'() cos c) F'() cos si.- Se f( ) - < si enonces: ) f no es inegrble en, pues no es coninu. b) f es inegrble en, y f( ) d. c) f es inegrble
.- Se F () ( ) d, enonces: cos Cálculo Inegrl ) F'() -(cos ) sen b) F'() cos c) F'() cos si.- Se f( ) - < si enonces: ) f no es inegrble en, pues no es coninu. b) f es inegrble en, y f( ) d. c) f es inegrble
5.1 LÍMITES INFINITOS 5.2 INTEGRANDOS INFINITOS
 MOISES VILLEA MUÑOZ 5 5. LÍMITES IFIITOS 5. ITEGRADOS IFIITOS Objeivo: Se reende que el esudine clcule inegrles sobre regiones no cods y resuelv roblems de licción relciondos con ls inegrles imrois 97
MOISES VILLEA MUÑOZ 5 5. LÍMITES IFIITOS 5. ITEGRADOS IFIITOS Objeivo: Se reende que el esudine clcule inegrles sobre regiones no cods y resuelv roblems de licción relciondos con ls inegrles imrois 97
ALGUNAS REFLEXIONES SOBRE LOS MODELOS ARIMA
 Dpo. de Esdísic,Esr.Ec.y O.E.I. TÉCNICAS DE ETRACCIÓN DE SEÑALES -Alguns considerciones finles sobre los modelos ARIMA -Inroducción l nálisis especrl de series emporles -Méodos de exrcción de señles bsdos
Dpo. de Esdísic,Esr.Ec.y O.E.I. TÉCNICAS DE ETRACCIÓN DE SEÑALES -Alguns considerciones finles sobre los modelos ARIMA -Inroducción l nálisis especrl de series emporles -Méodos de exrcción de señles bsdos
EJERCICIOS UNIDADES 1 y 2: MATRICES Y DETERMINANTES = 001 1 = A donde ( ) ( ) 2. B calcule la matriz X que verifique.
 ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
6.7 Teorema de Convolución y la delta de Dirac 409
 6.7 Teorem de Convolución y l del de Dirc 49 6.7 Teorem de Convolución y l del de Dirc En el nálisis de sisems lineles, como en los sisems vibrorios (mecánicos y elécricos), uno de los objeivos es conocer
6.7 Teorem de Convolución y l del de Dirc 49 6.7 Teorem de Convolución y l del de Dirc En el nálisis de sisems lineles, como en los sisems vibrorios (mecánicos y elécricos), uno de los objeivos es conocer
PROBLEMAS DE TEOREMA DE GREEN
 PROBLEMAS E TEOREMA E GREEN ENUNIAO EL TEOREMA Se un curv simple cerrd suve rozos oriend posiivmene se F(; (P;Q un cmpo vecoril cus funciones coordends ienen derivds prciles coninus sore un región ier
PROBLEMAS E TEOREMA E GREEN ENUNIAO EL TEOREMA Se un curv simple cerrd suve rozos oriend posiivmene se F(; (P;Q un cmpo vecoril cus funciones coordends ienen derivds prciles coninus sore un región ier
5014 Mecánica. Primera Parte (60 minutos) Hoja 1 de 2 L 1. ψ = Fecha de Examen:
 ech de Emen: 3-6- 5 Mecánic Primer pellido: Mrícul: Segundo pellido: Nombre: NOT: en el enuncido ls mgniudes ecoriles se escriben en negri (V), unque en l solución Vd. Debe represenrls con un flech ( V
ech de Emen: 3-6- 5 Mecánic Primer pellido: Mrícul: Segundo pellido: Nombre: NOT: en el enuncido ls mgniudes ecoriles se escriben en negri (V), unque en l solución Vd. Debe represenrls con un flech ( V
FACULTAD DE CIENCIAS SECCIÓN FÍSICAS PLAN DE ACOGIDA
 FACULTAD DE CIENCIAS SECCIÓN FÍSICAS LAN DE ACGIDA TÍTUL: Moimieno Recilíneo BJETIVS: Cinemáic es l pre de l Físic que se ocup de l descripción de los moimienos sin ender ls cuss que lo producen. Un prícul
FACULTAD DE CIENCIAS SECCIÓN FÍSICAS LAN DE ACGIDA TÍTUL: Moimieno Recilíneo BJETIVS: Cinemáic es l pre de l Físic que se ocup de l descripción de los moimienos sin ender ls cuss que lo producen. Un prícul
2. Estudio de la medición experimental de tensiones
 Sisem pr l medición del esdo de ensiones en membrns eiles. Esudio de l medición eperimenl de ensiones.1 Eensomerí:.1.1 Concepos fundmenles en ls bnds eensomérics:.1.1.1 Inroducción: L consne demnd de l
Sisem pr l medición del esdo de ensiones en membrns eiles. Esudio de l medición eperimenl de ensiones.1 Eensomerí:.1.1 Concepos fundmenles en ls bnds eensomérics:.1.1.1 Inroducción: L consne demnd de l
EXPRESIÓN MATRICIAL DE UN SISTEMA DE ECUACIONES DE PIMER GRADO SISTEMA DE CRAMER
 EXPRESIÓN MTRICIL DE UN SISTEM DE ECUCIONES DE PIMER GRDO Un sise de ecuciones lineles con n incógnis, x, x,, xn iene l for: x x n xn b x x n xn b x x n xn b Recordndo el produco ricil, podeos decir: x
EXPRESIÓN MTRICIL DE UN SISTEM DE ECUCIONES DE PIMER GRDO Un sise de ecuciones lineles con n incógnis, x, x,, xn iene l for: x x n xn b x x n xn b x x n xn b Recordndo el produco ricil, podeos decir: x
CINEMÁTICA DE LA PARTÍCULA
 CINEMÁTICA DE LA PARTÍCULA ÍNDICE 1. Inroducción. Reposo moimieno. Sisems de referenci 3. Vecores posición, elocidd celerción 4. Componenes inrínsecs de l celerción 5. Inegrción de ls ecuciones del moimieno
CINEMÁTICA DE LA PARTÍCULA ÍNDICE 1. Inroducción. Reposo moimieno. Sisems de referenci 3. Vecores posición, elocidd celerción 4. Componenes inrínsecs de l celerción 5. Inegrción de ls ecuciones del moimieno
SOLUCIONES EJERCICIOS SISTEMAS DE ECUACIONES
 SOLUCIONES EJERCICIOS SISTEMAS DE ECUACIONES Ejercicio nº.- Pon un ejemplo cundo se posible de un sisem de dos ecuciones con res incógnis que se: ) compible deermindo compible indeermindo c) incompible
SOLUCIONES EJERCICIOS SISTEMAS DE ECUACIONES Ejercicio nº.- Pon un ejemplo cundo se posible de un sisem de dos ecuciones con res incógnis que se: ) compible deermindo compible indeermindo c) incompible
Las siguientes matrices son, respectivamente, de orden 3 x 3, 3 x 2, 3 x 4 y 2 x )
 Álgebr y Geomerí nlíic Mrices- Deerminnes- Sisems de Ecuciones Fculd Regionl L Pl Ing. Vivin CPPELLO Mrices Un mriz es un conjuno de números colocdos en un deermind disposición ordendos en fils y columns.
Álgebr y Geomerí nlíic Mrices- Deerminnes- Sisems de Ecuciones Fculd Regionl L Pl Ing. Vivin CPPELLO Mrices Un mriz es un conjuno de números colocdos en un deermind disposición ordendos en fils y columns.
ˆ ˆ. FÍSICA 100 CERTAMEN # 2 Forma R 12 de junio de La pirámide de la figura está definida por los vectores a, b y
 FÍSICA 1 CERAMEN # Form R 1 de junio de 1 A. AERNO A. MAERNO NOMBRE ROL USM - Si su rol comienz con 9 coloque 9 ESE CERAMEN CONSA DE REGUNAS EN 8 ÁGINAS. IEMO: 15 MINUOS SIN CALCULADORA. SIN ELÉFONO CELULAR
FÍSICA 1 CERAMEN # Form R 1 de junio de 1 A. AERNO A. MAERNO NOMBRE ROL USM - Si su rol comienz con 9 coloque 9 ESE CERAMEN CONSA DE REGUNAS EN 8 ÁGINAS. IEMO: 15 MINUOS SIN CALCULADORA. SIN ELÉFONO CELULAR
Experimentos con una rueda de construcción casera. 1.- Estudio de un movimiento uniformemente acelerado
 Experimenos con un rued de consrucción cser 1.- Esudio de un movimieno uniformemene celerdo Meril Rued de mder con eje de rdio 5 mm Plno inclindo 1,10 m Cronómero Flexómero Fundmeno Sopore de elevción
Experimenos con un rued de consrucción cser 1.- Esudio de un movimieno uniformemene celerdo Meril Rued de mder con eje de rdio 5 mm Plno inclindo 1,10 m Cronómero Flexómero Fundmeno Sopore de elevción
La transformada de Laplace
 CAPÍTULO 6 L rnsformd de Lplce 6.7 Teorem de Convolución y l del de Dirc En el nálisis de sisems lineles, como en los sisems vibrorios (mecánicos y elécricos), uno de los objeivos es conocer l respues
CAPÍTULO 6 L rnsformd de Lplce 6.7 Teorem de Convolución y l del de Dirc En el nálisis de sisems lineles, como en los sisems vibrorios (mecánicos y elécricos), uno de los objeivos es conocer l respues
MATEMÁTICAS II TEMA 3 Sistemas de ecuaciones lineales: Problemas propuestos
 Álgebr: Sisems wwwmemicsjmmmcom José Mrí Mríne Medino MATEMÁTICAS II TEMA Sisems de ecuciones lineles: Problems propuesos Clsificción resolución de sisems por méodos elemenles Resuelve uilindo el méodo
Álgebr: Sisems wwwmemicsjmmmcom José Mrí Mríne Medino MATEMÁTICAS II TEMA Sisems de ecuciones lineles: Problems propuesos Clsificción resolución de sisems por méodos elemenles Resuelve uilindo el méodo
INTEGRAL DE RIEMANN-STIELTJES
 Prof. Enrique Meus Nieves Docorndo en Educción Memáic. INTEGRAL DE RIEMANN-STIELTJES L inegrl de Riemnn-Sieljes es un exensión del concepo de Inegrl de Riemnn que permie mplir el poencil de es herrmien.
Prof. Enrique Meus Nieves Docorndo en Educción Memáic. INTEGRAL DE RIEMANN-STIELTJES L inegrl de Riemnn-Sieljes es un exensión del concepo de Inegrl de Riemnn que permie mplir el poencil de es herrmien.
Matemáticas 2º Bachillerato MATRICES. columnas es muy antiguo, pero fue en el siglo XIX cuando J.J. Sylverster ( )
 TRICES emáics º chillero. Inroducción. Definición de mriz El concepo de mriz como un bl ordend de números escrios en fils y columns es muy niguo, pero fue en el siglo XIX cundo J.J. Sylverser (8-897) cuñó
TRICES emáics º chillero. Inroducción. Definición de mriz El concepo de mriz como un bl ordend de números escrios en fils y columns es muy niguo, pero fue en el siglo XIX cundo J.J. Sylverser (8-897) cuñó
Tema 10: Espacio Afin Tridimensional
 www.selecividd-cgrnd.co Te Espcio Afin Tridiensionl Se ll sise de referenci del espcio fín E l conjuno (O, u, u, u ). Siendo O un puno de E u, u, u res vecores libres que forn un bse de V. Ls recs OX,
www.selecividd-cgrnd.co Te Espcio Afin Tridiensionl Se ll sise de referenci del espcio fín E l conjuno (O, u, u, u ). Siendo O un puno de E u, u, u res vecores libres que forn un bse de V. Ls recs OX,
EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES
 IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (5-M-B-) Consider ls mrices 4 A = y B = 4 ) ( puno) Hll el deerminne de un mriz X que verifique l iguldd X AX = B b)
IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (5-M-B-) Consider ls mrices 4 A = y B = 4 ) ( puno) Hll el deerminne de un mriz X que verifique l iguldd X AX = B b)
Integrales impropias.
 Tem Inegrles impropis.. Inroducción. En el em nerior se h definido l inegrl de Riemnn con ls siguienes hipóesis Dom(f) = [, ] es un conjuno codo. f: [, ] IR esá cod en [, ]. Si lgun de ess condiciones
Tem Inegrles impropis.. Inroducción. En el em nerior se h definido l inegrl de Riemnn con ls siguienes hipóesis Dom(f) = [, ] es un conjuno codo. f: [, ] IR esá cod en [, ]. Si lgun de ess condiciones
FUNCIONES VECTORIALES
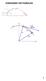 FUNCIONES VECTORIALES v - v e lo c i d d i n i c i l v v v lur inicil v r() P Vecor velocidd r() r Q r(+) INDICE FUNCIONES VECTORIALES FUNCIÓN VECTORIAL 4 Dominio de un función vecoril 5 Operciones con
FUNCIONES VECTORIALES v - v e lo c i d d i n i c i l v v v lur inicil v r() P Vecor velocidd r() r Q r(+) INDICE FUNCIONES VECTORIALES FUNCIÓN VECTORIAL 4 Dominio de un función vecoril 5 Operciones con
MODELOS ARIMA. Prof. Rafael de Arce Prof. Ramón Mahía Dpto. Economía Aplicada U.D.I. Econometría e Informática
 MODELOS ARIMA Prof. Rfel de Arce Prof. Rmón Mhí Dpo. Economí Aplicd U.D.I. Economerí e Informáic Progrm Ciius.- écnics de Previsión de vribles finnciers Págin INRODUCCIÓN En 97, Box Jenkins desrrollron
MODELOS ARIMA Prof. Rfel de Arce Prof. Rmón Mhí Dpo. Economí Aplicd U.D.I. Economerí e Informáic Progrm Ciius.- écnics de Previsión de vribles finnciers Págin INRODUCCIÓN En 97, Box Jenkins desrrollron
Taller 1 matemáticas básicas: Preparación primer parcial. Profesor Jaime Andrés Jaramillo. ITM
 Tller memáics básics: Preprción primer prcil. Profesor Jime Andrés Jrmillo. jimej@gmil.com. ITM. 0- Referenci: STEWART, Jmes oros. Precálculo. Quin edición. Méico: Thomson, 00. Números Reles. Simplific
Tller memáics básics: Preprción primer prcil. Profesor Jime Andrés Jrmillo. jimej@gmil.com. ITM. 0- Referenci: STEWART, Jmes oros. Precálculo. Quin edición. Méico: Thomson, 00. Números Reles. Simplific
es incompatible: a) Si m = 1 b) Si m = 2 c) Ninguna de las anteriores. Solución:, siendo r(a) = 2 y r(m) = 3 Sistema incompatible.
 nálisis eáico José rí ríne edino PROBLES DE SITES rouesos en eáenes) Preguns de io es. El sise es incoible: ) Si = b) Si = c) Ningun de ls neriores. 8 si r) =, SCD. Si =,, siendo r) = r) = Sise incoible.
nálisis eáico José rí ríne edino PROBLES DE SITES rouesos en eáenes) Preguns de io es. El sise es incoible: ) Si = b) Si = c) Ningun de ls neriores. 8 si r) =, SCD. Si =,, siendo r) = r) = Sise incoible.
En el tema anterior se ha definido la integral de Riemann con las siguientes hipótesis
 5 Fundmenos de Memáics : Cálculo inegrl en R Cpíulo Inegrles impropis En el em nerior se h definido l inegrl de Riemnn con ls siguienes hipóesis Domf = [, ] es un conjuno codo. f: [, ] R esá cod en [,
5 Fundmenos de Memáics : Cálculo inegrl en R Cpíulo Inegrles impropis En el em nerior se h definido l inegrl de Riemnn con ls siguienes hipóesis Domf = [, ] es un conjuno codo. f: [, ] R esá cod en [,
TEMA 3: ECUACIONES ECUACIONES DE 2º GRADO Las ecuaciones de 2º grado son de la forma ax 2 +bx+c=0 y su solución es:
 TEMA : ECUACIONES ECUACIONES DE º GRADO Ls ecuciones de º grdo son de l form +b+c=0 y su solución es: b b 4c Cundo b=o o c=0 son incomplets y se resuelven de l siguiente form. Cso b=0, por ejemplo: 6 7=0
TEMA : ECUACIONES ECUACIONES DE º GRADO Ls ecuciones de º grdo son de l form +b+c=0 y su solución es: b b 4c Cundo b=o o c=0 son incomplets y se resuelven de l siguiente form. Cso b=0, por ejemplo: 6 7=0
Hacia la universidad Aritmética y álgebra
 Solucionrio Solucionrio Hci l universidd riméic álger OPIÓN. Dds ls mrices ) lcul ls mrices. ) lcul l mri invers de. c) Resuelve l ecución mricil. ) 8 7 8 9 ) ( ), dj( ) c), [ ] 9 9 8 9. Resuelve el sisem
Solucionrio Solucionrio Hci l universidd riméic álger OPIÓN. Dds ls mrices ) lcul ls mrices. ) lcul l mri invers de. c) Resuelve l ecución mricil. ) 8 7 8 9 ) ( ), dj( ) c), [ ] 9 9 8 9. Resuelve el sisem
1.MATRICES. Definición : Se llama matriz de dimensiones m x n ( m filas y n columnas) a una. colección de datos expresados de la siguiente forma A=.
 .MATRICES. DEINICION, TERMINOLOGIA, TIPOS DE MATRICES Y OPERACIONES LINEALES: Definición : Se llm mri de dimensiones m n ( m fils n columns) un colección de dos epresdos de l siguiene form A=. m. m..........
.MATRICES. DEINICION, TERMINOLOGIA, TIPOS DE MATRICES Y OPERACIONES LINEALES: Definición : Se llm mri de dimensiones m n ( m fils n columns) un colección de dos epresdos de l siguiene form A=. m. m..........
En el tema anterior se ha definido la integral de Riemann con las siguientes hipótesis
 59 Memáics I : Cálculo inegrl en IR Tem 5 Inegrles impropis 5. Inroducción En el em nerior se h definido l inegrl de Riemnn con ls siguienes hipóesis Domf = [, ] es un conjuno codo. f: [, ] IR esá cod
59 Memáics I : Cálculo inegrl en IR Tem 5 Inegrles impropis 5. Inroducción En el em nerior se h definido l inegrl de Riemnn con ls siguienes hipóesis Domf = [, ] es un conjuno codo. f: [, ] IR esá cod
4. Modelos de series de tiempo
 4. Modelos de series de iempo Los modelos comunes para el análisis de series de iempo son los que se basan en modelos auorregresivos y modelos de medias móviles o una combinación de ambos. Es posible realizar
4. Modelos de series de iempo Los modelos comunes para el análisis de series de iempo son los que se basan en modelos auorregresivos y modelos de medias móviles o una combinación de ambos. Es posible realizar
Aplicación empírica de los modelos Feltham-Ohlson en función del signo del resultado anormal
 Aplicción empíric de los modelos Felhm-Ohlson en función del signo del resuldo norml Begoñ Giner Inchusi (Universidd de Vlenci y Rúl Iñiguez Sánchez (Universidd de Alicne Dirección de conco: Rúl Iñiguez
Aplicción empíric de los modelos Felhm-Ohlson en función del signo del resuldo norml Begoñ Giner Inchusi (Universidd de Vlenci y Rúl Iñiguez Sánchez (Universidd de Alicne Dirección de conco: Rúl Iñiguez
DEPARTAMENTO DE CIENCIAS DE LA ENERGIA Y MECANICA Laboratorio de Instrumentación Industrial Mecánica Laboratorio de Instrumentación Mecatrónica 1
 Lbororio de Insrumención Indusril Mecánic Lbororio de Insrumención Mecrónic 1 1. Tem: Simulción de un sensor medine su función de rnsferenci nálisis dinámico del mismo. 2. Objeivos: 3. Teorí.. Simulr el
Lbororio de Insrumención Indusril Mecánic Lbororio de Insrumención Mecrónic 1 1. Tem: Simulción de un sensor medine su función de rnsferenci nálisis dinámico del mismo. 2. Objeivos: 3. Teorí.. Simulr el
CAPÍTULO 1 FUNDAMENTOS TEÓRICOS
 Fundmenos Teóricos CAPÍTULO CAPÍTULO FUNDAMENTOS TEÓRICOS Anes de bordr el nálisis delldo de los modelos objeo de es esis, los modelos Felhm-Ohlson, en primer lugr es necesrio referirse ls definiciones
Fundmenos Teóricos CAPÍTULO CAPÍTULO FUNDAMENTOS TEÓRICOS Anes de bordr el nálisis delldo de los modelos objeo de es esis, los modelos Felhm-Ohlson, en primer lugr es necesrio referirse ls definiciones
EN EL PLANO (R 2 ) EN EL ESPACIO (R 3 ) ECUACIONES CONSTRUIR CLASIFICAR ECUACIONES CONSTRUIR CLASIFICAR. Resumen de Transformaciones Geométricas
 Resmen de Trnsformciones Geomérics EN EL PLNO (R ) EUIONES ONSTRUIR LSIFIR EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR Unidd Docene de Memáics de l E.T.S.I.T.G.. Resmen de Trnsformciones Geomérics Unidd Docene
Resmen de Trnsformciones Geomérics EN EL PLNO (R ) EUIONES ONSTRUIR LSIFIR EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR Unidd Docene de Memáics de l E.T.S.I.T.G.. Resmen de Trnsformciones Geomérics Unidd Docene
Tema 7: ÁLGEBRA DE MATRICES
 ÁLGER DE MTRICES Tem : ÁLGER DE MTRICES Índice. Concepo de mriz... Definición de mriz... Clsificción de ls mrices... Tls, grfos y mrices.. Operciones con mrices... Sum de mrices... Muliplicción de un número
ÁLGER DE MTRICES Tem : ÁLGER DE MTRICES Índice. Concepo de mriz... Definición de mriz... Clsificción de ls mrices... Tls, grfos y mrices.. Operciones con mrices... Sum de mrices... Muliplicción de un número
TRANSFORMACIONES EN EL ESPACIO (R 2 ) ECUACIONES
 TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR Unidd Docene de Memáics de l E.T.S.I.T.G.. EUIONES DE LOS MOVIMIENTOS, HOMOTEIS Y SEMEJNZS
TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR Unidd Docene de Memáics de l E.T.S.I.T.G.. EUIONES DE LOS MOVIMIENTOS, HOMOTEIS Y SEMEJNZS
ESTE MODELO SUSTITUYE AL ANTERIOR. FECHA: MODELO DE RESPUESTAS Objetivos 01 al 08.
 ESTE MODELO SUSTITUYE AL ANTERIOR FECHA: 5-- Seund Prue Prcil Lso - 7 /7 Universidd Ncionl Aier Memáics III Cód 7 Vicerrecordo Acdémico Cód Crrer: 6-8 Áre de Memáic Fech: -- OBJ PTA Clcul MODELO DE RESPUESTAS
ESTE MODELO SUSTITUYE AL ANTERIOR FECHA: 5-- Seund Prue Prcil Lso - 7 /7 Universidd Ncionl Aier Memáics III Cód 7 Vicerrecordo Acdémico Cód Crrer: 6-8 Áre de Memáic Fech: -- OBJ PTA Clcul MODELO DE RESPUESTAS
EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES
 IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (4-M;Jun-B-) (5 punos) Consider ls mrices A = y B = Deermin, si exise, l mriz X que verific AX + B = A + m (4-M-B-)
IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (4-M;Jun-B-) (5 punos) Consider ls mrices A = y B = Deermin, si exise, l mriz X que verific AX + B = A + m (4-M-B-)
Física General 1 Proyecto PMME - Curso 2007 Instituto de Física Facultad de Ingeniería UdelaR
 Físic Generl Proeco PMME - Curso 7 Insiuo de Físic Fculd de Inenierí UdelR TITULO MOVIMIENTO DE PROYECTIL AUTORES Andre Ferreir, Dieo Fonn, Ausin Mimbcs. INTRODUCCIÓN El siuiene rbjo r sobre el esudio
Físic Generl Proeco PMME - Curso 7 Insiuo de Físic Fculd de Inenierí UdelR TITULO MOVIMIENTO DE PROYECTIL AUTORES Andre Ferreir, Dieo Fonn, Ausin Mimbcs. INTRODUCCIÓN El siuiene rbjo r sobre el esudio
Sea a la longitud de la cuerda. Se trata de encontrar bajo qué ángulo á es máxima la distancia OP.
 Hoj de Problems Geomerí I 7. Un lzo corredizo, formdo por un cuerd, envuelve un column cilíndric de rdio r perfecmene lis, esndo sujeo el eremos libre de l cuerd. Averigur que disnci de l column esá el
Hoj de Problems Geomerí I 7. Un lzo corredizo, formdo por un cuerd, envuelve un column cilíndric de rdio r perfecmene lis, esndo sujeo el eremos libre de l cuerd. Averigur que disnci de l column esá el
CAPÍTULO 4 DISEÑO DE LA INVESTIGACIÓN Y METODOLOGÍA
 Diseño de l Invesigción y Meodologí CAPÍTULO 4 CAPÍTULO 4 DISEÑO DE LA INVESTIGACIÓN Y METODOLOGÍA Un vez revisdos los rbjos eóricos de Felhm-Ohlson y sus plicciones empírics, vmos proceder l relizción
Diseño de l Invesigción y Meodologí CAPÍTULO 4 CAPÍTULO 4 DISEÑO DE LA INVESTIGACIÓN Y METODOLOGÍA Un vez revisdos los rbjos eóricos de Felhm-Ohlson y sus plicciones empírics, vmos proceder l relizción
5. INDUCCIÓN MAGNÉTICA
 5. NDUCCÓN MAGNÉTCA 5.1 Flujo mgnéico. 5. ey de Frdy. 5.3 Generdores y Moores 5.4 nducnci. 5.5 Circuios. Energí mgnéic. 5.1 Flujo mgnéico. Φ E da Φ Φ m _ un _ espir m _ N _ espirs Φ BdA N BdA m BdA A A
5. NDUCCÓN MAGNÉTCA 5.1 Flujo mgnéico. 5. ey de Frdy. 5.3 Generdores y Moores 5.4 nducnci. 5.5 Circuios. Energí mgnéic. 5.1 Flujo mgnéico. Φ E da Φ Φ m _ un _ espir m _ N _ espirs Φ BdA N BdA m BdA A A
LA METODOLOGÍA DE VECTORES AUTORREGRESIVOS (VAR)
 LA METODOLOGÍA DE VECTORES AUTORREGRESIVOS (VAR) ESPECIFICACION La meodología VAR es, en ciera forma, una respuesa a la imposición de resricciones a priori que caraceriza a los modelos economéricos keynesianos:
LA METODOLOGÍA DE VECTORES AUTORREGRESIVOS (VAR) ESPECIFICACION La meodología VAR es, en ciera forma, una respuesa a la imposición de resricciones a priori que caraceriza a los modelos economéricos keynesianos:
EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES
 IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (5-M-B-) Consider ls mrices 4 A = y B = 4 ) ( puno) Hll el deerminne de un mriz X que verifique l iguldd X AX = B b)
IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (5-M-B-) Consider ls mrices 4 A = y B = 4 ) ( puno) Hll el deerminne de un mriz X que verifique l iguldd X AX = B b)
La valoración de acciones y la predicción de beneficios a través de los modelos Feltham-Ohlson
 L vlorción de cciones y l predicción de beneficios rvés de los modelos Felhm-Ohlson Begoñ Giner Inchusi (Universidd de Vlenci) y Rúl Iñiguez Sánchez (Universidd de Alicne) Dirección de conco: Rúl Iñiguez
L vlorción de cciones y l predicción de beneficios rvés de los modelos Felhm-Ohlson Begoñ Giner Inchusi (Universidd de Vlenci) y Rúl Iñiguez Sánchez (Universidd de Alicne) Dirección de conco: Rúl Iñiguez
FUNDAMENTOS DE PROGRAMACIÓN LINEAL
 18 de Septiembre de 2017 FUNDAMENTOS DE PROGRAMACIÓN LINEAL Ingenierí Industril Ingenierí Informátic Fcultd de Ingenierí Universidd Ctólic Andrés Bello Progrmción Linel José Luis Quintero 1 Puntos trtr
18 de Septiembre de 2017 FUNDAMENTOS DE PROGRAMACIÓN LINEAL Ingenierí Industril Ingenierí Informátic Fcultd de Ingenierí Universidd Ctólic Andrés Bello Progrmción Linel José Luis Quintero 1 Puntos trtr
Apuntes de A. Cabañó Matemáticas II SISTEMAS DE ECUACIONES LINEALES
 puntes de. Cbñó Mtemátics II SISTEMS DE ECUCIONES LINELES 8. Epresión mtricil de un sistem.clsificción de un sistem en términos del número de soluciones. 8. Teorem de RouchéFrobenius. 8. El método de eliminción
puntes de. Cbñó Mtemátics II SISTEMS DE ECUCIONES LINELES 8. Epresión mtricil de un sistem.clsificción de un sistem en términos del número de soluciones. 8. Teorem de RouchéFrobenius. 8. El método de eliminción
CAPITULO 4 DESARROLLO DE LA INVESTIGACIÓN. El desarrollo de la investigación comenzó con la obtención de los datos seguido de la
 CAPITULO 4 DESARROLLO DE LA INVESTIGACIÓN El desrrollo de l invesigción comenzó con l obención de los dos seguido de l comprobción de l vercidd de los mismos. Ese cpíulo drá conocer los medicmenos selecciondos.
CAPITULO 4 DESARROLLO DE LA INVESTIGACIÓN El desrrollo de l invesigción comenzó con l obención de los dos seguido de l comprobción de l vercidd de los mismos. Ese cpíulo drá conocer los medicmenos selecciondos.
Mecanismos de Transmisión y Reglas de Política Monetaria: La posición de la política monetaria como variable de estado
 ESUDIOS ECONÓMICOS Mecnismos de rnsmisión y Regls de Políic Moneri: L posición de l políic moneri como vrible de esdo Por: Crlos Brrer Chupis * Inroducción rs los episodios de elevd inflción en diferenes
ESUDIOS ECONÓMICOS Mecnismos de rnsmisión y Regls de Políic Moneri: L posición de l políic moneri como vrible de esdo Por: Crlos Brrer Chupis * Inroducción rs los episodios de elevd inflción en diferenes
elblogdematedeaida pág Discute según los valores del parámetro y resuelve cuando sea posible los sistemas de ecuaciones siguientes:
 elblogdeedeid pág curso - HOJA : EJERCCO REPAO DE TEMA - Discue según los vlores del práero resuelve cundo se posible los sises de ecuciones siguienes: ) 9 b) ) λ λ λ ; /;/;) b) - ); ) - Resuelve por Crer
elblogdeedeid pág curso - HOJA : EJERCCO REPAO DE TEMA - Discue según los vlores del práero resuelve cundo se posible los sises de ecuciones siguienes: ) 9 b) ) λ λ λ ; /;/;) b) - ); ) - Resuelve por Crer
OPCIÓN A. 1.A.- Dadas las matrices: a) Determinar la matriz inversa de B. b) Determinar una matriz X tal que A = BX
 IES Medierráneo de Málg Solución Seiembre Jun Crlos lonso Ginoni OPCIÓN..- Dds ls mrices: Deerminr l mri invers de b Deerminr un mri X l que X X X X X dj dj IES Medierráneo de Málg Solución Seiembre Jun
IES Medierráneo de Málg Solución Seiembre Jun Crlos lonso Ginoni OPCIÓN..- Dds ls mrices: Deerminr l mri invers de b Deerminr un mri X l que X X X X X dj dj IES Medierráneo de Málg Solución Seiembre Jun
Ecuaciones de 1 er y 2º grado
 Ecuciones de 1 er y º grdo Antes de empezr resolver estos tipos de ecuciones hemos de hcer un serie de definiciones previs, que irán compñds por lgunos ejemplos. Un iguldd lgebric está formd por dos epresiones
Ecuciones de 1 er y º grdo Antes de empezr resolver estos tipos de ecuciones hemos de hcer un serie de definiciones previs, que irán compñds por lgunos ejemplos. Un iguldd lgebric está formd por dos epresiones
Universidad Nacional de La Plata Facultad de Ciencias Naturales y Museo
 Universidd Ncionl de L Pl Fculd de Ciencis Nurles y Museo Cáedr de Memáic y Elemenos de Memáic signur: Elemenos de Memáic Conenidos de l Unidd Temáic Mrices: Sum y produco por un esclr. Propieddes. Produco
Universidd Ncionl de L Pl Fculd de Ciencis Nurles y Museo Cáedr de Memáic y Elemenos de Memáic signur: Elemenos de Memáic Conenidos de l Unidd Temáic Mrices: Sum y produco por un esclr. Propieddes. Produco
3.5.1 Trasformada de Laplace de la función escalón unitario
 .5. Trformd de Lplce de l función eclón unirio 0.5. Trformd de Lplce de l función eclón unirio Función Eclón Unirio Tmbién llmd función lo unidd de Heviide, y con frecuenci e uiliz en pliccione que rn
.5. Trformd de Lplce de l función eclón unirio 0.5. Trformd de Lplce de l función eclón unirio Función Eclón Unirio Tmbién llmd función lo unidd de Heviide, y con frecuenci e uiliz en pliccione que rn
MOVIMIENTO CIRCULAR. r en cualquier punto de su trayectoria. v 2 / R
 MOVIMIENTO CIRCULAR Es un ipo de movimieno en el plno, en el cul l pícul gi un disnci fij lededo de un puno llmdo ceno. El movimieno cicul puede se de dos ipos: Movimieno cicul unifome Movimieno cicul
MOVIMIENTO CIRCULAR Es un ipo de movimieno en el plno, en el cul l pícul gi un disnci fij lededo de un puno llmdo ceno. El movimieno cicul puede se de dos ipos: Movimieno cicul unifome Movimieno cicul
