UNIDAD 1 Números reales
|
|
|
- Soledad Rivero Redondo
- hace 8 años
- Vistas:
Transcripción
1 Pág. 1 de 6 I. Sabes clasificar los números en los distintos conjuntos numéricos (N, Z, Q, Á), representarlos en la recta real y reconocerlos en diferentes contextos? 1 Considera los números: 0,8; 1, ; ) ; π; ; 1 a) Expresa como cociente de dos enteros los que sea posible. Cuáles son irracionales? c) Alguno es natural? Y entero? 8 17 ) 11 a) 0,8 = = ; 1, = ; = Son irracionales, π y 1. c) Ninguno es natural. es entero. Si tienes dificultades, consulta la página de tu libro de texto. Clasifica los siguientes números según pertenezcan a los conjuntos N, Z, Q o Á. 7; ;,; π ; ;, 17; ) 8 1; 18 N 8 7; 18 Z 8 7; 18; 1 Q 8 ) 7; 18; 1 ; ;,;, 17 Á 8 ) 7; 18; 1 ; ;,;, 17; ; π 8 Si tienes dificultades, consulta la página de tu libro de texto.
2 Pág. de 6 Observa el diagrama y completa el cuadro adjunto. E D C 0,1 1,8 ) C' D' E' B 108 B' 19 A N ABB' ; 19; 108 Z ACC' ; 19; 108; ; ; 81 Q ) ADD' ; 19; 108; ; ; 81; ; 0,1; 1,8; Á ) 1 AEE' ; 19; 108; ; ; 81; ; 0,1; 1,8; ; ; ; Si tienes dificultades, consulta la página de tu libro de texto. Representa en la recta real los números y Si tienes dificultades, consulta la página de tu libro de texto. Cuáles de las siguientes ecuaciones tienen soluciones irracionales? a) 9x = 0 x 8 = 0 c) x + = 0 La ecuación x 8 = 0, cuya solución es x = ± 8 = ± Si tienes dificultades, consulta la página de tu libro de texto.
3 Pág. de 6 II. Identificas los números que pertenecen a un intervalo, conoces su notación y la sabes utilizar? 6 Representa el conjunto de números que cumple la desigualdad y exprésalo como un intervalo o semirrecta. a) Ì x < < x Ì a) [, 7) ] Si tienes dificultades, consulta las páginas 6 y 7 de tu libro de texto. 7 Representa gráficamente los intervalos A = (1, 6] y B = (, +@) y expresa cada uno de ellos como una desigualdad. a) A A 8 1 < x Ì 6 B 0 1 B 8 < x < +@ Si tienes dificultades, consulta las páginas 6 y 7 de tu libro de texto. 8 Representa y expresa como intervalo los números que verifican las siguientes condiciones: a) x é [, ) y x é [1, +@) x é 1] o x é [7, +@) a) 0 x é [1, ) 1 7 Cualquier x que pertenezca a 1] «[7, +@) Si tienes dificultades, consulta las páginas 6 y 7 de tu libro de texto. 9 Para qué valores de x es válida la expresión x +? Para x Ó. Si tienes dificultades, consulta la página 8 de tu libro de texto.
4 Pág. de 6 III. Manejas la notación científica y controlas el error cometido cuando das una aproximación? 10 Expresa en notación científica y calcula. a) , ,0000 0,0001 a), , 10 7, = = 7, , 10, 10 9 (1, 10 ) (7 10 ) 8 = 8, , Si tienes dificultades, consulta la página de tu libro de texto. 11 Calcula y expresa el resultado en notación científica. ( ) : ( ) = 1, Si tienes dificultades, consulta la página de tu libro de texto. 1 Da una cota del error absoluto de las siguientes mediciones: a) 1, c), Error absoluto < 0, Error absoluto < 0, 10 1 Error absoluto < 0, En cuál de ellas es menor el error relativo? En a) es menor el error relativo. Si tienes dificultades, consulta la página de tu libro de texto. 1 Da una cota del error relativo de las siguientes aproximaciones: a), Error relativo < 0,01 Error relativo < 0, Si tienes dificultades, consulta la página de tu libro de texto.
5 Pág. de 6 IV. Sabes identificar una potencia con una raíz y manejar con soltura la simplificación y las operaciones con radicales? 1 Expresa como potencia y efectúa después la operación. a) = 1/ / = (1/) + (/) = 7/6 = 6 7 a 10 = a a = a / = a a 1/ Si tienes dificultades, consulta la página 8 de tu libro de texto. 1 Simplifica los siguientes radicales: a) a = a a 1 = a c) 1 a b 8 = ab Si tienes dificultades, consulta la página 0 de tu libro de texto. 16 Opera y extrae factores fuera del radical. a) a 10ab 8a b a = 0a b : = 7 Si tienes dificultades, consulta la página 0 de tu libro de texto. 17 Efectúa. a) = = = = Si tienes dificultades, consulta la página 1 de tu libro de texto.
6 Pág. 6 de 6 18 Calcula el área total y el volumen de una pirámide cuadrangular regular cuya arista básica mide 8 cm, y la arista lateral, 1 cm. Expresa las soluciones con radicales. Altura de una cara = 8 cm Altura de la pirámide = 7 cm 6 7 Volumen = cm Área total = cm Si tienes dificultades, consulta las páginas 0, 1 y de tu libro de texto. 19 Halla el perímetro de este triángulo. Exprésalo con radicales. cm Solución: Perímetro = 10 + Si tienes dificultades, consulta las páginas 0, 1 y de tu libro de texto. 0 Racionaliza y simplifica. a) a) = 6( ) Si tienes dificultades, consulta la página de tu libro de texto.
1Soluciones a los ejercicios y problemas PÁGINA 36
PÁGINA 6 Pág. P RACTICA Números reales a) Cuáles de los siguientes números no pueden expresarse como cociente de dos números enteros? ;,7; ;, ; ),7; ) π; b)expresa como fracción aquellos que sea posible.
b) Expresa como fracción aquellos que sea posible. c) Cuáles son irracionales? a) No pueden expresarse como cociente: 3; 3π y 2 5.
PÁGINA 9 Entrénate 1 a) Cuáles de los siguientes números no pueden expresarse como cociente de dos números enteros? 2; 1,7; ; 4, 2; ),75; ) π; 2 5 b) Expresa como fracción aquellos que sea posible. c)
1Soluciones a los ejercicios y problemas
PÁGINA Pág. P R A C T I C A N ú m e r o s r e a l e s a) Cuáles de los siguientes números no pueden expresarse como cociente de dos números enteros? ;,7; ;, ; ),7; ) π; b)expresa como fracción aquellos
1Soluciones a las actividades de cada epígrafe PÁGINA 20
Soluciones a las actividades de cada epígrafe PÁGINA 0 RACIONALES Q ENTEROS Z NO RACIONALES 8,, 8,, NATURALES N ENTEROS NEGATIVOS FRACCIONARIOS (racionales no enteros) 8 0, 7,,, 8, 8,, 7 8 8,9;,8; ) 7
1Soluciones a los ejercicios y problemas
PÁGINA 8 Pág. 8 0 Divide y simplifica. a) 7 : b) : c) : 6 a) 7 : = 7 : = 9 b) : = : = = c) : = : = = 6 6 7 Reduce a índice común y efectúa. a) 6 b) : 6 c) 0 : 0 d) ( ) : ( ) 6 6 a) = b) = 0 6 0 8 78 6
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
Pág. Página 7 PRACTICA Aproximación y errores Expresa con un número adecuado de cifras significativas: a) Audiencia de un programa de televisión: 07 9 espectadores. b) Tamaño de un virus: 0,007 mm. c)
Ejercicios Tema 1. a) b) c) d) e) f) Ejercicio 6. Escribe en forma de intervalo y representa:
Ejercicios Tema 1 Números Reales Ejercicio 1. Clasifica los siguientes números en el lugar que conjunto que corresponde: a) b) c) Ejercicio 2. Clasifica los siguientes números: Ejercicio 3. a) Cuáles de
Tema 1: Aritmética. Repaso de 3º de ESO. NÚMEROS REALES. POTENCIAS Y RAÍCES. Ejercicios resueltos en video
Tema : Aritmética. Repaso de º de ESO. NÚMEROS REALES. POTENCIAS Y RAÍCES. EJERCICIOS Los conjuntos numéricos.. (º ESO) Cuáles de los números siguientes son racionales? e irracionales? Pon en forma de
TEMA 3: NÚMEROS REALES
. Intervalos y semirrectas TEMA : NÚMEROS REALES Ejemplo Dados los siguientes intervalos y semirrectas, exprésalos en forma de conjunto y represéntalos sobre la recta real:. El intervalo abierto de extremos
Soluciones a las actividades
Soluciones a las actividades BLOQUE I Aritmética. Los números reales. Potencias, radicales y logaritmos Los números reales. Números racionales e irracionales Calcula mentalmente el área de un cuadrado
Los números reales. 1. Números racionales e irracionales
Los números reales. Números racionales e irracionales Calcula mentalmente el área de un cuadrado de cm de lado. Expresa de forma exacta el lado, x, de un cuadrado de cm de área. P I E N S A Y C A L C U
Los números reales. 1. Números racionales e irracionales
Los números reales. Números racionales e irracionales Calcula mentalmente el área de un cuadrado de cm de lado. Expresa de forma exacta el lado, x, de un cuadrado de cm de área. P I E N S A Y C A L C U
REPASO DE ÁLGEBRA PRIMERA PARTE: RADICALES, LOGARITMOS Y POLINOMIOS
Ejercicio nº.- Simplifica: REPASO DE ÁLGEBRA PRIMERA PARTE: RADICALES, LOGARITMOS Y POLINOMIOS a) b) a a Ejercicio nº.- Epresa en forma de intervalo las soluciones de la desigualdad: El intervalo [, 6].
N Ú M E R O S R E A L E S
N Ú M E R O S R E A L E S 1. E L C O N J U N T O D E L O S N Ú M E R O S R E A L E S Al conjunto de todos los números que se pueden expresar mediante fracciones se le llama conjunto de los números racionales
CONJUNTO DE LOS NÚMEROS REALES
NÚMEROS REALES 1. EL CONJUNTO DE LOS NÚMEROS REALES Al conjunto de todos los números que se pueden expresar mediante fracciones se le llama conjunto de los números racionales y se representa por Q. Tanto
E J E R C I C I O S P R O P U E S T O S. Indica, sin realizar la división, el tipo de expresión decimal de estos números.
NÚMEROS REALES E J E R C I C I O S P R O P U E S T O S. Indica, sin realizar la división, el tipo de expresión decimal de estos números. a) b) 9 6 c) 7 d) 7 7 0 a) Periódico mixto c) 7 Periódico mixto
4 ; 3. d) 2 y 5 3. a) 2,2 b) c) 2,24 d) 2,236 e) 2,23607
EL NÚMERO REAL.- LOS NÚMEROS IRRACIONALES. NÚMEROS REALES - Indicar a qué conjuntos ( Ν, Ζ, Q, R ) pertenecen los siguientes números: -2 ; ; -4/ 5; 6/ 4; 4 ; 25 ; Ν ; 6/ 4 Ζ -2 ; 25 Q -4/ 5 ; 6 ; 4 ; 8
1. Potencias de exponente natural y entero. Solución: a) 8 b) 8 c) 8 d) 8. Solución: Solución: a) 2 5 b) 2 1 c) 2 0 d) 2 5
Potencias y radicales 1. Potencias de exponente natural y entero Calcula mentalmente las siguientes potencias: a) b) ) c) d) ) P I E N S A Y C A L C U L A a) 8 b) 8 c) 8 d) 8 1 Calcula mentalmente los
Los números reales. Calcula mentalmente el volumen de un cubo de arista 2 m y escribe el valor exacto de la arista de un cubo de volumen 2 m 3
Los números reales. Números racionales e irracionales Piensa y calcula Calcula mentalmente el volumen de un cubo de arista m y escribe el valor exacto de la arista de un cubo de volumen m V = = 8 m a =
1Soluciones a las actividades de cada epígrafe PÁGINA 20
Soluciones a las actividades de cada epígrafe PÁGINA 0 RACIONALES Q ENTEROS Z NO RACIONALES 8,, 8,, NATURALES N ENTEROS NEGATIVOS FRACCIONARIOS (racionales no enteros) 8 0,,,, 8, 8,, 8 8,;,8; ) ; 8 ; Pág.
a) Da una aproximación (con un número entero de metros) para las medidas del largo y del ancho del campo.
Modelos de EXAMEN Ejercicio nº 1.- Nos dicen que la medida de un campo de forma rectangular es de 45,236 m de largo por 38,54 m de ancho. Sin embargo, no estamos seguros de que las cifras decimales dadas
1. Números reales. Resuelve. BACHILLERATO Matemáticas I. Página 25
. Números reales Unidad. Números reales Resuelve Página A l F B d C. Demuestra que los triángulos ABF y EBD son semejantes (es decir, demuestra que sus ángulos son respectivamente iguales).. Si llamamos
CURSO: 1º bachillerato GRUPO: A Nº: FECHA: CALIF. 1. (1 puno) Representa sobre la recta real los siguientes conjuntos:
CURSO: 1º bachillerato GRUPO: A Nº: FECHA: CALIF. 1. (1 puno) Representa sobre la recta real los siguientes conjuntos: a) {x/ -5
Soluciones a las actividades
Soluciones a las actividades BLOQUE I Aritmética y álgebra. Los números reales. Álgebra Los números reales. Números racionales e irracionales Piensa y calcula Calcula mentalmente el volumen de un cubo
SOLUCIONARIO. UNIDAD 1: Conjuntos numéricos 18: : = = -9 ACTIVIDADES-PÁG. 8
UNIDAD : Conjuntos numéricos ACTIVIDADES-PÁG. 8. Factoriza los siguientes números: 84 = 7 40= 0 = 6 40=. Calcula el mcm y el mcd: y 60 = 60 = m.c.m.= =60 m.c.d. = = 70 y 90 70 = 7 90 = m.c.m. = 7 = 60
Enteros (Z):..., -3, -2, -1, 0, 1, 2, 3,... Números enteros (positivos o negativos), sin decimales. Incluye a los naturales.
Tema 1: Números Reales 1.1 Conjunto de los números Naturales (N): 0, 1, 2, 3. Números positivos sin decimales. Sirven para contar. Enteros (Z):..., -3, -2, -1, 0, 1, 2, 3,... Números enteros (positivos
Cuando se enumeran todos los elementos que componen el conjunto. A = { 1, 2, 3, 4, 5 }
LOS NÚMEROS REALES TEMA 1 IDEAS SOBRE CONJUNTOS Partiremos de la idea natural de conjunto y del conocimiento de si un elemento pertenece (* ) o no pertenece (* ) a un conjunto. Los conjuntos se pueden
CUADERNO DE REPASO DE VERANO
CUADERNO DE REPASO DE VERANO MATEMÁTICAS ACADÉMICAS 3º ESO Las actividades deben realizarse en estos folios, si algún proceso no te cabe en el hueco destinado para ello, lo haces en otra hoja o por detrás.
EJERCICIOS DE RECUPERACIÓN
EJERCICIOS DE RECUPERACIÓN Números Reales a) Halla, con ayuda de la calculadora, dando el resultado en notación científica con tres cifras significativas:, 48 10,54 10 4,5 10, 4 10 9 8 b) Da una cota para
Ejercicios Tema 1 El número real Matemáticas I 1º Bach. 1
Ejercicios Tema El número real Matemáticas I º Bach. TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN GRÁFICA DE NÚMEROS REALES EJERCICIO : Clasifica los siguientes números como 0 π ; ;,...; ; 6; ; ;,
MATEMÁTICAS 3º ESO PENDIENTES HOJA 1 GEOMETRÍA PLANA. 1.- Calcular el área y el perímetro de los siguientes polígonos:
MATEMÁTICAS º ESO PENDIENTES HOJA GEOMETRÍA PLANA.- Calcular el área y el perímetro de los siguientes polígonos: a) Un cuadrado de lado 5 cm de lado b) Un cuadrado de diagonal 0 cm. c) Un rectángulo de
EJERCICIOS DE MATEMÁTICAS. 1) Realiza las siguientes operaciones con números enteros y fraccionarios: a)
EJERCICIOS DE MATEMÁTICAS Realiza las siguientes operaciones con números enteros y fraccionarios: a 0 : 0 b 00 : c 7 0 d e 8 f 0 : g h i 0 j k l m 0 7 7 Simplifica la expresión, utilizando las propiedades
Potencias, radicales y logaritmos
Potencias, radicales y logaritmos 1. Potencias de exponente natural y entero Calcula mentalmente las siguientes potencias: a) b) ( ) c) d) ( ) P I E N S A Y C A L C U L A a) 8 b) 8 c) 8 d) 8 1 Calcula
OPCIÓN A. 1. (1 punto) Representa en la recta real el conjunto de valores reales x tales que 2 x y determínala mediante un intervalo.
EXAMEN: TEMAS 1 y BCT 1º 30/11/010 OPCIÓN A 1. (1 punto) Representa en la recta real el conjunto de valores reales x tales que x 1 3 1 y determínala mediante un intervalo. En primer lugar, desarrollamos
CURSO: 1º bachillerato GRUPO: A Nº: FECHA: CALIF. 1. (1 puno) Representa sobre la recta real los siguientes conjuntos:
CURSO: 1º bachillerato GRUPO: A Nº: FECHA: CALIF. 1. (1 puno) Representa sobre la recta real los siguientes conjuntos: a) {x/ -5
UNIDAD 6 La semejanza y sus aplicaciones
Pág. 1 de 5 I. Manejas la semejanza de figuras (mapas, planos, maquetas) para obtener medidas, incluidas áreas y volúmenes, de una a partir de la otra? 1 uáles de estas figuras son semejantes? Justifícalo
Prueba de evaluación. Nombre: Apellidos: Curso: Fecha: Calificación: Sean los números racionales representados por las fracciones,,, y.
Números racionales Prueba de evaluación Nombre: Apellidos: Curso: Fecha: Calificación: Sean los números racionales representados por las fracciones,,, y. Ordénalos 0 0 de menor a mayor y escribe sus fracciones
TEMA 1: NÚMEROS REALES 1.1 Numeros racionales Ejemplo:
TEMA : NÚMEROS REALES. Numeros racionales Ejemplo: 4... Entonces puedo expresar el "" de infinitas formas, siendo su fracción generatriz la que es irreducible. En nuestro caso Otro ejemplo de número racional
OBJETIVOS DE MATEMÁTICAS B 4º DE ESO
OBJETIVOS DE MATEMÁTICAS B 4º DE ESO UNIDAD 1 1.1. Domina la expresión decimal de un número o una cantidad y calcula o acota los errores absoluto y relativo en una aproximación. 1.2. Realiza operaciones
EJERCICIOS PROPUESTOS b) 2 20 x 8 x 5
EJERCICIOS PROPUESTOS 1.1 Halla el valor de x para que las siguientes fracciones sean equivalentes. a) 1 x 4 b) x 8 a) 1 4 x x 4 b) x 8 x 8 1. Expresa estas fracciones con el mismo denominador. a), 1 1
A = 1,84 B = 39,174 b) Halla el error absoluto y el error relativo que se cometen al tomar esas aproximaciones. 1,84 39,174
º ESO opción B EJERCICIOS MODELO TE PUEDEN SERVIR DE GUÍA JUNTO CON TU CUADERNO Y EL LIBRO PARA PREPARAR EL EXAMEN DE SEPTIEMBRE Debes entregarlos con el examen de septiembre Ejercicio nº.- a) Aproxima
f) b/a g) a ² h) b³ Rpta: son enteros: a), b), c), d), g), h).
Contenido 1 Ejercicios de Números Reales: Números naturales, enteros, racionales e irracionales. 1) Dados los siguientes conjuntos: a) N = {0,1,2,...} b) N* = {1,2,3,...} c) Z = {...-3,-2,-1,0,1,2,3,...}
a) 1,5 1,3:
1. Dados los siguientes números: 3,2 3 1 81 1,... Sitúa cada uno de ellos en su lugar correspondiente dentro del diagrama. Si alguno es racional indica de qué tipo es. 2. Efectúa las operaciones siguientes,
MATEMÁTICAS 3ºESO 18 de Junio de Nombre:
3ºESO 18 de Junio de 2010 Nombre: 1ª Evaluación 1. Enrique está enfermo y sus amigos han llamado para saber cómo se encuentr La llamada ha durado 15 minutos. Con Iván habló las 3/5 partes del tiempo; con
NÚMEROS REALES. El número áureo Para hallar la relación entre la diagonal y el lado del pentágono regular, da los siguientes
NÚMEROS REALES Página PARA EMPEZAR, REFLEXIONA Y RESUELVE El número áureo Para hallar la relación entre la diagonal y el lado del pentágono regular, da los siguientes pasos: a) Demuestra que los triángulos
Pon tres ejemplos de números racionales que tengan la parte decimal de distinto tipo. Hazlo en forma de fracción y da la forma decimal también.
Numeros Reales 1 Decimal Fracciones 1 Pon tres ejemplos de números racionales que tengan la parte decimal de distinto tipo. Hazlo en forma de fracción y da la forma decimal también. Qué es la parte decimal
1. Potencias de exponente natural y entero. Solución: a) 8 b) 8 c) 8 d) 8. Solución: Solución: a) 2 5 b) 2 1 c) 2 0 d) 2 5
Potencias y radicales 1. Potencias de exponente natural y entero Calcula mentalmente las siguientes potencias: a) b) ( ) c) d) ( ) P I E N S A Y C A L C U L A a) 8 b) 8 c) 8 d) 8 1 Calcula mentalmente
CURSO: GRUPO: Nº: FECHA: CALIF. 1. (1 puno) Representa sobre la recta real los siguientes conjuntos:
CURSO: GRUPO: Nº: FECHA: CALIF. 1. (1 puno) Representa sobre la recta real los siguientes conjuntos: {x/ -1
EJERCICIOS DE VERANO MATEMÁTICAS 3º ESO
EJERCICIOS DE VERANO MATEMÁTICAS 3º ESO Página 1 de 12 Entregar el día del examen de recuperación de matemáticas. Será condición indispensable para aprobar la asignatura. 1. Calcula: NUMEROS ENTEROS. FRACCIONES.
UNIDAD 6 La semejanza y sus aplicaciones
Pág. 1 de 5 I. Manejas la semejanza de figuras (mapas, planos, maquetas) para obtener medidas, incluidas áreas y volúmenes, de una a partir de la otra? 1 uáles de estas figuras son semejantes? Justifícalo
1 Calcula la forma fraccionaria o decimal (identificando cada una de sus partes), según corresponda de:
. NUMEROS REALES Calcula la forma fraccionaria o decimal (identificando cada una de sus partes), según corresponda de:,.. 8 0,... 0 Parte entera, anteperiodo, periodo 00 Parte entera, anteperiodo, periodo
OPERACIONES CON NÚMEROS REALES
OPERACIONES CON NÚMEROS REALES FRACCIONES ) Reduce a una fracción: + = + = 7 0 = ) Comprueba que el resultado de estas operaciones es un número entero: ( ) ( ) ( ) + + = 8 [ ( 7 0 ) ( )] ) De un solar
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
Pág. Página 22 La siguiente lista consta de todos los números escritos en la pizarra y algunos más: 0; ; ; 0,; 2 ; ; ; ; 2 ; 2 ; ; ; ;, ; ) π; Sitúalos, en tu cuaderno, sobre un cuadro como el de abajo.
Soluciones a las actividades
Soluciones a las actividades BLOQUE I Aritmética. Los números reales. Potencias, radicales y logaritmos Los números reales. Números racionales e irracionales a) Calcula mentalmente el área de un cuadrado
PREPARACIÓN CONTROL TEMA 1 4ºESO
1. (1,5 puntos). Efectúa las operaciones siguientes, expresando el resultado en forma de fracción irreducible: a) 4 2 4 8 13 : 5 3 5 7 14 4 2 b) 3 8 1 2 2 4 : 1 1 1 2 3 2 3 5 2. (1,5 puntos). Realiza las
CUARTO DE ESO. MATEMÁTICAS A
CUARTO DE ESO. MATEMÁTICAS A UNIDAD 1 1.1. Realiza operaciones combinadas con números enteros. 1.2. Realiza operaciones con fracciones. 1.3. Realiza operaciones y simplificaciones con potencias de exponente
b ( x + a ) ( x a ) c ( 3 a x ) ( a + 3 x ) 4-1 INGRESO A 4º AÑO - L. M. G. A. - Prueba de MATEMÁTICA CUESTIONARIO- ENERO/2004
4-1 INGRESO A 4º AÑO - L. M. G. A. - Prueba de MATEMÁTICA CUESTIONARIO- ENERO/2004 S i a a = 2 / 3, x = 2, halle el valor numérico de 3 a 3 x + 2 a 2 x 2 6 a b ( x + a ) ( x a ) c ( 3 a x ) ( a + 3 x )
EJEMPLO EJERCICIOS DE NÚMEROS PARA RECUPERAR. M2. Utiliza la notación científica para representar números grandes.
EJEMPLO EJERCICIOS DE NÚMEROS PARA RECUPERAR M1. Calcula correctamente potencias de base entera y exponente natural, utilizando las propiedades de las potencias. 1º. Calcula las siguientes potencias: a)
CONTENIDOS MÍNIMOS del ÁREA DE MATEMÁTICAS
Dpto. de Matemáticas IES Las Breñas 4º ESO OPCIÓN B CONTENIDOS MÍNIMOS del ÁREA DE MATEMÁTICAS 1: Números reales. Septiembre-2016 Números no racionales. Expresión decimal - Reconocimiento de algunos irracionales.
a) 12 = b) 45 = c) 54 a) 2 = 2 c) 9 c) 9 = 9 Tema 2 - Hoja 2: Raíz de un número
Tema - Hoja : Raíz de un número Expresa como producto de un número entero y un radical los siguientes radicales: a) a) = = = = = = Expresa en forma de raíz las siguientes potencias de exponente fraccionario:
Polinomios y fracciones
3 Polinomios y fracciones algebraicas. Binomio de Newton Desarrolla mentalmente: a) ( + ) b)( ) c) ( + )( ) P I E N S A Y C A L C U L A a) + + b) + c) ( + ) 3 A P L I C A L A T E O R Í A 6 3 5 y 5 4 y
TEMA 1 LOS NÚMEROS REALES
TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES.-LA RECTA REAL Los NÚMEROS RACIONALES: Se caracterizan porque pueden expresarse: En forma de fracción, es decir, como cociente b a de dos números enteros:
TEMA 1 LOS NÚMEROS REALES
TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES.-LA RECTA REAL Los NÚMEROS RACIONALES: Se caracterizan porque pueden expresarse: En forma de fracción, es decir, como cociente b a de dos números enteros:
Criterios de evaluación Matemáticas - B de 4º de ESO
UNIDAD Criterios de evaluación Matemáticas - B de 4º de ESO CRITERIOS GENERALES Unidad 1: Números reales - Dominar la expresión decimal de un número o una cantidad y calcular o acotar los errores absoluto
PRUEBA EXTAORDINAORIA DE SEPTIEMBRE DE 2014 CONTENIDOS MÍNIMOS DE MATEMÁTICAS
IES SAN BENITO PRUEBA EXTAORDINAORIA DE SEPTIEMBRE DE 2014 CONTENIDOS MÍNIMOS DE MATEMÁTICAS MATEMÁTICAS 1º ESO *SISTEMA DE NUMERACIÓN DECIMAL. N OS NATURALES. POTENCIAS Y RAICES Ordenación de los números
Tema 1. Racionales 2 2'4 0'1 2'1 1'15 3'1 1' Representa en la recta racional las siguientes fracciones:
Tema 1. Racionales 1.- Representa en la recta racional las siguientes fracciones: -1 y 4 b) - y 1. Calcula el valor de las siguientes expresiones: 7 5 4 1 4 b ) : c ) d) 8 4 1 5 5 : : 10 7 9 7 5 6 1 6
T E X T O D E L M A N U A L D E H T M L, W E B M A E S T R O, P O R F R A N C I S C O A R O C E N A
T E X T O D E L M A N U A L D E H T M L, W E B M A E S T R O, P O R F R A N C I S C O A R O C E N A Q U E S E E N C U E N T R A E N I N T E R N E T E N : h t t p : / / w w w. l a n d e r. e s / w e b m
TEMA 1: NÚMEROS REALES
. Numeros racionales Ejemplo: TEMA : NÚMEROS REALES 4.............................................. Entonces puedo expresar el "" de infinitas formas, siendo su fracción generatriz la que es irreducible.
Indica cuáles de los números son racionales y cuáles son irracionales.
SOLUCIONARIO ACTIVIDADES 06 0 08 09 040 Razona cuáles de los siguientes números decimales son racionales y cuáles son irracionales. a), e), b), f), c), g), d), h), a) Racional, periódico puro. e) Racional,
Números racionales e irracionales
Números racionales e irracionales. Divisibilidad Calcula mentalmente: a) M.C.D. (, 8) b) M.C.D. (, 8) c) M.C.D. (, 9, ) d) m.c.m. (, ) e) m.c.m. (, 9) f ) m.c.m. (,, ) P I E N S A Y C A L C U L A a) b)
Examen de Recuperación de la 1ª Evaluación - viernes 18 enero Nombre:...Curso: 4ºD
Examen de Recuperación de la 1ª Evaluación - viernes 18 enero 01 Nomre:...Curso: 4ºD 1. Dada la operación: 5,16 0,4 05 Halla, por separado, las fracciones generatrices irreduciles de los números decimales
CONTENIDOS MÍNIMOS DE MATEMÁTICAS - 1º ESO
CONTENIDOS MÍNIMOS DE MATEMÁTICAS - 1º ESO BLOQUE I: NÚMEROS Aplicar los criterios de divisibilidad para descomponer factorialmente números naturales. Calcular el M.C.D. y del m.c.m. de varios números
3Soluciones a los ejercicios y problemas
Soluciones a los ejercicios y problemas PÁGINA 0 Pág. P RACTICA Números reales a) Clasifica los siguientes números como racionales o irracionales: ; ;, ) 9 7;,; ; ; π b) Alguno de ellos es entero? c) Ordénalos
NÚMEROS REALES. El número áureo Para hallar la relación entre la diagonal y el lado del pentágono regular, da los siguientes
NÚMEROS REALES Página PARA EMPEZAR, REFLEXIONA Y RESUELVE El número áureo Para hallar la relación entre la diagonal y el lado del pentágono regular, da los siguientes pasos: a) Demuestra que los triángulos
Colegio ANTARES Inteligencias Múltiples Enseñamos a pensar y enseñamos a vivir ÁREA Y/O ASIGNATURA: MATEMÁTICAS. GRADO: OCTAVO PERIODO: PRIMER PERÍODO
ÁREA Y/O ASIGNATURA: MATEMÁTICAS. GRADO: OCTAVO PERIODO: PRIMER PERÍODO Reconocer el conjunto de los números Reales como la unión de Racionales e Irracionales. Simplificar expresiones algebraicas a través
TRABAJO PRÁCTICO Nº 1
TRABAJO PRÁCTICO Nº CONJUNTOS. NÚMEROS REALES Objetivos: Adquirir el concepto de conjunto. Operar adecuadamente con los conjuntos. Aprehender el concepto de función. Identificar números naturales, enteros,
Lección 1 Números Reales
Lección Números Reales 4º ESO MATEMÁTICAS ACADÉMICAS El número real 2 LECCIÓN. NÚMERO REAL.- CONJUNTOS NUMÉRICOS Números Naturales. Son los números más intuitivos y simples. Sirven, básicamente, para contar:
TAREAS DE VERANO MATERIA Y OPCIÓN: 3º ESO MATEMÁTICAS ACADÉMICAS, 3ºA
TAREAS DE VERANO MATERIA Y OPCIÓN: º ESO MATEMÁTICAS ACADÉMICAS, ºA NOMBRE DEL ALUMNO: CURSO: ºA LA REALIZACIÓN DE ESTAS TAREAS ES OBLIGATORIA. SI NO SE ENTREGAN EN LA FECHA DE LA PRUEBA O SU CALIFICACIÓN
1. [1p] Clasifica los siguientes números reales en racionales e irracionales, y escribe como fracción los que se puedan expresar de esa forma:
![1. [1p] Clasifica los siguientes números reales en racionales e irracionales, y escribe como fracción los que se puedan expresar de esa forma:](/thumbs/56/39229277.jpg "1. [1p] Clasifica los siguientes números reales en racionales e irracionales, y escribe como fracción los que se puedan expresar de esa forma:")
Matemáticas 3 o ESO. Recuperación de junio 2013/14 Primer Trimestre: Para recuperar el trimestre hay que obtener al menos 5 puntos 1. [1p] Clasifica los siguientes números reales en racionales e irracionales,
UNIDAD 11 Figuras en el espacio
Pág. 1 de 5 I. Conoces de cursos anteriores los poliedros regulares y algunas de sus características. Has reforzado ese conocimiento y lo has ampliado a los poliedros semirregulares? 1 Dibuja, a partir
( ) x p( x) d b ) a. 2) Dado el conjunto Re =! " y el predicado de una variable p( x): x = x
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS CURSO DE NIVELACIÓN 205 2S TERCERA EVALUACIÓN DE MATEMÁTICAS PARA INGENIERÍAS Y EDUCACIÓN
Propuesta de distribución v1.12 (feb-17) - Curriculum ESPAÑA
LEYENDA: (unidad interactiva) (ejercicios extra) P (en proceso) R (repaso) ARITMÉTICA Naturales Potencias Divisibilidad Fracciones Naturales (básico) Sistema decimal. Orden. Operaciones. Aproximación.
TRABAJO DE VERANO DE 4º DE ESO NOMBRE:...CURSO:. Página 1 Trabajo de Verano Matemáticas 4º ESO B. Curso 2014/15 REPASO DE FRACCIONES Y POTENCIAS
TRABAJO DE VERANO DE 4º DE ESO NOMBRE:....CURSO:. REPASO DE FRACCIONES Y POTENCIAS ) Efectúa: 6) Realiza las siguientes operaciones: ) Opera: ) Indica el conjunto numérico más pequeño entre N, Z, Q y R
MATEMÁTICAS 4ºESO (Opción A) Actividades de refuerzo 1 Curso Alumno/a:
MATEMÁTICAS 4ºESO (Opción A) Actividades de refuerzo 1 Curso 01-013 1. Calcula, paso a paso: 3 11 17 + + 3 4 3 4 1 + 3. Simplifica usando las propiedades de las potencias y expresa el resultado usando
UNIDAD 3 Ecuaciones, inecuaciones y sistemas
Pág. 1 de 4 I. Identificas las ecuaciones de primer y segundo grado, las bicuadradas, las que contienen radicales y las resuelves con soltura? 1 Resuelve las ecuaciones siguientes: a) (2x 3) 2 + (x 2)
4º E.S.O Opción A: DEPARTAMENTO DE MATEMÁTICAS
4º E.S.O Opción A: DEPARTAMENTO DE MATEMÁTICAS OBJETIVOS 1. Conocer, diferenciar y operar con cualquier número en cualquiera de sus formatos usando las aproximaciones adecuadas. 2. Conocer la importancia
Trabajo de Matemáticas AMPLIACIÓN 3º ESO
Trabajo de Matemáticas AMPLIACIÓN º ESO ACTIVIDADES DE AMPLIACIÓN TEMA : NÚMEROS FRACCIONARIOS O RACIONALES Problema nº Un grifo tarda en llenar un depósito horas y otro tarda en llenar el mismo depósito
Números. 1. Definir e identificar números primos y números compuestos.
MINIMOS DE MATEMÁTICAS DE 2º DE E.S.O. 1. Divisibilidad Números 1. Definir e identificar números primos y números compuestos. 2. Manejar con soltura el vocabulario propio de la divisibilidad: a es múltiplo/divisor
Materia: Matemáticas B Nivel: 4º ESO CURSO:
Materia: Matemáticas B Nivel: 4º ESO CURSO:2014-15 El Examen constará de 10 preguntas. Interpretación y uso de los números reales Representación de números en la recta numérica. Intervalos. Diferentes
I.E.S. El Galeón Curso CONTENIDOS MÍNIMOS MATEMÁTICAS 1º E.S.O.
Números naturales y enteros: -Comparar y ordenar números. -Representar en la recta. MATEMÁTICAS 1º E.S.O. -Realización de las cuatro operaciones (suma, resta, multiplicación y división) -Potencias con
CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS 3º DE ESO
CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS 3º DE ESO UNIDAD 1 1.1. Simplifica y compara fracciones y las sitúa de forma aproximada sobre la recta. 1.2. Realiza operaciones aritméticas con números fraccionarios.
Geometría del espacio
Áreas y volumenes de cuerpos geométricos Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los elementos de un poliedro son: Caras del poliedro: son los polígonos que lo
Ejercicios para la recuperación de matemáticas de 2º de ESO.
Ejercicios para la recuperación de matemáticas de 2º de ESO. Bloque I: Aritmética 1. Encuentra todos los números enteros que cumplen que su valor absoluto es menor que 10 y mayor que 6. 2. Calcula: a)
6. PROGRAMACIÓN DEL CURSO 4º A DE E. S. O.
6. PROGRAMACIÓN DEL CURSO 4º A DE E. S. O. 6.1 OBJETIVOS GENERALES DEL CURSO Reconocer las diferentes clases de números, y operar correctamente con ellos. Aplicaciones aritméticas. Conocer y manejar la
4. Expresa como una única potencia de base 2
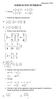0 9 9 9 0 8 0 : : Matemáticas º ESO EJERCICIOS NÚMEROS. Calcula: 6 : d c b a. Realiza las siguientes operaciones a b. Reduce a una única fracción:. Expresa como una única potencia de base 6 0 d c b a.
MATEMÁTICAS PENDIENTES 3º ESO EJERCICIOS PRUEBA I
Ejercicio nº 1.- MATEMÁTICAS PENDIENTES º ESO EJERCICIOS PRUEBA I a) Clasifica como naturales, enteros, racionales o irracionales los siguientes números: ) 1 1, 1, b) Representa sobre la recta los números:
Raíces y Radicales Preguntas de capítulo. Raíces y Radicales Problemas de capítulo
Raíces y Radicales Preguntas de capítulo 1. Cuáles son las propiedades de un? 2. Qué relación tienen la raíz cuadrada y el área de un? 3. Por qué ayuda saber de memoria los s perfectos? 4. Qué nos puede