11. Integrales múltiples.
|
|
|
- Josefa Gil Blázquez
- hace 5 años
- Vistas:
Transcripción
1 Tema 1. plicaciones del cálculo diferencial. urso 17/ Integrales múltiples. En este tema nos vamos a centrar en tratar de integrar funciones de varias variables. eniremos los conceptos de integral múltiple y cómo reducirlas a integrales simples Integrales dobles sobre rectángulos. ada una función de una variable, sabemos cómo integrarla en un intervalo (cerrado y acotado) de la forma [a, b], que son los conjuntos más simples y, en cierto sentido, los que generan a todos los demás. Pero en, tendremos que denir un nuevo tipo de conjuntos simples para poder integrar en ellos. Parece lógico tomar rectángulos del plano, es decir, conjuntos de la forma = [a, b] [c, d]. Incluso si nos plantamos integrar funciones de 3 variables, podremos pensar en elegir como conjuntos simples los paralelepípedos, es decir, conjuntos de la forma = [a, b] [c, d] [e, f]. En general, éstos van a ser los conjuntos elegidos. enición Sea f : = [a, b] [c, d] acotada en el rectángulo = [a, b] [c, d] (a) Si P 1 = {x, x 1,, x n } es una partición de [a, b] y P = {y, y 1,, y m } es una partición de [c, d], se obtiene una partición P = P 1 P de [a, b] [c, d] formada por los rectángulos de la forma i,j := [x i, x i+1 ] [y j, y j+1 ], 1 i n, 1 j m. (b) Sobre cada uno de los rectángulos construimos dos paralelepípedos de alturas: m ij = ínf{f(x, y) : (x, y) [x i, x i+1 ] [y j, y j+1 ]}, M ij = sup{f(x, y) : (x, y) [x i, x i+1 ] [y j, y j+1 ]} (c) Sumamos los volúmenes de los paralelepípedos de alturas m ij y M ij : U(f, P ) = n m M ij (x i+1 x i )(y j+1 y j ), L(f, P ) = i=1 j=1 n m m ij (x i+1 x i )(y j+1 y j ) i=1 j=1 (d) ecimos que f es Integrable (iemann) sobre si ínf{u(f, P )} = sup{l(f, P )}. En ese caso, denimos ese supremo e ínmo como la integral de iemann de f(x, y) sobre y lo denotaremos por f(x, y)dxdy. epartamento de nálisis Matemático 1 nálisis Matemático (Grado en Física)
2 Tema 1. plicaciones del cálculo diferencial. urso 17/18 Observación 11.. Esta denición de integral doble es fácilmente extrapolable a cualquier número de variables. Teorema 11.3 (Teorema de Fubini para rectángulos). Sea f : = [a, b] [c, d] una función acotada e integrable en. Supongamos que para cada y [c, d], la integral unidimensional (y) := b a Es decir, se cumple que f(x, y)dx existe. Entonces, si existe f(x, y)dxdy = d (y(dy, entonces coincidirá con la integral doble. c b a ( d c ) f(x, y)dy dx. e forma análoga, siempre que todo tenga sentido, podemos alterar el orden de integración en el Teorema de Fubini y escribir f(x, y)dxdy = d c ( b a ) f(x, y)dx dy. Interpretación geométrica: El Teorema de Fubini junto con el principio de avalieri nos garantizan que si f : (, + ) es una función acotada en el rectángulo, entonces f(x, y)dxdy representa el volumen del sólido S := {(x, y, z) 3 : (x, y), z f(x, y)}. Fig. 1: Interpretación geométrica de la integral doble en un rectángulo a través del Teorema de Fubini. Ejemplo Vamos a calcular (x sen y ye x )dxdy donde = [ 1, 1] [, π/]. plicando el Teorema de Fubini, vamos a integrar primero respecto de x y llamar (y) al resultado: (y) = 1 1 (x sen y ye x )dx = x sen y yex x=1 x= 1 = ey + y/e. epartamento de nálisis Matemático nálisis Matemático (Grado en Física)
3 Tema 1. plicaciones del cálculo diferencial. urso 17/18 Integrando ahora respecto de y, obtendremos el resultado nal (x sen y ye x )dxdy = π/ = (1/e e) (y)dy = π/ π/ ( ey + y/e)dy = ydy = (1/e e)π /8. Vamos a comprobar que, al intercambiar el orden de integración, no alteramos el resultado. (x sen y ye x )dxdy = = ( ) π/ (x sen y ye x )dy dx = 1 ( π e x /8 + x)dx = π e x /8 + x ( x cos y 1 ) y=π/ y e x dx = 1 x=1 x= 1 = (1/e e)π /8. enición Sea un subconjunto acotado del plano. Se dice que el conjunto tiene contenido nulo si para cada ε > existe un conjunto nito de rectángulos que recubre a y cuya suma de áreas no supera ε. y= icho de otro modo, un conjunto plano acotado de contenido nulo puede cubrirse con una cantidad nita de rectángulos cuya área total sea tan pequeña como se quiera. Las siguientes propiedades relativas a los conjuntos acotados de contenido nulo son sencillas consecuencias de esa denición. Propiedades (a) ualquier conjunto nito de puntos del plano tiene contenido nulo. (b) La unión de una cantidad nita de conjuntos de contenido nulo también es de contenido nulo. (c) Todo subconjunto de un conjunto de contenido nulo tiene contenido nulo. (d) Todo segmento de recta tiene contenido nulo. Teorema Sea f : una función acotada en un rectángulo. Si f es continua en, salvo en un conjunto de contenido nulo, entonces f es integrable en. En particular, las funciones continuas son integrables en rectángulos. epartamento de nálisis Matemático 3 nálisis Matemático (Grado en Física)
4 Tema 1. plicaciones del cálculo diferencial. urso 17/ Integrales dobles sobre regiones proyectables. Hasta ahora sólo hemos denido la integral doble sobre rectángulos pero, por ejemplo, no sobre un círculo. Esto se puede solucionar muy fácilmente de la siguiente forma. Sea un conjunto acotado, es decir, existe un rectángulo tal que. Sea f : una función acotada. iremos que f es integrable sobre si es integrable en la función f : dada por f(x, y) si (x, y) f(x, y) = en otro caso. En tal caso, escribiremos f(x, y)dxdy = f(x, y)dxdy. La integral doble,así denida, tiene propiedades similares a la integral de iemann. Propiedades Sean f, g : dos funciones integrables en y λ. Entonces, (a) f ± g es integrable en y (f ± g)(x, y)dxdy = f(x, y)dxdy ± g(x, y)dxdy. (b) αf es integrable en (αf)(x, y)dxdy = α f(x, y)dxdy. (c) Si f(x, y) g(x, y) (x, y), entonces f(x, y)dxdy (d) f es integrable en y f(x, y)dxdy f(x, y) dxdy g(x, y)dxdy. (e) Si = 1 y 1 tiene contenido nulo, entonces f es integrable en si y sólo si lo es en 1 y. En este caso: f(x, y)dxdy = f(x, y)dxdy + f(x, y)dxdy. 1 la vista del Teorema 11.7, incluso en el más simple de los casos en que el integrando sea una función constante, la integrabilidad de f sobre dependerá de lo complicada que sea la frontera del conjunto. Por ejemplo, si la frontera son segmentos de recta (pensemos que es un polígono), entonces la frontera de tendrá contenido nulo y, por tanto, las funciones continuas en serán integrables. En realidad, la frontera del conjunto de integración, necesitaría ser, en cierto modo, un conjunto de contenido nulo en sí mismo. El siguiente resultado nos permite determinar que la frontera de un conjunto plano es de contenido nulo. epartamento de nálisis Matemático 4 nálisis Matemático (Grado en Física)
5 Tema 1. plicaciones del cálculo diferencial. urso 17/18 Proposición Sea ϕ : [a, b] una función de una variable continua. Entonces, su gráca {(x, ϕ(x)) : a x b} es un conjunto de contenido nulo. on esta proposición, por ejemplo, una circunferencia es un conjunto de contenido nulo y podremos integrar sobre ella. El Teorema de Fubini nos proporciona una herramienta fundamental para el cálculo de integrales dobles sobre rectángulos, veamos cómo podemos extenderlo a otro tipo de regiones. enición Un conjunto se dice que es proyectable sobre el eje de abscisas si lo podemos escribir de la siguiente forma: = {(x, y) : x [a, b], α(x) y β(x)}, donde α y β son funciones continuas tales que α(x) β(x) x [a, b]. nálogamente se pueden denir los recintos proyectables sobre el eje de ordenadas como aquéllos conjuntos B que pueden escribirse de la forma B = {(x, y) : y [c, d], α(y) x β(y)}, donde α y β son funciones continuas tales que α(x) β(x) x [c, d]. d y=β (x) x=α (y) x=β (y) y=α (x) c a b Fig. : ecintos proyectables sobre el eje de abscisas (izquierda) y ordenadas (derecha). epartamento de nálisis Matemático 5 nálisis Matemático (Grado en Física)
6 Tema 1. plicaciones del cálculo diferencial. urso 17/18 Es claro que la frontera de recintos proyectables son de contenido nulo. demás, en una región proyectable sobre el eje de abscisas, para cada punto t [a, b] la recta vertical x = t corta a en un segmento que une la curva y = α(x) e y = β(x). nálogamente, en una región B proyectable sobre el eje de ordenadas, para cada punto t [c, d] la recta horizontal y = t corta a B en un segmento que une la curva x = α(y) y x = β(y). Ejemplo El círculo = {(x, y) : (x 1) + y 1} se puede escribir como recinto proyectable sobre ambos ejes: = {(x, y) : x, 1 (x 1) y 1 (x 1) } = {(x, y) : 1 y 1, 1 1 y x y } Teorema 11.1 (Teorema de Fubini sobre recintos proyectables.). Sea = {(x, y) : x [a, b], α(x) y β(x)} un recinto proyectable sobre el eje de abscisas. Sea f : una función acotada en y continua en. Entonces, existe f(x, y)dxdy y, además, se cumple que f(x, y)dxdy = b a ( ) β(x) f(x, y)dy dx. Existe una versión análoga de este resultado para recintos proyectables sobre el eje de ordenadas. α(x) En este caso, se tendrá que B f(x, y)dxdy = d ( ) β(y) f(x, y)dx dy. c α(y) omo hemos visto en el Ejemplo 11.11, hay recintos proyectables sobre ambos ejes. En tal caso, el orden de integración será indiferente, aunque suele ocurrir que una de las formas sea más complicada que la otra ambio de variables en integrales dobles. En esta sección vamos a tratar de generalizar la fórmula ϕ(b) ϕ(a) a integrales de dos variables. f(x) dx = b a f(ϕ(t))ϕ (t) dt epartamento de nálisis Matemático 6 nálisis Matemático (Grado en Física)
7 Tema 1. plicaciones del cálculo diferencial. urso 17/18 En la situación será la siguiente. Para calcular f(x, y)dxdy, realizaremos un cambio de variables h : (u, v) (x(u, v), y(u, v)) con el n de que el nuevo recinto de integración, o la nueva función a integrar sean más sencillos que los originales. Teorema Sea h : (u, v) (x(u, v), y(u, v)) una función inyectiva en con h( ) =. Sea f : una función integrable en. Entonces f(x, y)dxdy = f(x(u, v), y(u, v)) det(j h(u, v)) dudv donde J h(u, v) denota la matriz jacobiana del cambio de variables. Este teorema es fácilmente generalizable a cualquier dimensión n. demás, también es cierto si la función del cambio h deja de ser inyectiva en un conjunto de contenido nulo. Ejemplo omo primer ejemplo, vamos a usar los cambios de variables lineales, es decir, x = u + Bv En este caso, J h(u, v) = y = u + v. B = B. Si esta cantidad es no nula, h dene una biyección de en y, por tanto, f(x, y)dxdy = B f(u + Bv, u + v)dudv. omo aplicación, vamos a calcular (x y) e x+y dxdy, donde el cuadrado cuyos vértices son (, ), (1, 1), (, ) y (1, 1). x + y = u x = (u + v)/ Si hacemos el cambio de variables, el recinto se transforma en el rectángulo = [, ] [, ], por lo tanto, como J 1/ 1/ h(u, v) = 1/ 1/ = 1, se tiene x y = v y = (u v)/ que y) (x e x+y dxdy = 1 ( ) ( ) v e u dudv = e u du v dv = 4 e 1. 3 epartamento de nálisis Matemático 7 nálisis Matemático (Grado en Física)
8 Tema 1. plicaciones del cálculo diferencial. urso 17/ ambio a coordenadas polares. Ya vimos en el Tema 9 el cambio a coordenadas polares es x = r cos θ y = r sen θ cos θ con r y θ [, π). Su Jacobiano es det(j p (r, θ)) = sen θ r sen θ r cos θ = r. Por tanto, si una región se transforma en mediante el cambio de variables a coordenadas polares, tendremos que f(x, y)dxdy = f(r cos θ, r sen θ) r drdθ. Ejemplos (a) Vamos a calcular radio que está en el Primer uadrante. 4 x y dxdy, donde la parte del círculo centrado en el origen y La presencia de x + y así como la forma circular del recinto son claros indicios de que hay que usar el cambio a polares. Este cambio transforma, claramente, en = [, ] [, π/], por lo tanto, 4 x y dxdy = r ( ) π/ ( ) 4 r drdθ = dθ r(4 r ) 1/ dr = ( ) r= = π (4 r ) 3/ = 4π (b) Vamos a demostrar que e x dx = π. Para ello, vamos a calcular la siguiente integral doble e x y dxdy mediante el cambio a polares. Por un lado, por el Teorema de Fubini resulta que + ( + ) x y e dxdy = e x y dy dx = ( + ) ( + ) ( + = e x dx e y dy = e dx) x. r= epartamento de nálisis Matemático 8 nálisis Matemático (Grado en Física)
9 Tema 1. plicaciones del cálculo diferencial. urso 17/18 Por otro lado, si realizamos el cambio a polares resulta que x y e dxdy = = (,+ ) ( π,π) π + π dθ e r rdrdθ = re r dr = π 1 e r + = π. Por consiguiente, uniendo ambas partes, tenemos que de donde se deduce que (c) Vamos a calcular + ( + e dx) x = e x dx = π. x y e dxdy = π y x + y dxdy donde es el semicírculo x + (y 1) 1, y Las curvas que limitan el recinto quedan en polares y = 1 r sen θ = 1 r = 1/ sen θ x + y = y r = r sen θ r = sen θ. epartamento de nálisis Matemático 9 nálisis Matemático (Grado en Física)
10 Tema 1. plicaciones del cálculo diferencial. urso 17/18 sí pues, el recinto se transforma en := y x + y dxdy = r sen θ r rdrdθ = = 3π/4 π/4 { π 4 θ 3π } 4, 1 sen θ r sen θ. Por lo tanto, 3π/4 π/4 ( sen θ 1)dθ = ( ) sen θ sen θdr dθ = 1/ sen θ 3π/4 π/4 cos(θ)dθ = plicaciones geométricas y físicas Son muchas las aplicaciones de la integral doble de entre ellas destacamos las siguientes: álculo de áreas ado un recinto acotado del plano, decimos que es medible si existe y es nita la integral doble sobre de la función unidad, en cuyo caso dicho valor representa el área de : Área() = dxdy. Ejemplo alculemos el área de un círculo de radio a >. Lo haremos de dos formas: oordenadas cartesianas. La ecuación de la circunferencia es x + y = a. = {(x, y) : a x a, a x y a x }. a a x a a x a Área() = a dxdy = 4 dxdy = 4 a x dxdy = πa. a x oordenadas polares. En coordenadas polares la ecuación de la circunferencia es ρ = r, con θ [, π). Entonces el recinto en coordenadas polares es: = {(r, θ) : r a, θ π}. π a Área() = rdrdθ = rdrdθ = ) r=a (π r = πa. r= epartamento de nálisis Matemático 1 nálisis Matemático (Grado en Física)
11 Tema 1. plicaciones del cálculo diferencial. urso 17/ álculo de volúmenes El volumen del sólido S acotado inferiormente por el recinto plano y superiormente por la gráca de la supercie f : (función no negativa en ), viene dado por: V olumen(s) = f(x, y) dxdy. Si el sólido S está comprendido entre las grácas de dos supercies f, g : siendo f g en entonces S = {(x, y, z) : (x, y), f(x, y) z g(x, y) y su volumen será la integral: Volumen(S) = (g(x, y) f(x, y) dxdy. Los sólidos que vienen dados de esta última forma se dice que son xy-proyectables. e manera análoga se denen los volúmenes de sólidos xz-proyectables e yz-proyectables. Ejemplo Hallar el volumen del sólido limitado por z = 4 x y y el plano z =. En este caso, el volumen es V = (4 x y )dxdy, donde es el recinto interior a la intersección de la supercie y el plano z =, es decir, = {(x, y) : x + y 4}. Pasamos la integral a coordenadas polares: V = π r(4 r )dxdy = 8π entro de masa. Momentos de inercia Si tenemos una lámina de densidad variable, siendo la función densidad ρ : donde es la región plana que ocupa la lámina, entonces su masa viene dada por M = ρ(x, y)dxdy. Los momentos estáticos respecto a los ejes X e Y (respectivamente) de la lámina vienen dados por M x = yρ(x, y)dxdy, y M y = xρ(x, y)dxdy. epartamento de nálisis Matemático 11 nálisis Matemático (Grado en Física)
12 Tema 1. plicaciones del cálculo diferencial. urso 17/18 Y las coordenadas del centro de masa son: x = M y M, e ȳ = M x M. sí como la masa mide la resistencia de la materia a cambios en su movimiento rectilíneo, el momento de inercia mide la resistencia de la materia a cambios en su movimiento de rotación. Si denotamos por I x e I y los momentos de inercia de la lámina respecto de los ejes X e Y respectivamente, tenemos: I x = y ρ(x, y)dxdy, e I y = x ρ(x, y)dxdy. Ejemplo alcular la masa y el centro de masa de la lámina triangular de vértices (, ), (, 3) y (, 3), si su densidad en cada punto viene dada por ρ(x, y) = x + y. Haciendo un sencillo gráco se comprueba que la lámina está limitada por las rectas de ecuaciones x =, y = 3 y x = y 3. on esto, la masa de la lámina es: 3 y 3 M = (x + y)dxdy = dy (x + y)dx = 1 9 Por otro lado: M x = M y = y(x + y)dxdy = y(x + y)dxdy = 3 3 Luego las coordenadas del centro de masa son: y 3 dy y(x + y)dx = 1 9 dy ( x, ȳ) = y 3 3 x(x + y)dx = ( 17, 45 ). 3 y dy = 1. 3 y 3 dy = 45. y 3 dy = Integrales triples. nálogamente al caso n =, dada una función f : 3 acotada en un paralelepípedo = [a, b] [c, d] [p, q], se puede denir f(x, y, z)dxdydz, que representará un volumen en un espacio de cuatro dimensiones, es decir, el volumen de un sólido de cuatro dimensiones con base y altura en cada punto la que le asigna f(x, y, z). Esta integral se podrá de nuevo calcular mediante integrales iteradas: f(x, y, z)dxdydz = b a ( d ( q c p ) ) f(x, y, z)dz dy dx o cualquiera de las otras 5 formas resultantes de intercambiar los papeles de x, y y z. epartamento de nálisis Matemático 1 nálisis Matemático (Grado en Física)
13 Tema 1. plicaciones del cálculo diferencial. urso 17/18 También podemos integrar sobre recintos más generales: recintos proyectables. sí si tenemos V = {(x, y, z) 3 : a x b, c(x) y d(x), p(x, y) z q(x, y)}, donde c, d : [a, b] son funciones continuas con c(x) d(x) y p, q : son continuas en = {(x, y) : a x b, c(x) y d(x)} con p(x, y) q(x, y) y f : V 3 es una función acotada, podemos denir ( b ( d(x) ) ) q(x,y) f(x, y, z)dxdydz = f(x, y, z)dz dy dx. a c(x) p(x,y) Por supuesto, existen fórmulas análogas haciendo intercambiar los papeles de las 3 variables. Haciendo f 1, se tiene que Vol(V ) = dxdydz. V ambio de variables: cilíndricas y esféricas. on hipótesis análogas al caso de variables, se pude demostrar una fórmula para eel cambio de variables. Teorema Sea h : (u, v, w) 3 (x(u, v, w), y(u, v, w), z(u, v, w)) 3 una función inyectiva en V 3 con h(v ) = V. Sea f : V 3 una función integrable en V. Entonces f(x, y, z)dxdydz = f(x(u, v, w), y(u, v, w), z(u, v, w)) det(j h(u, v, w)) dudvdw V V donde J h(u, v, w) denota la matriz jacobiana del cambio de variables. oordenadas cilíndricas. Ya vimos en el Tema 9 el cambio a coordenadas cilíndricas x = r cos θ y = r sen θ z = z cos θ r sen θ cuyo Jacobiano es det(j c (r, θ, z)) = sen θ r cos θ = r. 1 epartamento de nálisis Matemático 13 nálisis Matemático (Grado en Física)
14 Tema 1. plicaciones del cálculo diferencial. urso 17/18 Por tanto, si una región V 3 se transforma en V 3 mediante el cambio de variables a coordenadas cilíndricas, tendremos que f(x, y, z)dxdydz = f(r cos θ, r sen θ, z) r drdθdz. V V Las coordenadas cilíndricas son especialmente útiles para la representación de supercies cilíndricas y supercies de revolución que tengan el eje OZ como eje de simetría: ilindro: x + y = a r = a. ono: x + y = z r = z. Paraboloide: Hiperboloide: x + y = z r = z. x + y z = a r = a + z. Ejemplo 11.. Hallar la integral (x + y )dxdydz siendo la supercie limitada por el paraboloide z = x + y y el plano z = 4. Vamos a describir en coordenadas cilíndricas. La proyección de sobre el plano XY es el círculo x + y 4, luego en cilíndricas será r y θ [, π]. La coordenada z varía desde el paraboloide, que tiene por ecuación en cilíndricas z = r, al plano cuya ecuación en cilíndricas es z = 4. Por último, la función integrando en cilíndricas es x + y r, y recordando que el jacobiano epartamento de nálisis Matemático 14 nálisis Matemático (Grado en Física)
15 Tema 1. plicaciones del cálculo diferencial. urso 17/18 de la transformación es r, la integral queda: π ( ( 4 ) ) ( ) (x + y )dxdydz = r 3 dz dr dθ = π r 3 (4 r )dr r = π(r 4 r6 6 ) r= = 3π r= 3. oordenadas esféricas. La función vectorial que dene las coordenadas esféricas en el espacio tiene por componentes: x(r, θ, ϕ) = r sen ϕ cos θ y(r, θ, ϕ) = r sen ϕ sen θ z(r, θ, ϕ) = r cos ϕ con r, θ [, π], ϕ [, π]. Por tanto su Jacobiano será sen ϕ cos θ r sen ϕ sen θ r cos ϕ sen θ det(j s (r, θ, ϕ)) = sen ϕ sen θ r sen ϕ cos θ r cos ϕ sen θ = r sen ϕ cos ϕ r sen ϕ Por tanto, si una región V 3 se transforma en V 3 mediante el cambio de variables a coordenadas esféricas, tendremos que f(x, y, z)dxdydz = f(r sen ϕ cos θ, r sen ϕ sen θ, r cos ϕ) r sen ϕ drdθdϕ. V V Las coordenadas esféricas son útiles para supercies como la esfera o el cono. Esfera: Semi ono (parte superior): x + y + z = a r = a. x + y = a z, z > ϕ = arctan(a). Ejemplo alcular la integral triple dxdydz siendo la supercie: = {(x, y, z) 3 : x + y z, x + y + z 9, z }. La supercie está limitada inferiormente por la hoja superior del cono z = x +y y superiormente por la esfera de ecuación x + y + z = 9. Vamos a describir en coordenadas esféricas. En coordenadas esféricas la ecuación de la esfera es r = x + y + z = 9, es decir r = 3; mientras que la del cono es r sen ϕ r cos ϕ, es decir, sen ϕ cos ϕ. Por otro lado, como z, debe ser epartamento de nálisis Matemático 15 nálisis Matemático (Grado en Física)
16 Tema 1. urso 17/18 plicaciones del cálculo diferencial. r cos ϕ, lo que equivale a que cos ϕ. omo de θ no obtenemos restricciones, debe ser θ [, π] (de hecho, la simetría del cono y la esfera así nos lo dice también). e aquí, la integral queda: ZZZ Z π Z (x + y )dxdydz = π 4 Z = π π 4 3 Z! Z r sen ϕdr dϕ dθ = π ϕ= π4 = 9π( 9 sen ϕdϕ = 18π cos ϕ π 4 r3 sen ϕ 3 r=3! dϕ r= ). ϕ= plicaciones geométricas y físicas álculo de volúmenes ado un sólido acotado del espacio triple sobre 3, decimos que es medible si existe y es nita la integral de la función unidad, en cuyo caso dicho valor representa el volumen de : ZZZ Vol() = dxdydz. Ejemplo 11.. alcular el volumen de la esfera de centro (,, ) y radio a. Para ello describiremos la esfera en coordenadas cilíndricas. La ecuación de la super cie esférica en coordenadas rectangulares es: con r a y θ π. x + y + z = a, Por tanto la esfera luego en coordenadas cilíndricas será r + z = a S = {(x, y, z) 3 : x + y + z a } expresada en coordenadas cilíndricas es: p p S = {(r, θ, z) : r a, θ π, a r z a r }. y su volumen viene dado por: epartamento de nálisis Matemático 16 nálisis Matemático (Grado en Física)
17 Tema 1. plicaciones del cálculo diferencial. urso 17/18 π a a r V(S) = rdrdθdz = S rdzdrdθ = a r a = π r (a a r dr = π r ) 3 3 π r=a r= ( a = 4π 3 a3. r ) a r dr dθ entro de masa. Momentos de inercia. Si tenemos un sólido tridimensional de densidad variable, siendo la función densidad ρ :, entonces su masa viene dada por M = ρ(x, y, z)dxdydz. Los momentos estáticos alrededor de los planos XY, Y Z y XZ, denotados M xy, M yz y M xz, respectivamente, se obtienen a partir de las siguientes expresiones: M xy = zρ(x, y, z)dxdydz, M yz = Las coordenadas del centro de masa o de gravedad son: xρ(x, y, z)dxdydz, y M xz = yρ(x, y, z)dxdydz. x = M yz M, ȳ = M xz M, y z = M xy M. Finalmente, el momento de inercia I xy respecto del plano XY se dene como I xy = z ρ(x, y, z) dxdydz, con fórmulas parecidas para los momentos I xz e I yz, respecto de los planos XZ e Y Z, respectivamente. El momento de inercia I L respecto de una recta L, se dene como I L = δ(x, y, z) ρ(x, y, z) dxdydz, siendo δ(x, y, z) la distancia de un punto genérico de a la recta L. En concreto, los momentos de inercia respecto de los ejes coordenados son I x = I xy + I xz, I y = I xy + I yz, I z = I xz + I yz. epartamento de nálisis Matemático 17 nálisis Matemático (Grado en Física)
18 Tema 1. plicaciones del cálculo diferencial. urso 17/18 Ejemplo alcular la masa del sólido comprendido entre los planos z = y z = 1 y y dentro del cilindro de ecuación x + 4y = 4, cuya densidad viene dada por ρ(x, y, z) = z. La masa del sólido viene dada por: 1 y M = zdxdydz. donde es la proyección del sólido sobre el plano XY : { 4 x = (x, y) : x, y } 4 x. Luego M = 1 y zdxdydz = El cálculo de los momentos estáticos dan: M xy = z dxdydz = 7π 3, M yz = xzdxdydz =, M xz = yzdxdydz = π. Por tanto el centro de masa tiene por coordenadas: 4 x 1 y zdzdydx = = 5π 4 x. y x = M yz M = 5π =, ȳ = M xz M = π 5π = 5, z = M xy M 7π = 3 5π = epartamento de nálisis Matemático 18 nálisis Matemático (Grado en Física)
Capítulo 3. Integración multidimensional. 1. Integrales de Riemann en rectángulos
 Capítulo 3 Integración multidimensional 1. Integrales de Riemann en rectángulos Definición (Partición de rectángulos). Consideremos el rectángulo [a, b] [c, d] y sean P 1 = {a = x 0, x 1,..., x n = b}
Capítulo 3 Integración multidimensional 1. Integrales de Riemann en rectángulos Definición (Partición de rectángulos). Consideremos el rectángulo [a, b] [c, d] y sean P 1 = {a = x 0, x 1,..., x n = b}
Teorema de Cambio de Variables para Integrales Dobles
 Universidad de Chile Facultad de Ciencias Físicas y Matemáticas epartamento de Ingeniería Matemática Cátedra - MA2A1 22 de Enero 2008 Teorema de Cambio de Variables para Integrales obles Cuál es la idea:
Universidad de Chile Facultad de Ciencias Físicas y Matemáticas epartamento de Ingeniería Matemática Cátedra - MA2A1 22 de Enero 2008 Teorema de Cambio de Variables para Integrales obles Cuál es la idea:
Tema 7. Integrales múltiples
 Tema 7 Integrales múltiples 7.. efinición. En esta sección estudiamos el cálculo de la integral de una función real de dos variables denominada integral doble. Se puede utilizar el esquema del tema anterior
Tema 7 Integrales múltiples 7.. efinición. En esta sección estudiamos el cálculo de la integral de una función real de dos variables denominada integral doble. Se puede utilizar el esquema del tema anterior
1. INTEGRALES MÚLTIPLES
 1. INTEGALES MÚLTIPLES 1. Calcular las siguientes integrales iteradas: 1. x x 7 y dy dx dx 1. x x y y dx dy 1 1 7. (1 + xy) dx dy 1 1 π/. x sen y dy dx 5. (x + y) dx dy 6/ 1 6. (x + y) 8 dx dy 616 5 1
1. INTEGALES MÚLTIPLES 1. Calcular las siguientes integrales iteradas: 1. x x 7 y dy dx dx 1. x x y y dx dy 1 1 7. (1 + xy) dx dy 1 1 π/. x sen y dy dx 5. (x + y) dx dy 6/ 1 6. (x + y) 8 dx dy 616 5 1
Tema 5: Funciones homogéneas
 Tema 5: Funciones homogéneas f se dice homogénea de grado α si se verifica: f(λ x) = λ α f( x), x, λ > 0 Propiedades: 1. Si f y g son homogéneas de grado α, entonces f ± g es también homogénea de grado
Tema 5: Funciones homogéneas f se dice homogénea de grado α si se verifica: f(λ x) = λ α f( x), x, λ > 0 Propiedades: 1. Si f y g son homogéneas de grado α, entonces f ± g es también homogénea de grado
9. DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES.
 9 DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES 91 Derivadas parciales y direccionales de un campo escalar La noción de derivada intenta describir cómo resulta afectada una función y = f(x) por un cambio
9 DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES 91 Derivadas parciales y direccionales de un campo escalar La noción de derivada intenta describir cómo resulta afectada una función y = f(x) por un cambio
Integrales Dobles. Hermes Pantoja Carhuavilca. Matematica II. Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos
 Integrales Dobles Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 76 CONTENIDO Integrales Dobles Introducción
Integrales Dobles Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 76 CONTENIDO Integrales Dobles Introducción
3 Integración en IR n
 a t e a POBLEMAS DE CÁLCULO II t i c a s 1 o Ings. Industrial y de Telecomunicación CUSO 29 21 3 Integración en I n 3.1 Integral múltiple. Problema 3.1 Calcula f en los siguientes casos: Q i) f(x, y) =
a t e a POBLEMAS DE CÁLCULO II t i c a s 1 o Ings. Industrial y de Telecomunicación CUSO 29 21 3 Integración en I n 3.1 Integral múltiple. Problema 3.1 Calcula f en los siguientes casos: Q i) f(x, y) =
AMPLIACIÓN DE CÁLCULO. Curso 2008/9. Hoja 1: Integración en varias variables.
 AMPLIACIÓN DE CÁLCULO. Curso 2008/9. Hoja 1: Integración en varias variables. 1. Calcular para =[0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcularlasintegralesdoblessiguientesenlosrecintosqueseindican:
AMPLIACIÓN DE CÁLCULO. Curso 2008/9. Hoja 1: Integración en varias variables. 1. Calcular para =[0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcularlasintegralesdoblessiguientesenlosrecintosqueseindican:
Integración doble Integrales dobles sobre regiones no rectangulares
 Nuestra intención es extender la definición de integral doble, de funciones continuas, sobre regiones más generales que el rectángulo. Para ello definiremos dos tipos de regiones en el plano, que llamaremos
Nuestra intención es extender la definición de integral doble, de funciones continuas, sobre regiones más generales que el rectángulo. Para ello definiremos dos tipos de regiones en el plano, que llamaremos
Contenido 1. Integrales Dobles 2. Integrales Triples
 Integración Contenido 1. Integrales Dobles 2 1.1. Integrales iteradas............................. 2 1.2. Regiones en R 2.............................. 3 1.3. Volumen..................................
Integración Contenido 1. Integrales Dobles 2 1.1. Integrales iteradas............................. 2 1.2. Regiones en R 2.............................. 3 1.3. Volumen..................................
EJERCICIOS DE CA LCULO II PARA GRADOS DE INGENIERI A Elaborados por Domingo Pestana y Jose Manuel Rodrı guez, con Arturo de Pablo y Elena Romera
 EJECICIOS E CA LCULO II PAA GAOS E INGENIEI A Elaborados por omingo Pestana y Jose Manuel odrı guez, con Arturo de Pablo y Elena omera 3 3. Integracio n en n Integral mu ltiple. f en los siguientes casos:
EJECICIOS E CA LCULO II PAA GAOS E INGENIEI A Elaborados por omingo Pestana y Jose Manuel odrı guez, con Arturo de Pablo y Elena omera 3 3. Integracio n en n Integral mu ltiple. f en los siguientes casos:
1 Funciones de Varias Variables
 EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
Lección 32: Algunas ideas sobre la integral doble. Introducción al Cálculo Infinitesimal I.T.I. Gestión
 Lección 32: Algunas ideas sobre la integral doble Introducción al Cálculo Infinitesimal I.T.I. Gestión Esquema: - Idea de integral doble - Teorema de Fubini - Cambio a coordenadas polares Integral doble
Lección 32: Algunas ideas sobre la integral doble Introducción al Cálculo Infinitesimal I.T.I. Gestión Esquema: - Idea de integral doble - Teorema de Fubini - Cambio a coordenadas polares Integral doble
Clase 14: Fórmula del Cambio de Variables
 Clase 4: Fórmula del Cambio de Variables C.J. Vanegas 4 de junio de 8 Recordemos.. Método de sustitución en integrales de una variable: b f(g(t))g (t) dt g(b) a g(a) f(s) ds s g(t) ds g (t)dt t a s g(a)
Clase 4: Fórmula del Cambio de Variables C.J. Vanegas 4 de junio de 8 Recordemos.. Método de sustitución en integrales de una variable: b f(g(t))g (t) dt g(b) a g(a) f(s) ds s g(t) ds g (t)dt t a s g(a)
Introducción al Cálculo. Integral en Varias Variables
 UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE CIENCIAS ESCUELA DE MATEMÁTICA LABORATORIO DE FORMAS EN GRUPOS Introducción al Cálculo Integral en Varias Variables Ramón Bruzual Marisela Domínguez Caracas,
UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE CIENCIAS ESCUELA DE MATEMÁTICA LABORATORIO DE FORMAS EN GRUPOS Introducción al Cálculo Integral en Varias Variables Ramón Bruzual Marisela Domínguez Caracas,
INTEGRALES DE FUNCIONES DE VARIAS VARIABLES
 INTEGALES DE FUNCIONES DE VAIAS VAIABLES [Versión preliminar] Prof. Isabel Arratia Z. Integrales dobles sobre rectángulos La integral de iemann para una función f de dos variables se define de manera similar
INTEGALES DE FUNCIONES DE VAIAS VAIABLES [Versión preliminar] Prof. Isabel Arratia Z. Integrales dobles sobre rectángulos La integral de iemann para una función f de dos variables se define de manera similar
Integrales dobles. Integrales dobles
 Integrales dobles Integrales iteradas b g2 (x) a g 1 (x) f(x, y) dydx ó d h2 (y) c h 1 (y) f(x, y) dxdy Los límites interiores de integración pueden ser variables respecto a la variable exterior de integración,
Integrales dobles Integrales iteradas b g2 (x) a g 1 (x) f(x, y) dydx ó d h2 (y) c h 1 (y) f(x, y) dxdy Los límites interiores de integración pueden ser variables respecto a la variable exterior de integración,
Integrales de lı nea y de superficie
 EJERIIO DE A LULO II PARA GRADO DE INGENIERI A Elaborados por Domingo Pestana y Jose Manuel Rodrı guez, con Arturo de Pablo y Elena Romera 4 4.1 Integrales de lı nea y de superficie Integrales sobre curvas
EJERIIO DE A LULO II PARA GRADO DE INGENIERI A Elaborados por Domingo Pestana y Jose Manuel Rodrı guez, con Arturo de Pablo y Elena Romera 4 4.1 Integrales de lı nea y de superficie Integrales sobre curvas
CÁLCULO INTEGRAL. HOJA 9.
 CÁLCULO INTEGRL. HOJ 9. EL TEOREM DEL CMIO DE VRILES. 1. Teorema (del cambio de variables). Sea g : U V un difeomorfismo de clase C 1 entre dos abiertos de R n, sea f : V R medible. Entonces f g es medible
CÁLCULO INTEGRL. HOJ 9. EL TEOREM DEL CMIO DE VRILES. 1. Teorema (del cambio de variables). Sea g : U V un difeomorfismo de clase C 1 entre dos abiertos de R n, sea f : V R medible. Entonces f g es medible
Integrales Triples Centro de Masa y Momento de Inercia Integrales Triples en Coordenadas Cilindricas Coordenadas Cilindricas. Integrales Triples
 Integrales Triples Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 30 CONTENIDO Integrales Triples Introducción
Integrales Triples Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 30 CONTENIDO Integrales Triples Introducción
7. Cambio de variables en integrales triples.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 011 1. Lección. Integrales múltiples. 7. Cambio de variables en integrales triples. El teorema del cambio de variables para integrales triples es análogo al de integrales
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 011 1. Lección. Integrales múltiples. 7. Cambio de variables en integrales triples. El teorema del cambio de variables para integrales triples es análogo al de integrales
INTEGRALES MÚLTIPLES
 INTEGALES MÚLTIPLES Introducción: Si f es una función definida sobre una región, la integral doble se puede interpretar como el volumen del sólido limitado superiormente por la superficie z = f(,, inferiormente
INTEGALES MÚLTIPLES Introducción: Si f es una función definida sobre una región, la integral doble se puede interpretar como el volumen del sólido limitado superiormente por la superficie z = f(,, inferiormente
Tema 4: Integración de funciones de varias variables
 Departamento de Matemáticas. Universidad de Jaén. Análisis Matemático II. Curso 29-21. Tema 4: Integración de funciones de varias variables 1. Evaluar las siguientes integrales iteradas e) f ) g) 1 2 1
Departamento de Matemáticas. Universidad de Jaén. Análisis Matemático II. Curso 29-21. Tema 4: Integración de funciones de varias variables 1. Evaluar las siguientes integrales iteradas e) f ) g) 1 2 1
Problemas de Análisis Vectorial y Estadístico
 Relación 1. Funciones Γ y β 1. Función Gamma Definimos la función gamma Γ(p) como: Demostrar que: Γ(p) = t (p 1) e t dt para p> a) Γ(1) = 1 b) Integrando por partes, ver que Γ(p) = (p 1)Γ(p 1) para p>1
Relación 1. Funciones Γ y β 1. Función Gamma Definimos la función gamma Γ(p) como: Demostrar que: Γ(p) = t (p 1) e t dt para p> a) Γ(1) = 1 b) Integrando por partes, ver que Γ(p) = (p 1)Γ(p 1) para p>1
Lectura 2 Ampliación de Matemáticas. Grado en Ingeniería Civil
 1 / 12 Lectura 2 Ampliación de Matemáticas. Grado en Ingeniería Civil Curso Académico 2011-2012 Cambio de variables 2 / 12 Idea básica: en ocasiones, la utilización de variables apropiadas en lugar de
1 / 12 Lectura 2 Ampliación de Matemáticas. Grado en Ingeniería Civil Curso Académico 2011-2012 Cambio de variables 2 / 12 Idea básica: en ocasiones, la utilización de variables apropiadas en lugar de
Cambio de Variables en la Integral Múltiple
 Capítulo 24 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Capítulo 24 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
6. Integrales triples.
 GRADO DE INGENIERÍA AEROESPACIAL. CRSO 0. Lección. Integrales múltiples. 6. Integrales triples. Integral triple en un prisma. El proceso para definir la integral triple f ( xyzdv,, ), de una función continua
GRADO DE INGENIERÍA AEROESPACIAL. CRSO 0. Lección. Integrales múltiples. 6. Integrales triples. Integral triple en un prisma. El proceso para definir la integral triple f ( xyzdv,, ), de una función continua
Cambio de Variables en la Integral Múltiple
 Capítulo 27 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Capítulo 27 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Tema 2. Ejercicios propuestos
 Tema 2. Ejercicios propuestos 1.- - Calcular 2.- - Calcular 3.- - Sea = x2 y2 dx dy, siendo = {(x, y) 2 : 1 x y 2, x y 4x}. (x2 +y2 )dx dy, donde = (x, y) 2 : x2 + y2 2y, x2 + y2 1, x 0. (x, y) 2 1 x 2
Tema 2. Ejercicios propuestos 1.- - Calcular 2.- - Calcular 3.- - Sea = x2 y2 dx dy, siendo = {(x, y) 2 : 1 x y 2, x y 4x}. (x2 +y2 )dx dy, donde = (x, y) 2 : x2 + y2 2y, x2 + y2 1, x 0. (x, y) 2 1 x 2
Integral Múltiple. María Muñoz Guillermo Matemáticas I(1 o Grado Ingeniería Electrónica Industrial y Automática) U.P.C.T.
 Integral Múltiple María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I(1 o Grado Ingeniería Electrónica Industrial y Automática) M. Muñoz (U.P.C.T.) Integral Múltiple Matemáticas I 1 / 19 Introducción
Integral Múltiple María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I(1 o Grado Ingeniería Electrónica Industrial y Automática) M. Muñoz (U.P.C.T.) Integral Múltiple Matemáticas I 1 / 19 Introducción
Ejercicios Resueltos de Cálculo III.
 Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
INTEGRALES MULTIPLES. Integral doble sobre rectángulos
 INTEGRALES MULTIPLES En este tema se estudia la integral de Riemann de funciones de varias variables. Como veremos, la forma de introducirla es similar a la de la integral de Riemann de funciones reales
INTEGRALES MULTIPLES En este tema se estudia la integral de Riemann de funciones de varias variables. Como veremos, la forma de introducirla es similar a la de la integral de Riemann de funciones reales
Matemáticas III Tema 5 Integrales de ĺınea
 Matemáticas III Tema 5 Integrales de ĺınea Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino órdoba, S. 2014. OW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia reative ommons Attribution- Nonomercial-ShareAlike
Matemáticas III Tema 5 Integrales de ĺınea Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino órdoba, S. 2014. OW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia reative ommons Attribution- Nonomercial-ShareAlike
Integrales Múltiples.
 CAPÍTULO 9 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
CAPÍTULO 9 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
Integrales Múltiples.
 CAPÍTULO 8 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
CAPÍTULO 8 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
UAM CSIC Grupo 911 Febrero Ejercicios Resueltos del Tema Asignatura de Matemáticas Grado en Química
 UAM I Grupo 911 Febrero 213 Ejercicios Resueltos del Tema 2.2.6 Asignatura de Matemáticas Grado en Química Lista de ejercicios en estas páginas: 1 7 y 9 12. Nota: Los ejercicios pueden contener errores,
UAM I Grupo 911 Febrero 213 Ejercicios Resueltos del Tema 2.2.6 Asignatura de Matemáticas Grado en Química Lista de ejercicios en estas páginas: 1 7 y 9 12. Nota: Los ejercicios pueden contener errores,
Examen final de Cálculo Integral
 Examen final de Cálculo Integral 8 de junio de (Soluciones) Cuestiones C Sí se puede asegurar que es integrable, como consecuencia del teorema 4. de los apuntes: Llamamos W y f : W R a la esfera y a la
Examen final de Cálculo Integral 8 de junio de (Soluciones) Cuestiones C Sí se puede asegurar que es integrable, como consecuencia del teorema 4. de los apuntes: Llamamos W y f : W R a la esfera y a la
Gu ıa Departamento Matem aticas U.V.
 Universidad de Valparaíso Instituto de Matemáticas Guía de Cálculo en Varias Variables Integración. Sean = [,] [,] {(x,y) : (x,y) < } y f : continua. a) Escriba lafuncióncaracterísticaχ demedianteunafunciónporparte,análogamente
Universidad de Valparaíso Instituto de Matemáticas Guía de Cálculo en Varias Variables Integración. Sean = [,] [,] {(x,y) : (x,y) < } y f : continua. a) Escriba lafuncióncaracterísticaχ demedianteunafunciónporparte,análogamente
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS. 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2.
 INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2. 1 1 4, 0 1 a.- (, ) = 2 1 4, 1 2 2 1 < 3, 0 < 1 b.- (, ) = 1 1 < 3, 1 2 3 3 4,
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2. 1 1 4, 0 1 a.- (, ) = 2 1 4, 1 2 2 1 < 3, 0 < 1 b.- (, ) = 1 1 < 3, 1 2 3 3 4,
3. Cambio de variables en integrales dobles.
 GADO DE INGENIEÍA AEOESPACIAL. CUSO. Lección. Integrales múltiples. 3. Cambio de variables en integrales dobles. Para calcular integrales dobles eiste, además del teorema de Fubini, otra herramienta fundamental
GADO DE INGENIEÍA AEOESPACIAL. CUSO. Lección. Integrales múltiples. 3. Cambio de variables en integrales dobles. Para calcular integrales dobles eiste, además del teorema de Fubini, otra herramienta fundamental
Integrales múltiples
 ntegrales múltiples Cálculo (2004) * El objetivo de este capítulo es definir y aprender a calcular integrales de funciones reales de varias variables, que llamamos integrales múltiples. Las motivación
ntegrales múltiples Cálculo (2004) * El objetivo de este capítulo es definir y aprender a calcular integrales de funciones reales de varias variables, que llamamos integrales múltiples. Las motivación
Ejercicios típicos del segundo parcial
 Ejercicios típicos del segundo parcial El segundo examen parcial consiste en tres ejercicios prácticos y dos teóricos, aunque esta frontera es muy difusa. Por ejemplo, el primer ejercicio de esta serie,
Ejercicios típicos del segundo parcial El segundo examen parcial consiste en tres ejercicios prácticos y dos teóricos, aunque esta frontera es muy difusa. Por ejemplo, el primer ejercicio de esta serie,
Lista de Ejercicios Complementarios
 Lista de Ejercicios omplementarios Matemáticas VI (MA-3) Verano. ean α >, β > y a, b R constantes. ea la superficie que es la porción del cono de ecuación z = α x + y que resulta de su intersección con
Lista de Ejercicios omplementarios Matemáticas VI (MA-3) Verano. ean α >, β > y a, b R constantes. ea la superficie que es la porción del cono de ecuación z = α x + y que resulta de su intersección con
Capítulo 5. Integrales sobre curvas y superficies
 Capítulo 5. Integrales sobre curvas y superficies 5.1. Integrales de funciones escalares sobre curvas 5.2. Integrales de campos vectoriales sobre curvas 5.3. Teorema de Green 5.4. Integrales sobre superficies
Capítulo 5. Integrales sobre curvas y superficies 5.1. Integrales de funciones escalares sobre curvas 5.2. Integrales de campos vectoriales sobre curvas 5.3. Teorema de Green 5.4. Integrales sobre superficies
Integración múltiple: integrales triples
 Problemas propuestos con solución Integración múltiple: integrales triples ISABEL MARRERO epartamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Integrales iteradas 1. Teorema
Problemas propuestos con solución Integración múltiple: integrales triples ISABEL MARRERO epartamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Integrales iteradas 1. Teorema
Cambio de variables en la integral múltiple.
 Cambio de variables en la integral múltiple. En este apartado vamos a generalizar la fórmula g(b) g(a) f(x) dx = b a f(g(t)) g (t) dt al caso de funciones de n variables. Como la región de integración
Cambio de variables en la integral múltiple. En este apartado vamos a generalizar la fórmula g(b) g(a) f(x) dx = b a f(g(t)) g (t) dt al caso de funciones de n variables. Como la región de integración
ANÁLISIS MATEMÁTICO II - Grupo Ciencias 2018 Práctica 9 Campos conservativos - Teorema de Green
 ANÁLISIS MATEMÁTIO II - Grupo iencias 018 Práctica 9 ampos conservativos - Teorema de Green A. ampos conservativos 1. Mostrar que F x, y) = y cos x) i + x sen y) j no es un campo vectorial gradiente..
ANÁLISIS MATEMÁTIO II - Grupo iencias 018 Práctica 9 ampos conservativos - Teorema de Green A. ampos conservativos 1. Mostrar que F x, y) = y cos x) i + x sen y) j no es un campo vectorial gradiente..
Teorema 1 (Cambio de Variable en R n ).
 Vamos a estudiar en este segundo capítulo sobre los cambios de variable para funciones de varias variables, algunos de los más habituales: los cambios de coordenadas a coordenadas polares en el plano,
Vamos a estudiar en este segundo capítulo sobre los cambios de variable para funciones de varias variables, algunos de los más habituales: los cambios de coordenadas a coordenadas polares en el plano,
A) Hallar el volumen del sólido formado cuando la región del primer cuadrante limitada por Z 4. 1 x 4 1 dx. Z b. p (x) h (x) dx.
 ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA I.T.I. Especialidad en Electricidad. Curso 4-5. Soluciones al Segundo Parcial de Fundamentos Matemáticos de la Ingeniería. PROBLEMA.- A) Hallar el volumen del
ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA I.T.I. Especialidad en Electricidad. Curso 4-5. Soluciones al Segundo Parcial de Fundamentos Matemáticos de la Ingeniería. PROBLEMA.- A) Hallar el volumen del
1. Teorema de Fubini. Teorema de Fubini.
 1. El teorema de Fubini nos va a dar una técnica para el cálculo de integrales de funciones de varias variables mediante el cálculo de varias integrales de funciones de una variable. partir de ahí se podrán
1. El teorema de Fubini nos va a dar una técnica para el cálculo de integrales de funciones de varias variables mediante el cálculo de varias integrales de funciones de una variable. partir de ahí se podrán
INTEGRACION EN VARIAS VARIABLES: Integrales dobles. 1. e x+y dy dx. 3. Evaluar las siguientes integrales en los recintos que se indican:
 INTEGACION EN VAIAS VAIABLES: Integrales dobles.. Evaluar las siguientes integrales iteradas: (x y + y )dy dx xye x+y dy dx ( x ln y)dy dx ln [((x + )(y + )] dx dy. 3 ; ; ; ln. 5. Sea I = [, ] [, 3]. Calcular
INTEGACION EN VAIAS VAIABLES: Integrales dobles.. Evaluar las siguientes integrales iteradas: (x y + y )dy dx xye x+y dy dx ( x ln y)dy dx ln [((x + )(y + )] dx dy. 3 ; ; ; ln. 5. Sea I = [, ] [, 3]. Calcular
Primera parte: Ejercicios de Integrales Múltiples Integración de Funciones de Varias Variables, grupo A, curso 15/16 Francisco José Freniche Ibáñez
 Primera parte: Ejercicios de Integrales Múltiples Integración de Funciones de Varias Variables, grupo, curso 5/6 Francisco José Freniche Ibáñez. Demuestra que si I R es un intervalo y f : I R es una función
Primera parte: Ejercicios de Integrales Múltiples Integración de Funciones de Varias Variables, grupo, curso 5/6 Francisco José Freniche Ibáñez. Demuestra que si I R es un intervalo y f : I R es una función
Integración múltiple
 Integración múltiple IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Integrales múltiples 1 3. Caso particular: la integral triple
Integración múltiple IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Integrales múltiples 1 3. Caso particular: la integral triple
Matemáticas III Tema 5 Integrales de línea
 Matemáticas III Tema 5 Integrales de línea Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino órdoba, S. 14. OW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia reative ommons ttribution- Nonomercial-Sharelike
Matemáticas III Tema 5 Integrales de línea Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino órdoba, S. 14. OW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia reative ommons ttribution- Nonomercial-Sharelike
Cálculo Integral (1º de los Grados en Matemáticas y en Física, Universidad de Cantabria) Examen final, 12 de junio de Soluciones.
 Examen final, 1 de junio de 17 Soluciones Cuestiones C 1 ) En este caso la condición es necesaria y suciente. Que es necesaria se demuestra en el apartado 3 4 del teorema 1.33. Que es suciente se sigue
Examen final, 1 de junio de 17 Soluciones Cuestiones C 1 ) En este caso la condición es necesaria y suciente. Que es necesaria se demuestra en el apartado 3 4 del teorema 1.33. Que es suciente se sigue
Integral Doble e Integral Triple
 www.cidse.itcr.ac.cr/revistamate Práctica 6 Integral Doble e Integral Triple Cambio de variable con coordenadas polares y coordenadas ciĺındricas. Cálculo Superior Instituto Tecnológico de Costa ica Escuela
www.cidse.itcr.ac.cr/revistamate Práctica 6 Integral Doble e Integral Triple Cambio de variable con coordenadas polares y coordenadas ciĺındricas. Cálculo Superior Instituto Tecnológico de Costa ica Escuela
9. Diferenciación de funciones reales de varias variables reales Diferenciación DERIVADAS PARCIALES
 9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
Vector Tangente y Vector Normal
 Vector Tangente y Vector Normal enición. ada una supercie S = f) descrita por la función f : R 2 R 3 fu, v) = xu, v), yu, v), zu, v)) de clase c con u, v) y dado un punto u, v ) denimos los vectores f
Vector Tangente y Vector Normal enición. ada una supercie S = f) descrita por la función f : R 2 R 3 fu, v) = xu, v), yu, v), zu, v)) de clase c con u, v) y dado un punto u, v ) denimos los vectores f
MA2112 Departamento de Matemáticas. f.ds = γ. ABC, con A(1, 0, 2), B(1, 3, 0), C(0, 1, -1) y f = (P, Q, R) = ( z, x+y, x).
 VRANO D 24 UNIVRSIDAD SIMON BOLIVAR P2A.- un segundo examen parcial de alguna fecha anterior. 1.- Calcule la integral : γ f.ds = γ Pdx+Qdy+Rdz, siendo γ la poligonal ABC, con A(1,, 2), B(1, 3, ), C(, 1,
VRANO D 24 UNIVRSIDAD SIMON BOLIVAR P2A.- un segundo examen parcial de alguna fecha anterior. 1.- Calcule la integral : γ f.ds = γ Pdx+Qdy+Rdz, siendo γ la poligonal ABC, con A(1,, 2), B(1, 3, ), C(, 1,
a n en las que n=1 s n = n + 1 Solución: a) Utilizando el criterios de D Alembert se obtiene que a n+1 n a n 3 > 1 n=1
 EJERCICIO DE FUNDAMENTO MATEMÁTICO eries. Estudia el carácter de las series (a El término general es a n en las que (b la suma parcial n-sima es a n n n+ 3 n, n,, 3,... s n n, n,, 3,... n + olución: a
EJERCICIO DE FUNDAMENTO MATEMÁTICO eries. Estudia el carácter de las series (a El término general es a n en las que (b la suma parcial n-sima es a n n n+ 3 n, n,, 3,... s n n, n,, 3,... n + olución: a
PEP 3. Responda 4 de los siguientes 9 problemas, escogiendo al menos uno de cada sección.
 Universidad de Santiago de Chile Cálculo odrigo Vargas do semestre 1 PEP Nombre: Nota: esponda de los siguientes 9 problemas, escogiendo al menos uno de cada sección. Sección 1. 1. Use coordenadas esféricas
Universidad de Santiago de Chile Cálculo odrigo Vargas do semestre 1 PEP Nombre: Nota: esponda de los siguientes 9 problemas, escogiendo al menos uno de cada sección. Sección 1. 1. Use coordenadas esféricas
Diferenciación SEGUNDA PARTE
 ANÁLISIS I MATEMÁTICA 1 ANÁLISIS II (Computación) Práctica 4 - Primer Cuatrimestre 009 Diferenciación SEGUNDA PARTE Regla de la Cadena 1 Sean f(u, v, w) = u + v 3 + wu y g(x, y) = x sen(y) Además, tenemos
ANÁLISIS I MATEMÁTICA 1 ANÁLISIS II (Computación) Práctica 4 - Primer Cuatrimestre 009 Diferenciación SEGUNDA PARTE Regla de la Cadena 1 Sean f(u, v, w) = u + v 3 + wu y g(x, y) = x sen(y) Además, tenemos
La puntuación depende del modo de resolución.
 Grupo B 16/17 Ampliación de Cálculo En todos los casos, se pide contestar razonadamente La puntuación depende del modo de resolución Ejercicio 1 (15 puntos por apartado) Una semiesfera sólida de densidad
Grupo B 16/17 Ampliación de Cálculo En todos los casos, se pide contestar razonadamente La puntuación depende del modo de resolución Ejercicio 1 (15 puntos por apartado) Una semiesfera sólida de densidad
1. Sea f una función definida en I = [1, 2] [1, 4] del siguiente modo: (x + y) 2, x y 2x, 0, en el resto.
![1. Sea f una función definida en I = [1, 2] [1, 4] del siguiente modo: (x + y) 2, x y 2x, 0, en el resto. 1. Sea f una función definida en I = [1, 2] [1, 4] del siguiente modo: (x + y) 2, x y 2x, 0, en el resto.](/thumbs/40/20516327.jpg) La integral múltiple Problemas resueltos. Sea f una función definida en I [, ] [, 4] del siguiente modo: { (x + y), x y x, f(x, y), en el resto. Indique, mediante un dibujo, la porción A del rectángulo
La integral múltiple Problemas resueltos. Sea f una función definida en I [, ] [, 4] del siguiente modo: { (x + y), x y x, f(x, y), en el resto. Indique, mediante un dibujo, la porción A del rectángulo
Funciones reales de varias variables
 PROBLEMAS DE CÁLCULO II Curso 2-22 2 Funciones reales de varias variables. Dibuja las curvas de niveles,,..., 5 y la representación gráfica de las siguientes funciones a) f(x, y) = 5 x y b) f(x, y) = x
PROBLEMAS DE CÁLCULO II Curso 2-22 2 Funciones reales de varias variables. Dibuja las curvas de niveles,,..., 5 y la representación gráfica de las siguientes funciones a) f(x, y) = 5 x y b) f(x, y) = x
Soluciones de los ejercicios del segundo examen parcial
 Matemáticas III GIC, curso 5 6 Soluciones de los ejercicios del segundo examen parcial EJERCICIO. Considera la integral doble π π ibuja la región del plano XY en la que se está integrando. Usa el teorema
Matemáticas III GIC, curso 5 6 Soluciones de los ejercicios del segundo examen parcial EJERCICIO. Considera la integral doble π π ibuja la región del plano XY en la que se está integrando. Usa el teorema
Universidad Técnica Federico Santamaría
 Integral de uperficie - Mate 4 UPEFICIE PAAMÉTICA e forma similar a como se describe una curva mediante una función vectorial r(t), en función de un parámetro t,se puede describir una superficie mediante
Integral de uperficie - Mate 4 UPEFICIE PAAMÉTICA e forma similar a como se describe una curva mediante una función vectorial r(t), en función de un parámetro t,se puede describir una superficie mediante
Integral de superficie.
 Tema 4 Integral de superficie. 4.1 uperficies. Definición 4.1 ean IR 2 un conjunto conexo y κ: IR 3 una función continua. La imagen = κ se llama superficie descrita por κ. También se dice que κ es una
Tema 4 Integral de superficie. 4.1 uperficies. Definición 4.1 ean IR 2 un conjunto conexo y κ: IR 3 una función continua. La imagen = κ se llama superficie descrita por κ. También se dice que κ es una
 Geraldine Cisneros 53 Integrales Múltiples y Sus Aplicaciones 2. INTEGRALES TRIPLES En esta sección se presenta la integral triple para funciones de tres variables, funciones del tipo f:b 3, tal como se
Geraldine Cisneros 53 Integrales Múltiples y Sus Aplicaciones 2. INTEGRALES TRIPLES En esta sección se presenta la integral triple para funciones de tres variables, funciones del tipo f:b 3, tal como se
+ ax 2 + bx) x. ( 2 sen(x) 0 (a + b sen(x) sen(2x))2 dx sea mínima.
 Facultad de Ingeniería - IMERL Cálculo - Curso. Práctico 8. Integrales paramétricas e integrales iteradas dobles y triples. Integrales múltiples. Cambio de variables, áreas, volúmenes, sumas de Riemann
Facultad de Ingeniería - IMERL Cálculo - Curso. Práctico 8. Integrales paramétricas e integrales iteradas dobles y triples. Integrales múltiples. Cambio de variables, áreas, volúmenes, sumas de Riemann
GUIA DE ESTUDIO PARA EL TEMA 2: INTEGRALES DE SUPERFICIE. 2) Para cada una de las superficies dadas determine un vector normal y la ecuación del
 GUIA DE ESTUDIO PARA EL TEMA 2: INTEGRALES DE SUPERFICIE PLANO TANGENTE Y VECTOR NORMAL. AREA DE UNA SUPERFICIE 1) En cada uno de los siguientes ejercicios se presenta una S dada en forma paramétrica,
GUIA DE ESTUDIO PARA EL TEMA 2: INTEGRALES DE SUPERFICIE PLANO TANGENTE Y VECTOR NORMAL. AREA DE UNA SUPERFICIE 1) En cada uno de los siguientes ejercicios se presenta una S dada en forma paramétrica,
Pauta Auxiliar N 10 Aplicaciones de la Integral I Viernes 1 de Junio de 2012
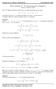 Pauta Auxiliar N Aplicaciones de la Integral I Viernes de Junio de P.- (P Examen Adicional - ) Sea A la región delimitada por las rectas y = x, y = ax, y = ax, a a) Calcule el área de A y el volumen del
Pauta Auxiliar N Aplicaciones de la Integral I Viernes de Junio de P.- (P Examen Adicional - ) Sea A la región delimitada por las rectas y = x, y = ax, y = ax, a a) Calcule el área de A y el volumen del
Práctica 7. sen 2 x cos x dx. c) 3x 2 x 2 dx. f) 3. Hallar el área encerrada por las curvas:
 ANÁLISIS I MATEMÁTICA ANÁLISIS (Computación) Práctica 7 I. epaso: integración en una variable. Calcular: sen x. b) π sen x. c) El área entre las curvas y = sen x, y =, x =, x = π.. Calcular: x sen x. b)
ANÁLISIS I MATEMÁTICA ANÁLISIS (Computación) Práctica 7 I. epaso: integración en una variable. Calcular: sen x. b) π sen x. c) El área entre las curvas y = sen x, y =, x =, x = π.. Calcular: x sen x. b)
MATEMÁTICAS 2. Curso 2016/17. Integración en varias variables.
 MATEMÁTICA 2. Curso 2016/17. Integración en varias variables. 1. Calcular para = [0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcular las integrales dobles siguientes
MATEMÁTICA 2. Curso 2016/17. Integración en varias variables. 1. Calcular para = [0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcular las integrales dobles siguientes
AMPLIACIÓN DE MATEMÁTICAS. Curso 2015/16. Integración en varias variables.
 AMPLIACIÓN DE MATEMÁTICA. Curso 2015/16. Integración en varias variables. 1. Calcular para = [0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcular las integrales dobles
AMPLIACIÓN DE MATEMÁTICA. Curso 2015/16. Integración en varias variables. 1. Calcular para = [0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcular las integrales dobles
Capítulo 4. Integración
 Capítulo 4. Integración En este capítulo vamos a estudiar cómo se puede hacer integración con funciones multivariables. Estudiaremos los siguientes temas: 4.1. Integral de Riemann, teorema de Fubini. 4..
Capítulo 4. Integración En este capítulo vamos a estudiar cómo se puede hacer integración con funciones multivariables. Estudiaremos los siguientes temas: 4.1. Integral de Riemann, teorema de Fubini. 4..
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen del 14 de Septiembre de 2000 Primera parte
 ÁLULO Primer curso de Ingeniero de Telecomunicación Examen del de Septiembre de Primera parte Ejercicio. Un flan tiene forma de tronco de paraboloide de revolución, siendo r y r losradiosdesusbasesyh su
ÁLULO Primer curso de Ingeniero de Telecomunicación Examen del de Septiembre de Primera parte Ejercicio. Un flan tiene forma de tronco de paraboloide de revolución, siendo r y r losradiosdesusbasesyh su
AMPLIACIÓN DE MATEMÁTICAS
 AMPLIACIÓN DE MATEMÁTICAS Examen de febrero EJECICIO ( h. 3 min.) 13 de junio de 9 1. En E 3 se considera el plano de ecuación x y z = 5. Se pide: a) Ecuaciones de la proyección ortogonal sobre dicho plano.
AMPLIACIÓN DE MATEMÁTICAS Examen de febrero EJECICIO ( h. 3 min.) 13 de junio de 9 1. En E 3 se considera el plano de ecuación x y z = 5. Se pide: a) Ecuaciones de la proyección ortogonal sobre dicho plano.
Análisis Matemático 2
 Análisis Matemático Resolución del coloquio de fecha 4/07/18 tema I con hipervínculos a videos on-line Autor: Martín Maulhardt Revisión: Fernando Acero y Ricardo Sirne Análisis Matemático II y II A Facultad
Análisis Matemático Resolución del coloquio de fecha 4/07/18 tema I con hipervínculos a videos on-line Autor: Martín Maulhardt Revisión: Fernando Acero y Ricardo Sirne Análisis Matemático II y II A Facultad
( ) x y dxdy. x y dxdy y. sin 2θ 2 = = = x y dxdy. 3 4y y ln. 1
 Cálculo II Exámenes esueltos Tercer Parcial. Evaluar la integral, pasando a coordenadas polares: Solución: haciendo los siguientes cambios, ( ) 4y 4y 4y x y y 4y 4y 4 4 4y x y sin θ x y = r ( sinθcosθ
Cálculo II Exámenes esueltos Tercer Parcial. Evaluar la integral, pasando a coordenadas polares: Solución: haciendo los siguientes cambios, ( ) 4y 4y 4y x y y 4y 4y 4 4 4y x y sin θ x y = r ( sinθcosθ
MATE1207 Cálculo Vectorial Tarea 2 Individual Entregue a su profesor en la Semana 11 (Ma Vi. 21 de Octubre)
 Universidad de los Andes Departamento de Matemáticas MAT27 Cálculo Vectorial Tarea 2 Individual ntregue a su profesor en la Semana (Ma. 8 - Vi. 2 de Octubre) Segundo xamen Parcial: Sábado 29 de Octubre,
Universidad de los Andes Departamento de Matemáticas MAT27 Cálculo Vectorial Tarea 2 Individual ntregue a su profesor en la Semana (Ma. 8 - Vi. 2 de Octubre) Segundo xamen Parcial: Sábado 29 de Octubre,
El Teorema de Fubini-Tonelli
 Capítulo 26 El Teorema de Fubini-Tonelli Veremos en este capítulo que el cálculo de una integral múltiple se reduce al de integrales simples. Concretamente se va a probar que si f(x, y) es una función
Capítulo 26 El Teorema de Fubini-Tonelli Veremos en este capítulo que el cálculo de una integral múltiple se reduce al de integrales simples. Concretamente se va a probar que si f(x, y) es una función
SERIE # 4 CÁLCULO VECTORIAL
 SERIE # 4 CÁLCULO VECTORIAL Página 1 1) Calcular 1 x y dy dx. 0 0 1 ) Evaluar la integral doble circunferencia x y 9. x 9 x da R, donde R es la región circular limitada por la 648 15 x y ) Calcular el
SERIE # 4 CÁLCULO VECTORIAL Página 1 1) Calcular 1 x y dy dx. 0 0 1 ) Evaluar la integral doble circunferencia x y 9. x 9 x da R, donde R es la región circular limitada por la 648 15 x y ) Calcular el
Cálculo III (0253) TEMA 3 INTEGRALES DOBLES Y TRIPLES Y SUS APLICACIONES. Semestre
 Cálculo III (05) Semestre -009 TEMA INTEGRALES DOBLES Y TRIPLES Y SUS APLICACIONES Semestre -009 Octubre 009 U.C.V. F.I.U.C.V. CÁLCULO III (05) - TEMA Las notas presentadas a continuación tienen como único
Cálculo III (05) Semestre -009 TEMA INTEGRALES DOBLES Y TRIPLES Y SUS APLICACIONES Semestre -009 Octubre 009 U.C.V. F.I.U.C.V. CÁLCULO III (05) - TEMA Las notas presentadas a continuación tienen como único
SERIE SUPERFICIES. 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones:
 SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
ANÁLISIS MATEMÁTICO II - Grupo Ciencias 2018 Comentarios y ejemplos - Práctica 10
 ANÁLII MATEMÁTICO II - Grupo Ciencias 218 Comentarios y ejemplos - Práctica 1 A. Parametrizaciones de superficies El concepto de parametrización de una superficie es análogo al de parametrización de una
ANÁLII MATEMÁTICO II - Grupo Ciencias 218 Comentarios y ejemplos - Práctica 1 A. Parametrizaciones de superficies El concepto de parametrización de una superficie es análogo al de parametrización de una
Plano Tangente y Vector Normal
 Plano Tangente y Vector Normal enición 1. ada una supercie S = φ) descrita por la función φ : R 2 R 3 φu, v) = xu, v), yu, v), zu, v)) de clase c 1 con u, v) y dado un punto u, v ) denimos los vectores
Plano Tangente y Vector Normal enición 1. ada una supercie S = φ) descrita por la función φ : R 2 R 3 φu, v) = xu, v), yu, v), zu, v)) de clase c 1 con u, v) y dado un punto u, v ) denimos los vectores
Tema 1 (Resultados).- Cónicas y Cuádricas.
 Ingenierías: Aeroespacial, Civil y Química Matemáticas I 010-011 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 1 (Resultados)- Cónicas y Cuádricas Ejercicio
Ingenierías: Aeroespacial, Civil y Química Matemáticas I 010-011 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 1 (Resultados)- Cónicas y Cuádricas Ejercicio
Clase 13 de febrero. Ejercicios propuestos números 1, 2 (página 19)
 Este documento contiene las actividades no presenciales propuestas al terminar la clase del día que se indica. Se sobreentiende que también se debe realizar el estudio de lo explicado en clase aunque no
Este documento contiene las actividades no presenciales propuestas al terminar la clase del día que se indica. Se sobreentiende que también se debe realizar el estudio de lo explicado en clase aunque no
Parametrización de superficies Integrales de superficie. h"p://www.sc.ehu.es/sqwpolim/metodos_matema6cos/
 Parametrización de superficies Integrales de superficie h"p://www.sc.ehu.es/sqwpolim/metodos_matema6cos/ Parametrización de una superficie en R 3 ea un dominio del espacio R 2, donde los puntos están definidos
Parametrización de superficies Integrales de superficie h"p://www.sc.ehu.es/sqwpolim/metodos_matema6cos/ Parametrización de una superficie en R 3 ea un dominio del espacio R 2, donde los puntos están definidos
En esta sección se presenta la integral triple para funciones de tres variables, funciones del tipo
 5. INTEGRALES TRIPLES En esta sección se presenta la integral triple para funciones de tres variables, funciones del tipo f:, tal como se hizo en la sección anterior para las integrales dobles. Así como
5. INTEGRALES TRIPLES En esta sección se presenta la integral triple para funciones de tres variables, funciones del tipo f:, tal como se hizo en la sección anterior para las integrales dobles. Así como
Integral definida. dx es diferencial de x, e indica cuál es la variable de la función que se integra.
 Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
5.2. El teorema de Fubini. TEMA 5. INTEGRALES DE FUNCIONES DE DOS VARIABLES.
 Tema 5 Integrales de funciones de dos variables. 5.. La integral doble como volumen. La integral de una función de dos variables está relacionada con zf H,L el cálculo del volumen encerrado entre el plano
Tema 5 Integrales de funciones de dos variables. 5.. La integral doble como volumen. La integral de una función de dos variables está relacionada con zf H,L el cálculo del volumen encerrado entre el plano
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS.
 UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS. Cálculo III, Examen Final. Semestre Primavera 1 Tiempo: 11 min. Problema 1 [1,5 puntos] La curvatura de una trayectoria
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS. Cálculo III, Examen Final. Semestre Primavera 1 Tiempo: 11 min. Problema 1 [1,5 puntos] La curvatura de una trayectoria
GUÍA DE EJERCICIOS - INTEGRALES MÚLTIPLES
 GUÍA DE EJERIIOS - INTEGRALES MÚLTIPLES 1. Escriba la expresión que permite calcular por integrales dobles: a. El área de una región plana R. b. El volumen de un sólido V, de altura z = f(x,y). c. La masa
GUÍA DE EJERIIOS - INTEGRALES MÚLTIPLES 1. Escriba la expresión que permite calcular por integrales dobles: a. El área de una región plana R. b. El volumen de un sólido V, de altura z = f(x,y). c. La masa
ANALISIS MATEMATICO II (Ciencias- 2011) Trabajo Práctico 8
 ANALISIS MATEMATIO II (iencias- 2011) Integrales sobre curvas (o de línea) Trabajo Práctico 8 1. Evaluar las siguientes integrales curvilíneas γ f ds. (a) f(x, y, z) = x + y + z ; r(t) = (sen t, cos t,
ANALISIS MATEMATIO II (iencias- 2011) Integrales sobre curvas (o de línea) Trabajo Práctico 8 1. Evaluar las siguientes integrales curvilíneas γ f ds. (a) f(x, y, z) = x + y + z ; r(t) = (sen t, cos t,
Integración en una variable (repaso)
 Análisis I Matemática I Análisis II (C) Primer Cuatrimestre - 28 Práctica 8: Integración Integración en una variable (repaso). Calcular: xsen x. sen 2 x cos x. xe x2. e x sen x. 3x 2 x 2 + x 2. ln x. 2.
Análisis I Matemática I Análisis II (C) Primer Cuatrimestre - 28 Práctica 8: Integración Integración en una variable (repaso). Calcular: xsen x. sen 2 x cos x. xe x2. e x sen x. 3x 2 x 2 + x 2. ln x. 2.
