CAPITULO II FUNCIONES VECTORIALES

Transcripción

1 CAPITULO II FUNCIONES VECTORIALES En el cpíulo nerior, cundo describimos l rec en el espcio, uilizmos un prámero en ls ecuciones pr enconrr ls coordends de los punos que conformn es rec. ecuciones prmérics b de l rec z z c cd coordend depende de el vlor que le demos l prámero, en ors plbrs, cd un esá en función de. f ), g ), z h ) Qué ps si cd puno de l rec le signmos un vecor de posición r i j z Tendrímos un vecor pr cd vlor de, o se que r es, su vez, un función de. r i j z r ) f ) i g ) j h ) r ) ) i b) j z c) Por ejemplo, pr l rec con ecuciones prmérics, l posición de cd z uno de sus punos es dd por r ) ) i ) j ), si bulmos dádole vlores pr enconrr lgunos vecores enemos r ) puno - i j 4 A,, 4 - i 4 j B,4, ij C,, i j D,, i j 8 E,,8 z Rec E D - C B A l rec dd por r ) ) i ) j ) 89

2 FUNCIÓN VECTORIAL Culquier función de l form r ) f ) i g ) j h ) f ), g ), h ) se conoce como función vecoril, con f, g h como funciones reles del prámero. se conocen como ls funciones componenes de r) ) En el plno, l función vecoril es r ) f ) i g ) j f ), g ). En el ejemplo nerior, no f como g h son funciones lineles de por éso l grfic de res ) un rec. Podemos usr un función vecoril pr rzr un curv demás describir su recori cómo se dibuj cundo crece). En oro ejemplo. Se l función vecoril. r) i j Si f ), g ) enonces, por lo no. Que es l ecución de un prábol en el plno. r-) r) Algunos de los vecores: r ) i 4 j, r ) i j, r), r) i j, r) i 4 j. L curv represend por : r) i j Cómo serí l curv r) i j? Enconremos lgunos vecores: r ) i 4 j, r ) i j, r), r) i j, r) i 4 j. Ps por los mismos punos que l curv de r-) r) l función nerior Qué cmbió? Cmbi el senido del rzo, hor es de derech izquierd conforme crece. r) i j Pr l curv definid por l función r ) cos,sen con donde ) cos. ) sen. Sumemos los cudrdos de cd función r 7 r 6 r r 4 r r r componene de r: ) cos sen. L gráfic es de un círculo de rdio cenrdo en el origen. - r 8 círculo unirio r)=<cos, sen > r r r cos,sen,, r r, 6 r r, 4, r r,, r4 r, r r,, r6 r,

3 r ) cos,sen, es l función de un curv en el espcio. Clculemos lgunos de sus punos pr. en incremenos de rd) cos sen z Cundo crece de, l curv describe un hélice hciendo dos espirles lrededor de un cilindro elípico, l ecución del cilindro l podemos obener omndo ls primers dos funciones componenes de r : cos e sen, de donde 9 cos sen ó 9 Dominio de un función vecoril El dominio de un función vecoril es l inersección de los dominios de sus funciones componenes. Por ejemplo, el dominio de r ) i 4 j son los vlores reles que se encuenrn en el inervlo,, ecepo cundo. El domino de l función r ) ln ) i j 4 es l inersección de los 4 dominios de f ) ln ), g ) D r 4 D D f g h ) 4 donde, ) D, - - /4 D h Df, g D / 4,, o se que D / 4,,. h r 9

4 Operciones con funciones vecoriles Sen r ) f ) i g ) j h ) k r ) f ) i g ) j h ) k funciones vecoriles un esclr: r ) r ) f ) f ) i g ) g ) j h ) h ) Sum: Diferenci: ) ) ) ) ) ) ) ) Múliplo esclr: r ) f ) i g ) j h ) r r f f i g g j h h Produco esclr: r ) r ) f ) f ) g ) g ) h ) h ) Produco vecoril: r ) r ) g ) h ) g ) h ) i f ) h ) f ) h ) j f ) g ) f ) g ) k Límies Coninuidd El límie de un función vecoril r ) f ) i g ) j h ) cundo eise solo sí eisen los limies en f, g h cundo. lim r ) lim f ) i lim g ) j lim h ) k Un función vecoril r ) es coninu en el puno donde siempre cundo el lim ) r punos del inervlo. eis. r ) es coninu en el inervlo I si r ) es coninu en cd uno de los Ejemplo: Deerminr el inervlo o inervlos) en que l funciön vecoril r ) ln ) i j 4 es coninu. 4 Solución: D / 4,,, es decir que puede omr vlores mores o El dominio de es r igules ¼ ecepo el. Probemos los límies con = ¼, = =: lim r ) lim ln ) i lim j lim 4 k ln i j /4 /4 /4 4 /4 4 6.i.7 j si eise el límie lim r ) lim ln ) i lim j lim 4 ln i j 7 4 no eise el límie 4 lim r ) lim ln ) i lim j lim 4 ln 4i j 4.86i.8 j.7 si eise el límie L función es coninu en odo el dominio de r, o se que es coninu en el inervlo / 4 en el inervlo. 9

5 Derivción de funciones vecoriles Pr derivr un función vecoril bs con derivr cd un de sus funciones componenes. Definición: l derivd de un función vecoril r se difine como r ) r ) r ) lim, siempre que el límie eis. Pr r ) f ) i g ) j h ) con f,g h funciones derivbles de, enonces ) ) f ) i g ) j h ) k f ) i g ) j h ) k r r r ) lim lim f ) f ) g ) g ) h ) h ) lim i lim j lim k f ) i g ) j h ) d dr r ) D r D r ) r ) d d Ors forms de noción pr l derivd: Ejemplo: sen ls funciones derivds. r ) i j s ) cos ) i sen ) j e k, hllr sus Solución: derivmos cd funcion componene ) 6 r i j s ) sen ) i cos ) j e k Propieddes de l derivd de funciones vecoriles Sen r s funciones vecoriles de, f un función derivble de un esclr. D r ) r ) derivd de un múliplo esclr D r ) s ) r ) s ) derivd de un sum/res D f ) r ) f ) r ) f ) r ) derivd de un produco D r ) s ) r ) s ) r ) s ) derivd del produco esclr D r ) s ) r ) s ) r ) s ) derivd del produco vecoril D r f )) r f )) f ) regl de l cden 7. si r ) f ) i g ) j h ) 8. enonces r ) f ) g ) h ) r ) r ) D r) derivd de l norm de r r ) 9. Si r ) r ) consne enonces r ) r ). Ejemplos: 9

6 Sen ls funciones vecoriles. r ) b. s ) c. D r ) s ) d. D ) r ) D r ) s ) e. f. D r ) s ) g. r ) r ) i j k s ) i j k, hllr: Solución:. r ) i j b. s ) i j k c. D ) ) ) ) 4 r s r s i j k d. D ) r ) ) r ) r ) )i j k) i j k 4 6 i j e. D ) ) r s i j k i j k i j k i j k 4 6 i j i j k f. D r ) s ) r ) s ) r ) s ) i j k i 6 j k i j 4 g. 6 r ) i j

7 Inegrción de funciones vecoriles Al igul que en el cso de l derivción, pr inegrr un función vecoril solo es necesrio inegrr cd un de sus funciones componenes. Definición: se r ) f ) i g ) j h ) un funcion vecoril con f, g h coninus en el inervlo cerrdo [,b], l inegrl indefinid de r ) es r ) d f ) d i g ) d j h ) d mienrs que l inegrl definid en el inervlo cerrdo [,b] de r ) es r ) d f ) d i g ) d j h ) d b b b b Cundo inegrmos r ) en un inegrl indefinid obenemos un consne de inegrción C, que es un vecor consne nos sirve pr diferencir un fmili de funciones vecoriles R) C ls primiivs de r) ) l que R ) r ) ó r ) d R ) C. r ) d f ) d i g ) d j h ) d ) ) ) k F C i G C j H C k F ) i G ) j H ) C i C j C R ) C Ejemplo: inegrr l función vecoril r ) i j Solución: r ) d ) d i d j d r ) d C i C j C i j C Ejemplo: inegrr l función vecoril r ) i 4j pr Solución: r ) d d i 4 d j d 4 r ) d i j 9 6 k i j k 4 4 Si conocemos l condición inicil de l función vecoril r ) podemos islr un de ls primiivs de l fmili de funciones que consiuen l inegrl definid de R ) r ) l que r ) R ) d 9

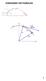
8 Ejemplo: hllr l primiiv de que r) i j R ) i 6 j sbiendo que R ) r ) 4 Solución: r ) R ) d d 6 d d i j C Si cundo, r) i j k C i j enonces C i j, por lo 4 no 4 r ) i j k C i j primiiv de r ) que cumple con l condición inicil. DESPLAZAMIENTO, VELOCIDAD Y ACELERACIÓN es l Consideremos que l función vecoril r ) indic l posición de un cuerpo que se mueve lo lrgo de un curv en el plno o el espcio en un iempo. Es posición l relcionmos con un puno, en el plno ó,, z en el espcio donde ls coordends,, z dependen, su vez, del iempo, l que ), ) z z) de mner que l posición del cuerpo es dd por l función r ) ) i ) j en el plno r ) ) i ) j z ) en el espcio Como sbemos, l velocidd promedio es l rzón de cmbio de posición del cuerpo en un inervlo de iempo. Se r el cmbio de posición el inervlo de mner que r r r r) de r ) es r ) lim l función posición r) P r r ) r ) r ) Velocidd promedio vm Vecor velocidd Conforme hcemos que el inervlo de se más coro, l velocidd promedio se Q irá cercndo l vlor que iene l velocidd en el insne velocidd insnne). r+) r ) r ) Vecor velocidd: v ) lim, si eise el límie. De l sección nerior vimos que l derivd ) ), por lo no l velocidd es igul l derivd de r v ) r ) ) i ) j en el plno v ) r ) ) i ) j z ) en el espcio 96

9 En l figur podemos nor que el vecor velocidd es ngene l curv ren ) el puno P. L mgniud de v represen l rpidez con l que se mueve el objeo en el iempo en el que esá en l posición P. L velocidd es un vecor mienrs que l rpidez es un esclr. De mner nálog que como lo hicimos con l velocidd, l celerción es l rzón de cmbio de ls velociddes con respeco del iempo rnscurrido. Se v el cmbio de velocidd en el inervlo l que v v v), l celerción en el puno P esá dd por v ) v ) ) lim v ). Definición de velocidd, celerción rpidez Sen, z funciónes derivbles de r ) ) i ) j l función posición en el plno ó r ) ) i ) j z ) en el espcio, definimos ls funciones velocidd celerción v ) r ) ) i ) j plno) v ) r ) ) i ) j z ) espcio) ) v ) r ) ) i ) j plno) ) v ) r ) ) i ) j z ) espcio) rpidez v ) r ) ) ) plno) v ) r ) ) ) + z ) espcio) cíd libre de un puerco Ejemplo: Un prícul se mueve siguiendo un recori mrcd por l función r ) i j k. Hllr velocidd, celerción rpidez pr,,, Solución: Velocidd: Acelerción: v ) r ) i j k ) v ) r ) j Rpidez: 4 v ) 4 v ) ) v ) - i j j 8.86 i j.6 i j j 8.86 i j 6 j.9 97

10 Ejemplo: Un prícul se mueve siguiendo un recori mrcd por l función r ) cos i sen j pr Trecori Hllr velocidd, celerción rpidez pr,,,,,, Solución: v ) ) v ) 6 j i 6 /6 i j 6 i 6 j 6 /4 6i j 6 / i j 6 i 6 j 6 / 6 j i 6 / 4 6i j 6 6 j i 6 Velocidd: v ) r ) 6sen i 6cos j Acelerción: ) ) cos sen Rpidez: v ) 6 sen cos 6 v i j Vecores posición velocidd. Ejemplo: Dibuje l recori de un prícul se mueve lo lrgo de un curv pln r ) i 4 j rce los vecores velocidd celerción con función pr pr,.,, 4. Solución: derivmos pr obener ls funciones velocidd celerción v ) r ) i 4 j ) v ) r ) j, evlumos: r ) v ) ) - i j i 6j j. i 4.7 j i j j i 7 j i j i 6j i j j - -) v-) v/) r-) v/4) v.) r.) v/) 8 4 v/6) r/) r/) r) r/4) r/) r4) - - r) v) v) r/6) r) r) v) v/) v4) Trecori r) 4 i j i 4j j Vecores posición, velocidd clerción -4 Noese que l celerción es consne hci bjo, de mner que, conforme l prícul se mueve hci el vérice de l prábol, l velocidd v decreciendo en mgniud crece de nuevo conforme se lej del vérice. 98

11 En el ejemplo nerior, podemos deducir l fórmul de l prábol que describe el movimieno usndo ls ecuciones prmérics ), ) 4 despejndo de l primer susiuendo en l segund: 4 Movimieno de proeciles Tiro prbólico ecución: Se denomin movimieno prbólico l relizdo por un objeo cu recori describe un prábol. Se corresponde con l recori idel de un proecil que se mueve en un medio que no ofrece resisenci l vnce que esá sujeo un cmpo grviorio uniforme. Tmbién es posible demosrr que puede ser nlizdo como l composición de dos movimienos recilíneos, un movimieno recilíneo uniforme horizonl movimieno recilíneo uniformemene celerdo vericl. 4 7 Supongmos hor que se lnz un proecil desde un posición en un ángulo de elevción con un velocidd inicil con mgniud v. Consideremos l recori del proecil en un plno vericl donde el suelo esá l lur del eje. v - v e lo c i d d i n i c i l v lur inicil v v, Desprecindo fricción, velocidd del vieno, ec. Consideremos l cción de l grvedd como l únic fuerz, despues del impulso inicil, que cú sobre el proecil. L fuerz de l grvedd sobre el proecil es F mg j que, de cuerdo l ª. Le de Newon que esipul que F m, enemos enonces que l celerción del proecil es igul g j g =. pie/s = 9.8 m/s ). Se ) g j l función vecoril de l celerción del proecil, l función que describe su velocidd l enconrmos inegrndo v ) ) d g d j g j C v donde C es un vecor que represen un velocidd consne. De ls condiciones iniciles enemos que v es l velocidd cundo, o se que v v) g) j C C, L velocidd del proecil es v ) g j v. 99

12 Siendo v l dirección mgniud de v, podemos describirl por sus componenes v v cosi vsen j e incluirl en l función de l velocidd v ) v cosi v sen g j Noe que l componene horizonl v cos es consne no depende de ) mienrs que l componene vericl es linel decreciene con respeco v descelerndo ). Pr describir l recori del proecil necesimos conocer su posición r ) l cul obenemos inegrndo l función velocidd r ) v ) d v cos d i v sen g d j v cos i v sen g j C con C como un vecor de posición consne. Si l posición inicil del proecil r i j, cundo enonces es es r r) v )cos i v ) sen g) j C C L función posición del proecil en culquier iempo r ) v cos i v sen g j L componene horizonl es linel en mienrs que l componene vericl es cudráic, lo cul eplic l recori prbólic. Ejemplo: Un le lnz un jblin que inici su recorrido desde un lur de 6 pies, con un velocidd inicil de 8 pies/s en un ángulo de 4. Qué lur lcnzrá l jblin?. Si l mrc mínim pr clificr l siguiene rond es de pies. Alcnzr el le l mrc con ese lnzmieno? 6 Solución: 4o Tommos l pun de l jblin como l prícul que vij siguiendo l recori rque ) describe l prábol. L velocidd con l que vij iene dos componenes, un horizonl v ) cos v, consne or vericl v ) sen v g que nos indic que l rpidez con l que sube v disminuendo hs llegr cero cundo lcnz l máim lur).

13 Podemos clculr el insne en que lleg su puno máimo resolviendo l ecución v ) sen v g pr. vsen 8 pies/ssen4.67 seg. g pies/s Susiuendo en l componene vericl de l recori: r ) v sen g obenemos l lur en ese insne: Alur máim: r.67) 6 pies 8 pie/s.67 s) sen 4 pie/s.67 s 47.7 pies Siundo el origen en el suelo juso debjo de l pun de l jblin l insne en el que inici el recorrido. Pr sber su posición con respeco l origen l momeno en que lcnz l lur máim, susiuimos.67 seg. en r ) v cos i v sen g j, donde 6 r.67) 8.67 cos 4 i sen 4.67 j 98.i 47.7 j Cundo lcnz su máim lur l jblin h recorrido horizonlmene 98. pies. Alcnce máimo Pr clculr el puno en el que l pun de l jblin oc el suelo usmos l componene vericl de l recori. Igulándol cero resolviendo pr : v sen g - L lur en ese iempo es cero 6 8 sen 6 - resolvemos ommos el vlor posiivo de.67 s El lcnce máimo es r v cos 8.67 cos4.87 pies. Por lo no el lnzmieno super l mrc requerid Grfic de l recori de l jblin en Ecel Cegorí vronil - Record mundil m. f), Record Olímpico 9.7 m 96 f)). Ejemplo: Un cñón dispr un proecil con un velocidd inicil de m/s lo dirige un blnco siudo sobre un lom de m de lo 4 m de disnci horizonl

14 como se muesr en l figur). Clcule el ángulo de dispro pr que el proecil impce en el blnco. m 4 m r ) 4i j en un ciero insne, o se que Solución: Si queremos dr en el blnco, el proecil deberá esr en l posición r ) v cos i v sen g j 4i j v cos 4 v sen g, despejmos en l ecución, l susiuimos en l ecución resolvemos pr : 4 de : cos 4 cos cos en : sen n 44.sec cos cos Uilizmos l idenidd rigonoméric sec n pr obener l ecución de 4 n 44. n 44.n 4 n 74. segundo grdo: De donde n eisen ángulos que resuelven el problem. El iempo que rd el proecil pr 9. es.47 s cos9. r.47).47 cos9. i.47 sen j 4i j 4 ngulo =

15 El iempo que rd el proecil pr 84. es.9 s cos84. r.9).9 cos84. i.9 sen j 4i j ngulo = 84. LONGITUD DE ARCO Dd un recori ), su celerción viene dd por su derivd segund ), si muliplicmos eso por l ms de un prícul obendremos, por l segund le de Newon, l fuerz relizd sobre ell l recorrer l recori. Por oro ldo, l longiud de rco de un recori ) enre los vlores b del prámero viene dd por: l σ ) σ ) d b Un cmpo vecoril es un función de R n en R n. Un líne de flujo de un cmpo vecoril es un recori cu derivd es igul l cmpo vecoril. PROBLEMAS.) Qué fuerz cú sobre un ms de kg que recorre l recori σ ) sen ; cos ; ) uniddes mks) pr el vlor de de segundo? SOLUCIÓN σ ) sen cos ;cos sen ; ) σ ) cos cos sen ; sen sen cos ;) σ) cos sen; sen cos;) F) σ) 4 cos sen; 4sen cos;) Nóese que es fuerz viene dd en Newons..) Se l recori σ ) ; ;log ), definid pr mor que. Hllr l longiud de rco de enre los punos ; ; ) 4; 4; log).

16 SOLUCIÓN Eminndo los dos punos comprndo con l le de l recori podemos comprobr que los vlores respecivos del prámero son = =. De modo que l longiud de rco enre mbos punos será: l σ) σ ) d ;; d d 4 d d d d log log ) Reprmerizr l recori σ ) cos ;sen ;cos ) con respeco l longiud de rco medid desde el puno donde = en l dirección en que se incremen. Considerr los vlores de ubicdos enre /, mbos incluidos. SOLUCIÓN Pr un ciero vlor, l longiud de rco medid desde el será: s l σ ) σ r) dr cos 9cos 9cos 4 r sen r sen r sen cos rdr r 9sen rcos r sen r) 4 r cos r sen cos r sen rdr sen r 4sen r cos r) r) 6cos sen r cos r) r sen dr rdr sen sen r) s dr De es mner, podemos epresr l recori en érminos de s, l longiud de rco, reemplzndo por su epresión en érminos de s: σ ) cos sen s s s ;sen sen ;cos sen / s s s / ; ; donde hemos usdo disins ideniddes rigonomérics, que dejmos l lecor descifrr. 4, 4.) Esbozr lguns línes de flujo de los cmpos vecoriles: ) F; ) = ; -) b) F; ) = ; -) SOLUCIÓN 4

17 ) Un líne de flujo de un cmpo vecoril F es un recori l que = F. De mner que enemos: ) ) ) ) ) )) ); )) / ); ) F σ L función derivd d, mienrs que l función derivd d -. No es difícil percibir que ls funciones que sisfcen ess relciones son ls funciones seno coseno. Tenemos sí: ) = sen ; cos) Ls línes de flujo serán, enonces, circunferencis de rdio cenrds en el origen. b) En ese cso, enemos: ) ) ) ) ) )) ); )) / ); ) F σ Ls funciones que sisfcen eso son ls eponenciles, sí endremos: ) = e ; be - ) )) = b = K.

18 Tendremos sí que ls línes de flujo serán un fmili de hipérbols = K, donde K puede ser posiivo o negivo. En l imgen, se hn represendo punos enre -. Vecores ngenes vecores normles Cundo rrepresen ) un movimieno de un prícul en el iempo, el vecor velocidd v ) pun en l dirección del movimieno es ngene l recori, como lo vimos e l sección nerior. Es crcerísic l podemos rsldr culquier curv suve r ) donde no necesrimene represene el iempo. L derivd r ) es el vecor ngene l curv. Ejemplo: Deermine l ecución de ls recs ngene norml l curv C represend r ) i j en el puno que corresponde. por l función vecoril Solución: L curv dd por res ) un prábol, que ps por P,) cundo. L derivd de r ) es r ) i j r ) i j i 4 j es un vecor, enonces ngene l curv C en el puno P. L rec ngene C en P es prlel l vecor r ) i 4 j o se que s 4s l ecución de l rec ngene es. l pendiene es m ) Pr l rec norml, l pendiene es mn, l ecución enonces es mt. T 6

19 Vecor ngene unirio. Definición: Se C un curv suve represend por l función vecoril r ) en un inervlo biero I. El vecor ngene unirio T ) en, se define como r ) T ), r ) r ) Ejemplo: Hllr el vecor ngene unirio l curv C dd por r ) i j k en el puno que corresponde. Solución: L derivd de r ) es r ) i j r ) 4 r ) el vecor ngene unirio es T ) i j pr El vecor ngene unirio es r ) 4 r ) T ) i j r ) 4 i j k El puno de l curv cundo es P,,) Ejemplo: Hllr los vecores unirios ngenes l curv dd por l función r ) cos i sen j en los punos correspondienes, / rd. Encuenre mbien un conjuno de ecuciones prmérics pr cd rec ngene l curv en esos punos. Solución: L derivd de r ) es r ) sen i cos j r ) sen cos sen cos 7

20 r el vecor ngene unirio es T ) ) sen i cosj k vecor ngene unirio en r ) r T) ) sen i cos j i j j r ) en / / ) cos / ) r T / ) sen i j k i j k i k r / ) en ) cos ) r T ) sen i j i j j r ) Recs ngenes en Pcos,sen,) P,,) T ),,, u T,, ecuciones prmérics:,, z en / Pcos /,sen /, / ) P,, / ) T / ),,, u T,, ecuciones prmérics,, z / en Pcos,sen, ) P,, ) T ),,, u T,, ecuciones prmérics:,, z Recs ngenes l hélice 8

21 Vecor norml principl unirio. En el plno, h dos vecores orogonles l vecor ngene T ), uno que pun hci denro de l curv oro hci fuer. vecores orogonles T en el plno T) En el espcio, eisen infinidd de vecores orogonles T ), uno de ellos es el vecor norml principl que se obiene medine l derivd del vecor T sbemos que si r ) r ) consne enonces r ) r ) como T ) T ) enonces T ) T ) T ) T ) son orogonles. ) Si normlizmos T ) obendremos el vecor norml principl unirio N ) Definición: Se C un curv suve represend por l función vecoril r ) en un inervlo biero I con T ) como vecor ngene unirio. Si T ), el vecor norml principl unirio en se define como T ) N ), si T ). T ) Ejemplo: Hllr el vecor ngene unirio el vecor norml principl l curv C dd r ) i j en el puno que corresponde. por Solución: L derivd de r ) es r ) i j r ) 4 4 r i j r ) ) el vecor ngene unirio es T ) i j pr el vecor ngene unirio es L derivd de T ) es j j r ) i T ) i j r ) i j j i j i j T ) T ) 9

22 el vecor norml principl es T ) i j N) i j T ) C pr el vecor norml principl es T ) ) i j N) i j T ) - - N) T) Ejemplo: Hllr los vecores ngene unirio norml principl l curv C dd por r ) cos i sen j en los punos donde,,,,,. 6 4 r sen Solución: r ) sen i cos j ) cos r ) el vecor ngene unirio es T ) cos i sen j T ) sen i cos j sen i cos j r ) T ) cos sen el vecor norml principl es T ) cos isen j N ) cos i sen j T ) r ) cosi sen j T ) sen icosj N ) cosisen j i /6 i j ĵ / ) i / î j / ) i / j = - - N) r) = T) =/6 /4 i j / ) i / j / ) i / j =/ =/ =/4 / / ) i / i j / ) i / j j / j î ĵ odos los vecores normles punn hci el cenro del círculo i ĵ î

23 Ejemplo: Hllr los vecores ngene unirio norml principl l curv C dd por r ) cos i sen j en los punos donde,,,. 4 Solución: r ) sen i cos j r sen ) cos vecor ngene unirio: r ) T ) sen i cosj sen i cosj T ) cosi sen j r ) T ) cos sen vecor norml principl: cosi sen j T ) N ) cosi sen j T ) T ) sen i cos j k r ) cos i sen j N ) cos i sen j i j k î /4 i j i j k i j / j i k ĵ i j k î z r) N) T) / Los vecores normles principles de l helice punn l eje z =/4 =

24 Vecor celerción componenes ngencil norml Como hemos observdo en lgunos de los ejemplos neriores, el vecor velocidd el vecor celerción no siempre son orogonles. En el cso del movimieno circulr ddo por r ) cos i sen j, velocidd l celerción son orogonles l rpidez es consne v sen ) cos, eso se d debido que l, el vecor celerción no conribue en nd en l dirección de l velocidd. v ) v ) consne enonces v ) v ). Recordemos que si En el problem del movimieno prbólico ) 4 r i j vemos que l celerción siempre es vericl consne ) ) j, mienrs que l velocidd v vrindo su dirección el ángulo enre mbs v cmbindo. L rpidez del movimieno es vrible v ) 4 4 el vecor celerción cú en dirección del movimieno posiivmene, umen-ndo l velocidd o en form negiv disminuéndol). 8 v.) v) v) v-) r.) 4 r) r) = - N) r) = r4) v4) - =/6 =/4 T) r-) Trecori r) =/ -) =/ -4 r ) cos i sen j ) 4 r i j Si velocidd celerción no son perpendiculres enonces podemos epresr l vecor celerción como l sum de vecores componenes orogonles, uno en dirección del movimieno, prlelo l velocidd, por lo no l vecor ngene unirio T ). L or componene serí prlel l vecor norml principl N ). Teorem: Si res ) el vecor posición de un curv suve C eise el vecor N ), enonces el vecor celerción ) r " ) se encuenr en el plno deermindo por T ) N ). T Ls proecciones de ) sobre los ) N vecores T ) N ) son ls componenes ngencil norml de l ecelerción. T) N) r) N) T) Pro T T T Pro N T N ) Componenes ngencil norml de l celerción

25 Ls proecciones de l celerción en dirección de los vecores T ) N ) son los vecores componenes de l celerción: T Pro Pro T T T T. N N N N N r v El vecor ngene unirio T r v, de donde v v T, l celerción es l derivd de l velocidd, o se: v D v T D v T v T T T T D v T v T D v T v T N N T N T N v componene ngencil: T T D v v T componene norml: v N N v T v T Ejemplo: Un objeo se mueve lo lrgo de l recori deermind por l función vecoril r ) i ) j. Clcule su posición, velocidd, rpidez, celerción, T ), N ), T N l insne. r) i ) j i Solución: Posición: Velocidd: ; v) i ) j i j v ) r ) i ) j Rpidez: 4 v ) ) 9 6 ; v) ) Vecor ngene unirio: T ) v ) i ) j v ) ; T ) i j i j Vecor norml principl: N ) T i j ) * ) 4 ) 9 6 T ; N ) i j i j * según el signo de : - sí es posiivo + si es negivo

26 Acelerción: ) v ) 6j ; ) 6 j N Componene ngencil: T 6j i j 6 T T ) Componene norml: v) N 6j i j 6 N - N) T) Acelercion: i j i j 6 ) 6 ) T N 6 6 i ) j ) i j ) T ) N ) 6 T T j i j ; 6 N N j i j en 6 i j 6 i j 6 ) TT ) NN) i j i j Ejemplo: Un objeo se mueve lo lrgo de l recori deermind por l función vecoril r ) cos isen j. Clcule su posición, velocidd, rpidez, celerción, T N l insne. Solución: Posición: r cos i sen j j Velocidd: v ) r ) sen i cos j ; v i 4

27 Rpidez: v ) sen cos l rpidez es consne ) Acelerción: ) r " ) cos i sen j ; cos i sen j j Componenes de l celerción: T i j i j v cos sen sen cos cos sen sen cos v cundo l rpidez es consne los vecores v ) ) son orogonles, v, l celerción no conribue en nd con el incremeno/decremeno de l velocidd, T ) N cos sen sen cos sen cos v i j i j k i j k v sen cos LONGITUD DE ARCO Y CURVATURA Supongmos que l función r ) ) i j z k represen l recori que sigue un cuerpo en el espcio. En un insne deermindo = sbremos l posición del móvil medine el vecor ró ) en =b su nuev posición rb. ) Qué ps si lo que desemos conocer es l disnci que recorrió desde el puno rhs ) rb ) siguiendo l recori r? ) D z r) r ) rb) Si el recorrido se efecur en líne rec no hbrí mucho problem, solo enemos que clculr l disnci enre los dos r) punos: D b b z b z z r) r ) Pero sobre un recori curv no es r) sí de direco, más, si no sbemos que nos recovecos uvo que relizr el cuerpo pr llegr de un puno oro. rb) z r) r ) rb) r) Podemos proimr l curv mendine pequeños segmenos de rec Si primos l curv en vrios segmenos clculmos l lon-giud de cd uno como si fuern recos, endrímos un proimción l longiud de l curv - enre más segmenos mejor l proimción.

28 Longiud de rco Tenemos l curv con función r ) ) i j z k, queremos sber l longiud de rco de l curv desde el puno correspondiene = hs el puno donde =b. Tomemos un pedcio de l s curv desde r ) r ) cu longiud llmremos r ) s. Si es mu pequeño enonces sumiremos que s se comporrá más como un segmeno de rec. r) En un rec, l disnci recorrid es igul l rpidez muliplicd por el inervlo de iempo. s r ) ) ) z ) z r+ D) Si summos odos esos pequeños inervlos endremos un proimción l longiud de l curv: ) ) ) S s z P cu pe re incremenndo el número de inervlos infinimene hce que, om-mos el límie pr obener l fórmul de longiud de rco de l curv. b b b S ) ) z ) d r ) d v ) d Ejemplo: Clcule l longiud de rco de l curv represend por l función r ) cos,sen desde hs. Solución: rco v ) r ) sen,cos, v ) sen cos 4 sen cos = - - r) = b longiud de rco S v ) d d 6

29 Ejemplo : Clcule l longiud de rco de l curv represend por l función r ) i j desde hs. Solución: v ) r ) i 4j, v ) 4 6 longiud de rco b S v ) d 6 d 4 6 ln ln 6 8 ln Ejemplo : Clcule l longiud de rco de l curv represend por l función r ) cos,sen, desde hs 4. Solución: v ) r ) sen,cos,, v ) sen cos longiud de rco b 4 4 S v d d ) Definición: Se C un curv suve dd por ren ) un inervlo cerrdo b,. Pr b, l función longiud de rco viene dd por z = C = b s ) r u ) du u ) u ) z u ) du l función longiud de rco es no-negiv. Mide l disnci sobre,, z hs el puno C desde el puno inicil,, z. L vrible s se denomin prámero longiud de rco. 7

30 Curvur Curvur es l medid de que n rápido se comb o uerce un curv. Por ejemplo, círculos pequeños se combn más rápido que círculos más grndes. B menor curvur A mor curvur Definición: se C un curv suve dd por r. ) L curvur de C en esá definid como T r ) r " ) K r r Si usmos el prámero longiud de rco s pr definir l función que describe l curv C, r s) s) i s) j z s) espcio), enonces l curvur esrí definid como l rzón de cmbio del vecor ngene unirio con respeco s. Tl que dt L curvur de C en s: K T s) ds Ejemplo: Clcule l curvur de un círculo de rdio R. Solución: Tomemos un círculo con cenro en el origen rdio R ddo por l función r ) Rcos i Rsen j, con r ) Rsen i Rcos j. r ) R sen R cos R R r ) R cos i sen j T ) cos i sen j ; r ) R T ) sen i cos j T sen ) cos R Rdio chico Curvur grnde K=/R R Rdio grnde Curvur pequeñ z = C = b l curvur del círculo de rdio R es T K r R 8

31 Si en lugr de omr el prámero lo hcemos con l longiud de rco s, donde ) sen ) cos ) s r u du R u R u du R du R s Tenemos que si s R enonces, por lo no si prmerizmos l ecución del R círculo en función de l longiud de rco s obenemos l función: s ) cos s r s R i Rsen j R R s donde ) sen s r s i cos j R R r s) s ) sen s T s i cos j r s) R R r s s R s R ) sen cos s ) cos s T s i sen j R R R curvur: K dt ) cos s sen s T s cos s sen s ds R R R R R R R R Ejemplo : Clcule l curvur de l curv C dd por,,. r ),, en Solución: Tenemos que r ) r " ) K donde r ), 4, r, r" ), 4, r ) 6 4 r ) r " ),, 4, r ) r " ) 4 6 susiuimos en K r ) r " ) r. K.46 ) K..4.) 6 K ) K.6 ) 8 9