U(r, θ) = Conjunto completo de operadores del dipolo puntual. Si usamos el operador asociado a la componente z del momento angular

Transcripción

1 Capítulo Dipolo puntual. Como vimos en la introucción al primer capítulo, la energía potencial que aquiere una partícula e carga eléctrica e cuano interacciona con un ipolo puntual es Ur, θ) = 4πϵ ep cos θ r. En este capítulo revisaremos las coniciones necesarias para que el potencial e ipolo puntual tenga estaos ligaos... Conjunto completo e operaores el ipolo puntual. Para analizar el problema e estaos ligaos e una partícula cargaa en presencia e un potencial e ipolo puntual resolvemos la ecuación e Schröinger inepeniente el tiempo, ĤΨ r) = EΨ r).) one Ĥ es el operaor hamiltoniano Ĥ = µ + U r)..) Escribieno explícitamente el operaor Laplaciano en coorenaas esféricas y la energía potencial U, tenemos [ Ĥ = r ) + sin θ ) + µ r r r r sin θ θ θ r sin + θ φ ep cos θ 4πϵ r Si usamos el operaor asociao a la componente z el momento angular ˆL z = i φ 3.3)

2 y efinimos el operaor angular ˆΩ = [ sin θ = sin θ θ θ sin θ ) + θ ) sin θ θ sin θ + µ ep cos θ φ 4πϵ + ˆL z sin θ + β cos θ.4) en el último renglón hemos hecho uso e la efinición el parámetro β, ecuación.4), β = µ entonces el operaor hamiltoniano se escribe como Ĥ = µ r r Claramente, los operaores Ĥ, ˆΩ y ˆL z conmutan entre sí [Ĥ, ˆΩ = [Ĥ, ˆLz = [ˆΩ, ˆL z = ep,.5) 4πϵ r ) + ˆΩ r µr..6) y forman, por lo tanto, un conjunto completo e operaores para escribir los estaos estacionarios el potencial e ipolo puntual. Estos estaos se representan por las eigenfunciones comunes a los tres operaores y se clasifican por los eigenvalores que toman ichos operaores, Ψ E,λ,m r, θ, φ). Por otro lao, si con F m φ) representamos la eigenfunción el operaor ˆL z, con eigenvalor m, ˆL z F m φ) = m F m φ).7) y con Y λ,m θ, φ) la eigenfunción e ˆΩ, con eigenvalor λ, ˆΩ Y λ,m θ, φ) = λ Y λ,m θ, φ).8) entonces, como el operaor ˆΩ es separable, la eigenfunción Y λ,m se escribirá como el proucto e la eigenfunción F m φ) y e una función e la variable θ, que enotamos con Θ λ,m θ), Y λ,m θ, φ) = Θ λ,m θ)f m φ).9) A su vez, las eigenfunciones el operaor hamiltoniano Ĥ son las eigenfunciones e la energía Ψ E,λ,m r, θ, φ) ĤΨ E,λ,m r, θ, φ) = EΨ E,λ,m r, θ, φ).) 4

3 y tomano en cuenta la separabilia el operaor hamiltoniano las eigenfunciones se escriben como el proucto e la función Y λ,m θ, φ) y e una función que sólo epene e la variable r, que enotamos con R E,λ r), Ψ E,λ,m r, θ, φ) = R E,λ r)y λ,m θ, φ) = R E,λ r)θ λ,m θ)f m φ).) así, los estaos estacionarios el sistema, Ψ E,λ,m r, θ, φ), están aos por el proucto e las tres funciones e variables separaas. Escribieno explícitamente caa operaor en la ecuación e eigenvalores corresponiente obtenemos ahora el sistema e ecuaciones iferenciales que satisfacen las funciones F m φ), Θ λ,m θ) y R E,λ r): F m φ) = imf m φ).) φ [ sin θ ) m sin θ θ θ sin θ β cos θ Θ λ,m θ) = λθ λ,m θ).3) [ r ) λr R µ r r r E,λ r) = ER E,λ r).4) La ecuación e la coorenaa φ ya fue resuelta en el capítulo anterior, sus soluciones son e la forma F m φ) = e imφ y representan los estaos e momento angular m alreeor el eje z. El eigenvalor, número m, es entero como resultao e imponer la conición e univaluamiento: F m φ) = F m φ + π). En las siguientes secciones trabajaremos con las ecuaciones para la coorenaa raial r y para la coorenaa angular θ. En particular, en la siguiente sección encontraremos información relevante sobre el eigenvalor λ.... Valor crítico el eigenvalor λ. Antes e resolver las ecuaciones iferenciales para θ y r, es importante conocer los valores posibles que puee tomar el eigenvalor λ, en lo que respecta al problema físico presente. La función e ona Ψ E,λ,m está normalizaa si caa una e las funciones separaas satisface su propia normalización, esto es: F m φ) = π e imφ.5) π Θ λ,m θ) sin θ θ =.6) R E,λ r) r r =.7) 5

4 Esto nos permite expresar el eigenvalor e la energía a partir e la ecuación.4). Multplicano por RE,λ r, integrano e cero a infinito y usano la normalización.7) obtenemos E = µ [ R r R ) + λr r r r R r r.8) one hemos omitio los subínices en la función raial, en el entenio e que Rr) = R E,λ r). A continuación hacemos el cambio e función Rr) = ur) r para esto necesitamos calcular la primera erivaa e la función Rr): Rr) r = r ur) r ur) r.9) multiplicano por r y erivano con respecto a r, obtenemos r Rr) ) = r ur) ) ur) = r ur).) r r r r r y sustituyeno este resultao, junto con el cambio e función.9), en la expresión para la energía.8), tenemos: [ E = u u µ r r r + λ u r r r r = µ u [ r + λ r ur.) Como poemos ver e la expresión anterior, el operaor e la energía equivale al operaor uniimensional Ô E = µ r + λ ).) r y e la normalización.7) se sigue que la función ur) está normalizaa, ur) r =.3) Ahora buscamos una escomposición el operaor ÔE en un proucto e operaores, e la siguiente forma: Ô E = µ r + a ) r r + b ) r con a y b constantes. Desarrollano el proucto Ô E = µ [ r + a b r 6 r ba + ) + r

5 y comparano con la forma original el operaor ÔE tenemos las relaciones: y De aquí obtenemos: por lo tanto, los valores posibles para a son: a b =, ba + ) = λ. a = b aa + ) = λ, a ± = ± + λ..4) 4 En resumen, poemos escribir el operaor ÔE como el proucto e operaores con erivaas e primer oren Ô E = µ r + a ) r r + a ). r Ahora regresamos a la expresión para la energía, ecuación.), y sustituimos la nueva forma el operaor, E = u µ r + a ) r r + a ) u r r [ = u u µ r r + a ) r u r + u a u r r + a ) r u r..5) La primera integral se puee calcular por partes u u r r + a ) u r u r = u r + a ) r u + u u = r r + a ) r u r. u r u r + a ) r u r one usamos el hecho que la función ur) se anula en el origen, ya que en r = el potencial es infinito, y cae a cero cuano r tiene a infinito por ser una función cuarao integrable. Sustituyeno en.5) el resultao obtenio, [ E = u u µ r r + a ) r u r + u a u r r + a ) r u r = µ = µ u r + a ) u r u r + a ) r u r ) u r + a u r u r + a ) r u r. 7

6 En particular, si a es real tenemos E = µ u r + a r u r > y para energías positivas no hay estaos ligaos. Entonces, para que haya estaos ligaos necesitamos que a no sea real y e la ecuación.4) esto ocurre cuano λ 4,.6) ésta es la restricción para los valores posibles el eigenvalor λ. Es ecir, λ =.5 es el valor crítico para que el potencial e ipolo puntual tenga estaos ligaos... Ecuación angular En esta sección estuiaremos las implicaciones e la ecuación iferencial.3): sin θ Θθ) ) [ m + sin θ θ θ sin θ + β cos θ Θθ) = λθθ), one omitimos los subínices e la función angular. Buscamos en esta ecuación una relación entre el eigenvalor λ, en particular su valor crítico, y la constante aimensional β. La ecuación iferencial se puee escribir en la forma ˆΩ mθθ) = λθθ).7) one el operaor ˆΩ m es ˆΩ m = sin θ ) + m sin θ θ θ sin + β cos θ.8) θ con λ sus eigenvalores y Θθ) sus eigenfunciones. Vieno la forma el operaor ˆΩ m, poemos reconocer en los primeros os términos al operaor cuarao el momento angular con componente L z = m, el cual está ao por esto es, ˆL = sin θ θ ˆΩ m = ˆL sin θ θ ) + m sin θ,.9) + β cos θ..3) Si β =, recuperamos el operaor ˆL y la ecuación.7) se reuce a: ˆL Θθ) = ll + )Θθ),.3) 8

7 lo cual es e esperarse ya que β contiene el momento ipolar p, y si éste es cero entonces el sistema se convierte en el problema e la partícula libre, que en la parte angular es escrito por los armónicos esféricos, que son eigenfunciones el operaor cuarao el momento angular. Ahora investigaremos la relación entre la constante aimensional β y el eigenvalor λ, con el fin e inferir la existencia e estaos ligaos. La manera e hacer esto es estuiano el estao base, es ecir, el estao posible e menor energía. Tanto el operaor ˆL como el término β cos θ tienen una cota inferior para sus respectivos eigenvalores, para ˆL es, resultao el eigenvalor l =, y para β cos θ es β, cuano θ toma el valor π. Por lo tanto los eigenvalores el operaor ˆΩ m tienen una cota inferior, aa por β, es ecir λ β. El eigenvalor aceptable más bajo, para el ipolo puntual, es λ = β. Ya habiamos visto que para tener estaos ligaos se necesita λ /4, esta limitación y la obtenia en el párrafo anterior nos eterminan el rango para el eigenvalor λ, esto es β λ /4, y para que se cumpla esto se requiere β /4, es ecir, el parámetro β tiene como cota inferior /4. En consecuencia, existe un valor crítico e β, y por lo tanto un valor crítico e la magnitu el ipolo, que permite la existencia e estaos ligaos para el ipolo puntual. A continuación encontraremos el valor numérico e β en icho estao crítico y lo compararemos con el valor crítico encontrao para el caso el ipolo físico. Dao que se busca el valor crítico e β, y esto ocurre cuano el eigenvalor λ toma el menor valor posible, y tomano en cuenta que en la ecuación.8) el término sin θ siempre es positivo, entonces el valor crítico ocurre para m =, que correspone a l =. Con esto, la ecuación quea, sin θ Θθ) ) + β cos θ Θθ) = λθθ), sin θ θ θ y espués e esarrollar la erivaa, Θ θ + cos θ Θ + λ β cos θ)θ =..3) sin θ θ Ahora hacemos el cambio e variable x = cos θ. Usano la regla e la caena: m θ = x θ x = sin θ x = x x 9

8 = θ θ = sin θ x sustituyeno estos operaores en.3) sin θ ) x = x x sin θ x ) x x = x ) x x x ) x Θ x xθ + βx + λ) Θ =.33) x que es exactamente igual a la ecuación iferencial para la variable η el capítulo, ecuación.34), con λ jugano el papel e C. En este caso resulta más eviente proponer como solución el esarrollo e Θθ) en la base e los polinomios e Legenre, porque el operaor ˆΩ es la suma el operaor ˆL y e β cos θ, y los polinomios e Legenre son eigenfunciones e ˆL en el caso m =. Con el esarrollo e Θx) en la base e los polinomios e Legenre ) Θx) = l P l x) l= sustituyeno en la ecuación iferencial.33) obtenemos una fórmula e recurrencia entre los coeficientes el esarrollo. Las relaciones e recurrencia son: λ + β 3 =,.34) l [λ ll + ) l + β l l + β l + l + 3 l+ =, l =,, ) Si corremos el ínice l, obtenemos el siguiente sistema e ecuaciones: λ + β 3 = β + λ ) + 5 β = 3 β + λ 6) β 3 = 3 5 β + λ ) β 4 = 4 7 β 3 + λ ) β 5 =.

9 que puee escribirse en forma matricial como β λ 3 β λ ) 5 β β λ 6) 3 β β λ ) 4 β = 4 β λ ) Este sistema homogéneo tiene soluciones istintas e cero para,,... sólo si el eterminante e la matriz es cero; es ecir, si los vectores columna, o renglón, son linealmente epenientes, β λ 3 β λ ) β 5 et β λ 6) 3 β β λ ) 4 β =.36) β λ ) ésta es una ecuación implícita para β en términos e λ, equivalente a la ecuación en fracciones continuas el capítulo, ecuación.43). Como la matriz es e oren infinito hay que hacer aproximaciones cortano la matriz en una submatriz e oren finito, por ejemplo 3 3 o 4 4, y calcular el eterminante con la conición e que sea igual a cero. Entre más grane sea la submatriz, mejor será la aproximación, pero más ifícil el cálculo. Cortano el eterminante en 4 4 y ejano el polinomio λβ) e tercer grao en β llegamos exactamente al mismo resultao que obtuvimos en el primer capítulo; e moo que el valor el momento ipolar mínimo para la existencia e estaos ligaos es igual para el ipolo puntual y para el ipolo físico; es ecir, el valor crítico es inepeniente el tamaño el ipolo. Aemás, sabemos que el valor crítico el eigenvalor λ, para la existencia e estaos ligaos, es λ =.5. Poemos sustituir este valor en el eterminante.36) y resolver numéricamente para β en el oren e aproximación que queramos. Por ejemplo, si resolvemos para un eterminante 8 8 obtenemos β = que comparao con el resultao obtenio en el primer capítulo, β =.75, confirma la afirmación hecha en el Apénice C sobre la convergencia rápia el parámetro β..3. Ecuación Raial La solución e la ecuación raial.4) ebe cumplir con coniciones en la frontera: ebe ser cero en el origen y, como la solución ebe ser normalizable, es ecir, ebe ser

10 cuarao integrable, ebe caer a cero cuano r. La ecuación raial es: µ [ r ) λr Rr) = ERr) r r r y para resolverla primero hacemos el cambio e función Rr) = ur) y usamos la relación r.), entonces la ecuación se transforma en µ r λ ) ur) = Eur)..37) r Como estamos interesaos en los estaos ligaos el ipolo, la energía es negativa y efinimos un nuevo parámetro k, meiante para tener la ecuación raial r λ r k = µ E,.38) ) ur) = k ur).39) Como solución e esta ecuación iferencial proponemos un proucto e funciones, una que escriba el comportamiento en el origen y otra que tiena a una constante cuano r : ur) = u r)qr).4) one u r) es la función que escribirá el comportamiento en el origen. Ahora veamos que ocurre cuano r. De la ecuación.39), tomano en cuenta que, conforme nos acercamos al origen, el término proporcional a k es espreciable comparao con el término proporcional a /r, la ecuación que satisface u r) es u r) r λ r u r) =.4) y la solución e esta ecuación es una potencia e r, por ejemplo u r) = r s. Sustituyeno en la ecuación obtenemos una ecuación algebraica para la potencia s cuya solución es: ss ) λ = por lo tanto, la solución cerca el origen es e la forma s ± = ± + λ,.4) 4 u r) = Ar s ±..43)

11 Si usamos la forma explícita s ± en u r): u r) = Ar r ± 4 +λ, = Ar e ± 4 +λ ln r. Vemos que, como λ /4, entonces la exponencial es imaginaria y u tiene un comportamiento onulatorio en la cercanía el origen ominao por la amplitu r /. La función, solución e la ecuación.4), hasta ahora se escribe como ur) = Ar s ± Qr).44) Por su parte, la ecuación que satisface la función Qr) se encuentra sustituyeno.44) en.39). Para eso calculamos la seguna erivaa e la función ur): ur) r u r = = s ± r ur) + Q r) Qr) ur) ) s± = r + Q r) ur) Qr) = = s ± r Q Q Q + Q Q [ Q Q Q Q [ Q Q + s ± r y sustituyeno en.39) tenemos, [ Q Q + s ± r ) ) s± u + r + Q s± Q Q ) s ± r + s ± r + s ± r Q Q + s ± s ± r Q Q + s ± s ± r u. Q Q + r + Q Q ) Q u k + λr ) u =. Multiplicano por Qr), y agrupano los términos proporcionales a Qr), encontramos ur) la ecuación iferencial, Q r + s ) ± Q s r r + ± s ± λ k Q = r y utilizano la ecuación.4), se reuce a Q r + s ± Q r r k Q =..45) Para trabajar con más comoia hacemos el cambio e variable x = kr; para ello, utilizamos la regla e la caena: r r = k x. = x r 3 x = k x, u ) u

12 Sustituimos en.45) y eliminamos un factor k para tener Qx) + s ± Qx) Qx) =..46) x x x Por la estructura e la ecuación, el origen es un punto singular regular, por lo tanto nos proponemos resolver esta ecuación iferencial con el métoo e Fröbenius usano como solución la serie e potencias, Qx) = C n x n..47) Sus erivaas son: Qx) x Qx) x = = n= nc n x n, n= nn )C n x n. n= y sustituyeno en.46) obtenemos la relación nn )C n x n + s ± n= n= nc n x n C n x n =, extrayeno el primer término e la seguna sumatoria y agrupano too en una sumatoria que comienza en n =, tenemos finalmente: s ± C x + {[nn + s ± ) C n C n } x n =. n= De la expresión anterior, utilizano la inepenencia lineal e las potencias e x, esto es, la combinación lineal se satisface solamente si los coeficientes son iguales a cero, obtenemos que: C = y la relación e recurrencia C n = n= nn + s ± ) C n n =, 3,....48) Por otro lao, como s ± = ± 4 + λ con λ /4, entonces s ± es un número complejo que poemos escribir como: con α un número real y positivo, ao por s ± = ± iα α = λ 4..49) 4

13 Así, sustituyeno la forma explícita e s ± en.48) obtenemos la fórmula e recurrencia C n = nn ± iα) C n..5) Como C =, los coeficientes impares e la serie, que se generan con la fórmula e recurrencia a partir e C, son cero. Sólo sobreviven los coeficientes pares. Corrieno la relación e recurrencia: C = C 4 = C 6 =. C n = ± iα) C 44 ± iα) C = 66 ± iα) C 4 = 4 ± iα)4 ± iα) C 4 6 ± iα)4 ± iα)6 ± iα) C 4 6 n n ± iα) ± iα)... n ± iα) C y usano la ientia e la función gamma, Γz + ) = zγz), los prouctos el enominaor se escriben como n ± iα)n ± iα) ± iα) ± iα) = y obtenemos el coeficiente C n en la forma C n = Γn + ± iα) Γ ± iα) Γ ± iα) n! n Γn + ± iα) C n =,,... Con estos resultaos la solución.47) quea: [ Q ± x) = C ± Γ ± iα) + n! n Γn + ± iα) xn,.5) n= y tenemos os soluciones, una por caa signo. El término igual a uno es incluío en la sumatoria como el caso n = y el factor Γ ± iα) es una constante inepeniente e n que puee ser absorbia por C ±. Por lo tanto, en términos e la coorenaa raial r, las funciones Q ± r) son: Q ± r) = C ± n= n!γn + ± iα) ) n kr..5) Comparano esta solución con la función Bessel moificaa e primer tipo, enotaa por I ν z): z ) n+ν I ν z) =,.53) n!γn + + ν) n= 5

14 z ) ν, vemos que, salvo por el factor global se trata e la misma función. Escribieno la función Q ± r) en la forma Q ± r) = C ± ) iα kr t= t!γt + ± iα) ) t±iα kr, ) iα k ientificano la función I ±iα kr) y absorbieno en C ± la constante, obtenemos finalmente las funciones Q ± r) en términos e la función Bessel moificaa e primer tipo: Q ± r) = C ± r iα I ±iα kr)..54) Con este resultao tenemos os soluciones para la función raial ur). De la ecuación.44), éstas son: u ± r) = Ar s ± r iα I ±iα kr) y como s ± = ± iα, quea u ± r) = Ar I±iα kr)..55) Son os las funciones para la parte raial. Pero aún quea peniente el problema e saber cuál es la solución que representa al problema físico. Ambas soluciones.55) satisfacen la conición e ser cero en el origen, pero las os ivergen cuano r. La respuesta es que la solución física es una combinación lineal e las os funciones u ± r). Dicha combinación lineal es la función Bessel moificaa e seguno tipo que, para ν no entero, está efinia como: K ν z) = π I ν z) I ν z).56) sin νπ y esta función, cuano se multiplica por r /, sí satisface las coniciones mencionaas. Ahora proceemos a hacer la combinación lineal e tal moo que recuperemos esta función. Sumano u r) y u + r), junto con la constante N apropiaa, la solución es: ur) = N π u r) u + r) sin iαπ = N π r I iα kr) I iα kr), sin iαπ e ientificano la función Bessel moificaa e seguno tipo, la solución e la parte raial que es normalizable es: ur) = Nr Kiα kr),.57) con N la constante e normalización. Ésta es una función real ya que Kiαkr) = π I iα kr) I iα kr) sin iαπ) = π I iα kr) + I iα kr) sin iαπ = K iα kr) 6

15 La constante e normalización se obtiene, a partir e.3), calculano la integral si hacemos el cambio y = kr quea N rkiαkr)r =..58) N k yk iαy)y =..59) La función Kiαy) se puee expresar en forma integral meiante la ientia, Watson entraa 3.7), K iαy) = y sustituyeno en la integral.59) quea: yk iαy)r = T cosh iαt e y cosh T cosh U cos αt T U U ye y cosh T cosh U y..6) La última integral se calcula meiante una integración por partes, con ayua e: ye ay y = a con a = cosh T cosh U real, positivo y mayor que cero. Así, ye y cosh T cosh U y = 4 cosh T cosh U. Sustituyeno este resultao en.6), la integral se reuce al proucto e os integrales inepenientes yk iαy)r = 8 T cosh iαt cosh T Calculamos caa integral por separao. La integral e la variable U: U cosh U = tanh U = y la integral e la variable T T cos αt cosh T = = T απ sinh απ cos αt cosh T U cosh U..6) one usamos la tabla e integrales e Grashteyn entraa 3.98). Sustituyeno estos resultaos en.6), ykiαy)y απ = sinh απ 7

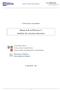
16 .6 u r r..4 Figura.: Gráfica e la función e ona raial normalizaa ur) con parámetros: k = y α = 5. y regresano a la expresión e normalización.59), obtenemos la constante e normalización ) k sinh απ N =.6) απ La forma final e la función raial normalizaa es ) k sinh απ ur) = r Kiα kr).63) απ con k = µ E y α = λ 4. Ahora estamos en coniciones e graficar la función raial ur). En la Figura. tenemos la gráfica e la función raial para la energía k = y el parámetro α = 5. De la gráfica se sigue que la función e ona oscila infinitamente conforme r ; en otras palabras, para cualquier energía negativa la función raial tiene un número infinito e noos cruces con el eje horizontal). Debio a que, en general, el estao base tiene cero noos, el primer estao excitao tiene uno y así sucesivamente, poemos concluir que el potencial el ipolo puntual no tiene estao base, solamente un número infinito e niveles e energía negativa que tiene a menos infinito, e moo que para cualquier energía siempre hay un estao e menor energía y éste, a su vez, tiene infinitos estaos e energía menores. Este resultao es congruente con la observación e que la ecuación raial para la energía, ecuación.4), es invariante e escala. La ecuación.4) es: r Rr) ) + λ Rr) = ERr) µ r r r r 8

17 vemos que si existe un estao ligao e energía E escrito por la función e ona raial Rr), entonces, para κ constante real y positiva, la función Rκr) también es solución e la ecuación pero con energía κ E. Pero la constante κ puee ser cualquier número; así que, si existe un estao ligao, existen estaos ligaos para cualquier energía y en consecuencia no hay estao base. Como veremos en el siguiente capítulo, la razón por la cual el potencial ipolar tiene estas anomalías es porque el operaor hamiltoniano el problema no es autoajunto. En la mecánica cuántica las variables inámicas e un sistema son escritas por operaores autoajuntos. En el siguiente capítulo estuiaremos la teoría e los operaores en el espacio e Hilbert y el métoo e extensiones autoajuntas e un operaor hermitiano, para luego aplicarlo al problema el ipolo puntual. 9