1. Convergencia monótona
|
|
|
- Lucía Rojas Castilla
- hace 7 años
- Vistas:
Transcripción
1 AMARUN Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2. Lección n 5: Teoremas clásicos EPN, verano 29 Todo el poder de la integral de Lebesgue está condensado en estos resultados. 1. Convergencia monótona Teorema 1 (Teorema de la convergencia monótona de Beppo Levi Sea (, A, µ un espacio medido y sean f una función A -medible y (f n n N una sucesión creciente de funciones A -medibles, ambas definidas sobre a valores en R +, tales que f(x = f n(x µ-c.t.p. Entonces f(xdµ(x = f n (xdµ(x. Demostración. La convergencia de la sucesión (f n n N se tiene en todo punto de. i Por la monotonía de la integral tenemos: f (xdµ(x f 1 (xdµ(x... f(xdµ(x; por lo tanto la sucesión ( f ndµ converge (eventualmente hacia + y su ite satisface n N f n (xdµ(x f(xdµ(x. (1 ii Sea (g n,k k N una sucesión creciente de funciones simples tales que f n = g n,k. k + Definimos h n : R + por h n = máx(g 1,n, g 2,n,..., g n,n de manera que la sucesión (h n n N es una sucesión creciente de funciones simples positivas, A -medibles que satisfacen h n f n y f = h n. Por la proposición del folleto y por la monoticidad de la integral se deduce que f(xdµ(x = h n (xdµ(x = Juntando (1 y (2 se obtiene el resultado deseado. Solo se tiene la convergencia µ-c.t.p. f n (xdµ(x. (2 Existe N que pertenece a A, de µ-medida nula, en donde no se tiene esta convergencia. Vemos que la función f1 N c satisface las hipótesis hechas en la primera parte de la demostración: f(x1 N c(xdµ(x = f n (x1 N c(xdµ(x. Dado que la función f n 1 N c = f n µ-c.t.p. y que f1 N c = f µ-c.t.p., en virtud de la proposición se tiene en µ-c.t.p. la igualdad f(xdµ(x = f n (xdµ(x. 1
2 Corolario 1 Sea (, A, µ un espacio medido y sea una serie S = n N f n cuyos términos f n son funciones A -medibles definidas sobre (, A, µ a valores en R +. Entonces la suma es medible y se tiene la identidad f n (xdµ(x. n N f n (xdµ(x = n N Definición 1 (Medida inducida por una función Sea (, A, µ un espacio medido y sea f : [, + ] una función A -medible. Definimos una nueva medida sobre el espacio medible (, A de la siguiente manera ν(a = f(xdµ(x. Verificación: (i Se tiene ν( = pues ν( = f(xdµ(x =. (ii Si (A n n N es una sucesión de conjuntos disjuntos de A y si notamos A = n N A n entonces ν(a = S f(xdµ(x = f(xdµ(x = ν(a n. n N An A n n N = Muy útil para construir nuevas medidas! Esta definición tiene repercusiones importantes en la teoría de la integración. 2. Lema de Fatou A n N Teorema 2 (Lema de Fatou Sea (, A, µ un espacio medido y sea (f n n N una sucesión de funciones A -medibles definidas sobre a valores en R +. Entonces se tiene la desigualdad: ínf f n(xdµ(x ínf f n (xdµ(x. Demostración. Para cada n N definimos una nueva función g n : R + de la siguiente forma: g n = ínf k n f k de manera que cada función g n es A -medible y se tiene, para todo x las relaciones g g 1... y ínf f n = g n. Puesto que tenemos la mayoración g n f n para todo n N, al aplicar el teorema de convergencia monótona de Beppo Levi obtenemos Lo que termina la demostración. ínf f n(xdµ(x = g n (xdµ(x ínf f n (xdµ(x. 2
3 3. Convergencia dominada Sin duda el teorema más famoso de la teoría de la integración. Teorema 3 (Teorema de la convergencia dominada de Lebesgue (T.C.D.L. Sea (, A, µ un espacio medido y sean f una función y (f n n N una sucesión de funciones, ambas A -medibles definidas sobre a valores en R o C. Hacemos las siguientes hipótesis: 1 para µ-casi todo x se tiene f n(x = f(x, 2 existe una función integrable g : R o C tal que se tenga, para todo n, la estimación f n (x g(x µ-casi en todas partes en. Entonces f es una función integrable y f n (xdµ(x = f(xdµ(x (3 Demostración. La integrabilidad de la función ite f se deduce de la integrabilidad de la función g: f(xdµ(x f(x dµ(x g(xdµ(x < +. Mostremos (3 suponiendo que las dos hipótesis se verifican para todo punto de y que g(x < + para todo x. La sucesión (g+f n n N es una sucesión de funciones positivas tales que (g+f(x = (g+f n(x, para todo x. Aplicamos el Lema de Fatou (teorema 2 para obtener la estimación (g + f(xdµ(x ínf (g + f n (xdµ(x de donde se obtiene, por la aditividad de la integral, la desigualdad f(xdµ(x ínf f n (xdµ(x. (4 Un argumento similar aplicado a la sucesión (g f n n N muestra que (g f(xdµ(x ínf (g f n (xdµ(x, es decir Gracias a las estimaciones (4 y (5 se obtiene la identidad deseada. f(xdµ(x ínf f n (xdµ(x. (5 Las hipótesis se verifican en µ-casi todas partes. Obsérvese que por el corolario del folleto, si se tiene g(xdµ(x < +, entonces se obtiene la estimación g(x < + µ-casi todas partes. Es posible entonces repetir el argumento utilizado en la demostración del teorema 1 considerando los conjuntos N y N c según si se tiene o no la convergencia. Convergencia en µ-c.t.p. + hipótesis de acotación (o dominación = f ndµ = f ndµ 3
4 Ejemplos (i Consideremos el ite siguiente: ( 1 nxe nx dx. Calculando directamente se puede ver que el ite tiende a cero; pero también se puede aplicar el T.C.D.L. a las funciones f n (x = nxe nx 1 [,1] (x. Tenemos f n (x para todo x y además se tienen las estimaciones f n (x 1 [,1] (x de modo que podemos aplicar el teorema 3 para escribir (ii Ahora estudiemos el ite a continuación: ( 1 1 nxe nx dx = nxe nx dx =. ( 1 nx 2 e nx2 dx. ya no es posible realizar un cálculo directo de la integral, = es necesario pasar por el T.C.D.L. Dado que las funciones f n (x = nx 2 e nx2 1 [,1] (x tienden a cero si n + y que se tienen las estimaciones f n (x 1 [,1] (x, podemos afirmar que el ite de la expresión anterior tiende a cero si n Integrales dependientes de un parámetro Teorema 4 (Continuidad con respecto a un parámetro Sea (, A, µ un espacio medido y sea (E, d un espacio métrico. Sea f : E K una función que verifica las tres condiciones siguientes: 1 para todo t E la función x f(x, t es medible, 2 para µ-casi todo x la función t f(x, t es continua en el punto t, 3 en µ-casi todas partes existe una función µ-integrable g : K tal que para todo t E se tiene la estimación f(x, t g(x Entonces, la función definida por es continua en el punto t. ϕ : E K t ϕ(t = f(x, tdµ(x (6 Demostración. Para verificar la continuidad de la función ϕ en el punto t, debemos probar que si (t n n N es una sucesión de puntos de E que converge hacia t, entonces ϕ(t n ϕ(t. Para ello utilizaremos dos funciones auxiliares ψ(x = f(x, t y ψ n (x = f(x, t n. Por la tercera hipótesis tenemos que ψ n (x g(x µ-casi todas partes para todo entero n. Por la segunda hipótesis tenemos que ψ n (x converge hacia ψ(x para µ-casi todo x y como las funciones ψ n son medibles (por la primera hipótesis, verificamos todas las condiciones para poder aplicar el teorema de convergencia dominada de Lebesgue: ϕ(t = ψ(xdµ(x = ψ n (xdµ(x = ϕ(t n, 4
5 Ejemplos (i Sea la función ϕ :], 1[ R t ϕ(t = + x t x dx. Notamos f(x, t la función definida sobre [, + [ ], 1[ determinada por f(x, t = xt 1 1+x. 1 la función x f(x, t es medible para todo t ], 1[ por ser el cociente de dos funciones medibles, 2 la función t f(x, t es continua para todo x [, + [, e(t 1 ln(x 3 para la hipótesis de dominación escribimos f(x, t = 1+x. Observamos que la función f(x, es creciente si x 1 y decreciente si x < 1; esto nos lleva a considerar a, b dos parámetros reales tales que < a < t < b < 1 y a definir una función g : [, + [ R de la siguiente forma: x a 1 1+x si < x < 1 g(x = x b 1 1+x si 1 x. Tenemos entonces la estimación f(x, t g(x válida para todo x [, + [ y además se tiene que + g(xdx < +. Dado que hemos verificado las hipótesis del teorema 4 = la función ϕ es continua sobre ], 1[. (ii Sea f : R C una función tal que + f(x dx < +. Definimos su Transformada de Fourier, notada F (f o ˆf, por la siguiente fórmula: F (f(ξ = ˆf(ξ = Verifiquemos las hipótesis de aplicación del teorema 4: + f(xe iξx dx. (7 1 la función x f(xe iξx es medible para todo ξ por ser el producto de dos funciones medibles, 2 la función ξ f(xe iξx es evidentemente continua para todo x, 3 la hipótesis de dominación se obtiene observando que f(xe iξx f(x. Aplicando el teorema de continuidad de la integral con respecto a un parámetro = la función ˆf : R C es continua. Corolario 2 (Continuidad de la integral con respecto a la cota superior Sea f una función integrable definida sobre la recta real R a valores en R y sea α R un real. Entonces la función definida por es continua para todo t > α. ϕ : t t α f(xdx (8 Prueba. Basta aplicar el teorema 4 a la función g(x, t = f(x1 [α,t] (x. En efecto, esta función g es continua en el punto t para todo x t y puesto que se tiene la mayoración g(x, t f(x podemos aplicar sin problema el resultado precedente y terminar la demostración. 5
6 Teorema 5 (Derivación bajo el signo integral Sea (, A, µ un espacio medido y sea I un intervalo abierto de R. Sea f : I K una función y suponemos que existe N un conjunto de µ-medida nula tales que 1 para todo t I la función x f(x, t es integrable, 2 la derivada parcial f t (x, t existe en todo punto x I en donde notamos = \ N. 3 existe una función integrable g : K tal que para todo x se tiene f (x, t t g(x en µ-casi todas partes. Entonces, la función definida por es derivable y se tiene ψ : I K t d dt ψ(t = f(x, tdµ(x f (x, tdµ(x. (9 t Demostración. Sea t un punto de I y sea (a n n N una sucesión de reales no nulos, lo suficientemente pequeños para que t + a n esté en I, y tales que a n. Definimos la función de manera que ϕ n (x = f(x, t + a n f(x, t a n ; ϕ n(x = f t (x, t. Por la fórmula de los crecimientos finitos, obtenemos ϕ n (x sup θ 1 f t (x, t + θa n g(x. Aplicamos el T.C.D.L. y obtenemos que la función ϕ : x f t (x, t es integrable y que f t (x, t dµ(x = ϕ n (xdµ(x = ψ(t + a n ψ(t a n. Dado que la sucesión (a n n N es arbitraria, tenemos que la función ψ es derivable en el punto t y por lo tanto se obtiene la fórmula (9 para la derivada de ψ. Ejemplos (i Consideramos la función f(x, t = 1 [,t[ (x definida sobre R a valores reales. Vemos que la derivada parcial f t (x, t existe para casi todo x (x t y es nula, pero las hipótesis del teorema 5 exigen más: hay que encontrar un conjunto N de medida nula tal que para todo x / N la derivada parcial existe para todo t. En este caso esto es imposible y si derivamos sin precaución obtenemos un resultado falso. Si por un lado tenemos t f (x, tdx =, t por otro lado tenemos d dtϕ(t = 1: esto muestra a posteriori no se puede aplicar el teorema de derivación bajo el signo integral si no se cumplen las hipótesis. 6
7 (ii El segundo ejemplo que tratamos aquí corresponde a la función f(x, t = xt x = e(t 1 ln(x 1 + x. Deseamos aplicar el teorema de derivación bajo el signo integral y para ello verificaremos las hipótesis necesarias. a vimos que esta función es continua y que es integrable para todo t ], 1[, lo que nos proporciona la primera hipótesis. Dado que se tiene para todo x [, + [ la identidad tf(x, t = ln(xf(x, t tenemos la segunda hipótesis. Finalmente si definimos, para < a < t < b < 1, la función g(x = ln(x xa 1 1+x ln(x xb 1 1+x si < x < 1 si 1 x; obtenemos la tercera hipótesis pues + g(xdx < +. Todo esto nos permite concluir que se tiene la identidad d dt ϕ(t = + 5. Integración en los espacios producto ln(x xt x dx. Principal objetivo: resolver integrales dobles por medio de integrales simples. pero qué es una integral doble? = Los ejemplos anteriores muestran la importancia de medir funciones que dependen de más de una sola variable. Cuando hay dos variables, definidas sobre dos espacios medidos distintos, hablaremos de integrales dobles. = Es necesario construir la integral sobre el producto de espacios medidos. σ-álgebras producto Sean (, A y (, B dos espacios medibles. Llamaremos un subconjunto del producto cartesiano un rectángulo de lados medibles si es de la forma A B para algún A A y algún B B. El conjunto de rectángulos medibles será notado por A B = {A B; A A, B B}. = Si = = R, dotado de la σ-álgebra de los Borelianos, un adoquín es un rectángulo de lados medibles. Definición 2 (σ-álgebra producto Sean (, A y (, B dos espacios medibles. Definimos el producto tensorial de las σ-álgebras A y B como la σ-álgebra engendrada A B = σ(a B. = si consideramos y dotados de las σ-álgebras A = {, } y B = {, } respectivamente, vemos que A B = {, }. 7
8 Teorema 6 Sean y dos espacios topológicos. Entonces la σ-álgebra boreliana del espacio producto contiene al producto de la σ-álgebra boreliana de por la σ-álgebra boreliana de : Bor( Bor( Bor(. Si y son espacios topológicos a base numerable de abiertos, entonces se tiene la identidad Bor( Bor( = Bor(. Corolario 3 Para todo p, q 1 tenemos Bor(R p+q = Bor(R p Bor(R q. Necesidad de congelar las variables = introducción de la noción de secciones. Definición 3 Sean y dos conjuntos y sea E un subconjunto de. Para todo x y todo y definimos las secciones E y y E x como E y = {x : (x, y E} y E x = {y : (x, y E}. Si f es una función definida sobre, entonces las secciones f y y f x están definidas por f y (x = f(x, y y f x (y = f(x, y. Proposición 1 Sean (, A y (, B dos espacios medibles. 1 Si E es un subconjunto de que pertenece a A B, entonces cada sección E x pertenece a B y cada sección E y pertenece a A. 2 Si f es una función A B-medible definida sobre a valores en K, entonces cada sección f x es B-medible y cada sección f y es A -medible. Prueba. 1 Supongamos que x y sea F la colección de todos los subconjuntos E de A B tales que E x pertenece a B. Vamos a mostrar que F es una σ-álgebra que coincide con A B. Si A A y B B, entonces A B A B y se tiene (A B x = { B si x A si x / A. (1 = todos los rectángulos de lados medibles pertenecen a F y en particular se tiene que F. = si E F, tenemos que E c F pues (E c x = {y : (x, y E c } = {y : (x, y E} c = (E x c. = si (E n n N F, entonces n N E n F puesto que ( n N E n x = n N (E n x. Estos tres puntos muestran que F es una σ-álgebra contenida en A B que contiene todos los rectángulos de lados medibles. Pero dado que A B es la más pequeña σ-álgebra que contiene este tipo de rectángulos se deduce F = A B. Un razonamiento similar demuestra que si E es un subconjunto de que pertenece a A B, entonces cada sección E y pertenece a A. 2 Para esta segunda parte vemos que si f es A B-medible entonces, para todo abierto U de K, el conjunto E = {(x, y : f(x, y U} pertenece a A B. Por la primera parte, para todo x y todo y, las secciones E x y E y son B-medibles y A -medibles respectivamente, lo que demuestra que f x y f y son medibles. 8
9 Proposición 2 Sean (, A, µ y (, B, ν dos espacios medidos σ-finitos. Si E pertenece a la σ-álgebra A B, entonces las funciones son A -medible y B-medible respectivamente. ϕ : R y ψ : R x ν(e x y µ(e y Prueba. 1. La medida ν es finita. Sea F la clase de los conjuntos E A B tales que la función x ν(e x es A -medible. Vamos a verificar que F = A B. Si A A y B B, utilizando la fórmula (1 podemos escribir ν((a B x = ν(b1 A (x, (11 de manera que el rectángulo A B pertenece a F pues la función ν(b1 A (x es A -medible. En particular, el espacio pertenece a F. Si E y F son dos conjuntos de A B tales que E F, entonces se tiene ν((f \ E x = ν(f x ν(e x que es una función A -medible, lo que muestra que F es estable por diferencia propia. Sea ahora (E n n N una sucesión creciente de conjuntos de A B. Vemos que se tiene la identidad ν(( n E n x = ν((e n x ; dado que la función ite es A -medible, se deduce que F es estable por diferencia propia y por unión numerable de sucesiones crecientes. Es por lo tanto una clase monótona. Puesto que la familia de rectángulos de lados medibles es estable por construcción de intersecciones finitas, el teorema del folleto nos proporciona la identidad F = A B. Obtenemos entonces que la aplicación x ν(e x es medible para cada conjunto E de A B. 2. La medida ν es σ-finita. Sea (D n n N una sucesión de conjuntos disjuntos que pertenecen a B, de medida finita con respecto a ν y tales que n N D n =. Para cada n definimos una medida finita ν n sobre B escribiendo ν n (B = ν(b D n. Tenemos pues que las funciones x ν n (E x son A -medibles para todo n. Dado que la identidad ν(e x = n N ν n(e x se verifica para todo x, se deduce la medibilidad que la aplicación x ν(e x. La función y µ n (E y puede ser tratada de manera totalmente similar lo que termina la demostración. 9
10 Medidas producto Teorema 7 Sean (, A, µ y (, B, ν dos espacios medidos σ-finitos. Existe entonces una sola medida definida sobre A B, llamada medida producto y notada µ ν tal que para todo A A y B B se tiene la relación para los rectángulos medibles: µ ν(a B = µ(aν(b. La medida con respecto a µ ν de un conjunto cualquiera E de A B está dada por µ ν(e = ν(e x dµ(x = µ(e y dν(y. (12 Nótese que esta fórmula permite calcular la medida de los conjuntos A B-medibles a partir de las medidas iniciales µ y ν. Obtenemos así un espacio medido sobre el producto cartesiano de y que notaremos (, A B, µ ν. Demostración. La medibilidad de las aplicaciones x ν(e x y y µ(e y para cada conjunto E A B se deduce de la proposición anterior. Podemos entonces definir las funciones (µ ν 1 y (µ ν 2 sobre A B determinadas por (µ ν 1 (E = µ(e y dν(y y (µ ν 2 (E = ν(e x dµ(x. Observamos sin problema que (µ ν 1 ( = (µ ν 2 ( =. Si (E n n N es una sucesión de conjuntos disjuntos de A B y si E = n E n y si y ; entonces (En y n N es una sucesión de conjuntos disjuntos de A tales que E y = n En y y por lo tanto se tiene µ(e y = n N µ(ey n. Podemos ahora aplicar el corolario 1, que nos permite intercambiar los símbolos y, para obtener las identidades siguientes: (µ ν 1 (E = µ(e y dν(y = µ(endν(y y = ν 1 (E n. n N n N(µ Deducimos entonces que la aplicación (µ ν 1 es numerablemente aditiva y, repitiendo este razonamiento, se obtiene un resultado totalmente análogo para (µ ν 2. Para el caso de los rectángulos medibles, es fácil verificar que si A A y B B entonces se tiene (µ ν 1 (A B = µ(aν(b = (µ ν 2 (A B. De todos estos puntos deducimos que (µ ν 1 y (µ ν 2 son medidas sobre A B que proporcionan los resultados deseados sobre los rectángulos de lados medibles. La unicidad de µ ν se obtiene entonces por el corolario del folleto y por el teorema de unicidad de las medidas, lo que implica en particular que (µ ν 1 = (µ ν 2 y que se tiene (12 para todo E A B. Corolario 4 Sea (, A B, µ ν un espacio medido producto y sea E A B, las proposiciones siguientes son equivalentes: 1 E es de µ ν-medida nula, 2 E x es de ν-medida nula para µ-casi todo x, 3 E y es de µ-medida nula para ν-casi todo y. 1
11 Ejemplos (i Sea = = R de manera que = R 2. Sea λ la medida de Lebesgue sobre R y λ 2 la medida de Lebesgue 2-dimensional. Vemos entonces que para todo adoquín Γ de la forma [a, b] [c, d] tenemos el mismo resultado aplicando λ 2 o λ λ: λ 2 (Γ = (b a(d c = λ([a, b]λ([c, d], lo que nos proporciona una segunda construcción de la medida de Lebesgue de R 2. (ii Sea ahora a y b dos puntos. Tenemos entonces entre las medidas de Dirac la relación δ a δ b = δ (a,b. Más generalmente si µ = i I α iδ ai y si ν = j J β jδ bj tenemos la fórmula µ ν = (i,j I J α i β j δ (ai,b j. Observación 1 Es importante insistir en las hipótesis de este teorema. En efecto, si no suponemos que las medidas que intervienen en este teorema son σ-finitas, no se tiene necesariamente la unicidad de la medida producto µ ν y además la fórmula (12 puede ser falsa. Demos un ejemplo clásico de esta situación: sea = [, 1], sea µ la medida de Lebesgue sobre la σ-álgebra Bor([, 1] y sea ν la medida de conteo del conjunto de partes (no numerable de = [, 1]. Nótese que esta medida ν no es σ-finita. Vemos entonces que la diagonal del cuadrado E = [, 1] [, 1] es un elemento de la σ-álgebra producto y se tiene ν(e x dµ(x = 1 µ(e y dν(y =. Teoremas de Fubini-Tonelli Estos teoremas nos permite evaluar integrales dobles por medio de integrales simples = resultados importantísimos! Teorema 8 (Tonelli Sean (, A, µ y (, B, ν dos espacios medidos σ-finitos y consideremos f : [, + ] una función A B-medible. Entonces 1 las funciones ϕ : [, + ] y ψ : [, + ] x f(x, ydν(y y f(x, ydµ(x son A -medibles y B-medibles respectivamente. 2 si las funciones ϕ y ψ son integrables sobre y respectivamente, la función f es integrable sobre y se tienen las identidades siguientes ( f(x, ydµ ν(x, y = f(x, ydµ(x dν(y = ( f(x, ydν(y dµ(x. (13 11
12 Demostración. Supongamos para empezar que E pertenece a la σ-álgebra producto A B y que f es la función indicatriz de E. Tenemos entonces que las secciones f x y f y son las funciones indicatrices de las secciones E x y E y de manera que se tienen las relaciones f x(ydν(y = ν(e x y f y (xdµ(x = µ(e y para todo x, y. Por la proposición 2 y por el teorema 7 obtenemos los puntos 1 y 2 para las funciones indicatrices de conjuntos, mientras que la aditividad y la homogeneidad de la integral implican que estos puntos siguen siendo válidos para las funciones simples A B-medibles. Sea ahora f una función A B-medible. Por el teorema de aproximación por medio de funciones simples, existe una sucesión (f n n N de funciones simples crecientes que convergen hacia f. El primer punto se deduce entonces por la estabilidad de las funciones medibles. El segundo punto se obtiene utilizando el teorema de convergencia monótona. Vemos entonces que se tienen estos dos puntos para todas las funciones positivas A B-medibles, terminando así la demostración. Teorema 9 (Fubini Sean (, A, µ y (, B, ν dos espacios medidos σ-finitos. Sea f una función definida sobre a valores en K, integrable con respecto a la medida producto µ ν. Entonces 1 para µ-casi todo punto x la sección f x es ν-integrable y para ν-casi todo punto y la sección f y es µ-integrable. 2 se tienen las relaciones siguientes: f(x, ydµ ν(x, y = = ( ( f(x, ydµ(x dν(y f(x, ydν(y dµ(x. (14 Demostración. Tratamos solamente el caso de funciones a valores reales pues el caso complejo se deduce fácilmente del primero utilizando argumentos ya explicitados anteriormente. Sea pues f una función integrable sobre (y por lo tanto A B-medible y sean f + y f las partes positivas y negativas de f. La proposición 1 nos asegura que las aplicaciones f x, (f + x y (f x son B-medibles y el teorema de Tonelli implica que las funciones x (f + x (ydν(y y x (f x (ydν(y son A -medibles y µ-integrables, y son por lo tanto finitas µ-c.t.p. por el corolario De manera que la función f x es ν-integrable para µ-casi todo x. Gracias a estos puntos tenemos entonces que la aplicación f(x, ydν(y pertenece al espacio L(, A, µ y el teorema de Tonelli nos permite escribir f(x, ydµ ν(x, y = f + (x, ydµ ν(x, y f (x, ydµ ν(x, y ( ( = f x + (ydν(y dµ(x fx (ydν(y dµ(x ( = f(x, ydν(y dµ(x. Con esto hemos terminado la demostración del teorema dado que un argumento totalmente similar se utiliza para tratar f y. 12
13 Observación 2 Los teoremas de Tonelli y de Fubini pueden parecer a primera vista muy similares, sin embargo son muy diferentes y son utilizados en situaciones distintas. El teorema de Tonelli nos dice que si las integrales simples existen y son finitas entonces la integral doble existe y es finita. Por el contrario, el teorema de Fubini tiene como hipótesis la integrabilidad doble a partir de la cual se deduce la finitud de las integrales simples. Ejemplos (i Si la inversión del orden de integración conduce a resultados distintos se obtiene a posteriori que el teorema de Fubini no se aplica. Consideremos por ejemplo = = [, 1] dotado de su σ-álgebra natural y la función f : [, 1] [, 1] R definida por f(x, y = x2 y 2 (x 2 + y 2 2 si (x, y (, (dado que el conjunto {(, } es de medida nula no es necesario definir la función en este punto. Observando que se tienen las identidades ( d x dx x 2 + y 2 = x2 y 2 (x 2 + y 2 2 y ( d y dy x 2 + y 2 = x2 y 2 (x 2 + y 2 2, estamos tentados en realizar los cálculos siguientes: 1 x 2 y 2 1 (x 2 + y 2 dx = 2 y y 1 x 2 y 2 (x 2 + y 2 2 dy = 1 x A partir de estos cálculos obtenemos el resultado contradictorio siguiente 1 1 y dy = π 4 y 1 1 x dx = π 4. Este ejemplo ilustra la necesidad de verificar cuidadosamente las hipótesis del teorema 9 antes de lanzarse en cálculos que pueden resultar falsos. En efecto, vemos sin mayor dificultad que f + (x, y = x2 y 2 1 (x 2 +y 2 2 [,1] (x1 [,x] (y y obtenemos entonces 1 ( 1 1 ( 1 f + x 2 y 2 (x, ydy dx = (x 2 + y [,1](x1 [,x] (ydy dx 1 ( y x 1 = dx x 2 + y 2 dx = 2x = +, de donde se deduce que la función f(x, y no es integrable con respecto a la medida producto y que por lo tanto no se puede aplicar el teorema de Fubini. (ii Un caso simple de aplicación del teorema de Tonelli se encuentra cuando se multiplica dos funciones integrables definidas sobre conjuntos distintos: sean (, A, µ y (, B, ν dos espacios medidos σ-finitos y sean g : [, + [ y h : [, + [ dos funciones µ y ν integrables respectivamente. Si definimos f(x, y = g(xh(y tenemos por el teorema de Tonelli que esta función es µ ν-integrable. En efecto las funciones ϕ : [, + ] y ψ : [, + ] x g(x h(ydν(y y h(y g(xdµ(x son integrables lo que nos permite escribir ( f(x, ydµ ν(x, y = ( g(xdµ(x h(ydν(y. 13
14 Integrales múltiples Sea pues ( 1, A 1, µ 1,..., ( n, A n, µ n una colección finita de n espacios σ-finitos. Observemos para empezar que existe una correspondencia inyectiva del conjunto ( 1 n 1 n sobre el conjunto 1 n determinada por ϕ((x 1,..., x n 1, x n = (x 1,..., x n para todo x i i, i = 1,..., n. Este hecho nos sugiere que podemos utilizar lo anterioremente expuesto para la construcción de espacios medidos múltiples. Definimos entonces la σ-álgebra A 1 A n sobre 1 n como la σ-álgebra engendrada por los rectángulos de la forma A 1 A n en donde A i A i para todo 1 i n: A 1 A n = σ{a 1 A n : A i A i ; 1 i n} Vemos entonces que la aplicación ϕ transforma los conjuntos que generan la σ-álgebra (A 1 A n 1 A n en los conjuntos que generan la σ-álgebra A 1 A n, de manera que un conjunto E 1 n pertenece a A 1 A n si y solo si ϕ 1 (E pertenece a (A 1 A n 1 A n. Esto nos permite entonces aplicar n 1 veces el teorema 7 para obtener una medida µ 1 µ n definida sobre A 1 A n que verifique la identidad siguiente µ 1 µ n (A 1 A n = n µ i (A i para todo A i A i con 1 i n, obteniendo así un espacio medido sobre el producto 1 n que notaremos ( 1 n, A 1 A n, µ 1 µ n. Los teoremas de Fubini-Tonelli generalizados a las integrales múltiples nos proporcionan resultados del tipo siguiente en donde se puede intercambiar el orden de integración, siempre y cuando se verifiquen las hipótesis necesarias: f(x 1, x 2, x 3 dµ ν η(x 1, x 2, x 3 = = = ( ( ( i=1 ( f(x 1, x 2, x 3 dη(x 3 ( 3 f(x 1, x 2, x 3 dν(x 2 ( 2 f(x 1, x 2, x 3 dµ(x 1 1 dν(x 2 dµ(x 1 dη(x 3 dµ(x 1 dν(x 2 dη(x 3 14
1. Funciones medibles
 AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 4: Construcción de la integral de Lebesgue EPN, verano 2009 1. Funciones medibles Un concepto de medibilidad
AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 4: Construcción de la integral de Lebesgue EPN, verano 2009 1. Funciones medibles Un concepto de medibilidad
1. Propiedades básicas de las medidas
 AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 2: σ-álgebras y medidas EPN, verano 2009 1. Propiedades básicas de las medidas Marco de trabajo: la
AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 2: σ-álgebras y medidas EPN, verano 2009 1. Propiedades básicas de las medidas Marco de trabajo: la
1. Unicidad de Medidas
 AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2. Lección n 3: Construcción de medidas, Medida de Lebesgue EPN, verano 2009 1. Unicidad de Medidas = Es imposible
AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2. Lección n 3: Construcción de medidas, Medida de Lebesgue EPN, verano 2009 1. Unicidad de Medidas = Es imposible
Teoremas de Tonelli y Fubini
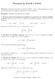 Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
Teoremas de Convergencia
 Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
El Teorema de Fubini-Tonelli
 Capítulo 26 El Teorema de Fubini-Tonelli Veremos en este capítulo que el cálculo de una integral múltiple se reduce al de integrales simples. Concretamente se va a probar que si f(x, y) es una función
Capítulo 26 El Teorema de Fubini-Tonelli Veremos en este capítulo que el cálculo de una integral múltiple se reduce al de integrales simples. Concretamente se va a probar que si f(x, y) es una función
Medida y Probabilidad
 Medida y Probabilidad Jorge Salazar 1 Enero 2015 1 Con el apoyo del Programa PROMETEO/SENESCYT del Gobierno del Ecuador. ii Contents 7 Integral de Lebesgue 1 7.1 Integración de funciones simples.................
Medida y Probabilidad Jorge Salazar 1 Enero 2015 1 Con el apoyo del Programa PROMETEO/SENESCYT del Gobierno del Ecuador. ii Contents 7 Integral de Lebesgue 1 7.1 Integración de funciones simples.................
El Teorema de Fubini-Tonelli
 Capítulo 23 El Teorema de Fubini-Tonelli Veremos en este capítulo que el cálculo de una integral múltiple se reduce al de integrales simples. Concretamente se va a probar que si f(x, y) es una función
Capítulo 23 El Teorema de Fubini-Tonelli Veremos en este capítulo que el cálculo de una integral múltiple se reduce al de integrales simples. Concretamente se va a probar que si f(x, y) es una función
1. MEDIDA E INTEGRACIÓN.
 1. MEDID E INTEGRCIÓN. En este capítulo repasamos algunos conceptos que se vieron en la asignatura mpliación de la Teoría de Funciones de Varias Variables. 1. MEDIDS POSITIVS. (1,1,1) Definición. Una σ-álgebra
1. MEDID E INTEGRCIÓN. En este capítulo repasamos algunos conceptos que se vieron en la asignatura mpliación de la Teoría de Funciones de Varias Variables. 1. MEDIDS POSITIVS. (1,1,1) Definición. Una σ-álgebra
Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2).
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 3: Lema de Baire y Teorema clásicos del Análisis Funcional EPN, verano 2012 Definición 1 (Espacio de
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 3: Lema de Baire y Teorema clásicos del Análisis Funcional EPN, verano 2012 Definición 1 (Espacio de
Integración de Funciones Reales
 Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Apuntes sobre la integral de Lebesgue
 Apuntes sobre la integral de Lebesgue Miguel Lacruz Martín Universidad de Sevilla 1. Medida de Lebesgue 1.1. Introducción La longitud l(i) de un intervalo I R se define habitualmente como la distancia
Apuntes sobre la integral de Lebesgue Miguel Lacruz Martín Universidad de Sevilla 1. Medida de Lebesgue 1.1. Introducción La longitud l(i) de un intervalo I R se define habitualmente como la distancia
1. Funciones Medibles
 1. Medibles Medibles simples... Hasta ahora hemos estudiado la medida de Lebesgue definida sobre los conjuntos de R n y sus propiedades. Vamos a aplicar ahora esta teoría al estudio de las funciones escalares
1. Medibles Medibles simples... Hasta ahora hemos estudiado la medida de Lebesgue definida sobre los conjuntos de R n y sus propiedades. Vamos a aplicar ahora esta teoría al estudio de las funciones escalares
Ejercicios de teoría de la medida
 Ejercicios de teoría de la medida Pedro Alegría Capítulo. Dada una aplicación F : Ω Ω, demostrar que: a) Si A es una σ-álgebra de Ω, A = {B Ω : F B) A} lo es de Ω. b) Si A es una σ-álgebra de Ω, A = F
Ejercicios de teoría de la medida Pedro Alegría Capítulo. Dada una aplicación F : Ω Ω, demostrar que: a) Si A es una σ-álgebra de Ω, A = {B Ω : F B) A} lo es de Ω. b) Si A es una σ-álgebra de Ω, A = F
Integral de Lebesgue
 Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
Parte 5: Integración en espacios producto.
 Parte 5: Integración en espacios producto. Definición 1 Sean (X; M, µ) y (Y, N, ν) espacios de medida. Se define la σ álgebra producto M N como la σ álgebra generada por los llamados rectángulos medibles,
Parte 5: Integración en espacios producto. Definición 1 Sean (X; M, µ) y (Y, N, ν) espacios de medida. Se define la σ álgebra producto M N como la σ álgebra generada por los llamados rectángulos medibles,
En primer lugar, vamos a precisar un concepto al que ya nos hemos referido anteriormente, el de σ-álgebra.
 Capítulo 20 Conjuntos de Borel Hemos demostrado ya que la familia M de los conjuntos medibles contiene a todos los abiertos de R n y, por tanto, a todos los conjuntos que podamos formar a partir de los
Capítulo 20 Conjuntos de Borel Hemos demostrado ya que la familia M de los conjuntos medibles contiene a todos los abiertos de R n y, por tanto, a todos los conjuntos que podamos formar a partir de los
Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 1: Aplicaciones Lineales EPN, verano 2012
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 1: Aplicaciones Lineales EPN, verano 212 Introducción Algunas fechas: 197: Noción de Operador lineal
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 1: Aplicaciones Lineales EPN, verano 212 Introducción Algunas fechas: 197: Noción de Operador lineal
1. Medida Exterior. Medida de Lebesgue en R n
 1. La integral de Lebesgue surge del desarrollo de la integral de Riemann, ante las dificultades encontradas en las propiedades de paso al ĺımite para calcular la integral de una función definida como
1. La integral de Lebesgue surge del desarrollo de la integral de Riemann, ante las dificultades encontradas en las propiedades de paso al ĺımite para calcular la integral de una función definida como
Teoría de la Probabilidad Tema 2: Teorema de Extensión
 Teoría de la Probabilidad Tema 2: Teorema de Extensión Alberto Rodríguez Casal 25 de septiembre de 2015 Definición Una clase (no vacía) A de subconjuntos de Ω se dice que es un álgebra si A es cerrada
Teoría de la Probabilidad Tema 2: Teorema de Extensión Alberto Rodríguez Casal 25 de septiembre de 2015 Definición Una clase (no vacía) A de subconjuntos de Ω se dice que es un álgebra si A es cerrada
Análisis real y complejo. Análisis Funcional
 UNIVERSIDAD DE SEVILLA Análisis real y complejo. Análisis Funcional Máster Universitario en Matemática Avanzada Luis Bernal González Departamento de Análisis Matemático Sevilla, febrero de 212 Disponible
UNIVERSIDAD DE SEVILLA Análisis real y complejo. Análisis Funcional Máster Universitario en Matemática Avanzada Luis Bernal González Departamento de Análisis Matemático Sevilla, febrero de 212 Disponible
Comisión de Pedagogía - Diego Chamorro Un (corto) panorama de Análisis Armónico (Nivel 3).
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Un (corto) panorama de Análisis Armónico (Nivel 3). Lección n : La ecuación de ondas como punto de partida UCE, otoño 04 Introducción El objetivo
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Un (corto) panorama de Análisis Armónico (Nivel 3). Lección n : La ecuación de ondas como punto de partida UCE, otoño 04 Introducción El objetivo
Medidas. Problemas para examen. Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez.
 Medidas Problemas para examen Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez. Sigma-álgebras 1. Propiedades elementales de σ-álgebras. Demuestre que una σ-álgebra es
Medidas Problemas para examen Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez. Sigma-álgebras 1. Propiedades elementales de σ-álgebras. Demuestre que una σ-álgebra es
1. Teoría de Littlewood-Paley
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis armónico y espacios funcionales (Nivel 3). Lección n 2: Teoría y Descomposiciones de Littlewood-Paley. EPN, verano 2010 1. Teoría de
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis armónico y espacios funcionales (Nivel 3). Lección n 2: Teoría y Descomposiciones de Littlewood-Paley. EPN, verano 2010 1. Teoría de
El Teorema de la Convergencia Dominada
 Capítulo 22 l Teorema de la Convergencia Dominada Los dos teoremas de convergencia básicos en la integración Lebesgue son el teorema de la convergencia monótona (Lema 19.10), que vimos el capítulo y el
Capítulo 22 l Teorema de la Convergencia Dominada Los dos teoremas de convergencia básicos en la integración Lebesgue son el teorema de la convergencia monótona (Lema 19.10), que vimos el capítulo y el
1. Convergencia en medida
 FACULTAD CS. FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA3801 Teoría de la Medida. Semestre 2009-02 Profesor: Jaime San Martín Auxiliares: Andrés Fielbaum y Cristóbal Guzmán Clase auxiliar 7 21 de Septiembre
FACULTAD CS. FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA3801 Teoría de la Medida. Semestre 2009-02 Profesor: Jaime San Martín Auxiliares: Andrés Fielbaum y Cristóbal Guzmán Clase auxiliar 7 21 de Septiembre
Notas de clase sobre la Transformada de Fourier
 Notas de clase sobre la Transformada de Fourier Pablo L. De Nápoli 3 de noviembre de 205. La definición de la transformada de Fourier Definición. Si f L ( ) definimos su transformada de fourier por f(ξ)
Notas de clase sobre la Transformada de Fourier Pablo L. De Nápoli 3 de noviembre de 205. La definición de la transformada de Fourier Definición. Si f L ( ) definimos su transformada de fourier por f(ξ)
2. CONSTRUCCIÓN DE MEDIDAS.
 2. CONSTRUCCIÓN DE MEDIDAS. 1. MEDIDAS EXTERIORES. (2,1,1) Definición. Una medida exterior es una aplicación µ : P(X) [0, + ] que cumple: (a) µ ( ) = 0. (b) Monotonía: Si A B, entonces µ (A) µ (B). (c)
2. CONSTRUCCIÓN DE MEDIDAS. 1. MEDIDAS EXTERIORES. (2,1,1) Definición. Una medida exterior es una aplicación µ : P(X) [0, + ] que cumple: (a) µ ( ) = 0. (b) Monotonía: Si A B, entonces µ (A) µ (B). (c)
Comisión de Pedagogía - Diego Chamorro Ecuaciones en Derivadas Parciales (Nivel 3).
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Ecuaciones en Derivadas Parciales (Nivel 3). Lección n 2: Soluciones clásicas de las ecuaciones de Navier-Stokes USFQ, noviembre 215 Índice
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Ecuaciones en Derivadas Parciales (Nivel 3). Lección n 2: Soluciones clásicas de las ecuaciones de Navier-Stokes USFQ, noviembre 215 Índice
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
Derivada de la función compuesta. Regla de la cadena
 Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
1. Teorema de Fubini. Teorema de Fubini.
 1. El teorema de Fubini nos va a dar una técnica para el cálculo de integrales de funciones de varias variables mediante el cálculo de varias integrales de funciones de una variable. partir de ahí se podrán
1. El teorema de Fubini nos va a dar una técnica para el cálculo de integrales de funciones de varias variables mediante el cálculo de varias integrales de funciones de una variable. partir de ahí se podrán
Comisión de Pedagogía - Diego Chamorro Ecuaciones en Derivadas Parciales (Nivel 3).
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Ecuaciones en Derivadas Parciales (Nivel 3). Lección n 1: Repaso de Ecuaciones Diferenciales Ordinarias UPS, julio 2015 Índice 1. Dos ejemplos
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Ecuaciones en Derivadas Parciales (Nivel 3). Lección n 1: Repaso de Ecuaciones Diferenciales Ordinarias UPS, julio 2015 Índice 1. Dos ejemplos
Espacios compactos. Se pretenden alcanzar las siguientes competencias específicas:
 4 Espacios compactos En este capítulo introducimos los conceptos de espacio y subespacio compacto. Se estudian propiedades de los conjuntos compactos, así como relación entre la compacidad y las funciones
4 Espacios compactos En este capítulo introducimos los conceptos de espacio y subespacio compacto. Se estudian propiedades de los conjuntos compactos, así como relación entre la compacidad y las funciones
Conjuntos Medibles. Preliminares
 Capítulo 18 Conjuntos Medibles Preliminares En el capítulo anterior vimos que la medida exterior de Lebesgue no resulta σ-aditiva en todo R n. Ahora vamos a construir una familia M de subconjuntos de R
Capítulo 18 Conjuntos Medibles Preliminares En el capítulo anterior vimos que la medida exterior de Lebesgue no resulta σ-aditiva en todo R n. Ahora vamos a construir una familia M de subconjuntos de R
Transformaciones lineales
 CAPíTULO 4 Transformaciones lineales En este capítulo estudiamos las primeras propiedades de las transformaciones lineales entre espacios vectoriales. 1. Construcciones de transformaciones lineales Lema
CAPíTULO 4 Transformaciones lineales En este capítulo estudiamos las primeras propiedades de las transformaciones lineales entre espacios vectoriales. 1. Construcciones de transformaciones lineales Lema
Recordemos que utilizaremos, como es habitual, la siguiente notación para algunos conjuntos de números que son básicos.
 Capítulo 1 Preliminares Vamos a ver en este primer capítulo de preliminares algunos conceptos, ideas y propiedades que serán muy útiles para el desarrollo de la asignatura. Se trata de resultados sobre
Capítulo 1 Preliminares Vamos a ver en este primer capítulo de preliminares algunos conceptos, ideas y propiedades que serán muy útiles para el desarrollo de la asignatura. Se trata de resultados sobre
El teorema del valor intermedio
 Ya hemos tratado en un artículo anterior el problema de la continuidad de una función. Ahora nos hemos de preguntar sobre las ventajas que, en análisis matemático, nos proporciona este hecho. Existen una
Ya hemos tratado en un artículo anterior el problema de la continuidad de una función. Ahora nos hemos de preguntar sobre las ventajas que, en análisis matemático, nos proporciona este hecho. Existen una
Continuidad y monotonía
 Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Cambio de Variables en la Integral Múltiple
 Capítulo 24 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Capítulo 24 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Funciones continuas e inyectivas
 Nuestro último teorema afirmaba que toda función continua en un intervalo cerrado y acotado tiene máximo y mínimo absolutos, pero nada nos informa sobre los puntos en los que se alcanzan. Bajo la hipótesis
Nuestro último teorema afirmaba que toda función continua en un intervalo cerrado y acotado tiene máximo y mínimo absolutos, pero nada nos informa sobre los puntos en los que se alcanzan. Bajo la hipótesis
Funciones continuas. Definición y propiedades
 Funciones continuas. Definición y propiedades Para la lectura de este artículo es recomendable haber leído con anterioridad otros tres artículos relacionados con las sucesiones de números reales y las
Funciones continuas. Definición y propiedades Para la lectura de este artículo es recomendable haber leído con anterioridad otros tres artículos relacionados con las sucesiones de números reales y las
El teorema de Lebesgue
 Capítulo 3 El teorema de Lebesgue En este capítulo estudiaremos un teorema que nos dice exactamente qué funciones son integrables y cuán grande puede ser la frontera de un conjunto para que éste tenga
Capítulo 3 El teorema de Lebesgue En este capítulo estudiaremos un teorema que nos dice exactamente qué funciones son integrables y cuán grande puede ser la frontera de un conjunto para que éste tenga
El Teorema de Stone-Weierstrass
 Capítulo 3 El Teorema de Stone-Weierstrass Vamos a ver en esta lección el teorema clásico de Weierstrass y la importante generalización del mismo dada por Stone. El teorema de Weierstrass El teorema de
Capítulo 3 El Teorema de Stone-Weierstrass Vamos a ver en esta lección el teorema clásico de Weierstrass y la importante generalización del mismo dada por Stone. El teorema de Weierstrass El teorema de
Espacios métricos completos
 5 Espacios métricos completos Comenzamos introduciendo las sucesiones de Cauchy, que relacionamos con las sucesiones convergentes. En el caso de que coincidan, se trata de un espacio métrico completo.
5 Espacios métricos completos Comenzamos introduciendo las sucesiones de Cauchy, que relacionamos con las sucesiones convergentes. En el caso de que coincidan, se trata de un espacio métrico completo.
ANÁLISIS FUNCIONAL Notas de curso. M.A. Rodríguez Departamento de Física Teórica II Universidad Complutense de Madrid
 ANÁLISIS FUNCIONAL Notas de curso M.A. Rodríguez Departamento de Física Teórica II Universidad Complutense de Madrid 2 de septiembre de 22 Índice general. La integral de Lebesgue 3.. Introducción............................................
ANÁLISIS FUNCIONAL Notas de curso M.A. Rodríguez Departamento de Física Teórica II Universidad Complutense de Madrid 2 de septiembre de 22 Índice general. La integral de Lebesgue 3.. Introducción............................................
Espacios topológicos. 3.1 Espacio topológico
 Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Cambio de variables en la integral múltiple.
 Cambio de variables en la integral múltiple. En este apartado vamos a generalizar la fórmula g(b) g(a) f(x) dx = b a f(g(t)) g (t) dt al caso de funciones de n variables. Como la región de integración
Cambio de variables en la integral múltiple. En este apartado vamos a generalizar la fórmula g(b) g(a) f(x) dx = b a f(g(t)) g (t) dt al caso de funciones de n variables. Como la región de integración
La Medida de Lebesgue. Problema de la Medida
 Capítulo 19 La Medida de Lebesgue. Problema de la Medida Hemos demostrado en el capítulo anterior que la medida exterior de Lebesgue es una medida sobre la familia M de los conjuntos medibles. Por definición,
Capítulo 19 La Medida de Lebesgue. Problema de la Medida Hemos demostrado en el capítulo anterior que la medida exterior de Lebesgue es una medida sobre la familia M de los conjuntos medibles. Por definición,
CÁLCULO II. Grado M+I. Sucesiones y series de funciones. Sucesiones y series de funciones 1 / 27. Grado M+I () CÁLCULO II
 CÁLCULO II Grado M+I Sucesiones y series de funciones Sucesiones y series de funciones 1 / Sucesiones funciones. Convergencia puntual Sucesión de funciones Definición Una sucesión de funciones será cualquier
CÁLCULO II Grado M+I Sucesiones y series de funciones Sucesiones y series de funciones 1 / Sucesiones funciones. Convergencia puntual Sucesión de funciones Definición Una sucesión de funciones será cualquier
Ejercicios Variable Real
 UNIVERSIDAD AUTÓNOMA DE MADRID FACULTAD DE MATEMÁTICAS Ejercicios Variable Real Antonio Córdoba (Manuel Mellado Cuerno) 1º Cuatrimestre del curso 2016-2017 manuel.mellado@estudiante.uam.es 2 Capítulo 1
UNIVERSIDAD AUTÓNOMA DE MADRID FACULTAD DE MATEMÁTICAS Ejercicios Variable Real Antonio Córdoba (Manuel Mellado Cuerno) 1º Cuatrimestre del curso 2016-2017 manuel.mellado@estudiante.uam.es 2 Capítulo 1
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias.
 Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Espacios compactos. 7.1 Espacios compactos
 58 Capítulo 7 Espacios compactos 7.1 Espacios compactos Definición 7.1.1 (Recubrimiento). Sea X un conjunto y sea S X. Un recubrimiento de S es una familia A = {A i } i I de subconjuntos de X tales que
58 Capítulo 7 Espacios compactos 7.1 Espacios compactos Definición 7.1.1 (Recubrimiento). Sea X un conjunto y sea S X. Un recubrimiento de S es una familia A = {A i } i I de subconjuntos de X tales que
Topología en R n. Continuidad de funciones de varias variables
 . Continuidad de funciones de varias variables María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I (1 o Grado en Ingeniería Electrónica Industrial y Automática) M. Muñoz (U.P.C.T.) Continuidad
. Continuidad de funciones de varias variables María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I (1 o Grado en Ingeniería Electrónica Industrial y Automática) M. Muñoz (U.P.C.T.) Continuidad
Espacios completos. 8.1 Sucesiones de Cauchy
 Capítulo 8 Espacios completos 8.1 Sucesiones de Cauchy Definición 8.1.1 (Sucesión de Cauchy). Diremos que una sucesión (x n ) n=1 en un espacio métrico (X, d) es de Cauchy si para todo ε > 0 existe un
Capítulo 8 Espacios completos 8.1 Sucesiones de Cauchy Definición 8.1.1 (Sucesión de Cauchy). Diremos que una sucesión (x n ) n=1 en un espacio métrico (X, d) es de Cauchy si para todo ε > 0 existe un
Sucesiones y series de funciones
 Sucesiones y series de funciones Renato Álvarez Nodarse Departamento de Análisis Matemático Facultad de Matemáticas. Universidad de Sevilla http://euler.us.es/ renato/ 8 de octubre de 2012 Sucesiones y
Sucesiones y series de funciones Renato Álvarez Nodarse Departamento de Análisis Matemático Facultad de Matemáticas. Universidad de Sevilla http://euler.us.es/ renato/ 8 de octubre de 2012 Sucesiones y
Cambio de Variables en la Integral Múltiple
 Capítulo 27 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Capítulo 27 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Terminaremos el capítulo con una breve referencia a la teoría de cardinales.
 TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
Sucesiones monótonas Monotonía. Tema 6
 Tema 6 Sucesiones monótonas Vamos a discutir ahora una importante propiedad de ciertas sucesiones de números reales: la monotonía. Como primer resultado básico, probaremos que toda sucesión monótona y
Tema 6 Sucesiones monótonas Vamos a discutir ahora una importante propiedad de ciertas sucesiones de números reales: la monotonía. Como primer resultado básico, probaremos que toda sucesión monótona y
Probabilidades y la Teoría de Integración
 Capítulo 2 Probabilidades y la Teoría de Integración Contents 2.0.2. σ-álgebras, variables aleatorias y leyes de probabilidad.............. 8 2.0.3. Integrales y esperanzas................................
Capítulo 2 Probabilidades y la Teoría de Integración Contents 2.0.2. σ-álgebras, variables aleatorias y leyes de probabilidad.............. 8 2.0.3. Integrales y esperanzas................................
Tema 1 EL TEOREMA DE PEANO. 1 Compacidad en C(I; R N ): el Teorema de Ascoli-
 Tema 1 EL TEOREMA DE PEANO En este tema vamos a probar que bajo la hipótesis de ser f continua en un entorno del punto (, y 0 ), se puede garantizar la existencia, aunque no necesariamente la unicidad,
Tema 1 EL TEOREMA DE PEANO En este tema vamos a probar que bajo la hipótesis de ser f continua en un entorno del punto (, y 0 ), se puede garantizar la existencia, aunque no necesariamente la unicidad,
Parte III. Medida e Integración en R n
 Parte III Medida e Integración en R n Capítulo 17 La Medida Exterior de Lebesgue en R n El cálculo de longitudes, áreas y volúmenes es uno de los asuntos matemáticos con más larga tradición histórica,
Parte III Medida e Integración en R n Capítulo 17 La Medida Exterior de Lebesgue en R n El cálculo de longitudes, áreas y volúmenes es uno de los asuntos matemáticos con más larga tradición histórica,
sup si A no es acotado.
 Capítulo 5 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Capítulo 5 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 2: Teorema de Hahn-Banach EPN, verano 2012
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 2: Teorema de Hahn-Banach EPN, verano 2012 1. Forma analítica Empecemos directamente con la primera
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 2: Teorema de Hahn-Banach EPN, verano 2012 1. Forma analítica Empecemos directamente con la primera
Práctica 1. Continuidad Ejercicios resueltos
 Práctica 1. Continuidad Ejercicios resueltos 1. Estudiar la continuidad de los campos escalares definidos por f(x, y) = x y x 2 + y 2 g(x, y) = x2 y x 2 + y 4 h(x, y) = x y2 x 2 + y 4 para todo (x, y)
Práctica 1. Continuidad Ejercicios resueltos 1. Estudiar la continuidad de los campos escalares definidos por f(x, y) = x y x 2 + y 2 g(x, y) = x2 y x 2 + y 4 h(x, y) = x y2 x 2 + y 4 para todo (x, y)
Parte 4: Teoremas de convergencia.
 Parte 4: Teoremas de convergencia. Como siempre, si no se dice lo contrario, se supone que (, M, µ) es un espacio de medida y trabajamos con funciones de dominio y recorrido contenido en C o R o R. Empezamos
Parte 4: Teoremas de convergencia. Como siempre, si no se dice lo contrario, se supone que (, M, µ) es un espacio de medida y trabajamos con funciones de dominio y recorrido contenido en C o R o R. Empezamos
1.3. El teorema de los valores intermedios
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 07-2 Importante: Visita regularmente http://www.dim.uchile.cl/calculo. Ahí encontrarás
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 07-2 Importante: Visita regularmente http://www.dim.uchile.cl/calculo. Ahí encontrarás
sup si A no es acotado.
 Capítulo 6 Espacios completos 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y
Capítulo 6 Espacios completos 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y
Elementos Básicos de Análisis Funcional en. Dr. Oldemar Rodríguez Rojas
 Elementos Básicos de Análisis Funcional en Análisis Numérico Dr. Oldemar Rodríguez Rojas Agosto 2008 Contents 1 Elementos Básicos de Análisis Funcional 2 1.1 Espacios normados...........................
Elementos Básicos de Análisis Funcional en Análisis Numérico Dr. Oldemar Rodríguez Rojas Agosto 2008 Contents 1 Elementos Básicos de Análisis Funcional 2 1.1 Espacios normados...........................
Análisis Real Apuntes de clase. Preparado por JC Trujillo O.
 Análisis Real Apuntes de clase Preparado por JC Trujillo O. Agosto - Diciembre 2013 Índice general 1 Números Reales 5 1 Clase 1-2013/07/29................................. 5 2 Los números reales..................................
Análisis Real Apuntes de clase Preparado por JC Trujillo O. Agosto - Diciembre 2013 Índice general 1 Números Reales 5 1 Clase 1-2013/07/29................................. 5 2 Los números reales..................................
Integrales múltiples
 ntegrales múltiples Cálculo (2004) * El objetivo de este capítulo es definir y aprender a calcular integrales de funciones reales de varias variables, que llamamos integrales múltiples. Las motivación
ntegrales múltiples Cálculo (2004) * El objetivo de este capítulo es definir y aprender a calcular integrales de funciones reales de varias variables, que llamamos integrales múltiples. Las motivación
Capítulo La integral de Riemann
 Capítulo 5 Integración 1. La integral de iemann Empecemos por recordar la integral de iemann de una función acotada f : [a, b]. Una partición P de [a, b] es un subconjunto finito P [a, b] tal que a, b
Capítulo 5 Integración 1. La integral de iemann Empecemos por recordar la integral de iemann de una función acotada f : [a, b]. Una partición P de [a, b] es un subconjunto finito P [a, b] tal que a, b
Departamento de Ingeniería Matemática - Universidad de Chile
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
ANÁLISIS FUNCIONAL Y ECUACIONES EN DERIVADAS PARCIALES HOJA 2: FORMULACIÓN DÉBIL DE PROBLEMAS ELÍPTICOS
 ANÁLSS FUNCONAL Y ECUACONES EN DERVADAS PARCALES HOJA : FORMULACÓN DÉBL DE PROBLEMAS ELÍPTCOS E. Sean X e Y dos espacios normados y sea T : X Y una aplicación lineal. Probar que las siguientes afirmaciones
ANÁLSS FUNCONAL Y ECUACONES EN DERVADAS PARCALES HOJA : FORMULACÓN DÉBL DE PROBLEMAS ELÍPTCOS E. Sean X e Y dos espacios normados y sea T : X Y una aplicación lineal. Probar que las siguientes afirmaciones
Continuidad de funciones reales y vectoriales de variable vectorial
 Capítulo 6 Continuidad de funciones reales y vectoriales de variable vectorial 6.1. Introducción Hasta el momento hemos estudiado funciones reales de variable real, es decir, funciones de la forma f :
Capítulo 6 Continuidad de funciones reales y vectoriales de variable vectorial 6.1. Introducción Hasta el momento hemos estudiado funciones reales de variable real, es decir, funciones de la forma f :
Reglas de derivación Sumas, productos y cocientes. Tema 4
 Tema 4 Reglas de derivación Aclarado el concepto de derivada, su significado analítico y sus interpretaciones geométrica y física, pasamos a desarrollar las reglas básicas para el cálculo de derivadas
Tema 4 Reglas de derivación Aclarado el concepto de derivada, su significado analítico y sus interpretaciones geométrica y física, pasamos a desarrollar las reglas básicas para el cálculo de derivadas
Ejercicios de Análisis Funcional
 Ejercicios de Análisis Funcional Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada ANÁLISIS FUNCIONAL Relación de Ejercicios N o 1 1. Dar un ejemplo de una distancia en un espacio
Ejercicios de Análisis Funcional Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada ANÁLISIS FUNCIONAL Relación de Ejercicios N o 1 1. Dar un ejemplo de una distancia en un espacio
Departamento de Matemáticas
 MA25 Clase 5: Series de potencias. Operaciones con series de potencias. Series de potencias Elaborado por los profesores Edgar Cabello y Marcos González Cuando estudiamos las series geométricas, demostramos
MA25 Clase 5: Series de potencias. Operaciones con series de potencias. Series de potencias Elaborado por los profesores Edgar Cabello y Marcos González Cuando estudiamos las series geométricas, demostramos
Límite superior y límite inferior de una sucesión
 Límite superior y límite inferior de una sucesión Objetivos. Definir las nociones de los límites superior e inferior de una sucesión y estudiar sus propiedades básicas. Requisitos. Supremo e ínfimo de
Límite superior y límite inferior de una sucesión Objetivos. Definir las nociones de los límites superior e inferior de una sucesión y estudiar sus propiedades básicas. Requisitos. Supremo e ínfimo de
Elementos de Teoría de la Medida, Análisis Funcional y Teoría de Distribuciones
 Elementos de Teoría de la Medida, Análisis Funcional y Teoría de Distribuciones Thelma: Mr. Dodd, how do you occupy your leisure? Dodd: Mrs. Cherie, all the excitement, the romance, the adventure that
Elementos de Teoría de la Medida, Análisis Funcional y Teoría de Distribuciones Thelma: Mr. Dodd, how do you occupy your leisure? Dodd: Mrs. Cherie, all the excitement, the romance, the adventure that
Sucesiones y convergencia
 Capítulo 2 Sucesiones y convergencia 1. Definiciones Una de las ideas fundamentales del análisis es la de límite; en particular, el límite de una sucesión. En este capítulo estudiaremos la convergencia
Capítulo 2 Sucesiones y convergencia 1. Definiciones Una de las ideas fundamentales del análisis es la de límite; en particular, el límite de una sucesión. En este capítulo estudiaremos la convergencia
2. El Teorema del Valor Medio
 2.24 45 2. El Teorema del Valor Medio Comenzaremos esta sección recordando dos versiones del teorema del valor medido para funciones de 1-variable y por tanto ya conocidas: 2.22 Sea f : [a, b] R R una
2.24 45 2. El Teorema del Valor Medio Comenzaremos esta sección recordando dos versiones del teorema del valor medido para funciones de 1-variable y por tanto ya conocidas: 2.22 Sea f : [a, b] R R una
Funciones convexas Definición de función convexa. Tema 10
 Tema 10 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones reales de variable real definidas en
Tema 10 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones reales de variable real definidas en
Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones
![Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones](/thumbs/49/25360651.jpg) Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
EJERCICIOS RESUELTOS. NÚMEROS Y FUNCIONES. CONTINUIDAD Y LÍMITE FUNCIONAL.
 EJERCICIOS RESUELTOS. NÚMEROS Y FUNCIONES. CONTINUIDAD Y LÍMITE FUNCIONAL. 1. Estúdiese la continuidad de la función f : R R, definida por f (x) = xe(1/x) si x = 0, f (0) = 1.. Sea f : R R continua, mayorada
EJERCICIOS RESUELTOS. NÚMEROS Y FUNCIONES. CONTINUIDAD Y LÍMITE FUNCIONAL. 1. Estúdiese la continuidad de la función f : R R, definida por f (x) = xe(1/x) si x = 0, f (0) = 1.. Sea f : R R continua, mayorada
E.T.S.I. INFORMÁTICOS (UPM) SOLUCIONES EXAMEN FINAL (16/6/2014) 2 n 2 +n. n = (n 2 + 1) (n 2 3n) n n 2 3n = lím. n + 1 n. n 2 n = 3 2
 MATEMÁTICA APLICADA CÁLCULO E.T.S.I. INFORMÁTICOS UPM o G.I.I. SOLUCIONES EXAMEN FINAL 6/6/04 er EXAMEN PARCIAL. Calcule los siguientes ites, si existen: a n + n 3n. b n n + 3 n +n a El ite presenta una
MATEMÁTICA APLICADA CÁLCULO E.T.S.I. INFORMÁTICOS UPM o G.I.I. SOLUCIONES EXAMEN FINAL 6/6/04 er EXAMEN PARCIAL. Calcule los siguientes ites, si existen: a n + n 3n. b n n + 3 n +n a El ite presenta una
1. Construcción de la Integral
 1. Construcción de la Integral La integral de Riemann en R n es una generalización de la integral de funciones de una variable. La definición que vamos a dar reproduce el método de Darboux para funciones
1. Construcción de la Integral La integral de Riemann en R n es una generalización de la integral de funciones de una variable. La definición que vamos a dar reproduce el método de Darboux para funciones
CARACTERIZACIONES DE LA COMPLETITUD DE R
 CARACTERIZACIONES DE LA COMPLETITUD DE R 1 Definición 1. Diremos que un cuerpo ordenado K es arquimediano si lím n n que decir que N, visto como subconjunto de K, no está acotado en K. = 0 en K. Esto es
CARACTERIZACIONES DE LA COMPLETITUD DE R 1 Definición 1. Diremos que un cuerpo ordenado K es arquimediano si lím n n que decir que N, visto como subconjunto de K, no está acotado en K. = 0 en K. Esto es
Departamento de Matemática Aplicada a la I.T. de Telecomunicación
 Departamento de Matemática Aplicada a la I.T. de Telecomunicación ASIGNATURA: CÁLCULO I (Examen Final) CONVOCATORIA: FEBRERO FECHA: de Enero de 3 Duración del examen: 3 horas Fecha publicación notas: 8--3
Departamento de Matemática Aplicada a la I.T. de Telecomunicación ASIGNATURA: CÁLCULO I (Examen Final) CONVOCATORIA: FEBRERO FECHA: de Enero de 3 Duración del examen: 3 horas Fecha publicación notas: 8--3
Teorema del Valor Medio
 Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Aplicaciones de las derivadas. El teorema del valor medio
 Aplicaciones de las derivadas. El teorema del valor medio Ya hemos hablado en un par de artículos anteriores del concepto de derivada y de su interpretación tanto desde el punto de vista geométrico como
Aplicaciones de las derivadas. El teorema del valor medio Ya hemos hablado en un par de artículos anteriores del concepto de derivada y de su interpretación tanto desde el punto de vista geométrico como
Tema 2: Series numéricas
 Tema 2: Series numéricas Una serie infinita (o simplemente serie) es una suma formal de infinitos términos a + a 2 + a 3 + + + Al número se le denomin-ésimo término de la serie Se llama sucesión de sumas
Tema 2: Series numéricas Una serie infinita (o simplemente serie) es una suma formal de infinitos términos a + a 2 + a 3 + + + Al número se le denomin-ésimo término de la serie Se llama sucesión de sumas
Sucesiones y Series Sucesiones
 Capítulo 6 Sucesiones y Series 6.. Sucesiones En particular estudiaremos las sucesiones de números reales, es decir, las que verifican la siguiente definición. Definición 6... Llamaremos sucesión a la
Capítulo 6 Sucesiones y Series 6.. Sucesiones En particular estudiaremos las sucesiones de números reales, es decir, las que verifican la siguiente definición. Definición 6... Llamaremos sucesión a la
Olimpiada Iberoamericana de Matemática Universitaria 2012 Problemas, soluciones y criterios
 Olimpiada Iberoamericana de Matemática Universitaria 202 Problemas, soluciones y criterios. Problemas. (3 puntos) Sea Z el anillo de los enteros. Los conjuntos Z, 2Z y 3Z son semigrupos con respecto a
Olimpiada Iberoamericana de Matemática Universitaria 202 Problemas, soluciones y criterios. Problemas. (3 puntos) Sea Z el anillo de los enteros. Los conjuntos Z, 2Z y 3Z son semigrupos con respecto a
Funciones de R m R n
 Funciones de R n R m Funciones de R m R n Una funcion f : R n R m es una función cuyo dominio es un subconjunto Ω R n. Denotada por f : Ω R m donde a cada x R n f le asigna un vector f(x) R m. Ejemplo.-
Funciones de R n R m Funciones de R m R n Una funcion f : R n R m es una función cuyo dominio es un subconjunto Ω R n. Denotada por f : Ω R m donde a cada x R n f le asigna un vector f(x) R m. Ejemplo.-
10. Series de potencias
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 7-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 7-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
Conjuntos Medibles. La identidad de Caratheodory
 Capítulo 18 Conjuntos Medibles La identidad de Caratheodory En el capítulo anterior vimos que la medida exterior de Lebesgue no resulta σ-aditiva en todo R n. Ahora vamos a construir una familia M de subconjuntos
Capítulo 18 Conjuntos Medibles La identidad de Caratheodory En el capítulo anterior vimos que la medida exterior de Lebesgue no resulta σ-aditiva en todo R n. Ahora vamos a construir una familia M de subconjuntos
Parte 2: Definición y ejemplos de topologías.
 Parte 2: Definición y ejemplos de topologías. 22 de marzo de 2014 1. Definiciones y propiedades básicas. Definición 1 Sea X un conjunto. Una familia T de subconjuntos de X es una topología de X si se cumplen:
Parte 2: Definición y ejemplos de topologías. 22 de marzo de 2014 1. Definiciones y propiedades básicas. Definición 1 Sea X un conjunto. Una familia T de subconjuntos de X es una topología de X si se cumplen:
Series de Fourier absolutamente convergentes
 Series de Fourier absolutamente convergentes Objetivos. Estudiar las propiedades principales de series de Fourier absolutamente convergentes. Ya hemos mostrado que los caracteres del grupo Z se pueden
Series de Fourier absolutamente convergentes Objetivos. Estudiar las propiedades principales de series de Fourier absolutamente convergentes. Ya hemos mostrado que los caracteres del grupo Z se pueden
