TEMA 2 FUNDAMENTOS Y APLICACIONES DE LA TEORIA DE GRAFOS. DIAGRAMAS EN ARBOL.
|
|
|
- Carlos Contreras Ortiz de Zárate
- hace 7 años
- Vistas:
Transcripción
1 1. Introducción. 2. Definición de grafo Grafo Simple Grafo General Grafo Orientado Grafo Nulo Grafo Completo Grafo Regular Grafo Bipartido. 3. Operaciones entre Grafos Isomorfismos y homomorfismos Combinaciones Supresiones y Contracciones Complementos. 4. Trayectorias. Grafos Eulerianos y Hamiltonianos Trayectorias Los puentes de Königsberg Grafos Eulerianos Grafos Hamiltonianos. 5. Matrices y Grafos Matriz de Adyacencia Matriz de Incidencia. 6. Planaridad y dualidad Grafos Planares Grafos Duales. 7. Diagramas en árbol La enumeración de árboles. 8. Coloreado de Grafos. 9. Aplicaciones de la teoría de Grafos El teorema matrimonial de Hall El teorema de Menger La teoría de matroides. 1/ 17
2 TEMA 2 FUNDAMENTOS Y APLICACIONES DE LA TEORIA DE GRAFOS. DIAGRAMAS EN ARBOL. 1. INTRODUCCIÓN. La teoría de grafos, que nació como una rama de la Topología, se ha convertido hoy en día en una herramienta matemática indispensable en campos tan diversos como la investigación operativa, la lingüística, la química, la física, la genética, la teoría de redes o la teoría de la decisión. Es por ello, que para casi cualquier rama de la ciencia, se hace indispensable el conocimiento, a través de conceptos globales, de las ideas básicas que sustentan a la denominada teoría de grafos. Este tema tiene por objetivo introducir al lector en estos conocimientos básicos a través de una breve pero, esperamos, clara exposición de las líneas generales de esta teoría. 2. DEFINICIÓN DE GRAFO. Se denomina grafo G al par (V(G), E(G)), en el que V(G) es un conjunto no vacío de elementos denominados vértices (también llamados nodos o puntos) y E(G) es un conjunto finito de pares no ordenados de elementos de V(G) denominados aristas (igualmente líneas). Al conjunto de elementos de V(G) se le denomina conjunto de vértices y al conjunto de elementos de E(G) conjunto de aristas. Así, sea el conjunto de vértices V(G)={u, v, w, z} y el conjunto de aristas E(G)={{u, v}, {u, w}, {w, z}}, se dice que {u, v} es la arista que une los puntos u y v, y se le designa de forma abreviada por uv. Si u=v la arista recibe el nombre de lazo. La representación de dicho grafo es la siguiente: Se dice que dos vértices u y w de un grafo G son adyacentes si el grafo contiene una arista que los une. Se dice también que los vértices son incidentes en dicha arista. Análogamente, se dice que dos aristas son adyacentes si tienen, al menos, un vértice en común. Se denomina grado de un vértice v de G al número de aristas que inciden en v, y se designará g(v) (un lazo en v contribuye de manera doble al grado de v). A un vértice de grado 0 se le denomina vértice aislado. A un vértice de grado 1 se le denomina vértice terminal o extremo. Un subgrafo de un grafo G, es un grafo cuyos vértices pertenecen a V(G) y cuyas aristas pertenecen a E(G). 2/ 17
3 En los siguientes apartados de este punto se expone la tipología más común de los grafos Grafo Simple. Se denomina grafo simple al grafo G={V(G), E(G)} que verifica que para todo u, v perteneciente a V(G), existe a lo sumo una única arista {u, v} de E(G) que los une. Grafo Simple [ u, v V(G)!{u, v} E(G)] Ejemplos de grafos simples serían los siguientes: 2.2. Grafo General. Se denomina grafo general o simplemente grafo, al grafo G=(V(G), E(G)), con V(G) conjunto de vértices y E(G) conjunto de aristas. De esta forma, un grafo general puede representar dos vértives unidos por más de una arista. Igualmente, una arista no tiene porque unir dos vértices diferentes, pudiéndose hablar de la arista {u, u}. A la arista que une un vértice consigo mismo se le denomina Lazo. La representación gráfica de este tipo sería: 2.3. Grafo Orientado. Un grafo orientado D, también denominados redes o digrafos, se define como un par (V(D), A(D)), donde V(D) es un conjunto finito no vacío de elementos llamados vértices, y A(D) es una familia finita de pares ordenados de elementos de V(D) llamados arcos (o aristas orientadas o di-aristas). En base a la existencia o no de lazos, podremos hablar de digrafos generales o digrafos simples. A continuación se muestra el diagrama del digrafo general (V(D), A(D)), con V(D)={u, v, w, z} y A(D)={uv, vv,uw, vw, wv, wu, wz} 3/ 17
4 2.4. Grafo Nulo. Se denomina grafo nulo a un grafo donde E(G) es vacío, es decir, el conjunto de aristas es el conjunto vacío. Obviamente en este tipo de grafo todo vértice es aislado Grafo Completo. Un grafo completo es un grafo simple en el que cualquier par de vértices son adyacentes. n Un grafo completo de n vértices n n tiene ( 1) = aristas. El resultado se 2 2 obtiene por combinaciones de n vértices tomados de dos en dos Grafo Regular. Se llama grafo regular a un grafo cuyos vértices tienen todos el mismo grado. Si el grado de cada vértice es r, se tiene un grafo regular de grado r. Todo grafo nulo es un grafo regular de grado 0. Todo grafo completo con n vértices es un grafo regular de grado n-1. Especial mención merece un tipo de grafo regular llamado grafo platónico, grafos formados por los cinco sólidos regulares (tetraedro, cubo, octaedro, dodecaedro e icosaedro) Grafo Bipartido. Sea un grafo G y sea su conjunto de vértices V(G) que puede ser expresado como la unión disjunta de dos subconjuntos de vértices V 1 y V 2 de forma que cada arista de G une un vértice de V 1 con otro de V 2, entonces se dice que G es un grafo bipartido y se escribe G(V 1, V 2 ). 3. OPERACIONES ENTRE GRAFOS Isomorfismo y Homomorfismo. Se dice que dos grafos G 1 y G 2 son isomorfos si existe una correspondencia biunívoca entre los vértices de G 1 y los de G 2, con la propiedad de que el número de aristas que unen cada dos vértices de G 1 es igual al número de aristas que unen los vértices correspondientes de G 2. 4/ 17
5 Veamos el ejemplo siguiente, donde G 1 tiene el conjunto de vértices {u, v, w, x, y, z} y G 2 tiene {l, m, n, p, q, r}. G 1 y G 2 son isomorfos bajo la correspondencia u l, v m, w n, x p, y q, z r Dos grafos son homomórficos (o idénticos salvo vértices de grado 2) si ambos pueden ser obtenidos a partir del mismo grafo insertando nuevos vértices de grado dos en sus aristas. Ejemplo: Sea el grafo G representado por el siguiente diagrama: G(V(G), E(G)) V(G)={v 1, v 2, v 3, v 4 } E(G)={v 1 v 2, v 1 v 3, v 3 v 2, v 2 v 4 } Construimos dos grafos homomórficos entre sí G 1 y G 2 a partir del anterior grafo G. Para ello, y partiendo de G, tomamos algunas de sus aristas y le insertamos un vértice de grado dos. Construimos G 1 : Sea la arista v 1 v 2 del grafo G, insertamos un nuevo vértice v de grado 2, de tal forma que el grafo G 1 resultante sería: De igual manera construimos G 2 : Sea la arista v 1 v 3 G, insertamos el vértice v de grado 2 de tal forma que el grafo resultante G 2 es: Se concluye que G 1 y G 2 son homomórficos. 3.2.Combinaciones. Sean dos grafos G 1 =(V(G 1 ); E(G 1 )) y G 2 =(V(G 2 ), E(G 2 )) con V(G 1 ) y V(G 2 ) disjuntos. Se define el grafo unión como G 1 G 2 tal que G 1 G 2 =(V(G 1 ) V(G 2 ), E(G 1 ), E(G 2 )). 5/ 17
6 Se dice que un grafo es conexo si no puede ser expresado como la unión de dos grafos, en caso contrario será inconexo. Cualquier grafo inconexo G puede verse expresado como la unión de un conjunto finito de grafos conexos. Un grafo circuito es un grafo conexo regular de grado dos. El grafo circuito de n vértices es designado C n. Igualmente, sean los grafos G 1 y G 2, se define el grafo suma, y se denota por G 1 +G 2 como la unión de ambos grafos, trazándose a continuación una arista entre cada vértice de G 1 y cada vértice de G 2. Sean los grafos G 1 =(V(G 1 ), E(G 1 )) con V(G 1 )={u, v, w, x, y, z} y G 2 =(V(G 2 ), E(G 2 )) con V(G 2 )={l, m, n} representados de la forma siguiente: Se representa el grafo G 1 G 2 de la forma: Y el grafo G 1 +G 2 como: 3.3.Supresiones y Contracciones. Sea F un conjunto de aristas del grafo G, se denomina G-F al grafo que se obtiene cuando se suprime en G el conjunto de aristas F. Análogamente, sea H un conjunto de vértices del grafo G, se denomina G-H al grafo que resulta cuando se suprimen en G los vértices que hay en H y las aristas que inciden en ellos. Sea el grafo G y en él la arista e, se denomina G/e al grafo obtenido de contraer en él la arista e, es decir, eliminar la arista, identificando a continuación sus extremos v y w, de forma que el vértice resultante es incidente a aquellas aristas que originalmente eran incidentes a v y w (excepto la propia arista e). En consecuencia, se llama 6/ 17
7 contracción de G a cualquier grafo que se obtiene a partir de G, después de efectuar contracciones de algunas de sus aristas. Sea el grafo G 1 =(V(G 1 ), E(G 1 )) con V(G 1 )={u, v, w, x} y E(G 1 )={uu, uv, vw, wu, wx, xv} y sea F={uw, xv}, se representa el grafo supresión G- F de la forma siguiente: 3.4.Complemento. Sea G un grafo simple, cuyo conjunto de vértices es V(G), el complemento(g) de G (denotado por G ) es el grafo simple que tiene a V(G) como conjunto de vértices, en el cual dos vértices son adyacentes si y sólo si no son adyacentes en G. Con el grafo G definido en el apartado anterior, se construye el grafo complemento de G de la siguiente forma: 4. TRAYECTORIAS. GRAFOS EULERIANOS Y HAMILTONIANOS. 4.1.Trayectorias. Sea una secuencia de aristas v 0 v 1, v 1 v 2,..., v m-1 v m, en la que todas las aristas son diferentes, entonces se le denomina cola. Si además los vértices v 0, v 1,..., v m, son diferentes (excepto el primero y el último que pudieran coincidir), la secuencia de aristas resultante se llama trayectoria. Una trayectoria es cerrada si v 0 =v m, y una trayectoria cerrada que posee al menos un lado es denominada circuito. Los siguientes ejemplos ilustran estas definiciones: Cola: Trayectoria: 7/ 17
8 Trayectoria cerrada: Al vértice v 0 se le denomina vértice inicial y al v m vértice final. La longitud de una secuencia de aristas es el número de aristas que posee. TEOREMA: Si G(V 1, V 2 ) es un grafo bipartido, todo circuito en G tiene longitud par. TEOREMA: Sea G un grafo simple de n vértices, si G tiene k componentes (subgrupos disjuntos) el número de aristas de G cumple la siguiente relación: n k m 1 (n k) (n k + 1) 2 m = número de aristas Se denomina conjunto desconectador de un grafo conexo G al conjunto de aristas de G cuya eliminación desconecta a G. Un conjunto corte será un conjunto desconectador del que ningún subconjunto suyo es un conjunto desconectador. Sea el grafo G, donde V(G)={v, w, x, y, z} y E(G)={vw, vx, wy, yz, wx, wz, xy, xz}, el conjunto de aristas D={wy, wz, xy, xz} es un conjunto desconectador de G, ya que si en G procedemos a la eliminación de las aristas de D queda el grafo inconexo que a continuación se expone Los Puentes de Königsberg. En el siglo XVIII, la ciudad de Königsberg, en Prusia, tenía dos islas y siete puentes según indica la figura: El alcalde de la ciudad escribió a Euler planteándole la siguiente cuestión: Es posible que una persona cruce los siete puentes pasando por cada uno de ellos una sola vez? 8/ 17
9 Euler probó que era imposible lo que el alcalde proponía. Sustituyó la isla y las orillas por puntos y los puentes por líneas que unían dichos puntos, obteniendo así el siguiente grafo: El grafo será recorrible si existe un camino que contenga todos los vértices y que pase por cada arista exactamente una vez. Supongamos que haya un camino que no empiece ni termine en un vértice u. Cada vez que el camino llegue a u debe de salir por otro que no haya sido utilizado. De esa manera, las aristas del camino incidentes con u deben aparecer de dos en dos, es decir, u es par. Así, si v es impar, el camino debe empezar y terminar en Q. Basándose en ese razonamiento, se deduce que no puede haber más de dos vértices que sean impares. El grafo anterior tiene cuatro vértices impares, por lo que no es recorrible Grafo Euleriano. Se denomina grafo euleriano, a un grafo conexo G que tiene una cola cerrada que incluye todas las aristas de G. TEOREMA de Euler: Un grafo es euleriano si y sólo si cada vértice es de grado par. Si tiene exactamente dos vértices impares es recorrible (la cola no será cerrada) y se llama semieuleriano. A continuación se muestran ejemplos de grafos no eulerianos, semieulerianos y eulerianos respectivamente Grafo Hamiltoniano. Se denomina grafo hamiltoniano, si existe un camino cerrado que contiene todos los vértices una sola vez (no tiene porque contener todas las aristas). Un grafo que posea una trayectoria que pase a través de cada vértice es denominado semihamiltoniano. Los siguientes ejemplos corresponden a un grafo no hamiltoniano, semihamiltoniano y hamiltoniano respectivamente. 9/ 17
10 5. MATRICES Y GRAFOS. Dado un grafo G con m vértices y n aristas, podemos asociar matrices a G, muy útiles para el cálculo Matriz de Adyacencia. Es la matriz A=(a ij ) de orden mx m definida por: k si v i es adyacentea v j donde k es el número de aristas que a ij = 0 en caso contrario unen el vértice v i con el v j La matriz de adyacencia es muy útil para decidir cuestiones de conexión, pues si A es la matriz de adyacencia de un grafo con m vértices donde m>1, entonces el término a ij de la matriz A n nos da el número de caminos de longitud n que van del vértice v i al vértice v j. La demostración se puede hacer por inducción en n Matriz de Incidencia. Es la matriz M=(m ij ) de orden mx m tal que m ij es 1 si el vértice v i es incidente con la arista e j y cero en caso contrario. 6. PLANARIDAD Y DUALIDAD Grafos Planares. Se denomina grafo planar a un grafo trazado en el plano de forma que ningún par de aristas se cortan geométricamente, excepto en el vértice que ambas inciden. Ejemplos de grafos planares son: Igualmente se dice que un grafo es planar si puede ser empotrado en el plano, es decir, dibujado sin cruces. A continuación se exponen algunos teoremas y corolarios referentes a la teoría de grafos planos. TEOREMA: El grafo K 3,3 (grafo bipartido completo con seis vértices y nueve aristas) y el grafo K 5 (grafo regular de grado cuatro, cinco vértices y diez aristas) son no planares. 10/ 17
11 La demostración de este teorema (que omitiremos en este tema dada su complejidad) se puede realizar de dos maneras distintas, por el teorema de Jordan o por la fórmula de Euler. TEOREMA de Kuratowski: Un grafo es planar si y sólo si no contiene ningún subgrafo que sea homomórfico a K 5 y K 3,3. Fórmula de Euler: el teorema o fórmula de Euler, relaciona el número de vértices, aristas y caras de un grafo plano conexo G. Sea un punto del plano x, se dice que x es disjunto de G si x no representa ni un vértice de G ni un punto que pertenezca a una arista de G. En este contexto, se define cara de G que contiene a x como al conjunto de todos los puntos del plano que pueden ser alcanzados desde x siguiendo una curva de Jordan, cuyos puntos sean todos disjuntos de G. Dos puntos del plano x e y son equivalentes si ambos son disjuntos de G y pueden ser unidos por una curva de Jordan cuyos puntos sean todos disjuntos de G. Esta relación de equivalencia sobre los puntos del plano disjuntos de G define clases de equivalencia a las que se denominan caras de G. TEOREMA: Si G es un grafo plano conexo, y sea n el número de vértices, m el número de aristas y f el de caras de G, se cumple la siguiente relación: n-m+f=2 (vértices aristas + caras = 2) dem. La demostración de este teorema se hace por la técnica matemática de la inducción, en este caso sobre el número de aristas m. Caso m=0 Sea el número de aristas m=0, y dado que G es conexo, se tiene que el número de vértices n=1 y f=1. Por tanto el teorema queda demostrado para m=0. Caso m-1 Hipótesis de inducción, suponemos ahora el teorema cierto para todos los grafos planos conexos tales que tiene m 1 aristas: n ( m 1) + (f 1) = 2 Caso m Sea ahora G un grafo planar conexo, y e una arista contenida en algún circuito de G. Entonces G e es un grafo planar conexo con n vértices, m 1 aristas y f 1 caras, de forma que G e verifica: n ( m 1) + (f 1) = 2 por la hipótesis de inducción. De aquí se desprende que G cumple el teorema: n m + f = 2. 11/ 17
12 COROLARIO: Si G es un grafo plano con n vértices, m aristas, f caras y k componentes, se cumple que: n m + f = k +1 COROLARIO: Si G es un grafo planar conexo simple de n vértices (n 3) y m aristas, se cumple m 3 n 6. TEOREMA: Todo grafo planar simple contiene un vértice cuyo grado es a lo sumo cinco. dem. Se supone, sin pérdida de generalidad, que el grafo es plano y conexo, y que contiene al menos tres vértices. Si todo vértice tuviera grado 6 como mínimo, se tendría que 6n 2m, con lo que se llega a una contradicción. Por tanto se tiene que el grado es a lo sumo de cinco Grafos Duales. Sea G un grafo plano, se llama grafo dual de G y se denota por G *, aquel construido de la siguiente manera: a) Se elige un punto v i en cada cara F i de G. Estos puntos son los vértices de G *. b) Por cada arista e G se traza una línea e * que atraviesa únicamente la arista e, y se unen los vértices v i pertenecientes a las caras adjuntas a e. Estas líneas son las aristas de G *. A continuación se ilustra este procedimiento de construcción con un ejemplo: Como teoremas significativos dentro de la teoría de grafos duales, se comentan los siguientes: TEOREMA: Si G es un grafo plano de n vértices, m aristas y f caras, y su dual G * tiene n * vértices, m * aristas y f * caras, se cumplen las siguientes relaciones: dem. n * = f m * = m f * = n La demostración de las dos primeras expresiones salen directamente a partir de la aplicación de la definición de dualidad. Para demostrar la tercera expresión, se ha de sustituir las dos primeras en la denominada fórmula de Euler. 12/ 17
13 7. DIAGRAMAS EN ÁRBOL. La teoría de árboles fue enunciada y elaborada por Cayley. Un grafo que no posee ningún circuito se denomina bosque, si además es un bosque conexo, se denomina árbol. Como ejemplos representativos de árboles se tienen los siguientes: Algunas de las propiedades características de los árboles son las siguientes: TEOREMA: Sea T un grafo con n vértices. Los siguientes enunciados son equivalentes: 1) T es un árbol. 2) T no contiene ningún circuito, y posee n 1 aristas. 3) T es conexo y tiene n 1 aristas. 4) T es conexo y cada arista es un istmo. 5) Cada dos vértices de T están conectados por una única trayectoria. 6) T no contiene ningún circuito, pero la adición de cualquier nueva arista crea exactamente un circuito. dem. Si n = 1 los seis enunciados son triviales. Supondremos, por tanto, que n 2. Para la demostración del teorema, demostraremos las implicaciones consecutivas, es decir, 1) 2) 3) 4) 5) 6) 1). 1) 2) T es árbol y por definición no contiene ningún circuito. Esto conlleva que la eliminación de cualquier arista va a dividir a T en dos grafos. Cada uno de estos grafos es un árbol. Por ello, y por inducción, el número de aristas en cada uno de los árboles es menor, en una unidad, que el número de vértices que tiene el grafo total. Por tanto, el número total de aristas de T es n 1. 2) 3) Si T fuera inconexo, entonces cada componente de T sería un grafo conexo sin ningún circuito y, por tanto, según se ha demostrado antes, el número de vértices de cada componente excedería en 1 del número de aristas. Por tanto, el número total de vértices de T excedería en al menos 2 del número total de aristas. Hemos llegado a una contradicción, pues T tiene n 1 aristas. Esto es porque se parte de una premisa falsa, es decir, el hecho de que T fuera inconexo. Por tanto T es conexo. 13/ 17
14 3) 4) La eliminación de cualquier arista daría lugar a un grafo con n vértices y n 2 aristas, que será inconexo. 4) 5) Como T es conexo, se sigue que cada par de vértices han de estar conectados por al menos una trayectoria. Dados dos vértices, si estos estuvieran conectados por dos trayectorias, entre ellos habría un circuito, contradicción con que toda arista es un istmo. 5) 6) Por reducción al absurdo, si T tuviese un circuito, cualquier par de vértices incluidos en el circuito estarían conectados por, al menos, dos trayectorias, lo que es una contradicción con las premisas. Si añadimos una arista e a T, se creará un circuito ya que los vértices incidentes a e ya están conectados en T. 6) 1) Supongamos que T no es un árbol, por tanto es inconexo. Si le añadimos cualquier arista que una un vértice de una componente a un vértice de otra, no se creará ningún circuito. Sin embargo, por el punto 6) se tiene que al añadir una nueva se crea un circuito, por tanto tenemos una contradicción. COROLARIO: Un bosque G con n vértices y k componentes tiene n k aristas. TEOREMA: Todo árbol G tiene al menos un vértice de grado 1. dem. Sean los vértices del árbol v 1, v 2,...,v n. Partiendo de v 1 vamos a su vecino v 2. Si el grado de v 2 es 1, ya está probado el teorema. En cualquier otro caso, vamos al vértice v 3 a través de otra arista. De esta forma se puede obtener el camino v 1 v 2 v 3... en el que ninguno de los v i son iguales por la definición de árbol. Como el número de vértices es finito, el camino tiene un último vértice v j. Evidentemente, éste tendrá grado 1, ya que se ha llegado a él y no se puede dejar. TEOREMA: Existe un único camino entre dos vértices cualesquiera v y w de un árbol. TEOREMA: Sea G un grafo conecto (dos vértices cualesquiera se encuentran unidos por un camino) de n vértices y n 1 aristas, entonces es un árbol La enumeración de árboles. La enumeración de grafos tiene por objeto encontrar el número de grafos no isomorfos que poseen una propiedad determinada. 14/ 17
15 En general, se denomina grafo etiquetado de n vértices a un grafo a cuyos vértices se le asignan números enteros de 1 a n, es decir, se trata de una aplicación biunívoca del conjunto de vértices de G sobre el conjunto {1, 2, 3,..., n}. El grafo etiquetado se designa (G,&) donde & es el etiquetado. Ejemplo de árbol etiquetado: TEOREMA: El número de árboles en los cuales el vértice v i tiene grado d i +1, v 2 tiene grado d 2 +1,..., v n tiene grado d n +1 viene determinado por el número combinatorio: dem. n 2 = (n 2)! d, d,..., d d 1!d 2!...d n! 1 2 n Como el grado de cada vértice es por lo menos 1, d i son enteros no negativos. Si se añaden los grados de cada vértice y se cuentan cada una de las n 1 aristas dos veces, se tiene (d 1 +1)+(d 2 +1)+...+(d n +1) = 2(n 1) A partir de aquí se tendrá la demostración del teorema. Ejemplo: Número de árboles con grado para el primer vértice 3, para el segundo 3 y del tercero al sexto 1. Como d 1 =d 2 =2 y d 3 =d 4 =d 5 =d 6 =0, entonces el número de árboles es 4 = 4! = 6 2,2,0,0,0,0 2!2! Dichos árboles son: TEOREMA de CAYLEY: Existen n n 2 árboles etiquetados diferentes de n vértices. Existen varios métodos de demostración para este teorema. Uno de ellos debido a Prufer y Clarke, y es: Se establece una correspondencia biunívoca entre el conjunto de árboles etiquetados de orden n y el conjunto de todos los símbolos ordenados (a 1, a 2,..., a n-2 ) 15/ 17
16 donde a i está definido como entero entre 1 y n. Dado que existen n n n n (n 2 veces) de tales símbolos, la demostración se tiene casi inmediata. 8. COLOREADO DE GRAFOS. Se dice que un grafo G sin lazos es k-coloreable si puede asignarse a cada uno de sus vértices uno de k colores dados de forma que ningún par de vértices adyacentes tengan el mismo color. Si es coloreable de grado k pero no de grado k 1, entonces G es k-cromático. Como ejemplo, sea el siguiente grafo 4-cromático. TEOREMA: Un grafo G cuyo máximo grado de vértice es &, entonces es (&+1)- coloreable. dem. Utilizaremos la inducción sobre el número de vértices. Si G tiene n vértices, si se suprime un vértice, el mayor grado para éste será &. Por hipótesis de inducción, este grafo es (&+1)-coloreable. TEOREMA: Si G es un grafo simple conexo no completo, si el mayor de los grados de sus vértices es & ( 3), entonces es &-coloreable. TEOREMA: Todo grafo planar es 5-coloreable. 9. APLICACIONES DE LA TEORÍA DE GRAFOS. Son varias las aplicaciones y usos que las distintas ciencias o áreas hacen de la teoría de grafos. La aplicación más importante dentro de la matemática moderna se encuentra en el campo de la combinatoria. Veamos algunos de los ejemplos más importantes: 9.1. El Teorema Matrimonial de Hall. Sea un conjunto finito de muchachos, cada uno de los cuales conoce a varias chicas. En qué condiciones se pueden formar los matrimonios de tal forma que cada uno de los muchachos se case con la chica que conoce? TEOREMA de Hall Una condición necesaria y suficiente para la solución del problema matrimonial es que cada conjunto de k jóvenes conozca colectivamente k chicas al menos (1 k m) El teorema de Menger. Determinación del número de trayectorias que unen dos vértices dados u, v de un grafo G. 16/ 17
17 TEOREMA de Menger. El número máximo de trayectorias de vértices disjuntos que conectan dos vértices diferentes no adyacentes v y w de G es igual al número mínimo de vértices de un subconjunto separador vw. TEOREMA: El teorema de Menger implica el teorema de Hall La teoría de Matroides. Aplicación de ciertos resultados de la teoría de grafos a la teoría transversal, donde aparece el concepto de matroide como un conjunto dotado de una estructura de independencia. Bibliografía. Algoritmos en Grafos y Redes. Aut. Blas Pelegrín, Lázaro Cánovas. Edit. P.P.U. Matemática Discreta y Combinatoria. Aut. Ralph Grimaldi. Edit. Addison-Wesley Iberoamericana. Lecciones de Optimización. Aut. Juan José Salazar. Edit. Universidad de La Laguna Graphs and Algorithms. Aut. M. Gondron, M. Minoux. Edit. Wiley-Intercience. Algebra y Matemática Discreta. Aut. J.A. Aledo Sánchez, J.C. Valverde Fajardo. Edit. Popular Libros. 17/ 17
Un grafo G = (V, E) se dice finito si V es un conjunto finito.
 1 Grafos: Primeras definiciones Definición 1.1 Un grafo G se define como un par (V, E), donde V es un conjunto cuyos elementos son denominados vértices o nodos y E es un subconjunto de pares no ordenados
1 Grafos: Primeras definiciones Definición 1.1 Un grafo G se define como un par (V, E), donde V es un conjunto cuyos elementos son denominados vértices o nodos y E es un subconjunto de pares no ordenados
Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre
 Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto. Típicamente, un grafo se representa
Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto. Típicamente, un grafo se representa
Minicurso de Teoría de Gráficas Escuela de Verano 2014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana
 Minicurso de Teoría de Gráficas Escuela de Verano 014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana Índice 1. Conceptos básicos 1 1.1. Nomenclatura...................................
Minicurso de Teoría de Gráficas Escuela de Verano 014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana Índice 1. Conceptos básicos 1 1.1. Nomenclatura...................................
Un grafo G es un par (V,E) donde V es un conjunto (llamado conjunto de vértices) y E un subconjunto de VxV (conjunto de aristas).
 TEMA 5.- GRAFOS 5.1.- DEFINICIONES BÁSICAS Un grafo G es un par (V,E) donde V es un conjunto (llamado conjunto de vértices) y E un subconjunto de VxV (conjunto de aristas). Gráficamente representaremos
TEMA 5.- GRAFOS 5.1.- DEFINICIONES BÁSICAS Un grafo G es un par (V,E) donde V es un conjunto (llamado conjunto de vértices) y E un subconjunto de VxV (conjunto de aristas). Gráficamente representaremos
Apuntes de Matemática Discreta 14. Grafos
 Apuntes de Matemática Discreta 14. Grafos Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 14 Grafos Contenido 14.1 Generalidades.....................................
Apuntes de Matemática Discreta 14. Grafos Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 14 Grafos Contenido 14.1 Generalidades.....................................
SISTEMA DE NUMEROS REALES
 SISTEMA DE NUMEROS REALES 1.1 Conjuntos Es una agrupación de objetos distintos (pero con algunas características en común), los que reciben el nombre de elementos. Generalmente se nombra a un conjunto
SISTEMA DE NUMEROS REALES 1.1 Conjuntos Es una agrupación de objetos distintos (pero con algunas características en común), los que reciben el nombre de elementos. Generalmente se nombra a un conjunto
Tema: Los Grafos y su importancia para la optimización de redes.
 Tema: Los Grafos y su importancia para la optimización de redes. Qué son los Grafos? Un grafo es una dupla G= {X,U}, donde X es un conjunto finito y no vacio de elementos llamados vértices y U es el conjunto
Tema: Los Grafos y su importancia para la optimización de redes. Qué son los Grafos? Un grafo es una dupla G= {X,U}, donde X es un conjunto finito y no vacio de elementos llamados vértices y U es el conjunto
Relaciones. Estructuras Discretas. Relaciones. Relaciones en un Conjunto. Propiedades de Relaciones en A Reflexividad
 Estructuras Discretas Relaciones Definición: relación Relaciones Claudio Lobos, Jocelyn Simmonds clobos,jsimmond@inf.utfsm.cl Universidad Técnica Federico Santa María Estructuras Discretas INF 152 Sean
Estructuras Discretas Relaciones Definición: relación Relaciones Claudio Lobos, Jocelyn Simmonds clobos,jsimmond@inf.utfsm.cl Universidad Técnica Federico Santa María Estructuras Discretas INF 152 Sean
b) Sea una relación de equivalencia en A y una operación en A. Decimos que y son compatibles si a b a c b c y c a c b para todo a, b, c A
 APENDICE Relaciones y Operaciones Compatibles 1 Definición: a) Sea A un conjunto y una relación entre elementos de A. Decimos que es una relación de equivalencia si es: i Reflexiva: a A, a a. ii Simétrica:
APENDICE Relaciones y Operaciones Compatibles 1 Definición: a) Sea A un conjunto y una relación entre elementos de A. Decimos que es una relación de equivalencia si es: i Reflexiva: a A, a a. ii Simétrica:
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Problemas y Conjeturas
 U UNIVERSITAT DE BARCELONA B Problemas y Conjeturas de la Teoría de Grafos (Trabajo Académicamente Dirigido) Autora: Cristina Araúz Lombardía Trabajo Académicamente Dirigido por F. Javier Soria de Diego
U UNIVERSITAT DE BARCELONA B Problemas y Conjeturas de la Teoría de Grafos (Trabajo Académicamente Dirigido) Autora: Cristina Araúz Lombardía Trabajo Académicamente Dirigido por F. Javier Soria de Diego
Caminos y Flujos optimales. Introducción a la Investigación de Operaciones 2007
 Caminos y Flujos optimales Introducción a la Investigación de Operaciones 2007 Contenido Definiciones básicas. Conexidad. Clausura transitiva. Esqueletos y caminos optimales. Redes. Flujos. Algoritmo de
Caminos y Flujos optimales Introducción a la Investigación de Operaciones 2007 Contenido Definiciones básicas. Conexidad. Clausura transitiva. Esqueletos y caminos optimales. Redes. Flujos. Algoritmo de
Tema 2. Fundamentos de la Teoría de Lenguajes Formales
 Departamento de Tecnologías de la Información Tema 2. Fundamentos de la Teoría de Lenguajes Formales Ciencias de la Computación e Inteligencia Artificial Índice 2.1. Alfabeto 2.2. Palabra 2.3. Operaciones
Departamento de Tecnologías de la Información Tema 2. Fundamentos de la Teoría de Lenguajes Formales Ciencias de la Computación e Inteligencia Artificial Índice 2.1. Alfabeto 2.2. Palabra 2.3. Operaciones
Espacios topológicos. 3.1 Espacio topológico
 Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS.
 UNIDAD 1.- CONCEPTOS REQUERIDOS CONJUNTOS. AXIOMAS DE PERTENENCIA, PARALELISMO, ORDEN Y PARTICIÓN. 1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS. 1.1 Determinaciones de un conjunto. Un conjunto queda determinado
UNIDAD 1.- CONCEPTOS REQUERIDOS CONJUNTOS. AXIOMAS DE PERTENENCIA, PARALELISMO, ORDEN Y PARTICIÓN. 1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS. 1.1 Determinaciones de un conjunto. Un conjunto queda determinado
LAS CIENCIAS DE LA PLANIFICACIÓN
 LAS CIENCIAS DE LA PLANIFICACIÓN 5. EL PROBLEMA DEL VIAJANTE (PV) (The Traveling Salesman Problem TSP) Un problema como el de las vacaciones, pero vital para las empresas, es el problema del viajante (PV):
LAS CIENCIAS DE LA PLANIFICACIÓN 5. EL PROBLEMA DEL VIAJANTE (PV) (The Traveling Salesman Problem TSP) Un problema como el de las vacaciones, pero vital para las empresas, es el problema del viajante (PV):
Estructuras Algebraicas
 Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
Conjuntos, relaciones y funciones Susana Puddu
 Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Introducción a la Teoría de Grafos
 Introducción a la Teoría de Grafos Flavia Bonomo fbonomo@dc.uba.ar do. Cuatrimestre 009 Árboles Un árbol es un grafo conexo y acíclico (sin ciclos). Un bosque es un grafo acíclico, o sea, una unión disjunta
Introducción a la Teoría de Grafos Flavia Bonomo fbonomo@dc.uba.ar do. Cuatrimestre 009 Árboles Un árbol es un grafo conexo y acíclico (sin ciclos). Un bosque es un grafo acíclico, o sea, una unión disjunta
NOCIONES PRELIMINARES (*) 1
 CONJUNTOS NOCIONES PRELIMINARES (*) 1 Conjunto no es un término definible, pero da idea de una reunión de cosas ( elementos ) que tienen algo en común. En matemática los conjuntos se designan con letras
CONJUNTOS NOCIONES PRELIMINARES (*) 1 Conjunto no es un término definible, pero da idea de una reunión de cosas ( elementos ) que tienen algo en común. En matemática los conjuntos se designan con letras
TEORÍA DE GRAFOS Ingeniería de Sistemas
 TEORÍA DE GRAFOS Ingeniería de Sistemas Código: MAT-31114 AUTORES Ing. Daniel Zambrano Ing. Viviana Semprún UNIDADES DE LA ASIGNATURA» UNIDAD I. Relaciones» UNIDAD II. Estructuras Algebraicas» UNIDAD III.
TEORÍA DE GRAFOS Ingeniería de Sistemas Código: MAT-31114 AUTORES Ing. Daniel Zambrano Ing. Viviana Semprún UNIDADES DE LA ASIGNATURA» UNIDAD I. Relaciones» UNIDAD II. Estructuras Algebraicas» UNIDAD III.
Terminaremos el capítulo con una breve referencia a la teoría de cardinales.
 TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
Tema 2.- Formas Cuadráticas.
 Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
Figura 3.1. Grafo orientado.
 Leyes de Kirchhoff 46. ECUACIONES DE INTERCONEXION. Leyes de Kirchhoff..1. Definiciones. Una red está formada por la interconexión de componentes en sus terminales; y deben cumplirse simultáneamente las
Leyes de Kirchhoff 46. ECUACIONES DE INTERCONEXION. Leyes de Kirchhoff..1. Definiciones. Una red está formada por la interconexión de componentes en sus terminales; y deben cumplirse simultáneamente las
Capítulo 6. Relaciones. Continuar
 Capítulo 6. Relaciones Continuar Introducción Una relación es una correspondencia entre dos elementos de dos conjuntos con ciertas propiedades. En computación las relaciones se utilizan en base de datos,
Capítulo 6. Relaciones Continuar Introducción Una relación es una correspondencia entre dos elementos de dos conjuntos con ciertas propiedades. En computación las relaciones se utilizan en base de datos,
Capítulo 4. Lógica matemática. Continuar
 Capítulo 4. Lógica matemática Continuar Introducción La lógica estudia la forma del razonamiento, es una disciplina que por medio de reglas y técnicas determina si un teorema es falso o verdadero, además
Capítulo 4. Lógica matemática Continuar Introducción La lógica estudia la forma del razonamiento, es una disciplina que por medio de reglas y técnicas determina si un teorema es falso o verdadero, además
Introducción a la Lógica
 Tema 0 Introducción a la Lógica En cualquier disciplina científica se necesita distinguir entre argumentos válidos y no válidos. Para ello, se utilizan, a menudo sin saberlo, las reglas de la lógica. Aquí
Tema 0 Introducción a la Lógica En cualquier disciplina científica se necesita distinguir entre argumentos válidos y no válidos. Para ello, se utilizan, a menudo sin saberlo, las reglas de la lógica. Aquí
Teoremas de Convergencia
 Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
Álgebra Lineal VII: Independencia Lineal.
 Álgebra Lineal VII: Independencia Lineal José María Rico Martínez Departamento de Ingeniería Mecánica División de Ingenierías, Campus Irapuato-Salamanca Universidad de Guanajuato email: jrico@salamancaugtomx
Álgebra Lineal VII: Independencia Lineal José María Rico Martínez Departamento de Ingeniería Mecánica División de Ingenierías, Campus Irapuato-Salamanca Universidad de Guanajuato email: jrico@salamancaugtomx
Máquinas Secuenciales, Autómatas y Lenguajes. Tema 3.1: Autómatas Finitos Deterministas
 Tema 3.1: Autómatas Finitos Deterministas Luis Peña luis.pena@urjc.es http://www.ia.urjc.es/cms/es/docencia/ic-msal Sumario Tema 3.1: Autómatas Finitos Deterministas. 1. Concepto de AFD 2. Equivalencia
Tema 3.1: Autómatas Finitos Deterministas Luis Peña luis.pena@urjc.es http://www.ia.urjc.es/cms/es/docencia/ic-msal Sumario Tema 3.1: Autómatas Finitos Deterministas. 1. Concepto de AFD 2. Equivalencia
BLOQUE 1. LOS NÚMEROS
 BLOQUE 1. LOS NÚMEROS Números naturales, enteros y racionales. El número real. Intervalos. Valor absoluto. Tanto el Cálculo como el Álgebra que estudiaremos en esta asignatura, descansan en los números
BLOQUE 1. LOS NÚMEROS Números naturales, enteros y racionales. El número real. Intervalos. Valor absoluto. Tanto el Cálculo como el Álgebra que estudiaremos en esta asignatura, descansan en los números
- Fernando Sánchez - Departamento de Matemáticas - Universidad de Extremadura. Topología
 - Fernando Sánchez - - 6 Topología Cálculo I en R 26 10 2015 Elementos de la topología en R. Una topología en un conjunto da un criterio para poder hablar de proximidad entre los elementos de un conjunto.
- Fernando Sánchez - - 6 Topología Cálculo I en R 26 10 2015 Elementos de la topología en R. Una topología en un conjunto da un criterio para poder hablar de proximidad entre los elementos de un conjunto.
Apuntes de Matemática Discreta 8. Relaciones de Equivalencia
 Apuntes de Matemática Discreta 8. Relaciones de Equivalencia Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 8 Relaciones de Equivalencia
Apuntes de Matemática Discreta 8. Relaciones de Equivalencia Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 8 Relaciones de Equivalencia
Soluciones a algunos ejercicios de Matemática Discreta 1.
 Soluciones a algunos ejercicios de Matemática Discreta 1. Eleonora Catsigeras * 23 de agosto de 2005 Práctico 1.- Ejercicio 5 Cuántos números naturales pares de tres dígitos (en base 10) tienen todos sus
Soluciones a algunos ejercicios de Matemática Discreta 1. Eleonora Catsigeras * 23 de agosto de 2005 Práctico 1.- Ejercicio 5 Cuántos números naturales pares de tres dígitos (en base 10) tienen todos sus
ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Enteros
 Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Z = N {0} N Enteros Las operaciones + y. son cerradas en Z, es decir la suma de dos números enteros es un número entero y el producto
Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Z = N {0} N Enteros Las operaciones + y. son cerradas en Z, es decir la suma de dos números enteros es un número entero y el producto
Sistemas de Ecuaciones Lineales y Matrices
 Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
John Venn Matemático y filósofo británico creador de los diagramas de Venn
 Georg Cantor Matemático Alemán creador de la teoría de conjuntos John Venn Matemático y filósofo británico creador de los diagramas de Venn August De Morgan Matemático ingles creador de leyes que llevan
Georg Cantor Matemático Alemán creador de la teoría de conjuntos John Venn Matemático y filósofo británico creador de los diagramas de Venn August De Morgan Matemático ingles creador de leyes que llevan
Fundamentos de la teoría de grafos
 Fundamentos de la teoría de grafos 3º I.T.I. de Sistemas Mª Teresa Cáceres Sansaloni 1 Tema 1: Nociones básicas Conceptos básicos sobre grafos. Representación de grafos. Multigrafos, grafos dirigidos y
Fundamentos de la teoría de grafos 3º I.T.I. de Sistemas Mª Teresa Cáceres Sansaloni 1 Tema 1: Nociones básicas Conceptos básicos sobre grafos. Representación de grafos. Multigrafos, grafos dirigidos y
Planaridad. Algoritmos y Estructuras de Datos III
 Planaridad Algoritmos y Estructuras de Datos III Por qué planares? Por qué planares? Por qué planares? Grafos planares Definiciones: Una representación planar de un grafo G es un conjunto de puntos en
Planaridad Algoritmos y Estructuras de Datos III Por qué planares? Por qué planares? Por qué planares? Grafos planares Definiciones: Una representación planar de un grafo G es un conjunto de puntos en
Una topología de los números naturales*
 Una topología de los números naturales* Divulgación Gabriel Ruiz Hernández Instituto de Matemáticas, UNAM 1 de septimebre de 1997 resumen En este trabajo vamos a describir un espacio topológico X con las
Una topología de los números naturales* Divulgación Gabriel Ruiz Hernández Instituto de Matemáticas, UNAM 1 de septimebre de 1997 resumen En este trabajo vamos a describir un espacio topológico X con las
Teoría de la Probabilidad Tema 2: Teorema de Extensión
 Teoría de la Probabilidad Tema 2: Teorema de Extensión Alberto Rodríguez Casal 25 de septiembre de 2015 Definición Una clase (no vacía) A de subconjuntos de Ω se dice que es un álgebra si A es cerrada
Teoría de la Probabilidad Tema 2: Teorema de Extensión Alberto Rodríguez Casal 25 de septiembre de 2015 Definición Una clase (no vacía) A de subconjuntos de Ω se dice que es un álgebra si A es cerrada
Recordemos que utilizaremos, como es habitual, la siguiente notación para algunos conjuntos de números que son básicos.
 Capítulo 1 Preliminares Vamos a ver en este primer capítulo de preliminares algunos conceptos, ideas y propiedades que serán muy útiles para el desarrollo de la asignatura. Se trata de resultados sobre
Capítulo 1 Preliminares Vamos a ver en este primer capítulo de preliminares algunos conceptos, ideas y propiedades que serán muy útiles para el desarrollo de la asignatura. Se trata de resultados sobre
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO
 DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
TRIGONOMETRÍA ESFÉRICA 2001 Kepler C k Ikastegia
 TRIGNMETRÍ ESFÉRI 2001 Kepler k Ikastegia 2 1.1 Introducción La Trigonometría es una rama de la Matemática en la que se analiza la medida de las partes de los triángulos, tanto de los triángulos planos
TRIGNMETRÍ ESFÉRI 2001 Kepler k Ikastegia 2 1.1 Introducción La Trigonometría es una rama de la Matemática en la que se analiza la medida de las partes de los triángulos, tanto de los triángulos planos
y cualquier par (x, y) puede escalarse, multiplicarse por un número real s, para obtener otro vector (sx, sy).
 UNIDAD II: VECTORES EN DOS Y TRES DIMENSIONES Un espacio vectorial (o espacio lineal) es el objeto básico de estudio en la rama de la matemática llamada álgebra lineal. A los elementos de los espacios
UNIDAD II: VECTORES EN DOS Y TRES DIMENSIONES Un espacio vectorial (o espacio lineal) es el objeto básico de estudio en la rama de la matemática llamada álgebra lineal. A los elementos de los espacios
CONTENIDOS. 1. Procesos Estocásticos y de Markov. 2. Cadenas de Markov en Tiempo Discreto (CMTD) 3. Comportamiento de Transición de las CMTD
 CONTENIDOS 1. Procesos Estocásticos y de Markov 2. Cadenas de Markov en Tiempo Discreto (CMTD) 3. Comportamiento de Transición de las CMTD 4. Comportamiento Estacionario de las CMTD 1. Procesos Estocásticos
CONTENIDOS 1. Procesos Estocásticos y de Markov 2. Cadenas de Markov en Tiempo Discreto (CMTD) 3. Comportamiento de Transición de las CMTD 4. Comportamiento Estacionario de las CMTD 1. Procesos Estocásticos
MÓDULO 8: VECTORES. Física
 MÓDULO 8: VECTORES Física Magnitud vectorial. Elementos. Producto de un vector por un escalar. Operaciones vectoriales. Vector unitario. Suma de vectores por el método de componentes rectangulares. UTN
MÓDULO 8: VECTORES Física Magnitud vectorial. Elementos. Producto de un vector por un escalar. Operaciones vectoriales. Vector unitario. Suma de vectores por el método de componentes rectangulares. UTN
Conjuntos Los conjuntos se emplean en muchas áreas de las matemáticas, de modo que es importante una comprensión de los conjuntos y de su notación.
 NÚMEROS REALES Conjuntos Los conjuntos se emplean en muchas áreas de las matemáticas, de modo que es importante una comprensión de los conjuntos y de su notación. Un conjunto es una colección bien definida
NÚMEROS REALES Conjuntos Los conjuntos se emplean en muchas áreas de las matemáticas, de modo que es importante una comprensión de los conjuntos y de su notación. Un conjunto es una colección bien definida
En una recta numérica el punto que representa el cero recibe el nombre de origen.
 1. Conjuntos numéricos Los conjuntos numéricos con los que has trabajado tanto en Enseñanza Básica como en Enseñanza Media, se van ampliando a medida que se necesita resolver ciertas problemáticas de la
1. Conjuntos numéricos Los conjuntos numéricos con los que has trabajado tanto en Enseñanza Básica como en Enseñanza Media, se van ampliando a medida que se necesita resolver ciertas problemáticas de la
Tema 2. Grupos. 3. El conjunto de matrices de orden 2 con coeficientes enteros (o reales) con la suma es un grupo conmutativo.
 Tema 2. Grupos. 1 Grupos Definición 1 Un grupo es una estructura algebraica (G, ) tal que la operación binaria verifica: 1. * es asociativa 2. * tiene elemento neutro 3. todo elemento de G tiene simétrico.
Tema 2. Grupos. 1 Grupos Definición 1 Un grupo es una estructura algebraica (G, ) tal que la operación binaria verifica: 1. * es asociativa 2. * tiene elemento neutro 3. todo elemento de G tiene simétrico.
Tema 3: Sistemas de ecuaciones lineales
 Tema 3: Sistemas de ecuaciones lineales 1. Introducción Los sistemas de ecuaciones resuelven problemas relacionados con situaciones de la vida cotidiana que tiene que ver con las Ciencias Sociales. Nos
Tema 3: Sistemas de ecuaciones lineales 1. Introducción Los sistemas de ecuaciones resuelven problemas relacionados con situaciones de la vida cotidiana que tiene que ver con las Ciencias Sociales. Nos
CAPÍTULO II TEORÍA DE CONJUNTOS
 TEORÍ DE ONJUNTOS 25 PÍTULO II TEORÍ DE ONJUNTOS 2.2 INTRODUIÓN Denotaremos los conjuntos con letras mayúsculas y sus elementos con letras minúsculas, si un elemento p pertenece a un conjunto escribiremos
TEORÍ DE ONJUNTOS 25 PÍTULO II TEORÍ DE ONJUNTOS 2.2 INTRODUIÓN Denotaremos los conjuntos con letras mayúsculas y sus elementos con letras minúsculas, si un elemento p pertenece a un conjunto escribiremos
El Teorema Fundamental del Álgebra
 El Teorema Fundamental del Álgebra 1. Repaso de polinomios Definiciones básicas Un monomio en una indeterminada x es una expresión de la forma ax n que representa el producto de un número, a, por una potencia
El Teorema Fundamental del Álgebra 1. Repaso de polinomios Definiciones básicas Un monomio en una indeterminada x es una expresión de la forma ax n que representa el producto de un número, a, por una potencia
PROBLEMAS RESUELTOS DE PREPARACIÓN PARA OPOSICIONES. Problemas 02
 PROBLEMAS RESUELTOS DE PREPARACIÓN PARA OPOSICIONES Problemas 0 Salvador Pérez Gómez pies3coma14@hotmail.com 4 de abril de 007 PROBLEMA 1 Sea n un número natural. Sea A n = n + n + 3n. a) Demostrar que
PROBLEMAS RESUELTOS DE PREPARACIÓN PARA OPOSICIONES Problemas 0 Salvador Pérez Gómez pies3coma14@hotmail.com 4 de abril de 007 PROBLEMA 1 Sea n un número natural. Sea A n = n + n + 3n. a) Demostrar que
APUNTES DE GEOMETRÍA ANALÍTICA
 CAPÍTULO 1: LA RECTA EN EL PLANO Conceptos Primitivos: Punto, recta, plano. APUNTES DE GEOMETRÍA ANALÍTICA Definición 1 (Segmento) Llamaremos segmento a la porción de una línea recta comprendida entre
CAPÍTULO 1: LA RECTA EN EL PLANO Conceptos Primitivos: Punto, recta, plano. APUNTES DE GEOMETRÍA ANALÍTICA Definición 1 (Segmento) Llamaremos segmento a la porción de una línea recta comprendida entre
Espacios Vectoriales www.math.com.mx
 Espacios Vectoriales Definiciones básicas de Espacios Vectoriales www.math.com.mx José de Jesús Angel Angel jjaa@math.com.mx MathCon c 007-009 Contenido. Espacios Vectoriales.. Idea Básica de Espacio Vectorial.................................
Espacios Vectoriales Definiciones básicas de Espacios Vectoriales www.math.com.mx José de Jesús Angel Angel jjaa@math.com.mx MathCon c 007-009 Contenido. Espacios Vectoriales.. Idea Básica de Espacio Vectorial.................................
Diagonal: es un segmento que une dos vértices no consecutivos del poliedro. Puede trazarse en una misma cara o entre distintas caras.
 CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones
![Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones](/thumbs/49/25360651.jpg) Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Definición y representación de los
 Definición y representación de los circuitos lógicos. LÁMARA R + - + - OBJETIVO GENERAL BATERÍA Utilizar el álgebra booleana para analizar y describir el funcionamiento de las combinaciones de las compuertas
Definición y representación de los circuitos lógicos. LÁMARA R + - + - OBJETIVO GENERAL BATERÍA Utilizar el álgebra booleana para analizar y describir el funcionamiento de las combinaciones de las compuertas
Semana05[1/14] Relaciones. 28 de marzo de Relaciones
![Semana05[1/14] Relaciones. 28 de marzo de Relaciones Semana05[1/14] Relaciones. 28 de marzo de Relaciones](/thumbs/50/26257926.jpg) Semana05[1/14] 28 de marzo de 2007 Introducción Semana05[2/14] Ya en los capítulos anteriores nos acercamos al concepto de relación. Relación Dados un par de conjuntos no vacíos A y B, llamaremos relación
Semana05[1/14] 28 de marzo de 2007 Introducción Semana05[2/14] Ya en los capítulos anteriores nos acercamos al concepto de relación. Relación Dados un par de conjuntos no vacíos A y B, llamaremos relación
La Distancia de un Punto a una Recta y de un Punto a un Plano, y un Teorema de Pitágoras en Tres Dimensiones
 58 Sociedad de Matemática de Chile La Distancia de un Punto a una Recta y de un Punto a un Plano, y un Teorema de Pitágoras en Tres Dimensiones Miguel Bustamantes 1 - Alejandro Necochea 2 El propósito
58 Sociedad de Matemática de Chile La Distancia de un Punto a una Recta y de un Punto a un Plano, y un Teorema de Pitágoras en Tres Dimensiones Miguel Bustamantes 1 - Alejandro Necochea 2 El propósito
Capítulo 3: Técnicas de Conteo Clase 2: Permutaciones y Combinaciones, Coeficientes Binomiales y Aplicaciones a Probabilidad Discreta
 Capítulo 3: Técnicas de Conteo Clase 2: Permutaciones y Combinaciones, Coeficientes Binomiales y Aplicaciones a Probabilidad Discreta Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática
Capítulo 3: Técnicas de Conteo Clase 2: Permutaciones y Combinaciones, Coeficientes Binomiales y Aplicaciones a Probabilidad Discreta Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática
MATEMÁTICASII Curso académico BLOQUE GEOMETRÍA. TEMA 1: VECTORES
 MATEMÁTICASII Curso académico 2015-2016 BLOQUE GEOMETRÍA. TEMA 1: VECTORES 1.1 VECTORES DEL ESPACIO. VECTORES LIBRES DEL ESPACIO Sean y dos puntos del espacio. Llamaremos vector (fijo) a un segmento orientado
MATEMÁTICASII Curso académico 2015-2016 BLOQUE GEOMETRÍA. TEMA 1: VECTORES 1.1 VECTORES DEL ESPACIO. VECTORES LIBRES DEL ESPACIO Sean y dos puntos del espacio. Llamaremos vector (fijo) a un segmento orientado
Matemáticas Discretas TC1003
 Matemáticas Discretas TC1003 Grafos: Básicos Departamento de Matemáticas / Centro de Sistema Inteligentes ITESM Grafos: Básicos Matemáticas Discretas - p. 1/12 Grafos: El tema de Teoría de Grafos apareció
Matemáticas Discretas TC1003 Grafos: Básicos Departamento de Matemáticas / Centro de Sistema Inteligentes ITESM Grafos: Básicos Matemáticas Discretas - p. 1/12 Grafos: El tema de Teoría de Grafos apareció
Figura en el espacio o cuerpo geométrico es el conjunto de puntos que no están contenidos en un mismo plano, es la porción de espacio limitado.
 Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
Unidad 6. Gráficas Planares
 Unidad 6. Gráficas Planares Una gráfica Planar es aquella que puede llegar a representarse en un plano de tal modo que no existe intersección de líneas excepto en los vértices. Una gráfica Plana es aquella
Unidad 6. Gráficas Planares Una gráfica Planar es aquella que puede llegar a representarse en un plano de tal modo que no existe intersección de líneas excepto en los vértices. Una gráfica Plana es aquella
COLEGIO NUESTRO SEÑOR DE LA BUENA ESPERANZA
 COLEGIO NUESTRO SEÑOR DE L UEN ESPERNZ signatura: NÁLISIS MTEMÁTICO 11º Profesor: Lic. EDURDO DURTE SUESCÚN TLLER OPERCIONES CON CONJUNTOS OPERCIONES CON CONJUNTOS En aritmética se suma, resta y multiplica,
COLEGIO NUESTRO SEÑOR DE L UEN ESPERNZ signatura: NÁLISIS MTEMÁTICO 11º Profesor: Lic. EDURDO DURTE SUESCÚN TLLER OPERCIONES CON CONJUNTOS OPERCIONES CON CONJUNTOS En aritmética se suma, resta y multiplica,
Capítulo 2: Inducción y recursión Clase 2: El principio de Inducción Fuerte
 Capítulo 2: Inducción y recursión Clase 2: El principio de Inducción Fuerte Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 2: Inducción y Recursión 1 / 20 Motivación
Capítulo 2: Inducción y recursión Clase 2: El principio de Inducción Fuerte Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 2: Inducción y Recursión 1 / 20 Motivación
Análisis y síntesis de sistemas digitales combinacionales
 Análisis Algoritmo de análisis, para un circuito lógico combinacional Síntesis. Conceptos Circuitos combinacionales bien construidos Circuitos combinacionales mal construidos Criterios de optimización
Análisis Algoritmo de análisis, para un circuito lógico combinacional Síntesis. Conceptos Circuitos combinacionales bien construidos Circuitos combinacionales mal construidos Criterios de optimización
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS.
 TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
Axiomas de separación
 CAPíTULO 6 Axiomas de separación Tema 1. Axiomas de separación: conceptos básicos El objetivo de este capítulo es considerar ciertas propiedades topológicas que comparten algunos espacios topológicos y
CAPíTULO 6 Axiomas de separación Tema 1. Axiomas de separación: conceptos básicos El objetivo de este capítulo es considerar ciertas propiedades topológicas que comparten algunos espacios topológicos y
Criterios de divisibilidad y Congruencias
 Criterios de divisibilidad y Congruencias Rafael F. Isaacs G. * Fecha: 9 de marzo de 2007 Cuando tenemos un número muy grande escrito en base 10 y deseamos saber si es múltiplo por ejemplo de 9 no necesitamos
Criterios de divisibilidad y Congruencias Rafael F. Isaacs G. * Fecha: 9 de marzo de 2007 Cuando tenemos un número muy grande escrito en base 10 y deseamos saber si es múltiplo por ejemplo de 9 no necesitamos
Grupos libres. Presentaciones.
 S _ Tema 12.- Grupos libres. Presentaciones. 12.1 Grupos libres. En el grupo Z de los enteros vimos una propiedad (cf. ejemplos.5), que lo caracteriza como grupo libre. Lo enunciamos al modo de una Propiedad
S _ Tema 12.- Grupos libres. Presentaciones. 12.1 Grupos libres. En el grupo Z de los enteros vimos una propiedad (cf. ejemplos.5), que lo caracteriza como grupo libre. Lo enunciamos al modo de una Propiedad
Eje 2. Razonamiento lógico matemático
 Razonamiento deductivo e inductivo La historia de las matemáticas se remonta al antiguo Egipto y Babilonia. Ante la necesidad de resolver problemas a través de errores y victorias, estas culturas lograron
Razonamiento deductivo e inductivo La historia de las matemáticas se remonta al antiguo Egipto y Babilonia. Ante la necesidad de resolver problemas a través de errores y victorias, estas culturas lograron
Probabilidad y Estadística
 Probabilidad y Estadística Probabilidad Conceptos como probabilidad, azar, aleatorio son tan viejos como la misma civilización. Y es que a diario utilizamos el concepto de probabilidad: Quizá llueva mañana
Probabilidad y Estadística Probabilidad Conceptos como probabilidad, azar, aleatorio son tan viejos como la misma civilización. Y es que a diario utilizamos el concepto de probabilidad: Quizá llueva mañana
Es trivial generalizar la definición al caso de varios conjuntos: A B C, etc.
 Tema 1 Espacios Vectoriales 1.1 Introducción Estas notas están elaboradas pensando simplemente en facilitar al estudiante una guía para el estudio de la asignatura, y en consecuencia se caracterizan por
Tema 1 Espacios Vectoriales 1.1 Introducción Estas notas están elaboradas pensando simplemente en facilitar al estudiante una guía para el estudio de la asignatura, y en consecuencia se caracterizan por
TEMA 3 ÁLGEBRA DE CONMUTACIÓN
 TEMA 3 ÁLGEBRA DE CONMUTACIÓN TEMA 3: Álgebra de Boole ÍNDICE. POSTULADOS DEL ÁLGEBRA DE CONMUTACIÓN 2. ÁLGEBRA DE BOOLE BIVALENTE O ÁLGEBRA DE CONMUTACIÓN 2. Teoremas del álgebra de conmutación 3. VARIABLES
TEMA 3 ÁLGEBRA DE CONMUTACIÓN TEMA 3: Álgebra de Boole ÍNDICE. POSTULADOS DEL ÁLGEBRA DE CONMUTACIÓN 2. ÁLGEBRA DE BOOLE BIVALENTE O ÁLGEBRA DE CONMUTACIÓN 2. Teoremas del álgebra de conmutación 3. VARIABLES
1. NÚMEROS PRIMOS Y COMPUESTOS.
 . NÚMEROS PRIMOS Y COMPUESTOS. De acuerdo a las propiedades ya vistas de los divisores, sabemos que: todo natural no nulo es divisor de sí mismo es divisor de todo número natural. Ahora: el natural tiene
. NÚMEROS PRIMOS Y COMPUESTOS. De acuerdo a las propiedades ya vistas de los divisores, sabemos que: todo natural no nulo es divisor de sí mismo es divisor de todo número natural. Ahora: el natural tiene
Matemáticas Discretas TC1003
 Matemáticas Discretas TC1003 Relaciones entre Conjuntos: Propiedades Departamento de Matemáticas / Centro de Sistema Inteligentes ITESM Relaciones entre Conjuntos: Propiedades Matemáticas Discretas - p.
Matemáticas Discretas TC1003 Relaciones entre Conjuntos: Propiedades Departamento de Matemáticas / Centro de Sistema Inteligentes ITESM Relaciones entre Conjuntos: Propiedades Matemáticas Discretas - p.
Poliedros Regulares Convexos
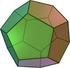 Poliedros Regulares Convexos Características y relaciones entre ellos AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 besode@alumni.uv.es Poliedros Regulares
Poliedros Regulares Convexos Características y relaciones entre ellos AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 besode@alumni.uv.es Poliedros Regulares
Anillo de polinomios con coeficientes en un cuerpo
 Capítulo 2 Anillo de polinomios con coeficientes en un cuerpo En el conjunto Z se ha visto cómo la relación ser congruente módulo m para un entero m > 1, es compatible con las operaciones suma y producto.
Capítulo 2 Anillo de polinomios con coeficientes en un cuerpo En el conjunto Z se ha visto cómo la relación ser congruente módulo m para un entero m > 1, es compatible con las operaciones suma y producto.
Subconjuntos notables de un Espacio Topológico
 34 Capítulo 4 Subconjuntos notables de un Espacio Topológico 4.1 Adherencia Definición 4.1.1 (Punto adherente). Sea (X, τ) un espacio topológico, y sea S un subconjunto de X. Diremos que x X es un punto
34 Capítulo 4 Subconjuntos notables de un Espacio Topológico 4.1 Adherencia Definición 4.1.1 (Punto adherente). Sea (X, τ) un espacio topológico, y sea S un subconjunto de X. Diremos que x X es un punto
Funciones integrables en R n
 Capítulo 1 Funciones integrables en R n Sean un subconjunto acotado de R n, y f : R una función acotada. Sea R = [a 1, b 1 ]... [a n, b n ] un rectángulo que contenga a. Siempre puede suponerse que f está
Capítulo 1 Funciones integrables en R n Sean un subconjunto acotado de R n, y f : R una función acotada. Sea R = [a 1, b 1 ]... [a n, b n ] un rectángulo que contenga a. Siempre puede suponerse que f está
POLÍGONOS POLÍGONOS. APM Página 1
 POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
Estudio de fallas asimétricas
 Departamento de Ingeniería Eléctrica Universidad Nacional de Mar del Plata Área Electrotecnia Estudio de fallas asimétricas Autor: Ingeniero Gustavo L. Ferro Prof. Adjunto Electrotecnia EDICION 2012 1.
Departamento de Ingeniería Eléctrica Universidad Nacional de Mar del Plata Área Electrotecnia Estudio de fallas asimétricas Autor: Ingeniero Gustavo L. Ferro Prof. Adjunto Electrotecnia EDICION 2012 1.
5 Autómatas de pila 5.1 Descripción informal. 5.2 Definiciones
 1 Curso Básico de Computación 5 Autómatas de pila 5.1 Descripción informal Un autómata de pila es esencialmente un autómata finito que controla una cinta de entrada provista de una cabeza de lectura y
1 Curso Básico de Computación 5 Autómatas de pila 5.1 Descripción informal Un autómata de pila es esencialmente un autómata finito que controla una cinta de entrada provista de una cabeza de lectura y
Punto. Recta. Semirrecta. Segmento. Rectas Secantes. Rectas Paralelas. Rectas Perpendiculares
 Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
2. SEÑALES Y SISTEMAS DISCRETOS EN EL TIEMPO. Una señal puede ser definida como una portadora física de información. Por ejemplo,
 2. SEÑALES Y SISTEMAS DISCRETOS EN EL TIEMPO Una señal puede ser definida como una portadora física de información. Por ejemplo, las señales de audio son variaciones en la presión del aire llevando consigo
2. SEÑALES Y SISTEMAS DISCRETOS EN EL TIEMPO Una señal puede ser definida como una portadora física de información. Por ejemplo, las señales de audio son variaciones en la presión del aire llevando consigo
Índice Proposiciones y Conectores Lógicos Tablas de Verdad Lógica de Predicados Inducción
 Curso 0: Matemáticas y sus Aplicaciones Tema 5. Lógica y Formalismo Matemático Leandro Marín Dpto. de Matemática Aplicada Universidad de Murcia 2012 1 Proposiciones y Conectores Lógicos 2 Tablas de Verdad
Curso 0: Matemáticas y sus Aplicaciones Tema 5. Lógica y Formalismo Matemático Leandro Marín Dpto. de Matemática Aplicada Universidad de Murcia 2012 1 Proposiciones y Conectores Lógicos 2 Tablas de Verdad
Tema 5 Algunas distribuciones importantes
 Algunas distribuciones importantes 1 Modelo Bernoulli Distribución Bernoulli Se llama experimento de Bernoulli a un experimento con las siguientes características: 1. Se realiza un experimento con dos
Algunas distribuciones importantes 1 Modelo Bernoulli Distribución Bernoulli Se llama experimento de Bernoulli a un experimento con las siguientes características: 1. Se realiza un experimento con dos
TRIÁNGULOS: RELACIONES DE DESIGUALDAD ENTRE SEGMENTOS Y ÁNGULOS
 TRIÁNGULOS: RELACIONES DE DESIGUALDAD ENTRE SEGMENTOS Y ÁNGULOS Introducción.- Anteriormente, a partir de la congruencia de triángulos, hemos estudiado las condiciones que han de verificarse para que dos
TRIÁNGULOS: RELACIONES DE DESIGUALDAD ENTRE SEGMENTOS Y ÁNGULOS Introducción.- Anteriormente, a partir de la congruencia de triángulos, hemos estudiado las condiciones que han de verificarse para que dos
LA FUNCIÓN INVERSA. Si R es una relación, la relación R definida por la proposiciones. (a, b) R (b, a) R. (a, b) R (c, b) R a = c
 LA FUNCIÓN INVERSA Existen diferentes definiciones de función inversa, aunque el concepto matemático es el mismo. Expondremos aquí tres de ellas, para efectos formales, ya que para hallar la inversa de
LA FUNCIÓN INVERSA Existen diferentes definiciones de función inversa, aunque el concepto matemático es el mismo. Expondremos aquí tres de ellas, para efectos formales, ya que para hallar la inversa de
RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES
 UNIDD 4 RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 00 Resolución de sistemas mediante determinantes x y Resuelve, aplicando x = e y =, los siguientes sistemas de ecuaciones: x 5y = 7 5x + 4y = 6x
UNIDD 4 RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 00 Resolución de sistemas mediante determinantes x y Resuelve, aplicando x = e y =, los siguientes sistemas de ecuaciones: x 5y = 7 5x + 4y = 6x
PRODUCTO CARTESIANO RELACIONES BINARIAS
 PRODUCTO CARTESIANO RELACIONES BINARIAS Producto Cartesiano El producto cartesiano de dos conjuntos A y B, denotado A B, es el conjunto de todos los posibles pares ordenados cuyo primer componente es un
PRODUCTO CARTESIANO RELACIONES BINARIAS Producto Cartesiano El producto cartesiano de dos conjuntos A y B, denotado A B, es el conjunto de todos los posibles pares ordenados cuyo primer componente es un
No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano.
 FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
CONTINUIDAD DE FUNCIONES. SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos.
 CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
Convergencia de sucesiones
 TEMA 4. CONVERGENCIA DE SUCESIONES 65 Tema 4. Convergencia de sucesiones Definición 5.4.1. Sea X un conjunto: una sucesión en X es una aplicación s : N X; denotaremos x n := s(n) y por S := {x n } n N
TEMA 4. CONVERGENCIA DE SUCESIONES 65 Tema 4. Convergencia de sucesiones Definición 5.4.1. Sea X un conjunto: una sucesión en X es una aplicación s : N X; denotaremos x n := s(n) y por S := {x n } n N
CAPÍTULO 2 NOCIONES BÁSICAS DE TEORÍA DE CONJUNTOS
 CAPÍTULO 2 NOCIONES BÁSICAS DE TEORÍA DE CONJUNTOS 2.1. NOCIONES PRIMITIVAS Consideraremos tres nociones primitivas: Conjunto, Elemento y Pertenencia. Conjunto Podemos entender al conjunto como, colección,
CAPÍTULO 2 NOCIONES BÁSICAS DE TEORÍA DE CONJUNTOS 2.1. NOCIONES PRIMITIVAS Consideraremos tres nociones primitivas: Conjunto, Elemento y Pertenencia. Conjunto Podemos entender al conjunto como, colección,
PRINCIPIOS DE LA DINÁMICA
 Capítulo 3 PRINCIPIOS DE LA DINÁMICA CLÁSICA 3.1 Introducción En el desarrollo de este tema, cuyo objeto de estudio son los principios de la dinámica, comenzaremos describiendo las causas del movimiento
Capítulo 3 PRINCIPIOS DE LA DINÁMICA CLÁSICA 3.1 Introducción En el desarrollo de este tema, cuyo objeto de estudio son los principios de la dinámica, comenzaremos describiendo las causas del movimiento
