Aplicacions de la derivada
|
|
|
- Marcos Bustos Cano
- hace 5 años
- Vistas:
Transcripción
1 Aplicacions de la derivada Números reales LITERATURA I MATEMÀTIQUES La vida, manual d ús Bartlebooth va proposar-li [al seu criat Smautf] que es jubilés ja fa molt de temps, però sempre s ha negat a fer-ho. La veritat és que té poca feina. Al matí prepara la roba de Bartlebooth i l ajuda a vestir-se. L afaitava fins fa cinc anys amb un matet que havia estat propietat d un avi de Bartlebooth, però hi veu molt malament i el pols ha començat a tremolar-li, motiu pel qual ha estat substituït per un oficial del senyor Pois, el perruquer del carrer Prony, que puja al pis cada matí. Bartlebooth ja no es mou de casa; gairebé no surt del despat en tot el dia. Smautf s està a l habitació contigua, amb la resta de criats, que no tenen gaire més feina que ell i passen l estona jugant a cartes i parlant del passat. [Ell, però, ha trobat una ocupació que l absorbei completament.] Smautf, molt al principi dels seus viatges, havia vist en un gran musichall de Londres un calculador prodigi i durant els vint anys de la seva volta al món, llegint i rellegint un vell tractat esparracat de passatemps matemàtics i aritmètics que havia descobert en una llibreria de vell d Inverness, es va aficionar al càlcul mental i, quan va tornar, era capaç d etreure arrels quadrades o cúbiques de nombres de nou ifres amb una rapidesa relativa. Quan aiò ja li començava a ser massa fàcil va entrar-li un frenesí pels factorials:! ;! ;! 6;! ; 5! 0; 6! 70; 7! 5.00; 8! 0.0;! 6.880; 0! ;!.6.800;! ; [...];! , o sigui més de mil milions de vegades set-cents vint-i-set mil milions. Smautf va actualment pel 76, però ja no troba paper de format prou gran; i, encara que el trobés, no hi hauria una taula prou llarga per estendre l. Cada vegada té menys seguretat en ell matei, i per aiò sempre està repetint els càlculs. Morellet va intentar desanimar-lo anys enrere dient-li que el nombre que s escriu, o sigui, nou elevat a nou elevat a nou, que és el nombre més gran que es pot escriure utilitzant només tres ifres, tindria, si l escrivíssim sencer, tres-cents setanta-nou milions de ifres; a raó d una ifra per segon, es trigarien onze anys a escriure l; i calculant dues ifres per centímetre, tindria mil vuit-cents quilòmetres de llargada. Malgrat aiò Smautf continuà alineant columnes i més columnes de ifres en dorsos de sobres, marges de quaderns i papers d embolicar carn. GEORGES PEREC
2 SOLUCIONARI La vida, manual d ús Georges Perec Al llarg d aquesta «complicada» novel la apareien un munt de personatges ecèntrics, dos dels quals, aquells que tenen alguna rellevància matemàtica, són els que surten en aquest paràgraf: Bartlebooth i Smautf. Bartlebooth va dedicar deu anys a iniciar-se en l art de l aquarel la. Després va recórrer el món durant vint anys pintant una aquarel la cada quinze dies en cinc-cents ports diferents. Quan n acabava una, l enviava a un artesà de París perquè l enganés en una placa de fusta i després la retallés, de manera que va formar un trencaclosques de set-centes cinquanta peces. Quan va acabar el seu periple, va tornar a França i es va estar vint anys més per reconstruir els cinc-cents trencaclosques a raó d un cada quinze dies. A mesura que els anava completant, el matei artesà, amb una tècnica especial, desenganava del suport l aquarel la reconstruïda i l enviava al matei lloc on l havia pintada. Allí la submergien en una solució detersiva de la qual sortia una altra vegada el full blanc i verge. D aquesta manera, no va quedar cap vestigi d aquella activitat que durant cinquanta anys va omplir del tot la vida de Bartlebooth. En totes les etapes, a Bartlebooth el va acompanyar el seu criat Smautf, el qual encara, malgrat els seus vuitanta anys, en té cura a casa seva de París i ocupa el temps amb els entrenaments matemàtics que hem vist en el tet escollit. Els factorials dels nombres naturals formen una successió creient, és a dir, una funció f ( )!, definida per a N, és creient. Estudia si la funció f ( ) ( )( ), definida per a qualsevol nombre real, també és creient. Perquè sigui creient s ha de verificar que, per a qualsevol valor de, R, amb < f ( ) < f ( ). Per a la funció f ( ) ( )( ) tenim que: < < ( )( ) < ( )( ) < f ( ) < f ( ) f ( ) creient 07
3 Aplicacions de la derivada ABANS DE COMENÇAR RECORDA 00 Determina el creiement i el decreiement d aquesta funció. Indica en quins punts assolei màims o mínims relatius i absoluts. La funció és decreient en ( `, ) (, ) ( 6, + `). i és creient en (, ) (, 6). Té un màim relatiu en (, ) i en (6, ). Té un mínim relatiu en (, ) i en (, ). Considerant la funció, no podem assegurar que presenti ni màims ni mínims absoluts. Y X 00 Una funció definida per a tots els nombres reals és decreient en l interval (, 5) i creient en la resta. Quins són els màims i els mínims? S assolei un màim en i un mínim en Si lim f( ) Li lim g( ) + `, calcula aquests límits: + ` + ` a) lim ( f( ) + g( )) + ` a) lim ( f( ) + g( )) + ` + ` b) lim ( f( ) g( )) + ` + ` b) lim ( f( ) g( )) + ` + ` si L > g c) lim ( f( )) ( ) Indeterminació si L + ` 0 si0< L < g c) lim ( f( )) ( ) +` ACTIVITATS 00 Troba el pendent de la recta tangent a la gràfica de la funció f ( ) 6 + en. f h f h ( ) lim ( ) ( ) lim ( ) h+ 6h lim h 0 h h 0 h h 0 h lim( + 6h) h 0 00 Quin és el pendent de la recta tangent a la gràfica de la funció f ( ) en? f h f h ( ) lim ( ) ( ) lim ( ) + + h+ h + h lim h 0 h h 0 h h 0 h lim( + h+ h ) h 0 00 Troba l equació de la recta tangent a la gràfica de la funció f ( ) + en el punt P (, ). Quina és l equació de la recta normal? 08
4 SOLUCIONARI f h f h ( ) lim ( ) ( ) lim ( ) h+ h lim h 0 h h 0 h h 0 h lim( + h) h 0 L equació de la recta tangent és: y ( + ) y + L equació de la recta normal és: y ( + ) y + 00 Calcula les equacions de les rectes tangents a la funció f () + en els punts i. Comprova que són paral leles a la recta y 6. f() 5 f h f h ( ) lim ( ) ( ) lim ( ) h+ 6h + h lim h 0 h h 0 h h 0 h lim( 6+ 6h+ h ) 6 h 0 L equació de la recta tangent és: y 5 6( ) y 6 f( ) f h f h ( ) lim ( ) ( ) lim ( ) h 6 h + h lim h 0 h h 0 h h 0 h lim( 6 6h+ h ) 6 h 0 L equació de la recta tangent és: y 6( + ) y Les rectes són paral leles a la recta y 6, perquè el seu pendent és Determina on creien i decreien aquestes funcions: a) f ( ) + + b) g ( ) + a) Com que f ( ) és contínua en R, estudiem el creiement per a tots els nombres reals. 6 ( ) 6 + 0, + En `,, + ` ( )> 0 f ( ) creient 6 6 En +, ( )< 0 f ( ) decreient b) Com que g ( ) és contínua en R, estudiem el creiement per a tots els nombres reals. g'( ) + 0 ± ( + ) En ( `, ) (, + `) g'( )< 0 g ( ) decreient En (, ) g'( )> 0 g ( ) creient 6 0
5 Aplicacions de la derivada 006 Troba els intervals de creiement i decreiement d aquestes funcions i comprova-ho gràficament: a) f ( ) + 5 b) g ( ) + 7 a) Com que f ( ) és contínua en R perquè és una funció polinòmica, estudiem el creiement per a tots els nombres reals. ( ) 0 En ( `, ) ( )> 0 f ( ) creient En (, + ` ) ( )< 0 f ( ) decreient Y f ( ) X b) Com que g ( ) és contínua en R perquè és una funció polinòmica, estudiem el creiement per a tots els nombres reals. g'( ) + 0 En `, g '( )< 0 g ( ) decreient En, + ` g'( )> 0 g ( ) creient Y g ( ) X 007 Estudia els intervals de creiement i decreiement d aquestes funcions, i calcula n els màims i els mínims: a) f( ) b) g ( ) + + a) f ( ) és contínua en R. ( ) 0 0 ( + ) En ( `, 0 ) ( )< 0 f ( ) decreient En ( 0, +` ) ( )> 0 f ( ) creient En 0 presenta un mínim, que té com a coordenades (0, ). 0
6 SOLUCIONARI b) g ( ) és contínua en R {. } g'( ) + 0 ( + ) Aií, doncs, estudiem el creiement en ( `, ),, i, + `. En (, ) `, g'( )> 0 g ( ) creient En, + ` g'( )< 0 g ( ) decreient En presenta un màim, que té com a coordenades,. 008 Troba les coordenades dels màims i els mínims de la funció següent: + f( ) ( ) 0 5 Com que f ( ) és contínua en R { 0 }, l etrem es troba en ( `, 0 ). ( ) ( 0) En `, En En ( )< 0 f ( ) decreient, ( )> 0 f ( ) creient presenta un mínim, que té com a coordenades,. 00 Troba els màims i els mínims d aquestes funcions mitjançant la derivada segona: a) f( ) b) g ( ) 6 + a) f ( ) és contínua en R { 0 } amb ( ) + 0 ± f"( ) 5 f" ( ) > 0 Mínim ( ) < Màim f" 0 b) g ( ) és contínua en R. g'( ) ( + ) 0 0,, g"( ) 6 ( + ) 8 g"( 0) > 0 0 Mínim g"( ) < 0 Màim g"( ) < 0 Màim 7
7 Aplicacions de la derivada 00 Utilitza la derivada segona per determinar els màims i els mínims de la funció següent: + f( ) + 6 f ( ) és contínua en R {, 0, }. ( ) ( + 6) f"( ) ( + ) f"( < ) 0 Màim 0 ( ) ( 6 + 8) ( ) ( + ) ( ) ( + ) 0 Determina on són còncaves i on són convees aquestes funcions: a) f ( ) 7 + b) g ( ) + a) Com que f ( ) és contínua en R, estudiem la concavitat per a tots els nombres reals. ( ) f"( ) 0 En `, f "( )< 0 f ( ) còncava En, + ` f"( )> 0 f ( ) convea b) Com que g ( ) és contínua en R, estudiem la concavitat per a tots els nombres reals. + g'( ) ( + ) g"( ) + 6 ( + ) ( ) ( ) ( 0) ( + ) ,, En `, 0, g'( )> 0 g ( ) convea En,, ` g'( )< 0 g ( ) còncava 0 Troba els intervals de concavitat i conveitat de les funcions següents, i comprova el resultat gràficament: a) f ( ) + b) g( ) 5 a) f ( ) és contínua en R; per tant, estudiem la concavitat per a tots els nombres reals. ( ) f"( ) < 0 f ( ) còncava
8 SOLUCIONARI Gràficament: Y X f ( ) b) g ( ) és contínua en R; per tant, estudiem la concavitat per a tots els nombres reals. g'( ) 0 g"( ) 0 < 0 g ( ) còncava Gràficament: Y X g ( ) 0 Estudia els intervals de concavitat i conveitat d aquestes funcions i, a partir d aquests intervals, determina els punts d infleió: a) f( ) + b) g ( ) + 7 a) f ( ) és contínua en R. ( ) + 6 f"( ) En ( `, ) f"( )< 0 f ( ) còncava En (, + ` ) f"( )> 0 f ( ) convea Aií, doncs, en trobem un punt d infleió. b) Com que el domini de g ( ) és R { 7, 0 }, estudiem la concavitat en ( `, 7 ), ( 7, 0 ), (0, 7) i ( 7, +` ). g'( ) ( + 7) 6 8 g"( ) 0 7 ( + 7) En ( `, 7) ( 0, 7 ) g"( )< 0 g ( ) còncava En ( 70, ) ( 7, + ` ) g"( )> 0 g ( ) convea Hi ha un punt d infleió en 7.
9 Aplicacions de la derivada 0 Estudia els intervals de concavitat i conveitat i els punts d infleió de les funcions següents: a) f ( ) b) g ( ) + a) ( ) 8 f"( ) 0 0 f"' ( ) f"' ( 0) 0 0 Punt d infleió En ( `, 0 ) f"( )< 0 f ( ) convea En ( 0, +` ) f"( )> 0 f ( ) còncava b) g'( ) g"( ) > 0 No hi ha punts d infleió i la funció és còncava en ( `, 0) ( 0 + `), perquè 0 no es troba en el domini. 05 Calcula els punts d infleió de les funcions següents mitjançant la derivada tercera: a) f( ) b) g ( ) 7 a) f '( ) + 6 f"( ) 0 6, 5 6 f"'( ) ( ) ( ) f"' 6 0, f"' 6 0 En 6 i en 6 presenta punts d infleió. + 7 b) g'( ) ( 7) g"( ) ( 7) g"' ( ) d infleió ( 7) 0 0 g"' ( 0) 0 En 0 presenta un punt 06 Troba els màims, els mínims o els punts d infleió d aquestes funcions: a) f ( ) 6 b) g( ) 7 5 a) ( ) 0 0 f"( ) f"' ( ) 80 f"' ( 0) 0
10 SOLUCIONARI IV) IV) f ( ) 0. f ( 0) 0 V) V) f ( ) 880. f ( 0) 0 VI) f ( ) La primera derivada no nul la té ordre parell i f VI) ( 0) < 0 En 0 assolei un màim. 6 b) g'( ) g"( ) g"' ( ) 60 g"' ( 0) 0 IV) IV) g ( ) 50. g ( 0) 0 V) V) g ( ) g ( 0) 0 VI) VI) g ( ) 5. 0 g ( 0) 0 VII) g ( ) L ordre de la primera derivada no nul la és imparell, per aiò en 0 presenta un punt d infleió Si obtenim el nombre de visitants d un museu mitjançant f( ), en què + és l hora en què l obren, quan rep un nombre més gran de visitants? 00 Hem de maimitzar aquesta funció: f( ) + ( ) ( + ) f" ( ) f" () < 0 En assolei un màim. ( + ) Aií, doncs, el nombre més gran de visitants el rep quan fa una hora que l han obert. 08 Troba el nombre real que minimitza aquesta funció: D ( ) (a ) + (b ) + (c ) a, b, c R D'( ) ( a ) ( b ) ( c ) D'( ) a+ b+ c+ 6 ( a+ b+ c) 0 ( a+ b+ c) a+ b+ c 6 a b c D"( ) 6> 0 En + + R té un mínim. 0 La capacitat de concentració d una saltadora d altura, en una competició d atletisme de tres hores de durada, està determinada per aquesta funció: f ( t ) 00 t ( t ) en què t mesura el temps en hores. Quin és el millor moment, en termes de capacitat de concentració, perquè la saltadora pugui batre la seva marca? ( t) t 0 t f"( t) 600 < 0 En t assolei un màim. Aií, doncs, el millor moment perquè la saltadora pugui batre la seva marca és al cap d una hora i mitja. 5
11 Aplicacions de la derivada 00 Troba dos nombres reals positius si saps que sumen 0 i que el producte dels seus quadrats és màim. Si anomenem i y els dos nombres reals positius, es complei que: + y 0 Hem de maimitzar la funció: P (, y) y P ( ) ( 0 ) ( ) P'( ) , 5, 0 Busquem quin és el nombre que maimitza la funció P ( ). P"( ) P"( 0) 00> 0 En 0 presenta un mínim. P"( 5) 00< 0 En 5 presenta un màim. P"( 0) 00> 0 En 0 presenta un mínim. Els dos nombres que busquem són 5 i y 5. 0 De tots els prismes rectes de base quadrada i que tinguin com a perímetre d una cara lateral 0 cm, troba les dimensions del que té volum màim. Anomenem la longitud de l aresta de la base i y l altura del prisma. Com que el perímetre d una cara lateral és de 0 cm, es complei que: + y 0 + y 5 y 5 La funció que hem d optimitzar és: V( ) ( 5 ) 5 V'( ) 0 0 0, 0 V"( ) 0 6 V"( 0) > 0, V"( 0) < 0 El màim es troba en 0. Les dimensions del prisma recte de base quadrada són: Aresta de la base: 0 cm Altura: 5 cm 0 Determina el punt de la gràfica de la funció que a cada nombre hi fa correspondre el seu doble i que té una distància mínima al punt (6, ). Quina és aquesta distància? La funció que a cada nombre hi fa correspondre el seu doble és: y Un punt que pertany a aquesta funció és (, ), i la funció que ens dóna la distància des d aquest punt a (6, ) és: d( ) ( 6) + ( ) Optimitzem la funció D( ) d( ) ( 6) + ( ). D'( ) ( 6) + ( ) D"( ) 0 > 0 En assolei un mínim. 5 Aií, doncs, la distància al punt (6, ) serà mínima en el punt, Entre tots els rectangles d àrea m, troba les dimensions del que té mínim el producte de les seves diagonals. 6
12 SOLUCIONARI Considerem i y les dimensions del rectangle, de manera que: y. La funció que hem d optimitzar està determinada per: d d d P y + y P + (, ) ( ) + 8 P'( ) 0 8 0, Com que la solució negativa no és vàlida, tenim que: 5 P" ( ) + P" ( ) > 0 En aquest punt hi ha un mínim. Les dimensions són, y, per tant, es tracta d un quadrat de costat m. 0 Un jardiner té 60 m de filferro que vol fer servir per construir una tanca en una zona rectangular i dividir-la en tres parts, de manera que vol posar el filat de les divisions paral leles en un dels costats del rectangle. Quines dimensions ha de tenir la zona tancada perquè l àrea sigui la més gran possible? y Anomenem i y les dimensions de la zona rectangular, i considerem que les divisions són paral leles als costats de mida. Per dividir la zona rectangular en tres parts necessitem dues divisions, per la qual cosa s ha de complir que: + y 60 + y 80 y 80 Hem d optimitzar la funció que ens dóna l àrea, és a dir: A (, y) y A ( ) ( 80 ) 80 A'( ) A"( ) < 0 En 0 assolei un màim. Aií, doncs, les dimensions de la zona rectangular han de ser 0 m i y 0 m. 05 Troba el pendent de la recta tangent a la gràfica de la funció f( ) en el punt d abscissa. El pendent coincidei amb el valor de la derivada en el punt. ( ) ( ) El pendent és. 06 Donada la funció f ( ) +, calcula el pendent de la tangent a la gràfica de la funció f en el punt d abcissa. ( ) + 6 ( ) 6 El pendent és. 7
13 Aplicacions de la derivada < 07 Donada la funció: f( ) 6 si si Calcula el pendent de la recta tangent a la gràfica de la funció en. f( ) 6 ( ) () El pendent és. 08 Donada la funció f( ), eistei algun punt de la gràfica en el qual la recta tingui pendent positiu? Justifica la resposta. ( ) < 0, R { } No eistei cap punt de la gràfica ( ) en el qual la recta tangent tingui pendent positiu. 0 Troba l equació de la tangent a la gràfica de cada una d aquestes funcions en els punts que s indiquen. a) y sin +, en π. b) y, en. c) y ln ( + 7), en 0. d) y +, en. a) f ( π) π ( ) cos + ( π) 0 L equació de la recta tangent és: y π 0( π) y π b) f ( ) ( ) + ( ) ( ) 6 L equació de la recta tangent és: y 6( + ) y c) f ( 0) ln 7 ( ) ( 0) L equació de la recta tangent és: y ln 7 0( 0) y ln 7 d) 0 f ( ) ( ) + 0 ln ( ) ln ln L equació de la recta tangent és: y ln ( + ) 00 Determina l equació de la tangent a la paràbola y en el punt A(, ). ( ) ( ) L equació de la recta tangent és: y ( ) y 8
14 SOLUCIONARI 0 Calcula l equació de la recta tangent a la corba + 6y 6 0 en el punt d abscissa i ordenada positiva. + 6y 6 0 6y 7 y ± Considerem el punt, 7. Aïllem y com a arrel positiva perquè és l ordenada positiva. y 6 y' 6 7 y'( ) L equació de la recta tangent és: y ( ) y Determina l equació de la recta tangent a la corba y 6 0 en el punt d abscissa i ordenada positiva. 7 6 y 6 0 y 8 y ± Considerem el punt, 7. Aïllem y com a arrel positiva perquè és l ordenada positiva. y 6 y' 6 y'( ) L equació de la recta tangent és: y ( ) y 7 0 Considera la funció f( ). Troba l epressió de la recta tangent a aquesta funció en. f ( ) ( ) ( ) ( ) La recta tangent és: y ( ) y + 6 y +
15 Aplicacions de la derivada 0 Donada la funció f( ) de f ( ) en 0. f ( 0) 0 + ( ) ( ) ( 0) Equació de la recta tangent: y, troba l equació de la recta tangent a la gràfica ( )( ) 05 Considera la funció f( ). Calcula l equació de la recta tangent a la corba en. 0 f ( ) ( ) ( ) 7 7 Equació de la recta tangent: 0 0 y ( + ) y + y Calcula l equació de la recta tangent a la gràfica de f () ( + ) e en el punt de tall f ( ) amb l ei X. Calculem el punt de tall amb l ei d abscisses: ( + ) e ( ) e ( + ) e ( ) e L equació de la recta tangent és: y e ( + ) 07 Considera la funció f( ) + 5. Determina els valors de a i b perquè l equació de la recta tangent a la gràfica de f ( ) en el punt sigui y a + b. f ( ) ( ) ( ) ( + 5) Equació de la recta tangent: y + ( + ) y + + y + a, b 0
16 SOLUCIONARI 08 Troba els valors de a i b perquè la recta tangent a la gràfica de f ( ) a b en el punt (, 5) sigui la recta y +. f() 5 a b 5 ( ) a ( ) a Com que el pendent de la recta tangent és resulta: a a Per tant: a b 5 b 5 b b 7 5 D aquesta manera tenim que: 7 f( ) + 0 Determina les equacions de la recta tangent i de la recta normal a la gràfica de la funció y ln en el punt d abscissa. f () 0 ( ) ( ) L equació de la recta tangent és: y L equació de la recta normal és: y ( ) y + 00 Troba les equacions de les rectes tangent i normal a les corbes següents en els punts que s indiquen: a) y e, en. b) y arcsin, en. a) f( ) e e ( ) e + e e + ( ) e L equació de la recta tangent és: y e e ( ) y e e L equació de la recta normal és: y e y e e ( ) + + e e b) f π ( ) π π L equació de la recta tangent és: y y + π L equació de la recta normal és: y π y + +
17 Aplicacions de la derivada 0 Determina les equacions de la recta tangent i de la recta normal a la gràfica de g( ) en el punt d abscissa. g( ) 5 g ( ) si g' ( ) + si < < > si si < < g'( ) L equació de la recta tangent és: y 5 ( ) y + L equació de la recta normal és: y 5 ( ) y + 0 Troba les equacions de les rectes tangent i normal a la corba y en el punt d ordenada i abscissa positiva ( + 6) 0 Hem de trobar les rectes que passen pel punt (, ). ( ) + 6 ( ) 0 L equació de la recta tangent és: y 0( ) y 0 6 L equació de la recta normal és: y ( ) y Determina en quins punts de la gràfica de la funció y + +, la recta tangent a aquesta funció és paral lela a la recta y + 7. Escriu les equacions de les rectes tangent i normal en els punts obtinguts. Si la recta tangent és paral lela a la recta y, resulta que: ( ) ( ) Aleshores, tenim que: Per tant, els punts de la gràfica que verifiquen la condició són: (0, ) i (, ) Equació de la recta tangent en (0, ): y y + Equació de la recta normal en (0, ): y y + Equació de la recta tangent en (, ): y + y Equació de la recta normal en (, ): y + ( ) y + y + 0 Calcula el valor de a perquè la recta tangent a la gràfica de la funció f ( ) a + 5, en el punt d abscissa, talli l ei X en el punt 5. Quina és l equació de la recta normal? f( ) a+ ( ) a + 5 ( ) 6a+ 5 L equació de la recta tangent és: y + a ( 6a+ 5)( ) y ( 6a+ 5) + a
18 SOLUCIONARI Si aquesta recta passa pel punt (5, 0), aleshores: ( 6a+ 5) 5+ a 0 a a Aií doncs, l equació de la recta tangent és: y ( ) y + 5 L equació de la recta normal és: y y 05 Donada la funció f ( ) + b + c, calcula els valors b i c si aquesta funció passa pel punt (, ) i en aquest punt l equació de la recta tangent és y. f () + b+ c b+ c 5 ( ) + b () + b Equació de la recta tangent: y ( + b)( ) y ( + b) + b+ + b 0 + b b f ( ) c b c 06 Troba els valors de a, b i c perquè les gràfiques de les funcions f ( ) + a + b i g ( ) + c passin pel punt (, ) i en aquest punt tinguin la mateia tangent. Si la gràfica de f passa pel punt (, ), aleshores: + a+ b a+ b I si la gràfica de g passa pel punt (, ), tenim que: + c c A més, si en aquest punt tenen la mateia tangent es verifica que: () g'() ( ) + a () + a + a a b 0 g' ( ) g' () 07 Troba el punt de la corba y en el qual la recta tangent és paral lela a la recta y. Les rectes són paral leles si tenen el matei pendent; aií doncs, busquem el punt que verifica que: ( ) ( ) Aleshores, tenim que: El punt té aquestes coordenades: (, ). 08 Troba els punts de la gràfica de f ( ) + en els quals la recta tangent és paral lela a la recta y. Si la recta tangent és paral lela a la recta y, resulta que: ( ) ( ) Aleshores, tenim que: Per tant, els punts de la gràfica que verifiquen la condició són (0, 0) i (, ).
19 Aplicacions de la derivada 0 Determina el punt de la paràbola y 7 + en el qual la recta tangent que passa per aquest punt és paral lela a la recta y Les rectes són paral leles si tenen el matei pendent; aií doncs, busquem el punt que verifica que: ( ) 5 ( ) 7 Aleshores, tenim que: 7 5 El punt té aquestes coordenades: (, ). 050 Troba el domini de la funció y log ( + + ) i els punts en els quals la tangent a la corba és paral lela a la bisectriu del primer quadrant. Nota: log significa logaritme neperià. + + > 0, R Domini R Com que la bisectriu del primer quadrant és la recta y, cal verificar que: + y' ( ) 0 0 Els punt són (0, 0) i (, log ). 05 Troba l equació de la paràbola y + b + c la recta tangent a la qual en el punt (, ) és paral lela a la bisectriu del primer quadrant. ( ) + b () + b La bisectriu del primer quadrant és la recta y. Si la recta tangent hi és paral lela, aleshores: + b b Aií doncs, l equació de la funció és de la forma: y + c Si passa pel punt (, ), tenim que: + c c Per tant, l equació de la paràbola és y Troba els valors de a, b i c perquè la corba f ( ) a + b + c passi pel punt (, ) i sigui tangent en l origen de coordenades a la bisectriu del primer quadrant. f() a+ b+ c ( ) a + b Passa pel punt (0, 0): f( 0) 0 c 0 Ha de ser tangent en aquest punt a la bisectriu del primer quadrant: ( 0) b Per tant, resulta: a+ b+ c a+ a Aií doncs, la funció és f( ) Considera la funció f( ). a) Troba els punts de la gràfica en els quals la recta tangent és paral lela a la recta + y b) Calcula les equacions d aquestes rectes tangents.
20 SOLUCIONARI a) Pendent de la recta + y Cal verificar que: ( ) ( ) ± b) f ( ) Recta tangent en, : y + y + + y ( ) + f ( ) + 7 Recta tangent en 7, : 7 y y + y ( ) 5 + si + < 05 Considera la funció: f( ) si si > Determina el punt de la gràfica en el qual la recta tangent té pendent 0. Qué més podem afirmar sobre aquest punt? Justifica la resposta. si < + < < ( ) si si > Si la recta tangent té pendent 0, cal verificar que: ( ) El punt té aquestes coordenades: (, ). A més, podem afirmar que és un punt de tall amb l ei X i un etrem relatiu. Com que f"( ) < 0 en l interval (, ), el punt (, ) és un màim. 055 Dibuia la paràbola f ( ) a) En quin punt de la gràfica la tangent és paral lela a l ei d abscisses? b) Troba l equació de la recta tangent a f ( ) en el punt P (, 0). Es tracta d una paràbola amb vèrte (, ). Punts de tall amb l ei X: (, 0) i (, 0). Punts de tall amb l ei Y: (0, 8). a) Perquè la tangent sigui paral lela a l ei d abscisses: ( ) (vèrte de la paràbola) Y f ( ) X 5
21 Aplicacions de la derivada b) ( ) 6 Equació de la tangent: y 0 ( ) y Considera f la funció amb domini els nombres reals menys el zero definida per f( ). a) Calcula l equació de la recta tangent i de la recta normal a la gràfica de f en el punt d abscissa. b) Determina els punts A i B de la gràfica de f per als quals les rectes tangents en A i B es tallen en el punt (, 8). a) f ( ) ( ) ( ) L equació de la recta tangent és: y ( ) y + L equació de la recta normal és: y y b) Considerem P p, un punt qualsevol de la gràfica de f. p ( p) p Aií doncs, la recta tangent en P és de la forma: y p y p ( p ) p + 8 p Si aquesta recta passa pel punt (, 8), tenim que: 8 p 8 + 8p + 8p 6 0 p + p 0 p p p Per tant, els punts que busquem són A(, ) i B(, ). 057 Troba els intervals de creiement i decreiement, i també els màims i els mínims, de les funcions polinòmiques següents: a) f( ) ( + ) b) g ( ) + c) h ( ) 8+ 6 d) i ( ) + e) j ( ) a) ( ) ( + ) , En `, ( 0, +` ) ( )> 0 f ( ) creient En, 0 ( )< 0 f ( ) decreient Per tant, f ( ) assolei un màim en i un mínim en 0. 6
22 SOLUCIONARI b) g'( ) +, 6 0, + En + `,, g'( )> 0 g ( ) creient + En, ( +`, ) g'( )< 0 g ( ) decreient Per tant, en un mínim. i en assolei dos màims, i en +, c) h'( ) 8+ 0, h"( ) h"( ) < 0 En aconseguei un màim. h"( ) 0 h"' ( ) h"' ( ) 0 En hi ha un punt d infleió. Aií doncs, h ( ) és creient en ( `, ) (, ) i és decreien en (, +` ). d) i'( ) + 0 ( + ) 0 0, En (, ) ` 0, + ( ) ` i' < 0 i ( ) decreient En 0, ( ) 0 i' > i ( ) creient En 0 aconseguei un mínim i en un màim. e) j ( ) si 0 si < 0 ( ) ( + ) si `,, ` si (, ) (, ) (, + ) j'( ) si ` ` si (, ) Aií, doncs j'( ) 0 0, per tant, els intervals en els quals hem d estudiar ( ) ( ) ( ) ( + ) el creiement i el decreiement són: `,,, 0, 0,,,. ` En (, 0) (,+ ` ) j ( ) (, ) j En `, 0 '( )> 0 i ( ) creient '( )< 0 i ( ) decreient La funció j ( ) assolei un màim en 0 i dos mínims en i. 058 Determina els intervals de creiement i decreiement i els etrems relatius d aquestes funcions racionals: a) f( ) + b) g ( ) c) h ( ) + d) i ( ) 5 7
23 Aplicacions de la derivada a) f és contínua en R {}. ( ) 0 0 ( ) En ( `, 0) (, + `) ( )> 0 f ( ) creient En ( 0, ) (, ) ( )< 0 f ( ) decreient En 0 assolei un màim, i en, un mínim. b) g és contínua en R { 0 }. g'( ) 0 < 0 g ( ) és decreient en tot el seu domini. ( 0 ) c) h és contínua en R. h'( ) + 0, ( + ) En ( `, ) (, + `) h'( )< 0 i ( ) decreient En ( ) Per tant, en d) i és contínua en R {} 5., h'( )> 0 h ( ) creient assolei un màim, i en un mínim. 5 5 i'( ) 0 0, ( 5) En (, ) (, ), ( ) ` i' < 0 i ( ) decreient 5 En, + ( ) 0 ` i' > i ( ) creient En 5 la funció aconseguei un mínim. 05 Considera la funció f( ). a) Troba l equació de la recta tangent a la corba y f ( ) en el punt d abscissa. b) Determina els intervals de creiement i decreiement, i els etrems, si eisteien. a) f ( ) ( ) ( ) Equació de la recta tangent: 8 ( ) 8 y ( ) y + y + 8
24 SOLUCIONARI b) Dom f R ( ) ( ) En ( `, 0) (, + `) ( ) > 0 f ( ) creient En 0,, ( ) < 0 f ( ) decreient En 0 aconseguei un màim i en un mínim. 060 Calcula els intervals de creiement i decreiement, i també els màims i els mínims, de les funcions eponencials següents: a) f( ) e c) h ( ) 6e b) g ( ) ( + ) e d) i ( ) e + + Les tres funcions són contínues en R. a) ( ) e ( 6 + ) 0, 0 En ( `, ) ( 0, + `) ( )> 0 f ( ) creient En (, 0) ( )< 0 f ( ) decreient En assolei un màim, i en 0, un mínim. b) g'( ) e ( + ) 0 En ( `, ) g'( )< 0 g ( ) decreient En (, + ` ) g'( )> 0 g ( ) creient En assolei un mínim. c) h'( ) e ( 6 6) 0 En ( `, ) h'( )> 0 h ( ) creient En ( +`, ) h'( )< 0 h ( ) decreient En assolei un màim. + + d) i'( ) ( + ) e En ( `, ) i' ( ) < 0 i ( ) decreient En (, + `) i' ( ) > 0 i ( ) creient En assolei un mínim. 06 Estudia el creiement i el decreiement i els etrems relatius d aquestes funcions logarítmiques: a) f( ) + ln b) g ( ) ln c) h ( ) ln d) i ( ) ln
25 Aplicacions de la derivada a) El domini de f és ( 0, +` ) i és contínua en tot el domini. ( ) + 0 En (0, ) ( )< 0 f ( ) decreient En ( +`, ) ( )> 0 f ( ) creient En assolei un mínim. b) El domini de g és ( 0, +` ) i és contínua en tot el domini. ln g'( ) 0 e En ( 0, e ) g'( )> 0 g ( ) creient ( ) En e, + ` g'( )< 0 g ( ) decreient En e assolei un màim. c) El domini de h és ( 0, +` ) i és contínua en tot el domini. h'( ) ln( ) + 0 e En 0, e h '( )< 0 h ( ) decreient En e, + ` h'( )> 0 h ( ) creient En assolei un mínim. e d) El domini de i és (0, + ) {} i és contínua en tot el domini. ln i'( ) 0 ln e ln En ( 0, ) (, e) i' ( ) < 0 i ( ) decreient En ( e, + `) i' ( ) > 0 i ( ) creient En e aconseguei un mínim. 06 Estudia el creiement i el decreiement d aquestes funcions trigonomètriques, i determina si assoleien màims o mínims en algun punt: a) f( ) cos π + c) h ( ) arctg b) g ( ) sin d) i ( ) cos a) f és contínua en R. ( ) sin π + cos 0 ± π Estudiem el creiement en ( π, π ) perquè les funcions de sinus i cosinus són periòdiques de període π. En π π π,, π ( )> 0 f ( ) creient En π π, ( )< 0 f ( ) decreient 0
26 SOLUCIONARI La funció té un màim en π i un mínim en π. Com que és una funció periòdica de període π, podem estendre el resultat a tota la recta real, de manera que es repeteiin indefinidament intervals de creiement i de decreiement, màims i mínims. b) g és contínua en R. g'( ) cos 0 cos 0 Estudiem el creiement en ( π, π ), perquè g' ( ) és periòdica de període π. g'( )> 0 en ( π, 0) ( 0, π) g ( ) creient No té etrems relatius. Si estenem el resultat a tota la recta real, g no té etrems relatius. c) h és contínua en R. h'( ) > 0 h ( ) creient en R No té etrems relatius. + d) i és contínua R. i'( ) + sin > 0, R i ( ) creient en R No té etrems relatius. 06 Determina els màims i els mínims d aquestes funcions per mitjà de la derivada segona: a) y 6 c) y ln ( + ) ( ) b) y + 8 d) y a) y' 0 8 ± 8 y" 6 ( ) > En 8 assolei un mínim. y" 8 0 ( ) < y" c) y' ( + ) 8 0 En 8 assolei un màim. y" + ( + ) 0 ± y"( ) > 0 En assolei un mínim. y"( ) < 0 En assolei un màim. c) y' y" + y" ( 0) > 0 En 0 assolei un mínim. ( + ) + 6 d) y' y" 8 y" ( 6 ) < 0 En 6 aconseguei un màim.
27 Aplicacions de la derivada 06 Troba els intervals de creiement i de decreiement i els màims i els mínims d aquestes funcions, a partir de la segona derivada. a) y ( + ) e b) y a) Domini R c) y e d) y y' ( + + ) e 0 No té etrems relatius. b) Domini R { } y' < 0 Funció decreient en tot el domini ( ) No té cap etrem relatiu. c) Domini R + 5 y' e + e e ( + ) , y" e ( + ) + e ( + ) e ( + + ) y"( 0) > 0 En 0 s aconseguei un mínim. y"( ) < 0 En s aconseguei un màim. Aií, en ( `, ) ( 0, + `) la funció és creient i en (, 0) és decreient. d) y + 5 Domini R { 0} 5 + y' > 0 Funció creient en tot el domini. No té etrems relatius. 065 Calcula els màims i els mínim absoluts de la funció f ( ) en l interval [, ]. Justifica que els punts trobats són màims o mínims absoluts. Els valors de la funció en els etrems de l interval són (, 5) i (, 5). ( ) , En (, ) ( ) < 0 f ( ) decreient En (, ) ( ) > 0 f ( ) creient En (, ) aconseguei un mínim relatiu, que com que és l únic en [, ] és, a més, mínim absolut, i en (, 5) i (, 5) aconseguei dos màims absoluts, perquè es tracta dels etrems de l interval i en tots dos f ( ) agafa el matei valor. 066 Donada la funció f( ) i decreiement. Dom f R { ± }, determina n els intervals de creiement ( ) + + > 0 f ( ) és creient en tot el domini. ( ) ( ) Aií doncs, els intervals de creiement són: ( `, ) (, ) (, + `)
28 SOLUCIONARI Considera la funció de variable real f( ). a) Determina n els intervals de creiement i decreiement. b) Troba n els etrems relatius. a) Dom f R { } 8 0 ( ) 0, 0 ( ) En ( `, ) ( 0, + `) ( ) > 0 f ( ) creient En (, ) (, 0) ( ) < 0 f ( ) decreient b) En s aconseguei un màim que té com a coordenades (, ). En 0 s aconseguei un mínim que té com a coordenades (0, 5). ( ) 068 Donada la funció real de variable real definida per f( ), calcula n + els màims i els mínims i determina n els intervals de creiement i decreiement. Dom f R { } ( ) 0, ( + ) En ( `, ) (, + `) ( ) > 0 f ( ) creient En (, ) (, ) ( ) < 0 f ( ) decreient En s aconseguei un màim que té com a coordenades (, ). En s aconseguei un mínim que té com a coordenades (, 0). 06 Comprova que la derivada en el punt de la funció f( ) ( +) és nul la i, tot i aií, no té un etrem relatiu. ( ) ( + ) ( ) 0, però, ( )> 0 per a tot valor real de ; per tant, f sempre és creient i no pot tenir cap etrem relatiu en. Aiò no contradiu el teorema: «Si una funció és derivable en un punt i hi té un etrem, aleshores la derivada és zero», perquè el cas recíproc no té per què ser cert, és a dir, si la derivada en un punt és zero, aiò no garantei que la funció tingui un etrem en aquest punt. 070 Comprova que la funció següent té un etrem relatiu en el punt 0 i la seva derivada en aquest punt no és nul la. f( ) si 0 si 0 Com que f és positiva en R { 0 } i val en 0 en aquest punt assolei un mínim. D altra banda, f no és derivable en 0. Aiò no contradiu el teorema enunciat a l activitat anterior perquè com que la funció no és derivable, no podem aplicar el teorema.
29 Aplicacions de la derivada 07 Considera la funció: + (, ) f( ) si 6 si [, ] Calcula els intervals de creiement i decreiement de f ( ) per als valors ( 6, ). ( ) ± En ( 6, ) ( ) > 0 f ( ) creient En (, ) ( ) < 0 f ( ) decreient 07 Una empresa de compra i venda d automòbils ha efectuat un estudi sobre els beneficis/pèrdues, en milers d euros, al llarg dels últims 0 anys i ha comprovat que s ajusten a la funció: Et demanem, justificant la resposta: Ft () t 8t + 8t si 0 t 0 a) En quins anys es produeien els valors màim i mínim d aquesta funció? b) Determina n els períodes de creiement i decreiement. c) Quins són els seus beneficis màims? d) Quins resultats va obtenir l empresa en l últim any de l estudi? a) F és contínua en [0, 0] perquè es tracta d una funció polinòmica. F'( t) t 6t t, t F"( t) 6t 6 F"( ) 8 6 8< 0 En t s aconseguei un màim. F"( ) 5 6 8> 0 En t s aconseguei un mínim. Aií doncs, el valor màim de la funció s aconseguei al cap de anys, i el mínim, al cap de anys. b) Períodes de creiement: (0, ) (, 0) Període de decreiement: (, ) c) F( ) El benefici puja a d) F( 0) És a dir, l empresa va obtenir un benefici de a 07 Per a cada valor de a es considera la funció f( ). + Calcula el valor de a perquè f ( ) tingui un mínim relatiu en.
30 SOLUCIONARI + a ( ) ( + ) Perquè hi hagi un mínim en s ha de complir que: + a ( ) a 0 a Troba els valors de a i b perquè la funció f ( ) a + b + + tingui un màim en el punt i un mínim en el punt. ( ) a + b + ( ) 0 a+ b+ 0 ( ) 0 a+ b+ 0 a+ b+ 0 a, b a+ b+ 0 6 k 075 Sigui la funció f( ). Determina el valor de k de manera que la funció tingui un màim en. En la funció determinada d aquesta manera, troba: a) El domini de definició. b) Els intervals de creiement i de decreiement de la funció, i també els màims i els mínims. k ( ) + ( ) 0 + k 0 k + f( ) + Dom f R { 0} ( ) 0 0 ± En ( `, ) (, + `) ( ) > 0 f ( ) creient En ( 0, ) ( 0, ) ( ) < 0 f ( ) decreient En aconseguei un màim amb aquestes coordenades: (, ); i en, un mínim amb aquestes coordenades: (, ). 076 Troba els paràmetres r, s i t perquè la funció f ( ) r + s + t tingui un màim en, un mínim en 0 i passi pel punt (, ). Passa per (, ) r + s+ t r + s+ t ( ) r + s Té un màim en ( ) 0 + r + s 0 Té un mínim en 0 ( 0) 0 s 0 Per tant, resulta: r + t r f( ) r 0 t 5 5
31 Aplicacions de la derivada 077 Troba els valors de a, b i c en la funció y a + b + c + d si saps que la seva tangent en el punt (, ) és la recta y + i que té un etrem en el punt (0, ). Passa per (, ) a+ b+ c+ d Passa per ( 0, ) d y' a + b + c y' () a+ b+ c S ha de verificar que: y'( ) a+ b+ c Té un etrem en el punt ( 0, ) y' ( 0) 0 c 0 Per tant, resulta: a + b + a y + a+ b b 078 Una entitat financera llença al mercat un pla d inversió la rendibilitat del qual, R, en euros ve donada per R() 0, , en què és la quantitat que s invertei. a) Quant ha d invertir un inversor si vol obtenir una rendibilitat màima? b) Calcula aquesta rendibilitat màima. 5 a) R'( ) 00, , R"( ) 00, < 0 En 50 la funció aconseguei un màim. Aií doncs, per obtenir una rendibilitat màima ha d invertir 50. b) R( 50) és la rendibilitat màima. 07 En la construcció d un túnel, el percentatge de roca fragmentada o de mala qualitat ve donat pel model matemàtic següent: R ( ) 5, si0 7 R ( ) representa aquest percentatge quan la distància a la boca del túnel és (en quilòmetres). Si en algun tram de la perforació el percentatge supera el 0 %, s hauran de reforçar les mesures de sosteniment i seguretat de l estructura. a) Indica en quins trams de la perforació el percentatge crei i en quins trams decrei. b) Assenyala els màims i els mínims (absoluts i relatius) i els punts d infleió de la corba. a) R'( ) + 8 0, 6 En (0, ) R'( )> 0 R ( ) creient En (, 6) R'( )< 0 R ( ) decreient En (6, 7) R'( )> 0 R ( ) creient Per tant, el percentatge crei en i de crei en (, 6). 6
32 SOLUCIONARI b) R"( ) 0 5, R"'( ) 0 En 5, hi ha un punt d infleió. Dels intervals de creiement i de decreiement que hem obtingut, i a partir del valor de la funció en [0, 7], deduïm que: En s aconseguei un màim relatiu i, a més, com que R() 7,5, aquest punt és el màim absolut de la funció. Té com a coordenades (, 7,5). En 6 s aconseguei un mínim relatiu que té com a coordenades (6, ). En, com que R(0) 5, s aconseguei el mínim absolut de la funció. Té com a coordenades (0, 5). 080 Un article de consum va estar a la venda durant 8 anys, i el seu preu P(t) (en milers d euros) va variar amb el temps t (en anys) que portava al mercat segons la funció: t + si 0 t Pt () 5 t + 5 si < t 8 Esbrina en quin moment es van assolir els preus màim i mínim i quins van ser aquests preus. En t la funció és contínua, perquè es complei que: P( ) P( ) 6+ 0 P( + 5 ) Per tant, la funció és contínua en (0, 8). 8t si 0< t < P'( t) 5 si < t < 8 En (0, ) P'( t)> 0 P(t) creient En (, 8) P'( t)< 0 P(t) decreient P( 0) P( ) 6+ 0 P( 8) El preu mínim es va aconseguir al començament de la venda, i va ser de.000 ; el preu màim es va aconseguir quan feia anys que es venia el producte, i va ser de El rendiment dels treballadors d una fàbrica (valorat en una escala de 0 a 00), durant una jornada de 8 hores, ve donat per la funció: 0t + 60t si 0 t < rt () 80 si t < t si 6 t 8 en què t és el temps en hores. a) Determina n els intervals de creiement i decreiement. Quin és el rendiment màim? b) En quins instants de la jornada laboral el rendiment se situa a la meitat de l escala? 7
33 Aplicacions de la derivada a) En t la funció és contínua, perquè es complei que: r( ) r( ) r( + ) 80 En t 6 la funció és contínua, perquè es complei que: r( 6 ) 80 r( 6) r( 6 + ) 80 Aií doncs, la funció és contínua en (0, 8). 0t + 60 si 0 < t < r'( t) 0 si < t < 6 5 si 6 < t < 8 En (0, ) r'( t) 0 0t t En (, 6) En (6, 8) r'( t) 0 r (t) constant r'( t)< 0 r (t) decreient En (0, ) r' () t > 0 r() tcreient En (, ) r' ( t ) < 0 r ( t ) decreient Per tant, el rendiment màim s aconseguei quan t, i té un valor de 0. b) El rendiment se situa a la meitat de l escala si r ( t ) 50. D aquesta manera, pot passar que: 0t + 60t 50 0 t + 6t 5 0 t, t 5 En aquest cas, només és vàlida la solució t, perquè l altra solució no és a (0, ). 70 5t t t 8 Aií doncs, el rendiment se situa a la meitat de l escala quan hagin passat o 8 hores. 08 L oferta d un bé si en coneiem el preu, p, és: p p Sp ( ) si 0 0 p 60p si 0 < p 0 Digues per a quin valor del preu s assoleien l oferta màima i la mínima. En p 0 la funció és contínua, perquè es complei que: S( 0) S( 0 ) 500 S( 0 + ) 500 Per tant, la funció és contínua en (0, 0). < p < S'( p) 0 si 0 0 p 60 si 0< p < 0 En (0, 0) S'( p)> 0 S(p) creient En (0, 0) S'( p) 0 p 60 0 p 0 En (0, 0) S'( p) < 0 S( p) decreient En (0, 0 ) S'( p) > 0 S( p) creient S( 0) 00 S( 0) 500 S( 0) 00 S( 0) 00 L oferta màima s aconseguei per a un valor del preu de 0, i l oferta mínima s aconseguei per a un valor del preu de 0. 8
34 SOLUCIONARI 08 La distància (en milles) entre un vaiell de pesca que va sortir a pescar durant un període de 0 dies i el seu port base ve donada per la funció: ( t ) t Mt () 6 6 si ( t) si 5 < t 0 en què t és el temps transcorregut, en dies, des de la sortida del port base. a) Després de quants dies és màima la distància del vaiell al port? A quantes milles es trobava? b) Durant quins períodes augmentava la distància al port base? En quins períodes disminuïa? c) A partir de quin dia, després d assolir la distància màima, es trobava a menys de milles del port base? a) En t 5 la funció és contínua, perquè es complei que: M( 5) M( 5 ) M( 5 + ) 0 ( t ) t M'( t) 6 si 0 < < 5 t si 5 < t < 0 En (0, 5) M'( t) 0 t + 0 t En (0, ) M' () t > 0 M() tcreient En (, 5) M' ( t ) < 0 M ( t ) decreient En (5, 0) M'( t)< 0 M(t) decreient M( 0) M( ) 6 M( 5) M( 0) 0 La distància del vaiell de pesca al port base és màima al cap de dies, i es trobava a 6 milles. b) La distància al port base augmentava en el període (0, ) i disminuïa en els períodes (, 5) i (5, 0). c) Com que en (, 5) la funció és decreient i M (5) 0, el dia que busquem estarà entre 5 i 0. Mt () < ( 0 t) < 0 t < 7 < t A partir del dia 7 es trobava sempre a menys de milles de distància del port base. 08 Determina els intervals de concavitat i de conveitat, i també els punts d infleió, de les funcions següents: a) y + + b) y + c) y 8 d) y e) y + f) y a) La funció és contínua en R. y' y" En ( `, ) y" < 0 Funció còncava En ( +`, ) y" > 0 Funció convea Aií, doncs, en assolei un punt d infleió.
35 Aplicacions de la derivada b) La funció és contínua en R. y' + 6 y" + 0 0, En ( `, ) ( 0, + `) y" > 0 Funció convea En (, 0 ) y" < 0 Funció còncava Aií, doncs, en i 0 assolei punts d infleió. c) La funció és contínua en R {, }. y' ( ) 6 + y" 0 No té punts d infleió. ( ) Aií, doncs, els intervals en els quals hem d estudiar la curvatura són: ( `, ), (, ), (, + `) En ( `, ) (, + `) y" > 0 Funció convea En (, ) y" < 0 Funció còncava d) La funció és contínua en R { 0 }. + 6 y' y" 8 < 0 en R { 0 } Funció còncava No té punts d infleió. e) La funció està definida en R. y' + y" > 0 en R Funció convea ( + ) + No té punts d infleió. f ) La funció està definida en ( `, ) (, + `). y' y" < 0 en tot el domini Funció còncava ( ) No té punts d infleió. 085 Estudia en quins intervals aquestes funcions són còncaves i en quins són convees. Calcula també els punts d infleió que tingui cadascuna. a) y ( ) e e) y b) y ln f) y c) y cos cos g) y d) y ln ( ) e 0
36 SOLUCIONARI a) La funció és contínua en R. y' ( ) e y" ( ) e 0 En ( `, ) y" < 0 Funció còncava En ( +`, ) y" > 0 Funció convea En assolei un punt d infleió. b) La funció és contínua en (0, +`). y' ln ln y" 0 ln e e ( ) y" < 0 Funció còncava ( ) En 0, e En e, + ` y" > 0 Funció convea En e assolei un punt d infleió. c) La funció és contínua en R. y' sin + sin y" cos + cos cos + (cos sin ) cos + (cos + cos ) 8 cos cos 0 Les solucions aproimades són: cos 077, 06, + kπ; 55, + kπ amb k R cos 065, 8, + kπ; 7, + kπ amb k R Estudiem la concavitat en (0, π) perquè la funció és periòdica: En ( 0; 0, 6) (, 8; 7, ) ( 55, ; π ) y" > 0 Funció convea En ( 06, ; 8, ) ( 7, ; 55, ) y" < 0 Funció còncava Aií, doncs, tots els punts que anul len y" són punts d infleió. d) La funció està definida en ( `, 0) (, + `). y' y" + < 0 en tot el domini Funció còncava ( ) No té punts d infleió. e) La funció és contínua en R. ln y' y" + ln ln 0 ± ln En + `, +, ` ln ln y" > 0 Funció convea + En, ln ln y" < 0 Funció còncava En l n i + l n assolei dos punts d infleió.
37 Aplicacions de la derivada f ) La funció està definida en ( `, 0) (, + `). y' ( ) y" ( ) ( + ) ( ) ( ) 0 No hi ha punts d infleió. ( ) A més, és negativa en tot el domini i, per tant, sempre és còncava. g) La funció està definida en R. e e y' e e e e y " ( ) e + e 0 En ( `, ) y" < 0 Funció còncava En (, + `) y" > 0 Funció convea En hi ha un punt d infleió. 086 Comprova que la funció f ( ) 7 té nul la la derivada segona en el punt 0 i, tot i aií, no té un punt d infleió. f( ) 7 ( ) 8 f" ( ) 8 f" ( 0) 0 En 0 no s aconseguei un punt d infleió, perquè f"( )< 0 per a qualsevol valor real de. Aií doncs, la funció sempre és còncava. 087 La derivada d una funció f és f ( ). Representa gràficament f i deduei d aquesta gràfica els intervals de creiement i de concavitat de f. Y ( ) X En ( `, ) (, + `) ( ) > 0 f ( ) creient En (, ) ( ) < 0 f ( ) decreient Aií doncs, en s aconseguei un màim, i en, un mínim. (0) 0, perquè ( ) presenta un mínim en 0. En ( `, 0) ( ) decreient f"( )< 0 f ( ) còncava En ( 0, +`) ( ) creient f"( )> 0 f ( ) convea Per tant, en 0 hi ha un punt d infleió.
38 SOLUCIONARI 088 Volem afegir a una casa una altra habitació rectangular de m de superfície. Determina quina longitud han de tenir les parets perquè el perímetre sigui el més petit possible i minimitzar la quantitat de maons que farem servir en aquesta ampliació.-- Si i y són les dimensions, tenim que: y y Com que la nova habitació serà un afegit de la casa, una de les parets hi ha de coincidir; d aquesta manera, no necessitem cap maó, perquè ja està construïda. Per tant, hem de minimitzar: P(, y) + y P ( ) + P'( ) 0 6, 6 Com que una longitud no pot ser negativa, tenim que: 6 y 6 Comprovem que en aquest punt s assolei un mínim: P" ( ) P" ( 6) > 0 Es tracta d un mínim. Les dimensions de l habitació són 6 m i y 6 m. 08 Volem delimitar una parcel la rectangular, enganada a la paret d una nau. Si disposen de 00 m de filat per fer la tanca, digues quines són les dimensions de la parcel la que té la superfície més gran. Anomenem i y les dimensions de la parcel la. Com que estarà enganada a la paret de la nau, s ha de complir que: + y 00 y 00 Es tracta de maimitzar la funció superfície, determinada per: S ( ) y S ( ) ( 00 ) 00 S'( ) S"( ) < 0 en R En 50 assolei un màim. Les dimensions de la parcel la són: 50 m i y 00 m. 00 Determina quines dimensions ha de tenir un paraigüer amb forma de prisma quadrat de 0 dm de volum perquè a l hora de fabricar-lo es gasti la quantitat de material més petita possible. Anomenem l aresta de la base i y l altura del prisma quadrangular. 0 Aleshores, s ha de complir que: y 0 y Com que un paraigüer no té base superior, hem de minimitzar la funció superfície, que està determinada per: 0 80 S (, y) + y S ( ) S'( ) S" ( ) + S" ( 0 ) > 0 Se assolei un mínim. Les dimensions del paraigüer són: 0 Aresta de la base 0 0 dm Altura y ( ) 0 dm 600.
39 Aplicacions de la derivada 0 Digues si tots els cilindres amb el matei volum tenen també la mateia superfície total. Quin té la superfície més petita? Considerem r i h les dimensions del radi de la base i de l altura del cilindre. Si V ( r, h ) és el volum: Vr (, h) Vr (, h) πrh h πr La superfície del cilindre que hem de minimitzar està determinada per: Vr (, h) V ( r, h) Sr (, h) πr + πrh πr + πr πr + πr r Com que el volum sempre és el matei, derivem respecte de r: Vr (, h) πr V(, r h) V( r, h ) S'( r, h) πr 0 r r r π Vr (, h) Vr (, h) S" (, r h) π + S" r π > 0 S assolei un mínim. Aií, doncs, no tots els cilindres amb el matei volum tenen també la mateia superfície total, i el que té la superfície més petita és d aquestes dimensions: r Vr (, h) π h Vr (, h ) π 0 De tots els cilindres que podem inscriure en una esfera de cm de radi, troba l altura i el radi del que té el volum més gran. Anomenem el radi de la base del cilindre i y la meitat de la seva altura, aií: R. Es verifica que: + y R + y 8 y La funció que hem de maimitzar és: V (, y) πh on h y. 8 V (, y) πy V ( ) π 8 π 8 6 R y 5 5 π( 6 ) π( 6 ) V'( ) 0 0, ( ) V ( ) En 0, 5 '( )> 0 V( ) creient En 5, + ` V'( )< 0 V( ) decreient Per tant, en 5 assolei un màim. Aií, doncs, l altura i el radi del cilindre de més volum que podem inscriure en una esfera de radi cm és: Radi: 5 cm Altura: cm
40 SOLUCIONARI 0 De tots els cons que podem inscriure en una esfera de cm de radi, determina l altura i el radi del que té el volum més gran. h r Anomenem r i h el radi i l altura del con. Es complei que: r + ( h ) 8 r 8 ( h ) h + 8h La funció que hem d optimitzar és: Vr (, h) πrh Vh ( ) π( h + 8hh ) π( h + 8h ) V'( h) π( h + 6h) π( h + h) 0 h 0, h V"( h) π( h+ ) V"( 0) > 0 Per a h 0 assolei un mínim. V"( ) < 0 Per a h assolei un màim. Aií, doncs, el con que té el volum més gran és el que té una altura de cm i un radi de la base 7 6 cm. 0 Amb un tros de filferro de cm de longitud podem formar diferents rectangles. Digues quin d aquests rectangles té la superfície màima. Considerem i y les dimensions del rectangle, de manera que: + y + y 6 Aií, doncs, la funció que hem de maimitzar és: S( ) ( 6 ) 6 S'( ) 6 0 S"( ) < 0 En assolei un màim. Per tant, les dimensions del rectangle de superfície màima són i, és a dir, un quadrat de costat cm. 05 Troba dos nombres que sumin 0 si saps que el seu producte és màim. Considerem i y els dos nombres que busquem. Es complei que: + y 0 y 0 P (, y) y P ( ) ( 0 ) 0 P'( ) P"( ) < 0 En 0 s aconseguei un màim i, per tant, els nombres són 0 i y 0. 5
41 Aplicacions de la derivada 06 Considera la funció següent: f( ) + ln Escriu l equació de la recta tangent a la gràfica d aquesta funció que té màim pendent en l interval [, e]. Com que necessitem que el pendent sigui màim, la funció que hem d optimitzar és la funció derivada primera: f '( ) + + f"( ) 0 6 f"' ( ) f"' ( ) < 0 En assolei un màim. f ( ) + ln L equació de la recta tangent en el punt, + l n amb pendent ( ) és: y + ln ( ) 07 Digues en quin punt de la paràbola y la tangent forma amb els eios de coordenades un triangle d àrea mínima. La funció de l enunciat representa una paràbola amb vèrte a l ei Y, per la qual cosa hi ha d haver dues solucions simètriques respecte d aquest ei, una al primer quadrant i una altra al segon. Considerem (a, a ) un punt de la paràbola del primer quadrant. y' y' ( a) a L equació de la recta tangent a la paràbola en el punt ( a, a ) és: y ( a ) a( a) y a + a + a Els punts d intersecció d aquesta recta amb els eios són: ( 0, a + ) i + a L àrea del triangle que es forma amb aquests punts i el punt (0, 0) és: a + ( a + ) Aa ( ) ( a + ) a a 6a ( a + ) ( a + ) A'( a) 6a que és la funció que hem d optimitzar. a + 8a 6 0 a ± a a és la solució del primer quadrant. a ( a + 6a) 8a( a + 8a 6) a + 6 A" ( a) A" 0 6a a > En 8, la tangent forma amb els eios un triangle d àrea mínima., 0. 6
42 SOLUCIONARI 08 Determina el punt de la paràbola y que es troba més pròim al punt (, 0). Considerem (, y) el punt de la paràbola que busquem. La distància d aquest punt al punt (, 0) està determinada per: d ( ) + ( y 0) La funció que hem d optimitzar és: D d ( ) + y D( ) ( ) + D'( ) ( ) + 0 és l única solució real. D" ( ) + D" () > 0 En assolei un mínim. Aií, doncs, el punt que busquem és (, ). 0 Determina les dimensions dels costats d un rectangle d àrea màima que està inscrit en una semicircumferència de 5 cm de radi, i que té un dels costats sobre el diàmetre d aquesta semicircumferència. y Considerem la meitat de la base del rectangle i y l altura. Es complei que: + y 5 y 5 La funció que hem d optimitzar és: A ( ) A'( ) , 5 5 En 0, 5 A'( )> 0 i en 5, + ` A'( )< 0 Per tant, en 5 assolei un màim. Aií, doncs, les dimensions del rectangle d àrea màima són: 5 cm i y 5 cm, és a dir, es tracta d un quadrat. 00 Entre tots els rectangles de m d àrea, troba les dimensions del que tingui mínim el producte de les diagonals. Considerem i y les dimensions del rectangle, de manera que: y. La funció que hem d optimitzar està determinada per: P d d d + y P + + ( ) 8 P'( ) 0 8 0, La solució vàlida és: 5 P" ( ) + P" ( ) > 0 En aquest punt assolei un mínim. Les dimensions són i y, és a dir, un quadrat de costat m. 7
43 Aplicacions de la derivada 0 De tots els triangles isòsceles inscrits en una circumferència de 5 cm de radi, troba les dimensions del que té l àrea més gran. Anomenem la meitat de la base del triangle, i y + 5 l altura. Es verifica que: + y 5 5 y La funció que hem d optimitzar està determinada per: Ay ( ) 5 y ( y + 5) ( y + 5) 5 y A'( y) 5 y + ( y + 5) y 5 y 5 y y 5y 0 5 y y 5y y 5, y La solució vàlida és la positiva. En 5, 5 A '( y )> 0 Funció creient 5 En, + ` A'( y)< 0 Funció decreient Aií, doncs, en y 5 assolei un màim. 5 y 5 5 Per tant, les dimensions del triangle d àrea més gran són: 75 Base: Altura: y El perímetre d un triangle isòsceles fa 0 m. Si gira al voltant de l altura que correspon al costat desigual, genera un con. Calcula els costats del triangle perquè el volum del con sigui màim. Pel teorema de Pitàgores: r + h g h g r Com que el perímetre del triangle és 0 m, tenim que: g+ r 0 g+ r 5 g 5 r Aií, doncs, si substituïm en l epressió de l altura obtenim: h g r ( 5 r) r 5 + r 0r r 5 0r La funció que hem d optimitzar és: π Vr (, h) πrh Vr () πr 5 0r 5r 0r π( 00r 50r ) r V'( r) r 0r r 5 La solució vàlida és r. Aií, doncs, les dimensions del triangle són: Base: m Costats: m g r h 8
44 SOLUCIONARI 0 Un taller artesanal està especialitzat en la producció d un tipus de joguines. Els costos de fabricació, C ( ), en euros, estan relacionats amb el nombre de joguines fabricades,, mitjançant l epressió: C ( ) El preu de venda de cada joguina és de 50. a) Planteja la funció d ingressos que obté el taller amb la venda de les joguines produïdes. b) Planteja la funció de beneficis, entesos com la diferència entre ingressos i costos de fabricació. c) Quantes joguines ha de fabricar per maimitzar beneficis? A quant pujaran aquests beneficis? a) I( ) 50 b) B ( ) I( ) C ( ) 50 ( ) c) B'( ) B"( ) 0 < 0 En 5 s aconseguei un màim. B( 5) Aií doncs, per maimitzar beneficis ha de vendre 5 joguines. Aquests beneficis pugen a B(5) La funció B( ) + 6 representa, en milers d euros, el benefici net d un procés de venda, en què és el nombre d articles venuts. Calcula el nombre d articles que s han de vendre per obtenir el benefici màim i determina aquest benefici màim. B ( ) + B ( ) ' ± La solució vàlida és (l altra no té sentit) ( ) 6 El benefici màim serà: B( ) +. Aií doncs, el benefici màim és de.000
La recta. La paràbola
 LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
+ 1= 0 té alguna arrel real (x en radians).
 Generalitat de Cataluna Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen r quadrimestre Nom i Cognoms: Grup: Data: ) Calculeu els its següents:
Generalitat de Cataluna Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen r quadrimestre Nom i Cognoms: Grup: Data: ) Calculeu els its següents:
x x 1 x 11= 7) y = 6 3x-2 12) y = e 5x (3x 2-6)
 Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
SOLUCIONARI Unitat 2. Comencem. Exercicis
 SOLUCIONARI Unitat Comencem Representa en paper mil limetrat la funció f() + 4. Traça amb la màima cura possible la recta tangent a la paràbola en el punt P(, ). Mesura amb un transportador l angle que
SOLUCIONARI Unitat Comencem Representa en paper mil limetrat la funció f() + 4. Traça amb la màima cura possible la recta tangent a la paràbola en el punt P(, ). Mesura amb un transportador l angle que
DERIVADES: exercicis bàsics ex D.1
 DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
DERIVADES. TÈCNIQUES DE DERIVACIÓ
 UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
SOLUCIONARI Unitat 1. Exercicis. Comencem. 1. La gràfica velocitat-temps corresponent a dos mòbils és la que pots veure a la dreta (fig. 1.3).
 SOLUCIONARI Unitat Comencem La funció f() és decreient en l interval (, ). Fes un raonament com el que em fet anteriorment per determinar on decrei amb més rapidesa, si ens movem prop de o si o fem prop
SOLUCIONARI Unitat Comencem La funció f() és decreient en l interval (, ). Fes un raonament com el que em fet anteriorment per determinar on decrei amb més rapidesa, si ens movem prop de o si o fem prop
UNITAT DIDÀCTICA 11 I NICIACIÓ AL CÀLCUL DE DERIVADES. APLICACIONS
 0 Matemàtiques UNITAT DIDÀCTICA Pàgina 80. a 0 km/h b 88 km/h Hi accedirà suaument. Pàgina 8. a Intenta assolir la velocitat de l autobús per accedir-hi suaument. b El passatger accedei suaument a l autobús;
0 Matemàtiques UNITAT DIDÀCTICA Pàgina 80. a 0 km/h b 88 km/h Hi accedirà suaument. Pàgina 8. a Intenta assolir la velocitat de l autobús per accedir-hi suaument. b El passatger accedei suaument a l autobús;
EXERCICIS MATEMÀTIQUES 1r BATXILLERAT
 Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
f x té màxims o mínims relatius. 6.- Determina els intervals de creixement i decreixement, màxims i mínims de les funcions següents: x
 EXERCICIS REPRESENTACIÓ DE FUNCIONS: - Estudia els intervals de monotonia (crei/decrei) de: f - Estudia si la funció f - Determina si la funció 4 té màims o mínims relatius e f té punts on la funció hi
EXERCICIS REPRESENTACIÓ DE FUNCIONS: - Estudia els intervals de monotonia (crei/decrei) de: f - Estudia si la funció f - Determina si la funció 4 té màims o mínims relatius e f té punts on la funció hi
f x té màxims o mínims relatius. 6.- Determina els intervals de creixement i decreixement, màxims i mínims de les funcions següents: x
 4- EXERCICIS REPRESENTACIÓ DE FUNCIONS: - Estudia els intervals de monotonia (crei/decrei) de: f - Estudia si la funció f - Determina si la funció 4 té màims o mínims relatius e f té punts on la funció
4- EXERCICIS REPRESENTACIÓ DE FUNCIONS: - Estudia els intervals de monotonia (crei/decrei) de: f - Estudia si la funció f - Determina si la funció 4 té màims o mínims relatius e f té punts on la funció
Sèrie 5. Resolució: 1. Siguin i les rectes de d equacions. a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i.
 Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Problemes d Anàlisi. Problema 4 Un granger desitja tancar en un terreny rectangular adjacent a un riu.
 Problemes d Anàlisi Càlcul diferencial Problema 1 Siga f : R R la funció donada per f() = a + b + c + d Determineu els coeficients a, b, c, d sabent que f té un etrem local en el punt d abscissa = 0, que
Problemes d Anàlisi Càlcul diferencial Problema 1 Siga f : R R la funció donada per f() = a + b + c + d Determineu els coeficients a, b, c, d sabent que f té un etrem local en el punt d abscissa = 0, que
TEMA 5 : Derivades. Tècniques de derivació. Activitats
 TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
Una funció és una relació entre dues variables, de tal manera que al variar el valor d'una d'elles va variant el valor de l'altra.
 UNITAT 7: FUNCIONS. Definició Una funció és una relació entre dues variables, de tal manera que al variar el valor d'una d'elles va variant el valor de l'altra. Eemple: Completa: f() g() - h() - - (-)
UNITAT 7: FUNCIONS. Definició Una funció és una relació entre dues variables, de tal manera que al variar el valor d'una d'elles va variant el valor de l'altra. Eemple: Completa: f() g() - h() - - (-)
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
Institut Jaume Balmes Aplicacions de les derivades I
 MS 1) Donada la funció y 6 + 8 a) Troba la recta tangent en el seu punt d'infleió. b) Troba la recta normal en el punt de 1 (1+0,5 1,5 punts) ) A la vista de la gràfica d'aquesta funció. a) Estudia la
MS 1) Donada la funció y 6 + 8 a) Troba la recta tangent en el seu punt d'infleió. b) Troba la recta normal en el punt de 1 (1+0,5 1,5 punts) ) A la vista de la gràfica d'aquesta funció. a) Estudia la
FUNCIONS. Característiques generals. 1) Indica el domini i el recorregut de les següents funcions: a) b) c)
 4ES 4 B FUNCINS Característiques generals ) Indica el domini i el recorregut de les següents funcions: a) b) c) ) Indica els punts de discontinuïtat de les següents funcions: a) b) c) ) De cadascuna de
4ES 4 B FUNCINS Característiques generals ) Indica el domini i el recorregut de les següents funcions: a) b) c) ) Indica els punts de discontinuïtat de les següents funcions: a) b) c) ) De cadascuna de
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2010
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 SÈRIE 1 Pregunta 1 3 1 lim = 3. Per tant, y = 3 és asímptota horitzontal de f. + 3 1 lim =. Per tant, = - és asímptota horitzontal
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 SÈRIE 1 Pregunta 1 3 1 lim = 3. Per tant, y = 3 és asímptota horitzontal de f. + 3 1 lim =. Per tant, = - és asímptota horitzontal
Equacions i sistemes de segon grau
 Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
1.- Sabem que el vector (2, 1, 1) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c. . cx by +2z = b
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
SOLUCIONARI Unitat 5
 SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
ANÁLISIS. 1 Junio Junio 98. y = 1al dar vuelta
 ANÁLISIS Junio 98 Junio 98 Un punto material recorre la parábola y = 7. Deducir razonadamente la posición, o posiciones, en que la distancia del punto al origen (0, 0) es mínima. Considera la superficie
ANÁLISIS Junio 98 Junio 98 Un punto material recorre la parábola y = 7. Deducir razonadamente la posición, o posiciones, en que la distancia del punto al origen (0, 0) es mínima. Considera la superficie
APLICACIONS DE LA DERIVADA
 0 APLICACIONS DE LA DERIVADA Pàgina 7 Relació del creiement amb el signe de la primera derivada Analitza de la mateia manera la corba següent: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f'
0 APLICACIONS DE LA DERIVADA Pàgina 7 Relació del creiement amb el signe de la primera derivada Analitza de la mateia manera la corba següent: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f'
SOLUCIONARI Unitat 3. Comencem. Exercicis
 SOLUCIONARI Unitat Comencem Troba i classifica les discontinuïtats que resenta la funció y. + - + + y la simlificació indica que a hi ha una discontinuïtat - ( + )( -) - evitable. A l eressió y hi trobem
SOLUCIONARI Unitat Comencem Troba i classifica les discontinuïtats que resenta la funció y. + - + + y la simlificació indica que a hi ha una discontinuïtat - ( + )( -) - evitable. A l eressió y hi trobem
Proves d accés a la Universitat per a més grans de 25 anys Convocatòria 2013
 Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
7. Calcula P (x ) Q (x ): P (x ) = 5x 4 + x 3 2x 2 5 Q (x ) = 7x 4 5x 2 + 3x + 2 P (x ) Q (x ) = 2x 4 + x 3 + 3x 2 3x 7
 50 SOLUCIONARI 5. Operacions amb polinomis 1. POLINOMIS. SUMA I RESTA PENSA I CALCULA Donat el cub de la figura, calcula en funció de : a) L àrea. b) El volum. a) A ( ) = 6 2 b) V ( ) = 3 CARNET CALCULISTA
50 SOLUCIONARI 5. Operacions amb polinomis 1. POLINOMIS. SUMA I RESTA PENSA I CALCULA Donat el cub de la figura, calcula en funció de : a) L àrea. b) El volum. a) A ( ) = 6 2 b) V ( ) = 3 CARNET CALCULISTA
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes. Nom i Cognoms: Grup: Data:
 Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen FINAL Nom i Cognoms: Grup: Data: -5-007 r BLOC: ) Trobeu els límits:
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen FINAL Nom i Cognoms: Grup: Data: -5-007 r BLOC: ) Trobeu els límits:
Col legi Maristes Sants-Les Corts. Departament de matemàtiques. té per asímptotes les rectes =
 Matemàtiques II Propostes recuperació 1a avaluació - 1/5 Col legi Maristes Sants-Les Corts Departament de matemàtiques Matemàtiques II PsPc. B2.A1 Tal i com alguns de vosaltres m heu demanat, us dono una
Matemàtiques II Propostes recuperació 1a avaluació - 1/5 Col legi Maristes Sants-Les Corts Departament de matemàtiques Matemàtiques II PsPc. B2.A1 Tal i com alguns de vosaltres m heu demanat, us dono una
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
TEMA 1 : Aplicacions de les derivades
 TEMA 1 : Aplicacions de les derivades 1.1. INFORMACIÓ EXTRETA DE LA PRIMERA DERIVADA 1.1.1 Creixement i decreixement de funcions Definició: f és creixent en x 0 existeix (x 0 - a, x 0 + a), un entorn del
TEMA 1 : Aplicacions de les derivades 1.1. INFORMACIÓ EXTRETA DE LA PRIMERA DERIVADA 1.1.1 Creixement i decreixement de funcions Definició: f és creixent en x 0 existeix (x 0 - a, x 0 + a), un entorn del
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2012
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció exponencial
 LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció eponencial La funció eponencial és de la forma f () = a, on a > 0, a 1 El valor a s anomena base de la funció eponencial.
LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció eponencial La funció eponencial és de la forma f () = a, on a > 0, a 1 El valor a s anomena base de la funció eponencial.
LA RECTA. Exercicis d autoaprenentatge 1. Siga la gràfica següent:
 LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
Al ser un quocient, el denominador no pot ser 0 i al ser una arrel d index senars no hi ha problema Dom = R\{x 3 +3x 2-6x-8=0}= R\{-4, 2, -1}.
 Col legi Maristes Sants-Les Corts Departament de matemàtiques Codi Sol PsP..- Troba el domini de les següents funcions. d) f ( ) 6 És un quocient de polinomis Dom R\{ -6} R\{,}. f) f ( ) És un quocient
Col legi Maristes Sants-Les Corts Departament de matemàtiques Codi Sol PsP..- Troba el domini de les següents funcions. d) f ( ) 6 És un quocient de polinomis Dom R\{ -6} R\{,}. f) f ( ) És un quocient
1.- Estudi de funcions Creixement i decreixement de funcions Extrems relatius i absoluts Derivabilitat de funcions
 .- Estudi de funcions..- Creiement i decreiement de funcions..- Etrems relatius i absoluts..- Derivabilitat de funcions.- Representació gràfica de funcions..- Introducció..- Domini de funcions..- Discontinuïtats.4.-
.- Estudi de funcions..- Creiement i decreiement de funcions..- Etrems relatius i absoluts..- Derivabilitat de funcions.- Representació gràfica de funcions..- Introducció..- Domini de funcions..- Discontinuïtats.4.-
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS
 Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
TEMES TREBALLATS A 3r d'eso
 TEMES TREBALLATS A r d'eso. Repàs de n d'eso. Nombres racionals. Equacions. Sistemes d'equacions de r grau. Funcions. Geometria en l'espai Recordeu que a part dels apunts teniu d'altres documents per preparar
TEMES TREBALLATS A r d'eso. Repàs de n d'eso. Nombres racionals. Equacions. Sistemes d'equacions de r grau. Funcions. Geometria en l'espai Recordeu que a part dels apunts teniu d'altres documents per preparar
avaluació diagnòstica educació secundària obligatòria competència matemàtica
 curs 2012-2013 avaluació diagnòstica educació secundària obligatòria competència matemàtica Nom i cognoms Grup Activitat 1: El telèfon mòbil Observa la figura següent, que representa la càrrega que queda
curs 2012-2013 avaluació diagnòstica educació secundària obligatòria competència matemàtica Nom i cognoms Grup Activitat 1: El telèfon mòbil Observa la figura següent, que representa la càrrega que queda
TEMA 2: Múltiples i Divisors
 TEMA 2: Múltiples i Divisors 4tESO CB Concepte de múltiple 6 és múltiple de 2 perquè 2 3 = 6 24 és múltiple de 8 perquè 8 3 = 24 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per 3
TEMA 2: Múltiples i Divisors 4tESO CB Concepte de múltiple 6 és múltiple de 2 perquè 2 3 = 6 24 és múltiple de 8 perquè 8 3 = 24 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per 3
Districte Universitari de Catalunya
 Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA
 DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
1. Indica si les següents expressions són equacions o identitats: a. b. c. d.
 Dossier d equacions de primer grau 1. Indica si les següents expressions són equacions o identitats: Solucions: Equació / Identitat / Identitat / Identitat 2. Indica els elements d aquestes equacions (membres,
Dossier d equacions de primer grau 1. Indica si les següents expressions són equacions o identitats: Solucions: Equació / Identitat / Identitat / Identitat 2. Indica els elements d aquestes equacions (membres,
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Prova d accés a la Universitat (2013) Matemàtiques II Model 1. (b) Suposant que a = 1, trobau totes les matrius X que satisfan AX + Id = A, on Id
 UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
Examen Final 17 de gener de 2013
 MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
11 Límits de funcions. Continuïtat i branques infinites
 Límits de funcions. Continuïtat i branques infinites Pàgina 7 A través d'una lupa a) A = + d " A = " + d A = 0 d "+ Soroll i silenci I = + d " 0 I = 0 d "+ Pàgina 75 a) Cert Cert Cert d) Cert e) Fals f)
Límits de funcions. Continuïtat i branques infinites Pàgina 7 A través d'una lupa a) A = + d " A = " + d A = 0 d "+ Soroll i silenci I = + d " 0 I = 0 d "+ Pàgina 75 a) Cert Cert Cert d) Cert e) Fals f)
8. Reflexiona: Si a<-3, pot se a<0?
 ACTIVITATS 1. Expressa amb nombres enters: a) L avió vola a una altura de tres mil metres b) El termòmetre marca tres graus sota zero c) Dec cinc euros al meu germà 2. Troba el valor absolut de: -4, +5,
ACTIVITATS 1. Expressa amb nombres enters: a) L avió vola a una altura de tres mil metres b) El termòmetre marca tres graus sota zero c) Dec cinc euros al meu germà 2. Troba el valor absolut de: -4, +5,
TEMA 2: Múltiples i Divisors. Activitats. 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per 3 ens doni 25
 TEMA 2: Múltiples i Divisors Activitats Concepte de múltiple 6 és múltiple de 2 perquè 2 3 = 6 24 és múltiple de 8 perquè 8 3 = 24 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per
TEMA 2: Múltiples i Divisors Activitats Concepte de múltiple 6 és múltiple de 2 perquè 2 3 = 6 24 és múltiple de 8 perquè 8 3 = 24 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS
 CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 85 Activitat 1 Calcula l àrea de la figura prenent com a unitat d àrea la quadrícula que hi ha indicada: Activitat Ens referirem a la unitat d àrea amb el símbol
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 85 Activitat 1 Calcula l àrea de la figura prenent com a unitat d àrea la quadrícula que hi ha indicada: Activitat Ens referirem a la unitat d àrea amb el símbol
corresponent de la primera pàgina de l examen.
 Oficina d Accés a la Universitat Pàgina 1 de 5 PAU 017 SÈRIE PAUTES PER ALS CORRECTORS RECORDEU: - Podeu valorar amb tants decimals com considereu convenient, però aconsellem no fer ho amb més de dos.
Oficina d Accés a la Universitat Pàgina 1 de 5 PAU 017 SÈRIE PAUTES PER ALS CORRECTORS RECORDEU: - Podeu valorar amb tants decimals com considereu convenient, però aconsellem no fer ho amb més de dos.
PAUTA D ESTIU MATEMÀ TIQUES 3R E.S.O. CURS
 PAUTA D ESTIU MATEMÀ TIQUES R E.S.O. CURS 00- Continguts: ) Fraccions: suma, resta, producte, divisió, castells, operacions combinades i fracció generatriu. ) Álgebra: suma, resta, producte i operacions
PAUTA D ESTIU MATEMÀ TIQUES R E.S.O. CURS 00- Continguts: ) Fraccions: suma, resta, producte, divisió, castells, operacions combinades i fracció generatriu. ) Álgebra: suma, resta, producte i operacions
Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 3 ÀREES I VOLUMS. Unitat 3 ÀREES I VOLUMS
 70 Unitat 3 ÀREES I VOLUMS què treballaràs? En acabar la unitat has de ser capaç de: Reconèixer unitats de mesura d una àrea. Interpretar fórmules d àrees de figures planes. Aplicar fórmules d àrees de
70 Unitat 3 ÀREES I VOLUMS què treballaràs? En acabar la unitat has de ser capaç de: Reconèixer unitats de mesura d una àrea. Interpretar fórmules d àrees de figures planes. Aplicar fórmules d àrees de
TEMA 4: Equacions exponencials i logarítmiques
 TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
y = m x x f x. Per determinar de totes aquestes rectes quina és la recta tangent, el que es fa és intentar aproximar el pendent m.
 Derivació Objectius: Usar el Maple en el càlcul de derivades i les seves aplicacions Definició de derivada La derivada d'una funció donada f en un punt és el pendent de la recta tangent a la corba 0 y
Derivació Objectius: Usar el Maple en el càlcul de derivades i les seves aplicacions Definició de derivada La derivada d'una funció donada f en un punt és el pendent de la recta tangent a la corba 0 y
AVALUACIÓ DE QUART D ESO
 AVALUACIÓ DE QUART D ESO FULLS DE RESPOSTES I CRITERIS DE CORRECCIÓ Competència matemàtica FULL DE RESPOSTES VERSIÓ AMB RESPOSTES competència matemàtica ENGANXEU L ETIQUETA IDENTIFICATIVA EN AQUEST ESPAI
AVALUACIÓ DE QUART D ESO FULLS DE RESPOSTES I CRITERIS DE CORRECCIÓ Competència matemàtica FULL DE RESPOSTES VERSIÓ AMB RESPOSTES competència matemàtica ENGANXEU L ETIQUETA IDENTIFICATIVA EN AQUEST ESPAI
Data de lliurament: divendres 8 d abril de 2016
 INS JÚLIA MINGUELL Matemàtiques 2n BAT. 18 març 2016 Dossier recuperació (2a AVAL.) DOSSIER de RECUPERACIÓ: 2a AVALUACIÓ Data de lliurament: divendres 8 d abril de 2016 Condicions: i) El no lliurament
INS JÚLIA MINGUELL Matemàtiques 2n BAT. 18 març 2016 Dossier recuperació (2a AVAL.) DOSSIER de RECUPERACIÓ: 2a AVALUACIÓ Data de lliurament: divendres 8 d abril de 2016 Condicions: i) El no lliurament
QUADERN d ESTUDI de RECTES TANGENTS
 QUADERN d ESTUDI de RECTES TANGENTS per a les PAU i 2n de Batxillerat Autor: Pepe Ródenas Borja pepe.rodenas.borja@gmail.com http://manifoldo.weebly.com Descripció del material: Aquest quadern consisteix
QUADERN d ESTUDI de RECTES TANGENTS per a les PAU i 2n de Batxillerat Autor: Pepe Ródenas Borja pepe.rodenas.borja@gmail.com http://manifoldo.weebly.com Descripció del material: Aquest quadern consisteix
La porció limitada per una línia poligonal tancada és un
 PLA Si n és el nombre de costats del polígon: El nombre de diagonals és La suma dels seus angles és 180º ( n 2 ). La porció limitada per una línia poligonal tancada és un Entre les seves propietats destaquem
PLA Si n és el nombre de costats del polígon: El nombre de diagonals és La suma dels seus angles és 180º ( n 2 ). La porció limitada per una línia poligonal tancada és un Entre les seves propietats destaquem
Resolucions de l autoavaluació del llibre de text
 Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
Exercicis de rectes en el pla
 Equacions de la recta 1. Escriu les diferents equacions de la recta que passa pel punt P(3, 4) i que té com a vector director el vector v = ( 5, 2). 2. Per a la recta d equació director. 6 + y = 1, escriu
Equacions de la recta 1. Escriu les diferents equacions de la recta que passa pel punt P(3, 4) i que té com a vector director el vector v = ( 5, 2). 2. Per a la recta d equació director. 6 + y = 1, escriu
FUNCIONS REALS. MATEMÀTIQUES-1
 FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES UNITAT 2 TEOREMA DE TALES.
 Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
Gràficament: una funció és contínua en un punt si en aquest punt el seu gràfica no es trenca
 Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Polinomis i fraccions algèbriques
 Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
Generalitat de Catalunya. 12 3x. x x x. lim. lim. 2 x. + = e) x +
 1) Una persona va invertir 6 000?comprant accions de dues empreses, A i B. Al cap d un any, el valor de les accions de l empresa A ha pujat un % i, en canvi, el valor de les accions de l empresa B ha baiat
1) Una persona va invertir 6 000?comprant accions de dues empreses, A i B. Al cap d un any, el valor de les accions de l empresa A ha pujat un % i, en canvi, el valor de les accions de l empresa B ha baiat
FUNCIONS EXPONENCIALS I LOGARÍTMIQUES. MATEMÀTIQUES-1
 FUNCIONS EXPONENCIALS I LOGARÍTMIQUES. 1. Funcions exponencials. 2. Equacions exponencials. 3. Definició de logaritme. Propietats. 4. Funcions logarítmiques. 5. Equacions logarítmiques. 1. Funcions exponencials.
FUNCIONS EXPONENCIALS I LOGARÍTMIQUES. 1. Funcions exponencials. 2. Equacions exponencials. 3. Definició de logaritme. Propietats. 4. Funcions logarítmiques. 5. Equacions logarítmiques. 1. Funcions exponencials.
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
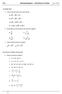 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera:
 Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
2n ESO A TREBALL D'ESTIU - MATEMÀTIQUES CURS
 INS PERE BORRELL C. Escoles Pies, 46 17520 PUIGCERDÂ Tel. 972880275 Fax 972141049 Departament de Matemàtiques 2n ESO A TREBALL D'ESTIU - MATEMÀTIQUES CURS 2015-2016 Exercicis que cal fer per preparar la
INS PERE BORRELL C. Escoles Pies, 46 17520 PUIGCERDÂ Tel. 972880275 Fax 972141049 Departament de Matemàtiques 2n ESO A TREBALL D'ESTIU - MATEMÀTIQUES CURS 2015-2016 Exercicis que cal fer per preparar la
PROBLEMES RESOLTS D OPTIMITZACIÓ.
 PROBLEMES RESOLTS D OPTIMITZACIÓ.. La concentració (en mil ligram ) d una substància durant les tres hores en les quals ha actuat un reactiu 0 t, vé donada per la unció C (t) = - t + 9t t + 8. Troba els
PROBLEMES RESOLTS D OPTIMITZACIÓ.. La concentració (en mil ligram ) d una substància durant les tres hores en les quals ha actuat un reactiu 0 t, vé donada per la unció C (t) = - t + 9t t + 8. Troba els
16 febrer 2016 Integrals exercicis. 3 Integrals
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 16 febrer 2016 Integrals exercicis 3 Integrals 28. Troba una funció primitiva de les següents funcions: () = 1/ () = 3 h() = 2 () = 4 () = cos () = sin () =
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 16 febrer 2016 Integrals exercicis 3 Integrals 28. Troba una funció primitiva de les següents funcions: () = 1/ () = 3 h() = 2 () = 4 () = cos () = sin () =
ACTIVITATS. a) b) c) d) INS JÚLIA MINGUELL 2n Batxillerat. dv, 18 de març Alumne:
 INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
1. RECTA TANGENT I NORMAL 2. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS
 APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO
 Generalitat de Catalunya Departament d Ensenyament Institut Pompeu Fabra DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO Nom i Cognoms:... INSTRUCCIONS: - Aquest dossier serveix per a preparar
Generalitat de Catalunya Departament d Ensenyament Institut Pompeu Fabra DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO Nom i Cognoms:... INSTRUCCIONS: - Aquest dossier serveix per a preparar
Indiqueu en quins punts Y = f(x) no és contínua, el tipus de discontinuïtats de cada cas i les asímptotes que presenta. (0,1 9 +0,8=1,7 punts)
 Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Nom: 1.- Trobeu la funció inversa o recíproca de la funció recorregut de la funció yf(). f ( ) Departament de Matemàtiques 1MA:
Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Nom: 1.- Trobeu la funció inversa o recíproca de la funció recorregut de la funció yf(). f ( ) Departament de Matemàtiques 1MA:
Tema 1: TRIGONOMETRIA
 Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
UNITAT DIDÀCTICA 10 L ÍMITS DE FUNCIONS. CONTINUÏTAT I BRANQUES INFINITES
 7 UNITAT DIDÀCTICA 0 Refleiona i resol Aproimacions successives El valor de la funció f () = + 5 0 per a = 5 no es pot obtenir directament perquè el denominador es fa zero. L obtindrem per aproimacions
7 UNITAT DIDÀCTICA 0 Refleiona i resol Aproimacions successives El valor de la funció f () = + 5 0 per a = 5 no es pot obtenir directament perquè el denominador es fa zero. L obtindrem per aproimacions
2 desembre 2015 Límits i número exercicis. 2.1 Límits i número
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
avaluació diagnòstica educació secundària obligatòria
 curs 2011-2012 avaluació diagnòstica educació secundària obligatòria competència matemàtica Nom i cognoms Grup INSTRUCCIONS Llegeix atentament cada pregunta abans de contestar-la. Si t equivoques, ratlla
curs 2011-2012 avaluació diagnòstica educació secundària obligatòria competència matemàtica Nom i cognoms Grup INSTRUCCIONS Llegeix atentament cada pregunta abans de contestar-la. Si t equivoques, ratlla
XXXV OLIMPÍADA MATEMÀTICA
 XXXV OLIMPÍADA MATEMÀTICA Primera fase (Catalunya) 10 de desembre de 1999, de 16 a 0h. 1. Amb quadrats i triangles equilàters de costat unitat es poden construir polígons convexos. Per exemple, es poden
XXXV OLIMPÍADA MATEMÀTICA Primera fase (Catalunya) 10 de desembre de 1999, de 16 a 0h. 1. Amb quadrats i triangles equilàters de costat unitat es poden construir polígons convexos. Per exemple, es poden
NOMBRES REALS: EXERCICIS
 NOMBRES REALS: EXERCICIS. Calcula la longitud dels segments indicats a continuació. Epressa n el resultat de manera eacta i utilitza la calculadora per obtenir-ne una aproimació arrodonida als centèsims:
NOMBRES REALS: EXERCICIS. Calcula la longitud dels segments indicats a continuació. Epressa n el resultat de manera eacta i utilitza la calculadora per obtenir-ne una aproimació arrodonida als centèsims:
UNITAT 3: SISTEMES D EQUACIONS
 UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
Unitat didàctica 5. Funcions elementals II
 Unitat didàctica 5. Funcions elementals II Et convé recordar Com s obtenen punts d una funció Per a la funció = +, calcula els punts següents: a) D abscissa = (, 8) b) D abscissa = (, ) c) D ordenada 0
Unitat didàctica 5. Funcions elementals II Et convé recordar Com s obtenen punts d una funció Per a la funció = +, calcula els punts següents: a) D abscissa = (, 8) b) D abscissa = (, ) c) D ordenada 0
Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 2015 Criteris de correcció Matemàtiques aplicades a les ciències socials
 Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 015 SÈRIE 1. Un arbre té un volum de 0 m i, per la qualitat de la seva fusta, es ven a 50 per metre cúbic. Cada any l'arbre augmenta el volum en 5 m.
Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 015 SÈRIE 1. Un arbre té un volum de 0 m i, per la qualitat de la seva fusta, es ven a 50 per metre cúbic. Cada any l'arbre augmenta el volum en 5 m.
( 2 3, utilitzeu la matriu inversa B 1 ( 1 4 ( 2 1. Matrius i determinants Sèrie 3 - Qüestió 4. Donada la matriu B =
 1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
Activitats de repàs DIVISIBILITAT
 Autor: Enric Seguró i Capa 1 CRITERIS DE DIVISIBILITAT Un nombre és divisible per 2 si acaba en 0 o parell (2,4,6,8). Ex: 10, 24, 62, 5.256, 90.070,... Un nombre és divisible per 3 si la suma de les seves
Autor: Enric Seguró i Capa 1 CRITERIS DE DIVISIBILITAT Un nombre és divisible per 2 si acaba en 0 o parell (2,4,6,8). Ex: 10, 24, 62, 5.256, 90.070,... Un nombre és divisible per 3 si la suma de les seves
TEMA 4 : Programació lineal
 TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
Institut d Educació Secundària. x b) A partir de la gràfica d aquesta funció, indica quin és el domini i el recorregut.
 Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques MS Àlgebra i uncions I Nom: Grup: ) Resol les següents equacions: a) 7+ 3+ c) 3 +
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques MS Àlgebra i uncions I Nom: Grup: ) Resol les següents equacions: a) 7+ 3+ c) 3 +
1. Què tenen en comú aquestes dues rectes? Com són entre elles? 2. En què es diferencien aquestes dues rectes?
 En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
COMISSIÓ GESTORA DE LES PROVES D ACCÉS A LA UNIVERSITAT COMISIÓN GESTORA DE LAS PRUEBAS DE ACCESO A LA UNIVERSIDAD
 COMISSIÓ GESTORA DE LES PROVES D ACCÉS A LA UNIVERSITAT COMISIÓN GESTORA DE LAS PRUEBAS DE ACCESO A LA UNIVERSIDAD PROVES D ACCÉS A LA UNIVERSITAT CONVOCATÒRIA: PRUEBAS DE ACCESO A LA UNIVERSIDAD CONVOCATORIA:
COMISSIÓ GESTORA DE LES PROVES D ACCÉS A LA UNIVERSITAT COMISIÓN GESTORA DE LAS PRUEBAS DE ACCESO A LA UNIVERSIDAD PROVES D ACCÉS A LA UNIVERSITAT CONVOCATÒRIA: PRUEBAS DE ACCESO A LA UNIVERSIDAD CONVOCATORIA:
UIB 2 + f (x) + f(x) ց ց ր ր Per tant, el punt ( 3. Una altra forma de veure-ho és calcular la derivada segona i mirar el signe en x = 3: 2 f (x) =
 El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
TEMA 2: Divisibilitat Activitats
 TEMA 2: Divisibilitat Activitats 1. 35 és múltiple de 5?. Raoneu la resposta 2. 48 és divisible per 6?. Raoneu la resposta 3. Completeu els deu primers múltiples de 8 8, 16,, 32,,,,,, 80 4. Quines de les
TEMA 2: Divisibilitat Activitats 1. 35 és múltiple de 5?. Raoneu la resposta 2. 48 és divisible per 6?. Raoneu la resposta 3. Completeu els deu primers múltiples de 8 8, 16,, 32,,,,,, 80 4. Quines de les
DE FORMA ALGEBRAICA CERTES SITUACIONS
 EXPRESSAR OBJECTIU DE FORMA ALGEBRAICA CERTES SITUACIONS NOM: CURS: DATA: LLENGUATGE NUMÈRIC I LLENGUATGE ALGEBRAIC El llenguatge en què intervenen nombres i signes d operacions l anomenem llenguatge numèric.
EXPRESSAR OBJECTIU DE FORMA ALGEBRAICA CERTES SITUACIONS NOM: CURS: DATA: LLENGUATGE NUMÈRIC I LLENGUATGE ALGEBRAIC El llenguatge en què intervenen nombres i signes d operacions l anomenem llenguatge numèric.
Examen FINAL M2 FIB-UPC 12 de juny de 2015
 Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
EXERCICIS - SOLUCIONS
 materials del curs de: MATEMÀTIQUES SISTEMES D EQUACIONS EXERCICIS - SOLUCIONS AUTOR: Xavier Vilardell Bascompte evi.vb@gmail.com www.elu.net CORRECCIÓ: Montse Ramos ÚLTIMA REVISIÓ: 1 d abril de 009 Aquests
materials del curs de: MATEMÀTIQUES SISTEMES D EQUACIONS EXERCICIS - SOLUCIONS AUTOR: Xavier Vilardell Bascompte evi.vb@gmail.com www.elu.net CORRECCIÓ: Montse Ramos ÚLTIMA REVISIÓ: 1 d abril de 009 Aquests
