MMII_L3_c2: Dominios de dependencia y de influencia. Problema no homogéneo: Principio de Duhamel.
|
|
|
- José Méndez Ruiz
- hace 5 años
- Vistas:
Transcripción
1 MMII_L3_c: Dominios de dependencia y de inflencia. roblema no homogéneo: rincipio de Dhamel. Gión de la clase : Esa lección es na coninación de la primera, segimos con el roblema de Cachy de la ecación de ondas. La pare mas novedosa es el rincipio de Dhamel (D) para resolver el problema no homogéneo (eisencia de ferzas eernas), qe es de aplicación no solo para el problema anerior, sino qe lo generalizaremos para ecaciones definidas por operadores reglares de Srm-Lioville. La referencia de consla para esa pare es el libro arial Differenial Eqaions de Erich Zaderer. La clase se inicia raando de generalizar la propiedad de qe la solción permanece consane a lo largo de la CC, propia del caso f diferene de cero y g =, al caso con g diferene de cero y f =. Sige con los imporanes concepos de dominio de dependencia y de inflencia, la clase finaliza con el D y s concreción al caso de la ecación de ondas qe nos ocpa. Libros de consla de esa clase, apare del ya mencionado, son los de Ecaciones Diferenciales en Derivadas arciales de H.F. Weinberger, y el libro Ecaciones en Derivadas arciales de Richard Habermann. Ejercicio recomendado: c F (,) f (,) g,, c, F, f ; g,, Esas noas son solo na ayda, qe ni preender ni peden ssiir a la asisencia a clase, donde se desarrollan los concepos, se aclararán las ddas y se sbsanaran posibles erraas, y a la consla de la bibliografía recomendada.
2 Noas de la clase MMII_L3_c Un ejemplo con g para complear la clase anerior, Ej-L3_c: c,,, c, f, g, Uilizando el concepo de fnción inegral podemos pasar a n problema donde la solción permanezca consane a lo largo de la CC, similar al caso con anerior,, G( ) g( s) ds c M,, donde M es n número sficiene grande, dependiene de la ecación. Con esa fnción, la solción del CH de arriba es: G( ) G( ) La inerpreación es similar al caso anerior, salvo qe ahora na de las ondas esá desfasada y iene n signo menos delane. G( + ) G( + la solción en = + ) G( + ) = =- - G( ) - G( - ) or lo qe represenando la solción (, ) es: - G( ) - G( - ) Ora forma de calclar la solción es direcamene ilizando la FD A: g() s ds 3
3 Dominio de dependencia de la solción La solción en el pno M de coordenadas ( M, M ) + dependerá como veremos de los pnos, : ( M -c M,), ( M +c M,). M -c=ce +c=ce Los pnos y se peden inerprear como los pnos casa y el pno M el pno efeco. Se peden esdiar res casos: f, g=: la solción es = f(+c) + f(-c), el dominio de dependencia es (DD(CH)) = {,}. De forma didácica diremos qe la solción en M f ( ) f ( ) sólo depende de los valores f() y f(): M ( ) f=, g : la solción es c c c g() s ds, el DD(CH) = in, el inerior del segmeno. La solción en M se pede epresar de la forma sigiene: ( M ) g( s) ds c f, g : la solción inclye los dos érminos aneriores, y el DD(CH)=, el segmeno, inclidos los dos pnos eremos, y (M) se pede epresar: f ( ) f ( ) ( M ) g( s) ds c Dominio de inflencia: Toma el pno de visa opeso al caso anerior, ahora nos cenramos en el pno casa de coordenadas ( o,); y bscamos los pnos efeco, donde llega s inflencia, pdiéndose presenar los mismos res casos qe en el aparado anerior. +c= -c= o
4 f, g= : el dominio de inflencia DI(( o,o))={ c = o }, qe son las dos semirrecas de la figra. f=, g : DI(( o,)) = cono abiero de vérice el pno ( o,) y generarices las dos semirrecas c = o. f, g : DI(( o,)) = cono cerrado de vérice el pno ( o,) y generarices las dos semirrecas c = o, inclidas las dos semirrecas. Ecación de ondas no homogénea Nos ocparemos del esdio del CH(EOD) no homogéneo, definido por la ecación no homogénea con condiciones iniciales homogéneas: c F(, ),, B (,), B (, o) rincipio de Dhamel (D). El D lo consideraremos en n coneo más general qe el problema no homogéneo de la ecación de ondas. Veamos s aplicación para las ecaciones hiperbólicas definidas mediane el operador L, qe iliza en s pare espacial el denominado operador reglar de Srm-Lioville (SL): n CH(D): L ( ) L F(, ) D,, siendo LSL ( p( ) ) q( ). SL La condición de reglaridad de L SL es:, q C, p C, p,, q ; mienras qe las condiciones iniciales del CH(D) son las ya indicadas en CH(EOD). En el caso pariclar qe los daos verifiqen: ( ), p ce=c, q y n, la ecación reslane, es la ecación de ondas nidimensional, qe nos ocpa: d d p q c d d ( ( ) ) ( ) ( ) El D se basa en la definición de n modelo ailiar (MA) homogéneo, qe se pede resolver por la FD A, s solción condcirá a la solción del CH(D). Ese MA se obiene mediane n cambio de origen de la variable emporal, consideremos el cambio de variable independiene (CVI). Ese MA vendrá definido por la variable dependiene: v(, ; ) v L v, D,, SL v(,; ), D F (, ) v (,; ), D ( )
5 , qe es n CH homogéneo con condiciones iniciales como las indicadas. Conocida s solción, podremos conocer la solción del CH(D) mediane la epresión: v(, ; ) d. Comprobaremos qe dicha epresión cmple las condiciones del CH(D): v(,, ) v (, ; ) d v (, ; ) v d, por la linealidad de los operadores: ecación original, se obendrá: SL SL SL L L v L vd, ssiyendo ese reslado en la F(, ) vd LSLv d F ( v LSLv) d, siendo ese úlimo érmino nlo por ser v solción del MA. Fala por comprobar qe cmple las condiciones iniciales: (,) v ; (,) v(,, ) v La solción del CH(D) no homogéneo se redce a resolver el CH(MA) qe es n problema homogéneo; en el caso pariclar de la EOD, el MA para aplicar el D es, La FD A da como solción: v c v D,,, v(, ; ), D v (, ; ) F(, ), D c( ) v F( s, ) ds c c( ) La solción del CH(EOD) no homogéneo es: c( ) (, ) F( s, ) ds d c c( ) De esa forma, el CH(EOD) compleo definido por: L F B Aplicando el principio de sperposición, iene como solción: B f g
6 (, ) ( f ( c) f ( c)) g( s) ds F( s, ) ds d c c La solción se pede inerprear: c c c( ) c( ) M(,) = El Teorema de Fbini eniende la solción como el área rayada de la gráfica; los pnos y son la casa, y el pno M el efeco: ( M ) Véase qe y vienen definidos por: ( ) ( ) c( ). Ej_L3_c: e B B. Aplicando el D: ( ) c M F. s ( ) e dsd e e d e e e ( ). Ora forma sería aplicando los méodos operacionales: L D D F e L (, ) robaremos solciones de la forma e, pero como L(, ) enemos problemas pes L (, ), es decir, e Ker L. En ese caso, probamos solciones de la forma: e L (, ), p e, siendo L D ya qe L D D.
7 Oro ipo de solción sería e 3 e L (, ), en ese caso, se esá viendo qe la solción no es única, pero el eorema de eisencia y nicidad afirma qe, si eise solción, ésa es única, pensar en la eplicación.
MMII_c5_L1: Formulación Débil de EDP_1o_cl: ondas de choque y de expansión
 MMII_c5_L: Formlación ébil de EP_o_cl: ondas de choqe de epansión Para resolver esas zonas donde la solción no esá definida porqe no pasa ningna crva caracerísica o pasan varias por el mismo pno, se inrodcirá
MMII_c5_L: Formlación ébil de EP_o_cl: ondas de choqe de epansión Para resolver esas zonas donde la solción no esá definida porqe no pasa ningna crva caracerísica o pasan varias por el mismo pno, se inrodcirá
MMII_L3_C5: Problema de la cuerda finita: Métodos directo y de las imágenes. Guión:
 MMII_L_C5: Problema de la cuerda finia: Méodos direco y de las imágenes. Guión: En esa lección se esudia el problema de una cuerda finia, por lo ano, es el problema con dos condiciones de conorno. Como
MMII_L_C5: Problema de la cuerda finia: Méodos direco y de las imágenes. Guión: En esa lección se esudia el problema de una cuerda finia, por lo ano, es el problema con dos condiciones de conorno. Como
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO 2011 (GENERAL) (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
 IES CSTELR BDJOZ PRUEB DE CCESO (LOGSE) UNIVERSIDD DE BLERES JUNIO (GENERL) (RESUELTOS por nonio Menguiano) MTEMÁTICS II Tiempo máimo: horas y minuos Conese de manera clara y razonada una de las dos opciones
IES CSTELR BDJOZ PRUEB DE CCESO (LOGSE) UNIVERSIDD DE BLERES JUNIO (GENERL) (RESUELTOS por nonio Menguiano) MTEMÁTICS II Tiempo máimo: horas y minuos Conese de manera clara y razonada una de las dos opciones
MMII_L1_c3: Método de Lagrange.
 MMII_L_c3: Método de Lagrange. Gión de la clase: Esta clase está centrada en plantearse la resolción de las ecaciones casi lineales de primer orden mediante el Método de Lagrange. El método eqivale a plantearse
MMII_L_c3: Método de Lagrange. Gión de la clase: Esta clase está centrada en plantearse la resolción de las ecaciones casi lineales de primer orden mediante el Método de Lagrange. El método eqivale a plantearse
IES CASTELAR BADAJOZ Examen Junio de 2011(General) Solución Antonio Mengiano Corbacho
 IES CASTELAR BADAJOZ Eamen Junio de (General) Anonio Mengiano Corbacho PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO (GENERAL) MATEMÁTICAS II Tiempo máimo: horas y minuos Conese de manera clara
IES CASTELAR BADAJOZ Eamen Junio de (General) Anonio Mengiano Corbacho PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO (GENERAL) MATEMÁTICAS II Tiempo máimo: horas y minuos Conese de manera clara
CAPÍTULO 5. INTEGRACIÓN DE FUNCIONES TRIGONOMÉTRICAS 5.1. Introducción 5.2. Cambios de variable 5.3. Transformación en sumas 5.4. Problemas resueltos
 CAPÍTULO 5. INTEGRACIÓN DE FUNCIONES TRIGONOMÉTRICAS 5.. Inroducción 5.. Cambios de variable 5.3. Transformación en sumas 5.4. Problemas resuelos 5.5. Inegración por recurrencia Capíulo 5 Inegración de
CAPÍTULO 5. INTEGRACIÓN DE FUNCIONES TRIGONOMÉTRICAS 5.. Inroducción 5.. Cambios de variable 5.3. Transformación en sumas 5.4. Problemas resuelos 5.5. Inegración por recurrencia Capíulo 5 Inegración de
Introducción a la Representación en Variable de
 ELC-3303 Teoría de Conrol Inrodcción a la Represenación en Variable de Esado Prof. Francisco M. Gonzalez-Longa fglonga@ieee.org hp://www.giaelec.org/fglonga/sp.hm Inrodcción a Represenación en Espacio
ELC-3303 Teoría de Conrol Inrodcción a la Represenación en Variable de Esado Prof. Francisco M. Gonzalez-Longa fglonga@ieee.org hp://www.giaelec.org/fglonga/sp.hm Inrodcción a Represenación en Espacio
Guía de Ejercicios 2 Econometría II
 Gía de Ejercicios Economería II.- Para el sigiene proceso : donde es n rido blanco con ariana. a Calcle la media la ariana marginal condicional del proceso. Compare los alores marginales condicionales.
Gía de Ejercicios Economería II.- Para el sigiene proceso : donde es n rido blanco con ariana. a Calcle la media la ariana marginal condicional del proceso. Compare los alores marginales condicionales.
parciales de segundo orden.
 MMII_L_c: Irodcció a las ecacioes e derivadas parciales de segdo orde. Gió: E esa lecció esableceremos las propiedades geerales de las ecacioes e derivadas parciales de segdo orde, qe lego va a ser esdiadas
MMII_L_c: Irodcció a las ecacioes e derivadas parciales de segdo orde. Gió: E esa lecció esableceremos las propiedades geerales de las ecacioes e derivadas parciales de segdo orde, qe lego va a ser esdiadas
ω ω ω y '' + 3 y ' y = 0 en la que al resolver se debe obtener la función y. dx = + d y y+ m = mg k dt d y dy dx dx = x y z d y dy u u x t t
 E.D.O para Ingenieros CAPITULO INTRODUCCIÓN A LAS ECUACIONES DIFERENCIALES Las ecuaciones diferenciales son ecuaciones en las que conienen derivadas, Por ejemplo: '' + ' = en la que al resolver se debe
E.D.O para Ingenieros CAPITULO INTRODUCCIÓN A LAS ECUACIONES DIFERENCIALES Las ecuaciones diferenciales son ecuaciones en las que conienen derivadas, Por ejemplo: '' + ' = en la que al resolver se debe
Errores de observación Sondebidosalaincorrectaobservación de quien realiza las medidas. El más común de este tipo es el error de paralaje.
 Gión de errores (2002) E.U.O. (U.C.M.) 1 1 Inrodcción Las ciencias experimenales son n conjno de disciplinas qe inenan dar na descripción de los fenómenos de la naraleza. Para poder canificar dichos fenómenos
Gión de errores (2002) E.U.O. (U.C.M.) 1 1 Inrodcción Las ciencias experimenales son n conjno de disciplinas qe inenan dar na descripción de los fenómenos de la naraleza. Para poder canificar dichos fenómenos
MMII_L3_c1: Lección 3: Ecuación de Ondas: Problema de Cauchy
 MMII_L3_1: Leión 3: Euaión de Ondas: Problema de Cauhy En esa leión se esudia la euaión de ondas de dimensión 1 espaial. La euaión de ondas de dimensiones espaiales superiores quedan omo un ejeriio volunario
MMII_L3_1: Leión 3: Euaión de Ondas: Problema de Cauhy En esa leión se esudia la euaión de ondas de dimensión 1 espaial. La euaión de ondas de dimensiones espaiales superiores quedan omo un ejeriio volunario
DERIVACIÓN BAJO EL SIGNO INTEGRAL. 1. Hallar el punto del intervalo [0,2] en el que la función =
![DERIVACIÓN BAJO EL SIGNO INTEGRAL. 1. Hallar el punto del intervalo [0,2] en el que la función = DERIVACIÓN BAJO EL SIGNO INTEGRAL. 1. Hallar el punto del intervalo [0,2] en el que la función =](/thumbs/52/30419199.jpg) DERIVACIÓN BAJO EL SIGNO INTEGRAL. Hallar el puno del inervalo [,] en el que la función F () d alcanza su valor mínimo. El mínimo de una función se alcanza en los punos donde su primera derivada es nula
DERIVACIÓN BAJO EL SIGNO INTEGRAL. Hallar el puno del inervalo [,] en el que la función F () d alcanza su valor mínimo. El mínimo de una función se alcanza en los punos donde su primera derivada es nula
130 Matemáticas I. Parte IV. I.T.I. en Electricidad. Prof: Jos Antonio Abia Vian
 30 Maemáicas I Pare IV Cálculo inegral en IR 3 Maemáicas I : Cálculo inegral en IR Tema Cálculo de primiivas. Primiiva de una función Definición 55.- Diremos ue la función F coninua en [a, b], es una primiiva
30 Maemáicas I Pare IV Cálculo inegral en IR 3 Maemáicas I : Cálculo inegral en IR Tema Cálculo de primiivas. Primiiva de una función Definición 55.- Diremos ue la función F coninua en [a, b], es una primiiva
RELACIÓN DE EJERCICIOS LÍMITES Y ASÍNTOTAS
 RELACIÓN DE EJERCICIOS LÍMITES Y ASÍNTOTAS. Calcla los sigientes límites: sen() (a) cos() sen() (b) cos(). Calcla los sigientes límites a) e b) a) e e sen() e. Calcla los sigientes límites: tg() sen()
RELACIÓN DE EJERCICIOS LÍMITES Y ASÍNTOTAS. Calcla los sigientes límites: sen() (a) cos() sen() (b) cos(). Calcla los sigientes límites a) e b) a) e e sen() e. Calcla los sigientes límites: tg() sen()
Ecuaciones de evolución como ecuaciones integrales
 22 (28) 46-51 Ecacione de evolción como ecacione inegrale Gonzalo orga 1 Lciano Barbani 2 1. Deparameno de Maemáica, Univeridad de acama. Copiapó, Chile 2. E-mail: gonzalo.aorga@da.cl 3. Inio de Maemáica
22 (28) 46-51 Ecacione de evolción como ecacione inegrale Gonzalo orga 1 Lciano Barbani 2 1. Deparameno de Maemáica, Univeridad de acama. Copiapó, Chile 2. E-mail: gonzalo.aorga@da.cl 3. Inio de Maemáica
MATEMÁTICAS I. TEMA 1: ECUACIONES Y SISTEMAS DE ECUACIONES
 Cód. 87 Avda. de San Diego, 8 Madrid Tel: 978997 98 Fa: 9789 Email: rldireccion@planalfa.es de No se auoria el uso comercial de ese Documeno. MATEMÁTICAS I. TEMA : ECUACIONES Y SISTEMAS DE ECUACIONES..
Cód. 87 Avda. de San Diego, 8 Madrid Tel: 978997 98 Fa: 9789 Email: rldireccion@planalfa.es de No se auoria el uso comercial de ese Documeno. MATEMÁTICAS I. TEMA : ECUACIONES Y SISTEMAS DE ECUACIONES..
CAPITULO 3º SOLUCIÓN ECUACIÓN DE ESTADO- 02. Ing. Diego A. Patiño G. M Sc, Ph.D.
 CPITULO 3º SOLUCIÓN ECUCIÓN DE ESTDO- Ing. Diego. Paiño G. M Sc Ph.D. Solción e ecaciones e esao no esacionarias Sea el sisema no esacionario escrio por las ecaciones El méoo aplicao para ecir la solción
CPITULO 3º SOLUCIÓN ECUCIÓN DE ESTDO- Ing. Diego. Paiño G. M Sc Ph.D. Solción e ecaciones e esao no esacionarias Sea el sisema no esacionario escrio por las ecaciones El méoo aplicao para ecir la solción
MMII_L1_c3: Clasificación de las ecuaciones. Formas Canónicas
 MMII_L_c3: Clasificación de las ecaciones. Fomas Canónicas Gión: En esta clase nos basamos en la definición de las Cvas Caacteísticas CC de la anteio paa intodci la clasificación de las ecaciones el tipo
MMII_L_c3: Clasificación de las ecaciones. Fomas Canónicas Gión: En esta clase nos basamos en la definición de las Cvas Caacteísticas CC de la anteio paa intodci la clasificación de las ecaciones el tipo
Ecuaciones de primer orden
 Capíulo 1 Ecuaciones de primer orden Problema 1.1 Hallar la solución general de la ecuación + 1 + 2 = 0. Hallar la solución que verifica (0) = 0 y la que verifica (1) = 0. k=-5 k=5 k=-1 Figura 1.1: Soluciones
Capíulo 1 Ecuaciones de primer orden Problema 1.1 Hallar la solución general de la ecuación + 1 + 2 = 0. Hallar la solución que verifica (0) = 0 y la que verifica (1) = 0. k=-5 k=5 k=-1 Figura 1.1: Soluciones
Forma diferencial de las leyes básicas. 5.1 Introducción Conservación de la masa Cantidad de movimiento...
 Capílo 5 Forma diferencial de las lees básicas Conenido 5. Inrodcción... 90 5. Conseración de la masa... 90 5.3 Canidad de moimieno... 9 5.3. Ecación de Eler... 96 5.3. Ecación de Bernolli... 00 5.3..
Capílo 5 Forma diferencial de las lees básicas Conenido 5. Inrodcción... 90 5. Conseración de la masa... 90 5.3 Canidad de moimieno... 9 5.3. Ecación de Eler... 96 5.3. Ecación de Bernolli... 00 5.3..
INTEGRACIÓN POR CAMBIO DE VARIABLE
 INTEGRCIÓN POR CMBIO DE VRIBLE Dada la inegral f( ) d, si consideramos como una función de ora variable, = g(), enonces d = g'() d, y susiuyendo en la inegral inicial se obiene f( g( )) g'( ) d. En el
INTEGRCIÓN POR CMBIO DE VRIBLE Dada la inegral f( ) d, si consideramos como una función de ora variable, = g(), enonces d = g'() d, y susiuyendo en la inegral inicial se obiene f( g( )) g'( ) d. En el
LA INTEGRAL INDEFINIDA
 Inegrales LA INTEGRAL INDEFINIDA Inegral indefinida: Primiiva (aniderivada) Primiivas (Aniderivadas) Dada la función F( es fácil hallar su derivada F (. El proceso inverso: enconrar F ( a parir de F (
Inegrales LA INTEGRAL INDEFINIDA Inegral indefinida: Primiiva (aniderivada) Primiivas (Aniderivadas) Dada la función F( es fácil hallar su derivada F (. El proceso inverso: enconrar F ( a parir de F (
Figura 11.1 Corriente en el diodo en función de la tensión aplicada en un diodo real. i D
 OS EFDOES OS EFDOES 11.1 ilización del diodo El diodo semicondcor se lo emplea en circios en los qe se qiere aproechar la diferene resisencia qe presena en n senido o en el oro. El gráfico de la corriene
OS EFDOES OS EFDOES 11.1 ilización del diodo El diodo semicondcor se lo emplea en circios en los qe se qiere aproechar la diferene resisencia qe presena en n senido o en el oro. El gráfico de la corriene
Movimiento uniformemente acelerado
 CINEMÁTICA DE LA PARTÍCULA Moimieno recilíneo Como su nombre lo indica, ese moimieno es el que iene lugar cuando una parícula se desplaza a lo largo de un rayeco reco. Describiremos res casos para el moimieno
CINEMÁTICA DE LA PARTÍCULA Moimieno recilíneo Como su nombre lo indica, ese moimieno es el que iene lugar cuando una parícula se desplaza a lo largo de un rayeco reco. Describiremos res casos para el moimieno
UNIDAD 1 Ecuaciones Diferenciales de Primer Orden
 UNIDAD UNIDAD Ecaciones Diferenciales de Primer Orden Definición Clasificación de las Ecaciones Diferenciales Una ecación diferencial es aqélla qe contiene las derivadas o diferenciales de na o más variables
UNIDAD UNIDAD Ecaciones Diferenciales de Primer Orden Definición Clasificación de las Ecaciones Diferenciales Una ecación diferencial es aqélla qe contiene las derivadas o diferenciales de na o más variables
Bibliografía: Ogata. Ingeniería de Control Moderna (cap. 3)
 OBJETIVOS. Linealización de modelos Reconocer n modelo lineal s ilidad prender a linealizar n modelo dinámico no lineal CONTENIDOS Linealidad / No linealidad Concepos No linealidades recenes en sisemas
OBJETIVOS. Linealización de modelos Reconocer n modelo lineal s ilidad prender a linealizar n modelo dinámico no lineal CONTENIDOS Linealidad / No linealidad Concepos No linealidades recenes en sisemas
Álgebras de Boole. Tema Álgebras de Boole
 Tema 5 Álgebras de Boole 5.1 Álgebras de Boole 5.1.1 Álgebras de Boole Definición 5.1.1. Un álgebra de Boole es una erna (A,, ) donde A es un conjuno y, : A A A son dos operaciones binarias inernas con
Tema 5 Álgebras de Boole 5.1 Álgebras de Boole 5.1.1 Álgebras de Boole Definición 5.1.1. Un álgebra de Boole es una erna (A,, ) donde A es un conjuno y, : A A A son dos operaciones binarias inernas con
2. Independencia del camino. Campos conservativos.
 GRADO DE INGENIERÍA AEROESPAIAL. URSO. Lección. álculo vecorial.. Independencia del camino. ampos conservaivos. Ha ocasiones en las que la inegral de un campo vecorial F, definido en una región U, a lo
GRADO DE INGENIERÍA AEROESPAIAL. URSO. Lección. álculo vecorial.. Independencia del camino. ampos conservaivos. Ha ocasiones en las que la inegral de un campo vecorial F, definido en una región U, a lo
1. Derivadas de funciones de una variable. Recta tangente.
 1. Derivadas de funciones de una variable. Reca angene. Derivadas Vamos a ver en ese capíulo la generalización del concepo de derivada de funciones reales de una variable a funciones vecoriales con varias
1. Derivadas de funciones de una variable. Reca angene. Derivadas Vamos a ver en ese capíulo la generalización del concepo de derivada de funciones reales de una variable a funciones vecoriales con varias
ECUACIONES DIFERENCIALES
 Tema 1 ECUACIONES DIFERENCIALES EJERCICIO 1 Comprobar que la función y() = c 2 ++3 es una solución del problema de valor inicial 2 y 2y + 2y = 6, y(0) = 3, y (0) = 1, (1.1) en <
Tema 1 ECUACIONES DIFERENCIALES EJERCICIO 1 Comprobar que la función y() = c 2 ++3 es una solución del problema de valor inicial 2 y 2y + 2y = 6, y(0) = 3, y (0) = 1, (1.1) en <
PONENCIA: DEMOSTRACIÓN, SIN CÁLCULO DIFERENCIAL, DE LAS ECUACIONES DE LA POSICIÓN EN EL MOVIMIENTO PARABÓLICO. Introducción
 PONENCIA: DEMOSTRACIÓN, SIN CÁLCULO DIFERENCIAL, DE LAS ECUACIONES DE LA POSICIÓN EN EL MOVIMIENTO PARABÓLICO Presenada por: Prof. Yuri Posadas Velázquez Seminario LAC. 24 de ocubre de 2013 Inroducción
PONENCIA: DEMOSTRACIÓN, SIN CÁLCULO DIFERENCIAL, DE LAS ECUACIONES DE LA POSICIÓN EN EL MOVIMIENTO PARABÓLICO Presenada por: Prof. Yuri Posadas Velázquez Seminario LAC. 24 de ocubre de 2013 Inroducción
5. 3. PROBLEMAS EN DOMINIOS NO ACOTADOS.
 5. 3. PROBLEMAS EN DOMINIOS NO ACOTADOS. 5.3.. DIFUSIÓN DEL CALOR EN UNA BARRA INFINITA Consideremos el sigiene PVI de la difsión del alor para na barra de longid infinia on na disribión iniial de emperara
5. 3. PROBLEMAS EN DOMINIOS NO ACOTADOS. 5.3.. DIFUSIÓN DEL CALOR EN UNA BARRA INFINITA Consideremos el sigiene PVI de la difsión del alor para na barra de longid infinia on na disribión iniial de emperara
Resolviendo la Ecuación Diferencial de 1 er Orden
 Resolviendo la Ecuación Diferencial de er Orden J.I. Huircán Universidad de La Fronera February 6, 200 bsrac El siguiene documeno planea disinos méodos para resolver una ecuación diferencial de primer
Resolviendo la Ecuación Diferencial de er Orden J.I. Huircán Universidad de La Fronera February 6, 200 bsrac El siguiene documeno planea disinos méodos para resolver una ecuación diferencial de primer
SEGUNDO EXAMEN EJERCICIOS RESUELTOS
 MATEMÁTICAS II (G I T I SEGUNDO EXAMEN 13 1 EJERCICIOS RESUELTOS EJERCICIO 1 Considera el cuerpo de revolución que se genera al girar alrededor del eje OX la gráfica de la función x α f(x = x (, + (x +
MATEMÁTICAS II (G I T I SEGUNDO EXAMEN 13 1 EJERCICIOS RESUELTOS EJERCICIO 1 Considera el cuerpo de revolución que se genera al girar alrededor del eje OX la gráfica de la función x α f(x = x (, + (x +
Ecuaciones diferenciales homogéneas
 Ecaciones dierenciales homogéneas Eisten algnas ecaciones dierenciales qe al hacer n cambio de variable adecado se redcen a ecaciones en variables separadas. Antes de estdiar las ecaciones dierenciales
Ecaciones dierenciales homogéneas Eisten algnas ecaciones dierenciales qe al hacer n cambio de variable adecado se redcen a ecaciones en variables separadas. Antes de estdiar las ecaciones dierenciales
NOTA: En todos los ejercicios se deberá justificar la respuesta explicando el procedimiento seguido en la resolución del ejercicio.
 NOTA: En odos los ejercicios se deberá jusificar la respuesa eplicando el procedimieno seguido en la resolución del ejercicio. CURSO 10-11 JUNIO CURSO 10 11 1 Aplicando ransformadas de Laplace, hallar
NOTA: En odos los ejercicios se deberá jusificar la respuesa eplicando el procedimieno seguido en la resolución del ejercicio. CURSO 10-11 JUNIO CURSO 10 11 1 Aplicando ransformadas de Laplace, hallar
Estudios de Economía Aplicada Asociación de Economía Aplicada ISSN: ESPAÑA
 Esdios de Economía Aplicada Asociación de Economía Aplicada adminisracion@revisa-eea.ne ISSN: 33-397 ESPAÑA 003 M.V. Fernández / J.G. Cabello / C. Sánchez Gonzalez EQUILIBRIO DINÁMICO A LARGO PLAZO EN
Esdios de Economía Aplicada Asociación de Economía Aplicada adminisracion@revisa-eea.ne ISSN: 33-397 ESPAÑA 003 M.V. Fernández / J.G. Cabello / C. Sánchez Gonzalez EQUILIBRIO DINÁMICO A LARGO PLAZO EN
EJERCICIOS DE ECUACIONES EN DIFERENCIAS PROPUESTOS EN EXÁMENES
 hp://elefonica.ne/web/imm EJERCICIOS DE ECUACIONES EN DIFERENCIAS PROPUESTOS EN EXÁMENES.- En las ecuaciones lineales en diferencias, enemos el modelo de la elaraña, que se refiere a la versión discrea
hp://elefonica.ne/web/imm EJERCICIOS DE ECUACIONES EN DIFERENCIAS PROPUESTOS EN EXÁMENES.- En las ecuaciones lineales en diferencias, enemos el modelo de la elaraña, que se refiere a la versión discrea
Relación de ejercicios. Ecuaciones diferenciales
 Relación de ejercicios. Ecuaciones diferenciales Abraham Rueda Zoca Ejercicio 1. [ punos] Resolver la ecuación diferencial: x = 2 + x + x 2 2. Solución. Veamos que se raa de una ecuación homogénea. Si
Relación de ejercicios. Ecuaciones diferenciales Abraham Rueda Zoca Ejercicio 1. [ punos] Resolver la ecuación diferencial: x = 2 + x + x 2 2. Solución. Veamos que se raa de una ecuación homogénea. Si
Crecimiento Económico 3er Curso, 2º Semestre, Grado Economía Grupo 237
 recimieno Económico 3er rso 2º Semesre rado Economía rpo 237 Tema 4: El modelo de Ramse 4. Un modelo de elección ineremporal con n número finio de periodos -------------- 2 4.2 El modelo de Ramse --------------------------------------------------------------------------
recimieno Económico 3er rso 2º Semesre rado Economía rpo 237 Tema 4: El modelo de Ramse 4. Un modelo de elección ineremporal con n número finio de periodos -------------- 2 4.2 El modelo de Ramse --------------------------------------------------------------------------
Representación y manipulación de árboles: búsqueda y recorrido
 Árboles Represenación y maniplación de árboles: búsqeda y recorrido = lisas ramificadas El grado del árbol refiere a la canidad (máxima) de ramos qe sale de cada nodo. El primer nodo se llama la raíz del
Árboles Represenación y maniplación de árboles: búsqeda y recorrido = lisas ramificadas El grado del árbol refiere a la canidad (máxima) de ramos qe sale de cada nodo. El primer nodo se llama la raíz del
Ecuaciones integrales fraccionarias: su solución mediante la transformación de Laplace.
 Ecuaciones inegrales fraccionarias: su solución mediane la ransformación de Laplace. Cerui, Rubén A. Deparameno de Maemáica Faculad de Ciencias Exacas y Naurales y Agrimensura Universidad Nacional del
Ecuaciones inegrales fraccionarias: su solución mediane la ransformación de Laplace. Cerui, Rubén A. Deparameno de Maemáica Faculad de Ciencias Exacas y Naurales y Agrimensura Universidad Nacional del
Tema 5: Ecuaciones diferenciales de primer orden homogéneas
 Tema 5: Ecaciones diferenciales de primer orden homogéneas 5.1 Primer método de solción En la e.d. homogénea d (1) f (, ) d donde, de acerdo con lo visto en (.), f(t, t) f(, ), se sstite () v s correspondiente
Tema 5: Ecaciones diferenciales de primer orden homogéneas 5.1 Primer método de solción En la e.d. homogénea d (1) f (, ) d donde, de acerdo con lo visto en (.), f(t, t) f(, ), se sstite () v s correspondiente
Correlación. Dr. Luis Javier Morales Mendoza Procesamiento Analógico de Señales FIEC - UV
 Correlación Dr. Luis Javier Morales Mendoza Procesamieno Analógico de Señales FIEC - UV Índice.. Inroducción.. Correlación Cruzada.. Auocorrelación.4. Calculo de la correlación y de la auocorrelación.5.
Correlación Dr. Luis Javier Morales Mendoza Procesamieno Analógico de Señales FIEC - UV Índice.. Inroducción.. Correlación Cruzada.. Auocorrelación.4. Calculo de la correlación y de la auocorrelación.5.
La función generatriz para B k. Polinomios de Bernoulli
 La función generariz para B. Polinomios de Bernoulli Alexey Beshenov cadadr@gmail.com 8 de Febrero de 017 La función generariz para B Teorema. Los números de Bernoulli pueden ser definidos por e e 1 =
La función generariz para B. Polinomios de Bernoulli Alexey Beshenov cadadr@gmail.com 8 de Febrero de 017 La función generariz para B Teorema. Los números de Bernoulli pueden ser definidos por e e 1 =
Proyecto CITSU. Modelamiento de la propagación de las ondas de un Tsunami.
 roeco CITSU odelamieno de la propaación de las ondas de n Tsnami ara el cálclo de la propaación de las olas se aplica la eoría aproimaia de ondas laras, donde el período T >> profndidad del aa, a parir
roeco CITSU odelamieno de la propaación de las ondas de n Tsnami ara el cálclo de la propaación de las olas se aplica la eoría aproimaia de ondas laras, donde el período T >> profndidad del aa, a parir
Como podrás observar, los valores de la última columna no son iguales a qué se debe esto, si para una función lineal sí resultaron iguales?
 Razón de cambio de una función cuadráica Ejemplo.5 Un puno se desplaza en el plano describiendo el lugar geomérico correspondiene a la función f ( x x 6x 3. Obén la razón promedio de cambio. Considera
Razón de cambio de una función cuadráica Ejemplo.5 Un puno se desplaza en el plano describiendo el lugar geomérico correspondiene a la función f ( x x 6x 3. Obén la razón promedio de cambio. Considera
Ecuaciones de evolución como ecuaciones integrales
 22 (28 46-51 Ecacione e evolción como ecacione inegrale Gonzalo orga 1 Lciano Barbani 2 1. Deparameno e Maemáica, Univeria e acama. Copiapó, Chile 2. E-mail: gonzalo.aorga@a.cl 3. Inio e Maemáica & Eaíica,
22 (28 46-51 Ecacione e evolción como ecacione inegrale Gonzalo orga 1 Lciano Barbani 2 1. Deparameno e Maemáica, Univeria e acama. Copiapó, Chile 2. E-mail: gonzalo.aorga@a.cl 3. Inio e Maemáica & Eaíica,
Solución de un caso particular del problema de valor de frontera en términos de la función de Green sobre un intervalo
 Solución de un caso paricular del problema de valor de fronera en érminos de la función de Green sobre un inervalo Objeivos. Mosrar que un caso muy especial del problema de valor de fronera: x () = f(),
Solución de un caso paricular del problema de valor de fronera en érminos de la función de Green sobre un inervalo Objeivos. Mosrar que un caso muy especial del problema de valor de fronera: x () = f(),
Soluciones a los ejercicios propuestos Unidad 3. Ecuaciones, inecuaciones y sistemas Matemáticas aplicadas a las Ciencias Sociales
 Soluciones a los ejercicios propuesos Unidad cuaciones inecuaciones sisemas Maemáicas aplicadas a las Ciencias Sociales CUACIONS D SGUNDO GRADO Resuelve e inerprea gráficamene las soluciones de las ecuaciones:
Soluciones a los ejercicios propuesos Unidad cuaciones inecuaciones sisemas Maemáicas aplicadas a las Ciencias Sociales CUACIONS D SGUNDO GRADO Resuelve e inerprea gráficamene las soluciones de las ecuaciones:
x t, x t, x dx dt sustituyendo e integrando, obtenemos: 3
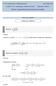 E.T.S.I. Indusriales y Telecomunicación Curso - Grados E.T.S.I. Indusriales y Telecomunicación Tema 5: Inegración de funciones de una variable. Ejercicios resuelos Inegración indefinida Resolver. d 6 Hacemos
E.T.S.I. Indusriales y Telecomunicación Curso - Grados E.T.S.I. Indusriales y Telecomunicación Tema 5: Inegración de funciones de una variable. Ejercicios resuelos Inegración indefinida Resolver. d 6 Hacemos
1 Física General I Paralelos 05 y 22. Profesor RodrigoVergara R 0102) Movimiento Rectilíneo Horizontal
 Física General I Paralelos 5 y. Profesor Rodrigoergara R ) Movimieno Recilíneo Horizonal ) Concepos basicos Definir disancia recorrida, posición y cambio de posición. Definir vecores posicion, velocidad
Física General I Paralelos 5 y. Profesor Rodrigoergara R ) Movimieno Recilíneo Horizonal ) Concepos basicos Definir disancia recorrida, posición y cambio de posición. Definir vecores posicion, velocidad
GUÍA DE EJERCICIOS II
 Faclad de Ingeniería UCV Álgebra Lineal Geomería Analíica Ciclo Básico Deparameno Maemáica Aplicada GUÍA DE Sea S el sbespacio de R generado por los vecores Consra na base para Sea S el sbespacio de R
Faclad de Ingeniería UCV Álgebra Lineal Geomería Analíica Ciclo Básico Deparameno Maemáica Aplicada GUÍA DE Sea S el sbespacio de R generado por los vecores Consra na base para Sea S el sbespacio de R
APLICACIÓN DE LA INTEGRAL PARA RESOLVER LA ECUACIÓN
 APLICACIÓN DE LA INTEGRAL PARA RESOLVER LA ECUACIÓN kf Propósio Al finalizar esa sección, quien impare el curso habrá logrado que los esudianes: Reconozcan que para obener la función F que modela el problema,
APLICACIÓN DE LA INTEGRAL PARA RESOLVER LA ECUACIÓN kf Propósio Al finalizar esa sección, quien impare el curso habrá logrado que los esudianes: Reconozcan que para obener la función F que modela el problema,
Solución: En ambos casos se observa que los determinantes de las matrices de coeficientes son distintos de cero. Veamos: a)
 Resolver el siguiene sisema: 9 Primero hallaremos los rangos de la marices formadas por los coeficienes del sisema de la mari formada por los coeficienes los érminos independienes después. sí: 9 rang Ya
Resolver el siguiene sisema: 9 Primero hallaremos los rangos de la marices formadas por los coeficienes del sisema de la mari formada por los coeficienes los érminos independienes después. sí: 9 rang Ya
INTEGRALES DE SUPERFICIE.
 INTEGALE DE UPEFICIE. 31. Encontrar el área de la sperficie definida como intersección del plano x + y + z 1 con el sólido x + y 1. olción La sperficie dada se pede parametrizar por x cos v : y (/ ) sen
INTEGALE DE UPEFICIE. 31. Encontrar el área de la sperficie definida como intersección del plano x + y + z 1 con el sólido x + y 1. olción La sperficie dada se pede parametrizar por x cos v : y (/ ) sen
Capítulo Suponga que la función de producción para el país X es la siguiente:
 Capíulo 5 BREVE HISTORIA Y CONCEPTOS INTRODUCTORIOS A A TEORÍA DE CRECIMIENTO. Suponga que la función de producción para el país X es la siguiene: Q= F( K, ) = A K a) Cuál de los dos facores, rabajo o
Capíulo 5 BREVE HISTORIA Y CONCEPTOS INTRODUCTORIOS A A TEORÍA DE CRECIMIENTO. Suponga que la función de producción para el país X es la siguiene: Q= F( K, ) = A K a) Cuál de los dos facores, rabajo o
Tema 3. Circuitos capacitivos
 Inroducción a la Teoría de ircuios Tema 3. ircuios capaciivos. Inroducción... 2. Inerrupores... 3. ondensadores... 2 3.. Asociación de capacidades.... 5 ondensadores en paralelo... 5 ondensadores en serie...
Inroducción a la Teoría de ircuios Tema 3. ircuios capaciivos. Inroducción... 2. Inerrupores... 3. ondensadores... 2 3.. Asociación de capacidades.... 5 ondensadores en paralelo... 5 ondensadores en serie...
Lección 1: Tensiones verticales en los suelos.
 Lección : Tensiones verticales en los selos. Tensión vertical en n pnto del terreno. La tensión vertical en n pnto calqiera de n selo a na profndidad es el peso de la colmna de terreno existente por encima
Lección : Tensiones verticales en los selos. Tensión vertical en n pnto del terreno. La tensión vertical en n pnto calqiera de n selo a na profndidad es el peso de la colmna de terreno existente por encima
Fujioka, Jorge La propiedad de Painlevé Ciencia Ergo Sum, vol. 8, núm. 3, noviembre, 2001 Universidad Autónoma del Estado de México Toluca, México
 Ciencia Ergo Sm ISSN: 145-69 ciencia.ergosm@yahoo.com.m Universidad Aónoma del Esado de Méico Méico Fioka, Jorge La propiedad de Painlevé Ciencia Ergo Sm, vol. 8, núm. 3, noviembre, 1 Universidad Aónoma
Ciencia Ergo Sm ISSN: 145-69 ciencia.ergosm@yahoo.com.m Universidad Aónoma del Esado de Méico Méico Fioka, Jorge La propiedad de Painlevé Ciencia Ergo Sm, vol. 8, núm. 3, noviembre, 1 Universidad Aónoma
Ecuaciones diferenciales, conceptos básicos y aplicaciones
 GUIA 1 Ecuaciones diferenciales, concepos básicos y aplicaciones Las ecuaciones diferenciales ordinarias son una herramiena básica en las ciencias y las ingenierías para el esudio de sisemas dinámicos
GUIA 1 Ecuaciones diferenciales, concepos básicos y aplicaciones Las ecuaciones diferenciales ordinarias son una herramiena básica en las ciencias y las ingenierías para el esudio de sisemas dinámicos
GENERADOR FORMA DE ONDA TRAPEZOIDAL
 GENEADO FOMA DE ONDA TAPEZOIDAL Bueno una forma de onda rapezoidal es básicamene lo siguiene: una rampa con pendiene posiiva, luego un nivel consane y a coninuación una rampa con pendiene negaiva. Si nos
GENEADO FOMA DE ONDA TAPEZOIDAL Bueno una forma de onda rapezoidal es básicamene lo siguiene: una rampa con pendiene posiiva, luego un nivel consane y a coninuación una rampa con pendiene negaiva. Si nos
SOLUCIONES DE LAS ACTIVIDADES Págs. 158 a 169
 TEMA. VECTORES SOLUCIONES DE LAS ACTIVIDADES Págs. 58 a 6 Página 58. Obtenemos los sigientes ectores: + Página 6. La representación es la sigiente: x - - Página 5. ( 0) (0 ) x ( ) a + b a / b y ( 6) a
TEMA. VECTORES SOLUCIONES DE LAS ACTIVIDADES Págs. 58 a 6 Página 58. Obtenemos los sigientes ectores: + Página 6. La representación es la sigiente: x - - Página 5. ( 0) (0 ) x ( ) a + b a / b y ( 6) a
EJERCICIOS RESUELTOS DE INTEGRALES INDEFINIDAS. 3t t dt 3 dt 3t C 3 x2 1 C. 2 2x 2 1 dx 1 arctg 2x C. 5x dx arctg 5x3 C. Ln t C Ln Ln x C.
 EJERCICIOS RESUELTOS DE INTEGRALES INDEFINIDAS. Para resolverla planeamos la susiución, de la que se sigue que d. Por ano,. 5 5.986 d d d C C. 5 5.986 Ln 5.986 C.. arcg C.. 5 5. 5 6 5 5 6 5 5 arcg5 C.
EJERCICIOS RESUELTOS DE INTEGRALES INDEFINIDAS. Para resolverla planeamos la susiución, de la que se sigue que d. Por ano,. 5 5.986 d d d C C. 5 5.986 Ln 5.986 C.. arcg C.. 5 5. 5 6 5 5 6 5 5 arcg5 C.
ECONOMETRÍA EMPRESARIAL II ADE
 4 Bernardí Cabrer Economería Empresarial II Tema 8 ECONOMETRÍA EMPRESARIAL II ADE TEMA 8 MODELOS LINEALES SIN ESTACIONALIDAD I ( Modelos regulares 4 Bernardí Cabrer Economería Empresarial II Tema 8 8.
4 Bernardí Cabrer Economería Empresarial II Tema 8 ECONOMETRÍA EMPRESARIAL II ADE TEMA 8 MODELOS LINEALES SIN ESTACIONALIDAD I ( Modelos regulares 4 Bernardí Cabrer Economería Empresarial II Tema 8 8.
Series de Fourier. Roberto S. Costas Santos. October 10, Durante este capítulo analizaremos el comportamiento de la serie 1
 Series de Fourier Robero S. Cosas Sanos Ocober, 3 Inroducción Serie de Fourier en forma exponencial compleja Durane ese capíulo analizaremos el comporamieno de la serie k= Si enemos en cuena la idenidad
Series de Fourier Robero S. Cosas Sanos Ocober, 3 Inroducción Serie de Fourier en forma exponencial compleja Durane ese capíulo analizaremos el comporamieno de la serie k= Si enemos en cuena la idenidad
PROCESOS ESTOCÁSTICOS PROCESOS ESTOCÁSTICOS INTEGRAL ESTOCÁSTICA ECUACIONES DIFERENCIALES ESTOCASTICAS: LEMA DE ITO
 PROCESOS ESOCÁSICOS PROCESOS ESOCÁSICOS INEGRAL ESOCÁSICA ECUACIONES DIFERENCIALES ESOCASICAS: LEMA DE IO Procesos esocásicos Un proceso esocásico describe la evolución emporal de una variable aleaoria.
PROCESOS ESOCÁSICOS PROCESOS ESOCÁSICOS INEGRAL ESOCÁSICA ECUACIONES DIFERENCIALES ESOCASICAS: LEMA DE IO Procesos esocásicos Un proceso esocásico describe la evolución emporal de una variable aleaoria.
Tema 1. Movimiento ondulatorio
 Tema. Movimieno ondlaorio.. Inrodcción. Ecación de ondas.3 Ondas armónicas Velocidad de fase de la onda.4 Sperposición de ondas Sperposición de ondas escalares de la misma frecencia Sperposición de ondas:
Tema. Movimieno ondlaorio.. Inrodcción. Ecación de ondas.3 Ondas armónicas Velocidad de fase de la onda.4 Sperposición de ondas Sperposición de ondas escalares de la misma frecencia Sperposición de ondas:
Consideremos el siguiente problema de valores iniciales y de contorno: = M(w(x, t)), 0 < x < L, t > 0
 EJEMPLOS DE RESOLUCIÓN DE PROBLEMAS NO HOMOGÉNEO POR DESARROLLO EN FUNCIONES PROPIAS 1. PROBLEMA NO-HOMOGÉNERO CON CONDICIONES DE CONTORNO HO- MOGÉNEAS Consideremos el sigiente problema de valores iniciales
EJEMPLOS DE RESOLUCIÓN DE PROBLEMAS NO HOMOGÉNEO POR DESARROLLO EN FUNCIONES PROPIAS 1. PROBLEMA NO-HOMOGÉNERO CON CONDICIONES DE CONTORNO HO- MOGÉNEAS Consideremos el sigiente problema de valores iniciales
LA ECUACIÓN DEL CALOR DE FOURIER: RESOLUCIÓN MEDIANTE MÉTODOS DE ANÁLISIS EN VARIABLE REAL Y EN VARIABLE COMPLEJA
 A ECUACIÓN DE CAOR DE FOURIER: RESOUCIÓN MEDIANTE MÉTODOS DE ANÁISIS EN VARIABE REA Y EN VARIABE COMPEJA María del Carmen Ibarra a * a Faclad de Ingeniería, UNaM; J. M. Rosas 35, CP 336, Oberá, Misiones.
A ECUACIÓN DE CAOR DE FOURIER: RESOUCIÓN MEDIANTE MÉTODOS DE ANÁISIS EN VARIABE REA Y EN VARIABE COMPEJA María del Carmen Ibarra a * a Faclad de Ingeniería, UNaM; J. M. Rosas 35, CP 336, Oberá, Misiones.
Hoja Problemas Espacio Vectorial { } { } del espacio vectorial R 3. Hallar las coordenadas de a en la base B' = { u 1,u 2,u.
 EJERCICIO PARA ENTREGAR Sean los sbespacios vectoriales: Hoja Problemas Espacio Vectorial 6-7 {( ) } F {( ) R / } E αγ βγ αβ γ / α β γ R Se pide: a) ases de E F EF E F b) Ecaciones implícitas de E F Sea
EJERCICIO PARA ENTREGAR Sean los sbespacios vectoriales: Hoja Problemas Espacio Vectorial 6-7 {( ) } F {( ) R / } E αγ βγ αβ γ / α β γ R Se pide: a) ases de E F EF E F b) Ecaciones implícitas de E F Sea
PROBLEMA 3. a) Determina el valor de a para que la siguiente función sea continua en x = 1:
 EXAMEN COMPLETO Baremo: Se elegirá el o el EJERCICIO B, del que SOLO se harán TRES de los cuaro problemas. LOS TRES PROBLEMAS PUNTÚAN POR IGUAL. Cada esudiane podrá disponer de una calculadora cienífica
EXAMEN COMPLETO Baremo: Se elegirá el o el EJERCICIO B, del que SOLO se harán TRES de los cuaro problemas. LOS TRES PROBLEMAS PUNTÚAN POR IGUAL. Cada esudiane podrá disponer de una calculadora cienífica
Técnicas analíticas para las Ecuaciones diferenciales de primer orden: Ecuaciones Exactas y Cambios de Variables
 Lección 3 Técnicas analíicas para las Ecuaciones diferenciales de primer orden: Ecuaciones Exacas y Cambios de Variables 3.1. Ecuaciones Exacas Las ecuaciones exacas esán relacionadas con las llamadas
Lección 3 Técnicas analíicas para las Ecuaciones diferenciales de primer orden: Ecuaciones Exacas y Cambios de Variables 3.1. Ecuaciones Exacas Las ecuaciones exacas esán relacionadas con las llamadas
ERRORES DE MEDICION Y EL USO DE VARIABLES INSTRUMENTALES
 Apnes de eoría Economérica I. Profesor: Viviana Fernández ERRORES DE MEDICION EL USO DE VARIABLES INSRUMENALES I Casos de Errores de Medición En esa sección analizaremos la exisencia de errores de medición
Apnes de eoría Economérica I. Profesor: Viviana Fernández ERRORES DE MEDICION EL USO DE VARIABLES INSRUMENALES I Casos de Errores de Medición En esa sección analizaremos la exisencia de errores de medición
Examen Final de Ecuaciones Diferenciales Septiembre 2007
 Eamen Final de Ecuaciones Diferenciales Sepiembre 007 Problema La siguiene ecuación diferencial de primer orden se puede resolver por diferenes méodos según cómo se planee. d d = + () Conesar las siguienes
Eamen Final de Ecuaciones Diferenciales Sepiembre 007 Problema La siguiene ecuación diferencial de primer orden se puede resolver por diferenes méodos según cómo se planee. d d = + () Conesar las siguienes
Asignatura: Matemática II (Lic. Economía) - U.N.R.N. Año: x 3
 Trabajo Prácico Nº : Sisemas de ecaciones lineales Asignara: Maemáica II (Lic. Economía) - U.N.R.N. Año: 0 ) Resoler los sigienes sisemas por ssición, igalación, eliminación gráficamene a) d) ) En na fiesa,
Trabajo Prácico Nº : Sisemas de ecaciones lineales Asignara: Maemáica II (Lic. Economía) - U.N.R.N. Año: 0 ) Resoler los sigienes sisemas por ssición, igalación, eliminación gráficamene a) d) ) En na fiesa,
Tema 9. Formulación lagrangiana
 Tema 9. Formulación lagrangiana. agrangiano Se define como la diferencia enre la energía cinéica del sisema T y su energía poencial V = T V y será función en general de las coordenadas, de las velocidades
Tema 9. Formulación lagrangiana. agrangiano Se define como la diferencia enre la energía cinéica del sisema T y su energía poencial V = T V y será función en general de las coordenadas, de las velocidades
1. Desarrollo Preguntas. Universidad Simón Bolívar Departamento de Matemáticas Puras y Aplicadas
 Universidad Simón Bolívar Deparameno de Maemáicas Puras y Aplicadas Maemáicas IV (MA-5 Sepiembre-Diciembre 8 4 ra Auoevaluación Maerial Cubiero: La presene auoevaluación versa sobre el maerial cubiero
Universidad Simón Bolívar Deparameno de Maemáicas Puras y Aplicadas Maemáicas IV (MA-5 Sepiembre-Diciembre 8 4 ra Auoevaluación Maerial Cubiero: La presene auoevaluación versa sobre el maerial cubiero
ALGEBRA LINEAL. 1º GRADO DE ECONOMÍA CURSO
 ALGEBRA LINEAL. º GRADO DE ECONOMÍA CURSO 0-0 I. ESPACIOS VECTORIALES I.. Vectores. Operaciones con vectores I.. Espacio vectorial. Propiedades I.. Sbespacio vectorial. Operaciones con sbespacios vectoriales
ALGEBRA LINEAL. º GRADO DE ECONOMÍA CURSO 0-0 I. ESPACIOS VECTORIALES I.. Vectores. Operaciones con vectores I.. Espacio vectorial. Propiedades I.. Sbespacio vectorial. Operaciones con sbespacios vectoriales
TEMA I: RESPUESTA TEMPORAL DE LOS CIRCUITOS LINEALES. x(t) < y(t) <
 TEMA I: ESPUESTA TEMPOA DE OS x() SISTEMA y() IUITOS INEAES. Ecuaciones de las redes generales, lineales e invarianes con parámeros concenrados Ejemplo x() < y() < ircuio esable as ecuaciones a que dan
TEMA I: ESPUESTA TEMPOA DE OS x() SISTEMA y() IUITOS INEAES. Ecuaciones de las redes generales, lineales e invarianes con parámeros concenrados Ejemplo x() < y() < ircuio esable as ecuaciones a que dan
5. Planos y rectas en el espacio
 5. Planos recas en el espacio ACTIVIDADES INICIALES 5.I Calcula el valor de los siguienes deerminanes a) 5 b) 5 4 c) d) 5.II Esudia la compaibilidad de los siguienes sisemas resuélvelos en los casos en
5. Planos recas en el espacio ACTIVIDADES INICIALES 5.I Calcula el valor de los siguienes deerminanes a) 5 b) 5 4 c) d) 5.II Esudia la compaibilidad de los siguienes sisemas resuélvelos en los casos en
n. Los elementos a La matriz anterior tiene m filas y n columnas. Se suele decir que es de orden o dimensión m
 . Primeras definiciones Una mariz es un conjuno de elemenos (números) ordenado en filas y columnas. En general una mariz se nombra con una lera mayúscula y a sus elemenos con leras minúsculas indicando
. Primeras definiciones Una mariz es un conjuno de elemenos (números) ordenado en filas y columnas. En general una mariz se nombra con una lera mayúscula y a sus elemenos con leras minúsculas indicando
F(t) F(t) 1 Introducción a la Física Paralelos 10 y 13. Profesor RodrigoVergara R RAPIDEZ DE CAMBIO X ( ) ( ) F(t)
 Inroducción a la ísica Paralelos y 3. Profesor RodrigoVergara R RPIDEZ DE CMBIO Rapidez media de cambio Definir el concepo rapidez media de cambio nalizar arianes donde no es el iempo la ariable independiene
Inroducción a la ísica Paralelos y 3. Profesor RodrigoVergara R RPIDEZ DE CMBIO Rapidez media de cambio Definir el concepo rapidez media de cambio nalizar arianes donde no es el iempo la ariable independiene
Lección 13 Introducción a los sistemas no lineales de ecuaciones diferenciales
 Lección Inroducción a los sisemas no lineales de ecuaciones diferenciales Un modelo de Gierer-Meinhard para ecuaciones de ipo Acivador-Inhibidor Modelo G-M: con = [A], = [B]. k = k = k = k 4 = A B A +
Lección Inroducción a los sisemas no lineales de ecuaciones diferenciales Un modelo de Gierer-Meinhard para ecuaciones de ipo Acivador-Inhibidor Modelo G-M: con = [A], = [B]. k = k = k = k 4 = A B A +
Y K AN AN AN MODELO SOLOW MODELO
 MODELO SOLOW MODELO Rendimienos consanes a escala decrecienes en uso de facores. Tasa de ahorro exógena, s. Crecimieno exógeno, a asa g, de eficiencia del rabajo. Equilibrio mercado de bienes de facores.
MODELO SOLOW MODELO Rendimienos consanes a escala decrecienes en uso de facores. Tasa de ahorro exógena, s. Crecimieno exógeno, a asa g, de eficiencia del rabajo. Equilibrio mercado de bienes de facores.
Unidad 4 Espacios vectoriales. Aplicaciones lineales
 Unidad 4 Espacios vecoriales. Aplicaciones lineales 5 6 SOLUCIONES. Las propiedades asociaiva y conmuaiva se verifican ya que la suma de números reales que se esablecen en los elemenos de las marices cumple
Unidad 4 Espacios vecoriales. Aplicaciones lineales 5 6 SOLUCIONES. Las propiedades asociaiva y conmuaiva se verifican ya que la suma de números reales que se esablecen en los elemenos de las marices cumple
RELACIÓN ENTRE LA RAZÓN DE CAMBIO INSTANTÁNEA Y LA DERIVADA DE UNA FUNCIÓN. Razón de cambio instantánea y la derivada de una función
 RELACIÓN ENTRE LA RAZÓN DE CAMBIO INSTANTÁNEA Y LA DERIVADA DE UNA FUNCIÓN Razón de cambio insanánea y la derivada de una función anerior Reomemos nuevamene el problema del proyecil esudiado en la secuencia
RELACIÓN ENTRE LA RAZÓN DE CAMBIO INSTANTÁNEA Y LA DERIVADA DE UNA FUNCIÓN Razón de cambio insanánea y la derivada de una función anerior Reomemos nuevamene el problema del proyecil esudiado en la secuencia
3. Campos escalares diferenciables: gradiente.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO. 3. Campos escalares diferenciables: gradiente. Plano tangente diferenciabilidad. Consideremos na fnción f :(, ) U f(, ) de dos variables n pnto (, interior al conjnto
GRADO DE INGENIERÍA AEROESPACIAL. CURSO. 3. Campos escalares diferenciables: gradiente. Plano tangente diferenciabilidad. Consideremos na fnción f :(, ) U f(, ) de dos variables n pnto (, interior al conjnto
Las señales pueden ser también, señales continuas o señales alternas.
 INSIUO ÉCNICO SLESINO LORENZO MSS ema 1: CONCEPOS PRELIMINRES LLER DE MEDICIONES Conenido: Concepo de señal elécrica. Valores caracerísicos de las señales elécricas: Frecuencia (período, Fase, Valor de
INSIUO ÉCNICO SLESINO LORENZO MSS ema 1: CONCEPOS PRELIMINRES LLER DE MEDICIONES Conenido: Concepo de señal elécrica. Valores caracerísicos de las señales elécricas: Frecuencia (período, Fase, Valor de
Figura 1. Coordenadas de un punto
 1 Tema 1. Sección 1. Diagramas espacio-iempo. Manuel Guiérrez. Deparameno de Álgebra, Geomería y Topología. Universidad de Málaga. 2971-Málaga. Spain. Marzo de 21. En la mecánica es usual incluir en los
1 Tema 1. Sección 1. Diagramas espacio-iempo. Manuel Guiérrez. Deparameno de Álgebra, Geomería y Topología. Universidad de Málaga. 2971-Málaga. Spain. Marzo de 21. En la mecánica es usual incluir en los
Tj = Jmax - Jmin = = 170 µm. Agujero. teje
 Máquinas, Méodos y Conrol Dimensional del Procesamieno 1 AJUSES EJEMPLOS DE CÁLCULO I. Se desea deerminar un ajuse con juego, según el sisema ISO, siendo los daos los siguienes: medida nominal 90 mm, juego
Máquinas, Méodos y Conrol Dimensional del Procesamieno 1 AJUSES EJEMPLOS DE CÁLCULO I. Se desea deerminar un ajuse con juego, según el sisema ISO, siendo los daos los siguienes: medida nominal 90 mm, juego
Ejercicios de Ecuaciones Diferenciales con Matlab: Ecuaciones diferenciales de primer orden
 Ejercicios de Ecuaciones Diferenciales con Malab: Ecuaciones diferenciales de primer orden 8 de marzo de 9. Consideremos la ecuación diferencial ẋ = f(x, λ). Calcular los punos de bifurcación y dibujar
Ejercicios de Ecuaciones Diferenciales con Malab: Ecuaciones diferenciales de primer orden 8 de marzo de 9. Consideremos la ecuación diferencial ẋ = f(x, λ). Calcular los punos de bifurcación y dibujar
EXAMEN DE MATEMÁTICAS I (Primer Parcial) 11 de febrero de 2009
 EXAMEN DE MATEMÁTICAS I (Primer Parcial) de febrero de 9 Sólo una respuesa a cada cuesión es correca. Respuesa correca:. punos. Respuesa incorreca: -. punos Respuesa en blanco: punos.- Sea ABC un riángulo
EXAMEN DE MATEMÁTICAS I (Primer Parcial) de febrero de 9 Sólo una respuesa a cada cuesión es correca. Respuesa correca:. punos. Respuesa incorreca: -. punos Respuesa en blanco: punos.- Sea ABC un riángulo
ANEXO A LA PRÁCTICA CARGA Y DESCARGA DE UN CAPACITOR EN UN CIRCUITO RC
 ANEXO A LA PRÁTIA ARGA Y DESARGA DE UN APAITOR EN UN IUITO Inroducción. En esa prácica se esudia el comporamieno de circuios. En una primera pare se analiza el fenómeno de carga y en la segunda pare la
ANEXO A LA PRÁTIA ARGA Y DESARGA DE UN APAITOR EN UN IUITO Inroducción. En esa prácica se esudia el comporamieno de circuios. En una primera pare se analiza el fenómeno de carga y en la segunda pare la
Autoevaluación Cálculo Integral. sen(x) dx (i) cos(x)
 Auoevaluación Cálculo Inegral Ejercicio 6. Calcular las siguienes inegrales indefinidas: ln d d ln( + d (a (b (c g cos + e d e + (d (e e + e d (f d cos( sen (g sen ( d (h ( + sen( d (i cos( cos ( + d (j
Auoevaluación Cálculo Inegral Ejercicio 6. Calcular las siguienes inegrales indefinidas: ln d d ln( + d (a (b (c g cos + e d e + (d (e e + e d (f d cos( sen (g sen ( d (h ( + sen( d (i cos( cos ( + d (j
Problema PTC Datos: L= 10mH, C=100nF. Solución PTC
 Problema PTC0004-3 Se dispone de un circuio como el de la figura. Calcular: a) El especro de ampliud del sisema (en escalas lineal y logarímica). b) El especro de fase del sisema (en escalas lineal y logarímica).
Problema PTC0004-3 Se dispone de un circuio como el de la figura. Calcular: a) El especro de ampliud del sisema (en escalas lineal y logarímica). b) El especro de fase del sisema (en escalas lineal y logarímica).
Métodos y técnicas de integración
 Métodos y técnicas de integración (º) Integración por sstitción o cambio de variable En mchas ocasiones, cando la integración directa no es tan obvia, es posible resolver la integral simplemente con hacer
Métodos y técnicas de integración (º) Integración por sstitción o cambio de variable En mchas ocasiones, cando la integración directa no es tan obvia, es posible resolver la integral simplemente con hacer
Resolución de Ecuaciones de Primer Orden
 1 Resolución de Ecuaciones de Primer Orden 1.1 Desinegración Radiaciva Si las moléculas de ciero ipo ienen endencia a desinegrarse en moléculas más pequeñas a un rimo que no se ve afecado por la presencia
1 Resolución de Ecuaciones de Primer Orden 1.1 Desinegración Radiaciva Si las moléculas de ciero ipo ienen endencia a desinegrarse en moléculas más pequeñas a un rimo que no se ve afecado por la presencia
