Capítulo 8. Estructura electrónica de moléculas diatómicas
|
|
|
- Laura Iglesias Acuña
- hace 8 años
- Vistas:
Transcripción
1 Cpítulo 8. Estuctu lctónic d moléculs ditómics Apoximción d Bon-Oppnhim Suponindo qu los núclos y lctons posn mss puntuls y dspcindo ls intccs spin-óit y ots considcs ltivists, l hmiltonino d un sistm d N núclos y n lctons s: Ĥ Tˆ Tˆ V Vˆ Vˆ [8.] N N NN Tˆ N N - h A Tˆ - h M m A A n i i N n n N Z A Z Vˆ N - Vˆ Vˆ NN A i Ai i j> i ij A B> A M. Bon y J.. Oppnhim popus tt spdmnt los movimintos nucls y lctónicos. Y qu los lctons s muvn mucho más ápidos qu los núclos, s pud consid qu los núclos pmncn fijos mints los lctons s muvn nt llos. El pim témino d l cución [8.] s nul y l último tom un vlo constnt. L cución d Schöding s pud scii como: ( Ĥ V l Ψ E Ψ [8.] NN El hmiltonino lctónico ( Ĥ l nglo los téminos, 3 y 4 d l cución [8.]. V NN spcific l pulsión nt núclos qu, como s h dicho ntiomnt, s contnt. L función d ond s pudn dsglos como poducto d funcs: Ψ (, A Ψ l (, A Ψ N ( A [8.3] Ψ l ( i, A s l función d ond lctónic qu dsci l moviminto d los lctons p un dtmind posición d los núclos. Ψ N ( A s l función d ond nucl qu dpnd sólo d ls coodnds nucls y qu s constnt si s supon qu los núclos stán fijos. ( Ĥ Vˆ Ψ Ĥ l NN Ψl ΨN E Ψl N Ψ N Ĥ l Ψl ΨN NN Ψl E Ψl ΨN l Ψ (E - Vˆ Ψ E Ψ [8.4] l NN l l l Vˆ A Z B AB Cpítulo 8. Moléculs Ditómics
![núclos y n lctons s: Ĥ Tˆ Tˆ V Vˆ Vˆ [8.] N N NN Tˆ N N - h A Tˆ - h M m A A n i i N n n N Z A Z Vˆ N - Vˆ Vˆ NN A i Ai i j> i ij A B> A M. Bon y J.](/docs-images/52/14145261/images/page_1.jpg ". Oppnhim popus tt spdmnt los movimintos nucls y lctónicos. Y qu los lctons s muvn mucho más ápidos qu los núclos, s pud consid qu los núclos pmncn fijos mints los lctons s muvn nt llos.")
2 P otn ls cuvs ngí-distnci s supon un configución fij d los núclos y s sulv l cución d Schöding. S pit l pocso ps difnts distncis intnucls. L ngí lctónic s utiliz como ngí potncil dl moviminto d los núclos. E(V st. xcit. Fig. 8.. Cuvs d ngí O. ntinlznt lctónic d los pimos stdos D O. nlznt lctónicos d l molécul d 3 (Å Ecución d Schöding p los nuclos: Ĥ N Ψ E Ψ [4.5] N N E s l ngí totl d l molécul (incluy l ngí lctónic y nucl. Molécul d hidógno L molécul más sncill qu pud xisti s l molécul d hidógno Fig. 8.. Molécul d El hmiltonino s: θ z O - h - - [8.6] m El sistm no tin simtí sféic (no s un sistm d fuzs cntls po lo qu Ĥ y Lˆ no conmutn. Ĥ y z Lˆ conmutn. Tinn conjunto d funcs popis comuns. Cpítulo 8. Moléculs Ditómics
![nlznt lctónicos d l molécul d 3 (Å Ecución d Schöding p los nuclos: Ĥ N Ψ E Ψ [4.5] N N E s l ngí totl d l molécul (incluy l ngí lctónic y nucl.](/docs-images/52/14145261/images/page_2.jpg "Molécul d hidógno L molécul más sncill qu pud xisti s l molécul d hidógno Fig. 8.. Molécul d El hmiltonino s: θ z O - h - - [8.")
3 Cmindo coodnds líptics confocls pudn nconts ls solucións xcts d l cución difncil ψ E ψ Coodnds líptics confocls: ξ η Cd nivl d ngí stá dolmnt dgndo (xcpto p m0 (Ef(m El nom d ls funcs d ond (oitls molculs dpnd dl vlo d m λ l númo cuántico dl qu dpnd L (y no xist l. z λ oitl σ π δ ϕ γ.997 ohs.06 Å D 0.06 ht.79 V 64.4 kcl/mol 3 Métodos poximdos Existn dos métodos poximdos p solv l cución d Schöding d un sistm molcul: Oitls Molculs(OM: S tt l molécul como si fu un átomo. S fijn los núclos y s sulv l cución d Schöding d un fom poximd. Los lctons s colocn n los oitls molculs otnidos (dsloclizdos tod l molécul Enlcs d Vlnci (EV: S pt d los átomos spdos. S vn ccndo y s considn ls intccs qu s fomn. Compción d los métodos: Amos métodos conducn sultdos simils. OM s más iguoso y sncillo, po conduc xpss mtmátics compljs. EV s más intuitivo y pmit simplific los cálculos mdint conocimintos químicos. Cpítulo 8. Moléculs Ditómics 3
4 Amos métodos sulvn l cución d Schöding d fom poximd, mplndo l método vicl. 4 Molécul d hidógno po Oitls Molculs y qu solv l cución d Schöding dl sistm: h - m - - Ψ E Ψ [8.7] L cución s sulv utilizndo l método vicl. L función vicl d pu s otin como cominción linl d oitls tómicos (poximción CLOA 4. Estdo fundmntl 4.. Cálculo d l ngí P l stdo fundmntl l función pud s: ϕ c Ψ s c Ψ s c s c s [8.8] ϕ * Ĥϕ dτ W E ϕ * ϕ dτ Ĥ (c s cc s c Ĥ s c Ĥ s ϕ * Ĥ ϕ c s Ĥ s c c s Ĥ s c c s Ĥ s c s Ĥ s * s Ĥs dτ Intgl d Coulom * s Ĥs dτ Intgl d nlc o sonnci ϕ * ϕ dτ c s s dτ c c s s dτ c s s s s dτs s dτ s s dτs (Intgl d Solpminto c c c c [8.9] c c c S c W dτ W y qu minimiz W con spcto c y c : 0 c Cpítulo 8. Moléculs Ditómics 4 W y 0 c
5 W c (c c (c c c S (c c c (c c S c c S (c c c c 0 W c (c c (c c (c c S c c S W 0 Ecucs sculs: c ( W c ( WS 0 c ( WS c ( W 0 W WS Dtminnt scul: 0 WS W [8.0] [8.] ( W ± ( WS W ( WS ( W S W [8.] S y qu clcul los vlos d y h s s dτ m h s - - s m dτ E 0 (E o. s dl átomo d hidógno s - s dτ K (ngí d tcción pomdio dl núclo y l lctón, dscito po s s s dτ (pulsión nt núclos E0 K [8.3] h s s dτ m h s - - s m dτ E 0 S Cpítulo 8. Moléculs Ditómics 5
![] S y qu clcul los vlos d y h s - - - s dτ m h s - - s m dτ E 0 (E o.](/docs-images/52/14145261/images/page_5.jpg "s dl átomo d hidógno s - s dτ K (ngí d tcción pomdio dl núclo y l lctón, dscito po s s s dτ (pulsión nt núclos")
6 s - s dτ J (intgl d cnj (J<0, dpnd dl solpminto nt los dos O.A. J no tin intptción clásic, sug dl hcho d qu l lctón pud st dscito po s o po s s s dτ S (E0 S J [8.4] Al sustitui [8.3] y [8.4] n W y W W W K J E0 W OM nlznt S K J E0 W OM ntinlznt S [8.5] 3 Fig Nivls ngéticos d W y W - (pulsión E 0 W W - nt núclos K J <0 S K J 3 <0 S Z Z S Z 3 Cpítulo 8. Moléculs Ditómics 6
![[8.4] Al sustitui [8.3] y [8.4] n W y W W W K J E0 W OM nlznt S K J E0 W OM ntinlznt S [8.](/docs-images/52/14145261/images/page_6.jpg "5] 3 Fig. 8.3. Nivls ngéticos d W y W - (pulsión E 0 W W - nt núclos K J <0 S K J 3 <0 S Z Z S")
7 Figu 8.4. psntción d l intgl d solpminto p dos oitls s hidognoids S tin un vlo pquño ± S J K Z ( Z / 0 J K 0,74 ( 0 /-0,7 0,4 ( 0 /-0,07 4 0,09 ( 0 /-4, ,074 ( 0 /-7,.0-6 Fig Cuv d ngí potncil-distnci d l molécul K, W K J E0 W S W E 0 J W E 0 J Cpítulo 8. Moléculs Ditómics 7
8 4.. Oitls Molculs Al sustitui W y W - n ls cucs sculs s pudn clcul los coficints d l cominción linl d cd OM. P l OM nlznt, s otin: c c S 0 S S c S c S S S S c ( S c ( S c ( S c ( S 0 c c ϕ c (s s [8.6] L constnt c s clcul nomlizndo l OM. ( s dτ s s dτ s dτ c ( S c (s s dτ c c ( S P l OM ntinlznt s otndí po un pocso nálogo: c - c ϕ- c (s - s [8.7] S 0 c ( S ϕ s s s -s ϕ - ( ϕ ( ϕ - Fig Oitls nlznt y ntinlznt d l molécul d Cpítulo 8. Moléculs Ditómics 8
![6] L constnt c s clcul nomlizndo l OM.](/docs-images/52/14145261/images/page_8.jpg "( s dτ s s dτ s dτ c ( S c (s s dτ c c ( S P l OM ntinlznt s otndí po un pocso nálogo: c - c ϕ- c (s - s [8.")
9 Nom: λ 0 σ ϕ(gd, simético con spcto l invsión σ g s ϕ-(ungd, ntisimético con spcto l invsión σ u s 4..3 sultdos y finmintos sultdos Si s sustituyn n ls cucs ntios ls funcs s s Z π 3 / Z / (Z s Z π 3 / Z / (Z S otin:.45 ohs D.78 V (.00 vlo xpimntl (.79 vlo xpimntl finminto. Cg fctiv (ζ El lctón s ncunt somtido un cg nucl supio Z. s ζ π 3 / ζ / s ζ π 3 / ζ / L cg fctiv s un pámto vicl y s clcul: E 0 ζ Los sultdos otnidos son:.0 ohs D.35 V ζ.4 c º finminto. Polizción d los OA L psnci ccn dl núclo poliz los oitls dl átomo, y vicvs. Los OA sán: ϕ s λ(p z ϕ s λ(p z L función vicl d pu sá: ϕ c ϕ c ϕ s 3 / 5 / ζ s ζs / ζ p ζ p / (p z cosθ π 4 π Los sultdos son: Cpítulo 8. Moléculs Ditómics 9.0 ohs D.73 V ζ s.46
10 ζ p.965 λ 0.38 P mjo los sultdos hí qu mpl funcs vicls más compljs. 4. Estdos xcitdos Cundo l disocis l molécul otnmos (s, s tom p l función d ond d pu vicl: ϕ c s c s El ttminto s nálogo l stdo fundmntl. W ; c c ϕ c (s s OM nlznt [8.8] c (dond S ( S s s dπ W - ; c - c ϕ- c (s - s OM ntinlznt [8.9] c ( S y son como n [8.3] y [8.4]. E 0 s ho l ngí dl OA hidognoid s. En los nuvos oitls: m 0 ; λ 0 σ ϕ (gd σ g s ϕ- (ungd σ u * s En los siguints stdos xcitdos sólo s cominn los qu tngn igul simtí. (p 0 con (p 0, (p x con (p x y (p y con (p y. - - σ u * p z - - (p z (p z Fig Intcción d oitls p z - - σ g p Cpítulo 8. Moléculs Ditómics 0
![W ; c c ϕ c (s s OM nlznt [8.8] c (dond S ( S s s dπ W - ; c - c ϕ- c (s - s OM ntinlznt [8.9] c ( S y son como n [8.3] y [8.4].](/docs-images/52/14145261/images/page_10.jpg "E 0 s ho l ngí dl OA hidognoid s.")
11 En stos oitls: m 0; λ 0 σ ϕ (gd σ g p ϕ- (ungd σ u * p - π * g p - z - - (p x (p x Fig Intcción - d oitls p x π u p x En stos oitls: m ; λ π ϕ (ungd π u p x ϕ- (gd π g * p x Los OM π u p y y π g * p y otnidos po cominción linl d los p y son nálogos los ntios po gidos 90. L cominción linl d OA tipo d, d OM tipo δ. Los OM tipo σ, π y δ tinn spctivmnt 0, y plnos nodls qu continn l j intnucl. L ngí d los OM p s: σ g s<σ u * s<σ g s<σ u * s<π u p x π u p y <σ g p<π g * p x π g * p y <σ u * p Cpítulo 8. Moléculs Ditómics
12 5 Molécul d hidógno po Oitls Molculs Fig Molécul d hidógno El miltonino molcul s: h Ĥ m h m [8.0] L función σ g s(σ g s( s un función vicl cptl. Al s un sistm con dos lctons l función d ond h d s ntisimétic, tin qu s un dtminnt d Slt. L función d ond OM poximd p l stdo fundmntl d l molécul d hidógno s: σ gs( α( σ gs( β( Ψ σ gs σ gs [8.] σ gs( α( σ gs( β( Ecución simil l [5.8] p l átomo d. Los sultdos otnidos son: 0.73 A (0.74 xp D 3.49 V (4.75 xp 6 Oitls Molculs d moléculs ditómics homonucls P ots moléculs ditómics homonucls s sigu l mismo citio qu l fom los átomos, s vn llnndo los OM po odn d ngí, tnindo n cunt qu cd OM pud ptis dos vcs, un p l función d spín α y ot β. En muchos csos l odn ngético d los OM s l mismo qu l otnido n l molécul d hidógno. Ejmplo 8.. Dtmin l configución lctónic dl N y clcul l digm d OM Solución: L molécul d N tin 4 lctons: Cpítulo 8. Moléculs Ditómics
![] σ gs( α( σ gs( β( Ecución simil l [5.8] p l átomo d. Los sultdos otnidos son: 0.73 A (0.74 xp D 3.49 V (4.](/docs-images/52/14145261/images/page_12.jpg "75 xp 6 Oitls Molculs d moléculs ditómics homonucls P ots moléculs ditómics homonucls s sigu l mismo citio qu l fom los átomos, s vn llnndo los OM po odn d ngí, tnindo n cunt qu cd OM pud ptis dos")
13 (σ g s (σ u * s (σ g s (σ u * s (π u p 4 (σ g p p x p y p z p x p y p z Fig Digm d los oitls molculs d l molécul d nitógno. N s s s s N P l O y l F hy un modificción n l ngí d los OM. Su configución s: O : KK (σ g s (σ u * s (σ g p (π u p 4 (π g * p F : KK (σ g s (σ u * s (σ g p (π u p 4 (π g * p 4 Odn d nlc n lct. nlznts - n lct. ntinlznts [8.] Tl 8.. Configución lctónic d moléculs ditómics. Moléc. Configución O.Enl. D (V (Å Témino (σ g s /.8.06 (σ g s (σ g s (σ * u s / 3.08 (σ g s (σ * u s 0 Li KK(σ g s..67 B KK(σ g s (σ * u s 0 B KK(σ g s (σ * u s (π u p C KK(σ g s (σ * u s (π u p N KK(σ g s (σ * u s (π u p 4 (σ g p 5/ 8.9. N KK(σ g s (σ * u s (π u p 4 (σ g p O KK(σ g s (σ * u s (σ g p (π u p 4 (π * g p 5/ 6.8. Cpítulo 8. Moléculs Ditómics 3 Σ g Σ g Σ u Σ g Σ g Σ g Σ g Σ g Π g?
14 O KK(σ g s (σ * u s (σ g p (π u p 4 (π * g p F KK(σ g s (σ * u s (σ g p (π u p 4 (π * g p Σ g Σ g 7 OM d moléculs ditómics htonucls Al constui los OM como CLOA l poximción más sncill s utiliz solo los OA qu tngn ngís simils y simtí dcud. Tl 8.. Nomncltu d téminos ngéticos Mol. homonucls ton. At. spdos Po simtí σ g s σ g σ σ * g s σ u σ σ g s σ g 3σ σ * g s σ u 4σ π u p π u π σ g 3s 3σ g 5σ π * g p π g π σ * u p 3σ u 6σ Ejmplo 8.. Clcul l configución lctónic d l molécul d CO. Solución: y un gn similitud con l molécul d N (son isolctónics. L cominción d OA s nálog. L molécul no tin cnto d simtí. L molécul psnt 4 lctons, su configución lctónic s: (σ (σ (3σ (4σ (π 4 (5σ Odn d nlc 3 Los nlcs stán polizdos: l contiución d los OA d mos átomos no s l mism. σ c C s C c O s O (c C c O ; CC OO Cpítulo 8. Moléculs Ditómics 4
15 6σ Fig. 8.. π 5σ π Digm d los oitls molculs d l molécul d CO. 4σ 3σ π σ C σ O C - O Ejmplo 8.3. Clcul l configución lctónic d l molécul d F Solución: Los OA s y s dl F tinn mno ngí qu l s dl. El OA p z dl F tin ngí simil l s dl. Los dos tinn m 0. S fom l cominción linl d oitls p z dl F ys dl. L minimizción d l intgl vicl dá dos conjuntos d vlos d los coficints qu poducn los OM nlznts y ntinlznts: 3σ c s c p z 4σ c 3 s c 4 p z Cpítulo 8. Moléculs Ditómics 5
16 4σ s p z p y p x 3σ σ s Fig. 8.. Digm d los oitls molculs d l molécul d F. F σ s F 8 Símolo d los stdos Cd conjunto d OM dgndos fom un sucp molcul. Sucp σ const d OM, dsci lctons Sucp π const d OM, dsci 4 lctons Sucp δ const d OM, dsci 4 lctons Sucp ϕ const d OM, dsci 4 lctons Dd un configución lctónic molcul, son posils difnts stdos d ngí dpndindo dl coplminto d spins y momntos nguls oitls. (coplminto simil l LS Ĥ conmut con Lˆ z y Ŝ z. M s l sum d los m individuls. Λ M Λ 0 3 Nom Σ Π Φ Multiplicidd: S S Témino: Λ M L m l m l σ m l 0; π m l ; M S m s m s S0, M S 0; S/, M S /; S, M S,0 (sg m l 0 m l 0 M L 0 MS/-/0 S0 Σ Cpítulo 8. Moléculs Ditómics 6
17 (σ g (σ u m l 0 m s / m l 0 m s - ½ m l3 0m s3 ½ M L 0, M S ½ (S/ Σ B (σ g (σ u (σ g (σ u (π u (π u. M L 0 M S. M L 0 M S -. M L 0 M S 0. M L 0 M S 0. M L M S 0 M L - M S 0 3 Σ Σ 9 Funcs d ond d SCF, d t-fock El método d t-fock s pud plic moléculs p dtmin su ngí y función d ond, d un mn simil qu átomos polilctónicos. Los oitls d F s dtminn mdint l solución d ls cucs d t-fock: Fˆ ε [8.3] i i i Fˆ s l opdo d t-fock o d Fock. oothn dmostó qu los OM d F pud xpss como cominción d un conjunto complto d funcs llmds funcs d s. Un s complt podí s l fomd po todos los OA d los átomos qu intvinn, ocupdos y no ocupdos. P vi s pud tom un s mínim, fomdo po los OA ocupdos. Los OA qu contiuyn un OM ddo dpnd d ls popidds d simtí dl OM. i s c χ ( [8.4] si s Cpítulo 8. Moléculs Ditómics 7
![Los oitls d F s dtminn mdint l solución d ls cucs d t-fock: Fˆ ε [8.3] i i i Fˆ s l opdo d t-fock o d Fock.](/docs-images/52/14145261/images/page_17.jpg "oothn dmostó qu los OM d F pud xpss como cominción d un conjunto complto d funcs llmds funcs d s. Un s complt podí s l fomd po todos los OA d los átomos qu intvinn, ocupdos y no ocupdos.")
18 En toí χ s d s un conjunto infinito d funcs. En l páctic s mpl un númo finito d funcs convnintmnt lgids. L cución [4.3] s tnsfom n: Fˆ Σ c si χ s Σ c si Fˆ χ s ε i Σ c si χ s [8.5] Multiplicndo po χ intgndo: s c si ( F s ε i S s 0 (,, 3, [8.6] F s < χ Fˆ χ s > S s < χ χ s > [8.7] L cución d oothn [4.6] indic qu s tinn un conjunto d cucs homogéns. P qu xist un solución distint d co, l dtminnt d oothn d los coficints d s co dt ( F s - ε i S s F s - ε i S s 0 [8.8] Dspués d c todo l pocso ittivo s otinn unos OM qu son un poximción los d F, y qu s h utilizdo un s mínim. El poducto ntisimtizdo d stos OM d l función d ond d cmpo utoconsistnt (SCF. Ejmplo 8.4: Cálculos n s mínim d l molécul d F Solución: Bs mínim p F : Fs, Fs, Fp z Fp x, Fp y y s. L molécul tin diz lctons. Po s zón l función d ond dl stdo fundmntl d l molécul d F s un dtminnt d Slt d 0x0. ( α( ( α( (3 α(3 (4 α(4 (5 α(5 Ψ N (6 α(6 (7 α(7 (8 α(8 (9 α(9 (0 α(0 ( β( ( β( (3 β(3 (4 β(4 (5 β(5 (6 β(6 (7 β(7 (8 β(8 (9 β(9 (0 β(0 ( α( ( β( En notción vid: Ψ ( α( 5 (0 α(0 5 ( β( 5 (0 β(0 5 Cd oitl i s otin como cominción linl d oitls tómicos (poximción CLOA c (s otinn 6 OM s c s c 3 p c 4 p c 5 p c 6 x y z s Cpítulo 8. Moléculs Ditómics 8
19 .000 s F (OA s 0.94 s 0.00 px 0.00 py 0.09 π z 0.5 s (E V (σ s 0.00 px 0.00 py 0.7 pz 0.5 s (E V (σ s.00 px 0.00 py pz 0.00 s (E V (OA s 0.00 px.00 py pz 0.00 s (E V (OA 6 6 (E V (oitl vitul (σ* (OM otnidos mdint l método PM3 A l mzcl d dos o más OA n un mismo átomo s llm hiidción. Estos oitls dsloclizdos tod l molécul son los dnomindos oitls cnónicos, qu son ls solucs d l cución d t-fock [8.3]. Dsd l punto d vist químico pud ints otn unos OM qu pmitn visuliz l fomción d nlcs. En l dtminnt d Slt s pudn sum o st colunms sin qu su vlo s v modificdo. Si s hc s modificción s pudn otn los oitls loclizdos. En l molécul d F los oitls ntuls son:.000 s (OA s pz s (E -.6 V (OM s pz (E V (OA híido. Cpítulo 8. Moléculs Ditómics 9
![Estos oitls dsloclizdos tod l molécul son los dnomindos oitls cnónicos, qu son ls solucs d l cución d t-fock [8.3]. Dsd l punto d vist químico pud ints otn unos OM qu pmitn visuliz l fomción d nlcs.](/docs-images/52/14145261/images/page_19.jpg "En l dtminnt d Slt s pudn sum o st colunms sin qu su vlo s v modificdo. Si s hc s modificción s pudn otn los oitls loclizdos. En l molécul d F los oitls ntuls son:.000 s (OA. 0.50 s 0.575 pz 0.")
20 4-0.5 py px (E V (OA híido py px (E V (OA híido Estos oitls loclizdos coincidn con los oitls clásicos fomdos po: OM nlznts loclizdos nt dos átomos OA d cp intn OA d ps d lctons solitios Ejmplo 8.5: Cálculos n s mínim d l molécul d CO. Solución: Bs mínim p CO : Os, Os, Op z Op x, Op y, Cs, Cs, Cp z Cp x, Cp y. L molécul tin 4 lctons. Po s zón l función d ond dl stdo fundmntl d l molécul d F s un dtminnt d Slt d 4x4. En notción vid: Ψ Los oitls cnónicos ocupdos son:.000 sc (OA..000 so (OA sc pxc 0.89 so pxo (E V (OM sc pxc so pxo (E V (OM pyc 0.56 pzc pyo pzo (E V (OM pyc pzc pyo pzo (E V (OM sc pxc 0.04 so 0.48 pxo (E V (OM Ejmplo 8.6: Cálculos n s mínim d l molécul d N. Solución: L molécul tin 4 lctons. Po s zón l función d ond dl stdo fundmntl d l molécul d N s un dtminnt d Slt d 4x4. Los OM cnónicos ocupdos son:.000 sn (OA.000 sn (OA sn pxn sn pxn (E V sn pxn sn pxn (E V pyn pzn 0.7 pyn pzn (E V pyn pzn pyn pzn (E V sn pxn sn pxn (E V Los OM loclizdos son:.000 sn (OA.000 sn (OA sn 0.64 pxn sn 0.64 pxn (E V (OM σ sn 0.47 pxn (E V (OA híido n N sn 0.47 pxn (E V (OA híido n N pyn pzn 0.7 pyn pzn (E V (OM π pyn pzn pyn pzn (E V (OM π Cpítulo 8. Moléculs Ditómics 0
21 0 Molécul d hidógno po Enlcs d Vlnci (EV Cundo los átomos stán spdos: f s (.s ( ó f s (.s ( Función d pu vicl: ϕ c f c f [8.9] Al minimiz l intgl vicl spcto ls constnts s otin un sistm d cucs sculs y un dtminnt scul. L función spcil qu dsci l nlc nt los dos s: ϕ c [s (s (s (s (] [8.30] c S ff dτ ( S Y qu l sistm tin dos lctons, l función d ond totl d s ntisimétic. Es l dnomind función d nlc d itl-london: ϕ c [s (s (s (s (][α(β(-α(β(] [8.3] sultdos: 0.80 Å D 3.0 V L función d itl-london pud psnts como: ϕ L ϕ cov s s ( α( ( α( S s ( β( ( β( s s ( β( ( β( s s ( α( ( α( { s s ss } Tmién s pudn tn n cunt spcis iónics. Ls funcs d ond iónics - son: ϕ s s ( α( ( α( s s ( β( ( β( s s ϕ s s ( α( ( α( s s ( β( ( β( s s L función totl s: ϕ c ϕ c ϕ c ϕ N( ϕ λϕ [8.3] v cov c > c c 3 ( λ cov Cpítulo 8. Moléculs Ditómics
22 Compción d ls dos toís El dsollo d l pt spcil d [8.] conduc, xcptundo l constnt d nomlizción : OM s (s (s (s (s (s (s (s ( l pt spcil d [8.3] s: ϕ L c [s (s (s (s (] y dos téminos d difnci s (s ( s (s ( s (s ( s (s ( P mjo l función d EV hy qu intoduci ls foms iónics: EV s (s (s (s (λ[s (s (s (s (] [8.33] EV s l función d sonnci iónico-covlnt. sultdos: λ 0.5 D 4.0 V. P mjo l función d OM hy liz cálculos post-f. Un posiilidd s liz intcción d configucs. L configución fundmntl p l s (σ g s. Ot sí (σ u * s [s (-s (][s (-s (] OM [s (s (][s (s (]γ[s (-s (][s (-s (] [8.34] Ls cucs [8.33] y [8.34] coincidn si γ λ γ Cpítulo 8. Moléculs Ditómics
23 Método d EV n ots moléculs En tods ls moléculs hy qu consid l función d ond covlnt y l función iónic. P l molécul d F: L función d itl London o covlnt s: ϕ L ϕ cov s s ( α( ( α( p p ( β( ( β( s s ( β( ( β( p p ( α( ( α( { s p s p } L función d ond iónic F - s: ϕ p p ( α( ( α( p p ( β( ( β( p p L función d ond iónic F - s: ϕ s s ( α( ( α( s s ( β( ( β( s s L función totl sá: ϕ v c ϕ cov c ϕ c ϕ 3 ϕ c ϕ c ϕ c ϕ N( ϕ λϕ (c >>>c 3 v cov 3 L constnt λ s un mdid d l polidd dl nlc. cov Cpítulo 8. Moléculs Ditómics 3
p m son términos semejantes
Páin dl Colio d Mtmátics d l ENP-UNAM Ocions con monomios olinomios Auto: D. José Mnul Bc Esinos OPERACIONES CON MONOMIOS Y POLINOMIOS UNIDAD IV IV. OPERACIONES CON MONOMIOS Un vil s un lmnto d un ómul,
Para que exista límite de una f(x) en un punto han de coincidir los límites laterales en dicho punto.
REPASO LÍMITES º BACH. RECORDAR: Para qu ista límit d una f() n un punto han d coincidir los límits latrals n dicho punto. A fctos dl f() no tnmos n cunta lo qu ocurr actamnt n a, sino n las a proimidads.
26 EJERCICIOS de LOGARITMOS
6 EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
Tema 2: Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla. Parte 6/7 Energía electrostática
Tm : Pincipios d l lctostátic, Antonio Gon nzálz Fná ándz Antonio Gonzálz Fnándz Dptmnto d Físic Aplicd III nivsidd d Svill Pt 6/7 Engí lctostátic Engí, tbjo y clo: l pim pincipio i i d l tmodinámic i
IES CASTELAR BADAJOZ Examen Junio de 2011(General) Solución Antonio Mengiano Corbacho UNIVERSIDAD DE EXTREMADURA MATEMÁTICAS II
IES CASTELAR BADAJOZ Emn Junio d (Gnrl) Antonio ngino Corbcho UNIVERSIDAD DE ETREADURA ATEÁTICAS II ATEÁTICAS II Timpo máimo: hor minutos Instruccions: El lumno lgirá un d ls dos opcions propusts Cd un
Ecuaciones de Poisson y Laplace
Elctc y Mgntsmo / Elctostátc Dfncón Los conuctos n lctostátc. mpo un cg puntul. plccons l Ly Guss Intgls supposcón. Potncl lctostátco Dfncón Intptcón. Intgls supposcón. Ecucons Posson y Lplc. oncons Intfs.oncons
la integral de línea de B alrededor de un trayecto cerrado
LEY DE AMPERE L ley de Guss de los cmpos elécticos implic el flujo de E tvés de un supeficie ced; estlece que este flujo es igul l cociente de l cg totl enced dento de l supeficie ente l constnte ε. En
4πε. q r 2. q r C 2 2
. ) A un distnci d. cm dl cnto d un sf conducto con cg cuyo dio s d. cm, l cmpo léctico s d 48 N/. uál s l cmpo léctico.6 cm dl cnto d l sf? ) A un distnci d. cm dl j d un cilindo conducto muy lgo con
TRANSFORMADORES EN PARALELO
TRNFORMDORE EN PRLELO. Trnsformdors d igul rzón d trnsformción Not: no s tomn n cunt ls pérdids n l firro. q q q llmrmos s cumpl b. Trnsformdors d rzón d trnsformción un poco distints Rfridos l scundrio:
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL
Cpít ulo RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL Dfiniions Pvis: I. ÁNGULO EN POSICIÓN NORMAL Llmo tmién n posiión nóni o stán. Es quél ángulo tigonométio uo véti oini on l oign l sistm
TRANSFORMACIONES GEOMÉTRICAS Proyectividad y homografía Homología y afinidad Inversión TEMA4. Objetivos y orientaciones metodológicas. 1.
TRNSRMINES GEMÉTRIS Poyctivi y homogfí Homologí y fini Invsión TEM4 IUJ GEMÉTRI bjtivos y ointcions mtoológics Est Tm tin como objtivos intouci l lumno n los conocimintos poyctivi, homogfí, homologí, fini
Por tanto,p(r) es la probabilidad de encontrar al electrón en esta envolvente.
LAS FUNCIONES DE ONDA PARA EL HIDROGENO qq Ddo qu : U k dpnd solnt d l distnci dil nt l núclo y l lctón, lgunos d los stdos pitidos p st átoo pudn s psntdos dint funcions d ond qu solo dpndn d L s sipl
Problema A.1. Obtener razonadamente, escribiendo todos los pasos del razonamiento utilizado: S, (2 puntos) y la matriz S -1, que es la
José Aulio Pin Romo JULIO MII www.pin.s EXAMEN DE ELECTIVIDAD JULIO. MATEMÁTICA II OPCIÓN A Poblm A.. Obtn ondmnt scibindo todos los psos dl onminto utilido: ) El vlo dl dtminnt d l mti ( puntos) l mti
Solución Tarea de Aproximaciones y errores de redondeo
Métodos numéicos y álgb linl CB0085 Apoximcions y os d dondo T d Apoximcions y os d dondo. Clcul l o bsoluto y l o ltivo si p y p 2.78 dond p s l vlo clculdo. : vlo l vlo clculdo 2.78 o bsoluto : vlo clculdo
47. Contesta a les qüestions següents referents a l àtom d hidrogen.
.6 Àtom d hidogn 7. Contst ls qüstions sgünts fnts l àtom d hidogn. n l ón l nom dls obitls cosponnts ls obitls qu s spcifiqun tvés dls nombs quàntics d l tul. b Assign cdscun d lls ls sus nombs quàntics
3. Explica en qué consisten la miopía y la hipermetropía. Qué lentes se usan para su corrección?
CANARIAS / JUNIO 0. LOGS / ÍSICA / XAMN COMPLTO D las dos opcions popustas, sólo hay qu dsaolla una opción complta. Cada poblma cocto val po ts puntos. Cada custión cocta val po un punto. OPCIÓN A Poblmas.
5. Convergencia de integrales impropias. Las funciones Γ y Β de Euler.
GRADO DE INGENIERÍA AEROESPACIAL. CURSO. Lcción. Intgals y aplicacions. 5. Convgncia d intgals impopias. Las funcions Γ y Β d Eul. La foma haitual d calcula una intgal impopia, po jmplo dl intgando, aplica
Solución de la ecuación de Schödinger para una partícula libre.
Solución d l cución d Schöding un tícul lib. Vmos nliz l volución tmol d l función d ond d un tícul lib con un jmlo concto. Ptimos d l siguint condición inicil: (; ) ik dond y k son dos constnts ls. Lo
Tomando como nivel de energía cero el nivel fundamental. Dada la diferencia de energía entre los niveles en la mayoría de los casos
Capíulo. La fucó d pacó ) Spaacó d la fucó d pacó S ha dmosado aom - / k [.] La ía dl l s ual a: k [.] + + + [.] + S los ados d lbad o accoa [.4] - / k - / k... [.5] ) Fucó d pacó lcóca omado como l d
Facultad de Ingeniería Física 1 Curso 5
Facultad d Ingniía Física Cuso 5 Índic Funt n moviminto con spcto al ai 3 Rsumn5 Ejcicio 5 Ejcicio 28 El obsvado stá n moviminto spcto a la unt n poso8 Rsumn Funt y obsvado n moviminto Ejcicio 3 Númo d
F U T S W W P V F W P V G U T S P V G F P V W P V P V W. nfec. G nfe C. Energía libre y fuerza electromotriz.
nrgí libr y furz lctromotriz. Dsd un punto d vist trmodinámico, sbmos qu tmprtur constnt, l disminución d l nrgí libr d Hlmholtz, F (pr un procso rvrsibl), rprsnt l trbjo totl (W) hcho sobr los lrddors,
Una variable es un elemento de una fórmula, proposición o algoritmo que puede adquirir o ser sustituido por un valor cualquiera.
Fcultd d Contduí Administción. UNAM Polinomios Auto: D. José Mnul Bc Esinos MATEMÁTICAS BÁSICAS POLINOMIOS OPERACIONES CON MONOMIOS Un vil s un lmnto d un ómul, oosición o loitmo u ud duii o s sustituido
Tema 4: Integrales Impropias
Prof. Susn López 1 Universidd Autónom de Mdrid Tem 4: Integrles Impropis 1 Integrl Impropi En l definición de un integrl definid f (x) se exigió que el intervlo [, b] fuese finito. Por otro ldo el teorem
IES Mediterráneo de Málaga Solución Septiembre 2013 Juan Carlos Alonso Gianonatti OPCIÓN A. se pide
IES Mditáno d Málg Solución Sptimb Jun los lonso Ginontti Ejcicio.- liicción máim puntos Dd l unción: 7 s pid ( 7 puntos Hll ls síntots d dich gic OPIÓN b ( 7 puntos Dtmin los intlos d cciminto dcciminto
Tema 2. Amplificadores Operacionales
Tma. mplificador Opracional Joaquín aquro Lópz Elctrónica, 007 Joaquín aquro Lópz mplificador Opracional (O): Índic.) Introducción a lo O.) Modlo implificado. Modlo Idal.3) Circuito Linal con O.4.) mplificador
Determinización: Construcción de Safra
Determinizción: Construcción de Sfr Ddo: Autómt de Büchi A = (Q,Σ,Q 0,δ,F) Supong que Q = {q 1,...,q n }. Vmos construir un utómt de Rin determinist B tl que L ω (A) = L ω (B), donde B está compuesto por:
r,, R r exp exp 1 cos cos 1
Como obtn función on y su ngí tvés cución Schöing. Rcomos qu función on s un cución mtmátic, qu cump citos quisitos, n cu s ncunt to infomción sistm, n st cso s tt infomción cion con ctón o núco. st función
D E C 9 & $ 9 B E F 10 $ 8
CADA LETRA CORRESPONDE A UN NÚMERO DEL 1 AL 5 AVERIGUA A QUE NÚMERO CORRESPONDE CADA UNA. D E C 9 & $ 9 B E F 10 & @ $ 8 B E F 10 $ $ # 14 5 12 12 29 7 10 14 31 Φ Π Δ 12 P E E 5 Χ Φ Φ 12 P P W 8 Χ Δ Φ
AUTOMATAS FINITOS Traductores
Universidd de Morón Lengujes Formles y Autómts AUTOMATAS FINITOS Trductores AUTOMATAS FINITOS Un utómt finito es un modelo mtemático que posee entrds y slids. Un utomát finito recie los elementos tester
FUNDAMENTOS MATEMÁTICOS (Grado en Ingeniería Informática) Práctica 7. INTEGRALES DEFINIDAS E IMPROPIAS
FUNDAMENTOS MATEMÁTICOS (Grdo n Ingnirí Informátic) Práctic 7. INTEGRALES DEFINIDAS E IMPROPIAS.- L intgrl dfinid d Rimnn. L intgrl dfinid d Rimnn surg prtir dl prolm dl cálculo d árs d suprficis dlimitds
Problemas Resueltos. el radio de la órbita circular, y la energía tiene el valor GMm 2 = a GM. 0. Es decir, 2 T 4π. GMm
Problmas sultos.0 Un satélit dscrib una órbita circular n torno a la Tirra. Si s cambia d rpnt la dircción d su vlocidad, pro no su módulo, studiar l cambio n su órbita y n su príodo. Al cambiar sólo la
RESPONSABILIDAD CIVIL
RESPONSABILIDAD CIVIL PRIVADA E MUEBLES XTOS CONTRACTUALES * C Ei * bs * G * C G 1 bs Rpd C Am Do 28 ESPECIFICACIONES Y ALCANCE DE LA CTURA ANIMALES DOMÉICOS I - Oe b Me i Rpd C e p v A, cfd c n v, r l
Repartido N 5. Limites ISCAB 3 EMT prof. Fernando Diaz
Reprtido N 5 Limites ISCAB EMT prof. Fernndo Diz El resultdo de un límite es un vlor de y en un función cundo el vlor de se proim mucho un vlor ddo sin llegr ser igul él. Es cercrse mucho un vlor en pr
Solución de los Problemas del Capítulo 3
1. Slccion l rspust corrct y xpliqu por qué. Un lctrón qu tin un n= y m= ) Db tnr un m s =+1/ b) Pud tnr un l= c) Pud tnr un l=, ó 1 d) Db tnr un l=1 L rspust corrct s l c) porqu si n=, los posibls vlors
3A,,. Prueba que M es un subespacio
.- Dtin os tis us X Y on tls qu: Y X Y X.- Estui l inpnni linl ls tis C.- Pu qu ls siguints tis son un s l spio vtoil ls tis us on.- S onsi l onjunto } R. Pu qu s un suspio vtoil.- Hll os tis us on os
8. Equilibrio químico en. reacciones gaseosas
Tnfomcione químic ndé Cedillo, T-50 cedillo@xnum.um.mx www.fqt.izt.um.mx/cedillo 8. Equiliio químico en eccione geo 8.1. ntecedente 8.. Contnte de equiliio 8.3. Condicione de equiliio 8.4. Cociente de
ÁÒÓÖÑ Ø ØÖº ÐÑÒØÓ ÔÖÓÔÙØÓ º ÊÐ ÑÞ ÅÖÒ Ý ÒÖ ËÖ ÊÑÖÞ ÔÙÐÓ ÔÓÖ Ð ÓÒÓ ØÓÖÐ Ð ÍÒÚÖ ÁÌ ¾¼¼¾º ÆÙ ØÖÓ ØÜØÓ Ø ÓØÓº Ä ÚÖ Ò ÕÙ Ù Ø Ø ÐÝÒÓ ÓÖÖ ÔÓÒ ÙÒ Öѹ ÔÖ Ò ÔÖ Ð Ï Ò Ð ÙÐ ÑÓ ÖÐÞÓ ÐÙÒ ÓÖÖÓÒ ÕÙ ÖÒ ÒÙ ØÖÓ ÓÒÓÑÒØÓº
Metálico: teoría de bandas
CP.: ELCES vn d Wl ( ) (Lnnd Jon) / q Iónico ( ) (Buckingm ) Covlnt ( ) D (Mo) Mtálico: toí d bnd - + - F + Enlc d hidógno Equm d ólido gún l tio d nlc Etuctu hgonl d Etuctu hgonl d hilo (nlc d hidógno)
9. MATRICES 189 9.1. DEFINICIÓN Y NOTACIONES... 189 9.2. OPERACIONES CON MATRICES... 190 9.3. MATRICES CUADRADAS... 192 9.3.1.
ÍNDICE 9. MATRICES 189 9.1. DEFINICIÓN Y NOTACIONES....................... 189 9.2. OPERACIONES CON MATRICES..................... 190 9.3. MATRICES CUADRADAS.......................... 192 9.3.1. Matrices
Estadística EIAE (UPM) Estadística p. 1
Ö Ó ÓÒØ ÒÙÓ ÑÓ ÐÓ p. 1 Ejercicio 1 A una gasolinera llegan, en media, 3 coches por minuto. Calcular la probabilidad de que a) En 1 minuto lleguen dos coches. b) En 1 minuto lleguen al menos dos coches.
PROBLEMAS RESUELTOS DE TRABAJO Y ENERGÍA
POLEMS ESUELOS E JO Y ENEGÍ Equip dct: ti J. Gc Mi Hádz Puc lfs l lmt POLEM U l d ms qu s mu 4 m/s pt iztlmt u lqu d md st u pfudidd d 5 cm. uál s l fuz mdi qu s lizd s l l p dtl?. F N d m S F l fuz mdi
(+) (+) ( ) 5/30/2013 (+) ( ) (+)
5/30/013 : Describe a los electrones en una molécula utilizando funciones de onda llamadas orbitales moleculares (OM). Los OM se forman por combinación lineal entre orbitales atómicos (OA) Estas combinaciones
CAPÍTULO 14: LAS EXPECTATIVAS: LOS INSTRUMENTOS BÁSICOS
CAPÍTULO 14: LAS EXPECTATIVAS: LOS INSTRUMENTOS BÁSICOS 14-1 Los tipos d intrés nominals y rals Slid 14.2 Los tipos d intrés xprsados n unidads d la monda nacional s dnominan tipos d intrés nominals. Los
4πε. r 1. r 2. E rˆ La carga puntual q 1
.3 L cg puntul q -5. nc está en el oigen l cg puntul q 3 nc está sobe el eje de ls en 3 cm. l punto P está en 4 cm. ) Clcule los cmpos elécticos debidos ls dos cgs en P. b) Obteng el cmpo eléctico esultnte
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID JUNIO 2008
UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID JUNIO El mn pnt o opcion, B. El lumno bá lgi UN Y SÓLO UN ll olv lo cuto jcicio qu cont. No pmit l uó clculo con cpci pntción gáfic. PUNTUCIÓN: L clificción
INFORME DE LA PRÁCTICA nº 2: LA RUEDA DE MAXWELL. Fernando Hueso González. Carlos Huertas Barra. (1º Fís.), L1, 21-XI-07 - 0 -
INFORME DE LA PRÁCTICA nº : LA RUEDA DE MAXWELL Fernndo Hueso González. Crlos Huerts Brr. (1º Fís.), L1, 1-XI-7 - - RESUMEN L práctic de l rued de Mxwell consiste en medir el tiempo que trd en descender
Integrales impropias
Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
CAPÍTULO 1. PROPAGACIÓN DE LAS ONDAS PLANAS UNIFORMES
CAPÍTULO 1. PROPAGACIÓN DE LAS ONDAS PLANAS UNIFORMES 1.1 Ecuación de onda. Las ecuaciones de Maxwell se publicaron en 1864, su principal función es predecir la propagación de la energía en formas de Onda.
Dpto. INGENIERÍA ENERGÉTICA Y FLUIDOMECÁNICA ESCUELA DE INGENIERÍAS INDUSTRIALES UNIVERSIDAD DE VALLADOLID
AIRE HÚMEDO Y PROCESOS PSICROMÉRICOS Introduccón. Crcterístcs del re úedo. Dgrs pscroétrcos. Análss de los procesos pscroétrcos báscos del re úedo ASIGNAURA: ERMODINÁMICA ÉCNICA RANSMISIÓN DE CALOR GRADO:
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE NAVARRA JUNIO 2012 (GENERAL) (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
IES CSTELR DJOZ nguino PRUE DE CCESO (LOGSE) UNIVERSIDD DE NVRR JUNIO (GENERL) (RESUELTOS por nonio nguino) TEÁTICS II Timpo máimo: hors minuos Rlir un d ls dos opcions propuss ( o ) OPCIÓN º) Esudi l
Validación del programa FERCIN para la calibración de las barras de control del reactor RP-10
Validación del programa FERCIN para la calibración de las barras de control del reactor RP-10 José Castro (1) jcastro@ipen.gob.pe; Magaly Zapata (2) magalibalcazar@yahoo.com; Rubén Bruna (3) rbruna@ipen.gob.pe
Matemáticas II CURVAS
CURVAS En este tema introduciremos nuevos conceptos relacionados con la curva y sus parametrizaciones. Definiciones.- Sea γ : I = [a,b] R n. Se dice que la curva es cerrada si γ(a) = γ(b). Se dice que
Si las cargas se atraen o repelen significa que hay una fuerza entre ellas. LEY DE COULOMB
Cuso: FISICA II CB 3U Ley de Coulomb (1736-186). Si ls cgs se ten o epelen signific que hy un fuez ente ells. LEY DE COULOMB L fuez ejecid po un cg puntul sobe ot Está diigid lo lgo de l líne que los une.
Practico 7 Fuerza y Leyes de Newton
008 Pctico 7 uez y Leyes de Newton ) Un bloque de 5.5 Kg. está inicilmente en eposo sobe un supeficie hoizontl sin ficción. Es empujdo con un fuez hoizontl constnte de 3.8 N. ) Cuál es su celeción? b)
XIV.- ALIMENTACIÓN AL RODETE CÁMARA ESPIRAL
XIV.- ALIMENTACIÓN AL OETE CÁMAA ESPIAL XIV..- IMENSIONAMIENTO PAA TUBINAS FANCIS (ELECTOCONSULT) c [m/s] 0,44 5,4 nq Figura 4.. Vlocia ntraa n la spiral n función la vlocia spcífica n s. Figura 4.. Esquma
Integrales impropias.
IX / 8 UNIVERSIDAD SIMON BOLIVAR MA nro-mrzo d 4 Dprtmnto d Mtmátics Purs y Aplicds. Intgrls impropis. Ejrcicios sugridos pr : los tms d ls clss dl 4 y 9 d mrzo d 4. Tms : Otrs forms indtrminds. Intgrls
1. INTEGRALES DEFINIDAS E IMPROPIAS
. INTEGRALES DEFINIDAS E IMPROPIAS.. INTEGRAL DEFINIDA Se y = f(x) definid pr todo x [, b]. Consideremos un prtiión P del intervlo [, b] P {x 0 = < x < x 2 < < x n = b} Sen P = máx{x i x i }, s n = n m
[ ] ( ) ( ) [ ] [ ] [ ] [ ] ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2. Opción A 4 A. u 4
![[ ] ( ) ( ) [ ] [ ] [ ] [ ] ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2. Opción A 4 A. u 4](/thumbs/88/115624296.jpg "[ ] ( ) ( ) [ ] [ ] [ ] [ ] ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2. Opción A 4 A. u 4")
IES Mditáno d Málg Solución Sptim 7 Jun Clo lono Ginontti Opción..- S qu l gáic d l unción () c l qu pc n l diujo - - - - - - - - ) Dtmin l unción [ punto] ) Clcul l á d l unción omd [ punto] [ ] [ ] [
Electromagnetismo II
Electomgnetismo II Semeste: 215-1 EXAMEN PARCIAL 2: Solución D. A. Reyes-Coondo Poblem 1 (2 pts.) Po: Jesús Cstejón Figueo ) Escibe ls cuto ecuciones de Mxwell en fom difeencil, escibiendo el nombe de
FORMACIÓN PROFESIONAL
FOMCIÓN POFIONL DIÑO CUICUL N UNIDD TÉCNIC CUDO 1228 D GOTO D 1985 INTUCCIÓN 0329 D 1986 DOGÓ L INTUCCIÓN 217 D 1972 Oscar Gaboa Carrillo FOMCION POFIONL: POCO MDINT L CUL L PON: DQUI Y DOLL CONOCIMINTO,
Cálculo con vectores
Unidd didáctic 1 Cálculo con vectoes 1.- Mgnitudes escles vectoiles. Son mgnitudes escles quells, como l ms, l tempetu, l enegí, etc., cuo vlo qued fijdo po un númeo (con su unidd coespondiente). Gáficmente
61.1 6.1. SERIES NUMÉRICAS INFINITAS 6.2. SERIES DE TÉRMINOS POSITIVOS 6.3. SERIES ALTERNANTES 6.4. SERIES DE POTENCIAS
Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Tema 4: Potencial eléctrico
1/38 Tem 4: Potencil Eléctico Fátim Msot Conde Ing. Industil 2007/08 Tem 4: Potencil Eléctico 2/38 Índice: 1. Intoducción 2. Enegí potencil eléctic 1. de dos cgs puntules 2. de un sistem de cgs 3. Intepetción
INTEGRAL DEFINIDA ÁREAS Y VOLUMENES
Intgrl indinid. gl d Brrow INTEGA DEFINIDA ÁEAS Y OUMENES siguint rgl, qu s s n l torm undmntl dl cálculo intgrl, rlcion l intgrl dinid con ls intgrls indinids prmit clculr ls intgrls dinids. intgrl dinid
TEMA 7. SUCESIONES NUMÉRICAS.
º EO Tem 7 TEMA 7. UCEIONE NUMÉRICA.. UCEIONE NUMÉRICA. Imgiemos el ecoido que efectú u bló que se h lzdo l suelo y midmos ls distcis ete bote y bote: Ls distcis fom u sucesió de úmeos: 0, 5, 0, 5,. U
Universidad Central de Venezuela Facultad de Farmacia Matemática - Física Prof. J. R. Morales
Universidd Centrl de Venezuel Fcultd de Frmci Mtemátic - Físic Prof J R Morles Guí de Vectores (Resumen de l Teorí) 1 En físic distinguiremos dos tipos de cntiddes: vectoriles esclres Ls cntiddes vectoriles
2. REPRESENTACIÓN ANALÍTICA Y GRÁFICA DE UN VECTOR
1. INTRODUCCIÓN CÁLCULO VECTORIAL Mgnitud: Es todo quello que se puede medir eperimentlmente. Ls mgnitudes físics se clsificn en esclres ectoriles. Mgnitud esclr: Es quell que iene perfectmente definid
A modo de repaso. Preliminares
UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
CONSIDERACIONES SOBRE LAS COMPUERTAS
Abril de 006 CONSDERACONES SOBRE LAS COMPUERTAS Cátedr de Mecánic de los Fluidos Escuel de ngenierí Mecánic Autores: ngeniero Edgr Blbstro ngeniero Gstón Bourges e-mil: gbourges@fcei.unr.edu.r 1 Abril
7. Integrales Impropias
Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Dierencil e Integrl 08-2 Bsdo en el punte del curso Cálculo (2d semestre), de Roerto Cominetti, Mrtín Mtml y Jorge
APUNTES DE MATEMÁTICAS
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
Reglamento de D i v er s i ones y E s p ec tá c u los P ú b li c os Ayuntamiento Constitucional de Zapotlanejo 2007-2009 e n t e M u n i c i Z a t n e j o, J a o, a h a t a n t e m u n i c i o h a g o
TRANSMISIÓN DE CALOR POR CONDUCCIÓN
ERMODINAMICA ÉCNICA Y RANSMISIÓN DE CAOR RANSMISIÓN DE CAOR POR RANSMISIÓN DE CAOR POR EN ESACIONARIO. Intoducción.. Balanc d ngía n una supfici plana. 3. Balanc d ngía n supficis cilíndicas y sféicas.
1 Introducción... 2. 2 Distribución exponencial... 2. 3 Distribución Weibull... 6. 4 Distribuciones Gamma y k-erlang... 10
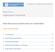Asignatura: Ingeniería Industrial Índice de Contenidos 1 Introducción... 2 2 Distribución exponencial... 2 3 Distribución Weibull... 6 4 Distribuciones Gamma y k-erlang... 10 5 Distribución log-normal...
ASIGNATURA: INGENIERIA DE PROCESOS III (ITCL 234) PROFESOR: Elton F. Morales Blancas
UNIVESIDD USTL DE CILE INSTITUTO DE CIENCI Y TECNOLOGI DE LOS LIMENTOS (ICYTL) / SIGNTU: INGENIEI DE POCESOS III (ITCL 34) POESO: Elton. Moals Blancas UNIDD : TNSEENCI DE CLO PO CONDUCCION (ESTDO ESTCIONIO)
GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1,0, la recta x 1 y z
GEOMETRÍA Junio 94. 1. Sin resolver el sistema, determina si la recta x 3y + 1 = 0 es exterior, secante ó tangente a la circunferencia (x 1) (y ) 1. Razónalo. [1,5 puntos]. Dadas las ecuaciones de los
Máquinas eléctricas de corriente alterna. Capítulo 2 Máquina Asíncrona
Universidad Carlos III de Madrid Dept. Ingenería eléctrica Máquinas eléctricas de corriente alterna Capítulo 2 Máquina Asíncrona David Santos Martín CAPÍTULO 2 Máquina Asíncrona 2.1.- Introducción 2.2.-
Siempre verifica que a 2 = b 2 + c 2 (Th. Pitágoras)
Págin 1 FIGURAS EN EL PLANO POLÍGONOS FIGURAS EN EL PLANO Y EN EL ESPACIO 1.- Polígono de 3 ldos: Tiángulo. B Los ángulos inteioes de culquie tiángulo sumn siempe 180º. El áe de culquie tiángulo se puede
UAM CSIC Grupo 911 Abril 2013. Ejercicios Resueltos de Equaciones Diferenciales Ordinarias. Asignatura de Matemáticas Grado en Química
UAM CSIC Grupo 911 Abril 201 Ejercicios Resueltos de Equaciones Diferenciales Ordinarias Asignatura de Matemáticas Grado en Química Nota: Los ejercicios pueden contener errores, agradecemos que se comuniquen
Funciones de varias variables
Capítulo 2 Funciones de varias variables 1. Definiciones básicas En este texto consideraremos funciones f : A R m, A R n. Dichas funciones son comúnmente denominadas como funciones de varias variables,
( ) ( ) ( ) ( ) BLOQUE A + = + IES Mediterráneo de Málaga Solución Junio 2012 Juan Carlos Alonso Gianonatti
IES Mditáno d Málg Solución Junio Jun Clos Alonso Ginontti BLOQUE A CUESTIÓN A..- ) Discut l guint stm d cucions n unción dl pámto [ 5 puntos] ) Rsul l stm cundo s comptil [ punto] λ λ λ Solución 8 Con
ENSAYOS DE MATERIALES
ENSAYOS DE MATERIALES Qué son los ensayos de materiales? Se denomina ensayo de materiales a toda prueba cuyo fin es determinar las propiedades de un material. Existen distintos ensayos, que nos darán las
Tema 6: Equilibrio químico.
Tema 6: Equilibrio químico. Equilibrio en las recciones químicas. Constante de equilibrio. Propiedades de las constantes de equilibrio. Constantes de equilibrio K c y K p. Equilibrio en mezclas heterogéneas.
Procesos Estacionarios. Francisco J. González Serrano. Universidad Carlos III de Madrid
PREDICCIÓN DE SEÑALES Procesos Estacionarios Francisco J. González Serrano Universidad Carlos III de Madrid Procesos Estacionarios A la hora de hacer predicciones parece obvio suponer que algo debe permanecer
Variables aleatorias continuas
Variables aleatorias continuas Hemos definido que una variable aleatoria X es discreta si I X es un conjunto finito o infinito numerable. En la práctica las variables aleatorias discretas sirven como modelos
x : N Q 1 x(1) = x 1 2 x(2) = x 2 3 x(3) = x 3
3 Sucesiones - Fernando Sánchez - - Cálculo I de números racionales 03 10 2015 Los números reales son aproximaciones que se van haciendo con números racionales. Estas aproximaciones se llaman sucesiones
Álgebra Vectorial. Principios de Mecánica. Licenciatura de Física. Curso 2007-2008. 1
Álgebra Vectorial Principios de Mecánica. Licenciatura de Física. Curso 2007-2008. 1 Indice. 1. Magnitudes Escalares y Vectoriales. 2. Vectores. 3. Suma de Vectores. Producto de un vector por un escalar.
PROBLEMAS DE ELECTROESTÁTICA
PBLMAS D LCTSTÁTICA I CAMP LCTIC N L VACI. Cagas puntuales. Cagas lineales. Cagas supeficiales 4. Flujo le de Gauss 5. Distibuciones cúbicas de caga 6. Tabajo enegía electostática 7. Poblemas Pof. J. Matín
REPRESENTACION GRAFICA.
REPRESENTACION GRAFICA. Calcular puntos notabls así como intrvalos d monotonía y curvatura d: ² - = 0 ; ² = ; = son los valors d qu anulan l dnominador D = R- y () = 0 ; - 4 = 0 ; = 0 posibl ma, min Monotonia:
Masa y composición isotópica de los elementos
Masa y composición isotópica de los elementos www.vaxasoftware.com Z Sím A isótopo Abndancia natral Vida Prodcto 1 H 1 1,00782503207(10) 99,9885(70) 1,00794(7) estable D 2 2,0141017780(4) 0,0115(70) estable
Integral Definida. Tema 6. 6.1 Introducción. 6.2 Definición de Integral Definida
Tem 6 Integrl Definid 6.1 Introducción En este tem estudiremos l Integrl Definid o Integrl de Riemnn, un concepto mtemático que esencilmente puede describirse como el límite de un sum cundo el número de
CAPÍTULO V MOMENTOS DE INERCIA. El momento de inercia de un área tiene la forma
sistci d Mtils. Cpítul V. CPÍTULO V MOMENTOS DE NEC 5.. Mmts d ici d ás El t d ici d u á ti l fm Mmt d ici spct dl j : Mmt d ici spct dl j : Nt qu l cdd qu v l itgd s l cti l j spct dl qu s clcul l t d
Resolución de problemas. Temas: VOR e ILS
Resolución de problemas. Temas: VOR e ILS Autor: Mario E. Casado García 3er Curso ITT ST Índice 1. Problema tema 5: VOR......3 2. Problema tema 7: ILS.....7 3. Referencias..12 2 1. Problema tema 5: VOR
q 1 q 2 Resp.: V A = 1800 V; V B = 0 V; W A - B = 450*10-7 Joul. 13 cm 13 cm 6 cm 4 cm 4 cm
UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA COMPLEJO DOCENTE EL SABINO DEPARTAMENTO DE MATEMÁTICA Y FÍSICA UNIDAD CURRICULAR: FÍSICA II PROFESORA CARMEN ADRIANA CONCEPCIÓN 1. Un potón (q potón
Manual de teoría: Trigonometría Matemática Bachillerato
Manual de teoría: Trigonometría Matemática Bachillerato Realizado por José Pablo Flores Zúñiga Trigonometría: José Pablo Flores Zúñiga Página Contenido: 4) Trigonometría 4. Trigonometría Básica 4. Funciones
1.3.4 Ejercicios resueltos sobre la función exponencial y logarítmica
.. Ejrcicios rsultos sobr l función ponncil rítmic. Us ls propidds d l función ponncil (torm ) pr simplificr totlmnt l siguint prsión:. Prub qu Simplifiqu inicilmnt l numrdor l dnomindor d l frcción. Así:
OPERACIONES MATEMÁTICAS
Cpítulo OPERACIONES MATEMÁTICAS OPERACIÓN MATEMÁTICA E un poo qu onit n l tnfoión un o á nti n ot ll ulto, jo it gl o oniion n l ul fin l opión. To opión táti pnt un gl finiión y un íolo qu l intifi llo
Ejercicios 2.2 Usando aritmética de cuatro dígitos de precisión, sume la siguiente expresión
CAPÍTULO EJERCICIOS RESUELTOS: ARITMÉTICA DE ORDENADORES Y ANÁLISIS DE ERRORES Ejercicios resueltos Ejercicios.1 Calcula la suma y la resta de los números a = 0.453 10 4, y b = 0.115 10 3, con una aritmética