EJERCICIOS DE LÍMITES DE FUNCIONES
|
|
|
- Veronica Caballero Santos
- hace 7 años
- Vistas:
Transcripción
1 EJERCICIOS DE LÍMITES DE FUNCIONES Ejercicio nº.- A partir de la gráica de (), calcula: c) d) e) 5 Ejercicio nº.- La guiente gráica corresponde a la unción (). Sobre ella, calcula los límites: c) d) e) Ejercicio nº.- Dada la guiente gráica de (), calcula los límites que se indican: c) d) e)
2 Ejercicio nº.- Calcula los guientes límites a partir de la gráica de (): c) d) e) Ejercicio nº 5.- Sobre la gráica de (), halla : c) d) e) Ejercicio nº.- Representa gráicamente los guientes resultados: g Ejercicio nº 7.- Para la unción, sabemosque : y Representa gráicamente estos dos límites.
3 Ejercicio nº.- Representa gráicamente: g Ejercicio nº 9.- Representa los guientes límites: Ejercicio nº.- Representa en cada caso los guientes resultados: g Ejercicio nº.- Calcula: c) sen Ejercicio nº.- Halla los límites guientes: c) log Ejercicio nº.- Resuelve: c) tg
4 Ejercicio nº.- Calcula ellímite de la unción en y en. Ejercicio nº 5.- Calcula los guientes límites: c) cos 9 Ejercicio nº.- Calcula el guiente límite y estudia el comportamiento de la unción por la izquierda y por la derecha de : Ejercicio nº 7.- Dada la unción, 5 calculaellímite de ( ) en. inormación que obtengas. Representala Ejercicio nº.- Calcula el guiente límite y estudia el comportamiento de la unción a la izquierda y a la derecha de : 9 Ejercicio nº 9.- Calcula el guiente límite y estudia el comportamiento de la unción por la izquierda y por la derecha de : Ejercicio nº.- Calcula el límite de la guiente unción en el punto y estudia su comportamiento por la izquierda y por la derecha:
5 Ejercicio nº.- Calcula ellímite cuando y cuando y representa la inormación que obtengas: Ejercicio nº.- delaguienteunción Halla ellímite cuando la inormación que obtengas: de las guientesunciones yrepresentagráicamente 5 Ejercicio nº.- Calcula los guientes límites y representa la inormación que obtengas: Ejercicio nº.- Calcula los guientes límites y representa el resultado que obtengas: Ejercicio nº 5.- Halla los guientes límites y representa gráicamente los resultados obtenidos: Ejercicio nº.- Calcula y representa gráicamente la inormación obtenida 5
6 Ejercicio nº 7.- Halla el límite guiente y representa la inormación obtenida: 5 Ejercicio nº.- Resuelve el guiente límite e interprétalo gráicamente. Ejercicio nº 9.- Calcula el guiente límite y representa gráicamente los resultados obtenidos: Ejercicio nº.- Calcula el guiente límite e interprétalo gráicamente: Ejercicio nº.- Resuelve los guientes límites y representa los resultados obtenidos Ejercicio nº.- Halla los guientes límites y representa gráicamente los resultados que obtengas:
7 Ejercicio nº.- Calcula los guientes límites y representa los resultados que obtengas: Ejercicio nº.- Halla ellímite cuando y cuando y representa los resultados que obtengas: delaguienteunción, Ejercicio nº 5.- Calcula los guientes límites y representa las ramas que obtengas: 5 5 Continuidad Ejercicio nº.- A partir de la gráica de ( ) señala es continua o no en y en. En el caso de no ser continua, indica la causa de la discontinuidad. 7
8 Ejercicio nº 7.- La guiente gráica corresponde a la unción : Di es continua o no en y en. Si en alguno de los puntos no es continua, indica cuál es la causa de la discontinuidad. Ejercicio nº.- Son continuas las guientes unciones en? Si alguna de ellas no lo es, indica la razón de la discontinuidad. Ejercicio nº 9.- Dada la gráica de : Es continua en?
9 en? Si no es continua en alguno de los puntos, indica cuál es la razón de la discontinuidad. Ejercicio nº.- Esta esla gráica de la unción : Es continua en =? en? Si no es continua en alguno de los puntos, indica la causa de la discontinuidad. Ejercicio nº.- Halla el valorde k para que seacontinua en : k Ejercicio nº.- Estudia la continuidad de: Ejercicio nº.- Comprueba la guiente unción es continua en 9
10 Ejercicio nº.- Averigua la guiente unción es continua en : Ejercicio nº 5.- Estudia la continuidad de la unción: 5
11 SOLUCIONES EJERC. LÍMITES DE FUNCIONES Ejercicio nº.- A partir de la gráica de (), calcula: c) d) e) 5 c) d) e) 5 Ejercicio nº.- La guiente gráica corresponde a la unción (). Sobre ella, calcula los límites: c) d) e) c) d) e)
12 Ejercicio nº.- Dada la guiente gráica de (), calcula los límites que se indican: c) d) e) c) d) e) Ejercicio nº.- Calcula los guientes límites a partir de la gráica de (): c) d) e) c) d) e)
13 Ejercicio nº 5.- Sobre la gráica de (), halla : c) d) e) c) d) e) Ejercicio nº.- Representa gráicamente los guientes resultados: g Ejercicio nº 7.- Para la unción, sabemosque : y Representa gráicamente estos dos límites.
14 Ejercicio nº.- Representa gráicamente: g o bien Por ejemplo: Ejercicio nº 9.- Representa los guientes límites: Ejercicio nº.- Representa en cada caso los guientes resultados: g
15 o bien Ejercicio nº.- Calcula: c) sen c) sen sen Ejercicio nº.- Halla los límites guientes: c) log 7 9 c) log log 5
16 Ejercicio nº.- Resuelve: tg c) c) tg tg Ejercicio nº.-. y en en ellímite de la unción Calcula 5 7 Ejercicio nº 5.- Calcula los guientes límites: 9 cos c) c) cos cos
17 Ejercicio nº.- Calcula el guiente límite y estudia el comportamiento de la unción por la izquierda y por la derecha de : Ejercicio nº 7.- Dada la unción, 5 calculaellímite de ( ) en. inormación que obtengas. Representala 5 Calculamos los límites laterales: 5 Ejercicio nº.- Calcula el guiente límite y estudia el comportamiento de la unción a la izquierda y a la derecha de : 9 9 Calculamos los límites laterales: 7
18 9 9 Ejercicio nº 9.- Calcula el guiente límite y estudia el comportamiento de la unción por la izquierda y por la derecha de : Calculamos los límites laterales: Ejercicio nº.- Calcula el límite de la guiente unción en el punto y estudia su comportamiento por la izquierda y por la derecha: Calculamos los límites laterales:
19 Ejercicio nº.- Calcula ellímite cuando y cuando y representa la inormación que obtengas: delaguienteunción Ejercicio nº.- Halla ellímite cuando la inormación que obtengas: de las guientesunciones yrepresentagráicamente 5 5 Ejercicio nº.- 9
20 Calcula los guientes límites y representa la inormación que obtengas: Ejercicio nº.- Calcula los guientes límites y representa el resultado que obtengas:
21 Ejercicio nº 5.- Halla los guientes límites y representa gráicamente los resultados obtenidos: Ejercicio nº.- Calcula y representa gráicamente la inormación obtenida Calculamos los límites laterales:
22 Ejercicio nº 7.- Halla el límite guiente y representa la inormación obtenida: Ejercicio nº.- Resuelve el guiente límite e interprétalo gráicamente. Ejercicio nº 9.- Calcula el guiente límite y representa gráicamente los resultados obtenidos:
23 Calculamos los límites laterales: Ejercicio nº.- Calcula el guiente límite e interprétalo gráicamente: Ejercicio nº.- Resuelve los guientes límites y representa los resultados obtenidos
24 Ejercicio nº.- Halla los guientes límites y representa gráicamente los resultados que obtengas: Ejercicio nº.- Calcula los guientes límites y representa los resultados que obtengas:
25 / Ejercicio nº.- Halla ellímite cuando y cuando y representa los resultados que obtengas: delaguienteunción, Ejercicio nº 5.- Calcula los guientes límites y representa las ramas que obtengas:
26 5 Continuidad Ejercicio nº.- A partir de la gráica de ( ) señala es continua o no en y en. En el caso de no ser continua, indica la causa de la discontinuidad. En =, sí es continua. En = es discontinua porque no está deinida, ni tiene límite inito. Tiene una rama ininita en ese punto (una asíntota vertical). Ejercicio nº 7.- La guiente gráica corresponde a la unción : Di es continua o no en y en. Si en alguno de los puntos no es continua, indica cuál es la causa de la discontinuidad.
27 En no es continua porque presenta un salto en ese punto. Observamos que. En sí es continua. Ejercicio nº.- Son continuas las guientes unciones en? Si alguna de ellas no lo es, indica la razón de la discontinuidad. No es continua en ; aunque esté deinida en, tiene el punto desplazado. Es una discontinuidad evitable porque eiste Sí es continua en.. Ejercicio nº 9.- Dada la gráica de : Es continua en? en? Si no es continua en alguno de los puntos, indica cuál es la razón de la discontinuidad. 7
28 Sí es continua en. No, en es discontinua porque no está deinida en ese punto. Como sí tiene límite en ese punto, es una discontinuidad evitable. Ejercicio nº.- Esta esla gráica de la unción : Es continua en =? en? Si no es continua en alguno de los puntos, indica la causa de la discontinuidad. No es continua en porque no está deinida, ni tiene límite inito en ese punto. Tiene una rama ininita en ese punto (una asíntota vertical). Sí es continua en. Ejercicio nº.- Halla el valorde k para que seacontinua en : k k Para que sea Ha de ser k. continua en,.
29 Ejercicio nº.- Estudia la continuidad de: Si, la unción es continua. Si : No escontinua en Ejercicio nº.- porque. Es decir, no tienelímiteenese punto. Comprueba la guiente unción es continua en Es continuaen porque. Ejercicio nº.- Averigua la guiente unción es continua en : Es continuaen porque. 9
30 Ejercicio nº 5.- Estudia la continuidad de la unción: 5 Si, la unción es continua. Si : 5 Tambiénescontinuaen porque.
EJERCICIOS DE LÍMITES DE FUNCIONES
EJERCICIOS DE LÍMITES DE FUNCIONES Ejercicio nº 1.- A partir de la gráica de (), calcula: c) d) e) 1 1 5 Ejercicio nº.- La guiente gráica corresponde a la unción (). Sobre ella, calcula los límites: c)
REPRESENTACIÓN DE FUNCIONES
REPRESENTACIÓN DE FUNCIONES Ejercicio nº.- Estudia y representa la siguiente unción: ( ) + 6 Ejercicio nº.- Dibuja la gráica de la unción: ( + ) ( ) Ejercicio nº.- Dada la unción: y sen sen, [0, ] a) Halla
TEMA 6: LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS
CONTINUIDAD TEMA 6: LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS 1- Representa gráficamente las siguientes funciones y di, de cada una de ellas, si es continua o discontinua: d) 2- Explica por qué
Representación de funciones
Representación de unciones Ejercicio nº.- Representa una unciónpolinómica, de la que sabemosque : lim ; lim Suderivadaes en Corta a los ejesen, en,.,,,,,,. Ejercicio nº.- Dibuja la gráica de la unción,
4.2. Continuidad de una función en un punto. (A) Una función f es continua en un punto x=a, cuando se cumplen las siguientes condiciones:
4. CONTINUIDAD DE UNA FUNCIÓN. 4.. Noción intuitiva de continuidad de una unción en un punto. La mayor parte de las unciones que manejamos a nivel elemental, presentan en sus gráicas una propiedad característica
Solución. - Verticales: En los puntos excluidos del dominio donde el límite quede de la forma k. 3( ) = Asíntota vertical. = + x 2.
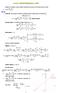Estudiar sus asíntotas y ramas ininitas valorando la posición de la unción respecto de ellas.. ( ) - Verticales: En los puntos ecluidos del dominio donde el límite quede de la orma D[ ( ) ] R { } 6 : Se
REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS
REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS DOMINIO - Polinomio : D = R - Cocientes : D = R {puntos que anulan el denominador} - Raíces de índice par : D = {Lo
Cálculo de límites. Ejercicio nº 1.- Haz una gráfica en la que se reflejen estos resultados: Ejercicio nº 2.-
Cálculo de ites Ejercicio nº.- Haz una gráica en la que se relejen estos resultados: d) Ejercicio nº.- Representa gráicamente los guientes resultados: 0 0 d) Ejercicio nº.- Representa en una gráica los
Asíntotas en una función.
Asíntotas en una unción. Las asíntotas son rectas a las cuales la unción se va aproimando indeinidamente, cuando por lo menos una de las variables ( o y) tienden al ininito. Deinición: Si un punto, y )
Límites y continuidad
Estudio de la continuidad de la función en el punto = : Comprobemos, como primera medida, que la función está definida en =. Para =, tenemos que determinar f() = + = 6 + = 8, luego eiste. Calculamos, entonces
BACHILLERATO Matemáticas I
Unidad. Lmites de funciones. Continuidad y ramas infinitas 5 Sobre la gráfica de la siguiente función f (), halla: a) lm " " f () b) lm f () c) lm f () " " d) lm f () e) lm f () f ) lm f () " " a) b) c)
LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS
LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS Página 7 PARA EMPEZAR, REFLEXIONA Y RESUELVE El valor de la función f () = + 5 para = 5 no se puede obtener directamente porque el denominador se hace
DERIVADAS. TÉCNICAS DE DERIVACIÓN
DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
CONTINUIDAD DEFINICIÓN CONTINUIDAD LATERAL. es continua en un punto. Una función. si:
CONTINUIDAD DEFINICIÓN Una función 1) l a ) f (a) ) f ( a) a un punto a Si una función no cumple alguna de estas condiciones es discontinua en : a CONTINUIDAD LATERAL Ejemplo a por la izquierda f ( a)
y con la semiamplitud δ =1. 2.
LÍMITE DE UNA FUNCIÓN UNIDAD II II. ENTORNOS Se denomina entorno de un punto a en, al intervalo abierto ( δ a δ ) semiamplitud del intervalo. a, donde δ es la El entorno de a, en notación de conjuntos
LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS
UNIDAD 8 LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS Página 6. Representa gráficamente las siguientes funciones y di, de cada una de ellas, si es continua o discontinua: < 0 a) y = + < b) y = 0
TEMA 2. FUNCIONES REALES DE VARIABLE REAL 2.3. CONCEPTO DE DERIVADA. CÁLCULO DE DERIVADAS
TEMA. FUNCIONES REALES DE VARIABLE REAL.. CONCEPTO DE DERIVADA. CÁLCULO DE DERIVADAS . FUNCIONES REALES DE VARIABLE REAL.. CONCEPTO DE DERIVAD. CÁLCULO DE DERIVADAS... Derivada de una unción en un punto...
y esboza su gráfica, apoyándote en la gráfica de f ( x ) que aparece debajo. 3 log + 1
Funciones Límites y continuidad Curso 06/7 Ejercicio puntos 0 Dadas las unciones = e, g = y h ( ) log ( ) =, se pide: Encuentra el dominio de la unción ( g h) Encuentra la unción y esboza su gráica, apoyándote
TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS
Tema 8 Límites de funciones, continuidad y asíntotas Matemáticas II º Bach 1 TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS 8.1 LÍMITE DE UNA FUNCIÓN 8.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite
LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS
UNIDAD 6 LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS Página 38. Representa gráficamente las siguientes funciones y di, de cada una de ellas, si es continua o discontinua: < 0 a) y = + 3 < b) y
APLICACIONES DE LA DERIVADA I. Ejercicios a resolver en la práctica. = x + 2. Determina y clasifica los puntos o valores
UNIVERSIDAD SIMÓN BOLÍVAR Enero-Marzo 010 DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-1111) Fecha de publicación: 0-0-010 Contenido Tercer Parcial APLICACIONES DE LA DERIVADA I Contenidos
TEMA 9. LÍMITES DE FUNCIONES
TEMA 9. LÍMITES DE UNCIONES Concepto intuitivo de límite de una unción en un punto. se lee límite cuando tiende a c de. c siniica que cuando toma valores cada vez más próimos a c c entonces los valores
Ejercicios: Límites y continuidad
. En los apartados siguientes, usar la gráfica de las funciones para hallar el límite si eiste: (a) (4 ) ( + ) (c) f(); f() = 4,! d 3 d d 0, = f(); f() = +,! 5 (f) d, = d 5 5 d 3 3. Calcula los siguientes
, 0 ; Decrece: 0 2, 0 ; 0, 2. d f x x x x. a f x. b f x. Solucionario tema 9: Estudio de Funciones. Ejercicio 1. Ejercicio 2
Solucionario tema 9: Estudio de Funciones Ejercicio Estudia la gráica siguiente: Dominio Recorrido 0, 4 Puntos de corte con los Ejes Con el Eje Y: 0, 4 Puntos máimos y mínimos: Máimo absoluto: 0, No hay
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas Función Derivada Función compuesta Derivada y f x y f x y f g x
Tabla de derivadas Función Derivada Función compuesta Derivada k ' 0 ' ' n ' ' ' e ' n n n n ' n ' e a ' ln ln log a a a ' ' e a ln ln a Reglas de derivación log a ' ' ' ' ' ' ' ' ' ln ' ' ' ' e a a '
f p) 2 3x f q) f r) 4 x f s) x 6 f t) f u) x 3x f v) x 7x x x 9x
.- Halla el dominio de deinición de las siguientes unciones polinómicas y racionales: a) b) 8 j) 9 4 d) 9 l) 7 ( ) 5 ( ) ( ) 4 p) q) r) 7 9 ( ) 8 7 9 ( ) 4 ( ) 4 ( ) ( ) s) 5 m) t) h) ( ) 7 ( ) 4 u) v)
TEMA 2: CONTINUIDAD DE FUNCIONES
TEMA : CONTINUIDAD DE FUNCIONES 1. Continuidad de una función en un punto Entre las primeras propiedades de las funciones aparece el concepto de continuidad. Durante mucho tiempo fue asumida como una idea
3 CONTINUIDAD. ( x) Introducción
CONTINUIDAD Introducción Inormalmente hablando, una unción deinida sobre un intervalo I es continua la curva que la representa, es decir el conjunto de los puntos (x, (x)), con x pertenecientes a I, está
Matemáticas II TEMA 7 Límites y continuidad de funciones Problemas Propuestos
Matemáticas II TEMA 7 Límites y continuidad de funciones Problemas Propuestos Definición de ites Demuestra, aplicando la definición, que ( ) Demuestra, aplicando la definición, que + + 8 Cálculo de ites
Procedimiento para determinar las asíntotas verticales de una función
DETERMINACIÓN DE ASÍNTOTAS EN UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición
TEMA 12 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES
Tema Derivadas. Aplicaciones Matemáticas I º Bacillerato TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES TASA DE VARIACIÓN MEDIA DE UNA FUNCIÓN EN UN INTERVALO EJERCICIO : Halla la tasa de variación
TEMA 11 LÍMITES, CONTINUIDAD Y ASÍNTOTAS
Tma Límits, continuidad y asíntotas Matmáticas I º Bachillrato TEMA LÍMITES, CONTINUIDAD ASÍNTOTAS CÁLCULO GRÁFICO DE LÍMITES EJERCICIO : Sobr la gráfica d f), halla : 8 8 8 f f c) f f ) f f f c) f f )
SOLUCIONES A LOS EJERCICIOS
SOLUCIONES A LOS EJERCICIOS Ejercicio nº.- a) Calcula utilizando la definición de logaritmo: log log log Sabiendo que log k calcula log ( k ). a) 5 5 5 7 log log log ( ) log k log logk log logk ( ) Ejercicio
TEMA 11 REPRESENTACIÓN DE FUNCIONES
Tema Representación de unciones Matemáticas II º Bachillerato TEMA REPRESENTACIÓN DE FUNCIONES EJERCICIO : Representa gráicamente la unción: Dominio R 8 respecto al origen. 8 Simetrías:. No es par ni impar:
(Apuntes en revisión para orientar el aprendizaje) Capítulo IV Variación de funciones. Extremos
(Apuntes en revisión para orientar el aprendizaje) Capítulo IV Variación de unciones. Etremos INTRODUCCIÓN En múltiples problemas de ingeniería se requiere optimizar una o varias de las variables que intervienen
LÍMITES Y CONTINUIDAD
U.C.V. F.I.U.C.V. CÁLCULO I (05) - TEMA Pág.: de 7. Compruebe los siguientes resultados o afirmaciones:.....5..7..9......5..7..9..... 7 + 5 + 8 5 + 6 + + + + 7 9 9 8 6 + + 6 + 6 8.....6..8..0......6. (a
SOLUCIONES ( ) ( ) ( ) 2 ( ) ( ) Fecha: La pendiente de la recta es m = = x = 4. x = 2 2x. Ejercicio nº 1.- Solución: La recta será:
Ejercicio nº.- Halla la ecuación de la recta tangente a la curva que sea paralela a la recta y. SOLUCIONES ' Fecha: La pendiente de la recta es m Cuando, y La recta será: Ejercicio nº.- y ( ) Averigua
a) lim x lim senx sen lim lim lim lim lim x x 2 lim Ejercicio nº 1.- Calcula: Solución: Ejercicio nº 2.-
Ejrcicio nº.- Calcula: c) 8 sn Evaluación: Fcha: c) 8 sn sn Ejrcicio nº.- Calcula l siguint it y studia l comportaminto d la unción por la izquirda y por la drcha d : Calculamos los its latrals: Ejrcicio
REPRESENTACIÓN DE FUNCIONES
REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
Denominadores: un denominador nunca se puede hacer cero. Ejemplo: 𝑓 𝑥 =
1. Continuidad de funciones. Una función es continua en 𝑥 = 𝑎, si se cumple: Existe 𝑓(𝑎). lim!! 𝑓 𝑥 = lim!!! 𝑓(𝑥) = lim!!! 𝑓 𝑥 𝒇 𝒂 = 𝐥𝐢𝐦𝒙 𝒂 𝒇 𝒙 Las funciones definidas por expresiones analíticas elementales
SOLUCIONES DE LAS ACTIVIDADES Págs. 239 a 257
TEMA. LÍMITES Y CONTINUIDAD SOLUCIONES DE LAS ACTIVIDADES Págs. 9 a 7 Página 9 Página. a) f() 0. a) f() 0, 0,0 0,00 0,000 f(),,9,99,999,9,99,999,9999 f() 00 0.000 0 6 0 8 b) f() 0 0, 0,0 0,00 0,000 f(),,0,00,000
En las figuras anteriores vemos algunos casos (no todos) que pueden presentarse al pasar por un punto x 0. (en este caso, para x 0 =2)
UNIVERSIDAD DEL VALLE PROFESOR CARLOS IVAN RESTREPO CONTINUIDAD. 1.- Continuidad en un punto. Continuidad lateral..- Continuidad en un intervalo. 3.- Operaciones con funciones continuas 4.- Discontinuidades.
Continuidad, límites y asíntotas
9 Continuidad, ites y asíntotas. Funciones especiales Piensa y calcula Completa la siguiente tabla: Parte entera de Parte decimal de Valor absoluto de 0,3 0,3,8,8 2,4 2,4 3,9 Ent () Dec () 3,9 0,3 0,3,8,8
2-LÍMITES Y CONTINUIDAD
-Distancia entre dos números: d(a,b)= -LÍMITES Y CONTINUIDAD Sea f una función a y L R 0 Propiedad- =L Ejemplos: -f()= + = = = ( = = =5 ( ) - = = = ( ) - = M > > para suficientemente próimos a a =a es
12.1 CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO
INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y = () en un intervalo
Límites y continuidad
Límites y continuidad.. Límites El ite por la izquierda de una función f en un punto 0, denotado como 0 f() es el valor al que se aproima f() cuando se acerca hacia 0 por la izquierda. De igual forma,
Unidad 9. Límites, continuidad y asíntotas
Unidad 9. Límites, continuidad y asíntotas. Límite de una función en un punto Piensa y calcula Halla mentalmente y completa la tabla siguiente:,9,99,,00,0, f () =,9,99,,00,0, f () =,9,99 3, 3 3,00 3,0
x 3 x x 2 9 x 2 x 6 x(x + 1)(x 2) x 4 x 3 14x x 1 4x x 2
. Calcula las asíntotas de las siguientes funciones: a) f() = 22 + 2 + 2 b) f() = 2 + + 2 2. Calcular el dominio de la función y = 3 3. Calcula el dominio de la función y = 2 + 9 4. Calcula el dominio
UNIDAD 9 LÍMITES DE FUNCIONES. CONTINUIDAD.
IES Padre Poveda (Guadi) UNIDAD 9 LÍMITES DE FUNCIONES. CONTINUIDAD.. Límite de una función en un punto... Límites laterales... Límite de una función en un punto.. Límites en el infinito... Comportamiento
9 Continuidad ACTIVIDADES INICIALES EJERCICIOS PROPUESTOS. 9.I. Dibuja la gráfica de las siguientes funciones.
9 Continuidad 9.I. Dibuja la gráfica de las guientes funciones. ACTIVIDADES INICIALES a) < f( ) > b) f ( ) 9.II. Escribe la epreón algebraica de la función. Y O X EJERCICIOS PROPUESTOS 9.. Indica las guientes
APUNTE: CONCEPTO DE DERIVADA
APUNTE: CONCEPTO DE DERIVADA UNIVERSIDAD NACIONAL DE RIO NEGRO Asignatura: Matemática Carreras: Lic en Economia Proesor: Pro Mabel Chrestia Semestre: ero Año: o Introducción al concepto de derivada de
TEMA 9 : LÍMITES DE FUNCIONES. CONTINUIDAD
MATEMÁTICAS I LÍMITES-CONTINUIDAD TEMA 9 : LÍMITES DE FUNCIONES. CONTINUIDAD 1. LÍMITES EN EL INFINITO En ocasiones interesa estudiar el comportamiento de una función (la tendencia) cuando los valores
LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS
LÍMITES DE FUNCIONES. CONTINUIDAD RAMAS INFINITAS Página 7 REFLEIONA RESUELVE Aproimaciones sucesivas Comprueba que: f () = 6,5; f (,9) = 6,95; f (,99) = 6,995 Calcula f (,999); f (,9999); f (,99999);
1 Consideramos la gráfica siguiente:
Conderamos la gráfica guiente: Determina, a la vista de la gráfica, el dominio de definición, metrías, el recorrido, la eistencia de asíntotas, los intervalos de crecimiento y decrecimiento. Justifica,
Colegio Diocesano Sagrado Corazón de Jesús
Colegio Diocesano Sagrado Corazón de Jesús MATEMÁTICAS I Actividades tipo eamen-recuperación de Pendientes / Nombre: Fecha de entrega: BLOQUE I: NÚMEROS REALES Ejercicio nº.- Clasiica los siguientes números
I.- Límite de una función
I.- Límite de una función a) En un punto En la mayoría de las funciones que vas a encontrarte, el límite, cuando tiende a un número real c, coincide con el valor numérico f(c), siempre que c pertenezca
TEMA 5 LÍMITE DE FUNCIONES. CONTINUIDAD
TEMA 5 LÍMITE DE FUNCIONES. CONTINUIDAD 5.1. VISIÓN INTUITIVA DE LA CONTINUIDAD. TIPOS DE DISCONTINUIDADES. La idea de función continua es la que puede ser construida con un solo trazo. DISCONTINUIDADES
LÍMITES Y CONTINUIDAD. 1º Bto. Sociales. CONCEPTO DE LÍMITE DE UNA FUNCIÓN LÍMITE DE UNA FUNCIÓN EN UN PUNTO CONCEPTO DE LÍMITE DE UNA FUNCIÓN
LÍMITES Y CONTINUIDAD º Bto. Sociales. CONCEPTO DE LÍMITE DE UNA FUNCIÓN Sea f() =. Vamos a darle valores a cercanos a y vamos a ver cómo se comporta f()..9.99.999.9999.99999 f() 4.8 4.98 4.998 4.9998
lim lim 3 2x + = lim lim 4 = es: lim = 2 x x x + 5 A) 4 B) 0 C) D) 2 E) lim x x 7 x+ lim Lim x lim 4x Sesión 5 Unidad II Límite de una función.
Sesión Unidad II Límite de una unción. 7.- Calcula el +.- El ite.- El E. Límites en el ininito 7 9 + 8 + A) B) 9 C) D) 0. 8.- El A) B) C) D) 0 + + + A) 0 B) C) D) - 9.- El valor del + 9 A) B) C) D) A)
( x) lim. lim. 2 no existe 4 y 1. lim + 5 C) 2 D) E) No existe. Sesión 4. Unidad II Límite de una función. A. Límites unilaterales.
Sesión.- Sea la unción ilustrada Unidad II Límite de una unción. A. Límites unilaterales..- Dado el dibujo de la unción, Determina ( ).- El - B) D) 0 - ( ) indicado en la siguiente igura de la graica Los
ASÍNTOTAS Y RAMAS. Ejercicio nº 1.- Halla las asíntotas verticales de: y sitúa la curva respecto a ellas. Ejercicio nº 2.-
ASÍNTOTAS Y RAMAS Ejercicio nº.- Halla las asíntotas verticales de: y sitúa la curva respecto a ellas. Ejercicio nº.- Halla las asíntotas verticales de la siguiente unción y sitúa la curva respecto a ellas:
LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS
LÍMITES DE FUNCIONES. CONTINUIDAD RAMAS INFINITAS Página 7 REFLEIONA RESUELVE Aproimaciones sucesivas Comprueba que: f () =,5; f (,9) =,95; f (,99) =,995 Calcula f (,999); f (,9999); f (,99999); A la vista
Es evidente la continuidad en En el punto, se tiene:
Tema 3 Continuidad Ejercicios Resueltos Ejercicio 1 Estudia la continuidad de la función La función puede expresarse como Para representarla basta considerar dos arcos de parábola: Es evidente la continuidad
LÍMITES Y CONTINUIDAD
Límite de un unción en un punto. Medinte tbls clcul: b c d 9. Teniendo en cuent l gráic de l unción, clcul los guientes límites: b c. A prtir de l gráic de l unción, comprueb que :. Clcul sen tg ý, teniendo
LÍMITES DE FUNCIONES. CONTINUIDAD
8 LÍMITES DE FUNCIONES. CONTINUIDAD REFLEXIONA Y RESUELVE Algunos ites elementales Utiliza tu sentido común para dar el valor de los siguientes ites: a 2, 3, 3 3 2 b 2, 3, 3 2 8 @ c 2, 3, 3 5 2 + 3 8 2
CONTINUIDAD Y DERIVABILIDAD 1.- CONTINUIDAD
CONTINUIDAD Y DERIVABILIDAD Continuidad. Derivabilidad. 1.- CONTINUIDAD 1.1 FUNCIÓN CONTINUA EN UN PUNTO Decimos que f es continua en a si: Lim f( ) = f( a) a Para que una función sea continua en un punto
x + x 2 +1 = 1 1 = 0 = lím
UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
TEMA 2. FUNCIONES REALES DE VARIABLE REAL 2.2. LÍMITES Y CONTINUIDAD
TEMA. FUNCIONES REALES DE VARIABLE REAL.. LÍMITES Y CONTINUIDAD . FUNCIONES REALES DE VARIABLE REAL.. LÍMITES Y CONTINUIDAD... LÍMITE DE UNA FUNCIÓN EN UN PUNTO... LÍMITES INFINITOS... LÍMITES EN EL INFINITO..4.
TEMA 8: LÍMITES DE FUNCIONES. CONTINUIDAD
TEMA 8: DE FUNCIONES. CONTINUIDAD 1. EN EL INFINITO En ocasiones interesa estudiar el comportamiento de una función (la tendencia) cuando los valores de se hacen enormemente grandes ( ) o enormemente pequeños
FUNCIONES. La variable x se denomina variable independiente y la variable y es la variable dependiente. x y
. DEFINICIÓN FUNCIONES Una unción real de variable real es una relación entre dos variables numéricas e y de orma que a cada valor de la variable le corresponde un único valor del la variable y. La variable
{( ) ( ) ( ) ( )} 4. FUNCIONES. B y f es una función de A en B definida por y = x 2 1, = x + 3, encuentra 5 pares que pertenezcan a la
4 FUNCIONES 4 Conceptos básicos Sean A y B dos conjuntos dados, una unción de A en B es una regla de correspondencia que asigna a cada elemento de A uno y solamente uno de B En una unción: A es el dominio
12 Representación de funciones
Representación de funciones ACTIVIDADES INICIALES.I. Factorizando previamente las epresiones, resuelve las siguientes ecuaciones: 3 a) 6 7 4 + 5 = 0 6 4 c) 4 + 4 = 0 7 b) 6 d) + + + + 3 = 0.II. Resuelve
Tema Derivadas. Aplicaciones Matemáticas CCSSI 1º Bachillerato 1
Tema Derivadas. Aplicaciones Matemáticas CCSSI 1º Bachillerato 1 EJERCICIO : A partir de la gráica de (): a b c Cuáles son los puntos de corte con los ejes? Di cuáles son sus asíntotas. Indica la posición
Estudio de funciones mediante límites y derivadas
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
el blog de mate de aida CSI: Límites y continuidad. . Se lee x tiende a x por la derecha. , se expresa así: , se expresa así: por la derecha)
pág. LÍMITE DE UNA FUNCIÓN EN UN PUNTO gnifica que toma valores cada vez más próimos a. Se lee tiende a. Ejemplo: ;,9;,;,;,8;,;,9;,;,999; Es una secuencia de números cada vez más próimos a. Escribimos.
LÍMITES, CONTINUIDAD, ASÍNTOTAS LÍMITE DE UNA FUNCIÓN. Límite de una función en un punto
LÍMITES, CONTINUIDAD, ASÍNTOTAS LÍMITE DE UNA FUNCIÓN Límite de una función en un punto xc Se lee: El límite cuando x tiende a c de f(x) es l Notas: - Que x se aproxima a c significa que toma valores muy
CONTINUIDAD Y DERIVABILIDAD. DERIVADAS
CONTINUIDAD Y DERIVABILIDAD. DERIVADAS. Dada la función f (), (, ), definir f () y f () de forma que f sea continua sen(π ) en todo el intervalo cerrado [, ]. : f () f () π 5 si. Estudiar la continuidad
Trabajo Práctico N 5
Trabajo Práctico N 5 Asíntota Continuidad Algunos ejemplos para tener en cuenta Asíntotas. Asíntota vertical (AV) Decimos que la recta = a es AV de f() f() = ± f() = ± a + Por ejemplo, para hallar la AV
RESUMEN DE ANÁLISIS MATEMÁTICAS II
RESUMEN DE ANÁLISIS MATEMÁTICAS II 1. DOMINIO DE DEFINICIÓN Y CONTINUIDAD 1.1. FUNCIONES ELEMENTALES (No tienen puntos angulosos) Tipo de función f (x) Dom (f) Continuidad Polinómicas P(x) R Racional P(x)/Q(x)
TEMA 6 : LÍMITES DE FUNCIONES. CONTINUIDAD
TEMA 6 : DE FUNCIONES. CONTINUIDAD. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. Ejercicio: Observa la gráfica siguiente: a) Estudia el dominio, el recorrido y la continuidad de f(). b) Indica si eisten los límites
Procedimiento para determinar las asíntotas verticales de una función
DETERMINACIÓN DE ASÍNTOTAS EN UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición
Procedimiento para determinar las asíntotas verticales de una función
DETERMINACIÓN DE ASÍNTOTAS EN UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD = 3 2
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
Continuidad. 4.2 Tipos de discontinuidades CAPÍTULO. De una función que no es continua en un punto se dice que es discontinua en dicho punto.
CAPÍTULO Continuidad. Tipos de discontinuidades De una función que no es continua en un punto se dice que es discontinua en dicho punto. Vamos a clasificar las discontinuidades de una función. Discontinuidad
Cálculo Diferencial e Integral - Límite y continuidad. Farith J. Briceño N.
Cálculo Diferencial e Integral - Límite y continuidad. Farith J. Briceño N. Objetivos a cubrir Código : MAT-CDI.5 Límites laterales. Cálculo de límites. Límites en el infinito. Límites infinitos Límites
FACULTAD de INGENIERÍA Análisis Matemático A
FACULTAD de INGENIERÍA Anális Matemático A Página FACULTAD de INGENIERÍA Anális Matemático A g( ) g( ) g () d) g( ) 6) Encuentre los guientes ites endo f ( ) a cada paso indicando el álgebra de ites utilizado.
1) Calcula el dominio de las siguientes funciones: x 4x. = 2x. c) f ( x) = 1+ log. x 1. f ( x)
EJERCICIOS DE MATEMÁTICAS II TEMA (FUNCIONES) ) Calcula el dominio de las siguientes funciones: f ( ) f ( ) + + + f ( ) 4 ln f ( ) f ( ) ln f ( ) ln sen ( ) e g) f ( ) e f ( ) ln + h) ( ) i) f ( ) e tg
TEMA 9: FUNCIONES, LÍMITES Y CONTINUIDAD
º CONCEPTOS PREVIOS Ejercicio º Valor absoluto a,b, TEMA 9: FUNCIONES, LÍMITES Y CONTINUIDAD º Intervalos: a, b, a, b, a, b Semirrectas:, a, -,a, a,, a, Representa gráficamente las siguientes funciones,
9 Continuidad. Solucionario ACTIVIDADES INICIALES EJERCICIOS PROPUESTOS. 9.I. Dibuja la gráfica de las siguientes funciones.
Solucionario 9 Continuidad 9.I. Dibuja la gráfica de las guientes funciones. ACTIVIDADES INICIALES a) < f( ) > b) f ( ) a) Si (, ). El segmento de recta pasa por el punto (, ) y se acerca al (, ). Si [,
Determina las asíntotas de las siguientes funciones e interpreta gráficamente los resultados:
Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS Determina las asíntotas de las siguientes funciones e interpreta gráficamente los resultados: ) f ( ) 4 f ( ) es una función polinómica
LÍMITES Y CONTINUIDAD
LÍMITES Y CONTINUIDAD Tema 4: LÍMITES Y CONTINUIDAD. Índice:. Límite de una función en un punto. Límites laterales.. Límites en el infinito.. Cálculo de límites... Propiedades de los límites... Límites
Continuidad y ramas infinitas. El aumento A producido por cierta lupa viene dado por la siguiente ecuación: A = 2. lm í
Unidad. Límites de funciones. Continuidad y ramas infinitas Resuelve Página 7 A través de una lupa AUMENTO DISTANCIA (dm) El aumento A producido por cierta lupa viene dado por la siguiente ecuación: A
TEMA 9- LÍMITES Y CONTINUIDAD MATEMÁTICAS I 1º BACHILLERATO 1 TEMA 9 LÍMITES DE FUNCIONES, CONTINUIDAD Y RAMAS INFINITAS
TEMA 9- LÍMITES Y CONTINUIDAD MATEMÁTICAS I 1º BACHILLERATO 1 TEMA 9 LÍMITES DE FUNCIONES, CONTINUIDAD Y RAMAS INFINITAS TEMA 9- LÍMITES Y CONTINUIDAD MATEMÁTICAS I 1º BACHILLERATO 9.1. LÍMITE DE UNA FUNCIÓN
Problemas Tema 2 Enunciados de problemas de Límite y Continuidad
página /2 Problemas Tema 2 Enunciados de problemas de Límite y Continuidad Hoja. Estudiar la continuidad y derivabilidad de la función f ()=. solución: continua en toda la recta real. Punto anguloso en
Lamberto Cortázar Vinuesa la función se va a - infinito x 2 2x
http://matematicas-tic.wikispaces.com Lamberto Cortázar Vinuesa 07 LÍMITES EN EL INFINITO. ASÍNTOTAS EJERCICIOS WIKI Idea Se trata de estudiar lo que sucede con la unción () cuando damos a valores tan
DERIVADAS. TÉCNICAS DE DERIVACIÓN
DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 55 REFLEXIONA Y RESUELVE Tangentes a una curva y f ( 5 5 Halla, mirando la gráfica y las rectas trazadas, f'(, f'( y f'(. f'( 0; f'( ; f'( Di otros tres puntos
Continuidad de funciones
Apuntes Tema 3 Continuidad de funciones 3.1 Continuidad de funciones Def.: Dada una función f(x), diremos que es continua en x = a, si cumple la siguiente condición: En caso de que no cumpla esta condición,
REPRESENTACIÓN DE FUNCIONES
8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
Cálculo de derivadas. Aplicaciones. 1ºBHCS
Pág. de 5 Cálculo de derivadas. Aplicaciones. ºBHCS Ejercicio nº.- Consideramos la unción: Halla la tasa de variación media en el intervalo [0, ] e indica si () crece o decrece en ese intervalo. TVM Ejercicio
Problemas Tema 2 Solución a problemas de Límite y Continuidad - Hoja 02 - Todos resueltos
página 1/11 Problemas Tema 2 Solución a problemas de Límite y Continuidad - Hoja 02 - Todos resueltos Hoja 2. Problema 1 Resuelto por Sara Aparicio (noviembre 2014) 1. Estudiar la continuidad y derivabilidad