Representación de funciones
|
|
|
- Elisa Parra Carrizo
- hace 7 años
- Vistas:
Transcripción
1 Representación de unciones Ejercicio nº.- Representa una unciónpolinómica, de la que sabemosque : lim ; lim Suderivadaes en Corta a los ejesen, en,.,,,,,,. Ejercicio nº.- Dibuja la gráica de la unción, sabiendoque: Suderivadase anula en,. Solocorta a los ejesen,. Sus asíntotas son:, La posición de la curva respecto a las asíntotas es: e lim ; lim ; lim ; lim Ejercicio nº.- Haz la gráica de una unción, Es continua. sabiendo que : lim ; lim Su deriv adase anula en Corta a los ejesenlospuntos Ejercicio nº.-,, en, en,.,,,,,,,,. Representa una unción (), de la que sabemos lo siguiente: La derivada no se anula en ningún punto. La unción es decreciente. Corta a los ejes en (, ) en (, ) lim ; lim Tiene una asíntota horizontal en. Además:
2 Ejercicio nº 5.- Representa gráicamente una unción Su deriv adase anula en No corta a los ejes. lim ; lim, en,. Tiene una asíntota oblicua, que es. Además: (), de la que conocemoslo siguiente : Ejercicio nº 6.- La siguiente gráica corresponde a la unción (): a En qué puntos se anula la derivada? b Cuáles son sus asíntotas? c Indica la posición de la curva respecto a sus asíntotas verticales. Ejercicio nº 7.- La siguiente gráica corresponde a la unción (). A partir de ella, indica: a Máimos mínimos. b s de corte con los ejes. c Ramas ininitas. d Intervalos de crecimiento de decrecimiento.
3 Ejercicio nº 8.- A partir de la gráica de (), di cuáles son sus asíntotas, indica la posición de la curva respecto a ellas halla los intervalos de crecimiento de decrecimiento de la unción: Ejercicio nº 9.- Dada la gráica de (), di cuáles son sus asíntotas e indica la posición de la curva respecto a ellas. Halla también los intervalos de crecimiento de decrecimiento de la unción: Ejercicio nº.- A partir de la gráica de (): a b c Cuáles son los puntos de corte con los ejes? Di cuáles son sus asíntotas. Indica la posición de la curva respecto a las asíntotas verticales.
4 Ejercicio nº.- Representa la siguiente unción, estudiando los aspectos que consideres más relevantes: Ejercicio nº.- Estudia representa la siguiente unción: Ejercicio nº.- Estudia representa la siguiente unción: Ejercicio nº.- Estudia representa la unción: Ejercicio nº 5.- Estudia representa la unción: Ejercicio nº 6.- Representa gráicamente la siguiente unción, estudiando previamente los aspectos que consideres más relevantes: Ejercicio nº 7.- Estudia representa la siguiente unción: Ejercicio nº 8.- Estudia representa la unción: Ejercicio nº 9.- Dada la unción: estudia sus aspectos más relevantes represéntala gráicamente.
5 Ejercicio nº.- Estudia representa la siguiente unción: Ejercicio nº.- Estudia representa la siguiente unción: Ejercicio nº.- Dada la unción: estudia sus aspectos más relevantes represéntala gráicamente. Ejercicio nº.- Representa gráicamente la siguiente unción, estudiando los aspectos que consideres más relevantes: Ejercicio nº.- Estudia representa la unción: Ejercicio nº 5.- Estudia representa la siguiente unción: Ejercicio nº 6.- Dada la unción estudia sus aspectos más relevantes represéntala gráicamente. 5
6 Ejercicio nº 7.- Estudia representa la siguiente unción: Ejercicio nº 8.- Estudia representa la unción: Ejercicio nº 9.- Estudia representa la siguiente unción: Ejercicio nº.- Representa gráicamente la siguiente unción, estudiando previamente los aspectos que consideres más relevantes: Ejercicio nº.- Estudia representa la siguiente unción: Ejercicio nº.- Dada la unción estudia sus aspectos más relevantes represéntala gráicamente., Ejercicio nº.- Estudia representa la unción: 6
7 Ejercicio nº.- Estudia representa la unción: Ejercicio nº 5.- Representa gráicamente la siguiente unción, estudiando previamente los aspectos que consideres más relevantes: Ejercicio nº 6.- Representa gráicamente la siguiente unción, estudiando previamente los aspectos que consideres más relevantes: Ejercicio nº 7.- Estudia representa la unción: Ejercicio nº 8.- Estudia representa la unción: Ejercicio nº 9.- Dada la unción estudia sus aspectos más relevantes represéntala gráicamente. Ejercicio nº.- Estudia representa la siguiente unción: 5 7
8 SOLUCIONES Representación de unciones Ejercicio nº.- Representa una unciónpolinómica, de la que sabemosque : lim ; lim Suderivadaes en Corta a los ejesen, en,.,,,,,,. Ejercicio nº.- Dibuja la gráica de la unción, sabiendoque: Suderivadase anula en,. Solocorta a los ejesen,. Sus asíntotas son:, La posición de la curva respecto a las asíntotas es: e lim ; lim ; lim ; lim 8
9 Ejercicio nº.- Haz la gráica de una unción, Es continua. sabiendo que : lim ; lim Su deriv adase anula en Corta a los ejesenlospuntos,, en, en,.,,,,,,,,. Ejercicio nº.- Representa una unción (), de la que sabemos lo siguiente: La derivada no se anula en ningún punto. La unción es decreciente. Corta a los ejes en (, ) en (, ) lim ; lim Tiene una asíntota horizontal en. Además: 9
10 Ejercicio nº 5.- Representa gráicamente una unción Su deriv adase anula en No corta a los ejes. lim ; lim, en,. Tiene una asíntota oblicua, que es. Además: (), de la que conocemoslo siguiente : Ejercicio nº 6.- La siguiente gráica corresponde a la unción ():
11 a En qué puntos se anula la derivada? b Cuáles son sus asíntotas? c Indica la posición de la curva respecto a sus asíntotas verticales. ' a) Ha unmáimoen b Asíntotas verticales:, Asíntota horizontal:, lim ; lim c) lim ; lim Ejercicio nº 7.- La siguiente gráica corresponde a la unción (). A partir de ella, indica: a Máimos mínimos. b s de corte con los ejes. c Ramas ininitas. d Intervalos de crecimiento de decrecimiento. a) ' Ha unmínimoen ' Ha unmáimoen,,,,,,,. b) c) lim ; lim, d) Decrece en, en, ; crece en,. Ejercicio nº 8.- A partir de la gráica de (), di cuáles son sus asíntotas, indica la posición de la curva respecto a ellas halla los intervalos de crecimiento de decrecimiento de la unción:
12 Asíntota vertical: Posición de la curva: lim ; lim Asíntota horizontal: Posición de la curva: Si, Si, La unciónescrecienteen, en,. Ejercicio nº 9.- Dada la gráica de (), di cuáles son sus asíntotas e indica la posición de la curva respecto a ellas. Halla también los intervalos de crecimiento de decrecimiento de la unción: Asíntota vertical: Posición de la curva: lim ; lim Asíntota horizontal: Posición de la curva:
13 Si Si,, La unciónesdecreciente en, en,. Ejercicio nº.- A partir de la gráica de (): a b c Cuáles son los puntos de corte con los ejes? Di cuáles son sus asíntotas. Indica la posición de la curva respecto a las asíntotas verticales. a (, ) b Asíntotas verticales:, Asíntota horizontal: c) lim ; lim lim ; lim Ejercicio nº.- Representa la siguiente unción, estudiando los aspectos que consideres más relevantes: lim ; lim s de corte con los ejes:,,, Con el eje Y = = s singulares:
14 ', 6, 6 Gráica: Ejercicio nº.- Estudia representa la siguiente unción: lim ; lim s de corte con los ejes: Con el eje Y ( ),,, s singulares: ' s 7,,. Gráica:
15 Ejercicio nº.- Estudia representa la siguiente unción: lim ; lim s de corte con los ejes: Con el eje Y :, (,) (, ) s singulares: ' 6 (,) (, ) Gráica: Ejercicio nº.- Estudia representa la unción: 5
16 lim ; lim s de corte con los ejes:. Cambio z z z z No corta aleje. no nos da un valorreal para. Y, s singulares: ', Gráica: Ejercicio nº 5.- Estudia representa la unción: lim ; lim s de corte con los ejes: (, ) (, ) (, ) Con el eje Y = = (,) s singulares: 6
17 ' (, ) (, ) (, ) Gráica: Ejercicio nº 6.- Representa gráicamente la siguiente unción, estudiando previamente los aspectos que consideres más relevantes: Dominio R {} s de corte con los ejes: Y,, Asíntotas verticales: lim ; lim Asíntota oblicua: es asíntota oblicua. Si, Si, La curvaestá por encima de la asíntota. Lacurva está por debajodelaasíntota. s singulares: 7
18 8 ',, ' Gráica: Ejercicio nº 7.- Estudia representa la siguiente unción: Dominio R {} s de corte con los ejes:, eje Con el, eje el Con Y Asíntota vertical: lim lim ; Asíntota oblicua: es asíntota oblicua. encimadelaasíntota. Lacurva está por, Si debajodelaasíntota. Lacurva está por, Si s singulares:
19 9 ' 8,, ' Gráica: Ejercicio nº 8.- Estudia representa la unción: Dominio R {} s de corte con los ejes:, eje el Con, eje el Con Y Asíntota vertical: lim lim ; Asíntota horizontal: con, con, lim lim s singulares: ' No tiene puntos singulares. Gráica:
20 Ejercicio nº 9.- Dada la unción: estudia sus aspectos más relevantes represéntala gráicamente. Dominio R {} s de corte con los ejes: Y,, Asíntota vertical: lim ; lim Asíntota horizontal: lim, con lim, con s singulares: ' 9 9 No tiene puntos singulares. Gráica:
21 Ejercicio nº.- Estudia representa la siguiente unción: Dominio R {} s de corte con los ejes: Y,, Asíntota vertical: lim ; lim Asíntota horizontal: lim, con lim, con s singulares: ' 6 6 No tiene puntos singulares. Gráica:
22 Ejercicio nº.- Estudia representa la siguiente unción: Dominio R {} s de corte con los ejes:, Y, Asíntota vertical: lim ; lim Rama parabólica pues el grado del numerador es dos unidades maor que el grado del denominador. lim ; lim s singulares ' 6 6 ',, 7 Gráica:
23 Ejercicio nº.- Dada la unción: estudia sus aspectos más relevantes represéntala gráicamente. Dominio R {} s de corte con los ejes:,,; Con el eje Y No corta al eje Y, pues no pertenece al dominio. Asíntota vertical: lim ; lim Rama parabólica pues el grado del numerador es de dos unidades maor que el del denominador. lim ; lim s singulares: ' ', Gráica:
24 Ejercicio nº.- Representa gráicamente la siguiente unción, estudiando los aspectos que consideres más relevantes: Dominio R {} s de corte con los ejes:,,; Con el eje Y No corta el eje Y, pues no está en el dominio. Asíntota vertical: lim ; lim Rama parabólica pues el grado del numerador es dos unidades maor que el del denominador. lim ; lim s singulares: ' ', Gráica:
25 Ejercicio nº.- Estudia representa la unción: Dominio R { } s de corte con los ejes:, Y, Asíntota vertical: lim ; lim Rama parabólica pues el grado del numerador es dos unidades maor que el del denominador. lim ; lim s singulares: ' 6 6 ',, 7 Gráica: 5
26 Ejercicio nº 5.- Estudia representa la siguiente unción: Dominio R {} s de corte con los ejes: s,, Con el eje Y No corta al eje Y, pues no está en el dominio. Asíntota vertical: lim ; lim Rama parabólica pues el grado del numerador es tres unidades maor que el del denominador. lim ; lim s singulares: ' No tiene puntos singulares. Gráica: 6
27 Ejercicio nº 6.- Dada la unción estudia sus aspectos más relevantes represéntala gráicamente. Dominio R {} s de corte con los ejes: No corta aleje Con el eje Y No corta al eje Y, pues no pertenece al dominio. Asíntota vertical: lim ; lim Asíntota horizontal:. lim, con lim, con s singulares: ' No tiene puntos singulares. Gráica: 7
28 Ejercicio nº 7.- Estudia representa la siguiente unción: Dominio R {, } s de corte con los ejes: Y,, Asíntotas verticales:, lim ; lim lim ; lim Asíntota horizontal: lim, con lim, con s singulares: ' 6 6 ' 6, Gráica: 8
29 Ejercicio nº 8.- Estudia representa la unción: Dominio R {, } s de corte con los ejes: Y,, Asíntotas verticales:, lim ; lim lim ; lim Asíntota horizontal: lim, con lim, con s singulares: ' ', Gráica: 9
30 Ejercicio nº 9.- Estudia representa la siguiente unción: Dominio R {, } s de corte con los ejes: s,,, Con el eje Y Asíntotas verticales:, lim ; lim lim ; lim Asíntota horizontal: lim, con lim, con s singulares: ' ' 8 6 6, Gráica:
31 Ejercicio nº.- Representa gráicamente la siguiente unción, estudiando previamente los aspectos que consideres más relevantes: Dominio R s de corte con los ejes: Y,, No tiene asíntotas verticales. Asíntota horizontal: lim, con lim, con s singulares: ' ', Gráica:
32 Ejercicio nº.- Estudia representa la siguiente unción: Dominio R s de corte con los ejes:, eje Con el, eje el Con Y Asíntotas verticales: No tiene Asíntota oblicua: es asíntota oblicua. debajodelaasíntota. Lacurva está por, Si encimadelaasíntota. Lacurva está por, Si s singulares:, ' ' Gráica:
33 Ejercicio nº.- Dada la unción estudia sus aspectos más relevantes represéntala gráicamente., Dominio R {} s de corte con los ejes:,6, 6; Con el eje Y No corta el eje Y, pues no está en el dominio. Asíntota vertical: lim ; lim Asíntota oblicua: Si, Si, s singulares: es asíntota oblicua. Lacurva está por encimadelaasíntota. Lacurva está por encimadelaasíntota.
34 , ' ' Gráica: Ejercicio nº.- Estudia representa la unción: Dominio: Dominio R {} s de corte con los ejes:, eje Con el, eje el Con Y Asíntota vertical: lim lim ; ; Asíntota oblicua: es asíntota oblicua. encimadelaasíntota. Lacurva está por, Si debajodelaasíntota. Lacurva está por, Si
35 5 s singulares: 6 ' 6, ' no vale, pues no está en el dominio.. 7, Gráica: Ejercicio nº.- Estudia representa la unción: Dominio: Dominio R {} s de corte con los ejes:, eje Con el, eje el Con Y
36 6 Asíntota vertical: lim lim ; ; Asíntota oblicua: es asíntota oblicua. encimadelaasíntota. Lacurva está por, Si debajodelaasíntota. Lacurva está por, Si s singulares: 6 ' 6, ' no vale, pues no está en el dominio.. 7, Gráica: Ejercicio nº 5.- Representa gráicamente la siguiente unción, estudiando previamente los aspectos que consideres más relevantes:
37 7 Dominio R s de corte con los ejes:, eje Con el, eje el Con Y Asíntotas verticales: No tiene. Asíntota oblicua: asíntota oblicua. es debajodelaasíntota. Lacurva está por, Si encimadelaasíntota. Lacurva está por, Si s singulares: ', 6 ' Gráica: Ejercicio nº 6.- Representa gráicamente la siguiente unción, estudiando previamente los aspectos que consideres más relevantes:
38 8 Dominio R {, } s de corte con los ejes:, eje el Con,; s,;, eje el Con Y Asíntotas verticales:, lim lim lim lim ; ; Rama parabólica pues el grado del numerador es dos unidades maor que el del denominador. lim lim ; s singulares: ' 6 ; ;, ' z z z z No tiene solución Gráica:
39 9 Ejercicio nº 7.- Estudia representa la unción: Dominio R {} s de corte con los ejes: eje nocorta al eje Con el Con el eje Y No corta al eje Y, pues no está en el dominio. Asíntota vertical: lim lim ; Rama parabólica pues el grado del numerador es dos unidades maor que el del denominador. lim ; lim s singulares: ',, s ' Gráica:
40 Ejercicio nº 8.- Estudia representa la unción: Dominio = R s de corte con los ejes: Y,, Asíntotas verticales: No tiene. Rama parabólica pues el grado del numerador es dos unidades maor que el del denominador. lim ; lim s singulares: ', Gráica Ejercicio nº 9.- Dada la unción estudia sus aspectos más relevantes represéntala gráicamente.
41 Dominio R {} s de corte con los ejes: eje Con el Si z z z z,, s Con el eje Y No corta el eje Y porque, no está en el dominio. Asíntota vertical: lim lim ; Rama parabólica pues el grado del numerador es dos unidades maor que el del denominador. lim lim ; s singulares: 6 ',, s ' Gráica:
42 Ejercicio nº.- Estudia representa la siguiente unción: 5 Dominio = R s de corte con los ejes: Y,, Asíntotas verticales: No tiene. Rama parabólica (pues el grado del numerador es tres unidades maor que el del denominador). lim ; lim s singulares: ' ' , Gráica: 5
REPRESENTACIÓN DE FUNCIONES
REPRESENTACIÓN DE FUNCIONES Ejercicio nº.- Estudia y representa la siguiente unción: ( ) + 6 Ejercicio nº.- Dibuja la gráica de la unción: ( + ) ( ) Ejercicio nº.- Dada la unción: y sen sen, [0, ] a) Halla
SOLUCIONES ( ) ( ) ( ) 2 ( ) ( ) Fecha: La pendiente de la recta es m = = x = 4. x = 2 2x. Ejercicio nº 1.- Solución: La recta será:
Ejercicio nº.- Halla la ecuación de la recta tangente a la curva que sea paralela a la recta y. SOLUCIONES ' Fecha: La pendiente de la recta es m Cuando, y La recta será: Ejercicio nº.- y ( ) Averigua
REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS
REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS DOMINIO - Polinomio : D = R - Cocientes : D = R {puntos que anulan el denominador} - Raíces de índice par : D = {Lo
Página 322. 3. Representa: a) y = b) y = c) y = cos 2x + cos x. a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales:
Página. Representa: e e a) y = b) y = c) y = cos + cos e a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales: f () = +@ 8 0 f () = +@ 8 0 + Asíntota vertical: = 0 f () = 0. Además, f () > 0
Tema Derivadas. Aplicaciones Matemáticas CCSSI 1º Bachillerato 1
Tema Derivadas. Aplicaciones Matemáticas CCSSI 1º Bachillerato 1 EJERCICIO : A partir de la gráica de (): a b c Cuáles son los puntos de corte con los ejes? Di cuáles son sus asíntotas. Indica la posición
x + x 2 +1 = 1 1 = 0 = lím
UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
TEMA 12 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES
Tema Derivadas. Aplicaciones Matemáticas I º Bacillerato TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES TASA DE VARIACIÓN MEDIA DE UNA FUNCIÓN EN UN INTERVALO EJERCICIO : Halla la tasa de variación
Autor: Antonio Rivero Cuesta, Tutor C.A. Palma de Mallorca
Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
APLICACIONES DE LA DERIVADA I. Ejercicios a resolver en la práctica. = x + 2. Determina y clasifica los puntos o valores
UNIVERSIDAD SIMÓN BOLÍVAR Enero-Marzo 010 DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-1111) Fecha de publicación: 0-0-010 Contenido Tercer Parcial APLICACIONES DE LA DERIVADA I Contenidos
TEMA 11 REPRESENTACIÓN DE FUNCIONES
Tema Representación de unciones Matemáticas II º Bachillerato TEMA REPRESENTACIÓN DE FUNCIONES EJERCICIO : Representa gráicamente la unción: Dominio R 8 respecto al origen. 8 Simetrías:. No es par ni impar:
EJERCICIOS DE LÍMITES DE FUNCIONES
EJERCICIOS DE LÍMITES DE FUNCIONES Ejercicio nº.- A partir de la gráica de (), calcula: c) d) e) 5 Ejercicio nº.- La guiente gráica corresponde a la unción (). Sobre ella, calcula los límites: c) d) e)
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas Función Derivada Función compuesta Derivada y f x y f x y f g x
Tabla de derivadas Función Derivada Función compuesta Derivada k ' 0 ' ' n ' ' ' e ' n n n n ' n ' e a ' ln ln log a a a ' ' e a ln ln a Reglas de derivación log a ' ' ' ' ' ' ' ' ' ln ' ' ' ' e a a '
12.1 CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO
INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y = () en un intervalo
FUNCIONES RACIONALES. HIPÉRBOLAS
www.matesronda.net José A. Jiménez Nieto FUNCIONES RACIONALES. HIPÉRBOLAS 1. FUNCIÓN DE PROPORCIONALIDAD INVERSA El área de un rectángulo es 18 cm 2. La siguiente tabla nos muestra algunas medidas que
Cálculo de derivadas. Aplicaciones. 1ºBHCS
Pág. de 5 Cálculo de derivadas. Aplicaciones. ºBHCS Ejercicio nº.- Consideramos la unción: Halla la tasa de variación media en el intervalo [0, ] e indica si () crece o decrece en ese intervalo. TVM Ejercicio
REPRESENTACIÓN GRÁFICA DE FUNCIONES
REPRESENTACIÓN GRÁFICA DE FUNCIONES a. Dominio de definición: D = Dom f() = { R eiste f()} b. Puntos de corte con los ejes: Con el eje OX (abscisas): f() = 0 : (,0). Ninguno, uno o más puntos. Con el eje
(Apuntes en revisión para orientar el aprendizaje) Capítulo IV Variación de funciones. Extremos
(Apuntes en revisión para orientar el aprendizaje) Capítulo IV Variación de unciones. Etremos INTRODUCCIÓN En múltiples problemas de ingeniería se requiere optimizar una o varias de las variables que intervienen
Asíntotas en una función.
Asíntotas en una unción. Las asíntotas son rectas a las cuales la unción se va aproimando indeinidamente, cuando por lo menos una de las variables ( o y) tienden al ininito. Deinición: Si un punto, y )
Estudio de funciones mediante límites y derivadas
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Solución. - Verticales: En los puntos excluidos del dominio donde el límite quede de la forma k. 3( ) = Asíntota vertical. = + x 2.
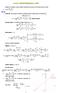Estudiar sus asíntotas y ramas ininitas valorando la posición de la unción respecto de ellas.. ( ) - Verticales: En los puntos ecluidos del dominio donde el límite quede de la orma D[ ( ) ] R { } 6 : Se
REPRESENTACIÓN DE FUNCIONES
8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2015 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
1. f(x) = x3 1 x 2. 2. f(x) = x2 9 x 2 4. 3. f(x) = x 3 x + 2. x 3 (x 1) 2. 4. f(x) = 5. f(x) = x + 5 x 2 9. 6. f(x) = x2 3 x 2. x 2 3 x 2. 7.
. f() =. f() = 9. f() =. f() = ( ). f() = 9 6. f() = 7. f() =. f() = 9. f() = p. f() =. f() =. f() = ( ). f() = 9. f() = ( ) . f() = Función racional con asíntota oblícua. Einamos los puntos que anulan
BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE. ESTUDIO DE LA GRÁFICA DE UNA FUNCIÓN
BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE. ESTUDIO DE LA GRÁFICA DE UNA FUNCIÓN Crecimiento y decrecimiento. Extremos absolutos y relativos. Concavidad y convexidad. Asíntotas.
UNIDAD 8 Representación de funciones
Pág. de 6 Representa las siguientes funciones racionales: y 5 + 7 es raíz del denominador y no lo es del numerador, es asíntota vertical. Veamos la posición de la curva respecto a ella estudiando sus signos
Bloque II. Análisis. Autoevaluación. BACHILLERATO Matemáticas aplicadas a las Ciencias Sociales I. Página 210
Matemáticas aplicadas a las Ciencias Sociales I Autoevaluación Página 0 Observa la gráfica de la función y f () y a partir de ella responde: a) Cuál es su dominio de definición? su recorrido? b) Representa
TEMA 12 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES.
TEMA DERIVADAS Y APLICACIONES MATEMÁTICAS I º Bach. TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. Tasa d variación mdia. Cálculo y signiicado EJERCICIO : Considramos la unción:. Halla la tasa
Tipos de Funciones. 40 Ejercicios para practicar con soluciones. 1 Representa en los mismos ejes las siguientes funciones: 1 x
Tipos de Funciones. 40 Ejercicios para practicar con soluciones Representa en los mismos ejes las siguientes funciones: a) y = ; b) y = ; c) y = y= y= y= Representa las siguientes funciones: a) y = b)
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
Autoevaluación. Bloque IV. Análisis. BACHILLERATO Matemáticas I. Página Observa la gráfica de la función y = f (x) y a partir de ella responde:
Autoevaluación Página Observa la gráfica de la función y = f () y a partir de ella responde: a) Cuál es su dominio de definición? su recorrido? b) Representa gráficamente: y = f ( + ); y = f () + ; y =
REPRESENTACIÓN GRÁFICA DE FUNCIONES
Página 1 de 5 REPRESENTACIÓN GRÁFICA DE FUNCIONES 1 Determinar en cuál de los siguientes intervalos la función f(x) = ln (x+1) es estrictamente cóncava. A (-, 0) B [-1, 1] C (-1, ) D Nunca es estrictamente
REPRESENTACIÓN DE FUNCIONES
REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
Representaciones gráficas
1 MAJ99 Representaciones gráficas 1. Se considera la función 3 f ( ) 1 60 3 (a) Hállense sus máimos y mínimos. (b) Determínense sus intervalos de crecimiento y decrecimiento. (c) Represéntese gráficamente.
1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6
![1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6](/thumbs/40/21103079.jpg "1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6")
ejerciciosyeamenes.com PROBLEMAS DE DERIVADAS 1. Calcula la tasa de variación media de la función +- en los intervalos: a) [- 1,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación media
Ejercicios de representación de funciones
Ejercicios de representación de funciones Representar las siguientes funciones, estudiando su: Dominio. Simetría. Puntos de corte con los ejes. Asíntotas y ramas parabólicas. Crecimiento y decrecimiento.
1Tema 11 Representación de funciones
1Tema 11 Representación de funciones 1. Del estudio a la gráfica. a) Representa una función y f () sabiendo que: Dominio: 0 Corta a OX en = 1. Asín. horizontal y = 0: Asín. vertical = 0: Si Si Si Si, y
Grado en Química Bloque 1 Funciones de una variable
Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 4: FUNCIONES
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
JUNIO 2010. Opción A. 1 1.- Dada la parábola y = 3 área máxima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola.
Junio 00 (Prueba Específica) JUNIO 00 Opción A.- Dada la parábola y 3 área máima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola., y la recta y 9, hallar las dimensiones
Página 194 EJERCICIOS Y PROBLEMAS PROPUESTOS. Tasa de variación media PARA PRACTICAR UNIDAD
UNIDAD Página 9 EJERCICIOS PROBLEMAS PROPUESTOS PARA PRACTICAR Tasa de variación media Calcula la tasa de variación media de esta función en los intervalos: a) [, 0] b) [0, ] c) [, 5] 0 5 f (0) f ( ) a)
Resoluciones de la autoevaluación del libro de texto. cos x. (x + 3) x = 1 x = 3
BLOQUE IV Análisis Resoluciones de la autoevaluación del libro de teto Pág. de 7 Halla el dominio de definición de las funciones siguientes: a) y = log ( ) b) y = cos a) y = log ( ); > 0 8 < ; Dom = (
ASÍNTOTAS Y RAMAS. Ejercicio nº 1.- Halla las asíntotas verticales de: y sitúa la curva respecto a ellas. Ejercicio nº 2.-
ASÍNTOTAS Y RAMAS Ejercicio nº.- Halla las asíntotas verticales de: y sitúa la curva respecto a ellas. Ejercicio nº.- Halla las asíntotas verticales de la siguiente unción y sitúa la curva respecto a ellas:
DERIVADAS. TÉCNICAS DE DERIVACIÓN
DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
x = 1 Asíntota vertical
EJERCICIO Sea la función f ( ). a) Indique el dominio de definición de f, sus puntos de corte con los ejes, sus máimos mínimos, eisten, sus intervalos de crecimiento decrecimiento. b) Obtenga las ecuaciones
Representación gráfica de funciones. Un ejemplo resuelto. Para comprobar si tiene asíntotas oblicuas, calculamos el límite cuando x tiende a -
Representación gráica de unciones. Un ejemplo resuelto Consideremos la unción deinida por la epresión + =. Dominio Debemos ecluir del dominio los valores de que anulan el denominador. Así, el dominio Dom
Determina las asíntotas de las siguientes funciones e interpreta gráficamente los resultados:
Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS Determina las asíntotas de las siguientes funciones e interpreta gráficamente los resultados: ) f ( ) 4 f ( ) es una función polinómica
REPRESENTACIÓN DE FUNCIONES
REPRESENTACIÓN DE FUNCIONES REFLEXIONA Y RESUELVE Descripción de una gráfica Traza unos ejes coordenados sobre papel cuadriculado y representa una curva, lo más sencilla posible, que cumpla las siguientes
Ejercicios de representación de funciones
Ejercicios de representación de funciones 1.- Representar las siguientes funciones, estudiando su: Dominio. Simetría. Puntos de corte con los ejes. Asíntotas y ramas parabólicas. Crecimiento y decrecimiento.
FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN
FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN 1 FUNCIONES FUNCIÓN REAL DE VARIABLE REAL Una función real de variable real es una relación que asocia a cada número real, (variable independiente),
Apuntes Matemáticas 2º de bachillerato. Tema 5. Estudio de funciones
Apuntes Tema 5 Estudio de funciones 5.1 Dominio Hay que determinar para qué intervalos de números reales, o puntos aislados, la función existe o está definida. Para ello tenemos que prestar atención a
ANÁLISIS (Selectividad)
ANÁLISIS (Selectividad) 1 Sea f : R R la función definida por f() ln ( +1). (a) Determina los intervalos de crecimiento y decrecimiento y los etremos relativos de la función f (puntos donde se alcanzan
EXAMEN DE MATEMATICAS II 2ª ENSAYO (1) Apellidos: Nombre:
EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
P. A. U. LAS PALMAS 2005
P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
REPRESENTACIÓN DE CURVAS - CCSS
REPRESENTACIÓN DE CURVAS - CCSS Esquema Para representar gráficamente una función se debe estudiar: 1. Dominio. Puntos de corte con los ejes coordenados. Paridad y periodicidad 4. Asíntotas 5. Monotonía
Colegio Portocarrero. Curso 2014-2015. Departamento de matemáticas. Análisis y programación lineal
Análisis y programación lineal Problema 1: La gráfica de la función derivada de una función f es la parábola de vértice (0, 2) que corta al eje de abscisas en los puntos ( 3, 0) y (3, 0). A partir de dicha
Hacia la universidad Análisis matemático
Hacia la universidad Análisis matemático OPCIÓN A. a) Deriva las funciones f( ) = 8, g ( ) =, h ( ) = e. f( ) si 0 b) Indica si la función m ( ) = es continua en =. g ( ) si < c) Escribe la ecuación de
Colegio Portocarrero. Curso Departamento de matemáticas. Análisis. (Límites/Asíntotas/Continuidad/Derivadas/Aplicaciones de las derivadas)
Análisis (Límites/Asíntotas/Continuidad/Derivadas/Aplicaciones de las derivadas) Problema 1: Sea la función Determina: a) El dominio de definición. b) Las asíntotas si existen. c) El o los intervalos de
Tema 8: Iniciación al cálculo de derivadas. Aplicaciones
Tema 8: Iniciación al cálculo de derivadas. Aplicaciones Ejercicio 1. Hallar el valor de la derivada de la función y 5 en los puntos 1, 0 y. Solución: En 1 : T.V.M. 1,1 h h Por tanto, f (1) lím ( h) h0
Procedimiento para determinar las asíntotas verticales de una función
DETERMINACIÓN DE ASÍNTOTAS EN UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición
Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones.
Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones. 0.. Concepto de derivada. Definición. Sea f : S R R, a (b, c) S. Decimos que f es derivable en a si existe: f(x) f(a)
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2002 MATEMÁTICAS II TEMA 4: FUNCIONES
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 00 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio 1, Opción A Junio, Ejercicio 1, Opción B Reserva 1, Ejercicio 1, Opción B Reserva 1, Ejercicio, Opción A
CRECIMIENTO Y DECRECIMIENTO. MÁXIMOS Y MÍNIMOS.
pág.1 CRECIMIENTO Y DECRECIMIENTO. MÁXIMOS Y MÍNIMOS. En la figura se observa la recta tangente a una función creciente. La recta tangente es siempre creciente también para cualquier punto, por lo que
5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días
![5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días](/thumbs/40/21102307.jpg "5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días")
. [204] [ET-A] Una empresa ha realizado un estudio sobre los beneficios, en miles de euros, que ha obtenido en los últimos 0 años. La función a la que se ajustan dichos beneficios viene dada por B(t) =
Tema 4: FUNCIONES Y LÍMITES. 1º Bachillerato Sociales. Lomce
º Bachillerato Sociales. Lomce. DOMINIO. CONCEPTO DE LIMITES. LIMITES EN UN PUNTO 4. INDETERMINACIONES 5. LIMITES EN EL INFINITO 6. PROPIEDADES DE LIMITES.-Calcula el dominio: a f ( b f ( c f ( d f (.-
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 4: FUNCIONES
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Teoría Tema 9 Representación gráfica de funciones
página 1/24 Teoría Tema 9 Representación gráfica de funciones Índice de contenido Gráficas de funciones...2 Gráfica de una parábola...3 Gráfica de un polinomio de grado 3...6 Gráfica de un cociente de
5 GUÍA PARA REALIZAR ESTUDIO DE FUNCIÓN
5 GUÍA PARA REALIZAR ESTUDIO DE UNCIÓN ) Determinar el Dominio de la función. ) Hallar, si eisten, las Intersecciones con los Ejes de Coordenadas Signo. ( Int. con eje y, hacer = Int. con eje, hacer y
Matemáticas aplicadas a las CC.SS. II
Tema Nº 8 Aplicaciones de las Derivadas ( 17! Determina las dimensiones de una ventana rectangular que permita pasar la máima cantidad de luz, sabiendo que su marco debe medir 4 m. ---oooo--- La ventana
SOLUCIONES HOJA 5: APLICACIONES DE LA DERIVADA 1
MATEMÁTICAS:º BACHILLERATO SOLUCIONES HOJA 5: APLICACIONES DE LA DERIVADA.- Calcular los etremos relativos de las siguientes funciones: a) f ( ) D(f) (Por ser polinómica) ; Posibles máimos o mínimos 6
TEMA 9. Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Problemas Resueltos
64 TEMA 9. Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Problemas Resueltos Crecimiento y decrecimiento. Máimos y mínimos relativos; puntos de infleión. Dada la función
Examen de Matemáticas 2 o de Bachillerato Mayo 2003
Examen de Matemáticas o de Bachillerato Mayo 1. (a) Dibuja el recinto limitado por las curvas y = e x+, y = e x y x =. (b) Halla el área del recinto considerado en el apartado anterior. (a) El dominio
Aplicaciones de la derivada
CAPÍTULO 8 Aplicaciones de la derivada 8. Máimos mínimos locales Si f. 0 / f./ para cada cerca de 0, es decir, en un intervalo abierto que contenga a 0, diremos que f alcanza un máimo local o un máimo
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 5: INTEGRALES
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Matemáticas Febrero 2013 Modelo A
Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
ANTES DE COMENZAR RECUERDA
ANTES DE COMENZAR RECUERDA 00 Determina cuáles de estos vectores son paralelos y cuáles son perpendiculares a v (, ). a) v ( 6, ) b) v (, ) c) v (, ) a) v v Los vectores son paralelos. b) v v 0 Los vectores
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2008 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 008 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
< La recta y = -4/5 es una asíntota horizontal en +4. < La misma recta es también asíntota en -4. < y asíntota y = -4/5 = -0,8
Ramas infinitas de una curva. Asíntotas horizontales Ejemplo 1. Analizar si la curva tiene o no asíntotas horizontales Análisis del comportamiento de la función en +4 : x 6 +4 < La recta y = -4/5 es una
ANÁLISIS. Página a) Escribe la expresión analítica de esta función. b) Observa la gráfica y di el valor de los siguientes límites:
II ANÁLISIS Página 00 a) Escribe la epresión analítica de esta función. b) Observa la gráfica y di el valor de los siguientes ites: f (); f (); f () 8 @ 8 4 ( + ), Ì a) f () = 3 4, > 8 +@ 4 5 b) f () =
Montesion. Examen final 2ª evaluación Tel.:
Montesion. Eamen final ª evaluación Tel.: 665.516.510 1º Los gastos de mantenimiento de la maquinaria de una determinada empresa, G () (en miles de euros), vienen dados en función del tiempo, en meses,
y con la semiamplitud δ =1. 2.
LÍMITE DE UNA FUNCIÓN UNIDAD II II. ENTORNOS Se denomina entorno de un punto a en, al intervalo abierto ( δ a δ ) semiamplitud del intervalo. a, donde δ es la El entorno de a, en notación de conjuntos
TEMA 7. Representación gráfica de funciones y Optimización Problemas Resueltos
Matemáticas Aplicadas a las Ciencias Sociales II. Soluciones de los problemas propuestos. Tema 7 TEMA 7. Representación gráfica de funciones y Optimización Problemas Resueltos Crecimiento y decrecimiento.
Apellidos: Nombre: Curso: 1º Grupo: C Día: 2- III- 16 CURSO
EXAMEN DE MATEMÁTICAS GRÁFICAS E INTEGRALES Apellidos: Nombre: Curso: º Grupo: C Día: - III- 6 CURSO 05-6. [ punto] Estudia si las siguientes funciones presentan simetría par (respecto del eje de ordenadas)
10 Representación de funciones
0 Representación de funciones Página 99 Límites y derivadas para representar una función 5 lm í x f (x) = lm í x + f (x) = lm í f (x) = + lm í f (x) = + x x + f ( 9) = 0; f ' (0) = 0; f () = 0 f ' (0)
1.- Sea la función f definida por f( x)
Solución Eamen Final de la 3ª Evaluación de º Bcto..- Sea la función f definida por f( ) a) El dominio de la función es Dom( f) estudiando las asíntotas verticales:, por tanto vamos a empezar La función
Gráficamente: una función es continua en un punto si en dicho punto su gráfica no se rompe. Función continua en x = 0 Función no continua en x = 0
Funciones continuas Funciones continuas Continuidad de una función Si x 0 es un número, la función f(x) es continua en este punto si el límite de la función en ese punto coincide con el valor de la función
9. Rectas e hipérbolas
08 SOLUCIONARIO 9. Rectas e hipérbolas Representa gráficamente las siguientes ecuaciones. Di cuáles son funciones y clasifícalas: 8. y =. FUNCIONES CONSTANTES LINEALES PIENSA CALCULA y = Halla mentalmente
Resoluciones de la autoevaluación del libro de texto. (x + 3) x = 1 x = 3
Resoluciones de la autoevaluación del libro de teto Pág. de 6 a) Escribe la epresión analítica de esta función. b) Observa la gráfica y di el valor de los siguientes ites: f (); f (); f () 8 @ 8 4 ( +
RESOLUCIÓN DE ACTIVIDADES
RESOLUCIÓN DE ACTIVIDADES Actividades iniciales. En las siguientes funciones estudia las características: dominio, los puntos de corte con los ejes, las simetrías, la periodicidad, las asíntotas, la monotonía,
8 Límites y continuidad
Solucionario 8 Límites y continuidad ACTIVIDADES INICIALES 8.I. Simplifica las epresiones siguientes. a) 7 9 c) 3 6 5 b) 3 a) 7 9 ( 3) ( 3) ( 4) 3) 4 3 b) 3 8 4 d) ( )( 3)( ) 4 8 4 ( )( 4) ( )( ) 4 c)
x = 0, la recta tangente a la gráfica de f (x)
CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
"""##$##""" !!!""#""!!! """##$##""" (c) Verdadero siempre que los términos en grado p = q se anulen.
Unidad nº 0 FFUNCI IONEES POLLI INÓMICAS YY RACIONALLEES! 7 AUTOEVALUACIÓN Halla la suma y el producto de los polinomios P() y Q() - - 5 -. P() + Q() 5 - +.. P() Q() ( ) ( 5 ) - 6 5 5 + + 0 + - 6 5 + 5
FUNCIÓN RACIONAL. 1 es racional x. es racional. es racional. es racional. es racional. El dominio de toda función racional es igual al conjunto ( ) 0
FUNCIÓN RACIONAL Función Racional. Dados polinomios p( ) q( ) tales que no tienen actores comunes, se deine la unción racional como la unción ormada por el cociente de los polinomios Ejemplos de unciones
GRÁFICA DE FUNCIONES
GRÁFICA DE FUNCIONES. Función cuadrática. Potencia. Eponencial 4. Logarítmica 5. Potencia de eponente negativo 6. Seno 7. Coseno 8. Tangente 9. Valor absoluto. Dominio. Puntos de corte con los ejes. Simetrías.
FUNCIONES CUADRÁTICAS. PARÁBOLAS
FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
TEMA 11: ESTUDIO LOCAL Y GLOBAL DE FUNCIONES. OPTIMIZACIÓN
TEMA 11: ESTUDIO LOCAL Y GLOBAL DE FUNCIONES. OPTIMIZACIÓN ESTUDIO DE LA MONOTONÍA DEF.- Una función es CRECIENTE en un intervalo I del dominio de la función si: x1 < x2 I f ( x1 ) f ( x2). Si se cumple
RESUMEN PARA HACER EL ANÁLISIS COMPLETO DE UNA FUNCIÓN:
RESUMEN PARA HACER EL ANÁLISIS COMPLETO DE UNA FUNCIÓN: Ejemplo: 1 Dominio Representación de en el intervalo [,] Los puntos que no pertenecen al dominio de una función racional, son aquellos que anulan