CURSO DE INGRESO AREA MATEMATICA
|
|
|
- Dolores Valdéz Pinto
- hace 9 años
- Vistas:
Transcripción
1 Uiversidd Niol de Misioes UNIVERSIDAD NACIONAL DE MISIONES FACULTAD DE INGENIERÍA CURSO DE INGRESO AREA MATEMATICA el ietífio explor lo que existe, el igeiero re lo que u h existido Krm Ju Muel de Ross Tel/Fx E-mil :[email protected] Oerá Misioes CP 60
2 SISTEMA DE ACCESO COMÚN A LAS CARRERAS DE INGENIERÍA DE LA UNM III AREA MATEMATICA OBJETIVOS Ojetivos Geerles Atulizr los ooimietos mtemátios ásios dquiridos e el ivel medio/polimodl. Logrr el mejo propido del leguje mtemátio. Desrrollr hiliddes pr l presetió esrit de u proeso mtemátio. Fmilirizrse e l letur ompresiv e iterpretió de textos de mtemáti. Desrrollr hiliddes pr relior el leguje lítio o el leguje gráfio. Geerr proesos de rzomietos lógios, retivos y dedutivos. Promover el desrrollo de hiliddes de estudio resposle, trjo idepediete y oopertivo. Ojetivos espeífios Atulizr los ooimietos ásios de ls operioes o úmeros y sus propieddes. Idetifir ls fuioes poliómis, sus diferetes represetioes y elemetos rterístios. Utilizr operioes o poliomios e simplifiió y resoluió de euioes rioles. Resolver prolems utilizdo euioes de primer grdo o u y dos iógits. Resolver prolems utilizdo sistems de dos euioes o dos iógits. Alizr omprtivmete el álulo lítio y l represetió gráfi. Utilizr distitos sistems de mediió de águlos distiguiedo el más deudo e determidos sos Formulr y resolver prolems utilizdo l trigoometrí.
3 CONTENIDOS Tem : Cojutos Numérios Números: Nturles, Eteros, Rioles, Irrioles y Reles. Operioes y propieddes. Notió ietífi. Orde. Represetió e l ret uméri. Apliió de ls propieddes de ls resoluioes de euioes e ieuioes. Número omplejos. Form iómi. Tem : Fuioes Poliómis Poliomios. Operioes o poliomios. Divisiilidd de poliomios: Teorem del Resto y Teorem del ftor. Ftoreo. Simplifiió de expresioes rioles. Fuioes Poliómis. Gráfios. Iterseió o los ejes. Fuió liel. Fuió udráti. Tem : Euioes y Sistems de Euioes Lieles Euioes de primer grdo o u y o dos vriles. Soluió líti y gráfi. Sistems de dos euioes o dos vriles. Resoluió líti por igulió, sustituió o elimiió. Iterpretió geométri de ls distits soluioes. Tem : Trigoometrí Sistems de mediió de águlos. Relioes trigoométris de u águlo. Relió fudmetl de l trigoometrí. Círulo trigoométrio. Fuioes trigoométris. Represetió gráfi. Idetiddes trigoométris. Apliioes: Resoluió de triágulos retágulos y oliuágulos, Form trigoométri de los úmeros omplejos.
4 SISTEMA DE ACCESO COMÚN A LAS CARRERAS DE INGENIERÍA DE LA UNM INDICE GENERAL OBJETIVOS CONTENIDOS III. UNIDAD : CONJUNTOS NUMÉRICOS 6 III.. LOS NÚMEROS NATURALES 6 III.. LOGARITMO DE UN NÚMERO REAL 7 III.. LOS NÚMEROS COMPLEJOS 9 III.. TRABAJO PRÁCTICO: CONJUNTOS NUMÉRICOS III. UNIDAD : FUNCIONES POLINÓMICAS 9 III.. POLINOMIOS 9 III.. OPERACIONES ENTRE POLINOMIOS 0 III.. FACTORIZACIÓN DE POLINOMIOS 6 III.. APLICACIONES DEL FACTOREO 9 III.. FUNCIONES POLINÓMICAS 0 III..6 TRABAJO PRÁCTICO: FUNCIONES POLINÓMICAS 6 III. UNIDAD : ECUACIONES DE PRIMER GRADO 66 III.. ECUACIONES DE PRIMER GRADO 66 III.. SISTEMA DE ECUACIONES 7 III.. TRABAJO PRÁCTICO: ECUACIONES DE PRIMER GRADO 8 III.. TRABAJO PRÁCTICO: SISTEMA DE ECUACIONES 8 III. UNIDAD : TRIGONOMETRÍA 88 III.. SISTEMAS DE MEDICIÓN DE ÁNGULOS 88 III.. RELACIONES TRIGONOMÉTRICAS DE UN ÁNGULO 9 III.. RESOLUCIÓN DE TRIÁNGULOS 97 III.. TRABAJO PRÁCTICO: TRIGONOMETRÍA 0
5 III. UNIDAD : CONJUNTOS NUMÉRICOS III.. NUMEROS. OPERACIONES. PROPIEDADES III... Los Números Nturles Cd dí, e uestr oversió, por l televisió, e l letur de por ejemplo u dirio, o e el trjo está presete l ide de ojuto. Ejemplos: Al psr por l plz se levtó u dd de ploms. E el dirio leemos que uestro equipo de fútol preferido gó el prtido. Todos etedemos que u dd es u ojuto de pájros, el equipo de fútol es u ojuto de jugdores. E todos estos ejemplos, se trt de sióimos de l plr ojuto y o u defiiió. E mtemáti, utilizmos el térmio ojuto si u defiiió previ y o el mismo sigifido que se le d e l vid diri. Otro ejemplo: El ojuto de ls ots musiles Este ojuto serí A {do, re, mi, f, sol, l, si} Costtemete reliomos ojutos o distitos fies; uo de ellos es el de otr sus elemetos. Pr otr utilizmos los úmeros turles. Al priipio, el homre fue reliodo ojutos pr otr sus elemetos. Al omprr tiddes, se eró uestr oió tul de otr medite orrespodeis, por ejemplo, o prtes del uerpo: tego tts vs omo dedos e u mo. Cd v se relio o u úio dedo; los elemetos del ojuto v se puede prer o el ojuto de los dedos de l mo; deimos, etoes, que estos dos ojutos so oordiles, o que tiee el mismo rdil. El rdil de u ojuto fiito es u úmero turl Ejemplos: El rdil del ojuto de vs es el úmero. El rdil del ojuto de ots musiles es 7. El rdil del ojuto vío es 0. Al ojuto de los úmeros turles lo desigmos o N: N 0 {0,,,,,,... } Ls propieddes de N 0 so:. Es ifiito ( ).. Tiee primer elemeto: ero. No tiee último elemeto.. Todo úmero turl tiee u suesor. U úmero turl y su suesor se die oseutivos.. Todo úmero (exepto ero) tiee u teesor.. El suesor de u úmero turl es myor que él y su teesor es meor. Simólimete: < < 6
6 SISTEMA DE ACCESO COMÚN A LAS CARRERAS DE INGENIERÍA DE LA UNM 6. Etre dos úmeros turles existe siempre u úmero fiito de úmeros turles. Por eso se die que es u ojuto disreto. III... Los Números Negtivos Etoes, el homre ooe los úmeros turles desde el mometo e que tuvo eesidd de otr, pero éstos o le lz pr expresr muhs situioes. Ejemplos: Ls temperturs jo ero El sldo deudor de u uet ri Por eso fue eesri l reió de los úmeros egtivos. Los úmeros egtivos so los opuestos de los úmeros turles distitos de ero. El 0 o es i positivo i egtivo. El ojuto o grupo de los úmeros eteros es l uió del ojuto de los úmeros eteros egtivos, el ojuto que tiee ero omo úio elemeto y el ojuto de los úmeros eteros positivos. Al ojuto de los úmeros eteros lo desigmos o Z Z {...,,,, 0,,,,...} Ls propieddes de Z so:. Es ifiito ( ).. No tiee primero i último elemeto.. Todo úmero etero tiee u suesor. U úmero etero y su suesor se die oseutivos.. Todo úmero etero tiee u teesor.. El suesor de u úmero etero es myor que él y su teesor es meor. Simólimete: < < 6. Etre dos úmeros eteros existe siempre u úmero fiito de úmeros eteros. Por eso, el ojuto de úmeros eteros es disreto. III... Los Números Friorios Estos úmeros surge de l eesidd de expresr frioes de uidd. Ejemplos: Tomás omió tres de ls utro prtes de ls que ost su tlet de hoolte dividido 7
7 Se llm frió u oiete de úmeros eteros. Todo úmero que puede ser expresdo medite u frió es u úmero riol. A este ojuto de úmeros lo desigmos o l letr Q. Todo úmero etero se puede expresr omo u frió o deomidor. Ejemplos: ; Todo úmero riol se puede expresr omo úmero deiml exto o periódio. Ejemplos: 0, ; 0, ) 0 Dos frioes, y, que umple l odiió d so equivletes. Esto d sigifi que expres el mismo úmero riol. L uió del ojuto Z de úmeros eteros y el ojuto de úmeros friorios que o represet úmeros eteros es el ojuto Q de los úmeros rioles. Ls propieddes de Q so:. Es ifiito ( ).. No tiee primero i último elemeto.. Etre dos úmeros rioles existe ifiitos rioles. Por ello, se die que el ojuto de úmeros rioles es deso. Ejemplo: Etre y se puede eotrr ttos rioles omo se quier. Bst overtir ests frioes e otrs equivletes de deomidor myor Como oseuei de l propiedd terior, igú úmero riol tiee suesor i teesor.. Q es u ojuto ordedo por l relió meor o igul.. Si los úmeros rioles y so frioes irreduiles, se umple que: > d > d d 8
8 SISTEMA DE ACCESO COMÚN A LAS CARRERAS DE INGENIERÍA DE LA UNM Ejemplos: > porque > 6 < porque tod frió egtiv es meor que ulquier frió positiv. 7 < porque tod frió uyo umerdor es myor que el deomidor es myor que l uidd. L represetió e l ret uméri de los distitos úmeros que hemos visto hst quí es: Nturles Eteros Rioles L pregut: los úmeros rioles omplet l ret uméri?. O, l mism pregut o otrs plrs, qued putos de l ret los que o les orrespode igú úmero riol? III... Los Números Irrioles L euió x 0 o tiee soluió e el mpo de los úmeros rioles. L soluió est euió requiere l desripió de los úmeros irrioles. Los úmeros irrioles so quellos uy expresió deiml es ifiit y o tiee u período, por ejemplo: El úmero pi: π + El úmero de oro: φ Ls ríes de ídie pr de úmeros turles uyos resultdos o so turles Ejemplo: ; 6 ; 8 ; et. Ls ríes de ídie impr de úmeros eteros uyos resultdos o so eteros Ejemplo: 7 ; ; et. 9
9 Por tto: Los úmeros irrioles o se puede expresr omo u frió o omo u oiete de dos eteros. Pr oteer u úmero irriol, es sufiiete esriir u úmero uys ifrs deimles se ifiits y o presete periodiidd. Por ejemplo:,... L otió pr los úmeros irrioles será I. III... Los Números Reles L uió del ojuto Q de úmeros rioles y el ojuto I de úmeros irrioles es el ojuto R de los úmeros reles, que puede represetrse medite u ret otiu llmd ret rel. Cd puto de est ret represet u úmero rel, y d úmero rel le orrespode u úio puto sore l ret. Por ello, o los úmeros reles se omplet l ret uméri. Ls propieddes de R so:. Es ifiito ( ).. No tiee primero i último elemeto.. Etre dos úmeros reles existe siempre u úmero ifiito de reles. Se die que el ojuto de úmeros reles es deso.. Nigú úmero rel tiee suesor i teesor.. El ojuto R es u ojuto totlmete ordedo por l relió meor o igul. 6. Es u ojuto otiuo porque omplet l ret uméri Hemos visto los úmeros turles, eteros, rioles y reles. U úmero turl es tmié etero, y u úmero etero puede esriirse omo u úmero riol utilizdo u frió que teg u e el deomidor. Si m es etero, etoes m m es riol Teemos sí dos grdes grupos de úmeros: los rioles y los irrioles. Estos dos grdes grupos form el ojuto de los úmeros reles. R Q I Z N 0
10 SISTEMA DE ACCESO COMÚN A LAS CARRERAS DE INGENIERÍA DE LA UNM Los úmeros reles tmpoo so l soluió tods ls euioes (omo, por ejemplo x + 0 ), si emrgo os port l estrutur eesri pr omezr trjr o situioes mtemátis e ls que utilizremos ls operioes y sus propieddes defiids e los distitos ojutos umérios que desriimos teriormete. Idir si ls siguietes firmioes so verdders o flss. E so de flsedd, justifi tu respuest: ) ) )., d) El produto de dos úmeros irrioles es siempre otro úmero irriol... e) El udrdo de u úmero irriol siempre es u úmero riol... f) El produto de u etero por u irriol es u úmero irriol... III...6 Operioes e los distitos Cojutos Numérios. Propieddes Desrrollremos otiuió ls operioes fudmetles y lgus de sus propieddes osiderdo los dos grdes grupos de úmeros: los rioles y los irrioles III...6. Adiió y Sustrió de Números Rioles Pr sumr o restr frioes de igul deomidor, el resultdo es otr frió de igul deomidor que ls dds, y uyos umerdores se otiee sumdo o restdo los umerdores ddos. E símolos: ± ± Cudo summos o restmos frioes de distito deomidor, usmos frioes equivletes ls dds que teg igul deomidor. E símolos: Ejemplos: d ± ± d d III..6. Multipliió y Divisió de Números Rioles Pr multiplir frioes, hemos: d d
11 Pr dividir frioes, hemos: d d d ( o 0) Ejemplos: III...6. Poteiió y Rdiió de Números Rioles 0 Si p es u úmero riol y k u etero positivo; p si p 0 ; p p ; p k p p p p k ftores p k p p k ftores p si p 0 Si p es u úmero riol y u úmero turl; p q q p Cudo relizmos ls operioes o úmeros (summos, restmos, multiplimos, et.) hy ierts regls que deemos respetr; este ojuto de regls ls deomimos propieddes. Cooer ests propieddes y mejrls o soltur es importte. No vmos exhiir e este uderillo u list exhustiv de propieddes sio sólo quells que se utiliz o freuei y se olvid o filidd. E so de olvidos de propieddes que o figur quí deerís reurrir u texto de EGB o Polimodl pr osultr l respeto. Se osider,, úmeros que perteee R (esto sigifi que tmié se umple ls propieddes e los otros ojutos umérios porque R los iluye) ) ) ) ) + + ( + ) omuttividd de l sum omuttividd del produto distriutividd del produto respeto l sum distriutividd del oiete respeto de l sum deir Si emrgo o hy u propiedd distriutiv si l sum está e el deomidor, es Por ejemplo:, y o es igul + 8 Ls propieddes ) y ) vle tmié pr l rest. Es deir
12 SISTEMA DE ACCESO COMÚN A LAS CARRERAS DE INGENIERÍA DE LA UNM ) ) ( ) Sigmos o más propieddes III...6. Propieddes de ls Operioes sore Igulddes ) 6) 7) 8) Si etoes + + Si etoes Si y 0 etoes Si 0 etoes 0 ó 0 o ms Vemos u pliió. Resolver l euió ( x ) x + Comezmos multiplido mos miemros por. ( x ) ( x + ) ( x ) ( x + ) x x + x x + + x x distriuimos summos e mos miemros restmos x e mos miemros dividimos por es l soluió e mos miemros III...6. Propieddes de ls Operioes sore Desigulddes 9) 0) ) Si < Si < Si < etoes y > 0 y < 0 + < + etoes < etoes > Vemos u pliió. Resolver l ieuió ( x ) > x + Comezmos dividiedo mos miemros por
13 ( x ) x + > x > x + x > x + + x > x < summos e mos miemros restmos x e mos miemros multiplimos por mos miemros Oservr que e el último pso se tuvo que dividir por u úmero egtivo, y esto mió el setido de l desiguldd. III Regls de Sigos ) ) ) ( ) ( ) ( ) ( ) ( ) Y filmete u regl importte que os oviee teer e uet udo opermos o frioes: ) III Algus Propieddes de l Poteiió y l Rdiió 6) 7) 8) ( ) m m + m m ( ). y De ests propieddes se dedue que m m El ítem 8 mr l propiedd distriutiv de l poteiió respeto del produto y oiete. E mio o vle l propiedd distriutiv de l poteiió o respeto l sum o l rest, es deir: ( + ) + y ( ) + mietrs que + Ejemplo: ( ) 9 U diferei de udrdos se ftoriz sí: ( ) ( + ) udrdo de u iomio se resuelve de est form: e tto el ( + ) ( + ) ( + ) ( ) ( ) ( ) + +
14 SISTEMA DE ACCESO COMÚN A LAS CARRERAS DE INGENIERÍA DE LA UNM Si l operió es l rdiió, lgus propieddes so: 9) 0) ) m m Bie, es hor de omezr l ejeritió dode utilizrá ls operioes y propieddes desrrollds hst quí. III Módulo de u Número Rel El módulo o vlor soluto de u úmero rel x es l disti etre ese úmero y ero. Se simoliz sí: x Ejemplo:... Si x 0 x x Si x < 0 x x Otr form de expresr el modulo de u úmero rel x es: x x Ejemplo: x 6 x 6 x 6 x 6 ó x 6 III Propieddes del Módulo. 0.. o 0. Desiguldd trigulr: + +. x Ejemplo: Resuelv l euió: + x 6 Aplimos l propiedd e el primer térmio del primer miemro: x + x x 6 ; omo, teemos: + x 6 + x 6 sdo ftor omú x 6 x 6 multiplido miemro miemro por x 6 6 6
15 Por defiiió: x x x Por lo tto el ojuto soluió de l euió es S {, } III Operioes o Rdiles III Simplifiió: Si es impr Si es pr Si el ídie y el expoete del rdido tiee u divisor omú myor que, se simplifi dividiédolos por ese divisor omú. E so de que éste se pr se tom el vlor soluto del rdido. Ejemplo: ( ) 6 III Adiió y Sustrió: Rdiles semejtes: so quellos que tiee el mismo ídie y el mismo rdido. Al sumr o l restr rdiles semejtes, se otiee u expresió de u solo térmio. Ejemplo: + 7 Se puede extrer del rdil todos los ftores uyos expoetes se myores o igules que el ídie. Pr ello, se ftoriz el rdido, se desompoe los ftores e form oveiete, se distriuye l ríz o respeto l produto y se simplifi. Ejemplo: Pr sumr o pr restr rdiles, se he sí: - Si los rdiles so úmeros ompuestos, se ftoriz. - Se simplifi todos los rdiles posiles. - Se extre todos los ftores posiles de d rdil. - Si hy rdiles semejtes, se grup e u solo termio. - L sum o l rest de rdiles o semejtes se dej expresd. Ejemplo: III Multipliió y Divisió: Si los rdiles tiee igul ídie, se pli ests fórmuls.. 6
16 SISTEMA DE ACCESO COMÚN A LAS CARRERAS DE INGENIERÍA DE LA UNM Rdiles de ídies distitos: se us rdiles equivletes de modo tl que todos teg el mismo ídie. Ejemplo: ( ) III Riolizió de Deomidores: Cosiste e trsformr u expresió que otiee rdiles e su deomidor e otr equivlete, uyo deomidor se etero. Ejemplos: ( ) ( ) III Expoetes Rioles: Pr ulquier úmero turl myor que y 0 se umple que: k k. Ls poteis de expoete riol umple ls misms propieddes que ls poteis de expoete etero. Pr operr, e lguos sos oviee expresr los rdiles omo poteis y trjr o ests plido sus propieddes. + Ejemplo:.. 6 III.. LOGARITMO DE UN NÚMERO REAL El logritmo e se de u úmero es el úmero, si elevdo l expoete d omo resultdo. E símolos: log es l se del logritmo y dee ser u úmero rel positivo y distito de. es el rgumeto del logritmo y dee ser u úmero rel positivo. y log x (se lee: logritmo e se de x ) 7
17 Ejemplos: ) log ddo que ) log ddo que III... Propieddes de los Logritmos ) log ( x y) log x + log y ) log ( ) y log x x ) log logx log y y x y ) Culquier se : log () y log () 0 III... Cmio de se: Supogmos que queremos verigur log utilizdo l luldor ietífi. Pr pesr y ompletr Podemos proeder sí: segú l defiiió de logritmo, log x x Aplimos logritmos deimles mos miemros log x log Aplimos l propiedd pr jr el expoete x log Despejmos x ; pero x log, etoes log... log Este proedimieto se llm mio de se, y os permite mir l se de u logritmo por otr más oveiete (hemos elegido se 0, pero podrímos her elegido ulquier otr). Si llmmos w l se elegid, podemos plir diretmete l siguiete fórmul: log log log w w Así podemos oteer o l luldor ietífi el logritmo de u úmero e ulquier se. L uev se que elegimos será 0 o e log 0 Por ejemplo: log 0... Este logritmo se resuelve utilizdo l log luldor ietífi. 8
18 SISTEMA DE ACCESO COMÚN A LAS CARRERAS DE INGENIERÍA DE LA UNM U uestió de otió... log ( ) [ log ( ) ] Cudo lemos log si her referei l se se etederá que o referimos l se 0, es deir, 0. Ls luldors tom est oveió. III.. LOS NÚMEROS COMPLEJOS Los úmeros omplejos surge por l eesidd de resolver situioes omo l que plte l siguiete euió: x + 0 x R Situioes omo l presetd requiere l mpliió de R pr dr respuest, por ejemplo, el vlor de x ( x ) que result de l euió plted. Tl mpliió origi el ojuto de los úmeros omplejos C. Ates de defiir úmero omplejo pr que pueds ompreder mejor defiimos pr ordedo de úmeros reles. Pr ordedo so dos elemetos ddos e u ierto orde. E símolos: (, ), dode se llm primer ompoete y segud ompoete Por ejemplo: (, ) (,) (,) es deir que si mimos el orde de ls ompoetes estmos e presei de dos pres ordedos distitos. Número omplejo es todo pr ordedo de úmeros reles., / R R C {( ) } L otió usul es (,) z dode (primer ompoete) se deomi prte rel de z y (segud ompoete) se deomi prte imgiri U úmero omplejo tmié se puede expresr e form iómi: z + i El omplejo z (, ) expresdo omo pr ordedo e form iómi serí z + i Al úmero i se llm uidd imgiri que umple: i Si l prte rel es ul, el úmero omplejo es imgirio puro 9
19 Si l prte imgiri es ul, el úmero omplejo es u úmero rel El ojuto R está iluido e el ojuto C L últim rterísti euid sore los úmeros omplejos die: El ojuto R está iluido e el ojuto C. Cómo justifirís est firmió? Ejemplos: El úmero omplejo + i se represet e el plo medite el puto de oordeds (; ). El eje horizotl se llm eje rel, y el eje vertil eje imgirio. z + i z i z z i z z z z A d úmero omplejo le orrespode u puto del plo y d puto del plo le orrespode u úmero omplejo. El eje rel otiee úimete los úmeros reles, y el eje imgirio, úimete los imgirios puros. Dos omplejos so ojugdos si y sólo si tiee l mism prte rel, y sus prtes imgiris so opuests Ejemplo: z + i y z i III... Operioes e C III... Sum y Rest Pr sumr y restr úmeros omplejos se sum o rest ls prtes reles y ls prtes imgiris Ejemplos: Ddos los omplejos z (, ) z (, ) 0
20 SISTEMA DE ACCESO COMÚN A LAS CARRERAS DE INGENIERÍA DE LA UNM Presetmos u ejemplo de sum E form de pr ordedo: z + z (+ ( ), + ) (, ) E form iómi: z + z ( i) + ( + i) i III... Multipliió E este so es eesrio seprr l multipliió de úmeros omplejos e form de pr ordedo y e form iómi. E form de pr ordedo: se defie (,) (,d) ( d, d + ) E form iómi: se pli l propiedd distriutiv de l multipliió respeto l sum y rest ( i) ( + di) + di + i + di + ( d) + (d + ) i Pr ejemplifir osidermos los mismos omplejos utilizdos e l sum y rest E form de pr ordedo: ( ( ) ( ), + ( ) ( ) ) ( 0,0) z z E form iómi: ( i) ( i) z z i + i i + 0i ( ) i 0 + 0i III... Divisió E form de pr ordedo: se defie (, ) (, d) (, ) + d d, + d Es deir, que se trsform e u multipliió.
21 E form iómi: se multipli el dividedo y el divisor por el omplejo ojugdo del divisor + i + di ( + i) ( di) ( + di) ( di) + ( di) + i di + d ( + d) (d ) i + d Ejemplos: Ddos los omplejos z (, ) z (, ) E form de pr ordedo: z z (, ), (, ), y se resuelve omo l multipliió y ejemplifid teriormete. 0 0 E form iómi: i + i ( i) ( i) 6i + i ( + i) ( i) 0 ( ) + () i
RADICALES. 1.2.1 Teorema fundamental de la radicación. 1.2.3 Reducción de radicales a índice común. 1.2.4 Potenciación de exponente fraccionario
 RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 4º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
POTENCIA DE UN NÚMERO.
 INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resoluió Nº de oviere./0 Seretri De Eduió Distritl REGISTRO DANE Nº00-00099 Teléfoo Brrio Bstids St Mrt DEPARTAMENTO DE MATEMATICAS DOCENTE: LIC-ING.
INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resoluió Nº de oviere./0 Seretri De Eduió Distritl REGISTRO DANE Nº00-00099 Teléfoo Brrio Bstids St Mrt DEPARTAMENTO DE MATEMATICAS DOCENTE: LIC-ING.
NÚMEROS NATURALES. DIVISIBILIDAD
 NÚMEROS NATURALES. DIVISIBILIDAD NÚMEROS NATURALES Los úeros turles so los que sirve pr otr: 1,,, So ifiitos y for u ojuto que se deoi N. Está ordedos, lo que os perite represetrlos sore u ret uyo orige
NÚMEROS NATURALES. DIVISIBILIDAD NÚMEROS NATURALES Los úeros turles so los que sirve pr otr: 1,,, So ifiitos y for u ojuto que se deoi N. Está ordedos, lo que os perite represetrlos sore u ret uyo orige
TEMA 3: RESOLUCIÓN DE SISTEMAS DE ECUACIONES MEDIANTE DETERMINANTES.
 TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES. º BCH(CN) TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES..-INTRODUCCIÓN. L resoluió de sistems de euioes está ligd l estudio
TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES. º BCH(CN) TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES..-INTRODUCCIÓN. L resoluió de sistems de euioes está ligd l estudio
Unidad-4: Radicales (*)
 Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
( ) ( ) El principio de inducción
 El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas son equivalentes porque 2 10 4 5.
 Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Tema 2 Sucesiones Matemáticas I 1º Bachillerato. 1
 Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
TEMA 2: NÚMEROS RACIONALES: FRACCIONES.
 TEMA NÚMEROS RACIONALES FRACCIONES.. Cojuto e los Núeros Rioles, Q. El ojuto e los úeros rioles es u pliió e los úeros eteros, los que se le ñe uevos úeros que se ostruye o úeros eteros y se ll FRACCIONES.
TEMA NÚMEROS RACIONALES FRACCIONES.. Cojuto e los Núeros Rioles, Q. El ojuto e los úeros rioles es u pliió e los úeros eteros, los que se le ñe uevos úeros que se ostruye o úeros eteros y se ll FRACCIONES.
Sucesiones. Universidad Diego Portales CALCULO II
 Suesioes Uiversidd Diego Portles U suesió se puede defiir omo u list de úmeros esritos e orde defiido:,,,...,,... El úmero es el primer térmio;, el segudo térmio y e geerl, es el -ésimo térmio. Cosiderremos
Suesioes Uiversidd Diego Portles U suesió se puede defiir omo u list de úmeros esritos e orde defiido:,,,...,,... El úmero es el primer térmio;, el segudo térmio y e geerl, es el -ésimo térmio. Cosiderremos
Potencias y radicales
 Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
1. Números reales. 2. Raíces y potencias. 3. Operaciones con radicales. Matemáticas 4º ESO
 Mteátis º ESO 1. Núeros reles Clsifiió de los úeros reles Frió geertriz de u úero deil Reresetió de úeros rioles e l ret rel Aroxiioes Itervlos. Ríes y oteis Proieddes de ls oteis de exoete riol Rdiles
Mteátis º ESO 1. Núeros reles Clsifiió de los úeros reles Frió geertriz de u úero deil Reresetió de úeros rioles e l ret rel Aroxiioes Itervlos. Ríes y oteis Proieddes de ls oteis de exoete riol Rdiles
Progresiones aritméticas y geométricas
 Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Potencias y Radicales
 Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
Z={...,-4,-3,-2,-1,0,1,2,3,4,...}
 TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
FUNDAMENTOS DE MATEMÁTICA MATERIAL CON FINES DIDÁCTICOS UNEFA NÚCLEO TÁCHIRA PRODUCTOS NOTABLES.
 PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
Matrices. Matrices especiales
 UNIVERSIDD UÓNO DE NUEVO EÓN FUD DE INGENIERÍ EÁNI Y EÉRI tries triz: ojuto de eleetos ordedos e fils y olus os eleetos puede ser úeros reles o oplejos E este urso solo se osider tries o eleetos reles
UNIVERSIDD UÓNO DE NUEVO EÓN FUD DE INGENIERÍ EÁNI Y EÉRI tries triz: ojuto de eleetos ordedos e fils y olus os eleetos puede ser úeros reles o oplejos E este urso solo se osider tries o eleetos reles
Integral de Riemann. Tema Sumas inferiores y superiores Particiones de un intervalo Sumas inferiores y superiores
 4 Mtemátis I : Cálulo itegrl e IR Tem 3 Itegrl de Riem 3. Sums iferiores y superiores 3.. Prtiioes de u itervlo Defiiió 26.- Se llm prtiió de u itervlo errdo [, ] ulquier ojuto fiito de putos P = {,,...,
4 Mtemátis I : Cálulo itegrl e IR Tem 3 Itegrl de Riem 3. Sums iferiores y superiores 3.. Prtiioes de u itervlo Defiiió 26.- Se llm prtiió de u itervlo errdo [, ] ulquier ojuto fiito de putos P = {,,...,
Ejemplo: 5. Cambio de base: Ejemplo: No existe el logaritmo de un número con base negativa. No existe el logaritmo de un número negativo.
 III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
1.3.6 Fracciones y porcentaje
 Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
TEMA 2 ECUACIONES, INECUACIONES Y SISTEMAS
 TEMA ECUACIONES INECUACIONES Y SISTEMAS CURSO CERO MATEMÁTICAS:. ECUACIONES INECUACIONES Y SISTEMAS.. ECUACIONES DE PRIMER GRADO... Método geerl de resolució de ecucioes EJEMPLO: Resolver 4 5 6 (+7) =
TEMA ECUACIONES INECUACIONES Y SISTEMAS CURSO CERO MATEMÁTICAS:. ECUACIONES INECUACIONES Y SISTEMAS.. ECUACIONES DE PRIMER GRADO... Método geerl de resolució de ecucioes EJEMPLO: Resolver 4 5 6 (+7) =
Tema 1 Los números reales Matemáticas CCSS1 1º Bachillerato 1
 Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
Matemáticas B 4º E.S.O. Tema 1 Los números Reales 1 3º ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS. Simplificar la fracción, si es posible N = 50
 Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
Matemáticas 1 1 EJERCICIOS RESUELTOS: Sucesiones numéricas. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación. Universidad de Cantabria
 Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
Introducción a los métodos lineales en dominio de la frecuencia
 Itrouió los métoos lieles e omiio e l freuei Mrio Estévez Báez Arés Mho Grí José M. Estévez Crrer 3 Mteril pulio origilmete e formto html e: lirosiertos:itrouio los_metoos_lieles_e_el_omiio_e_l_freuei.
Itrouió los métoos lieles e omiio e l freuei Mrio Estévez Báez Arés Mho Grí José M. Estévez Crrer 3 Mteril pulio origilmete e formto html e: lirosiertos:itrouio los_metoos_lieles_e_el_omiio_e_l_freuei.
C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA. CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Patricia Cardona
 C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Ptrici Crdo COMPLEJO EDUCATIVO Dr. OSCAR ABDALA CONTENIDOS DE REVISIÓN CONJUTOS NUMÉRICOS Nturles: N = 1
C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Ptrici Crdo COMPLEJO EDUCATIVO Dr. OSCAR ABDALA CONTENIDOS DE REVISIÓN CONJUTOS NUMÉRICOS Nturles: N = 1
POTENCIACIÓN Y RADICACIÓN EN. Recordemos en primer lugar algunas definiciones y propiedades de la potenciación y de la radicación de números reales:
 POTENCIACIÓN Y RADICACIÓN EN Recordemos e primer lugr lgus defiicioes y propieddes de l potecició y de l rdicció de úmeros reles: PROPIEDADES DE LA POTENCIACIÓN Poteci de expoete cero : 0 = por defiició,
POTENCIACIÓN Y RADICACIÓN EN Recordemos e primer lugr lgus defiicioes y propieddes de l potecició y de l rdicció de úmeros reles: PROPIEDADES DE LA POTENCIACIÓN Poteci de expoete cero : 0 = por defiició,
1.6. BREVE REPASO DE LOGARITMOS.
 .. BREVE REPASO DE LOGARITMOS. Sistems de ritmos. Si ulquier número positivo puede tomrse omo Bse, eiste infinito número de sistems de logritmos, pero trdiionlmente, solo se utilizn dos sistems: o ritmos
.. BREVE REPASO DE LOGARITMOS. Sistems de ritmos. Si ulquier número positivo puede tomrse omo Bse, eiste infinito número de sistems de logritmos, pero trdiionlmente, solo se utilizn dos sistems: o ritmos
Si quieres que algo se haga, encárgaselo a una persona ocupada Proverbio chino
 i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
Tema 1. Números Reales. Intervalos y Radicales
 Tem. Números Reles. Itervlos y Rdicles. El cojuto de úmeros reles.... Cojutos de l rect rel. Itervlos y etoros..... Opercioes co cojutos, uió e itersecció..... Notció cietífic.... Potecis y Rdicles...
Tem. Números Reles. Itervlos y Rdicles. El cojuto de úmeros reles.... Cojutos de l rect rel. Itervlos y etoros..... Opercioes co cojutos, uió e itersecció..... Notció cietífic.... Potecis y Rdicles...
POTENCIAS.- a determina la potencia de base a y exponente n, significa que hemos de multiplicar a por si mismo n veces.
 POTENCIAS.- determi l oteci de se y exoete, sigific ue hemos de multilicr or si mismo veces. Defiició: L otció Bse Exoet El exoete,, idic ls veces ue se reite l se e el roducto de ést or si mism. L se,,
POTENCIAS.- determi l oteci de se y exoete, sigific ue hemos de multilicr or si mismo veces. Defiició: L otció Bse Exoet El exoete,, idic ls veces ue se reite l se e el roducto de ést or si mism. L se,,
Matemática 1 Capítulo 4
 Mtemátic Cpítulo 4 Comitori Ejemplo Cuáts comids diferetes que coste de u plto pricipl y u eid puede hcerse prtir del siguiete meú? Etrds Sop Esld Pltos priciples Pst Miles de pollo Filete de pescdo Beids
Mtemátic Cpítulo 4 Comitori Ejemplo Cuáts comids diferetes que coste de u plto pricipl y u eid puede hcerse prtir del siguiete meú? Etrds Sop Esld Pltos priciples Pst Miles de pollo Filete de pescdo Beids
UNIDAD 1 NÚMEROS REALES. es el sucesor de n. 4) Todo número natural tiene antecesor excepto el 1:, donde n 1
 Uiversidd Nciol de Slt Fcultd de Igeierí Aputes de Curso Me prepro pr estudir Igeierí UNIDAD 1 NÚMEROS REALES CONJUNTOS NUMÉRICOS El cojuto de los Núeros Nturles ( N ) Los úeros que se eple pr cotr 1,2,3,4,...
Uiversidd Nciol de Slt Fcultd de Igeierí Aputes de Curso Me prepro pr estudir Igeierí UNIDAD 1 NÚMEROS REALES CONJUNTOS NUMÉRICOS El cojuto de los Núeros Nturles ( N ) Los úeros que se eple pr cotr 1,2,3,4,...
TEMA 1. VECTORES Y MATRICES 1.4. APLICACIONES
 TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Licenciatura en Electrónica y Computación: Métodos Numéricos
 CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
LOS NÚMEROS REALES. n, se llaman números irracionales. Una diferencia entre los
 LOS NÚMEROS REALES Los úmeros,, so usdos pr cotr Normlmete se los cooce como el cojuto de los úmeros turles, dicho cojuto se lo deot ormlmete co l letr N, sí N {,,K } Si se sum dos úmeros turles el resultdo
LOS NÚMEROS REALES Los úmeros,, so usdos pr cotr Normlmete se los cooce como el cojuto de los úmeros turles, dicho cojuto se lo deot ormlmete co l letr N, sí N {,,K } Si se sum dos úmeros turles el resultdo
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas
 Números turles. Sistem de umerció deciml Como y sbes, el sistem de umerció deciml utiliz diez cifrs o dígitos distitos:,,,, 4, 5, 6, 7, 8 y 9. Además, es u sistem posiciol porque cd cifr o dígito tiee
Números turles. Sistem de umerció deciml Como y sbes, el sistem de umerció deciml utiliz diez cifrs o dígitos distitos:,,,, 4, 5, 6, 7, 8 y 9. Además, es u sistem posiciol porque cd cifr o dígito tiee
Matemáticas 1 EJERCICIOS RESUELTOS:
 Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
En este capítulo expondremos brevemente (a modo de repaso) conceptos básicos sobre los sistemas de numeración.
 Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
Definición: Llamamos función exponencial a una función que se expresa de la forma: x. ( x)
 FUNCIÓN EXPONENCIAL Defiició: Llmmos fució epoecil u fució que se epres de l form: f = = co > 0 ( ), dode f ( ) : R R > 0 Ates de trbjr específicmete, co ls fucioes epoeciles, recordemos lguos coceptos
FUNCIÓN EXPONENCIAL Defiició: Llmmos fució epoecil u fució que se epres de l form: f = = co > 0 ( ), dode f ( ) : R R > 0 Ates de trbjr específicmete, co ls fucioes epoeciles, recordemos lguos coceptos
LÍMITES DE SUCESIONES. EL NÚMERO e
 www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
Capítulo 7. Series Numéricas y Series de Potencias.
 Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
Cuestionario Respuestas
 Cuestionrio Respuests Copright 2014, MtemtiTu Derehos reservdos 1) Un ineuión o desiguldd on un vrile (inógnit) es un enunido en que se presentn dos epresiones, l menos un on l vrile entre ells uno de
Cuestionrio Respuests Copright 2014, MtemtiTu Derehos reservdos 1) Un ineuión o desiguldd on un vrile (inógnit) es un enunido en que se presentn dos epresiones, l menos un on l vrile entre ells uno de
Fracciones equivalentes
 6 Aritméti Friones equivlentes Reflexiones diionles Frión unitri. Es quell frión uyo numerdor es igul. Friones equivlentes. Son ls que representn l mism ntidd, un undo el numerdor y el denomindor sen distintos,
6 Aritméti Friones equivlentes Reflexiones diionles Frión unitri. Es quell frión uyo numerdor es igul. Friones equivlentes. Son ls que representn l mism ntidd, un undo el numerdor y el denomindor sen distintos,
SESIÓN 11 SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I
 Mtemátis I SESIÓN SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I I. CONTENIDOS:. Conepto y representión geométri.. Métodos de soluión: o Igulión o Sustituión. o Reduión (sum y rest). o Determinnte.
Mtemátis I SESIÓN SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I I. CONTENIDOS:. Conepto y representión geométri.. Métodos de soluión: o Igulión o Sustituión. o Reduión (sum y rest). o Determinnte.
1. Discutir según los valores del parámetro k el sistema
 . Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
. Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
2.- Dadas las matrices A y B. Calcula A+B, A-B, A 2, B 2, AB, BA
 ejeriiosemees.om MTRICES Y DETERMINNTES. Dds ls mtries Hllr ) ) B ).B d) B. e) +B f) C. g) C.B h) C.D i) j) B k) + l) B.B uioes. Dds ls mtries B. Clul +B, B,, B, B, B uió D C B.B / / / / / / / / B / /
ejeriiosemees.om MTRICES Y DETERMINNTES. Dds ls mtries Hllr ) ) B ).B d) B. e) +B f) C. g) C.B h) C.D i) j) B k) + l) B.B uioes. Dds ls mtries B. Clul +B, B,, B, B, B uió D C B.B / / / / / / / / B / /
COLEGIO SAN FRANCISCO DE SALES Prof. Cecilia Galimberti
 COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
16/11/2015. Tema 1: Números reales REALES. Racionales (Q) Irracionales (I) Naturales (N) REALES (I) (Q) (Z) (N)
 rrcioles () //0 Te : úeros reles úeros reles (rcioles e irrcioles) Aproxició de úeros reles L rect rel Vlor soluto tervlo y seirrects Potecis de expoete etero otció cietífic dicles Potecis de expoete frcciorio
rrcioles () //0 Te : úeros reles úeros reles (rcioles e irrcioles) Aproxició de úeros reles L rect rel Vlor soluto tervlo y seirrects Potecis de expoete etero otció cietífic dicles Potecis de expoete frcciorio
Sucesiones de funciones
 Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Matemáticas aplicadas a las Ciencias Sociales
 Mtemátics plicds ls Ciecis Sociles SERIE RESUELVE El liro Mtemátics plicds ls Ciecis Sociles I pr. er curso de Bchillerto, es u or colectiv coceid, diseñd y cred e el Deprtmeto de Edicioes Eductivs de
Mtemátics plicds ls Ciecis Sociles SERIE RESUELVE El liro Mtemátics plicds ls Ciecis Sociles I pr. er curso de Bchillerto, es u or colectiv coceid, diseñd y cred e el Deprtmeto de Edicioes Eductivs de
3 Potencias y raíces de números
 Potecis y ríces de úeros reles. Potecis de expoete turl. Defiició. El producto tiee sus siete fctores igules. Este producto se puede idicr de for brevid coo. se ll poteci, y l fctor, bse. El úero de veces
Potecis y ríces de úeros reles. Potecis de expoete turl. Defiició. El producto tiee sus siete fctores igules. Este producto se puede idicr de for brevid coo. se ll poteci, y l fctor, bse. El úero de veces
Este documento es de distribución gratuita y llega gracias a www.cienciamatematica.com El mayor portal de recursos educativos a tu servicio!
 Este documeto es de distribució grtuit y lleg grcis Cieci Mtemátic El myor portl de recursos eductivos tu servicio! Los poliomios de Beroulli y sus pliccioes Pblo De Nápoli versió 0.. Los poliomios de
Este documeto es de distribució grtuit y lleg grcis Cieci Mtemátic El myor portl de recursos eductivos tu servicio! Los poliomios de Beroulli y sus pliccioes Pblo De Nápoli versió 0.. Los poliomios de
Enteros (Z) Son todos los números que puede expresarse como el cociente de dos nº enteros, siendo el denominador distinto de cero
 www.clseslcrt.co Clsificció de Núeros Reles Te.- Núeros Reles Reles R Rcioles Q Irrcioles Ι Eteros Z Nturles N Negtivos Deciles Exctos Frcciorios Deciles Periódicos Puros Deciles Periódicos Mixtos Rcioles
www.clseslcrt.co Clsificció de Núeros Reles Te.- Núeros Reles Reles R Rcioles Q Irrcioles Ι Eteros Z Nturles N Negtivos Deciles Exctos Frcciorios Deciles Periódicos Puros Deciles Periódicos Mixtos Rcioles
se llama ecuación polinómica de primer grado con una incógnita. Dos ecuaciones son equivalentes cuando admiten el mismo conjunto solución.
 Euiones e ineuiones de Primer Grdo on un inógnit Se P () un euión polinómi, on P() un polinomio, resolver l mism es enontrr los eros o ríes de P(), es deir, los vlores de que nuln diho polinomio. X se
Euiones e ineuiones de Primer Grdo on un inógnit Se P () un euión polinómi, on P() un polinomio, resolver l mism es enontrr los eros o ríes de P(), es deir, los vlores de que nuln diho polinomio. X se
MATEMÁTICA. 2.- La simplificación de: 3.- Al Simplificar: Se obtiene: A) B) C) D) E) β αβ. 5.- Simplificar. A) 1 B) a -30 C) a 30 D) a E) 3 a
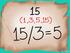 TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
FÓRMULA DE TAYLOR 1. Introducción formula de Taylor Brook Taylor 2. Objetivos Aproximación de funciones por polinomios f(x) P(x) f(x)
 FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
7. Fallas Asimétricas
 Friso M. Gozlez-Lott Cpítulo 7 7. Flls Asimétris 7. troduió U r proporió de ls flls e lo sistems elétrios de potei so simétrios, flls simétris trvés de impedis (ortoiruitos moofásios, ifásios, ifásios
Friso M. Gozlez-Lott Cpítulo 7 7. Flls Asimétris 7. troduió U r proporió de ls flls e lo sistems elétrios de potei so simétrios, flls simétris trvés de impedis (ortoiruitos moofásios, ifásios, ifásios
Álgebra para ingenieros de la Universidad Alfonso X
 Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
En donde x representa la incógnita, y a, b y c son constantes.
 FUNCIÓN CUADRÁTICA. Cundo los elementos de un onjunto los elementos de un onjunto se soin medinte un regl de orrespondeni definid por un euión de segundo grdo en, l llmmos funión de segundo grdo o udráti.
FUNCIÓN CUADRÁTICA. Cundo los elementos de un onjunto los elementos de un onjunto se soin medinte un regl de orrespondeni definid por un euión de segundo grdo en, l llmmos funión de segundo grdo o udráti.
TEMA 1. ÁLGEBRA LINEAL
 Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
La integral. 1.5 Definición de la integral. Sumas de Riemann Aproximación del área de una región
 APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
Ejercicios: 1. Coloca donde corresponda los siguientes números: N Z Q FRACCIONARIOS I
 TEMA : LOS NÚMEROS REALES LOS NÚMEROS REALES. CLASIFICACIÓN. Detro del cojuto de los úeros reles distiguios: NATURALES. Se desig co l letr N y so los úeros si deciles y positivos 0,,,,. ENTEROS. Se desig
TEMA : LOS NÚMEROS REALES LOS NÚMEROS REALES. CLASIFICACIÓN. Detro del cojuto de los úeros reles distiguios: NATURALES. Se desig co l letr N y so los úeros si deciles y positivos 0,,,,. ENTEROS. Se desig
Aplicaciones del cálculo integral
 Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Unidad 7: Sucesiones. Solución a los ejercicios
 Mtemátics º Uidd 7: Sucesioes Uidd 7: Sucesioes. Solució los ejercicios Ejercicio Ecuetr el térmio geerl de ls siguietes sucesioes: ),,,,,... 5 6 7 b ) 0,, 8,5,, 5... b 5 6 c ) 0,,,,,,... 5 6 7 c Ejercicio
Mtemátics º Uidd 7: Sucesioes Uidd 7: Sucesioes. Solució los ejercicios Ejercicio Ecuetr el térmio geerl de ls siguietes sucesioes: ),,,,,... 5 6 7 b ) 0,, 8,5,, 5... b 5 6 c ) 0,,,,,,... 5 6 7 c Ejercicio
1. Aplicar la definición para hallar, sin calculadora, el valor de las siguientes potencias:
 EJERCICIOS de POTENCIAS º ESO FICHA : Potecis de expoete IN RECORDAR:... Defiició de poteci ( veces). Aplicr l defiició pr hllr, si clculdor, el vlor de ls siguietes potecis: ) b) ( ) c) d) ( ) e) f) (
EJERCICIOS de POTENCIAS º ESO FICHA : Potecis de expoete IN RECORDAR:... Defiició de poteci ( veces). Aplicr l defiició pr hllr, si clculdor, el vlor de ls siguietes potecis: ) b) ( ) c) d) ( ) e) f) (
SenB. SenC. c SenC = 3.-
 TRIANGULOS OBLICUANGULOS Se llmn oliuángulos por que los ldos son oliuos on relión uno l otro, no formndo nun ángulos retos. Hy seis elementos fundmentles en un tringulo: los tres ldos y los tres ángulos,
TRIANGULOS OBLICUANGULOS Se llmn oliuángulos por que los ldos son oliuos on relión uno l otro, no formndo nun ángulos retos. Hy seis elementos fundmentles en un tringulo: los tres ldos y los tres ángulos,
DEFINICIONES BÁSICAS, EXPONENTES Y RADICALES
 . TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
. TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
Potencias, Raíces y logaritmos
 Potecis, Ríces y logritmos El ivetor del jedrez, le preseto su ovedos creció l rey de Dirhm, e l idi, este quedo t fscido por el juego que le ofreció culquier cos que el deser como recompes. Ate este
Potecis, Ríces y logritmos El ivetor del jedrez, le preseto su ovedos creció l rey de Dirhm, e l idi, este quedo t fscido por el juego que le ofreció culquier cos que el deser como recompes. Ate este
m 2 9 8 La fórmula cuadrática que se usó para construir el ejemplo anterior es un caso particular
 Funión Cudráti Unidd Conepto Un negoio de deorión, Alfomri Confort, onfeion tpies udrdos que miden entre metros de ldo, on diseños elusivos pedido. Queremos ver que superfiie tiene los tpies. Teniendo
Funión Cudráti Unidd Conepto Un negoio de deorión, Alfomri Confort, onfeion tpies udrdos que miden entre metros de ldo, on diseños elusivos pedido. Queremos ver que superfiie tiene los tpies. Teniendo
( ) ( ) 10. 18 = y el número 12 también es múltiplo del 3 ya que. 6 = y el número 8 también es múltiplo del 2 ya que. 3.
 Pági del Colegio de Mtemátics de l ENP-UNAM El cmpo de los úmeros reles Autor: Dr. José Muel Becerr Espios EL CAMPO DE LOS NÚMEOS EALES UNIDAD III III. NÚMEOS NATUALES Los úmeros turles so quellos que
Pági del Colegio de Mtemátics de l ENP-UNAM El cmpo de los úmeros reles Autor: Dr. José Muel Becerr Espios EL CAMPO DE LOS NÚMEOS EALES UNIDAD III III. NÚMEOS NATUALES Los úmeros turles so quellos que
TEMA 1. FUNCIONES REALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES
 FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
ECUACIONES DE SEGUNDO GRADO. Resolver la ecuación de segundo grado aplicando propiedades de la
 ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
RAZONES TRIGONOMÉTRICAS EN EL TRIÁNGULO RECTÁNGULO
 Geometrí y Trigonometrí Rzones trigonométris en el triángulo retángulo 7. RZONES TRIGONOMÉTRIS EN EL TRIÁNGULO RETÁNGULO 7.1 onepto de trigonometrí Trigonometrí L plr trigonometrí es un volo ltino ompuesto
Geometrí y Trigonometrí Rzones trigonométris en el triángulo retángulo 7. RZONES TRIGONOMÉTRIS EN EL TRIÁNGULO RETÁNGULO 7.1 onepto de trigonometrí Trigonometrí L plr trigonometrí es un volo ltino ompuesto
TEMA 1 FUNDAMENTOS 1.1 LÓGICA DE PROPOSICIONES.
 AESO A LA UNIVERSIDAD Mtemátis Aplids ieis Soiles etro Asoido de Plm de Mllor Autor: Atoio Rivero uest TEMA FUNDAMENTOS. LÓGIA DE PROPOSIIONES... Proposiioes. Proposiió, orió que siempre podemos firmr
AESO A LA UNIVERSIDAD Mtemátis Aplids ieis Soiles etro Asoido de Plm de Mllor Autor: Atoio Rivero uest TEMA FUNDAMENTOS. LÓGIA DE PROPOSIIONES... Proposiioes. Proposiió, orió que siempre podemos firmr
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES
 AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El sistem de los úmeros reles es u cojuto o vcío deotdo por R co dos opercioes
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El sistem de los úmeros reles es u cojuto o vcío deotdo por R co dos opercioes
PROBLEMAS Y EJERCICIOS RESUELTOS
 PROGRESIONES 3º ESO PÁGINA EJERCICIOS RESUELTOS DE PROGRESIONES ARITMÉTICAS Y GEOMÉTRICAS UN POCO DE HISTORIA: UN NIÑO LLAMADO GAUSS Hce poco más de dos siglos, u mestro lemá que querí pz y trquilidd e
PROGRESIONES 3º ESO PÁGINA EJERCICIOS RESUELTOS DE PROGRESIONES ARITMÉTICAS Y GEOMÉTRICAS UN POCO DE HISTORIA: UN NIÑO LLAMADO GAUSS Hce poco más de dos siglos, u mestro lemá que querí pz y trquilidd e
Guía Práctica N 12 RAÍCES FUNCIÓN RAÍZ CUADRADA
 Fuete: PreUiversitrio Pedro de Vldivi Guí Práctic N RAÍCES FUNCIÓN RAÍZ CUADRADA DEFINICIÓN : Si es u etero pr positivo es u rel o egtivo, etoces es el úico rel, o egtivo, tl que = = =, 0 DEFINICIÓN :
Fuete: PreUiversitrio Pedro de Vldivi Guí Práctic N RAÍCES FUNCIÓN RAÍZ CUADRADA DEFINICIÓN : Si es u etero pr positivo es u rel o egtivo, etoces es el úico rel, o egtivo, tl que = = =, 0 DEFINICIÓN :
TEMA1: MATRICES Y DETERMINANTES:
 TEM: MTRICES Y DETERMINNTES: MTRICES: U triz de diesió, es u tbl ford por fils y colus. j i siedo ij,.,,., ) ( Por ejeplo: Se ll Mtriz Fil l que tiee u sol fil, ejeplo: Se ll Mtriz Colu l que tiee u sol
TEM: MTRICES Y DETERMINNTES: MTRICES: U triz de diesió, es u tbl ford por fils y colus. j i siedo ij,.,,., ) ( Por ejeplo: Se ll Mtriz Fil l que tiee u sol fil, ejeplo: Se ll Mtriz Colu l que tiee u sol
UNIDAD I. Números Reales
 UNIDAD I Números Reles CONJUNTOS Defiició: U cojuto es u colecció ie defiid de ojetos. Deotremos los cojutos co letrs myúsculs A, B, C, etc. Los ojetos que compoe el cojuto recie el omre de elemetos o
UNIDAD I Números Reles CONJUNTOS Defiició: U cojuto es u colecció ie defiid de ojetos. Deotremos los cojutos co letrs myúsculs A, B, C, etc. Los ojetos que compoe el cojuto recie el omre de elemetos o
Tema IV Elección Social. El Análisis Positivo, Votación, Teorema de May, Teorema de Imposibilidad de Arrow
 Tem IV Eleión Soil El Análisis Positivo, Votión, Teorem de My, Teorem de Imposiilidd de Arrow 1 Qué hiimos en el tem nterior? Repso Estudimos ul deerí ser l ominión de reursos (en un eonomí de intermio)
Tem IV Eleión Soil El Análisis Positivo, Votión, Teorem de My, Teorem de Imposiilidd de Arrow 1 Qué hiimos en el tem nterior? Repso Estudimos ul deerí ser l ominión de reursos (en un eonomí de intermio)
