P O L I T E C N I C O 1 CAPÍTULO 1: ÁNGULOS. I. Generalización del concepto de ángulo. Ángulo plano convexo. Definición: al conjunto de puntos
|
|
|
- Ignacio Murillo Fidalgo
- hace 6 años
- Vistas:
Transcripción
1 Trignmetría 3º Añ Matemática Cód P r f. J u a n C a r l s B u e P r f. D a n i e l a C a n d i P r f. V e r ó n i c a F i l t t i P r f. M a r í a d e l L u á n M a r t í n e z P r f. N e m í L a g r e c a Dpt. de Matemática
2 CAPÍTULO : ÁNGULOS I. Generalización del cncept de ángul Ángul plan cnve Definición: Llamams ángul plan cnve de vértice b se l simbliza abc ba al cnunt de punts del plan barrids pr la semirrecta al pasar de una psición inicial P a una psición final P, describiend el punt a un arc de circunferencia menr igual que una semicircunferencia igual a una circunferencia. Gráficamente: a P Eempl b Ángul plan cóncav Definición: c P Llamams ángul plan cóncav se l simbliza ba abc cóncav al cnunt de punts del plan barrids pr la semirrecta al pasar de una psición inicial P a una psición final P, describiend el punt a un arc de circunferencia mar que una semicircunferencia menr que una circunferencia. Gráficamente: Eempl a P b c P P O L I T E C N I C O
3 Trignmetría Matemática II. Ánguls rientads En situacines de la vida ctidiana cuand un bet gira, a veces, es necesari saber en qué sentid l hace, es decir, desde el punt vista matemátic saber en qué sentid se mueve la semirrecta que genera el ángul. Es decir: Llamams ángul psitiv a td aquel generad en el sentid cntrari al mvimient de las aguas del rel. P ˆ 60º 3 rad A la medida de un ángul psitiv le antepnems el sign (+) para indicar en qué sentid fue generad. Figura P Llamams ángul negativ a td aquel generad en el mism sentid que se mueven las aguas del rel. P ˆ 30º 6 rad A la medida de un ángul negativ le antepnems el sign (-) para indicar en qué sentid fue generad. P Observación: Es necesari tener en cuenta que la medida de un ángul es un númer n negativ. El sign indica slamente el sentid en el que es generad. Si l hace en sentid antihrari, pr simplicidad, se mite la escritura del sign psitiv. Entnces, cnsiderand el ángul de la Figura ; se puede escribir: 60 rad 3 III. Ánguls simétrics u puests P O L I T E C N I C O
4 Definición: Ds ánguls sn puests simétrics, si pseen igual medida se generan a partir de una misma semirrecta en sentids cntraris. α α α α sn puests PROBLEMA. Cnstrue el ángul simétric u puest de,, en cada cas IV. Ánguls mares que una vuelta Hasta el mment se ha trabaad cn ánguls menres e iguales a 360 ( π rad ). Per a veces en la vida ctidiana ns encntrams cn situacines dnde se hace necesari utilizar ánguls mares de 360, así cm en la rtación de una rueda que gira sbre su ee. Pr eempl gráfics de ánguls mares que 360º pdrían ser: P O L I T E C N I C O 3
5 Trignmetría Matemática PROBLEMA:. Cmpleta, indicand el valr del ángul, de acuerd a l indicad en cada apartad: a) ˆ =... w wˆ 35 b) ˆ... θ π θ rad 4 V. Ánguls cterminales: Definición: Llamams ánguls cterminales a aquells dnde las psicines de las semirrectas iniciales finales sn cincidentes difieren en un númer enter de vueltas En símbls: Eempls: es cterminal cn k ; k Z 4 P O L I T E C N I C O
6 P P P P Observación: Al cnunt de ls ánguls definids en este apartad l llamarems cnunt de ánguls generalizads. PROBLEMA 3. Determina cuáles de ls siguientes ánguls sn cterminales teniend en cuenta que sus lads iniciales cinciden: 300º 50º 0º rad 405º rad 4 3 VI. Relación entre el cnunt de ls ánguls generalizads el cnunt de ls númers reales: Sean G el cnunt de ls ánguls generalizads, R el cnunt de ls númers reales una le que a cada ángul le hace crrespnder un únic númer real, que es su medida en radianes acmpañada de un sign más mens que, cm a sabems, indica su sentid de generación. Además a cada númer de R le hace crrespnder un únic ángul de G, quedand así definida una función biectiva entre ambs cnunts. Mediante un diagrama sagitari se representa la función f / f: G R 4 P O L I T E C N I C O 5
7 Trignmetría Matemática CAPÍTULO : FUNCIONES TRIGONOMÉTRICAS I. Ánguls en psición nrmal Definición: Direms que un ángul está en psición nrmal respect a un cuand su vértice cincide cn el rigen su lad inicial cn el semiee psitiv de las ;, i Ls ánguls de las siguientes figuras están en psición nrmal i i Sabems que al cnsiderar en el plan el sistema ;, i, éste queda dividid en cuatr regines que numeradas según el sentid de gir antihrari sn: III II 0 i I IV Cada una de estas regines recibe el nmbre de CUADRANTE. Así, para simblizar cada cuadrante indicarems: Ic (Primer cuadrante), IIc (Segund cuadrante), IIIc (Tercer cuadrante) IVc (Cuart cuadrante) Direms que un ángul es del primer cuadrante cuand, clcad en psición nrmal, su lad final está incluid en dich cuadrante n cincide cn ls semiees psitivs (definicines semeantes se aplican a ls trs cuadrantes). 6 P O L I T E C N I C O
8 Ls ánguls en ls cuales el lad final cincide cn alguns de ls cuatr semiees del sistema de referencia se llaman ánguls cuadrangulares PROBLEMA 4. Cmpleta, cnsiderand en cada cas el ángul en el a) Si b) Si c) Si d) Si es del I c entnces es del... entnces rad rad 3 es del III c entnces... rad...es un ángul cuadrangular 0 ; Cnsiderems nuevamente un sistema de referencia rtnrmal figura ubiquems la circunferencia C(;r) ; i,, según crrespnda cm se indica en la q s i p Sea ˆ un ángul generalizad cualquiera en psición nrmal. Para ese ángul tendrems una psición final s de la semirrecta generadra además un únic punt de intersección de s ' cn la circunferencia que llamarems q. En resumen tenems las siguientes crrespndencias (n biectivas): Entnces: ˆ s ' q A cada ángul generalizad le crrespnde un únic punt de la circunferencia. A cada punt de la circunferencia n le crrespnde un únic ángul. P O L I T E C N I C O 7
9 Trignmetría Matemática Eempl: q p Obsérvese que dad un sistema rtnrmal a cada punt q del plan le crrespnde un únic par de númers (; ) que sn sus crdenadas. De acuerd a l epuest: Dada una circunferencia C(; r) se verifica que: A cada ángul generalizad le crrespnde un par rdenad de númers reales (; ) Es decir queda definida una función n biectiva: ˆ ; II. Definición de las funcines trignmétricas: sen csen de un ángul. Una aplicación de Reales en Reales. Dads en un sistema rtnrmal ;; i, una circunferencia C, radianes) en psición nrmal p; / s ' C, r p s ' r p( ; ) i s r, un ángul (en 8 P O L I T E C N I C O
10 Definims las siguientes relacines trignmétricas: rdenada de p sen del ángul = sen r medida radi de C( ; r) csen del ángul = cs abscisa de p r medida radi de C( ; r) Para recrdar: Sen se abrevia sen en inglés sin cm se bserva en la calculadra Csen se abrevia cs Estas relacines definidas, serán funcines? Para respnder a esta pregunta cnsiderems C (; r ) C (; r ) cm muestra la figura C ds circunferencias cualesquiera de radis p ( ; ) C p p p ( ; ) i b c b = c = p b = p c = r r Ntams que decir: bp cp. Lueg las medidas de sus lads sn prprcinales, es p b p b p ; p c p c p Teniend en cuenta p ( ; ), p ( ; ) ; las prpiedades de las prprcines las definicines de las relacines trignmétricas dadas, entnces las igualdades anterires pdems epresarlas así: sen cs r r r r De l epuest pdems determinar que las relacines definidas: n dependen de la circunferencia elegida tienen para cada ángul un únic valr En cnclusión las relacines trignmétricas definidas sn funcines P O L I T E C N I C O 9
11 Trignmetría Matemática Entnces definims: Función SENO Dad un ángul llamams sen al cciente entre la rdenada del punt p (intersección entre el lad terminal del ángul la circunferencia) la medida del radi de la circunferencia. En símbls sen r cn R Función COSENO Dad un ángul llamams cs al cciente entre la abscisa del punt p (intersección entre el lad terminal del ángul la circunferencia) la medida del radi de la circunferencia. En símbls cs cn R r PROBLEMA 5. Cnsiderand al ángul α en ls distints cuadrantes, cmpleta el cuadr cn ls signs (+) (-) según crrespnda sen cs Ic IIc IIIc IVc 0 P O L I T E C N I C O
12 V. Relación Pitagórica: Dada una circunferencia C(;r), un ángul un punt p(; ) m p ( ;) p=r q En el triángul rectángul qp resulta: p () Per: p = r; q = qp = m = ; entnces reemplazand en la epresión () ns queda: Entnces: r 0 Dividiend ambs miembrs de la igualdad pr ) Cm r cs r r r r r () ; sen, la epresión () resulta: r (r Aclaración: En general: n n (senν) =sen ν n n n (csν) =cs ν n El hech de ecluir para el valr n = se debe a n crear cnfusines cn la función inversa. cs sen Esta epresión se la cnce cm Relación Pitagórica, vincula el sen el csen del mism ángul. P O L I T E C N I C O
13 Trignmetría Matemática III. Circunferencia trignmétrica En la definición de las funcines sen csen hems pensad en una circunferencia de radi r cualquiera. Entre ls valres que puede asumir r cnsiderems r =. La circunferencia de radi igual a la denminams circunferencia trignmétrica. Si C(;r) es una circunferencia trignmétrica, un ángul en radianes de lad final s C(;r) s' p ; Teniend en cuenta la definición de sen csen de un ángul, ns queda: sen cs r r s' resulta: Entnces en tda circunferencia trignmétrica el sen del ángul es la rdenada el csen C α i p(;) es la abscisa, del punt p (intersección entre s' la C(;r)). En símbls: sen = cs = IV. Valres de las funcines trignmétricas de ánguls particulares En l sucesiv, para simplificar la btención de cada una de las epresines trabaarems cn la circunferencia trignmétrica ns referirems indistintamente al ángul al númer real que l identifica. a) Funcines sen csen del ángul 0 i p Observams en la figura que cuand = 0 el punt p tiene cm rdenada 0 cm abscisa, es decir, según la definición de las funcines sen csen: sen 0 0 cs 0 P O L I T E C N I C O
14 b) Funcines sen csen del ángul p i Observams en la figura que cuand el punt p tiene cm rdenada el númer cm abscisa el 0, es decir, según la definición de las funcines sen csen resulta: sen cs 0 c) Funcines sen csen del ángul 6 Para determinar las funcines sen csen del ángul crdenadas del punt p. 6 debems encntrar las Cmencems marcand el punt p, simétric de p cn respect al ee unams dich punt cn el rigen del sistema. Así pdems bservar el el pp '? pp ', qué clase de triángul es p 6 m p P O L I T E C N I C O 3
15 Trignmetría Matemática p ôp' = pr cnstrucción. () 3 p = p' pr ser radis de la circunferencia trignmétrica. Lueg: El triángul pp' es isósceles pp' p' p () De () () pp' pp es equiángul ' es equiláter lueg: p p pp' Siend m bisectriz de pp' en el triángul pp' mediana de dich triángul, lueg: equiláter, entnces m es mediatriz pm = es la rdenada de p, entnces sen 6 Pr aplicación del Terema de Pitágras en el triángul pm : p pm m 3 m m m es la abscisa de p, entnces 3 cs 6 En resumen 3 sen cs P O L I T E C N I C O
16 d) Funcines sen csen del ángul 4 Para determinar las funcines sen csen del ángul 4 debems encntrar las crdenadas del punt p. p es radi de la circunferencia trignmétrica p Cnsiderems el triángul pm, dnde: 4 m i pôm 4 mˆ p = pr cnstrucción pr cnstrucción ˆ pm 4 Entnces el triángul pm es isósceles, m mp; además p =, aplicand el Terema de Pitágras en dich triángul : p pm m pm pm pm es la rdenada de p, entnces: sen 4 Cm m es la abscisa de p, tenems: cs 4 En resumen sen cs 4 4 P O L I T E C N I C O 5
17 Trignmetría Matemática e) Funcines sen csen del ángul 3 Para determinar las funcines sen csen del ángul 3, cnstruams p ' simétric de p respect del ee. p m p Resulta así que p' p pr l tant el pp ' es isósceles. Además lueg p' m = pp' 3 mp mp 6 pr cnstrucción, i Cm el pp' tres ánguls mide Lueg: es isósceles el ángul puest a la base mide 3 3, entnces cada un de ls, el triángul es equiángul en cnsecuencia es equiláter: p = p = pp = m es bisectriz de p Cm p ' ô de dich triángul. Entnces:, en el pp' equiláter, entnces m es mediatriz mediana () () pm mp' m p pm 3 3 m 4 4 de () () 3 p ; Lueg: cs 3 sen P O L I T E C N I C O
18 PROBLEMAS 6. Cmpleta según crrespnda sen 0... cs0... sen... cs... sen... cs( )... sen( )... cs( )... sen( 3 )... cs( 4 )... sen(6 )... sen... cs... 3 cs( )... cs... 3 sen Determina ls valres eacts de en cada apartad a) b) c) d) sen cs sen cs sen sen cs 4 sen sen cs sen sen cs cs Cmpleta la siguiente tabla indicand a qué cuadrante pertenece el ángul cs 0 cs 0 sen 0 sen 0 9. Verifica las siguientes identidades a) b) c) a) 4 sen.cs cs - sen (sen cs ) (sen - cs ) 3 sen sen cs sen - sen cs cs sen P O L I T E C N I C O 7
19 Trignmetría Matemática 0. Encuentra el valr del: a) b) c) cs si sen si cs si 5 sen 6 cs 3 4 sen CAPITULO 3. ESTUDIO DE LA FUNCIÓN SENO, COSENO Y TANGENTE A md de eempl cmenzarems estudiand en frma cmpleta, la función sen. I. FUNCIÓN SENO Dad f : R -; / f() sen a) Dmini de definición de la le De acuerd a la definición de la función sen pdems epresar que Dm(f) R b) Cnunt imagen Si cnsiderams ls infinits ánguls generads (en ambs sentids) a partir del semiee psitiv de las, cm se bserva en la figura, pdems epresar que ls psibles valres de las rdenadas de ls punts de intersección del lad terminal del ángul cn la Im f -; circunferencia trignmétrica varían entre. Resulta entnces: a b e i c d c) Biectividad Para estudiar si la función es biectiva, tendrems que analizar si es surectiva e inectiva simultáneamente. 8 P O L I T E C N I C O
20 Surectividad: a la función sen la definims sbre su cnunt imagen, entnces es surectiva. Inectividad: la función n es inectiva, a que pr definición de ánguls cterminales es inmediat que: sen sen( k ) cn k Z; R k i Del análisis anterir cncluims que la función sen n es biectiva. d) Peridicidad Pr definición de ánguls cterminales recrdand la definición de función periódica, resulta: sen sen k cn kz sen sen sen 4 sen Entnces pdems cncluir que f e) Paridad k k k sen es periódica, de períd Cnsiderems un ángul cualquiera su puest (-) cm muestra la figura - i P O L I T E C N I C O 9
21 Trignmetría Matemática Pdems bservar que ls punts b c sn simétrics respect del ee pr l tant tienen rdenadas puestas. En cnsecuencia: sen = -sen (-) R f es impar f) Crecimient Sabems que la función sen es impar periódica cn períd 0; estudiarems el crecimient en el cnunt. Pr l tant d c b a i e Observems en la circunferencia que el sen de crece hasta llegar a, en hasta llegar a 0, en. Resumiend: La función f() sen en 0; : f) Intersección cn ls ees es creciente en 0 ; es decreciente en ; decrece cn el ee f() 0 sen 0 k cn k Z ls punts k ; 0 Gf (gráfica de la función) el punt 0; 0 Gf cn el ee 0 f(0) sen0 0 0 P O L I T E C N I C O
22 Cmpleta, resumiend td l estudiad de la función sen: Dmini:... Cnunt imagen:... Surectiva:... Inectiva:... Biectiva:... Periódica:... Períd:... Par:... Impar:... Intersección cn el ee :... Intersección cn el ee :... Cn las cnclusines anterires estams en cndicines de graficar la función sen. g) Gráfica PROBLEMA:. Representa gráficamente las siguientes funcines e indica dmini de definición de la le cnunt imagen. a) sen si 0 g() sen si 0 sen si b) s() sen c) r() sen 4 d) l() sen P O L I T E C N I C O
23 Trignmetría Matemática e) m() sen sen f) t() sen sen II. FUNCIÓN COSENO Cnsiderems un sistema de referencia trignmétrica ls ánguls ; i; centrad en una circunferencia según se muestra en la fugura. Observand el gráfic cmparand ls triánguls ac bd, pdems cncluir que resultan cngruentes. Lueg las medidas de ls lads hmólgs sn iguales, es decir: ac = d c = db b d b c a Teniend en cuenta las crdenadas de ls punts a(a ; a ) b(b ; b ), las igualdades anterires pdems epresarlas: () () a b a b Además sabems que: sen a cs( ) b cs a sen( ) b de () () resulta: sen cs cs sen De la relación cs sen, pdems cncluir que para cnstruir la gráfica de la función csen bastará efectuar una traslación hrizntal a la gráfica de la función sen: sen csen P O L I T E C N I C O
24 De acuerd cn l estudiad sbre la función sen teniend en cuenta la btención de la gráfica de la función csen, prpnems para el lectr estudiar para ésta última: a) Dmini de definición de la le cnunt imagen b) Biectividad peridicidad c) Paridad d) Crecimient e) Intersección cn ls ees crdenads Relacines especiales Dad que la función csen es simétrica respect del ee, la función sen tiene la misma gráfica desplazada sen es simétrica respect de la recta = en el sentid psitiv del ee, resulta que la gráfica del pr l tant: 0.5 lueg: Es decir: sen sen sen cs sen cs 3 El csen de un ángul el sen de su cmplementari sn iguales P O L I T E C N I C O 3
25 Trignmetría Matemática PROBLEMA. Representa gráficamente las siguientes funcines e indica dmini de definición de la le su cnunt imagen: a) g() 3cs b) () cs c) c() cs cs III. FUNCIÓN TANGENTE Definición: Definirems una nueva función trignmétrica que a cada númer real le hace crrespnder un únic númer que resulta de efectuar el cciente entre el sen de el csen de, a la que llamarems tangente de e indicarems tg. Simbólicamente: Estudi de la función tangente sen tg ; cs 0 cs a) Dmini de definición de la le La función tangente estará definida para aquells valres dnde el cs sea distint de cer, es decir: Dmf R / k ;kz b) Cnunt imagen Para determinar el cnunt imagen de la función tangente, intentarems encntrar un punt cua rdenada representa a la tangente de cada un de ls ánguls del dmini. Sea entnces una circunferencia trignmétrica, un sistema de referencia ; i; ls punts aa ; a ; b ; 0 pp ; p 4 P O L I T E C N I C O
26 a c i p b R Cnsiderems un ángul cualquiera del primer cuadrante una recta R dnde esté incluida la semirrecta (psición final de ), al trazar una recta perpendicular al ee que pase pr el punt b(;0), queda determinad el punt p, intersección de la recta = cn la psición final del ˆ ˆ a Así resulta que el ac pb c b pb es semeante al dnde ac a; c a ; pb p b Entnces pdems epresar: sen a p tg cs a ac pr l tant sus lads sn prprcinales lueg: tg p Es decir: El númer que representa la tangente de un ángul es la rdenada del punt de intersección del lad terminal del mism cn la recta de ecuación =. De este md si cnsiderams un ángul cualquiera en el cuart cuadrante también pdems bservar que el númer que representa la tangente del ángul es la rdenada del punt de intersección de la semirrecta final del ángul cn la recta de ecuación =. Para encntrar la tangente de un ángul del II c del III c, basta cn determinar, el punt de intersección de la semirrecta final del ángul cn la recta de ecuación: = -. En ests cass la tangente del ángul es la rdenada puesta de la del punt de intersección. Cn tdas estas cnsideracines, prcedems a determinar el cnunt imagen de la función tangente: Si 0 tg 0 P O L I T E C N I C O 5
27 Trignmetría Matemática Si se aprima a desde valres menres a, el valr de la tangente es mar que cualquier númer psitiv dad. En símbls: tg pues la recta R tiende a ser paralela al ee. Observams que cuand el valr del ángul va creciend también crece el valr de la tangente del ángul, cmpletand así tds ls punts de abscisa de la () Si se aprima a desde valres mares que tangente es menr que cualquier númer negativ dad., el valr de la bp En símbls: tg Observams que cuand el valr del ángul va decreciend también decrece el valr de la tangente del ángul, cmpletand así tds ls punts de abscisa de la bq () i p p p b q De () () bservams que cn sól estudiar la tangente para ánguls de I c IV c quedan cubiertas tds ls punts de la recta = que relacinad cn el ee ns permite determinar que: Im(f) =R q q 6 P O L I T E C N I C O
28 c) Biectividad peridicidad a(a ;a ) d(d ;d ) a d c b i Además sabems que: a = sen a = cs Si cnsiderams entnces es elemental que el punt d es el simétric de a respect de, lueg: d = sen d = cs cm: d a sen sen( ) sen d a cs cs( ) cs Entnces: tg( ) tg En cnclusión: La función tangente es PERIÓDICA de períd Pr ser una función periódica n es inectiva pr l tant: f() tg NO ES BIYECTIVA P O L I T E C N I C O 7
29 Trignmetría Matemática d) Paridad: Cnsiderems una circunferencia trignmétrica centrada en un sistema ánguls ; i ; ls a(a;a) - i a (a ;a ) Teniend en cuenta que a es simétric de a respect del ee pr cnstrucción, resulta: sen a sen sen( ) a' a cs a cs cs( ) a' a a a' a a a' a tg tg tg( ) () De () () Lueg: tg tg( ) La función tangente es IMPAR, pr l tant su gráfica resulta SIMÉTRICA RESPECTO DEL PUNTO (0; 0) e) Gráfica de la función tangente P O L I T E C N I C O
30 f) Crecimient: Deams al lectr el estudi del crecimient de la función tangente en el períd ; g) Intersección cn ls ees Intersección cn el ee 0 f() 0 tg 0 k cn k Z, k ;0 G ls punts f Intersección cn el ee 0 f(0) 0 tg0 0 (0;0) Gf PROBLEMAS: 3. Representa gráficamente e indica dmini recrrid de cada un de las siguientes funcines a) f() tg 3 b) g() tg 3 4. Dada f : ; R / f() tg -, determina: a) gráfica de f() b) un interval dnde f es creciente. c) la gráfica de g()/ g() f() d) 3 z / z f( ) f Calcula cs sen sabiend que tg 3 CAPITULO 4: OTRAS FUNCIONES TRIGONOMÉTRICAS DE USO FRECUENTE Sabems que una función, si es periódica, n es biectiva, lueg n admite función inversa. En particular las funcines trignmétricas pr ser periódicas n tienen inversa. Sin embarg es psible restringir ls dminis de dichas funcines, de tal manera que resulten biectivas. Entnces llamams funcines trignmétricas inversas, a las inversas de las funcines trignmétricas restringidas a dminis cnvenientes adptads cnvencinalmente de la frma que se indica a cntinuación: P O L I T E C N I C O 9
31 Trignmetría Matemática a) Se llama función arc sen la indicams arcsen a la inversa de la función sen tmand cm dmini de definición de la función sen el interval: ; es decir: arcsen sen ; De la gráfica de la función sen de la gráfica de la función inversa de una función dada, resulta que la gráfica de la función arc sen es : =arcsen = 0.5 =sen Dm ( arcsen) ; Im ( arcsen) ; b) Se llama función arc csen la indicams arccs a la inversa de la función csen tmand cm dmini de definición de esta última el interval 0;. Es decir arccs cs ; 0 La gráfica resultante se muestra en la siguiente figura: 30 P O L I T E C N I C O
32 = = arccs 0 = cs Dm (arccs) (arccs) ; Im 0; c) Se llama arc tangente la indicams arctg a la inversa de la función tangente, tmand cm dmini de definición para ésta última, el interval ; Es decir: arctg tg ; - La gráfica es la que se muestra en la siguiente figura: = tg = = arctg 0 Dm ( arctg ) R Im ( arctg ) ; P O L I T E C N I C O 3
33 Trignmetría Matemática PROBLEMAS: 6. Calcula el valr de empleand tu calculadra a) arcsen b) arccs 3 c) cs arcsen 7 d) sen arcsen 4 e) sen arccs 5 arcsen arccs0 f) arcsen Recuerda: En tu calculadra bservarás que las funcines circulares inversas se indican: Función arc sen sin Función arc cs cs Función arc tg tan II- FUNCIONES RECÍPROCAS Habiend definid las funcines sen, csen tangente pasams ahra a definir sus crrespndientes funcines recíprcas, de las siguiente manera: Función Csecante: Se llama función csecante de un númer, la indicams csec, a la recíprca de la función sen. Es decir: Dm (cs ec) csec R sen / k;k Z Im (cs ec) ; ; 3 P O L I T E C N I C O
34 Función Secante: Se llama función secante de un númer, la indicams sec, a la recíprca de la función csen. Es decir: sec cs Dm (sec) R / Im (sec) k ;k Z ; ; Función Ctangente: Se llama función ctangente de un númer, la indicams ctg, al cciente entre el csen de el sen de. Es decir Dm ctg) cs ctg sen ( R / k;k Z Im ( ctg) R PROBLEMAS 7. Calcula tdas las funcines trignmétricas del 0 < <,sabiend que sen 0, 65 P O L I T E C N I C O 33
35 Trignmetría Matemática 8. Demuestra las siguientes identidades: a) ctg csec b) sec csec sec csec c) sec csec tg sec csec tg d) tg sen sec sen 3 cs e) sec csec ctg tg f) sen cs csec cs sen g) tg ctg tg tg ctg ctg h) sec sen tg csec sen cs sen cs i) 9. Calcula a) csec, sabiend que II c cs = -0,4 b) sec, si sen = - 0, tg > 0 c) ctg, si cs = 0,5 IV c d) cs sen,sabiend que la csec= 5 0. Si: tg β = - 0,5 β es un ángul del segund cuadrante, calcula el valr eact de: sen β + csβ. 34 P O L I T E C N I C O
36 III. REDUCCIÓN AL PRIMER CUADRANTE Teniend en cuenta ls gráfics que se presentan a cntinuación en la circunferencia trignmétrica, resuelve la siguiente actividad: Qué relación puede establecerse entre las funcines trignmétricas de cas? en cada Cas I Cnsiderams que sn suplementaris es decir ; Además supndrems, el cas en el que ˆ I ˆ c ; IIc b p a m i Analiza la cngruencia de ls bp am, cnclue cmpleta: sen.....cs.....tg..... P O L I T E C N I C O 35
37 Trignmetría Matemática Cas II: Supngams que difieren en, es decir ; En este cas que I c ; IIIc Analiza cmpleta, teniend presente l efectuad en el cas I b i a Cas III: sen.....cs.....tg..... sn cmplementaris a una vuelta u puests, supngams En este cas I c ; IVc ; a b i Analiza nuevamente cmpleta: sen.....cs.....tg..... Observación: El análisis se ha realizad para I, per sn válidas para cualquier ángul; habría que estudiar, pr separad, el cas en el que pertenezca al segund, al tercer al cuart cuadrante; para pder generalizar las cnclusines btenidas. Supnems que la tarea está realizada. Entenderems pr reducir al primer cuadrante la tarea de epresar las funcines trignmétricas de un ángul del II c, III c IV c en relación a las funcines trignmétricas de un ángul del I c, a partir de prpiedades que ls vinculen (suplementaris, difieren en, etc. ) c 36 P O L I T E C N I C O
38 PROBLEMAS. Siend I c, analiza cmpleta: sen( )... cs( )... tg( ).... Verifica las siguientes identidades: a) cs( ) sen( ) tg sen b) c) d) e) f) sen cs cs tg cs tg cs sec tgw.sec w sen w senw sen cs sec cs sen cs sen sen cs tg ct g P O L I T E C N I C O 37
FUNCIONES REALES DE VARIABLE REAL
 FUNCIONES REALES DE VARIABLE REAL CONCEPTOS BÁSICOS Se llama función real de variable real a cualquier aplicación f : D R cn D Œ R, es decir, a cualquier crrespndencia que ascia a cada element de D un
FUNCIONES REALES DE VARIABLE REAL CONCEPTOS BÁSICOS Se llama función real de variable real a cualquier aplicación f : D R cn D Œ R, es decir, a cualquier crrespndencia que ascia a cada element de D un
LÍMITE DE UNA FUNCIÓN
 Unidad didáctica 7. Funcines reales de variable real Autras: Glria Jarne, Esperanza Minguillón, Trinidad Zabal LÍMITE DE UNA FUNCIÓN De frma intuitiva se puede definir el límite de una función en un punt
Unidad didáctica 7. Funcines reales de variable real Autras: Glria Jarne, Esperanza Minguillón, Trinidad Zabal LÍMITE DE UNA FUNCIÓN De frma intuitiva se puede definir el límite de una función en un punt
DERIVADA DE UNA FUNCIÓN REAL
 Unidad didáctica 7 Funcines reales de variable real Autras: Glria Jarne, Esperanza Minguillón, Trinidad Zabal DERIVADA DE UNA FUNCIÓN REAL CONCEPTOS BÁSICOS Dada una función real y f( ) y un punt D en
Unidad didáctica 7 Funcines reales de variable real Autras: Glria Jarne, Esperanza Minguillón, Trinidad Zabal DERIVADA DE UNA FUNCIÓN REAL CONCEPTOS BÁSICOS Dada una función real y f( ) y un punt D en
Tema 4B. Inecuaciones
 1 Tema 4B. Inecuacines 1. Intrducción Una inecuación es una desigualdad en la que aparecen númers y letras ligads mediante las peracines algebraicas. Ls signs de desigualdad sn: , Las inecuacines
1 Tema 4B. Inecuacines 1. Intrducción Una inecuación es una desigualdad en la que aparecen númers y letras ligads mediante las peracines algebraicas. Ls signs de desigualdad sn: , Las inecuacines
o o 2 1 2 2 24 α = + α = + α = α =
 Tema 7 Trignmetría Matemáticas 4º ESO 1 TEMA 7 TRIGONOMETRÍA UNIDADES DE MEDIDAS DE ÁNGULOS EJERCICIO 1 a) Pasa a radianes ls siguientes ánguls: 10 y 70 b) Pasa a grads ls ánguls: 7π rad 6 y,5 rad π 7π
Tema 7 Trignmetría Matemáticas 4º ESO 1 TEMA 7 TRIGONOMETRÍA UNIDADES DE MEDIDAS DE ÁNGULOS EJERCICIO 1 a) Pasa a radianes ls siguientes ánguls: 10 y 70 b) Pasa a grads ls ánguls: 7π rad 6 y,5 rad π 7π
Tema 2 APUNTES DE MATEMÁTICAS TEMA 2: TRIGONOMETRÍA 1º BACHILLERATO
 Tema APUNTES DE MATEMÁTICAS TEMA : TRIGONOMETRÍA 1º BACHILLERATO Tema TEMA : TRIGONOMETRÍA... 1 1. Definición de Ángul... 4 1.1. MEDIDA DE LOS ÁNGULOS... 4 1.1.1. Grad sexagesimal... 4 1.1.. Radián (rad)...
Tema APUNTES DE MATEMÁTICAS TEMA : TRIGONOMETRÍA 1º BACHILLERATO Tema TEMA : TRIGONOMETRÍA... 1 1. Definición de Ángul... 4 1.1. MEDIDA DE LOS ÁNGULOS... 4 1.1.1. Grad sexagesimal... 4 1.1.. Radián (rad)...
REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES
 Unidad didáctica 7. Funcines reales de variable real Autras: Glria Jarne, Esperanza Minguillón, Trinidad Zabal REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES CRECIMIENTO Y DECRECIMIENTO Dada una función real
Unidad didáctica 7. Funcines reales de variable real Autras: Glria Jarne, Esperanza Minguillón, Trinidad Zabal REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES CRECIMIENTO Y DECRECIMIENTO Dada una función real
en los siguientes polígonos regulares:
 1) Halla el valr de Xˆ, Yˆ, Zˆ en ls siguientes plígns regulares: a. El ángul Xˆ es el ángul central del pentágn regular, pr l que 360º mide la quinta parte de 360º: ˆX 7º Para calcular Yˆ pdems hacer
1) Halla el valr de Xˆ, Yˆ, Zˆ en ls siguientes plígns regulares: a. El ángul Xˆ es el ángul central del pentágn regular, pr l que 360º mide la quinta parte de 360º: ˆX 7º Para calcular Yˆ pdems hacer
Física. fisica.ips.edu.ar
 Mvimient Circular Segunda Parte Física fisica.ips.edu.ar www.ips.edu.ar 3º Añ Cód- 7305-16 P r f. L i l i a n a G r i g i n i P r f. M a r c e l a P a l m e g i a n i P r f. M a r í a E u g e n i a G d
Mvimient Circular Segunda Parte Física fisica.ips.edu.ar www.ips.edu.ar 3º Añ Cód- 7305-16 P r f. L i l i a n a G r i g i n i P r f. M a r c e l a P a l m e g i a n i P r f. M a r í a E u g e n i a G d
TRIGONOMETRÍA. 1. Ángulos. 2. Razones trigonométricas de ángulos agudos
 TRIGONOMETRÍA 1 Ángulos Hasta ahora se han considerado los ángulos como la porción del plano comprendida entre dos semirrectas con el origen común De esta manera, el ángulo está comprendido entre 0 y 360
TRIGONOMETRÍA 1 Ángulos Hasta ahora se han considerado los ángulos como la porción del plano comprendida entre dos semirrectas con el origen común De esta manera, el ángulo está comprendido entre 0 y 360
ÁLGEBRA Y GEOMETRÍA ANALÍTICA SUPERFICIES CUÁDRICAS SUPERFICIES
 SUPERFICIES En el área de estudi del electrmagnetism ns encntrams cn la guiente tuación: Ds superficies cilíndricas caxiales cuys radis sn de cm y de 3 cm respectivamente, llevan cargas eléctricas iguales
SUPERFICIES En el área de estudi del electrmagnetism ns encntrams cn la guiente tuación: Ds superficies cilíndricas caxiales cuys radis sn de cm y de 3 cm respectivamente, llevan cargas eléctricas iguales
Unidad 3: Razones trigonométricas.
 Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
LA RECTA INTRODUCCIÓN.
 LA RECTA INTRODUCCIÓN. En la vida diaria es cmún escuchar eclamar alguna de las siguiente frases esta calle está mu inclinada ó bien la siguiente esta calle tiene mucha pendiente en las que siempre tmams
LA RECTA INTRODUCCIÓN. En la vida diaria es cmún escuchar eclamar alguna de las siguiente frases esta calle está mu inclinada ó bien la siguiente esta calle tiene mucha pendiente en las que siempre tmams
Ejemplo: En este ejemplo veremos cómo podemos utilizar un coaxial slotted line para calcular la impedancia de carga Z L.
 91 Ejempl: En este ejempl verems cóm pdems utilizar un caxial sltted line para calcular la impedancia de carga. Un caxial sltted line tiene una pequeña abertura lngitudinal (i.e. slit) en su cnductr exterir.
91 Ejempl: En este ejempl verems cóm pdems utilizar un caxial sltted line para calcular la impedancia de carga. Un caxial sltted line tiene una pequeña abertura lngitudinal (i.e. slit) en su cnductr exterir.
Ejercicios de Diferenciabilidad
 Ejercicis de Dierenciabilidad ) a) Obtener un valr aprimad de (-,05) + (,0). b) Calcular aprimadamente sen (,6) e /,57 (ejercici 0 capítul, []) 0.0 teniend en cuenta la aprimación ) El larg el anch de
Ejercicis de Dierenciabilidad ) a) Obtener un valr aprimad de (-,05) + (,0). b) Calcular aprimadamente sen (,6) e /,57 (ejercici 0 capítul, []) 0.0 teniend en cuenta la aprimación ) El larg el anch de
cx + d k; ax 2 + bx + c 0&a 1 x 2 + b 1 x + c 1 a 2 x 2 + b 2 x + c 2, con a 1 a 2
 Ls númers reales 1 OBJETIVOS PARTICULARES. Al terminar este capítul, el alumn debe ser capaz de: Identificar númers naturales, enters, racinales, irracinales y reales. Cncer prpiedades algebraicas y de
Ls númers reales 1 OBJETIVOS PARTICULARES. Al terminar este capítul, el alumn debe ser capaz de: Identificar númers naturales, enters, racinales, irracinales y reales. Cncer prpiedades algebraicas y de
TEMA 8: TRANSFORMACIONES EN EL PLANO
 TEMA 8: TRANSFORMACIONES EN EL PLANO Matías Arce, Snsles Blázquez, Tmás Ortega, Cristina Pecharrmán 1. INTRODUCCIÓN...1 2. SIMETRÍA AXIAL...2 3. SIMETRÍA CENTRAL...3 4. TRASLACIONES...3 5. GIROS...4 6.
TEMA 8: TRANSFORMACIONES EN EL PLANO Matías Arce, Snsles Blázquez, Tmás Ortega, Cristina Pecharrmán 1. INTRODUCCIÓN...1 2. SIMETRÍA AXIAL...2 3. SIMETRÍA CENTRAL...3 4. TRASLACIONES...3 5. GIROS...4 6.
ELIMINATORIA, 28 de marzo de 2009 PROBLEMAS
 ELIMINATORIA, 28 de marz de 2009 PROBLEMAS 1. Ana y Pedr viven en la m ism a calle (sbre la m ism a banquet a). De un lad de la casa de Ana hay 2 casas y del tr hay 13 casas. Pedr vive en la casa que está
ELIMINATORIA, 28 de marz de 2009 PROBLEMAS 1. Ana y Pedr viven en la m ism a calle (sbre la m ism a banquet a). De un lad de la casa de Ana hay 2 casas y del tr hay 13 casas. Pedr vive en la casa que está
ASIGNATURA: MATEMÁTICA. Contenido: TRIGONOMETRÍA I TEORÍA
 ASIGNATURA: MATEMÁTICA Contenido: TRIGONOMETRÍA I TEORÍA Docente: Teneppe María Gabriela Medida de ángulos: Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas
ASIGNATURA: MATEMÁTICA Contenido: TRIGONOMETRÍA I TEORÍA Docente: Teneppe María Gabriela Medida de ángulos: Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas
UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA
 C u r s o : Matemática Material N 18 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA GUÍA TEÓRICO PRÁCTICA Nº 15 SISTEMA CARTESIANO ORTOGONAL Para determinar la posición de los puntos de un plano usando
C u r s o : Matemática Material N 18 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA GUÍA TEÓRICO PRÁCTICA Nº 15 SISTEMA CARTESIANO ORTOGONAL Para determinar la posición de los puntos de un plano usando
UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA
 C u r s o : Matemática Material N 8 GUÍA TEÓRICO PRÁCTICA Nº 5 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA SISTEMA CARTESIANO ORTOGONAL Para determinar la posición de los puntos de un plano usando
C u r s o : Matemática Material N 8 GUÍA TEÓRICO PRÁCTICA Nº 5 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA SISTEMA CARTESIANO ORTOGONAL Para determinar la posición de los puntos de un plano usando
1. Ángulos orientados
 NOCIONES ELEMENTALES DE TRIGONOMETRIA En lo que sigue se repasan conceptos elementales de trigonometría, que serán utilizados en temas posteriores de la asignatura.. Ángulos orientados Un ángulo orientado
NOCIONES ELEMENTALES DE TRIGONOMETRIA En lo que sigue se repasan conceptos elementales de trigonometría, que serán utilizados en temas posteriores de la asignatura.. Ángulos orientados Un ángulo orientado
Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6
 página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
APARATO DE OSCILACIÓN GIRATORIA. Cálculo de momentos de Inercia
 APARATO DE OSCILACIÓN GIRATORIA Cálcul de mments de Inercia 1. OBJETIVO Estudi de las vibracines de trsión aplicadas a la determinación cuantitativa de mments de inercia de distints bjets. Cmprbación experimental
APARATO DE OSCILACIÓN GIRATORIA Cálcul de mments de Inercia 1. OBJETIVO Estudi de las vibracines de trsión aplicadas a la determinación cuantitativa de mments de inercia de distints bjets. Cmprbación experimental
TEMA 8. ENERGÍA Y TRABAJO
 TEMA 8. ENERGÍA Y TRABAJO 8.1 CONCEPTO DE ENERGÍA De frma general, se puede decir que la energía es una prpiedad de tds ls cuerps que hace psible la interacción entre ells. Tda la energía del Univers estuv
TEMA 8. ENERGÍA Y TRABAJO 8.1 CONCEPTO DE ENERGÍA De frma general, se puede decir que la energía es una prpiedad de tds ls cuerps que hace psible la interacción entre ells. Tda la energía del Univers estuv
, si X toma valores muy grandes positivos, f(x) se va aproximando a l. o., si X toma valores muy grandes negativos, f(x) se va aproximando a l.
 3.8 Límites en el infinit En casines interesa cnsiderar el cmprtamient de una función cuand la variable independiente tiende, n a un valr cncret, sin a valres muy grandes, tant psitivs cm negativs. En
3.8 Límites en el infinit En casines interesa cnsiderar el cmprtamient de una función cuand la variable independiente tiende, n a un valr cncret, sin a valres muy grandes, tant psitivs cm negativs. En
Nombre: Nº. Ejercicio nº 1.- Traza la mediatriz de estos segmentos y responde: Qué tienen en común todos los puntos de esa recta que has trazado?
 Nmbre: Nº Ejercici nº 1.- Traza la mediatriz de ests segments y respnde: Qué tienen en cmún tds ls punts de esa recta que has trazad? Ejercici nº 2.- Ejercici nº 3.- Tiene algún eje de simetría esta figura?
Nmbre: Nº Ejercici nº 1.- Traza la mediatriz de ests segments y respnde: Qué tienen en cmún tds ls punts de esa recta que has trazad? Ejercici nº 2.- Ejercici nº 3.- Tiene algún eje de simetría esta figura?
Teoría elemental de conjuntos
 Tería elemental de cnjunts Lógica prpsicinal Una prpsición es cualquier enunciad lógic al que se le pueda asignar un valr de verdad (1) falsedad (0). Dada una prpsición p, se define la negación de p cm
Tería elemental de cnjunts Lógica prpsicinal Una prpsición es cualquier enunciad lógic al que se le pueda asignar un valr de verdad (1) falsedad (0). Dada una prpsición p, se define la negación de p cm
1. Ángulos Referencia angular. TRIGONOMETRÍA La palabra, TRI-GONO-METRÍA, etimológicamente significa relación entre los lados
 IES Joan Ramon Benaprès TRIGNMETRÍA La palabra, TRI-GN-METRÍA, etimológicamente significa relación entre los lados y ángulos de un triángulo 1 Ángulos Definición 1 (Ángulo) Un ángulo es la abertura de
IES Joan Ramon Benaprès TRIGNMETRÍA La palabra, TRI-GN-METRÍA, etimológicamente significa relación entre los lados y ángulos de un triángulo 1 Ángulos Definición 1 (Ángulo) Un ángulo es la abertura de
CRISTALOGRAFÍA GEOMÉTRICA. TEMA 3 SIMETRÍA y REDES
 CRISTALOGRAFÍA GEOMÉTRICA TEMA 3 SIMETRÍA y REDES ÍNDICE 3.1 Simetría cntenida en las redes 3.2 Cncept de simetría 3.3 Operacines de simetría 3.4 Elements de simetría 3.5 Traslación 3.6 Rtación y eje de
CRISTALOGRAFÍA GEOMÉTRICA TEMA 3 SIMETRÍA y REDES ÍNDICE 3.1 Simetría cntenida en las redes 3.2 Cncept de simetría 3.3 Operacines de simetría 3.4 Elements de simetría 3.5 Traslación 3.6 Rtación y eje de
Matemáticas TRABAJO. Funciones Trigonométricas
 Matemáticas TRABAJO Funciones Trigonométricas 2 En este trabajo trataremos de mostrar de una forma práctica las funciones trigonométricas, con sus formas de presentación, origen y manejos. También se incluirán
Matemáticas TRABAJO Funciones Trigonométricas 2 En este trabajo trataremos de mostrar de una forma práctica las funciones trigonométricas, con sus formas de presentación, origen y manejos. También se incluirán
1. a) Qué significa una potencia de exponente negativo?... ; b)
 MATEMÁTICAS - SEPTIEMBRE TAREA DE VERANO 4º E.S.O.-B 1. a) Qué significa una potencia de eponente negativo?..... b) Simplificar: b 1) : b 4 ) b ) 9 1 b 4) 1 4. Simplificar potencias: a) 4 ( ) d) 9000 0'000000006
MATEMÁTICAS - SEPTIEMBRE TAREA DE VERANO 4º E.S.O.-B 1. a) Qué significa una potencia de eponente negativo?..... b) Simplificar: b 1) : b 4 ) b ) 9 1 b 4) 1 4. Simplificar potencias: a) 4 ( ) d) 9000 0'000000006
CONDUCTOR EN EQULIBRIO ELECTROSTÁTICO
 CONDUCTOR EN EQULIBRIO ELECTROSTÁTICO Un cnductr en euilibri electrstátic tiene las siguientes prpiedades: El camp eléctric es cer en punts situads dentr del cnductr. Cualuier carga en exces ue se clue
CONDUCTOR EN EQULIBRIO ELECTROSTÁTICO Un cnductr en euilibri electrstátic tiene las siguientes prpiedades: El camp eléctric es cer en punts situads dentr del cnductr. Cualuier carga en exces ue se clue
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS
 FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS PARA EMPEZAR, REFLEXIONA Y RESUELVE 1. Aunque el método para resolver las siguientes preguntas se sistematiza en la página siguiente, puedes resolverlas ahora: a) Cuántos
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS PARA EMPEZAR, REFLEXIONA Y RESUELVE 1. Aunque el método para resolver las siguientes preguntas se sistematiza en la página siguiente, puedes resolverlas ahora: a) Cuántos
U.E CRUZ VITALE Prof.Zuleidi Zambrano Matemática 4to A Y B
 U.E CRUZ VITALE Prof.Zuleidi Zambrano Matemática 4to A Y B TEORIA PARA LA ELABORACIÓN DEL CUENTO. ( PERSONAS, DEFENSA) TRIGONOMETRÍA ETIMOLÓGICAMENTE: Trigonometría, es la parte de la matemática que estudia
U.E CRUZ VITALE Prof.Zuleidi Zambrano Matemática 4to A Y B TEORIA PARA LA ELABORACIÓN DEL CUENTO. ( PERSONAS, DEFENSA) TRIGONOMETRÍA ETIMOLÓGICAMENTE: Trigonometría, es la parte de la matemática que estudia
TRIGONOMETRÍA. MATEMÁTICAS I 1º Bachillerato Ciencias de la Salud y Tecnológico. 1.- Ángulos en la Circunferencia.
 TRIGONOMETRÍA MATEMÁTICAS I 1º Bachillerato Ciencias de la Salud y Tecnológico 1.- Ángulos en la Circunferencia. 2.- Razones Trigonométricas de un Triángulo Rectángulo. 3.- Valores del Seno, Coseno y Tangente
TRIGONOMETRÍA MATEMÁTICAS I 1º Bachillerato Ciencias de la Salud y Tecnológico 1.- Ángulos en la Circunferencia. 2.- Razones Trigonométricas de un Triángulo Rectángulo. 3.- Valores del Seno, Coseno y Tangente
Seno (matemáticas) Coseno Tangente
 Seno (matemáticas), una de las proporciones fundamentales de la trigonometría. En un triángulo rectángulo, el valor del seno (que suele abreviarse sen) de un ángulo agudo es igual a la longitud del cateto
Seno (matemáticas), una de las proporciones fundamentales de la trigonometría. En un triángulo rectángulo, el valor del seno (que suele abreviarse sen) de un ángulo agudo es igual a la longitud del cateto
Forma de medir los ángulos en números reales
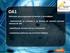 Angulo orientado Un ángulo orientado α consiste de un vértice O, una semirrecta (l i ) de origen O llamada lado inicial, otra semirrecta (l t ) de origen O llamada lado terminal, un giro g alrededor de
Angulo orientado Un ángulo orientado α consiste de un vértice O, una semirrecta (l i ) de origen O llamada lado inicial, otra semirrecta (l t ) de origen O llamada lado terminal, un giro g alrededor de
TRIGONOMETRIA. Trigonometría plana
 TRIGONOMETRIA Trigonometría, rama de las matemáticas que estudia las relaciones entre los lados y los ángulos de triángulos, de las propiedades y aplicaciones de las funciones trigonométricas de ángulos.
TRIGONOMETRIA Trigonometría, rama de las matemáticas que estudia las relaciones entre los lados y los ángulos de triángulos, de las propiedades y aplicaciones de las funciones trigonométricas de ángulos.
CÁLCULO I ANEXO: FUNCIONES TRIGONOMÉTRICAS
 1 CÁLCULO I ANEXO: FUNCIONES TRIGONOMÉTRICAS Departamento de Matemática Aplicada a los Recursos Naturales José Carlos Bellido Muñoz Félix Miguel de las Heras García Julián Herranz Calzada Antonio Ruíz
1 CÁLCULO I ANEXO: FUNCIONES TRIGONOMÉTRICAS Departamento de Matemática Aplicada a los Recursos Naturales José Carlos Bellido Muñoz Félix Miguel de las Heras García Julián Herranz Calzada Antonio Ruíz
EJERCICIOS DE RELACIONES TRIGONOMÉTRICAS (TEMA 1)
 Colegio Diocesano Asunción de Nuestra Señora Ávila Tema EJERCICIOS DE RELACIONES TRIGONOMÉTRICAS (TEMA ).- Dados los ángulos = º y = 7º, calcula: a) + b) c) d).- Dados los ángulos = º 7 y = 7º, calcula:
Colegio Diocesano Asunción de Nuestra Señora Ávila Tema EJERCICIOS DE RELACIONES TRIGONOMÉTRICAS (TEMA ).- Dados los ángulos = º y = 7º, calcula: a) + b) c) d).- Dados los ángulos = º 7 y = 7º, calcula:
Funciones Trigonométricas
 UNIVERSIDAD LA REPÚBLICA ESCUELA DE INGENIERÍA FUNDAMENTOS DE LA MATEMÁTICA PROF. FRANCISCA GONZÁLEZ AY. GABRIEL SORIA TRABAJO: Funciones Trigonométricas FECHA: 22 de septiembre de 1999 INTEGRANTES: CARLOS
UNIVERSIDAD LA REPÚBLICA ESCUELA DE INGENIERÍA FUNDAMENTOS DE LA MATEMÁTICA PROF. FRANCISCA GONZÁLEZ AY. GABRIEL SORIA TRABAJO: Funciones Trigonométricas FECHA: 22 de septiembre de 1999 INTEGRANTES: CARLOS
Solución: Solución: 5. Calcula los siguientes ángulos en grados, minutos y segundos
 3 Razones trigonométricas. Razones trigonométricas o circulares Piensa y calcula En una circunferencia de radio R = m, calcula mentalmente y de forma eacta la longitud de: a) la circunferencia. b) la semicircunferencia.
3 Razones trigonométricas. Razones trigonométricas o circulares Piensa y calcula En una circunferencia de radio R = m, calcula mentalmente y de forma eacta la longitud de: a) la circunferencia. b) la semicircunferencia.
5 Geometría analítica plana
 Solucionario Geometría analítica plana ACTIVIDADES INICIALES.I. Halla las coordenadas del punto medio del segmento de extremos A(, ) y B(8, ). El punto medio es M(, 8)..II. Dibuja un triángulo isósceles
Solucionario Geometría analítica plana ACTIVIDADES INICIALES.I. Halla las coordenadas del punto medio del segmento de extremos A(, ) y B(8, ). El punto medio es M(, 8)..II. Dibuja un triángulo isósceles
EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES
 EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES 1 er PARCIAL 1. Obtén los valores reales que cumplen las siguientes condiciones: x+ x 3 5 x 1/ =1. Opera y expresa el resultado en notación científic (5,
EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES 1 er PARCIAL 1. Obtén los valores reales que cumplen las siguientes condiciones: x+ x 3 5 x 1/ =1. Opera y expresa el resultado en notación científic (5,
Funciones (continuación)
 Nivelación de Matemática MTHA UNLP Funciones (continuación) Funciones trigonométricas Consideremos un ángulo x y seleccionemos un punto (a, b) sobre el rayo que determina dicho ángulo Sea R = a + b, la
Nivelación de Matemática MTHA UNLP Funciones (continuación) Funciones trigonométricas Consideremos un ángulo x y seleccionemos un punto (a, b) sobre el rayo que determina dicho ángulo Sea R = a + b, la
José Antonio Jiménez Nieto
 TRIGONOMETRÍA. UNIDADES PARA MEDIR ÁNGULOS Un ángulo es una porción de plano limitada por dos semirrectas que tienen un origen común. Las unidades que más frecuentemente se utilizan para medir ángulos
TRIGONOMETRÍA. UNIDADES PARA MEDIR ÁNGULOS Un ángulo es una porción de plano limitada por dos semirrectas que tienen un origen común. Las unidades que más frecuentemente se utilizan para medir ángulos
PLANIFICACIÓN DE LA SESIÓN DE APRENDIZAJE
 PLANIFICACIÓN DE LA SESIÓN DE APRENDIZAJE Grad: Tercer Duración: 2 hras pedagógicas UNIDAD 6 NÚMERO DE SESIÓN 5/15 I. TÍTULO DE LA SESIÓN Empleams el gniómetr para hallar alturas y ánguls de elevación
PLANIFICACIÓN DE LA SESIÓN DE APRENDIZAJE Grad: Tercer Duración: 2 hras pedagógicas UNIDAD 6 NÚMERO DE SESIÓN 5/15 I. TÍTULO DE LA SESIÓN Empleams el gniómetr para hallar alturas y ánguls de elevación
Física General 1 M O V I M I E N T O D E U N H O M B R E B A L A. Ronit Kremer, Noelia Pacheco.
 Prect PE - Curs 7 Institut de Física O V I I E N T O D E U N H O B R E B A L A Rnit Kremer, Nelia Pachec. INTRODUCCIÓN: OBJETIVO: Dad el siguiente ejercici: Ejercici 11, práctic. imient de un hmbre bala.
Prect PE - Curs 7 Institut de Física O V I I E N T O D E U N H O B R E B A L A Rnit Kremer, Nelia Pachec. INTRODUCCIÓN: OBJETIVO: Dad el siguiente ejercici: Ejercici 11, práctic. imient de un hmbre bala.
TEMA 0 FUNCIONES ***************
 TEMA 0. Definición y terminología.. Funciones conocidas. 3. Operaciones con funciones. 4. Funciones inversas. FUNCIONES ***************. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable
TEMA 0. Definición y terminología.. Funciones conocidas. 3. Operaciones con funciones. 4. Funciones inversas. FUNCIONES ***************. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable
Semana06[1/24] Trigonometría. 4 de abril de Trigonometría
![Semana06[1/24] Trigonometría. 4 de abril de Trigonometría Semana06[1/24] Trigonometría. 4 de abril de Trigonometría](/thumbs/58/41677169.jpg) Semana06[1/4] 4 de abril de 007 Medida de ángulos en radianes Semana06[/4] Consideremos la circunferencia de radio 1 y centrada en el origen de la figura. P α A x Ángulo positivo Dado un punto P en la
Semana06[1/4] 4 de abril de 007 Medida de ángulos en radianes Semana06[/4] Consideremos la circunferencia de radio 1 y centrada en el origen de la figura. P α A x Ángulo positivo Dado un punto P en la
Página 209 PARA RESOLVER. 44 Comprueba que el triángulo de vértices A( 3, 1), B(0, 5) y C(4, 2) es rectángulo
 44 Comprueba que el triángulo de vértices A(, ), B(0, ) y C(4, ) es rectángulo y halla su área. Veamos si se cumple el teorema de Pitágoras: AB = (0 + ) + ( ) = AC = (4 + ) + ( ) = 0 BC = 4 + ( ) = 0 +
44 Comprueba que el triángulo de vértices A(, ), B(0, ) y C(4, ) es rectángulo y halla su área. Veamos si se cumple el teorema de Pitágoras: AB = (0 + ) + ( ) = AC = (4 + ) + ( ) = 0 BC = 4 + ( ) = 0 +
Trigonometría. 1. Ángulos:
 Trigonometría. Ángulos: - Ángulos en posición estándar: se ubican en un sistema de coordenadas XY. El vértice será el origen (0,0) y el lado inicial coincide con el eje X positivo. - Ángulos positivos:
Trigonometría. Ángulos: - Ángulos en posición estándar: se ubican en un sistema de coordenadas XY. El vértice será el origen (0,0) y el lado inicial coincide con el eje X positivo. - Ángulos positivos:
TEMAS 4 Y 5 TRIGONOMETRÍA
 Temas 4 y 5 Trigonometría Matemáticas I º Bachillerato TEMAS 4 Y 5 TRIGONOMETRÍA UNIDADES DE MEDIDAS DE ÁNGULOS EJERCICIO a Pasa a radianes los siguientes ángulos: y 7 b) Pasa a grados los ángulos: 7 rad
Temas 4 y 5 Trigonometría Matemáticas I º Bachillerato TEMAS 4 Y 5 TRIGONOMETRÍA UNIDADES DE MEDIDAS DE ÁNGULOS EJERCICIO a Pasa a radianes los siguientes ángulos: y 7 b) Pasa a grados los ángulos: 7 rad
es el lugar geométrico de los puntos p tales que ; R (1)
 LA RECTA DEL PLANO ECUACIÓN VECTORIAL Y ECUACIONES PARAMÉTRICAS La recta en el plano como lugar geométrico Dados un punto p un vector no nulo u, la recta T paralela a u que pasa por p es el lugar geométrico
LA RECTA DEL PLANO ECUACIÓN VECTORIAL Y ECUACIONES PARAMÉTRICAS La recta en el plano como lugar geométrico Dados un punto p un vector no nulo u, la recta T paralela a u que pasa por p es el lugar geométrico
DECANATURA DE: ELECTRONICA ASIGNATURA: TRIGONOMETRÍA CÓDIGO: O15101 DOCENTE: DIANA MARCELA DOMINGUEZ PIEDRAHITA
 1 DECANATURA DE: ELECTRONICA PLANEACIÓN PARA EL DESARROLLO DE CONTENIDOS PROGRAMÁTICOS PROGRAMA : TECNOLOGÍA ELECTRONICA Códig: GDO - FR - 48 Versión: 001 Página 1 de 9 ASIGNATURA: TRIGONOMETRÍA CÓDIGO:
1 DECANATURA DE: ELECTRONICA PLANEACIÓN PARA EL DESARROLLO DE CONTENIDOS PROGRAMÁTICOS PROGRAMA : TECNOLOGÍA ELECTRONICA Códig: GDO - FR - 48 Versión: 001 Página 1 de 9 ASIGNATURA: TRIGONOMETRÍA CÓDIGO:
TEMA 8 FUENTES DEL CAMPO MAGNETICO
 Fundaments Físics de la nfrmática Escuela Superir de nfrmática Curs 09/10 Departament de Física Aplicada TEMA 8 FUENTES DEL CAMPO MAGNETCO 8.1.- Un prtón (carga +e), que se mueve cn una velcidad de v =
Fundaments Físics de la nfrmática Escuela Superir de nfrmática Curs 09/10 Departament de Física Aplicada TEMA 8 FUENTES DEL CAMPO MAGNETCO 8.1.- Un prtón (carga +e), que se mueve cn una velcidad de v =
Trigonometría Cálculo I
 Trigonometría Cálculo I Estimado estudiante, para que se te haga más fácil la aplicación de trigonometría en Cálculo I, es necesario que revises y repases los siguientes conceptos: Ángulos de Referencia
Trigonometría Cálculo I Estimado estudiante, para que se te haga más fácil la aplicación de trigonometría en Cálculo I, es necesario que revises y repases los siguientes conceptos: Ángulos de Referencia
ECUACIÓN DE LA RECTA. 6. Hallar la ecuación de la recta que pase por el punto A ( 1, 2) y que determina en el eje X un segmento de longitud 6.
 ECUACIÓN DE LA RECTA 1. El ángulo de inclinación de una recta mide 53º y pasa por los puntos ( 3, n) y ( 5, 4). Hallar el valor de n. A) 1 /5 B) 8 /5 C) 1 /5 D) 8 /5 E) 7 /3. Qué tipo de triángulo es el
ECUACIÓN DE LA RECTA 1. El ángulo de inclinación de una recta mide 53º y pasa por los puntos ( 3, n) y ( 5, 4). Hallar el valor de n. A) 1 /5 B) 8 /5 C) 1 /5 D) 8 /5 E) 7 /3. Qué tipo de triángulo es el
TRIGONOMETRÍA. π radianes. 1.- ÁNGULOS Y SUS MEDIDAS. 1.1 Los ángulos orientados
 TRIGONOMETRÍA.- ÁNGULOS Y SUS MEDIDAS. Los ángulos orientados Son aquellos que además de tener una cierta su amplitud ésta viene acompañada de un signo que nos indica un orden de recorrido (desde la semirrecta
TRIGONOMETRÍA.- ÁNGULOS Y SUS MEDIDAS. Los ángulos orientados Son aquellos que además de tener una cierta su amplitud ésta viene acompañada de un signo que nos indica un orden de recorrido (desde la semirrecta
RECTAS Y PLANOS EN EL ESPACIO. donde OP y OP
 RECTAS Y ANOS EN E ESACIO A RECTA EN R Ecacines de la recta En el espaci R se determina na recta si se cnce n pnt de ella dirección representada pr n ectr n nl Figra a Recta en R Cm se bsera en la Figra
RECTAS Y ANOS EN E ESACIO A RECTA EN R Ecacines de la recta En el espaci R se determina na recta si se cnce n pnt de ella dirección representada pr n ectr n nl Figra a Recta en R Cm se bsera en la Figra
GUIA DE ESTUDIO PARA EXAMEN EXTRAORDINARIO NOMBRE DEL ALUMNO: GRUPO: FECHA:
 CENTRO DE BACHILLERATO TECNOLOGICO INDUSTRIAL Y DE SERVICIOS N 281 SEMS DGETI DEPARTAMENTO DE SERVICIOS DOCENTES ASIGNATURA: GEOMETRIA Y TRIGONOMETRIA GUIA DE ESTUDIO PARA EXAMEN EXTRAORDINARIO NOMBRE
CENTRO DE BACHILLERATO TECNOLOGICO INDUSTRIAL Y DE SERVICIOS N 281 SEMS DGETI DEPARTAMENTO DE SERVICIOS DOCENTES ASIGNATURA: GEOMETRIA Y TRIGONOMETRIA GUIA DE ESTUDIO PARA EXAMEN EXTRAORDINARIO NOMBRE
APELLIDOS Y NOMBRE:...
 1º BACHILLERATO Fecha: 6-09-011 PRUEBA INICIAL APELLIDOS Y NOMBRE:... NORMAS El eamen se realizará con tinta de un solo color: azul ó negro No se puede usar corrector Se valorará potivamente: ortografía,
1º BACHILLERATO Fecha: 6-09-011 PRUEBA INICIAL APELLIDOS Y NOMBRE:... NORMAS El eamen se realizará con tinta de un solo color: azul ó negro No se puede usar corrector Se valorará potivamente: ortografía,
Razones trigonométricas DE un ángulo agudo de un triángulo
 RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO RAZONAMIENTO Y DEMOSTRACIÓN Calcula razones trigonométricas en un triángulo rectángulo. Demuestra identidades trigonométricas elementales Demuestra identidades
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO RAZONAMIENTO Y DEMOSTRACIÓN Calcula razones trigonométricas en un triángulo rectángulo. Demuestra identidades trigonométricas elementales Demuestra identidades
TEMA 4: TRIGONOMETRÍA. RAZONES TRIGONOMÉTRICAS
 IES IGNACIO ALDECOA 19 TEMA 4: TRIGONOMETRÍA. RAZONES TRIGONOMÉTRICAS 4.1 Medida de ángulos. Equivalencias. Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas
IES IGNACIO ALDECOA 19 TEMA 4: TRIGONOMETRÍA. RAZONES TRIGONOMÉTRICAS 4.1 Medida de ángulos. Equivalencias. Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas
1 Si los puntos ( 6, 2), ( 2, 6) y (2, 2) son vértices de un cuadrado, cuál es el cuarto vértice?
 Pág. 1 Puntos 1 Si los puntos ( 6, 2), ( 2, 6) y (2, 2) son vértices de un cuadrado, cuál es el cuarto vértice? 2 Los puntos ( 2, 3), (1, 2) y ( 2, 1) son vértices de un rombo. Cuáles son las coordenadas
Pág. 1 Puntos 1 Si los puntos ( 6, 2), ( 2, 6) y (2, 2) son vértices de un cuadrado, cuál es el cuarto vértice? 2 Los puntos ( 2, 3), (1, 2) y ( 2, 1) son vértices de un rombo. Cuáles son las coordenadas
UNIDAD IV TRIGONOMETRÍA
 UNIDAD IV TRIGONOMETRÍA http://www.ilustrados.com/publicaciones/epyuvklkkvpfesxwjt.php Objetivos: Al finalizar esta unidad, el alumno deberá ser hábil en: Comprender las definiciones de las relaciones
UNIDAD IV TRIGONOMETRÍA http://www.ilustrados.com/publicaciones/epyuvklkkvpfesxwjt.php Objetivos: Al finalizar esta unidad, el alumno deberá ser hábil en: Comprender las definiciones de las relaciones
PÉNDULO FÍSICO AMORTIGUADO. Estudio del movimiento ondulatorio libre y amortiguado.
 Labratri de Física PÉNDULO FÍSICO AMORTIGUADO 1. OBJETIVO Estudi del mvimient ndulatri libre y amrtiguad.. FUNDAMENTO TEÓRICO Se denmina péndul físic a cualquier sólid rígid capaz de scilar alrededr de
Labratri de Física PÉNDULO FÍSICO AMORTIGUADO 1. OBJETIVO Estudi del mvimient ndulatri libre y amrtiguad.. FUNDAMENTO TEÓRICO Se denmina péndul físic a cualquier sólid rígid capaz de scilar alrededr de
SITUACIONES DONDE SE USA FUNCIÓN LINEAL I
 SITUACIONES DONDE SE USA FUNCIÓN LINEAL I Función Oferta y Función Demanda de un Mercad. Ejercicis prpuests: 1) Cnsidere la relación 8p +0Q 000 0, dnde p es el preci de un prduct. a) Da la función explícita
SITUACIONES DONDE SE USA FUNCIÓN LINEAL I Función Oferta y Función Demanda de un Mercad. Ejercicis prpuests: 1) Cnsidere la relación 8p +0Q 000 0, dnde p es el preci de un prduct. a) Da la función explícita
(tema 9 del libro) 1. FUNCIÓNES EXPONENCIALES
 (tema 9 del libro). FUNCIÓNES EXPONENCIALES Son funciones de la forma f ( ) a donde a 0 y a. Su dominio es todo R y van a estar acotadas inferiormente por 0, que es su ínfimo. Todas pasan por el punto
(tema 9 del libro). FUNCIÓNES EXPONENCIALES Son funciones de la forma f ( ) a donde a 0 y a. Su dominio es todo R y van a estar acotadas inferiormente por 0, que es su ínfimo. Todas pasan por el punto
Tema 6: Trigonometría.
 Tema 6: Trigonometría. Comenzamos un tema, para mi parecer, muy bonito, en el que estudiaremos algunos aspectos importantes de la geometría, como son los ángulos, las principales razones e identidades
Tema 6: Trigonometría. Comenzamos un tema, para mi parecer, muy bonito, en el que estudiaremos algunos aspectos importantes de la geometría, como son los ángulos, las principales razones e identidades
FUNCIÓN. La Respuesta correcta es D
 FUNCIONES FUNCIÓN La Respuesta correcta es D FUNCIÓN Función Continua: Es aquella en la que su gráfica se puede recorrer en forma ininterrumpida en toda su extensión. FUNCIÓN Función Discontinua: Es aquella
FUNCIONES FUNCIÓN La Respuesta correcta es D FUNCIÓN Función Continua: Es aquella en la que su gráfica se puede recorrer en forma ininterrumpida en toda su extensión. FUNCIÓN Función Discontinua: Es aquella
Ángulos y razones trigonométricas
 Departamento Matemáticas TEMAS 3 y 4. Trigonometría Nombre CURSO: 1 BACH CCNN 1 Ángulos y razones trigonométricas 1. Hallar las razones trigonométricas de los ángulos agudos del siguiente triángulo rectángulos.
Departamento Matemáticas TEMAS 3 y 4. Trigonometría Nombre CURSO: 1 BACH CCNN 1 Ángulos y razones trigonométricas 1. Hallar las razones trigonométricas de los ángulos agudos del siguiente triángulo rectángulos.
GUIA SEMANAL DE APRENDIZAJE PARA EL GRADO OCTAVO
 GUIA SEMANAL DE APRENDIZAJE PARA EL GRADO OCTAVO IDENTIFICACIÓN AREA: Matemáticas. ASIGNATURA: Matemáticas. DOCENTE. Juan Gabriel Chacón c. GRADO. Octav. PERIODO: Segund UNIDAD: Ecuacines inecuacines lineales
GUIA SEMANAL DE APRENDIZAJE PARA EL GRADO OCTAVO IDENTIFICACIÓN AREA: Matemáticas. ASIGNATURA: Matemáticas. DOCENTE. Juan Gabriel Chacón c. GRADO. Octav. PERIODO: Segund UNIDAD: Ecuacines inecuacines lineales
Actividad 8: Lectura Capítulo 5
 Actividad 8: Lectura Capítulo 5 Fecha de inicio Fecha de Cierre 10/OCT/13 00:00 02/NOV/13 23:55 Ángulos y el círculo trigonométrico Ángulos En Geometría se estudiaron los ángulos, clases, propiedades y
Actividad 8: Lectura Capítulo 5 Fecha de inicio Fecha de Cierre 10/OCT/13 00:00 02/NOV/13 23:55 Ángulos y el círculo trigonométrico Ángulos En Geometría se estudiaron los ángulos, clases, propiedades y
1. Contesta: función sea creciente? 2. Representa la función: ( ) = Representa la siguiente función definida a trozos:
 IES SAULO TORÓN Matemáticas 4º ESO RECUPERACIÓN 3ª Evaluación 1. Contesta: a) Pon un ejemplo de una función de proporcionalidad directa. b) En la función () = +, explica el significado de m. Cómo debe
IES SAULO TORÓN Matemáticas 4º ESO RECUPERACIÓN 3ª Evaluación 1. Contesta: a) Pon un ejemplo de una función de proporcionalidad directa. b) En la función () = +, explica el significado de m. Cómo debe
GEOMETRÍA. (x 1) 2 +(y 2) 2 =1. Razónalo. x y + z = 2. :3x 3z +1= 0 es doble de la distancia al plano π 2. : x + y 1= 0. Razónalo.
 GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
LA RECTA Y SUS ECUACIONES
 UNIDAD LA RECTA Y SUS ECUACIONES EJERCICIOS RESUELTOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas correspondientes a las rectas en el plano y sus ecuaciones. Objetivo. Recordarás
UNIDAD LA RECTA Y SUS ECUACIONES EJERCICIOS RESUELTOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas correspondientes a las rectas en el plano y sus ecuaciones. Objetivo. Recordarás
Sistemas de numeración
 Indice 1. Intrduccin 2. Sistema de numeración binari 3. Operacines Binarias 4. Bibligrafía (Internet) www.mngrafias.cm Sistemas de numeración 1. Intrducción La imprtancia del sistema decimal radica en
Indice 1. Intrduccin 2. Sistema de numeración binari 3. Operacines Binarias 4. Bibligrafía (Internet) www.mngrafias.cm Sistemas de numeración 1. Intrducción La imprtancia del sistema decimal radica en
GEOMETRÍA Y TRIGONOMETRÍA
 REPÚLI OLIVRIN E VENEZUEL UNIVERSI EXPERIMENTL POLITÉNI E L FUERZ RM NIONL (UNEF) GEOMETRÍ Y TRIGONOMETRÍ a = b + c URSO E INUIÓN UNIVERSITRI (EJERIIOS) UNEF. Ejercicis de Gemetría y Trignmetría. -.. Generalidades
REPÚLI OLIVRIN E VENEZUEL UNIVERSI EXPERIMENTL POLITÉNI E L FUERZ RM NIONL (UNEF) GEOMETRÍ Y TRIGONOMETRÍ a = b + c URSO E INUIÓN UNIVERSITRI (EJERIIOS) UNEF. Ejercicis de Gemetría y Trignmetría. -.. Generalidades
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA ANA COLO HERRERA HECTOR PATRITTI PARA LOS CURSOS DE MATEMATICA DE LOS BACHILLERATOS TECNOLÓGICOS DEL C.E.T.P. APLICACIONES DE LA DERIVADA Ejercicis resuelts PROF. ANA COLO HERRERA
APLICACIONES DE LA DERIVADA ANA COLO HERRERA HECTOR PATRITTI PARA LOS CURSOS DE MATEMATICA DE LOS BACHILLERATOS TECNOLÓGICOS DEL C.E.T.P. APLICACIONES DE LA DERIVADA Ejercicis resuelts PROF. ANA COLO HERRERA
Unidad III: Termoquímica. 3. 1. Calores estándar de formación
 67.30 - Cmbustión - Unidad III 5 Unidad III: Termquímica 3.. Calres estándar de frmación El calr estándar de frmación de una sustancia, H f (kcal/ml), se define cm el calr invlucrad cuand se frma un ml
67.30 - Cmbustión - Unidad III 5 Unidad III: Termquímica 3.. Calres estándar de frmación El calr estándar de frmación de una sustancia, H f (kcal/ml), se define cm el calr invlucrad cuand se frma un ml
INSTITUCIÓN EDUCATIVA GABRIEL TRUJILLO CORREGIMIENTO DE CAIMALITO, PEREIRA
 INSTITUCIÓN EDUCATIVA GABRIEL TRUJILLO CORREGIMIENTO DE CAIMALITO, PEREIRA Lo peor no es cometer un error, sino tratar de justificarlo, en vez de aprovecharlo como aviso providencial de nuestra ligereza
INSTITUCIÓN EDUCATIVA GABRIEL TRUJILLO CORREGIMIENTO DE CAIMALITO, PEREIRA Lo peor no es cometer un error, sino tratar de justificarlo, en vez de aprovecharlo como aviso providencial de nuestra ligereza
ELECTIVA I PROGRAMA DE FISICA Departamento de Física y Geología Universidad de Pamplona Marzo de 2010 NESTOR A. ARIAS HERNANDEZ - UNIPAMPLONA
 ELECTIVA I PROGRAMA DE FISICA Departament de Física y Gelgía Universidad de Pamplna Marz de 2010 En esta sección ns enfcarems en una clase muy limitada, per imprtante que invlucra mdificacines sencillas
ELECTIVA I PROGRAMA DE FISICA Departament de Física y Gelgía Universidad de Pamplna Marz de 2010 En esta sección ns enfcarems en una clase muy limitada, per imprtante que invlucra mdificacines sencillas
3.1 Situaciones que involucran funciones trigonométricas
 3.1 Situaciones que involucran funciones trigonométricas Ejemplo 1) La traectoria de un proectil disparado con una inclinación respecto a la horizontal con una velocidad inicial v 0 es una parábola. Epresa
3.1 Situaciones que involucran funciones trigonométricas Ejemplo 1) La traectoria de un proectil disparado con una inclinación respecto a la horizontal con una velocidad inicial v 0 es una parábola. Epresa
UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN FACULTAD DE CIENCIAS-ESCUELA DE FÍSICA FÍSICA MECÁNICA MÓDULO #2: FUNDAMENTOS SOBRE VECTORES
 UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN FACULTAD DE CIENCIAS-ESCUELA DE FÍSICA FÍSICA MECÁNICA MÓDULO #2: FUNDAMENTOS SOBRE VECTORES Dieg Luis Aristizábal R., Rbert Restrep A., Tatiana Muñz H. Prfesres,
UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN FACULTAD DE CIENCIAS-ESCUELA DE FÍSICA FÍSICA MECÁNICA MÓDULO #2: FUNDAMENTOS SOBRE VECTORES Dieg Luis Aristizábal R., Rbert Restrep A., Tatiana Muñz H. Prfesres,
EE525M ANTENAS 2009-1 ARREGLO DE FUENTES PUNTUALES, PARTE I
 EE55M ANTENAS 9-1 Este capitul incluye ls siguientes tópics: ARREGLO DE FUENTES PUNTUALES, PARTE I -Ejempl de arregl de ds fuentes puntuales. -Multiplicación de patrón. -Síntesis de patrón. -Fuentes n
EE55M ANTENAS 9-1 Este capitul incluye ls siguientes tópics: ARREGLO DE FUENTES PUNTUALES, PARTE I -Ejempl de arregl de ds fuentes puntuales. -Multiplicación de patrón. -Síntesis de patrón. -Fuentes n
Razones trigonométricas.
 Razones trigonométricas. Matemáticas I 1 Razones trigonométricas. Medidas de ángulos. Medidas en grados (Deg.) El grado es el ángulo plano que teniendo su vértice en el centro de un círculo intercepta
Razones trigonométricas. Matemáticas I 1 Razones trigonométricas. Medidas de ángulos. Medidas en grados (Deg.) El grado es el ángulo plano que teniendo su vértice en el centro de un círculo intercepta
Tema 1: Cinemática. Capítulo 2: Movimiento de proyectiles y Movimiento circular
 Tema 1: Cinemática Capítul : Mimient de pryectiles y Mimient circular TEMA 1: CINEMÁTICA Capítul : Mimient de pryectiles Trayectria Tiemp de uel Alcance (cta final) Ejempl de tir parabólic Mimient de Pryectiles
Tema 1: Cinemática Capítul : Mimient de pryectiles y Mimient circular TEMA 1: CINEMÁTICA Capítul : Mimient de pryectiles Trayectria Tiemp de uel Alcance (cta final) Ejempl de tir parabólic Mimient de Pryectiles
TEMAS 4 Y 5 TRIGONOMETRÍA
 Temas 4 y 5 Trigonometría Matemáticas I º Bachillerato TEMAS 4 Y 5 TRIGONOMETRÍA UNIDADES DE MEDIDAS DE ÁNGULOS EJERCICIO a Pasa a radianes los siguientes ángulos: y 7 b) Pasa a grados los ángulos: 7 rad
Temas 4 y 5 Trigonometría Matemáticas I º Bachillerato TEMAS 4 Y 5 TRIGONOMETRÍA UNIDADES DE MEDIDAS DE ÁNGULOS EJERCICIO a Pasa a radianes los siguientes ángulos: y 7 b) Pasa a grados los ángulos: 7 rad
TRIGONOMETRIA. π radianes <> 180º
 TRIGONOMETRIA La trigonometría estudia las relaciones existentes entre los ángulos y los lados de un triángulo. La base de su estudio es el ángulo. Angulo es la porción del plano limitada por dos semirrectas
TRIGONOMETRIA La trigonometría estudia las relaciones existentes entre los ángulos y los lados de un triángulo. La base de su estudio es el ángulo. Angulo es la porción del plano limitada por dos semirrectas
PRACTICA DE GEOMETRIA TRIGONOMETRIA SEGUNDO PARCIAL CIRCUNFERENCIA
 CURSO PRE FACULTATIVO II-01 PRACTICA DE GEOMETRIA TRIGONOMETRIA SEGUNDO PARCIAL CIRCUNFERENCIA 1. En una circunferencia de centro O, se traza el diámetro AB y se prolonga hasta el punto C a partir del
CURSO PRE FACULTATIVO II-01 PRACTICA DE GEOMETRIA TRIGONOMETRIA SEGUNDO PARCIAL CIRCUNFERENCIA 1. En una circunferencia de centro O, se traza el diámetro AB y se prolonga hasta el punto C a partir del
Capítulo 7. Trigonometría del triángulo rectángulo. Contenido breve. Presentación. Módulo 17 Medición de ángulos. Módulo 18 Ángulos notables
 Capítulo 7 Trigonometría del triángulo rectángulo Contenido breve Módulo 17 Medición de ángulos Módulo 18 Ángulos notables La trigonometría se utiliza para realizar medidas indirectas de posición y distancias.
Capítulo 7 Trigonometría del triángulo rectángulo Contenido breve Módulo 17 Medición de ángulos Módulo 18 Ángulos notables La trigonometría se utiliza para realizar medidas indirectas de posición y distancias.
1 Razones trigonométricas de la suma
 1 Raznes trignmétricas de la suma Ejercici 1 Utilizand las siguientes fórmulas ( + ) = cs + cs ( ) = cs cs cs( + ) = cs cs cs( + ) = cs cs + tan( + ) = tan + tan 1 tan tan calcula 15 ; cs 15 ; tan 15 75
1 Raznes trignmétricas de la suma Ejercici 1 Utilizand las siguientes fórmulas ( + ) = cs + cs ( ) = cs cs cs( + ) = cs cs cs( + ) = cs cs + tan( + ) = tan + tan 1 tan tan calcula 15 ; cs 15 ; tan 15 75
HOTEL RURAL. Taller de modelado de objetos. Ingeniería del Software Curso 2005-2006. Salamanca, 16-XI-2005. Trabajo realizado por:
 Taller de mdelad de bjets HOTEL RURAL Salamanca, 16-XI-2005 Trabaj realizad pr: Javier Trujill Hernández Javier Rubi Alamill Fernand Buitrag Alns El Htel Rural Un pequeñ htel rural necesita una aplicación
Taller de mdelad de bjets HOTEL RURAL Salamanca, 16-XI-2005 Trabaj realizad pr: Javier Trujill Hernández Javier Rubi Alamill Fernand Buitrag Alns El Htel Rural Un pequeñ htel rural necesita una aplicación
Además de la medida, que estudiaremos a continuación, consideraremos que los ángulos tienen una orientación de acuerdo con el siguiente convenio:
 Trigonometría La trigonometría trata sobre las relaciones entre los ángulos y los lados de los triángulos. El concepto fundamental sobre el que se trabaja es el de ángulo. Dos semirrectas con un origen
Trigonometría La trigonometría trata sobre las relaciones entre los ángulos y los lados de los triángulos. El concepto fundamental sobre el que se trabaja es el de ángulo. Dos semirrectas con un origen
TEMA 8: FUNCIONES. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
 2009 TEMA 8: FUNCIONES. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 1º E.S.O. TEMA 08: Funciones. TEMA 08: FUNCIONES. 1. Correspondencia.
2009 TEMA 8: FUNCIONES. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 1º E.S.O. TEMA 08: Funciones. TEMA 08: FUNCIONES. 1. Correspondencia.
PSU Resolución Ensayo 3 Matemática
 PSU Resolución Ensayo Matemática Indicaciones generales Este cuadernillo contiene la resolución de cada pregunta del Ensayo de Matemática. Te permitirá conocer preliminarmente tu puntaje de acuerdo a tus
PSU Resolución Ensayo Matemática Indicaciones generales Este cuadernillo contiene la resolución de cada pregunta del Ensayo de Matemática. Te permitirá conocer preliminarmente tu puntaje de acuerdo a tus
INSTITUCION EDUCATIVA NUESTRA SEÑORA DE BELEN
 RAZONES TRIGONOMÉTRICAS EN EL TRIÁNGULO RECTÁNGULO Las funciones trigonométricas estudiadas en la circunferencia unitaria se pueden describir en triángulos rectángulos a partir de las relaciones entre
RAZONES TRIGONOMÉTRICAS EN EL TRIÁNGULO RECTÁNGULO Las funciones trigonométricas estudiadas en la circunferencia unitaria se pueden describir en triángulos rectángulos a partir de las relaciones entre
