Gráfica de la función coseno de x (cos x)
|
|
|
- Hugo Lozano Ortiz de Zárate
- hace 6 años
- Vistas:
Transcripción
1 Gráfica de la función coseno de x (cos x) Empecemos por trazar la gráfica de la función coseno de x que se simboliza como cos x, x es el argumento de la función. El dominio de esta función son todos los valores que puede tomar x, démosle valores en grados, pero recordando que estos grados se pueden transformar a radianes y estos son números reales. Como ya vimos los grados son positivos si se miden en sentido contrario a las manecillas del reloj y negativos si se miden en el mismo sentido, con ayuda de tu calculadora evaluemos algunos valores de x en grados para delinear a esta función, también puedes darle valores en radianes usando el modo en radianes, trata de reproducir los valores que se encuentran en la siguiente tabla completándola y traza la gráfica. x (grados) f(x)=cosx Como te puedes dar cuenta al marcar la gráfica si sigues aumentando los grados la curva se va repitiendo y que si le das valores negativos, los valores de la función se van repitiendo, o sea que su gráfica es como una onda que se extiende desde menos infinito hasta infinito, repitiéndose la curva cada, esta es la razón por la cual se dice que es periódica y su período es de 6 º que en términos de π equivale a π. Cuál es el dominio de la función? D= 8
2 También podrás observar que los valores que toma la función no pasan de ni bajan de, oscila entre estos valores, por lo tanto el rango de esta función es: R = Además cruza al eje x en: Ahora hagamos lo mismo que hemos hecho con las funciones vistas en las unidades anteriores primero veamos que pasa si le sumamos o restamos una cantidad determinada. Ejemplo ) Traza la gráfica de las siguientes funciones y da su dominio y su rango: a) f(x) = cos x + b) g(x) = cos x Solución: Completa la siguiente tabla en base a la tabla que ya hiciste para la función cos x y localiza los puntos en el plano (traza la gráfica de cada una de las funciones) x (grados) f(x)= cos x + g(x)= cos x
3 Si observas las dos gráficas y las comparas con la original notaras que lo único que paso es que una subió dos unidades y la otra bajo tres unidades, así que el dominio y el rango para cada una de ellas es: a) f(x) = cos x +, D= R = b) g(x) = cos x, D = R = Y ambas funciones se siguen repitiendo cada, o sea que su periodo es: P =. Qué puedes concluir de lo anterior? Estas funciones no cruzan el eje x por lo tanto no tienen ceros, hasta qué cantidad se le tendría que sumar o restar para que cruzaran o tocaran el eje x? Ejemplo ) Ahora vamos a multiplicar por una cantidad, traza las gráficas de las siguientes funciones: a) F(x) = cos x b) G(x) = ½ cos x c) H(x) = cos x Solución: Completa la tabla y traza las respectivas gráficas en el plano.
4 X F(x)=cos x G(x)=½ cos x H(x)= cos x
5 Puedes observar que para las tres funciones su periodo sigue siendo P =, o sea que se repite cada 6 ; su dominio es el mismo también D = Pero el rango cambia para cada una de ellas ahora es: R F = R G = R H = Cruzan al eje x en: A la cantidad por la cual multiplicamos a la función le vamos a llamar amplitud y lo que hace esta cantidad es: Ahora vamos a ver que pasa si esta cantidad es negativa. Ejemplo ) Traza las gráficas de las siguientes funciones y analízalas: a) g(x) = cos x b) h(x) = ½ cos x c) j(x) = cos x Solución: Completa la tabla x (grados) G(x)= cos x h(x)= ½ cos x j(x)= cos x x (grados) G(x)= cos x -9 7 h(x)= ½ cos x j(x)= cos x
6 Ahora la parte positiva se convierte en negativa y la negativa se convierte en positiva, al multiplicar la función por un número negativo la gráfica se Los ceros de la función no cambian ya que siguen cruzando al eje x en 9 + n8 con n = ±, ±,... El dominio es el mismo para las tres funciones: D = Y el intervalo del rango se hace más ancho o más angosto según sea la magnitud de la amplitud: R g = R h = R j = Cuándo le agregamos o restamos un valor a x, Crees saber que es lo que pasará? Si no es así haz la siguiente tabla y traza la gráfica. Ejemplo 4) A la función cos x, al valor de x vamos a sumarle y restarle, vamos analizar las funciones: F(x) = cos( x + ) y G(x) = cos (x ) Solución: Completa la tabla y traza las gráficas. x cos x F(x) = G(x) = X cos x F(x) = G(x) = cos( x + ) cos (x ) cos( x + ) cos (x )
7 Su dominio y su rango siguen siendo los mismos que la función Y cuando le aumentamos la gráfica se recorre Cuando le restamos la gráfica se recorre Cambia su periodo?, P =, su amplitud A =. Qué podemos concluir? Ejemplo 5) Si a x la multiplicamos por un número y luego aplicamos la función coseno, veamos que pasa; analiza las siguientes funciones: a) f(x) = cos x b) g(x) = cos x c) h(x) = cos (.5 x) Solución: Completa la tabla y traza la gráfica X cos x f(x) = cos x g(x) = cos x h(x) = cos (.5 x) X cos x f(x) = cos x g(x) = cos x h(x) = cos (.5 x)
8 Su dominio sigue siendo, todos los números reales y los valores que toman las funciones siguen estando entre la franja desde hasta así que su rango tampoco cambia esta en el intervalo Si te das cuenta entre y 6 la función f(x) = cos x se duplica o sea que la uve se repite dos veces esto quiere decir que su periodo ahora es de P = = 6 /; para g(x) = cos x la uve se repite cada así que su periodo es P = ; mientras que para h(x) = cos (.5 x) la uve se repite hasta los, por lo que su periodo es P = =. Con esto podemos afirmar lo siguiente: Si a x la multiplicamos por un número b, y luego aplicamos la función coseno, su gráfica cambia modificándose su periodo como P =. O sea que entre y 6 se repite b veces la uve. Cambiaron los ceros de cada una de las funciones. Enuméralos: a) b) c) Ejemplo 6) Analiza la función G(x) = - cosx + y traza su gráfica. Solución: El que esta multiplicando a x hace que cambie su periodo, ahora se va a repetir veces entre y 6, así que tiene un periodo de: P = El signo menos que se encuentra antes del coseno hace que se invierta sobre el eje, por lo que la uve se voltea, ahora el se lo estamos sumando a la función coseno así que sube unidades, cuando x=, G() = - + =, ahora a la mitad del periodo x=9, la original valdría pero como se invierte es y además le sumamos nos queda G(9 ) = +=4; donde termina la uve x= 8 5
9 en la original sería pero la invertimos así que es y le sumamos nos queda G(8 ) = -+= con esto ya la podemos delinear y dar el dominio. D = y el rango, R = Así que en base a la original delinea a G(x) G(x) tiene ceros, ya que, y su amplitud vale. Ejercicios) Analiza las siguientes funciones y traza su gráfica: ) F(x) = 4 cos x ) G(x) = 5 cos x ) H(x) = cos x + 4) I(x) = cos (x + π/6) 5) K(x) = cos (x 4 ) 6) M(x) = cos x Gráfica de la función seno de x (sen x) Nuevamente vamos a darle valores a x en grados y apliquemos la función seno, completa la tabla verificando los valores que se dan y recuerda el modo en que debe estar tu calculadora es en grados (deg o D): x f(x)=sen x X
10 f(x) = sen x Cuál es el dominio de la función? D = y el rango, R = La forma de esta función ahora es una onda que empieza en y termina en 6 y vuelve a repetirse hacia delante, en los negativos, empieza en 6 y termina en así que podemos decir que es simétrica con respecto al origen. Se repite cada por lo que su periodo es P = =. Enumera los ceros de esta función:..., -8,,,,... a partir de cada. Si sobre esta misma gráfica trazas la función g(x) = cos x Si te das cuenta es como si recorrieras hacia la derecha 9 la función cos x, o sea que sen x =, así que las dos funciones se comportan de manera similar su dominio son todos los números reales y su rango va desde hasta y cada 6 se repiten. Ahora vamos hacer lo mismo que hicimos con la función coseno, solamente que sin hacer las tablas, solamente trata de comprobar para algunos valores. Ejemplo) Analiza cada una de las siguientes funciones y traza su gráfica: a) f(x) = sen x 5 b) g(x) = sen x + Solución: En el inciso a) primero le damos un valor a x en grados y aplicamos la función seno y luego le restamos 5 unidades. Si recuerdas cuando hicimos esto 7
11 con la función coseno de x, simplemente se recorrió sobre el eje y, (bajo), así que teniendo la original de la función seno traza la función f(x) = sen x 5, bajándola 5 unidades. En el inciso b) aplicamos la función seno a x y le sumamos unidades, por lo que ahora subimos unidades la original y tenemos la gráfica de g(x) = sen x El dominio es D f = y el rango, R = D g = y su rango, R = Su periodo es P = y su amplitud A =. Los ceros de la función son: Así que si a la función sen x le sumamos o restamos una cantidad dada, la gráfica se desplaza sobre el eje, ya sea o hacia Ejemplo ) Analiza la función h(x) = sen (x + 6 ) y traza su gráfica. Solución: Crees saber como es la gráfica?. Lo que sucedía con la función coseno era que se recorría sobre el eje x, así que dale valores a x y ahora evalúa la función sen (x + 6 ) y confirma que lo que tienes que hacer es recorrer cada punto de la original 6 hacia la izquierda 8
12 El dominio y el rango de esta función son: D =, R = El periodo es P =, tiene una amplitud A = Enumera los ceros de la función: Si a x le aumentamos o restamos cierta cantidad y luego aplicamos la función seno, la gráfica se desplaza sobre el eje, ya sea a la o a la respectivamente. Ejemplo ) Analiza y traza la gráfica de cada una de las funciones: a) F(x) = 4 sen x b) G(x) = sen x Solución: Para el inciso a) la función esta multiplicada por 4, así que el menos la invierte sobre el eje y el 4 cambia su amplitud que ahora es de A= Así que su dominio es. D =, y como la amplitud es 4, el ancho del rango se hace más grande, R =, su periodo es P = ; con esto ya la puedes delinear comprobando para algunos valores. Para el inciso b) la función esta multiplicada por positivo así que queda de la misma forma que la original, solamente cambia su amplitud que ahora es A = Su dominio es D = y R = P =, comprueba con algunos valores. Los ceros de estas dos funciones son: 9
13 Cuando a la función seno la multiplicamos por una cantidad determinada a lo que sucede es que cambia su y si esta cantidad es negativa la invierte sobre el eje. Ejemplo 4) Traza la gráfica de cada una de las siguientes funciones y analízalas: a) M(x) = sen x b) P(x) = sen x Solución: Como se esta multiplicando a x en un caso por y en otro por, lo que sucede es que su periodo cambia como en la función coseno y ahora se va a repetir dos veces en el intervalo de a 6 en el inciso a) y veces en el inciso b), en el primer caso su periodo es P = y en el segundo caso P = Comprueba con algunos valores Los ceros de cada una de las funciones son: 4
14 Si a x la multiplicamos por un número b y luego aplicamos la función seno, la gráfica se va a repetir b veces en el intervalo de a 6, o sea que su periodo ahora es P =, su dominio son todos los números y su rango va desde hasta. Ejercicios) Analiza cada una de las siguientes funciones y traza su gráfica: ) P(x) = sen x ) Q(x) = - sen x + 4 ) R(x) = - sen x + ) S(x) = 5 sen x 5) T(x) = sen (x + π/4) 6) U(x) = sen πx Gráfica de la función tangente de x (tan x) Por último analicemos la función tangente de la misma manera que en las anteriores con ayuda de tu calculadora completa la siguiente tabla y marca los puntos en el plano. (puedes darle más valores para delinearla mejor) x f(x)=sen x x f(x)=sen x
15 Como te habrás dado cuenta tu calculadora marca error cuando queremos sacar tangente de 9 y para algunos múltiplos de este valor como son:, y ; por qué crees que marque error? El dominio de la función tangente es el conjunto de todos los números reales, excepto los múltiplos impares de (9 ), mientras que su rango es:. Esta función es simétrica con respecto, por lo que es una función impar. Cuando nos acercamos a 9 por la derecha por ejemplo 88, 89 la función se extiende hacia arriba y cuando nos acercamos por la izquierda por ejemplo 9, 9, la función por lo que podemos decir que x = 9 (x = π/) es una asíntota vertical. Enumera las demás asíntotas verticales: Es periódica esta función?, se repite cada, así que su periodo es P = = En cuanto a su forma empieza en y en 45 vale y se extiende hacia arriba pegándose por la derecha a la asíntota x=π/, después se extiende hacia abajo ahora pegándose por la izquierda a la asíntota y volviendo a llegar a cero cuando x = 8 (x=π) y se vuelve a repetir, así que las asíntotas están separadas o π radianes. Cuáles son los ceros de la función tan x? Sigamos realizando otros ejemplos para que te quede claro lo que le sucede a esta función al realizarle los diferentes cambios que ya hicimos con las funciones seno y coseno. Ejermplo ) Analiza las funciones y traza su respectiva gráfica, a) f(x) = tan x + b) g(x) = tan x Solución: Las asíntotas siguen siendo las mismas ya que sigue siendo la misma función tan x, así que las marcamos sobre el plano; como a la función se le está sumando unidades o restando unidades la gráfica se va a desplazar sobre el eje y en el inciso a) sube y en el inciso b) baja, con respecto a la original se sube el eje x unidades o lo bajamos unidades y reproducimos la gráfica, en el plano que se te da solamente trazamos un ciclo de la original, puedes trazar más ciclos. El dominio y el rango de las funciones es: D f =, R f = D g =, R g = 4
16 Las asíntotas son: Los ceros de la función f los podemos encontrar igualándola a cero y encontrando las raíces de esta ecuación: tan x + =, tan x =, la función tangente la despejamos como tan -, así que x = tan - ( ), la calculadora debe estar en modo grados (deg o D), así que x = y cada 8 que es el periodo vamos encontrar otra raíz, por lo tanto las raíces de f son: x = n(8 ) con n =, ±, ±,... Ahora encuentra los ceros de la función g: Verifica que coincidan con la gráfica. Si a la función tangente le sumamos o restamos una cantidad d que es lo que sucede: Ejemplo ) Analiza y traza la gráfica de las funciones: a) F(x) = tan (x + ) b) G(x) = tan ( x 4 ) Solución: Ahora como a x le sumamos o le restamos 4 la gráfica se va a desplazar sobre el eje x, a la izquierda y 4 a la derecha, por lo que las 4
17 asíntotas también se van a desplazar al igual que la gráfica y su periodo sigue siendo P = Las asíntotas verticales son: D =, R = Los ceros de la función son: Cruza al eje y en Las asíntotas verticales se encuentran en: D =, R = Los ceros de la función son: Cruza al eje y en. Verifica con la calculadora algunos valores para ver si coinciden con tu gráfica. Escribe lo que puedes concluir: 44
18 Ejemplo ) Analiza y traza la gráfica de la función Q(x) = tan x Solución: Como la variable x se esta multiplicando por el argumento de la función tangente llega más rápido a 9, o sea cuando x =, por lo que este valor nos da una asíntota vertical y su periodo ahora es P = 8/ =, después de cada 6 vamos a encontrar una asíntota, por lo que las asíntotas verticales se presentan en: x = Las marcamos sobre el plano y ahora el dominio y el rango son: D =, R = Evalúa en algunos valores entre y y reproduce la gráfica Los ceros de la función son: De lo anterior, si multiplicamos a x por un número b y luego aplicamos la función tangente, lo que cambia es el y este lo calculamos como P = /b. Como consecuencia de esto cambia:, y los ceros de la función. Ejemplo 4) Analiza las funciones y traza su gráfica: a) M(x) = tan x b) N(x) = ½ tan x Solución: Ahora se esta multiplicando a la función tangente por una cantidad, por lo que vamos a tener un alargamiento en la primera ya que estamos multiplicando por y una compresión en la segunda por que estamos multiplicando por un número entre y (/), así que cada valor de la original se triplica para el inciso a) y de divide a la mitad para el inciso b); no cambian: las asíntotas verticales, el dominio, el rango y lo ceros de la función. Las asíntotas verticales se presentan en: D=, R = Los ceros de ambas funciones se encuentran en : 45
19 Ejercicios) Analiza las siguientes funciones y traza sus respectivas gráficas ) F(x) = tan ( x) ) G(x) = tan x ) H(x) = tan ( x π/) 4) J(x) = tan πx/ 5) K(x) = tan x/ 6) L(x) = tan ( x).4 Definición de función periódica Una función f es periódica si existe un número real positivo p tal que f( x + p) = f(x) para toda x del dominio de f. El número positivo p, si es que existe se llama el periodo de f. En los casos anteriores al periodo le hemos llamado P y para la función seno y coseno es de π, mientras que para la función tangente es de π. A la parte de las gráficas de la función seno y coseno correspondiente al intervalo [, π] se le llama ciclo y para la función tangente un ciclo corresponde a la gráfica en el intervalo [, π]. Asi por ejemplo puedes verificar con tu calculadora que: sen ( +(6 )= sen sen ( + (6 )) = sen sen (45 (6 )) = sen cos (6 + 5(6)) = cos tan (75 6 ) = tan tan (π/ + π) = tan cos (π/4-4π) = cos tan ( + 8 ) = tan Así que: sen [x + n(π)] = sen x, cos [x + n(π)] = cos x y tan [x + n(π)] = tan x con n = ±, ±, ±,... 46
FUNCIONES TRIGONOMÉTRICAS
 FUNCIONES TRIGONOMÉTRICAS DEFINICIÓN PREVIA: Una función periódica es aquella que se repite una y otra vez en una dirección horizontal. El periodo de una función periódica es la longitud de un ciclo (o
FUNCIONES TRIGONOMÉTRICAS DEFINICIÓN PREVIA: Una función periódica es aquella que se repite una y otra vez en una dirección horizontal. El periodo de una función periódica es la longitud de un ciclo (o
Para cada cada valor de la función original lo multiplicas por 3 lo recorres 45 a la derecha y lo subes 5 unidades.
 3.5 Gráficas de las funciones: f(x) = a sen (bx + c) + d f(x) = a cos (bx + c) + d f(x) = a tan (bx + c) + d en donde a, b, c, y d son números reales En la sección 3.4 ya realizamos algunos ejemplos en
3.5 Gráficas de las funciones: f(x) = a sen (bx + c) + d f(x) = a cos (bx + c) + d f(x) = a tan (bx + c) + d en donde a, b, c, y d son números reales En la sección 3.4 ya realizamos algunos ejemplos en
Las desigualdades involucran los símbolos: < menor que, >,
 . Noción de intervalo en la recta real Un intervalo es un conjunto de números reales que satisfacen una desigualdad, por lo que un intervalo puede ser cerrado, abierto o semiabierto, lo podemos representar
. Noción de intervalo en la recta real Un intervalo es un conjunto de números reales que satisfacen una desigualdad, por lo que un intervalo puede ser cerrado, abierto o semiabierto, lo podemos representar
x =, x = 6 esta es la raíz de g
 1.4 TEOREMAS Y TÉCNICAS DE EXPLORACIÓN APLICABLES A FUNCIONES POLINOMIALES PARA LA OBTENCIÓN DE SUS CEROS. Como ya vimos la función lineal es una función polinomial de primer grado donde el coeficiente
1.4 TEOREMAS Y TÉCNICAS DE EXPLORACIÓN APLICABLES A FUNCIONES POLINOMIALES PARA LA OBTENCIÓN DE SUS CEROS. Como ya vimos la función lineal es una función polinomial de primer grado donde el coeficiente
3.1 Situaciones que involucran funciones trigonométricas
 3.1 Situaciones que involucran funciones trigonométricas Ejemplo 1) La traectoria de un proectil disparado con una inclinación respecto a la horizontal con una velocidad inicial v 0 es una parábola. Epresa
3.1 Situaciones que involucran funciones trigonométricas Ejemplo 1) La traectoria de un proectil disparado con una inclinación respecto a la horizontal con una velocidad inicial v 0 es una parábola. Epresa
Profesorado de Nivel Medio y Superior en Biología Matemática - 1º Cuatrimestre Año 2013 FUNCIÓN CUADRÁTICA
 Matemática - º Cuatrimestre Año 0 FUNCIÓN CUADRÁTICA Hemos definido anteriormente la función lineal como una función f: R R de la forma f()a+b con a R y b R, que se representa en el plano mediante una
Matemática - º Cuatrimestre Año 0 FUNCIÓN CUADRÁTICA Hemos definido anteriormente la función lineal como una función f: R R de la forma f()a+b con a R y b R, que se representa en el plano mediante una
Unidad 3: Razones trigonométricas.
 Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
Módulo 3: Gráfica de las Funciones Trigonométricas
 x Módulo : Gráfica de las Funciones Trigonométricas Una función es una relación entre los valores x de un conjunto (dominio) los elementos de un conjunto (llamado codominio o rango), en la cual a cada
x Módulo : Gráfica de las Funciones Trigonométricas Una función es una relación entre los valores x de un conjunto (dominio) los elementos de un conjunto (llamado codominio o rango), en la cual a cada
x= 3 y y=f(x)
 4.10 Gráficas de funciones logarítmicas. Empecemos por recordar las que ya hicimos en la sección 4.8, en esta sección trazamos la función logaritmo base 2 de x, conociendo su inversa y reflejándola sobre
4.10 Gráficas de funciones logarítmicas. Empecemos por recordar las que ya hicimos en la sección 4.8, en esta sección trazamos la función logaritmo base 2 de x, conociendo su inversa y reflejándola sobre
CONCEPTOS CLAVE DE LA UNIDAD 3
 CONCEPTOS CLAVE DE LA UNIDAD 3 1. Razón trigonométrica seno. Si θ es la medida de algún ángulo interior agudo en cualquier triángulo rectángulo, entonces a la razón que hay de la longitud del cateto opuesto
CONCEPTOS CLAVE DE LA UNIDAD 3 1. Razón trigonométrica seno. Si θ es la medida de algún ángulo interior agudo en cualquier triángulo rectángulo, entonces a la razón que hay de la longitud del cateto opuesto
Las Funciones Trigonométricas. Sección 5.3 Funciones Trigonométricas de números reales
 5 Las Funciones Trigonométricas Sección 5.3 Funciones Trigonométricas de números reales Qué hemos visto? Si el lado inicial de un ángulo,, coincide con la parte del eje de x que se encuentra en el primer
5 Las Funciones Trigonométricas Sección 5.3 Funciones Trigonométricas de números reales Qué hemos visto? Si el lado inicial de un ángulo,, coincide con la parte del eje de x que se encuentra en el primer
Las Funciones Trigonométricas. Sección 5.3 Funciones Trigonométricas de números reales
 5 Las Funciones Trigonométricas Sección 5.3 Funciones Trigonométricas de números reales Dominios Se presentan los dominios de las funciones trigonométricas : Campo de valores Para cada θ en el dominio
5 Las Funciones Trigonométricas Sección 5.3 Funciones Trigonométricas de números reales Dominios Se presentan los dominios de las funciones trigonométricas : Campo de valores Para cada θ en el dominio
1 x (rad) 0 π/2 π 3π/2 2π cos x x Para representarla, recomiendo que se haga una tabla dando al argumento
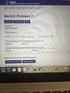 . A partir de las funciones: y = sen, y = cos, y = e, y = Ln, e y = ² representar las siguientes funciones: i. y = cos 2 y = cos Función periódica. = 2π 2π T ; ω Coeficiente de la. T = = 2π ω (rad) 0 π/2
. A partir de las funciones: y = sen, y = cos, y = e, y = Ln, e y = ² representar las siguientes funciones: i. y = cos 2 y = cos Función periódica. = 2π 2π T ; ω Coeficiente de la. T = = 2π ω (rad) 0 π/2
TEMA 1: NÚMEROS REALES
 . Numeros racionales Ejemplo: TEMA : NÚMEROS REALES 4.............................................. Entonces puedo expresar el "" de infinitas formas, siendo su fracción generatriz la que es irreducible.
. Numeros racionales Ejemplo: TEMA : NÚMEROS REALES 4.............................................. Entonces puedo expresar el "" de infinitas formas, siendo su fracción generatriz la que es irreducible.
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
Parciales Matemática CBC Parciales Resueltos - Exapuni.
 Parciales Matemática CBC 2012 Parciales Resueltos - Exapuni www.exapuni.com.ar Compilado de primeros parciales del 2012 Parcial 1 1) Sea. Hallar todos los puntos de la forma, tales que la distancia entre
Parciales Matemática CBC 2012 Parciales Resueltos - Exapuni www.exapuni.com.ar Compilado de primeros parciales del 2012 Parcial 1 1) Sea. Hallar todos los puntos de la forma, tales que la distancia entre
FUNCIÓN BÁSICA DEL SENO Y DEL COSENO, GRÁFICAS Y CARACTERÍSTICAS
 FUNCIÓN BÁSICA DEL SENO Y DEL COSENO, GRÁFICAS Y CARACTERÍSTICAS Sugerencias para quien imparte el curso: Es importante que la interacción con los alumnos dentro del salón de clases sea lo más activa posible,
FUNCIÓN BÁSICA DEL SENO Y DEL COSENO, GRÁFICAS Y CARACTERÍSTICAS Sugerencias para quien imparte el curso: Es importante que la interacción con los alumnos dentro del salón de clases sea lo más activa posible,
TEMA 5. FACTORIZACIÓN DE POLINOMIOS.
 TEMA 5. FACTORIZACIÓN DE POLINOMIOS. 1. SACAR FACTOR COMÚN Cuando todos los términos de un polinomio, P(x), son múltiplos de un mismo monomio, M(x), podemos extraer M(x) como factor común. Por ejemplo:
TEMA 5. FACTORIZACIÓN DE POLINOMIOS. 1. SACAR FACTOR COMÚN Cuando todos los términos de un polinomio, P(x), son múltiplos de un mismo monomio, M(x), podemos extraer M(x) como factor común. Por ejemplo:
Límites y continuidad. Cálculo 1
 Límites y continuidad Cálculo 1 Razones de cambio y límites La rapidez promedio de un móvil es la distancia recorrida durante un intervalo de tiempo dividida entre la longitud del intervalo. Ejemplo 1
Límites y continuidad Cálculo 1 Razones de cambio y límites La rapidez promedio de un móvil es la distancia recorrida durante un intervalo de tiempo dividida entre la longitud del intervalo. Ejemplo 1
UNIDAD 4: FUNCIONES POLINOMIALES Y RACIONALES
 UNIDAD 4: FUNCIONES POLINOMIALES Y RACIONALES En la Sección anterior se abordó contenidos relacionados con las funciones y gráficas, continuamos aprendiendo más sobre funciones; en la presente unidad abordaremos
UNIDAD 4: FUNCIONES POLINOMIALES Y RACIONALES En la Sección anterior se abordó contenidos relacionados con las funciones y gráficas, continuamos aprendiendo más sobre funciones; en la presente unidad abordaremos
Nuestro primer ejemplo nos dice: Escribe la ecuación de una línea que es perpendicular a la grafica de Y= ½x + 4 y pasa por los puntos (0,-1).
 CGT.5.G.3-Pam Beach-Write the equation of a line perpendicular to a line through a point. La lección de hoy es sobre escribir una ecuación de una línea perpendicular a una línea dado un punto. El cuál
CGT.5.G.3-Pam Beach-Write the equation of a line perpendicular to a line through a point. La lección de hoy es sobre escribir una ecuación de una línea perpendicular a una línea dado un punto. El cuál
Apuntes Matemáticas 2º de bachillerato. Tema 5. Estudio de funciones
 Apuntes Tema 5 Estudio de funciones 5.1 Dominio Hay que determinar para qué intervalos de números reales, o puntos aislados, la función existe o está definida. Para ello tenemos que prestar atención a
Apuntes Tema 5 Estudio de funciones 5.1 Dominio Hay que determinar para qué intervalos de números reales, o puntos aislados, la función existe o está definida. Para ello tenemos que prestar atención a
Capitulo VI: Funciones.
 Funciones o Aplicaciones: Capitulo VI: Funciones. Ejemplo de función: Sean: A = {, 2, 3 } B = { a, b, c, d, e } F = { (;a) (2;b) (3;e) } es una función de A en B, porque a cada elemento de A, le corresponde
Funciones o Aplicaciones: Capitulo VI: Funciones. Ejemplo de función: Sean: A = {, 2, 3 } B = { a, b, c, d, e } F = { (;a) (2;b) (3;e) } es una función de A en B, porque a cada elemento de A, le corresponde
Función cuadrática. Ecuación de segundo grado completa
 Función cuadrática Una función cuadrática es aquella que puede escribirse como una ecuación de la forma: f(x) = ax 2 + bx + c donde a, b y c (llamados términos) son números reales cualesquiera y a es distinto
Función cuadrática Una función cuadrática es aquella que puede escribirse como una ecuación de la forma: f(x) = ax 2 + bx + c donde a, b y c (llamados términos) son números reales cualesquiera y a es distinto
CLASE 2. Sergio Stive Solano Sabié. Agosto de 2011. Catálogo de funciones básicas Transformaciones de funciones Combinaciones de funciones
 CLASE 2 Sergio Stive Solano Sabié Agosto de 2011 CLASE 2 Sergio Stive Solano Sabié Agosto de 2011 Función lineal Definición 1.1 Decimos que y es una función lineal de x, si la gráfica de y es una recta.
CLASE 2 Sergio Stive Solano Sabié Agosto de 2011 CLASE 2 Sergio Stive Solano Sabié Agosto de 2011 Función lineal Definición 1.1 Decimos que y es una función lineal de x, si la gráfica de y es una recta.
GIMNASIO VIRTUAL SAN FRANCISCO JAVIER Valores y Tecnología para la Formación Integral del Ser Humano UNIDAD I FUNCIONES
 UNIDAD I FUNCIONES Una función es una correspondencia entre dos conjuntos, que asocia a cada elemento del primer conjunto exactamente un elemento del otro conjunto. Una función f definida entre dos conjuntos
UNIDAD I FUNCIONES Una función es una correspondencia entre dos conjuntos, que asocia a cada elemento del primer conjunto exactamente un elemento del otro conjunto. Una función f definida entre dos conjuntos
Límite de una función
 Límite de una función El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x 0. Es decir el valor al que tienden
Límite de una función El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x 0. Es decir el valor al que tienden
Funciones Parte 1. Prof. Derwis Rivas Olivo
 Universidad de Los ndes Facultad de Ingeniería Escuela ásica de Ingeniería Departamento de Cálculo Funciones Parte 1 Prof. Derwis Rivas Olivo 1.- Dadas las funciones f : R R / f(x) = x 3 + x 3 y g : R
Universidad de Los ndes Facultad de Ingeniería Escuela ásica de Ingeniería Departamento de Cálculo Funciones Parte 1 Prof. Derwis Rivas Olivo 1.- Dadas las funciones f : R R / f(x) = x 3 + x 3 y g : R
CURSO CERO DE MATEMATICAS. Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García
 INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
Apuntes de dibujo de curvas
 Apuntes de dibujo de curvas El objetivo de estas notas es dar unas nociones básicas sobre dibujo de curvas definidas por medio de ecuaciones cartesianas explícitas o paramétricas y polares: 1. Curvas en
Apuntes de dibujo de curvas El objetivo de estas notas es dar unas nociones básicas sobre dibujo de curvas definidas por medio de ecuaciones cartesianas explícitas o paramétricas y polares: 1. Curvas en
Límite de una función
 Idea intuitiva de límite Límite de una función El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x 0. Es
Idea intuitiva de límite Límite de una función El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x 0. Es
Senos (truco): (Coseno truco = pero el cero ponerlo del 90 a la izquierda y /2.
 SENOS, COSENOS Y TANGENTES (REPASO): Grados Radianes Seno Coseno Tangente 0 0 0 1 0 30 pi / 6 un medio Raíz de 3 / 2 raíz de 3 / 3 45 pi / 4 raíz de 2 / 2 Raíz de 2 / 2 1 60 pi /3 raíz de 3 / 2 Un medio
SENOS, COSENOS Y TANGENTES (REPASO): Grados Radianes Seno Coseno Tangente 0 0 0 1 0 30 pi / 6 un medio Raíz de 3 / 2 raíz de 3 / 3 45 pi / 4 raíz de 2 / 2 Raíz de 2 / 2 1 60 pi /3 raíz de 3 / 2 Un medio
ESTUDIO COMPLETO Y REPRESENTACIÓN DE UNA FUNCIÓN
 ESTUDIO COMPLETO Y REPRESENTACIÓN DE UNA FUNCIÓN Teoría Práctica Los pasos a seguir para el estudio completo y representación de una Función son los siguientes: ) Hallar el Dominio de la función. En dicho
ESTUDIO COMPLETO Y REPRESENTACIÓN DE UNA FUNCIÓN Teoría Práctica Los pasos a seguir para el estudio completo y representación de una Función son los siguientes: ) Hallar el Dominio de la función. En dicho
TEMA 8: FUNCIONES. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
 2009 TEMA 8: FUNCIONES. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 1º E.S.O. TEMA 08: Funciones. TEMA 08: FUNCIONES. 1. Correspondencia.
2009 TEMA 8: FUNCIONES. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 1º E.S.O. TEMA 08: Funciones. TEMA 08: FUNCIONES. 1. Correspondencia.
FUNCIONES y = f(x) ESO3
 Las correspondencias entre conjunto de valores o magnitudes se pueden expresar de varias formas: con un enunciado, con una tabla, con una gráfica, o con una fórmula o expresión algebraica o analítica.
Las correspondencias entre conjunto de valores o magnitudes se pueden expresar de varias formas: con un enunciado, con una tabla, con una gráfica, o con una fórmula o expresión algebraica o analítica.
Si se pueden obtener las imágenes de x por simple sustitución.
 TEMA 0: REPASO DE FUNCIONES FUNCIONES: TIPOS DE FUNCIONES Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción,
TEMA 0: REPASO DE FUNCIONES FUNCIONES: TIPOS DE FUNCIONES Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción,
CONTINUIDAD DE FUNCIONES. SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos.
 CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
Expliquemos con exactitud qué queremos decir con valores máximos y mínimos.
 Introducción: Ahora que conocemos las reglas de derivación nos encontramos en mejor posición para continuar con las aplicaciones de la derivada. Veremos cómo afectan las derivadas la forma de la gráfica
Introducción: Ahora que conocemos las reglas de derivación nos encontramos en mejor posición para continuar con las aplicaciones de la derivada. Veremos cómo afectan las derivadas la forma de la gráfica
REPRESENTACIÓN DE FUNCIONES
 8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
II. TRIGONOMETRÍA. A. ÁNGULOS Y SUS MEDIDAS Un ángulo es la abertura que existe ebtre dos líneas que se cortan.
 II. TRIGONOMETRÍA La trigonometría se encarga del estudio de la medida de los triángulos, es decir de la medida de sus ángulos y sus lados. A. ÁNGULOS Y SUS MEDIDAS Un ángulo es la abertura que eiste ebtre
II. TRIGONOMETRÍA La trigonometría se encarga del estudio de la medida de los triángulos, es decir de la medida de sus ángulos y sus lados. A. ÁNGULOS Y SUS MEDIDAS Un ángulo es la abertura que eiste ebtre
Problemas Tema 1 Solución a problemas de Repaso de 1ºBachillerato - Hoja 02 - Todos resueltos
 página /9 Problemas Tema Solución a problemas de Repaso de ºBachillerato - Hoja 02 - Todos resueltos Hoja 2. Problema. Sea f x )=a x 3 +b x 2 +c x+d un polinomio que cumple f )=0, f ' 0)=2, y tiene dos
página /9 Problemas Tema Solución a problemas de Repaso de ºBachillerato - Hoja 02 - Todos resueltos Hoja 2. Problema. Sea f x )=a x 3 +b x 2 +c x+d un polinomio que cumple f )=0, f ' 0)=2, y tiene dos
1 Método de la bisección. 1.1 Teorema de Bolzano Teorema 1.1 (Bolzano) Contenido
 E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
El subconjunto en el que se define la función se llama dominio o campo existencia de la función. Se designa por D.
 Concepto de función Función real de variable real es toda correspondencia f que asocia a cada elemento de un determinado subconjunto de números reales, llamado dominio, otro número real (uno y sólo uno).
Concepto de función Función real de variable real es toda correspondencia f que asocia a cada elemento de un determinado subconjunto de números reales, llamado dominio, otro número real (uno y sólo uno).
Apellidos: Nombre: para x 1, determina sus asíntotas. 4. Halla el valor de los parámetros m y n para que la función f sea continua en todo.
 EXAMEN DE MATEMÁTICAS CONTINUIDAD Y DERIVABILIDAD Apellidos: Nombre: Curso: º Grupo: C Día: 3- II- 6 CURSO 05-6. Halla el dominio de definición y recorrido de las funciones a) f(x)= 9 b) g(x)= 4. Calcula
EXAMEN DE MATEMÁTICAS CONTINUIDAD Y DERIVABILIDAD Apellidos: Nombre: Curso: º Grupo: C Día: 3- II- 6 CURSO 05-6. Halla el dominio de definición y recorrido de las funciones a) f(x)= 9 b) g(x)= 4. Calcula
Fundamentos matemáticos. Tema 8 Ecuaciones diferenciales
 Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
FUNCIONES POLINÓMICAS
 PRÁCTICAS CON DERIVE 28 NUM.de MATRÍCULA FECHA... APELLIDOS /Nombre...PC PRÁCTICA CUATRO. FUNCIONES ELEMENTALES FUNCIONES POLINÓMICAS Dado un entero n 0, la función f(x) =a 0 x n + a 1 x n 1 + a 2 x n
PRÁCTICAS CON DERIVE 28 NUM.de MATRÍCULA FECHA... APELLIDOS /Nombre...PC PRÁCTICA CUATRO. FUNCIONES ELEMENTALES FUNCIONES POLINÓMICAS Dado un entero n 0, la función f(x) =a 0 x n + a 1 x n 1 + a 2 x n
CONCEPTOS QUE DEBES DOMINAR
 INTERVALOS CONCEPTOS QUE DEBES DOMINAR Un intervalo es un conjunto infinito de números reales comprendidos entre dos extremos, que pueden estar incluidos en él o no. 1. Intervalo abierto (a, b): Comprende
INTERVALOS CONCEPTOS QUE DEBES DOMINAR Un intervalo es un conjunto infinito de números reales comprendidos entre dos extremos, que pueden estar incluidos en él o no. 1. Intervalo abierto (a, b): Comprende
27/01/2011 TRIGONOMETRÍA Página 1 de 7
 β 27/01/2011 TRIGONOMETRÍA Página 1 de 7 Notación en un triángulo: En un triángulo cualquiera llamaremos a, b y c a sus lados y A, B y C a sus vértices de forma que A sea el vértice formado por los lados
β 27/01/2011 TRIGONOMETRÍA Página 1 de 7 Notación en un triángulo: En un triángulo cualquiera llamaremos a, b y c a sus lados y A, B y C a sus vértices de forma que A sea el vértice formado por los lados
Destreza Encontrar intervalo entre -2 π y 2 π en que una función dada es creciente o decreciente. Actividad de aprendizaje Juego del seno coseno
 Semana 1 Actividades para el logro de las tareas de desempeño Día:1 Día: Día:3 Día:4 Día:5 ES.F.4.4 Cómo evaluar funciones trigonométricas para un número real dado. Cómo representar las funciones trigonométricas
Semana 1 Actividades para el logro de las tareas de desempeño Día:1 Día: Día:3 Día:4 Día:5 ES.F.4.4 Cómo evaluar funciones trigonométricas para un número real dado. Cómo representar las funciones trigonométricas
FUNCIONES TRIGONOMÉTRICAS
 UNIDAD 3 FUNCIONES TRIGONOMÉTRICAS Concepto clave: 1. Razones trigonométricas Si A es un ángulo interior agudo de un triángulo rectángulo y su medida es, entonces: sen longitud del cateto opuesto al A
UNIDAD 3 FUNCIONES TRIGONOMÉTRICAS Concepto clave: 1. Razones trigonométricas Si A es un ángulo interior agudo de un triángulo rectángulo y su medida es, entonces: sen longitud del cateto opuesto al A
el blog de mate de aida CS II: Representación de funciones y optimización.
 Pág.1 CRECIMIENTO Y DECRECIMIENTO. En la figura se observa la recta tangente a una función creciente. La recta tangente es siempre creciente también para cualquier punto, por lo que su pendiente será positiva
Pág.1 CRECIMIENTO Y DECRECIMIENTO. En la figura se observa la recta tangente a una función creciente. La recta tangente es siempre creciente también para cualquier punto, por lo que su pendiente será positiva
Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 7: Lunes 22 - Viernes 27 de Abril. Contenidos
 Coordinación de Matemática I (MAT01) 1 er Semestre de 013 Semana 7: Lunes - Viernes 7 de Abril Cálculo Contenidos Clase 1: Álgebra de límites. Teorema del Sandwich. Cálculo de límites. Límites trigonométricos.
Coordinación de Matemática I (MAT01) 1 er Semestre de 013 Semana 7: Lunes - Viernes 7 de Abril Cálculo Contenidos Clase 1: Álgebra de límites. Teorema del Sandwich. Cálculo de límites. Límites trigonométricos.
RECONOCER EL GRADO, EL TÉRMINO Y LOS COEFICIENTES DE UN POLINOMIO
 OBJETIVO RECONOCER EL GRADO, EL TÉRMINO Y LOS COEICIENTES DE UN POLINOMIO NOMBRE: CURSO: ECHA: Un polinomio es una expresión algebraica formada por la suma de monomios, que son los términos del polinomio.
OBJETIVO RECONOCER EL GRADO, EL TÉRMINO Y LOS COEICIENTES DE UN POLINOMIO NOMBRE: CURSO: ECHA: Un polinomio es una expresión algebraica formada por la suma de monomios, que son los términos del polinomio.
(A) Primer parcial. si 1 x 1; x 3 si x>1. (B) Segundo parcial
 CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E700 1) x 5 > 1. A) Primer parcial ) Sean las funciones ft) t +,gy) y 4&hw) w. Encontrar f/h, g f, f g y sus dominios. ) Graficar la función x + six
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E700 1) x 5 > 1. A) Primer parcial ) Sean las funciones ft) t +,gy) y 4&hw) w. Encontrar f/h, g f, f g y sus dominios. ) Graficar la función x + six
TEMA 0: REPASO DE FUNCIONES
 TEMA 0: REPASO DE FUNCIONES Recordamos que una función real de variable real es una aplicación de un subconjunto de los números reales A en el conjunto de los números reales de forma que a cada elemento
TEMA 0: REPASO DE FUNCIONES Recordamos que una función real de variable real es una aplicación de un subconjunto de los números reales A en el conjunto de los números reales de forma que a cada elemento
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS
 FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS PARA EMPEZAR, REFLEXIONA Y RESUELVE 1. Aunque el método para resolver las siguientes preguntas se sistematiza en la página siguiente, puedes resolverlas ahora: a) Cuántos
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS PARA EMPEZAR, REFLEXIONA Y RESUELVE 1. Aunque el método para resolver las siguientes preguntas se sistematiza en la página siguiente, puedes resolverlas ahora: a) Cuántos
INSTRUCTIVO PARA TUTORÍAS
 INSTRUCTIVO PARA TUTORÍAS Las tutorías corresponden a los espacios académicos en los que el estudiante del Politécnico Los Alpes puede profundizar y reforzar sus conocimientos en diferentes temas de cara
INSTRUCTIVO PARA TUTORÍAS Las tutorías corresponden a los espacios académicos en los que el estudiante del Politécnico Los Alpes puede profundizar y reforzar sus conocimientos en diferentes temas de cara
ECUACIÓN GENERAL DE LA RECTA
 ECUACIÓN GENERAL DE LA RECTA Sugerencias para quien imparte el curso En los ejemplos que se proponen, se debe tratar en la medida de lo posible que el propio alumno encuentre las respuestas y llegue a
ECUACIÓN GENERAL DE LA RECTA Sugerencias para quien imparte el curso En los ejemplos que se proponen, se debe tratar en la medida de lo posible que el propio alumno encuentre las respuestas y llegue a
Funciones Racionales y Asíntotas
 y Asíntotas Carlos A. Rivera-Morales Precálculo 2 y Asíntotas Tabla de Contenido 1 Asíntotas de :Asíntotas Asíntotas Verticales y Asíntotas Horizontales y Asíntotas Asíntotas de :Asíntotas Definición:
y Asíntotas Carlos A. Rivera-Morales Precálculo 2 y Asíntotas Tabla de Contenido 1 Asíntotas de :Asíntotas Asíntotas Verticales y Asíntotas Horizontales y Asíntotas Asíntotas de :Asíntotas Definición:
INTERVALOS Y SEMIRRECTAS.
 el blog de mate de aida CSI: Inecuaciones pág 1 INTERVALOS Y SEMIRRECTAS La ordenación de números permite definir algunos conjuntos de números que tienen una representación geométrica en la recta real
el blog de mate de aida CSI: Inecuaciones pág 1 INTERVALOS Y SEMIRRECTAS La ordenación de números permite definir algunos conjuntos de números que tienen una representación geométrica en la recta real
Trigonometría. 1. Ángulos:
 Trigonometría. Ángulos: - Ángulos en posición estándar: se ubican en un sistema de coordenadas XY. El vértice será el origen (0,0) y el lado inicial coincide con el eje X positivo. - Ángulos positivos:
Trigonometría. Ángulos: - Ángulos en posición estándar: se ubican en un sistema de coordenadas XY. El vértice será el origen (0,0) y el lado inicial coincide con el eje X positivo. - Ángulos positivos:
TRIGONOMETRÍA. π radianes. 1.- ÁNGULOS Y SUS MEDIDAS. 1.1 Los ángulos orientados
 TRIGONOMETRÍA.- ÁNGULOS Y SUS MEDIDAS. Los ángulos orientados Son aquellos que además de tener una cierta su amplitud ésta viene acompañada de un signo que nos indica un orden de recorrido (desde la semirrecta
TRIGONOMETRÍA.- ÁNGULOS Y SUS MEDIDAS. Los ángulos orientados Son aquellos que además de tener una cierta su amplitud ésta viene acompañada de un signo que nos indica un orden de recorrido (desde la semirrecta
Desigualdades con Valor absoluto
 Resolver una desigualdad significa encontrar los valores para los cuales la incógnita cumple la condición. Para ver ejemplos de las diferentes desigualdades que hay, haga Click sobre el nombre: Desigualdades
Resolver una desigualdad significa encontrar los valores para los cuales la incógnita cumple la condición. Para ver ejemplos de las diferentes desigualdades que hay, haga Click sobre el nombre: Desigualdades
Funciones Racionales y Asíntotas
 Funciones Racionales y Carlos A. Rivera-Morales Precálculo II Funciones Racionales y Tabla de Contenido 1 2 3 Verticales y Horizontales Funciones Racionales y : Contenido Discutiremos: qué es una función
Funciones Racionales y Carlos A. Rivera-Morales Precálculo II Funciones Racionales y Tabla de Contenido 1 2 3 Verticales y Horizontales Funciones Racionales y : Contenido Discutiremos: qué es una función
Tema 4 Funciones elementales Matemáticas CCSSI 1º Bachillerato 1
 Tema 4 Funciones elementales Matemáticas CCSSI 1º Bachillerato 1 TEMA 4 - FUNCIONES ELEMENTALES 4.1 CONCEPTO DE FUNCIÓN DEFINICIÓN : Una función real de variable real es una aplicación de un subconjunto
Tema 4 Funciones elementales Matemáticas CCSSI 1º Bachillerato 1 TEMA 4 - FUNCIONES ELEMENTALES 4.1 CONCEPTO DE FUNCIÓN DEFINICIÓN : Una función real de variable real es una aplicación de un subconjunto
Lo rojo sería la diagonal principal.
 MATRICES. Son listas o tablas de elementos y que tienen m filas y n columnas. La dimensión de la matriz es el número se filas y de columnas y se escribe así: mxn (siendo m el nº de filas y n el de columnas).
MATRICES. Son listas o tablas de elementos y que tienen m filas y n columnas. La dimensión de la matriz es el número se filas y de columnas y se escribe así: mxn (siendo m el nº de filas y n el de columnas).
RESUMEN PARA EL ESTUDIO
 RESUMEN PARA EL ESTUDIO 1. Números de siete cifras U. millón CM DM UM C D U Cómo se lee 2 8 9 6 7 8 2 Cómo se descompone: 2.896.782 = 2 U. millón + 8 CM + 9 DM + 6 UM + 7 C + 8 D + 2 U Cómo se compone:
RESUMEN PARA EL ESTUDIO 1. Números de siete cifras U. millón CM DM UM C D U Cómo se lee 2 8 9 6 7 8 2 Cómo se descompone: 2.896.782 = 2 U. millón + 8 CM + 9 DM + 6 UM + 7 C + 8 D + 2 U Cómo se compone:
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO. Análisis Matemático
 Análisis Matemático Unidad 4 - Límite de una función en un punto Límite de una función en un punto El límite de una función para un valor de x es el valor al que la función tiende en los alrededores de
Análisis Matemático Unidad 4 - Límite de una función en un punto Límite de una función en un punto El límite de una función para un valor de x es el valor al que la función tiende en los alrededores de
Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o
![Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o](/thumbs/49/25449703.jpg) DERIVADAS Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o El teorema de Lagrange dice que: f(3) - f(-1) =
DERIVADAS Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o El teorema de Lagrange dice que: f(3) - f(-1) =
1.- Ángulo de inclinación
 Unidad II.- La línea recta. Todos tenemos la idea intuitiva de lo que es una recta. Las propiedades fundamentales de la recta, de acuerdo a los Axiomas de Euclides, son: Por dos puntos distintos pasa una
Unidad II.- La línea recta. Todos tenemos la idea intuitiva de lo que es una recta. Las propiedades fundamentales de la recta, de acuerdo a los Axiomas de Euclides, son: Por dos puntos distintos pasa una
FUNCIONES. Anexo. halla, de ser posible: a) El dominio de h b) los ceros c) los polos d) intervalos de crecimiento y de decrecimiento.
 FUNCIONES Anexo ) Se quiere alquilar un automóvil y para eso se visitan dos empresas. En una de ellas el costo es de $65 por día. La otra en cambio no cobra por día, sino $3,5 por kilómetro recorrido.
FUNCIONES Anexo ) Se quiere alquilar un automóvil y para eso se visitan dos empresas. En una de ellas el costo es de $65 por día. La otra en cambio no cobra por día, sino $3,5 por kilómetro recorrido.
Polinomios. 1.- Funciones cuadráticas
 Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
Clase 4 Funciones polinomiales y racionales
 Clase 4 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo de 2014 Polinomios Definición Se llama polinomio en x a toda expresión de la forma p(x) = a 0 + a 1x+ +a n
Clase 4 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo de 2014 Polinomios Definición Se llama polinomio en x a toda expresión de la forma p(x) = a 0 + a 1x+ +a n
Funciones Cuadráticas en una Variable Real
 en una Variable Real Carlos A. Rivera-Morales Precálculo I Tabla de Contenido Contenido adrática : Contenido Discutiremos: qué es una función cuadrática : Contenido Discutiremos: qué es una función cuadrática
en una Variable Real Carlos A. Rivera-Morales Precálculo I Tabla de Contenido Contenido adrática : Contenido Discutiremos: qué es una función cuadrática : Contenido Discutiremos: qué es una función cuadrática
1º BACHILLERATO MATEMÁTICAS CIENCIAS SOCIALES TEMA 4.- LÍMITES, CONTINUIDAD Y DERIVADAS
 1º BACHILLERATO MATEMÁTICAS CIENCIAS SOCIALES TEMA 4.- LÍMITES, CONTINUIDAD Y DERIVADAS 1 1.- LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite de una función f por la izquierda de un punto x = a. Es el valor al
1º BACHILLERATO MATEMÁTICAS CIENCIAS SOCIALES TEMA 4.- LÍMITES, CONTINUIDAD Y DERIVADAS 1 1.- LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite de una función f por la izquierda de un punto x = a. Es el valor al
Cálculo Diferencial en una variable
 Tema 2 Cálculo Diferencial en una variable 2.1. Derivadas La derivada nos proporciona una manera de calcular la tasa de cambio de una función Calculamos la velocidad media como la razón entre la distancia
Tema 2 Cálculo Diferencial en una variable 2.1. Derivadas La derivada nos proporciona una manera de calcular la tasa de cambio de una función Calculamos la velocidad media como la razón entre la distancia
Factorización de polinomios FACTORIZACIÓN DE POLINOMIOS
 FACTORIZACIÓN DE POLINOMIOS 1. Polinomios Un monomio es el producto de un número real por una o más letras que pueden estar elevadas a exponentes que sean números naturales. La suma de los exponentes de
FACTORIZACIÓN DE POLINOMIOS 1. Polinomios Un monomio es el producto de un número real por una o más letras que pueden estar elevadas a exponentes que sean números naturales. La suma de los exponentes de
3. Funciones reales de una variable real. Límites. Continuidad 1
 3. Funciones reales de una variable real. Límites. Continuidad 1 Una función real de variable real es una aplicación f : D R, donde D es un subconjunto de R denominado dominio de f. La función f hace corresponder
3. Funciones reales de una variable real. Límites. Continuidad 1 Una función real de variable real es una aplicación f : D R, donde D es un subconjunto de R denominado dominio de f. La función f hace corresponder
Los números enteros. Dado que los enteros contienen los enteros positivos, se considera a los números naturales son un subconjunto de los enteros.
 Los números enteros Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde
Los números enteros Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde
CURSO 2013/2014 RESUMEN LÍMITES Y CONTINUIDAD 2, ,61 2,01 4,0401 1,99 3,9601 2,001 4, ,999 3,
 RESUMEN LÍMITES Y CONTINUIDAD Límite de una función en un punto El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan
RESUMEN LÍMITES Y CONTINUIDAD Límite de una función en un punto El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan
lím lím Veamos como ejemplo el límite de la función polinómica f(x)=3x 2-8 en 1: x 1 (3x2 )-lím 8 x 1 =2 x 1 x)2 -lím x 1 8 =
 LÍMITES LECCIÓN 7 Índice: Cálculo de ites en un punto. Epresión indeterminada L/0. Epresión indeterminada 0/0. Algunos ites de funciones irracionales. Otras técnicas básicas para el cálculo de ites. Problemas..-
LÍMITES LECCIÓN 7 Índice: Cálculo de ites en un punto. Epresión indeterminada L/0. Epresión indeterminada 0/0. Algunos ites de funciones irracionales. Otras técnicas básicas para el cálculo de ites. Problemas..-
1. Dominio, simetría, puntos de corte y periodicidad
 Estudio y representación de funciones 1. Dominio, simetría, puntos de corte y periodicidad 1.1. Dominio Al conjunto de valores de x para los cuales está definida la función se le denomina dominio. Se suele
Estudio y representación de funciones 1. Dominio, simetría, puntos de corte y periodicidad 1.1. Dominio Al conjunto de valores de x para los cuales está definida la función se le denomina dominio. Se suele
FUNCIONES. Función. π k π +, k } (los puntos que quitamos anulan el coseno). 2. tg x: {x / x =
 Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
TEMA 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS
 TEMA 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS 1.- POLINOMIOS Recordemos que un monomio es una expresión algebraica (combinación de letras y números) en la que las únicas operaciones que aparecen entre las
TEMA 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS 1.- POLINOMIOS Recordemos que un monomio es una expresión algebraica (combinación de letras y números) en la que las únicas operaciones que aparecen entre las
Primera parte: Funciones trigonome tricas (cont). Tiempo estimado: 1.3 h
 1. DATOS DE IDENTIFICACIÓN Asignatura: Cálculo Diferencial Docente: Alirio Gómez Programa : INGENIERÍA Semestre: 4 Fecha de elaboración: 21-07-2013 Guía Nº: 2 Título: Funciones. Alumno: Grupo: CB-N-2 Primera
1. DATOS DE IDENTIFICACIÓN Asignatura: Cálculo Diferencial Docente: Alirio Gómez Programa : INGENIERÍA Semestre: 4 Fecha de elaboración: 21-07-2013 Guía Nº: 2 Título: Funciones. Alumno: Grupo: CB-N-2 Primera
TEMA 3: CONTINUIDAD DE FUNCIONES
 TEMA 3: CONTINUIDAD DE FUNCIONES. Valor Absoluto Trabajaremos en el campo de los números reales, R. Para el estudio de las propiedades de las funciones necesitamos el concepto de valor absoluto de un número
TEMA 3: CONTINUIDAD DE FUNCIONES. Valor Absoluto Trabajaremos en el campo de los números reales, R. Para el estudio de las propiedades de las funciones necesitamos el concepto de valor absoluto de un número
TRIGONOMETRÍA ANALÍTICA
 TRIGONOMETRÍA ANALÍTICA....4 Los alumnos comenzaron a estudiar funciones trigonométricas en el Capítulo 7, cuando aprendieron sobre radianes la transformación de funciones trigonométricas. Aquí aprenderán
TRIGONOMETRÍA ANALÍTICA....4 Los alumnos comenzaron a estudiar funciones trigonométricas en el Capítulo 7, cuando aprendieron sobre radianes la transformación de funciones trigonométricas. Aquí aprenderán
TEMA 7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES 7.1 CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO
 TEMA 7 DERIVADAS Y APLICACIONES MATEMÁTICAS CCSSI º Bac TEMA 7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES 7. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Definición : Se llama
TEMA 7 DERIVADAS Y APLICACIONES MATEMÁTICAS CCSSI º Bac TEMA 7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES 7. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Definición : Se llama
Una función es una relación o correspondencia entre dos magnitudes o variables x e y, de manera que a cada valor
 RESUMEN TEORÍA FUNCIONES: 4º ESO Op. B DEFINICIONES: Una función es una relación o correspondencia entre dos magnitudes o variables x e y, de manera que a cada valor de x le corresponde un único valor
RESUMEN TEORÍA FUNCIONES: 4º ESO Op. B DEFINICIONES: Una función es una relación o correspondencia entre dos magnitudes o variables x e y, de manera que a cada valor de x le corresponde un único valor
Unidad II. Si una función f(x) tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en unaconstante.
 Unidad II Integral indefinida y métodos de integración. 2.1 Definición de integral indefinida. Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones
Unidad II Integral indefinida y métodos de integración. 2.1 Definición de integral indefinida. Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones
Los Conjuntos de Números
 Héctor W. Pagán Profesor de Matemática Mate 40 Debemos recordar.. Los conjuntos de números 2. Opuesto. Valor absoluto 4. Operaciones de números con signo Los Conjuntos de Números Conjuntos importantes
Héctor W. Pagán Profesor de Matemática Mate 40 Debemos recordar.. Los conjuntos de números 2. Opuesto. Valor absoluto 4. Operaciones de números con signo Los Conjuntos de Números Conjuntos importantes
1.4.6) Identificación de tipos de raíz: Enteras, racionales, reales, complejas y su multiplicidad.
 Los divisores del término independiente son fundamentales para aplicar el teorema de las raíces racionales (segundo método), el cual estudiaremos con mayor detalle en el siguiente punto. Por el momento
Los divisores del término independiente son fundamentales para aplicar el teorema de las raíces racionales (segundo método), el cual estudiaremos con mayor detalle en el siguiente punto. Por el momento
Unidad II. 2.1 Concepto de variable, función, dominio, condominio y recorrido de una función.
 Unidad II Funciones 2.1 Concepto de variable, función, dominio, condominio y recorrido de una función. Función En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio)
Unidad II Funciones 2.1 Concepto de variable, función, dominio, condominio y recorrido de una función. Función En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio)
Formulas Matemáticas
 B A C a TRIGONOMETRÍA Radian Grados sen a cos a tag a 0 2π 0 0 1 0 π/6 30º 1 / 2 3 / 2 3 / 3 π/4 45º 2 / 2 2 / 2 1 π/3 60º 3 / 2 1 / 2 3 π/2 90º 1 0 π 180º 0-1 0 3π/2 270º -1 0 sen a = B / C cos a = A
B A C a TRIGONOMETRÍA Radian Grados sen a cos a tag a 0 2π 0 0 1 0 π/6 30º 1 / 2 3 / 2 3 / 3 π/4 45º 2 / 2 2 / 2 1 π/3 60º 3 / 2 1 / 2 3 π/2 90º 1 0 π 180º 0-1 0 3π/2 270º -1 0 sen a = B / C cos a = A
UNIDAD IV DISTANCIA ENTRE DOS PUNTOS
 UNIDAD IV DISTANCIA ENTRE DOS PUNTOS Dados los puntos: P(x1, y1) y Q(x2, y2), del plano, hallemos la distancia entre P y Q. Sin pérdida de generalidad, tomemos los puntos P y Q, en el primer cuadrante
UNIDAD IV DISTANCIA ENTRE DOS PUNTOS Dados los puntos: P(x1, y1) y Q(x2, y2), del plano, hallemos la distancia entre P y Q. Sin pérdida de generalidad, tomemos los puntos P y Q, en el primer cuadrante
DIVISION: Veamos una división: Tomamos las dos primeras cifra de la izquierda del dividendo (57).
 DIVISION: Dividir es repartir un número en grupos iguales (del tamaño que indique el divisor). Por ejemplo: 45/ 5 es repartir 45 en grupos de 5. Los términos de la división son: Dividendo: es el número
DIVISION: Dividir es repartir un número en grupos iguales (del tamaño que indique el divisor). Por ejemplo: 45/ 5 es repartir 45 en grupos de 5. Los términos de la división son: Dividendo: es el número
FUNCIONES 1. DEFINICION DOMINIO Y RANGO
 1. DEFINICION DOMINIO Y RANGO FUNCIONES Antes de definir función, uno de los conceptos fundamentales y de mayor importancia de todas las matemáticas, plantearemos algunos ejercicios que nos eran de utilidad
1. DEFINICION DOMINIO Y RANGO FUNCIONES Antes de definir función, uno de los conceptos fundamentales y de mayor importancia de todas las matemáticas, plantearemos algunos ejercicios que nos eran de utilidad
Integral indefinida. Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.
 Integral indefinida 1. Integración Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x). Se dice, entonces,
Integral indefinida 1. Integración Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x). Se dice, entonces,
Límites y Continuidad de funciones
 CAPITULO Límites y Continuidad de funciones Licda. Elsie Hernández Saborío Instituto Tecnológico de Costa Rica Escuela de Matemática Revista digital Matemática, educación e internet (www.cidse.itcr.ac.cr)
CAPITULO Límites y Continuidad de funciones Licda. Elsie Hernández Saborío Instituto Tecnológico de Costa Rica Escuela de Matemática Revista digital Matemática, educación e internet (www.cidse.itcr.ac.cr)
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS
 FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Página 8. Aunque el método para resolver las siguientes preguntas se sistematiza en la página siguiente, puedes resolverlas ahora: a) Cuántos radianes corresponden
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Página 8. Aunque el método para resolver las siguientes preguntas se sistematiza en la página siguiente, puedes resolverlas ahora: a) Cuántos radianes corresponden
