UNITATS 4 i 5: VECTORS I GEOMETRIA ANALÍTICA
|
|
|
- Laura Alcaraz Villalobos
- hace 5 años
- Vistas:
Transcripción
1 UNITATS 4 i 5: VECTORS I GEOMETRIA ANALÍTICA Nom i Llinatges: Curs r de Batxillerat Matemàtiques I IES M. Àngels Cardona
2 Índex 4.1 Definició i elements d un vector 4.2 Operacions amb vectors 4.3 Combinació lineal de vectors i bases 4.4 Producte escalar de dos vectors i les seves aplicacions 5.1 Punts i vectors en el pla 5.2 Equacions d una recta 5.3 Paral lelisme i perpendicularitat de rectes 5.4 Posició relativa de dues rectes i intersecció de rectes 5.5 Angle entre dues rectes 5.6 Distància entre dos punts 5.7 Distància d un punt a una recta 5.8 Equacions de la circumferència i l el lipse 5.9 Autoavaluació 5.10 Aplicacions informàtiques i positius 5.11 Solucions a les activitats del llibre Nota: Els següents apunts han estat elaborats (durant els caps de setmana d Octubre i Novembre de 2013) en base al llibre de text emprat a classe: Matemàtiques I de l editorial Anaya. En cap cas pretenen substituir el llibre, només volen ser un complement que faciliti el treball de l alumne. És evident que per completar coneixements es recomana fer una lectura atenta, seriosa i completa del llibre.
3 4.1 Definició i elements d un vector Definició: En general en matemàtiques un vector és qualsevol element d un espai vectorial (conjunt amb operació interna i externa) però en aquest tema considerarem només un tipus molt concret de vectors, els vectors d un espai euclidià de dues dimensions que es poden representar geomètricament com a segments de recta dirigits. Així, qualsevol vector vindrà determinat per dos punts A i B. Al vector que té origen en A i final en B l escrivim AB. També podem representar un vector sense indicar-ne l origen i final: u, v, w.... El mòdul d un vector és la distància que hi ha entre A i B i s escriu AB o AB La direcció d un vector és la direcció de la recta en què es troba el vector i la de totes les seves paral leles. Cada direcció admet dos sentits. Diem que dos vectors són iguals si tenen la mateixa direcció, sentit i mòdul i per tant, al operar amb un vector és com fer-ho amb qualsevol dels vectors que són iguals a aquest. Exemple: Donats els vectors que apareixen a la figura que tens més avall: a) Troba n dos d igual direcció però sentit contrari. b) Troba n dos d igual mòdul però direcció diferent. c) Digues quin és el que té major mòdul. d) Dibuixa un vector d igual direcció que u però mòdul doble i sentit contrari. e) Dibuixa un vector d igual direcció i sentit que v però amb mòdul la meitat. 4.2 Operacions amb vectors Entre els vectors també podrem definir les operacions de suma, resta, producte per un escalar i producte escalar. Vegem com es realitzen aquestes operacions tant gràficament com analíticament. 1
4 Exemple: Donats els vectors: u = (1, 3); v = ( 2, 3); w = (0, 2) ; farem les següents operacions gràficament i analíticament: ANALÍTICAMENT GRÀFICAMENT a) 2u + v b) 1 2 u v c) u + v 2w d) 1 2u v + w 2 Sol: a) (0,9); b) (5/2, -3/2); c) (-1,10); d) (3,5/2) Deures: Pàg. 175: Ex. 1; Pàg. 182: Ex. 1, 2, 3, 4, 5, 6, 7 i 8. 2
5 4.3 Combinació lineal de vectors i bases Donat un conjunt de vectors u, v, w... qualsevol expressió de la forma au +b v +c w +... s anomena combinació lineal dels vectors u, v, w... Exemple: a) Donats els vectors u =(2,-3); v =(-4,3); w =(-2,-5) forma una combinació lineal dels tres vectors. b) Escriu el vector w com a combinació lineal dels vectors u i v. Sol: 13 8 w = u + v 3 3 c) També ho podem fer gràficament. Expressa els vectors a i b com a combinació lineal dels vectors u i v : Sol: a = 6u + 3v ; b = 4 u + 1 v Important: Donat un parell de vectors amb direccions diferents, qualsevol altre vector es pot posar de forma única com a combinació lineal d aquests dos vectors. Deures: Pàg. 183: Ex. 12, 13, 14 i 15. Pàg. 184: Ex. 34 Definició: Anomenam base del conjunt de vectors del pla a qualsevol parell de vectors x, y que no tenguin la mateixa direcció. Així, qualsevol vector del pla es podrà posar com a combinació lineal d aquest parell de forma única. 3
6 Exemple 1: Donats els vectors a =(2,3) i b =(-2,3) explica perquè formen una base del conjunt de vectors del pla. Escriu el vector (3,5) en aquesta base Sol: ( 3,5 ) =, B Exemple 2: Escriu els vectors següents en funció de la base formada pels vectors a i b : Sol: u =(1,4); t =(-1,7); z =(-1,-1); x =(2 5, -5 5); y =(0,-4) Nota: Tot i que alguns dels resultats serien igualment vàlids, a partir d ara considerarem tot vector expressat en una base ortonormal (dos vectors perpendiculars i de mòdul 1) Deures: Pàg. 182: Ex. 9; Pàg Ex Producte escalar de dos vectors i les seves aplicacions A) Donats dos vectors u i v en definim el seu producte escalar (un nombre) com: u v = u v cos ( u, v ) És a dir, a partir de dos vectors obtenim un nombre. u = Nota: Si les coordenades dels vectors són ( u, u ) ; v = ( v, v ) compleix que: u v = u v + u v Exemples: 1) Donats els vectors u =(3,-2), v =(1,2) i w =(-2,5) troba: a) u v = , llavors es 4
7 b) (2u ) (-3v )= c) 2u (v -3 w )= Sol: a) -1; b) 6; c) 94 2) Donats els vectors u i v dels que només sabem que tenen mòdul 2 i 3 respectivament i que a més formen un angle de 60 graus. Troba: a) u v = b) u (u - v )= Sol: a) 3; b) 1 Deures: Pàg. 176: Ex. 1, 2 i 3; Pàg. 183: Ex. 18, 19 i 20. B) Càlcul del mòdul d un vector donades les seves coordenades: Sigui u =(a,b), llavors tenim que: u = a + b 2 2 Exemple: Troba el mòdul del vector u =(-3,6). Sol: u = 3 5 Definició: A un vector de mòdul 1 se l anomena unitari. 2 2 Exemple 1: Comprova que el vector v =, és unitari. 2 2 Obtenció de vectors unitaris: Donat un vector qualsevol, u = ( u, u ) 1 2 és relativament fàcil trobar un vector amb la mateixa direcció i sentit que u però unitari. Bastarà multiplicar-lo per l invers del seu mòdul: 1 v = ( u1, u2 ) u Exemple: Donat el vector u =(-1,2): a) Comprova que no és unitari. b) Troba un parell de vectors unitaris amb la mateixa direcció que u Sol: a) u = 5 ; b), ;, Deures: Pàg. 183: Ex. 21, 22, 23, 24, 25 i 26. 5
8 C) Aplicacions del producte escalar de dos vectors: El producte escalar de vectors ens servirà, bàsicament, per tres coses : C.1) Comprovar si dos vectors són perpendiculars (ortogonals): u v u v = Exemple 1: Comprova si els vectors u =(3,-2) i v =(1,2) són perpendiculars. 0 Sol: No ho són. Exemple 2: Donat el vector u =(3,-2) troba n 4 que siguin paral lels a u i altres 4 que siguin perpendiculars a u. Mira, també, si (4 5, -3) és paral lel a u. Exemple 3: Troba el valor de k de forma que el vector (-3,k) sigui: - Paral lel a u =(3,-2): - Per perpendicular a u : Sol: a) k=2; b) k=-9/2 C.2) Calcular l angle que formen dos vectors: cos (, ) cos, u v + u v u v = u v + u v = u v = u v u v u v = u v ( ) Exemple 1: Troba l angle que formen els vectors u =(3,-2) i v =(1,2) Sol: 97º7 30 Exemple 2: Donat u =(4,-3) i v =(5,k), troba el valor de k de forma que els dos vectors formin un angle de 60º. Sol: k = 11 6
9 Exemple 3: Donats dos vectors u i v unitaris que formen un angle de 60º, troba a + b i a b 2. Pista: Demostra primer que u = u u. Sol: a) 3 ; b) 1 Deures: Pàg. 178: Ex. 4; Pàg. 184: Ex. 27, 28, 29, 30, 31, 32, 35 (igual que exemple 3 del punt C.2), 37, 40, 41, Punts i vectors en el pla Nota: Tot i que molts dels conceptes explicats es poden estendre a qualsevol sistema de referència, a partir d ara considerarem un sistema de referència amb una base ortonormal {O, e 1, e 2 }. D aquesta manera, cada vegada que ens referim al punt A(a,b) ens referim l element O+a e 1 +b e 2 A) Coordenades del vector que uneix dos punts: AB = B A = x x, y y Donats A(x 1,y 1 ) i B(x 2,y 2 ), tenim que: ( ) Exemple: Donats els punts A(2,-3) i B(-5,7), troba: AB = BA = Sol: a) (-7,10); b) (7,-10) B) Pendent d una recta que té la mateixa direcció que un vector donat: u = a, b, el pendent d una recta que té la mateixa direcció que el Donat un vector ( ) vector és : recta. m u b =. En aquest cas diem que aquest vector és el vector director de la a Exemple: Troba el pendent d una recta que té per vector director: u = ( 3, 5) v = ( 2, 4) w = ( 5,0) Un vector perpendicular a u : Sol: a) -5/3; b) 2; c) 0; d) No definida; e) 3/5 x = ( 0,7) Exemple 2: Troba un vector director per cadascuna de les rectes de les quals en sabem el seus pendents: m 1 =3 m 2 =-3/5 m 3 =0 Sol: a) (1,3); b) (5,-3); c) (1,0) 7
10 Nota: Si el pendent d una recta és m, el de la recta perpendicular serà: I per tant, m m = C) Punts alineats Els punts A, B i C estaran alineats sempre que els vectors AB i BC per exemple, siguin paral lels. És a dir, sempre que els pendents de les rectes de les quals en són vectors directors siguin les mateixes. Per tant, per saber si tres punts estan alineats bastarà comprovar si aquests pendents coincideixen. Vegem-ho millor amb un parell d exemples. Exemple 1: Digues si els punts A(2,3), B(-3,4) i C(7,9) estan alineats. Sol: No hi estan. Exemple 2: Troba x perquè els punts A(2,3), B(-3,4) i C(7,x) estiguin alineats. Sol: x=2 Deures: Pàg. 189: Ex. 1, 2, 3; Pàg. 206: 2 D) Punt mitjà entre altres dos punts Trobar el punt mitjà entre altres dos punts es pot fer de manera raonada però existeix una fórmula que ens ajuda a anar una mica més ràpid. És la que pots veure a la figura adjunta de la dreta. Anem a demostrar com s obté aquesta fórmula. Dem: 8
11 Exemple1: Troba, emprant la fórmula, el punt mitjà entre els punts A(2,3) i B(-7,8) Sol: (-5/2, 11/2) Exemple 2: Troba, de forma raonada, el punt mitjà entre els punts A(2,3) i B(-7,8) Exemple 3: De la mateixa manera que en el cas anterior, troba els dos punts que divideixen el segment format pels punts A(2,3) i B(10,15) en tres parts iguals. I en quatre parts iguals? Sol: En tres parts: (14/3, 7) i (22/3,11). En quatre parts (4,6); (6,9); (8,12). E) Simètric d un punt respecte a un altre. Si cercam el simètric de A respecte de B, el punt B serà el punt mitjà entre el punt A i aquest simètric A que cercam (mira la figura). Això ens dóna una pista de com trobar el simètric d un punt respecte d un altre. Exemple: Troba el simètric del punt A(2,3) respecte del punt B(5,7). Sol: A =(8,11) Deures: Pàg. 190: Ex. 4abc; Pàg. 206: Ex. 3, 4, 5 i 6; Pàg. 209: 50, 52, 9
12 5.2 Equacions d una recta Bàsicament per definir una recta necessitam dues coses: a) Un punt P pel que passa b) Un vector director, d, que, com diu el nom, ens marcarà la direcció que segueix la recta. Equacions de la recta i pas d una a una altra: Equació vectorial: ( x,y ) = ( p, p ) + t ( d, d ) Equació contínua: x p1 y p2 = d d 1 2 Equació explícita: y=mx+n (m és el pendent i n l ordenada a l origen) Equacions paramètriques: x = p1 + td1 y = p2 + td2 Equació implícita o general: Ax+By+C=0 (A,B) és un vector perpendicular a la recta. Equació punt-pendent: y=y 0 +m(x-x 0 ) (x 0,y 0 ) és un punt pel que passa m és el pendent de la recta Exemple 1: Escriu de totes les formes anteriors l equació de la recta que passa pels punts A(-2,3) i B(-6,8) Sol: (x,y)=(-2,3)+t(-4,5); 5 y = ( x ) x = 2 4t ; y = 3 + 5t x + 2 y 3 = ; 5x+4y-2=0; 4 5 5x 1 y = + ;
13 Exemple 2: Donada la recta 2x-3y=5 escriu-la de totes les formes que s han explicat. Troba n també tres punts qualssevol. Sol: (1,-1); (-2,-3); (4,1); (x,y)=(1,-1)+t(3,2); 2 y = ( x ) x = 1+ 3t ; y = 1 + 2t x 1 y + 1 = ; -2x+3y+5=0; 3 2 Deures: Pàg. 193: Ex. 1, 2 i 3; Pàg. 206: Ex. 7ab, 8ab; 9ab; 10ab; 11ab; 12 Exemple 3: Troba l equació de la mediatriu del segment A(1,5) i B(-3,7) expressant-la en forma contínua i general. Troba, a més, dos punts d aquesta mediatriu. Sol: 2x-y+8=0 Exemple 4: Donat el triangle de vèrtexs A(-3,1), B(4,0) i C(0,2) troba n el circumcentre. Nota: Recorda que el circumcentre és el punt en el que es tallen les mediatrius dels tres costats d un triangle. Sol: Mediatriu BC: 2x-y-3=0; Mediatriu AC: x+y+1=0; Circumcentre: (2/3,-5/3) 11
14 5.3 Paral lelisme i perpendicularitat de rectes Depenent de la forma en la que tinguem expressada una recta seguirem una estratègia o una altra per saber si dues rectes són paral leles o perpendiculars. Així ens podem fer les següents preguntes: - Quan són paral leles dues rectes? a) Si tenen el mateix pendent o b) Si tenen vectors directors proporcionals - Quan són perpendiculars dues rectes? a) Si m m =-1 (on m i m són els pendents de les rectes) Exemple: Si una recta té pendent 2/3, una recta perpendicular a aquesta té pendent: o b) Si els vectors directors són perpendiculars. Exemples: A) Digues si les dues rectes següents són paral leles, perpendiculars o cap de les dues coses: x = 2 3t r: 2x+3y-7=0 s: y = 5 Sol: Cap de les dues. B) Escriu una recta perpendicular i una altra paral lela a la recta r: 4x-7y+8=0 que passin pel punt (-2,3). Sol: (x,y)=(-2,3)+t(7,4); (x,y)=(-2,3)+t(4,-7) x 2 y C) Troba una recta perpendicular i una paral lela a la recta s: = que a més 3 2 passin pel punt (2,3). Escriu-les de totes les maneres que sàpigues. Paral lela: Sol. paral leles: (x,y)=(2,3)+t(3,-2); y 2x = + ; y = 3 ( x 2) x = 2 + 3t ; y = 3 2t x 2 y 3 = ; 2x+3y-13=0;
15 Perpendicular: x = 2 + 2t x 2 y 3 Sol. perpendicular: (x,y)=(2,3)+t(2,3); ; = ; 3x-2y=0; y=(3/2)x; y = 3 + 3t y = 3+ ( x 2) 2 Deures: Pàg. 197: Ex. 1, 3 i 4; Pàg. 206: 13a, 14a, 15a, 17 i Posició relativa de dues rectes i intersecció de rectes En el pla, dues rectes poden tallar-se o no. En cas que no es tallin diem que són paral leles i en cas que es tallin podem tenir dos casos, que siguin la mateixa recta però expressades de formes diferents i en diem coincidents o que només tenguin un punt en comú i en diem secants. Anem a veure com podem distingir aquests tres casos. COINCIDENTS PARAL LELES SECANTS Representació A partir del punt i del vector director Vectors directors proporcionals. Punts comuns Vectors directors proporcionals. Cap punt comú. Vectors directors no proporcionals A partir de les equacions implícites Ax+By+C=0 A x+b y+c =0 A = B = C A' B ' C ' A = B C A' B ' C ' A A' B B ' En cas que siguin secants, per obtenir-ne el punt de tall haurem de resoldre el sistema format per les dues equacions de les dues rectes. Anem a veure n millor uns quants exemples. Exemple: Troba la posició relativa de les següents rectes i, en cas que es tallin, troba n el punt de tall. A) r: 2x+3y-4=0; s: (x,y)=(2,0)+t(6,-4) Sol: Coincidents. 13
16 B) r: y=3x-2; s: x 2 1 y = 2 6 Sol: Paral leles x = 2 3t C) r: y = 5t s: x=0 Sol: Es tallen al punt (0,10/3) x = 2 3t x + 2 y 1 D) r: s: = y = 3 5t 3 2 Sol: Es tallen al punt (8/3, 37/9) E) Troba k de forma que les dues rectes següents siguin: a) Paral leles; b) Perpendiculars. r: 2x+ky+8=0 s: x+y-5=0 Sol: Per paral leles: k=2; per perpendiculars: k=-2. Deures: Pàg. 199: Ex. 1; Pàg. 207: 25c, 26, 27, 29b 14
17 5.5 Angle entre dues rectes L angle format per dues rectes serà igual a l angle que formin els seus vectors directors però considerant sempre un angle agut. Si per calcular l angle que formen els vectors directors de la recta empram la fórmula vista al punt 4.4 podem obtenir angles majors que 90º. Per evitar-ho emprarem una petita modificació d aquella amb la que sempre obtindrem l angle agut. u1 v1 + u2 v2 cos ( u, v ) = u v On u = ( u, u ) i v = ( v, v ) són els vectors directors de les rectes. En cas que tinguem les rectes expressades en forma explícita o només en coneguem els pendents, existeix una altra fórmula que ens permet trobar l angle que formen les rectes. És la següent: m1 m2 tgα = 1 + m m 1 2 On α és l angle que formen les rectes i m 1 i m 2 són els pendents de les rectes. Exemple 1: Troba l angle que formen les dues rectes següents de dues formes diferents: a) Trobant-ne els dos vectors directors; b) Trobant-ne els pendents. x 2 1 y r: y=2x-2; s: = 2 6 Sol: Formen un angle de 45º Exemple 2: Troba el valor de k de forma que l angle que formin aquestes dues rectes sigui de 45º: r: 2x+ky+8=0 s: 2x+y-5=0 Sol: k=6 i k=-2/3 Deures: Pàg. 200: Ex. 1; Pàg. 208: 32, 33 i 34 15
18 5.6 Distància entre dos punts Com sembla evident, la distància entre dos punts és igual al mòdul del vector que els uneix. Per tant, donats els punts P(x 1, y 1 ) i Q(x 2, y 2 ) obtenim la següent fórmula: d P Q PQ x x y y (, ) = = ( ) + ( ) Exemple 1: Troba la distància entre els punts A(1,-3) i B(4,5) Sol: 73 u Exemple 2: Troba el valor de k de forma que els punts A(2,3) i B(4,k) sigui 7. Sol: k 1 = ; k 2 = Distància d un punt a una recta La distància del punt P(a,b) a la recta r: Ax+By+C=0 ve donada per la següent fórmula: Aa + Bb + C (, ) = 2 2 d P r A + B Exemple: Donades les rectes r: 2x+3y+5=0, s: 4x+6y-2=0 i el punt P(2,-3), troba: a) La distància del punt a la recta s. Sol: u b) Comprova si el punt pertany a cap de les dues rectes Sol: Només a r. c) Comprova que les dues rectes són paral leles 16
19 d) Troba la distància entre les rectes Sol: Exemple 2: Donat el triangle de vèrtexs A(1,2), B(7,3) i C(3,6), troba n el perímetre, els angles, l àrea i digues de quin tipus és segons (equilàter, isòsceles, escalè). Solucions: P= ; A=11u 2 ; és escalè; angles: 53º58 21 ; 46º19 56 ; 79º41 43 Deures: Pàg. 201: Ex. 1; Pàg. 208: 35a, 37, 40a, 41, 43, 44, 17
20 Súper-exemple final: Troba el circumcentre, el baricentre i l ortocentre del següent triangle. Ves comprovant, sobre el dibuix, que els resultats que obtens són correctes. Circumcentre: Baricentre: 18
21 Ortocentre: Sol: Circumcentre: (81/4, 20/7); Baricentre: (17/3, 11/3); Ortocentre: (38/7, 37/7) Deures: Pàg. 209: Ex. 64, 65, 71, 73, 74, 75, 79 (a partir del dibuix), Pàg. 211: 87; 5.8 Equacions de la circumferència i l el lipse -Circumferència: Com tots sabem, es pot definir una circumferència com el lloc geomètric format per tots els punts que estan a distància constant d un altre que s anomena centre. A la distància a la que estan se l anomena radi. Així, l equació d una circumferència de centre (A,B) i radi r ve donada per la següent equació: ( ) ( ) x A + y B = r Exemples: Troba l equació de les següents circumferències. Sol: a) x 2 +y 2 =4; b) (x-4) 2 +(y-3) 2 =1 19
22 Sol: (x-4) 2 +(y-6) 2 =13 - El lipse: Donats dos punts F 1 i F 2 anomenats focus, i una distància k, anomenada constant de l el lipse (sempre major que la distància entre els focus), s anomena el lipse al lloc geomètric dels punts P la suma de distàncies a F 1 i a F 2 dels quals és igual a k. És a dir: d(p,f 1 )+ d(p,f 2 )=k. Així, l equació reduïda d una el lipse de semieixos a i b, i centre (A,B) ve donada per: ( x A) ( y B) a = b Exemples: Troba les equacions de les següents el lipses = 1 ( ; e2: )2 2 x + 0'5 y + = 1 ( ) 2 ( ) 2 x 8 y 3 ; e3: + = '25 6' '25 4 ( x + 4 ) ( y 6 ) Sol: e1: 20
23 5.9 Autoavaluació Els exercicis del llibre que es proposen per a preparar l examen són els següents: Pàgina 185: 1, 2ab, 3, 4, 5, 6, 7 i 9. Pàgina 211: 1, 2, 3, 5, 6 i Aplicacions informàtiques i positius Amb aquests positius intentarem reproduir el que vam fer junts al punt 5.7. Dibuixarem un triangle i en trobarem els punts notables. 1) Has d'anar a la pàgina web: Veuràs que apareixen uns eixos de coordenades. 2) Ara has de dibuixar un triangle com i on vulguis. Ho podràs fer amb el botó que veus a la imatge de la dreta. Una vegada seleccionat només has d'anar amb el ratolí damunt on vulguis posar cadascun dels tres vèrtexs del triangle a la part dels eixos de coordenades. Per acabar has de tornar a clicar damunt el primer vèrtex que hagis dibuixat. Et quedarà una cosa com la següent: Circumcentre : Com saps, per trobar el circumcentre hem de trobar les tres mediatrius dels costats. Només has de seleccionar el botó Mediatriu i quan el tenguis seleccionat fer click amb el ratolí damunt del costat del que vulguis trobar-ne la mediatriu. Et quedarà una cosa com la següent: Com veus ja tenim les tres mediatrius i el circumcentre. Si t hi fixes a l esquerra hi apareixen les equacions dels punts, les mediatrius... 21
24 Ara només et queda guardar el que has fet en pdf, per exemple. Per fer-ho has de seguir la següent ruta: Fitxer->Exporta->Construcció interactiva a pàgina web->pdf Nota: També pots fer una captura de pantalla si t és més còmode. Ortocentre: Has de tornar a dibuixar el triangle (emprarem un triangle per cada punt notable). Una vegada el tenguis, farem una perpendicular a cada costat que passi pel vèrtex contrari. Seleccionarem el que pots veure a la figura de la dreta. Aquesta opció ens fa una recta perpendicular a un costat que passa pel punt que noltros vulguem. Per tant, quan haguem fet clic en aquesta opció marcarem primer el costat i després el vèrtex contrari al costat i així ja tindrem la primera altura: Fent el mateix procés pels altres dos costats obtindrem les tres altures i per tant, l'ortocentre: Baricentre: Per trobar el baricentre hauràs de trobar primer el punt mitjà de cada costat del triangle. Per trobar-lo hauràs de seleccionar el que pots veure a la següent figura, PUNTO MEDIO O CENTRO. I després marcar el costat del que en vols trobar el punt mig. Hauràs de repetir el mateix pels tres costats. Quant tenguis els tres punts mitjos dibuixats només has de fer les tres medianes. Es a dir, una recta que passi per un dels vèrtexs i pel punt mig de l altre costat i el mateix altres dues vegades pels altres dos costats: 22
25 Pàg 171: IES M.ÀNGELS CARDONA 1r Batx. Matemàtiques I CURS Incentre: El punt de tall de les tres bisectrius dels tres angles s anomena incentre. Investiga una mica com fer la bisectriu d un angle, dibuixa les tres bisectrius dels tres angles i al seu punt de tall hi trobaràs l incentre. POSITIUS: 1r positiu: Dibuixa amb geogebra un triangle amb els vèrtexs als punts A(-2,1), B(3,2) i C(0,k) on k= 4 pels nombres de llista de 1 a 5; k=5 pels nombres de llista de 6 a 10; k=6 pels nombres de llista de 11 a 15; k=-2 pels nombres de llista de 16 a 20; k=-3 pels nombres de llista de 21 a 25; k=-4 pels nombres de llista de 26 a 30 Troba el circumcentre, l incentre, el baricentre i l ortocentre amb el programa informàtic i envia una captura de pantalla per cadascun dels punts notables del triangle. 2n positiu: Troba el circumcentre i el baricentre del triangle analíticament i comprova que es troba situat on has vist amb el programa geogebra Solucions a les activitats del llibre U7: VECTORS Pàg 175: 1) a) (-3,6); b) (-3,9); c) (-17/3,41/3); d) (-1,11/2) Pàg 176: 1) a) 3 3 ; b) 3 3 c) -3 3 ; d) ; e) 16; f) -9/4 2) 97º ) 3/2; 65/2 Pàg 178: 4) a) -15, -15; b) 5; 10, 161º33 54 ; c) k=4/3; d) (4,3), (4/5,3/5), dos perpendiculars unitaris són: (4/5,3/5) i (-4/5, -3/5) 23
26 Pàg 182 : 1) Tenen mateix mòdul però diferent direcció; b) Mateixa direcció, sentit i mòdul; c) Mateixa direcció i sentit però el mòdul de BM és la meitat que el de DE; d) El mòdul de OS és menor que el de OE i són perpendiculars. 2) NC=BN=FR=RE; AS=SF=CP=PD 3) a) CD=2CP; b) MN=(1/2)AC; c) OP=-OS; d) NB=(-1/2)BC 4) a) AF+BC=AE b) AS+CC=SF; c) OP+SO=FD; d) AM+AM=AB 5) a) AC; b) AB=DC; c) BA-CD; d) AA=0; e) AC; f) 2DC 6) 7) b=x+y-z; c=x-y+z 8) 9) u=(-1/2,1/2); v=(3/4,1); w=(3/2,1) Pàgina 183: 10) a=(2,2); b=(0,-3); c=(-1,0), d=(-1,3) 11) (2,3) 12) a) (-7,21/2); b) (-9/5,72/5); (-17/6,2) 13) b=(-20,22) 14) m=-5/4, n=-15/4 15) a=5b-4c 16) a) Sí; b) No 17) a) 2; b) -2; c) 4; d) -4 18) a) -6; b) -13; c) 12 19) a) k=2; b) k=30; c) k=-15/2 20) a) 22; b) 29; c) (-15,-6); d) (20,30) 21) Per ordre: 13; 13;10;1; 5; 2 22) m=4/5; m=-4/5 23) 78º28 34,6 24) a) 112º22 48 ; b) 90º; c) 135º 25) a) -10; b) 3 i -3 26) a) (3/5, -4/5); (-3/5, 4/5); b) (8,6), (-8,-6); c) (4/5, 3/5); (-4/5,-3/5) Pàgina 184: 27) (-8,6) i (8,-6) 28) (-1/4,3/4) 29) Dues solucions: a=3, b=15/2 i a=-3, b=-15/2 30) k=-4/3, k=-8/3 ± 10 31) k = 73 32) Dues solucions: k=8 i b=4 o k=-8 i b=-4 33) Dues solucions: u=(0,1) i u=(4/5, -3/5) 34) a=(-1/2)x+2y; b=(1/2)x+2y; c=(1/2)x-y 35) 7 36) 20 37) 34 tots dos 38) 2 tots dos 39) 90º 40) 4/3 i -3/4 24
27 41) -2 36; ) Dues solucions: (4 46, 0 27) i (-2 46, 3 73) 43) Dues solucions: 3 3 3, 3 + o , ) ) ; 14/ ) 1 47) (3,6) i (2,-1) 48) 120º Pàgina 185: 50) Tots són nombres menys el b que és un vector 51) Sí No, Sí, No 52) 0, 90, 180 i ) a), i , ; b) (40/13, 8/13) i (-40/13, -8/13) ) a) AC=a+b; BD=-a+b; b) AC BD=0 1) AUTOAVALUACIÓ 2) a) 1/2; b) -3; c) 3/2 3) a=2u-3v 4) a) 2 3 ; b) 2, 2; c) 30º 5) a) k=-2; b) k=4, k=-4 6) Dues solucions: ( 1, 3) i ( 1, 3) 7) Dues solucions: (-3,4) i (3,-4) 8) -3 9) 1 i 3 U8: GEOMETRIA ANALÍTICA. PROBLEMES AFINS I MÈTRICS Pàg 189: 1) MN=(-9,-6); NM=(9,6) 2) Hi estan 3) k=-5/3 Pàg 190: 4) a) (11/2,4); b) (13,-11); c) (-2,19); d) (5,5); e) (4,7) Pàg 193: 1) a) x-y=0; b) -4x-6y+24=0; c) y-5=0; d) x-3=0 2) 2x-y+3=0; Paramètriques: x=t, y=3+2t; Contínua: (x-0)/1=(y-3)/2 3) a) (0,2) i (-3,0) per exemple; c) x=-3t; y=2-2t; d) y=(2/3)x+2; Pàg 194: 1) (x+3)/11=(y-5)/-1 2) (x-4)/-10=(y-0)/4 3) 32x-8y+7=0 Pàg 197: 1) Paral lela: x=4-5t; y=-3+2t; Perpendicular: x=4+2t, y=-3+5t 2) a) (5,3); b) -5/3; c) (-3,5) 3) a) (x-5)/3=(y+3)/1; b) 3x+y-4=0; c) y=(1/3)x+1 4) 5x-2y+23=0; 2x+5y-14=0 Pàg 199: 1) Paral leles, secants, secants i paral leles 25
28 Pàg 200: 1) a) 10º18 17,45 ; b) 57º31 43,71 ; c) 2º43 34,72 Pàg 201: 1) d(p,q)=17; d(p,r)=3/5; d(p,s)=3; d(q,r)=16/5; d(q,s)=12 2) 24 u 2 Pàg 206: 1) Sí, No, Sí 2) k=-11/5 3) B=(8,-7) 4) (5,2) 5) (2,2) 6) (2,6) 7) a) (x,y)=(-3,7)+k(4,-1); x=-3+4t, y=7-t; Punts: (1,6); (5,5); (9,4), (13,3); (17,2) b) (x,y)=(-1,0)+k(0,2); x=-1, y=2k; Punts: (-1,2), (-1,4), (-1,6), (-1,8), (-1,10) 8) a) 7x+6y-30=0; b) x-3=0; c) y=0 9) a) x=t, y=2t; b) x=7, y=t; c) x=t, y=2; d) x=-3t, y=t; e) x=1+3t, y=-1+2t ; f) x=-1+2t, y=1-t 10) a) (x+1)/2=y/-3; b) (x-2)/0=y/3; c) x/1=(y+1)/-3; d) (x-2)/2=(y+1)/1 11) a) x+2y-1=0; b) 5x+y-3=0; c) y-2=0; d) 15x+10y-4=0 12) a) x=t, y=0; b) x=0, y=t 13) Per ordre, vector director, vector normal i pendent: a) (2,5); (-5,2); 5/2; b) (2,4); (-4,2); 2; c) (0,1), (1,0), No en té. d) (3,1), (-1,3), 1/3 14) Pertany a la tercera i la quarta 15) a) -1; b) 0; c) 5/2 Pàgina 207: 16) a) y=(-1/5)x-16/5; b) y=5x+15 17) a) x=3+t; y=2-3t; b) x-1=y+3; c) y=-3; d) y=-3 18) 2x-3y-6=0 19) 3x-4y+8=0 20) a) x=-3+2t, y=1; b) x=5-t; y=-2+2t; c) x=1+2t, y=3-3t; d) x=-3+4t; y=2-6t 21) a) y=(2/3)x; b) y=(-3/2)x+7/2 22) a) y=-2+m(x-3); b) 7x+4y-13=0; c) 2x+y-4=0; d) 5x-12y-39=0 23) (1,-2) 24) y=-2x+7 25) a) (-3,-1); b) (2,-1); c) (2,-1/2) 26) k=2; t=-1 27) k=4 28) k=-11/2 Pàgina 208: 29) a) Paral leles; b) Secants; c) Secants; 30) a) 45; b) 90; c) 45; d) 63º26 5,82 31) 56º18 35,8 32) 26º33 54,2 33) n= 3 34) m=3; i dues solucions per n: n=30 i n=-6/5 35) a) 4 2 ; b) 5 2 ; c) ) k=-2 37) a=-5 o a=-1 38) ) a) 4 5 ; b) 21/4; c) 9/2 40) a) 12/5; b) 9/2; c) 3; d) ) c=10 o c=-10 42) ) a) 2 10 ; b) ; c) 10u2 44) 12 5u 2 45) 25u 2 26
29 Pàgina 209: IES M.ÀNGELS CARDONA 1r Batx. Matemàtiques I CURS ) p:7x-4y+9=0; s: x=2; r:y=-3/2; t: x+2y-1=0 47) -3 48) a) 5x-7y-18=0; b) 6x-18y-12=0; c) 5x-7y-6=0 49) 6x-4y-5=0 50) (1/3,2) i (8/3,3) 51) (17/3, 0) 53) (-4/5,8/5) 54) 71/2 55) 46/5 56) Mediana: ) Dos punts: ( , ) ; Altura: ) (8,8) i ( , ) 59) (1/8, 15/8); (5/4,3/4) 60) Dos valors: 9 i ) (-5/3, 3); A= ) Dues rectes: y=(-3/2)x+9/2 i y=(2/3)x-6/3 63) Dos valors: o ) Angles: 60º15 18,4 ; 34º30 30,7 ; 85º ) 29º44 41,6 ; 46º13 7,9 ; 104º2 10,5 Pàgina 210: 66) Dues solucions: y= 3 x+2; y=- 3 x+2; 67) y=3x+5/2; y=(-1/3)x+5/ ) (-6,-6); (2,-2) 69) y 2 = ( x + 2) i y 2 = ( x + 2) ) r: x-y+1=0; Dues solucions a la segona recta: x-y+7=0; x-5=0 71) (3,-3) 72) A=(0,4); C=(-6,-2); Àrea=24u 2 73) Ortocentre: (21/11, 103/11); Circumcentre: (1/22, -37/22) 74) (16/5, 8/5) 75) a) (2,-4); (-6,0); b) 108º26 5,8 ; 71º ) (0,2); (10/3, -4/3); (8/3,10/3) 77) (-15,0) i (3/7,0) 78) Dos punts: (13/2, 3) i (-11/2, -3) 79) A=9/2 u 2 80) A=21/2 u 2 81) Dues solucions: (-9/2,-9) i (-3/2, 3) 82) 3/4 83) r: 18x+y+13=0; s: 15x+11y-40=0 84) 2x+3y+5=0 Pàgina 211: 87) a) Passa per (0,0); b) És una recta horitzontal; c) És una recta vertical 89) B=(1,1); C=(-1,4); D=(-4,2); longitud del costat: 26 90) Dues solucions: C=(8,4) i D=(7,0) o C=(0,6) i D=(-1,2) 91) Perímetre=16 2 ; Vèrtexs: ( 1 2 3, 2 3 ) i ( , 2 3 ) 92) Dues solucions: y=-2x+18; y=-2x-18 93) Dues solucions: D(1,2) i C(5,6) o D=(1/2, 3/2) i C=(5/2,7/2) AUTOAVALUACIÓ 1) a) (1,3); b) k=-7; 2) a) x=3+5t, y=2+t; x-5y+7=0; b) y=-x/3, x/3=y/-1 3) a) 5x-2y-16=0; b) 2x+3y-6=0; 4) a(x-5)+b(y-1)=0; y=1 5) a) Perpendiculars; b) secants; 6) k= 3 ; 7) a) 11, -1; b) k=1, k=-3/2 27
Tema 2: GEOMETRIA ANALÍTICA AL PLA
 Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Exercicis de rectes en el pla
 Equacions de la recta 1. Escriu les diferents equacions de la recta que passa pel punt P(3, 4) i que té com a vector director el vector v = ( 5, 2). 2. Per a la recta d equació director. 6 + y = 1, escriu
Equacions de la recta 1. Escriu les diferents equacions de la recta que passa pel punt P(3, 4) i que té com a vector director el vector v = ( 5, 2). 2. Per a la recta d equació director. 6 + y = 1, escriu
TEMA 4 : Geometria analítica al pla. Vectors i la Recta. Activitats
 TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
j Unitat 6. Rectes en el pla
 MATEMÀTIQUES 9 4. Calcula a a sabent que a b, b b 4 i que l angle que formen els vectors a i b mesura 0º. b b 4 b 4 b a b a b cos a a cos 0º a cos 0º a a a 9. Els punts A(, ), B(, ) i C(, ) són tres vèrtexs
MATEMÀTIQUES 9 4. Calcula a a sabent que a b, b b 4 i que l angle que formen els vectors a i b mesura 0º. b b 4 b 4 b a b a b cos a a cos 0º a cos 0º a a a 9. Els punts A(, ), B(, ) i C(, ) són tres vèrtexs
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA
 DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
GEOMETRIA ANALÍTICA DEL PLA. MATEMÀTIQUES-1
 GEOMETRIA ANALÍTICA DEL PLA. 1. Vectors en el pla.. Equacions de la recta. 3. Posició relativa de dues rectes. 4. Paral lelisme de rectes. 5. Producte escalar de dos vectors. 6. Perpendicularitat de rectes.
GEOMETRIA ANALÍTICA DEL PLA. 1. Vectors en el pla.. Equacions de la recta. 3. Posició relativa de dues rectes. 4. Paral lelisme de rectes. 5. Producte escalar de dos vectors. 6. Perpendicularitat de rectes.
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
1.- Elements d una recta Vector director d una recta Vector normal d una recta Pendent d una recta
 .- Elements d una recta..- Vector director d una recta..- Vector normal d una recta.3.- Pendent d una recta.- Equacions d una recta..- Equació ectorial, paramètrica i contínua..- Equació explícita.3.-
.- Elements d una recta..- Vector director d una recta..- Vector normal d una recta.3.- Pendent d una recta.- Equacions d una recta..- Equació ectorial, paramètrica i contínua..- Equació explícita.3.-
Geometria / GE 2. Perpendicularitat S. Xambó
 Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
Geometria analítica del pla
 8 Geometria analítica del pla Objectius Aquesta quinzena aprendràs a: Reconèixer els elements d'un vector identificant quan dos vectors són equipol lents. Fer operacions amb vectors lliures tant analíticament
8 Geometria analítica del pla Objectius Aquesta quinzena aprendràs a: Reconèixer els elements d'un vector identificant quan dos vectors són equipol lents. Fer operacions amb vectors lliures tant analíticament
Geometria Analítica del pla
 Geometria Analítica del pla Continguts 1. Vectors Vectors fixos i vectors lliures Operacions amb vectors Combinació lineal de vectors Punt mitjà d un segment Producte escalar Aplicacions del producte escalar
Geometria Analítica del pla Continguts 1. Vectors Vectors fixos i vectors lliures Operacions amb vectors Combinació lineal de vectors Punt mitjà d un segment Producte escalar Aplicacions del producte escalar
Resolucions de l autoavaluació del llibre de text
 Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
VECTORS I RECTES AL PLA. Exercici 1 Tenint en compte quin és l'origen i quin és l'extrem, anomena els següents vectors: D
 VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
Vector unitari Els vectors unitaris tenen de mòdul la unitat. Calculem el vector unitari del vector següent manera: ( ) ( )
 GEOMETRIA EN L ESPAI VECTORS EN L ESPAI OPERACIONS AMB VECTORS Un vector és un segment orientat en l espai que té un mòdul, una direcció i un sentit coneguts: té un extrem i un origen (Exemple: vector
GEOMETRIA EN L ESPAI VECTORS EN L ESPAI OPERACIONS AMB VECTORS Un vector és un segment orientat en l espai que té un mòdul, una direcció i un sentit coneguts: té un extrem i un origen (Exemple: vector
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES UNITAT 2 TEOREMA DE TALES.
 Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
TEMA 6 : Geometria en l espai. Activitats
 TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
= 1+ β, essent α i β paràmetres reals. a la recta r 2. i el pla Π d equació
 Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
1. Què tenen en comú aquestes dues rectes? Com són entre elles? 2. En què es diferencien aquestes dues rectes?
 En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera:
 Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
GEOMETRIA ANALÍTICA PLANA
 GEOMETRIA ANALÍTICA PLANA Un vector fix és un segment orientat que va del punt A (origen) al punto B (extrem). M òdul del vector AB, es representa pe r. : É s la long itud del segment Direc ció del vector
GEOMETRIA ANALÍTICA PLANA Un vector fix és un segment orientat que va del punt A (origen) al punto B (extrem). M òdul del vector AB, es representa pe r. : É s la long itud del segment Direc ció del vector
Proves d accés a la Universitat per a més grans de 25 anys Convocatòria 2013
 Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
8 Geometria analítica
 Geometria analítica INTRODUCCIÓ Els vectors s utilitzen en diverses branques de la física que fan servir magnituds vectorials, per això és important que els alumnes en coneguin els elements i les operacions.
Geometria analítica INTRODUCCIÓ Els vectors s utilitzen en diverses branques de la física que fan servir magnituds vectorials, per això és important que els alumnes en coneguin els elements i les operacions.
SOLUCIONARI Unitat 5
 SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2012
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Deduce razonadamente en que casos los planos π 1 y π 2 son o no paralelos:
 GEOMETRÍA Junio 98 Deduce razonadamente en que casos los planos y son o no paralelos: a) : x + y + z = y : x + y z = 4 b) : x y + z = 4 y : x y + z = Obtén la distancia entre los planos y cuando sean paralelos.
GEOMETRÍA Junio 98 Deduce razonadamente en que casos los planos y son o no paralelos: a) : x + y + z = y : x + y z = 4 b) : x y + z = 4 y : x y + z = Obtén la distancia entre los planos y cuando sean paralelos.
GEOMETRIA PLANA 1. ELS ANGLES 1.1. DEFINICIÓ 1.2. CLASSIFICACIÓ
 GEOMETRIA PLANA 1. ELS ANGLES 1.1. DEFINICIÓ Representem un punt A en un pla i tracem dues semirectes amb origen en aquest punt. El punt A serà el vèrtex de l angle i cada semirecta serà el costat. 1..
GEOMETRIA PLANA 1. ELS ANGLES 1.1. DEFINICIÓ Representem un punt A en un pla i tracem dues semirectes amb origen en aquest punt. El punt A serà el vèrtex de l angle i cada semirecta serà el costat. 1..
GEOMETRÍA ANALÍTICA PLANA
 GEOMETRÍA ANALÍTICA PLANA Un vector fijo es un segmento orientado que va del punto A (origen) al punto B (extremo). Módulo del vector : Es la longitud del segmento AB, se representa por. Dirección del
GEOMETRÍA ANALÍTICA PLANA Un vector fijo es un segmento orientado que va del punto A (origen) al punto B (extremo). Módulo del vector : Es la longitud del segmento AB, se representa por. Dirección del
Sèrie 5. Resolució: 1. Siguin i les rectes de d equacions. a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i.
 Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
10 Àlgebra vectorial. on 3, -2 i 4 són les projeccions en els eixos x, y, y z respectivament.
 10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
ACTIVITATS. a) b) c) d) INS JÚLIA MINGUELL 2n Batxillerat. dv, 18 de març Alumne:
 INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
UNITAT 3: SISTEMES D EQUACIONS
 UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
TRIANGLES. TEOREMA DE PITÀGORES.
 TRIANGLES. TEOREMA DE PITÀGORES. Un triangle ABC és la figura geomètrica del plànol formada per 3 segments anomenats costats els extrems dels quals es tallen a en 3 punts anomenats vèrtexs. Els vèrtexs
TRIANGLES. TEOREMA DE PITÀGORES. Un triangle ABC és la figura geomètrica del plànol formada per 3 segments anomenats costats els extrems dels quals es tallen a en 3 punts anomenats vèrtexs. Els vèrtexs
Sector circular i Segment circular.
 Tema: poligons, circumferència i cercle Activitats de consolidació Pàgina 1 de 8 1. Explica quines són les semblances i diferències entre: Línia poligonal i polígon. Circumferència i cercle. Sector circular
Tema: poligons, circumferència i cercle Activitats de consolidació Pàgina 1 de 8 1. Explica quines són les semblances i diferències entre: Línia poligonal i polígon. Circumferència i cercle. Sector circular
1.- Sabem que el vector (2, 1, 1) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c. . cx by +2z = b
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
j Introducció al càlcul vectorial
 FÍSICA 00 9 j Introducció al càlcul vectorial j Activitats finals h Qüestions 1. La suma dels vectors unitaris i, j és un altre vector unitari? Justifiqueu la resposta fent un gràfic. Els vectors unitaris
FÍSICA 00 9 j Introducció al càlcul vectorial j Activitats finals h Qüestions 1. La suma dels vectors unitaris i, j és un altre vector unitari? Justifiqueu la resposta fent un gràfic. Els vectors unitaris
UN POLÍGON és una superficie plana
 UNITAT 10 - FIGURES PLANES RECORDA 4t. Primària UN POLÍGON és una superficie plana limitada per segments rectes. Cadascún d aquests segments és un COSTAT i cada punt on s uneixen dos costats forman un
UNITAT 10 - FIGURES PLANES RECORDA 4t. Primària UN POLÍGON és una superficie plana limitada per segments rectes. Cadascún d aquests segments és un COSTAT i cada punt on s uneixen dos costats forman un
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES B =,
 RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES PAU LOGSE 999 Sèrie Problema : (Incomplet Donats els punts de l'espai A (,,0, B ( 0,,0, C (,0,0 i D ( 0,,0 a Són coplanaris? Formen
RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES PAU LOGSE 999 Sèrie Problema : (Incomplet Donats els punts de l'espai A (,,0, B ( 0,,0, C (,0,0 i D ( 0,,0 a Són coplanaris? Formen
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
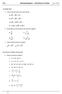 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
Prova d accés a la Universitat (2013) Matemàtiques II Model 1. (b) Suposant que a = 1, trobau totes les matrius X que satisfan AX + Id = A, on Id
 UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
LA RECTA. Exercicis d autoaprenentatge 1. Siga la gràfica següent:
 LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS
 Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
FITXA 1: Polígons. Conceptes
 FITXA 1: Polígons. Conceptes A.1. REPASSA ELS TEUS CONEIXEMENTS. 1. Escriu la lletra de les figures equilàteres. A, D 2. Escriu el nom de les figures equiangulars. A, D 3. Anomena les figures que tenen
FITXA 1: Polígons. Conceptes A.1. REPASSA ELS TEUS CONEIXEMENTS. 1. Escriu la lletra de les figures equilàteres. A, D 2. Escriu el nom de les figures equiangulars. A, D 3. Anomena les figures que tenen
c) C = (c ij ) de tres files i tres columnes per a) u r = (1, 2, 3, 4), c) u r = (1, 1, 1), v r = (2, 4, 8) i w r = (3, 9, 27)
 SOLUCONAR Unitat 8 Comencem Cada 100 g de producte d un determinat aliment conté 0,06 g de vitamina A, 0,3 g de vitamina B i 0, g de calci. Anàlogament, un altre aliment conté 0,1 g de vitamina A, 0, g
SOLUCONAR Unitat 8 Comencem Cada 100 g de producte d un determinat aliment conté 0,06 g de vitamina A, 0,3 g de vitamina B i 0, g de calci. Anàlogament, un altre aliment conté 0,1 g de vitamina A, 0, g
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
I. SISTEMA DIÈDRIC 3. DISTÀNCIES I ANGLES DIBUIX TÈCNIC
 DIBUIX TÈCNIC I. SISTEMA DIÈDRIC 3. DISTÀNCIES I ANGLES 1. Dist. d un punt a una recta - Abatiment del pla format per la recta i el punt 2. Dist. d un punt a un pla - Canvi de pla posant el pla de perfil
DIBUIX TÈCNIC I. SISTEMA DIÈDRIC 3. DISTÀNCIES I ANGLES 1. Dist. d un punt a una recta - Abatiment del pla format per la recta i el punt 2. Dist. d un punt a un pla - Canvi de pla posant el pla de perfil
Polinomis i fraccions algèbriques
 Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
Gràficament: una funció és contínua en un punt si en aquest punt el seu gràfica no es trenca
 Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
FITXA 1: Angles consecutius i adjacents
 FITXA 1: Angles consecutius i adjacents A.1. OBSERVA AQUESTES FIGURES I FES EL QUE S INDICA: Consecutius Adjacents Oposats 1. Col loca aquests noms en la figura corresponent: angles adjacents, angles oposats
FITXA 1: Angles consecutius i adjacents A.1. OBSERVA AQUESTES FIGURES I FES EL QUE S INDICA: Consecutius Adjacents Oposats 1. Col loca aquests noms en la figura corresponent: angles adjacents, angles oposats
La recta. La paràbola
 LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
EXERCICIS MATEMÀTIQUES 1r BATXILLERAT
 Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
TEMA 1: Trigonometria
 TEMA 1: Trigonometria La trigonometria, és la part de la geometria dedicada a la resolució de triangles, es a dir, a determinar els valors dels angles i dels costats d un triangle. 1.1 MESURA D ANGLES
TEMA 1: Trigonometria La trigonometria, és la part de la geometria dedicada a la resolució de triangles, es a dir, a determinar els valors dels angles i dels costats d un triangle. 1.1 MESURA D ANGLES
DOSSIER DE RECUPERACIÓ 3r ESO
 DOSSIER DE RECUPERACIÓ 3r ESO INS MARIANAO. Departament de matemàtiques La correcta realització d aquest dossier, i la posterior entrega el dia de l examen puntuarà un 20% de la nota total. Les activitats
DOSSIER DE RECUPERACIÓ 3r ESO INS MARIANAO. Departament de matemàtiques La correcta realització d aquest dossier, i la posterior entrega el dia de l examen puntuarà un 20% de la nota total. Les activitats
Districte Universitari de Catalunya
 Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
TEMA 4: Equacions exponencials i logarítmiques
 TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
TEMA 4 : Programació lineal
 TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
Foto: El teorema de Tales a la ciutat de París, Autora: Tamara Victoria Fernández
 Foto: El teorema de Tales a la ciutat de París, Autora: Tamara Victoria Fernández Matemàtiques 1r ESO T. tales 1 Matemàtiques 1r ESO T. tales 2 Teorema de Tales A.1 Utilitzant tota la plana apaïsada d
Foto: El teorema de Tales a la ciutat de París, Autora: Tamara Victoria Fernández Matemàtiques 1r ESO T. tales 1 Matemàtiques 1r ESO T. tales 2 Teorema de Tales A.1 Utilitzant tota la plana apaïsada d
Equacions i sistemes de segon grau
 Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
QUADERN d ESTUDI de RECTES TANGENTS
 QUADERN d ESTUDI de RECTES TANGENTS per a les PAU i 2n de Batxillerat Autor: Pepe Ródenas Borja pepe.rodenas.borja@gmail.com http://manifoldo.weebly.com Descripció del material: Aquest quadern consisteix
QUADERN d ESTUDI de RECTES TANGENTS per a les PAU i 2n de Batxillerat Autor: Pepe Ródenas Borja pepe.rodenas.borja@gmail.com http://manifoldo.weebly.com Descripció del material: Aquest quadern consisteix
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2008 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
QUADERN D ESTIU 4t ESO MATEMÀTIQUES
 QUADERN D ESTIU t ESO MATEMÀTIQUES Alumne:... Curs/Grup:... Data:... Professor/a:... INS Antoni de Martí i Franquès Departament de Matemàtiques Curs 0-0 Valoració del/de la professor/a: TREBALL D ESTIU
QUADERN D ESTIU t ESO MATEMÀTIQUES Alumne:... Curs/Grup:... Data:... Professor/a:... INS Antoni de Martí i Franquès Departament de Matemàtiques Curs 0-0 Valoració del/de la professor/a: TREBALL D ESTIU
UNITAT 3: TRIGONOMETRIA
 UNITAT 3: TRIGONOMETRIA 1. Angles Anomenem angle a l'espai del pla tancat per dues semirectes que tenen un mateix origen. Podem classificar els angles segons la seva obertura en tres tipus: agut, recte
UNITAT 3: TRIGONOMETRIA 1. Angles Anomenem angle a l'espai del pla tancat per dues semirectes que tenen un mateix origen. Podem classificar els angles segons la seva obertura en tres tipus: agut, recte
Proporcionalitat geomètrica
 Proporcionalitat geomètrica Guió de treball de l alumne/a...del grup... Raó entre dos segments 1. Amb el GeoGebra obriu l arxiu MArao.html, us trobareu dos segments a i b, els quals podeu seleccionar les
Proporcionalitat geomètrica Guió de treball de l alumne/a...del grup... Raó entre dos segments 1. Amb el GeoGebra obriu l arxiu MArao.html, us trobareu dos segments a i b, els quals podeu seleccionar les
Problemes de Geometria per a l ESO 178
 Problemes de Geometria per a l EO 17 1771- alculeu el perímetre de la figura KöMaL, K04 01 19 19 olució: onsiderem el pentàgon DE Les rectes i DE s intersecten en el punt P PD = 90º PD = DE = 01 19 = 0
Problemes de Geometria per a l EO 17 1771- alculeu el perímetre de la figura KöMaL, K04 01 19 19 olució: onsiderem el pentàgon DE Les rectes i DE s intersecten en el punt P PD = 90º PD = DE = 01 19 = 0
La porció limitada per una línia poligonal tancada és un
 PLA Si n és el nombre de costats del polígon: El nombre de diagonals és La suma dels seus angles és 180º ( n 2 ). La porció limitada per una línia poligonal tancada és un Entre les seves propietats destaquem
PLA Si n és el nombre de costats del polígon: El nombre de diagonals és La suma dels seus angles és 180º ( n 2 ). La porció limitada per una línia poligonal tancada és un Entre les seves propietats destaquem
Àmbit de les matemàtiques, de la ciència i de la tecnologia M14 Operacions numèriques UNITAT 2 LES FRACCIONS
 M1 Operacions numèriques Unitat Les fraccions UNITAT LES FRACCIONS 1 M1 Operacions numèriques Unitat Les fraccions 1. Concepte de fracció La fracció es representa per dos nombres enters que s anomenen
M1 Operacions numèriques Unitat Les fraccions UNITAT LES FRACCIONS 1 M1 Operacions numèriques Unitat Les fraccions 1. Concepte de fracció La fracció es representa per dos nombres enters que s anomenen
Tema 1: TRIGONOMETRIA
 Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
PROVES D ACCÉS A CICLES FORMATIUS DE GRAU SUPERIOR Convocatòria maig de 2005 DIBUIX TÈCNIC
 PROVES D ACCÉS A CICLES FORMATIUS DE GRAU SUPERIOR Convocatòria maig de 2005 DIBUIX TÈCNIC 1º A Donada la perspectiva de la figura dibuixa, a mà alçada, les tres vistes de la mateixa Dada la perspectiva
PROVES D ACCÉS A CICLES FORMATIUS DE GRAU SUPERIOR Convocatòria maig de 2005 DIBUIX TÈCNIC 1º A Donada la perspectiva de la figura dibuixa, a mà alçada, les tres vistes de la mateixa Dada la perspectiva
EXERCICIS - SOLUCIONS
 materials del curs de: MATEMÀTIQUES SISTEMES D EQUACIONS EXERCICIS - SOLUCIONS AUTOR: Xavier Vilardell Bascompte xevi.vb@gmail.com ÚLTIMA REVISIÓ: 21 d abril de 2009 Aquests materials han estat realitzats
materials del curs de: MATEMÀTIQUES SISTEMES D EQUACIONS EXERCICIS - SOLUCIONS AUTOR: Xavier Vilardell Bascompte xevi.vb@gmail.com ÚLTIMA REVISIÓ: 21 d abril de 2009 Aquests materials han estat realitzats
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 9 PAU 2006 Pautes de correcció
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 9 PAU 006 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 9 PAU 006 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
XXXV OLIMPÍADA MATEMÀTICA
 XXXV OLIMPÍADA MATEMÀTICA Primera fase (Catalunya) 10 de desembre de 1999, de 16 a 0h. 1. Amb quadrats i triangles equilàters de costat unitat es poden construir polígons convexos. Per exemple, es poden
XXXV OLIMPÍADA MATEMÀTICA Primera fase (Catalunya) 10 de desembre de 1999, de 16 a 0h. 1. Amb quadrats i triangles equilàters de costat unitat es poden construir polígons convexos. Per exemple, es poden
TEMA 3: Polinomis 3.1 DEFINICIONS:
 TEMA 3: Polinomis 3.1 DEFINICIONS: Anomenarem monomi qualsevol expressió algèbrica formada per la multiplicació d un nombre real i d una variable elevada a un exponent natural. El nombre es diu coeficient
TEMA 3: Polinomis 3.1 DEFINICIONS: Anomenarem monomi qualsevol expressió algèbrica formada per la multiplicació d un nombre real i d una variable elevada a un exponent natural. El nombre es diu coeficient
Semblança. Teorema de Tales
 Semblança. Teorema de Tales Dos polígons són semblants si el angles corresponents són iguals i els costats corresponents són proporcionals. ABCDE A'B'C'D'E' si: Â = Â',Bˆ = Bˆ', Ĉ = Ĉ', Dˆ = Dˆ', Ê = Ê'
Semblança. Teorema de Tales Dos polígons són semblants si el angles corresponents són iguals i els costats corresponents són proporcionals. ABCDE A'B'C'D'E' si: Â = Â',Bˆ = Bˆ', Ĉ = Ĉ', Dˆ = Dˆ', Ê = Ê'
DERIVADES. TÈCNIQUES DE DERIVACIÓ
 UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 2007
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 007 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 007 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
VECTORS EN EL PLA. EQUACIÓ VECTORIAL DE LA RECTA ESQUEMA 1. VECTORS EN EL PLA 2. OPERACIONS AMB VECTORS 3. EQUACIONS PARAMÈTRIQUES DE LA RECTA
 VECTORS EN EL PL. EQUCIÓ VECTORIL DE L RECT ESQUEM 1. VECTORS EN EL PL 2. OPERCIONS M VECTORS 3. EQUCIONS PRMÈTRIQUES DE L RECT 1. VECTORS EN EL PL En un sistema d eixos cartesians, cada punt es descriu
VECTORS EN EL PL. EQUCIÓ VECTORIL DE L RECT ESQUEM 1. VECTORS EN EL PL 2. OPERCIONS M VECTORS 3. EQUCIONS PRMÈTRIQUES DE L RECT 1. VECTORS EN EL PL En un sistema d eixos cartesians, cada punt es descriu
DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES 2n d ESO
 Institut Galileo Galilei Departament de Matemàtiques Curs 015-16 DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES n d ESO A continuació tens una sèrie d'exercicis i activitats relacionats amb els continguts treballats
Institut Galileo Galilei Departament de Matemàtiques Curs 015-16 DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES n d ESO A continuació tens una sèrie d'exercicis i activitats relacionats amb els continguts treballats
QUINZENA 6 (VECTORS AL PLA): OBSERVACIONS
 QUINZENA 6 (VECTORS AL PLA): OBSERVACIONS 1. Sobre el significat dels vectors, de les operacions amb vectors, i sobre el concepte de combinació lineal. Aquests temes s entenen prou bé al llibre. Però,
QUINZENA 6 (VECTORS AL PLA): OBSERVACIONS 1. Sobre el significat dels vectors, de les operacions amb vectors, i sobre el concepte de combinació lineal. Aquests temes s entenen prou bé al llibre. Però,
Els fulls de càlcul. Tabla 1 : Calculadora
 Els fulls de càlcul Els Fulls de càlcul tenen etiquetes de columna (A, B, C,...) i etiquetes de files (1, 2, 3,...). Aquestes etiquetes constitueixen les coordenades per les quals s identifica una cel
Els fulls de càlcul Els Fulls de càlcul tenen etiquetes de columna (A, B, C,...) i etiquetes de files (1, 2, 3,...). Aquestes etiquetes constitueixen les coordenades per les quals s identifica una cel
Definir els límits d integració en dominis 3D (R 3 ) Càlcul 2 - Aula Lliure
 Definir els límits d integració en dominis 3D (R 3 ) Càlcul 2 - Aula Lliure Quim Primavera 2017 Introducció Estem a l espai (R 3 ) i els punts del domini tenen tres components: (x, y, z). El nostre domini
Definir els límits d integració en dominis 3D (R 3 ) Càlcul 2 - Aula Lliure Quim Primavera 2017 Introducció Estem a l espai (R 3 ) i els punts del domini tenen tres components: (x, y, z). El nostre domini
REPRESENTACIÓ DE FUNCIONS
 1. FUNCIONS PRINCIPALS REPRESENTACIÓ DE FUNCIONS 1.1 Rectes Forma: 4 5 1.2 Paràboles Forma: 1.3 Funcions amb radicals Forma: 1.4 Funcions de proporcionalitat inversa Forma: 1.5 Exponencials Forma: 2 1.6
1. FUNCIONS PRINCIPALS REPRESENTACIÓ DE FUNCIONS 1.1 Rectes Forma: 4 5 1.2 Paràboles Forma: 1.3 Funcions amb radicals Forma: 1.4 Funcions de proporcionalitat inversa Forma: 1.5 Exponencials Forma: 2 1.6
VECTORS EN L ESPAI. Pàgina 130. Pàgina 131. Problema 1. Troba l àrea d aquest paral lelogram en funció de l angle α: Área = 8 5 sen α = 40 sen α cm 2
 VECTORS EN L ESPAI Pàgina 130 Problema 1 Troba l àrea d aquest paral lelogram en funció de l angle α: Área = 8 sen α = 40 sen α cm cm α 8 cm Troba l àrea d aquest triangle en funció de l angle β: β a b
VECTORS EN L ESPAI Pàgina 130 Problema 1 Troba l àrea d aquest paral lelogram en funció de l angle α: Área = 8 sen α = 40 sen α cm cm α 8 cm Troba l àrea d aquest triangle en funció de l angle β: β a b
Manual per a consultar la nova aplicació del rendiment acadèmic dels Graus a l ETSAV
 Manual per a consultar la nova aplicació del rendiment acadèmic dels Graus a l ETSAV Versió: 1.0 Data: 19/01/2017 Elaborat: LlA-CC Gabinet Tècnic ETSAV INDEX Objectiu... 3 1. Rendiment global dels graus...
Manual per a consultar la nova aplicació del rendiment acadèmic dels Graus a l ETSAV Versió: 1.0 Data: 19/01/2017 Elaborat: LlA-CC Gabinet Tècnic ETSAV INDEX Objectiu... 3 1. Rendiment global dels graus...
2.Igualtat. 3.Gir. 4.Simetria. 6.Semblança. 7.Escales
 DIBUIX TÈCNIC 3. TRANSFORMACIONS GEOMÈTRIQUES. ESCALES 1.Transformacions isomètriques 2.Igualtat 3.Gir 4.Simetria 5.Transformacions isomòrfiques 6.Semblança 7.Escales COL LEGI ST. JOSEP SANT SADURNÍ D
DIBUIX TÈCNIC 3. TRANSFORMACIONS GEOMÈTRIQUES. ESCALES 1.Transformacions isomètriques 2.Igualtat 3.Gir 4.Simetria 5.Transformacions isomòrfiques 6.Semblança 7.Escales COL LEGI ST. JOSEP SANT SADURNÍ D
Geogebra és un programa de llicència lliure i multiplataforma per l aprenentatge i ensenyament de les matemàtiques a tots els nivells.
 Espiral de Fibonacci Geogebra 1. Introducció al programa Geogebra és un programa de llicència lliure i multiplataforma per l aprenentatge i ensenyament de les matemàtiques a tots els nivells. Teniu una
Espiral de Fibonacci Geogebra 1. Introducció al programa Geogebra és un programa de llicència lliure i multiplataforma per l aprenentatge i ensenyament de les matemàtiques a tots els nivells. Teniu una
Ordinador 3... un cop d ull per dins!
 Ordinador 3... un cop d ull per dins! FES UN TASTET, SENSE POR! Ara que el ratolí, el teclat, etc. no tenen cap secret per tu, descobrirem l ordinador per dins i com funciona. 1. Ja tens l ordinador obert,
Ordinador 3... un cop d ull per dins! FES UN TASTET, SENSE POR! Ara que el ratolí, el teclat, etc. no tenen cap secret per tu, descobrirem l ordinador per dins i com funciona. 1. Ja tens l ordinador obert,
Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 8 PAU SÈRIE 3 Pautes de correcció (PAU 2002) MATEMÀTIQUES
 Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 8 SÈRIE 3 () MATEMÀTIQUES Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta
Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 8 SÈRIE 3 () MATEMÀTIQUES Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta
DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO
 Generalitat de Catalunya Departament d Ensenyament Institut Pompeu Fabra DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO Nom i Cognoms:... INSTRUCCIONS: - Aquest dossier serveix per a preparar
Generalitat de Catalunya Departament d Ensenyament Institut Pompeu Fabra DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO Nom i Cognoms:... INSTRUCCIONS: - Aquest dossier serveix per a preparar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2010
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 SÈRIE 1 Pregunta 1 3 1 lim = 3. Per tant, y = 3 és asímptota horitzontal de f. + 3 1 lim =. Per tant, = - és asímptota horitzontal
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 SÈRIE 1 Pregunta 1 3 1 lim = 3. Per tant, y = 3 és asímptota horitzontal de f. + 3 1 lim =. Per tant, = - és asímptota horitzontal
LLOCS GEOMÈTRICS. CÒNIQUES
 LLOCS GEOMÈTRICS. CÒNIQUES Pàgina REFLEXIONA I RESOL Còniques obertes: paràboles i hipèrboles Completa la taula següent, en què a és l angle que formen les generatrius amb l eix, e, de la cònica i b l
LLOCS GEOMÈTRICS. CÒNIQUES Pàgina REFLEXIONA I RESOL Còniques obertes: paràboles i hipèrboles Completa la taula següent, en què a és l angle que formen les generatrius amb l eix, e, de la cònica i b l
Càlcul d'àrees i volums.
 Càlcul d'àrees i volums. Exemple 1. Donada la figura següent: Calcula'n: superfície volum Resolució: Fixem-nos que la superfície està formada per tres objectes.: 1. la base del cilindre 2. la paret del
Càlcul d'àrees i volums. Exemple 1. Donada la figura següent: Calcula'n: superfície volum Resolució: Fixem-nos que la superfície està formada per tres objectes.: 1. la base del cilindre 2. la paret del
1. RECTA TANGENT I NORMAL 2. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS
 APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
Resultat final, sense desenvolupar, dels exercicis i problemes proposats de cada unitat i de l apartat Resolució de problemes. En queden exclosos
 DE S L U S RE S I V I C LES Resultat final, sense desenvolupar, dels exercicis i problemes proposats de cada unitat i de l apartat Resolució de problemes. En queden exclosos aquells exercicis que requereixen
DE S L U S RE S I V I C LES Resultat final, sense desenvolupar, dels exercicis i problemes proposats de cada unitat i de l apartat Resolució de problemes. En queden exclosos aquells exercicis que requereixen
TEMA 1: EXPRESSIONS ALGEBRAIQUES. Activitats
 TEMA 1: EXPRESSIONS ALGEBRAIQUES Activitats 1.- Expressa en llenguatge algebraic: a) El doble d un nombre. b) El doble d un nombre menys tres unitats. c) El doble d un nombre menys tres unitats, més un
TEMA 1: EXPRESSIONS ALGEBRAIQUES Activitats 1.- Expressa en llenguatge algebraic: a) El doble d un nombre. b) El doble d un nombre menys tres unitats. c) El doble d un nombre menys tres unitats, més un
Generalitat de Catalunya Departament d Educació Institut El Palau. Nivell: 1r ESO. Matèria: Matemàtiques. Nom:
 Nivell: 1r ESO Matèria: Matemàtiques Nom: Unitat 1: Divisibilitat Múltiples i divisors 1. Digues si són certes o falses les frases següents i el perquè: a) 4 és divisor de 32 b) 12 és un divisor de 4.
Nivell: 1r ESO Matèria: Matemàtiques Nom: Unitat 1: Divisibilitat Múltiples i divisors 1. Digues si són certes o falses les frases següents i el perquè: a) 4 és divisor de 32 b) 12 és un divisor de 4.
DOSSIER DE RECUPERACIÓ CURS VISUAL I PLÀSTICA 3ESO PROF: CATERINA PUPPO
 INSTITUT ELS TRES TURONS ÀMBIT ARTÍSTIC DOSSIER DE RECUPERACIÓ CURS 2017-2018 VISUAL I PLÀSTICA 3ESO PROF: CATERINA PUPPO Per superar l assignatura s ha de presentar a l exàmen de setembre junt amb el
INSTITUT ELS TRES TURONS ÀMBIT ARTÍSTIC DOSSIER DE RECUPERACIÓ CURS 2017-2018 VISUAL I PLÀSTICA 3ESO PROF: CATERINA PUPPO Per superar l assignatura s ha de presentar a l exàmen de setembre junt amb el
GEOMETRIA Optativa 1r d ESO
 GEOMETRIA Optativa 1r d ESO Dossier d estiu per a recuperar la matèria al setembre. S haurà d entregar el dia de l examen. L examen valdrà un 50% i aquest dossier l altre 50%. S han d escriure tots els
GEOMETRIA Optativa 1r d ESO Dossier d estiu per a recuperar la matèria al setembre. S haurà d entregar el dia de l examen. L examen valdrà un 50% i aquest dossier l altre 50%. S han d escriure tots els
Proporcionalitat i percentatges
 Proporcionalitat i percentatges Proporcions... 2 Propietats de les proporcions... 2 Càlul del quart proporcional... 3 Proporcionalitat directa... 3 Proporcionalitat inversa... 5 El tant per cent... 6 Coneixement
Proporcionalitat i percentatges Proporcions... 2 Propietats de les proporcions... 2 Càlul del quart proporcional... 3 Proporcionalitat directa... 3 Proporcionalitat inversa... 5 El tant per cent... 6 Coneixement
