0 si dos índices coinciden 1 si jkl es permutación impar de 123. = εjkl i X l (2) = εjkl i P l (3) = εjkl i L l (4)
|
|
|
- José Francisco Ferreyra Muñoz
- hace 5 años
- Vistas:
Transcripción
1 Momento angular
2 Operador momento angular L = R P, L j = ε jkl X k P l (1) Tensor antisimétrico ε jkl = 0 si dos índices coinciden 1 si jkl es permutación par de si jkl es permutación impar de 123 Relaciones de conmutación [ Lj, X k ] = εjkl i X l (2) [ Lj, P k ] = εjkl i P l (3) [ Lj, L k ] = εjkl i L l (4) Módulo al cuadrado L 2 = L 2 x + L 2 y + L 2 z, [ L 2, L j ] = 0 1
3 En general, un momento angular es un operador J = J x u x + J y u y + J z u z cuyas componentes verifican [ Jj, J k ] = εjkl i J l. En consecuencia, J 2 = J 2 x + J 2 y + J 2 z verifica [ J 2, J ] = 0. Por tanto, podemos buscar autovectores comunes a J 2 y J z (elegimos el eje z como eje polar) 2
4 DEFINICIONES Y NOTACIÓN Operadores escalera J + = J x + ij y J = J x ij y Conmutadores [ Jz, J + ] = J+ [J z, J ] = J [ J+, J ] = 2 Jz [ J 2, J ± ] = [ J 2, J z ] = 0 Relación con J 2 J + J = J 2 x + J 2 y i [J x, J y ] = J 2 J 2 z + J z J J + = J 2 x + J 2 y + i [J x, J y ] = J 2 J 2 z J z J 2 = 1 2 ( J+ J + J J + ) + J 2 z 3
5 AUTOVECTORES Y AUTOVALORES Es claro que, para cualquier estado ψ se tiene que J 2 0 ya que J 2 i = ψ J2 i ψ = J i ψ 2 0. Autovalores de J 2 además serán λ 2, con λ 0, y λ = 0 si y sólo si J i ψ = 0, i. Autovalores de J z serán m y los autovectores comunes a J 2 y J z los denotaremos kλm (J 2 y J z no forman en general un CCOC) J 2 kλm = λ 2 kλm (5) J z kλm = m kλm (6) 4
6 Se verifica la desigualdad entre autovalores λ m 2. (λ m 2 ) 2 = kλm (J 2 J 2 z ) kλm = kλm (J 2 x + J 2 y ) kλm 0. Utilizando que J z J ± = [J z, J ± ]+J ± J z = ± J ± +J ± J z = J ± (J z ± ) y que [ J 2 ], J ± = 0 se tiene que J z J + kλm = (m + 1) J + kλm (7) J 2 J + kλm = λ 2 J + kλm (8) J z J kλm = (m 1) J kλm (9) J 2 J kλm = λ 2 J kλm (10) 5
7 La condición λ m 2 limita la magnitud de m. Por tanto, ha de existir un valor máximo de m, llamémosle j tal que Multiplicando por J, J + kλj = 0 J J + kλj = (J 2 J 2 z J z ) kλj En consecuencia, = 2 (λ j 2 j) kλj = 0.(11) λ = j 2 + j = j(j + 1) También ha de existir un valor mínimo de m, sea j, tal que J kλj = 0. Aplicando J + se obtiene que λ = j (j 1), de lo que se deduce j = j. 6
8 Como los valores de m varían en una unidad, deber ser j j entero, esto es, j ha de ser entero o semientero, j = 0, 1 2, 1, 3 2, 2, 5 2,... y para un valor dado de j, los posibles valores de m son m = j, j + 1,..., j 1, j. CAMBIO DE NOTACIÓN: Indexamos los autovectores con j en lugar de λ = j(j + 1), escribiremos kjm. J 2 kjm = j(j + 1) 2 kjm (12) J z kjm = m kjm (13) Es sencillo demostrar que J ± kjm = = (j m)(j ± m + 1) kjm ± 1 j(j + 1) m(m ± 1) kjm ± 1. 7 (14)
9 Como consecuencia de las relaciones de conmutación, en cualquier estado ψ, J x J y 2 J z. Para poder dar con toda precisión las tres componentes del momento angular debemos tener que J = 0, pero además necesitaremos, dado que J x = J y = J z = 0, J 2 x = J 2 y = J 2 z = 0, esto es, ha de verificarse J ψ = 0, J 2 ψ = 0. El único estado en que se pueden medir con toda precisión las tres componentes del momento angular es el vector k00. Para todos los demás estados, las fluctuaciones cuánticas hacen imposible medir las tres componentes simultáneamente. 8
10 MOMENTO ANGULAR ORBITAL Coordenadas esféricas x = r sin θ cos φ y = r sin θ sin φ z = r cos φ, (15) donde r 0, 0 θ π, 0 φ < 2π. El elemento de volumen es d r = r 2 drdω dω = sin θdθdφ. (16) Expresiones de las componentes de L ( L x = i sin φ θ + cos φ tan θ φ, (17) ( L y = i cos φ θ + sin φ ) tan θ φ, (18) L z = i φ. (19) A partir de ellas, ( L 2 = 2 θ tan θ θ + 1 ) sin 2 θ φ 2 (20), L ± = e ±iφ ( ) ± θ + i cot θ φ. (21) ) 9
11 Representación de posiciones: ecuación de autovalores y autofunciones, teniendo en cuenta que L sólo actúa sobre las variables angulares L 2 Yl m (θ, φ) = l(l + 1) 2 Yl m (θ, φ), (22) L z Yl m (θ, φ) = m Yl m (θ, φ). (23) Estas ecuaciones sólo tienen una única solución linealmente independiente para cada pareja de autovalores l(l + 1) y m. Incluyendo la dependencia respecto de r, ψ klm (r, θ, φ) = f klm (r)y m l (θ, φ). (24) Normalización: dω Yl m (θ, φ) 2 = 1, (25) 0 dr r2 f klm (r) 2 = 1. (26) 10
12 Tenemos que L z Y l m (θ, φ) = i φ Yl m (θ, φ) = myl m (θ, φ), (27) por tanto, Yl m (θ, φ) = Fl m (θ)e imφ. (28) La función de onda es monovaluada: φ y φ+2π corresponden al mismo punto del espacio, e im2π = 1, m es entero, l es entero. (29) Vamos a demostrar que todos los valores enteros no negativos son posibles para el número cuántico l, L + Yl l (θ, φ) = 0. (30) 11
13 Por tanto, ( d dθ l cot θ cuya solución es ) Fl l (θ) = 0, (31) F l l (θ) = c l (sin θ) l, (32) lo que significa que existe una única función l. i. Y l l (θ, φ) = c l (sin θ) l e ilφ. (33) Actuando con L, obtenemos sucesivamente el resto de autofunciones Yl l 1,..., Yl m,..., Yl l, que también son únicas. Las autofunciones Yl m (θ, φ), con la elección de la fase para c l c l = ( 1)l (2l + 1)! 2 l, (34) l! 4π se denominan ARMÓNICOS ESFÉRICOS. 12
14 Armónicos esféricos para l = 0, 1 y 2 Y0 0 = 1 4π Y 1 ±1 (θ, φ) = 3 8π sin θe±iφ Y1 0 3 (θ, φ) = 4π cos θ Y 2 ±2 15 (θ, φ) = 32π sin2 θe ±2iφ Y 2 ±1 15 (θ, φ) = sin θ cos θe±iφ 8π Y2 0 5 (θ, φ) = ( 3 cos 2 θ 1 ) 16π 13
15 Propiedades de los armónicos esféricos (comp. A V I ) L ± Y m l (θ, φ) = Ortonormalidad 2π 0 dφ π l(l + 1) m(m ± 1) Y m±1 l (θ, φ). (35) dθ sin θ Y m l 0 Cualquier función de los ángulos f(θ, φ) = c lm = Paridad +l l=0 m= l 2π π 0 dφ 0 (θ, φ)y m l (θ, φ) = δ ll δ mm. (36) c lm Y m l (θ, φ), (37) dθ sin θ Y m l (θ, φ)f(θ, φ). (38) Yl m (θ, φ) = ( 1) l Yl m (π θ, π + φ). (39) Conjugado Yl m (θ, φ) = ( 1) m Yl m (θ, φ). (40) 14
16 Base estándar del espacio de las funciones de onda de una partícula sin espín Los operadores L 2 y L z no constituyen un CCOC para el espacio de las funciones de onda de una partícula sin espín. En general, hay que introducir un índice k para denotar la degeneración existente una vez fijados (l, m). ψ klm ( r) = R klm (r)y m l (θ, φ). (41) Por ser autofunción de L 2 y L z, L ± ψ klm ( r) = l(l + 1) m(m ± 1) ψ klm±1 ( r), (42) y como L ± sólo actúa sobre las variables angulares, L ± ψ klm ( r) = R klm (r)l ± Yl m (θ, φ) = l(l + 1) m(m ± 1) R klm (r) Yl m±1 (θ, φ). (43) Por tanto, R klm±1 (r) = R klm (r). (44) 15
17 La parte radial no puede depender de m, esto es, ψ klm ( r) = R kl (r)y m l (θ, φ). (45) Relación de ortonormalidad d rψ klm ( r)ψ k l m ( r) = δ kk δ ll δ mm. (46) En consecuencia, 0 dr r2 R kl (r)r k l (r) = δ kk, (47) ya que los armónicos esféricos son ortogonales para l l. 16
18 Predicciones físicas Sea una función de onda arbitraria ψ( r) = k donde c klm = +l l=0 m= l 0 dr r2 R kl (r) 2π 0 dφ π o c klm R kl (r)y m l (θ, φ), (48) dθ sin θ Y m l (θ, φ)ψ(r, θ, φ). (49) La probabilidad de una medida conjunta de L 2 y L z es P L 2,L z (l, m) = k c klm 2, (50) y si sólo medimos L 2 o L z las probabilidades respectivas son P L 2(l) = +l m= l P Lz (m) = l m P L 2,L z (l, m), (51) P L 2,L z (l, m). (52) 17
19 Como el momento angular sólo actúa sobre las variables (θ, φ), sólo la dependencia en éstas es relevante para los cálculos anteriores, ψ(r, θ, φ) = +l l=0 m= l a lm (r)y m l (θ, φ),(53) a lm (r) = c klm R kl (r). (54) k Debido a la ortogonalidad de las funciones radiales, 0 dr r2 a lm (r) 2 = k = k k c klm c k lm dr 0 r2 Rkl (r)r k l (r) c klm 2, (55) y a lm (r) = 2π 0 dφ π 0 dθ sin θ Y m l (θ, φ)ψ(r, θ, φ). (56) 18
El átomo de hidrógeno
 El átomo de hiógeno Antonio. árquez Departamento de Química Física Universidad de Sevilla Curso 017/018 Índice 1. Ecuación de Schrodinger 1. Orbitales hiogenoides 5 3. Función de distribución radial 7
El átomo de hiógeno Antonio. árquez Departamento de Química Física Universidad de Sevilla Curso 017/018 Índice 1. Ecuación de Schrodinger 1. Orbitales hiogenoides 5 3. Función de distribución radial 7
Apuntes de la asignatura Química Física II (Licenciatura en Química) Tema 6: Momento angular
 Apuntes de la asignatura Química Física II Licenciatura en Química) Tema 6: Momento angular Ángel José Pére Jiméne Dept. de Química Física Univ. Alicante) Índice 1. Momento angular en Mecánica Clásica.
Apuntes de la asignatura Química Física II Licenciatura en Química) Tema 6: Momento angular Ángel José Pére Jiméne Dept. de Química Física Univ. Alicante) Índice 1. Momento angular en Mecánica Clásica.
1.1 DEFINICIÓN CLÁSICA DEL MOMENTO ANGU- LAR
 Chapter MOMENTO ANGULAR La teoría del momento angular en mecánica cuántica es de gran importancia tanto por el número como por la variedad de sus consecuencias. A partir de la espectroscopía rotacional,
Chapter MOMENTO ANGULAR La teoría del momento angular en mecánica cuántica es de gran importancia tanto por el número como por la variedad de sus consecuencias. A partir de la espectroscopía rotacional,
FÍSICA 4 PRIMER CUATRIMESTRE DE 2015 GUÍA 9: POTENCIALES EN 2-D Y 3-D, MOMENTO ANGULAR, ÁTOMO DE HIDRÓGENO, ESPÍN
 FÍSICA 4 PRIMER CUATRIMESTRE DE 2015 GUÍA 9: POTENCIALES EN 2-D Y 3-D, MOMENTO ANGULAR, ÁTOMO DE HIDRÓGENO, ESPÍN 1. Considere el siguiente potencial (pozo infinito): { 0 x a; y b y z c V(x)= sino Escribiendo
FÍSICA 4 PRIMER CUATRIMESTRE DE 2015 GUÍA 9: POTENCIALES EN 2-D Y 3-D, MOMENTO ANGULAR, ÁTOMO DE HIDRÓGENO, ESPÍN 1. Considere el siguiente potencial (pozo infinito): { 0 x a; y b y z c V(x)= sino Escribiendo
El ÁTOMO de HIDRÓGENO
 El ÁTOMO de HIDRÓGENO Dr. Andres Ozols Dra. María Rebollo FIUBA 006 Dr. A. Ozols 1 ESPECTROS DE HIDROGENO espectros de emisión espectro de absorción Dr. A. Ozols ESPECTROS DE HIDROGENO Secuencias de las
El ÁTOMO de HIDRÓGENO Dr. Andres Ozols Dra. María Rebollo FIUBA 006 Dr. A. Ozols 1 ESPECTROS DE HIDROGENO espectros de emisión espectro de absorción Dr. A. Ozols ESPECTROS DE HIDROGENO Secuencias de las
EL ÁTOMO DE HIDRÓGENO
 EL ÁTOMO DE HIDRÓGENO El átomo de hidrógeno constituye uno de los pocos sistemas de interés químico que admite una solución exacta de la ecuación de Schröedinger. Para todos los demás sólo es factible
EL ÁTOMO DE HIDRÓGENO El átomo de hidrógeno constituye uno de los pocos sistemas de interés químico que admite una solución exacta de la ecuación de Schröedinger. Para todos los demás sólo es factible
MECANICA CUANTICA AVANZADA FIM 8440 (6)
 MECANICA CUANTICA AVANZADA FIM 8440 (6) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 1er. Semestre 2012 Rotaciones y Rotaciones y Si J es el momento angular de un sistema,
MECANICA CUANTICA AVANZADA FIM 8440 (6) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 1er. Semestre 2012 Rotaciones y Rotaciones y Si J es el momento angular de un sistema,
Ayudantía 11: Resumen Mecánica Cuántica
 Pontificia Universidad Católica de Chile Facultad de Física FIZ03 Física Cuántica I Ayudantía 11: Resumen Mecánica Cuántica Fabián Cádiz 0.1. Principios 0.1.1. El espacio de Hilbert La primera etapa en
Pontificia Universidad Católica de Chile Facultad de Física FIZ03 Física Cuántica I Ayudantía 11: Resumen Mecánica Cuántica Fabián Cádiz 0.1. Principios 0.1.1. El espacio de Hilbert La primera etapa en
Examen de Física Cuántica I
 UNIVERSIDAD COMPLUTENSE DE MADRID FACULTAD DE CIENCIAS FISICAS 9 de Junio de 2017 Examen de Física Cuántica I Nombre y Apellidos: Firma y DNI: Los alumnos que se presentan a toda la asignatura tienen que
UNIVERSIDAD COMPLUTENSE DE MADRID FACULTAD DE CIENCIAS FISICAS 9 de Junio de 2017 Examen de Física Cuántica I Nombre y Apellidos: Firma y DNI: Los alumnos que se presentan a toda la asignatura tienen que
Matemática Avanzada. Clase Nro. 22
 Matemática Avanzada Clase Nro. 22 Octavio Miloni Facultad de Cs. Astronómicas y Geofísicas - Universidad Nacional de La Plata / 28 Aplicaciones a la Física Matemática Teoria del Potencial Problema de Contorno
Matemática Avanzada Clase Nro. 22 Octavio Miloni Facultad de Cs. Astronómicas y Geofísicas - Universidad Nacional de La Plata / 28 Aplicaciones a la Física Matemática Teoria del Potencial Problema de Contorno
Física cuántica I Grupo C 2015/16 Examen final 22 de junio de 2016
 UNIVERSIDAD COMPLUTENSE DE MADRID DEPARTAMENTO DE FÍSICA TEÓRICA I GRADO EN FÍSICA Física cuántica I Grupo C 15/1 Examen final de junio de 1 Nombre: Soluciones Firma: Problema 1 (1 punto). Un haz de radiación
UNIVERSIDAD COMPLUTENSE DE MADRID DEPARTAMENTO DE FÍSICA TEÓRICA I GRADO EN FÍSICA Física cuántica I Grupo C 15/1 Examen final de junio de 1 Nombre: Soluciones Firma: Problema 1 (1 punto). Un haz de radiación
Estructura de la Materia. Átomo de Hidrógeno. Martha M. Flores Leonar FQ UNAM. 16 de abril de 2018
 Estructura de la Materia Átomo de Hidrógeno Martha M. Flores Leonar FQ UNAM 16 de abril de 2018 ÁTOMO DE HIDRÓGENO z θ r φ y x Ψ (r, θ, φ) = R (r) Θ (θ) Φ (φ) (1) Ĥ = 2 2µ 2 kze2 r (2) ĤΨ (r, θ, φ) = EΨ
Estructura de la Materia Átomo de Hidrógeno Martha M. Flores Leonar FQ UNAM 16 de abril de 2018 ÁTOMO DE HIDRÓGENO z θ r φ y x Ψ (r, θ, φ) = R (r) Θ (θ) Φ (φ) (1) Ĥ = 2 2µ 2 kze2 r (2) ĤΨ (r, θ, φ) = EΨ
HOJA DE PROBLEMAS 1: ENUNCIADOS
 Tema: ESTRUCTURA ELECTRÓNICA DE LOS ÁTOMOS HOJA DE PROBLEMAS 1: ENUNCIADOS 1. ( ) Para describir el estado fundamental de una partícula que se encuentra en una caja de potencial unidimensional definida
Tema: ESTRUCTURA ELECTRÓNICA DE LOS ÁTOMOS HOJA DE PROBLEMAS 1: ENUNCIADOS 1. ( ) Para describir el estado fundamental de una partícula que se encuentra en una caja de potencial unidimensional definida
Problemas de Mecánica Cuántica (para el Exámen Predoctoral)
 Problemas de Mecánica Cuántica (para el Exámen Predoctoral) 1 Formalismo general 1. Problema: Consideremos un sistema cuántico que contiene sólo dos estados linealmente independientes 1 y 2, 1 = 2 = (
Problemas de Mecánica Cuántica (para el Exámen Predoctoral) 1 Formalismo general 1. Problema: Consideremos un sistema cuántico que contiene sólo dos estados linealmente independientes 1 y 2, 1 = 2 = (
t t, r ( t) = r(t). (8.1)
 Capítulo 8 Inversión temporal 8.1. Inversión temporal en mecánica clásica Sean x(t) y p(t) la posición y el momento lineal de una partícula en función del tiempo. La operación de inversión temporal, además
Capítulo 8 Inversión temporal 8.1. Inversión temporal en mecánica clásica Sean x(t) y p(t) la posición y el momento lineal de una partícula en función del tiempo. La operación de inversión temporal, además
Funciones de Legendre - Fórmulas
 Funciones de Legendre - Fórmuas Agustín Nieto Departamento de Física Universidad de Oviedo 8 de mayo de Resumen Se dan fórmuas reacionadas os poinomios de Legendre, as funciones asociadas de Legendre y
Funciones de Legendre - Fórmuas Agustín Nieto Departamento de Física Universidad de Oviedo 8 de mayo de Resumen Se dan fórmuas reacionadas os poinomios de Legendre, as funciones asociadas de Legendre y
Respuestas de la Serie 2
 Respuestas de la Serie 2 1. N h 2 Ĥ = 2 2M I I=1 }{{} A n h 2 2 + 2m i }{{} B N N I=1 J>I kz 2 e 2 R I R J } {{ } C N n kze 2 I } i R I r i {{} D + n n ke 2 r j>i i r j }{{} E a) En el orden en el que
Respuestas de la Serie 2 1. N h 2 Ĥ = 2 2M I I=1 }{{} A n h 2 2 + 2m i }{{} B N N I=1 J>I kz 2 e 2 R I R J } {{ } C N n kze 2 I } i R I r i {{} D + n n ke 2 r j>i i r j }{{} E a) En el orden en el que
ESTRUCTURA DE LA MATERIA
 7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 0 7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 1 7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 1 7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 3 7/03/18 FUNDAMENTOS
7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 0 7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 1 7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 1 7/03/18 FUNDAMENTOS DE LA MECÁNICA CUÁNTICA 3 7/03/18 FUNDAMENTOS
TEMA 2. Modelo mecanocuántico. ntico del átomo de
 TEMA. Modelo mecanocuántico ntico del átomo de hidrógeno Aunque la teoría de Bohr y la etensión de Somerfeld conducen a resultados satisfactorios para el átomo de hidrógeno su aplicación tropezaba con
TEMA. Modelo mecanocuántico ntico del átomo de hidrógeno Aunque la teoría de Bohr y la etensión de Somerfeld conducen a resultados satisfactorios para el átomo de hidrógeno su aplicación tropezaba con
Física Cuántica Partículas idénticas.
 Física Cuántica Partículas idénticas. José Manuel López y Luis Enrique González Universidad de Valladolid Curso 2004-2005 p. 1/18 Partículas idénticas Qué son varias partículas idénticas? Las que tienen
Física Cuántica Partículas idénticas. José Manuel López y Luis Enrique González Universidad de Valladolid Curso 2004-2005 p. 1/18 Partículas idénticas Qué son varias partículas idénticas? Las que tienen
Ecuaciones diferenciales en derivadas parciales Método de separación de variables
 Ecuaciones diferenciales en derivadas parciales Método de separación de variables 1. Ecuaciones diferenciales en derivadas parciales. El problema de las condiciones de contorno. 2. La ecuación de Laplace
Ecuaciones diferenciales en derivadas parciales Método de separación de variables 1. Ecuaciones diferenciales en derivadas parciales. El problema de las condiciones de contorno. 2. La ecuación de Laplace
Rotaciones. R es ortogonal. Esto es :RR T = 1, donde R T ij =R ji. En efecto. R T R =1, R es una matriz ortogonal
 Rotaciones Convención de Einstein: Dos índices repetidos en un monomio significan la suma de esos índices de 1 a la dimensión del espacio. Las rotaciones son transformaciones lineales, definidas por la
Rotaciones Convención de Einstein: Dos índices repetidos en un monomio significan la suma de esos índices de 1 a la dimensión del espacio. Las rotaciones son transformaciones lineales, definidas por la
Hoja de Problemas 5. Física Atómica.
 Hoja de Problemas 5. Física Atómica. Fundamentos de Física III. Grado en Física. Curso 25/26. Grupo 56. UAM. 3-3-26 Problema En 896 el astrónomo americano Edward Charles Pickering observó unas misteriosas
Hoja de Problemas 5. Física Atómica. Fundamentos de Física III. Grado en Física. Curso 25/26. Grupo 56. UAM. 3-3-26 Problema En 896 el astrónomo americano Edward Charles Pickering observó unas misteriosas
Apuntes de la asignatura Química Física II (Licenciatura en Química) Tema 7: El átomo de hidrógeno
 Apuntes de la asignatura Química Física II (Licenciatura en Química) Tema 7: El átomo de hidrógeno Ángel José Pérez Jiménez Dept. de Química Física (Univ. Alicante) Índice 1. Partícula sometida a un potencial
Apuntes de la asignatura Química Física II (Licenciatura en Química) Tema 7: El átomo de hidrógeno Ángel José Pérez Jiménez Dept. de Química Física (Univ. Alicante) Índice 1. Partícula sometida a un potencial
4 Momentos Angulares
 4 Momentos Angulares Estudiaremos en este capítulo la forma como se hace la adición de dos momentos angulares independientes en mecánica cuántica. Introduciremos los llamados coeficientes de Clebsh-Gordan
4 Momentos Angulares Estudiaremos en este capítulo la forma como se hace la adición de dos momentos angulares independientes en mecánica cuántica. Introduciremos los llamados coeficientes de Clebsh-Gordan
Vibración y rotación en mecánica cuántica
 Vibración y rotación en mecánica cuántica Antonio M. Márquez Departamento de Química Física Universidad de Sevilla Ultima actualización de marzo de 017 Índice 1. Oscilador armónico monodimensional 1. Cuantización
Vibración y rotación en mecánica cuántica Antonio M. Márquez Departamento de Química Física Universidad de Sevilla Ultima actualización de marzo de 017 Índice 1. Oscilador armónico monodimensional 1. Cuantización
Átomos Hidrogenoides
 Átomos Hidrogenoides Gonzalo Abal Instituto de Física Facultad de Ingeniería Montevideo, Uruguay August 18, 2004 Contents 1 Introducción 1 2 Potenciales con simetría esférica 2 2.1 Armónicos Esféricos.........................
Átomos Hidrogenoides Gonzalo Abal Instituto de Física Facultad de Ingeniería Montevideo, Uruguay August 18, 2004 Contents 1 Introducción 1 2 Potenciales con simetría esférica 2 2.1 Armónicos Esféricos.........................
Química Física II. Tema II
 Química Física II. Tema II TEMA II: LA ECUACIÓN DE SCHRÖDINGER 1. La ecuación de Schrödinger independiente del tiempo 2. La ecuación de Schrödinger dependiente del tiempo 3. Principio de incertidumbre
Química Física II. Tema II TEMA II: LA ECUACIÓN DE SCHRÖDINGER 1. La ecuación de Schrödinger independiente del tiempo 2. La ecuación de Schrödinger dependiente del tiempo 3. Principio de incertidumbre
El átomo de hidrógeno
 El átomo de hiógeno Antonio M. Márquez Departamento de Química Física Universidad de Sevilla Curso 15-16 Problema 1 Calcule la probabilidad de que un electrón 1s del H se encuentre entre r r. La probabilidad
El átomo de hiógeno Antonio M. Márquez Departamento de Química Física Universidad de Sevilla Curso 15-16 Problema 1 Calcule la probabilidad de que un electrón 1s del H se encuentre entre r r. La probabilidad
LOS POSTULADOS DE LA MECÁNICA CUÁNTICA
 LOS POSTULADOS DE LA MECÁNICA CUÁNTICA POSTULADO I Cualquier estado de un sistema dinámico de N partículas puede ser descrito por una función de las 3N coordenadas y del tiempo: La cantidad Ψ(q 1, q 2,...,
LOS POSTULADOS DE LA MECÁNICA CUÁNTICA POSTULADO I Cualquier estado de un sistema dinámico de N partículas puede ser descrito por una función de las 3N coordenadas y del tiempo: La cantidad Ψ(q 1, q 2,...,
El átomo de hidrógeno
 El átomo de hiógeno Antonio M. Márquez Departamento de Química Física Universidad de Sevilla Curso 16-17 Problema 1 Calcule la probabilidad de que un electrón 1s del H se encuentre entre r y r. Solución
El átomo de hiógeno Antonio M. Márquez Departamento de Química Física Universidad de Sevilla Curso 16-17 Problema 1 Calcule la probabilidad de que un electrón 1s del H se encuentre entre r y r. Solución
Capítulo 3. Átomos Hidrogenoides.
 Capítulo 3. Átomos Hidrogenoides. Objetivos: Introducción del concepto de orbital atómico Descripción de los números cuánticos en los orbitales atómicos Justificación cualitativa de la cuantización de
Capítulo 3. Átomos Hidrogenoides. Objetivos: Introducción del concepto de orbital atómico Descripción de los números cuánticos en los orbitales atómicos Justificación cualitativa de la cuantización de
Lección: Modelos cuánticos útiles en Química
 Lección: Modelos cuánticos útiles en Química TEMA: Introducción 1 Adolfo Bastida Pascual Universidad de Murcia. España. I. La partícula en una caja de potencial.. 2 I.A. Ecuación de Schrödinger...........
Lección: Modelos cuánticos útiles en Química TEMA: Introducción 1 Adolfo Bastida Pascual Universidad de Murcia. España. I. La partícula en una caja de potencial.. 2 I.A. Ecuación de Schrödinger...........
Física cuántica I - Colección de ejercicios cortos
 Física cuántica I - Colección de ejercicios cortos http://teorica.fis.ucm.es En las siguientes cuestiones una y sólo una de las cuatro respuestas ofrecidas es correcta. Dígase cuál. Es conveniente hacer
Física cuántica I - Colección de ejercicios cortos http://teorica.fis.ucm.es En las siguientes cuestiones una y sólo una de las cuatro respuestas ofrecidas es correcta. Dígase cuál. Es conveniente hacer
Gráficas de las partes angulares En la figura presentamos la gráfica de la función s: (1/4π) 1/2
 Gráficas de las partes angulares En la figura presentamos la gráfica de la función s: (1/4π) 1/2 La función s es un círculo porque siempre vale (1/4π) 1/2 independientemente del valor de los ángulos θ
Gráficas de las partes angulares En la figura presentamos la gráfica de la función s: (1/4π) 1/2 La función s es un círculo porque siempre vale (1/4π) 1/2 independientemente del valor de los ángulos θ
Métodos Matemáticos en Física Lección 7A: Coordenadas curvilíneas (app_d_apl)
 Lección 7A: Coordenadas curvilíneas (app_d_apl) Operadores diferenciales: gradiente, divergencia y laplaciano Recordatorio: Coordenadas cartesianas Gradiente 1 Divergencia 2 1 Leccion: Coordenadas curvilíneas
Lección 7A: Coordenadas curvilíneas (app_d_apl) Operadores diferenciales: gradiente, divergencia y laplaciano Recordatorio: Coordenadas cartesianas Gradiente 1 Divergencia 2 1 Leccion: Coordenadas curvilíneas
Orbitas tridimensionales y cuanticas a partir de la teoria ECE2: Mecanica Cuantica Lagrangiana.
 Orbitas tridimensionales y cuanticas a partir de la teoria ECE2: Mecanica Cuantica Lagrangiana. por M. W. Evans y H. Eckardt Civil List YAlAS / UPlTEC (www.aias.us, www.upitec.org, www.archive.org, www.webarchive.org.uk,
Orbitas tridimensionales y cuanticas a partir de la teoria ECE2: Mecanica Cuantica Lagrangiana. por M. W. Evans y H. Eckardt Civil List YAlAS / UPlTEC (www.aias.us, www.upitec.org, www.archive.org, www.webarchive.org.uk,
Apuntes de la asignatura Química Física II (Licenciatura en Química) Tema 4: Postulados de la Mecánica Cuántica
 Apuntes de la asignatura Química Física II (Licenciatura en Química) Tema 4: Postulados de la Mecánica Cuántica Ángel José Pérez Jiménez Dept. de Química Física (Univ. Alicante) Índice 1. Descripción de
Apuntes de la asignatura Química Física II (Licenciatura en Química) Tema 4: Postulados de la Mecánica Cuántica Ángel José Pérez Jiménez Dept. de Química Física (Univ. Alicante) Índice 1. Descripción de
Estructura electrónica de los átomos
 Estructura electrónica de los átomos Partículas subatómicas Protón (p) 1,673 10-27 Kg + 1,602 10-19 C Goldstein (1886) Electrón (e) 9,109 10-31 Kg - 1,602 10-19 C Thomson (1897) Neutrón (n) 1,673 10-27
Estructura electrónica de los átomos Partículas subatómicas Protón (p) 1,673 10-27 Kg + 1,602 10-19 C Goldstein (1886) Electrón (e) 9,109 10-31 Kg - 1,602 10-19 C Thomson (1897) Neutrón (n) 1,673 10-27
Serie de problemas para el curso. Química Cuantica I
 erie de problemas para el curso Química Cuantica I Matemáticas Tema Resuelva todos los problemas del capítulo de la referencia B6 y compare sus resultados con las soluciones que se incluyen al final de
erie de problemas para el curso Química Cuantica I Matemáticas Tema Resuelva todos los problemas del capítulo de la referencia B6 y compare sus resultados con las soluciones que se incluyen al final de
Simetría de funciones de onda y Principio de Pauli. Rueda Carlos Alberto Tinajero Verónica Tavera Hernández Rosario
 Simetría de funciones de onda y Principio de Pauli Rueda Carlos Alberto Tinajero Verónica Tavera Hernández Rosario Introducción. En el espectro de emisión del sodio la línea amarilla es la más intensa
Simetría de funciones de onda y Principio de Pauli Rueda Carlos Alberto Tinajero Verónica Tavera Hernández Rosario Introducción. En el espectro de emisión del sodio la línea amarilla es la más intensa
= r t r. r t r. x y z = senφ cos φ. z por lo que la representacion matricial de esta rotación es
 Introducción 1. CARACTERIZACION DE UN SISTEMA CUANTICO Y SIMETRIAS En Mecánica Cuántica, las propiedades de los sistemas físicos están contenidas en el vector de estado ψ que vive en un espacio lineal
Introducción 1. CARACTERIZACION DE UN SISTEMA CUANTICO Y SIMETRIAS En Mecánica Cuántica, las propiedades de los sistemas físicos están contenidas en el vector de estado ψ que vive en un espacio lineal
Síntesis de problemas con simetría esférica.
 Síntesis de problemas con simetría esférica. 1. Ondas esféricas. Supongamos que tenemos la ecuación de ondas en d = 3 u tt = c u (1) y vamos a buscar soluciones que espacialmente, solo dependen de la variable
Síntesis de problemas con simetría esférica. 1. Ondas esféricas. Supongamos que tenemos la ecuación de ondas en d = 3 u tt = c u (1) y vamos a buscar soluciones que espacialmente, solo dependen de la variable
9. Observables de dispersión en el formalismo de matriz S.
 Mecánica Cuántica Avanzada Carlos Pena 9-9. Observables de dispersión en el formalismo de matriz S. [Ros XI.7, Sch 8.2, Ynd 22.3] Probabilidades de transición: regla de oro de Fermi generalizada En términos
Mecánica Cuántica Avanzada Carlos Pena 9-9. Observables de dispersión en el formalismo de matriz S. [Ros XI.7, Sch 8.2, Ynd 22.3] Probabilidades de transición: regla de oro de Fermi generalizada En términos
Métodos Matemáticos en Física
 Lección 7A: Coordenadas curvilíneas (app_d_apl) Operadores diferenciales: gradiente, divergencia y laplaciano Recordatorio: Coordenadas cartesianas Gradiente 1 Divergencia 2 1 Leccion: Coordenadas curvilíneas
Lección 7A: Coordenadas curvilíneas (app_d_apl) Operadores diferenciales: gradiente, divergencia y laplaciano Recordatorio: Coordenadas cartesianas Gradiente 1 Divergencia 2 1 Leccion: Coordenadas curvilíneas
Química Física II. Curso Serie L02. Problemas de una partícula
 Química Física II. Curso 009-00. Serie L0. Problemas de una partícula. La función de onda de una partícula libre que se mueve en una dimensión con energía constante es Ψ k (x, t) = ψ k (x)e iωt = Ae ikx
Química Física II. Curso 009-00. Serie L0. Problemas de una partícula. La función de onda de una partícula libre que se mueve en una dimensión con energía constante es Ψ k (x, t) = ψ k (x)e iωt = Ae ikx
Sistemas de coordenadas
 Sistemas de coordenadas. Introducción En un sistema de coordenadas un punto se representa como la intersección de tres superficies ortogonales llamadas superficies coordenadas del sistema: u u u = cte
Sistemas de coordenadas. Introducción En un sistema de coordenadas un punto se representa como la intersección de tres superficies ortogonales llamadas superficies coordenadas del sistema: u u u = cte
2. Método de separación de variables
 APUNTES DE AMPIACIÓN DE MATEMÁTICAS II PARA INGENIEROS DE TEECOMUNICACIONES Elaborados por Arturo de Pablo, Domingo Pestana y José Manuel Rodríguez 2. Método de separación de variables 2.1. Separación
APUNTES DE AMPIACIÓN DE MATEMÁTICAS II PARA INGENIEROS DE TEECOMUNICACIONES Elaborados por Arturo de Pablo, Domingo Pestana y José Manuel Rodríguez 2. Método de separación de variables 2.1. Separación
Matemática Avanzada. Clase Nro. 20
 Matemática Avanzada Clase Nro. 20 Octavio Miloni Facultad de Cs. Astronómicas y Geofísicas - Universidad Nacional de La Plata / 2 Ecuación de Legendre Polinomios de Legendre Ecuación Diferencial de Legendre
Matemática Avanzada Clase Nro. 20 Octavio Miloni Facultad de Cs. Astronómicas y Geofísicas - Universidad Nacional de La Plata / 2 Ecuación de Legendre Polinomios de Legendre Ecuación Diferencial de Legendre
Colominas I., Gómez H. Problemas de EDPs en la matemática aplicada 63/117
 Colominas I., Gómez H. Problemas de EDPs en la matemática aplicada 63/117 5. Se desea estudiar la distribución estacionaria de temperaturas en el interior de una esfera homogénea de radio R, centrada en
Colominas I., Gómez H. Problemas de EDPs en la matemática aplicada 63/117 5. Se desea estudiar la distribución estacionaria de temperaturas en el interior de una esfera homogénea de radio R, centrada en
2. MECANICA CUANTICA DE SISTEMAS ELEMENTALES.
 . MECANICA CUANTICA DE SISTEMAS EEMENTAES... MOVIMIENTO TRASACIONA. A PARTÍCUA IBRE. Partícula de masa m moviéndose en la dimensión no sometida a fueras eternas: V( 0 Operador amiltoniano del sistema:
. MECANICA CUANTICA DE SISTEMAS EEMENTAES... MOVIMIENTO TRASACIONA. A PARTÍCUA IBRE. Partícula de masa m moviéndose en la dimensión no sometida a fueras eternas: V( 0 Operador amiltoniano del sistema:
Anarmonicidad y resonancias en vibraciones de moléculas
 Anarmonicidad y resonancias en vibraciones de moléculas PRINCIPIOS DE ESTRUCTURA DE LA MATERIA DR. LUIS ALBERTO VICENTE HINESTROZA WILLIAM GARCÍA SANTOS ARMANDO MARTÍNEZ DE LA PEÑA ELIA MÉNDEZ VARGAS Ciencia
Anarmonicidad y resonancias en vibraciones de moléculas PRINCIPIOS DE ESTRUCTURA DE LA MATERIA DR. LUIS ALBERTO VICENTE HINESTROZA WILLIAM GARCÍA SANTOS ARMANDO MARTÍNEZ DE LA PEÑA ELIA MÉNDEZ VARGAS Ciencia
Rotación y vibración de moléculas poliatómicas
 Rotación y vibración de moléculas poliatómicas Química Física Aplicada, UAM (Química Física Aplicada, UAM) Rotación y vibración de moléculas poliatómicas 1 / 1 Movimiento de rotación en moléculas poliatómicas
Rotación y vibración de moléculas poliatómicas Química Física Aplicada, UAM (Química Física Aplicada, UAM) Rotación y vibración de moléculas poliatómicas 1 / 1 Movimiento de rotación en moléculas poliatómicas
TEORIA ELECTROMAGNETICA FIZ 0321 (2)
 TEORIA ELECTROMAGNETICA FIZ 0321 (2) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 2do. Semestre 2006 Solución de problemas de electrostática Ecuación de Laplace Coordenadas
TEORIA ELECTROMAGNETICA FIZ 0321 (2) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 2do. Semestre 2006 Solución de problemas de electrostática Ecuación de Laplace Coordenadas
Polinomios de Legendre.
 . Introducción. Polinomios de Legendre. Los polinomios de Legendre constituyen una base ortogonal en el espacio de funciones definidas entre [, ]. Son soluciones de la familia de ecuaciones diferenciales
. Introducción. Polinomios de Legendre. Los polinomios de Legendre constituyen una base ortogonal en el espacio de funciones definidas entre [, ]. Son soluciones de la familia de ecuaciones diferenciales
Teorema 1 (Cambio de Variable en R n ).
 Vamos a estudiar en este segundo capítulo sobre los cambios de variable para funciones de varias variables, algunos de los más habituales: los cambios de coordenadas a coordenadas polares en el plano,
Vamos a estudiar en este segundo capítulo sobre los cambios de variable para funciones de varias variables, algunos de los más habituales: los cambios de coordenadas a coordenadas polares en el plano,
Física Cuántica Atomos multielectrónicos.
 Física Cuántica Atomos multielectrónicos. José Manuel López y Luis Enrique González Universidad de Valladolid Curso 2004-2005 p. 1/19 Atomos multielectrónicos. Tenemos un sistema formado por un núcleo
Física Cuántica Atomos multielectrónicos. José Manuel López y Luis Enrique González Universidad de Valladolid Curso 2004-2005 p. 1/19 Atomos multielectrónicos. Tenemos un sistema formado por un núcleo
MATEMÁTICA D y D 1 Módulo I: Análisis de Variable Compleja
 Matemática D y D MATEMÁTICA D y D Módulo I: Análisis de Variable Compleja Unidad 0 Números Complejos Mag. María Inés Baragatti Números complejos. Generalidades Un número complejo es un par ordenado de
Matemática D y D MATEMÁTICA D y D Módulo I: Análisis de Variable Compleja Unidad 0 Números Complejos Mag. María Inés Baragatti Números complejos. Generalidades Un número complejo es un par ordenado de
Física Teórica 2. Primer cuatrimestre de Guía 4: Dinámica cuántica
 Física Teórica Primer cuatrimestre de 018 Guía 4: Dinámica cuántica 1. La representación matricial del Hamiltoniano correspondiente a un fotón propagándose en dirección del eje óptico de un cristal de
Física Teórica Primer cuatrimestre de 018 Guía 4: Dinámica cuántica 1. La representación matricial del Hamiltoniano correspondiente a un fotón propagándose en dirección del eje óptico de un cristal de
Física Teórica II Práctica 8: Teoría de Perturbaciones Parte I: Perturbaciones Independientes del Tiempo
 Física Teórica II Parte I: Perturbaciones Independientes del Tiempo 1. Si los estados vibracionales de una molécula diatómica dipolar pueden ser descriptos adecuadamente por un potencial armónico unidimensional,
Física Teórica II Parte I: Perturbaciones Independientes del Tiempo 1. Si los estados vibracionales de una molécula diatómica dipolar pueden ser descriptos adecuadamente por un potencial armónico unidimensional,
Por otra parte, una función es antisimétrica o impar cuando f(x) = -f(-x), por lo que, en este caso:
 Problemas de la Lección.) Justifíquese la simetría o asimetría de las funciones: a) Ψ () = cos() b) Ψ() = /sen() c) Ψ() = ( + )( - ) d) Ψ() = ep(-a ) e) Ψ() = F()F(-) f) Ψ() = ( - 4). Se dice que una función
Problemas de la Lección.) Justifíquese la simetría o asimetría de las funciones: a) Ψ () = cos() b) Ψ() = /sen() c) Ψ() = ( + )( - ) d) Ψ() = ep(-a ) e) Ψ() = F()F(-) f) Ψ() = ( - 4). Se dice que una función
Ejemplos de interferencia
 Tema 2_2 Ejemplos de interferencia El efecto fotoeléctrico Hipótesis de Plank: Sólo fotones con frecuencia mayor que un umbral Energía cinética del electrón emitido Qué tipo de partícula es el fotón?
Tema 2_2 Ejemplos de interferencia El efecto fotoeléctrico Hipótesis de Plank: Sólo fotones con frecuencia mayor que un umbral Energía cinética del electrón emitido Qué tipo de partícula es el fotón?
Fotones, electrones, y. Dualidad onda partícula. Dualidad onda partícula. Ventaja de los electrones. Fotos enviadas por Sebastián Gómez (curso 2007)
 Fotones, electrones, y. Dualidad onda partícula partículas cuánticas ó paquetes de onda Se difractan si interactúan con objetos de tamaño comparable con su λ. Es decir en ese caso se comportan como ondas.
Fotones, electrones, y. Dualidad onda partícula partículas cuánticas ó paquetes de onda Se difractan si interactúan con objetos de tamaño comparable con su λ. Es decir en ese caso se comportan como ondas.
Producto tensorial entre tensores
 Tensores cartesianos Producto tensorial entre tensores Producto tensorial entre tensores Se define el producto tensorial entre los tensores S CT(m) y T CT(n) como el tensor S T CT(n + m): S T = S i1...i
Tensores cartesianos Producto tensorial entre tensores Producto tensorial entre tensores Se define el producto tensorial entre los tensores S CT(m) y T CT(n) como el tensor S T CT(n + m): S T = S i1...i
El campo magnético de las corrientes estacionarias
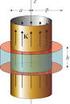 El campo magnético de las corrientes estacionarias Introducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
El campo magnético de las corrientes estacionarias Introducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
dx = x El tensor x/ X se denomina tensor gradiente de la deformación F = x
 Capítulo 2 Cinemática El desarrollo de las expresiones contenidas en este capítulo se lleva a cabo en un sistema de referencia general cartesiano {I 1 I 2 I 3 }. La notación es, con algunas diferencias,
Capítulo 2 Cinemática El desarrollo de las expresiones contenidas en este capítulo se lleva a cabo en un sistema de referencia general cartesiano {I 1 I 2 I 3 }. La notación es, con algunas diferencias,
Mecánica Cuántica. Curso propedéutico Mauricio Fortes 21/10/09 IFUNAM. mfb (IFUNAM) MQ-3 21/10/09 1 / 30
 Mecánica Cuántica Curso propedéutico 2009 Mauricio Fortes IFUNAM 21/10/09 mfb (IFUNAM) MQ-3 21/10/09 1 / 30 Sitio web http://www.fisica.unam.mx/personales/fortes mfb (IFUNAM) MQ-3 21/10/09 2 / 30 Postulados
Mecánica Cuántica Curso propedéutico 2009 Mauricio Fortes IFUNAM 21/10/09 mfb (IFUNAM) MQ-3 21/10/09 1 / 30 Sitio web http://www.fisica.unam.mx/personales/fortes mfb (IFUNAM) MQ-3 21/10/09 2 / 30 Postulados
Definición 13.1 Definimos el conjunto de los polinomios de Laguerre {L n (t)} n N 0 mediante una cualquiera de las siguientes ecuaciones:
 Capítulo 13 Polinomios de Laguerre 13.1 Definición Definición 13.1 Definimos el conjunto de los polinomios de Laguerre {} n N mediante una cualquiera de las siguientes ecuaciones: = e t dn ( t n e t) =
Capítulo 13 Polinomios de Laguerre 13.1 Definición Definición 13.1 Definimos el conjunto de los polinomios de Laguerre {} n N mediante una cualquiera de las siguientes ecuaciones: = e t dn ( t n e t) =
EJERCICIOS PAU MATEMÁTICAS II ARAGÓN Autor: Fernando J. Nora Costa-Ribeiro Más ejercicios y soluciones en fisicaymat.wordpress.com
 GEOMETRÍA 1- Dados el punto P(1,-1,0) y la recta : 1 0 3 3 0 a) Determine la ecuación general del plano (Ax+By+Cz+D=0) que contiene al punto P y a la recta s. b) Determine el ángulo que forman el plano
GEOMETRÍA 1- Dados el punto P(1,-1,0) y la recta : 1 0 3 3 0 a) Determine la ecuación general del plano (Ax+By+Cz+D=0) que contiene al punto P y a la recta s. b) Determine el ángulo que forman el plano
1. Clasifica las siguientes cónicas dando su ecuación reducida, centro o vértice y ejes (si es posible): (1.d) x 2 + y 2 + 2x + 1 = 0
 Clasificación de cónicas.. Clasifica las siguientes cónicas dando su ecuación reducida, centro o vértice y ejes si es posible:.a x xy + y + x y + 0.b x + xy y 6x + y 0.c x + xy + y x y 0.d x + y + x +
Clasificación de cónicas.. Clasifica las siguientes cónicas dando su ecuación reducida, centro o vértice y ejes si es posible:.a x xy + y + x y + 0.b x + xy y 6x + y 0.c x + xy + y x y 0.d x + y + x +
25 1. Conceptos fundamentales
 25 1. Conceptos fundamentales Problemas propuestos Problema 1.1. Si X,Y,Z son operadores, demostrad las propiedades siguientes utilizando la notación de bras y kets. a)(xy) = Y X y más generalmente(xy
25 1. Conceptos fundamentales Problemas propuestos Problema 1.1. Si X,Y,Z son operadores, demostrad las propiedades siguientes utilizando la notación de bras y kets. a)(xy) = Y X y más generalmente(xy
1. ESPACIO EUCLÍDEO. ISOMETRÍAS
 1 1. ESPACIO EUCLÍDEO. ISOMETRÍAS Muchos de los fenómenos que se investigan en la geometría utilizan nociones como las de longitud de un vector y ángulo entre vectores. Para introducir estos dos conceptos
1 1. ESPACIO EUCLÍDEO. ISOMETRÍAS Muchos de los fenómenos que se investigan en la geometría utilizan nociones como las de longitud de un vector y ángulo entre vectores. Para introducir estos dos conceptos
Campo de un hilo infinito. Fuerzas magnéticas. Teorema de Ampère. Campo magnético de una espira circular
 El campo magnético de las corrientes estacionarias ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
El campo magnético de las corrientes estacionarias ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
Ayudantía 13: Potencial central y primera descripción de átomos
 Pontificia Universidad Católica de Chile Facultad de Física FIZ3 Física Cuántica I Ayudantía 13: Potencial central y primera descripción de átomos Fabián Cádiz.1. Movimiento en un potencial central Consideremos
Pontificia Universidad Católica de Chile Facultad de Física FIZ3 Física Cuántica I Ayudantía 13: Potencial central y primera descripción de átomos Fabián Cádiz.1. Movimiento en un potencial central Consideremos
Métodos Matemáticos para Físicos II
 Métodos Matemáticos para Físicos II Profesor: Federico Pardo Casas Facultad de Ciencias Universidad Nacional de Ingeniería Lima, PERÚ Pardo Casas, Federico UNI Ciencias Física) CF391 Ciclo 2013 I 1 / 22
Métodos Matemáticos para Físicos II Profesor: Federico Pardo Casas Facultad de Ciencias Universidad Nacional de Ingeniería Lima, PERÚ Pardo Casas, Federico UNI Ciencias Física) CF391 Ciclo 2013 I 1 / 22
Procesamiento Cuántico de Datos. Miguel Arizmendi, Gustavo Zabaleta. 17 de noviembre de Sitio web: www3..mdp.edu.ar/fes/procq.
 Procesamiento Cuántico de Datos Miguel Arizmendi, Gustavo Zabaleta 17 de noviembre de 2016 Sitio web: www3..mdp.edu.ar/fes/procq.html Mecánica Cuántica y Qubits Qubits El qubit o bit cuántico es la unidad
Procesamiento Cuántico de Datos Miguel Arizmendi, Gustavo Zabaleta 17 de noviembre de 2016 Sitio web: www3..mdp.edu.ar/fes/procq.html Mecánica Cuántica y Qubits Qubits El qubit o bit cuántico es la unidad
2. El conjunto de los números complejos
 Números complejos 1 Introducción El nacimiento de los números complejos se debió a la necesidad de dar solución a un problema: no todas las ecuaciones polinómicas poseen una solución real El ejemplo más
Números complejos 1 Introducción El nacimiento de los números complejos se debió a la necesidad de dar solución a un problema: no todas las ecuaciones polinómicas poseen una solución real El ejemplo más
Problemas. a a 0 a 0 A =
 Problemas 1. La representación matricial del Hamiltoniano correspondiente a un fotón propagandose en dirección del eje óptico de un cristal de cuarzo usando como base los estados de polarización lineal
Problemas 1. La representación matricial del Hamiltoniano correspondiente a un fotón propagandose en dirección del eje óptico de un cristal de cuarzo usando como base los estados de polarización lineal
π, los niveles de energía que existen y la degeneración, o número de
 EXAMEN DE SEPTIEMBRE DE QUÍMICA FÍSICA (3º Curso de Químicas): 9/9/8. ) a) Que propiedades poseen las funciones propias de un operador hermítico. b) Indicar para una configuración π, los nieles de energía
EXAMEN DE SEPTIEMBRE DE QUÍMICA FÍSICA (3º Curso de Químicas): 9/9/8. ) a) Que propiedades poseen las funciones propias de un operador hermítico. b) Indicar para una configuración π, los nieles de energía
Tema 14 11/02/2005. Tema 8. Mecánica Cuántica. 8.1 Fundamentos de la mecánica cuántica
 Tema 14 11/0/005 Tema 8 Mecánica Cuántica 8.1 Fundamentos de la mecánica cuántica 8. La ecuación de Schrödinger 8.3 Significado físico de la función de onda 8.4 Soluciones de la ecuación de Schrödinger
Tema 14 11/0/005 Tema 8 Mecánica Cuántica 8.1 Fundamentos de la mecánica cuántica 8. La ecuación de Schrödinger 8.3 Significado físico de la función de onda 8.4 Soluciones de la ecuación de Schrödinger
+V(x,y,z).ψ(x,y,z,t) = i.h
 Ecuación n de Schrödinger -h ( Ψ Ψ Ψ ) m Ψ +V(x,y,z).ψ(x,y,z,t) = i.h x y z t h = h / π i = (-1) 1/ ψ(x,y,z,t)... función (compleja) de onda V(x,y,z)... función de energía potencial ψ (x,y,z,t)... puede
Ecuación n de Schrödinger -h ( Ψ Ψ Ψ ) m Ψ +V(x,y,z).ψ(x,y,z,t) = i.h x y z t h = h / π i = (-1) 1/ ψ(x,y,z,t)... función (compleja) de onda V(x,y,z)... función de energía potencial ψ (x,y,z,t)... puede
Electromagnetismo. Introducción. Líneas de campo magnético. Experimento de Oersted. El campo magnético de las corrientes estacionarias
 El campo magnético de las corrientes estacionarias Electromagnetismo Andrés Cantarero Sáez Curso 25-26 Grupo C ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo
El campo magnético de las corrientes estacionarias Electromagnetismo Andrés Cantarero Sáez Curso 25-26 Grupo C ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo
Deformaciones. Contenidos
 Lección 2 Deformaciones Contenidos 2.1. Concepto de deformación................... 14 2.2. Deformación en el entorno de un punto.......... 15 2.2.1. Vector deformación. Componentes intrínsecas........
Lección 2 Deformaciones Contenidos 2.1. Concepto de deformación................... 14 2.2. Deformación en el entorno de un punto.......... 15 2.2.1. Vector deformación. Componentes intrínsecas........
UNIVERSIDAD SANTO TOMAS SECCIONAL BUCARAMANGA. División de Ingenierías - Facultad de Química Ambiental
 UNIVERSIDAD SANTO TOMAS SECCIONAL BUCARAMANGA División de Ingeniería Facultad de Química Ambiental Nombre de Asignatura: QUÍMICA CUÁNTICA Àrea: Básicas de Química Fisicoquímica Créditos: 3 Modalidad: Teórica
UNIVERSIDAD SANTO TOMAS SECCIONAL BUCARAMANGA División de Ingeniería Facultad de Química Ambiental Nombre de Asignatura: QUÍMICA CUÁNTICA Àrea: Básicas de Química Fisicoquímica Créditos: 3 Modalidad: Teórica
El espacio R n. Tema El conjunto R n El espacio vectorial R n
 Tema 1 El espacio R n En este primer tema de la asignatura recordaremos algunos conceptos ya estudiados acerca del conjunto R n y las estructuras sobre él definidas. Se presentarán por tanto bastantes
Tema 1 El espacio R n En este primer tema de la asignatura recordaremos algunos conceptos ya estudiados acerca del conjunto R n y las estructuras sobre él definidas. Se presentarán por tanto bastantes
Espectroscopía atómica
 C A P Í T U L O 6 Espectroscopía atómica 6.. ENUNCIADOS Y SOLUCIONES DE LOS PROBLEMAS PROBLEMAS 6. Demuestre la regla de selección angular del átomo hidrogenoide m = 0, ±. Para m m 2π 0 e im Φ e imφ dφ
C A P Í T U L O 6 Espectroscopía atómica 6.. ENUNCIADOS Y SOLUCIONES DE LOS PROBLEMAS PROBLEMAS 6. Demuestre la regla de selección angular del átomo hidrogenoide m = 0, ±. Para m m 2π 0 e im Φ e imφ dφ
Apuntes del Modelo del átomo hidrogenoide.
 Apuntes del Modelo del átomo hidrogenoide. Dr. Andrés Soto Bubert Un átomo hidrogenoide es aquel que tiene un solo electrón de carga e, rodeando un núcleo de carga +Ze. Átomos que cumplen esta descripción
Apuntes del Modelo del átomo hidrogenoide. Dr. Andrés Soto Bubert Un átomo hidrogenoide es aquel que tiene un solo electrón de carga e, rodeando un núcleo de carga +Ze. Átomos que cumplen esta descripción
SEMINARIO 1: ELEMENTOS DIFERENCIALES DE LÍNEA, SUPERFICIE Y VOLUMEN
 SEMINARIO 1: ELEMENTOS DIFERENCIALES DE LÍNEA, SUPERFICIE Y VOLUMEN Sistemas de coordenadas 3D Transformaciones entre sistemas Integrales de línea y superficie SISTEMA COORDENADO CARTESIANO O RECTANGULAR
SEMINARIO 1: ELEMENTOS DIFERENCIALES DE LÍNEA, SUPERFICIE Y VOLUMEN Sistemas de coordenadas 3D Transformaciones entre sistemas Integrales de línea y superficie SISTEMA COORDENADO CARTESIANO O RECTANGULAR
Anuladores. Objetivos. Definir el concepto de anuladores y estudiar sus propiedades principales.
 Anuladores Objetivos. Definir el concepto de anuladores y estudiar sus propiedades principales. Requisitos. Espacio dual, espacio bidual, base dual.. Definición (anulador de un subconjunto de un espacio
Anuladores Objetivos. Definir el concepto de anuladores y estudiar sus propiedades principales. Requisitos. Espacio dual, espacio bidual, base dual.. Definición (anulador de un subconjunto de un espacio
Tema 14 Mecánica Cuántica
 Tema 14 Mecánica Cuántica 1 14.1 Fundamentos de la mecánica cuántica 14. La ecuación de Schrödinger 14.3 Significado físico de la función de onda 14.4 Soluciones de la ecuación de Schrödinger para el átomo
Tema 14 Mecánica Cuántica 1 14.1 Fundamentos de la mecánica cuántica 14. La ecuación de Schrödinger 14.3 Significado físico de la función de onda 14.4 Soluciones de la ecuación de Schrödinger para el átomo
Fotones, electrones, y. partículas cuánticas ó paquetes de onda
 Fotones, electrones, y. partículas cuánticas ó paquetes de onda Larrondo 2009 Dualidad onda partícula Se difractan si interactúan con objetos de tamaño comparable con su λ. Es decir en ese caso se comportan
Fotones, electrones, y. partículas cuánticas ó paquetes de onda Larrondo 2009 Dualidad onda partícula Se difractan si interactúan con objetos de tamaño comparable con su λ. Es decir en ese caso se comportan
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1. Se llama producto escalar sobre un espacio vectorial real V a cualquier aplicación
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 6 Espacios euclídeos 6.1 Producto escalar. Espacio euclídeo Se llama producto escalar sobre un espacio vectorial real V a cualquier aplicación
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 6 Espacios euclídeos 6.1 Producto escalar. Espacio euclídeo Se llama producto escalar sobre un espacio vectorial real V a cualquier aplicación
Universidad Nacional Autónoma de México Facultad de Ciencias Geometría Analítica II Tarea 1
 Universidad Nacional Autónoma de México Facultad de Ciencias Geometría Analítica II Tarea. Completa las igualdades usando el dibujo. γ β = α β = β + θ = θ + ε + ω = θ + ε = β + θ + ω = α + ε = β + δ =.
Universidad Nacional Autónoma de México Facultad de Ciencias Geometría Analítica II Tarea. Completa las igualdades usando el dibujo. γ β = α β = β + θ = θ + ε + ω = θ + ε = β + θ + ω = α + ε = β + δ =.
Rotación de moléculas diatómicas
 Rotación de moléculas diatómicas Química Física Aplicada, UAM 23 de enero de 2011 (Química Física Aplicada, UAM) Rotación de moléculas diatómicas 23 de enero de 2011 1 / 29 Movimiento nuclear en moléculas
Rotación de moléculas diatómicas Química Física Aplicada, UAM 23 de enero de 2011 (Química Física Aplicada, UAM) Rotación de moléculas diatómicas 23 de enero de 2011 1 / 29 Movimiento nuclear en moléculas
, SZ } como. i de estados propios de { ˆ s
 Función de onda de spin de una partícula de spin S Si ψ es la función de onda de spin de una partícula de spin S, puede expandirse en la base Sσ de estados propios de {ˆ S, SZ } como ψ = S σ= S C σ Sσ.
Función de onda de spin de una partícula de spin S Si ψ es la función de onda de spin de una partícula de spin S, puede expandirse en la base Sσ de estados propios de {ˆ S, SZ } como ψ = S σ= S C σ Sσ.
Principios de Estructura de la Materia Equipo 4. Solución de la ecuación de Schrödinger para un rotor rígido
 Principios de Estructura de la Materia Equipo 4 Ramírez Palma Lillian Gisela Rendón Gaytán Fernando Torres Alcalá Andrea Villanueva Sánchez Luis Felipe Solución de la ecuación de Schrödinger para un rotor
Principios de Estructura de la Materia Equipo 4 Ramírez Palma Lillian Gisela Rendón Gaytán Fernando Torres Alcalá Andrea Villanueva Sánchez Luis Felipe Solución de la ecuación de Schrödinger para un rotor
FÍSICA MODERNA FÍSICA CUÁNTICA. José Luis Rodríguez Blanco
 FÍSICA MODERNA FÍSICA CUÁNTICA José Luis Rodríguez Blanco CRISIS DE LA FÍSICA CLÁSICA Problemas de la Física Clásica a finales del siglo XIX, principios del XX Espectros discontinuos de gases Efecto fotoeléctrico
FÍSICA MODERNA FÍSICA CUÁNTICA José Luis Rodríguez Blanco CRISIS DE LA FÍSICA CLÁSICA Problemas de la Física Clásica a finales del siglo XIX, principios del XX Espectros discontinuos de gases Efecto fotoeléctrico
Cálculo diferencial e integral 3
 Cálculo diferencial e integral 3 Guía 1 1. Sean a 1,..., a n R n. Demuestra que el conjunto { W = x = (x 1,..., x n ) R n es un subespacio vectorial de R n. } n a i x i = 0 i=1 2. Sean W y V subespacios
Cálculo diferencial e integral 3 Guía 1 1. Sean a 1,..., a n R n. Demuestra que el conjunto { W = x = (x 1,..., x n ) R n es un subespacio vectorial de R n. } n a i x i = 0 i=1 2. Sean W y V subespacios
