CRITERIO DE ESTABILIDAD DE ROUTH
|
|
|
- Teresa Parra Montes
- hace 7 años
- Vistas:
Transcripción
1 CRITERIO DE ESTABIIDAD DE ROUTH INGENIERÍA DE CONTRO.C. EIZABETH GPE. ARA HDZ.
2 INGENIERÍA DE CONTRO.C. EIZABETH GPE. ARA HDZ. Criterio e etili e Routh-Hurwitz El prolem má importte e lo item e otrol liel tiee que ver o l etili. U item e otrol e etle i y ólo i too lo polo e lzo erro e euetr e el emiplo izquiero el plo. Coieremo l iguiete fuió e trferei e lzo erro. ( ) ( ) ( ) ( ) A B R C m m m m E oe l y l o otte y m. Criterio e etili e Routh. El riterio e etili e Routh permite etermir l ti e polo e lzo erro que e euetr e el emiplo ereho el plo (ríe poitiv) i teer que ftorizr el poliomio. Ete riterio e etili ólo e pli lo poliomio o u ti fiit e térmio. Proeimieto e el riterio e etili e Routh:. Eri el poliomio e el eomior e l form iguiete: E oe lo oefiiete o tie rele. Supoemo que ; e eir e elimi ulquier ríz ero.. Si lguo e lo oefiiete e ero o egtivo te l preei e l meo u oefiiete poitivo hy u ríz o ríe imgiri o que tiee prte rele poitiv. E tl o el item o e etle. oiió eeri pero o ufiiete pr l etili e que too lo oefiiete e l euió eté preete y teg igo poitivo.. Si too lo oefiiete o poitivo oree lo oefiiete el poliomio e regloe y olum e uero o el ptró o rreglo iguiete: 6 g f e e o oefiiete et. e evlú el moo iguiete:
3 INGENIERÍA DE CONTRO.C. EIZABETH GPE. ARA HDZ. 6 evluió otiú ht que to l rette o ero. El riterio e etili e Routh- Hurwitz plte que el úmero e ríe e l euió o prte rele poitiv e igul l úmero e mio e igo e lo oefiiete e l primer olum el rreglo. oiió eeri y ufiiete pr que to l ríe e l euió e euetre e el emiplo izquiero el plo e que too lo oefiiete e l euió e poitivo y que too lo térmio e l primer olum el rreglo teg igo poitivo. Ejemplo Coiere el poliomio iguiete: o primero o regloe e otiee iretmete el poliomio o. El rreglo e oefiiete erí 6 Hy o mio e igo e lo oefiiete e l primer olum. Eto igifi que exite o ríe o prte rele poitiv. Oerve que el reulto o e moifi uo lo oefiiete e ulquier regló e multipli por o e ivie etre u úmero poitivo pr implifir el álulo.
4 Ejemplo Apliió el riterio e etili e Routh l álii e u item e otrol. Coiere el item e l figur. Determie el rgo e vlore e pr l etili. fuió e trferei e lzo erro e C R ( ) ( ) ( )( ) euió rteríti e El rreglo e oefiiete e ovierte e 9 Pr l etili ee er poitiv y too lo oefiiete e l primer olum ee e erlo tmié. 9 > > Por tto pr que el item e otrol e etle el rgo e erí Cuo 9 9 > > el Coefiiete e l primer olum e l fil e he ero eto igifi que exite ríe imgiri y el item e vuelve oiltorio y mtemátimete l oilió e mtiee e u mplitu otte. Se puee lulr l ríe imgiri oiero u poliomio uxilir el uál e otiee tomo lo oefiiete e l fil que e euetr rri oe e geeró el ero. euió erí ± 9 ±.86 j omo 9 INGENIERÍA DE CONTRO.C. EIZABETH GPE. ARA HDZ.
5 Co epeile Si el térmio e l primer olum e ulquier regló e ero pero lo térmio rette o o ero o o hy térmio rette el térmio ero e utituye o u úmero poitivo muy pequeño ε y e evlú el reto el rreglo. Ejemplo oiere l euió El rreglo e oefiiete e ε Si el igo el oefiiete que etá eim el ero ( ε ) e igul l igo que etá jo e él quiere eir que hy u pr e ríe imgiri. Ejemplo Si too lo oefiiete e ulquier regló o ero igifi que exite ríe o mgitue igule y igo opueto y/o o ríe imgiri ojug. E ete o l evluió el reto el rreglo otiú meite l formió e u poliomio uxilir o lo oefiiete el último regló y meite el empleo e lo oefiiete e l eriv e ete poliomio e el regló iguiete. Tle ríe e euetr epejo el poliomio uxilir que iempre e pr. Pr u poliomio uxilir e gro exite pre e ríe igule y opuet. Por ejemplo oiere l euió: El rreglo e oefiiete e 8 8 Poliomio uxilir P Regló ero ( ) Too lo térmio el regló oefiiete el regló o ero. Depué e form el poliomio uxilir prtir e lo P e El poliomio uxilir ( ) P ( ) 8 lo ul ii que hy o pre e ríe e igul mgitu y igo opueto. Eto pre e otiee reolvieo l euió el poliomio uxilir ( ) P o repeto e P. eriv e ( ) ( ) P 8 96 INGENIERÍA DE CONTRO.C. EIZABETH GPE. ARA HDZ.
6 o oefiiete e l últim euió utituye lo térmio el regló el rreglo. Por oiguiete el rreglo e oefiiete e ovierte e ( ) P Coefiiete e No exite mio e igo e l primer olum o hy ríe o prte rel poitiv i emrgo i hy ríe imgiri. Depejo l ríe el poliomio uxilir Oteemo P ( ) 8 ± j.86 ± j.6 INGENIERÍA DE CONTRO 6.C. EIZABETH GPE. ARA HDZ.
7 Ejemplo Determie el rgo e vlore e pr l etili. euió rteríti e El rreglo e oefiiete e ovierte e ( ) Pr l etili ee er poitiv y too lo oefiiete e l primer olum ee e erlo tmié. > > < 6 Por tto pr que el item e otrol e etle el rgo e erí < < 6 Cuo 6 el item e vuelve oiltorio y mtemátimete l oilió e mtiee e u mplitu otte. INGENIERÍA DE CONTRO.C. EIZABETH GPE. ARA HDZ.
8 Ejemplo 6 Determie l etili pr iguiete item euió rteríti e El rreglo e oefiiete e ovierte e ε 6 ε ε ε 6 ε 6 Como el igo rri y jo e ε o iferete exite o mio e igo e lo oefiiete e l primer olum hy o ríe o prte rel poitiv el item e ietle INGENIERÍA DE CONTRO 8.C. EIZABETH GPE. ARA HDZ.
9 Ejemplo Determie l etili pr iguiete item euió rteríti e El rreglo e oefiiete e Poliomio uxilir P( ) Too lo térmio el regló oefiiete el regló o ero. Etoe e form el poliomio uxilir prtir e lo El poliomio uxilir P( ) P e ( ) 6 lo ul ii que hy o ríe e igul mgitu y igo opueto. eriv e P ( ) o repeto e ( ) P o oefiiete el regló e l euió e utituye por el poliomio etermio. Por oiguiete el rreglo e oefiiete e ovierte e ( ) P Coefiiete e Exite o mio e igo e l primer olum hy o ríe o prte rel poitiv. Pero tmié exite ríe imgiri por el ero que e formó e el regló Depejo l ríe el poliomio uxilir P ( ) 6 Oteemo l o ríe imgiri ± j. INGENIERÍA DE CONTRO 9.C. EIZABETH GPE. ARA HDZ.
10 Prolem De l iguiete euioe rteríti etermie l etili el item (o ) 6. INGENIERÍA DE CONTRO.C. EIZABETH GPE. ARA HDZ.
Estabilidad en el Plano Complejo
 Cpítulo Etili e el Plo Complejo Itrouió L etili e u item liel e lzo erro e etermi prtir e l uiió e lo polo e lzo erro e el plo Si lguo e eto polo e euetr e el emiplo ereho el plo, etoe oforme umet el tiempo,
Cpítulo Etili e el Plo Complejo Itrouió L etili e u item liel e lzo erro e etermi prtir e l uiió e lo polo e lzo erro e el plo Si lguo e eto polo e euetr e el emiplo ereho el plo, etoe oforme umet el tiempo,
Criterios de Estabilidad de Routh y Jury. M.I. Ricardo Garibay Jimenez 2006
 Criterio de Etbilidd de Routh y Jury M.I. Rirdo Griby Jimeez 6 Criterio de Routh U poliomio (... A tiee ríe etble (o prte rel egtiv i e umple odiioe. Neeidd todo lo oefiiete y o poitivo Sufiiei El igo
Criterio de Etbilidd de Routh y Jury M.I. Rirdo Griby Jimeez 6 Criterio de Routh U poliomio (... A tiee ríe etble (o prte rel egtiv i e umple odiioe. Neeidd todo lo oefiiete y o poitivo Sufiiei El igo
ESTABILIDAD. estable, si sometido a una perturbación, éste, luego de un tiempo, vuelve a su
 ESTABIIDAD El álii de lo ite de otrol e e gr prte e el ooiieto de u etilidd olut y reltiv ESTABIIDAD ABSOUTA: u ite liel ivrite e el tiepo e etle, i oetido u perturió, éte, luego de u tiepo, vuelve u odiió
ESTABIIDAD El álii de lo ite de otrol e e gr prte e el ooiieto de u etilidd olut y reltiv ESTABIIDAD ABSOUTA: u ite liel ivrite e el tiepo e etle, i oetido u perturió, éte, luego de u tiepo, vuelve u odiió
Criterio de Estabilidad de Routh-Hurwitz
 Criterio de Etbilidd de Routh-Hurwitz F Pr l etbilidd BIBO, l ríce de l ecució crcterític, o lo polo de C()/R(), o puede etr loclizdo e el emiplo derecho del plo o e eje j, todo debe quedr e el emiplo
Criterio de Etbilidd de Routh-Hurwitz F Pr l etbilidd BIBO, l ríce de l ecució crcterític, o lo polo de C()/R(), o puede etr loclizdo e el emiplo derecho del plo o e eje j, todo debe quedr e el emiplo
Definiciones de estabilidad BIBO
 Tem. Etilidd de Sitem Itroducció TEORÍA DE ONTROL L oció de etilidd e fudmetl e el derrollo de item de cotrol y e prticulr pr lo item retrolimetdo. L ueci de et propiedd vuelve iútil e l práctic culquier
Tem. Etilidd de Sitem Itroducció TEORÍA DE ONTROL L oció de etilidd e fudmetl e el derrollo de item de cotrol y e prticulr pr lo item retrolimetdo. L ueci de et propiedd vuelve iútil e l práctic culquier
Criterio de Estabilidad de Routh-Hurwitz
 Criterio de Etbilidd de Routh-Hurwitz F Pr l etbilidd BIBO, l ríce de l ecució crcterític +G()H() =, o lo polo de C()/R(), o puede etr loclizdo e el emiplo derecho del plo o e eje j, todo debe quedr e
Criterio de Etbilidd de Routh-Hurwitz F Pr l etbilidd BIBO, l ríce de l ecució crcterític +G()H() =, o lo polo de C()/R(), o puede etr loclizdo e el emiplo derecho del plo o e eje j, todo debe quedr e
Teoría de Sistemas y Señales
 Teorí de Sitem y Señle Criterio lgerio de etilidd Criterio de Routh Autor Dr. Jun Crlo Gómez Criterio Algerio de Etilidd pr SE en TC Promo que l ondiión neeri y ufiiente pr que un SE en TC repreentdo por
Teorí de Sitem y Señle Criterio lgerio de etilidd Criterio de Routh Autor Dr. Jun Crlo Gómez Criterio Algerio de Etilidd pr SE en TC Promo que l ondiión neeri y ufiiente pr que un SE en TC repreentdo por
ESTABILIDAD. 1. Concepto de estabilidad. 2. Criterio de Routh-Hurwitz. Métodos algebraicos para el análisis de estabilidad.
 Uiveridd Crlo III de Mdrid Señle y Sitem ESTABILIDAD Método lgerio pr el álii de etilidd.. Coepto de etilidd.. Criterio de Roth-Hrwitz. Dolore Blo, Rmó Brer, Mrí Mlfz y Migel Ágel Slih Uiveridd Crlo III
Uiveridd Crlo III de Mdrid Señle y Sitem ESTABILIDAD Método lgerio pr el álii de etilidd.. Coepto de etilidd.. Criterio de Roth-Hrwitz. Dolore Blo, Rmó Brer, Mrí Mlfz y Migel Ágel Slih Uiveridd Crlo III
MATEMÁTICAS 2º DE ESO LOE
 MATEMÁTICAS º DE ESO LOE TEMA II: FRACCIONES Los sigifios e u frió. Frioes propis e impropis. Equivlei e frioes. Amplifiió y simplifiió. Frió irreuile. Reuió e frioes omú eomior. Comprió e frioes. Operioes
MATEMÁTICAS º DE ESO LOE TEMA II: FRACCIONES Los sigifios e u frió. Frioes propis e impropis. Equivlei e frioes. Amplifiió y simplifiió. Frió irreuile. Reuió e frioes omú eomior. Comprió e frioes. Operioes
tiene derivada continua hasta de orden 1
 Cálulo Numério Progrmió Apli INTERPOLACIÓN SEGMENTARIA O SPLINES L otruió e poliomio e iterpolió e gro lto uque utifile teórimete plte muo prolem Por u lo, l form e l fuió poliómi e gro lto meuo o repoe
Cálulo Numério Progrmió Apli INTERPOLACIÓN SEGMENTARIA O SPLINES L otruió e poliomio e iterpolió e gro lto uque utifile teórimete plte muo prolem Por u lo, l form e l fuió poliómi e gro lto meuo o repoe
Algunas propiedades de los Números reales. Números reales (R) c d
 Profesoro e Nivel Meio y Superior e Biologí Mtemáti º Cutrimestre Año 0 Prof. Mrí Ele Ruiz Algus propiees e los Números reles (Este mteril tiee omo ojeto presetr u seleió e oeptos orrespoietes l Ui, pr
Profesoro e Nivel Meio y Superior e Biologí Mtemáti º Cutrimestre Año 0 Prof. Mrí Ele Ruiz Algus propiees e los Números reles (Este mteril tiee omo ojeto presetr u seleió e oeptos orrespoietes l Ui, pr
Operaciones con Fracciones
 Operioes o Frioes Reuió e frioes Frioes o igul eomior: De os frioes que tiee el mismo eomior es meor l que tiee meor umeror. Frioes o igul umeror: De os frioes que tiee el mismo umeror es meor l que tiee
Operioes o Frioes Reuió e frioes Frioes o igul eomior: De os frioes que tiee el mismo eomior es meor l que tiee meor umeror. Frioes o igul umeror: De os frioes que tiee el mismo umeror es meor l que tiee
Sucesiones. Universidad Diego Portales CALCULO II
 Suesioes Uiversidd Diego Portles U suesió se puede defiir omo u list de úmeros esritos e orde defiido:,,,...,,... El úmero es el primer térmio;, el segudo térmio y e geerl, es el -ésimo térmio. Cosiderremos
Suesioes Uiversidd Diego Portles U suesió se puede defiir omo u list de úmeros esritos e orde defiido:,,,...,,... El úmero es el primer térmio;, el segudo térmio y e geerl, es el -ésimo térmio. Cosiderremos
tiene dimensión 3 2. El elemento a 21 = 3.
 Tem. MTRICES Defiiió e mtriz U mtriz e imesió m es u ojuto e úmeros ispuestos e fils y m olums. sí:... m... m : : : :... m L mtriz terior tmié se puee eotr por ( ) m El elemeto ij es el que oup l fil i
Tem. MTRICES Defiiió e mtriz U mtriz e imesió m es u ojuto e úmeros ispuestos e fils y m olums. sí:... m... m : : : :... m L mtriz terior tmié se puee eotr por ( ) m El elemeto ij es el que oup l fil i
( ) ( ) El principio de inducción
 El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
En resumen, en las raíces de la ecuación característica está la información sobre el patrón de la respuesta temporal de un sistema.
 Aálii Culittivo l Rput mporl u Sitm Si oo l fuió trfri G() u o itm y l tr x(t), pu vlur l li y(t) prtir : hio lugo l trformió ivr: y(t) y() G() x() L y() L G( ) x() L fuió trfri G() pu xprr omo u oit poliomio
Aálii Culittivo l Rput mporl u Sitm Si oo l fuió trfri G() u o itm y l tr x(t), pu vlur l li y(t) prtir : hio lugo l trformió ivr: y(t) y() G() x() L y() L G( ) x() L fuió trfri G() pu xprr omo u oit poliomio
Integrales Dobles. Vimos que este problema estaba relacionado con el cálculo de una primitiva de
 Pro. Erique Mteus Nieves otoro e Euió Mtemáti Itegrles oles Itrouió. E el primer urso e Fumetos se plteó el prolem e hllr el áre omprei etre l grái e u uió positiv y x, el eje OX y ls rets x, x. ih áre
Pro. Erique Mteus Nieves otoro e Euió Mtemáti Itegrles oles Itrouió. E el primer urso e Fumetos se plteó el prolem e hllr el áre omprei etre l grái e u uió positiv y x, el eje OX y ls rets x, x. ih áre
UNIDAD 1.- Números reales (temas 1 del libro)
 UNIDAD.- Núeros reles (tes el libro). NUMEROS NATURALES Y ENTEROS Co los úeros turles otos los eleetos e u ojuto (úero ril). O bie expresos l posiió u ore que oup u eleeto e u ojuto (oril). Se represet
UNIDAD.- Núeros reles (tes el libro). NUMEROS NATURALES Y ENTEROS Co los úeros turles otos los eleetos e u ojuto (úero ril). O bie expresos l posiió u ore que oup u eleeto e u ojuto (oril). Se represet
TEMA 2: NÚMEROS RACIONALES: FRACCIONES.
 TEMA NÚMEROS RACIONALES FRACCIONES.. Cojuto e los Núeros Rioles, Q. El ojuto e los úeros rioles es u pliió e los úeros eteros, los que se le ñe uevos úeros que se ostruye o úeros eteros y se ll FRACCIONES.
TEMA NÚMEROS RACIONALES FRACCIONES.. Cojuto e los Núeros Rioles, Q. El ojuto e los úeros rioles es u pliió e los úeros eteros, los que se le ñe uevos úeros que se ostruye o úeros eteros y se ll FRACCIONES.
COSAS DE DIVISORES Y HOTELES
 COSAS DE DIVISORES Y HOTELES E est sesió trtremos de resolver el siguiete rolem: Prolem: El hotel de ls mil hitioes. Cuet ue e ierto ís hí u gr hotel ue teí 000 hitioes y otros ttos emledos. Estos, u dí
COSAS DE DIVISORES Y HOTELES E est sesió trtremos de resolver el siguiete rolem: Prolem: El hotel de ls mil hitioes. Cuet ue e ierto ís hí u gr hotel ue teí 000 hitioes y otros ttos emledos. Estos, u dí
Clase 16. Tema: Racionalización de expresiones. Matemáticas 9. Bimestre: I Número de clase: 16. Tipo 1. Esta clase tiene video.
 Bimestre: I Número de lse: 16 Mtemátis Clse 16 Est lse tiee video Tem: Riolizió de expresioes Atividd 46 1 Le l siguiete iformió sore l riolizió. E mtemátis es omú eotrros o expresioes rioles que otiee
Bimestre: I Número de lse: 16 Mtemátis Clse 16 Est lse tiee video Tem: Riolizió de expresioes Atividd 46 1 Le l siguiete iformió sore l riolizió. E mtemátis es omú eotrros o expresioes rioles que otiee
1) CONCEPTOS 2) MONOMIOS TEMA : EXPRESIONES ALGEBRAICAS
 TEMA EXPRESIONES ALGEBRAICAS CONCEPTOS U EXPRESIÓN ALGEBRAICA es el ojuto e úmeros letrs que se omi o los sigos e ls operioes mtemátis sum, rest, multipliió, ivisió poteiió. Ejemplo El VALOR NUMÉRICO e
TEMA EXPRESIONES ALGEBRAICAS CONCEPTOS U EXPRESIÓN ALGEBRAICA es el ojuto e úmeros letrs que se omi o los sigos e ls operioes mtemátis sum, rest, multipliió, ivisió poteiió. Ejemplo El VALOR NUMÉRICO e
RADICALES. 1.2.1 Teorema fundamental de la radicación. 1.2.3 Reducción de radicales a índice común. 1.2.4 Potenciación de exponente fraccionario
 RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
3. Se ha observado que el acero de compresión contribuye a reducir las Deformaciones a Largo Plazo.
 VIGS RENGULRES DOBLEENE RDS. El ero de ompreió vee e eerio por:. L dimeioe de l eió o retrigid por oiderioe rquitetói. E ete o, el oreto e ompreió o e pz de reitir el mometo tute por lo tto, e ñde ero
VIGS RENGULRES DOBLEENE RDS. El ero de ompreió vee e eerio por:. L dimeioe de l eió o retrigid por oiderioe rquitetói. E ete o, el oreto e ompreió o e pz de reitir el mometo tute por lo tto, e ñde ero
FUNDAMENTOS DE MATEMÁTICA MATERIAL CON FINES DIDÁCTICOS UNEFA NÚCLEO TÁCHIRA PRODUCTOS NOTABLES.
 PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
Tema 4. Análisis de la Respuesta Temporal de Sistemas LTI. Automática. 2º Curso del Grado en Ingeniería en Tecnología Industrial
 Deprtmeto de Igeierí de Sitem y Automátic Tem 4. Aálii de l Repuet Temporl de Sitem LTI Automátic º Curo del Grdo e Igeierí e Tecologí Idutril Deprtmeto de Igeierí de Sitem y Automátic Coteido Tem 4.-
Deprtmeto de Igeierí de Sitem y Automátic Tem 4. Aálii de l Repuet Temporl de Sitem LTI Automátic º Curo del Grdo e Igeierí e Tecologí Idutril Deprtmeto de Igeierí de Sitem y Automátic Coteido Tem 4.-
Matemáticas II (Bachillerato de Ciencias). Soluciones de los problemas propuestos. Tema 1 1. TEMA 1. Matrices Problemas Resueltos.
 Meáis (hillero e ieis) Soluioes e los proles propuesos Te wwweisjo José Mrí Mríez Meio TEM Mries Proles Resuelos Operioes o ries Ds, y, hll os úeros y pr que se verifique que Soluió Esriieo l euió exei
Meáis (hillero e ieis) Soluioes e los proles propuesos Te wwweisjo José Mrí Mríez Meio TEM Mries Proles Resuelos Operioes o ries Ds, y, hll os úeros y pr que se verifique que Soluió Esriieo l euió exei
Análisis de Sistemas Lineales. Modelado en variables de fase
 Aálii e Sitem Liele Moelo e vrile e fe A B Coteio C D Moelo e vrile e fe Co : Si eriv e l fció e etr Co : Co geerl Ejemplo ejercicio Moelo e vrile e fe A B pr el co, q C D E moelo e vrile e eto, e el cl
Aálii e Sitem Liele Moelo e vrile e fe A B Coteio C D Moelo e vrile e fe Co : Si eriv e l fció e etr Co : Co geerl Ejemplo ejercicio Moelo e vrile e fe A B pr el co, q C D E moelo e vrile e eto, e el cl
D E T E R M I N A N T E S M A T R I Z I N V E R S A
 º DE BACHILLERATO DETERMINANTES D E T E R M I N A N T E S ----------- M A T R I Z I N V E R S A DETERMINANTES I. Determites. II. Primers pliioes de los determites. I. Determites.. Defiió álulo de u determite.
º DE BACHILLERATO DETERMINANTES D E T E R M I N A N T E S ----------- M A T R I Z I N V E R S A DETERMINANTES I. Determites. II. Primers pliioes de los determites. I. Determites.. Defiió álulo de u determite.
Tema 2 Sucesiones Matemáticas I 1º Bachillerato. 1
 Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
1. Números reales. 2. Raíces y potencias. 3. Operaciones con radicales. Matemáticas 4º ESO
 Mteátis º ESO 1. Núeros reles Clsifiió de los úeros reles Frió geertriz de u úero deil Reresetió de úeros rioles e l ret rel Aroxiioes Itervlos. Ríes y oteis Proieddes de ls oteis de exoete riol Rdiles
Mteátis º ESO 1. Núeros reles Clsifiió de los úeros reles Frió geertriz de u úero deil Reresetió de úeros rioles e l ret rel Aroxiioes Itervlos. Ríes y oteis Proieddes de ls oteis de exoete riol Rdiles
CURIOSIDADES MATEMATICAS EL TRIANGULO DE PASCAL GENERALIZADO
 CURIOSIDADES MATEMATICAS EL TRIANGULO DE PASCAL GENERALIZADO JOSÉ FRANCISCO LEGUIZAMÓN ROMERO GRUPO DE INVESTIGACIÓN PIRÁMIDE LÍNEA MEDIOS EDUCATIVOS EN MATEMÁTICAS FACULTAD DE CIENCIAS DE LA EDUCACIÓN
CURIOSIDADES MATEMATICAS EL TRIANGULO DE PASCAL GENERALIZADO JOSÉ FRANCISCO LEGUIZAMÓN ROMERO GRUPO DE INVESTIGACIÓN PIRÁMIDE LÍNEA MEDIOS EDUCATIVOS EN MATEMÁTICAS FACULTAD DE CIENCIAS DE LA EDUCACIÓN
entonces A.B es: A) 4 B) 2 C) 1 D) 1/2 E) 1/4 a b. a b a b 4... Calcula: A) 1 B) 2 C) 2 D) 3 E) 2 2 x x A) 1 B) x C) A) 7 B) 8 C) 9 D) 10 E) 6
 Rzomieto Lógio. Efetú: E = ÁLGEBRA DOENTE: Dr. Rihrd Herrer A. TEORIA DE EXPONENTES 8 A 0, B 0, D E 6. Simplifi: 6..80 9..0 A B D E. Hll el vlor de: M A B 6 D / E. Simplifi: ; si: > 0 A B D E. lul: S :
Rzomieto Lógio. Efetú: E = ÁLGEBRA DOENTE: Dr. Rihrd Herrer A. TEORIA DE EXPONENTES 8 A 0, B 0, D E 6. Simplifi: 6..80 9..0 A B D E. Hll el vlor de: M A B 6 D / E. Simplifi: ; si: > 0 A B D E. lul: S :
TECNOLOGÍA ELÉCTRICA. UNIDAD DIDÁCTICA 1 CONCEPTOS BÁSICOS Y PROBLEMAS RESUELTOS
 L Uiversidd er TECNOLOGÍA ELÉCTRICA. UNIDAD DIDÁCTICA 1 CONCEPTOS BÁSICOS Y PROBLEMAS RESUELTOS 1.- POTENCIA EN SISTEMAS DE CORRIENTE ALTERNA E los iruitos de orriete lter, l produto etre tesió e itesidd
L Uiversidd er TECNOLOGÍA ELÉCTRICA. UNIDAD DIDÁCTICA 1 CONCEPTOS BÁSICOS Y PROBLEMAS RESUELTOS 1.- POTENCIA EN SISTEMAS DE CORRIENTE ALTERNA E los iruitos de orriete lter, l produto etre tesió e itesidd
Matrices. Matrices especiales
 UNIVERSIDD UÓNO DE NUEVO EÓN FUD DE INGENIERÍ EÁNI Y EÉRI tries triz: ojuto de eleetos ordedos e fils y olus os eleetos puede ser úeros reles o oplejos E este urso solo se osider tries o eleetos reles
UNIVERSIDD UÓNO DE NUEVO EÓN FUD DE INGENIERÍ EÁNI Y EÉRI tries triz: ojuto de eleetos ordedos e fils y olus os eleetos puede ser úeros reles o oplejos E este urso solo se osider tries o eleetos reles
. De manera sucesiva, si x se multiplica por si misma n veces, se
 Fcultd de Cotdurí Adiistrció UNAM Lees de eoetes ritos Autor: Dr José Muel Becerr Esios MATEMÁTICAS BÁSICAS LEYES DE EXPONENTES Y LOGARITMOS LEYES DE EXPONENTES Se u úero rel Si se ultilic or sí iso se
Fcultd de Cotdurí Adiistrció UNAM Lees de eoetes ritos Autor: Dr José Muel Becerr Esios MATEMÁTICAS BÁSICAS LEYES DE EXPONENTES Y LOGARITMOS LEYES DE EXPONENTES Se u úero rel Si se ultilic or sí iso se
MATEMÁTICAS LOS NÚMEROS REALES 4º DE ESO
 MATEMÁTICAS LOS NÚMEROS REALES º DE ESO 1. Núeros reles Clsifiió de los úeros reles Frió geertriz de u úero deil Reresetió de úeros rioles e l ret rel Aroxiioes Itervlos. Ríes y oteis Proieddes de ls oteis
MATEMÁTICAS LOS NÚMEROS REALES º DE ESO 1. Núeros reles Clsifiió de los úeros reles Frió geertriz de u úero deil Reresetió de úeros rioles e l ret rel Aroxiioes Itervlos. Ríes y oteis Proieddes de ls oteis
FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS PRODUCTOS NOTABLES
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS GRADO 8 TALLER Nº SEMESTRE II RESEÑA HISTÓRICA PRODUCTOS NOTABLES Psl, Blise (-: filósofo, mtemátio físio frés, osiderdo u de ls metes
FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS GRADO 8 TALLER Nº SEMESTRE II RESEÑA HISTÓRICA PRODUCTOS NOTABLES Psl, Blise (-: filósofo, mtemátio físio frés, osiderdo u de ls metes
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Determine las ecuaciones vectorial, paramétricas y simétricas de la recta que., siendo D(4, 0, -1) y T(2, -3, 1).
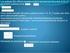 Vetores Cooreos Ilustrió 38 Determie ls euioes vetoril prmétris y simétris e l ret que ps por el puto A- 3 y es prlel l vetor DT sieo D4 0 - y T -3. Soluió Desigemos est ret por L A DT Se Px y z tl que
Vetores Cooreos Ilustrió 38 Determie ls euioes vetoril prmétris y simétris e l ret que ps por el puto A- 3 y es prlel l vetor DT sieo D4 0 - y T -3. Soluió Desigemos est ret por L A DT Se Px y z tl que
Tema 4. Análisis de la Respuesta Temporal de Sistemas LTI. Automática. 2º Curso del Grado en Ingeniería en Tecnología Industrial
 Tem 4. Aálii de l Repuet Temporl de Sitem LTI de Sitem y Automátic Automátic º Curo del Grdo e Igeierí e Tecologí Idutril Coteido de Sitem y Automátic Tem 4.- Aálii de l repuet temporl de item LTI 4..
Tem 4. Aálii de l Repuet Temporl de Sitem LTI de Sitem y Automátic Automátic º Curo del Grdo e Igeierí e Tecologí Idutril Coteido de Sitem y Automátic Tem 4.- Aálii de l repuet temporl de item LTI 4..
Licenciatura en Electrónica y Computación: Métodos Numéricos
 CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
POTENCIA DE UN NÚMERO.
 INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resoluió Nº de oviere./0 Seretri De Eduió Distritl REGISTRO DANE Nº00-00099 Teléfoo Brrio Bstids St Mrt DEPARTAMENTO DE MATEMATICAS DOCENTE: LIC-ING.
INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resoluió Nº de oviere./0 Seretri De Eduió Distritl REGISTRO DANE Nº00-00099 Teléfoo Brrio Bstids St Mrt DEPARTAMENTO DE MATEMATICAS DOCENTE: LIC-ING.
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES
 AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El siste e los úeros reles es u ojuto o vío eoto por o os operioes iters
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El siste e los úeros reles es u ojuto o vío eoto por o os operioes iters
2.- Dadas las matrices A y B. Calcula A+B, A-B, A 2, B 2, AB, BA
 ejeriiosemees.om MTRICES Y DETERMINNTES. Dds ls mtries Hllr ) ) B ).B d) B. e) +B f) C. g) C.B h) C.D i) j) B k) + l) B.B uioes. Dds ls mtries B. Clul +B, B,, B, B, B uió D C B.B / / / / / / / / B / /
ejeriiosemees.om MTRICES Y DETERMINNTES. Dds ls mtries Hllr ) ) B ).B d) B. e) +B f) C. g) C.B h) C.D i) j) B k) + l) B.B uioes. Dds ls mtries B. Clul +B, B,, B, B, B uió D C B.B / / / / / / / / B / /
(3x, 6y) = ( 1, 5): (2, y) = (6x, 6x 6y):
 . Reliz ls siguietes opeioes o pes uéios ) ( ) ( ) ) [ ( ) ( )] ½ ( ) 6 ( ) ) ( ) ( ) (6 ) ( ) ) (x y) (x y) ( ) ( ) Soluió. 6. ( ) ( ) ( 6 ( ) ) ( 9 7). [ ( ) ( )] ½ ( ) 6 ( ) ( ) ( ) (6 ) ( 6) ( ). (
. Reliz ls siguietes opeioes o pes uéios ) ( ) ( ) ) [ ( ) ( )] ½ ( ) 6 ( ) ) ( ) ( ) (6 ) ( ) ) (x y) (x y) ( ) ( ) Soluió. 6. ( ) ( ) ( 6 ( ) ) ( 9 7). [ ( ) ( )] ½ ( ) 6 ( ) ( ) ( ) (6 ) ( 6) ( ). (
Departamento de Ingenierías Eléctrica y Electrónica Universidad del Norte
 chritianq@uninorte.edu.co Departamento de Ingeniería Eléctrica y Electrónica Univeridad del Norte El problema má importante de lo itema de control lineal tiene que ver con la etabilidad. Un itema de control
chritianq@uninorte.edu.co Departamento de Ingeniería Eléctrica y Electrónica Univeridad del Norte El problema má importante de lo itema de control lineal tiene que ver con la etabilidad. Un itema de control
WhittiLeaks Los apuntes que ellos no quieren que sepas de
 Métodos umérios WittiLes Los putes que ellos o quiere que seps de ITBA mo 7 WittiLes Resume Métodos umérios Pso Pr u fuió defiid e u itervlo: f (, ) ( ) el pso se defie por: ; dode es l tidd de divisioes
Métodos umérios WittiLes Los putes que ellos o quiere que seps de ITBA mo 7 WittiLes Resume Métodos umérios Pso Pr u fuió defiid e u itervlo: f (, ) ( ) el pso se defie por: ; dode es l tidd de divisioes
En donde x representa la incógnita, y a, b y c son constantes.
 FUNCIÓN CUADRÁTICA. Cundo los elementos de un onjunto los elementos de un onjunto se soin medinte un regl de orrespondeni definid por un euión de segundo grdo en, l llmmos funión de segundo grdo o udráti.
FUNCIÓN CUADRÁTICA. Cundo los elementos de un onjunto los elementos de un onjunto se soin medinte un regl de orrespondeni definid por un euión de segundo grdo en, l llmmos funión de segundo grdo o udráti.
CONTROL II. Tema: CRITERIOSDE ESTABILIDAD ALGEBRAICOS: HURWITS Y ROUTH-HURWITZ. Prof. Ing. Carlos F. Martín
 CONTROL II Tem: CRITERIOSDE ESTABILIDAD ALGEBRAICOS: URWITS Y ROUT-URWITZ Prof Ig Crlo F Mrtí CONTROL II (Elo y Bio) Profeor Ig Crlo Frcico Mrtí Itroducció De lo etudio de l ecucioe diferecile liele co
CONTROL II Tem: CRITERIOSDE ESTABILIDAD ALGEBRAICOS: URWITS Y ROUT-URWITZ Prof Ig Crlo F Mrtí CONTROL II (Elo y Bio) Profeor Ig Crlo Frcico Mrtí Itroducció De lo etudio de l ecucioe diferecile liele co
Juan Antonio González Mota Profesor de Matemáticas del Colegio Juan XIII Zaidín de Granada
 Ju Atoio Goále Mot Profesor de Mtemátis del Colegio Ju XIII Zidí de Grd ESPACIOS VECTORIALES CONCEPTO DE ESPACIO VECTORIAL. Se V u ojuto ulquier R el ojuto de úmeros reles. E V defiimos dos lees de omposiió:
Ju Atoio Goále Mot Profesor de Mtemátis del Colegio Ju XIII Zidí de Grd ESPACIOS VECTORIALES CONCEPTO DE ESPACIO VECTORIAL. Se V u ojuto ulquier R el ojuto de úmeros reles. E V defiimos dos lees de omposiió:
Temario Curso Propedéutico de Matemáticas
 Terio Curso Propeéutio e Mteátis Sesió, Sesió Sesió.- El Cojuto e Núeros Reles. Operioes o úeros rioles. Propiees. Operioes leris. Su, Rest, Lees e los Epoetes pr el Prouto l Divisió Aleri. Sesió. -Riles
Terio Curso Propeéutio e Mteátis Sesió, Sesió Sesió.- El Cojuto e Núeros Reles. Operioes o úeros rioles. Propiees. Operioes leris. Su, Rest, Lees e los Epoetes pr el Prouto l Divisió Aleri. Sesió. -Riles
FUNCIONES POLINÓMICAS
 Prof.: Lui Tfererry FUNCIONES POLINÓMICAS POLINOMIOS Los poliomios so importtes. El volume de u ilidro r h y su áre totl es rh r. ic El pitl fil produido por u pitl C durte t meses l i% ul, es C. t. 00
Prof.: Lui Tfererry FUNCIONES POLINÓMICAS POLINOMIOS Los poliomios so importtes. El volume de u ilidro r h y su áre totl es rh r. ic El pitl fil produido por u pitl C durte t meses l i% ul, es C. t. 00
1, 4, 16, 64,. Cuál regla define esta sucesión? Puedes indicar los próximos dos elementos?
 UCEIONE Prof. Evel Dávil Cálculo Reviso ABRIL 0 U sucesió o sucesió cosiste e u eumerció o listo e elemetos los cules los escribe u regl o ptró por tto el ore e sus elemetos es fumetl.,,,,. Cuál regl efie
UCEIONE Prof. Evel Dávil Cálculo Reviso ABRIL 0 U sucesió o sucesió cosiste e u eumerció o listo e elemetos los cules los escribe u regl o ptró por tto el ore e sus elemetos es fumetl.,,,,. Cuál regl efie
Guía Práctica N 12 RAÍCES FUNCIÓN RAÍZ CUADRADA
 Fuete: PreUiversitrio Pedro de Vldivi Guí Práctic N RAÍCES FUNCIÓN RAÍZ CUADRADA DEFINICIÓN : Si es u etero pr positivo es u rel o egtivo, etoces es el úico rel, o egtivo, tl que = = =, 0 DEFINICIÓN :
Fuete: PreUiversitrio Pedro de Vldivi Guí Práctic N RAÍCES FUNCIÓN RAÍZ CUADRADA DEFINICIÓN : Si es u etero pr positivo es u rel o egtivo, etoces es el úico rel, o egtivo, tl que = = =, 0 DEFINICIÓN :
Tema 9. Determinantes.
 Uidd.Determites Tem. Determites.. Coeptos previos, permutioes. Defiiió geerl de determites. Determite de mtries de orde y orde.. Determite mtries udrds de orde. Determite mtries udrds de orde. Determite
Uidd.Determites Tem. Determites.. Coeptos previos, permutioes. Defiiió geerl de determites. Determite de mtries de orde y orde.. Determite mtries udrds de orde. Determite mtries udrds de orde. Determite
LOS NÚMEROS REALES. Los número 1,2,3 se denominan números naturales. El conjunto de los números naturales se representan con la letra N, así
 LOS NÚMEROS REALES Los número,, se enominn números nturles. El onjunto e los números nturles se representn on l letr N, sí N {,,K } Si se sumn os números nturles el resulto es otro nturl, pero si se rest
LOS NÚMEROS REALES Los número,, se enominn números nturles. El onjunto e los números nturles se representn on l letr N, sí N {,,K } Si se sumn os números nturles el resulto es otro nturl, pero si se rest
Cuaderno de Matemáticas para el Verano
 Colegio Alás Msplos ºESO Cuero e Mteátis pr el Vero ºESO Deprteto e Mteátis 0-0 Colegio Alás Msplos ºESO.- Oper los siguietes riles, reoro que uo hy sus o rests etro e u ríz hy que sr ftor oú tes e poer
Colegio Alás Msplos ºESO Cuero e Mteátis pr el Vero ºESO Deprteto e Mteátis 0-0 Colegio Alás Msplos ºESO.- Oper los siguietes riles, reoro que uo hy sus o rests etro e u ríz hy que sr ftor oú tes e poer
Cuaderno de Matemáticas para el Verano
 Cuero e Mteátis pr el Vero ºESO Deprteto e Mteátis 0-0 .- Oper los siguietes riles, reoro que uo hy sus o rests etro e u ríz hy que sr ftor oú tes e poer etrer. ) ) ) 0 9 0 9 : h) i) j) k) l) ) : ) o)
Cuero e Mteátis pr el Vero ºESO Deprteto e Mteátis 0-0 .- Oper los siguietes riles, reoro que uo hy sus o rests etro e u ríz hy que sr ftor oú tes e poer etrer. ) ) ) 0 9 0 9 : h) i) j) k) l) ) : ) o)
σ c de los conductores metálicos es alta,
 EC3 ORIA DE ONDAS 4.5 GUÍAS DE ONDAS METÁLICAS CON CONDUCTORES REALES 4.5. Eeto e l outivi iit el outor e los s e propgió Tl oo se estleió e l seió 3.6. pr el so e ls líes e trsisió reles el eeto e l outivi
EC3 ORIA DE ONDAS 4.5 GUÍAS DE ONDAS METÁLICAS CON CONDUCTORES REALES 4.5. Eeto e l outivi iit el outor e los s e propgió Tl oo se estleió e l seió 3.6. pr el so e ls líes e trsisió reles el eeto e l outivi
Análisis de Programas Recursivos
 Arturo Díz Pérez Aálisis y Diseño e Algoritmos Aálisis e Progrms Recursivos Arturo Díz Pérez Itroucció Progrms Recursivos Aálisis e Fucioes Recursivs Relcioes e recurreci pr evlur progrms recursivos Aálisis
Arturo Díz Pérez Aálisis y Diseño e Algoritmos Aálisis e Progrms Recursivos Arturo Díz Pérez Itroucció Progrms Recursivos Aálisis e Fucioes Recursivs Relcioes e recurreci pr evlur progrms recursivos Aálisis
3.- Solución de sistemas de ecuaciones lineales
 .- Solució de sistes de ecucioes lieles U siste de ecucioes lieles e icógits tiee l for geerl: + + + +... + +... + +... + (.) L solució de estos sistes de ecucioes lieles ls podeos ctlogr segú l tl. Siste
.- Solució de sistes de ecucioes lieles U siste de ecucioes lieles e icógits tiee l for geerl: + + + +... + +... + +... + (.) L solució de estos sistes de ecucioes lieles ls podeos ctlogr segú l tl. Siste
DETERMINANTES. A toda matriz cuadrada se le puede hacer corresponder un número (determinante) cuyo cálculo se puede hacer de las siguientes maneras:
 Deterites DETERMINNTES. DEFINICIÓN. tod tri udrd se le uede her orresoder u úero (deterite uo álulo se uede her de ls siguietes ers:.. DETERMINNTE DE SEGUNDO ORDEN. det Es deir, es el roduto de los eleetos
Deterites DETERMINNTES. DEFINICIÓN. tod tri udrd se le uede her orresoder u úero (deterite uo álulo se uede her de ls siguietes ers:.. DETERMINNTE DE SEGUNDO ORDEN. det Es deir, es el roduto de los eleetos
Progresiones aritméticas y geométricas
 Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
1. Números reales. 2. Raíces y potencias. 3. Operaciones con radicales. Matemáticas 3º ESO
 Mteátis º ESO 1. Núeros reles Clsifiió de los úeros reles Aroxiió de deiles Itervlos. Ríes y oteis Notió ietífi. Oerioes Rdiió. Proieddes de ls oteis de exoete riol Rdiles equivletes Silifir rdiles Extrió
Mteátis º ESO 1. Núeros reles Clsifiió de los úeros reles Aroxiió de deiles Itervlos. Ríes y oteis Notió ietífi. Oerioes Rdiió. Proieddes de ls oteis de exoete riol Rdiles equivletes Silifir rdiles Extrió
3) El espacio fuera de la esfera de radio b. Al potencial en toda esa región lo denotaremos como V 3 (r; ) y lo escribiremos
 . U esfer coductor de rdio se mtiee potecil V. Está roded por u cscró esférico cocétrico, de rdio, que tiee u desidd super cil de crg () = cos, dode es u costte co ls uiddes propids es l coorded polr..
. U esfer coductor de rdio se mtiee potecil V. Está roded por u cscró esférico cocétrico, de rdio, que tiee u desidd super cil de crg () = cos, dode es u costte co ls uiddes propids es l coorded polr..
{ } + S = = S, para S. a converge si su sucesión de sumas parciales converge, es decir,
 Esuel de Igeierí Cetro de Ciei Bási Cálulo de Vrile Rel Guí teóri Series Series Iiits: Deiiió: Se { } u suesió iiit. L epresió, se deoi serie iiit o serie y se deot por: { } S S S S S S S S - U serie es
Esuel de Igeierí Cetro de Ciei Bási Cálulo de Vrile Rel Guí teóri Series Series Iiits: Deiiió: Se { } u suesió iiit. L epresió, se deoi serie iiit o serie y se deot por: { } S S S S S S S S - U serie es
Álgebra para ingenieros de la Universidad Alfonso X
 Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
RAÍCES Y SUS PROPIEDADES Guía para el aprendizaje (Presentar el día martes 29 de abril 2014)
 NOMBRE DEL ESTUDIANTE:: RAÍCES Y SUS PROPIEDADES Guí pr el predizje (Presetr el dí mrtes 9 de ril 0) CURSO: RADICALES Se llm ríz -ésim de u úmero, se escrie, u úmero que elevdo de. 9, porque 9 7, porque.0,
NOMBRE DEL ESTUDIANTE:: RAÍCES Y SUS PROPIEDADES Guí pr el predizje (Presetr el dí mrtes 9 de ril 0) CURSO: RADICALES Se llm ríz -ésim de u úmero, se escrie, u úmero que elevdo de. 9, porque 9 7, porque.0,
1. CONJUNTOS DE NÚMEROS
 Águed Mt y Miguel Reyes, Dpto. de Mtemátic Aplicd, FI-UPM. 1 1. CONJUNTOS DE NÚMEROS 1.1. NÚMEROS REALES Culquier úmero rciol tiee u expresió deciml fiit o periódic y vicevers, es decir, culquier expresió
Águed Mt y Miguel Reyes, Dpto. de Mtemátic Aplicd, FI-UPM. 1 1. CONJUNTOS DE NÚMEROS 1.1. NÚMEROS REALES Culquier úmero rciol tiee u expresió deciml fiit o periódic y vicevers, es decir, culquier expresió
Ejemplo: 5. Cambio de base: Ejemplo: No existe el logaritmo de un número con base negativa. No existe el logaritmo de un número negativo.
 III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
Compensación: diseño de Gc. Ejemplo 1: Sea una planta Gs () =
 Compenión: ieño e G Ejemplo : Se un plnt G () =, e neeit relimentr l ( + )( + )( + ) plnt. El enor utilio tenú vee l li (G LCBF =) y lo requerimiento el item relimento on lo iguiente: ) Anho e bn, BW=r/eg
Compenión: ieño e G Ejemplo : Se un plnt G () =, e neeit relimentr l ( + )( + )( + ) plnt. El enor utilio tenú vee l li (G LCBF =) y lo requerimiento el item relimento on lo iguiente: ) Anho e bn, BW=r/eg
Definiciones. Los valores de los términos necesarios para empezar a calcular se llaman condiciones iniciales.
 Deprtmeto de Mtemáti plid. ETSIIf. UPM. Vitori Zrzos Rodríguez RELCIONES DE RECURRENCI Defiiioes Relió de reurrei o reursiv pr l suesió { } es u epresió que relio el térmio geerl de l suesió o uo o más
Deprtmeto de Mtemáti plid. ETSIIf. UPM. Vitori Zrzos Rodríguez RELCIONES DE RECURRENCI Defiiioes Relió de reurrei o reursiv pr l suesió { } es u epresió que relio el térmio geerl de l suesió o uo o más
Sucesiones de Números Reales
 Apédice A Sucesioes de Números Reles A.. Defiicioes U sucesió de úmeros reles es u correspodeci A que soci, cd úmero turl, u úmero rel A ( ) El cojuto de los úmeros turles, cotiee ifiitos elemetos e u
Apédice A Sucesioes de Números Reles A.. Defiicioes U sucesió de úmeros reles es u correspodeci A que soci, cd úmero turl, u úmero rel A ( ) El cojuto de los úmeros turles, cotiee ifiitos elemetos e u
SISTEMAS DE ECUACIONES LINEALES: TEOREMA DE ROUCHÉ- FROBENIUS
 R.F.- - SISTES DE ECUCIONES INEES: TEORE DE ROUCHÉ- FROBENIUS Recordeos que u siste de ecucioes co icógits es u siste de l for: Dode: ij so úeros reles se ll coeficietes del siste,,,, so úeros reles recie
R.F.- - SISTES DE ECUCIONES INEES: TEORE DE ROUCHÉ- FROBENIUS Recordeos que u siste de ecucioes co icógits es u siste de l for: Dode: ij so úeros reles se ll coeficietes del siste,,,, so úeros reles recie
RADICALES. Entre los números reales se encuentran los radicales, que se pueden expresar como raíz de un índice n 2 de un número real.
 RADICALES Etre los úeros reles se euetr los rdiles, ue se uede exresr oo ríz de u ídie de u úero rel. Ríz eési de u úero rel. Si R y Ν, o, direos ue l ríz eési de es u úero rel r y lo otreos sí: r, si
RADICALES Etre los úeros reles se euetr los rdiles, ue se uede exresr oo ríz de u ídie de u úero rel. Ríz eési de u úero rel. Si R y Ν, o, direos ue l ríz eési de es u úero rel r y lo otreos sí: r, si
SISTEMAS DE ECUACIONES
 . Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
. Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
a se denomina serie a es convergente y SERIES = si r <1 S n La suma de los términos de una sucesión infinita { } n n=1 infinita o simplemente serie
 SERIES L sum de los térmios de u suesió ifiit { } = ifiit o simplemete serie se deomi serie Y se represet o el símbolo = Defiiió: = 4 KK Dd l serie = ésim sum pril = 4 K K, se desigrá S su S = = = 4 K
SERIES L sum de los térmios de u suesió ifiit { } = ifiit o simplemete serie se deomi serie Y se represet o el símbolo = Defiiió: = 4 KK Dd l serie = ésim sum pril = 4 K K, se desigrá S su S = = = 4 K
Potencias y Radicales
 Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
Análisis del Lugar Geométrico de las Raíces (LGR) o Método de Evans
 Análii del Lugar Geométrio de la Raíe (LGR) o Método de Evan La araterítia báia de la repueta tranitoria de un itema en lazo errado e relaiona etrehamente on la ubiaión de lo polo en lazo errado. Si el
Análii del Lugar Geométrio de la Raíe (LGR) o Método de Evan La araterítia báia de la repueta tranitoria de un itema en lazo errado e relaiona etrehamente on la ubiaión de lo polo en lazo errado. Si el
DETERMINANTES. 1. Calcular el valor del determinante. Solución: Determinante tipo Van der Mondem. sustituyendo en la primera expresión
 DETERMINANTES. lulr el vlor el eterminnte ² ² ² Soluión: Sno ftor omún e en lª fil Sno ftor omún e en l ª fil ² ² ² ² ² ² Determinnte tipo Vn er Monem. ² ² ² ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) sustituyeno
DETERMINANTES. lulr el vlor el eterminnte ² ² ² Soluión: Sno ftor omún e en lª fil Sno ftor omún e en l ª fil ² ² ² ² ² ² Determinnte tipo Vn er Monem. ² ² ² ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) sustituyeno
GUÍA Nº 5 POTENCIAS Y NOTACIÓN CIENTÍFICA. a, (n veces) 2) Si a es un número real distinto de cero y n es un número natural, entonces, 5 c) 6 f)
 Poteci GUÍA Nº POTENCIAS Y NOTACIÓN CIENTÍFICA ) Si es u úero rel y es u úero turl, etoces,...., ( veces) ) Si es u úero rel distito de cero y es u úero turl, etoces, ) Si es u úero rel distito de cero,
Poteci GUÍA Nº POTENCIAS Y NOTACIÓN CIENTÍFICA ) Si es u úero rel y es u úero turl, etoces,...., ( veces) ) Si es u úero rel distito de cero y es u úero turl, etoces, ) Si es u úero rel distito de cero,
TEMA 8: MATRICES. Para notar una matriz se utiliza o: una letra mayúscula, por ejemplo A, o también a
 emáis º hillero. Profesor: rí José Sáhez Queveo TE : TRES. DENÓN DE TRZ. GULDD DE TRES. TPOS DE TRES. OPERONES ON TRES..- SU DE TRES..- PRODUTO DE UN Nº REL POR UN TRZ..- PRODUTO DE TRES. TRNSORONES ELEENTLES
emáis º hillero. Profesor: rí José Sáhez Queveo TE : TRES. DENÓN DE TRZ. GULDD DE TRES. TPOS DE TRES. OPERONES ON TRES..- SU DE TRES..- PRODUTO DE UN Nº REL POR UN TRZ..- PRODUTO DE TRES. TRNSORONES ELEENTLES
SISTEMA DE ECUACIONES LINEALES
 SISTEM DE ECUCIONES LINELES Defiició: Llmremos sistem de m ecucioes co icógits, u cojuto de ecucioes de l form: m.... m..... m m (S) Los elemetos so los coeficietes del sistem. ij Los elemetos i so ls
SISTEM DE ECUCIONES LINELES Defiició: Llmremos sistem de m ecucioes co icógits, u cojuto de ecucioes de l form: m.... m..... m m (S) Los elemetos so los coeficietes del sistem. ij Los elemetos i so ls
Control Eléctrico y Accionamientos Teoría de Circuitos I Unidad 5: Redes múltiples en régimen permanente
 otrol létrio iomietos Teorí e iruitos i : Rees múltiples e régime permete -..- oeptos geerles er e iruitos rees elétris -..- Métoos e soluió e rees -...- Métoo e superposiió -...- Métoo e ls itesies e
otrol létrio iomietos Teorí e iruitos i : Rees múltiples e régime permete -..- oeptos geerles er e iruitos rees elétris -..- Métoos e soluió e rees -...- Métoo e superposiió -...- Métoo e ls itesies e
I.E.S Padre Juan Ruíz Aritmética Hinojosa del Duque
 I.E.S Pdre Ju Ruíz Aritméti Hiojos del Duque PROPIEDADES DE LA ARITMÉTICA Y ERRORES MÁS COMUNES NÚMEROS ENTEROS Elimir prétesis: Del mismo sigo, sle + De distito sigo, sle + (+) = + ( ) = + + ( ) = (+)
I.E.S Pdre Ju Ruíz Aritméti Hiojos del Duque PROPIEDADES DE LA ARITMÉTICA Y ERRORES MÁS COMUNES NÚMEROS ENTEROS Elimir prétesis: Del mismo sigo, sle + De distito sigo, sle + (+) = + ( ) = + + ( ) = (+)
Ecuaciones de recurrencia
 Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
Utilizando la fórmula que nos proporciona el número de divisores se tiene que:
 Hoj de Prolems º Alger IV /. Hllr u úmero etero A que o teg ms ftores primos que, y 7, siedo demás que ª tiee divisores más que A y que ª tiee divisores ms que A. Clulr tmié l sum de todos los divisores
Hoj de Prolems º Alger IV /. Hllr u úmero etero A que o teg ms ftores primos que, y 7, siedo demás que ª tiee divisores más que A y que ª tiee divisores ms que A. Clulr tmié l sum de todos los divisores
El proeso de idetifiió E tr d s 5 Defiiió del experimeto reoleió de dtos Es orreto el experimeto? Dtos ideudos H que filtrr los dtos? Limp
 Idetifiió de Sistems 5 Ojetivo de l Idetifiió de Sistems: Oteer u ue modelo (geerlmete liel del sistem empledo u tidd de trjo rzole. Perturioes o ruido: e(t 8 6 4 4 6 8 4 6 Etrds: u(t Desripió del sistem?
Idetifiió de Sistems 5 Ojetivo de l Idetifiió de Sistems: Oteer u ue modelo (geerlmete liel del sistem empledo u tidd de trjo rzole. Perturioes o ruido: e(t 8 6 4 4 6 8 4 6 Etrds: u(t Desripió del sistem?
TEMA 3: RESOLUCIÓN DE SISTEMAS DE ECUACIONES MEDIANTE DETERMINANTES.
 TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES. º BCH(CN) TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES..-INTRODUCCIÓN. L resoluió de sistems de euioes está ligd l estudio
TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES. º BCH(CN) TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES..-INTRODUCCIÓN. L resoluió de sistems de euioes está ligd l estudio
los coeficientes 10 y 30 tienen los factores comunes 2, 5 y 10, se saca el mayor factor común: 10, de las letras el factor 2
 CASO I: CUANDO TODOS LOS TÉRMINOS DE UN POLINOMIO TIENEN UN FACTOR COMÚN ) Fctor comú moomio. Ejemplos: descompoer e fctores ) fctor comú como coeficiete de u prétesis; detro de los prétesis se escrie
CASO I: CUANDO TODOS LOS TÉRMINOS DE UN POLINOMIO TIENEN UN FACTOR COMÚN ) Fctor comú moomio. Ejemplos: descompoer e fctores ) fctor comú como coeficiete de u prétesis; detro de los prétesis se escrie
TERCER PERÍODO 2015 CASO I: CUANDO TODOS LOS TÉRMINOS DE UN POLINOMIO TIENEN UN FACTOR COMÚN
 TERCER PERÍODO 01 CASO I: CUANDO TODOS LOS TÉRMINOS DE UN POLINOMIO TIENEN UN FACTOR COMÚN ) Fctor comú moomio. Ejemplos: descompoer e fctores ) fctor comú como coeficiete de u prétesis; detro de los prétesis
TERCER PERÍODO 01 CASO I: CUANDO TODOS LOS TÉRMINOS DE UN POLINOMIO TIENEN UN FACTOR COMÚN ) Fctor comú moomio. Ejemplos: descompoer e fctores ) fctor comú como coeficiete de u prétesis; detro de los prétesis
1. SISTEMAS DE ECUACIONES LINEALES Es un conjunto de expresiones algebraicas de la forma:
 CRISTIN ROND HERNÁNDEZ Sistes de ecucioes SISTEMS DE ECUCIONES. Sistes de ecucioes lieles. Epresió tricil de u siste. Clsiicció de sistes de ecucioes. Teore de Rouché-Fröeius. Discusió de sistes 6. Método
CRISTIN ROND HERNÁNDEZ Sistes de ecucioes SISTEMS DE ECUCIONES. Sistes de ecucioes lieles. Epresió tricil de u siste. Clsiicció de sistes de ecucioes. Teore de Rouché-Fröeius. Discusió de sistes 6. Método
GUÍA DE EJERCICIOS III
 Fult e Igeierí UCV Álger Liel Geometrí líti 5 Cilo Básio GUÍ DE EJECICIOS III rsformioes lieles: Demuestre e so si l trsformió el esio vetoril V e el esio vetoril W es liel e w : B oe B es g u mtri fij
Fult e Igeierí UCV Álger Liel Geometrí líti 5 Cilo Básio GUÍ DE EJECICIOS III rsformioes lieles: Demuestre e so si l trsformió el esio vetoril V e el esio vetoril W es liel e w : B oe B es g u mtri fij
CAPITULO 3 SISTEMAS DE ECUACIONES LINEALES ...
 LGEBR SUPERIOR Y LINEL.. INTRODUCCION. CPITULO SISTEMS DE ECUCIONES LINELES Se llm ecució liel ó ecució de primer grdo, u ecució que relcio cierto úmero coocido, co u ó má icógit, e et ecució cd icógit
LGEBR SUPERIOR Y LINEL.. INTRODUCCION. CPITULO SISTEMS DE ECUCIONES LINELES Se llm ecució liel ó ecució de primer grdo, u ecució que relcio cierto úmero coocido, co u ó má icógit, e et ecució cd icógit
TEMA 1. VECTORES Y MATRICES 1.4. APLICACIONES
 TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
Potencias y radicales
 Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
1.-INTEGRAL DEFINIDA.
 INTEGRAL DEFINIDA .-INTEGRAL DEFINIDA. e y ƒ( u fució cotiu e u itervlo [, ]. Not.- Pr simplificr l demostrció se cosider positiv, ƒ( > 0, e todo puto del itervlo. e divide el itervlo [, ] e "" suitervlos
INTEGRAL DEFINIDA .-INTEGRAL DEFINIDA. e y ƒ( u fució cotiu e u itervlo [, ]. Not.- Pr simplificr l demostrció se cosider positiv, ƒ( > 0, e todo puto del itervlo. e divide el itervlo [, ] e "" suitervlos
( ) ( )( )( ) ( ) ( )( )
 Algebra uiversitaria UNIDAD III. POLINOMIOS 3.. Técicas elemetales para buscar raíces Recordado la defiició de raíz U poliomio P(x) tiee ua raíz r si y solo si P(r) = 0. Recordar el teorema de factorizació
Algebra uiversitaria UNIDAD III. POLINOMIOS 3.. Técicas elemetales para buscar raíces Recordado la defiició de raíz U poliomio P(x) tiee ua raíz r si y solo si P(r) = 0. Recordar el teorema de factorizació
EXPRESIÓN DECIMAL DE LOS NÚMEROS RACIONALES ABSOLUTOS:
 Mtemátic II do Mgisterio IFD Celoes XPRSIÓN DCIMAL D LOS NÚMROS RACIONALS ABSOLUTOS: Vmos clsificr los úmeros rcioles solutos e dos cojutos disjutos D y D P ( D D φ ). P D Q D P Se / el represette cóico
Mtemátic II do Mgisterio IFD Celoes XPRSIÓN DCIMAL D LOS NÚMROS RACIONALS ABSOLUTOS: Vmos clsificr los úmeros rcioles solutos e dos cojutos disjutos D y D P ( D D φ ). P D Q D P Se / el represette cóico
