En resumen, en las raíces de la ecuación característica está la información sobre el patrón de la respuesta temporal de un sistema.
|
|
|
- Xavier Cárdenas Macías
- hace 7 años
- Vistas:
Transcripción
1 Aálii Culittivo l Rput mporl u Sitm Si oo l fuió trfri G() u o itm y l tr x(t), pu vlur l li y(t) prtir : hio lugo l trformió ivr: y(t) y() G() x() L y() L G( ) x() L fuió trfri G() pu xprr omo u oit poliomio : G() N() D() m m m L rí l poliomio umror N() omi ro l fuió trfri, mitr qu l rí l omior D() l llm polo. Culmt, l turlz l rí l omior o l qu trmi l ptró l rput tmporl u ñl tr y o prmit u ooimito ulittivo l iámi l itm. Dio t rtríti t importt qu l omior u fuió trfri, uo lo igul ro, lo omi Euió Crtríti l Sitm: D()... S pu hr l iguit orvio rpto l uiió lo polo l fuió trfri:. Polo rl y itito p, p, t. L rput tmporl trá ompot l pt pt form C, C, t. moo qu lo tritorio ovrgrá ro i lo polo o gtivo.. Polo rl múltipl. E t o, pr u polo p o multiplii r, l fuió tmporl qu rultrí l trformió ivr otrí térmio l form C C C C!! (r )! r r pt t t... t y vl lo iho t, i p gtivo, uo t, y(t).. Polo ompljo ojugo j. L rput rult oiltori, o u ompot tmporl l form C t ( t ). Sgú uál l igo l iuoi mplifirá ( > ) o rá ( < ). l frui l oilió. m E rum, l rí l uió rtríti tá l iformió or l ptró l rput tmporl u itm.
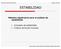
2 C p t p C p t p C t ( t ) C t ( t ) Figur : Rput tmporl gú l uiió lo polo l uió rtríti Euió Crtríti lo Sitm Lzo Crro Coirmo u itm lzo rro, uyo igrm loqu rprt l Figur. G G r G Gv Gp ( - ) CONROLADOR ELEMENO FNAL DE CONROL PROCESO y Gt Ruio Miió ELEMENO DE MEDCON-RANSMSON Figur : Digrm Bloqu u Sitm Lzo Crro
3 El itm v omtio itit prturio (,, ) qu ii itito puto l lzo. L voluió l vril mi y rultrá l otriuió l prturio y lo mio l vlor o r: G Gp Gt G Gt y() G Gv Gp Gt G Gv Gp Gt G Gv Gp Gt G Gp Gv Gt r G Gv Gp Gt Qu vii qu, ipitmt uál l ñl tr oir, l uió rtríti impr l mim. A tl uió l omirá Euió Crtríti l Sitm Lzo Crro: N() E( ) G() Gv() Gp() Gt() D() y l turlz u rí iirá uál l ptró l rput tmporl l lzo rro uo v omtio mio l tr. Orvo uiomt l Euió Crtríti, pu ottr qu p lo lmto qu utr tro l lzo, to, otrolor, lmto fil otrol, proo í mimo y lmto trmiió-miió. Por lo tto, l ptró rput u lzo vi trmio por lo lmto l lzo, ipitmt uál l prturió iit. [] Etili lo Sitm Lzo Crro El opto Etili importi mulr Cotrol Automátio. Exit itit form fiirl. U fiiió, lmtl i quir, pro ituitiv, l ooi omo BBO-tili (ou iput ou output tility): U itm i qu tl i pr to tr ot prou u li ot, ipitmt u to iiil.
4 SSEMA ESABLE ENRADA ACOADA SSEMA MARGNALMENE ESABLE SSEMA NESABLE RESPUESAS DE LA VARABLE MEDDA Figur : Equm itm o itit rtríti tili Lo tritorio l li pu rlior o l rí l uió rtríti tl omo vio t. D moo qu l opto Etili pu fiir térmio mtmátio má prio l iguit form: U itm tl i l rí l uió rtríti o rl gtiv o omplj ojug o prt rl gtiv. O iho form má ompt, i to l rí utr l miplo izquiro l vril omplj.
5 Compot mgiri ω σ jω σ Compot Rl REGÓN ESABLE REGÓN NESABLE Figur : Crtrizió l tili gú l uiió l rí l Euió Crtríti Si lgu ríz ui l j imgirio, oti u itm o tili mrgil, ir, u itm qu hll l límit tr l tili y l itili. Hy lgu orvio qu mtr rlizr: Si quir r i u itm tl o o, trí o lizr l rí l uió rtríti. Como trt u poliomio, l rí o pu lulr o u fórmul xplíit, lvo xpio. Por lo tto, pr lizr l tili, rí rurrir u proimito umério. Orvo l uió rtríti [], qu vii qu l rí (y por lo tto l tili l itm lzo rro) p l G(), to, l otrolor. Como, pu lgir l tipo otrolor (fuió trfri) y l vlor u prámtro (itoizió). Si l proo y lo lmto miió y tuió y tá fijo, pu oluir to qu l tili l itm otrol prá u juiio lió l tipo y itoizió l otrolor. Critrio Etili Routh Pr iir i u itm lzo rro tl olo rquir r i xit rí l uió rtríti l miplo rho, y o rio oor u vlor. El t
6 Routh prmit itifir l úmro rí l miplo rho trvé u proimito rltivmt impl. Primro xprr l umror l uió rtríti form poliomil: - - N ()... [] - Hy qu vrifir qu poitiv, lo otrrio, multiplir lo mimro l uió por. PASO (oiió ri) El poliomio [] r omplto, to, igú i r ulo, lo otrrio, l mo u ríz otrrá l miplo rho. Si lguo lo ofiit,,,,..., -, gtivo, to l mo u ríz ui l miplo rho y o rio igú álii iiol rquir. Má ú, l úmro mio igo igul l ti rí l miplo rho (orm lo igo Drt). Si too lo ofiit Routh qu po fil: PASO (oiió ufiit),,,..., -, o poitivo otruir l Arrglo... f g..... L o primr fil otruy o lo ofiit,,,..., -,. Si impr grg u olum ro y i pr, l gu fil omplt o u.
7 g f L o primr fil otruy o lo ofiit l poliomio rtrítio Lo ofiit l fil uiguit omput o lo ofiit l o fil imit trior. Por jmplo, l trr fil otruy o l iguit oprio:..... g f (-) (-) Lo ofiit l trr fil lt otruy trvé oprio mplo l o fil imit trior L fórmul pr l ómputo lo itito lmto l Arrglo Routh o: Et proimito otiu ht qu omplt l fil éim. El rrglo fil ti u trutur trigulr. Exmio lo ofiit l primr olum l rrglo, g, f,...,,,, i lgú ofiit gtivo, l mo u ríz tá l miplo rho y l itm rá itl. Má ú, l úmro mio igo ii l ti rí tl miplo.
8 El úmro mio igo rult igul l úmro rí l miplo rho... f g..... Apliió l Critrio Routh Pr vr l poiili tuio ri l t Routh, propo tuir u itm lzo rro rtrizo por l fuio trfri l Figur. r ( - ) CONROLADOR ELEMENO FNAL DE CONROL PROCESO y ELEMENO DE MEDCON-RANSMSON Figur. Ejmplo u itm lzo rro E t o, l fuio trfri lo itito lmto l lzo ti prámtro qu pu hr io otio yo (itifiió) o prtir molo mtmátio. S l um qu m ott timpo o poitiv (ituió orml lo proo). El otrolor lgio l tipo itgrl puro y u úio prámtro itoí (timpo itgrl). El itrrogt qu trt rpor qué rgo vlor l porá igr moo qu l itm tg u omportmito tl? E itrt otr qu o h iluio igu iformió or l prturio qu pu ftr l itm. Hy qu rorr qu l tili l itm lzo rro p xluivmt lo lmto l lzo. Pr tuir l tili pltr l uió rtríti: E( ) G() Gv() Gp() Gt() ruio omú omior rult: ( ) ( )
9 ) ( ) ( ) ( ) ( D() N() Pr qu t oit igul ro, l umror r igul ro. E oui, l uió l qu hy qu plir l álii Routh : ) ( N() PASO Como vit, l poliomio omplto. Pr gurr qu o xit mio igo lo ofiit mtr qu umpl qu PASO S otruir l rrglo Routh qu otrá utro fil, io l o primr otrui o lo ofiit l poliomio origil y rto oti o l oprio ript t. pioo l primr olum, pr qu o xit mio igo y oui pu gurr l tili, urg u gu oiió: y omo l omior myor qu ro, pr qu umpl t rtriió rá r y por lo tto
10 D t form, i l prouto l gi poitivo, l vlor timpo itgrl míimo miil rí: (mi) y orrporí u itm o tili ríti o mrgil (rput prturio o oilio oti). E ovit hr u orvió t puto. El ritrio tili Routh prmit hr u trtmito mtmátio forml y rlior lo prámtro l fuio trfri o lo l otrolor, tlio lo límit y l rtriio. Eto o porí hr o l mro ómputo umério l rí l uió qu olo portrí iformió pr vlor trmio lo prámtro ( t o gi, ott timpo y timpo itgrl). Limitio y xtio l Critrio Etili Routh Hy qu rorr qu l hrrmit qu propuo irv uo l fuio trfri tá ivoluro poliomio. S qu Cotrol Proo químio u ompot iámi muy ifui l timpo murto. Si t iámi tá prt l uió rtríti, l ómputo l rí impli rolvr u uió trt pr l qu o pli l proimito Routh. L oluió má impl trformr l rtro timpo u fuió riol uo u ri tru ylor: L L ( L)!! ( L)! pro l rultr u itm o ul o otituy u u proximió. U oluió, tmié proxim, oit rmplzr l timpo murto por u oit ri ooi omo Aproximió Pè: L L ( L) L ( L) qu ti u ol vtj: oti u proximió orrpoit u itm ul y l rror truió mor pr u mimo úmro térmio
CRITERIO DE ESTABILIDAD DE ROUTH
 CRITERIO DE ESTABIIDAD DE ROUTH INGENIERÍA DE CONTRO.C. EIZABETH GPE. ARA HDZ. INGENIERÍA DE CONTRO.C. EIZABETH GPE. ARA HDZ. Criterio e etili e Routh-Hurwitz El prolem má importte e lo item e otrol liel
CRITERIO DE ESTABIIDAD DE ROUTH INGENIERÍA DE CONTRO.C. EIZABETH GPE. ARA HDZ. INGENIERÍA DE CONTRO.C. EIZABETH GPE. ARA HDZ. Criterio e etili e Routh-Hurwitz El prolem má importte e lo item e otrol liel
MCD Y MCM DE POLINOMIOS FRACCIONES ALGEBRAICAS
 TRILE pítulo MD Y MM DE POLINOMIOS FRAIONES ALGEBRAIAS Rgl pr lulr l MM y MD Poliomios :. S ftoriz los poliomios os.. El MD strá formo por l multipliió toos los ftors primos omus los poliomios os, osiros
TRILE pítulo MD Y MM DE POLINOMIOS FRAIONES ALGEBRAIAS Rgl pr lulr l MM y MD Poliomios :. S ftoriz los poliomios os.. El MD strá formo por l multipliió toos los ftors primos omus los poliomios os, osiros
= 0 ' = 0 ' Fracciones equivalentes (productos cruzados iguales): c. Fracción generatriz:
 Dprtmto Mtmátis http://www.olgiovirggri.org/so/mt.htm Aritméti. ARITMÉTICA... Cojutos umérios. I Númros tros: úmros turls Númros riols: os juto o sus opustos (úmros imls prióios gtivos). Númros turls:
Dprtmto Mtmátis http://www.olgiovirggri.org/so/mt.htm Aritméti. ARITMÉTICA... Cojutos umérios. I Númros tros: úmros turls Númros riols: os juto o sus opustos (úmros imls prióios gtivos). Númros turls:
Soluciones a los ejercicios, problemas y cuestiones Unidad 2. Polinomios y fracciones algebraicas Matemáticas aplicadas a las Ciencias Sociales I
 Soluios los jriios prolms ustios Ui oliomios rios lgris Mtmátis plis ls Ciis Soils I EJECICIOS SUMA ESTA Y MULTILICACIÓN DE OLINOMIOS Dos los poliomios Dtrmi si stá ruios si so ompltos ii su gro Clul trmi
Soluios los jriios prolms ustios Ui oliomios rios lgris Mtmátis plis ls Ciis Soils I EJECICIOS SUMA ESTA Y MULTILICACIÓN DE OLINOMIOS Dos los poliomios Dtrmi si stá ruios si so ompltos ii su gro Clul trmi
Enfrentando. cesantía INUND. ntía INUNDAC
 frto i F f I C D tí IU o B t B o t tr it D D o I o CS SUICID F i F i f f I C tí IUD B to B o t t i D D tr o o CS SUICIDI F F i i f f tí IUDCI to B B o t t tr i D o I ID IC U o FCS S i i f f I CI tí IUDC
frto i F f I C D tí IU o B t B o t tr it D D o I o CS SUICID F i F i f f I C tí IUD B to B o t t i D D tr o o CS SUICIDI F F i i f f tí IUDCI to B B o t t tr i D o I ID IC U o FCS S i i f f I CI tí IUDC
Criterios de Estabilidad de Routh y Jury. M.I. Ricardo Garibay Jimenez 2006
 Criterio de Etbilidd de Routh y Jury M.I. Rirdo Griby Jimeez 6 Criterio de Routh U poliomio (... A tiee ríe etble (o prte rel egtiv i e umple odiioe. Neeidd todo lo oefiiete y o poitivo Sufiiei El igo
Criterio de Etbilidd de Routh y Jury M.I. Rirdo Griby Jimeez 6 Criterio de Routh U poliomio (... A tiee ríe etble (o prte rel egtiv i e umple odiioe. Neeidd todo lo oefiiete y o poitivo Sufiiei El igo
1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }
![1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x } 1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }](/thumbs/74/71224437.jpg) IES P Pov (Gui Mtmátis II UNIDD : INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los vlos,,
IES P Pov (Gui Mtmátis II UNIDD : INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los vlos,,
Estabilidad en el Plano Complejo
 Cpítulo Etili e el Plo Complejo Itrouió L etili e u item liel e lzo erro e etermi prtir e l uiió e lo polo e lzo erro e el plo Si lguo e eto polo e euetr e el emiplo ereho el plo, etoe oforme umet el tiempo,
Cpítulo Etili e el Plo Complejo Itrouió L etili e u item liel e lzo erro e etermi prtir e l uiió e lo polo e lzo erro e el plo Si lguo e eto polo e euetr e el emiplo ereho el plo, etoe oforme umet el tiempo,
Formulario de matemáticas
 Forlro tát lgr- Sgo (+) (+) = + (-) (-) = + (+) (-) = - (-) (+) = - (+) / (+) = + (-) / (-) = + (+) / (-) = - (-) / (+) = - Fro Proto otl ftorzó ( ) ( ) ( ) ( ) ( ) ()() ()( ) ( )( ) ()( ) L lo ot rl log
Forlro tát lgr- Sgo (+) (+) = + (-) (-) = + (+) (-) = - (-) (+) = - (+) / (+) = + (-) / (-) = + (+) / (-) = - (-) / (+) = - Fro Proto otl ftorzó ( ) ( ) ( ) ( ) ( ) ()() ()( ) ( )( ) ()( ) L lo ot rl log
1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }
![1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x } 1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }](/thumbs/64/51459891.jpg) IES P Pov (Gui Mtmátis II UNIDD INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ (Positiv [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los
IES P Pov (Gui Mtmátis II UNIDD INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ (Positiv [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los
ESTABILIDAD. estable, si sometido a una perturbación, éste, luego de un tiempo, vuelve a su
 ESTABIIDAD El álii de lo ite de otrol e e gr prte e el ooiieto de u etilidd olut y reltiv ESTABIIDAD ABSOUTA: u ite liel ivrite e el tiepo e etle, i oetido u perturió, éte, luego de u tiepo, vuelve u odiió
ESTABIIDAD El álii de lo ite de otrol e e gr prte e el ooiieto de u etilidd olut y reltiv ESTABIIDAD ABSOUTA: u ite liel ivrite e el tiepo e etle, i oetido u perturió, éte, luego de u tiepo, vuelve u odiió
FILTRADO DIGITAL FIR E IIR
 Promito Digitl Sñl Aquiiió y Promito Sñl Biológi Fult Igirí y Cii Ext y turl FILRADO DIGIAL FIR E IIR L uió priipl u iltro igitl, irimir l rui u ñl tr irt x[], ovirtiéol u ñl li y[]. Pr llo, prt u ñl igitli
Promito Digitl Sñl Aquiiió y Promito Sñl Biológi Fult Igirí y Cii Ext y turl FILRADO DIGIAL FIR E IIR L uió priipl u iltro igitl, irimir l rui u ñl tr irt x[], ovirtiéol u ñl li y[]. Pr llo, prt u ñl igitli
FRACCIONARIOS Y DECIMALES
 FRACCIONARIOS Y DECIMALES Hg clck obr l t qu coultr: 1. Núro Frccoro - Frccoro grl - Frccoro hoogéo y htrogéo - Clfccó lo frccoro - Frcco quvlt - Ruccó frcco (plfccó) - Covró frccoro cl 2. Núro Dcl Núro
FRACCIONARIOS Y DECIMALES Hg clck obr l t qu coultr: 1. Núro Frccoro - Frccoro grl - Frccoro hoogéo y htrogéo - Clfccó lo frccoro - Frcco quvlt - Ruccó frcco (plfccó) - Covró frccoro cl 2. Núro Dcl Núro
Análisis de Fourier para Señales y Sistemas de Tiempo Discreto
 Aálii d Fourir pr Sñl y Sitm d impo Dicrto Rput d u itm LI l pocil compl [] h[] y [ ] h [ ] [ ] h [ ] [ ] Si y h h H [ ] [ ] [ ] [ ] ( [ ] ( H Autofució d lo Sitm LI Autovlor ocido y Si r rformd Si rformd
Aálii d Fourir pr Sñl y Sitm d impo Dicrto Rput d u itm LI l pocil compl [] h[] y [ ] h [ ] [ ] h [ ] [ ] Si y h h H [ ] [ ] [ ] [ ] ( [ ] ( H Autofució d lo Sitm LI Autovlor ocido y Si r rformd Si rformd
PROGRESIONES. Capítulo TRILCE. Progresión aritmética (P.A.) 3. Número de términos (n)
 TRILCE Cpítulo 7 PROGRESIONES Progrsió ritméti (PA) Es qull susió or l qu térmio, xpto l primro, s igul l térmio trior umto u vlor ostt llmo rzó l progrsió Rprstió u PA r r ( )r Númro térmios () r 4 Térmios
TRILCE Cpítulo 7 PROGRESIONES Progrsió ritméti (PA) Es qull susió or l qu térmio, xpto l primro, s igul l térmio trior umto u vlor ostt llmo rzó l progrsió Rprstió u PA r r ( )r Númro térmios () r 4 Térmios
ECUACIONES DIFERENCIALES DE ORDEN SUPERIOR. Ecuaciones lineales homogéneas con coeficientes constates de orden dos y superior.
 Prof Eriqu Mtus Nivs Dotordo Eduió Mtmáti ECUACIONES DIFERENCIALES DE ORDEN SUPERIOR Euios lils homogés o ofiits ostts d ord dos suprior Apliqu l método d rduió pr dtrmir u soluió d l uió o homogé dd los
Prof Eriqu Mtus Nivs Dotordo Eduió Mtmáti ECUACIONES DIFERENCIALES DE ORDEN SUPERIOR Euios lils homogés o ofiits ostts d ord dos suprior Apliqu l método d rduió pr dtrmir u soluió d l uió o homogé dd los
Sucesiones. Universidad Diego Portales CALCULO II
 Suesioes Uiversidd Diego Portles U suesió se puede defiir omo u list de úmeros esritos e orde defiido:,,,...,,... El úmero es el primer térmio;, el segudo térmio y e geerl, es el -ésimo térmio. Cosiderremos
Suesioes Uiversidd Diego Portles U suesió se puede defiir omo u list de úmeros esritos e orde defiido:,,,...,,... El úmero es el primer térmio;, el segudo térmio y e geerl, es el -ésimo térmio. Cosiderremos
tiene dimensión 3 2. El elemento a 21 = 3.
 Tem. MTRICES Defiiió e mtriz U mtriz e imesió m es u ojuto e úmeros ispuestos e fils y m olums. sí:... m... m : : : :... m L mtriz terior tmié se puee eotr por ( ) m El elemeto ij es el que oup l fil i
Tem. MTRICES Defiiió e mtriz U mtriz e imesió m es u ojuto e úmeros ispuestos e fils y m olums. sí:... m... m : : : :... m L mtriz terior tmié se puee eotr por ( ) m El elemeto ij es el que oup l fil i
( ) ( ) El principio de inducción
 El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
61.1 6.1. SERIES NUMÉRICAS INFINITAS 6.2. SERIES DE TÉRMINOS POSITIVOS 6.3. SERIES ALTERNANTES 6.4. SERIES DE POTENCIAS
 Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
206 MÉTODOS NUMÉRICOS
 6 MÉTODOS UMÉRICOS.. Alguos hhos mortts r ls rs vs wto: ls sguts so lgus ls ros más mortts ls rs vs wto: (. S s u rmutó K ) ( ) K tos [ K ] [ K ] CASO PARTICULAR: [ ] [ ] ( Est ro s osu l u l olomo trolt
6 MÉTODOS UMÉRICOS.. Alguos hhos mortts r ls rs vs wto: ls sguts so lgus ls ros más mortts ls rs vs wto: (. S s u rmutó K ) ( ) K tos [ K ] [ K ] CASO PARTICULAR: [ ] [ ] ( Est ro s osu l u l olomo trolt
SUCESIONES DE POTENCIAS ITERATIVAS GENERADAS POR a.
 SUCESIONES DE POTENCIAS ITERATIVAS GENERADAS POR. Jorg E. Hráz U. Eith C. Hráz Uivri Pá, Ctro Rgiol Uivritrio Vrgu, Ecul Mtátic. RESUMEN E l prt trjo tui l ució i i potci itrtiv gr por, > 0; í coo l oluili
SUCESIONES DE POTENCIAS ITERATIVAS GENERADAS POR. Jorg E. Hráz U. Eith C. Hráz Uivri Pá, Ctro Rgiol Uivritrio Vrgu, Ecul Mtátic. RESUMEN E l prt trjo tui l ució i i potci itrtiv gr por, > 0; í coo l oluili
CAPITULO 6.- LA TRANSFORMADA DE LAPLACE.
 PITUO 6.- TRSFORD DE PE. 6. Irocció. 6. rform plc. 6.3 rform plc ilrl. 6.4 Ivrió l rform plc. 6.5 Solció ccio ifrcil co coicio iicil. 6.6 rform plc ilrl. 6.7 álii im mi l rform plc. 6. Irocció. Grlizmo
PITUO 6.- TRSFORD DE PE. 6. Irocció. 6. rform plc. 6.3 rform plc ilrl. 6.4 Ivrió l rform plc. 6.5 Solció ccio ifrcil co coicio iicil. 6.6 rform plc ilrl. 6.7 álii im mi l rform plc. 6. Irocció. Grlizmo
Criterio de Estabilidad de Routh-Hurwitz
 Criterio de Etbilidd de Routh-Hurwitz F Pr l etbilidd BIBO, l ríce de l ecució crcterític, o lo polo de C()/R(), o puede etr loclizdo e el emiplo derecho del plo o e eje j, todo debe quedr e el emiplo
Criterio de Etbilidd de Routh-Hurwitz F Pr l etbilidd BIBO, l ríce de l ecució crcterític, o lo polo de C()/R(), o puede etr loclizdo e el emiplo derecho del plo o e eje j, todo debe quedr e el emiplo
1.2 INTEGRACION, DIFERENCIACIÓN DE FUNCIONES Y EXPANSIONES EN SERIES. (1.2_CvR_T_062, Revisión: , C2, C3, C4)
 . INTEGRACION, DIFERENCIACIÓN DE FUNCIONES Y EXPANSIONES EN SERIES. (._CvR_T_06, Rvisió: 5-0-06, C, C3, C4).. DERIVADA DE UNA FUNCIÓN. Dfiició: f f ( ) f ( ) lim, si l límit ist. 0 Notció: f ', f ( ) E.g.:
. INTEGRACION, DIFERENCIACIÓN DE FUNCIONES Y EXPANSIONES EN SERIES. (._CvR_T_06, Rvisió: 5-0-06, C, C3, C4).. DERIVADA DE UNA FUNCIÓN. Dfiició: f f ( ) f ( ) lim, si l límit ist. 0 Notció: f ', f ( ) E.g.:
( ) [ ( )] ( ) MATEMÁTICAS BÁSICAS PRODUCTOS NOTABLES. a + b se puede obtener multiplicando término a término:
![( ) [ ( )] ( ) MATEMÁTICAS BÁSICAS PRODUCTOS NOTABLES. a + b se puede obtener multiplicando término a término: ( ) [ ( )] ( ) MATEMÁTICAS BÁSICAS PRODUCTOS NOTABLES. a + b se puede obtener multiplicando término a término:](/thumbs/40/21276395.jpg) Fult Cotuí Aiitió. UNAM Pouto otl Auto: D. Joé Mul B Eio MATEMÁTICAS BÁSICAS PRODUCTOS NOTABLES CONCEPTO DE PRODUCTO NOTABLE Tto l ultiliió li oo l itéti iu u loito uo o ou l ulto. Si o, it outo lio u
Fult Cotuí Aiitió. UNAM Pouto otl Auto: D. Joé Mul B Eio MATEMÁTICAS BÁSICAS PRODUCTOS NOTABLES CONCEPTO DE PRODUCTO NOTABLE Tto l ultiliió li oo l itéti iu u loito uo o ou l ulto. Si o, it outo lio u
n o ó i Mi nombre: Mi numero de orden: Cuadernillo 1 periodo II MOMENTO DE LA MOVILIZACIÓN NACIONAL POR LA MEJORA DE LOS APRENDIZAJES
 l bim cm CACIÓN EDU bim cm DOS TO C u m ó i c c i d r t m m i trá d D qu d r p d i, r u q rd p l rd m p d T d 2 d u g S g prid Mi mbr: Cudrill 1 Mi umr d rd: II MOMENTO DE LA MOVILIZACIÓN NACIONAL POR
l bim cm CACIÓN EDU bim cm DOS TO C u m ó i c c i d r t m m i trá d D qu d r p d i, r u q rd p l rd m p d T d 2 d u g S g prid Mi mbr: Cudrill 1 Mi umr d rd: II MOMENTO DE LA MOVILIZACIÓN NACIONAL POR
Definiciones de estabilidad BIBO
 Tem. Etilidd de Sitem Itroducció TEORÍA DE ONTROL L oció de etilidd e fudmetl e el derrollo de item de cotrol y e prticulr pr lo item retrolimetdo. L ueci de et propiedd vuelve iútil e l práctic culquier
Tem. Etilidd de Sitem Itroducció TEORÍA DE ONTROL L oció de etilidd e fudmetl e el derrollo de item de cotrol y e prticulr pr lo item retrolimetdo. L ueci de et propiedd vuelve iútil e l práctic culquier
a se denomina serie a es convergente y SERIES = si r <1 S n La suma de los términos de una sucesión infinita { } n n=1 infinita o simplemente serie
 SERIES L sum de los térmios de u suesió ifiit { } = ifiit o simplemete serie se deomi serie Y se represet o el símbolo = Defiiió: = 4 KK Dd l serie = ésim sum pril = 4 K K, se desigrá S su S = = = 4 K
SERIES L sum de los térmios de u suesió ifiit { } = ifiit o simplemete serie se deomi serie Y se represet o el símbolo = Defiiió: = 4 KK Dd l serie = ésim sum pril = 4 K K, se desigrá S su S = = = 4 K
ESTABILIDAD. 1. Concepto de estabilidad. 2. Criterio de Routh-Hurwitz. Métodos algebraicos para el análisis de estabilidad.
 Uiveridd Crlo III de Mdrid Señle y Sitem ESTABILIDAD Método lgerio pr el álii de etilidd.. Coepto de etilidd.. Criterio de Roth-Hrwitz. Dolore Blo, Rmó Brer, Mrí Mlfz y Migel Ágel Slih Uiveridd Crlo III
Uiveridd Crlo III de Mdrid Señle y Sitem ESTABILIDAD Método lgerio pr el álii de etilidd.. Coepto de etilidd.. Criterio de Roth-Hrwitz. Dolore Blo, Rmó Brer, Mrí Mlfz y Migel Ágel Slih Uiveridd Crlo III
tiene derivada continua hasta de orden 1
 Cálulo Numério Progrmió Apli INTERPOLACIÓN SEGMENTARIA O SPLINES L otruió e poliomio e iterpolió e gro lto uque utifile teórimete plte muo prolem Por u lo, l form e l fuió poliómi e gro lto meuo o repoe
Cálulo Numério Progrmió Apli INTERPOLACIÓN SEGMENTARIA O SPLINES L otruió e poliomio e iterpolió e gro lto uque utifile teórimete plte muo prolem Por u lo, l form e l fuió poliómi e gro lto meuo o repoe
Integrales Dobles. Vimos que este problema estaba relacionado con el cálculo de una primitiva de
 Pro. Erique Mteus Nieves otoro e Euió Mtemáti Itegrles oles Itrouió. E el primer urso e Fumetos se plteó el prolem e hllr el áre omprei etre l grái e u uió positiv y x, el eje OX y ls rets x, x. ih áre
Pro. Erique Mteus Nieves otoro e Euió Mtemáti Itegrles oles Itrouió. E el primer urso e Fumetos se plteó el prolem e hllr el áre omprei etre l grái e u uió positiv y x, el eje OX y ls rets x, x. ih áre
RESPUESTA TEMPORAL: PULSOS CONFORMADOS (Dominio del tiempo y Dominio de Laplace)
 ádr d Torí d ircio pn d Plo onormdo nrodcción RESPEST TEMPORL: PLSOS ONFORMDOS Dominio dl impo y Dominio d Lplc S mpln con ñl priódic o d orm pcil, l q dcomponn n ncion clón, rmp y dplzmino mporl Dominio
ádr d Torí d ircio pn d Plo onormdo nrodcción RESPEST TEMPORL: PLSOS ONFORMDOS Dominio dl impo y Dominio d Lplc S mpln con ñl priódic o d orm pcil, l q dcomponn n ncion clón, rmp y dplzmino mporl Dominio
Electrónica Básica. Álgebra de Boole. Electrónica Digital. José Ramón Sendra Sendra Dpto. de Ingeniería Electrónica y Automática ULPGC
 Eletrói Bási Álger de Boole Eletrói Digitl José Rmó Sedr Sedr Dpto. de Igeierí Eletrói y Automáti ULPGC 2 Ciruito de omutió p.e. sistem de otrol idustril sistem teleóio ordedor et. El Álger de Boole sirve
Eletrói Bási Álger de Boole Eletrói Digitl José Rmó Sedr Sedr Dpto. de Igeierí Eletrói y Automáti ULPGC 2 Ciruito de omutió p.e. sistem de otrol idustril sistem teleóio ordedor et. El Álger de Boole sirve
MÉTODO INDUCTIVO. Capítulo TRILCE
 pítulo É V l É V r lys prtir l osrvión los hhos, mint l gnrlizión l omportminto osrvo; n rli, lo qu rliz s un spi gnrlizión, sin qu por mio l lógi pu onsguir un mostrión ls its lys o onjunto onlusions.
pítulo É V l É V r lys prtir l osrvión los hhos, mint l gnrlizión l omportminto osrvo; n rli, lo qu rliz s un spi gnrlizión, sin qu por mio l lógi pu onsguir un mostrión ls its lys o onjunto onlusions.
2.- Dadas las matrices A y B. Calcula A+B, A-B, A 2, B 2, AB, BA
 ejeriiosemees.om MTRICES Y DETERMINNTES. Dds ls mtries Hllr ) ) B ).B d) B. e) +B f) C. g) C.B h) C.D i) j) B k) + l) B.B uioes. Dds ls mtries B. Clul +B, B,, B, B, B uió D C B.B / / / / / / / / B / /
ejeriiosemees.om MTRICES Y DETERMINNTES. Dds ls mtries Hllr ) ) B ).B d) B. e) +B f) C. g) C.B h) C.D i) j) B k) + l) B.B uioes. Dds ls mtries B. Clul +B, B,, B, B, B uió D C B.B / / / / / / / / B / /
Primer Parcial de Introducción a la Investigación de Operaciones Fecha: 5 de mayo de 2015
 Primr Pril Introuión l Invstigión Oprions Fh: 5 myo 2015 INDICACIONES Durión l pril: 3 hrs. Esriir ls hojs un solo lo. No s prmit l uso mtril ni lulor. Numrr ls hojs. Ponr nomr y númro éul n l ángulo suprior
Primr Pril Introuión l Invstigión Oprions Fh: 5 myo 2015 INDICACIONES Durión l pril: 3 hrs. Esriir ls hojs un solo lo. No s prmit l uso mtril ni lulor. Numrr ls hojs. Ponr nomr y númro éul n l ángulo suprior
ERROR EN ESTADO ESTACIONARIO
 UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD DE INGENIEÍA MECÁNICA Y EÉCICA EO EN ESADO ESACIONAIO INGENIEÍA DE CONO M.C. EIZABEH GPE. AA HDZ. M.C. OSÉ MANUE OCHA NÚÑEZ UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD
UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD DE INGENIEÍA MECÁNICA Y EÉCICA EO EN ESADO ESACIONAIO INGENIEÍA DE CONO M.C. EIZABEH GPE. AA HDZ. M.C. OSÉ MANUE OCHA NÚÑEZ UNIVESIDAD AUÓNOMA DE NUEVO EÓN FACUAD
EsyGes INFORME ESTADÍSTICAS DE LA CONSTRUCCIÓN DATOS GENERALES. Consultoría de Gestión. Mutilva Alta Navarra TFNO: FAX:
 EG Cultrí Gtió INFORME ESTADÍSTICAS DE LA CONSTRUCCIÓN DATOS GENERALES Mutil Alt Nrr TFNO: 4 52 12 FAX: 4 52 12 Eil: iitrió@. ÍNDICE 1.1 Cu Art Ct.... 3 1.2 El.... 3 1.3 Eluió Pri l Mtril.... 4 1.4 Eluió
EG Cultrí Gtió INFORME ESTADÍSTICAS DE LA CONSTRUCCIÓN DATOS GENERALES Mutil Alt Nrr TFNO: 4 52 12 FAX: 4 52 12 Eil: iitrió@. ÍNDICE 1.1 Cu Art Ct.... 3 1.2 El.... 3 1.3 Eluió Pri l Mtril.... 4 1.4 Eluió
La obtención y proyección de tablas de mortalidad empleando curvas spline
 X Ruó Nol Ivtgó Dmogá Méo Méo, DF, - Novm L otó poó tl motl mplo uv pl Aljo M Vlé El Colgo Méo ovm Itouó El ál uméo popoo l tumto téo o p llv o too lo pomto mtmáto tt o lgotmo qu pmt u muló o álulo E l
X Ruó Nol Ivtgó Dmogá Méo Méo, DF, - Novm L otó poó tl motl mplo uv pl Aljo M Vlé El Colgo Méo ovm Itouó El ál uméo popoo l tumto téo o p llv o too lo pomto mtmáto tt o lgotmo qu pmt u muló o álulo E l
EJERCICIOS DE REFUERZO DE ECUACIONES 4º ESO A
 Dprtmnto Cinis Mtmátis ºA Euions, sistms inuions Colio Con Espin Prosor Ánl Fuiio Mrtínz EJERCICIOS DE REFUERZO DE ECUACIONES º ESO A Rsolvr ls siuints uions: - = - = + + = = + = + = - = - -=- - = - -
Dprtmnto Cinis Mtmátis ºA Euions, sistms inuions Colio Con Espin Prosor Ánl Fuiio Mrtínz EJERCICIOS DE REFUERZO DE ECUACIONES º ESO A Rsolvr ls siuints uions: - = - = + + = = + = + = - = - -=- - = - -
SEMEJANZA DE TRIÁNGULOS
 IES ÉLAIOS Curso - Ruprión ª Evluión ÁREA: MATEMÁTICAS º ESO OPCIÓN B TEMAS,, 6 y 7 ACTIVIDADES DE RECUPERACIÓN DE LA ª EVALUACIÓN SEMEJANZA DE TRIÁNGULOS. S quir onstruir un prtrr on orm triángulo rtángulo.
IES ÉLAIOS Curso - Ruprión ª Evluión ÁREA: MATEMÁTICAS º ESO OPCIÓN B TEMAS,, 6 y 7 ACTIVIDADES DE RECUPERACIÓN DE LA ª EVALUACIÓN SEMEJANZA DE TRIÁNGULOS. S quir onstruir un prtrr on orm triángulo rtángulo.
Criterio de Estabilidad de Routh-Hurwitz
 Criterio de Etbilidd de Routh-Hurwitz F Pr l etbilidd BIBO, l ríce de l ecució crcterític +G()H() =, o lo polo de C()/R(), o puede etr loclizdo e el emiplo derecho del plo o e eje j, todo debe quedr e
Criterio de Etbilidd de Routh-Hurwitz F Pr l etbilidd BIBO, l ríce de l ecució crcterític +G()H() =, o lo polo de C()/R(), o puede etr loclizdo e el emiplo derecho del plo o e eje j, todo debe quedr e
ERROR EN ESTADO ESTACIONARIO
 UNIVESIDAD AUÓNOMA DE NUEVO LEÓN FACULAD DE INGENIEÍA MECÁNICA Y ELÉCICA EO EN ESADO ESACIONAIO INGENIEÍA DE CONOL M.C. ELIZABEH GPE. LAA HDZ. M.C. OSÉ MANUEL OCHA NÚÑEZ UNIVESIDAD AUÓNOMA DE NUEVO LEÓN
UNIVESIDAD AUÓNOMA DE NUEVO LEÓN FACULAD DE INGENIEÍA MECÁNICA Y ELÉCICA EO EN ESADO ESACIONAIO INGENIEÍA DE CONOL M.C. ELIZABEH GPE. LAA HDZ. M.C. OSÉ MANUEL OCHA NÚÑEZ UNIVESIDAD AUÓNOMA DE NUEVO LEÓN
Tema 9. Determinantes.
 Uidd.Determites Tem. Determites.. Coeptos previos, permutioes. Defiiió geerl de determites. Determite de mtries de orde y orde.. Determite mtries udrds de orde. Determite mtries udrds de orde. Determite
Uidd.Determites Tem. Determites.. Coeptos previos, permutioes. Defiiió geerl de determites. Determite de mtries de orde y orde.. Determite mtries udrds de orde. Determite mtries udrds de orde. Determite
UNIVERSIDAD FRANCISCO DE PAULA SANTANDER FACULTAD DE CIENCIAS BASICAS DEPARTAMENTO DE MATEMATICAS Y ESTADISTICA GUIA No. 1. ECUACIONES DIFERENCIALES
 UNIVERSIDAD FRANCISCO DE PAULA SANTANDER FACULTAD DE CIENCIAS BASICAS DEPARTAMENTO DE MATEMATICAS Y ESTADISTICA GUIA No.. ECUACIONES DIFERENCIALES ECUACIONES DIFERENCIALES U cució ircil s u cució l qu
UNIVERSIDAD FRANCISCO DE PAULA SANTANDER FACULTAD DE CIENCIAS BASICAS DEPARTAMENTO DE MATEMATICAS Y ESTADISTICA GUIA No.. ECUACIONES DIFERENCIALES ECUACIONES DIFERENCIALES U cució ircil s u cució l qu
SUCESIONES. El límite de una potencia es igual al límite de la base elevado al límite del exponente.
 SUCESIONES 1. El it d l sucsió d térmio grl A) B) 1 C) 0 + 1 3 + + 3 vl: (Covoctori juio 001. Exm tipo G) El it d u potci s igul l it d l bs lvdo l it dl xpot. + 1 1 Límit d l bs: 3 + 3 Límit dl xpot:
SUCESIONES 1. El it d l sucsió d térmio grl A) B) 1 C) 0 + 1 3 + + 3 vl: (Covoctori juio 001. Exm tipo G) El it d u potci s igul l it d l bs lvdo l it dl xpot. + 1 1 Límit d l bs: 3 + 3 Límit dl xpot:
Árboles binarios. Árbol: definición. Árbol (del latín arbor oris):
 Árol: iniión Árols inrios Árol (l ltín ror oris): Plnt prnn, trono lñoso y lvo, qu s rmii irt ltur l sulo. (otrs, vr Rl Ami Espñol ) Frno Guii Polno Esul Innirí Inustril Pontiii Univrsi Ctóli Vlpríso,
Árol: iniión Árols inrios Árol (l ltín ror oris): Plnt prnn, trono lñoso y lvo, qu s rmii irt ltur l sulo. (otrs, vr Rl Ami Espñol ) Frno Guii Polno Esul Innirí Inustril Pontiii Univrsi Ctóli Vlpríso,
Emailing an Application and supporting documents into CCMS
 How to Emil n Applition into CCMS Emiling n Applition n upporting oumnt into CCMS With th nw Chil Cr Mngmnt Sytm (CCMS) our lint n provir now hv th ility to mil oumnt. Complting th oumnt urtly will nur
How to Emil n Applition into CCMS Emiling n Applition n upporting oumnt into CCMS With th nw Chil Cr Mngmnt Sytm (CCMS) our lint n provir now hv th ility to mil oumnt. Complting th oumnt urtly will nur
Compensación: diseño de Gc. Ejemplo 1: Sea una planta Gs () =
 Compenión: ieño e G Ejemplo : Se un plnt G () =, e neeit relimentr l ( + )( + )( + ) plnt. El enor utilio tenú vee l li (G LCBF =) y lo requerimiento el item relimento on lo iguiente: ) Anho e bn, BW=r/eg
Compenión: ieño e G Ejemplo : Se un plnt G () =, e neeit relimentr l ( + )( + )( + ) plnt. El enor utilio tenú vee l li (G LCBF =) y lo requerimiento el item relimento on lo iguiente: ) Anho e bn, BW=r/eg
Teoría de Sistemas y Señales
 Teorí de Sitem y Señle Criterio lgerio de etilidd Criterio de Routh Autor Dr. Jun Crlo Gómez Criterio Algerio de Etilidd pr SE en TC Promo que l ondiión neeri y ufiiente pr que un SE en TC repreentdo por
Teorí de Sitem y Señle Criterio lgerio de etilidd Criterio de Routh Autor Dr. Jun Crlo Gómez Criterio Algerio de Etilidd pr SE en TC Promo que l ondiión neeri y ufiiente pr que un SE en TC repreentdo por
Matemáticas II (Bachillerato de Ciencias). Soluciones de los problemas propuestos. Tema 1 1. TEMA 1. Matrices Problemas Resueltos.
 Meáis (hillero e ieis) Soluioes e los proles propuesos Te wwweisjo José Mrí Mríez Meio TEM Mries Proles Resuelos Operioes o ries Ds, y, hll os úeros y pr que se verifique que Soluió Esriieo l euió exei
Meáis (hillero e ieis) Soluioes e los proles propuesos Te wwweisjo José Mrí Mríez Meio TEM Mries Proles Resuelos Operioes o ries Ds, y, hll os úeros y pr que se verifique que Soluió Esriieo l euió exei
MATEMÁTICAS 2º DE ESO LOE
 MATEMÁTICAS º DE ESO LOE TEMA II: FRACCIONES Los sigifios e u frió. Frioes propis e impropis. Equivlei e frioes. Amplifiió y simplifiió. Frió irreuile. Reuió e frioes omú eomior. Comprió e frioes. Operioes
MATEMÁTICAS º DE ESO LOE TEMA II: FRACCIONES Los sigifios e u frió. Frioes propis e impropis. Equivlei e frioes. Amplifiió y simplifiió. Frió irreuile. Reuió e frioes omú eomior. Comprió e frioes. Operioes
Reducción de. Estados equivalentes. Reducción de estados equivalentes. Ejemplo. Tabla de estados Mario Medina C. 1
 Ruión stos quivlnts Mrio Min. mriomin@u.l Ruión stos quivlnts Proso isño ntrior no sgur l númro mínimo stos Ruión númro stos Ru l númro lip-lops Ru l lógi ominionl Asignión vrils sto tmién pu ruir lógi
Ruión stos quivlnts Mrio Min. mriomin@u.l Ruión stos quivlnts Proso isño ntrior no sgur l númro mínimo stos Ruión númro stos Ru l númro lip-lops Ru l lógi ominionl Asignión vrils sto tmién pu ruir lógi
HUMANIDADES Y CIENCIAS DE LA EDUCACIÓN
 Flt HUMANIDADES Y CIENCIAS DE LA EDUCACIÓN Gr Eió Priri Uivri Jé GRADO EN EDUCACIÓN PRIMARIA PRESENTACIÓN DEL GRADO Pr l btió l títl Gr Eió Priri r l Uivri Jé brá rr 240 ECTS. Et títl it r l rfió M y M
Flt HUMANIDADES Y CIENCIAS DE LA EDUCACIÓN Gr Eió Priri Uivri Jé GRADO EN EDUCACIÓN PRIMARIA PRESENTACIÓN DEL GRADO Pr l btió l títl Gr Eió Priri r l Uivri Jé brá rr 240 ECTS. Et títl it r l rfió M y M
Sus términos son antecedente y consecuente. Proporción. Una proporción es una igualdad entre dos razones.
 Rzón y proporión. Rzón. Rzón entre os números y es el oiente. Sus términos son nteeente y onseuente. Proporión. Un proporión es un igul entre os rzones. Se lee es omo es.,, y son los términos e l proporión.
Rzón y proporión. Rzón. Rzón entre os números y es el oiente. Sus términos son nteeente y onseuente. Proporión. Un proporión es un igul entre os rzones. Se lee es omo es.,, y son los términos e l proporión.
CAPÍTULO 2 PROCESAMIENTO DE CALCOGENUROS POR SOLUCIÓN
 APÍTULO 2 PROESAMIENTO DE ALOGENUROS POR SOLUIÓN 2.1 INTRODUIÓN E iió t j ió irti q í ti ti i t r q h rr r ti r r i í i ifrt t. L r r friió í iviir r : r fíi i q it tá r rt t r ifrt i fíi; r qíi r óit
APÍTULO 2 PROESAMIENTO DE ALOGENUROS POR SOLUIÓN 2.1 INTRODUIÓN E iió t j ió irti q í ti ti i t r q h rr r ti r r i í i ifrt t. L r r friió í iviir r : r fíi i q it tá r rt t r ifrt i fíi; r qíi r óit
Progresiones aritméticas y geométricas
 Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
DEFINICIÓN 1: Sea G = (V, A) un digrafo conexo y sin lazos. Se dice que G es una RED o RED DE TRANSPORTE si se verifican:
 REDES DE TRANSORTE E un pliión digro ponrdo l lujo irulión un ien un uente un tino ddo. Lo iene puen er por ejemplo litro petróleo que luyen por tuerí llmd teleóni tré un item omuniión et. Oerión: el peo
REDES DE TRANSORTE E un pliión digro ponrdo l lujo irulión un ien un uente un tino ddo. Lo iene puen er por ejemplo litro petróleo que luyen por tuerí llmd teleóni tré un item omuniión et. Oerión: el peo
UNIDAD 1.- Números reales (temas 1 del libro)
 UNIDAD.- Núeros reles (tes el libro). NUMEROS NATURALES Y ENTEROS Co los úeros turles otos los eleetos e u ojuto (úero ril). O bie expresos l posiió u ore que oup u eleeto e u ojuto (oril). Se represet
UNIDAD.- Núeros reles (tes el libro). NUMEROS NATURALES Y ENTEROS Co los úeros turles otos los eleetos e u ojuto (úero ril). O bie expresos l posiió u ore que oup u eleeto e u ojuto (oril). Se represet
ISSN: Número 37. Marzo de 2014 páginas 57-70
 www.ism.org/w/uio ISSN: 85-4 Númro 7. rzo 4 págis 57-7 U ls torí grupos uso progrsios ritmétis gométris y mtris urs or impr Josph Friso This Arrz Eilmo Crvjl Fh rpió: /4/ Fh ptió: 5// Rsum Astrt Rsumo
www.ism.org/w/uio ISSN: 85-4 Númro 7. rzo 4 págis 57-7 U ls torí grupos uso progrsios ritmétis gométris y mtris urs or impr Josph Friso This Arrz Eilmo Crvjl Fh rpió: /4/ Fh ptió: 5// Rsum Astrt Rsumo
MATEMÁTICAS PARA LA COMPUTACIÓN CAPÍTULO 6. RELACIONES
 MATEMÁTICAS PARA LA COMPUTACIÓN CAPÍTULO. RELACIONES DIAGRAMAS DE HASSE. AUTOR: JOSÉ ALFREDO JIMÉNEZ MURILLO AVC APOYO VIRTUAL PARA EL CONOCIMIENTO Digrms Hss Un rlión R:A B s orn pril o prilmnt orn si
MATEMÁTICAS PARA LA COMPUTACIÓN CAPÍTULO. RELACIONES DIAGRAMAS DE HASSE. AUTOR: JOSÉ ALFREDO JIMÉNEZ MURILLO AVC APOYO VIRTUAL PARA EL CONOCIMIENTO Digrms Hss Un rlión R:A B s orn pril o prilmnt orn si
CIENCIAS EXPERIMENTALES
 Fult CIENCIAS EXPERIMENTALES Gr Bilí Uivri Jé GRADO EN BIOLOGÍA PRESENTACIÓN DEL GRADO El Gr Bilí u titulió rátr itífi qu ti m bjtiv frmr l lum l imit l vi t u ft l ut vit mlulr ht l tui l itm rfi l l
Fult CIENCIAS EXPERIMENTALES Gr Bilí Uivri Jé GRADO EN BIOLOGÍA PRESENTACIÓN DEL GRADO El Gr Bilí u titulió rátr itífi qu ti m bjtiv frmr l lum l imit l vi t u ft l ut vit mlulr ht l tui l itm rfi l l
En un grafo se puede recorrer la información de diferentes maneras para llegar de un punto a otro.
 CAMINOS Y CIRCUITOS En un grfo s pu rorrr l informión ifrnts mnrs pr llgr un punto otro. Cmino Ciruito (Cilo) Ciruito simpl longitu n Cmino simpl longitu n ulquir suni noos n l qu pr son ynts. Es un mino
CAMINOS Y CIRCUITOS En un grfo s pu rorrr l informión ifrnts mnrs pr llgr un punto otro. Cmino Ciruito (Cilo) Ciruito simpl longitu n Cmino simpl longitu n ulquir suni noos n l qu pr son ynts. Es un mino
FUNCIONES DERIVABLES EN UN INTERVALO
 DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. FUNCIONES DERIVABLES EN UN INTERVALO Ls unions qu son ontinus n un intrvlo rrdo [, ] y drivls n un intrvlo irto, tinn propidds importnts. Torm d Roll.
DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. FUNCIONES DERIVABLES EN UN INTERVALO Ls unions qu son ontinus n un intrvlo rrdo [, ] y drivls n un intrvlo irto, tinn propidds importnts. Torm d Roll.
MÓDULO Nº5 COMPARADORES Y SUMADORES
 MÓULO Nº OMPRORES Y SUMORES UNI: LÓGI OMINTORI TEMS: omprors. Sumors. OJETIVOS: Explir qu s un ompror y sus prinipls rtrístis. Explir qu s un sumor y sus prinipls rtrístis.. omprors: ESRROLLO E TEMS En
MÓULO Nº OMPRORES Y SUMORES UNI: LÓGI OMINTORI TEMS: omprors. Sumors. OJETIVOS: Explir qu s un ompror y sus prinipls rtrístis. Explir qu s un sumor y sus prinipls rtrístis.. omprors: ESRROLLO E TEMS En
ALELUYA. D A Bmi F#mi ALELUYA, ALELU ALELUYA G D A ALELUYA, ALELUYA. D A Bmi F#mi ALELUYA, ALELU ALELUYA, G D A D ALELUYA, ALELUUUYA SANTO
 NTR UNTS VS --0 1---3-3-3 1---5-5 1 3 0 --1---3---5-5-5---3---6-6---3---5---1 UNTS VS SINO NIÑO T R ON MIS VRSOS T I QU T MB //POO POO ON L TIMPO mi OLVINOM TI mi POR MINOS QU S LJN M PRI// HOY H VULTO
NTR UNTS VS --0 1---3-3-3 1---5-5 1 3 0 --1---3---5-5-5---3---6-6---3---5---1 UNTS VS SINO NIÑO T R ON MIS VRSOS T I QU T MB //POO POO ON L TIMPO mi OLVINOM TI mi POR MINOS QU S LJN M PRI// HOY H VULTO
( ) [ ( )] ( ) PRODUCTOS NOTABLES Y FACTORIZACIÓN UNIDAD V V.1 PRODUCTOS NOTABLES. a + b se puede obtener multiplicando término a término:
![( ) [ ( )] ( ) PRODUCTOS NOTABLES Y FACTORIZACIÓN UNIDAD V V.1 PRODUCTOS NOTABLES. a + b se puede obtener multiplicando término a término: ( ) [ ( )] ( ) PRODUCTOS NOTABLES Y FACTORIZACIÓN UNIDAD V V.1 PRODUCTOS NOTABLES. a + b se puede obtener multiplicando término a término:](/thumbs/48/24308156.jpg) Pági l Colgio Mtátis l ENP-UNAM Proutos otls toriió Autor: Dr. José Mul Brr Esios PRODUCTOS NOTABLES Y FACTORIZACIÓN UNIDAD V V. PRODUCTOS NOTABLES Tto l ultiliió lgri oo l ritéti s sigu u lgorito uos
Pági l Colgio Mtátis l ENP-UNAM Proutos otls toriió Autor: Dr. José Mul Brr Esios PRODUCTOS NOTABLES Y FACTORIZACIÓN UNIDAD V V. PRODUCTOS NOTABLES Tto l ultiliió lgri oo l ritéti s sigu u lgorito uos
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE QUÍMICA DEPARTAMENTO DE MATEMÁTICAS Ecuaciones Diferenciales [Guia]
![UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE QUÍMICA DEPARTAMENTO DE MATEMÁTICAS Ecuaciones Diferenciales [Guia] UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE QUÍMICA DEPARTAMENTO DE MATEMÁTICAS Ecuaciones Diferenciales [Guia]](/thumbs/80/80848373.jpg) UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE QUÍMICA DEPARTAMENTO DE MATEMÁTICAS Ecucio Difrcil [Gui] E l hoj d orcio or l úmro d rgu, l drrollo qu juifiqu u ru, u ru co i crrd u rcágulo lugo u
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE QUÍMICA DEPARTAMENTO DE MATEMÁTICAS Ecucio Difrcil [Gui] E l hoj d orcio or l úmro d rgu, l drrollo qu juifiqu u ru, u ru co i crrd u rcágulo lugo u
Ecuaciones de recurrencia
 Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
1) CONCEPTOS 2) MONOMIOS TEMA : EXPRESIONES ALGEBRAICAS
 TEMA EXPRESIONES ALGEBRAICAS CONCEPTOS U EXPRESIÓN ALGEBRAICA es el ojuto e úmeros letrs que se omi o los sigos e ls operioes mtemátis sum, rest, multipliió, ivisió poteiió. Ejemplo El VALOR NUMÉRICO e
TEMA EXPRESIONES ALGEBRAICAS CONCEPTOS U EXPRESIÓN ALGEBRAICA es el ojuto e úmeros letrs que se omi o los sigos e ls operioes mtemátis sum, rest, multipliió, ivisió poteiió. Ejemplo El VALOR NUMÉRICO e
Determine las ecuaciones vectorial, paramétricas y simétricas de la recta que., siendo D(4, 0, -1) y T(2, -3, 1).
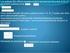 Vetores Cooreos Ilustrió 38 Determie ls euioes vetoril prmétris y simétris e l ret que ps por el puto A- 3 y es prlel l vetor DT sieo D4 0 - y T -3. Soluió Desigemos est ret por L A DT Se Px y z tl que
Vetores Cooreos Ilustrió 38 Determie ls euioes vetoril prmétris y simétris e l ret que ps por el puto A- 3 y es prlel l vetor DT sieo D4 0 - y T -3. Soluió Desigemos est ret por L A DT Se Px y z tl que
Aquauno Video 2 Plus
 Cont l progrmor l grifo. Aquuno Vio 2 Plus Pág. 1 Guí uso 3 START STOP RESET CANCEL 3 4 5 6 3 4 5 6 3 4 5 6 Cli! Pr Aquuno Vio 2 (ó.): 8454-8428 Pr Aquuno Vio 2 Plus (ó.): 8412 Ar l móulo progrmión, prsionno
Cont l progrmor l grifo. Aquuno Vio 2 Plus Pág. 1 Guí uso 3 START STOP RESET CANCEL 3 4 5 6 3 4 5 6 3 4 5 6 Cli! Pr Aquuno Vio 2 (ó.): 8454-8428 Pr Aquuno Vio 2 Plus (ó.): 8412 Ar l móulo progrmión, prsionno
ANÁLISIS DE LA RESPUESTA TRANSITORIA
 CAPITULO ANÁLISIS DE LA RESPUESTA TRANSITORIA. INTRODUCCIÓN Ua la caractrítica má importat lo itma cotrol u rputa traitoria. Como l propóito lo itma cotrol proporcioar ua rputa aa, frcutmt u rputa traitoria
CAPITULO ANÁLISIS DE LA RESPUESTA TRANSITORIA. INTRODUCCIÓN Ua la caractrítica má importat lo itma cotrol u rputa traitoria. Como l propóito lo itma cotrol proporcioar ua rputa aa, frcutmt u rputa traitoria
Matemáticas II Bloque VI Carlos Tiznado Torres
 Mtmátis II loqu VI rlos Tizno Torrs IRUNFERENI El írulo y l irunfrni son os ojtos gométrios qu hn llmo l tnión y hn sio l ojto stuio un grn númro mtmátios s timpos ntiguos, sino más grn utili práti pr
Mtmátis II loqu VI rlos Tizno Torrs IRUNFERENI El írulo y l irunfrni son os ojtos gométrios qu hn llmo l tnión y hn sio l ojto stuio un grn númro mtmátios s timpos ntiguos, sino más grn utili práti pr
Definiciones. Los valores de los términos necesarios para empezar a calcular se llaman condiciones iniciales.
 Deprtmeto de Mtemáti plid. ETSIIf. UPM. Vitori Zrzos Rodríguez RELCIONES DE RECURRENCI Defiiioes Relió de reurrei o reursiv pr l suesió { } es u epresió que relio el térmio geerl de l suesió o uo o más
Deprtmeto de Mtemáti plid. ETSIIf. UPM. Vitori Zrzos Rodríguez RELCIONES DE RECURRENCI Defiiioes Relió de reurrei o reursiv pr l suesió { } es u epresió que relio el térmio geerl de l suesió o uo o más
{ } + S = = S, para S. a converge si su sucesión de sumas parciales converge, es decir,
 Esuel de Igeierí Cetro de Ciei Bási Cálulo de Vrile Rel Guí teóri Series Series Iiits: Deiiió: Se { } u suesió iiit. L epresió, se deoi serie iiit o serie y se deot por: { } S S S S S S S S - U serie es
Esuel de Igeierí Cetro de Ciei Bási Cálulo de Vrile Rel Guí teóri Series Series Iiits: Deiiió: Se { } u suesió iiit. L epresió, se deoi serie iiit o serie y se deot por: { } S S S S S S S S - U serie es
D E T E R M I N A N T E S M A T R I Z I N V E R S A
 º DE BACHILLERATO DETERMINANTES D E T E R M I N A N T E S ----------- M A T R I Z I N V E R S A DETERMINANTES I. Determites. II. Primers pliioes de los determites. I. Determites.. Defiió álulo de u determite.
º DE BACHILLERATO DETERMINANTES D E T E R M I N A N T E S ----------- M A T R I Z I N V E R S A DETERMINANTES I. Determites. II. Primers pliioes de los determites. I. Determites.. Defiió álulo de u determite.
APUNTE: TRIGONOMETRIA
 APUNTE: TRIGONOMETRIA UNIVERSIDAD NACIONAL DE RIO NEGRO Asigntur: Mtemáti Crrers: Li. en Eonomí Profesor: Prof. Mel S. Chresti Cutrimestre: ero Año: 06 o Coneptos Previos o Definiión de ángulo Un ángulo
APUNTE: TRIGONOMETRIA UNIVERSIDAD NACIONAL DE RIO NEGRO Asigntur: Mtemáti Crrers: Li. en Eonomí Profesor: Prof. Mel S. Chresti Cutrimestre: ero Año: 06 o Coneptos Previos o Definiión de ángulo Un ángulo
Seguridad Sanitaria Internacional
 7 Abri 2007 Sguri Sitri Itrcio Oció pr ibiizr obr pcto cv u mui. E objtivo guri itri itr gobiro/orgizcio/ mpr ivrtir u pr forjr u porvir má guro. Efrm mrgt/pimióg y u brot; propgció VIH/SIDA, mrgci humitri
7 Abri 2007 Sguri Sitri Itrcio Oció pr ibiizr obr pcto cv u mui. E objtivo guri itri itr gobiro/orgizcio/ mpr ivrtir u pr forjr u porvir má guro. Efrm mrgt/pimióg y u brot; propgció VIH/SIDA, mrgci humitri
TP: "POTENCIACIÓN" exponente. "n" veces a. Definición conveniente: Todo número real distinto de cero elevado a la cero da 1(uno) En símbolos: a 0 : a
 TP: "POTENCIACIÓN" Defiiió Ddo u ierto úmero rel, llmremos "potei eésim de " l produto de por sí mismo u tidd de vees; siedo u úmero turl. E símolos: se expoete........ p POTENCIA ENÉSIMA de Ej:.. 8 ""
TP: "POTENCIACIÓN" Defiiió Ddo u ierto úmero rel, llmremos "potei eésim de " l produto de por sí mismo u tidd de vees; siedo u úmero turl. E símolos: se expoete........ p POTENCIA ENÉSIMA de Ej:.. 8 ""
APLICACIONES DE LA DIFERENCIAL
 DEINICIÓN DE UNCIÓN DIERENCIABLE Se die que u uió es diereible e u puto si su iremeto puede esribirse de l orm g η es tl que g o depede de los iremetos η udo. Ejemplo: Determir si l uió es diereible. Clulemos
DEINICIÓN DE UNCIÓN DIERENCIABLE Se die que u uió es diereible e u puto si su iremeto puede esribirse de l orm g η es tl que g o depede de los iremetos η udo. Ejemplo: Determir si l uió es diereible. Clulemos
26 EJERCICIOS de LOGARITMOS
 6 EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
6 EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
OPERACIONES MATEMÁTICAS
 Cpítulo OPERACIONES MATEMÁTICAS OPERACIÓN MATEMÁTICA E un poo qu onit n l tnfoión un o á nti n ot ll ulto, jo it gl o oniion n l ul fin l opión. To opión táti pnt un gl finiión y un íolo qu l intifi llo
Cpítulo OPERACIONES MATEMÁTICAS OPERACIÓN MATEMÁTICA E un poo qu onit n l tnfoión un o á nti n ot ll ulto, jo it gl o oniion n l ul fin l opión. To opión táti pnt un gl finiión y un íolo qu l intifi llo
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL
 Cpít ulo RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL Dfiniions Pvis: I. ÁNGULO EN POSICIÓN NORMAL Llmo tmién n posiión nóni o stán. Es quél ángulo tigonométio uo véti oini on l oign l sistm
Cpít ulo RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL Dfiniions Pvis: I. ÁNGULO EN POSICIÓN NORMAL Llmo tmién n posiión nóni o stán. Es quél ángulo tigonométio uo véti oini on l oign l sistm
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
E.T.S.I. Industriales y Telecomunicación Curso Grados E.T.S.I. Industriales y Telecomunicación
 E.T.S.I. Idustrils y Tlcomuicció Curso 00-0 Grdos E.T.S.I. Idustrils y Tlcomuicció Asigtur: Cálculo I Tm : Sucsios y Sris Numérics. Sris d Potcis. Ejrcicios propustos Obtr los cutro primros térmios, sí
E.T.S.I. Idustrils y Tlcomuicció Curso 00-0 Grdos E.T.S.I. Idustrils y Tlcomuicció Asigtur: Cálculo I Tm : Sucsios y Sris Numérics. Sris d Potcis. Ejrcicios propustos Obtr los cutro primros térmios, sí
PROBLEMAS DE ÁLGEBRA DE MATRICES
 Mtemátis Álger e mtries José Mrí Mrtínez Meino PROLEMS DE ÁLGER DE MTRCES Oservión: L myorí e estos ejeriios proeen e ls prues e Seletivi D l mtriz enuentr tos ls mtries P tles que P P Soluión: Se ese
Mtemátis Álger e mtries José Mrí Mrtínez Meino PROLEMS DE ÁLGER DE MTRCES Oservión: L myorí e estos ejeriios proeen e ls prues e Seletivi D l mtriz enuentr tos ls mtries P tles que P P Soluión: Se ese
Clase 16. Tema: Racionalización de expresiones. Matemáticas 9. Bimestre: I Número de clase: 16. Tipo 1. Esta clase tiene video.
 Bimestre: I Número de lse: 16 Mtemátis Clse 16 Est lse tiee video Tem: Riolizió de expresioes Atividd 46 1 Le l siguiete iformió sore l riolizió. E mtemátis es omú eotrros o expresioes rioles que otiee
Bimestre: I Número de lse: 16 Mtemátis Clse 16 Est lse tiee video Tem: Riolizió de expresioes Atividd 46 1 Le l siguiete iformió sore l riolizió. E mtemátis es omú eotrros o expresioes rioles que otiee
Superintendencia de Servicios Sanitarios - SISS
 up v - I u u u u uó ul Rgó Pbló ub g l públ l m Pbló ub m gu v l m Fm g gu v vé l Públ vé m lv % Pbló m gu v bl Mpl 6.553.090 4.845.302 100,0% 0,0% 100,0% Vlpí 1.336.468 1.336.428 100,0% 0,0% 100,0% O
up v - I u u u u uó ul Rgó Pbló ub g l públ l m Pbló ub m gu v l m Fm g gu v vé l Públ vé m lv % Pbló m gu v bl Mpl 6.553.090 4.845.302 100,0% 0,0% 100,0% Vlpí 1.336.468 1.336.428 100,0% 0,0% 100,0% O
FÓRMULA DE TAYLOR 1. Introducción formula de Taylor Brook Taylor 2. Objetivos Aproximación de funciones por polinomios f(x) P(x) f(x)
 FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
r o d e M i r i a m c a n t a a l a b a n z a s a d i o s Hombres y Mujeres Ordinarios... Poder Superordinario
 H r o d f Hombr y Mujr Ordinrio... Podr Suprordinrio 9 M i r i m c n t b n z d i o C u r r í c u o h r o d F 2 0 1 2 www.miionrington.org Ningun prt d t currícuo podrá r rpubicd in prmio. Siént ibr d rproduciro
H r o d f Hombr y Mujr Ordinrio... Podr Suprordinrio 9 M i r i m c n t b n z d i o C u r r í c u o h r o d F 2 0 1 2 www.miionrington.org Ningun prt d t currícuo podrá r rpubicd in prmio. Siént ibr d rproduciro
126 l lg l g g b b t p p ñ ñ ñ l l l.. - p t p r l cl clí í í l L fc c u c i l y b ft i i cr cró ó ó l p b g,, i d,, p pm i l g i l ft i i g d r f i m
 SOBR BRE LA NEFRITIS CRON ONIC ICA DEL PERR RRO Y DEL GATO EL PELIGR IGRO DE PRACTI CTICAR CAR OPERAC RACION IONES EN LOS -BRIGH IGHTIC TICOS" Pr l Prf. HEBR BRAN ANT y Prf f. ju ANTO TOIN INE l El V r
SOBR BRE LA NEFRITIS CRON ONIC ICA DEL PERR RRO Y DEL GATO EL PELIGR IGRO DE PRACTI CTICAR CAR OPERAC RACION IONES EN LOS -BRIGH IGHTIC TICOS" Pr l Prf. HEBR BRAN ANT y Prf f. ju ANTO TOIN INE l El V r
WhittiLeaks Los apuntes que ellos no quieren que sepas de
 Métodos umérios WittiLes Los putes que ellos o quiere que seps de ITBA mo 7 WittiLes Resume Métodos umérios Pso Pr u fuió defiid e u itervlo: f (, ) ( ) el pso se defie por: ; dode es l tidd de divisioes
Métodos umérios WittiLes Los putes que ellos o quiere que seps de ITBA mo 7 WittiLes Resume Métodos umérios Pso Pr u fuió defiid e u itervlo: f (, ) ( ) el pso se defie por: ; dode es l tidd de divisioes
TP: "POTENCIACIÓN" exponente. "n" veces a. Definición conveniente: Todo número real distinto de cero elevado a la cero da 1(uno) En símbolos: a 0: a
 TP: "POTENCIACIÓN" Defiiió Ddo u ierto úmero rel, llmremos "potei eésim de " l produto de por sí mismo u tidd de vees; siedo u úmero turl. E símolos: se expoete........ p POTENCIA ENÉSIMA de Ej:.. "" vees
TP: "POTENCIACIÓN" Defiiió Ddo u ierto úmero rel, llmremos "potei eésim de " l produto de por sí mismo u tidd de vees; siedo u úmero turl. E símolos: se expoete........ p POTENCIA ENÉSIMA de Ej:.. "" vees
CAPITULO 3 SISTEMAS DE ECUACIONES LINEALES ...
 LGEBR SUPERIOR Y LINEL.. INTRODUCCION. CPITULO SISTEMS DE ECUCIONES LINELES Se llm ecució liel ó ecució de primer grdo, u ecució que relcio cierto úmero coocido, co u ó má icógit, e et ecució cd icógit
LGEBR SUPERIOR Y LINEL.. INTRODUCCION. CPITULO SISTEMS DE ECUCIONES LINELES Se llm ecució liel ó ecució de primer grdo, u ecució que relcio cierto úmero coocido, co u ó má icógit, e et ecució cd icógit
Algunas propiedades de los Números reales. Números reales (R) c d
 Profesoro e Nivel Meio y Superior e Biologí Mtemáti º Cutrimestre Año 0 Prof. Mrí Ele Ruiz Algus propiees e los Números reles (Este mteril tiee omo ojeto presetr u seleió e oeptos orrespoietes l Ui, pr
Profesoro e Nivel Meio y Superior e Biologí Mtemáti º Cutrimestre Año 0 Prof. Mrí Ele Ruiz Algus propiees e los Números reles (Este mteril tiee omo ojeto presetr u seleió e oeptos orrespoietes l Ui, pr
x a es una serie de la forma que el radio de convergencia de la serie geométrica es el intervalo abierto
 ERIE DE POTENCIA ERIE DE POTENCIA. Diició. U sri d pocis c s u sri d l orm c c c c... c... Por jmplo. i c y l sri d pocis om l orm....... Por jmplo. i c y l sri d pocis om l orm....... TEOREMA. El cojuo
ERIE DE POTENCIA ERIE DE POTENCIA. Diició. U sri d pocis c s u sri d l orm c c c c... c... Por jmplo. i c y l sri d pocis om l orm....... Por jmplo. i c y l sri d pocis om l orm....... TEOREMA. El cojuo
