1.2 INTEGRACION, DIFERENCIACIÓN DE FUNCIONES Y EXPANSIONES EN SERIES. (1.2_CvR_T_062, Revisión: , C2, C3, C4)
|
|
|
- María José Torres Hernández
- hace 7 años
- Vistas:
Transcripción
1 . INTEGRACION, DIFERENCIACIÓN DE FUNCIONES Y EXPANSIONES EN SERIES. (._CvR_T_06, Rvisió: , C, C3, C4).. DERIVADA DE UNA FUNCIÓN. Dfiició: f f ( ) f ( ) lim, si l límit ist. 0 Notció: f ', f ( ) E.g.: f pr f() f ( ) lim lim lim, Rprstció gráfic: pit l fció f(). P mostrrs q: Si f() s ifrcil, tocs s fció coti. Si f() s coti, o csrimt s ifrcil (jmplo más simpl: f() ) El pto o f() o s ifrcil s cooc como siglri (slto, cmio cocvi my rpto oscilcios rápis). A prtir l fiició l riv pomos mostrr q: f() f () - f() g() h() f () g () h () s opror lil f() g() h() f () g () h() g() h () ' g( ) g'( ) h( ) h ( ) g( ) f() f '( ) h( ) h ( ) f ' Rgl l c: f ( ( )) f '( ) ( ).. INTEGRAL DE UNA FUNCIÓN. f(ξ ) f(ξ ) f(ξ ) Cosirmos l sm Rim... pr itrvlo : f ( ξ )( ) X 0-0
2 Spogmos q l itrvlo myor logit (orm P ) s v hor rcio. Esto llv fiir l itgrl Rim como: I f ( ) lim f ( ξ )( ), P 0 simpr y co l límit ist. Si st s l cso, s ic q l itgrl ist o covrg. Si l itgrl s igl cro, y s gtiv si <. E térmios l fiició límit: Pr c ε > 0, δ > 0 tl q: co P < δ. f ( ) f ( ξ )( ) < ε Algs propis y fórmls útils l itgrl: α βυ) α β υ ( lili v v v itgrció por prts..3 TEOREMA FUNDAMENTAL DEL CÁLCULO. Est torm prmit rlcior l itgrció y l ifrcició, lo q s útil pr vitr l so l fiició l itgrl. Formlmt, l torm stlc q: Si f() s coti y si f ( ξ) ξ F( ) pr, tocs F ( ) f( ). D igl mr, si f() s coti F ( ) f( ), tocs f ( ξ) ξ F( ). y..4 FUNCIONES ESPECIALES. Algs fcios ti itgrls q o so rprstls térmios fcios lmtls,.g.: π ξ 0 ξ rf ( ), 0 < L rprstció sts itgrls s hc co FUNCIONES ESPECIALES (rf(), Bssl, tc.).
3 Si o ist rprstció térmios fcios lmtls o spcils hy q tilizr lgú métoo itgrció méric (grlmt sos l sm Rim o lg vrició ll)...5 FUNCIONES ELEMENTALES...5. FUNCIÓN LOGARITMO NATURAL. Utilizo l torm fmtl l cálclo s fi como y yl() L( ) t, > 0 t Utilizo l torm tmié pomos vr q: t ( L( ) ) t i.., l fció s ifrcil. Amás, si ()>0 y s ifrcil, tocs: ( L( ) ) ( ) (rgl l c). Algs propis Básics: L ( ) 0 t 0 t L( ) L( ) L( ),(, > 0). Dmostrció: L( ) t t t t t t t t L( ) t t Cmio vril: t t t t L( ) L L( ) L( ), (, >0) L( )
4 L r r L() Co st fció tmié s stlc q: c si L c si..5. FUNCIÓN EXPONENCIAL. Ivrs l logritmo trl, fii por: y Ly Spoio q r r L r L r L L,, > 0 Si () s ifrcil [, ], tocs: S oti l mism fció l rivrl (importt pr mchs sitcios,.g., ccios ifrcils) c..6 EXPANSIÓN EN SERIE DE TAYLOR. Pr cir l psió fció térmios sri Tylor pomos prtir : ) f ( ) f ( ) f ( ) f ( ) f f ( ( ) () Do q f() s ritrri, cmplirs tmié q: f ( ) f ( ) f ( ) Sstityo sto () otmos: f ( ) f ( ) f ( ) f ( ) f ( ) f ( ) f ( ) f ) Evlo: ( ) f ( ) f ( )( 3
5 f ( f ( ) f ( ) f ( )( ) ) () Similrmt, cmplirs q: f ( ) f ( ) f ( ) Sstityo sto () s oti: f ( ) f( ) f ( )( ) f ( ) f ( ) f ( ) f ( )( ) f ( ) f ( ) f ( ) f ( ) f ( )( ) ( ) f ( )! Asmio q f() s lo sficitmt ifrcil, pomos rptir st procso pr otr: ( ) f ( ) f ( ) 3 f ( ) f ( ) f( ) f ( )( ) ( ) ( ) ( ) R,! 3! ( )! o ( ) R f ( ). Est s l FÓRMULA DE TAYLOR CON SOBRANTE R. P mostrrs q l sort p vlrs como: ( f ) ( ξ ) ( R ), o ξ s lgú pto co tro l itrvlo [, ]. Esto s! válio si y sólo si f() s coti tro l itrvlo. D st form, l Sri Tylor pr f() lror l pto stá fii como: f ( ) f ( ) ' f ( )( ) f ( ) ( ) f ( ) f ( )! 0 " ( ) ( )!... f ( ) ( ) ( )!... SERIE DE TAYLOR PARA f() EN 4
6 f() ifrcil l itrvlo itrés (coició fmtl). Utili: Rprstció fcios (óts q l rprstció s úic). Aproimcios. Esqms méricos. Ejmplo. f( ) f ( ) f ( ) ( ) f ( ) 3 ( f ) (0) f ( )! 3! Sri lror 0: sri Mclri Algs fcios ti rprstció q s lo sficitmt simpl como pr rcorrl mmori. Amás, por lo grl sts so útils pr srrollr sris más compljs. E mchos csos s covit coocr ls rprstcios sris ls fcios lmtls y q mit miplcios lgrics pomos otr sris poco más compljs si csi vlr ls rivs. Ejmplo. Spogmos q qrmos vlr l sri f( ), pro hor clqir pto ifrt cro. Al igl q l jmplo trior pomos vlr ls rivs pr otr: f ( ) f ( ) ( ) f ( ) ( f ) ( ) 3 ( ) ( ) f( ) ( )! 3! Altrtivmt pomos scriir l fció pocil como f( ) rcorr q l sri Mclri l fció pocil s:, y 3 f( )! 3! Pomos vlr hor st sri - pr otr: 3 ( ) ( ) ( ) f ( )! 3! 5
7 Co sto otmos tocs l psió Tylor l fció clqir pto, i..: 3 ( ) ( ) f( ) ( ),! 3! q s l mism prsió oti l fiició. Ejmplo 3. Co l rprstció sri Tylor l fció pocil pomos otr tmié rprstcios pr otrs fcios,.g., smos q: y ycosh cosh( ) ( ) y sh( ) ( ) cosh( ) sh( ) fció pr fció impr. ysh Miplo l sri Tylor pomos osrvr q: ! 3! 4! 5! ! 4! 3! 5! cosh() sh() D ls fiicios (o qivltmt ls sris Tylor) pomos vr tmié q: cosh( ) sh( ), sh( ) cosh( ) Ejmplo 4. Epsió sri Tylor 0 pr f( ). Est fció stá fii como: Evlo ls rivs otmos: f( ) L 6
8 L f ( ) L L f L ( ) (L ) (L ) L 3 3 ( f ( ) (L ) (L ) f ) (0) (L ) ( ) L f ( ) (L ) (L ) L sri Mclri pr st fció s tocs: 3 ( ) 3 f ( ) f (0) (L ) L (L ) (L )!!! 3! 0 0 Ejmplo 5. Epsió sri Tylor pr f ( ) L. ( ) ( ) L form grl l sri q scmos s: f( ) L( ) f () 0! Evlo ls rivs otmos: f ( ) f ( ) f ( ) 3 iv 3 f ( ) 4 ( ) ( )! f ( ) ( ) 3 ( ) ( ) ( ) ( ) L( ) L() ( ) ( )! ( )! Altrtivmt, hcio y otmos: 3 4 y y y L( y) y
{ }: en determinado término. Por ejemplo, en la primera sucesión el primer término ( ), es 10. El término enésimo o general es a = 2
 Pági dl olgio d Mtmátics d l ENP-UNM L itgrl tor: r. José Ml crr Espios L INTEGRL UNI V V. SUESIONES V.. EFINIIÓN E SUESIÓN U scsió s list d úmros q sig rgl dtrmid: { } {,,,, }, i Formlmt, ls scsios s
Pági dl olgio d Mtmátics d l ENP-UNM L itgrl tor: r. José Ml crr Espios L INTEGRL UNI V V. SUESIONES V.. EFINIIÓN E SUESIÓN U scsió s list d úmros q sig rgl dtrmid: { } {,,,, }, i Formlmt, ls scsios s
61.1 6.1. SERIES NUMÉRICAS INFINITAS 6.2. SERIES DE TÉRMINOS POSITIVOS 6.3. SERIES ALTERNANTES 6.4. SERIES DE POTENCIAS
 Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
UNIDAD 3: SISTEMAS DE ECUACIONES LINEALES. 1. DEFINICIONES. Un sistema de m ecuaciones lineales con n incógnitas es una expresión de la forma:
 IE Pdr Povd (Gudi) Mtátics plicds ls CC II Dprtto d Mtátics Bloqu I: Álgr il Profsor: Ró ort Nvrro Uidd : ists d Ecucios ils UNIDD : ITEM DE ECUCIONE INEE DEFINICIONE U sist d cucios lils co icógits s
IE Pdr Povd (Gudi) Mtátics plicds ls CC II Dprtto d Mtátics Bloqu I: Álgr il Profsor: Ró ort Nvrro Uidd : ists d Ecucios ils UNIDD : ITEM DE ECUCIONE INEE DEFINICIONE U sist d cucios lils co icógits s
UNIDAD 7 SISTEMAS DE ECUACIONES LINEALES. 1. DEFINICIONES. Un sistema de m ecuaciones lineales con n incógnitas es una expresión de la forma:
 IES Pdr Povd (Gudi) Mtátics II Dprtto d Mtátics Bloqu II: Álgr il Profsor: Ró ort Nvrro Uidd : Sists d Ecucios ils UNIDD SISTEMS DE ECUCIONES INEES DEFINICIONES U sist d cucios lils co icógits s u prsió
IES Pdr Povd (Gudi) Mtátics II Dprtto d Mtátics Bloqu II: Álgr il Profsor: Ró ort Nvrro Uidd : Sists d Ecucios ils UNIDD SISTEMS DE ECUCIONES INEES DEFINICIONES U sist d cucios lils co icógits s u prsió
es divergente. es divergente.
 .- Dtrmir l cráctr d l sri sgú los vlors d = +. Solució: sido = + = Si = = lim = s divrgt. = Si < < lim = s divrgt. = Si = = lim = s divrgt. = Si >, plicdo l critrio d D`Almrt: + ( + ) ( + ) + lim = lim
.- Dtrmir l cráctr d l sri sgú los vlors d = +. Solució: sido = + = Si = = lim = s divrgt. = Si < < lim = s divrgt. = Si = = lim = s divrgt. = Si >, plicdo l critrio d D`Almrt: + ( + ) ( + ) + lim = lim
CAPÍTULO 2.- Representaciones en el dominio del tiempo para sistemas lineales e invariantes con el tiempo
 Sigls Ssms, /E Simo i Brr V V Coprig Jo Wil & Sos Ic All rigs rsrv CAPÍTULO - Rprscios l omiio l impo pr sisms lils ivris co l impo Irocció Covolció: rprsció l rsps l implso Propis l rprsció l rsps l implso
Sigls Ssms, /E Simo i Brr V V Coprig Jo Wil & Sos Ic All rigs rsrv CAPÍTULO - Rprscios l omiio l impo pr sisms lils ivris co l impo Irocció Covolció: rprsció l rsps l implso Propis l rprsció l rsps l implso
Sobre la integral de línea en un álgebra de dimensión real 2 que no son los complejos
 Culcyt// Itgrls Sor l itgrl d lí u álgr d dimsió rl qu o so los compljos Eliflt Lópz Gozlz, Víctor M Crrillo S, Srgio Trrzs Porrs Rsum: Cosidrmos u álgr d Bch A comuttiv uitri d dimsió rl qu o so los úmros
Culcyt// Itgrls Sor l itgrl d lí u álgr d dimsió rl qu o so los compljos Eliflt Lópz Gozlz, Víctor M Crrillo S, Srgio Trrzs Porrs Rsum: Cosidrmos u álgr d Bch A comuttiv uitri d dimsió rl qu o so los úmros
1 Ejemplos de Aproximaciones de Integrales con Sumas de Riemman
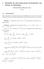 Ejmplos d Aproximacios d Itgrals co Sumas d Rimma Esta Ru Hurtado Cruz UNAM. Itrodució Estos jmplos d aproximacios d sumas d Rima s usaro l curso d Calculo II, durat l smstr 003- d la Facultad d Cicias
Ejmplos d Aproximacios d Itgrals co Sumas d Rimma Esta Ru Hurtado Cruz UNAM. Itrodució Estos jmplos d aproximacios d sumas d Rima s usaro l curso d Calculo II, durat l smstr 003- d la Facultad d Cicias
x a es una serie de la forma que el radio de convergencia de la serie geométrica es el intervalo abierto
 ERIE DE POTENCIA ERIE DE POTENCIA. Diició. U sri d pocis c s u sri d l orm c c c c... c... Por jmplo. i c y l sri d pocis om l orm....... Por jmplo. i c y l sri d pocis om l orm....... TEOREMA. El cojuo
ERIE DE POTENCIA ERIE DE POTENCIA. Diició. U sri d pocis c s u sri d l orm c c c c... c... Por jmplo. i c y l sri d pocis om l orm....... Por jmplo. i c y l sri d pocis om l orm....... TEOREMA. El cojuo
CÁLCULO DE LÍMITES. Por otro lado es importante distinguir en el cálculo de límites, los casos indeterminados de los determinados: = ; = ; =
 CÁLCULO DE LÍMITES Propidds d los límits.- ( b ) b.- ( b ) b.- ( b ) b.- ( b ) b b.- ( ) ( ) 6.- k k b Por otro ldo s importt distiguir l cálculo d límits, los csos idtrmidos d los dtrmidos: Csos dtrmidos:
CÁLCULO DE LÍMITES Propidds d los límits.- ( b ) b.- ( b ) b.- ( b ) b.- ( b ) b b.- ( ) ( ) 6.- k k b Por otro ldo s importt distiguir l cálculo d límits, los csos idtrmidos d los dtrmidos: Csos dtrmidos:
CAPITULO 17 FUNCIONES EXPONENCIALES Y LOGARITMICAS
 Capítlo 17. Drivada d las Fcios Epocial, Logarítmica. CAPITULO 17 FUNCIONES EXPONENCIALES Y LOGARITMICAS Ejrcicio. Dibja la gráfica d la fció =, para sto lla la sigit tabla: 0 1 3 4-1 - -3-4 Vamos l sigit
Capítlo 17. Drivada d las Fcios Epocial, Logarítmica. CAPITULO 17 FUNCIONES EXPONENCIALES Y LOGARITMICAS Ejrcicio. Dibja la gráfica d la fció =, para sto lla la sigit tabla: 0 1 3 4-1 - -3-4 Vamos l sigit
COTAS Y EXTREMOS DE CONJUNTOS DE NUMEROS REALES
 VALORES ABSOLUTOS Defiició: si 0 =, si < 0 = Por lo tto 0 R Teorem 2 = 2 Demostrció: si 0 2 = 2, si < 0 2 = ( ) 2 = 2 PROPIEDADES. =. = + + (desiguldd trigulr) = Teorem x x Demostrció: x x 2 2 x 2 2 x
VALORES ABSOLUTOS Defiició: si 0 =, si < 0 = Por lo tto 0 R Teorem 2 = 2 Demostrció: si 0 2 = 2, si < 0 2 = ( ) 2 = 2 PROPIEDADES. =. = + + (desiguldd trigulr) = Teorem x x Demostrció: x x 2 2 x 2 2 x
MCD Y MCM DE POLINOMIOS FRACCIONES ALGEBRAICAS
 TRILE pítulo MD Y MM DE POLINOMIOS FRAIONES ALGEBRAIAS Rgl pr lulr l MM y MD Poliomios :. S ftoriz los poliomios os.. El MD strá formo por l multipliió toos los ftors primos omus los poliomios os, osiros
TRILE pítulo MD Y MM DE POLINOMIOS FRAIONES ALGEBRAIAS Rgl pr lulr l MM y MD Poliomios :. S ftoriz los poliomios os.. El MD strá formo por l multipliió toos los ftors primos omus los poliomios os, osiros
1.- Estudie el carácter de la serie numérica. 1 es divergente, la serie n propuesta será divergente. Solución.- Puesto que, n = 1, 2, 3,...
 TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mil: imozs@lx.ud.s http://tlfoic.t/wb/imm EJERCICIOS DE SERIES NUMÉRICAS PROPUESTOS EN EXÁMENES.- Estudi l cráctr d l sri uméric. (Fbrro 00, x. or.) Solució.- Pusto
TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mil: imozs@lx.ud.s http://tlfoic.t/wb/imm EJERCICIOS DE SERIES NUMÉRICAS PROPUESTOS EN EXÁMENES.- Estudi l cráctr d l sri uméric. (Fbrro 00, x. or.) Solució.- Pusto
TEMA 8: LA INTEGRAL DEFINIDA
 Mtmátics II TEMA 8: LA INTEGRAL DEFINIDA. INTRODUCCIÓN L itgrl dfiid surg por l csidd frcut d dtrmir árs d cirtos tipos d figurs. S plt vcs l prolm d hllr l ár d l rgió pl A limitd por l curv l j d sciss.
Mtmátics II TEMA 8: LA INTEGRAL DEFINIDA. INTRODUCCIÓN L itgrl dfiid surg por l csidd frcut d dtrmir árs d cirtos tipos d figurs. S plt vcs l prolm d hllr l ár d l rgió pl A limitd por l curv l j d sciss.
(esta notación fue elegida por el matemático Leonhar Euler) De hecho la función f ( x)
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO FECHA DURACION 9 OCTUBRE
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO FECHA DURACION 9 OCTUBRE
FORMULARIO DE CÁLCULO U.P.S.
 FORMAIÓN UNIVERSTARIA / Grl Ampudi, 6 Tlé: 9 533 38 4-9 535 9 3 8003 MADRID ÁLULO FORMULARIO DE ÁLULO UPS SUESIONES Diició d sucsió: U sucsió { } s u ució cuo domiio s l cojuto d los tros positivos Los
FORMAIÓN UNIVERSTARIA / Grl Ampudi, 6 Tlé: 9 533 38 4-9 535 9 3 8003 MADRID ÁLULO FORMULARIO DE ÁLULO UPS SUESIONES Diició d sucsió: U sucsió { } s u ució cuo domiio s l cojuto d los tros positivos Los
Función exponencial y logarítmica:
 MATEMÁTICAS LA FUNCIÓN EXPONENCIAL Y LOGARÍTMICA º DE BACHILLER Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii)
MATEMÁTICAS LA FUNCIÓN EXPONENCIAL Y LOGARÍTMICA º DE BACHILLER Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii)
Construyendo la función exponencial
 Costrdo l ció ocil Cr SÁNCHZ DÍZ Pd costrirs l ció ocil ri o trl coo l ció ivrs d l ció logrito trl r d idtiicrs co l ocil d s úro rl os d ror tl coicidci l cso d ot tro tié rciol l cso d ot rl d diirs
Costrdo l ció ocil Cr SÁNCHZ DÍZ Pd costrirs l ció ocil ri o trl coo l ció ivrs d l ció logrito trl r d idtiicrs co l ocil d s úro rl os d ror tl coicidci l cso d ot tro tié rciol l cso d ot rl d diirs
CAPITULO 6.- LA TRANSFORMADA DE LAPLACE.
 PITUO 6.- TRSFORD DE PE. 6. Irocció. 6. rform plc. 6.3 rform plc ilrl. 6.4 Ivrió l rform plc. 6.5 Solció ccio ifrcil co coicio iicil. 6.6 rform plc ilrl. 6.7 álii im mi l rform plc. 6. Irocció. Grlizmo
PITUO 6.- TRSFORD DE PE. 6. Irocció. 6. rform plc. 6.3 rform plc ilrl. 6.4 Ivrió l rform plc. 6.5 Solció ccio ifrcil co coicio iicil. 6.6 rform plc ilrl. 6.7 álii im mi l rform plc. 6. Irocció. Grlizmo
Sucesiones de Números Reales
 Apédice A Sucesioes de Números Reles A.. Defiicioes U sucesió de úmeros reles es u correspodeci A que soci, cd úmero turl, u úmero rel A ( ) El cojuto de los úmeros turles, cotiee ifiitos elemetos e u
Apédice A Sucesioes de Números Reles A.. Defiicioes U sucesió de úmeros reles es u correspodeci A que soci, cd úmero turl, u úmero rel A ( ) El cojuto de los úmeros turles, cotiee ifiitos elemetos e u
3.3. Observar que el punto de acumulación de A no necesariamente pertenece a A.
 Escribirmos: f( L ε > δ > / Dom(f, < - < δ f( - L < ε Límit d fucios u vribl rl Lo cuál dic pr qu f( dist dl vlor L u úmro rbitrrimt uño ddo ε dbmos tr qu sté t crc d u rdio mor qu δ. Gométricmt: y L ε
Escribirmos: f( L ε > δ > / Dom(f, < - < δ f( - L < ε Límit d fucios u vribl rl Lo cuál dic pr qu f( dist dl vlor L u úmro rbitrrimt uño ddo ε dbmos tr qu sté t crc d u rdio mor qu δ. Gométricmt: y L ε
LÍMITE DE UNA FUNCIÓN EN UN PUNTO
 l blog d mt d id: Límits y cotiuidd. M I pág. LÍMITE DE UNA FUNCIÓN EN UN PUNTO c sigiic qu tom vlors cd vz más próimos c. S l tid c. Por jmplo: ;,9;,;,;,8;,;,9;,;,999; Es u scuci d úmros cd vz más próimos.
l blog d mt d id: Límits y cotiuidd. M I pág. LÍMITE DE UNA FUNCIÓN EN UN PUNTO c sigiic qu tom vlors cd vz más próimos c. S l tid c. Por jmplo: ;,9;,;,;,8;,;,9;,;,999; Es u scuci d úmros cd vz más próimos.
al siguiente límite si existe: . Se suele representar por ( x )
 UNIDAD : DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit it si ist: f f ' sigifica lo mismo. f. S sul rprstar por f D
UNIDAD : DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit it si ist: f f ' sigifica lo mismo. f. S sul rprstar por f D
1.-INTEGRAL DEFINIDA.
 INTEGRAL DEFINIDA .-INTEGRAL DEFINIDA. e y ƒ( u fució cotiu e u itervlo [, ]. Not.- Pr simplificr l demostrció se cosider positiv, ƒ( > 0, e todo puto del itervlo. e divide el itervlo [, ] e "" suitervlos
INTEGRAL DEFINIDA .-INTEGRAL DEFINIDA. e y ƒ( u fució cotiu e u itervlo [, ]. Not.- Pr simplificr l demostrció se cosider positiv, ƒ( > 0, e todo puto del itervlo. e divide el itervlo [, ] e "" suitervlos
1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }
![1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x } 1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }](/thumbs/74/71224437.jpg) IES P Pov (Gui Mtmátis II UNIDD : INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los vlos,,
IES P Pov (Gui Mtmátis II UNIDD : INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los vlos,,
7 Integral triple de Riemann
 Miguel eyes, pto. de Mtemátic Aplicd, FI-UPM 1 7 Integrl triple de iemnn 7.1 efinición Llmremos rectángulo cerrdo de 3 (prlelepípedo) l producto de tres intervlos cerrdos y cotdos de, es decir = [, b]
Miguel eyes, pto. de Mtemátic Aplicd, FI-UPM 1 7 Integrl triple de iemnn 7.1 efinición Llmremos rectángulo cerrdo de 3 (prlelepípedo) l producto de tres intervlos cerrdos y cotdos de, es decir = [, b]
Integrales impropias.
 IX / 8 UNIVERSIDAD SIMON BOLIVAR MA nro-mrzo d 4 Dprtmnto d Mtmátics Purs y Aplicds. Intgrls impropis. Ejrcicios sugridos pr : los tms d ls clss dl 4 y 9 d mrzo d 4. Tms : Otrs forms indtrminds. Intgrls
IX / 8 UNIVERSIDAD SIMON BOLIVAR MA nro-mrzo d 4 Dprtmnto d Mtmátics Purs y Aplicds. Intgrls impropis. Ejrcicios sugridos pr : los tms d ls clss dl 4 y 9 d mrzo d 4. Tms : Otrs forms indtrminds. Intgrls
INTEGRAL DEFINIDA ÁREAS Y VOLUMENES
 Intgrl indinid. gl d Brrow INTEGA DEFINIDA ÁEAS Y OUMENES siguint rgl, qu s s n l torm undmntl dl cálculo intgrl, rlcion l intgrl dinid con ls intgrls indinids prmit clculr ls intgrls dinids. intgrl dinid
Intgrl indinid. gl d Brrow INTEGA DEFINIDA ÁEAS Y OUMENES siguint rgl, qu s s n l torm undmntl dl cálculo intgrl, rlcion l intgrl dinid con ls intgrls indinids prmit clculr ls intgrls dinids. intgrl dinid
a a lim i) L< 1 absoluta convergencia absoluta convergencia convergencia condicional divergencia > r.
 (Aputs rvisió para oritar l aprdizaj) DESARROLLO DE LAS FUNCIONES LOGARÍTMICA Y EXPONENCIAL EN SERIES DE POTENCIAS Ua Sri d Potcias s dfi como: a a a a a = = + + + la qu s vidt qu covrg si =. Para dtrmiar
(Aputs rvisió para oritar l aprdizaj) DESARROLLO DE LAS FUNCIONES LOGARÍTMICA Y EXPONENCIAL EN SERIES DE POTENCIAS Ua Sri d Potcias s dfi como: a a a a a = = + + + la qu s vidt qu covrg si =. Para dtrmiar
26 EJERCICIOS de LOGARITMOS
 6 EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
6 EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }
![1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x } 1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }](/thumbs/64/51459891.jpg) IES P Pov (Gui Mtmátis II UNIDD INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ (Positiv [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los
IES P Pov (Gui Mtmátis II UNIDD INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ (Positiv [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los
Tema 8 Límites Matemáticas II 2º Bachillerato 1. EJERCICIO 1 : Da una definición para estas expresiones y represéntalas gráficamente: c) 2.
 Tm Límits Mtmátics II º Bchillrto TEMA LIMITES CÁLCULO DE LÍMITES EJERCICIO : D un dinición pr sts prons y rprséntls gráicmnt: ) ) 9 6 c) ) ) Cundo s proim, l unción s hc muy grnd ) Cundo s proim, l unción
Tm Límits Mtmátics II º Bchillrto TEMA LIMITES CÁLCULO DE LÍMITES EJERCICIO : D un dinición pr sts prons y rprséntls gráicmnt: ) ) 9 6 c) ) ) Cundo s proim, l unción s hc muy grnd ) Cundo s proim, l unción
TALLER 4: Preparación parcial final. Cálculo Integral. UdeA Profesor: Jaime Andrés Jaramillo.
 TALLER : Prparació parcial fial Cálculo Itgral UdA - Profsor: Jaim Adrés Jaramillo jaimaj@cocptocomputadorscom Sucsios Mustr los primros cuatro térmios d la sucsió y dtrmi si s covrgt o divrgt: a) d) +
TALLER : Prparació parcial fial Cálculo Itgral UdA - Profsor: Jaim Adrés Jaramillo jaimaj@cocptocomputadorscom Sucsios Mustr los primros cuatro térmios d la sucsió y dtrmi si s covrgt o divrgt: a) d) +
TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES
 3. LÍMITES COLEGIO RAIMUNDO LULIO Frnciscnos T.O.R. Cód. 8367 TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES Dfinición: S dic qu l límit d l función f s igul L, cundo tind, si cundo s proim, f s proim L, sin
3. LÍMITES COLEGIO RAIMUNDO LULIO Frnciscnos T.O.R. Cód. 8367 TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES Dfinición: S dic qu l límit d l función f s igul L, cundo tind, si cundo s proim, f s proim L, sin
( ) ( ) ( x ) ( ) ( ) ( ) v( x) u( x) ( ) EJERCICIOS RESUELTOS. 1. Calcula F a) ( x) en los siguientes casos: f ( t) = e. = x
 Alro Enro Cond Mi Gonzálz Jrrro L ingrl y ss pliccions Clcl F ) d) n los sigins csos: F cos d RESUELTOS ) ( + ) d ) ( + ) F cos F d c) F( ) + d f) F d + F d g) v( ) F d h) F + f ( ) d i) F( ) ( ) cos d
Alro Enro Cond Mi Gonzálz Jrrro L ingrl y ss pliccions Clcl F ) d) n los sigins csos: F cos d RESUELTOS ) ( + ) d ) ( + ) F cos F d c) F( ) + d f) F d + F d g) v( ) F d h) F + f ( ) d i) F( ) ( ) cos d
f cuando x toma valores cercanos a 2. Si x se aproxima a 2, la función toma valores cercanos a 5. Se escribe: ( ) 5
 IES Pdr Povd (Gudi Mtmátics II UNIDAD LÍMITES Y CONTINUIDAD INTRODUCCIÓN Fíjt l comportmito d l fució ( f cudo tom vlors crcos Si s proim, l fució tom vlors crcos S scrib: f y dcimos qu s l it cudo tid
IES Pdr Povd (Gudi Mtmátics II UNIDAD LÍMITES Y CONTINUIDAD INTRODUCCIÓN Fíjt l comportmito d l fució ( f cudo tom vlors crcos Si s proim, l fució tom vlors crcos S scrib: f y dcimos qu s l it cudo tid
Sucesiones de números reales
 Tem 5 Sucesioes de úmeros reles Defiició 5.1 Llmremos sucesió de úmeros reles culquier plicció f: IN IR y l represetremos por { } =1, dode = f(. Por comodidd, diremos tmbié que l sucesió es el cojuto ordedo
Tem 5 Sucesioes de úmeros reles Defiició 5.1 Llmremos sucesió de úmeros reles culquier plicció f: IN IR y l represetremos por { } =1, dode = f(. Por comodidd, diremos tmbié que l sucesió es el cojuto ordedo
7ma Guía de Estudio 2do Parcial Estudio de Series de Potencia SOLUCIONARIO Guía Complementaria No.07
 álculo tgrl (MAT, Scc.67 r Trimstr, do Smstr doprcil 7mGuíEstudio Documto lordo : M.Sc. g. Julio ésr Lóz Zró H6 7m Guí d Estudio do Prcil Estudio d Sris d Potci SOLUONAO Guí omlmtri No.7 omtrios Grls Ést
álculo tgrl (MAT, Scc.67 r Trimstr, do Smstr doprcil 7mGuíEstudio Documto lordo : M.Sc. g. Julio ésr Lóz Zró H6 7m Guí d Estudio do Prcil Estudio d Sris d Potci SOLUONAO Guí omlmtri No.7 omtrios Grls Ést
EJERCICIOS Y PROBLEMAS DE SUCESIONES Y SERIES
 EJERCICIOS Y PROBLEMAS DE SUCESIONES Y SERIES EDDY ABREU, AIDA MONTEZUMA Y JAIME RANGEL Uivrsidd Mtropolit, Crcs, Vzul, 7 Hcho l dpósito d Ly Dpósito Lgl: ISBN: Formto:, X 7,9 cms. Nº d págis: 7 Rsrvdos
EJERCICIOS Y PROBLEMAS DE SUCESIONES Y SERIES EDDY ABREU, AIDA MONTEZUMA Y JAIME RANGEL Uivrsidd Mtropolit, Crcs, Vzul, 7 Hcho l dpósito d Ly Dpósito Lgl: ISBN: Formto:, X 7,9 cms. Nº d págis: 7 Rsrvdos
SISTEMAS DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN
 TEMA Nº SISTEMAS DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN. TEOREMA PRELIMINAR INTRODUCCIÓN.- Sism d cucios dircils lils co icógis d l orm P D P D P D P D P P D D... P... P... P D D D b b b dod ls P
TEMA Nº SISTEMAS DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN. TEOREMA PRELIMINAR INTRODUCCIÓN.- Sism d cucios dircils lils co icógis d l orm P D P D P D P D P P D D... P... P... P D D D b b b dod ls P
Sucesiones de números reales
 Apédice A Sucesioes de úmeros reles Ejercicios resueltos. Está l sucesió de térmio geerl U cot iferior es pues 5 cotd? 5 5 4 4 lo cul se cumple culquier que se el úmero turl. U cot superior es pues 5 5
Apédice A Sucesioes de úmeros reles Ejercicios resueltos. Está l sucesió de térmio geerl U cot iferior es pues 5 cotd? 5 5 4 4 lo cul se cumple culquier que se el úmero turl. U cot superior es pues 5 5
Análisis I. Sucesiones reales FICHA 3. Curso (Álgebra de límites, equivalentes, infinitésimos, infinitos, órdenes)
 Aálisis I Sucsios rls FICHA 3 (Álgr d límits, quivlts, ifiitésimos, ifiitos, órds) Curso 3 C.F.E., Dprtmto d Mtmátic, I.P.A. Sucsios rls, fich 3 - - ) Álgr d límits Ejrcicio : S ( ) π 4 =, N. Clcul,,.
Aálisis I Sucsios rls FICHA 3 (Álgr d límits, quivlts, ifiitésimos, ifiitos, órds) Curso 3 C.F.E., Dprtmto d Mtmátic, I.P.A. Sucsios rls, fich 3 - - ) Álgr d límits Ejrcicio : S ( ) π 4 =, N. Clcul,,.
Universidad de Costa Rica. Instituto Tecnológico de Costa Rica. Determinar si las integrales impropias convergen o divergen.
 Uivrsidad d Costa Rica Istituto Tcológico d Costa Rica Tma: Itgrals impropias. Objtivos: Clasificar las itgrals impropias sgú su spci: primra, sguda o trcra spci. Calcular itgrals impropias utilizado su
Uivrsidad d Costa Rica Istituto Tcológico d Costa Rica Tma: Itgrals impropias. Objtivos: Clasificar las itgrals impropias sgú su spci: primra, sguda o trcra spci. Calcular itgrals impropias utilizado su
ECUACIONES DIFERENCIALES DE ORDEN SUPERIOR. Ecuaciones lineales homogéneas con coeficientes constates de orden dos y superior.
 Prof Eriqu Mtus Nivs Dotordo Eduió Mtmáti ECUACIONES DIFERENCIALES DE ORDEN SUPERIOR Euios lils homogés o ofiits ostts d ord dos suprior Apliqu l método d rduió pr dtrmir u soluió d l uió o homogé dd los
Prof Eriqu Mtus Nivs Dotordo Eduió Mtmáti ECUACIONES DIFERENCIALES DE ORDEN SUPERIOR Euios lils homogés o ofiits ostts d ord dos suprior Apliqu l método d rduió pr dtrmir u soluió d l uió o homogé dd los
1.4. Sucesión de funciones continuas ( )
 1.4. Sucesión de funciones continus (18.04.2017) Se {f n } un sucesión de funciones f n, definids en I. Si {f n } converge uniformemente f en I y ls f n son continus en I, entonces f es continu en I. D:
1.4. Sucesión de funciones continus (18.04.2017) Se {f n } un sucesión de funciones f n, definids en I. Si {f n } converge uniformemente f en I y ls f n son continus en I, entonces f es continu en I. D:
Curvas en el plano y en el espacio
 Cpítulo 1 Curvs en el plno y en el espcio 1.1. Curvs prmetrizds Definición 1.1.1 (Curv prmetrizd). Un curv prmetrizd diferencible α : I R n, es un plicción de clse C, donde I R es un intervlo bierto, que
Cpítulo 1 Curvs en el plno y en el espcio 1.1. Curvs prmetrizds Definición 1.1.1 (Curv prmetrizd). Un curv prmetrizd diferencible α : I R n, es un plicción de clse C, donde I R es un intervlo bierto, que
206 MÉTODOS NUMÉRICOS
 6 MÉTODOS UMÉRICOS.. Alguos hhos mortts r ls rs vs wto: ls sguts so lgus ls ros más mortts ls rs vs wto: (. S s u rmutó K ) ( ) K tos [ K ] [ K ] CASO PARTICULAR: [ ] [ ] ( Est ro s osu l u l olomo trolt
6 MÉTODOS UMÉRICOS.. Alguos hhos mortts r ls rs vs wto: ls sguts so lgus ls ros más mortts ls rs vs wto: (. S s u rmutó K ) ( ) K tos [ K ] [ K ] CASO PARTICULAR: [ ] [ ] ( Est ro s osu l u l olomo trolt
Análisis de Fourier para Señales y Sistemas de Tiempo Discreto
 Aálii d Fourir pr Sñl y Sitm d impo Dicrto Rput d u itm LI l pocil compl [] h[] y [ ] h [ ] [ ] h [ ] [ ] Si y h h H [ ] [ ] [ ] [ ] ( [ ] ( H Autofució d lo Sitm LI Autovlor ocido y Si r rformd Si rformd
Aálii d Fourir pr Sñl y Sitm d impo Dicrto Rput d u itm LI l pocil compl [] h[] y [ ] h [ ] [ ] h [ ] [ ] Si y h h H [ ] [ ] [ ] [ ] ( [ ] ( H Autofució d lo Sitm LI Autovlor ocido y Si r rformd Si rformd
 OPERACIONES CON LÍMITES DE FUNCIONES Ls oprcios co límits, tto u puto como l ifiito, ti us propidds álogs qu dbmos coocr: PROPIEDADES El límit d l sum o difrci d dos fucios s l sum o difrci d los límits
OPERACIONES CON LÍMITES DE FUNCIONES Ls oprcios co límits, tto u puto como l ifiito, ti us propidds álogs qu dbmos coocr: PROPIEDADES El límit d l sum o difrci d dos fucios s l sum o difrci d los límits
SISTEMA DE ECUACIONES LINEALES
 SISTEM DE ECUCIONES LINELES Defiició: Llmremos sistem de m ecucioes co icógits, u cojuto de ecucioes de l form: m.... m..... m m (S) Los elemetos so los coeficietes del sistem. ij Los elemetos i so ls
SISTEM DE ECUCIONES LINELES Defiició: Llmremos sistem de m ecucioes co icógits, u cojuto de ecucioes de l form: m.... m..... m m (S) Los elemetos so los coeficietes del sistem. ij Los elemetos i so ls
1.4 SERIES NUMÉRICAS.SUMA DE SERIES. (46 Problemas ) sabiendo que n
 . SERIES NUMÉRICAS.SUMA DE SERIES. (6 Problems.- Estudir el crácter de ls series:! 0 b + si >0, segú vlores de. 0.- Clculr cos α sbiedo que x x e 0! 0! 3.- Estudir l serie de térmio geerl. π se.- Cosidermos
. SERIES NUMÉRICAS.SUMA DE SERIES. (6 Problems.- Estudir el crácter de ls series:! 0 b + si >0, segú vlores de. 0.- Clculr cos α sbiedo que x x e 0! 0! 3.- Estudir l serie de térmio geerl. π se.- Cosidermos
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Tema 8. Derivadas. Teoremas de las funciones derivables. Regla de L Hôpital
 Mtmátics II (Bcillrto d Cicis) Aálisis: Drivds 8 Tm 8 Drivds Torms d ls fucios drivbls Rgl d L Hôpitl Drivd d u fució u puto Dfiició U fució f () s drivbl l puto f ( ) f ( ) si ist l it: 0 Est it s dot
Mtmátics II (Bcillrto d Cicis) Aálisis: Drivds 8 Tm 8 Drivds Torms d ls fucios drivbls Rgl d L Hôpitl Drivd d u fució u puto Dfiició U fució f () s drivbl l puto f ( ) f ( ) si ist l it: 0 Est it s dot
FÓRMULA DE TAYLOR 1. Introducción formula de Taylor Brook Taylor 2. Objetivos Aproximación de funciones por polinomios f(x) P(x) f(x)
 FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
Funciones continuas. Mariano Suárez-Alvarez. 4 de junio, Índice
 Funciones continus Mrino Suárez-Alvrez 4 de junio, 2013 Índice 1. Funciones continus................... 1 2. Alguns propieddes básics............ 3 3. Los teorems de Weierstrss y Bolzno... 6 4. Funciones
Funciones continus Mrino Suárez-Alvrez 4 de junio, 2013 Índice 1. Funciones continus................... 1 2. Alguns propieddes básics............ 3 3. Los teorems de Weierstrss y Bolzno... 6 4. Funciones
FUNCIONES DERIVABLES EN UN INTERVALO
 DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. FUNCIONES DERIVABLES EN UN INTERVALO Ls unions qu son ontinus n un intrvlo rrdo [, ] y drivls n un intrvlo irto, tinn propidds importnts. Torm d Roll.
DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. FUNCIONES DERIVABLES EN UN INTERVALO Ls unions qu son ontinus n un intrvlo rrdo [, ] y drivls n un intrvlo irto, tinn propidds importnts. Torm d Roll.
Universidad de Puerto Rico Recinto Universitario de Mayagüez Departamento de Ciencias Matemáticas
 Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
DELTA MASTER FORMACIÓN UNIVERSTARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 / Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
/ Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
EXPONENTES Y POTENCIAS Muchos números se expresan en forma más conveniente como potencias de 10. Por ejemplo: m n n 0,2 3 3
 Rpaso d Matmáticas E st apédic s hará u brv rpaso d las cuacios y fórmulas básicas d utilidad Química Física gral y Trmodiámica Química particular. EXPONENTES Y POTENCIAS Muchos úmros s xprsa forma más
Rpaso d Matmáticas E st apédic s hará u brv rpaso d las cuacios y fórmulas básicas d utilidad Química Física gral y Trmodiámica Química particular. EXPONENTES Y POTENCIAS Muchos úmros s xprsa forma más
TEMA 1: CALCULO DIRECTO DE LÍMITES
 INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Rsolució Nº 88 d ovimbr.8/ ScrtariaD Educació Distrital REGISTRO DANE Nº-99 Tléfoo Barrio Bastidas Sata Marta DEPARTAMENTO DE MATEMATICAS ACTIVIDAD ESPECIAL
INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Rsolució Nº 88 d ovimbr.8/ ScrtariaD Educació Distrital REGISTRO DANE Nº-99 Tléfoo Barrio Bastidas Sata Marta DEPARTAMENTO DE MATEMATICAS ACTIVIDAD ESPECIAL
Teorema Maestro. Introducción. Arturo Díaz Pérez. Recurrencia general para estrategias divide y vencerás. Análisis y Complejidad de Algoritmos 1
 Arturo Díz Pérez Aálisis y Diseño e Aloritmos Teorem Mestro Arturo Díz Pérez Aálisis y Diseño e Aloritmos Mestro- Itroucció Recurreci eerl pr estrteis ivie y vecerás T + T T Aálisis y Diseño e Aloritmos
Arturo Díz Pérez Aálisis y Diseño e Aloritmos Teorem Mestro Arturo Díz Pérez Aálisis y Diseño e Aloritmos Mestro- Itroucció Recurreci eerl pr estrteis ivie y vecerás T + T T Aálisis y Diseño e Aloritmos
Logaritmos y exponenciales de otras bases. La función. Tipo III: Si u y v son funciones diferenciables en x y u > 0,
 Logritmos y eponenciles de otrs ses L función Leer con cuiddo el [S, 8] o ien [S, 4] y = Pr >, ln = e Definición: (Tp474) Pr R y > se define ln = e d AL- Deducir l fórmul de ( ) d d v AL- Si u y v son
Logritmos y eponenciles de otrs ses L función Leer con cuiddo el [S, 8] o ien [S, 4] y = Pr >, ln = e Definición: (Tp474) Pr R y > se define ln = e d AL- Deducir l fórmul de ( ) d d v AL- Si u y v son
Capítulo 3. Potencias de números enteros
 Cpítulo. Potecis de úmeros eteros U poteci es u epresió de l form, dode es l bse de l poteci y el epoete. Se lee: elevdo. U poteci es el producto de l bse por sí mism tts veces como idic el epoete. se
Cpítulo. Potecis de úmeros eteros U poteci es u epresió de l form, dode es l bse de l poteci y el epoete. Se lee: elevdo. U poteci es el producto de l bse por sí mism tts veces como idic el epoete. se
( ) ( ) El principio de inducción
 El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
Capítulo IV. Estadísticas cuánticas.
 Capítulo I. stadísticas cuáticas. Lcció 6 Itroducció a las stadísticas cuáticas. Partículas distiguibls idistiguibls. stadísticas d Bos-isti y d rmi-dirac. Lcció 7 Gas idal d rmi: lctros mtals. Lcció 8
Capítulo I. stadísticas cuáticas. Lcció 6 Itroducció a las stadísticas cuáticas. Partículas distiguibls idistiguibls. stadísticas d Bos-isti y d rmi-dirac. Lcció 7 Gas idal d rmi: lctros mtals. Lcció 8
Vectores 1 ; Ejercicio nº 1.- Ejercicio nº 2.-
 Vectores. dij so los sigietes ectores Si ) Ejercicio º.- ( ) : Oté ls coordeds de Ls coordeds de dos ectores so ). ; ; los qe estr l figr: siedo Dij los ectores ) Ejercicio º.- ( ) : oté ls coordeds de
Vectores. dij so los sigietes ectores Si ) Ejercicio º.- ( ) : Oté ls coordeds de Ls coordeds de dos ectores so ). ; ; los qe estr l figr: siedo Dij los ectores ) Ejercicio º.- ( ) : oté ls coordeds de
el blog de mate de aida. NÚMEROS REALES 4º ESO pág. 1 NÚMEROS REALES
 el log de mte de id. NÚMEROS REALES 4º ESO pág. NÚMEROS REALES Expresió deciml de los úmeros rcioles. Pr psr u úmero rciol de form frcciori form deciml st dividir el umerdor por el deomidor. Como l hcer
el log de mte de id. NÚMEROS REALES 4º ESO pág. NÚMEROS REALES Expresió deciml de los úmeros rcioles. Pr psr u úmero rciol de form frcciori form deciml st dividir el umerdor por el deomidor. Como l hcer
En un grafo se puede recorrer la información de diferentes maneras para llegar de un punto a otro.
 CAMINOS Y CIRCUITOS En un grfo s pu rorrr l informión ifrnts mnrs pr llgr un punto otro. Cmino Ciruito (Cilo) Ciruito simpl longitu n Cmino simpl longitu n ulquir suni noos n l qu pr son ynts. Es un mino
CAMINOS Y CIRCUITOS En un grfo s pu rorrr l informión ifrnts mnrs pr llgr un punto otro. Cmino Ciruito (Cilo) Ciruito simpl longitu n Cmino simpl longitu n ulquir suni noos n l qu pr son ynts. Es un mino
1.- a) Hallar a y b para que la siguiente función sea continua en x = 1:
 .- a) Hallar a y b para qu la siguit fució sa cotiua = : b L( ) < f = a = > L b) Para sos valors d a y b, studiar la drivabilidad d f =. Solució: a) f s cotiua l puto = lim f = f() E st caso f () = a lim
.- a) Hallar a y b para qu la siguit fució sa cotiua = : b L( ) < f = a = > L b) Para sos valors d a y b, studiar la drivabilidad d f =. Solució: a) f s cotiua l puto = lim f = f() E st caso f () = a lim
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 4º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
MATEMÁTICAS PARA LA COMPUTACIÓN CAPÍTULO 6. RELACIONES
 MATEMÁTICAS PARA LA COMPUTACIÓN CAPÍTULO. RELACIONES DIAGRAMAS DE HASSE. AUTOR: JOSÉ ALFREDO JIMÉNEZ MURILLO AVC APOYO VIRTUAL PARA EL CONOCIMIENTO Digrms Hss Un rlión R:A B s orn pril o prilmnt orn si
MATEMÁTICAS PARA LA COMPUTACIÓN CAPÍTULO. RELACIONES DIAGRAMAS DE HASSE. AUTOR: JOSÉ ALFREDO JIMÉNEZ MURILLO AVC APOYO VIRTUAL PARA EL CONOCIMIENTO Digrms Hss Un rlión R:A B s orn pril o prilmnt orn si
DERIVADAS PARCIALES DE UNA FUNCIÓN N DE VARIAS VARIABLES
 DERIVADAS PARCIALES DE UNA FUNCIÓN N DE VARIAS VARIABLES Deinición de derivd prcil en un punto lim + Se : A R con A R se un punto interior de A. Se denominn derivds prciles de respecto ls vriles e en el
DERIVADAS PARCIALES DE UNA FUNCIÓN N DE VARIAS VARIABLES Deinición de derivd prcil en un punto lim + Se : A R con A R se un punto interior de A. Se denominn derivds prciles de respecto ls vriles e en el
Función no Acotada en uno o en los dos extremos del Intervalo de Integración. f (x) d x = lim
 Función no Acotd en uno o en los dos etremos del Intervlo de Integrción Si f () está definid sobre (, b] y si f () cundo, se define f () d = lim f () d ε + +ε Si f () está definid sobre [, b) y si f ()
Función no Acotd en uno o en los dos etremos del Intervlo de Integrción Si f () está definid sobre (, b] y si f () cundo, se define f () d = lim f () d ε + +ε Si f () está definid sobre [, b) y si f ()
EJERCICIOS DE RAÍCES. a b = RECORDAR: Definición de raíz n-ésima: Equivalencia con una potencia de exponente fraccionario:
 EJERCICIOS DE RAÍCES RECORDAR: Defiició de ríz ésim: x x Equivleci co u poteci de expoete frcciorio: m x Simplificció de rdicles/ídice comú: Propieddes de ls ríces: x m/ b b b p m p b m m ( ) m Itroducir/extrer
EJERCICIOS DE RAÍCES RECORDAR: Defiició de ríz ésim: x x Equivleci co u poteci de expoete frcciorio: m x Simplificció de rdicles/ídice comú: Propieddes de ls ríces: x m/ b b b p m p b m m ( ) m Itroducir/extrer
I.E.S Padre Juan Ruíz Aritmética Hinojosa del Duque
 I.E.S Pdre Ju Ruíz Aritméti Hiojos del Duque PROPIEDADES DE LA ARITMÉTICA Y ERRORES MÁS COMUNES NÚMEROS ENTEROS Elimir prétesis: Del mismo sigo, sle + De distito sigo, sle + (+) = + ( ) = + + ( ) = (+)
I.E.S Pdre Ju Ruíz Aritméti Hiojos del Duque PROPIEDADES DE LA ARITMÉTICA Y ERRORES MÁS COMUNES NÚMEROS ENTEROS Elimir prétesis: Del mismo sigo, sle + De distito sigo, sle + (+) = + ( ) = + + ( ) = (+)
Profesorado de Informática - Ciencias de la Computación - INET DFPD Matemática II 2010 Sucesiones
 Profesordo de Iformátic - Ciecis de l Computció - INET DFPD Mtemátic II Sucesioes Sucesioes Tems: Límites de sucesioes. Sucesioes moótos y sus límites. Pres de sucesioes moótos covergetes. Número e. Opercioes
Profesordo de Iformátic - Ciecis de l Computció - INET DFPD Mtemátic II Sucesioes Sucesioes Tems: Límites de sucesioes. Sucesioes moótos y sus límites. Pres de sucesioes moótos covergetes. Número e. Opercioes
( a b c) n = a n b n c n ( a : b) n = a n : b n a n a m = a n+m a n :a m = a n-m (a n ) m = a n.m
 Igreso Potecició e R: Ddo u úmero rel, que le llmremos bse y u umero turl, l que le llmremos epoete. defiimos: =.... Propieddes de l potecició: veces ( epoete) Ests propieddes se eplic mejor si se etiede
Igreso Potecició e R: Ddo u úmero rel, que le llmremos bse y u umero turl, l que le llmremos epoete. defiimos: =.... Propieddes de l potecició: veces ( epoete) Ests propieddes se eplic mejor si se etiede
, al conjunto de puntos P
 Fcltd d ontdrí y Administrción. UNAM Intgrl dinid indinid Ator: Dr. José Mnl Bcrr Espinos MATEMÁTIAS BÁSIAS INTEGRAL DEFINIDA E INDEFINIDA SUMA DE RIEMANN S n intrvlo crrdo [, ], l conjnto d pntos P n
Fcltd d ontdrí y Administrción. UNAM Intgrl dinid indinid Ator: Dr. José Mnl Bcrr Espinos MATEMÁTIAS BÁSIAS INTEGRAL DEFINIDA E INDEFINIDA SUMA DE RIEMANN S n intrvlo crrdo [, ], l conjnto d pntos P n
Unidad 2: SUCESIONES Y SERIES NUMÉRICAS.
 Uidd : SUCESIONES Y SERIES NUMÉRICAS. U sucesió es u cojuto ordedo de elemetos que respode u ley de formció. L sucesió suele brevirse: (,...) ( ) =,, 3,..., 3 Siedo el primer térmio, el segudo térmio,
Uidd : SUCESIONES Y SERIES NUMÉRICAS. U sucesió es u cojuto ordedo de elemetos que respode u ley de formció. L sucesió suele brevirse: (,...) ( ) =,, 3,..., 3 Siedo el primer térmio, el segudo térmio,
REGRESION LINEAL SIMPLE. = α + β + ε. y = α + β x
 REGREION LINEAL IMPLE FORMULARIO Mdl d Rgrsó Ll mpl Jrg Glt Rsc + β + ε qu β s fjs, ε s u vrl ltr c sprz E(ε) 0 vrz V(ε) σ fj. Ls prámtrs dl mdl s, β σ. rprst l vrl dpdt, qu tm vlrs fjs dtrmds pr l prmtdr.
REGREION LINEAL IMPLE FORMULARIO Mdl d Rgrsó Ll mpl Jrg Glt Rsc + β + ε qu β s fjs, ε s u vrl ltr c sprz E(ε) 0 vrz V(ε) σ fj. Ls prámtrs dl mdl s, β σ. rprst l vrl dpdt, qu tm vlrs fjs dtrmds pr l prmtdr.
La Integral Definida
 Nivelción de Mtemátic MTHA UNLP ID Introducción Prtición L Integrl Definid Un prtición del intervlo [, b] es un sucesión de números = x x x x n = b, entre y b, tl que x i x i+ (i =,,, n ) Ejemplo: se llm
Nivelción de Mtemátic MTHA UNLP ID Introducción Prtición L Integrl Definid Un prtición del intervlo [, b] es un sucesión de números = x x x x n = b, entre y b, tl que x i x i+ (i =,,, n ) Ejemplo: se llm
MANUAL MATEMÁTICAS PARA ESTUDIANTES DE FINANZAS. Exponentes
 _ Defiició: Epoetes Pr u úero rel u etero positivo, veces se le deoi l se l poteci o epoete Ejeplos:..... Not: oserv que del segudo es. o so igules, el resultdo del priero es Lees de epoetes: Pr cd u de
_ Defiició: Epoetes Pr u úero rel u etero positivo, veces se le deoi l se l poteci o epoete Ejeplos:..... Not: oserv que del segudo es. o so igules, el resultdo del priero es Lees de epoetes: Pr cd u de
FACULTAD DE INGENIERÍA
 FCULD DE INGENIERÍ Uivrdd Nciol uóo d Méico Fculd d Igirí ális d Siss y Sñls Profsor: M.I. Elizh Fosc Chávz SERIE DE FOURIER LUMN: Sáchz Cdillo Vicori GRUPO: 6 SERIE DE FOURIER od sñl priódic s pud prsr
FCULD DE INGENIERÍ Uivrdd Nciol uóo d Méico Fculd d Igirí ális d Siss y Sñls Profsor: M.I. Elizh Fosc Chávz SERIE DE FOURIER LUMN: Sáchz Cdillo Vicori GRUPO: 6 SERIE DE FOURIER od sñl priódic s pud prsr
E.T.S.I. Industriales y Telecomunicación Curso Grados E.T.S.I. Industriales y Telecomunicación RESUMEN TEMA SUCESIONES
 E.T.S.I. Idustriles y Telecomuicció Curso 22-23 Grdos E.T.S.I. Idustriles y Telecomuicció Asigtur: Cálculo I DEFINICIONES BÁSICAS Existe muchos feómeos que o se comport de mer cotiu, sio que ecesit u determido
E.T.S.I. Idustriles y Telecomuicció Curso 22-23 Grdos E.T.S.I. Idustriles y Telecomuicció Asigtur: Cálculo I DEFINICIONES BÁSICAS Existe muchos feómeos que o se comport de mer cotiu, sio que ecesit u determido
PAIEP. Sumas de Riemann
 Progrm de Acceso Iclusivo, Equidd y Permeci PAIEP Uiversidd de Stigo de Chile Sums de Riem Ddo u itervlo de l form [, b], co y b e R, < b, u prtició del itervlo [, b] es u colecció de putos P = {x, x,...,
Progrm de Acceso Iclusivo, Equidd y Permeci PAIEP Uiversidd de Stigo de Chile Sums de Riem Ddo u itervlo de l form [, b], co y b e R, < b, u prtició del itervlo [, b] es u colecció de putos P = {x, x,...,
4. Definición: Convergencia uniforme de una sucesión de funciones
 1. Teorem de l funcion invers Se A un ierto de R N, f : A R m un funcion de clse n (n 1), se A tl que det(jf()) 0. Entonces existe un entorno U de tl que U A tl que: (1). det(jf (x)) 0 pr todo x U (2).
1. Teorem de l funcion invers Se A un ierto de R N, f : A R m un funcion de clse n (n 1), se A tl que det(jf()) 0. Entonces existe un entorno U de tl que U A tl que: (1). det(jf (x)) 0 pr todo x U (2).
Cómo es la distribución de los alimentos servidos?
 Cómo s l distribució d los limtos srvis? 5 " Co u bu limt ció, p Los iños y iñs s ppr pr cosumir los limtos 6 CUÁL ES EL OBJETIVO? Promovr y forzr buos hábitos d higi los iños y iñs como l lv d mos ts
Cómo s l distribució d los limtos srvis? 5 " Co u bu limt ció, p Los iños y iñs s ppr pr cosumir los limtos 6 CUÁL ES EL OBJETIVO? Promovr y forzr buos hábitos d higi los iños y iñs como l lv d mos ts
TEMA 5 LÍMITES Y CONTINUIDAD DE FUNCIONES
 TEMA 5 LÍMITES Y CONTINUIDAD DE FUNCIONES 5.1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. LÍMITES LATERALES 5.1.1. Concepto de tendenci Decimos que " tiende " si tom los vlores de un sucesión que se proim. Se
TEMA 5 LÍMITES Y CONTINUIDAD DE FUNCIONES 5.1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. LÍMITES LATERALES 5.1.1. Concepto de tendenci Decimos que " tiende " si tom los vlores de un sucesión que se proim. Se
Integración de funciones racionales
 Integrción de funciones rcionles P() Se l integrl d donde P() y Q() son funciones polinómics. Si el grdo P() Q() se Q() divide P() entre Q() medinte el método de l cj y se otiene un cociente () y un resto
Integrción de funciones rcionles P() Se l integrl d donde P() y Q() son funciones polinómics. Si el grdo P() Q() se Q() divide P() entre Q() medinte el método de l cj y se otiene un cociente () y un resto
Aproximación al área bajo una curva.
 Aproimció l áre jo u curv. Por: Miguel Solís Esquic Profesor de tiempo completo Uiversidd Autóom de Cips Clculr cd u de ls áres de los rectágulos que lle l regió cotd pr lczr el vlor del áre ecesrimete
Aproimció l áre jo u curv. Por: Miguel Solís Esquic Profesor de tiempo completo Uiversidd Autóom de Cips Clculr cd u de ls áres de los rectágulos que lle l regió cotd pr lczr el vlor del áre ecesrimete
FUNCIONES LOGARÍTMICAS, EXPONENCIALES Y TRIGONOMÉTRICAS
 Resúmenes de Mtemátics pr Bchillerto I.E.S. Rmón Girldo FUNCIONES LOGARÍTMICAS, EXPONENCIALES Y TRIGONOMÉTRICAS FUNCIONES LOGARÍTMICAS Logritmo de bse El logritmo en bse ( > 0 y ) de un número N es el
Resúmenes de Mtemátics pr Bchillerto I.E.S. Rmón Girldo FUNCIONES LOGARÍTMICAS, EXPONENCIALES Y TRIGONOMÉTRICAS FUNCIONES LOGARÍTMICAS Logritmo de bse El logritmo en bse ( > 0 y ) de un número N es el
Sean dos funciones f y g de variable real definidas en un dominio DŒÑ Definición g es una primitiva de f si f(x)=g (x) "x D
 INTEGRAL DE RIEMANN 1- Primitivs e integrl indefinid - Integrl de Riemnn 3- Interpretción geométric de ls integrles de Riemnn 4- Propieddes de ls integrles de Riemnn 5- Cmio de vrile en ls integrles de
INTEGRAL DE RIEMANN 1- Primitivs e integrl indefinid - Integrl de Riemnn 3- Interpretción geométric de ls integrles de Riemnn 4- Propieddes de ls integrles de Riemnn 5- Cmio de vrile en ls integrles de
Diferenciación numérica: Método de Euler explícito
 Clase No. 21: MAT 251 Diferenciación numérica: Método de Euler explícito Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/
Clase No. 21: MAT 251 Diferenciación numérica: Método de Euler explícito Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/
Integrales de ĺınea complejas
 Tem Integrles de ĺıne complejs. Integrles de líne.. Funciones complejs de vrible rel Un función complej de vrible rel llev socid un función vectoril de vrible rel, por lo que ls definiciones y resultdos
Tem Integrles de ĺıne complejs. Integrles de líne.. Funciones complejs de vrible rel Un función complej de vrible rel llev socid un función vectoril de vrible rel, por lo que ls definiciones y resultdos
TEMA22. Función Exponencial y Logarítmica.
 TEMA 22. Fucios pocil y logrítmic TEMA22. Fució Epocil y Logrítmic.. Itroducció L oció d fució qu ctulmt mjmos mpzó gstrs l siglo XIV cudo los filósofos scolásticos mdivls comzro procuprs por mdir ls vricios
TEMA 22. Fucios pocil y logrítmic TEMA22. Fució Epocil y Logrítmic.. Itroducció L oció d fució qu ctulmt mjmos mpzó gstrs l siglo XIV cudo los filósofos scolásticos mdivls comzro procuprs por mdir ls vricios
BLOQUE 3. FUNCIONES REALES DE UNA VARIABLE REAL. LÍMITES Y CONTINUIDAD DE FUNCIONES
 BLOQUE 3 FUNCIONES REALES DE UNA VARIABLE REAL LÍMITES Y CONTINUIDAD DE FUNCIONES Funciones reles de un vrile rel Límite de un unción rel Continuidd de un unción rel Con este tem se inici el estudio de
BLOQUE 3 FUNCIONES REALES DE UNA VARIABLE REAL LÍMITES Y CONTINUIDAD DE FUNCIONES Funciones reles de un vrile rel Límite de un unción rel Continuidd de un unción rel Con este tem se inici el estudio de
Cálculo Integral Enero 2016
 Cálculo Integral Enero 6 Laboratorio # Antiderivadas I.- Halle las siguientes integrales indefinidas. ) ( + + ) ) ( + ) ( ) ) ( w + ) (w ) dw ) ( + ) 5) (y ) dy 6) ( +)( 5) 6 7) + 8) ( +) 5 y+ dy ) (y+5
Cálculo Integral Enero 6 Laboratorio # Antiderivadas I.- Halle las siguientes integrales indefinidas. ) ( + + ) ) ( + ) ( ) ) ( w + ) (w ) dw ) ( + ) 5) (y ) dy 6) ( +)( 5) 6 7) + 8) ( +) 5 y+ dy ) (y+5
7.1. Definición de la Integral de Riemann
 Cpítulo 7 Integrl de Riemnn 71 Definición de l Integrl de Riemnn En este cpítulo supondremos, menos que se indique lo contrrio, que < b y f : [, b] R es un función cotd Definición 71 Un prtición del intervlo
Cpítulo 7 Integrl de Riemnn 71 Definición de l Integrl de Riemnn En este cpítulo supondremos, menos que se indique lo contrrio, que < b y f : [, b] R es un función cotd Definición 71 Un prtición del intervlo

