1 Ejemplos de Aproximaciones de Integrales con Sumas de Riemman
|
|
|
- Mercedes Venegas Silva
- hace 6 años
- Vistas:
Transcripción
1 Ejmplos d Aproximacios d Itgrals co Sumas d Rimma Esta Ru Hurtado Cruz UNAM. Itrodució Estos jmplos d aproximacios d sumas d Rima s usaro l curso d Calculo II, durat l smstr 003- d la Facultad d Cicias d la UNAM. Ejmplo suitrvalos. Dmostrar qu x3 dx = cosidrado particios Solució. Cosidrmos la partició P={a, a +, a +, a + 3,..., a + k,..., a + = } como a + = tocs = a qu s la amplitud d los itrvalo d sta partició. tocs x3 dx = = = fx k x k = [a 3 + 3a k + 3ak + k 3 3 ] a 3 + 3a k + 3ak + k 3 3 = a3 + +3a +3 a a = a a3 + 3 a + a + a a + k a a a + a + 3 a a a + 3 a3 a++ + a +
2 = a a3 + 3 a a a + + a3 + a + + = a a a a + a a 3 + a =a 3 a + 3 a 3a a +a 3 3 a +3a 3 a + 3 a+ 3 a a 3 + a = a Ejmplo x dx = a cosidrado particios suitrvalos. Dmostrar qu Solució. Cosidrmos la partició P={a, aq, aq,..., aq k,..., aq = } como aq = tocs q = por lo qu si tocs q a xk = aq k aq k = aq k q la cual 0 si x dx = fx k x k = aq k q aq k = a q k aq k q = aq k q k q = a = q a q q k q k q q q = q q + q a q q q = q + a q a = q a q k k q = a = q q a q q q = a = q + a q a q = a
3 Ejmplo 3 Dmostrar qu Sxdx = Cos + Cosa cosidrado particios suitrvalos. Solució. Cosidrmos la partició P={a, a +, a +, a + 3,..., a + k,..., a + = } como a + = tocs = a qu s la amplitud d los itrvalo d sta partició. tocs Sxdx = fx k x k = = [Sa + + Sa Sa + ] Multiplicado por s otmos s s [ s s Sa + k ] [Sa + + Sa Sa + ] Sa + + s Sa s Utilizado la idtidad trigoomtrica Sx Sy = Cosx y Cosx + y y simpr qu o sa multiplo d π s oti s Cosa + Cosa Cosa + Cosa Cosa + Cosa + = Sa + s Cosa + Cosa Cosa + 3 Cosa Cosa + Cosa Pusto qu a + =, la itgral s covirt l limit s Cosa + Cosa + + = s Cosa + Cos + =Cosa Cos 3
4 Ejmplo Dmostrar qu Cosxdx = S Sa cosidrado particios suitrvalos. Solució. Cosidrmos la partició P={a, a +, a +, a + 3,..., a + k,..., a + = } como a + = tocs = a qu s la amplitud d los itrvalo d sta partició. tocs Cosxdx = fx k x k = = [Cosa + + Cosa Cosa + ] Multiplicado por s otmos s s [ s Cosa + k ] [Cosa + + Cosa Cosa + ] s Cosa + + s Cosa s Cosa + Utilizado la idtidad trigoomtrica S α S β = S α + β + S α β y l co d qu S α = S α s Sa+ 3 +S a +Sa+ 5 +S a Sa S a 5 + Sa S a S + + a+ +S a s S a + S + = S Sa Ejmplo 5 Dmostrar qu x xdx = a cosidrado particios suitrvalos. Solució. Cosidrmos la partició P={a, a +, a +, a + 3,..., a + k,..., a + = } como a + = tocs = a qu s la amplitud d los itrvalo d sta partició.
5 tocs x dx = fx k x k = a+k = a k = a k a k = 0 = a [ ] [ k = a ] a como = a y y = a a = = 0 = y = a = tmos qu a [ ] = a [ a a ] a Usarmos l co d qu α = Logα Por lo qu a = Log a = a asi pus a [ a a a ] [ a ] [ = a a a = a a a ] = a a Ejmplo Mdiat la dfiició, calcul x + dx cosidrado particios suitrvalos. Solució. Cosidrmos la partició P={a, a +, a +, a + 3,..., a + k,..., a + = } como a + = tocs = a qu s la amplitud d los itrvalo d sta partició. tocs 5
6 x + dx = + + [a + k + ] = fx k x k = a + k + a + k + = a + = a + + a + = a a a =a a + a + + a = a a + a + a = aa + a + = aa + + =a 3 a + 3 a 3a a +a 3 3 a +3a 3 a + 3 a+ 3 a a 3 + a = a Ejmplo 7 Mdiat la dfiició, calcul 5 x dx cosidrado particios suitrvalos. Solució. Cosidrmos la partició P={, +, +, + 3,..., + k,..., + = 5} como + = tocs = 5 = 3 qu s la amplitud d los itrvalo d sta partició. tocs x dx = = = fx k x k = + k [ ] +k+k = Si + = 5 = 3 = 3 por lo qu
7 =+ + + =+8+9= = =
Universidad de Costa Rica. Instituto Tecnológico de Costa Rica. Determinar si las integrales impropias convergen o divergen.
 Uivrsidad d Costa Rica Istituto Tcológico d Costa Rica Tma: Itgrals impropias. Objtivos: Clasificar las itgrals impropias sgú su spci: primra, sguda o trcra spci. Calcular itgrals impropias utilizado su
Uivrsidad d Costa Rica Istituto Tcológico d Costa Rica Tma: Itgrals impropias. Objtivos: Clasificar las itgrals impropias sgú su spci: primra, sguda o trcra spci. Calcular itgrals impropias utilizado su
MATEMÁTICA D Módulo I: Análisis de Variable Compleja. Teoría de Residuos
 Matmática D MATEMÁTIA D Módulo I: Aálisis d Variabl omplja Uidad Toría d siduos Mag. María Iés Baragatti Sigularidads S dic qu s ua sigularidad aislada d f( si f( o s aalítica pro sí s aalítica u toro
Matmática D MATEMÁTIA D Módulo I: Aálisis d Variabl omplja Uidad Toría d siduos Mag. María Iés Baragatti Sigularidads S dic qu s ua sigularidad aislada d f( si f( o s aalítica pro sí s aalítica u toro
al siguiente límite si existe: . Se suele representar por ( x )
 UNIDAD : DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit it si ist: f f ' sigifica lo mismo. f. S sul rprstar por f D
UNIDAD : DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit it si ist: f f ' sigifica lo mismo. f. S sul rprstar por f D
a a lim i) L< 1 absoluta convergencia absoluta convergencia convergencia condicional divergencia > r.
 (Aputs rvisió para oritar l aprdizaj) DESARROLLO DE LAS FUNCIONES LOGARÍTMICA Y EXPONENCIAL EN SERIES DE POTENCIAS Ua Sri d Potcias s dfi como: a a a a a = = + + + la qu s vidt qu covrg si =. Para dtrmiar
(Aputs rvisió para oritar l aprdizaj) DESARROLLO DE LAS FUNCIONES LOGARÍTMICA Y EXPONENCIAL EN SERIES DE POTENCIAS Ua Sri d Potcias s dfi como: a a a a a = = + + + la qu s vidt qu covrg si =. Para dtrmiar
INTEGRAL INDEFINIDA. Derivación. Integración
 TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA FUNCIÓN PRIMITIVA. F() s ua primitiva d f() si F ()= f(). Esto s prsa así: f() = F'() = F() La itgració s la opració ivrsa a la drivació, d modo qu: FUNCIONES
TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA FUNCIÓN PRIMITIVA. F() s ua primitiva d f() si F ()= f(). Esto s prsa así: f() = F'() = F() La itgració s la opració ivrsa a la drivació, d modo qu: FUNCIONES
Antiderivada o Primitiva
 Antiderivada o Promitiva agosto 2012 En esta Presentación... En esta Presentación veremos: Definición de Antiderivada. En esta Presentación... En esta Presentación veremos: Definición de Antiderivada.
Antiderivada o Promitiva agosto 2012 En esta Presentación... En esta Presentación veremos: Definición de Antiderivada. En esta Presentación... En esta Presentación veremos: Definición de Antiderivada.
MÉTODOS MATEMÁTICOS DE LA FÍSICA II Segunda Parte. 10 de Febrero de 2005.
 MÉTODOS MATEMÁTICOS DE LA FÍSICA II Segunda Parte. 0 de Febrero de 005. Tenéis 3 horas para hacer estos ejercicios. Podéis usar una versión de los apuntes como están en la red, sin ninguna anotación. No
MÉTODOS MATEMÁTICOS DE LA FÍSICA II Segunda Parte. 0 de Febrero de 005. Tenéis 3 horas para hacer estos ejercicios. Podéis usar una versión de los apuntes como están en la red, sin ninguna anotación. No
INTEGRAL INDEFINIDA. Derivación. Integración
 TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA. FUNCIÓN PRIMITIVA F() s ua primitiva d f() si F ()= f(). Esto s prsa así: La itgració s la opració ivrsa a la drivació, d modo qu: f() F'() F() FUNCIONES PRIMITIVAS
TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA. FUNCIÓN PRIMITIVA F() s ua primitiva d f() si F ()= f(). Esto s prsa así: La itgració s la opració ivrsa a la drivació, d modo qu: f() F'() F() FUNCIONES PRIMITIVAS
Universidad Simón Bolívar Departamento de Matemáticas Puras y Aplicadas Enero - Marzo, 2008
 Universidad Simón Bolívar Departamento de Matemáticas Puras y Aplicadas Enero - Marzo, 8 MA- Practica: semana y/o Ejercicios sugeridos para la semana y/o. Cubre el siguiente material: Propiedades de la
Universidad Simón Bolívar Departamento de Matemáticas Puras y Aplicadas Enero - Marzo, 8 MA- Practica: semana y/o Ejercicios sugeridos para la semana y/o. Cubre el siguiente material: Propiedades de la
Universidad de Puerto Rico Recinto Universitario de Mayagüez Departamento de Ciencias Matemáticas
 Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
Antiderivada o Primitiva
 Octubre 2013 En esta Presentación... En esta Presentación veremos: Definición de Antiderivada En esta Presentación... En esta Presentación veremos: Definición de Antiderivada Ejemplos En esta Presentación...
Octubre 2013 En esta Presentación... En esta Presentación veremos: Definición de Antiderivada En esta Presentación... En esta Presentación veremos: Definición de Antiderivada Ejemplos En esta Presentación...
Problemas Tema 2: Sistemas
 SISTEMAS Y CIRCUITOS ~ PROBLEMAS Curso Académico 00900 Problmas Tma Sismas PROBLEMA. Dados los siguis sismas impo coiuo las sñals d rada idicadas, drmi las sñals d salida corrspodis ( ) x sñal d rada x
SISTEMAS Y CIRCUITOS ~ PROBLEMAS Curso Académico 00900 Problmas Tma Sismas PROBLEMA. Dados los siguis sismas impo coiuo las sñals d rada idicadas, drmi las sñals d salida corrspodis ( ) x sñal d rada x
1.2 INTEGRACION, DIFERENCIACIÓN DE FUNCIONES Y EXPANSIONES EN SERIES. (1.2_CvR_T_062, Revisión: , C2, C3, C4)
 . INTEGRACION, DIFERENCIACIÓN DE FUNCIONES Y EXPANSIONES EN SERIES. (._CvR_T_06, Rvisió: 5-0-06, C, C3, C4).. DERIVADA DE UNA FUNCIÓN. Dfiició: f f ( ) f ( ) lim, si l límit ist. 0 Notció: f ', f ( ) E.g.:
. INTEGRACION, DIFERENCIACIÓN DE FUNCIONES Y EXPANSIONES EN SERIES. (._CvR_T_06, Rvisió: 5-0-06, C, C3, C4).. DERIVADA DE UNA FUNCIÓN. Dfiició: f f ( ) f ( ) lim, si l límit ist. 0 Notció: f ', f ( ) E.g.:
Formulas de Newton-Cotes
 Formulas de Newton-Cotes. Usando las reglas del Trapecio, Punto Medio, Simpson y las formulas de Newton-Cotes abiertas con n =,, aproxime el valor de las siguientes Integrales. Construya una tabla para
Formulas de Newton-Cotes. Usando las reglas del Trapecio, Punto Medio, Simpson y las formulas de Newton-Cotes abiertas con n =,, aproxime el valor de las siguientes Integrales. Construya una tabla para
MATEMÁTICAS II (PAUU XUÑO 2011)
 MATEMÁTICAS II (PAUU XUÑO 0) OPCIÓN A. a) Sean C, C, C 3 las columnas primera, segunda y tercera, respectivamente, de una matriz cuadrada M de orden 3 con det (M ) = 4. Calcula enunciando las propiedades
MATEMÁTICAS II (PAUU XUÑO 0) OPCIÓN A. a) Sean C, C, C 3 las columnas primera, segunda y tercera, respectivamente, de una matriz cuadrada M de orden 3 con det (M ) = 4. Calcula enunciando las propiedades
TEMA 1: CALCULO DIRECTO DE LÍMITES
 INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Rsolució Nº 88 d ovimbr.8/ ScrtariaD Educació Distrital REGISTRO DANE Nº-99 Tléfoo Barrio Bastidas Sata Marta DEPARTAMENTO DE MATEMATICAS ACTIVIDAD ESPECIAL
INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Rsolució Nº 88 d ovimbr.8/ ScrtariaD Educació Distrital REGISTRO DANE Nº-99 Tléfoo Barrio Bastidas Sata Marta DEPARTAMENTO DE MATEMATICAS ACTIVIDAD ESPECIAL
1.- a) Hallar a y b para que la siguiente función sea continua en x = 1:
 .- a) Hallar a y b para qu la siguit fució sa cotiua = : b L( ) < f = a = > L b) Para sos valors d a y b, studiar la drivabilidad d f =. Solució: a) f s cotiua l puto = lim f = f() E st caso f () = a lim
.- a) Hallar a y b para qu la siguit fució sa cotiua = : b L( ) < f = a = > L b) Para sos valors d a y b, studiar la drivabilidad d f =. Solució: a) f s cotiua l puto = lim f = f() E st caso f () = a lim
Ejercicios resueltos de Álgebra, hoja 3. Beatriz Graña Otero
 Ejercicios resueltos de Álgebra, hoja. Beatriz Graña Otero 5 de Diciembre de 8 B.G.O. 47.- Sobre el R-espacio vectorial E de dimensión 4, sea la métrica cuya matriz asociada a la base B = {e, e, e, e 4
Ejercicios resueltos de Álgebra, hoja. Beatriz Graña Otero 5 de Diciembre de 8 B.G.O. 47.- Sobre el R-espacio vectorial E de dimensión 4, sea la métrica cuya matriz asociada a la base B = {e, e, e, e 4
EXPONENTES Y POTENCIAS Muchos números se expresan en forma más conveniente como potencias de 10. Por ejemplo: m n n 0,2 3 3
 Rpaso d Matmáticas E st apédic s hará u brv rpaso d las cuacios y fórmulas básicas d utilidad Química Física gral y Trmodiámica Química particular. EXPONENTES Y POTENCIAS Muchos úmros s xprsa forma más
Rpaso d Matmáticas E st apédic s hará u brv rpaso d las cuacios y fórmulas básicas d utilidad Química Física gral y Trmodiámica Química particular. EXPONENTES Y POTENCIAS Muchos úmros s xprsa forma más
ANÁLISIS DE FOURIER CAPÍTULO CUATRO TIEMPO DISCRETO Introducción
 CAPÍTULO CUATRO AÁLISIS DE FOURIER TIEMPO DISCRETO 4. Itroducció Las técicas dl aálisis d Fourir timpo cotiuo dsarrolladas l capítulo atrior ti mucho valor l aálisis d las propidads d sñals y sistmas d
CAPÍTULO CUATRO AÁLISIS DE FOURIER TIEMPO DISCRETO 4. Itroducció Las técicas dl aálisis d Fourir timpo cotiuo dsarrolladas l capítulo atrior ti mucho valor l aálisis d las propidads d sñals y sistmas d
Tema 11. Limite de funciones. Continuidad
 Tma. Limit d fucios. Cotiuidad. Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito
Tma. Limit d fucios. Cotiuidad. Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito
Entonces el volumen del k-ésimo cilindro es. n n) πar2 k 2. k 2 = πar2 k 2 n(n + 1)(2n + 1) 6
 Uidad 1 Itegrales Múltiples 1.2 Itegral de ua fució de dos variables como volume Volumees Cuado deimos volume aceptaremos el hecho de que si se trata de u cubo de lado a etoces V cubo) = a 3 y si se trata
Uidad 1 Itegrales Múltiples 1.2 Itegral de ua fució de dos variables como volume Volumees Cuado deimos volume aceptaremos el hecho de que si se trata de u cubo de lado a etoces V cubo) = a 3 y si se trata
es divergente. es divergente.
 .- Dtrmir l cráctr d l sri sgú los vlors d = +. Solució: sido = + = Si = = lim = s divrgt. = Si < < lim = s divrgt. = Si = = lim = s divrgt. = Si >, plicdo l critrio d D`Almrt: + ( + ) ( + ) + lim = lim
.- Dtrmir l cráctr d l sri sgú los vlors d = +. Solució: sido = + = Si = = lim = s divrgt. = Si < < lim = s divrgt. = Si = = lim = s divrgt. = Si >, plicdo l critrio d D`Almrt: + ( + ) ( + ) + lim = lim
Tema 7. Integrales múltiples
 Tema 7 Integrales múltiples 7.. efinición. En esta sección estudiamos el cálculo de la integral de una función real de dos variables denominada integral doble. Se puede utilizar el esquema del tema anterior
Tema 7 Integrales múltiples 7.. efinición. En esta sección estudiamos el cálculo de la integral de una función real de dos variables denominada integral doble. Se puede utilizar el esquema del tema anterior
Noviembre 2006, Versión 1.1. Ejercicio 1 Resuelve las siguientes ecuaciones diferenciales ordinarias. 1. 4y 00 + y 0 =0. 2. y 00 y 0 6y =0.
 E.T.S. Minas: Métodos Matemáticos Ejercicios resueltos Tema 8 EDOs de orden superior Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Curso 006/07
E.T.S. Minas: Métodos Matemáticos Ejercicios resueltos Tema 8 EDOs de orden superior Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Curso 006/07
1. CÁLCULO DE PRIMITIVAS
 1 1. CÁLCULO DE PRIMITIVAS Definición 1.1. Primitiva. Una función F (x) es primitiva de f(x) si F (x) = f(x) para todo x del dominio de f. Obsérvese que si F (x) es primitiva de f(x), entonces F (x) +
1 1. CÁLCULO DE PRIMITIVAS Definición 1.1. Primitiva. Una función F (x) es primitiva de f(x) si F (x) = f(x) para todo x del dominio de f. Obsérvese que si F (x) es primitiva de f(x), entonces F (x) +
Ecuaciones diferenciales de orden superior
 Práctica 2 Ecuaciones diferenciales de orden superior 2.1. Introducción Una ED de orden n es una ecuación de la forma o escrito en forma normal g(x, y, y,...,y (n) ) = 0 (2.1) y (n) = f(x, y, y,...,y (n
Práctica 2 Ecuaciones diferenciales de orden superior 2.1. Introducción Una ED de orden n es una ecuación de la forma o escrito en forma normal g(x, y, y,...,y (n) ) = 0 (2.1) y (n) = f(x, y, y,...,y (n
Sistemas de ecuaciones diferenciales lineales
 695 Aálisis matmático para Igiría M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA CAPÍTULO Sistmas d cuacios difrcials lials d primr ord Cuado s studia matmáticamt ua situació d la ralidad, l modlo qu s
695 Aálisis matmático para Igiría M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA CAPÍTULO Sistmas d cuacios difrcials lials d primr ord Cuado s studia matmáticamt ua situació d la ralidad, l modlo qu s
2.8.3 Solución de las ecuaciones diferenciales lineales no homogéneas por el método de variación de parámetros
 .8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros 59.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros Variació d parátros U procdiito
.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros 59.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros Variació d parátros U procdiito
Funciones de Una Variable Real II: Cálculo de Primitivas
 Universidad de Murcia Departamento Matemáticas Funciones de Una Variable Real II: Cálculo de Primitivas B. Cascales, J. M. Mira y L. Oncina Universidad de Murcia http://webs.um.es/beca Grado en Matemáticas
Universidad de Murcia Departamento Matemáticas Funciones de Una Variable Real II: Cálculo de Primitivas B. Cascales, J. M. Mira y L. Oncina Universidad de Murcia http://webs.um.es/beca Grado en Matemáticas
Formulas Matemáticas
 B A C a TRIGONOMETRÍA Radian Grados sen a cos a tag a 0 2π 0 0 1 0 π/6 30º 1 / 2 3 / 2 3 / 3 π/4 45º 2 / 2 2 / 2 1 π/3 60º 3 / 2 1 / 2 3 π/2 90º 1 0 π 180º 0-1 0 3π/2 270º -1 0 sen a = B / C cos a = A
B A C a TRIGONOMETRÍA Radian Grados sen a cos a tag a 0 2π 0 0 1 0 π/6 30º 1 / 2 3 / 2 3 / 3 π/4 45º 2 / 2 2 / 2 1 π/3 60º 3 / 2 1 / 2 3 π/2 90º 1 0 π 180º 0-1 0 3π/2 270º -1 0 sen a = B / C cos a = A
Auxiliar 6: Interpolación Mediante Spline Cúbicos
 Universidad de Chile Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Matemática Semestre Otoño 27 Cálculo Numérico MAA-2 Profesor: Gonzalo Hernández Auxiliar: Gonzalo Ríos Fecha:
Universidad de Chile Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Matemática Semestre Otoño 27 Cálculo Numérico MAA-2 Profesor: Gonzalo Hernández Auxiliar: Gonzalo Ríos Fecha:
1. Derivada de la función compuesta
 Cátedra de Matemática Matemática Facultad de Arquitectura Universidad de la República 213 Segundo semestre Ya nos hemos encontrado con la idea de que las propiedades del cálculo de integrales y del cálculo
Cátedra de Matemática Matemática Facultad de Arquitectura Universidad de la República 213 Segundo semestre Ya nos hemos encontrado con la idea de que las propiedades del cálculo de integrales y del cálculo
Teoría de Sistemas y Señales
 Toría d Sistmas y Sñals Trasparias: Aálisis ruial d sñals TD Autor: Dr. Jua Carlos Gómz Aálisis ruial d Sñals Timpo Disrto. Sri d ourir d Sñals Timpo Disrto Sa () ua sñal priódia o príodo, s dir: ( ) +
Toría d Sistmas y Sñals Trasparias: Aálisis ruial d sñals TD Autor: Dr. Jua Carlos Gómz Aálisis ruial d Sñals Timpo Disrto. Sri d ourir d Sñals Timpo Disrto Sa () ua sñal priódia o príodo, s dir: ( ) +
11 INTRODUCCIÓN A LA DINÁMICA NO LINEAL (BIFURCACIONES, CAOS)
 INTRODUCCIÓN A LA DINÁMICA NO LINEAL (BIFURCACIONES, CAOS) Los sistmas o lials pud llgar a tr comportamitos ralmt sorprdts alguos casos: por u lado pud llgar a tr diámicas totalmt difrts sgú l valor qu
INTRODUCCIÓN A LA DINÁMICA NO LINEAL (BIFURCACIONES, CAOS) Los sistmas o lials pud llgar a tr comportamitos ralmt sorprdts alguos casos: por u lado pud llgar a tr diámicas totalmt difrts sgú l valor qu
MÉTODOS MATEMÁTICOS II
 MÉTODOS MATEMÁTICOS II (Licenciatura de Física. Curso 2007-2008) Boletín de problemas a evaluar correspondientes a los Temas I y II Fecha de entrega: Viernes, 23 de Noviembre de 2007 1. Calcula los siguientes
MÉTODOS MATEMÁTICOS II (Licenciatura de Física. Curso 2007-2008) Boletín de problemas a evaluar correspondientes a los Temas I y II Fecha de entrega: Viernes, 23 de Noviembre de 2007 1. Calcula los siguientes
Aproximación de funciones derivables mediante polinomios: Fórmulas de Taylor y Mac-Laurin
 Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
1.- Estudie el carácter de la serie numérica. 1 es divergente, la serie n propuesta será divergente. Solución.- Puesto que, n = 1, 2, 3,...
 TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mil: imozs@lx.ud.s http://tlfoic.t/wb/imm EJERCICIOS DE SERIES NUMÉRICAS PROPUESTOS EN EXÁMENES.- Estudi l cráctr d l sri uméric. (Fbrro 00, x. or.) Solució.- Pusto
TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mil: imozs@lx.ud.s http://tlfoic.t/wb/imm EJERCICIOS DE SERIES NUMÉRICAS PROPUESTOS EN EXÁMENES.- Estudi l cráctr d l sri uméric. (Fbrro 00, x. or.) Solució.- Pusto
3º B.D. opción Social-Económico Matemática III. Parábola.
 Parábola. Definición: Lugar geométrico de los puntos del plano que equidistan de un punto fijo F, llamado foco y de una recta fija z llamada directriz. Siendo F no perteneciente a z. Entonces siendo P
Parábola. Definición: Lugar geométrico de los puntos del plano que equidistan de un punto fijo F, llamado foco y de una recta fija z llamada directriz. Siendo F no perteneciente a z. Entonces siendo P
Selectividad Matemáticas II junio 2015, Andalucía (versión 3)
 Selectividad Matemáticas II junio 05, Andalucía (versión 3) Pedro González Ruiz 7 de junio de 05. Opción A Problema. Se quiere construir un depośito abierto de base cuadrada y paredes verticales con capacidad
Selectividad Matemáticas II junio 05, Andalucía (versión 3) Pedro González Ruiz 7 de junio de 05. Opción A Problema. Se quiere construir un depośito abierto de base cuadrada y paredes verticales con capacidad
Cálculo 20. Semestre B-2015 Prof. José Prieto Correo: 1. Teoremas sobre funciones derivables
 Cálculo 20. Semestre B-2015 Prof. José Prieto Correo: prieto@ula.ve 1. Teoremas sobre funciones derivables Problema 1 Determine si la función dada satisface las hipótesis del Teorema de Bolzano sobre el
Cálculo 20. Semestre B-2015 Prof. José Prieto Correo: prieto@ula.ve 1. Teoremas sobre funciones derivables Problema 1 Determine si la función dada satisface las hipótesis del Teorema de Bolzano sobre el
Señales y Sistemas. Análisis de Fourier.
 Sñals y Sistmas Aálisis d Fourir. Itroducció El foqu d st capítulo s la rprstació d sñals utilizado sos y cosos ( otras palabras, xpocials complas). El studio d sñals y sistmas utilizado xpocials complas
Sñals y Sistmas Aálisis d Fourir. Itroducció El foqu d st capítulo s la rprstació d sñals utilizado sos y cosos ( otras palabras, xpocials complas). El studio d sñals y sistmas utilizado xpocials complas
Ejercicios de Variables Aleatorias
 Ejercicios de Variables Aleatorias Elisa M. Molanes-López, Depto. Estadística, UC3M Transformaciones de variables aleatorias Ejercicio. Sea X una v.a. continua con función de densidad dada por: /, si
Ejercicios de Variables Aleatorias Elisa M. Molanes-López, Depto. Estadística, UC3M Transformaciones de variables aleatorias Ejercicio. Sea X una v.a. continua con función de densidad dada por: /, si
Tema 16: Ecuaciones diferenciales II: Ecuaciones lineales de orden superior
 Tema 16: Ecuaciones diferenciales II: Ecuaciones lineales de orden superior 1 Ecuaciones diferenciales lineales de orden mayor que 1 Una ecuación diferencial lineal (en adelante ecuación lineal) de orden
Tema 16: Ecuaciones diferenciales II: Ecuaciones lineales de orden superior 1 Ecuaciones diferenciales lineales de orden mayor que 1 Una ecuación diferencial lineal (en adelante ecuación lineal) de orden
Sobre la integral de línea en un álgebra de dimensión real 2 que no son los complejos
 Culcyt// Itgrls Sor l itgrl d lí u álgr d dimsió rl qu o so los compljos Eliflt Lópz Gozlz, Víctor M Crrillo S, Srgio Trrzs Porrs Rsum: Cosidrmos u álgr d Bch A comuttiv uitri d dimsió rl qu o so los úmros
Culcyt// Itgrls Sor l itgrl d lí u álgr d dimsió rl qu o so los compljos Eliflt Lópz Gozlz, Víctor M Crrillo S, Srgio Trrzs Porrs Rsum: Cosidrmos u álgr d Bch A comuttiv uitri d dimsió rl qu o so los úmros
SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA 1: Problema Nº 5.34 Oppenheim
 SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA : Problma Nº 5.3 Opphim Obsrv l siguit sistma: Dtrmi y() Solució: El traycto d arriba produc, al multiplicar por Cos(/), traslació dl spctro
SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA : Problma Nº 5.3 Opphim Obsrv l siguit sistma: Dtrmi y() Solució: El traycto d arriba produc, al multiplicar por Cos(/), traslació dl spctro
Elementos de Cálculo en Varias Variables
 Elementos de Cálculo en Varias Variables Departamento de Matemáticas, CSI/ITESM 5 de octubre de 009 Índice Introducción Derivada parcial El Jacobiano de una Función 5 Derivadas Superiores 5 5 Derivada
Elementos de Cálculo en Varias Variables Departamento de Matemáticas, CSI/ITESM 5 de octubre de 009 Índice Introducción Derivada parcial El Jacobiano de una Función 5 Derivadas Superiores 5 5 Derivada
Examen de Matemáticas II (Junio 2014) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas II (Junio 04) Selectividad-Opción A Tiempo: 90 minutos Problema (3 puntos) Dadas las matrices α β γ x 0 A = γ 0 α ; X = y ; B = 0 O = 0 β γ z 0 se pide: (,5 puntos). Calcula α, β
Examen de Matemáticas II (Junio 04) Selectividad-Opción A Tiempo: 90 minutos Problema (3 puntos) Dadas las matrices α β γ x 0 A = γ 0 α ; X = y ; B = 0 O = 0 β γ z 0 se pide: (,5 puntos). Calcula α, β
1. Empleando sustitución universal, calcular: dx.
 Escuela Superior Politécnica del Litoral Práctica 1.4 de Cálculo Integral 1. Empleando sustitución universal, calcular: a) b) 1 sen(x) + cos(x) dx. 1 3 + 5cos(x) dx. c) d) sen(x) 1 sen(x) dx. dx 8 4sen(x)
Escuela Superior Politécnica del Litoral Práctica 1.4 de Cálculo Integral 1. Empleando sustitución universal, calcular: a) b) 1 sen(x) + cos(x) dx. 1 3 + 5cos(x) dx. c) d) sen(x) 1 sen(x) dx. dx 8 4sen(x)
Espacios vectoriales euclídeos.
 Univrsidad d Jaén Dpartamnto d Matmáticas (Ara d Álgbra) Curso 4/5 PRÁCTICA Nº 6 Espacios vctorials uclídos. En sta práctica vamos a vr cómo introducir un producto scalar y trabajar con él n Mathmatica
Univrsidad d Jaén Dpartamnto d Matmáticas (Ara d Álgbra) Curso 4/5 PRÁCTICA Nº 6 Espacios vctorials uclídos. En sta práctica vamos a vr cómo introducir un producto scalar y trabajar con él n Mathmatica
, pero lím. 1 x3 1. (x 1) x(x + 1) = x = x 1 1 x 3 = que es una forma indeterminada. (x + 2) (1 + x + x 2 ) = 3
 Ana María Albornoz R. Ejercicios resueltos. Calcular los siguientes ites algebraicos + + 5 + + + 0 0 + pero + 0 0 0, pero 0 + + + 4 que es una forma indeterminada. Pero + + + + + + + + + + + + + + + +
Ana María Albornoz R. Ejercicios resueltos. Calcular los siguientes ites algebraicos + + 5 + + + 0 0 + pero + 0 0 0, pero 0 + + + 4 que es una forma indeterminada. Pero + + + + + + + + + + + + + + + +
INTEGRALES. EL PROBLEMA DEL ÁREA I
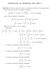 INTEGRALES. EL PROBLEMA DEL ÁREA I Ejercicio : En este ejercicio vamos a practicar el cálculo de la integral indefinida haciendo uso de la integral inmediata: (f(x)) n f (x)dx n = (f(x))n+ + K (K constante)
INTEGRALES. EL PROBLEMA DEL ÁREA I Ejercicio : En este ejercicio vamos a practicar el cálculo de la integral indefinida haciendo uso de la integral inmediata: (f(x)) n f (x)dx n = (f(x))n+ + K (K constante)
Familiarizarse con las propiedades y las principales técnicas de integración.
 Capítulo 7 Integración Objetivos Familiarizarse con las propiedades y las principales técnicas de integración. 7.1. Definición y propiedades Sea f(x) una función real. Una primitiva o integral indefinida
Capítulo 7 Integración Objetivos Familiarizarse con las propiedades y las principales técnicas de integración. 7.1. Definición y propiedades Sea f(x) una función real. Una primitiva o integral indefinida
1. Teorema de Fubini. Teorema de Fubini.
 1. El teorema de Fubini nos va a dar una técnica para el cálculo de integrales de funciones de varias variables mediante el cálculo de varias integrales de funciones de una variable. partir de ahí se podrán
1. El teorema de Fubini nos va a dar una técnica para el cálculo de integrales de funciones de varias variables mediante el cálculo de varias integrales de funciones de una variable. partir de ahí se podrán
Integración por Partes III. Método Tabular
 Integración por Partes III Método Tabular I.) INTEGRALES NO CÍCLICAS El método tabular te va a permitir desarrollar cierto tipo de integrales sin tener que utilizar todos los pasos de la integración por
Integración por Partes III Método Tabular I.) INTEGRALES NO CÍCLICAS El método tabular te va a permitir desarrollar cierto tipo de integrales sin tener que utilizar todos los pasos de la integración por
ESPACIOS VECTORIALES Y APLICACIONES LINEALES
 Departamento de Matemática Aplicada II E.E.I. ÁLGEBRA Y ESTADÍSTICA Boletín n o (010-011 ESPACIOS VECTORIALES Y APLICACIONES LINEALES 1. En el espacio vectorial ordinario R 4 estudiar cuáles de los siguientes
Departamento de Matemática Aplicada II E.E.I. ÁLGEBRA Y ESTADÍSTICA Boletín n o (010-011 ESPACIOS VECTORIALES Y APLICACIONES LINEALES 1. En el espacio vectorial ordinario R 4 estudiar cuáles de los siguientes
Contenidos de los preliminares
 Preliminares del tema 3 Contenidos de los preliminares Algunas primitivas Una primitiva por cambio de variable Igualdades notables Ecuaciones bicuadradas Construcción de un polinomio de segundo grado a
Preliminares del tema 3 Contenidos de los preliminares Algunas primitivas Una primitiva por cambio de variable Igualdades notables Ecuaciones bicuadradas Construcción de un polinomio de segundo grado a
CÁLCULO NUMÉRICO (0258)
 CÁLCULO NUMÉRICO (58) Tema 5. Diferenciación e Integración Numérica Enero 5. Utilice la fórmula para calcular la derivada de f(x) = cos(x) en utilizar la fórmula. f(x + ) f(x) f'(x) x = y con =.. Estime
CÁLCULO NUMÉRICO (58) Tema 5. Diferenciación e Integración Numérica Enero 5. Utilice la fórmula para calcular la derivada de f(x) = cos(x) en utilizar la fórmula. f(x + ) f(x) f'(x) x = y con =.. Estime
Unidad Temática Cálculo de primitivas
 Unidad Temática 5 5.1 Análisis Matemático (Ingeniería Informática) Departamento de Matemática Aplicada Facultad de Informática Universidad Politécnica de Valencia Contenidos 1 Integración Primitiva Integración
Unidad Temática 5 5.1 Análisis Matemático (Ingeniería Informática) Departamento de Matemática Aplicada Facultad de Informática Universidad Politécnica de Valencia Contenidos 1 Integración Primitiva Integración
La integral de Riemann
 L integrl de Riemnn 1 Vmos dr un definición precis de l integrl de un función definid en un intervlo. Este tiene que ser un intervlo cerrdo y cotdo, es decir [,] con < R, y l definición que dremos de integrl
L integrl de Riemnn 1 Vmos dr un definición precis de l integrl de un función definid en un intervlo. Este tiene que ser un intervlo cerrdo y cotdo, es decir [,] con < R, y l definición que dremos de integrl
Series de números reales
 Tema 6 Series de úmeros reales 6. Series de úmeros reales. Defiició 6. Sea {a } ua sucesió de úmeros reales y cosideremos la sucesió {S }, defiida por S = a + a + + a, para cada IN, que llamaremos sucesió
Tema 6 Series de úmeros reales 6. Series de úmeros reales. Defiició 6. Sea {a } ua sucesió de úmeros reales y cosideremos la sucesió {S }, defiida por S = a + a + + a, para cada IN, que llamaremos sucesió
Álgebra Matricial y Optimización Ma130
 Álgebra Matricial y Optimización Ma130 Elementos de Cálculo en Varias Variables Departamento de Matemáticas ITESM Elementos de Cálculo en Varias Variables Ma130 - p. 1/47 En esta lectura se dará una revisión
Álgebra Matricial y Optimización Ma130 Elementos de Cálculo en Varias Variables Departamento de Matemáticas ITESM Elementos de Cálculo en Varias Variables Ma130 - p. 1/47 En esta lectura se dará una revisión
Ejercicios Resueltos de Clasificación de Funciones
 Istituto Tecológico de Ciudad Madero Uidad I. Complejidad Computacioal Capitulo. Clasificació de Algoritmos Ejercicios Resueltos de Clasificació de Fucioes.. Determie si f ( ) perteece a la clase idicada
Istituto Tecológico de Ciudad Madero Uidad I. Complejidad Computacioal Capitulo. Clasificació de Algoritmos Ejercicios Resueltos de Clasificació de Fucioes.. Determie si f ( ) perteece a la clase idicada
Sucesiones y series de números reales
 38 Matemáticas : Cálculo diferecial e IR Capítulo Sucesioes y series de úmeros reales Sucesioes Defiició 37- Llamaremos sucesió de úmeros reales a cualquier aplicació f: N R y la represetaremos por { a,
38 Matemáticas : Cálculo diferecial e IR Capítulo Sucesioes y series de úmeros reales Sucesioes Defiició 37- Llamaremos sucesió de úmeros reales a cualquier aplicació f: N R y la represetaremos por { a,
INTEGRALES DEFINIDAS Y CÁLCULOS DE ÁREAS
 INTEGRALES DEFINIDAS Y CÁLCULOS DE ÁREAS CÁLCULO AUTOMÁTICO DE INTEGRALES DEFINIDAS La integral de una función definida puede obtenerse en DERIVE tecleando el icono Cálculo integral,, También puede obtenerse
INTEGRALES DEFINIDAS Y CÁLCULOS DE ÁREAS CÁLCULO AUTOMÁTICO DE INTEGRALES DEFINIDAS La integral de una función definida puede obtenerse en DERIVE tecleando el icono Cálculo integral,, También puede obtenerse
( x ) 2 SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD. 1 Saca factor común: 2 Expresa los polinomios siguientes como cuadrado de un binomio:
 Pág. 1 Página 95 PRACTICA Factor común e identidades notables 1 Saca factor común: a) 9x 2 + 6x 3 b) 2x 3 6x 2 + 4x c) 10x 3 5x 2 d) x 4 x 3 + x 2 x a) 9x 2 +6x 3 = 3(3x 2 + 2x 1) b) 2x 3 6x 2 + 4x = 2x(x
Pág. 1 Página 95 PRACTICA Factor común e identidades notables 1 Saca factor común: a) 9x 2 + 6x 3 b) 2x 3 6x 2 + 4x c) 10x 3 5x 2 d) x 4 x 3 + x 2 x a) 9x 2 +6x 3 = 3(3x 2 + 2x 1) b) 2x 3 6x 2 + 4x = 2x(x
Práctico 7 - Desarrollo de Taylor. 1. Polinomio de Taylor. Universidad de la República Cálculo 1 Facultad de Ingeniería - IMERL Segundo Semestre 2016
 Universidad de la República Cálculo Facultad de Ingeniería - IMERL Segundo Semestre 206 Práctico 7 - Desarrollo de Taylor. Polinomio de Taylor. El polinomio de Mc Laurin de orden 4 asociado a una cierta
Universidad de la República Cálculo Facultad de Ingeniería - IMERL Segundo Semestre 206 Práctico 7 - Desarrollo de Taylor. Polinomio de Taylor. El polinomio de Mc Laurin de orden 4 asociado a una cierta
Herramientas digitales de auto-aprendizaje para Matemáticas
 ir Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura ir ir Índice. Definiciones y propiedades Método de por
ir Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura ir ir Índice. Definiciones y propiedades Método de por
Práctico Preparación del Examen
 Cálculo Diferencial e Integral (Áreas Tecnológicas) Segundo Semestre 4 Universidad de la República Práctico Preparación del Examen Límites, funciones y continuidad Ejercicio Sea log(+x ) f(x) =, si x
Cálculo Diferencial e Integral (Áreas Tecnológicas) Segundo Semestre 4 Universidad de la República Práctico Preparación del Examen Límites, funciones y continuidad Ejercicio Sea log(+x ) f(x) =, si x
Preguntas Total Puntuación obtenida
 1 SEGUNDO PARCIAL DE MATEMÁTICAS. GRADO DE INGENIERÍA CIVIL Preguntas 1 2 3 4 5 6 7 8 9 10 Total Puntuación obtenida Observaciones 1. Las preguntas 1-6 son eliminatorias. Sólo se corregirá el examen completo
1 SEGUNDO PARCIAL DE MATEMÁTICAS. GRADO DE INGENIERÍA CIVIL Preguntas 1 2 3 4 5 6 7 8 9 10 Total Puntuación obtenida Observaciones 1. Las preguntas 1-6 son eliminatorias. Sólo se corregirá el examen completo
I.T. INDUSTRIAL METODOS ESTADÍSTICOS. FORMULARIO I. ESTADISTICA DESCRIPTIVA Xv.a. Media x = n n i x 2 Varianza poblacional σ 2 i
 I.T. INDUSTRIAL METODOS ESTADÍSTICOS FORMULARIO I. ESTADISTICA DESCRIPTIVA Xv.a k modalidades x 1,x,..., x k ; datos i x i Media x = i x Variaza poblacioal σ i = x i (x i x) Variaza muestral S = 1 (x i
I.T. INDUSTRIAL METODOS ESTADÍSTICOS FORMULARIO I. ESTADISTICA DESCRIPTIVA Xv.a k modalidades x 1,x,..., x k ; datos i x i Media x = i x Variaza poblacioal σ i = x i (x i x) Variaza muestral S = 1 (x i
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
UNIVERSIDAD TECNOLÓGICA DE JALISCO DIVISIÓN ELECTRÓNICA Y AUTOMATIZACIÓN
 AGOSTO 6 TITULO DE LA PRACTICA: Solución d la tranformada d la laplac por mdio dl torma fundamntal ASIGNATURA: Matmática III HOJA: DE: UNIDAD TEMATICA: Tranformada d Laplac FECHA DE REALIZACIÓN: d Agoto
AGOSTO 6 TITULO DE LA PRACTICA: Solución d la tranformada d la laplac por mdio dl torma fundamntal ASIGNATURA: Matmática III HOJA: DE: UNIDAD TEMATICA: Tranformada d Laplac FECHA DE REALIZACIÓN: d Agoto
Funciones de Clase C 1
 Capítulo 7 Funciones de Clase C 1 Vamos a considerar ahora la extensión a varias variables del concepto de función de clase C 1. Cada vez que establezcamos una propiedad de las funciones diferenciables,
Capítulo 7 Funciones de Clase C 1 Vamos a considerar ahora la extensión a varias variables del concepto de función de clase C 1. Cada vez que establezcamos una propiedad de las funciones diferenciables,
Lección: Ortogonalidad y Series de Fourier
 Lección: Ortogonalidad y Series de Fourier Dr. Miguel Angel Uh Zapata, Centro de Investigación en Matemáticas, Unidad Mérida Facultad de Matemáticas, UADY Octubre 2015 Miguel Uh Lección: Ortogonalidad
Lección: Ortogonalidad y Series de Fourier Dr. Miguel Angel Uh Zapata, Centro de Investigación en Matemáticas, Unidad Mérida Facultad de Matemáticas, UADY Octubre 2015 Miguel Uh Lección: Ortogonalidad
Álgebra y Álgebra II - Segundo Cuatrimestre 2017 Práctico 4 - Espacios Vectoriales
 Álgebra y Álgebra II - Segundo Cuatrimestre 2017 Práctico 4 - Espacios Vectoriales (1) Sea n N. Mostrar que el conjunto de polinomios sobre R de grado menor que n es un subespacio vectorial de R[x]. Este
Álgebra y Álgebra II - Segundo Cuatrimestre 2017 Práctico 4 - Espacios Vectoriales (1) Sea n N. Mostrar que el conjunto de polinomios sobre R de grado menor que n es un subespacio vectorial de R[x]. Este
TEORÍA DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 3: Sucesiones y series. Domingo Pestana Galván José Manuel Rodríguez García
 TEORÍA DE CÁLCULO I Para Grados e Igeiería Capítulo 3: Sucesioes y series Domigo Pestaa Galvá José Mauel Rodríguez García Figuras realizadas co Arturo de Pablo Martíez TEMA 3. Sucesioes y series 3. Sucesioes
TEORÍA DE CÁLCULO I Para Grados e Igeiería Capítulo 3: Sucesioes y series Domigo Pestaa Galvá José Mauel Rodríguez García Figuras realizadas co Arturo de Pablo Martíez TEMA 3. Sucesioes y series 3. Sucesioes
RESUMEN DE CARACTERÍSTICAS DE LAS FUNCIONES REALES. CONTINUIDAD
 RESUMEN DE CARACTERÍSTICAS DE LAS FUNCIONES REALES. CONTINUIDAD. ACOTACIÓN DE FUNCIONES COTA SUPERIOR KR s cota suprior d f( ) D s f( ) K Cualquir nº mayor qu una cota suprior también s una cota suprior.
RESUMEN DE CARACTERÍSTICAS DE LAS FUNCIONES REALES. CONTINUIDAD. ACOTACIÓN DE FUNCIONES COTA SUPERIOR KR s cota suprior d f( ) D s f( ) K Cualquir nº mayor qu una cota suprior también s una cota suprior.
CÁLCULO DE LÍMITES. Por otro lado es importante distinguir en el cálculo de límites, los casos indeterminados de los determinados: = ; = ; =
 CÁLCULO DE LÍMITES Propidds d los límits.- ( b ) b.- ( b ) b.- ( b ) b.- ( b ) b b.- ( ) ( ) 6.- k k b Por otro ldo s importt distiguir l cálculo d límits, los csos idtrmidos d los dtrmidos: Csos dtrmidos:
CÁLCULO DE LÍMITES Propidds d los límits.- ( b ) b.- ( b ) b.- ( b ) b.- ( b ) b b.- ( ) ( ) 6.- k k b Por otro ldo s importt distiguir l cálculo d límits, los csos idtrmidos d los dtrmidos: Csos dtrmidos:
Selectividad Matemáticas II junio 2012, Andalucía
 Selectividad Matemáticas II junio 0, Andalucía Pedro González Ruiz 0 de junio de 0. Opción A Problema. Sea la función f : R R definida por f(x) = e x (x ).. Calcular las asíntotas de f.. Hallar los extremos
Selectividad Matemáticas II junio 0, Andalucía Pedro González Ruiz 0 de junio de 0. Opción A Problema. Sea la función f : R R definida por f(x) = e x (x ).. Calcular las asíntotas de f.. Hallar los extremos
Respuesta en frecuencia. Procesado Digital de Señales.4º Ingeniería Electrónica. Universitat de València. Profesor Emilio Soria.
 Rspusta frcucia. Procsado Digital d Sñals.4º Igiría Elctróica. Uivrsitat d Valècia. Profsor Emilio Soria. 1 Itrés uso PDS. Ti l mismo uso qu sistmas cotiuos: dtrmiar la salida d u sistma stado stacioario;
Rspusta frcucia. Procsado Digital d Sñals.4º Igiría Elctróica. Uivrsitat d Valècia. Profsor Emilio Soria. 1 Itrés uso PDS. Ti l mismo uso qu sistmas cotiuos: dtrmiar la salida d u sistma stado stacioario;
IES Fco Ayala de Granada Sobrantes de 2011 ( Modelo 3) Solución Germán-Jesús Rubio Luna
 IES Fco Ayala de Granada Sobrantes de 11 ( Modelo 3) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo 3 del 11 [ 5 puntos] Dada la función f : R R definida por f(x) ax 3 + bx +cx, determina
IES Fco Ayala de Granada Sobrantes de 11 ( Modelo 3) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo 3 del 11 [ 5 puntos] Dada la función f : R R definida por f(x) ax 3 + bx +cx, determina
Sucesiones y Series de Funciones
 Sucesiones y Series de Funciones Consideremos una sucesión {f n }, donde f n : I R R, entonces decimos que {f n } es una sucesión de funciones. Ejemplos: i) {f n }, donde f n : R R está dada por Tenemos
Sucesiones y Series de Funciones Consideremos una sucesión {f n }, donde f n : I R R, entonces decimos que {f n } es una sucesión de funciones. Ejemplos: i) {f n }, donde f n : R R está dada por Tenemos
TERCER TRABAJO EN GRUPO Grupo 10
 TERCER TRABAJO EN GRUPO Grupo 10 Problema 1.- Se considera la ecuación x 3 + x + mx 6 = 0. Utilizando el Teorema de Bolzano demostrar que: (i) Si m > 3 la ecuación tiene al menos una raíz real menor que.
TERCER TRABAJO EN GRUPO Grupo 10 Problema 1.- Se considera la ecuación x 3 + x + mx 6 = 0. Utilizando el Teorema de Bolzano demostrar que: (i) Si m > 3 la ecuación tiene al menos una raíz real menor que.
ÁLGEBRA LINEAL I Práctica 5
 ÁLGEBRA LINEAL I Práctica 5 Espacios vectoriales (Curso 2014 2015) 1. En el espacio vectorial real IR 2 consideramos los siguientes subconjuntos: (a) A = {(x y) IR 2 x 2 + y 2 = 1}. (b) B = {(x y) IR 2
ÁLGEBRA LINEAL I Práctica 5 Espacios vectoriales (Curso 2014 2015) 1. En el espacio vectorial real IR 2 consideramos los siguientes subconjuntos: (a) A = {(x y) IR 2 x 2 + y 2 = 1}. (b) B = {(x y) IR 2
Ejercicio 44 Calcula el volumen limitado por la superficie z = 1+2x+3y y los cuatro lados verticales del rectángulo D = [1, 2] [0, 1]. (x + y)dxdy.
![Ejercicio 44 Calcula el volumen limitado por la superficie z = 1+2x+3y y los cuatro lados verticales del rectángulo D = [1, 2] [0, 1]. (x + y)dxdy. Ejercicio 44 Calcula el volumen limitado por la superficie z = 1+2x+3y y los cuatro lados verticales del rectángulo D = [1, 2] [0, 1]. (x + y)dxdy.](/thumbs/69/60069071.jpg) BLOQUE II Itegració múltiple Ejercicio 44 Calcula el volume limitado por la superficie z = x3y y los cuatro lados verticales del rectágulo = [, ] [0, ]. Ejercicio 45 Sea = {(x, y) R : 0 x, x y x }. Calcular
BLOQUE II Itegració múltiple Ejercicio 44 Calcula el volume limitado por la superficie z = x3y y los cuatro lados verticales del rectágulo = [, ] [0, ]. Ejercicio 45 Sea = {(x, y) R : 0 x, x y x }. Calcular
LÍMITE DE FUNCIONES. lim. lim. lim. LÍMITE DE UNA FUNCIÓN CUANDO x + LÍMITE FINITO. DEFINICIÓN
 LÍMITE DE FUNCIONES LÍMITE DE UNA FUNCIÓN CUANDO LÍMITE FINITO. DEFINICIÓN Cuando la función pud comportars d divrsas manras: f l Al aumntar los valors d, los valors d f s aproiman a un cirto númro l.
LÍMITE DE FUNCIONES LÍMITE DE UNA FUNCIÓN CUANDO LÍMITE FINITO. DEFINICIÓN Cuando la función pud comportars d divrsas manras: f l Al aumntar los valors d, los valors d f s aproiman a un cirto númro l.
Operador Diferencial y Ecuaciones Diferenciales
 Operador Diferencial y Ecuaciones Diferenciales. Operador Diferencial Un operador es un objeto matemático que convierte una función en otra, por ejemplo, el operador derivada convierte una función en una
Operador Diferencial y Ecuaciones Diferenciales. Operador Diferencial Un operador es un objeto matemático que convierte una función en otra, por ejemplo, el operador derivada convierte una función en una
Relación de ejercicios 6
 Relación de ejercicios 6 Ecuaciones Diferenciales y Cálculo Numérico Grado en Ingeniería de Tecnologías de Telecomunicación Mayo de 2017 Ejercicio 6.1. 1. Construye, usando la base canónica del espacio
Relación de ejercicios 6 Ecuaciones Diferenciales y Cálculo Numérico Grado en Ingeniería de Tecnologías de Telecomunicación Mayo de 2017 Ejercicio 6.1. 1. Construye, usando la base canónica del espacio
Series de Fourier en varias variables. García Hernández Samuel Reporte de proyecto semestral.
 Introducción. Series de Fourier en varias variables. García Hernández Samuel Reporte de proyecto semestral. Esta pequeña introducción motivaremos un poco el estudio de las series de Fourier en varias variables.
Introducción. Series de Fourier en varias variables. García Hernández Samuel Reporte de proyecto semestral. Esta pequeña introducción motivaremos un poco el estudio de las series de Fourier en varias variables.
BACHILLERATO FÍSICA A. HERRAMIENTAS MATEMÁTICAS DE LA FÍSICA. Dpto. de Física y Química. R. Artacho
 BACHILLERATO FÍSICA A. HERRAMIENTAS MATEMÁTICAS DE LA FÍSICA R. Artacho Dpto. de Física y Química ÍNDICE 1. Áreas y volúmenes de figuras geométricas. Funciones trigonométricas 3. Productos de vectores
BACHILLERATO FÍSICA A. HERRAMIENTAS MATEMÁTICAS DE LA FÍSICA R. Artacho Dpto. de Física y Química ÍNDICE 1. Áreas y volúmenes de figuras geométricas. Funciones trigonométricas 3. Productos de vectores
BI_UII Más ejemplos de construcción de una segunda solución a partir de otra ya conocida (secc ) 469
 BI_UII Más jmplos d onstruión d una sgunda soluión a partir d otra a onoida (s..6.) 69 Apéndi BI_UII Más jmplos d onstruión d una sgunda soluión a partir d otra a onoida. (s..6.) Ejmplo BI. Sindo soluión
BI_UII Más jmplos d onstruión d una sgunda soluión a partir d otra a onoida (s..6.) 69 Apéndi BI_UII Más jmplos d onstruión d una sgunda soluión a partir d otra a onoida. (s..6.) Ejmplo BI. Sindo soluión
3º B.D. opción Físico-Matemática Matemática II. Parábola.
 Parábola. Definición: Lugar geométrico de los puntos del plano que equidistan de un punto fijo F, llamado foco y de una recta fija z llamada directriz. Siendo F no perteneciente a z. Entonces siendo P
Parábola. Definición: Lugar geométrico de los puntos del plano que equidistan de un punto fijo F, llamado foco y de una recta fija z llamada directriz. Siendo F no perteneciente a z. Entonces siendo P
UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERÍA INSTITUTO DE CIENCIAS BASICAS
 UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERÍA INSTITUTO DE CIENCIAS BASICAS Álgebra Ejercicios Trigonometría Plana Material para el alumno. Recopilado y preparado por los profesores Isabel Arratia
UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERÍA INSTITUTO DE CIENCIAS BASICAS Álgebra Ejercicios Trigonometría Plana Material para el alumno. Recopilado y preparado por los profesores Isabel Arratia
1. Se trata en primer lugar de calcular la transformada de Fourier F[f]. Para ello
![1. Se trata en primer lugar de calcular la transformada de Fourier F[f]. Para ello 1. Se trata en primer lugar de calcular la transformada de Fourier F[f]. Para ello](/thumbs/73/68677028.jpg) 1. Enunciados 1.1. Primer ejercicio Sea f(x := e x, x R. 1. Se trata en primer lugar de calcular la transformada de Fourier F[f]. Para ello a Asegurar que existe probando que la función f es absolutamente
1. Enunciados 1.1. Primer ejercicio Sea f(x := e x, x R. 1. Se trata en primer lugar de calcular la transformada de Fourier F[f]. Para ello a Asegurar que existe probando que la función f es absolutamente
Teoría de la Integración
 Licenciatura en Matemáticas y Física Universidad de Antioquia 1 Introducción 2 3 Introducción Para toda persona con formación matemática superior, es conocida la teoría de la integración de Riemann. Sin
Licenciatura en Matemáticas y Física Universidad de Antioquia 1 Introducción 2 3 Introducción Para toda persona con formación matemática superior, es conocida la teoría de la integración de Riemann. Sin




