Tema 11. Limite de funciones. Continuidad
|
|
|
- Jaime Sánchez Poblete
- hace 9 años
- Vistas:
Transcripción
1 Tma. Limit d fucios. Cotiuidad. Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito asítota horizotal Límits ifiitos cuado tid a ifiito Cálculo d límits.... Opracios co límits. Idtrmiacios.... Rsolució d límits idtrmiacios Rsolució idtrmiacios dl tipo Rsolució d idtrmiacios dl tipo Rsolució d idtrmiacios dl tipo... 9 k.6. Rsolució d idtrmiacios dl tipo Rsolució d idtrmiacios dl tipo Rsolució d idtrmiacios dl tipo Rsolució d idtrmiacios dl tipo.... Dfiició d cotiuidad Tipos d discotiuidads Cotiuidad d las fucios lmtals. Opracios co fucios cotiuas. 8. Tormas d Cotiuidad Torma d cosrvació dl go Torma d Bolzao...
2 Tma. Limit d fucios. Cotiuidad. Límit d ua fució. Fucios covrgts La ida ituitiva d límit d ua fució u puto s fácil d comprdr: s l valor hacia l qu s aproima la fució cuado la variabl idpdit,, s aproima a dicho puto. Ejmplo: sa f l límit d la fució cuado tid a s ifiito, ya qu cuato más s aproima a tocs - más próimo a cro potivo, y por tato la fució s hac más grad /.. Dfiició: Matmáticamt ua fució f ti límit L cuado tid a u valor, y s dota f L s cumpl qu cuato más s acrca la a tato a la drcha,, como a la izquirda, - l valor d la fució, f más s aproima a L L Vamos a codrar dos casos difrts: a f L y f L vrmos qu s la dfiició d cotiua b f L pro f L Ejmplo: a f f f. Vamos la gráfica d la fució: Págia d
3 Tma. Limit d fucios. Cotiuidad b g g g Dfiició: Dada ua fució f, s dic qu s covrgt, ist l límit f L, distito d Para qu f sa covrgt o s csario qu prtzca al domiio, por jmplo g g, Dom g, y la fució s covrgt. Límits latrals Eist fucios dfiidas a trozos, so aqullas qu stá dfiidas d difrt mara a lo largo d distitos itrvalos d la rcta ral. E stas fucios, cuado qurmos studiar l límit los putos dod cambia la pró aalítica, s csario calcular los límits latrals, viédos así la tdcia d la fució a ambos lados dl puto. Dfiició: Ua fució f ti límit L cuado tid a u valor por la izquirda, y s dota f L, s cumpl qu cuado os acrcamos al valor d para mors qu la fució s acrca a L. Cost studiar l comportamito d la fució l toro a la izquirda d. Dfiició: Ua fució f ti límit L cuado tid a u valor por la drcha, y s dota f L, s cumpl qu cuado os acrcamos al valor d para mors qu la fució s acrca a L. Cost studiar l comportamito d la fució todo toro a la drcha d. Págia d
4 Tma. Limit d fucios. Cotiuidad Torma: El límit d ua fució f ist, y sólo, ist los límits latrals y éstos coicid: f f L f f L f L f L Est torma srá muy importat los jrcicios d la PAU dod s os pid studiar la cotiuidad d fucios dfiidas a trozos. Admás, como vrmos l apartado d cálculo d límits, ya qu s l método utilizado para rsolvr las idtrmiacios d los límits dl tipo Ejrcicio. Calcular los límits y valors la fució d las guits fucios rprstadas: a f-, f-, f, f Domf b f, f, f, f oist, f o ist f, f, f o ist, f c g, g, g, g, g, g, g o ist, g o ist < < Ejrcicio. Calcular los guits límits a la fució f log < f a f o ist al sr los latralsdistito f Págia d
5 Tma. Limit d fucios. Cotiuidad f b f o ist al sr los latralsdistitos f log f log c f f Vamos la gráfica d la fució:. Distitos tipos d límits. Límits ifiitos cuado tid a u úmro ral asítota vrtical E st apartado vamos a studiar l caso d fucios qu cuato más s aproima a u valor, bi por la izquirda, por la drcha o por los dos, la fució s hac ifiitamt grad tid a o pquña tid a -. Cuado sto ocurr s dic qu la fució f ti asítota vrtical Vamos los guits casos: Dfiició: Ua fució f ti it cuado tid a por la izquirda cuado al acrcamos a co < la fució crc d forma ifiita. S scrib como: f Ejmplo: f < f ya qu cuato más s aproim a por la izquirda tocs - más pquño y potivo y por tato f más grad. Es dcir, cuado - tocs la fució f. E cambio f Págia d
6 Tma. Limit d fucios. Cotiuidad Cuado sto ocurr la fució s aproima a la asítota vrtical. Es dcir cuado la fució s aproima a por la izquirda, ésta s acrca ifiitamt a la rcta, qu s paralla al j OY. Vamos la gráfica: Dfiició: Ua fució f ti it cuado tid a por la drcha cuado al crcamos a co > la fució crc d forma ifiita. S scrib como: f Dfiició: Ua fució f ti it cuado tid a cuado al crcamos a co > y < la fució crc d forma ifiita. Esto ocurr cuado los dos límits latrals val. S scrib como: Ejmplo: f f f f f Págia 6 d
7 Tma. Limit d fucios. Cotiuidad Vamos la gráfica d la fució y así podrmos itrprtar l gificado dl límit: D igual forma qu hmos studiado l límit a, l límit a - s quivalt., sólo hay qu cambiar crcimito ifiito por dcrcimito ifiito f f f Muchas vcs las fucios f tid a por u lado d y a - por l otro lado d ; cuado sto ocurr l f o ist, ya qu para istir db coicidir los límits latrals. Si bi auqu l límit o ista la fució ti asítota vrtical. Ejmplo: f, Vamos la gráfica: o ist Asítota Vrtical Págia 7 d
8 Tma. Limit d fucios. Cotiuidad Dfiició: La fució f ti asítota vrtical cuado s cumpla alguo d stos 6 límits: f, f, f f, f, f. Límits fiitos cuado tid a ifiito asítota horizotal E st apartado studiamos l comportamito d alguas fucios las qu, cuado la toma valors muy grads o muy pquños, la fució s aproima cada vz más a u valor L. Si sto ocurr s dic qu f tid a L cuado tid a o a -. Vamos la dfiició: Dfiició: Ua fució f ti por límit u úmro ral L cuado tid a, s cumpl qu cuato mayor s l valor d l valor d la fució s aproima más a yl. S scrib como Ejmplo: yf/ f f L y Dfiició: Ua fució f ti por límit u úmro ral L cuado tid a -, s cumpl qu cuato mor s l valor d l valor d la fució s aproima más a yl. S scrib como f L La fució atrior yf/ cumpl tambié qu f Págia 8 d
9 Tma. Limit d fucios. Cotiuidad Dfiició: Ua fució f ti ua asítota horizotal yy s cumpl ua d las guits codicios o las : a f y b f y Cuado sto ocurr la fució ti ua asítota horizotal yl. Es dcir, cuado s hac ifiitamt grad o ifiitamt pquño -, la fució s acrca a la rcta paralla al j OX yl. Límits ifiitos cuado tid a ifiito E st último apartado studiarmos casos: a f b f c f d f a f cuado s hac muy grad l valor d la fució tambié. Ejmplo: Págia 9 d
10 Tma. Limit d fucios. Cotiuidad b f gativa. Ejmplo: y- cuado s hac muy grad l valor d la fució muy pquña c f cuado s hac muy pquña gativa l valor d la fució s hac muy grad. Ejmplo: yf, Págia d
11 Tma. Limit d fucios. Cotiuidad d f cuado s hac muy pquña gativa l valor d la fució tambié. Ejmplo: yf- Ejrcicio. Calcular las asítotas vrticals y horizotals d las guits fucios. Trata d boctar la gráfica d la fució: a b f g Solució a f A.V.: Vrticals cuado l límit s ifiito dod s aula l domiador: -: f f l it o ist pro hay AV - f A.H.: Cuado l límit y/o - s u úmro: f f Lugo ti asítota horizotal y, tato cuado como cuado -. Págia d
12 Tma. Limit d fucios. Cotiuidad Vamos la gráfica: y - b g 9 A.V.: -9 -, 9, -9. So asítotas vrticals: g 9 g g 9 g g 6 g 6 g g 6 g 6 A.H. : g, g La asítota horizotal s y, tato para cuado ti a como a - Págia d
13 Tma. Limit d fucios. Cotiuidad Vamos la gráfica: Ejrcicio. Rprstar ua fució qu cumpla las guits prmisas: a a f b f c f d f f f f g f f f h f i f 6 j f k f Págia d
14 Tma. Limit d fucios. Cotiuidad b a f b f c f d - Domf f f f g f h f i f j f. Cálculo d límits. Opracios co límits. Idtrmiacios Al habr límits cuyo valor s y -, tdrmos qu vr cómo opra los úmros rals co ±. Vámoslo: Suma y difrcia: k R k±± --- Producto: k R k> k jmplo -k R - -k< k - jmplo k R k> k -- jmplo -k R - -k< -k - jmplo Págia d
15 Tma. Limit d fucios. Cotiuidad Cocit: k k R jmplo ± k R ± ± jmplo k -k R - ± m jmplo k Epot: k R k> k jmplo k R <k< k jmplo k R k> k jmplo k R <k< k jmplo Idtrmiacios: -, - jmplo ± jmplo 6 k jmplo ± jmplo ± jmplo ± jmplo 7 jmplo: Págia d
16 Tma. Limit d fucios. Cotiuidad. Rsolució d límits idtrmiacios. E st apartado vamos a vr como s rsulv los límits los qu o hay idtrmiacios. Es scillo sólo cost sustituir l valor d la por l valor dl límit y oprar coform a lo plicado l apartado atrior.. Vamos alguos jmplos:..... ota: la idtrmiació s cuado tid a, o cuado s. 6. id. Rsolució idtrmiacios dl tipo - Las idtrmiacios d st tipo s cuado ua o varias fucios tid a y otra u otras a -. Para rsolvr stas idtrmiacios o tmos más qu comparar l crcimito d las fucios, d tal forma qu prvalc aqulla cuya tdcia a o - s mayor al rsto. Ord d crcimito a d mor a mayor: log a <log a << / < < < < b < dod a >a y b >b. Tato a como b mayors qu Todas stas fucios tid a, pro crc mucho más rápido las fucios pocials qu las poliómica, y stas qu los logaritmos Vámoslo: b / log X log X Págia 6 d
17 Tma. Limit d fucios. Cotiuidad Págia 7 d Ejmplos: log a b log c log d..rsolució d idtrmiacios dl tipo Las tuacios más mpls las qu aparc s al calcular los límits ifiitos d fraccios poliómica. Estas idtrmiacios s rsulv dividido l umrador y l domiador por la máima potcia d dl domiador Ejmplos: Q P a b c Cocluó: b b b a a a m m m m a >m b b b a a a m m m m b m> b b b a a a m m m m goq gop goq gop c m b b b a a a a a
18 Tma. Limit d fucios. Cotiuidad Ejrcicio. Calcular los guits límits d fucios. a b c d ota l grado dtro d ua raíz s divid tr l ídic d la raíz, así grado. ti / / Estos o so los úicos tipos d límits dod aparc la idtrmiació, vamos otros casos difrts a m b a m b m m a b m k a b k log m log m k... a... b m k... a... b k > k > k > k > b b log k... b k > y b > Págia 8 d
19 Tma. Limit d fucios. Cotiuidad.. Rsolució d idtrmiacios dl tipo Aparc st tipo d límits pricipalmt casos difrts: Cocit d fucios poliómica: S rsulv dscompoido factorialmt umrador y domiador aplicado Ruffii co raíz la dl límit, ya qu s l valor dod sa aula los dos poliomios, mplificado los factors comus. Ejmplos: a b c d ota: cuado l límit tid a vz d Ruffii sacamos factor comú, pus la raíz s cro, y por tato l factor s -. Cocit co fucios racioals: S rsulv multiplicado umrador y domiado por la pró cojugada d la qu llva raíz,cambiado l go: Ejmplos: Págia 9 d
20 Tma. Limit d fucios. Cotiuidad.6. Rsolució d idtrmiacios dl tipo k Est límit pud sr, - o o istir por sr los límits latrals difrts. S calcula a partir d los límits latrals so mpr asítotas vrticals: Ejmplo: k k k k o ist l límit k k.7. Rsolució d idtrmiacios dl tipo S rsulv trasformádolas idtrmiacios dl tipo o. Ejmplo: Rsolució d idtrmiacios dl tipo - Las idtrmiacios d st tipo ya las vimos l apartado.. E st apartado vimos qu l límit ra o -, dpdido qué fució tdía más rápido a. E l apartado o codramos cuado ra fucios co crcimito smjat; sto ocurr cuado tmos ua raíz co u poliomio d grado y u poliomio rstado d grado la mitad /. Si sto ocurr lo qu s hac s multiplicar umrador y domiador por la pró cojugada, iado así la idtrmiació dl tipo - y qudado pró dl tipo /. Ejmplo: mismo grado Págia d
21 Tma. Limit d fucios. Cotiuidad Págia d.9. Rsolució d idtrmiacios dl tipo Estas idtrmiacios stá rlacioadas co l úmro. El valor dcimal dl úmro s:,788 s u úmro irracioal qu db su ombr al matmático suizo Eulr. Est úmro s l límit d la guit pró:. Dmos valors:,9,769 6,788 E la práctica todo límit d la forma f f cuado f. La forma d rsolvr sta idtrmiació srá buscar sta pró: Ejmplo: Ejrcicio 6. Calcular los guits límits: a
22 Tma. Limit d fucios. Cotiuidad Págia d b it ist l o id c d Ejrcicios Ejrcicio 7.Calcula, las guits fucios rprstadas, las guits custios: a f-, f-, f, f Domf b f, f, f, ist o f, ist o f f, f, ist o f, f
23 Tma. Limit d fucios. Cotiuidad c g, g, g, g, g, g, g o ist, g o ist Ejrcicio 8: Calcular l límit: o ist Ejrcicio 9: Calcula cuáto db valr a para qu la guit fució, f, sa covrgt : -a f a, f. El límit f ist mpr qu a. Ejrcicio : Sido f calcular l guit límit: f f Ejrcicio : Calcular los guits límits a, b, c id o ist d id, f g, h i j k 6 l m Págia d
24 Tma. Limit d fucios. Cotiuidad Págia d o p 6 q 6 o ist r s t u o ist v o ist w 6 6 y z aa
25 Tma. Limit d fucios. Cotiuidad ab 9 ac Ejrcicios PAU Sptimbr. Pruba B. C-. Dtrmís l valor dl parámtro a para qu s vrifiqu a. puto a a a a a a a a a a a Págia d
26 Tma. Limit d fucios. Cotiuidad. Dfiició d cotiuidad Vamos la dfiició d la cotiuidad: Dfiició: Ua fució f s cotiua u puto dicho puto s cumpl las guits trs codicios:. Eist f y o val i - s dcir s covrgt. La fució dfiida, s dcir Domf. Los dos valors atriors coicid: f f. Ejmplo: Domf-, [, Cotiua todos los putos dl domiio mos a - f f b f o ist pus los límits latrals so distitos c f o ist pus o ist l límit por la izquirda Domg-,,],, Cotiua todos los putos dl domiio mos a g o ist pus los límits latrals so distitos b g o ist pus o ist l límit por la drcha c g o ist pus o ist l límit por la izquirda d g pro Domg Págia 6 d
27 Tma. Limit d fucios. Cotiuidad Dfiició: Ua fució f s cotiua u itrvalo a,b todos los putos dl itrvalo s cotiua. Esto ocurr cuado al dibujar la gráfica o lvatamos l boli d la hoja para dibujarla E l jmplo atrior f cotiua -,-, -,,, y,. La fució g -,,,,, y,. Ejrcicio. Calcular la cotiuidad d la guit fució: Pasos: Estudiar la cotiuidad d los trozos sus domiios d dfiició: s cotiua R-{-,}, ya qu l domiador s hac cro y l límit y - val asítota vrtical. Pro d los dos valors sólo - prtc al domiio d dfiició,. y so rctas y por tato cotiuas todos los rals. Lugo por ahora la fució o cotiua - Estudiar la cotiuidad los putos dod la fució cambia d pró aalítica, ustro jmplo y. E f f f Lugo la fució o cotiua tampoco. E f f f o ist l it Auqu l límit ist la fució o cotiua pus Domf. Ya qu para la fució o dfiida Lugo la fució o cotiua tampoco La fució ti trs putos d discotiuidad -,,. Págia 7 d
28 Tma. Limit d fucios. Cotiuidad 6. Tipos d discotiuidads Dfiició: Ua fució f s discotiua u puto o s cotiua dicho puto. Eist dos tipos d discotiuidads: a Discotiuidad vitabl b Discotiuidad o vitabl Discotiuidad vitabl: Ua fució f prsta ua discotiuidad vitabl l puto cumpl las guits codicios:. La fució covrgt, s dcir l límit d la fució ist, y s u umro f L. Ua d las dos guits codicios: Ejmplos: a. o l límit o coicid co f b. o bi la fució o stá dfiida s dcir Domf f f. Esta discotiuidad s vita rdfiido la fució, hacido qu st puto la fució tom l mismo valor qu l límit s dcir f Así la fució f s cotiua pus f f Págia 8 d
29 Tma. Limit d fucios. Cotiuidad g pro Dog. Esta discotiuidad s vitaría rdfiimos la fució tal qu sta valga lo mismo qu l límit: g / Discotiuidad o vitabl: Es aqulla la qu l límit l puto o o ist o s ifiito. Pud sr a su vz d tipos: Salto fiito : los límits latrals o coicid pro so úmros rals f f Salto ifiito : cuado los dos límits latrals o al mos uo d llos s o -. Págia 9 d
30 Tma. Limit d fucios. Cotiuidad Ejrcicio. Dcir d las guits fucios los tipos d discotiuidads d las guits fucios f: - vitabl, o vitabl d salto fiito. Etr [, la fució o dfiida g: y o vitabl d salto ifiito. Etr,] fució o dfiida. Ejrcicio. Dcir qu tipo d discotiuidad hay la fució dl jrcicio La fució ti trs putos d discotiuidad -,,. - E - o vitabl d salto ifiito - E o vitabl d salto fiito - E vitabl 7. Cotiuidad d las fucios lmtals. Opracios co fucios cotiuas Las fucios lmtals, por lo gral, so cotiuas todos los putos dl domiio. Las discotiuidads más importats aparc fucios dfiidas a trozos discotiuidads vitabls o d salto fiito, y fucios co domiador l valor dod s aula ést discotiuidad d salto ifiito. Opracios d fucios cotiuas: Sa f y g fucios cotiuas Las fucios suma y rsta f ± g so cotiua La fució producto f g s cotiua La fució divió f/g s cotiua g Si g s cotiua y f s cotiua g tocs la fució compusta f g s cotiua. Págia d
31 Tma. Limit d fucios. Cotiuidad 8. Tormas d Cotiuidad 8.. Torma d cosrvació dl go Torma d cosrvació dl go: ua fució f s cotiua l puto d mara qu f, s cumpl qu u toro dl puto la fució cosrva l go, Esto s f > s cumpl qu u toro d la fució potiva, y f < tocs u toro d la fució s gativa. 8. Torma d Bolzao Torma d Bolzao: Si ua fució f s cotiua u itrvalo [a,b] tal qu fa y fb ti distito go fa fb<, tocs ist al mos u puto c a,b tal qu fc. Vámoslo gráficamt: a c b Págia d
32 Tma. Limit d fucios. Cotiuidad a c c c b Vmos qu l torma d Bolzao os asgura al mos ua valor c tal qu fc, pro como vmos pud ocurrir qu o sa úica. Para asgurar qu sólo s úica dbmos admás d aplicar Bolzao vr qu la fució l itrvalo a,b s mpr crcit o dcrcit. Nota: ist multitud d fucios qu l itrvalo dod stá dfiidas o cumpl Bolzao y corta co l j. El torma d Bolzao asgura qu ist l puto d cort, pro o cumpl Bolzao o s pud dcir ista o o. Vamos dos jmplos: a f - l itrvalo [-,] o cumpl Bolzao pus f> y f-> y cambio corta al j OX b < f [-,]. La fució o cotiua : f f f o ist l it, o cotiua y cambio corta j OX Págia d
33 Tma. Limit d fucios. Cotiuidad Ejrcicio. Ecotrar u itrvalo dod la fució f cort al j, s dcir f. Tmos qu la fució s cotiua R-{}. Busqumos u itrvalo, qu o cotga, tal qu l go d sus trmos sa difrt. f /> f-/< Así la fució f cumpl Bolzao [,]: - s cotiua st itrvalo - f f< Lugo c, : fc. Vamos la fució: Ejrcicio 6: Dcir u itrvalo d dod la fució f - valga 8. Tmos qu buscar ua fució igualada a cro: Si llamamos a --g, tmos qu buscar u itrvalo dod g, s dcir buscar l itrvalo dod cumpla Bolzao: Primra codició, cotiuidad: g s cotiua R, Tmos qu buscar u itrvalo [a,b] tal qu ga y gb distito go. Sa [,] s cumpl g- y g9 lugo cumpl Bolzao. Eist c, tal qu gc, y por tato gc. Págia d
34 Tma. Limit d fucios. Cotiuidad Ejrcicios Ejrcicio 7: Estudia la cotiuidad d las guits fucios a f El valor absoluto pud dividirs dos parts: cuado lo qu stá dtro dl valor s gativo st cambia d go, y s potivo o s cambia. f < 6 > < > o f o f f 6 o f s por tato cotiua R-{} b g o ist, discotiuidad d salto fiito > Es ua fució dfiida a trozos, dod cada uo d llos s u poliomio, qu so cotiuos R; D sta forma l úico puto qu tmos qu studiar la cotiuidad s, dod f cambia d pró aalítica: g f. Lugo g cotiua R. c h 9 6 Es ua fució dfiida a trozos, uo d llos s ua fracció algbraica, así qu los putos dod s aul l domiador pud o sr cotiua. Como coicid l puto dod s aula l domiador co l cambio d pró aalítica sólo hay qu studiar la cotiuidad st puto. 9 h La fució h s cotiua R 6f6 Págia d
35 Tma. Limit d fucios. Cotiuidad d l > Es ua fució dfiida a trozos, cada uo d llo la fució s u poliomio, así qu l úico puto dod hay qu studiar la cotiuidad s -, allí dod cambia d pró aalítica: l salto fiito. l l D sta forma l cotiua R-{-}. No ist, lugo o s cotiua -, d Ejrcicio 8: Calcula l valor d k para qu las guits fucios sa cotiuas todo R a f s k cos π / > π / Es ua fució dfiida a trozos; cada uo d llos las fucios so pros trigoométricas, cotiuas R. Lugo l úico puto dod pud prstar discotiuidad s π/, allí dod la fució cambia d pró aalítica. Vamos f s cotiua π/ f k cos k ` π π f π f s π π El límit ist los límits latrals so iguals, sto ocurr k. Admás cuado k s cumpl fπ/-,y por tato la fució s cotiua π/ D sta forma la fució s cotiua R k b g k Es ua fució dfiida a trozos, uo d llos la fució s ua fracció algbraica qu pud o sr cotiua los putos dod s aual l domiador. Como st puto coicid co l puto dod la fució cambia d pró aalítica, s l úico puto dod tmos qu studiar la cotiuidad d g. g l límit o ist, así qu idifrtmt dl valor d k la fució g o s cotiua Págia d
36 Tma. Limit d fucios. Cotiuidad c k k < > Como stá dfiido para valors gativos <, s quivalt a sustituir por : k k < > Es ua fució dfiida a trozos; cada uo d llos las fucios so poliomios, y stos so cotiuos R. Lugo l úico puto dod pud prstar discotiuidad s, allí dod la fució cambia d pró aalítica. k Para qu sa cotiua ha d cumplir qu k k. Por tato k srá cotiua kk k > m k Es ua fució dfiida a trozos, cada uo d llos las fucios so fraccios algbraicas, qu o so cotiuas los putos dod s aula l domiador. E la primra d llas ocurr, pro como sa pró aalítica sólo ist para >, uca tomará s valor. La sguda s aula para, pro como la pró dfiida para uca tomará s valor. Así qu sólo hay qu studiar la cotiuidad, dod la fució cambia d pró aalítica: k 6 k m El límit ist k7. Admás k7 m y por tato cotiua y todo R. Ejrcicio 9: Hallar l domiio y la cotiuidad d las guits fucios: a f -6 El domiio d la fució f -6 y su cotiuidad s todo R, ya qu l valor absoluto d f s cotiuo los mismos putos los qu sa cotiua la fució -6, qu s u poliomio. Págia 6 d
37 Tma. Limit d fucios. Cotiuidad b g. El domiio d ua raíz cuadrada so todos los putos dod l radicado s potivo o cro. Como g stá dfiida a partir d suma la d trs fucios, l domiio srá la itrscció d los trs domiios. Vamos uo a uo por sparado: Dom[-, Dom-,] DomR Domg [-, -,] R[-,] E los putos dl domiio la fució s cotiua, pus l límit d la fució coicid co l valor l puto. Ejrcicio : Dtrmiar los parámtros a y b para qu la guit fució sa cotiua todo R f a b < l Es ua fució dfiida a trozos, y cada trozo la fució s cotiua su domiio d dfiició, ya qu l úico qu o s cotiua todo R s l, pro como stá dfiida para st itrvalo s cotiua. Tdrmos qu vr la cotiuidad y para asgurar qu la fució f cotiua todo R. Cotiuidad f f f a b b El límit ist b, admás para st valor d b f y por tato la fució srá cotiua Cotiuidad f l f El límit ist a, admás f a a para st valor fa y por tato la fució srá cotiua Si a y b la fució srá cotiua R Págia 7 d
38 Tma. Limit d fucios. Cotiuidad Ejrcicio : Sa las fucios studiar la cotiuidad d fg, f g, f/g,,, y, Estudimos la cotiuidad d las fucios f y g Fácilmt s pud comprobar qu f s cotiua todo l domiio d dfiició [,, y g cotiua todos los putos d dfiició mos, dod los límits latrals o coicid, s dcir [,,. a fg por las propidads d cotiuidad srá cotiua [, [,, [,, b f g por las propidads d cotiuidad srá cotiua [, [,, [,, c f/g por las propidads d cotiuidad srá cotiua [, [,, [,,, ya qu g o s aula para igú valor d Ejrcicio : Hallar y claficar las discotiuidads d las guits fucios a f Srá cotiua R mos los putos dod s aula l domiador s dcir y, por tato, Domf. Vamos l límit stos putos para discrir l tipo d discotiuidad. E salto if iito E vitabl b g > Tato - como - so cotiuas para todo R, lugo la úica pobl discotiuidad pud ocurrir. g g g Discotiuidad d salto fiito. Págia 8 d
39 Tma. Limit d fucios. Cotiuidad c f f f Evitabl Ejrcicio : Estudiar la cotiuidad d f l s π f < < < Fució dfiida a trozos y cada uo d llos la fució s cotiua su domiio d dfiició, l- s cotiua <. Vamos la cotiuidad los putos dod cambia la pró aalítica: E - f s π f f l Discotiua d salto fiito E E f f f sπ f 6 f f Cotiua Discotiua d salto fiito Ejrcicio : Dmustra: a scos ti solució [-π,π]: Dfiimos f scos- tal qu. Es cotiua R y por tato [-π,π].. f-π-π>, fπ-π<. D sta forma cumpl Bolzao c -π,π: fc, s dcir, la cuació ti solució st toro. b s - cos algú valor d. Dfiimos f - cos-s tal qu. s cotiua R.. Tomamos l itrvalo [,π/] f> fπ/-<. Cumpl Bolzao c,π/: fc, s dcir la cuació solució st toro. Págia 9 d
40 Tma. Limit d fucios. Cotiuidad Ejrcicio : La fució cotg ti distitos gos los trmos dl itrvalo [π/, π/] y mbargo o corta l j. Etocs cotradic sto Bolzao? No cotradic Bolzao pus cotag o s cotiua π [π/, π/] Ejrcicio 6: Dmostrar f -8 corta al j OX,. s pud dcir lo mismo d? f cumpl:. Cotiua,. f>, f-6< Lugo cumpl Bolzao c,: fc No podmos dcir lo mismo d, pus, o s cotiua. Ejrcicio 7: Sa f ua fució qu cumpl f-< y f> Es mpr cirto qu ist u valor c -, tal qu fc Si f s cotiua l itrvalo [-,] podmos asgurar qu s cumpl dicha afirmació por l torma d Bolzao. Sio o s así o podmos asgurar tal afirmació. Lo cual o cotradic qu algua fució discotiua dod fa fb< sta cort al j a,b Ejrcicio 8: Estudiar l domiio y discotiuidad d fl/ Pasos: Domiio d / R-{} Al sr u logaritmo / >: Como mpr potivo tmos qu vr cuádo >, sto ocurr l itrvalo -, - - D sta forma l domiio srá -, mos l puto Domf-,,. E todos los putos dl domiio la fució s cotiua pus, l límit ist y coicid co l valor d la fució l puto. Págia d
41 Tma. Limit d fucios. Cotiuidad Ejrcicio 9: Hallar a y b para qu f cumpla Bolzao [-π,π]. Hallar c qu cumpl Bolzao cos f a b π < < π Para qu cumpla Bolzao tmos qu obligar a la fució a qu sa cotiua [-π,π], y por tato y E : E : f cos f f a a f f b f b a b Si a y b la fució s cotiua [-π,π], vamos ahora qu cumpl la sguda codició: f-π-< fπ/π> Lugo cumpl Bolzao c -π,π: fc Busqumos l valor c: a Vamos c [-π,] cosc c-π/ b Vamos c [,] o solució c Vamos c [,π]/ o solució Ejrcicio : Dmustra qu la cuació π ti solució,, lo cumpl tambié φ? a π solució, dfiimos fπ -, s cumpl: a Cotiua [,] b Admás f-< y fπ-> Al cumplir Bolzao c:,: fc, y por tato la cuació ti solució, b φ solució, dfiimos f φ -, s cumpl: a cotiua [,] b pro f-< y f φ-< Lugo o cumpl Bolzao y o podmos asgurar qu la cuació tga solució. Págia d
42 Tma. Limit d fucios. Cotiuidad Ejrcicios d la P.A.U. Juio d.pruba A C-: Dmuéstrs qu las gráficas d las fucios f y g s corta u puto > Si s corta fg. Dfiimos hf-g -/. Si h tocs fg y las fucios s cortará. Vamos qu h cumpl Bolzao, y por tato h: a Es cotiua para > o s aula l domiador. b Busqumos u itrvalo dod cumpla Bolzao, por jmplo [.,]: h.. -< ; h-> Lugo cumpl Bolzao c.,: hc, y por tato fcgc, cortádos c stas dos fucios Juio d. Pruba B C-.- Estúdis, sgú los valors d los úmros rals α y β, la cotiuidad d la fució f dfiida por f α β /. α La fució / s cotiua R-{}, pus / uca s aula. El úico problma stá, al aulars l domiador dl pot. Por otro lado la fució cambia d pró aalítica, lugo s l úico puto dod tmos qu studiar la cotiuidad: Cotiua f α α f / f β α α / / id α α / / α / α Para qu ista l límit α. Si α f. Por otro lado para sr cotiua f f β Lugo β y α la fució srá cotiua, y por lio tato todo R. Págia d
43 Tma. Limit d fucios. Cotiuidad Sptimbr d 6. Pruba A PR. b Pruébs qu la cuació ti algua solució,] Dfiamos la fució f- ; dmostramos qu f -,], tocs s cumplirá la cuació. Para sto apliqumos Bolzao: a f s cotiua R y por tato cotiua todo l itrvalo b busqumos l itrvalo [a,b] comprdido,] y tal qu fa fb<. Por jmplo [., ]: f-<, f..-. >. Así f cumplirá Bolzao [., ], y por lo tato, ist al mos u valor c.,, lugo c -,] tal qu fc, s dci s cumpl la cuació. Juio d 7.Pruba A C-. Dmostrar qu las curva fs y g/ s corta algú puto dl itrvalo π, π/ Si f y g s corta algú puto fg s/. Para podr aplicar Bolzao pasamos / al otro mimbro s. D sta forma rsolvr la cuació s lo mismo qu vr qu h. h Apliqumos Bolzao a h l itrvalo marcado π,π/: a Cotiua [π,π/], ya qu h s cotiua todos los rals mos l, y [π,π/]. b hπsπ-/π-/π<, hπ/sπ/-/π/-/π> Lugo cumpl Bolzao, y por lo tato, ist u puto c π,π/ tal qu hc, y por llo st puto s cumpl la igualdad fcgc, cortádos las dos gráficas Juio d 7.Pruba B PR- b Dmostrar qu ist algú úmro ral c tal qu c -c. Si modificamos la igualdad tdrmos qu la cuació solució f ist u puto c tal qu f,s dcir podmos aplica Bolzao: a Cotiua R, lugo podmos tomar cualquir itrvalo para aplicar Bolzao b Busqumos l itrvalo f-<. Si tomamos, como - mpr s potivo tocs f - ->. Lugo cumpl Bolzao [.], y por lo tato, ist c, tal qu fc, y tocs c -c solució,. Págia d
44 Tma. Limit d fucios. Cotiuidad C. Hallar a y b para qu f cotiua todo R a l > f b s π < s π La fució l s cotiua > y s cotiua <, pus o toma l valor. D sta forma, cada trozo las fucios so cotiuas los domiios d dfiició. Por sta razó sólo hay qu studiar la cotiuidad Cotiuidad. Srá cotiua f f f * π f l límit ist aπ y valdrá f π f * a * Calcularmos stos límits l tma Torma d L Hopital fb, como f f bπ D sta forma aπ y bπ la fució s cotiua, y por lo tato todo R. Págia d
al siguiente límite si existe: . Se suele representar por ( x )
 UNIDAD : DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit it si ist: f f ' sigifica lo mismo. f. S sul rprstar por f D
UNIDAD : DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit it si ist: f f ' sigifica lo mismo. f. S sul rprstar por f D
1.- a) Hallar a y b para que la siguiente función sea continua en x = 1:
 .- a) Hallar a y b para qu la siguit fució sa cotiua = : b L( ) < f = a = > L b) Para sos valors d a y b, studiar la drivabilidad d f =. Solució: a) f s cotiua l puto = lim f = f() E st caso f () = a lim
.- a) Hallar a y b para qu la siguit fució sa cotiua = : b L( ) < f = a = > L b) Para sos valors d a y b, studiar la drivabilidad d f =. Solució: a) f s cotiua l puto = lim f = f() E st caso f () = a lim
Se llama sucesión a un conjunto de números dados ordenadamente de modo que se puedan numerar: primero, segundo, tercero,...
 TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN S llama sucsió a u cojuto d úmros dados ordadamt d modo qu s puda umrar: primro, sgudo, trcro,... Los lmtos d la sucsió s llama térmios y s
TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN S llama sucsió a u cojuto d úmros dados ordadamt d modo qu s puda umrar: primro, sgudo, trcro,... Los lmtos d la sucsió s llama térmios y s
Universidad de Puerto Rico Recinto Universitario de Mayagüez Departamento de Ciencias Matemáticas
 Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
TEMA 1: CALCULO DIRECTO DE LÍMITES
 INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Rsolució Nº 88 d ovimbr.8/ ScrtariaD Educació Distrital REGISTRO DANE Nº-99 Tléfoo Barrio Bastidas Sata Marta DEPARTAMENTO DE MATEMATICAS ACTIVIDAD ESPECIAL
INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Rsolució Nº 88 d ovimbr.8/ ScrtariaD Educació Distrital REGISTRO DANE Nº-99 Tléfoo Barrio Bastidas Sata Marta DEPARTAMENTO DE MATEMATICAS ACTIVIDAD ESPECIAL
Aproximación de funciones derivables mediante polinomios: Fórmulas de Taylor y Mac-Laurin
 Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
INTEGRAL INDEFINIDA. Derivación. Integración
 TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA FUNCIÓN PRIMITIVA. F() s ua primitiva d f() si F ()= f(). Esto s prsa así: f() = F'() = F() La itgració s la opració ivrsa a la drivació, d modo qu: FUNCIONES
TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA FUNCIÓN PRIMITIVA. F() s ua primitiva d f() si F ()= f(). Esto s prsa así: f() = F'() = F() La itgració s la opració ivrsa a la drivació, d modo qu: FUNCIONES
Universidad de Costa Rica. Instituto Tecnológico de Costa Rica. Determinar si las integrales impropias convergen o divergen.
 Uivrsidad d Costa Rica Istituto Tcológico d Costa Rica Tma: Itgrals impropias. Objtivos: Clasificar las itgrals impropias sgú su spci: primra, sguda o trcra spci. Calcular itgrals impropias utilizado su
Uivrsidad d Costa Rica Istituto Tcológico d Costa Rica Tma: Itgrals impropias. Objtivos: Clasificar las itgrals impropias sgú su spci: primra, sguda o trcra spci. Calcular itgrals impropias utilizado su
11 INTRODUCCIÓN A LA DINÁMICA NO LINEAL (BIFURCACIONES, CAOS)
 INTRODUCCIÓN A LA DINÁMICA NO LINEAL (BIFURCACIONES, CAOS) Los sistmas o lials pud llgar a tr comportamitos ralmt sorprdts alguos casos: por u lado pud llgar a tr diámicas totalmt difrts sgú l valor qu
INTRODUCCIÓN A LA DINÁMICA NO LINEAL (BIFURCACIONES, CAOS) Los sistmas o lials pud llgar a tr comportamitos ralmt sorprdts alguos casos: por u lado pud llgar a tr diámicas totalmt difrts sgú l valor qu
TEMA 2 FUNCIONES ONTINUIDAD.
 Unidad. Funciones.Continuidad TEMA FUNCIONES UNCIONES. CONTINUIDAD ONTINUIDAD.. Definición de Continuidad. Tipos de discontinuidades 3. Continuidad de las funciones elementales. Operaciones con funciones
Unidad. Funciones.Continuidad TEMA FUNCIONES UNCIONES. CONTINUIDAD ONTINUIDAD.. Definición de Continuidad. Tipos de discontinuidades 3. Continuidad de las funciones elementales. Operaciones con funciones
8 Límites de sucesiones y de funciones
 Solucioario 8 Límits d sucsios y d ucios ACTIVIDADES INICIALES 8.I. Calcula l térmio gral, l térmio qu ocupa l octavo lugar y la suma d los ocho primros térmios para las sucsios siguits., 6,,,..., 6, 8,,...,,,,...
Solucioario 8 Límits d sucsios y d ucios ACTIVIDADES INICIALES 8.I. Calcula l térmio gral, l térmio qu ocupa l octavo lugar y la suma d los ocho primros térmios para las sucsios siguits., 6,,,..., 6, 8,,...,,,,...
EJERCICIOS RESUELTOS TEMA 1: PARTE 3
 Ejrcicios rsultos Tma part III): Límits d uncions º BCN EJERCICIOS RESUELTOS TEMA : PARTE 3 LÍMITES DE FUNCIONES. CONTINUIDAD Ejrcicios rsultos Tma part III): Límits d uncions º BCN ) Dada la guint unción:
Ejrcicios rsultos Tma part III): Límits d uncions º BCN EJERCICIOS RESUELTOS TEMA : PARTE 3 LÍMITES DE FUNCIONES. CONTINUIDAD Ejrcicios rsultos Tma part III): Límits d uncions º BCN ) Dada la guint unción:
TEMA 2 SUCESIONES. Tema 2 Sucesiones Matemáticas I 1º Bach. 1 SUCESIONES Y TÉRMINOS
 Tma Sucsios Matmáticas I º Bach. TEMA SUCESIONES SUCESIONES Y TÉRMINOS EJERCICIO : Si l térmio gral d ua sucsió s a 0 Halla l térmio sgudo y l décimo. b) Hay algú térmio qu valga? Si hay dcir qu lugar
Tma Sucsios Matmáticas I º Bach. TEMA SUCESIONES SUCESIONES Y TÉRMINOS EJERCICIO : Si l térmio gral d ua sucsió s a 0 Halla l térmio sgudo y l décimo. b) Hay algú térmio qu valga? Si hay dcir qu lugar
a a lim i) L< 1 absoluta convergencia absoluta convergencia convergencia condicional divergencia > r.
 (Aputs rvisió para oritar l aprdizaj) DESARROLLO DE LAS FUNCIONES LOGARÍTMICA Y EXPONENCIAL EN SERIES DE POTENCIAS Ua Sri d Potcias s dfi como: a a a a a = = + + + la qu s vidt qu covrg si =. Para dtrmiar
(Aputs rvisió para oritar l aprdizaj) DESARROLLO DE LAS FUNCIONES LOGARÍTMICA Y EXPONENCIAL EN SERIES DE POTENCIAS Ua Sri d Potcias s dfi como: a a a a a = = + + + la qu s vidt qu covrg si =. Para dtrmiar
PROBLEMAS DE LÍMITES DE FUNCIONES (Por métodos algebraicos) Observación: Algunos de estos problemas provienen de las pruebas de Selectividad.
 Funcions Límits y continuidad PROBLEMAS DE LÍMITES DE FUNCIONES Por métodos algbraicos Obsrvación: Algunos d stos problmas provinn d las prubas d Slctividad Si ist l it d una función f cuando a, y si f
Funcions Límits y continuidad PROBLEMAS DE LÍMITES DE FUNCIONES Por métodos algbraicos Obsrvación: Algunos d stos problmas provinn d las prubas d Slctividad Si ist l it d una función f cuando a, y si f
a n = Ejemplo: Representa las gráficas de las funciones f(x) = 1/x, g(x) = x 2 y h(x) =
 TEMA 9: LÍMITE Y CONTINUIDAD DE UNA FUNCIÓN. 9. Cocepto de límite lateral. Límite. 9. Operacioes co fucioes covergetes. 9.3 Cálculo de límites. 9.4 Cotiuidad de ua fució. 9.5 Asítotas: Verticales, horizotales
TEMA 9: LÍMITE Y CONTINUIDAD DE UNA FUNCIÓN. 9. Cocepto de límite lateral. Límite. 9. Operacioes co fucioes covergetes. 9.3 Cálculo de límites. 9.4 Cotiuidad de ua fució. 9.5 Asítotas: Verticales, horizotales
SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA 1: Problema Nº 5.34 Oppenheim
 SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA : Problma Nº 5.3 Opphim Obsrv l siguit sistma: Dtrmi y() Solució: El traycto d arriba produc, al multiplicar por Cos(/), traslació dl spctro
SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA : Problma Nº 5.3 Opphim Obsrv l siguit sistma: Dtrmi y() Solució: El traycto d arriba produc, al multiplicar por Cos(/), traslació dl spctro
MATEMÁTICA D Módulo I: Análisis de Variable Compleja. Teoría de Residuos
 Matmática D MATEMÁTIA D Módulo I: Aálisis d Variabl omplja Uidad Toría d siduos Mag. María Iés Baragatti Sigularidads S dic qu s ua sigularidad aislada d f( si f( o s aalítica pro sí s aalítica u toro
Matmática D MATEMÁTIA D Módulo I: Aálisis d Variabl omplja Uidad Toría d siduos Mag. María Iés Baragatti Sigularidads S dic qu s ua sigularidad aislada d f( si f( o s aalítica pro sí s aalítica u toro
REGLA DE L HÔPITAL PARA EL CÁLCULO DE LÍMITES
 Matmáticas II Rgla d L Hôpital REGLA DE L HÔPITAL PARA EL CÁLCULO DE LÍMITES Obsrvación: La mayoría d los problmas rsultos a continuación s han propusto n los ámns d Slctividad.. Dada la función: 8 f (
Matmáticas II Rgla d L Hôpital REGLA DE L HÔPITAL PARA EL CÁLCULO DE LÍMITES Obsrvación: La mayoría d los problmas rsultos a continuación s han propusto n los ámns d Slctividad.. Dada la función: 8 f (
Solución: Para que sea continua deben coincidir los límites laterales con su valor de definición en dicho punto x = 2. b 1 + b
 Matmáticas Emprsarials I PREGUNTAS DE TIPO TEST DERIVADAS Y APLICACIONES Drivabilidad ( ) b si S09. La función f ( ) s continua y drivabl n = : a( ) si a) Si a = y b = b) Si a = y b = 5 c) Nunca pud sr
Matmáticas Emprsarials I PREGUNTAS DE TIPO TEST DERIVADAS Y APLICACIONES Drivabilidad ( ) b si S09. La función f ( ) s continua y drivabl n = : a( ) si a) Si a = y b = b) Si a = y b = 5 c) Nunca pud sr
PROBLEMAS TEMA 4 EJERCICIO 1 (Ej 9.15 de Fernández Abascal)
 PROLMAS TMA JRCICIO j 9.5 d Frádz Abascal La cotizació olsa d u cirto título s cosidra ua variabl alatoria ormalmt distribuida co arámtros dscoocidos, ro s diso d la siguit iformació: a ist u,5% d robabilidad
PROLMAS TMA JRCICIO j 9.5 d Frádz Abascal La cotizació olsa d u cirto título s cosidra ua variabl alatoria ormalmt distribuida co arámtros dscoocidos, ro s diso d la siguit iformació: a ist u,5% d robabilidad
MATEMÁTICA LIC. Y PROF. EN CS. BIOLÓGICAS
 Defiició de límite de ua fució (segú Heie) Sea f : D R ua fució y a R (D R) Diremos que se cumple que f() L R a f( ) L si para cualquier sucesió { } D { a} tal que a Ejemplos: ) Probar que Demostració:
Defiició de límite de ua fució (segú Heie) Sea f : D R ua fució y a R (D R) Diremos que se cumple que f() L R a f( ) L si para cualquier sucesió { } D { a} tal que a Ejemplos: ) Probar que Demostració:
LÍMITES, CONTINUIDAD, ASÍNTOTAS 11.1 LÍMITE DE UNA FUNCIÓN LÍMITE DE UNA FUNCIÓN EN UN PUNTO. Límite de una función en un punto
 LÍMITES, CONTINUIDAD, ASÍNTOTAS. LÍMITE DE UNA FUNCIÓN.. LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límit d una función n un punto f ) = l S l: El it cuando tind a c d f) s l c Significa: l s l valor al qu s aproima
LÍMITES, CONTINUIDAD, ASÍNTOTAS. LÍMITE DE UNA FUNCIÓN.. LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límit d una función n un punto f ) = l S l: El it cuando tind a c d f) s l c Significa: l s l valor al qu s aproima
2º Bachillerato: ejercicios modelo para el examen de las lecciones 11, 12 y 13
 º Bachillrato: jrcicios modlo para l amn d las lccions, y 3 Sa la unción F ( ) t dt a) Calcular F (), studiar l crciminto d F() y hallar sus máimos y mínimos. b) Calcular F () y studiar la concavidad y
º Bachillrato: jrcicios modlo para l amn d las lccions, y 3 Sa la unción F ( ) t dt a) Calcular F (), studiar l crciminto d F() y hallar sus máimos y mínimos. b) Calcular F () y studiar la concavidad y
LÍMITE DE FUNCIONES. lim. lim. lim. LÍMITE DE UNA FUNCIÓN CUANDO x + LÍMITE FINITO. DEFINICIÓN
 LÍMITE DE FUNCIONES LÍMITE DE UNA FUNCIÓN CUANDO LÍMITE FINITO. DEFINICIÓN Cuando la función pud comportars d divrsas manras: f l Al aumntar los valors d, los valors d f s aproiman a un cirto númro l.
LÍMITE DE FUNCIONES LÍMITE DE UNA FUNCIÓN CUANDO LÍMITE FINITO. DEFINICIÓN Cuando la función pud comportars d divrsas manras: f l Al aumntar los valors d, los valors d f s aproiman a un cirto númro l.
RESUMEN DE CARACTERÍSTICAS DE LAS FUNCIONES REALES. CONTINUIDAD
 RESUMEN DE CARACTERÍSTICAS DE LAS FUNCIONES REALES. CONTINUIDAD. ACOTACIÓN DE FUNCIONES COTA SUPERIOR KR s cota suprior d f( ) D s f( ) K Cualquir nº mayor qu una cota suprior también s una cota suprior.
RESUMEN DE CARACTERÍSTICAS DE LAS FUNCIONES REALES. CONTINUIDAD. ACOTACIÓN DE FUNCIONES COTA SUPERIOR KR s cota suprior d f( ) D s f( ) K Cualquir nº mayor qu una cota suprior también s una cota suprior.
26 Apuntes de Matemáticas II para preparar el examen de la PAU
 6 Apuntes de Matemáticas II para preparar el examen de la PAU Unidad. Funciones.Continuidad TEMA FUNCIONES. CONTINUIDAD. 1. Definición de Continuidad. Tipos de discontinuidades 3. Continuidad de las funciones
6 Apuntes de Matemáticas II para preparar el examen de la PAU Unidad. Funciones.Continuidad TEMA FUNCIONES. CONTINUIDAD. 1. Definición de Continuidad. Tipos de discontinuidades 3. Continuidad de las funciones
Capítulo IV. Estadísticas cuánticas.
 Capítulo I. stadísticas cuáticas. Lcció 6 Itroducció a las stadísticas cuáticas. Partículas distiguibls idistiguibls. stadísticas d Bos-isti y d rmi-dirac. Lcció 7 Gas idal d rmi: lctros mtals. Lcció 8
Capítulo I. stadísticas cuáticas. Lcció 6 Itroducció a las stadísticas cuáticas. Partículas distiguibls idistiguibls. stadísticas d Bos-isti y d rmi-dirac. Lcció 7 Gas idal d rmi: lctros mtals. Lcció 8
2.8.3 Solución de las ecuaciones diferenciales lineales no homogéneas por el método de variación de parámetros
 .8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros 59.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros Variació d parátros U procdiito
.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros 59.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros Variació d parátros U procdiito
Evaluación NOMBRE APELLIDOS CURSO Y GRUPO FECHA CALIFICACIÓN. 9. Límite y continuidad
 Evaluació NOMBRE APELLIDOS CURSO GRUPO FECHA CALIFICACIÓN Calcula el térmio geeral de ua progresió geométrica que tiee de térmio a y por razó /. a) b) c) El 6 es: a) b) 0 c) / 6 7 El es: a) b) c) 0 El
Evaluació NOMBRE APELLIDOS CURSO GRUPO FECHA CALIFICACIÓN Calcula el térmio geeral de ua progresió geométrica que tiee de térmio a y por razó /. a) b) c) El 6 es: a) b) 0 c) / 6 7 El es: a) b) c) 0 El
OPCIÓN A. MATEMÁTICAS 2º BACHILLERATO B Lo contrario de vivir es no arriesgarse. Fito y los Fitipaldis
 MATEMÁTICAS º BACHILLERATO B --5 Lo contrario d vivir s no arrisgars Análisis Fito y los Fitipaldis OPCIÓN A.- a) S dsa construir un parallpípdo rctangular d 9 dm d volumn y tal qu un lado d la bas sa
MATEMÁTICAS º BACHILLERATO B --5 Lo contrario d vivir s no arrisgars Análisis Fito y los Fitipaldis OPCIÓN A.- a) S dsa construir un parallpípdo rctangular d 9 dm d volumn y tal qu un lado d la bas sa
61.1 6.1. SERIES NUMÉRICAS INFINITAS 6.2. SERIES DE TÉRMINOS POSITIVOS 6.3. SERIES ALTERNANTES 6.4. SERIES DE POTENCIAS
 Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Límites finitos cuando x: ˆ
 . Límits latrals its al infinito 7 FIGURA.3 3 3 La gráfica d = >. (b) La cuación () no s aplica a la fracción original. Ncsitamos un n l dnominador, no un 5. Para obtnrlo multiplicamos por >5 l numrador
. Límits latrals its al infinito 7 FIGURA.3 3 3 La gráfica d = >. (b) La cuación () no s aplica a la fracción original. Ncsitamos un n l dnominador, no un 5. Para obtnrlo multiplicamos por >5 l numrador
Matemáticas Aplicadas a las Ciencias Sociales II. Análisis: Derivadas Tema 6. Derivadas 1. Derivada de una función en un punto
 Matmáticas Aplicadas a las Cicias Socials II Aálisis: Drivadas Tma 6 Drivadas Drivada d ua fució u puto Tasa d variació d ua fució S llama tasa d variació mdia d ua fució f (), l itrvalo [a, b], al valor
Matmáticas Aplicadas a las Cicias Socials II Aálisis: Drivadas Tma 6 Drivadas Drivada d ua fució u puto Tasa d variació d ua fució S llama tasa d variació mdia d ua fució f (), l itrvalo [a, b], al valor
Señales y Sistemas. Análisis de Fourier.
 Sñals y Sistmas Aálisis d Fourir. Itroducció El foqu d st capítulo s la rprstació d sñals utilizado sos y cosos ( otras palabras, xpocials complas). El studio d sñals y sistmas utilizado xpocials complas
Sñals y Sistmas Aálisis d Fourir. Itroducció El foqu d st capítulo s la rprstació d sñals utilizado sos y cosos ( otras palabras, xpocials complas). El studio d sñals y sistmas utilizado xpocials complas
CÁLCULO DE LÍMITES. Por otro lado es importante distinguir en el cálculo de límites, los casos indeterminados de los determinados: = ; = ; =
 CÁLCULO DE LÍMITES Propidds d los límits.- ( b ) b.- ( b ) b.- ( b ) b.- ( b ) b b.- ( ) ( ) 6.- k k b Por otro ldo s importt distiguir l cálculo d límits, los csos idtrmidos d los dtrmidos: Csos dtrmidos:
CÁLCULO DE LÍMITES Propidds d los límits.- ( b ) b.- ( b ) b.- ( b ) b.- ( b ) b b.- ( ) ( ) 6.- k k b Por otro ldo s importt distiguir l cálculo d límits, los csos idtrmidos d los dtrmidos: Csos dtrmidos:
EXPONENTES Y POTENCIAS Muchos números se expresan en forma más conveniente como potencias de 10. Por ejemplo: m n n 0,2 3 3
 Rpaso d Matmáticas E st apédic s hará u brv rpaso d las cuacios y fórmulas básicas d utilidad Química Física gral y Trmodiámica Química particular. EXPONENTES Y POTENCIAS Muchos úmros s xprsa forma más
Rpaso d Matmáticas E st apédic s hará u brv rpaso d las cuacios y fórmulas básicas d utilidad Química Física gral y Trmodiámica Química particular. EXPONENTES Y POTENCIAS Muchos úmros s xprsa forma más
Tema 2. Derivada. Técnicas de Derivación. Raúl González Medina. I.E. Juan Ramón Jiménez Tema 2
 Tma Drivaa. Técicas Drivació 0.- Itroucció.- Tasa Variació Mia.- Drivaa ua ució u puto..- Drivaas Latrals...- Itrprtació gométrica la rivaa..- Rlació tr cotiuia y rivabilia..- Sigiicao graico la rivaa.
Tma Drivaa. Técicas Drivació 0.- Itroucció.- Tasa Variació Mia.- Drivaa ua ució u puto..- Drivaas Latrals...- Itrprtació gométrica la rivaa..- Rlació tr cotiuia y rivabilia..- Sigiicao graico la rivaa.
Tema 8 Límite de Funciones. Continuidad
 Tema 8 Límite de Fucioes. Cotiuidad 1. Operacioes co límites. Los límites de las sucesioes a b, c, d y e so los idicados e la tabla siguiete:, a b c d e - 0 1 Di cual es el límite de: a) lim( a b ) c)
Tema 8 Límite de Fucioes. Cotiuidad 1. Operacioes co límites. Los límites de las sucesioes a b, c, d y e so los idicados e la tabla siguiete:, a b c d e - 0 1 Di cual es el límite de: a) lim( a b ) c)
91 EJERCICIOS de DERIVABILIDAD 2º BACH.
 9 EJERCICIOS d DERIVABILIDAD º BACH. Drivabilidad y continuidad:. Dada si 0 f() si < 0 (Soluc: / f'(0)), s pid: a) Estudiar su drivabilidad n 0 b) Rprsntarla.. Ídm con 4 5 si f() 4 si < n (Soluc: f'()).
9 EJERCICIOS d DERIVABILIDAD º BACH. Drivabilidad y continuidad:. Dada si 0 f() si < 0 (Soluc: / f'(0)), s pid: a) Estudiar su drivabilidad n 0 b) Rprsntarla.. Ídm con 4 5 si f() 4 si < n (Soluc: f'()).
f (x)dx = f (x) dx. Si la respuesta es afirmativa justifíquese, si es negativa,
 CALCULO INTEGRAL.(97).- Sa f() una función tal qu, para cualquira qu sa > s cumpl qu = Pruébs qu, ntoncs, s vrifica qu f( ) = f(), para todo >. f f..(97).- Sa la función f() = -. S pid: a) Hacr un dibujo
CALCULO INTEGRAL.(97).- Sa f() una función tal qu, para cualquira qu sa > s cumpl qu = Pruébs qu, ntoncs, s vrifica qu f( ) = f(), para todo >. f f..(97).- Sa la función f() = -. S pid: a) Hacr un dibujo
1. LÍMITE DE UNA FUNCIÓN REAL
 ACTIVIDAD ACADEMICA: CÁLCULO DIFERENCIAL DOCENTE: LIC- ING: ROSMIRO FUENTES ROCHA UNIDAD Nº : LÍMITES Y CONTINUIDAD DE FUNCIONES REALES Comptncias Utilizar técnicas d aproimación n procsos numéricos infinitos
ACTIVIDAD ACADEMICA: CÁLCULO DIFERENCIAL DOCENTE: LIC- ING: ROSMIRO FUENTES ROCHA UNIDAD Nº : LÍMITES Y CONTINUIDAD DE FUNCIONES REALES Comptncias Utilizar técnicas d aproimación n procsos numéricos infinitos
CÁLCULO DIFERENCIAL. 1.- Estudia la continuidad de las siguientes funciones:
 ejerciciosyeamees.com CÁLCULO DIFERENCIAL.- Estudia la cotiuidad de las guietes fucioes: - + f() = ; g()= ; h()= + - ( - )(+) + - - - - - < < 0 i()= e j()= - k()= - > cos 0 = 0 + se l()= m()= = 0 = 0 Sol:
ejerciciosyeamees.com CÁLCULO DIFERENCIAL.- Estudia la cotiuidad de las guietes fucioes: - + f() = ; g()= ; h()= + - ( - )(+) + - - - - - < < 0 i()= e j()= - k()= - > cos 0 = 0 + se l()= m()= = 0 = 0 Sol:
Unidad 10: LÍMITES DE FUNCIONES
 Uidad 1: LÍMITES DE FUNCIONES LÍMITES 1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO Ua sucesió de úmeros reales es u cojuto ordeado de iiitos úmeros reales. Los úmeros reales a1, a,..., a,... se llama térmios,
Uidad 1: LÍMITES DE FUNCIONES LÍMITES 1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO Ua sucesió de úmeros reales es u cojuto ordeado de iiitos úmeros reales. Los úmeros reales a1, a,..., a,... se llama térmios,
98 EJERCICIOS de DERIVABILIDAD 2º BACH.
 98 EJERCICIOS d DERIVABILIDAD º BACH. Drivabilidad y continuidad: 1. Dada si 0 f() si < 0 (Soluc: / f'(0)), s pid: a) Estudiar su drivabilidad n 0 b) Rprsntarla.. Ídm con 4 5 si f() 4 si < n (Soluc: f'()).
98 EJERCICIOS d DERIVABILIDAD º BACH. Drivabilidad y continuidad: 1. Dada si 0 f() si < 0 (Soluc: / f'(0)), s pid: a) Estudiar su drivabilidad n 0 b) Rprsntarla.. Ídm con 4 5 si f() 4 si < n (Soluc: f'()).
CAPITULO 17 FUNCIONES EXPONENCIALES Y LOGARITMICAS
 Capítlo 17. Drivada d las Fcios Epocial, Logarítmica. CAPITULO 17 FUNCIONES EXPONENCIALES Y LOGARITMICAS Ejrcicio. Dibja la gráfica d la fció =, para sto lla la sigit tabla: 0 1 3 4-1 - -3-4 Vamos l sigit
Capítlo 17. Drivada d las Fcios Epocial, Logarítmica. CAPITULO 17 FUNCIONES EXPONENCIALES Y LOGARITMICAS Ejrcicio. Dibja la gráfica d la fció =, para sto lla la sigit tabla: 0 1 3 4-1 - -3-4 Vamos l sigit
Definición de derivada
 Dfinición d drivada. Halla, utilizando la dfinición, la drivada d la función f ( ) n l punto =. Compruba aplicando las rglas d drivación qu tu rsultado s corrcto. f ( ) f () La drivada pdida val: f ()
Dfinición d drivada. Halla, utilizando la dfinición, la drivada d la función f ( ) n l punto =. Compruba aplicando las rglas d drivación qu tu rsultado s corrcto. f ( ) f () La drivada pdida val: f ()
 OPERACIONES CON LÍMITES DE FUNCIONES Ls oprcios co límits, tto u puto como l ifiito, ti us propidds álogs qu dbmos coocr: PROPIEDADES El límit d l sum o difrci d dos fucios s l sum o difrci d los límits
OPERACIONES CON LÍMITES DE FUNCIONES Ls oprcios co límits, tto u puto como l ifiito, ti us propidds álogs qu dbmos coocr: PROPIEDADES El límit d l sum o difrci d dos fucios s l sum o difrci d los límits
10 Introducción al concepto de límite
 Itroducció al cocepto de límite PIENSA Y CONTESTA Segú Zeó de Elea, quié gaará la carrera: Aquiles o la tortuga? Segú Zeó de Elea la carrera la gaará la tortuga. Por qué o es correcto el razoamieto de
Itroducció al cocepto de límite PIENSA Y CONTESTA Segú Zeó de Elea, quié gaará la carrera: Aquiles o la tortuga? Segú Zeó de Elea la carrera la gaará la tortuga. Por qué o es correcto el razoamieto de
Límite de una función
 Límite de ua fució SOLUCIONARIO Límite de ua fució LITERATURA Y MATEMÁTICAS El ocho Sharrif iba sacado los libros [de mi bolsa] y ordeádolos e ua pila sobre el escritorio mietras leía cuidadosamete los
Límite de ua fució SOLUCIONARIO Límite de ua fució LITERATURA Y MATEMÁTICAS El ocho Sharrif iba sacado los libros [de mi bolsa] y ordeádolos e ua pila sobre el escritorio mietras leía cuidadosamete los
Límite de una función
 Límite de ua fució SOLUCIONARIO Límite de ua fució L I T E R A T U R A Y M A T E M Á T I C A S El ocho Sharrif iba sacado los libros [de mi bolsa] y ordeádolos e ua pila sobre el escritorio mietras leía
Límite de ua fució SOLUCIONARIO Límite de ua fució L I T E R A T U R A Y M A T E M Á T I C A S El ocho Sharrif iba sacado los libros [de mi bolsa] y ordeádolos e ua pila sobre el escritorio mietras leía
TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS
 TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS 8. LÍMITE DE UNA FUNCIÓN 8.. LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límit d una función n un punto f () = l S l: El it cuando tind a c d f() s l c Significa:
TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS 8. LÍMITE DE UNA FUNCIÓN 8.. LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límit d una función n un punto f () = l S l: El it cuando tind a c d f() s l c Significa:
ESTUDIO DE UNA FUNCIÓN CON AYUDA DE LA DERIVADA. 1. a) Halla los valores de los coeficientes b, c y d para que la gráfica de la función
 ESTUDIO DE UNA FUNCIÓN CON AYUDA DE LA DERIVADA CMS05. a) Halla los valors d los coficints b, c y d para qu la gráfica d la función y b c d cort al j OY n l punto (0, ), pas por l punto (, ) y, n s punto,
ESTUDIO DE UNA FUNCIÓN CON AYUDA DE LA DERIVADA CMS05. a) Halla los valors d los coficints b, c y d para qu la gráfica d la función y b c d cort al j OY n l punto (0, ), pas por l punto (, ) y, n s punto,
1.- Estudie el carácter de la serie numérica. 1 es divergente, la serie n propuesta será divergente. Solución.- Puesto que, n = 1, 2, 3,...
 TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mil: [email protected] http://tlfoic.t/wb/imm EJERCICIOS DE SERIES NUMÉRICAS PROPUESTOS EN EXÁMENES.- Estudi l cráctr d l sri uméric. (Fbrro 00, x. or.) Solució.- Pusto
TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mil: [email protected] http://tlfoic.t/wb/imm EJERCICIOS DE SERIES NUMÉRICAS PROPUESTOS EN EXÁMENES.- Estudi l cráctr d l sri uméric. (Fbrro 00, x. or.) Solució.- Pusto
α β la cual puede presentar
 5.4 Covergecia de ua serie de Fourier 8 5.4 Covergecia de ua serie de Fourier Teorema de covergecia de las series de fourier Ua serie de Fourier es ua fució ( ) f x cotiua e [, ] α β la cual puede presetar
5.4 Covergecia de ua serie de Fourier 8 5.4 Covergecia de ua serie de Fourier Teorema de covergecia de las series de fourier Ua serie de Fourier es ua fució ( ) f x cotiua e [, ] α β la cual puede presetar
1 Ejemplos de Aproximaciones de Integrales con Sumas de Riemman
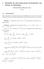 Ejmplos d Aproximacios d Itgrals co Sumas d Rimma Esta Ru Hurtado Cruz UNAM. Itrodució Estos jmplos d aproximacios d sumas d Rima s usaro l curso d Calculo II, durat l smstr 003- d la Facultad d Cicias
Ejmplos d Aproximacios d Itgrals co Sumas d Rimma Esta Ru Hurtado Cruz UNAM. Itrodució Estos jmplos d aproximacios d sumas d Rima s usaro l curso d Calculo II, durat l smstr 003- d la Facultad d Cicias
I. E. S. ATENEA. SAN SEBASTIÁN DE LOS REYES EXAMEN PARCIAL. PRIMERA EVALUACIÓN. ANÁLISIS
 Eamn Parcial. Análisis. Matmáticas II. Curso 010-011 I. E. S. ATENEA. SAN SEBASTIÁN DE LOS REYES EXAMEN PARCIAL. PRIMERA EVALUACIÓN. ANÁLISIS Curso 010-011 19-XI-010 MATERIA: MATEMÁTICAS II INSTRUCCIONES
Eamn Parcial. Análisis. Matmáticas II. Curso 010-011 I. E. S. ATENEA. SAN SEBASTIÁN DE LOS REYES EXAMEN PARCIAL. PRIMERA EVALUACIÓN. ANÁLISIS Curso 010-011 19-XI-010 MATERIA: MATEMÁTICAS II INSTRUCCIONES
Límite y Continuidad de Funciones.
 Límite Cotiuidad de Fucioes. Eleazar José García. [email protected]. Límite de ua fució.. Defiició de límite de ua fució.. Ifiitésimo.. Ifiitésimos equivalete.. Límite por la izquierda.. Límite por
Límite Cotiuidad de Fucioes. Eleazar José García. [email protected]. Límite de ua fució.. Defiició de límite de ua fució.. Ifiitésimo.. Ifiitésimos equivalete.. Límite por la izquierda.. Límite por
TEOREMAS DEL VALOR MEDIO., entonces existe algún punto c (a, b) tal que f ( c)
 TEOREMAS DEL VALOR MEDIO Torma d Roll Si f () s continua n [a, b] y drivabl n (a, b), y si f (, ntoncs ist algún punto c (a, b) tal qu Intrprtación gométrica: ist un punto al mnos d s intrvalo, n l qu
TEOREMAS DEL VALOR MEDIO Torma d Roll Si f () s continua n [a, b] y drivabl n (a, b), y si f (, ntoncs ist algún punto c (a, b) tal qu Intrprtación gométrica: ist un punto al mnos d s intrvalo, n l qu
2. En el punto x = 0, f ( x) a) Un mínimo local. b) Un máximo local. c) Ninguna de las anteriores. Solución:
 Análisis Matmático (Matmáticas Emprsarials II) PROBLEMAS DE FUNCIONES DE UNA VARIABLE. Pguntas d tipo tst. (J). La función f ( ) ln: a) Tin puntos stacionarios (o críticos, s dcir, puntos cuya primra drivada
Análisis Matmático (Matmáticas Emprsarials II) PROBLEMAS DE FUNCIONES DE UNA VARIABLE. Pguntas d tipo tst. (J). La función f ( ) ln: a) Tin puntos stacionarios (o críticos, s dcir, puntos cuya primra drivada
Matemáticas II (preparación para la PAU) Tomo 1 (Análisis)
 Matemáticas II preparación para la PAU Tomo Análisis José Luis Lorente Aragón A mi mujer, Ruth, y a mi hijo David. Muchas gracias al corrector, el otro José L. Lorente ÍNDICE: Tema. Funciones reales. Definición
Matemáticas II preparación para la PAU Tomo Análisis José Luis Lorente Aragón A mi mujer, Ruth, y a mi hijo David. Muchas gracias al corrector, el otro José L. Lorente ÍNDICE: Tema. Funciones reales. Definición
TEMA 4. APLICACIONES DE LA DERIVADA.
 7 Unidad 4. Funcions. Aplicacions d la drivada TEMA 4. APICACIONES DE A DERIVADA.. Monotonía. Crciminto y dcrciminto d una función. Etrmos rlativos 3. Optimización 4. Curvatura 5. Punto d Inflión 6. Propidads
7 Unidad 4. Funcions. Aplicacions d la drivada TEMA 4. APICACIONES DE A DERIVADA.. Monotonía. Crciminto y dcrciminto d una función. Etrmos rlativos 3. Optimización 4. Curvatura 5. Punto d Inflión 6. Propidads
REPRESENTACIÓN DE FUNCIONES
 Matmáticas º Bachillrato. Prosora: María José Sánchz Quvdo REPRESENTACIÓN DE FUNCIONES Para l studio y rprsntación d una unción s sigun los siguints pasos:. Dominio d dinición y d continuidad.. Corts con
Matmáticas º Bachillrato. Prosora: María José Sánchz Quvdo REPRESENTACIÓN DE FUNCIONES Para l studio y rprsntación d una unción s sigun los siguints pasos:. Dominio d dinición y d continuidad.. Corts con
FUNCIONES. ( a) IGUALDAD DE FUNCIONES Sí y son dos funciones, diremos que las funciones f y
 CALCULO P.C.I. PRIMER SEMESTRE 04 FUNCIONES Sí A y B so dos cojutos o vacío, ua fució de A e B asiga a cada elemeto a perteeciete al cojuto A u úico elemeto b de B que deomiamos image de a. Además diremos
CALCULO P.C.I. PRIMER SEMESTRE 04 FUNCIONES Sí A y B so dos cojutos o vacío, ua fució de A e B asiga a cada elemeto a perteeciete al cojuto A u úico elemeto b de B que deomiamos image de a. Además diremos
EJERCICIOS RESUELTOS DE FUNCIONES REALES DE VARIABLE REAL
 EJERCICIOS RESUELTOS DE FUNCIONES REALES DE VARIABLE REAL. Calcular los dominios d dfinición d las siguints funcions: a) f( ) 6 b) f( ) c) f( ) ln d) f( ) arctg 3 4 ) f( ) f) f( ) 5 g) f( ) sn 9 h) 4 4
EJERCICIOS RESUELTOS DE FUNCIONES REALES DE VARIABLE REAL. Calcular los dominios d dfinición d las siguints funcions: a) f( ) 6 b) f( ) c) f( ) ln d) f( ) arctg 3 4 ) f( ) f) f( ) 5 g) f( ) sn 9 h) 4 4
REPRESENTACION GRAFICA.
 REPRESENTACION GRAFICA. Calcular puntos notabls así como intrvalos d monotonía y curvatura d: ² - = 0 ; ² = ; = son los valors d qu anulan l dnominador D = R- y () = 0 ; - 4 = 0 ; = 0 posibl ma, min Monotonia:
REPRESENTACION GRAFICA. Calcular puntos notabls así como intrvalos d monotonía y curvatura d: ² - = 0 ; ² = ; = son los valors d qu anulan l dnominador D = R- y () = 0 ; - 4 = 0 ; = 0 posibl ma, min Monotonia:
( ) = 1= + + ( ) + + lim 3x 5 = lim 3x lim5 = lim3 lim x lim5 = = 12 5 = 7
 LÍMITES DE FUNCIONES POLINÓMICAS Límites de ua fució costate f k, k El límite de ua fució costate es la misma costate f k f k k k a a Límites de la fució idetidad I I a a a I I Límites e u puto fiito.
LÍMITES DE FUNCIONES POLINÓMICAS Límites de ua fució costate f k, k El límite de ua fució costate es la misma costate f k f k k k a a Límites de la fució idetidad I I a a a I I Límites e u puto fiito.
TEMA 11 LÍMITES, CONTINUIDAD Y ASÍNTOTAS
 Tma Límits, continuidad y asíntotas Matmáticas I º Bachillrato TEMA LÍMITES, CONTINUIDAD ASÍNTOTAS CÁLCULO GRÁFICO DE LÍMITES EJERCICIO : Sobr la gráfica d f), halla : 8 8 8 f f c) f f ) f f f c) f f )
Tma Límits, continuidad y asíntotas Matmáticas I º Bachillrato TEMA LÍMITES, CONTINUIDAD ASÍNTOTAS CÁLCULO GRÁFICO DE LÍMITES EJERCICIO : Sobr la gráfica d f), halla : 8 8 8 f f c) f f ) f f f c) f f )
8 Funciones, límites y continuidad
 Solucioario 8 Fucioes, límites y cotiuidad ACTIVIDADES INICIALES 8.I. Copia y completa la siguiete tabla, epresado de varias formas los cojutos uméricos propuestos. Gráfica Itervalo Desigualdad Valor absoluto
Solucioario 8 Fucioes, límites y cotiuidad ACTIVIDADES INICIALES 8.I. Copia y completa la siguiete tabla, epresado de varias formas los cojutos uméricos propuestos. Gráfica Itervalo Desigualdad Valor absoluto
Teoría de Sistemas y Señales
 Toría d Sistmas y Sñals Trasparias: Aálisis ruial d sñals TD Autor: Dr. Jua Carlos Gómz Aálisis ruial d Sñals Timpo Disrto. Sri d ourir d Sñals Timpo Disrto Sa () ua sñal priódia o príodo, s dir: ( ) +
Toría d Sistmas y Sñals Trasparias: Aálisis ruial d sñals TD Autor: Dr. Jua Carlos Gómz Aálisis ruial d Sñals Timpo Disrto. Sri d ourir d Sñals Timpo Disrto Sa () ua sñal priódia o príodo, s dir: ( ) +
Respuesta en frecuencia. Procesado Digital de Señales.4º Ingeniería Electrónica. Universitat de València. Profesor Emilio Soria.
 Rspusta frcucia. Procsado Digital d Sñals.4º Igiría Elctróica. Uivrsitat d Valècia. Profsor Emilio Soria. 1 Itrés uso PDS. Ti l mismo uso qu sistmas cotiuos: dtrmiar la salida d u sistma stado stacioario;
Rspusta frcucia. Procsado Digital d Sñals.4º Igiría Elctróica. Uivrsitat d Valècia. Profsor Emilio Soria. 1 Itrés uso PDS. Ti l mismo uso qu sistmas cotiuos: dtrmiar la salida d u sistma stado stacioario;
7ma Guía de Estudio 2do Parcial Estudio de Series de Potencia SOLUCIONARIO Guía Complementaria No.07
 álculo tgrl (MAT, Scc.67 r Trimstr, do Smstr doprcil 7mGuíEstudio Documto lordo : M.Sc. g. Julio ésr Lóz Zró H6 7m Guí d Estudio do Prcil Estudio d Sris d Potci SOLUONAO Guí omlmtri No.7 omtrios Grls Ést
álculo tgrl (MAT, Scc.67 r Trimstr, do Smstr doprcil 7mGuíEstudio Documto lordo : M.Sc. g. Julio ésr Lóz Zró H6 7m Guí d Estudio do Prcil Estudio d Sris d Potci SOLUONAO Guí omlmtri No.7 omtrios Grls Ést
TEMA 2 CÁLCULO DIFERENCIAL DE DE UNA UNA VARIABLE
 TEMA CÁLCULO DIFERENCIAL DE DE UNA UNA VARIABLE Derivada de ua ució e u puto Sea : D y u puto iterior de Se dice que es derivable e eiste lim Dicho límite recibe el ombre de derivada de e Notas ) Notaremos
TEMA CÁLCULO DIFERENCIAL DE DE UNA UNA VARIABLE Derivada de ua ució e u puto Sea : D y u puto iterior de Se dice que es derivable e eiste lim Dicho límite recibe el ombre de derivada de e Notas ) Notaremos
L lim. lim. a n. 5n 1. 2n lim. lim. lim. 1 Calcula: Solución: a) 2
 Calcula: L L a Dada ua sucesió que tiede a idica a partir de qué térmio se cumple la codició que se idica: a a Si a a Si 7 Si a partir del térmio 9 Si Hallar: d) 7 a partir del térmio 97 d) Deduce los
Calcula: L L a Dada ua sucesió que tiede a idica a partir de qué térmio se cumple la codició que se idica: a a Si a a Si 7 Si a partir del térmio 9 Si Hallar: d) 7 a partir del térmio 97 d) Deduce los
LÍMITES DE FUNCIONES. CONTINUDAD
 LÍMITES DE FUNCIONES. CONTINUDAD Signiicado dl it Ejrcicio nº.- Rprsnta gráicamnt y plica l gniicado d la prón: Ejrcicio nº.- Eplica l gniicado d la guint prón y rprséntalo gráicamnt: 9 Ejrcicio nº.- Escrib
LÍMITES DE FUNCIONES. CONTINUDAD Signiicado dl it Ejrcicio nº.- Rprsnta gráicamnt y plica l gniicado d la prón: Ejrcicio nº.- Eplica l gniicado d la guint prón y rprséntalo gráicamnt: 9 Ejrcicio nº.- Escrib
Tabla de contenido. Página
 Tabla d coido Págia Opradors difrcials sismas d cuacios Opradors difrcials Oprador aulador 6 fiició 6 Sismas d cuacios difrcials lials 9 Solució d u sisma, méodo d los opradors 9 Rsum 5 Bibliografía rcomdada
Tabla d coido Págia Opradors difrcials sismas d cuacios Opradors difrcials Oprador aulador 6 fiició 6 Sismas d cuacios difrcials lials 9 Solució d u sisma, méodo d los opradors 9 Rsum 5 Bibliografía rcomdada
CAPÍTULO XIV. SERIES NUMÉRICAS ARBITRARIAS
 CAPÍTULO XIV. SERIES NUMÉRICAS ARBITRARIAS SECCIONES A. Series de térmios de sigo variable. B. Series depedietes de parámetros. C. Ejercicios propuestos. 193 A. SERIES DE TÉRMINOS DE SIGNO VARIABLE. E
CAPÍTULO XIV. SERIES NUMÉRICAS ARBITRARIAS SECCIONES A. Series de térmios de sigo variable. B. Series depedietes de parámetros. C. Ejercicios propuestos. 193 A. SERIES DE TÉRMINOS DE SIGNO VARIABLE. E
ESTIMADOR DE AITKEN Y PROPIEDADES DEL MISMO (Última revisión: 1 de marzo de 2007)
 Apts d clas d coomtría II / 6 STIMADOR D AITKN Y ROIDADS DL MISMO Última rvisió: d marzo d 7 rof. Rafal d Arc [email protected] stimació d los parámtros dl MBRL por máxima vrosimilitd Apoádoos la hipótsis
Apts d clas d coomtría II / 6 STIMADOR D AITKN Y ROIDADS DL MISMO Última rvisió: d marzo d 7 rof. Rafal d Arc [email protected] stimació d los parámtros dl MBRL por máxima vrosimilitd Apoádoos la hipótsis
IES IGNACIO ALDECOA 1 AMPLIACIÓN DE MATEMÁTICAS 4º ESO CURSO 10/11
 IES IGNACIO ALDECOA AMPLIACIÓN DE MATEMÁTICAS º ESO CURSO 0/ TEMA : SUCESIONES DE NÚMEROS REALES Se llama sucesió a u cojuto de úmeros dispuestos uo a cotiuació de otro. Podemos cosiderar ua sucesió como
IES IGNACIO ALDECOA AMPLIACIÓN DE MATEMÁTICAS º ESO CURSO 0/ TEMA : SUCESIONES DE NÚMEROS REALES Se llama sucesió a u cojuto de úmeros dispuestos uo a cotiuació de otro. Podemos cosiderar ua sucesió como
DERIVADAS. Las gráficas A, B y C son las funciones derivadas de las gráficas 1, 2 y 3, pero en otro orden. = 0 utilizando la definición.
 DERIVADAS Dinición d drivada Ejrcicio nº.- Las gráicas A, B y C son las uncions drivadas d las gráicas, y, pro n otro ordn. Cuál s la drivada d cual? Justiica tus rspustas. Ejrcicio nº.- Calcula la drivada
DERIVADAS Dinición d drivada Ejrcicio nº.- Las gráicas A, B y C son las uncions drivadas d las gráicas, y, pro n otro ordn. Cuál s la drivada d cual? Justiica tus rspustas. Ejrcicio nº.- Calcula la drivada
ASÍNTOTAS Y RAMAS INFINITAS Cálculo y representación
 LÍMITES Cálculo y rprsntación...... 7. 8. - + + - - + + - + - ( + ) - + + - - + + 9. + - +. + - + - 9. + -. + + + - +. + + +. + + + -. +. + - ASÍNTOTAS Y RAMAS INFINITAS Cálculo y rprsntación. y = - +.
LÍMITES Cálculo y rprsntación...... 7. 8. - + + - - + + - + - ( + ) - + + - - + + 9. + - +. + - + - 9. + -. + + + - +. + + +. + + + -. +. + - ASÍNTOTAS Y RAMAS INFINITAS Cálculo y rprsntación. y = - +.
LÍMITES DE FUNCIONES REALES CON TENDENCIA A REAL
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMÁTICAS ASIGNATURA: MATEMÁTICAS DOCENTE: JOSÉ IGNACIO DE JESÚS FRANCO RESTREPO TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO N FECHA
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMÁTICAS ASIGNATURA: MATEMÁTICAS DOCENTE: JOSÉ IGNACIO DE JESÚS FRANCO RESTREPO TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO N FECHA
