Matemática II Tema 17: integrales dobles en coordenadas polares
|
|
|
- José Ángel Cruz Cabrera
- hace 6 años
- Vistas:
Transcripción
1 Matemática II Tema 7: integrales dobles en coordenadas polares Índice Integrales dobles en coordenadas polares Coordenadas polares límites de integración Ejemplos de aplicación 2 Sustitución en integrales múltiples 4 Sustitución en integrales dobles 4 Trabajo práctico 6 Ejemplos con Sage 7 Cálculo de integrales dobles en polares 7 Integrales dobles en coordenadas polares Coordenadas polares límites de integración r r, ) P, ) Coordenadas polares r, ) de un punto, ) Un punto P con coordenadas cartesianas, ) también puede ser localizado por sus coordenadas polares r, ). Ambos juegos de coordenadas se relacionan por las transformaciones r cos r r sin tan Figura : coordenadas cartesianas coordenadas polares de un punto P del plano. En muchas integrales dobles, la región de integración, la función f, ), o ambos, son epresados más fácilmente en coordenadas polares r, ). r Motivación: simplificar una integral difícil Consideremos, por ejemplo, el calcular el volumen V, sobre la región del plano definida por : 2 + 2, bajo la paraboloide z 2 2. Iterando dos integrales en coordenadas cartesianas quedaría Figura 2: región de integración :
2 tema 7: integrales dobles en coordenadas polares 2 V 2 2 ) da lo cual puede costar bastante resolver ) d d La misma integral doble, pero en coordenadas polares, quedará V 2 2 ) da r 2 ) da Pero para iterar esta integral debemos conocer la epresión del elemento de área da en polares... + d da d d + d da d d r dr dr El cambio de coordenadas transforma la región en una región. Se necesita un factor r para igualar los elementos de área da d d r } dr {{ } r da da Ahora podemos iterar la integral doble, más fácilmente, en coordenadas polares Ejemplos de aplicación Ejemplo. Evaluar V 2 2 ) da r 2 ) r da 2π 2π /4 [ r 2 2π /4 [] 2π π/2 r 2 ) r dr 2 r4 4 ] e d d donde es la región semicircular acotada por el eje la curva 2. 2 π π/2 r r da r r + dr Figura 3: interpretación geométrica de un pequeño elemento de área da, en coordenadas cartesianas en coordenadas polares. r r 2π Figura 4: la transformación de coordenadas cartesianas a polares simplifica la región de integración.
3 tema 7: integrales dobles en coordenadas polares 3 {, ) } {r, ) π r }. Entonces la integral doble se iterará como e d d π π π e r2 r dr [/2 e r2] /2 e ) /2 e ) π /2 e ) [] π π/2 e ) 2,7 Ejemplo 2. Evaluar la integral ) d d. Integrando con respecto de la variable nos quedará ) 2 ) 3 /2 d 3 π/2 2 la cual es dificil de resolver sin utilizar un software o tablas Las cosas mejoran si cambiamos a coordenadas polares 2 π/2 π/2 [ r 4 4 π/2 /4 π/8, ) d d r 2) r dr ] r Figura 5: la región de integración del ejemplo 2. π/2 r r + cos 2 Ejemplo 3. Determinar los límites para integrar una f r, ) sobre la región que está dentro de la cardioide r + cos fuera de la circunferencia r. π/2 r. Bosquejar las curvas frontera. 2. Un rao desde el origen corta primero a r después a r + cos, entonces Figura 6: la región de integración del ejemplo 3. r + cos
4 tema 7: integrales dobles en coordenadas polares 4 3. Los raos deben barrer desde π/2 hasta π/2. 4. Entonces la integral quedaría π/2 +cos π/2 f r, ) r dr Sustitución en integrales múltiples Sustitución en integrales dobles Transformación de coordenadas uv en Supongamos que una región del plano uv se transforma en una región del plano por medio de las ecuaciones gu, v) hu, v) v u, v), ) u Cualquier función f, ), definida en, puede ser considerada como una función compuesta f gu, v), hu, v) ) definida en. Si g, h f tienen derivadas parciales continuas, entonces f, ) d d f gu, v), hu, v) ) Ju, v) du dv donde aparece un factor, un valor absoluto, de una función Ju, v) llamada jacobiano de la transformación de coordenadas. Jacobiano de una transformación de coordenadas Definición jacobiano). El jacobiano o determinante jacobiano de la transformación de coordenadas gu, v), hu, v) es Ju, v) u u v v u El jacobiano también suele anotarse como Ju, v), ) u, v) v u v Ejemplo 4. Determinar el jacobiano para la transformación de coordenadas polares r cos, r sin.
5 tema 7: integrales dobles en coordenadas polares 5. El jacobiano será u v Jr, ) cos r sin sin r cos u v ) r cos 2 + sin 2 r } {{ } 2. Como Jr, ) r r, para las integrales dobles se cumplirá f, ) d d f r cos, r sin ) r dr
6 tema 7: integrales dobles en coordenadas polares 6 Trabajo práctico. En cada caso, cambie la integral cartesiana a una integral polar equivalente, luego evalue esta integral polar. i) ii) iii) iv) v) vi) vii) a a 2 2 a a d d d d d d 2 + 2) d d 2 + 2) d d 2 d d ln 2 ln 2) 2 2 e d d Pista: dibuje un bosquejo de cada región de integración.
Integrales Dobles. Hermes Pantoja Carhuavilca. Matematica II. Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos
 Integrales Dobles Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 76 CONTENIDO Integrales Dobles Introducción
Integrales Dobles Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 76 CONTENIDO Integrales Dobles Introducción
Tema 3. Integrales dobles y triples y sus aplicaciones Septiembre {(x,y)/0 x 2, 0 y } x. I = f(x, y)dydx. 2 4 x. 2 4 x.
 CÁLCULO III (05) Tema. Integrales dobles y triples y sus aplicaciones eptiembre 06. Dibuje la región de integración y calcule las integrales dobles siguientes: d. e. f. g. yda, donde es la región limitada
CÁLCULO III (05) Tema. Integrales dobles y triples y sus aplicaciones eptiembre 06. Dibuje la región de integración y calcule las integrales dobles siguientes: d. e. f. g. yda, donde es la región limitada
Teorema de Cambio de Variables para Integrales Dobles
 Universidad de Chile Facultad de Ciencias Físicas y Matemáticas epartamento de Ingeniería Matemática Cátedra - MA2A1 22 de Enero 2008 Teorema de Cambio de Variables para Integrales obles Cuál es la idea:
Universidad de Chile Facultad de Ciencias Físicas y Matemáticas epartamento de Ingeniería Matemática Cátedra - MA2A1 22 de Enero 2008 Teorema de Cambio de Variables para Integrales obles Cuál es la idea:
INTEGRALES DE FUNCIONES DE VARIAS VARIABLES
 INTEGALES DE FUNCIONES DE VAIAS VAIABLES [Versión preliminar] Prof. Isabel Arratia Z. Integrales dobles sobre rectángulos La integral de iemann para una función f de dos variables se define de manera similar
INTEGALES DE FUNCIONES DE VAIAS VAIABLES [Versión preliminar] Prof. Isabel Arratia Z. Integrales dobles sobre rectángulos La integral de iemann para una función f de dos variables se define de manera similar
3. Cambio de variables en integrales dobles.
 GADO DE INGENIEÍA AEOESPACIAL. CUSO. Lección. Integrales múltiples. 3. Cambio de variables en integrales dobles. Para calcular integrales dobles eiste, además del teorema de Fubini, otra herramienta fundamental
GADO DE INGENIEÍA AEOESPACIAL. CUSO. Lección. Integrales múltiples. 3. Cambio de variables en integrales dobles. Para calcular integrales dobles eiste, además del teorema de Fubini, otra herramienta fundamental
COORDENADAS POLARES O CILÍNDRICAS
 COORDENADAS POLARES O CILÍNDRICAS Para definir la posición de un punto en un plano (o en el espacio) podemos utilizar distintos tipos de coordenadas, siendo las más normales las coordenadas rectangulares
COORDENADAS POLARES O CILÍNDRICAS Para definir la posición de un punto en un plano (o en el espacio) podemos utilizar distintos tipos de coordenadas, siendo las más normales las coordenadas rectangulares
PRIMITIVAS E INTEGRAL DEFINIDA Ejercicios de selectividad
 PRIMITIVAS E INTEGRAL DEFINIDA Ejercicios de selectividad Sea f : R R la función definida por f() = e /. (a) En qué punto de la gráfica de f la recta tangente a ésta pasa por el origen de coordenadas?
PRIMITIVAS E INTEGRAL DEFINIDA Ejercicios de selectividad Sea f : R R la función definida por f() = e /. (a) En qué punto de la gráfica de f la recta tangente a ésta pasa por el origen de coordenadas?
Integrales Múltiples.
 CAPÍTULO 8 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
CAPÍTULO 8 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS. 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2.
 INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2. 1 1 4, 0 1 a.- (, ) = 2 1 4, 1 2 2 1 < 3, 0 < 1 b.- (, ) = 1 1 < 3, 1 2 3 3 4,
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2. 1 1 4, 0 1 a.- (, ) = 2 1 4, 1 2 2 1 < 3, 0 < 1 b.- (, ) = 1 1 < 3, 1 2 3 3 4,
1. INTEGRALES MÚLTIPLES
 1. INTEGALES MÚLTIPLES 1. Calcular las siguientes integrales iteradas: 1. x x 7 y dy dx dx 1. x x y y dx dy 1 1 7. (1 + xy) dx dy 1 1 π/. x sen y dy dx 5. (x + y) dx dy 6/ 1 6. (x + y) 8 dx dy 616 5 1
1. INTEGALES MÚLTIPLES 1. Calcular las siguientes integrales iteradas: 1. x x 7 y dy dx dx 1. x x y y dx dy 1 1 7. (1 + xy) dx dy 1 1 π/. x sen y dy dx 5. (x + y) dx dy 6/ 1 6. (x + y) 8 dx dy 616 5 1
SERIE # 4 CÁLCULO VECTORIAL
 SERIE # 4 CÁLCULO VECTORIAL Página 1 1) Calcular 1 x y dy dx. 0 0 1 ) Evaluar la integral doble circunferencia x y 9. x 9 x da R, donde R es la región circular limitada por la 648 15 x y ) Calcular el
SERIE # 4 CÁLCULO VECTORIAL Página 1 1) Calcular 1 x y dy dx. 0 0 1 ) Evaluar la integral doble circunferencia x y 9. x 9 x da R, donde R es la región circular limitada por la 648 15 x y ) Calcular el
Contenido 1. Integrales Dobles 2. Integrales Triples
 Integración Contenido 1. Integrales Dobles 2 1.1. Integrales iteradas............................. 2 1.2. Regiones en R 2.............................. 3 1.3. Volumen..................................
Integración Contenido 1. Integrales Dobles 2 1.1. Integrales iteradas............................. 2 1.2. Regiones en R 2.............................. 3 1.3. Volumen..................................
INTEGRALES MÚLTIPLES
 INTEGALES MÚLTIPLES Introducción: Si f es una función definida sobre una región, la integral doble se puede interpretar como el volumen del sólido limitado superiormente por la superficie z = f(,, inferiormente
INTEGALES MÚLTIPLES Introducción: Si f es una función definida sobre una región, la integral doble se puede interpretar como el volumen del sólido limitado superiormente por la superficie z = f(,, inferiormente
ECUACIONES DIFERENCIALES DE VARIABLES SEPARABLES ESTUDIO CUALITATIVO
 ECUACIONES DIFERENCIALES DE VARIABLES SEPARABLES ESTUDIO CUALITATIVO E. SÁEZ Sean Ω R 2 un conjunto abierto del plano, P,Q : Ω R funciones continuas. P R Ω Q Fig. 0 Definición.- La epresión P(,)d+ Q(,)d
ECUACIONES DIFERENCIALES DE VARIABLES SEPARABLES ESTUDIO CUALITATIVO E. SÁEZ Sean Ω R 2 un conjunto abierto del plano, P,Q : Ω R funciones continuas. P R Ω Q Fig. 0 Definición.- La epresión P(,)d+ Q(,)d
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
Datos del alumno. Criterios de desempeño. Criterios de desempeño. 7. Determina las coordenadas a partir de un punto en el plano.
 Bloque I Actividad 2: Puntos y líneas en el plano. AGNATURA 2. Entrega con limpieza. 3. Entrega con orden el trabajo. 4. Muestra actitud de respeto ante sus compañeros y maestros. 5. Muestra honestidad
Bloque I Actividad 2: Puntos y líneas en el plano. AGNATURA 2. Entrega con limpieza. 3. Entrega con orden el trabajo. 4. Muestra actitud de respeto ante sus compañeros y maestros. 5. Muestra honestidad
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2004 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 4 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 4 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
INTEGRALES EN REGIONES POLARES 1 INTEGRALES DOBLES EN COORDENADAS POLARES
 INTEGRALES EN REGIONES POLARES 1 INTEGRALES DOBLES EN COORDENADAS POLARES Hasta el momento hemos tratado integrales dobles en las cuales la región de integración es una región rectangular de la forma *(
INTEGRALES EN REGIONES POLARES 1 INTEGRALES DOBLES EN COORDENADAS POLARES Hasta el momento hemos tratado integrales dobles en las cuales la región de integración es una región rectangular de la forma *(
División Departamento Licenciatura. Asignatura: Horas/semana: Horas/semestre: Obligatoria X Teóricas 4.0 Teóricas 64.0
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA PROGRAMA DE ESTUDIO CÁLCULO VECTORIAL CIENCIAS BÁSICAS 3 8 Asignatura Clave Semestre Créditos COORDINACIÓN DE MATEMÁTICAS INGENIERÍA CIVIL
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA PROGRAMA DE ESTUDIO CÁLCULO VECTORIAL CIENCIAS BÁSICAS 3 8 Asignatura Clave Semestre Créditos COORDINACIÓN DE MATEMÁTICAS INGENIERÍA CIVIL
Superficies Parametrizadas y Áreas
 Superficies Parametrizadas y Áreas 1 Superficies Parametrizadas y Áreas Hasta ahora hemos estudiado (tema de matemáticas 5) superficies definidas como gráficas de funciones de la forma z = f (x, y). El
Superficies Parametrizadas y Áreas 1 Superficies Parametrizadas y Áreas Hasta ahora hemos estudiado (tema de matemáticas 5) superficies definidas como gráficas de funciones de la forma z = f (x, y). El
Matemáticas Especiales II Clase 8 Aspectos Geométricos II. Geometría de los cambios de coordenadas
 Matemáticas Especiales II Clase 8 Aspectos Geométricos II Geometría de los cambios de coordenadas Octavio Miloni Facultad de Cs. Astronómicas y Geofísicas - Universidad Nacional de La Plata Octavio Miloni
Matemáticas Especiales II Clase 8 Aspectos Geométricos II Geometría de los cambios de coordenadas Octavio Miloni Facultad de Cs. Astronómicas y Geofísicas - Universidad Nacional de La Plata Octavio Miloni
( ) () i ( ) ( ) ( ) cálculos. Por ejemplo, dada una región de integración D de la forma indicada en la figura (i) tenemos:
 Universidad iego Portales Facultad de Ingeniería. Instituto de Ciencias Básicas Asignatura: Cálculo III Laboratorio N 9, Integrales Multiples. Introducción. En este laboratorio estudiamos las integrales
Universidad iego Portales Facultad de Ingeniería. Instituto de Ciencias Básicas Asignatura: Cálculo III Laboratorio N 9, Integrales Multiples. Introducción. En este laboratorio estudiamos las integrales
INTEGRALES MÚLTIPLES. 9 xy c) 4
 de 6 TRABAJO PRÁCTICO Nº A.M. II - INTEGRALES MÚLTIPLES INTEGRALES DOBLES - Calcule las siguientes integrales: a d d d d d b d d sen e 6 d d --. Grafique la región de integración eprese la integral invirtiendo
de 6 TRABAJO PRÁCTICO Nº A.M. II - INTEGRALES MÚLTIPLES INTEGRALES DOBLES - Calcule las siguientes integrales: a d d d d d b d d sen e 6 d d --. Grafique la región de integración eprese la integral invirtiendo
y = 2x + 8x 7, y = x 4. y = 4 x, y = x + 2, x = 2, x = 3. x = 16 y, x = 6 y. y = a x, y = x, x y = a. (1 x)dx. y = 9 x, y = 0.
 . Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
. Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
Soluciones de los ejercicios del segundo examen parcial
 Matemáticas III GIC, curso 5 6 Soluciones de los ejercicios del segundo examen parcial EJERCICIO. Considera la integral doble π π ibuja la región del plano XY en la que se está integrando. Usa el teorema
Matemáticas III GIC, curso 5 6 Soluciones de los ejercicios del segundo examen parcial EJERCICIO. Considera la integral doble π π ibuja la región del plano XY en la que se está integrando. Usa el teorema
Cambio de variables. ISABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna 1.
 Cambio de variables IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Cambio de variables 1 2.1. El teorema del cambio de variables
Cambio de variables IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Cambio de variables 1 2.1. El teorema del cambio de variables
INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA. APLICACIONES
 INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA. APLICACIONES. a) Eplicar el concepto de función primitiva. b) Sea f () = e + 8, justificar si es primitiva de alguna de las siguientes funciones: g () = e + 8 h
INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA. APLICACIONES. a) Eplicar el concepto de función primitiva. b) Sea f () = e + 8, justificar si es primitiva de alguna de las siguientes funciones: g () = e + 8 h
INTEGRALES TRIPLES. 46. Dada la integral la integral de todas las formas posibles. f(x, y, z) dzdydx, dibujar la región de integración y escribir
 INTEGALES TIPLES. 46. Dada la integral la integral de todas las formas posibles. f(,, ) ddd, dibujar la región de integración escribir Teniendo en cuenta la gráfica adjunta, si D 1, D 2 D 3 son las proecciones
INTEGALES TIPLES. 46. Dada la integral la integral de todas las formas posibles. f(,, ) ddd, dibujar la región de integración escribir Teniendo en cuenta la gráfica adjunta, si D 1, D 2 D 3 son las proecciones
Análisis Matemático I (Ing. de Telecomunicación), Examen final, 26 de enero de 2010 RESPUESTAS A AMBOS MODELOS
 Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
Integración múltiple: integrales dobles
 Problemas propuestos con solución Integración múltiple: integrales dobles ISABEL MAEO epartamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice. Integrales iteradas 2. Teorema
Problemas propuestos con solución Integración múltiple: integrales dobles ISABEL MAEO epartamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice. Integrales iteradas 2. Teorema
Universidad Icesi Departamento de Matemáticas y Estadística
 Universidad Icesi Departamento de Matemáticas y Estadística Solución del tercer eamen parcial del curso Cálculo una variable Grupo: Uno Período: Inicial del año Prof: Rubén D. Nieto C. PUNTO. a. Después
Universidad Icesi Departamento de Matemáticas y Estadística Solución del tercer eamen parcial del curso Cálculo una variable Grupo: Uno Período: Inicial del año Prof: Rubén D. Nieto C. PUNTO. a. Después
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2017 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 7 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 7 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.
 SEMESTRE 018-1 SERIE CURVAS EN EL PLANO POLAR 1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.. Determinar las coordenadas polares del punto C simétrico
SEMESTRE 018-1 SERIE CURVAS EN EL PLANO POLAR 1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.. Determinar las coordenadas polares del punto C simétrico
Integral Doble e Integral Triple
 www.cidse.itcr.ac.cr/revistamate Práctica 6 Integral Doble e Integral Triple Cambio de variable con coordenadas polares y coordenadas ciĺındricas. Cálculo Superior Instituto Tecnológico de Costa ica Escuela
www.cidse.itcr.ac.cr/revistamate Práctica 6 Integral Doble e Integral Triple Cambio de variable con coordenadas polares y coordenadas ciĺındricas. Cálculo Superior Instituto Tecnológico de Costa ica Escuela
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2011 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Tema 5: Funciones homogéneas
 Tema 5: Funciones homogéneas f se dice homogénea de grado α si se verifica: f(λ x) = λ α f( x), x, λ > 0 Propiedades: 1. Si f y g son homogéneas de grado α, entonces f ± g es también homogénea de grado
Tema 5: Funciones homogéneas f se dice homogénea de grado α si se verifica: f(λ x) = λ α f( x), x, λ > 0 Propiedades: 1. Si f y g son homogéneas de grado α, entonces f ± g es también homogénea de grado
TEMA 5: LA INTEGRAL DEFINIDA
 Alonso Fernández Galián TEMA 5: LA INTEGRAL DEFINIDA Originalmente el Cálculo Diferencial e Integral estaba fuertemente vinculado a la geometría analítica. Ya vimos la aplicación de las derivadas al cálculo
Alonso Fernández Galián TEMA 5: LA INTEGRAL DEFINIDA Originalmente el Cálculo Diferencial e Integral estaba fuertemente vinculado a la geometría analítica. Ya vimos la aplicación de las derivadas al cálculo
Ejercicio reto. Definición. Circunferencia con centro en el origen. ENCUENTRO # 60 TEMA:Secciones cónicas. CONTENIDOS: 1. Circunferencia.
 ENCUENTRO # 60 TEMA:Secciones cónicas. CONTENIDOS: 1. Circunferencia. Ejercicio reto 1. La ecuación de la recta que pasa por M(π, 0) y por la intersección de las rectas con ecuaciones: 3x 2y 1=0, x 4y+
ENCUENTRO # 60 TEMA:Secciones cónicas. CONTENIDOS: 1. Circunferencia. Ejercicio reto 1. La ecuación de la recta que pasa por M(π, 0) y por la intersección de las rectas con ecuaciones: 3x 2y 1=0, x 4y+
Integración doble Integrales dobles sobre regiones no rectangulares
 Nuestra intención es extender la definición de integral doble, de funciones continuas, sobre regiones más generales que el rectángulo. Para ello definiremos dos tipos de regiones en el plano, que llamaremos
Nuestra intención es extender la definición de integral doble, de funciones continuas, sobre regiones más generales que el rectángulo. Para ello definiremos dos tipos de regiones en el plano, que llamaremos
MÉTODOS MATEMÁTICOS II
 MÉTODOS MATEMÁTICOS II (Licenciatura de Física. Curso 2007-2008) Boletín de problemas a evaluar correspondientes a los Temas I y II Fecha de entrega: Viernes, 23 de Noviembre de 2007 1. Calcula los siguientes
MÉTODOS MATEMÁTICOS II (Licenciatura de Física. Curso 2007-2008) Boletín de problemas a evaluar correspondientes a los Temas I y II Fecha de entrega: Viernes, 23 de Noviembre de 2007 1. Calcula los siguientes
Técnicas de Integración
 Técnicas de Integración Índice Capítulo único: Técnicas de Integración. Integración Directa....................................... Integración por Sustitución.................................. Integración
Técnicas de Integración Índice Capítulo único: Técnicas de Integración. Integración Directa....................................... Integración por Sustitución.................................. Integración
El cálculo de la viga superior no presenta mayores problemas, ya que su volumen corresponde al de un prisma recto cuyas dimensiones se indican:
 Consideremos el problema: Usted es un ingeniero civil y se le ha encargado la tarea de construir un puente. Para ello necesita cubicar (dimensionar), para saber la cantidad de material necesario para hacer
Consideremos el problema: Usted es un ingeniero civil y se le ha encargado la tarea de construir un puente. Para ello necesita cubicar (dimensionar), para saber la cantidad de material necesario para hacer
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2003 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Junio, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Junio, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva, Ejercicio,
UNIVERSIDAD AUTONOMA DE BAJA CALIFORNIA
 UNIVERSIDAD AUTONOMA DE BAJA CALIFORNIA DIRECCION GENERAL DE ASUNTOS ACADEMICOS PROGRAMA DE ASIGNATURA POR COMPETENCIAS I. DATOS DE IDENTIFICACIÓN 1. Unidad Académica: Facultad de Ciencias 2. Programa
UNIVERSIDAD AUTONOMA DE BAJA CALIFORNIA DIRECCION GENERAL DE ASUNTOS ACADEMICOS PROGRAMA DE ASIGNATURA POR COMPETENCIAS I. DATOS DE IDENTIFICACIÓN 1. Unidad Académica: Facultad de Ciencias 2. Programa
ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA Ingeniería Técnica Industrial, Especialidad de Electricidad
 ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA Ingeniería Técnica Industrial, Especialidad de Electricidad Fundamentos Matemáticos de la Ingeniería Diciembre de 5. Primera parte Tiempo: horas. Se recuerda
ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA Ingeniería Técnica Industrial, Especialidad de Electricidad Fundamentos Matemáticos de la Ingeniería Diciembre de 5. Primera parte Tiempo: horas. Se recuerda
INTRODUCCIÓN A LAS MATEMÁTICAS SUPERIORES. Tema 3 EL PLANO Y LAS GRÁFICAS EL PLANO CARTESIANO. COORDENADAS Y DISTANCIA ENTRE PUNTOS.
 INTRODUCCIÓN A LAS MATEMÁTICAS SUPERIORES Tema EL PLANO Y LAS GRÁFICAS EL PLANO CARTESIANO. COORDENADAS Y DISTANCIA ENTRE PUNTOS. C.- Qué es cómo se representa un sistema de coordenadas cartesianas rectangulares
INTRODUCCIÓN A LAS MATEMÁTICAS SUPERIORES Tema EL PLANO Y LAS GRÁFICAS EL PLANO CARTESIANO. COORDENADAS Y DISTANCIA ENTRE PUNTOS. C.- Qué es cómo se representa un sistema de coordenadas cartesianas rectangulares
7. Cambio de variables en integrales triples.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 011 1. Lección. Integrales múltiples. 7. Cambio de variables en integrales triples. El teorema del cambio de variables para integrales triples es análogo al de integrales
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 011 1. Lección. Integrales múltiples. 7. Cambio de variables en integrales triples. El teorema del cambio de variables para integrales triples es análogo al de integrales
SERIE # 2 CÁLCULO VECTORIAL
 SERIE # CÁLCULO VECTORIAL SERIE 1) Calcular las coordenadas del punto P de la curva: en el que el vector P 1, 1, r t es paralelo a r t Página 1 t1 r t 1 t i ( t ) j e k ) Una partícula se mueve a lo largo
SERIE # CÁLCULO VECTORIAL SERIE 1) Calcular las coordenadas del punto P de la curva: en el que el vector P 1, 1, r t es paralelo a r t Página 1 t1 r t 1 t i ( t ) j e k ) Una partícula se mueve a lo largo
Universidad Nacional Autónoma de México Centro de Investigación en Energía. Programa de Estudio
 Universidad Nacional Autónoma de Centro de Investigación en Energía Programa de Estudio Cálculo Vectorial 2 10 Asignatura Clave Semestre Créditos Ciencias Básicas Ciclo Matemáticas Área Asignatura: Horas:
Universidad Nacional Autónoma de Centro de Investigación en Energía Programa de Estudio Cálculo Vectorial 2 10 Asignatura Clave Semestre Créditos Ciencias Básicas Ciclo Matemáticas Área Asignatura: Horas:
Examen de Matemáticas 2 o de Bachillerato Mayo 2003
 Examen de Matemáticas o de Bachillerato Mayo 1. (a) Dibuja el recinto limitado por las curvas y = e x+, y = e x y x =. (b) Halla el área del recinto considerado en el apartado anterior. (a) El dominio
Examen de Matemáticas o de Bachillerato Mayo 1. (a) Dibuja el recinto limitado por las curvas y = e x+, y = e x y x =. (b) Halla el área del recinto considerado en el apartado anterior. (a) El dominio
Tema 4: Integración de funciones de varias variables
 Departamento de Matemáticas. Universidad de Jaén. Análisis Matemático II. Curso 29-21. Tema 4: Integración de funciones de varias variables 1. Evaluar las siguientes integrales iteradas e) f ) g) 1 2 1
Departamento de Matemáticas. Universidad de Jaén. Análisis Matemático II. Curso 29-21. Tema 4: Integración de funciones de varias variables 1. Evaluar las siguientes integrales iteradas e) f ) g) 1 2 1
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2010 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Máximos y mínimos usando la segunda derivada
 Máimos mínimos usando la segunda derivada Ahora que sabemos que la segunda derivada nos da información acerca de la primera derivada, vamos a utilizarla para calcular los máimos mínimos de funciones. Ya
Máimos mínimos usando la segunda derivada Ahora que sabemos que la segunda derivada nos da información acerca de la primera derivada, vamos a utilizarla para calcular los máimos mínimos de funciones. Ya
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 26 de Junio de 2007 Primera parte
 CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 6 de Junio de 7 Primera parte Ejercicio. Determinar los puntos de máxima y mínima pendiente de la gráfica de la función y = +x, x. Solución.
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 6 de Junio de 7 Primera parte Ejercicio. Determinar los puntos de máxima y mínima pendiente de la gráfica de la función y = +x, x. Solución.
EJERCICIOS DE DERIVADAS PARCIALES. ), demostrar que y x = 0. es una solución de + = 0 x. z 7. Si z = f(f(x)+g(y)), demostrar que = 0
 EJERCICIOS DE DERIVADAS PARCIALES. z. En cada ejercicio hallar ; de la primera forma comprobar usando la segunda forma: a) z = ln + = [ ln( + ln( + ] e + e e e + b) z = e + e = e ( ) + c) z = ln = [ ln
EJERCICIOS DE DERIVADAS PARCIALES. z. En cada ejercicio hallar ; de la primera forma comprobar usando la segunda forma: a) z = ln + = [ ln( + ln( + ] e + e e e + b) z = e + e = e ( ) + c) z = ln = [ ln
Ejercicios típicos del segundo parcial
 Ejercicios típicos del segundo parcial El segundo examen parcial consiste en tres ejercicios prácticos y dos teóricos, aunque esta frontera es muy difusa. Por ejemplo, el primer ejercicio de esta serie,
Ejercicios típicos del segundo parcial El segundo examen parcial consiste en tres ejercicios prácticos y dos teóricos, aunque esta frontera es muy difusa. Por ejemplo, el primer ejercicio de esta serie,
Sistemas no lineales
 Tema 4 Sistemas no lineales Dpto. Matemática Aplicada I E.T.S. de Arquitectura Universidad de Sevilla Curso 2005 2006 Tema 4. Sistemas no lineales 1. Sistemas no lineales de ecuaciones diferenciales. Integrales
Tema 4 Sistemas no lineales Dpto. Matemática Aplicada I E.T.S. de Arquitectura Universidad de Sevilla Curso 2005 2006 Tema 4. Sistemas no lineales 1. Sistemas no lineales de ecuaciones diferenciales. Integrales
OPCIÓN A. MATEMÁTICAS 2º BACHILLERATO B Lo que te llevará al final, serán tus pasos, no el camino. Fito y los Fitipaldis
 MATEMÁTICAS º BACHILLERATO B 9--4 Lo que te llevará al final, serán tus pasos, no el camino Análisis Fito y los Fitipaldis OPCIÓN A.- a) Hallar las dimensiones que hacen mínimo el coste de un contenedor
MATEMÁTICAS º BACHILLERATO B 9--4 Lo que te llevará al final, serán tus pasos, no el camino Análisis Fito y los Fitipaldis OPCIÓN A.- a) Hallar las dimensiones que hacen mínimo el coste de un contenedor
Técnicas de Integración. Integración por Partes (I)
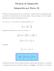 Técnicas de Integración Integración por Partes (I El método de integración por partes es un método que te permite separar una integral (que tiene un producto de dos funciones en una integral simple y lista
Técnicas de Integración Integración por Partes (I El método de integración por partes es un método que te permite separar una integral (que tiene un producto de dos funciones en una integral simple y lista
Tema 4A: Integración Doble ENUNCIADO Y RESPUESTA AL EJERCICIO: ENUNCIADO
 Ejercicio de Seguimiento de Aprendizaje Tema 4A: Integración Doble FECHA: 8/05/1 TIEMPO RECOMENDADO: 1/ Hora Puntuación/TOTAL:,5/10 Halle el área total encerrada por la curva: Y RESPUESTA AL EJERCICIO:
Ejercicio de Seguimiento de Aprendizaje Tema 4A: Integración Doble FECHA: 8/05/1 TIEMPO RECOMENDADO: 1/ Hora Puntuación/TOTAL:,5/10 Halle el área total encerrada por la curva: Y RESPUESTA AL EJERCICIO:
PRÁCTICA INTEGRACIÓN MÚLTIPLE. CAMBIO DE VARIABLE CURSO CÁLCULO II. Práctica 2 (16/02/2016)
 PRÁTIA INTEGRAIÓN MÚLTIPLE. AMBIO DE VARIABLE URSO 015-016 ÁLULO II Prácticas Matlab Práctica (16/0/016) Objetivos o alcular integrales dobles mediante cambio de variable o Definir dominios regulares en,
PRÁTIA INTEGRAIÓN MÚLTIPLE. AMBIO DE VARIABLE URSO 015-016 ÁLULO II Prácticas Matlab Práctica (16/0/016) Objetivos o alcular integrales dobles mediante cambio de variable o Definir dominios regulares en,
Funciones de 2 variables.
 Funciones de variables. INTRODUCCIÓN En el curso anterior estudiamos las funciones reales de variable real, donde estaban involucradas únicamente dos variables (, ). Una de ellas era la variable independiente
Funciones de variables. INTRODUCCIÓN En el curso anterior estudiamos las funciones reales de variable real, donde estaban involucradas únicamente dos variables (, ). Una de ellas era la variable independiente
FUNCIONES DE DOS VARIABLES
 FUNCIONES DE DOS VARIABLES - Funciones de dos variables reales - Límites 3- Continuidad de funciones de dos variables 4- Derivabilidad de funciones de dos variables 5- Diferenciabilidad de funciones de
FUNCIONES DE DOS VARIABLES - Funciones de dos variables reales - Límites 3- Continuidad de funciones de dos variables 4- Derivabilidad de funciones de dos variables 5- Diferenciabilidad de funciones de
Integrales dobles. Integrales dobles
 Integrales dobles Integrales iteradas b g2 (x) a g 1 (x) f(x, y) dydx ó d h2 (y) c h 1 (y) f(x, y) dxdy Los límites interiores de integración pueden ser variables respecto a la variable exterior de integración,
Integrales dobles Integrales iteradas b g2 (x) a g 1 (x) f(x, y) dydx ó d h2 (y) c h 1 (y) f(x, y) dxdy Los límites interiores de integración pueden ser variables respecto a la variable exterior de integración,
FACULTAD DE CIENCIAS DEL MAR. FUNDAMENTOS MATEMÁTICOS II. Convocatoria Extraordinaria de Diciembre de 2002.
 FAULTAD DE IENIAS DEL MAR. FUNDAMENTOS MATEMÁTIOS II. onvocatoria Extraordinaria de Diciembre de. xydx x y dy a lo largo de la elipse.- alcular + ( ) contrario al de las agujas del reloj. x y + = recorrida
FAULTAD DE IENIAS DEL MAR. FUNDAMENTOS MATEMÁTIOS II. onvocatoria Extraordinaria de Diciembre de. xydx x y dy a lo largo de la elipse.- alcular + ( ) contrario al de las agujas del reloj. x y + = recorrida
TEMA 3: CÁLCULO DE FUNCIONES DE VARIAS VARIABLES
 TEMA : CÁLCULO DE FUNCIONES DE AIAS AIABLES. Hallar f,. f, f,. 4 4. Hallar el valor de la función f, en los puntos de la circunferencia.. Calcular los guientes límites: cos lim,, sen lim,, c, lim con,
TEMA : CÁLCULO DE FUNCIONES DE AIAS AIABLES. Hallar f,. f, f,. 4 4. Hallar el valor de la función f, en los puntos de la circunferencia.. Calcular los guientes límites: cos lim,, sen lim,, c, lim con,
TEORIA MATEMATICAS 5 PRIMER PARCIAL
 Def: Grafica de una función TEORIA MATEMATICAS 5 PRIMER PARCIAL Sea:. Definimos la grafica de f como el subconjunto de formado por los puntos, de en los que es un punto de U. Simbólicamente grafica es:
Def: Grafica de una función TEORIA MATEMATICAS 5 PRIMER PARCIAL Sea:. Definimos la grafica de f como el subconjunto de formado por los puntos, de en los que es un punto de U. Simbólicamente grafica es:
( ) x y dxdy. x y dxdy y. sin 2θ 2 = = = x y dxdy. 3 4y y ln. 1
 Cálculo II Exámenes esueltos Tercer Parcial. Evaluar la integral, pasando a coordenadas polares: Solución: haciendo los siguientes cambios, ( ) 4y 4y 4y x y y 4y 4y 4 4 4y x y sin θ x y = r ( sinθcosθ
Cálculo II Exámenes esueltos Tercer Parcial. Evaluar la integral, pasando a coordenadas polares: Solución: haciendo los siguientes cambios, ( ) 4y 4y 4y x y y 4y 4y 4 4 4y x y sin θ x y = r ( sinθcosθ
Ejercicios Resueltos de Cálculo III.
 Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Energía almacenada en el campo magnético.
 c Rafael R. Boix y Francisco Medina 1 Energía almacenada en el campo magnético. Consideremos una espira conductora, modelada mediante la curva Γ, por la que circula una corriente estacionaria de intensidad
c Rafael R. Boix y Francisco Medina 1 Energía almacenada en el campo magnético. Consideremos una espira conductora, modelada mediante la curva Γ, por la que circula una corriente estacionaria de intensidad
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-07-2-M-2-00-202 CURSO: Matemática Intermedia I SEMESTRE: Segundo CÓDIGO DEL CURSO: 07 TIPO DE EXAMEN: Segundo
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-07-2-M-2-00-202 CURSO: Matemática Intermedia I SEMESTRE: Segundo CÓDIGO DEL CURSO: 07 TIPO DE EXAMEN: Segundo
En este curso nos centraremos en un nuevo concepto de curva la cual estará descrita por una o mas ecuaciones denominadas ecuaciones paramétricas.
 Unidad I - Curvas en R ecuaciones paramétricas.. Ecuaciones paramétricas En cursos anteriores se ha considerado a una curva como una sucesión de pares ordenados ubicados en un plano rectangular provenientes
Unidad I - Curvas en R ecuaciones paramétricas.. Ecuaciones paramétricas En cursos anteriores se ha considerado a una curva como una sucesión de pares ordenados ubicados en un plano rectangular provenientes
1 Funciones de Varias Variables
 EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
FUNDAMENTOS MATEMÁTICOS (Grado en Ingeniería Informática) Práctica 4. DERIVACIÓN
 FUNDAMENTOS MATEMÁTICOS (Grado en Ingeniería Informática) Práctica 4. DERIVACIÓN 1.- Derivada de una función en un punto. El estudio de la derivada de una función en un punto surge con el problema geométrico
FUNDAMENTOS MATEMÁTICOS (Grado en Ingeniería Informática) Práctica 4. DERIVACIÓN 1.- Derivada de una función en un punto. El estudio de la derivada de una función en un punto surge con el problema geométrico
UNIDAD I. DIFERENCIALES E INTEGRAL INDEFINIDA. Actividad 1. DIFERENCIALES
 CENTRO DE ESTUDIOS DE BACHILLERATO Nº 4/ LIC. JESÚS REYES HEROLES GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO ASIGNATURA PROFESOR SEMESTRE CÁLCULO INTEGRAL L. M. A. JUAN MANUEL VALDEZ CHÁVEZ 0 0 B SEXTO
CENTRO DE ESTUDIOS DE BACHILLERATO Nº 4/ LIC. JESÚS REYES HEROLES GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO ASIGNATURA PROFESOR SEMESTRE CÁLCULO INTEGRAL L. M. A. JUAN MANUEL VALDEZ CHÁVEZ 0 0 B SEXTO
Matemática II Tema 14: valores extremos
 Matemática II Tema 14: valores extremos 2012 2013 Índice Valores extremos y puntos silla 1 Criterio de las derivadas para extremos locales 1 Máximos y mínimos absolutos 5 Trabajo práctico 7 Valores extremos
Matemática II Tema 14: valores extremos 2012 2013 Índice Valores extremos y puntos silla 1 Criterio de las derivadas para extremos locales 1 Máximos y mínimos absolutos 5 Trabajo práctico 7 Valores extremos
EJERCICIOS DE CA LCULO II PARA GRADOS DE INGENIERI A Elaborados por Domingo Pestana y Jose Manuel Rodrı guez, con Arturo de Pablo y Elena Romera
 EJECICIOS E CA LCULO II PAA GAOS E INGENIEI A Elaborados por omingo Pestana y Jose Manuel odrı guez, con Arturo de Pablo y Elena omera 3 3. Integracio n en n Integral mu ltiple. f en los siguientes casos:
EJECICIOS E CA LCULO II PAA GAOS E INGENIEI A Elaborados por omingo Pestana y Jose Manuel odrı guez, con Arturo de Pablo y Elena omera 3 3. Integracio n en n Integral mu ltiple. f en los siguientes casos:
La Diferencial de Fréchet
 Capítulo 6 La Diferencial de Fréchet Es bien conocido que una función de una variable f es derivable en un punto a si y sólo si su gráfica admite una recta tangente (no vertical) en el punto (a, f(a)).
Capítulo 6 La Diferencial de Fréchet Es bien conocido que una función de una variable f es derivable en un punto a si y sólo si su gráfica admite una recta tangente (no vertical) en el punto (a, f(a)).
PROBLEMAS DE INTEGRALES INDEFINIDAS
 PROBLEMAS DE INTEGRALES INDEFINIDAS Integración por partes. Mediante la integración por partes, hallar una primitiva de la función y = Ln (1 + x) Calcular una primitiva de una función, es hallar su
PROBLEMAS DE INTEGRALES INDEFINIDAS Integración por partes. Mediante la integración por partes, hallar una primitiva de la función y = Ln (1 + x) Calcular una primitiva de una función, es hallar su
Representación gráfica y uso de curvas conicas
 Representación gráfica y uso de curvas conicas Representará gráficamente y algebraicamente curvas canónicas, partiendo de la definición de su lugar geométrico y aplicando técnicas y procedimientos, para
Representación gráfica y uso de curvas conicas Representará gráficamente y algebraicamente curvas canónicas, partiendo de la definición de su lugar geométrico y aplicando técnicas y procedimientos, para
Tema 7. Integrales múltiples
 Tema 7 Integrales múltiples 7.. efinición. En esta sección estudiamos el cálculo de la integral de una función real de dos variables denominada integral doble. Se puede utilizar el esquema del tema anterior
Tema 7 Integrales múltiples 7.. efinición. En esta sección estudiamos el cálculo de la integral de una función real de dos variables denominada integral doble. Se puede utilizar el esquema del tema anterior
Volumen de Sólidos de Revolución
 60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
Guía Semanas 13 y RESUMEN. Universidad de Chile. Ingeniería Matemática. Triedro de vectores y factores escalares. Supongamos que r.
 1. RESUMEN Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08-1 Ingeniería Matemática Guía Semanas 13 y 14 Triedro de vectores y factores
1. RESUMEN Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08-1 Ingeniería Matemática Guía Semanas 13 y 14 Triedro de vectores y factores
Unidad 5 - Trabajo Práctico 5 Parte 1 Elementos de Matemática
 06 Unidad 5 - Trabajo Práctico 5 Parte Unidad 5 Integral indefinida. Primitivas inmediatas. Uso de tablas de integrales. Integración por descomposición, por sustitución y por partes. Integral definida:
06 Unidad 5 - Trabajo Práctico 5 Parte Unidad 5 Integral indefinida. Primitivas inmediatas. Uso de tablas de integrales. Integración por descomposición, por sustitución y por partes. Integral definida:
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2001 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Lectura 2 Ampliación de Matemáticas. Grado en Ingeniería Civil
 1 / 12 Lectura 2 Ampliación de Matemáticas. Grado en Ingeniería Civil Curso Académico 2011-2012 Cambio de variables 2 / 12 Idea básica: en ocasiones, la utilización de variables apropiadas en lugar de
1 / 12 Lectura 2 Ampliación de Matemáticas. Grado en Ingeniería Civil Curso Académico 2011-2012 Cambio de variables 2 / 12 Idea básica: en ocasiones, la utilización de variables apropiadas en lugar de
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/2010. Solución al primer examen parcial. x - x 3 1
 UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
OCW-Universidad de Málaga, (2014). Bajo licencia. Creative Commons Attribution- NonComercial-ShareAlike 3.
 OCW-Universidad de Málaga, http://ocw.uma.es (014). Bajo licencia Creative Commons Attribution- NonComercial-ShareAlike 3.0 Spain Matemáticas III Relación de ejercicios Tema 1 Ejercicios Ej. 1 Encuentra
OCW-Universidad de Málaga, http://ocw.uma.es (014). Bajo licencia Creative Commons Attribution- NonComercial-ShareAlike 3.0 Spain Matemáticas III Relación de ejercicios Tema 1 Ejercicios Ej. 1 Encuentra
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2014 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Por el teorema de Green, si llamamos D al interior del cuadrado, entonces. dxdy. y. x P. 1 dx. 1 (4x 3 2y) dy =
 TEOREMA E GREEN. 1. Calcular y dx x dy, donde es la frontera del cuadrado [ 1, 1] [ 1, 1] orientada en sentido contrario al de las agujas del reloj. Por el teorema de Green, si llamamos al interior del
TEOREMA E GREEN. 1. Calcular y dx x dy, donde es la frontera del cuadrado [ 1, 1] [ 1, 1] orientada en sentido contrario al de las agujas del reloj. Por el teorema de Green, si llamamos al interior del
Coordenadas polares. Si P es un punto cualquiera del plano, su posición queda determinada con el par ( r, ), donde: Ejemplo
 Coordenadas polares Sobre el plano elijamos un punto O, que denominamos Polo (u origen) y un rayo con origen O, que denominamos Eje Polar 1 2 Si P es un punto cualquiera del plano, su posición queda determinada
Coordenadas polares Sobre el plano elijamos un punto O, que denominamos Polo (u origen) y un rayo con origen O, que denominamos Eje Polar 1 2 Si P es un punto cualquiera del plano, su posición queda determinada
MATE-1207 Cálculo Vectorial Taller 2 - Preparación Segundo Parcial P2. (a) Si f(x,y), g(x,y) son dos funciones continuas en D, entonces
 Universidad de los Andes epartamento de Matemáticas MATE-27 Cálculo Vectorial Taller 2 - Preparación Segundo Parcial P2. Conteste Falso o Verdadero. Justifique matemáticamente. (a) Si f(x,y), g(x,y) son
Universidad de los Andes epartamento de Matemáticas MATE-27 Cálculo Vectorial Taller 2 - Preparación Segundo Parcial P2. Conteste Falso o Verdadero. Justifique matemáticamente. (a) Si f(x,y), g(x,y) son
Tema 1. Números Complejos
 Tema 1. Números Complejos Prof. William La Cruz Bastidas 27 de septiembre de 2002 Capítulo 1 Números Complejos Definición 1.1 Un número complejo, z, es un número que se expresa como z = x + iy o, de manera
Tema 1. Números Complejos Prof. William La Cruz Bastidas 27 de septiembre de 2002 Capítulo 1 Números Complejos Definición 1.1 Un número complejo, z, es un número que se expresa como z = x + iy o, de manera
Integral definida. dx es diferencial de x, e indica cuál es la variable de la función que se integra.
 Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
+ ax 2 + bx) x. ( 2 sen(x) 0 (a + b sen(x) sen(2x))2 dx sea mínima.
 Facultad de Ingeniería - IMERL Cálculo - Curso. Práctico 8. Integrales paramétricas e integrales iteradas dobles y triples. Integrales múltiples. Cambio de variables, áreas, volúmenes, sumas de Riemann
Facultad de Ingeniería - IMERL Cálculo - Curso. Práctico 8. Integrales paramétricas e integrales iteradas dobles y triples. Integrales múltiples. Cambio de variables, áreas, volúmenes, sumas de Riemann
UNIDAD IX: APLICACIONES DE LAS INTEGRALES DEFINIDAS.
 UNIDAD IX: APLICACIONES DE LAS INTEGRALES DEFINIDAS. Área de un sector en coordenadas polares. Área de una superficie de revolución. Volumen de un sólido de revolución. Objetivos Instructivos. Con esta
UNIDAD IX: APLICACIONES DE LAS INTEGRALES DEFINIDAS. Área de un sector en coordenadas polares. Área de una superficie de revolución. Volumen de un sólido de revolución. Objetivos Instructivos. Con esta
PLAN DE EVALUACIÓN ACREDITACIÓN
 PLAN DE EVALUACIÓN ACREDITACIÓN ASIGNATURA: MATEMÁTICAS III SEDE: ESTATAL SEMESTRE: TERCERO BLOQUES: I y II PERIODO: 2016-2 CORTE: 1 DESEMPEÑO A DEMOSTRAR Uno o más desempeños pueden asociarse con una.
PLAN DE EVALUACIÓN ACREDITACIÓN ASIGNATURA: MATEMÁTICAS III SEDE: ESTATAL SEMESTRE: TERCERO BLOQUES: I y II PERIODO: 2016-2 CORTE: 1 DESEMPEÑO A DEMOSTRAR Uno o más desempeños pueden asociarse con una.
Examen de Matemáticas II (Modelo 2015) Selectividad-Opción A Tiempo: 90 minutos
 Eamen de Matemáticas II (Modelo 2015) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Dadas las matrices 2 4 2 2 0 A = 1 m m ; B = 0 X = y O = 0 1 2 1 1 z 0 (1 punto). Estudiar el rango
Eamen de Matemáticas II (Modelo 2015) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Dadas las matrices 2 4 2 2 0 A = 1 m m ; B = 0 X = y O = 0 1 2 1 1 z 0 (1 punto). Estudiar el rango
a) Analice la continuidad en (1,0). E1) Dada F : IR 2 π g : D IR 2 I R 2 2 2
 Ejemplos de parcial de Análisis Matemático II Los ítems E1, E, E3 E4 corresponden a la parte práctica Los ítems T1 T son teóricos (sólo para promoción) T1) Sea F : IR IR diferenciable tal que F(,) 00 =
Ejemplos de parcial de Análisis Matemático II Los ítems E1, E, E3 E4 corresponden a la parte práctica Los ítems T1 T son teóricos (sólo para promoción) T1) Sea F : IR IR diferenciable tal que F(,) 00 =
Ecuación Diferenciales Homogéneas de Primer Orden
 Ecuación Diferenciales Homogéneas de Primer Orden 1. Funciones Homogéneas de grado n Definicion: Diremos que una función f(, y) es homogénea de grado n si f(t, ty) = t n f(, y) si w = y f(, y) = n g(w)
Ecuación Diferenciales Homogéneas de Primer Orden 1. Funciones Homogéneas de grado n Definicion: Diremos que una función f(, y) es homogénea de grado n si f(t, ty) = t n f(, y) si w = y f(, y) = n g(w)
