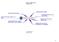
Figura 1: Esquema de las tablas simplex de inicio y general.

Tamaño: px

Comenzar la demostración a partir de la página:

Download "Figura 1: Esquema de las tablas simplex de inicio y general."

Ana Blanco Quiroga
hace 7 años
Vistas:

1 RELACIONES PRIMAL-DUAL Los cambios que se hacen en el modelo original de programación lineal afectan a los elementos de la tabla óptima actual el que se tenga en el momento, que a su vez puede afectar la optimalidad y/o la factibilidad de la solución actual. Por esta razón estudiaremos cómo se re-calculan los elementos de la tabla símplex óptima para reflejar los nuevos cambios. Planteamiento de la tabla símplex Figura 1: Esquema de las tablas simplex de inicio y general. La figura 1 es una representación esquemática de las tablas símplex de inicio y general. En la tabla de inicio, los coeficientes de las restricciones abajo de las variables de inicio forman una matriz identidad: todos los elementos de la diagonal principal iguales a 1 y fuera de la diagonal principal iguales a cero. Con este arreglo, las demás iteraciones de la tabla símplex, generadas con las operaciones de fila de Gauss-Jordan modificarán los elementos de la matriz identidad para producir la llamada matriz in- 1

2 versa. Como veremos en el resto de este capítulo, la matriz inversa es la clave del cálculo de todos los elementos de la tabla símplex asociada. Solución dual óptima Las soluciones primal y dual se relacionan en forma tan estrecha que la solución óptima del problema primal produce en forma directa con unos pocos de cálculos adicionales la solución óptima del dual. En esta sección se describen dos métodos para calcular este resultado. Método 1 Valores óptimos de las variables duales Vector fila de los coeficientes objetivos originales de las variables básicas óptimas primales Inversa primal óptima Los elementos del vector fila de los coeficientes objetivos del primal original deben aparecer en el mismo orden que aparecen las variables básicas en la columna Básica de la tabla símplex. Método 2 La solución dual óptima se puede determinar resolviendo las siguientes ecuaciones: Coeficiente z-primal óptimo de cualquier variables x j Lado izquierdo de la j-ésima restricción dual Lado derecho de la j-ésima restricción dual Observe con cuidado que, como el dual del problema dual es en sí mismo el problema primal compruébelo, los métodos presentados se pueden aplicar en forma simétrica para determinar la solución óptima del primal a partir de la del dual. Esto podría implicar ventajas de cómputo si la cantidad de variables en el primal fuera bastante menor que la cantidad de restricciones. Ya que la cantidad de cálculos símplex depende mucho de la cantidad de restricciones, en este caso es más eficiente resolver el dual, a partir del cual se pueda determinar entonces la solución del primal. Ejemplo Se tiene la siguiente programación lineal: 2

3 Maximizar z 5x x 2 + 4x 3 sujeta a x 1 + 2x 2 + x x 1 x 2 + 3x 3 8 x k 0, k. Para preparar el problema para su solución con método símplex se agrega una holgura x 4 en la primera restricción, y una R artificial en la segunda. Los problemas primal y dual asociado resultantes se definen así: Primal Primal en forma de ecuación Maximizar z 5x x 2 + 4x 3 MR Minimizar w 10y 1 + 8y 2 sujeta a sujeta a x 1 + 2x 2 + x 3 + x 4 10 y 1 + 2y 2 5 2x 1 x 2 + 3x 3 + R 8 2y 1 y 2 12 x 1, x 2, x 3, R 0 y 1 + 3y 2 4 y 1 0 y 2 M y 2 no restringida La tabla 1 muestra la tabla primal óptima. La matriz inversa óptima, que se señala bajo las variables de inicio x 4 y R es Inversa óptima Cuadro 1: Tabla óptima del primal, ejemplo Básica x 1 x 2 x 3 x 4 R Solución z 0 0 3/5 29/5 2/5 + M 274/5 x /5 12/5 x /5 26/5 Ahora indicaremos cómo se determinan los valores duales óptimos usando los dos métodos que se citaron al iniciar esta sección. Método 1. Primero se observa que las variables primales óptimas aparecen en la tabla en orden de la fila, primero x 2 y después x 1. Eso quiere decir que los elementos de 3

4 los coeficientes originales del objetivo para las dos variables deben aparecer en el mismo orden, que es: Coeficiente objetivo originales Coeficiente de x 2, Coeficiente de x 1 12, 5 Así, los valores duales óptimos se calculan como sigue: y 1, y 2 Coeficientes objetivo Inversa óptima originales x 2, x 1 12, 5 29/5, 2/5 Método 2. Como el problema dual tiene dos variables se necesitan dos ecuaciones para llegar a la solución. Tomaremos las restricciones duales asociadas con las variables primales de inicio, x 4 y R. Como se ve en la definición de dual, las restricciones duales asociadas con las variables primales de inicio son: Variable de inicio x 4 : y 1 0 Variable de inicio R : y 2 M También, de acuerdo con la tabla óptima tabla 1, Coeficiente z de x 4 29/5 Entonces, de acuerdo con el método 2, Coeficiente z de R 2/5 + M 29/5 y 1 0 y 1 29/5 2/5 + M y 2 M y 2 2/5 4

5 Nótese que en cada ecuación interviene exactamente una variable, y por tanto la solución dual está disponible de inmediato. Éste es siempre el caso de las restricciones duales asociadas con las variables de inicio. En realidad, las restricciones duales asociadas con dos variables primales cualesquiera se podrían usar exactamente igual, para obtener la solución dual. Por ejemplo, en la tabla óptima, las variables primales x 1, y x 3 producirán las siguientes ecuaciones respectivas verifíquelo!: y 1 + 2y y 1 + 3y 2 4 3/5 La solución de estas dos ecuaciones produce los mismos valores duales óptimos, y 1 29/5 y y 2 2/5. Sin embargo, obsérvese que las ecuaciones que se obtienen no son tan sencillas como las asociadas con x 4 y R convénzase usted mismo: dos variables cualesquiera de x 1, x 2, x 3, x 4 y R producirán la misma solución. Cálculos con la tabla símplex En esta sección se indica cómo se puede generar toda la tabla símplex en cualquier iteración, a partir de los datos originales del problema y la inversa asociada con la iteración. Usando la distribución de la tabla símplex previamente expuesta, se puede dividir los cálculos en dos tipos: 1. Columnas de restricción lados izquierdo y derecho. 2. fila objetivo z. Cálculos de columnas de restricción. En cualquier iteración símplex, una columna del lado izquierdo o derecho se calcula como sigue: Columna de restricción en la iteración i Inversa en la iteración i Columna original de restricción Fómula 1 Cálculos de fila objetivo z. En cualquier iteración símplex, el coeficiente de x j en la función objetivo se calcula como sigue: 5

6 Coeficiente de la variable x j en la ecuación primal de z Lado izquierdo de la restricción dual correspondiente Lado derecho de la restricción dual correspondiente Nótese que la fórmula 2 es igual a la que se usó en el método 2, que acabamos de ver, para determinar la solución dual óptima. Ejemplo Se usará la programación lineal del ejemplo para ilustrar la aplicación de las fórmulas 1 y 2. De acuerdo con la tabla óptima de la tabla 1, Fómula 2 Inversa óptima El uso de la fórmula 1 se ilustra calculando todas las columnas de lado izquierdo y lado derecho de la tabla óptima: Columna de x1 Inversa en la Columna de iteración óptima x 1 original De manera parecida se calculan las siguientes columnas de restricción: Columna de x2 2 1 Columna de x /5 3 7/5 6

7 Columna de x4 Columna de R Columna de lado derecho en la iteración óptima 1 2/5 0 1/5 0 1/5 1 2/5 x2 x /5 26/5 A continuación se demostrará cómo se hacen los cálculos de la fila objetivo, con la fórmu la 2. Los valores óptimos de las variables duales y 1, y 2 29/5, 2/5, se calcularon en el ejemplo 4.2-1, con dos métodos distintos. Estos valores se usan en la fórmula 2 para determinar los coeficientes asociados de z como sigue: Coeficiente x 1 en z y 1 + 2y / /5 5 0 Coeficiente x 2 en z 2y 1 y /5 2/ Coeficiente x 3 en z y 1 + 3y / /5 4 3/5 Coeficiente x 4 en z y /5 0 29/5 Coeficiente R en z y 2 M 2/5 M 2/5 + M Es importante observar que los cálculos con las fórmulas 1 y 2 se pueden aplicar en cualquier iteración, sea de los problemas primales o duales. Todo lo que se necesita es la inversa asociada con la iteración primal o dual, y los datos de la programación lineal original. Valor objetivo primal y dual En los problemas primal-dual, si uno es de maximización el otro debe ser de minimización. Desde este punto de vista, los valores objetivo en los dos problemas se relacionan de la siguiente manera: Para cualquier par de soluciones primales y duales factibles, Valor objetivo en el problema de Maximización Valor objetivo en el problema de Minimización 7

8 En el óptimo, la relación es válida estrictamente como ecuación. Obsérvese que la relación no especifica cuál problema es primal y cuál es dual. En este caso sólo importa el sentido de la optimización maximización o minimización. Ejemplo En el ejemplo 4.2-1, x 1 0, x 2 0, x 3 8/3 y y 1 6, y 2 0 son soluciones factibles primal y dual. Los valores asociados de las funciones objetivo son z y w 60. También, la solución óptima de los dos problemas, que es x 1 26/5, x 2 12/5, x 3 0 y y 1 29/5, y 2 2/5 producen z w 54,8. Ambos cálculos demuestran la relación mencionada. La relación indica que para todas las soluciones primales y duales factibles, el valor objetivo en el problema de minimización establece siempre una cota superior del valor objetivo en el problema de maximización. Dado que las iteraciones sucesivas del problema de maximización obtienen valores crecientes de z, y las del problema de minimización obtienen valores decrecientes de w, al final, en el curso de las iteraciones, se llegará a un punto de equilibrio donde los valores objetivo de maximización y de minimización deben ser iguales; esto es, z w. 8

Documentos relacionados

Dualidad 1. 1 Formas simétricas. 2 Relación primal-dual. 3 Dualidad: el caso general. 4 Teoremas de dualidad. 5 Condiciones de holgura complementaria.

Dualidad 1. 1 Formas simétricas. 2 Relación primal-dual. 3 Dualidad: el caso general. 4 Teoremas de dualidad. 5 Condiciones de holgura complementaria. Dualidad 1 1 Formas simétricas. 2 Relación primal-dual. 3 Dualidad: el caso general. 4 Teoremas de dualidad. Condiciones de holgura complementaria. 6 Solución dual óptima en la tabla. 7 Interpretación