SLUD Resolver problemas con Máxima In memoriam William Schelter
|
|
|
- Margarita Cortés Castellanos
- hace 8 años
- Vistas:
Transcripción
1 SLUD 2006 Resolver problemas con Máxima In memoriam William Schelter Robert Dodier Proyecto Máxima Libero este documento por el GNU General Public License version 2
2 Características generales de Máxima Toda cosa es una expresión (casi todas) Máxima = colección de funciones para trasformar expresiones Soluciones perezosas y la actitud laissez faire Distinguir entre evaluación y simplificación
3 Máxima como calculador perezoso (%i1) F : m * a; (%o1) a m (%i2) a : 9.81; (%o2) 9.81 (%i3) F; (%o3) a m (%i4) F; (%o4) 9.81 m (%i5) S : sum (g(i, x), i, 0, 6); (%o5) g(6, x) + g(5, x) + g(4, x) + g(3, x) + g(2, x) + g(1, x) + g(0, x) (%i6) g(i, x) := x^i / i!; i x (%o6) g(i, x) := -- i!
4 (%i7) S; x x x x x (%o7) x (%i8) x : 1; (%o8) 1 (%i9) S; 1957 (%o9) (%i10) %, numer; (%o10) (%i11) %e, numer; (%o11)
5 Definición de funciones (%i1) F (m, a) := m * a; (%o1) F(m, a) := m a (%i2) F (100, 9.81); (%o2) (%i3) F (100, g); (%o3) 100 g (%i4) apply (F, [100, g]); (%o4) 100 g (%i5) L1 : [100, 200, 300]; (%o5) [100, 200, 300] (%i6) L2 : [a, b, c]; (%o6) [a, b, c] (%i7) map (F, L1, L2); (%o7) [100 a, 200 b, 300 c]
6 Función sin nombre: lambda Máxima reconoce a funciones sin nombre en algunos contextos en los que se espere una función (%i1) L1 : [100, 200, 300]; (%o1) [100, 200, 300] (%i2) L2 : [a, b, c]; (%o2) [a, b, c] (%i3) map (lambda ([m, a], m * a), L1, L2); (%o3) [100 a, 200 b, 300 c] (%i4) apply (lambda ([m, a], m * a), [1234, x + u]); (%o4) 1234 (x + u)
7 Gráficos Máxima puede hacer gráficos de 2 o 3 dimensiones plot2d(expr, [x, a, b]) hacer un gráfico de expr de variable x entre limites a y b plot2d([discrete, x, y]) hacer un gráfico de datos discretos, en las listas x y y plot3d gráficos de 3 dimensiones Se puede eligir entre formatos Gnuplot o Openmath (Tcl/Tk) Para hacer gráficos, hay varias opciones arcanas. Se refiere a la documentación.
8 Ejemplo de gráfico 2-dimensional plot2d ([gamma(x), 1/gamma(x)], [x, -4.5, 5], [y, -10, 10]); gamma(x) 1/gamma(x)
9 Ejemplo de gráfico 3-dimensional plot3d ([cos(x)*(3 + y*cos(x/2)), sin(x)*(3 + y*cos(x/2)), y*sin(x/2)], [x, -%pi, %pi], [y, -1, 1], [ grid, 50, 15]); Function
10 Números Números enteros. Precisión no fija. Computación rapida con funciones especializadas GMP (%i1) 2^100; (%o1) (%i2) 100!; (%o2) \ \ (%i3) is (100! > 2^100); (%o3) true (%i4) primep (2^ ); (%o4) false (%i5) ifactors (2^ ); (%o5) [[17, 1], [401, 1], [61681, 1], [340801, 1], [ , 1], [ , 1]]
11 Números racionales. Raciones de números enteros (%i1) 1/4-1/5; 1 (%o1) (%i2) 2^100 / 100!; (%o2) 8/ \ \ (%i3) 17 * 2^100 / 100! - 29 * 2^101 / 101!; (%o3) 8/ \ \
12 Números de coma flotante y precisión fija (IEEE 754). Máxima usa solamente la precisión doble (64 bits) (%i1) /5; (%o1) (%i2) float (1/4-1/5); (%o2) 0.05 (%i3) sin (1); (%o3) sin(1) (%i4) sin (1.0); (%o4) Números de coma flotante y precisión no fija ( bigfloat ) (%i1) fpprec : 50; (%o1) 50 (%i2) fpprintprec : 50; (%o2) 50 (%i3) bfloat (%pi); (%o3) b0 (%i4) sin (1b0); (%o4) b-1
13 Números complejos. Máxima no reconoce como tipo distinto, sino como expresión de forma a + b i (%i1) c : a + b * %i; (%o1) %i b + a (%i2) realpart (c); (%o2) a (%i3) imagpart (c); (%o3) b (%i4) exp (c); %i b + a (%o4) %e (%i5) demoivre (exp (c)); a (%o5) %e (%i sin(b) + cos(b))
14 Polinomios (%i1) P : (x - 1) * (x - 2) * (x + 3); (%o1) (x - 2) (x - 1) (x + 3) (%i2) Q : expand (P); 3 (%o2) x - 7 x + 6 (%i3) factor (Q); (%o3) (x - 2) (x - 1) (x + 3) (%i4) solve (Q = 0, x); (%o4) [x = 1, x = 2, x = - 3] (%i5) subst (first (%), Q); (%o5) 0
15 (%i6) solve (Q = 1, x); - 3/2 sqrt(3) %i 1 3 sqrt(697) %i 5 1/3 (%o6) [x = ( ) ( ) sqrt(3) %i 1 7 ( ) , x = - 3/2 3 sqrt(697) %i 5 1/3 3 ( ) 2 2-3/2 sqrt(3) %i 1 3 sqrt(697) %i 5 1/3 ( ) ( ) sqrt(3) %i 1 7 ( ) 2 2
16 , x = - 3/2 3 sqrt(697) %i 5 1/3 3 ( ) 2 2-3/2 3 sqrt(697) %i 5 1/3 7 ( ) ] 2 2-3/2 3 sqrt(697) %i 5 1/3 3 ( ) 2 2 (%i7) allroots (Q - 1); (%o7) [x = , x = , x = ]
17 Funciones matemáticas Máxima tiene una gran collección de funciones básicas. Se muestran algunos debajo. También tiene paquetes de polinómios ortogonales y funciones hipergeometricas y muchas otras funciones. (%i1) sin (u); (%o1) sin(u) (%i2) sin (%pi * u - v / w); v (%o2) - sin(- - %pi u) w (%i3) sin (0); (%o3) 0 (%i4) sin (%pi); (%o4) 0 (%i5) sin (1); (%o5) sin(1)
18 (%i6) sin (1/2); 1 (%o6) sin(-) 2 (%i7) sin (0.5); (%o7) (%i8) sin (1) + cos (1); (%o8) sin(1) + cos(1) (%i9) %, numer; (%o9) Unos ejemplos de gráficos que se pueden hacer. plot2d ([sin, cos, tan], [x, -0.5, 7], [y, -3, 3]); plot2d ([sinh, cosh, tanh], [x, -2, 2], [y, -10, 10]); plot2d ([bessel_j (0, x), bessel_j (1, x)], [x, -0.5, 10], [y, -3, 3]);
19 map, apply Listas, conjuntos, y matrices (%i1) L : [1, 1, 2, 2, a, a, b, b]; (%o1) [1, 1, 2, 2, a, a, b, b] (%i2) length (L); (%o2) 8 (%i3) first (L); (%o3) 1 (%i4) last (L); (%o4) b (%i5) [length (L), first (L), last (L)]; (%o5) [8, 1, b] (%i6) makelist (sin (i), i, 1, 5); (%o6) [sin(1), sin(2), sin(3), sin(4), sin(5)]
20 (%i1) L : [a, b, x, 0, 1, 2]; (%o1) [a, b, x, 0, 1, 2] (%i2) map (F, L); (%o2) [F(a), F(b), F(x), F(0), F(1), F(2)] (%i3) map (sin, L); (%o3) [sin(a), sin(b), sin(x), 0, sin(1), sin(2)] (%i4) map (lambda ([e], e + 1), L); (%o4) [a + 1, b + 1, x + 1, 1, 2, 3] (%i5) apply (concat, L); (%o5) abx012 (%i6) apply (max, L); (%o6) max(x, b, a, 2)
21 (%i1) C : {1, 1, 2, 2, a, a, b, b}; (%o1) {1, 2, a, b} (%i2) cardinality (C); (%o2) 4 (%i3) subsetp ({1, 2, a}, C); (%o3) true (%i4) powerset (C); (%o4) {{}, {1}, {1, 2}, {1, 2, a}, {1, 2, a, b}, {1, 2, b}, {1, a}, {1, a, b}, {1, b}, {2}, {2, a}, {2, a, b}, {2, b}, {a}, {a, b}, {b}} (%i5) permutations (C); (%o5) {[1, 2, a, b], [1, 2, b, a], [1, a, 2, b], [1, a, b, 2], [1, b, 2, a], [1, b, a, 2], [2, 1, a, b], [2, 1, b, a], [2, a, 1, b], [2, a, b, 1], [2, b, 1, a], [2, b, a, 1], [a, 1, 2, b], [a, 1, b, 2], [a, 2, 1, b], [a, 2, b, 1], [a, b, 1, 2], [a, b, 2, 1], [b, 1, 2, a], [b, 1, a, 2], [b, 2, 1, a], [b, 2, a, 1], [b, a, 1, 2], [b, a, 2, 1]}
22 (%i1) M : matrix ([3, -1/5], [-1/5, %pi]); [ 1 ] [ ] [ 5 ] (%o1) [ ] [ 1 ] [ - - %pi ] [ 5 ] (%i2) transpose (M); [ 1 ] [ ] [ 5 ] (%o2) [ ] [ 1 ] [ - - %pi ] [ 5 ] (%i3) N : transpose (M). M; [ 226 %pi 3 ] [ ] [ ]
23 (%o3) [ ] [ %pi ] [ %pi + -- ] [ ] (%i4) invert (N); [ 2 1 ] [ %pi + -- ] [ 25 ] [ ] [ 2 1 ] [ 226 (%pi + --) ] [ 25 %pi 3 %pi 3 ] [ ( ) ( ) ] [ ] (%o4) Col 1 = [ ] [ %pi 3 ] [ ] [ 5 5 ] [ ] [ 2 1 ]
24 [ 226 (%pi + --) ] [ 25 %pi 3 %pi 3 ] [ ( ) ( ) ] [ ] [ %pi 3 ] [ ] [ 5 5 ] [ ] [ 2 1 ] [ 226 (%pi + --) ] [ 25 %pi 3 %pi 3 ] [ ( ) ( ) ] Col 2 = [ ] [ ] [ 226 ] [ ] [ 2 1 ] [ 226 (%pi + --) ] [ 25 %pi 3 %pi 3 ] [ 25 ( ( ) ( )) ]
25 [ ] (%i5) ratsimp (N); [ 226 %pi + 3 ] [ ] [ 25 5 ] (%o5) [ ] [ 2 ] [ %pi %pi + 1 ] [ ] [ 5 25 ] (%i6) vcm : eigenvalues (M); 2 sqrt(25 %pi %pi + 229) - 5 %pi - 15 (%o6) [[ , 10 2 sqrt(25 %pi %pi + 229) + 5 %pi ], [1, 1]] 10 (%i7) vcn : eigenvalues (N);
26 (%o7) 2 2 (5 %pi + 15) sqrt(25 %pi %pi + 229) - 25 %pi [[ , (5 %pi + 15) sqrt(25 %pi %pi + 229) + 25 %pi ], 50 [1, 1]] (%i8) vcm, numer; (%o8) [[ , ], [1, 1]] (%i9) vcm^2, numer; (%o9) [[ , ], [1, 1]] (%i10) vcn, numer; (%o10) [[ , ], [1, 1]]
27 Integrales símbolicos Máxima tiene una implementación del algoritmo Risch y otros para integrales símbolicos (%i1) I : exp(x) * sin(2 * x) * cos(3 * x); x (%o1) %e sin(2 x) cos(3 x) (%i2) integrate (I, x); x x %e (sin(5 x) - 5 cos(5 x)) %e (sin(x) - cos(x)) (%o2) (%i3) integrate (I, x, 0, 1); %e sin(5) 5 %e cos(5) %e sin(1) %e cos(1) 2 (%o3)
28 Integrales númericos También podemos realizar aproximaciones numéricas por funciones de QUADPACK (originalmente de Fortran) (%i1) I : exp(x) * sin(2 * x) * cos(3 * x); x (%o1) %e sin(2 x) cos(3 x) (%i2) quad_qags (I, x, 0, 1); (%o2) [ , E-15, 21, 0] (%i3) (integrate (I, x, 0, 1)), numer; (%o3)
29 Ecuaciones diferenciales ode2 para resolver una ecuación diferencial ic1 y ic2 para problemas de valores inicial bc2 para problemas de valores de frontera
30 (%i1) x^2 * diff(y, x) + 3 * y * x = sin(x)/x; 2 dy sin(x) (%o1) x x y = dx x (%i2) ode2 (%, y, x); %c - cos(x) (%o2) y = x (%i3) ic1 (%, x = %pi, y = 0); cos(x) + 1 (%o3) y = x
31 (%i1) diff(y, x, 2) + y * diff(y, x)^3 = 0; 2 d y dy 3 (%o1) y (--) = 0 2 dx dx (%i2) soln : ode2 (%, y, x); 3 y + 6 %k1 y (%o2) = x + %k2 6
32 (%i1) diff(y, x, 2) + y * diff(y, x)^3 = 0; 2 d y dy 3 (%o1) y (--) = 0 2 dx dx (%i2) soln : ode2 (%, y, x); 3 y + 6 %k1 y (%o2) = x + %k2 6 (%i3) ratsimp (ic2 (soln, x = 0, y = 0, diff(y, x) = 2)); 3 2 y - 3 y (%o3) = x 6
33 (%i4) bc2 (soln, x = 0, y = 1, x = 1, y = 3); 3 y - 10 y 3 (%o4) = x
34 Álgebra lineal Por lo largo de la historia de Máxima, habían sido varios paquetes de funciones de álgebra lineal Lo más reciente se llama linearalgebra, que tiene funciones de LU descomposición, computación del espacio nulo y su complemento, y otros (%i1) M : matrix ([a, 1], [2, b]); [ a 1 ] (%o1) [ ] [ 2 b ] (%i2) load (linearalgebra); (%o2) /usr/share/maxima/5.10.0/share/linearalgebra/linearalgebra.mac
35 (%i3) LU : lu_factor (M); [ a 1 ] [ ] (%o3) [[ 2 2 ], [1, 2], generalring] [ - b - - ] [ a a ] (%i4) get_lu_factors (LU); [ 1 0 ] [ a 1 ] [ 1 0 ] [ ] [ ] (%o4) [[ ], [ 2 ], [ 2 ]] [ 0 1 ] [ - 1 ] [ 0 b - - ] [ a ] [ a ] (%i5) lu_backsub (LU, matrix ([3], [4])); [ 6 ] [ ] [ a ] [ ] [ 2 ] [ b - - ] [ a ]
36 [ ] (%o5) [ a ] [ ] [ 6 ] [ ] [ a ] [ ] [ 2 ] [ b - - ] [ a ] (%i6) ratsimp (%); [ 3 b - 4 ] [ ] [ a b - 2 ] (%o6) [ ] [ 4 a - 6 ] [ ] [ a b - 2 ]
37 (%i2) M2 : matrix ([x, - 1/2], [1/3, y]); [ 1 ] [ x - - ] [ 2 ] (%o2) [ ] [ 1 ] [ - y ] [ 3 ] (%i3) nullspace (M2); 1 Proviso: {x # 0, y # 0} 6 x (%o3) span()
38 (%i4) M3 : matrix ([x, - 1/2], [- 2 * x, 1]); [ 1 ] [ x - - ] (%o4) [ 2 ] [ ] [ - 2 x 1 ] (%i5) nullspace (M3); Proviso: {x # 0} [ 1 ] (%o5) span([ ]) [ 2 x ] (%i6) columnspace (M3); Proviso: {x # 0} [ x ] (%o6) span([ ]) [ - 2 x ]
39 Estadística y tratamiento de datos Para funciones de probabilidad y estadística, paquetes adicionales distrib y descriptive (%i1) load (descriptive); (%o1) /usr/share/maxima/5.10.0/share/contrib/descriptive/descriptive.mac (%i2) X : [1.1, 2.2, 3.3, 4.4, 5.5, 6.6, 7.7]; (%o2) [1.1, 2.2, 3.3, 4.4, 5.5, 6.6, 7.7] (%i3) mean (X); (%o3) 4.4 (%i4) std (X); (%o4) 2.2 (%i5) load (distrib); (%o5) /usr/share/maxima/5.10.0/share/contrib/distrib/distrib.mac (%i6) quantile_normal (0.95, mean(x), std(x)); (%o6)
40 Gráficas estadísticas. Ejemplo: histograma de ejemplares de una distribución normal (%i1) load (descriptive); (%o1) /usr/share/maxima/5.10.0/share/contrib/descriptive/descriptive.mac (%i2) load (distrib); (%o2) /usr/share/maxima/5.10.0/share/contrib/distrib/distrib.mac (%i3) X : random_normal (10, 1, 100)$ (%i4) histogram (X, nclasses = 12); (%o4) 0
41 Fr x
42 A continuación. Un diagrama de dispersión de ejemplares de una distribución normal bidimensional (%i5) Y : random_normal (10, 1, 100)$ (%i6) S : matrix ([5, - 1], [- 1, 7]); [ 5-1 ] (%o6) [ ] [ ] (%i7) load (cholesky); Warning - you are redefining the Maxima function cholesky (%o7) /usr/share/maxima/5.10.0/share/contrib/cholesky.mac (%i8) L : cholesky (S), numer; [ ] (%o8) [ ] [ ] (%i9) XY : transpose (matrix (X, Y))$ (%i10) dataplot (XY. transpose (L)); (%o10) 0
43 y x
44 Derivación del estimador de probabilidad máxima (%i1) pdf[i] := exp (- (1/2) * (x[i] - mu)^2 / sigma2) / sqrt(sigma2) / sqrt(2 * %pi); 1 2 (- -) (x - mu) 2 i exp( ) sigma sqrt(sigma2) (%o1) pdf := i sqrt(2 %pi) (%i2) logexpand : all; (%o2) all (%i3) declare (sum, linear); (%o3) done
45 (%i4) FPL : sum (log (pdf[i]), i, 1, n); n ==== \ 2 > (x - mu) / i ==== n log(sigma2) i = 1 log(%pi) n log(2) n (%o4) sigma2 2 2 (%i5) dmu : diff (FPL, mu); n ==== \ > x - mu n / i ==== i = 1 (%o5) sigma2
46 (%i6) dsigma2 : diff (FPL, sigma2); n ==== \ 2 > (x - mu) / i ==== i = 1 n (%o6) sigma2 2 sigma2
47 (%i7) solve (dmu = 0, mu); n ==== \ > x / i ==== i = 1 (%o7) [mu = ] n (%i8) solve (dsigma2 = 0, sigma2); n ==== \ 2 > (x - mu) / i ==== i = 1 (%o8) [sigma2 = ] n
Introducción al Cálculo Simbólico a través de Maple
 1 inn-edu.com ricardo.villafana@gmail.com Introducción al Cálculo Simbólico a través de Maple A manera de introducción, podemos decir que los lenguajes computacionales de cálculo simbólico son aquellos
1 inn-edu.com ricardo.villafana@gmail.com Introducción al Cálculo Simbólico a través de Maple A manera de introducción, podemos decir que los lenguajes computacionales de cálculo simbólico son aquellos
Prácticas de Mecánica Computacional. Introducción a Maxima y TEX MACS
 Prácticas de Mecánica Computacional. Introducción a Maxima y TEX MACS 1 Introducción por Felipe Gabaldón Correo-e: felipe.gabaldon@upm.es 6 January 010 El objetivo de este documento es proporcionar una
Prácticas de Mecánica Computacional. Introducción a Maxima y TEX MACS 1 Introducción por Felipe Gabaldón Correo-e: felipe.gabaldon@upm.es 6 January 010 El objetivo de este documento es proporcionar una
RELACIONES DE RECURRENCIA
 Unidad 3 RELACIONES DE RECURRENCIA 60 Capítulo 5 RECURSIÓN Objetivo general Conocer en forma introductoria los conceptos propios de la recurrencia en relación con matemática discreta. Objetivos específicos
Unidad 3 RELACIONES DE RECURRENCIA 60 Capítulo 5 RECURSIÓN Objetivo general Conocer en forma introductoria los conceptos propios de la recurrencia en relación con matemática discreta. Objetivos específicos
Números aleatorios. Contenidos
 Números aleatorios. Contenidos 1. Descripción estadística de datos. 2. Generación de números aleatorios Números aleatorios con distribución uniforme. Números aleatorios con otras distribuciones. Método
Números aleatorios. Contenidos 1. Descripción estadística de datos. 2. Generación de números aleatorios Números aleatorios con distribución uniforme. Números aleatorios con otras distribuciones. Método
Álgebra Lineal. Sesión de Prácticas 6: Ortogonalidad. Método de Gram-Schmidt. Complemento ortogonal y mejor aproximación
 Álgebra Lineal Sesión de Prácticas 6: Ortogonalidad. Método de Gram-Schmidt. Complemento ortogonal y mejor aproximación Primero Grado Ingeniería Informática Departamento de Matemática Aplicada Facultad
Álgebra Lineal Sesión de Prácticas 6: Ortogonalidad. Método de Gram-Schmidt. Complemento ortogonal y mejor aproximación Primero Grado Ingeniería Informática Departamento de Matemática Aplicada Facultad
De aquí sale el proyecto MACsyma (MAC s SYmbolic MAnipulator)
 El proyecto Matemáticas y Computación (MAC) se inicia en la década de los años 60 en el MIT (con el apoyo financiero de los Departamentos de Defensa y Energía de los EE.UU.) para atender sus necesidades
El proyecto Matemáticas y Computación (MAC) se inicia en la década de los años 60 en el MIT (con el apoyo financiero de los Departamentos de Defensa y Energía de los EE.UU.) para atender sus necesidades
Complemento Microsoft Mathematics
 Complemento Microsoft Mathematics El complemento Microsoft Mathematics es un conjunto de herramientas que se pueden usar para realizar operaciones matemáticas y trazado de gráficas con expresiones o ecuaciones
Complemento Microsoft Mathematics El complemento Microsoft Mathematics es un conjunto de herramientas que se pueden usar para realizar operaciones matemáticas y trazado de gráficas con expresiones o ecuaciones
Cursada Primer Semestre 2015 Guía de Trabajos Prácticos Nro. 2
 Temas: Programación en MATLAB: Sentencias, expresiones y variables. Estructuras de control. Operadores relacionales y lógicos. Programación de funciones. Aritmética finita: Representación de números en
Temas: Programación en MATLAB: Sentencias, expresiones y variables. Estructuras de control. Operadores relacionales y lógicos. Programación de funciones. Aritmética finita: Representación de números en
Introducción al sistema Wolfram Mathematica
 Introducción al sistema Wolfram Mathematica Expresiones Usamos la interfaz gráfica ( Notebook ) de Wolfram Mathematica. Para calcular una expresión en Notebook, hay que oprimir Shift-Enter (Mayús-Intro).
Introducción al sistema Wolfram Mathematica Expresiones Usamos la interfaz gráfica ( Notebook ) de Wolfram Mathematica. Para calcular una expresión en Notebook, hay que oprimir Shift-Enter (Mayús-Intro).
Manual básico de Maxima
 Asignatura: Cálculo Grado de Ingeniería. Departamento de Matemática Aplicada I 2 Índice general 1. Cómo utilizo este Manual?................... 4 2. Preguntas básicas sobre Maxima................. 4 2.1.
Asignatura: Cálculo Grado de Ingeniería. Departamento de Matemática Aplicada I 2 Índice general 1. Cómo utilizo este Manual?................... 4 2. Preguntas básicas sobre Maxima................. 4 2.1.
INTRODUCCIÓN A Maxima
 INTRODUCCIÓN A Maxima Ing. Matías De la Puente 1. Introducción El sistema de álgebra computacional Maxima 1 es un motor de cálculo simbólico escrito en lenguaje Lisp publicado bajo
INTRODUCCIÓN A Maxima Ing. Matías De la Puente 1. Introducción El sistema de álgebra computacional Maxima 1 es un motor de cálculo simbólico escrito en lenguaje Lisp publicado bajo
Semana 3 [1/28] Derivadas. 2 de agosto de Derivadas
![Semana 3 [1/28] Derivadas. 2 de agosto de Derivadas Semana 3 [1/28] Derivadas. 2 de agosto de Derivadas](/thumbs/88/116142499.jpg) Semana 3 [1/28] 2 de agosto de 2007 Funciones derivables Semana 3 [2/28] Derivabilidad en un punto Función derivable en un punto Diremos que f : (a, b) Ê es derivable en el punto x (a, b), si existe el
Semana 3 [1/28] 2 de agosto de 2007 Funciones derivables Semana 3 [2/28] Derivabilidad en un punto Función derivable en un punto Diremos que f : (a, b) Ê es derivable en el punto x (a, b), si existe el
Medidas de tendencia central o de posición: situación de los valores alrededor
 Tema 10: Medidas de posición y dispersión Una vez agrupados los datos en distribuciones de frecuencias, se calculan unos valores que sintetizan la información. Estudiaremos dos grandes secciones: Medidas
Tema 10: Medidas de posición y dispersión Una vez agrupados los datos en distribuciones de frecuencias, se calculan unos valores que sintetizan la información. Estudiaremos dos grandes secciones: Medidas
PENDIENTES DE MATEMÁTICAS DE 2º ESO (CURSO 2014-2015)
 PENDIENTES DE MATEMÁTICAS DE 2º ESO (CURSO 2014-2015) CRITERIOS E INDICADORES Se detallan a continuación los criterios de evaluación junto con sus indicadores de contenidos asociados. En negrita se indican
PENDIENTES DE MATEMÁTICAS DE 2º ESO (CURSO 2014-2015) CRITERIOS E INDICADORES Se detallan a continuación los criterios de evaluación junto con sus indicadores de contenidos asociados. En negrita se indican
I.E.S.MEDITERRÁNEO CURSO 2015 2016 DPTO DE MATEMÁTICAS PROGRAMA DE RECUPERACIÓN DE LOS APRENDIZAJES NO ADQUIRIDOS EN MATEMÁTICAS DE 3º DE E.S.O.
 PROGRAMA DE RECUPERACIÓN DE LOS APRENDIZAJES NO ADQUIRIDOS EN MATEMÁTICAS DE 3º DE E.S.O. Este programa está destinado a los alumnos que han promocionado a cursos superiores sin haber superado esta materia.
PROGRAMA DE RECUPERACIÓN DE LOS APRENDIZAJES NO ADQUIRIDOS EN MATEMÁTICAS DE 3º DE E.S.O. Este programa está destinado a los alumnos que han promocionado a cursos superiores sin haber superado esta materia.
Introducción. Maxima se puede obtener de la página web: http://maxima.sourceforge.net/es/
 Introducción Maxima es un programa de cálculo simbólico que realiza cálculos matemáticos tanto en forma numérica como simbólica, a este tipo de programa se les llama CAS o SAC. Este programa y sus manuales
Introducción Maxima es un programa de cálculo simbólico que realiza cálculos matemáticos tanto en forma numérica como simbólica, a este tipo de programa se les llama CAS o SAC. Este programa y sus manuales
Preliminares. Tipos de variables y Expresiones
 Preliminares. Tipos de variables y Expresiones Felipe Osorio Instituto de Estadística Pontificia Universidad Católica de Valparaíso Marzo 5, 2015 1 / 20 Preliminares Computadoras desarrollan tareas a un
Preliminares. Tipos de variables y Expresiones Felipe Osorio Instituto de Estadística Pontificia Universidad Católica de Valparaíso Marzo 5, 2015 1 / 20 Preliminares Computadoras desarrollan tareas a un
Nano Taller de Python
 Charla 5: Programación Funcional Royal Institute of Technology (KTH), Estocolmo, Suecia Grupo de Nanomateriales (GNM), Santiago, Chile 13 de enero 2009, de 13:00 a 14:00 Parte I Programación
Charla 5: Programación Funcional Royal Institute of Technology (KTH), Estocolmo, Suecia Grupo de Nanomateriales (GNM), Santiago, Chile 13 de enero 2009, de 13:00 a 14:00 Parte I Programación
Cálculo científico y técnico con HP49g/49g+/48gII/50g Módulo 3: Aplicaciones Tema 3.7 Polinomio interpolador
 Cálculo científico y técnico con HP49g/49g+/48gII/50g Módulo 3: Aplicaciones Tema 3.7 Polinomio interpolador Francisco Palacios Escuela Politécnica Superior de Ingeniería Manresa Universidad Politécnica
Cálculo científico y técnico con HP49g/49g+/48gII/50g Módulo 3: Aplicaciones Tema 3.7 Polinomio interpolador Francisco Palacios Escuela Politécnica Superior de Ingeniería Manresa Universidad Politécnica
Supervisado por: Alfonsa García, Francisco García, Rafael Miñano y Blanca Ruiz
 2011 Departamento de Matemática Aplicada EU Informática 1 [MINI MANUAL WXMAXIMA] Elaborado por: Rubén Haro Sanz Supervisado por: Alfonsa García, Francisco García, Rafael Miñano y Blanca Ruiz Trabajo parcialmente
2011 Departamento de Matemática Aplicada EU Informática 1 [MINI MANUAL WXMAXIMA] Elaborado por: Rubén Haro Sanz Supervisado por: Alfonsa García, Francisco García, Rafael Miñano y Blanca Ruiz Trabajo parcialmente
>> 10.5 + 3.1 % suma de dos números reales, el resultado se asigna a ans
 Universidad de Concepción Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Matemática Cálculo Numérico (521230) Laboratorio 1: Introducción al Matlab Matlab es una abreviatura para
Universidad de Concepción Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Matemática Cálculo Numérico (521230) Laboratorio 1: Introducción al Matlab Matlab es una abreviatura para
3.1. Trabajando con distintos tipos de números
 3 Capítulo Aritmética 3.1. Trabajando con distintos tipos de números 3.1.1. Números enteros Maxima (y wxmaxima) pueden trabajar con números enteros con cualquier número de dígitos. Pero por defecto, cuando
3 Capítulo Aritmética 3.1. Trabajando con distintos tipos de números 3.1.1. Números enteros Maxima (y wxmaxima) pueden trabajar con números enteros con cualquier número de dígitos. Pero por defecto, cuando
Ejercicios. 1. Definir en Maxima las siguientes funciones y evaluarlas en los puntos que se indican:
 Ejercicios. 1. Definir en Maxima las siguientes funciones y evaluarlas en los puntos que se indican: 2. Graficar las funciones anteriores, definiendo adecuadamente los rangos de x e y, para visualizar
Ejercicios. 1. Definir en Maxima las siguientes funciones y evaluarlas en los puntos que se indican: 2. Graficar las funciones anteriores, definiendo adecuadamente los rangos de x e y, para visualizar
VII. Estructuras Algebraicas
 VII. Estructuras Algebraicas Objetivo Se analizarán las operaciones binarias y sus propiedades dentro de una estructura algebraica. Definición de operación binaria Operaciones como la suma, resta, multiplicación
VII. Estructuras Algebraicas Objetivo Se analizarán las operaciones binarias y sus propiedades dentro de una estructura algebraica. Definición de operación binaria Operaciones como la suma, resta, multiplicación
Desarrollar y aplicar estrategias para resolver problemas Determinar si un gráfico es lineal dibujando puntos en una situación dada
 MANEJO DE DATOS Analizar gráficos o diagramas de situaciones dadas para identificar información específica Recoger datos, dibujar los datos usando escalas apropiadas y demostrar una comprensión de las
MANEJO DE DATOS Analizar gráficos o diagramas de situaciones dadas para identificar información específica Recoger datos, dibujar los datos usando escalas apropiadas y demostrar una comprensión de las
f(x) = 0; x [a, b] de la que, por simplicidad, suponemos que f : [a, b] R es una función derivable tres veces.
![f(x) = 0; x [a, b] de la que, por simplicidad, suponemos que f : [a, b] R es una función derivable tres veces. f(x) = 0; x [a, b] de la que, por simplicidad, suponemos que f : [a, b] R es una función derivable tres veces.](/thumbs/27/10938495.jpg) Práctica 5 Método de Newton 5.1. Introducción En esta práctica damos al alumno un guión y una relación de referencias para que con su trabajo personal, que estimamos de 6 horas, realice un pequeño estudio
Práctica 5 Método de Newton 5.1. Introducción En esta práctica damos al alumno un guión y una relación de referencias para que con su trabajo personal, que estimamos de 6 horas, realice un pequeño estudio
PROBLEMA 1. 1. [1.5 puntos] Obtener la ecuación de la recta tangente en el punto ( 2, 1) a la curva dada implícitamente por y 3 +3y 2 = x 4 3x 2.
![PROBLEMA 1. 1. [1.5 puntos] Obtener la ecuación de la recta tangente en el punto ( 2, 1) a la curva dada implícitamente por y 3 +3y 2 = x 4 3x 2. PROBLEMA 1. 1. [1.5 puntos] Obtener la ecuación de la recta tangente en el punto ( 2, 1) a la curva dada implícitamente por y 3 +3y 2 = x 4 3x 2.](/thumbs/27/11795036.jpg) PROBLEMA. ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA Ingeniería Técnica en Diseño Industrial Fundamentos Matemáticos de la Ingeniería Soluciones correspondientes a los problemas del Primer Parcial 7/8.
PROBLEMA. ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA Ingeniería Técnica en Diseño Industrial Fundamentos Matemáticos de la Ingeniería Soluciones correspondientes a los problemas del Primer Parcial 7/8.
Máster Universitario en Ingeniería de Caminos, Canales y Puertos Introducción al Análisis Numérico
 Máster Universitario en Ingeniería de Caminos, Canales y Puertos Introducción al Análisis Numérico Departamento de Matemática Aplicada Universidad Granada Introducción El Cálculo o Análisis Numérico es
Máster Universitario en Ingeniería de Caminos, Canales y Puertos Introducción al Análisis Numérico Departamento de Matemática Aplicada Universidad Granada Introducción El Cálculo o Análisis Numérico es
Algorítmica y Lenguajes de Programación. MATLAB (i)
 Algorítmica y Lenguajes de Programación MATLAB (i) MATLAB. Introducción MATLAB es un entorno interactivo que utiliza como tipos de datos básicos vectores y matrices de flotantes que no requieren ser dimensionados.
Algorítmica y Lenguajes de Programación MATLAB (i) MATLAB. Introducción MATLAB es un entorno interactivo que utiliza como tipos de datos básicos vectores y matrices de flotantes que no requieren ser dimensionados.
INTEGRALES DEFINIDAS Y CÁLCULOS DE ÁREAS
 INTEGRALES DEFINIDAS Y CÁLCULOS DE ÁREAS CÁLCULO AUTOMÁTICO DE INTEGRALES DEFINIDAS La integral de una función definida puede obtenerse en DERIVE tecleando el icono Cálculo integral,, También puede obtenerse
INTEGRALES DEFINIDAS Y CÁLCULOS DE ÁREAS CÁLCULO AUTOMÁTICO DE INTEGRALES DEFINIDAS La integral de una función definida puede obtenerse en DERIVE tecleando el icono Cálculo integral,, También puede obtenerse
Curso de GNU Octave y L A TEXpara el apoyo a la investigación en ingeniería
 Curso de GNU Octave y L A TEXpara el apoyo a la investigación en ingeniería Red de investigaciones y Tecnología Avanzada - RITA Facultad de ingeniería Universidad Distrital Francisco José de Caldas Copyleft
Curso de GNU Octave y L A TEXpara el apoyo a la investigación en ingeniería Red de investigaciones y Tecnología Avanzada - RITA Facultad de ingeniería Universidad Distrital Francisco José de Caldas Copyleft
Proyecto de Innovación Docente: Guía multimedia para la elaboración de un modelo econométrico.
 1 Primeros pasos en R. Al iniciarse R (ver Figura 16), R espera la entrada de órdenes y presenta un símbolo para indicarlo. El símbolo asignado, como puede observarse al final, es > Figura 16. Pantalla
1 Primeros pasos en R. Al iniciarse R (ver Figura 16), R espera la entrada de órdenes y presenta un símbolo para indicarlo. El símbolo asignado, como puede observarse al final, es > Figura 16. Pantalla
4. Sucesiones y funciones
 1 4. Sucesiones y funciones Mathematica dispone de herramientas para hacer sumas de series numéricas, derivadas de funciones de una y varias variables, cálculo de primitivas de funciones de una variable,
1 4. Sucesiones y funciones Mathematica dispone de herramientas para hacer sumas de series numéricas, derivadas de funciones de una y varias variables, cálculo de primitivas de funciones de una variable,
CAPITULO 4 JUSTIFICACION DEL ESTUDIO. En este capítulo se presenta la justificación del estudio, supuestos y limitaciones de
 CAPITULO 4 JUSTIFICACION DEL ESTUDIO En este capítulo se presenta la justificación del estudio, supuestos y limitaciones de estudios previos y los alcances que justifican el presente estudio. 4.1. Justificación.
CAPITULO 4 JUSTIFICACION DEL ESTUDIO En este capítulo se presenta la justificación del estudio, supuestos y limitaciones de estudios previos y los alcances que justifican el presente estudio. 4.1. Justificación.
Álgebra Lineal Tutorial básico de MATLAB
 Escuela de Matemáticas. Universidad Nacional de Colombia, Sede Medellín. 1 VECTORES Álgebra Lineal Tutorial básico de MATLAB MATLAB es un programa interactivo para cómputos numéricos y visualización de
Escuela de Matemáticas. Universidad Nacional de Colombia, Sede Medellín. 1 VECTORES Álgebra Lineal Tutorial básico de MATLAB MATLAB es un programa interactivo para cómputos numéricos y visualización de
4. Se considera la función f(x) =. Se pide:
 Propuesta A 1. Queremos realizar una inversión en dos tipos de acciones con las siguientes condiciones: Lo invertido en las acciones de tipo A no puede superar los 10000 euros. Lo invertido en las acciones
Propuesta A 1. Queremos realizar una inversión en dos tipos de acciones con las siguientes condiciones: Lo invertido en las acciones de tipo A no puede superar los 10000 euros. Lo invertido en las acciones
Capítulo VI DESIGUALDADES E INECUACIONES
 Capítulo VI DESIGUALDADES E INECUACIONES 6.1 DEFINICIONES: a. Desigualdad: Se denomina desigualdad a toda expresión que describe la relación entre al menos elementos escritos en términos matemáticos, y
Capítulo VI DESIGUALDADES E INECUACIONES 6.1 DEFINICIONES: a. Desigualdad: Se denomina desigualdad a toda expresión que describe la relación entre al menos elementos escritos en términos matemáticos, y
El Método de Monte Carlo. Curso de Estadística TAE, 2005 J.J. Gómez-Cadenas
 El Método de Monte Carlo Curso de Estadística TAE, 2005 J.J. Gómez-Cadenas El método de Monte Carlo es una técnica numérica para calcular probabilidades y otras cantidades relacionadas, utilizando secuencias
El Método de Monte Carlo Curso de Estadística TAE, 2005 J.J. Gómez-Cadenas El método de Monte Carlo es una técnica numérica para calcular probabilidades y otras cantidades relacionadas, utilizando secuencias
facilidades para cálculo matemático y Dispone de toolboxes especializados: Control Systems, Neural Netword, Optimization, etc.
 MATLAB Introducción al MATLAB MATLAB = MATrix LABoratory Es un entorno de computación que presenta facilidades para cálculo matemático y visualización gráfica Dispone de toolboxes especializados: Control
MATLAB Introducción al MATLAB MATLAB = MATrix LABoratory Es un entorno de computación que presenta facilidades para cálculo matemático y visualización gráfica Dispone de toolboxes especializados: Control
SLUD Programación de Máxima In memoriam William Schelter
 SLUD 2006 Programación de Máxima In memoriam William Schelter Robert Dodier Proyecto Máxima Libero este documento por el GNU General Public License version 2 Toda cosa es expresión Toda cosa en Máxima
SLUD 2006 Programación de Máxima In memoriam William Schelter Robert Dodier Proyecto Máxima Libero este documento por el GNU General Public License version 2 Toda cosa es expresión Toda cosa en Máxima
Introducción a MATLAB/ OCTAVE. Fundamentos Físicos de la Informática, 2006
 Introducción a MATLAB/ OCTAVE Fundamentos Físicos de la Informática, 006 Matlab/ Octave Matlab es un lenguaje de programación orientado al cálculo numérico, principalmente matricial Octave es un programa
Introducción a MATLAB/ OCTAVE Fundamentos Físicos de la Informática, 006 Matlab/ Octave Matlab es un lenguaje de programación orientado al cálculo numérico, principalmente matricial Octave es un programa
Parámetros y estadísticos
 Parámetros y estadísticos «Parámetro»: Es una cantidad numérica calculada sobre una población y resume los valores que esta toma en algún atributo Intenta resumir toda la información que hay en la población
Parámetros y estadísticos «Parámetro»: Es una cantidad numérica calculada sobre una población y resume los valores que esta toma en algún atributo Intenta resumir toda la información que hay en la población
Nombre de la asignatura: METODOS NUMERICOS. Carrera : Ingeniería Mecánica. Clave de la asignatura: ACB- 9311 Clave local:
 Nombre de la asignatura: METODOS NUMERICOS Carrera : Ingeniería Mecánica Clave de la asignatura: ACB- 9 Clave local: Horas teoría horas practicas créditos: -0-8.- UBICACIÓN DE LA ASIGNATURA A) RELACIÓN
Nombre de la asignatura: METODOS NUMERICOS Carrera : Ingeniería Mecánica Clave de la asignatura: ACB- 9 Clave local: Horas teoría horas practicas créditos: -0-8.- UBICACIÓN DE LA ASIGNATURA A) RELACIÓN
INSTITUCIÓN EDUCATIVA HÉCTOR ABAD GÓMEZ
 INSTITUCIÓN EDUCATIVA HÉCTOR ABAD GÓMEZ CONTENIDOS DEL AREA PERIODO: 01 MATEMATICAS Y ESTADISTICA DOCENTE: ADRIANA ZULAY VILLA URIBE GRADO 8 MATEMÁTICAS Objetivos: Explicar y justificar la importancia
INSTITUCIÓN EDUCATIVA HÉCTOR ABAD GÓMEZ CONTENIDOS DEL AREA PERIODO: 01 MATEMATICAS Y ESTADISTICA DOCENTE: ADRIANA ZULAY VILLA URIBE GRADO 8 MATEMÁTICAS Objetivos: Explicar y justificar la importancia
Ejercicios 2.2 Usando aritmética de cuatro dígitos de precisión, sume la siguiente expresión
 CAPÍTULO EJERCICIOS RESUELTOS: ARITMÉTICA DE ORDENADORES Y ANÁLISIS DE ERRORES Ejercicios resueltos Ejercicios.1 Calcula la suma y la resta de los números a = 0.453 10 4, y b = 0.115 10 3, con una aritmética
CAPÍTULO EJERCICIOS RESUELTOS: ARITMÉTICA DE ORDENADORES Y ANÁLISIS DE ERRORES Ejercicios resueltos Ejercicios.1 Calcula la suma y la resta de los números a = 0.453 10 4, y b = 0.115 10 3, con una aritmética
Métodos Computacionales 0302390
 Métodos Computacionales 0302390 Fecha de actualización Tue, 28 Jul 2015 06:28:33-050 Usuario que realiza la actualización Facultad Autorización Vicedecano Última versión del curso 1 Número de Acta del
Métodos Computacionales 0302390 Fecha de actualización Tue, 28 Jul 2015 06:28:33-050 Usuario que realiza la actualización Facultad Autorización Vicedecano Última versión del curso 1 Número de Acta del
Sistemas Numéricos Cambios de Base Errores
 Cálculo Numérico Definición: es el desarrollo y estudio de procedimientos (algoritmos) para resolver problemas con ayuda de una computadora. π + cos ( x) dx 0 Tema I: Introducción al Cálculo Numérico Sistemas
Cálculo Numérico Definición: es el desarrollo y estudio de procedimientos (algoritmos) para resolver problemas con ayuda de una computadora. π + cos ( x) dx 0 Tema I: Introducción al Cálculo Numérico Sistemas
Álgebra Matricial y Optimización Ma130
 Álgebra Matricial y Optimización Ma130 Descripción del Curso Departamento de Matemáticas ITESM Descripción del Curso Ma130 - p. 1/8 El objetivo de este curso es presentar al estudiante algunas de las herramientas
Álgebra Matricial y Optimización Ma130 Descripción del Curso Departamento de Matemáticas ITESM Descripción del Curso Ma130 - p. 1/8 El objetivo de este curso es presentar al estudiante algunas de las herramientas
Generación de números aleatorios
 Generación de números aleatorios Marcos García González (h[e]rtz) Verano 2004 Documento facilitado por la realización de la asignatura Métodos informáticos de la física de segundo curso en la universidad
Generación de números aleatorios Marcos García González (h[e]rtz) Verano 2004 Documento facilitado por la realización de la asignatura Métodos informáticos de la física de segundo curso en la universidad
Revista digital Matemática, Educación e Internet (www.cidse.itcr.ac.cr/revistamate/). Vol. 8, N o 2. 2007
 Sección Tecnologías de Internet Revista digital Matemática, Educación e Internet (www.cidse.itcr.ac.cr/revistamate/). Vol. 8, N o 2. 2007 Hacia una propuesta didáctica para la enseñanza de Métodos Numéricos
Sección Tecnologías de Internet Revista digital Matemática, Educación e Internet (www.cidse.itcr.ac.cr/revistamate/). Vol. 8, N o 2. 2007 Hacia una propuesta didáctica para la enseñanza de Métodos Numéricos
Álgebra y Matemática Discreta Sesión de Prácticas 1
 Álgebra y Matemática Discreta Sesión de Prácticas 1 (c) 2013 Leandro Marín, Francisco J. Vera, Gema M. Díaz 16 Sep 2013-22 Sep 2013 Estructuras Algebraicas La Estructura como Variable Tenemos una gran
Álgebra y Matemática Discreta Sesión de Prácticas 1 (c) 2013 Leandro Marín, Francisco J. Vera, Gema M. Díaz 16 Sep 2013-22 Sep 2013 Estructuras Algebraicas La Estructura como Variable Tenemos una gran
Carrera: Ingeniería Civil CIE 0524
 1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos: Investigación de Operaciones Ingeniería Civil CIE 0524 2 2 6 2.- HISTORIA DEL
1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos: Investigación de Operaciones Ingeniería Civil CIE 0524 2 2 6 2.- HISTORIA DEL
CONTENIDOS MÍNIMOS BLOQUE III: ÁLGEBRA
 CONTENIDOS MÍNIMOS BLOQUE III: ÁLGEBRA Interpolación de términos en una sucesión. Cálculo del término general de sucesiones muy sencillas. Distinción entre progresiones aritméticas y geométricas. Interpolación
CONTENIDOS MÍNIMOS BLOQUE III: ÁLGEBRA Interpolación de términos en una sucesión. Cálculo del término general de sucesiones muy sencillas. Distinción entre progresiones aritméticas y geométricas. Interpolación
Trabajando en la ventana de comandos en el programa gretl.
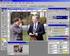 Proyecto de Innovación Docente: Guía multimedia para la elaboración de un modelo econométrico. 1 Trabajando en la ventana de comandos en el programa gretl. Gretl permite trabajar mediante comandos y funciones,
Proyecto de Innovación Docente: Guía multimedia para la elaboración de un modelo econométrico. 1 Trabajando en la ventana de comandos en el programa gretl. Gretl permite trabajar mediante comandos y funciones,
Ecuaciones y sistemas de ecuaciones en Maple
 Ecuaciones y sistemas de ecuaciones en Maple José Luis Torres Rodríguez * Febrero Maple proporciona al usuario un conjunto de funciones para manipulación y solución de ecuaciones y sistemas de ecuaciones,
Ecuaciones y sistemas de ecuaciones en Maple José Luis Torres Rodríguez * Febrero Maple proporciona al usuario un conjunto de funciones para manipulación y solución de ecuaciones y sistemas de ecuaciones,
Planeación de la Recolección de Datos. Planeacion de Recoleccion de Datos
 Planeación de la Recolección de Datos Qué Son los datos? Recolección de Datos Contenido Por Qué Es Importante la Recolección de Datos? Estrategias de Muestreo Estrategias para la Definición de Datos Base
Planeación de la Recolección de Datos Qué Son los datos? Recolección de Datos Contenido Por Qué Es Importante la Recolección de Datos? Estrategias de Muestreo Estrategias para la Definición de Datos Base
Diagonalización de matrices
 diagonalizacion.nb Diagonalización de matrices Práctica de Álgebra Lineal, E.U.A.T., Grupos ºA y ºB, 2005 Algo de teoría Qué es diagonalizar una matriz? Para estudiar una matriz suele ser conveniente expresarla
diagonalizacion.nb Diagonalización de matrices Práctica de Álgebra Lineal, E.U.A.T., Grupos ºA y ºB, 2005 Algo de teoría Qué es diagonalizar una matriz? Para estudiar una matriz suele ser conveniente expresarla
1. Trace la curva definida por las ecuaciones paramétricas y elimine el parámetro para deducir la ecuación cartesiana de la curva:
 1. Trace la curva definida por las ecuaciones paramétricas y elimine el parámetro para deducir la ecuación cartesiana de la curva: a) x = senθ, y = cosθ, 0 θ π t b), t x = e y = e + 1 c) x = senθ, y =
1. Trace la curva definida por las ecuaciones paramétricas y elimine el parámetro para deducir la ecuación cartesiana de la curva: a) x = senθ, y = cosθ, 0 θ π t b), t x = e y = e + 1 c) x = senθ, y =
Tema 4: Empezando a trabajar con ficheros.m
 Tema 4: Empezando a trabajar con ficheros.m 1. Introducción Como ya se comentó en el punto 3 del tema1, en Matlab tienen especial importancia los ficheros M de extensión.m. Contienen conjuntos de comandos
Tema 4: Empezando a trabajar con ficheros.m 1. Introducción Como ya se comentó en el punto 3 del tema1, en Matlab tienen especial importancia los ficheros M de extensión.m. Contienen conjuntos de comandos
Tratamiento y Transmisión de Señales Ingenieros Electrónicos SEGUNDA PRÁCTICA
 Tratamiento y Transmisión de Señales Ingenieros Electrónicos SEGUNDA PRÁCTICA NOTA: en toda esta práctica no se pueden utilizar bucles, para que los tiempos de ejecución se reduzcan. Esto se puede hacer
Tratamiento y Transmisión de Señales Ingenieros Electrónicos SEGUNDA PRÁCTICA NOTA: en toda esta práctica no se pueden utilizar bucles, para que los tiempos de ejecución se reduzcan. Esto se puede hacer
1. TEMPORALIZACIÓN POR EVALUACIONES DE LOS CONTENIDOS
 1. TEMPORALIZACIÓN POR EVALUACIONES DE LOS CONTENIDOS Primera Evaluación TEMA 1. NÚMEROS REALES Distintos tipos de números. Recta real. Radicales. Logaritmos. Notación científica. Calculadora. TEMA 2.
1. TEMPORALIZACIÓN POR EVALUACIONES DE LOS CONTENIDOS Primera Evaluación TEMA 1. NÚMEROS REALES Distintos tipos de números. Recta real. Radicales. Logaritmos. Notación científica. Calculadora. TEMA 2.
Integración por el método de Monte Carlo
 Integración por el método de Monte Carlo Georgina Flesia FaMAF 7 de abril 2015 El método de Monte Carlo El método de Monte Carlo es un procedimiento general para estudiar procesos mediante la seleccion
Integración por el método de Monte Carlo Georgina Flesia FaMAF 7 de abril 2015 El método de Monte Carlo El método de Monte Carlo es un procedimiento general para estudiar procesos mediante la seleccion
Organización del Computador. Prof. Angela Di Serio
 Punto Flotante Muchas aplicaciones requieren trabajar con números que no son enteros. Existen varias formas de representar números no enteros. Una de ellas es usando un punto o coma fijo. Este tipo de
Punto Flotante Muchas aplicaciones requieren trabajar con números que no son enteros. Existen varias formas de representar números no enteros. Una de ellas es usando un punto o coma fijo. Este tipo de
TÉCNICO SUPERIOR UNIVERSITARIO EN TECNOLOGÍAS DE LA INFORMACIÓN Y COMUNICACIÓN
 TÉCNICO SUPERIOR UNIVERSITARIO EN TECNOLOGÍAS DE LA INFORMACIÓN Y COMUNICACIÓN HOJA DE ASIGNATURA CON DESGLOSE DE UNIDADES TEMÁTICAS 1. Nombre de la asignatura Desarrollo de habilidades del pensamiento
TÉCNICO SUPERIOR UNIVERSITARIO EN TECNOLOGÍAS DE LA INFORMACIÓN Y COMUNICACIÓN HOJA DE ASIGNATURA CON DESGLOSE DE UNIDADES TEMÁTICAS 1. Nombre de la asignatura Desarrollo de habilidades del pensamiento
IES La Serna Matemáticas Aplicadas a las Ciencias Sociales II. Comunidad de Madrid. Año 08. Septiembre. Opción B. Ejercicio 1.
 IES La Serna Matemáticas Aplicadas a las Ciencias Sociales II. Comunidad de Madrid. Año 08. Septiembre. Opción B. Ejercicio. ( puntos) Se desea invertir una cantidad de dinero menor o igual que 000 euros,
IES La Serna Matemáticas Aplicadas a las Ciencias Sociales II. Comunidad de Madrid. Año 08. Septiembre. Opción B. Ejercicio. ( puntos) Se desea invertir una cantidad de dinero menor o igual que 000 euros,
Álgebra Lineal Taller N o 2 con Matlab
 Álgebra Lineal Taller N o con Matlab Tema: Introducción a las transformaciones lineales. Determinantes. Valores y vectores propios de matrices de orden n:diagonaliación de matrices de orden n. plicación
Álgebra Lineal Taller N o con Matlab Tema: Introducción a las transformaciones lineales. Determinantes. Valores y vectores propios de matrices de orden n:diagonaliación de matrices de orden n. plicación
ANÁLISIS DE CORRELACIÓN EMPLEANDO EXCEL Y GRAPH
 ANÁLISIS DE CORRELACIÓN EMPLEANDO EXCEL Y GRAPH Cuando se estudian en forma conjunta dos características (variables estadísticas) de una población o muestra, se dice que estamos analizando una variable
ANÁLISIS DE CORRELACIÓN EMPLEANDO EXCEL Y GRAPH Cuando se estudian en forma conjunta dos características (variables estadísticas) de una población o muestra, se dice que estamos analizando una variable
8.1. Introducción... 1. 8.2. Dependencia/independencia estadística... 2. 8.3. Representación gráfica: diagrama de dispersión... 3. 8.4. Regresión...
 Tema 8 Análisis de dos variables: dependencia estadística y regresión Contenido 8.1. Introducción............................. 1 8.2. Dependencia/independencia estadística.............. 2 8.3. Representación
Tema 8 Análisis de dos variables: dependencia estadística y regresión Contenido 8.1. Introducción............................. 1 8.2. Dependencia/independencia estadística.............. 2 8.3. Representación
BOLETÍN OFICIAL DEL ESTADO UNIVERSIDADES
 Núm. 240 Miércoles 7 de octubre de 2015 Sec. III. Pág. 92578 III. OTRAS DISPOSICIONES UNIVERSIDADES 10792 Resolución de 11 de septiembre de 2015, de la Universidad de Almería, por la que se publica la
Núm. 240 Miércoles 7 de octubre de 2015 Sec. III. Pág. 92578 III. OTRAS DISPOSICIONES UNIVERSIDADES 10792 Resolución de 11 de septiembre de 2015, de la Universidad de Almería, por la que se publica la
CIRCUITOS ARITMÉTICOS. Tema 5: CIRCUITOS ARITMÉTICOS
 Tema 5: CIRCUITOS ARITMÉTICOS Contenido: * Aritmética binaria. * Circuito semisumador. Sumador completo. * Operaciones con n bits. Sumador paralelo con arrastre serie. * Circuito sumador-restador. * Sumador
Tema 5: CIRCUITOS ARITMÉTICOS Contenido: * Aritmética binaria. * Circuito semisumador. Sumador completo. * Operaciones con n bits. Sumador paralelo con arrastre serie. * Circuito sumador-restador. * Sumador
Capítulo 1: Sistemas de representación numérica Introducción. Dpto. de ATC, Universidad de Sevilla - Página 1 de 8
 Dpto. de ATC, Universidad de Sevilla - Página de Capítulo : INTRODUCCIÓN SISTEMAS DE REPRESENTACIÓN NUMÉRICA Introducción Bases de numeración Sistema decimal Sistema binario Sistema hexadecimal REPRESENTACIÓN
Dpto. de ATC, Universidad de Sevilla - Página de Capítulo : INTRODUCCIÓN SISTEMAS DE REPRESENTACIÓN NUMÉRICA Introducción Bases de numeración Sistema decimal Sistema binario Sistema hexadecimal REPRESENTACIÓN
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2015 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 1: MATRICES. Junio, Ejercicio 1, Opción B
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 015 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 1: MATRICES Junio, Ejercicio 1, Opción B 3 Sean las matrices A 0 3, B y C 0 1 1 5 1 3 0 a) Calcule las
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 015 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 1: MATRICES Junio, Ejercicio 1, Opción B 3 Sean las matrices A 0 3, B y C 0 1 1 5 1 3 0 a) Calcule las
Práctica 1. Introducción a Sage.
 1 de 9 07/07/2010 12:07 To print higher-resolution math symbols, click the Hi-Res Fonts for Printing button on the jsmath control panel. If the math symbols print as black boxes, turn off image alpha channels
1 de 9 07/07/2010 12:07 To print higher-resolution math symbols, click the Hi-Res Fonts for Printing button on the jsmath control panel. If the math symbols print as black boxes, turn off image alpha channels
Módulo 9 Sistema matemático y operaciones binarias
 Módulo 9 Sistema matemático y operaciones binarias OBJETIVO: Identificar los conjuntos de números naturales, enteros, racionales e irracionales; resolver una operación binaria, representar un número racional
Módulo 9 Sistema matemático y operaciones binarias OBJETIVO: Identificar los conjuntos de números naturales, enteros, racionales e irracionales; resolver una operación binaria, representar un número racional
Formatos y Operadores
 Formatos y Operadores Formatos numéricos format short long hex bank short e short g long e long g rational coma fija con 4 decimales (defecto) coma fija con 15 decimales cifras hexadecimales números con
Formatos y Operadores Formatos numéricos format short long hex bank short e short g long e long g rational coma fija con 4 decimales (defecto) coma fija con 15 decimales cifras hexadecimales números con
Selectividad Septiembre 2009 SEPTIEMBRE 2009. Opción A
 SEPTIEMBRE 2009 Opción A 1.- Como cada año, el inicio del curso académico, una tienda de material escolar prepara una oferta de 600 cuadernos, 500 carpetas y 400 bolígrafos para los alumnos de un IES,
SEPTIEMBRE 2009 Opción A 1.- Como cada año, el inicio del curso académico, una tienda de material escolar prepara una oferta de 600 cuadernos, 500 carpetas y 400 bolígrafos para los alumnos de un IES,
SLUD El sistema de computación simbólica, Máxima In memoriam William Schelter
 SLUD 2006 El sistema de computación simbólica, Máxima In memoriam William Schelter Robert Dodier Proyecto Máxima Libero este documento por el GNU General Public License version 2 Por qué la computación
SLUD 2006 El sistema de computación simbólica, Máxima In memoriam William Schelter Robert Dodier Proyecto Máxima Libero este documento por el GNU General Public License version 2 Por qué la computación
Modelos de líneas de transmisión en estado estacionario... 2
 Modelos de líneas de transmisión en estado estacionario Prof Ing Raúl ianchi Lastra Cátedra: CONTENIDO Modelos de líneas de transmisión en estado estacionario Introducción Constantes del cuadripolo Modelos
Modelos de líneas de transmisión en estado estacionario Prof Ing Raúl ianchi Lastra Cátedra: CONTENIDO Modelos de líneas de transmisión en estado estacionario Introducción Constantes del cuadripolo Modelos
Estadística con Excel Informática 4º ESO ESTADÍSTICA CON EXCEL
 1. Introducción ESTADÍSTICA CO EXCEL La estadística es la rama de las matemáticas que se dedica al análisis e interpretación de series de datos, generando unos resultados que se utilizan básicamente en
1. Introducción ESTADÍSTICA CO EXCEL La estadística es la rama de las matemáticas que se dedica al análisis e interpretación de series de datos, generando unos resultados que se utilizan básicamente en
Elementos de Probabilidad y Estadística Segundo de Economía Examen del 26 de junio de 2006 DURACIÓN: 2 horas
 Elementos de Probabilidad y Estadística Segundo de Economía Examen del 6 de junio de 6 DURACIÓN: horas. a) Se realizan lanzamientos de un dado regular. i) Calcular la probabilidad de obtener exactamente
Elementos de Probabilidad y Estadística Segundo de Economía Examen del 6 de junio de 6 DURACIÓN: horas. a) Se realizan lanzamientos de un dado regular. i) Calcular la probabilidad de obtener exactamente
Se podría entender como una matriz de filas y columnas. Cada combinación de fila y columna se denomina celda. Por ejemplo la celda A1, B33, Z68.
 Departamento de Economía Aplicada: UDI de Estadística. Universidad Autónoma de Madrid Notas sobre el manejo de Excel para el análisis descriptivo y exploratorio de datos. (Descriptiva) 1 1 Introducción
Departamento de Economía Aplicada: UDI de Estadística. Universidad Autónoma de Madrid Notas sobre el manejo de Excel para el análisis descriptivo y exploratorio de datos. (Descriptiva) 1 1 Introducción
Si f es derivable, definimos al diferencial de una función (df), como el producto de la derivada de f por un incremento de la variable ( x).
 2 Integrales Indefinidas y Métodos de Integración La integral Indefinida o antiderivada es el nombre que recibe la operación inversa a la derivada. Es decir, dada una función F aquella consiste en encontrar
2 Integrales Indefinidas y Métodos de Integración La integral Indefinida o antiderivada es el nombre que recibe la operación inversa a la derivada. Es decir, dada una función F aquella consiste en encontrar
Funciones a trozos. Imágenes de funciones definidas a trozos.
 Funciones a trozos. Imágenes de funciones definidas a trozos. En matemáticas, una función definida a trozos (también conocida como función por partes) es una función cuya definición (la regla que define
Funciones a trozos. Imágenes de funciones definidas a trozos. En matemáticas, una función definida a trozos (también conocida como función por partes) es una función cuya definición (la regla que define
Tema 3: Variables aleatorias y vectores aleatorios bidimensionales
 Estadística 38 Tema 3: Variables aleatorias y vectores aleatorios bidimensionales El concepto de variable aleatoria surge de la necesidad de hacer más manejables matemáticamente los resultados de los experimentos
Estadística 38 Tema 3: Variables aleatorias y vectores aleatorios bidimensionales El concepto de variable aleatoria surge de la necesidad de hacer más manejables matemáticamente los resultados de los experimentos
Estructura de Computadores
 Estructura de Computadores Tema 2. Representación de la información Departamento de Informática Grupo de Arquitectura de Computadores, Comunicaciones y Sistemas UNIVERSIDAD CARLOS III DE MADRID Contenido
Estructura de Computadores Tema 2. Representación de la información Departamento de Informática Grupo de Arquitectura de Computadores, Comunicaciones y Sistemas UNIVERSIDAD CARLOS III DE MADRID Contenido
SISTEMAS DE ECUACIONES LINEALES
 SISTEMAS DE ECUACIONES LINEALES INTRODUCCIÓN En el presente documento se explican detalladamente dos importantes temas: 1. Descomposición LU. 2. Método de Gauss-Seidel. Se trata de dos importantes herramientas
SISTEMAS DE ECUACIONES LINEALES INTRODUCCIÓN En el presente documento se explican detalladamente dos importantes temas: 1. Descomposición LU. 2. Método de Gauss-Seidel. Se trata de dos importantes herramientas
Modelación y Simulación en Física. Guia 3(v1): Raíces.
 Modelación y Simulación en Física. Guia 3(v1): Raíces. Prof. Francisco Santibáñez Calderón. francisco.santibanez@ucv.cl Laboratorio de Mecanica de Materiales Complejos. 3 de octubre de 2013 Metodos Numericos
Modelación y Simulación en Física. Guia 3(v1): Raíces. Prof. Francisco Santibáñez Calderón. francisco.santibanez@ucv.cl Laboratorio de Mecanica de Materiales Complejos. 3 de octubre de 2013 Metodos Numericos
13. Técnicas de simulación mediante el método de Montecarlo
 13. Técnicas de simulación mediante el método de Montecarlo Qué es la simulación? Proceso de simulación Simulación de eventos discretos Números aleatorios Qué es la simulación? Simulación = técnica que
13. Técnicas de simulación mediante el método de Montecarlo Qué es la simulación? Proceso de simulación Simulación de eventos discretos Números aleatorios Qué es la simulación? Simulación = técnica que
Las Matemáticas En Ingeniería
 Las Matemáticas En Ingeniería 1.1. Referentes Nacionales A nivel nacional se considera que el conocimiento matemático y de ciencias naturales, sus conceptos y estructuras, constituyen una herramienta para
Las Matemáticas En Ingeniería 1.1. Referentes Nacionales A nivel nacional se considera que el conocimiento matemático y de ciencias naturales, sus conceptos y estructuras, constituyen una herramienta para
Soluciones de la Tarea 2 Análisis Numérico I
 Soluciones de la Tarea 2 Análisis Numérico I Dr. Miguel Angel Uh Zapata Ejercicio 2.1 Programar en Matlab: Una función que dado los valores a y b del intervalo [a, b], dibuje ambas gráficas de las funciones
Soluciones de la Tarea 2 Análisis Numérico I Dr. Miguel Angel Uh Zapata Ejercicio 2.1 Programar en Matlab: Una función que dado los valores a y b del intervalo [a, b], dibuje ambas gráficas de las funciones
guía para LOS PADRES APOYANDO A SU HIJO EN LA PREPARATORIA (HIGH SCHOOL) MATEMÁTICAS
 guía para LOS PADRES APOYANDO A SU HIJO EN LA PREPARATORIA (HIGH SCHOOL) MATEMÁTICAS HS Las escuelas de los Estados Unidos de América están trabajando para brindar una enseñanza de mayor calidad nunca
guía para LOS PADRES APOYANDO A SU HIJO EN LA PREPARATORIA (HIGH SCHOOL) MATEMÁTICAS HS Las escuelas de los Estados Unidos de América están trabajando para brindar una enseñanza de mayor calidad nunca
CAPÍTULO 6 SIMULACIONES Y RESULTADOS
 CAPÍTULO 6 SIMULACIONES Y RESULTADOS 6.1 Proceso de Simulación Las simulaciones fueros llevadas a cabo empleando como herramienta la Versión 6.5 Release 13 de Matlab. Para lo cual fue empleado un banco
CAPÍTULO 6 SIMULACIONES Y RESULTADOS 6.1 Proceso de Simulación Las simulaciones fueros llevadas a cabo empleando como herramienta la Versión 6.5 Release 13 de Matlab. Para lo cual fue empleado un banco
Carrera: SCB - 0419 4-0-8. Participantes. Representantes de la academia de sistemas y computación de los Institutos Tecnológicos.
 1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos Investigación de operaciones Ingeniería en Sistemas Computacionales SCB - 0419
1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos Investigación de operaciones Ingeniería en Sistemas Computacionales SCB - 0419
Matemáticas I. Carrera: IFM - 0423 3-2-8. Participantes. Representantes de la academia de sistemas y computación de los Institutos Tecnológicos.
 1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos Matemáticas I Licenciatura en Informática IFM - 0423 3-2-8 2.- HISTORIA DEL PROGRAMA
1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos Matemáticas I Licenciatura en Informática IFM - 0423 3-2-8 2.- HISTORIA DEL PROGRAMA
Pruebas de. Hipótesis
 Pruebas de ipótesis Pruebas de ipótesis Otra manera de hacer inferencia es haciendo una afirmación acerca del valor que el parámetro de la población bajo estudio puede tomar. Esta afirmación puede estar
Pruebas de ipótesis Pruebas de ipótesis Otra manera de hacer inferencia es haciendo una afirmación acerca del valor que el parámetro de la población bajo estudio puede tomar. Esta afirmación puede estar
TEMA 7: Análisis de la Capacidad del Proceso
 TEMA 7: Análisis de la Capacidad del Proceso 1 Introducción Índices de capacidad 3 Herramientas estadísticas para el análisis de la capacidad 4 Límites de tolerancia naturales 1 Introducción La capacidad
TEMA 7: Análisis de la Capacidad del Proceso 1 Introducción Índices de capacidad 3 Herramientas estadísticas para el análisis de la capacidad 4 Límites de tolerancia naturales 1 Introducción La capacidad
2. SISTEMAS LINEALES DE PRIMER ORDEN (I)
 2. SISTEMAS LINEALES DE PRIMER ORDEN (I) 2.1 INTRODUCCIÓN DOMINIO TIEMPO Un sistema lineal de primer orden con una variable de entrada, " x ( ", y una variable salida, " y( " se modela matemáticamente
2. SISTEMAS LINEALES DE PRIMER ORDEN (I) 2.1 INTRODUCCIÓN DOMINIO TIEMPO Un sistema lineal de primer orden con una variable de entrada, " x ( ", y una variable salida, " y( " se modela matemáticamente
Simulación de Curvas de Rendimiento empleando Componentes Principales: Una aplicación para los Fondos de Pensiones. Banco Central de Reserva del Perú
 Simulación de Curvas de Rendimiento empleando Componentes Principales: Una aplicación para los Fondos de Pensiones Banco Central de Reserva del Perú - Gonzalo Chávez - Paul Zanabria 1 Introducción La proyección
Simulación de Curvas de Rendimiento empleando Componentes Principales: Una aplicación para los Fondos de Pensiones Banco Central de Reserva del Perú - Gonzalo Chávez - Paul Zanabria 1 Introducción La proyección
4 APLICACIONES LINEALES. DIAGONALIZACIÓN
 4 APLICACIONES LINEALES DIAGONALIZACIÓN DE MATRICES En ocasiones, y con objeto de simplificar ciertos cálculos, es conveniente poder transformar una matriz en otra matriz lo más sencilla posible Esto nos
4 APLICACIONES LINEALES DIAGONALIZACIÓN DE MATRICES En ocasiones, y con objeto de simplificar ciertos cálculos, es conveniente poder transformar una matriz en otra matriz lo más sencilla posible Esto nos
Carrera: 2-2-6. Participantes
 1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Investigación de Operaciones Ingeniería Civil Clave de la asignatura: Horas teoría-horas práctica-créditos 2-2-6 2.- HISTORIA DEL PROGRAMA Lugar
1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Investigación de Operaciones Ingeniería Civil Clave de la asignatura: Horas teoría-horas práctica-créditos 2-2-6 2.- HISTORIA DEL PROGRAMA Lugar
