Energía almacenada en el campo magnético.

Tamaño: px

Comenzar la demostración a partir de la página:

Download "Energía almacenada en el campo magnético."

Fernando Caballero Olivares
hace 7 años
Vistas:

1 c Rafael R. Boix y Francisco Medina 1 Energía almacenada en el campo magnético. Consideremos una espira conductora, modelada mediante la curva Γ, por la que circula una corriente estacionaria de intensidad I. Sea Φ e m el ujo magnético estacionario creado por la espira a través de su propia supercie, y sea A(r) el potencial vector magnético creado por la espira conductora en todos los puntos del espacio. La energía magnética almacenada en la espira conductora viene dada por: U m = 1 2 IΦe m = I A(r) dr = 1 IA(r) dr (1) 2 Γ 2 Γ donde dr es un vector desplazamiento innitesimal denido en cada punto de la espira en el sentido de la corriente. Consideremos ahora un conductor no liforme que ocupa un volumen acotado τ en el espacio, y consideremos un sistema de coordenadas con origen en el centro geométrico de τ. Por el conductor circula una corriente estacionaria de densidad volumétrica de corriente J(r). Sean A(r) y B(r) el potencial vector magnético y el campo magnético creados en todos los puntos del espacio por el conductor no liforme. Para obtener la energía magnética almacenada en el conductor no liforme, basta descomponer dicho conductor en tubos de co-

2 c Rafael R. Boix y Francisco Medina 2 rriente de sección transversal innitesimal que pueden ser tratados como conductores liformes. Mediante la ecuación (1) se puede obtener una expresión para la energía magnética innitesimal almacenada en cada uno de esos tubos de corriente, y si se integra dicha expresión para todos los tubos de corriente que se pueden denir en el conductor no liforme, se llega a que la energía magnética almacenada en el conductor vendrá dada por: U m = 1 J(r) A(r)dτ (2) 2 τ Sea ahora τ esfera un volumen esférico centrado en el origen de coordenadas de radio R +, y sea S esfera la supercie esférica que limita a τ esfera. Dado que J(r) es un campo vectorial que sólo toma valores no nulos en τ (ya que la densidad volumétrica de corriente es nula fuera de τ), podemos extender el dominio de integración de la ecuación (2) a todo el volumen τ esfera, esto es: U m = 1 J(r) A(r)dτ (3) 2 τ esfera Por otro lado, dado que la corriente que circula por el conductor no liforme es estacionaria, se cumple que B(r) = µ 0 J(r), y en consecuencia, la ecuación (3) se puede reescribir: U m = 1 τ esfera ( B(r)) A(r)dτ (4)

3 c Rafael R. Boix y Francisco Medina 3 Si ahora hacemos uso de la identidad vectorial (A B) = ( A) B ( B) A y utilizamos que A = B, se obtiene que el integrando de la ecuación (4) se puede escribir: ( B) A = ( A) B (A B) = B 2 (A B) (5) y si sustituimos la ecuación (5) en la ecuación (4), se obtiene la siguiente expresión para la energía magnética almacenada en el conductor no liforme: U m = 1 τ esfera B 2 dτ 1 τ esfera (A B) dτ (6) Si aplicamos ahora el teorema de la divergencia a la segunda integral de volumen de la ecuación (6), se llega a que: (A B) dτ = (A B) ds (7) τ esfera S esfera Dado que la supercie S esfera está situada en el innito, desde los puntos de S esfera el conductor no liforme se va a ver como si fuera un dipolo magnético puntual situado en el origen de coordenadas, con lo cual, se va a cumplir que A] Sesfera 1 y que B] R 2 Sesfera 1 R 3 (téngase en cuenta que el potencial vector creado por un dipolo puntual decae como el inverso del cuadrado de la distancia al dipolo, y el campo magnético, como el inverso del cubo de la distancia al dipolo). Y como ds] Sesfera = R 2 senθdθdϕu r, se vericará que la integral de supercie de la ecuación (7) se anula ya que: (A B) ds 1 0 si R (8) S esfera R3 Si ahora hacemos uso de las ecuaciones (7) y (8) en la ecuación

4 c Rafael R. Boix y Francisco Medina 4 (6), la expresión para la energía magnética almacenada por el conductor no liforme puede reescribirse de la siguiente manera: ( ) 1 U m = lím B 2 dτ = 1 B 2 dτ (9) R τ esfera todo el espacio La ecuación (9) también se puede escribir: U m = w m (r)dτ (10) todo el espacio donde el campo escalar w m (r) representa la densidad volumétrica de energía magnética, dada por: w m (r) = 1 B(r) B(r) (11) Aunque la ecuación (9) ha sido deducida para conductores no liformes, dicha ecuación también permite obtener la energía magnética almacenada en conductores laminares y liformes por los que circulan corrientes estacionarias. No obstante, hay que tener en cuenta que en el caso de los conductores liformes, la ecuación (9) da un valor innito de la energía magnética cuando dichos conductores se modelan mediante una curva cuya sección transversal tiene área nula (esto es lógico si se piensa que la energía magnética de un conductor liforme también se puede calcular mediante la ecuación U m = 1 2 LI2 L es la autoinducción del conductor e I la intensidad que lo atraviesa, y que L toma un valor innito cuando el conductor liforme se modela mediante una curva). Las ecuaciones (2) y (9) son completamente equivalentes a la hora de calcular la energía magnética almacenada en un conductor no liforme que transporta corrientes estacionarias. Sin embargo,

5 c Rafael R. Boix y Francisco Medina 5 mientras que la ecuación (2) parece indicar que la energía está almacenada en las corrientes que circulan por el conductor (ya que la integral involucrada en el cálculo de la energía sólo se extiende al volumen ocupado por el conductor), la ecuación (9) parece indicar que la energía está almacenada en el campo magnético que crean esas corrientes. La ecuación (9) indica que la energía magnética almacenada por un conductor que transporta corriente estacionaria (o por un conjunto de conductores que transportan corrientes estacionarias) siempre es una cantidad mayor o igual que cero (U m 0). Este hecho tiene sus implicaciones. Consideremos un conjunto de N espiras por las que circulan corrientes estacionarias de intensidades I i (i = 1,..., N) (vea la gura adjunta), y supongamos que los ujos magnéticos a través de las espiras valen Φ e mi (i = 1,..., N). Sea L = (L ij ) (i, j = 1,..., N) la matriz inducción del conjunto de espiras y sea Z = (Z ij ) (i, j = 1,..., N) la matriz inversa de L. La energía magnética del conjunto de espiras puede calcularse mediante las ecuaciones: U m = 1 N N I i L ij I j (12) 2 U m = 1 2 i=1 N i=1 j=1 N Φ e miz ij Φ e mj (13) j=1

6 c Rafael R. Boix y Francisco Medina 6 Dado que U m 0, las ecuaciones (12) y (13) nos indican que la energía magnética de un conjunto de espiras es una forma cuadrática denida positiva, tanto de las intensidades que circulan por las espiras como de los ujos magnéticos a través de las espiras. En el caso concreto en que sólo tenemos dos espiras, la ecuación (12) se puede reescribir: U m = 1 2 L 11I1 2 + L 12 I L 22I2 2 = 1 2 L 1I1 2 + MI L 2I2 2 [ = 1 ( ) 2 ( ) ] I1 I1 2 I2 2 L 1 + 2M + L 2 = 1 2 I2 2 [ ( L1 ( ) I1 + M ) 2 + (L 2 M 2 ) ] (14) L1 Y en particular, si se cumple que I 1 = M L 1, entonces se cumple ( L1 ( ) ) también que I1 + M L1 = 0, y en ese caso, la energía magnética pasa a valer: U m ]I 1 = 1 I2 = L M 1 2 I2 2 (L 2 M 2 ) (15) Ahora bien, cuando I 1 = M L 1, se debe seguir cumpliendo que U m 0. Por tanto, de acuerdo con la ecuación (15), se debe cumplir que: 1 2 I2 2 (L 2 M 2 ) 0 = L 2 M 2 0 = M 2 L 1 L 2 L 1 L 1 = k 2 L 1 L 2 L 1 L 2 = k 2 1 = 1 k +1 (16) con lo cual, queda demostrado que el valor absoluto del coeciente de acoplamiento entre dos espiras es menor o igual que 1. L 1 L 1

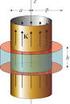
7 c Rafael R. Boix y Francisco Medina 7 Ejemplo Consideremos un solenoide toroidal de sección transversal rectangular. El solenoide se ha construido con un bobinado uniforme de N vueltas de un hilo conductor por el que circula una corriente estacionaria de intensidad I. La sección transversal del solenoide es un rectángulo de dimensiones (b a) h (vea la gura adjunta). Si suponemos que el solenoide está contenido en la región 0 z h y tomamos como eje z el eje de revolución del solenoide (vea la gura adjunta), el campo magnético creado por el solenoide en todos los puntos del espacio viene dado por: z=0 B = ρ=a µ 0 NI 2πρ u ϕ a < ρ < b y 0 < z < h 0 en otro caso De acuerdo con la ecuación (9), la energía magnética almacenada por el solenoide toroidal valdrá: U m = 1 B 2 dτ todo el espacio = 1 z=h ρ=b ϕ=2π µ 2 0N 2 4π 2 ρ ρdϕdρdz = µ ( ) 0 b 2 4π N 2 h ln (17) a ϕ=0 Por otro lado, de acuerdo con la ecuación (12), la energía magnética del solenoide toroidal está relacionada con su autoinducción

8 c Rafael R. Boix y Francisco Medina 8 L mediante la ecuación: U m = 1 2 LI2 (18) con lo cual, la autoinducción del solenoide toroidal puede calcularse a partir de la energía magnética mediante la ecuación: L = 2U m = µ 0N 2 ( ) h b ln (19) 2π a La ecuación (19) proporciona una alternativa para el cálculo de la autoinducción de un conductor en términos de la energía magnética almacenada.

Documentos relacionados

Rotacional del campo magnético creado por corrientes estacionarias. Ley de Ampère

c Rafael R. Boix y Francisco Medina 1 Rotacional del campo magnético creado por corrientes estacionarias. Ley de Ampère Consideremos un conductor que ocupa un volumen τ. Sea r el vector de posición de