Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada
|
|
|
- María Luz Cordero Carmona
- hace 6 años
- Vistas:
Transcripción
1 Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227C) Clase09-01 Elizabeth Villota Cerna Semestre 2010II - UNI 29/10/ Estabilidad En general, puede ser difícil obtener una solución explícita de las ecuaciones diferenciales no lineales que modelan un sistema dinámico. Sin embargo, a menudo no necesitamos conocer las soluciones explícitas de las ecuaciones del modelo. En su lugar, estamos interesados en el comportamiento de las soluciones a medida que el tiempo tiende a infinito. Adicionalmente, en muchos sistemas físicos un pequeño cambio en las condiciones iniciales resulta en un pequeño cambio en la solución. Específicamente si un sistema es perturbado de la posición de reposo, o de la posición de equilibrio, luego comienza a moverse. A grosso modo, podemos decir que una posición de equilibrio es estable si para pequeñas perturbaciones el sistema no se va muy lejos de esta posición. Este concepto es ilustrado mediante una bola que descansa en equilibrio en una hoja de metal doblada en varias formas con secciones transversales como mostrado en la Fig. 1. Esta figura presenta 4 escenarios posibles. Despreciando fuerzas de fricción, una pequeña perturbación del equilibrio lleva a: 1. Movimiento oscilatorio alrededor del punto de eequilibrio independientemente de la magnitud de las perturbaciones iniciales. Es este caso la posición de equilibrio es globalmente estable. 2. La nueva posición es también un equilibrio, y la bola permanecerá en esta posición. Aqui la posición de equilibrio es estable. 3. La bola se aleja y no retorna a la posición de equilibrio. La posición de equilibrio es inestable. 4. Movimiento oscilatorio en torno al equilibrio, a menos que la perturbación sea muy grande y la bola se vea forzada a oscilar en una nueva posición de equilibrio. La posición de equilibrio es localmente estable. (1) (2) (3) (4) Figura 1: Ilustración de posiciones de equilibrio estables e inestables. Si se toma en cuenta la fricción, el movimiento oscilatorio decrecerá permanentemente hasta que la bola retorne al punto de equilibrio como en los puntos 1 y 4 arriba. Nos referimos a tales posiciones de equilibrio como siendo asintóticamente estables. En la discusión de conceptos de estabilidad, implícitamente, se asume, como en el punto 4, que existe una región pequeña para las perturbaciones iniciales permitidas para la cual los movimientos subsecuentes convergen a la posición de equilibrio. Sin embargo, si, como en el punto 1, cualquier perturbación inicial conlleva a un movimiento que converge a la posición de equilibrio, entonces tenemos estabilidad asintótica global, que tambien se refiere como estabilidad asintótica en la grande.
2 8.1. Definiciones básicas de estabilidad Consideramos una clase de sistemas dinámicos modelados por la ecuación: ẋ(t) = f(t,x(t)), x(t o ) = x o, (1) donde x R n es el vector de estados y f : R R n R n es una función vectorial con los componentes: f i (t,x 1,x 2,...,x n ) : R R n R, i = 1,2,...,n. Asumiendo que los f i s son contínuos y que tienen derivadas parciales de primer orden contínuas. Bajo estas suposiciones, la solución de ẋ(t) = f(t,x(t)), x(t o ) = x o, existe y es única. Denotamos la solución como x(t) = x(t;t o,x o ). Si los f i s no dependen explícitamente de t, luego el sistema es representado como ẋ(t) = f(t,x(t)) = f(x(t)) y es llamado autónomo; de otra forma es llamado no autónomo. Un punto de equilibrio o estado es un vector constante, digamos x e, tal que: f(t,x e ) = 0, para todo t. Observese que un estado de equilibrio x e es una solución constante de (1). Si x e es un punto de equilibrio, siempre se puede transferir este punto de equilibrio al origen de R n mediante la definición de la siguiente variable: x = x x e. Asumamos que esto ya ha sido hecho para un punto de equilibrio en consideración. Entonces, tenemos: f(t,0) = 0 para todo t. A continuación introducimos definiciones básicas de estabilidad según Lyapunov ( ). En las siguientes consideraciones usaremos la norma Euclidiana estándar de un vector. Entonces, si x R n, luego: x = x 2 = (x T x) 1/2. Definición 1. Se dice que un estado de equilibrio x e es estable si para cualquier t o dado y cualquier escalar positivo ǫ, existe un escalar positivo δ = δ(t o,ǫ) tal que si x(t o ) x e < δ, luego x(t;t o,x o ) x e < ǫ para todo t t o. Friedland (ver referencias al final) realiza el siguiente comentario sobre la definición de estabilidad: Si esta definición epsilonica los deja frios, piensen en una competencia entre Ud, el diseñador del sistema, y un adversario (naturaleza?). El adversario escoge una región en el espacio de estados de radio ǫ y lo desafia a encontrar otra región, de radio δ, tal que si el estado inicial comienza dentro de tu región, luego permanecerá dentro de la región escogida por el adversario. Si Ud puede hacerlo, el sistema es estable. Definición 2. Un estado de equilibrio x e se dice que convergente, o atrayente, si para cualquier t o dado existe un escalar positivo δ 1 = δ 1 (t o ) tal que si x(t o ) x e < δ 1, entonces lím x(t;t o,x o ) = x e. t Reescribiremos la Definición 2 como sigue. Un estado de equilibrio x e es convergente si para cualquier t o existe un escalar positivo δ 1 = δ 1 (t o ) tal que si x(t o ) x e < δ 1, entonces para cualquier ǫ 1 > 0 dado existe T = T(ǫ 1,t o,x o ) tal que x(t;t o,x o ) x e < ǫ 1 para todo t > t o + T. Definición 3. Un estado de equilibrio x e es asintóticamente estable si es estable y convergente. Definición 4. Un estado de equilibrio x e se dice que es uniformemente estable si el escalar positivo δ = δ(t o,ǫ) introducido en la Definición 1 puede ser tomado independientemente del tiempo inicial t o. Clase09-01, pág. 2
3 Definición 5. Un estado de equilibrio x e se dice que es uniformemente convergente, o uniformente atrayente, si el escalar positivo δ 1 = δ 1 (t o ) y T = T(ǫ 1,t o,x o ) introducido en la Definición 2 son independientes del tiempo inicial t o. Las dos últimas definiciones permiten introducir la noción de estabilidad asintótica uniforme. Definición 6. Un estado de equilibrio x e se dice que es uniformemente asintóticamente estable si es uniformemente estable y uniformemente convergente. Nótese que la solución x(t) = x e debe primero ser estable para luego calificar como asintóticamente estable. Esto para prevenir que la trayectoria del sistema se aleje arbitrariamente del estado de equilibrio antes de que converja al mismo. Nótese también que el concepto de estabilidad y estabilidad asintótica segun Lyapunov son conceptos locales. Ellos se aplican al comportamiento del sistema en una pequeña vecindad del punto de equilibrio. Un caso especial de estabilidad asintótica uniforme es estabilidad exponencial uniforme que implica estabilidad uniforme e impone un requerimiento adicional que todas las soluciones que se originan cerca al punto de equilibrio dado, x e = 0, se acercan al equilibrio exponencialmente a medida que t. Más rigurosamente, decimos que x e = 0 es exponencialmente uniformemente estable si es estable y existen dos constantes positivas finitas γ y λ tal que para cualquier t o y x o, cualquier solución comenzando en la vecindad de cero satisface: x(t) γe λ(t to) x o. Nótese que γ no es menos que la unidad, y uniformidad implica que γ y λ son independientes de t o (ver Fig. 2). x 0 x 0 t 0 x(t) t^0 x^(t) t Figura 2: Ilustración de estabilidad exponencial uniforme: un límite de decaimiento exponencial es independiente del tiempo inicial t o. Un estado de equilibrio es inestable si no es estable. Una definición ǫ δ de inestabilidad es dada a continuación. Definición 7. Un estado de equilibrio x e se dice que es inestable si existe un ǫ > 0 tal que para cualquier δ > 0 existe x(t o ) tal que si x(t o ) x e < δ, entonces x(t 1 ) x e 0 para algún t 1 > t o. Una interpretación geométrica en dos dimensiones de las definiciones arriba está mostrada en la Fig. 3. Asumiendo que x e = 0 es el estado de equilibrio. Si el estado de equilibrio es estable, como en la Fig. 3(a), entonces dado un circulo externo de radio ǫ, entonces existe un circulo interno de radio δ tal que las trayectorias comenzando dentro del circulo-δ nunca dejen el circulo-ǫ. Si el estado de equilibrio es asintóticamente estable, entonces las trayectorias tienden al estado de equilibrio a medida que t tiende al. Esta situación es descrita en la Fig. 3(b). Finalmente, si el estado de equilibrio es inestable, como en la Fig. 3(c), entonces existe un circulo-ǫ tal que para cualquier circulo-δ existe una trayectoria comenzando dentro del mismo que deja el circulo-ǫ en algún tiempo posterior. Una interpretación geométrica del escenario descrito arriba en una dimensión está dada en la Fig. 4. Clase09-01, pág. 3
4 x 2 x 2 x 2 x(t 0 ) x 1 x(t 0 ) x 1 x 1 x(t 0 ) (a) (b) (c) Figura 3: Ilustración de conceptos de estabilidad en dos dimensiones. (a) Estado de equilibrio estable en el sentido de Lyapunov. (b) Estado de equilibrio asintóticamente estable. (c) Estado de equilibrio inestable. x(t) x(t) 0 t 0 t (a) (b) x(t) 0 t (c) Figura 4: Ilustración de conceptos de estabilidad en una dimensión. (a) Estado de equilibrio estable en el sentido de Lyapunov. (b) Estado de equilibrio asintóticamente estable. (c) Estado de equilibrio inestable Estabilidad según Lyapunov Sea V (x) = V (x 1,x 2,...,x n ) : R n R una función de valor real y sea S R n sea una región compacta conteniendo el origen x = 0 en su interior. Definición 8. Decimos que una función V = V (x) es semi definida positiva en S, con respecto a x = 0, si: 1. V es continuamente diferenciable, esto es, V C V (0) = V (x) 0 para todo x S. Definición 9. Decimos que una función V = V (x) es definida positiva en S, con respecto a x = 0, si: 1. V es continuamente diferenciable, esto es, V C V (0) = V (x) > 0 para todo x S \ {0}. El simbolo S \ {0} en el punto 3 arriba denota el conjunto {x : x S,x 0}. Definición 10. Decimos que una función V = V (x) es (semi)definida positiva globalmente si las definiciones arriba se cumplen para todo x R n ; de otra forma se dice que V = V (x) es (semi) definida positiva localmente. Clase09-01, pág. 4
5 Las funciones semidefinida negativa y definida negativa son definidas de la misma forma pero revertiendo los signos de desigualdad en el punto 3 de las dos definiciones de arriba. Nota: Para observar la diferencia entre funciones definida positiva y semi definida positiva, suponga que x R 2 y sea: V 1 (x) = x 2 1 V 2 (x) = x x 2 2. Ambas funciones V 1 y V 2 son siempre no negativas. Sin embargo, es posible que V 1 sea cero aún en el caso de que x 0. Especificamente, si fijamos x = (0,c), donde c R es cualquier número diferente de cero, entonces V 1 (x) = 0. Por otro lado, V 2 (x) = 0 si y solo si x = (0,0). Entonces V 1 (x) es semi definida positiva y V 2 (x) es definida positiva. Teorema 1. Sea V una función no negativa en R n y sea V la derivada en función del tiempo de V a lo largo de las trayectorias de la dinámica del sistema (1): V = V dx x dt = V x f(t,x(t)). Sea S r = S r (0) una bola de radio r alrededor del origen. Si existe r > 0 tal que V es definida positiva y V es semi definida negativa para todo x S r, luego x = 0 es localmente estable según Lyapunov. Si V es definida positiva y V es definida negativa para todo x S r, luego x = 0 es localmente asintóticamente estable. Demostración. Ver demostración del Teorema 3.1 en Nonlinear Systems, de H.K. Khalil, Notas: 1. Una función V que satisface las condiciones del teorema es llamada función de Lyapunov. 2. V (x) se puede definir como una función de energia que limita el tamaño de x. A continuación damos una interpretación geométrica del teorema de Lyapunov. Primero, nótese que la función: dv (x(t)) V =, dt puede ser expresada, usando la regla de la cadena como: V = V T ẋ = V ẋ cos θ, donde θ es el ángulo entre los vectores V y ẋ. Si ẋ = 1, entonces V T ẋ puede ser entendida como el incremento de V, evaluado en el punto x, en la dirección ẋ. Entonces, V < 0 si y solo si 90 o < θ < 270 o. En ese caso, el vector velocidad ẋ(t) apunta en la dirección de decrecimiento de V. Ilustramos la discusión presentando Fig. 5. V x V c 1 V c 2 c 1 Figura 5: Interpretación geométrica del teorema de Lyapunov. Notas: 1. P: Cómo encontramos la función de Lyapunov? R (antes del 2000): adivinar R (después del 2000): SOSTOOLS (MATLAB Toolbox), para sistemas polinomiales con coeficientes conocidos Clase09-01, pág. 5
6 2. Teorema inverso: si x e = 0 es asintóticamente estable entonces existe V definida positiva y V definida negativa. Esto implica, que si uno busca, uno puede encontrar una función de Lyapunov. 3. A menudo el caso de V (x) = x T Px funciona, donde P R n n es una matriz simétrica (P = P T ). La condición que V es definida positiva es equivalente a la condición que P una matriz definida positiva: x T Px > 0 para todo x 0, que se puede escribir como P > 0. Se puede mostrar que si P es simétrica y definida positiva entonces todos sus autovalores son reales y positivos. Los conjuntos nivel de x T Px son elipsoides Ejemplo 1 Sea el sistema: ẋ 1 = x 1 x 2 ẋ 2 = x 2, determinar la estabilidad del punto de equilibrio x = 0. Usando Luego x = 0 es globalmente asintóticamente estable. V (x) = x x 2 2 > 0, x 0 V (x) = 2x 1 ẋ 1 + 2x 2 ẋ 2 = 2x 2 1 2x 1 x 2 2x 2 2 = (x 1 + x 2 ) 2 x 2 1 x 2 2 < 0, x Ejemplo 2. Funciones de Lyapunov motivadas por la fisica del problema: péndulo Considere el péndulo, de masa unitaria, longitud unitaria, donde x 1 es el ángulo del péndulo con la vertical, y x 2 es la velocidad angular del péndulo. ẋ 1 = x 2 ẋ 2 = g sen x 1 Para demostrar que x e = 0 (péndulo apuntando hacia abajo) es un punto de equilibrio estable, considere la siguiente función como candidata a función de Lyapunov: V (x) = g(1 cos x 1 ) + x2 2 2, definida sobre el conjunto {x R n : π < x 1 < π} {0}. Luego, V (x) = [ g sen x 1 x 2 [ x 2 g sen x 1 = 0, entonces el punto de equilibrio x e = 0 es estable. Es el punto x e = 0 asintóticamente estable? Ejemplo 3. Funciones de Lyapunov motivadas por la fisica del problema: péndulo con fricción Considere el péndulo del ejemplo anterior pero esta vez incluya fricción unitaria: Sea la función de Lyapunov candidata: ẋ 1 = x 2 ẋ 2 = g sen x 1 x 2 V (x) = g(1 cos x 1 ) + x2 2 2, definida sobre el conjunto {x R n : π < x 1 < π} {0}. Luego, V (x) = [ g sen x 1 x 2 [ x 2 g sen x 1 x 2 = x 2 2, Clase09-01, pág. 6
7 entonces V (x) es semidefinida negativa. No es definida negativa porque V (x) = 0 para x 2 = 0 independientemente del valor de x 1 ; esto es V (x) = 0 a lo largo del eje x 1. De ahí que solo podamos concluir que el origen es estable. Sin embargo, si graficaramos el diagrama de plano de fase de la ecuación del péndulo se podría observar que el origen es asintóticamente estable. La función de Lyapunov no demuestra este último hecho. A continuación se presenta un teorema (corolario) enunciado por LaSalle que nos permitirá extender las conclusiones de estabilidad del origen usando funciones de Lyapunov. Corolario 1 Sea x = 0 un punto de equilibrio para el sistema (1). Sea V : S R una función definida positiva contínuamente diferenciable en el dominio S que contiene al origen x = 0, tal que V (x) 0 en S. Sea M = {x S V (x) = 0} y suponer que ninguna solución puede estar en M, excepto la solución trivial. Luego el origen es asintóticamente estable. Demostración Ver Khalil, Sección Principio de Invariancia Ejemplo 4. Funciones de Lyapunov motivadas por la fisica del problema: control de posición de un robot Una tarea fundamental en robótica para los manipuladores es transferir objetos de un punto a otro, el problema de control de posición de un robot. Muchas de las aplicaciones venían haciendo uso de controladores proporcionales derivativos; sin embargo, no se presentaba una justificación teórica para la estabilidad de tales sistemas de control debido a la dinámica altamente no lineal del robot. Un robot consiste en un número de eslabones conectadas por juntas translacionales o rotacionales, siendo que el último eslabón posee una especie de efector (actuador final). La dinámica de un brazo robótico de n-eslabones puede ser representado por: H(q) q + b(q, q) + g(q) = τ, donde q es el vector n-dimensional que describe la posición de las juntas, τ es el vector de torques de entrada, g es el vector de torques gravitacionales, b representa las fuerzas de Coriolis y fuerzas centripetas causadas por el movimiento de los eslabones, y H es la matriz de inercias n n del brazo robotico. Considere un controlador compuesto por un término proporcional derivativo y un término de compensación de gravedad. τ = K D q K P q + g(q), donde K D y K P son matrices constantes definidas negativas. Con la ayuda de un entendimiento físico del problema, se puede encontrar una función de Lyapunov para un sistema robótico complejo. Primero, nótese que la matriz de inercia H(q) es definida positiva para cualquier q. Segundo, el término de control PD puede ser interpretado como una combinación de resortes y amortiguadores. Este análisis sugiere la siguiente función de Lyapunov candidata: V = 1 2 [ qt H q + q T K p q, donde el primer término representa la energia cinética del manipulador, y el segundo término denota la energia potencial artificial asociada al resorte virtual en la ley de control. Para calcular la derivada de la función V se puede usar el teorema de energia en mecánica que estipula que la variación en la energia cinética es igual a la potencia dotada por las fuerzas externas. Entonces: V = q T (τ g) + q T K P q. Substituyendo la ley de control en la ecuación arriba se tiene: V = q T K D q 0. Y del Teorema 1, el origen es estable. Analizando el caso cuando V (q, q) = 0: q = 0 y siendo que el brazo no puede atorarse en una posición tal que q 0 (que puede mostrarse fácilmente notando que la aceleración es diferente de cero en tales situaciones), el brazo robótico debe establecerse en q = 0. Luego, usando el Corolario 1, el origen es en realidad globalmente asintóticamente estable. Dos lecciones se pueden sacar de este ejemplo prático: 1) usar las propiedades físicas como sea posible cuando se analice el comportamiento del sistema, y 2) conceptos físicos como energia nos llevan a elecciones acertadas de funciones de Lyapunov. Clase09-01, pág. 7
8 Figura 6: Un manipulador robótico Funciones de Lyapunov para sistemas lineales Considere un sistema dinámico lineal invariante en el tiempo modelado por la ecuación: Consideramos la función de Lyapunov cuadrática: ẋ = Ax, x(t o ) = x o. V (x) = x T Px, donde P es una matriz n n real simétrica. La derivada en función del tiempo de V (x(t)) evaluada en la solución de ẋ = Ax es: dv (x(t)) = dt V (t) = ẋ T (t)px(t) + x T (t)pẋ(t). Sustituyendo ẋ = Ax y ẋ T = x T A T en la ecuación arriba resulta en: V = x T A T Px + x T PAx = x T (A T P + PA)x. El requerimiento que la función V sea definida positiva es equivalente a que la matriz P sea definida positiva (P > 0); y el requerimiento que V sea definida negativa es equivalente a la condición: Q = A T P + PA < 0, (2) (como matriz). Luego el problema se centra en determinar si la matriz simétrica Q definida por la denominada ecuación de Lyapunoven (2) es definida negativa. Si este es el caso luego V satisface las condiciones del Teorema 1, y el origen es globalmente asintóticamente estable Ejemplo 1 Sea un sistema lineal donde: es asintóticamente estable. Eligiendo P como: P = A = [ [ , = I 2 > 0. Luego, Q = A T P + PA = [ , Clase09-01, pág. 8
9 que es indefinida. Entonces, a menos que Q resultase definida negativa, nada se puede inferir acerca de la estabilidad asintótica, usando el teorema de Lyapunov, para cuando comenzamos con P y luego calculamos Q. Una forma más útil de estudiar la estabilidad de sistemas lineales usando funciones cuadráticas es encontrando una matriz P para una función Q definida negativa dada; así: elegir una matriz Q definida negativa resolver para P de la ecuación de Lyapunov en (2) verficar si P es definida positiva Si P es definida positiva, luego x T Px es una función de Lyapunov para el sistema lineal y la estabilidad asintótica global está garantizada Ejemplo 2 Considere el sistema lineal: dx 1 dt dx 2 dt con a,b,c > 0, para el cual tenemos: [ a 0 A = b c = ax 1 = bx 1 cx 2. P = [ p11 p 12. p 21 p 22 Elegimos Q = I R 2 2 y la ecuación de Lyapunov correspondiente es: [ [ [ [ a b p11 p 12 p11 p + 12 a 0 = 0 c p 21 p 22 p 21 p 22 b c [ y resolviendo para los elementos de P tenemos: P = o la correspondiente función de Lyapunov: [ b 2 +ac+c 2 2a 2 c+2ac 2 b 2c(a+c) b 2c(a+c) 1 2 V (x) = b2 + ac + c 2 b 2a 2 c + 2ac 2 x2 1 2c(a + c) x 1x x2 2. Es fácil verificar que P (verificar los autovalores) y por construcción V = I < 0. Entonces el origen es globalmente asintóticamente estable. Fuente: Capítulo 4 del libro Systems and Control de Stanislaw H. Zak, Oxford University Press, Fuente: Nonlinear Systems, de H.K. Khalil, Macmillan Publishing Company, Fuente: Nonlinear Systems Analysis, de M. Vidyasagar, Prentice-Hall, Second Edition, Fuente: Advanced Control System Design, de B. Friedland, Prentice-Hall, Clase09-01, pág. 9
Carlos Mario Vélez S. Universidad EAFIT. Temas 1. Generalidades sobre estabilidad 2. Estabilidad de Lyapunov
 Objetivo específico Presentar la teoría de estabilidad de Lyapunov aplicada a sistema lineales y no lineales e ilustrar su uso en el análisis y diseño de sistemas no lineales Temas.. Método directo de
Objetivo específico Presentar la teoría de estabilidad de Lyapunov aplicada a sistema lineales y no lineales e ilustrar su uso en el análisis y diseño de sistemas no lineales Temas.. Método directo de
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada
 Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 7C) Clase-b Elizabeth Villota Cerna Semestre II - UNI 8/9/.3.
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 7C) Clase-b Elizabeth Villota Cerna Semestre II - UNI 8/9/.3.
Análisis de Sistemas No Lineales
 Análisis de Sistemas No Lineales Análisis de Estabilidad: Caso No Autónomo Dr. Fernando Ornelas Tellez Universidad Michoacana de San Nicolas de Hidalgo Morelia, Michoacán Sistemas de Control Dr. Fernando
Análisis de Sistemas No Lineales Análisis de Estabilidad: Caso No Autónomo Dr. Fernando Ornelas Tellez Universidad Michoacana de San Nicolas de Hidalgo Morelia, Michoacán Sistemas de Control Dr. Fernando
Prof. Virginia Mazzone - Mariana Suarez
 SISTEMAS NO LINEALES SISTEMAS DE SEGUNDO ORDEN Prof. Virginia Mazzone - Prof. Mariana Suarez 1 Introducción Método de isoclinas Ejemplos 3 Introducción Un sistema de segundo orden autónomo está representado
SISTEMAS NO LINEALES SISTEMAS DE SEGUNDO ORDEN Prof. Virginia Mazzone - Prof. Mariana Suarez 1 Introducción Método de isoclinas Ejemplos 3 Introducción Un sistema de segundo orden autónomo está representado
8.4. CRITERIO DE ESTABILIDAD POR EL METODO DIRECTO DE LIAPUNOV
 8.4. CRITERIO DE ESTAB.: METODO DE LIAPUNOV 309 8.4. CRITERIO DE ESTABILIDAD POR EL METODO DIRECTO DE LIAPUNOV Consideremos el sistema autónomo dx = F (x, y) dt (8.32) dt = G(x, y), y supongamos que tiene
8.4. CRITERIO DE ESTAB.: METODO DE LIAPUNOV 309 8.4. CRITERIO DE ESTABILIDAD POR EL METODO DIRECTO DE LIAPUNOV Consideremos el sistema autónomo dx = F (x, y) dt (8.32) dt = G(x, y), y supongamos que tiene
EJERCICIOS RESUELTOS Y PROPUESTOS
 UNIVERSIDAD NACIONAL DE INGENIERÍA Facultad de Ingeniería Mecánica MT 227 Control Moderno y Óptimo EJERCICIOS RESUELTOS Y PROPUESTOS Estabilidad según Lyapunov (1) Un buen modelo de un niño impulsandose
UNIVERSIDAD NACIONAL DE INGENIERÍA Facultad de Ingeniería Mecánica MT 227 Control Moderno y Óptimo EJERCICIOS RESUELTOS Y PROPUESTOS Estabilidad según Lyapunov (1) Un buen modelo de un niño impulsandose
CAPITULO 4 ESTABILIDAD. Ing. Diego Alejandro Patiño G. M. Sc., Ph. D.
 CAPITULO 4 ESTABILIDAD Ing. Diego Alejandro Patiño G. M. Sc., Ph. D. Estabilidad Cada punto donde la bola se puede detener es un punto de equilibrio. A y F: puntos inestables: un cambio infinitesimal en
CAPITULO 4 ESTABILIDAD Ing. Diego Alejandro Patiño G. M. Sc., Ph. D. Estabilidad Cada punto donde la bola se puede detener es un punto de equilibrio. A y F: puntos inestables: un cambio infinitesimal en
Estabilidad. Sea un sistema dinámico, autónomo y estacionario lineal o no lineal, con x a como vector de estado. Un punto se dice de equilibrio si
 Estabilidad Sea un sistema dinámico, autónomo y estacionario lineal o no lineal, dx a (t) dt = F(x a (t)) con x a como vector de estado. Un punto se dice de equilibrio si dx a (t) dt = F(c) = 0. Para saber
Estabilidad Sea un sistema dinámico, autónomo y estacionario lineal o no lineal, dx a (t) dt = F(x a (t)) con x a como vector de estado. Un punto se dice de equilibrio si dx a (t) dt = F(c) = 0. Para saber
Sistemas autónomos. Introducción a la teoría cualitativa.
 Lección 4 Sistemas autónomos. Introducción a la teoría cualitativa. 4.1 Sistemas autónomos. Mapas de fase. En esta lección nos centraremos en el estudio de sistemas autónomos, es decir, aquellos que pueden
Lección 4 Sistemas autónomos. Introducción a la teoría cualitativa. 4.1 Sistemas autónomos. Mapas de fase. En esta lección nos centraremos en el estudio de sistemas autónomos, es decir, aquellos que pueden
MT227 Sistemas Lineales. Función de transferencia. Elizabeth Villota
 MT227 Sistemas Lineales. Función de transferencia Elizabeth Villota 1 Sistemas Lineales Sistema no lineal, forma espacio de estados: Sea la salida correspondiente a la condición inicial y entrada escrita
MT227 Sistemas Lineales. Función de transferencia Elizabeth Villota 1 Sistemas Lineales Sistema no lineal, forma espacio de estados: Sea la salida correspondiente a la condición inicial y entrada escrita
VI. Sistemas de dos grados de libertad
 Objetivos: 1. Describir que es un sistema de dos grados de.. Deducir las ecuaciones diferenciales de movimiento para un sistema de dos grados de masa-resorte-amortiguador, con amortiguamiento viscoso y
Objetivos: 1. Describir que es un sistema de dos grados de.. Deducir las ecuaciones diferenciales de movimiento para un sistema de dos grados de masa-resorte-amortiguador, con amortiguamiento viscoso y
CÁLCULO II Grados en Ingeniería
 CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
PROGRAMA DE FÍSICA I TEORÍA
 Pág. 1/5 UNIVERSIDAD NACIONAL EXPERIMENTAL DEL TÁCHIRA VICE RECTORADO ACADÉMICO DECANATO DE DOCENCIA DEPARTAMENTO DE MATEMÁTICA Y FÍSICA PROGRAMA DE FÍSICA I TEORÍA Código: 0846203T Teoría: 4 horas/semana
Pág. 1/5 UNIVERSIDAD NACIONAL EXPERIMENTAL DEL TÁCHIRA VICE RECTORADO ACADÉMICO DECANATO DE DOCENCIA DEPARTAMENTO DE MATEMÁTICA Y FÍSICA PROGRAMA DE FÍSICA I TEORÍA Código: 0846203T Teoría: 4 horas/semana
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS
 Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
VECTORES : Las Cantidades Vectoriales cantidades escalares
 VECTORES En física hay dos tipos de cantidades: Las Cantidades Vectoriales son aquellas que tiene tanto magnitud como dirección y sentido sobre la dirección), mientras que las cantidades escalares son
VECTORES En física hay dos tipos de cantidades: Las Cantidades Vectoriales son aquellas que tiene tanto magnitud como dirección y sentido sobre la dirección), mientras que las cantidades escalares son
Esta relación se obtiene mediante el denominado modelo dinámico, que relaciona matemáticamente:
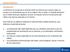 Introducción La dinámica se ocupa de la relación entre las fuerzas que actúan sobre un cuerpo y el movimiento que en el se origina. Por lo tanto, el modelo dinámico de un robot tiene por objetivo conocer
Introducción La dinámica se ocupa de la relación entre las fuerzas que actúan sobre un cuerpo y el movimiento que en el se origina. Por lo tanto, el modelo dinámico de un robot tiene por objetivo conocer
Robótica 4. Control de robots F. Hugo Ramírez Leyva
 Robótica 4. Control de robots F. Hugo Ramírez Leyva Cubículo 3 Instituto de Electrónica y Mecatrónica hugo@mixteco.utm.mx Marzo 2012 Representación en Variables de estado Un sistema dinámico no lineal
Robótica 4. Control de robots F. Hugo Ramírez Leyva Cubículo 3 Instituto de Electrónica y Mecatrónica hugo@mixteco.utm.mx Marzo 2012 Representación en Variables de estado Un sistema dinámico no lineal
UNIVERSIDAD TECNOLÓGICA DE PEREIRA FACULTAD DE TECNOLOGÍAS ESCUELA DE TECNOLOGÍA MECÁNICA FUNDAMENTACIÓN CIENTÍFICA
 UNIVERSIDAD TECNOLÓGICA DE PEREIRA FACULTAD DE TECNOLOGÍAS ESCUELA DE TECNOLOGÍA MECÁNICA ASIGNATURA: CÓDIGO: ÁREA: REQUISITO: FÍSICA I CB234 FUNDAMENTACIÓN CIENTÍFICA Matemática I CB15 con nota 2.0 HORAS
UNIVERSIDAD TECNOLÓGICA DE PEREIRA FACULTAD DE TECNOLOGÍAS ESCUELA DE TECNOLOGÍA MECÁNICA ASIGNATURA: CÓDIGO: ÁREA: REQUISITO: FÍSICA I CB234 FUNDAMENTACIÓN CIENTÍFICA Matemática I CB15 con nota 2.0 HORAS
Capítulo VI. Diferenciabilidad de funciones de varias variables
 Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada
 Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227C) Clase5-2 Elizabeth Villota Cerna Semestre 2I - UNI
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 227C) Clase5-2 Elizabeth Villota Cerna Semestre 2I - UNI
Una aplicación al péndulo de Furuta
 Capítulo 4 Una aplicación al péndulo de Furuta Los péndulos invertidos se han convertido en unos dispositivos muy populares para el análisis de control no-lineal y para propósitos educativos. El primer
Capítulo 4 Una aplicación al péndulo de Furuta Los péndulos invertidos se han convertido en unos dispositivos muy populares para el análisis de control no-lineal y para propósitos educativos. El primer
Ambiente gráfico de simulación de un péndulo.
 Ambiente gráfico de simulación de un péndulo. J. A. Mijares, F. Reyes, S. Vergara, D. Rojas, J. Salome Av. San Claudio y 18 Sur, C.U. San Manuel, Edificio 109-A, 7570, Puebla, Pue. Grupo de robótica, FCE-BUAP
Ambiente gráfico de simulación de un péndulo. J. A. Mijares, F. Reyes, S. Vergara, D. Rojas, J. Salome Av. San Claudio y 18 Sur, C.U. San Manuel, Edificio 109-A, 7570, Puebla, Pue. Grupo de robótica, FCE-BUAP
Semana 13 Análisis cualitativo de Sistemas No Lineales Retratos de Fase
 Matemáticas Aplicadas MA101 Semana 13 Análisis cualitativo de Sistemas No Lineales Retratos de Fase Elizabeth Villota Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Sistemas de coeficientes
Matemáticas Aplicadas MA101 Semana 13 Análisis cualitativo de Sistemas No Lineales Retratos de Fase Elizabeth Villota Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Sistemas de coeficientes
Capítulo 2 Resolución de la Ecuación de Oscilación
 ELC-3054 Sistemas de Potencia II Capítulo Resolución de la Ecuación de Oscilación Prof. Francisco M. González-Longatt fglongatt@ieee.org http://www.giaelec.org/fglongatt/sp.htm Sistemas de Potencia II
ELC-3054 Sistemas de Potencia II Capítulo Resolución de la Ecuación de Oscilación Prof. Francisco M. González-Longatt fglongatt@ieee.org http://www.giaelec.org/fglongatt/sp.htm Sistemas de Potencia II
Mediante este programa se persigue desarrollar las siguientes habilidades:
 PROPÓSITO: El programa de esta asignatura está dirigido a los estudiantes del primer semestre de la Facultad de Ingeniería, con la finalidad de ofrecerles una capacitación teórica práctica en los principios
PROPÓSITO: El programa de esta asignatura está dirigido a los estudiantes del primer semestre de la Facultad de Ingeniería, con la finalidad de ofrecerles una capacitación teórica práctica en los principios
Estabilidad entrada-salida LTI
 Estabilidad p. 1/24 Estabilidad entrada-salida LTI En un sistema inestable cualquier perturbación, por pequeña que sea, llevará a estados y/o salidas a crecer sin límite o hasta que el sistema se queme,
Estabilidad p. 1/24 Estabilidad entrada-salida LTI En un sistema inestable cualquier perturbación, por pequeña que sea, llevará a estados y/o salidas a crecer sin límite o hasta que el sistema se queme,
Cinemática y Dinámica
 Cinemática y Dinámica Cinética de la partícula Objetivo: El alumno aplicará las leyes de Newton en la resolución de ejercicios de movimiento de la partícula en un plano, donde intervienen las causas que
Cinemática y Dinámica Cinética de la partícula Objetivo: El alumno aplicará las leyes de Newton en la resolución de ejercicios de movimiento de la partícula en un plano, donde intervienen las causas que
2DA PRÁCTICA CALIFICADA
 2DA PRÁCTICA CALIFICADA DINÁMICA (IC 244) ALUMNOS : CARITAS BARRIENTOS, Ronald ROBLES ROCHA, Hamilton TORRES PÉREZ, Walter A. TORO VELARDE, William DOCENTE : Ing. CASTRO PÉREZ, Cristian CINÉTICA DE UNA
2DA PRÁCTICA CALIFICADA DINÁMICA (IC 244) ALUMNOS : CARITAS BARRIENTOS, Ronald ROBLES ROCHA, Hamilton TORRES PÉREZ, Walter A. TORO VELARDE, William DOCENTE : Ing. CASTRO PÉREZ, Cristian CINÉTICA DE UNA
Lugar Geométrico de las Raíces Herramienta para diseño de sistemas de control
 Lugar Geométrico de las Raíces Herramienta para diseño de sistemas de control Elizabeth Villota Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica UNI-FIM 1 Modelado Modelo: representación
Lugar Geométrico de las Raíces Herramienta para diseño de sistemas de control Elizabeth Villota Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica UNI-FIM 1 Modelado Modelo: representación
Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena
 1 Universidad Simón Bolívar. Preparaduría nº 3. christianlaya@hotmail.com ; @ChristianLaya Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena Derivada
1 Universidad Simón Bolívar. Preparaduría nº 3. christianlaya@hotmail.com ; @ChristianLaya Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena Derivada
III. Vibración con excitación armónica
 Objetivos: 1. Definir que es vibración con excitación.. Analizar la respuesta de un sistema no amortiguado con excitación. 3. Analizar la respuesta de un sistema amortiguado con excitación. 4. Analizar
Objetivos: 1. Definir que es vibración con excitación.. Analizar la respuesta de un sistema no amortiguado con excitación. 3. Analizar la respuesta de un sistema amortiguado con excitación. 4. Analizar
Dinámica del movimiento rotacional
 Dinámica del movimiento rotacional Torca, momento angular, momento cinético o momento de torsión: La habilidad de una fuerza para rotar o girar un cuerpo alrededor de un eje. τ = r F r= es la posición
Dinámica del movimiento rotacional Torca, momento angular, momento cinético o momento de torsión: La habilidad de una fuerza para rotar o girar un cuerpo alrededor de un eje. τ = r F r= es la posición
VALORES Y VECTORES PROPIOS
 VALORES Y VECTORES PROPIOS En diversos campos de la ingeniería y las matemáticas surge el problema de calcular los valores escalares λ y los vectores x 0 tales que para la matriz cuadrada A se cumple Ax
VALORES Y VECTORES PROPIOS En diversos campos de la ingeniería y las matemáticas surge el problema de calcular los valores escalares λ y los vectores x 0 tales que para la matriz cuadrada A se cumple Ax
El Sistema de Lorenz
 Capítulo 4 El Sistema de Lorenz Este sistema fué encontrado por E. Lorenz en el año 1963, el objetivo que Lorenz tenía, era el de, mediante este sistema, poder predecir el clima. Los resultados no fueron
Capítulo 4 El Sistema de Lorenz Este sistema fué encontrado por E. Lorenz en el año 1963, el objetivo que Lorenz tenía, era el de, mediante este sistema, poder predecir el clima. Los resultados no fueron
1 Control Óptimo. 1.1 Introducción Problema típico de control óptimo
 1 Control Óptimo 1.1 Introducción El control óptimo es una rama del control moderno que se relaciona con el diseño de controladores para sistemas dinámicos tal que se minimice una función de medición que
1 Control Óptimo 1.1 Introducción El control óptimo es una rama del control moderno que se relaciona con el diseño de controladores para sistemas dinámicos tal que se minimice una función de medición que
UNIVERSIDAD JUAREZ AUTONOMA DE TABASCO DIVISIÓN ACADEMICA DE CIENCIAS BIOLÓGICAS LICENCIATURA EN INGENIERIA AMBIENTAL PROGRAMA DE ESTUDIOS: MECANICA
 UNIVERSIDAD JUAREZ AUTONOMA DE TABASCO DIVISIÓN ACADEMICA DE CIENCIAS BIOLÓGICAS LICENCIATURA EN INGENIERIA AMBIENTAL PROGRAMA DE ESTUDIOS: MECANICA ASIGNATURA: MECANICA CARRERA: INGENIERIA AMBIENTAL CREDITOS:
UNIVERSIDAD JUAREZ AUTONOMA DE TABASCO DIVISIÓN ACADEMICA DE CIENCIAS BIOLÓGICAS LICENCIATURA EN INGENIERIA AMBIENTAL PROGRAMA DE ESTUDIOS: MECANICA ASIGNATURA: MECANICA CARRERA: INGENIERIA AMBIENTAL CREDITOS:
ECUACIONES DIFERENCIALES ORDINARIAS. HOJA 8. Conjuntos invariantes
 ECUACIONES DIFERENCIALES ORDINARIAS. HOJA 8. CONJUNTOS INVARIANTES Y CONJUNTOS LÍMITE. ESTABILIDAD POR EL MÉTODO DE LIAPUNOV. Conjuntos invariantes 1. Definición. Se dice que un conjunto D Ω es positivamente
ECUACIONES DIFERENCIALES ORDINARIAS. HOJA 8. CONJUNTOS INVARIANTES Y CONJUNTOS LÍMITE. ESTABILIDAD POR EL MÉTODO DE LIAPUNOV. Conjuntos invariantes 1. Definición. Se dice que un conjunto D Ω es positivamente
, la ley anterior se convierte en la ecuación de movimiento de la partícula: una ecuación diferencial para la posición r,
 Repaso de la mecánica de Newton Arrancamos de la segunda ley de Newton sin aclaraciones que vendrán más tarde. (1.1) Especificada la fuerza, la ley anterior se convierte en la ecuación de movimiento de
Repaso de la mecánica de Newton Arrancamos de la segunda ley de Newton sin aclaraciones que vendrán más tarde. (1.1) Especificada la fuerza, la ley anterior se convierte en la ecuación de movimiento de
La función, definida para toda, es periódica si existe un número positivo tal que
 Métodos con series de Fourier Definición: Función periódica La función, definida para toda, es periódica si existe un número positivo tal que para toda. El número en un periodo de la función. Si existe
Métodos con series de Fourier Definición: Función periódica La función, definida para toda, es periódica si existe un número positivo tal que para toda. El número en un periodo de la función. Si existe
Convolución: Un proceso natural en los sistemas lineales e invariantes en el tiempo.
 Convolución: Un proceso natural en los sistemas lineales e invariantes en el tiempo. Introducción. En este documento se describe como el proceso de convolución aparece en forma natural cuando se trata
Convolución: Un proceso natural en los sistemas lineales e invariantes en el tiempo. Introducción. En este documento se describe como el proceso de convolución aparece en forma natural cuando se trata
Indice. Cinemática de la Partícula Introducción
 Indice Cinemática de la Partícula Introducción Un fenómeno que siempre está presente y que observamos a nuestro alrededor es el movimiento. La cinemática es la parte de la Física que describe los posibles
Indice Cinemática de la Partícula Introducción Un fenómeno que siempre está presente y que observamos a nuestro alrededor es el movimiento. La cinemática es la parte de la Física que describe los posibles
MOVIMIENTO OSCILATORIO O VIBRATORIO
 MOVIMIENTO OSCILATORIO O VIBRATORIO 1. Movimiento armónico simple (MAS). 2. Ecuaciones del MAS. 3. Dinámica del MAS. 4. Energía del MAS. 5. El oscilador armónico. 6. El péndulo simple. Física 2º bachillerato
MOVIMIENTO OSCILATORIO O VIBRATORIO 1. Movimiento armónico simple (MAS). 2. Ecuaciones del MAS. 3. Dinámica del MAS. 4. Energía del MAS. 5. El oscilador armónico. 6. El péndulo simple. Física 2º bachillerato
Universidad Pontificia Bolivariana. Escuela de Ingenierías. Centro Ciencia Básica
 Universidad Pontificia Bolivariana. Escuela de Ingenierías. Centro Ciencia Básica Curso: Fundamentos de mecánica. 2015 20 Programación por semanas (teoría y práctica) Texto de apoyo Serway-Jewtt novena
Universidad Pontificia Bolivariana. Escuela de Ingenierías. Centro Ciencia Básica Curso: Fundamentos de mecánica. 2015 20 Programación por semanas (teoría y práctica) Texto de apoyo Serway-Jewtt novena
Cinemática del sólido rígido
 Cinemática del sólido rígido Teoría básica para el curso Cinemática del sólido rígido, ejercicios comentados α δ ω B B A A P r B AB A ω α O Ramírez López-Para, Pilar Loizaga Garmendia, Maider López Soto,
Cinemática del sólido rígido Teoría básica para el curso Cinemática del sólido rígido, ejercicios comentados α δ ω B B A A P r B AB A ω α O Ramírez López-Para, Pilar Loizaga Garmendia, Maider López Soto,
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 01/02
 Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
Tema 2: Movimiento unidimensional
 Tema 2: Movimiento unidimensional FISICA I, 1º Grado en Ingeniería Electrónica, Robótica y Mecatrónica Escuela Técnica Superior de Ingeniería Universidad de Sevilla 1 Índice Introducción Vector de posición
Tema 2: Movimiento unidimensional FISICA I, 1º Grado en Ingeniería Electrónica, Robótica y Mecatrónica Escuela Técnica Superior de Ingeniería Universidad de Sevilla 1 Índice Introducción Vector de posición
Examen de Física-1, 1 Ingeniería Química Examen final. Enero de 2013 Problemas (Dos puntos por problema).
 Examen de Física-1, 1 Ingeniería Química Examen final. Enero de 013 Problemas Dos puntos por problema. Problema 1 Primer parcial: El radio de una noria de feria mide 5 m y da una vuelta en 10 s. a Hállese
Examen de Física-1, 1 Ingeniería Química Examen final. Enero de 013 Problemas Dos puntos por problema. Problema 1 Primer parcial: El radio de una noria de feria mide 5 m y da una vuelta en 10 s. a Hállese
Ecuaciones Diferenciales Ordinarias MA26A Sistemas No Lineales
 Ecuaciones Diferenciales Ordinarias MA26A Sistemas No Lineales Profesor: Axel Osses, Auxiliares: Jorge Lemus,Oscar Peredo 7 de Noviembre del 2005 1. Definiciones y Propiedades Definición 1 (SNLA). Dado
Ecuaciones Diferenciales Ordinarias MA26A Sistemas No Lineales Profesor: Axel Osses, Auxiliares: Jorge Lemus,Oscar Peredo 7 de Noviembre del 2005 1. Definiciones y Propiedades Definición 1 (SNLA). Dado
MODELACION EN VARIABLES DE ESTADO
 CAPÍTULO VIII INGENIERÍA DE SISTEMAS I MODELACION EN VARIABLES DE ESTADO 8.1. DEFINICIONES Estado: El estado de un sistema dinámico es el conjunto más pequeño de variables de modo que el conocimiento de
CAPÍTULO VIII INGENIERÍA DE SISTEMAS I MODELACION EN VARIABLES DE ESTADO 8.1. DEFINICIONES Estado: El estado de un sistema dinámico es el conjunto más pequeño de variables de modo que el conocimiento de
Capítulo 10. Rotación de un Cuerpo Rígido
 Capítulo 10 Rotación de un Cuerpo Rígido Contenido Velocidad angular y aceleración angular Cinemática rotacional Relaciones angulares y lineales Energía rotacional Cálculo de los momentos de inercia Teorema
Capítulo 10 Rotación de un Cuerpo Rígido Contenido Velocidad angular y aceleración angular Cinemática rotacional Relaciones angulares y lineales Energía rotacional Cálculo de los momentos de inercia Teorema
Estudia las propiedades geométricas de las trayectorias que describen los cuerpos en movimiento mecánico, independientemente de la masa del cuerpo y
 CINEMÁTICA CINEMÁTICA (MRU) CONCEPTO DE CINEMÁTICA Estudia las propiedades geométricas de las trayectorias que describen los cuerpos en movimiento mecánico, independientemente de la masa del cuerpo y de
CINEMÁTICA CINEMÁTICA (MRU) CONCEPTO DE CINEMÁTICA Estudia las propiedades geométricas de las trayectorias que describen los cuerpos en movimiento mecánico, independientemente de la masa del cuerpo y de
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada
 Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 7C) Clase - Elizabeth Villota Cerna Semestre 9 I - UNI 3/7/9
Universidad Nacional de Ingeniería - Facultad de Ingeniería Mecánica Departamento Académico de Ingeniería Aplicada CONTROL MODERNO Y ÓPTIMO (MT 7C) Clase - Elizabeth Villota Cerna Semestre 9 I - UNI 3/7/9
1. TEORIA DE ESTABILIDAD DE SISTEMAS DINAMICOS
 1. TEORIA DE ESTABILIDAD DE SISTEMAS DINAMICOS El Segundo Método de Lyapunov (caso autónomo) Este reporte presenta el método directo de Lyapunov para determinar la estabilidad o estabilidad asintótica
1. TEORIA DE ESTABILIDAD DE SISTEMAS DINAMICOS El Segundo Método de Lyapunov (caso autónomo) Este reporte presenta el método directo de Lyapunov para determinar la estabilidad o estabilidad asintótica
Campo Eléctrico. Es el portador de la fuerza eléctrica. q 2. q 1
 Campo Eléctrico Es el portador de la fuerza eléctrica. q 1 q 2 E1 E2 Por qué se usa el campo eléctrico? Porque es útil simplificar el problema separándolo en partes. Porque nos permite pensar en una situación
Campo Eléctrico Es el portador de la fuerza eléctrica. q 1 q 2 E1 E2 Por qué se usa el campo eléctrico? Porque es útil simplificar el problema separándolo en partes. Porque nos permite pensar en una situación
Teoria de Semigrupos y su estabilidad. Jaime E. Muñoz Rivera LNCC IM-UFRJ
 Teoria de Semigrupos y su estabilidad Jaime E. Muñoz Rivera LNCC IM-UFRJ La ecuación de primera orden Cuando A es un número real la solución es dada por : Para sistemas de ecuaciones diferenciales introducimos:
Teoria de Semigrupos y su estabilidad Jaime E. Muñoz Rivera LNCC IM-UFRJ La ecuación de primera orden Cuando A es un número real la solución es dada por : Para sistemas de ecuaciones diferenciales introducimos:
Lección 2: Funciones vectoriales: límite y. continuidad. Diferenciabilidad de campos
 Lección 2: Funciones vectoriales: límite y continuidad. Diferenciabilidad de campos vectoriales 1.1 Introducción En economía, frecuentemente, nos interesa explicar la variación de unas magnitudes respecto
Lección 2: Funciones vectoriales: límite y continuidad. Diferenciabilidad de campos vectoriales 1.1 Introducción En economía, frecuentemente, nos interesa explicar la variación de unas magnitudes respecto
Semana 06 EDO de orden alto - Aplicaciones
 Matemáticas Aplicadas MA101 Semana 06 EDO de orden alto - Aplicaciones Elizabeth Villota Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Aplicaciones Ecuaciones diferenciales de orden
Matemáticas Aplicadas MA101 Semana 06 EDO de orden alto - Aplicaciones Elizabeth Villota Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Aplicaciones Ecuaciones diferenciales de orden
INDICE Capitulo 1. Introducción: La Física y la Medición Capitulo 2. Vectores Capitulo 3. Movimiento de una Dimensión
 INDICE Capitulo 1. Introducción: La Física y la Medición 1 1.1. Estándares de longitud, masa tiempo 2 1.2. Densidad y masa atómica 5 1.3. Análisis dimensional 6 1.4. Conversión de unidades 8 1.5. Cálculos
INDICE Capitulo 1. Introducción: La Física y la Medición 1 1.1. Estándares de longitud, masa tiempo 2 1.2. Densidad y masa atómica 5 1.3. Análisis dimensional 6 1.4. Conversión de unidades 8 1.5. Cálculos
CONCEPTO DE CINEMÁTICA: es el estudio del movimiento sin atender a las causas que lo producen
 CINEMÁTICA CONCEPTO DE CINEMÁTICA: es el estudio del movimiento sin atender a las causas que lo producen CONCEPTO DE MOVIMIENTO: el movimiento es el cambio de posición, de un cuerpo, con el tiempo (este
CINEMÁTICA CONCEPTO DE CINEMÁTICA: es el estudio del movimiento sin atender a las causas que lo producen CONCEPTO DE MOVIMIENTO: el movimiento es el cambio de posición, de un cuerpo, con el tiempo (este
4.- ANALISIS DE SISTEMAS EN TIEMPO CONTINUO
 ANALISIS DE SISTEMAS EN TIEMPO CONTINUO Dinámica de Sistemas 4. 4.- ANALISIS DE SISTEMAS EN TIEMPO CONTINUO 4..- Efecto de los polos en el comportamiento del sistema. 4..- Estabilidad. 4.3.- Análisis de
ANALISIS DE SISTEMAS EN TIEMPO CONTINUO Dinámica de Sistemas 4. 4.- ANALISIS DE SISTEMAS EN TIEMPO CONTINUO 4..- Efecto de los polos en el comportamiento del sistema. 4..- Estabilidad. 4.3.- Análisis de
Semana 10 Matrices y vectores - Sistemas de EDOs
 Matemáticas Aplicadas MA101 Semana 10 Matrices y vectores - Sistemas de EDOs Elizabeth Villota Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Matrices y vectores Sean dos EDOs lineales
Matemáticas Aplicadas MA101 Semana 10 Matrices y vectores - Sistemas de EDOs Elizabeth Villota Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Matrices y vectores Sean dos EDOs lineales
3. Funciones de varias variables
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
VELOCIDAD Y ACELERACION. RECTA TANGENTE.
 VELOCIDAD Y ACELERACION. RECTA TANGENTE. 3. Describir la trayectoria y determinar la velocidad y aceleración del movimiento descrito por las curvas siguientes: (a) r (t) = i 4t 2 j + 3t 2 k. (b) r (t)
VELOCIDAD Y ACELERACION. RECTA TANGENTE. 3. Describir la trayectoria y determinar la velocidad y aceleración del movimiento descrito por las curvas siguientes: (a) r (t) = i 4t 2 j + 3t 2 k. (b) r (t)
( + )= ( ) ( ) tiene periodo si es cualquier periodo de ( ). + =cos( +2 )=cos + = ( +2 )=. cosnt+ sinnt) ( )~ Métodos con series de Fourier
 Métodos con series de Fourier Definición: Función periódica La función (), definida para toda, es periódica si existe un número positivo tal que (+)=() para toda. El número en un periodo de la función.
Métodos con series de Fourier Definición: Función periódica La función (), definida para toda, es periódica si existe un número positivo tal que (+)=() para toda. El número en un periodo de la función.
Semana 03 Interpretaciones Gráficas de las EDO - Aplicaciones
 Matemáticas Aplicadas MA101 Semana 03 Interpretaciones Gráficas de las EDO - Aplicaciones Elizabeth Villota Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Interpretación Gráfica A menudo
Matemáticas Aplicadas MA101 Semana 03 Interpretaciones Gráficas de las EDO - Aplicaciones Elizabeth Villota Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Interpretación Gráfica A menudo
MODELOS DE SERIES DE TIEMPO 1. Modelos capaces de predecir, interpretar y evaluar hipótesis con datos económicos y financieros.
 MODELOS DE SERIES DE TIEMPO 1 Introducción Modelos capaces de predecir, interpretar y evaluar hipótesis con datos económicos y financieros. Originalmente tuvieron como objetivo hacer predicciones. Descomposición
MODELOS DE SERIES DE TIEMPO 1 Introducción Modelos capaces de predecir, interpretar y evaluar hipótesis con datos económicos y financieros. Originalmente tuvieron como objetivo hacer predicciones. Descomposición
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias.
 Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
BOLILLA 3 DESPLAZAMIENTO, VELOCIDAD Y ACELERACION
 BOLILLA 3 DESPLAZAMIENTO, VELOCIDAD Y ACELERACION 1. INTRODUCCION A LA CINEMATICA El origen de la dinámica se remonta a los primeros experimentos realizados por Galileo Galilei (1564-1642). Pero a partir
BOLILLA 3 DESPLAZAMIENTO, VELOCIDAD Y ACELERACION 1. INTRODUCCION A LA CINEMATICA El origen de la dinámica se remonta a los primeros experimentos realizados por Galileo Galilei (1564-1642). Pero a partir
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
CINEMÁTICA DE UNA PARTÍCULA. Ing. Ronny Altuve
 UNIVERSIDAD ALONSO DE OJEDA FACULTAD DE INGENIERÍA Escuela de Industrial/Computación CINEMÁTICA DE UNA PARTÍCULA Elaborado por: Ing. Ronny Altuve Ciudad Ojeda, Junio de 2015 INTRODUCCIÓN MECÁNICA Mecánica
UNIVERSIDAD ALONSO DE OJEDA FACULTAD DE INGENIERÍA Escuela de Industrial/Computación CINEMÁTICA DE UNA PARTÍCULA Elaborado por: Ing. Ronny Altuve Ciudad Ojeda, Junio de 2015 INTRODUCCIÓN MECÁNICA Mecánica
TEORÍA DE CÁLCULO II PARA GRADOS DE INGENIERÍA Elaborada por Domingo Pestana y José Manuel Rodríguez 1. CÁLCULO DIFERENCIAL EN VARIAS VARIABLES
 TEORÍA DE CÁLCULO II PARA GRADOS DE INGENIERÍA Elaborada por Domingo Pestana y José Manuel Rodríguez 1 CÁLCULO DIFERENCIAL EN VARIAS VARIABLES 11 CONCEPTOS BÁSICOS Definición La norma de un vector x =
TEORÍA DE CÁLCULO II PARA GRADOS DE INGENIERÍA Elaborada por Domingo Pestana y José Manuel Rodríguez 1 CÁLCULO DIFERENCIAL EN VARIAS VARIABLES 11 CONCEPTOS BÁSICOS Definición La norma de un vector x =
II. Vibración libre de un sistema de un grado de libertad
 Objetivos: 1. Definir que es vibración libre. 2. Recordar el método de diagrama de cuerpo libre para deducir las ecuaciones de movimiento. 3. Introducir el método de conservación de energía para deducir
Objetivos: 1. Definir que es vibración libre. 2. Recordar el método de diagrama de cuerpo libre para deducir las ecuaciones de movimiento. 3. Introducir el método de conservación de energía para deducir
2 o Bachillerato. Conceptos básicos
 Física 2 o Bachillerato Conceptos básicos Movimiento. Cambio de posición de un cuerpo respecto de un punto que se toma como referencia. Cinemática. Parte de la Física que estudia el movimiento de los cuerpos
Física 2 o Bachillerato Conceptos básicos Movimiento. Cambio de posición de un cuerpo respecto de un punto que se toma como referencia. Cinemática. Parte de la Física que estudia el movimiento de los cuerpos
1. Ecuaciones lineales con coeficientes constantes. Ecuaciones de primer orden. 2. Encontrar la solución de los siguientes problemas de valor inicial.
 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes problemas de valor inicial. ẋ =5x, x0) =.. ẋ + x =0, x) =.. ẋ + x = te t, x0) =. si
. Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes problemas de valor inicial. ẋ =5x, x0) =.. ẋ + x =0, x) =.. ẋ + x = te t, x0) =. si
Tema II: Dinámica en el espacio de fases
 Tema II: Dinámica en el espacio de fases 1. Las ecuaciones de Hamilton Para sistemas autónomos en los que H no depende de t, es una constante del movimiento por lo que H(p, q = α (1.1 Esta ecuación determina
Tema II: Dinámica en el espacio de fases 1. Las ecuaciones de Hamilton Para sistemas autónomos en los que H no depende de t, es una constante del movimiento por lo que H(p, q = α (1.1 Esta ecuación determina
LECCIONES DEL CURSO DE MODELACIÓN MATEMÁTICA Y COMPUTACIONAL
 LECCIONES DEL CURSO DE MODELACIÓN MATEMÁTICA Y COMPUTACIONAL POSGRADOS DE CIENCIAS DE LA TIERRA Y DE CIENCIA E INGENIERÍA DE LA COMPUTACIÓN UNAM AUTORES: Ismael Herrera Revilla 1 Basado en el Libro Mathematical
LECCIONES DEL CURSO DE MODELACIÓN MATEMÁTICA Y COMPUTACIONAL POSGRADOS DE CIENCIAS DE LA TIERRA Y DE CIENCIA E INGENIERÍA DE LA COMPUTACIÓN UNAM AUTORES: Ismael Herrera Revilla 1 Basado en el Libro Mathematical
Momento angular de una partícula. Momento angular de un sólido rígido
 Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
Funciones Reales de Varias Variables
 Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 162 CONTENIDO Funciones
Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 162 CONTENIDO Funciones
Observar el efecto de las fuerzas en un sistema de movimiento mixto.
 PRÁCTICA DEMOSTRATIVA N 3 (MOVIMIENTO CIRCULAR) Ing. Francisco Franco Web: http://mgfranciscofranco.blogspot.com/ Fuente de información: Trabajo de grado de Mónica A. Camacho D. y Wilson H. Imbachi M.
PRÁCTICA DEMOSTRATIVA N 3 (MOVIMIENTO CIRCULAR) Ing. Francisco Franco Web: http://mgfranciscofranco.blogspot.com/ Fuente de información: Trabajo de grado de Mónica A. Camacho D. y Wilson H. Imbachi M.
Vibraciones Linealización de ecuaciones diferenciales
 Vibraciones Linealización de ecuaciones diferenciales MScAA Marcos Knoblauch Departamento de Aeronáutica Universidad Nacional de La Plata Introducción Este documento contiene las ecuaciones y conceptos
Vibraciones Linealización de ecuaciones diferenciales MScAA Marcos Knoblauch Departamento de Aeronáutica Universidad Nacional de La Plata Introducción Este documento contiene las ecuaciones y conceptos
IES Francisco Giner de los Ríos 2016/2017 Física y Química 1º Bachillerato nocturno (FQ NB1B-Noct) UD 8. El movimiento
 UD 8. El movimiento 1- Sistemas de referencia. 2- Magnitudes vectoriales. 3- Interpretaciones gráficas de los movimientos. 4- Componentes intrínsecas de la aceleración. 1- Sistemas de referencia: 1.1.
UD 8. El movimiento 1- Sistemas de referencia. 2- Magnitudes vectoriales. 3- Interpretaciones gráficas de los movimientos. 4- Componentes intrínsecas de la aceleración. 1- Sistemas de referencia: 1.1.
Programa de Doctorado en Física Pontificia Universidad Católica de Valparaíso Universidad Técnica Federico Santa María
 1 Mecánica Clásica - II Semestre 2014 Programa de Doctorado en Física Pontificia Universidad Católica de Valparaíso Universidad Técnica Federico Santa María Problema 1. Una barra rígida (de altura despreciable)
1 Mecánica Clásica - II Semestre 2014 Programa de Doctorado en Física Pontificia Universidad Católica de Valparaíso Universidad Técnica Federico Santa María Problema 1. Una barra rígida (de altura despreciable)
Diferencial de una función 1
 Cálculo _Comisión y Año 7 Diferencial de una función Dada una función y f (, derivable en x, se define: Diferencial de f, en x, al producto de la derivada de la función en dicho punto, por el incremento
Cálculo _Comisión y Año 7 Diferencial de una función Dada una función y f (, derivable en x, se define: Diferencial de f, en x, al producto de la derivada de la función en dicho punto, por el incremento
2. Continuidad y derivabilidad. Aplicaciones
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Tema 6: Cinética de la partícula
 Tema 6: Cinética de la partícula FISICA I, 1º Grado en Ingeniería Civil Departamento Física Aplicada III Escuela Técnica Superior de Ingeniería Universidad de Sevilla Índice Introducción Trabajo mecánico
Tema 6: Cinética de la partícula FISICA I, 1º Grado en Ingeniería Civil Departamento Física Aplicada III Escuela Técnica Superior de Ingeniería Universidad de Sevilla Índice Introducción Trabajo mecánico
Tema 9: Introducción a la Dinámica
 Tema 9: Introducción a la Dinámica 1º Ingenieros Aeronáuticos Escuela Técnica Superior de Ingenieros Universidad de Sevilla 1 Situación en la asignatura Primer Parcial Introducción Mecánica Cinemática
Tema 9: Introducción a la Dinámica 1º Ingenieros Aeronáuticos Escuela Técnica Superior de Ingenieros Universidad de Sevilla 1 Situación en la asignatura Primer Parcial Introducción Mecánica Cinemática
Función exponencial compleja
 Función exponencial compleja Genaro Luna Carreto * Los números reales y los complejos satisfacen los axiomas de campo, pero los segundos, no satisfacen los axiomas de orden. Sin embargo, a raíz de que
Función exponencial compleja Genaro Luna Carreto * Los números reales y los complejos satisfacen los axiomas de campo, pero los segundos, no satisfacen los axiomas de orden. Sin embargo, a raíz de que
UNIVERSIDAD CENTROCCIDENTAL LISANDRO ALVARADO DECANATO DE CIENCIAS Y TECNOLOGÍA DIRECCIÓN DE PROGRAMA INGENIERIA DE PRODUCCIÓN
 UNIVERSIDAD CENTROCCIDENTAL LISANDRO ALVARADO DECANATO DE CIENCIAS Y TECNOLOGÍA DIRECCIÓN DE PROGRAMA INGENIERIA DE PRODUCCIÓN PROGRAMA DE LA ASIGNATURA PROGRAMA: Ingeniería de Producción DEPARTAMENTO:
UNIVERSIDAD CENTROCCIDENTAL LISANDRO ALVARADO DECANATO DE CIENCIAS Y TECNOLOGÍA DIRECCIÓN DE PROGRAMA INGENIERIA DE PRODUCCIÓN PROGRAMA DE LA ASIGNATURA PROGRAMA: Ingeniería de Producción DEPARTAMENTO:
Matrices. Operaciones con matrices.
 Matrices. Operaciones con matrices. Ejercicio. Dadas las matrices ( ) ( ) 4 A = B = ( ) C = D = 4 5 ( ) 4 E = F = seleccione las que se pueden sumar y súmelas. Ejercicio. Dadas las matrices ( ) ( ) A =
Matrices. Operaciones con matrices. Ejercicio. Dadas las matrices ( ) ( ) 4 A = B = ( ) C = D = 4 5 ( ) 4 E = F = seleccione las que se pueden sumar y súmelas. Ejercicio. Dadas las matrices ( ) ( ) A =
Cátedra Matemática del PIT. Gradiente y Derivada Direccional
 Cátedra Matemática del PIT Gradiente y Derivada Direccional Propósito de la Unidad Hallar y usar las derivadas direccionales de una función de dos variables. Hallar el gradiente de una función de dos variables.
Cátedra Matemática del PIT Gradiente y Derivada Direccional Propósito de la Unidad Hallar y usar las derivadas direccionales de una función de dos variables. Hallar el gradiente de una función de dos variables.
Ejercicios: Estimando π con métodos Monte Carlo y cálculo del mayor autovalor de una matriz
 Ejercicios: Estimando π con métodos Monte Carlo y cálculo del mayor autovalor de una matriz 6 de marzo de 05. Cálculo de π con métodos Monte Carlo El objetivo de este ejercicio consiste en estimar el valor
Ejercicios: Estimando π con métodos Monte Carlo y cálculo del mayor autovalor de una matriz 6 de marzo de 05. Cálculo de π con métodos Monte Carlo El objetivo de este ejercicio consiste en estimar el valor
Ecuaciones diferenciales
 de primer orden 21 de noviembre de 2016 de primer orden Introducción Introducción a las ecuaciones diferenciales Las primeras ecuaciones diferenciales surgen al tratar de resolver ciertos problemas de
de primer orden 21 de noviembre de 2016 de primer orden Introducción Introducción a las ecuaciones diferenciales Las primeras ecuaciones diferenciales surgen al tratar de resolver ciertos problemas de
Física I. Dr. Roberto Pedro Duarte Zamorano (Responsable) Dr. Mario Enrique Álvarez Ramos (Colaborador) Dr. Ezequiel Rodríguez Jáuregui (Colaborador)
 Física I Dr. Roberto Pedro Duarte Zamorano (Responsable) Dr. Mario Enrique Álvarez Ramos (Colaborador) Dr. Ezequiel Rodríguez Jáuregui (Colaborador) Webpage: http://paginas.fisica.uson.mx/qb 2015 Departamento
Física I Dr. Roberto Pedro Duarte Zamorano (Responsable) Dr. Mario Enrique Álvarez Ramos (Colaborador) Dr. Ezequiel Rodríguez Jáuregui (Colaborador) Webpage: http://paginas.fisica.uson.mx/qb 2015 Departamento
Límites y continuidad. Cálculo 1
 Límites y continuidad Cálculo 1 Razones de cambio y límites La rapidez promedio de un móvil es la distancia recorrida durante un intervalo de tiempo dividida entre la longitud del intervalo. Ejemplo 1
Límites y continuidad Cálculo 1 Razones de cambio y límites La rapidez promedio de un móvil es la distancia recorrida durante un intervalo de tiempo dividida entre la longitud del intervalo. Ejemplo 1
Nombre de la asignatura: Control no Lineal. Carrera: Ingeniería Electrónica
 1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Control no Lineal Carrera: Ingeniería Electrónica Clave de la asignatura: Horas teoría - horas práctica créditos: 3-2-8 2.- HISTORIA DEL PROGRAMA Lugar
1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Control no Lineal Carrera: Ingeniería Electrónica Clave de la asignatura: Horas teoría - horas práctica créditos: 3-2-8 2.- HISTORIA DEL PROGRAMA Lugar
SEGUNDA EVALUACIÓN. FÍSICA Marzo 18 del 2015 (11h30-13h30)
 SEGUNDA EVALUACIÓN DE FÍSICA Marzo 18 del 2015 (11h30-13h30) Como aspirante a la ESPOL me comprometo a combatir la mediocridad y actuar con honestidad, por eso no copio ni dejo copiar" NOMBRE: FIRMA: VERSION
SEGUNDA EVALUACIÓN DE FÍSICA Marzo 18 del 2015 (11h30-13h30) Como aspirante a la ESPOL me comprometo a combatir la mediocridad y actuar con honestidad, por eso no copio ni dejo copiar" NOMBRE: FIRMA: VERSION
ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO
 ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO Nombre: Marilyn Chela Curso: 1 nivel de Ing. Química TEMA: Relación entre la Dinámica Lineal y la Dinámica Rotacional. Dinámica rotacional: Se trabaja con el
ESCUELA SUPERIOR POLITÉCNICA DE CHIMBORAZO Nombre: Marilyn Chela Curso: 1 nivel de Ing. Química TEMA: Relación entre la Dinámica Lineal y la Dinámica Rotacional. Dinámica rotacional: Se trabaja con el
Clasificación de Ecuaciones Diferenciales Parciales
 Clasificación de Ecuaciones Diferenciales Parciales Yarko Niño C. y Paulo Herrera R. Departamento de Ingeniería Civil, Universidad de Chile Semestre Primavera 2011 Calendario Cátedras sólo los miércoles.
Clasificación de Ecuaciones Diferenciales Parciales Yarko Niño C. y Paulo Herrera R. Departamento de Ingeniería Civil, Universidad de Chile Semestre Primavera 2011 Calendario Cátedras sólo los miércoles.
