Cinemática en una dimensión
|
|
|
- Concepción Lucero Sevilla
- hace 8 años
- Vistas:
Transcripción
1 Capítulo 2. Cinemática en una dimensión La meánica, la más antiüa de las ciencias físicas es el estudio del movimiento de los cuerpos. 1. Distinción entre cinemática y dinámica Cuando describimos el mvimiento nos ocupamos de la parte de la mecánica que llamamos cinemática. Cuando relacionamos el movimiento con las fuerzas que intervienen en él y con las propiedades de los cuerposen movimiento, nos ocupamos de la dinámica. 2. Concepto de partícula Matemáticamente una partícula se considera como un punto, como un objeto sin tamaño de manera que no hay que hacer consideraciones de rotación o vibración. En realidad no existe en la naturaleza nada que pueda llamarse un objeto sin extensión. Sin embaro, los objetos reales a menudo se comportan, con ran aproximación como partículas. Un cuerpo no necesita ser realmente pequeño para poder ser tratado como partícula. Por ejemplo, con respecto a la distancia tierra sol, el sol y la tierra pueden ser tratados ordinariamente como partículas: R T 3. Espacio y tiempo D = 10 5 Vamos a tratar estos dos conceptos no desde un punto de vista filosófico ( Qué son?) sino en su relación con el movimiento de los cuerpos. 17
2 18 Capítulo Movimiento A un cuerpo le asinaremos una posición en el espacio en un instante de tiempo. Como varie una en función del otro nos proporcionará su movimiento Medida Intuitivamente estamos introduciendo la observación cuantitativa, es decir la medición. Con un patrón de lonitud podemos medir la distacia recorrida y con un patrón de tiempo el tiempo empleado. El hecho de que Galileo se plantease tales medidas dió luar al nacimieto de la Física como ciencia, separándose así de la filosofía para la cual los razonamientos sobre los hechos naturales eran suficiente prueba de los mismos Homoeneidad del tiempo En lo que hemos dicho hasta ahora es imprescindible hacer una suposición de partida: el patrón de tiempo no varía con el transcurso del mismo. Como no podemos contrastarlo experimentalmente consideramos la homoeneidad del tiempo como una hipótesis necesaria. 4. Movimiento en una dimensión 4..1 Posición Puesto que el movimiento se realiza en una recta, llamaremos i al vector unitario en la dirección positiva, de manera que la posición de la partícula e un instante dado será: r(t) = x(t) i (4.1) Podemos representar la curva x(t) que denominaremos trayectoria de la partícula 4..2 Velocidad Da cuenta de la rapidez con que varía la posición con el tiempo y se define como: v(t) = dr(t) r(t) = = ẋ i (4.2) dt
3 Cinemática en una dimensión 19 t Aceleración Fiura 2..1: Posición,velocidad y tiempo Da cuenta de la rapidez con que varía la velocidad con el tiempo y se define como: 4..4 Ejemplos Ejemplo 1 a(t) = v(t) = d2 r(t) = ẍ i (4.3) dt 2 Es posible que una persona camine a través de una habitación con velocidad neativa y aceleración positiva?. Poner un ejemplo y hacer un ráfico. Suponamos que inicialmente su velocidad es v = v 0 i donde v 0 > 0 y que acelera con una aceleración constante a = a 0 i con a 0 > 0. El movimiento será: x = ( v 0 t + a 0 t 2 /2) i de forma que v = ( v 0 + a 0 t) i que está diriida en la dirección neativa del eje x en el intervalo temporal 0 < t < v 0 / mientras que la aceleración está siempre diriida en la dirección positiva del eje x
4 20 Capítulo 2 5. Condiciones iniciales Conocida la aceleración que tiene una partícula en una dimensión a = a(t) i (5.4) podemos determinar su velocidad y posición mediante dos interaciones sucesivas. En cada interación hay que introducir una constante arbitraria. Ello sinifica que hay infinitas trayectorias posibles con la misma aceleración, tantas como los diferentes valosres de las constantes arbitrarias. El movimiento concreto de una partícula dada dependerá de los valores particulares que tomen estas constantes. Para fijarlas hay que conocer la posición y la velocidad inicial 5..1 Posición inicial 5..2 Velocidad inicial 6. Movimiento uniformemente acelerado 6..1 Caída libre (Resnick 3-10, 3-11)
5 Cinemática en una dimensión 21 Problemas el Tema II ( ) 1.) La posición de una partícula que se mueve a lo laro del eje de las x depende del tiempo de acuerdo con la ecuación x = a 0 t 2 b 0 t 3 en donde x está en cm y t en seundos a) Que dimensiones y unidades deben tener a 0 y b 0? b) Suponamos que en dichas unidades los valores de a 0 y b 0 son 3 y 1 respectivamente.si parte del arien, Cuanto tarda la partícula en recorrer la máxima distancia posible hacia la derecha? c) En que posición se encuentra al cabo de los primeros 4 seundos?. Con que velocidad?. Con que aceleración?. 2.) Una partícula que parte del reposo desde el orien, tiene una aceleración que aumenta linealmente con el tiempo a = kt siendo el cambio de la aceleración k = 1, 5 m/s 3 a) Hacer una ráfica de a en función de t durante el primer intervalo de 10s b) Hacer la ráfica de v en función de t en el mismo período y calcular la velocidad a los 5s de empezar el movimiento c) Hacer la ráfica correspondiente de x en función de t y determinar lo que ha avanzado la partícula en los primeros 5 s y en los siuientes 5 3.) La posición de una partícula que se mueve a lo laro del eje x varía con el tiempo seún la ecuación x = v 0 k (1 e kt ) en la cual v 0 y k son constantes a) Hacer una ráfica de x en función de t b) Determinar la distancia total que recorre la partícula c) Demostrar que la aceleración está diriida en sentido contrario a la velocidad d) Razonar como se puede requerir un tiempo infinito para recorrer una distancia finita 4.) Un coche sale de una ciudad a 70km/h. Al cabo de 15 minutos otro coche sale del mismo luar a 80Km/H. Cuanto tiempo tarda el seundo coche en alcanzar al primero y a qué distancia de la ciudad ocurre? 5.) Una ciudad A se encuentra 54Km al norte de otra ciudad B. Si un coche sale de A hacia el sur a 60Km/h y al mismo tiempo otro sale de B hacia A a 75Km/h, determinar a que distancia de A se cruzan y cuanto tiempo después de haber salido 6.) Una partícula siue un movimiento rectilíneo dado por ẍ = 6at bω 3 sen(ωt). En t = 0 su velocidad y posición son cero. Determinar la posición y velocidad en cualquier instante
6 22 Capítulo 2 7.) Una partícula siue un movimiento rectilíneo con una velocidad dada por v = k/x donde k es una constante positiva. Si para t = 0 se encuentra en x = 2, determinar posición, velocidad y aceleración como funciones del tiempo 8.) Una partícula se mueve en en el seno de un líquido con una aceleración opuesta a la velocidad en forma a = kv 2. Determinar la velocidad en función del tiempo y de la posición si las condiciones iniciales son x = 0 y v = v 0 cuando t = 0. 9.) Si un cuerpo recorre la mitad de su distancia total de caida libre durante el último seundo de su movimiento a partir del reposo, calcular el tiempo y la altura desde la cual cae. 10.) Un lobo va subiendo a razón de 12 m/se. Cuando se encuentra a 80 m sobre el suelo suelta un paquete. Cuanto tiempo tarda el paquete en llear al suelo? 11.) Un paracaidista después de saltar, cae sin rozamiento durante 50 m hasta que se abre el paracaidas que le frena a razón de 2 m/s 2. LLea al suelo con una velocidad de 3 m/s a) Cuanto tiempo ha estado en el aire? b) Desde que altura saltó? 12.) Una pelota se lanza al aire con velocidad v 0. Demostrar que la altura que alcanza es la mitad de la que alcanzaría en el mismo tiempo si no hubiese ravedad. 13.) Una pelota se lanza al aire con velocidad v 0. En cada rebote pierde 2/3 de la velocidad. Calcular el tiempo que tarda en pararse y el espacio recorrido durante ese tiempo. Determinar cual sería la velocidad equivalente a la que se hubiera tenido que mover un cuerpo con movimiento uniforme para recorrer la misma distancia en el mismo tiempo. 14.) Se suelta una moneda al borde de un acantilado de 105 m de altura. Con qué velocidad debe lanzarse una piedra 1 seundo después para que alcance a la moneda a 15 m del suelo?
7 Cinemática en una dimensión Problemas 1.) La posición de una partícula que se mueve a lo laro del eje de las x depende del tiempo de acuerdo con la ecuación x = a 0 t 2 b 0 t 3 en donde x está en cm y t en seundos a) Que dimensiones y unidades deben tener a 0 y b 0? b) Suponamos que en dichas unidades los valores de a 0 y b 0 son 3 y 1 respectivamente.si parte del arien, Cuanto tarda la partícula en recorrer la máxima distancia posible hacia la derecha? c) En que posición se encuentra al cabo de los primeros 4 seundos?. Con que velocidad?. Con que aceleración?. a) [a 0 ] = LT 2 [b 0 ] = LT 3 b) dx dt = 0 = 2a 0t 3b 0 t 2 = 0 = t = 2a 0 3b 0 = 2s x(t = 2s) = 4cm c) x(t = 4s) = 16cm v = 2a 0 t 3b 0 t 2 = v(t = 4s) = 24cm/s a = 2a 0 6b 0 t = a(t = 4s) = 18cm/s 2
8 24 Capítulo t Problema 1: Posición, velocidad y aceleración
9 Cinemática en una dimensión 25 2.) Una partícula que parte del reposo desde el orien, tiene una aceleración que aumenta linealmente con el tiempo a = kt siendo el cambio de la aceleración k = 1, 5 m/s 3 a) Hacer una ráfica de a en función de t durante el primer intervalo de 10s b) Hacer la ráfica de v en función de t en el mismo período y calcular la velocidad a los 5s de empezar el movimiento c) Hacer la ráfica correspondiente de x en función de t y determinar lo que ha avanzado la partícula en los primeros 5 s y en los siuientes t Problema 2: Posición, velocidad y aceleración
10 26 Capítulo 2 3.) La posición de una partícula que se mueve a lo laro del eje x varía con el tiempo seún la ecuación x = v 0 k (1 e kt ) en la cual v 0 y k son constantes a) Hacer una ráfica de x en función de t b) Determinar la distancia total que recorre la partícula c) Demostrar que la aceleración está diriida en sentido contrario a la velocidad d) Razonar como se puede requerir un tiempo infinito para recorrer una distancia finita a) t 1 Problema 3: Posición, velocidad y aceleración b) el máximo de x se alcanza cuando lueo dx dt = 0 = 0 = v 0e kt = t = x m = x(t = ) = v 0 k
11 Cinemática en una dimensión 27 c) d) Iual que Aquiles y la tortua v = dx dt = v 0e kt a = dv dt = kv 0e kt = kv
12 28 Capítulo 2 4.) Un coche sale de una ciudad a 70km/h. Al cabo de 15 minutos otro coche sale del mismo luar a 80Km/H. Cuanto tiempo tarda el seundo coche en alcanzar al primero y a qué distancia de la ciudad ocurre? Sea v 1 = 70km/h = /3600m/s = 700m/36/s v 2 = 80km/h = 800m/36s t 0 = 15s t Problema 4: Posición de los dos coches El movimiento del primer coche será x 1 = v 1 t el del seundo x 2 = v 2 (t t 0 ) Por tanto coinciden al cabo de un tiempo T despues de la salida del primer coche tal que v 1 T = v 2 (T t 0 ) T = v 2 t 0 = 1 v 2 v 1 1 v t 1 0 v 2 T = 15s1 7/8 = 120s = 2h. En este periodo han recorrido un espacio x 1 (T ) = 70km/h.2h = 140Km
13 Cinemática en una dimensión 29 5.) Una ciudad A se encuentra 54Km al norte de otra ciudad B. Si un coche sale de A hacia el sur a 60Km/h y al mismo tiempo otro sale de B hacia A a 75Km/h, determinar a que distancia de A se cruzan y cuanto tiempo después de haber salido Sea v 1 = 60km/h = /3600m/s = 600m/36/s v 2 = 75km/h = 7500m/36s x 0 = 54km t Problema 5: Posición de los dos coches Tomando el orien en A El movimiento del primer coche será x 1 = v 1 t el del seundo x 2 = x0 v 2 t Por tanto coinciden al cabo de un tiempo T despues de la salida del primer coche tal que v 1 T = x0 v 2 T T = x 0 v 2 + v 1 = En este periodo han recorrido un espacio 54km 135km/h = 0.4h x 1 (T ) = 60km/h.(0.4h) = 24Km
14 30 Capítulo 2 6.) Una partícula siue un movimiento rectilíneo dado por ẍ = 6at bω 3 sen(ωt). En t = 0 su velocidad y posición son cero. Determinar la posición y velocidad en cualquier instante Interando ẍ = 6at bω 3 sen(ωt) ẋ = 3at 2 + bω 2 cos(ωt) + c 1 con las condiciones iniciales dadas c 1 = bω 2 Interando la velocidad v = 3at 2 + bω 2 cos(ωt) bω 2 x = at 3 + bω sin(ωt) + c 2 donde c 2 = 0 de acuerdo con las condiciones iniciales
15 Cinemática en una dimensión 31 7.) Una partícula siue un movimiento rectilíneo con una velocidad dada por v = k/x donde k es una constante positiva. Si para t = 0 se encuentra en x = 2, determinar posición, velocidad y aceleración como funciones del tiempo Problema 7: Posición, velocidad y aceleración Interando dx dt = k/x 1/2x 2 kt + c 1 = 0 con las condiciones iniciales dadas c 1 = 2 x = 2kt + 4 derivando v = k 2kt + 4 k 2 a = ( 2kt + 4) 3
16 32 Capítulo 2 8.) Una partícula se mueve en en el seno de un líquido con una aceleración opuesta a la velocidad en forma a = kv 2. Determinar la velocidad en función del tiempo y de la posición si las condiciones iniciales son x = 0 y v = v 0 cuando t = 0. interando interando de nuevo o bien, eliminando el tiempo Problema 8: Gráfica de v en función de x a = kv 2 dv v 2 = kdt 1 v = kt + 1 v 0 = v = x = 1 k ln v 0 v v = v 0 e kx v v 0 kt
17 Cinemática en una dimensión 33 9.) Si un cuerpo recorre la mitad de su distancia total de caida libre durante el último seundo de su movimiento a partir del reposo, calcular el tiempo y la altura desde la cual cae. Las condiciones iniciales son y por tanto z(0) = h ż(0) = 0 z = h 1 2 t2 v = t El tiempo total T de caida corresponde a z(t ) = 0 = h 1 2 T 2 = T = + 2h (1) Sea t 0 = 1s, entonces en T t 0 recorre h 2 z(t t 0 ) = h 2 = h 1 2 (T t 0) 2 h = T t 0 = + (2) Combinando (1) y (2) 2h h = ( h 2 1) = 1 ( h 2 + 1) = t 0 Despejando h: h = ( 2 + 1) 2 t 2 0 = 57.1 m T = (2 + 2)t 0 = 3.4 s
18 34 Capítulo 2 10.) Un lobo va subiendo a razón de 12 m/se. Cuando se encuentra a 80 m sobre el suelo suelta un paquete. Cuanto tiempo tarda el paquete en llear al suelo? La altura inicial es: Su velocidad inicial es lueo h = 80 m v 0 = 12 m/s z = h + v 0 t 1 2 t2 El tiempo que tarda en llear al suelo es: z(t ) = 0 = h + v 0 T 1 2 T 2 = 0 T = v 0 [ h v 2 0 ] = 5.4 s
19 Cinemática en una dimensión ) Un paracaidista después de saltar, cae sin rozamiento durante 50 m hasta que se abre el paracaidas que le frena a razón de 2 m/s 2. LLea al suelo con una velocidad de 3 m/s a) Cuanto tiempo ha estado en el aire? b) Desde que altura saltó? Sea h 1 = 50m Es la composición de dos movimientos acelerados Hasta que se abre el paracaidas h > z > h 2 = h h 1, 0 < t < T 1 Caída con acelración, posición inicial h y velocidad inicial cero z = h 1 2 t2 v = t Este movimiento termina en el momento que se abre el paracaidas, lo que ocurrirá en el instante t = T 1 tal que z = h h 1 = h 2. Por lo tanto: h 1 = 1 2 T 1 2 2h 1 = T 1 = = 3.2 s La velocidad en ese instante será v 1 = v(t 1 ) = 2h 1 = 31.3 m/s Al abrirse al paracaidas h 2 > z > 0, T 1 < t < T 2 Caída con aceleración a, posición inicial h 2 = h(t 1 ) y velocidad inicial v 1 = v(t 1 ) z = h 2 + v 1 (t T 1 ) a(t T 1) 2 v = v 1 + a(t T 1 ) Lleará al suelo en el instante t = T 2 tal que z(t 2 ) = 0 yv 2 = v(t 2 ) donde v 2 = 3m/s. Por tanto 0 = z(t 2 ) = h 2 + v 1 (T 2 T 1 ) a(t 2 T 1 ) 2 Por tanto T 2 T 1 = v 2 v 1 a v 2 = v(t 2 ) = v 1 + a(t 2 T 1 ) = s = T 2 = s h 2 = v2 1 v 2 2 2a = m
20 36 Capítulo 2 12.) Una pelota se lanza al aire con velocidad v 0. Demostrar que la altura que alcanza es la mitad de la que alcanzaría en el mismo tiempo si no hubiese ravedad. La ecuación del ovimiento es z = v 0 t 1 2 t2 v = v 0 t La altura que alcanza corresponde al instante T en que v = 0. Por tanto: T = v 0 lueo h = z(t ) = v2 0 2 h = v 0 T 2
21 Cinemática en una dimensión ) Una pelota se lanza al aire con velocidad v 0. En cada rebote pierde 2/3 de la velocidad. Calcular el tiempo que tarda en pararse y el espacio recorrido durante ese tiempo. Determinar cual sería la velocidad equivalente a la que se hubiera tenido que mover un cuerpo con movimiento uniforme para recorrer la misma distancia en el mismo tiempo. Como hemos visto en el problema anterior En el primer rebote (subida y bajada) emplearía un tiempo T 1 = 2v 0 y recorrería una distancia h 1 = v2 0 En el seundo la velocidad inicial es v 0 q donde q = 1 : Por tanto: 3 y recorrería una distancia En el rebote n ésimo: y recorrería una distancia Lueo el tiempo total será T 2 = 2v 0q h 1 = v2 0q 2 T n = 2v 0q n h n = v2 0q 2n T = = lim k k n=0 Como q < 1, q k 0 y por tanto T n = n=0 n=0 2v 0 qn 2v 0 2v 0 qn = lim k ( ) 1 q k+1 1 q
22 38 Capítulo 2 En cuanto a h Es decir y por tanto T = 2v 0 h = = lim k k n=0 ( ) 1 = 3v 0 1 q h n = n=0 n=0 v 2 0 q2n v0 2 v q2n 0 2 = lim k h = v2 0 lueo la velocidad equivalente es ( ) 1 = 9v2 0 1 q 2 8 h = v q T V = v q = 3v 0 4 ( ) 1 q 2k+2 1 q 2
23 Cinemática en una dimensión ) Se suelta una moneda al borde de un acantilado de 105 m de altura. Con qué velocidad debe lanzarse una piedra 1 seundo después para que alcance a la moneda a 15 m del suelo? x m = h 1/2t 2 x p = h v 0 (t t 0 ) 1/2(t t 0 ) 2 lueo t = 2(h h 0 )/ = 4.3s v 0 (t t 0 ) = 1/2(t) 2 1/2(t t 0 ) 2 v = t 0 2 2t t 0 t t 0 = 11.3m/s
EJERCICIOS RESUELTOS 1º DE BACHILLERATO (Hnos. Machado): EJERCICIOS DE REFUERZO 1º EVALUACIÓN (Cinemática) Por Álvaro Téllez Róbalo
 EJERCICIOS RESUELTOS 1º DE BACHILLERATO (Hnos. Machado): EJERCICIOS DE REFUERZO 1º EVALUACIÓN (Cinemática) Por Álvaro Téllez Róbalo 1. El vector posición de un punto, en función del tiempo, viene dado
EJERCICIOS RESUELTOS 1º DE BACHILLERATO (Hnos. Machado): EJERCICIOS DE REFUERZO 1º EVALUACIÓN (Cinemática) Por Álvaro Téllez Róbalo 1. El vector posición de un punto, en función del tiempo, viene dado
Ideas básicas sobre movimiento
 Ideas básicas sobre movimiento Todos conocemos por experiencia qué es el movimiento. En nuestra vida cotidiana, observamos y realizamos infinidad de movimientos. El desplazamiento de los coches, el caminar
Ideas básicas sobre movimiento Todos conocemos por experiencia qué es el movimiento. En nuestra vida cotidiana, observamos y realizamos infinidad de movimientos. El desplazamiento de los coches, el caminar
Movimiento Rectilíneo Uniforme
 Movimiento Rectilíneo Uniforme 1. Teoría La mecánica es la parte de la física encargada de estudiar el movimiento y el reposo de los cuerpos, haciendo un análisis de sus propiedades y causas. La mecánica
Movimiento Rectilíneo Uniforme 1. Teoría La mecánica es la parte de la física encargada de estudiar el movimiento y el reposo de los cuerpos, haciendo un análisis de sus propiedades y causas. La mecánica
TRABAJO Y ENERGÍA: CHOQUES
 . TRABAJO Y ENERGÍA: CHOQUES Una bola de acero que cae verticalmente rebota en una placa ríida que forma un ánulo con la horizontal. Calcular para que la bola sala con una velocidad horizontal después
. TRABAJO Y ENERGÍA: CHOQUES Una bola de acero que cae verticalmente rebota en una placa ríida que forma un ánulo con la horizontal. Calcular para que la bola sala con una velocidad horizontal después
1. El vector de posición de una partícula viene dado por la expresión: r = 3t 2 i 3t j.
 1 1. El vector de posición de una partícula viene dado por la expresión: r = 3t 2 i 3t j. a) Halla la posición de la partícula para t = 3 s. b) Halla la distancia al origen para t = 3 s. 2. La velocidad
1 1. El vector de posición de una partícula viene dado por la expresión: r = 3t 2 i 3t j. a) Halla la posición de la partícula para t = 3 s. b) Halla la distancia al origen para t = 3 s. 2. La velocidad
Ejercicios de cinemática
 Ejercicios de cinemática 1.- Un ciclista recorre 32,4 km. en una hora. Calcula su rapidez media en m/s. (9 m/s) 2.- La distancia entre dos pueblos es de 12 km. Un ciclista viaja de uno a otro a una rapidez
Ejercicios de cinemática 1.- Un ciclista recorre 32,4 km. en una hora. Calcula su rapidez media en m/s. (9 m/s) 2.- La distancia entre dos pueblos es de 12 km. Un ciclista viaja de uno a otro a una rapidez
Observa el diagrama del centro y determina cual de los siguientes corresponde a un diagrama v-t para ese movimiento
 De las gráficas. Indica aquellas que presentan movimiento rectilíneo uniforme así como las que pertenecen al movimiento rectilíneo uniformemente acelerado Observa el diagrama del centro y determina cual
De las gráficas. Indica aquellas que presentan movimiento rectilíneo uniforme así como las que pertenecen al movimiento rectilíneo uniformemente acelerado Observa el diagrama del centro y determina cual
1. El vector de posición de una partícula, en unidades del SI, queda determinado por la expresión: r (t)=3t i +(t 2 2 t) j.
 IES ARQUITECTO PEDRO GUMIEL BA1 Física y Química UD 1: Cinemática 1. El vector de posición de una partícula, en unidades del SI, queda determinado por la expresión: r (t)=3t i +(t t) j. a) Determina los
IES ARQUITECTO PEDRO GUMIEL BA1 Física y Química UD 1: Cinemática 1. El vector de posición de una partícula, en unidades del SI, queda determinado por la expresión: r (t)=3t i +(t t) j. a) Determina los
CINEMÁTICA I FYQ 1º BAC CC.
 www.matyfyq.com Página 1 de 5 Pregunta 1: La posición de una partícula en el plano viene dada por la ecuación vectorial: r(t) = (t 2 4) i + (t + 2) j En unidades del SI calcula: a) La posición de la partícula
www.matyfyq.com Página 1 de 5 Pregunta 1: La posición de una partícula en el plano viene dada por la ecuación vectorial: r(t) = (t 2 4) i + (t + 2) j En unidades del SI calcula: a) La posición de la partícula
3. Una pelota se lanza desde el suelo hacia arriba. En un segundo llega hasta una altura de 25 m. Cuál será la máxima altura alcanzada?
 Problemas de Cinemática 1 o Bachillerato Caída libre y tiro horizontal 1. Desde un puente se tira hacia arriba una piedra con una velocidad inicial de 6 m/s. Calcula: a) Hasta qué altura se eleva la piedra;
Problemas de Cinemática 1 o Bachillerato Caída libre y tiro horizontal 1. Desde un puente se tira hacia arriba una piedra con una velocidad inicial de 6 m/s. Calcula: a) Hasta qué altura se eleva la piedra;
A continuación voy a colocar las fuerzas que intervienen en nuestro problema.
 ísica EL PLANO INCLINADO Supongamos que tenemos un plano inclinado. Sobre él colocamos un cubo, de manera que se deslice sobre la superficie hasta llegar al plano horizontal. Vamos a suponer que tenemos
ísica EL PLANO INCLINADO Supongamos que tenemos un plano inclinado. Sobre él colocamos un cubo, de manera que se deslice sobre la superficie hasta llegar al plano horizontal. Vamos a suponer que tenemos
Solución Actividades Tema 4 MOVIMIENTOS RECTILÍNEOS Y CIRCULARES. INTRODUCCIÓN A LA CINEMÁTICA.
 Solución Actividades Tema 4 MOVIMIENTOS RECTILÍNEOS Y CIRCULARES. INTRODUCCIÓN A LA CINEMÁTICA. Actividades Unidad 4. Nos encontramos en el interior de un tren esperando a que comience el viaje. Por la
Solución Actividades Tema 4 MOVIMIENTOS RECTILÍNEOS Y CIRCULARES. INTRODUCCIÓN A LA CINEMÁTICA. Actividades Unidad 4. Nos encontramos en el interior de un tren esperando a que comience el viaje. Por la
Cajón de Ciencias. Ejercicios resueltos de Movimiento rectilíneo uniforme
 Ejercicios resueltos de Movimiento rectilíneo uniforme 1) Pasar de unidades las siguientes velocidades: a) de 36 km/h a m/s b) de 10 m/s a km/h c) de 30 km/min a cm/s d) de 50 m/min a km/h 2) Un móvil
Ejercicios resueltos de Movimiento rectilíneo uniforme 1) Pasar de unidades las siguientes velocidades: a) de 36 km/h a m/s b) de 10 m/s a km/h c) de 30 km/min a cm/s d) de 50 m/min a km/h 2) Un móvil
PRÁCTICA 2 CINEMÁTICA DEL MOVIMIENTO RECTILÍNEO
 INGENIERÍA QUÍMICA 1 er curso FUNDAMENTOS FÍSICOS DE LA INGENIERÍA PRÁCTICA 2 CINEMÁTICA DEL MOVIMIENTO RECTILÍNEO Departamento de Física Aplicada Escuela Politécnica Superior de la Rábida. II. Movimiento
INGENIERÍA QUÍMICA 1 er curso FUNDAMENTOS FÍSICOS DE LA INGENIERÍA PRÁCTICA 2 CINEMÁTICA DEL MOVIMIENTO RECTILÍNEO Departamento de Física Aplicada Escuela Politécnica Superior de la Rábida. II. Movimiento
Problemas de Física 1 o Bachillerato
 Problemas de Física o Bachillerato Principio de conservación de la energía mecánica. Desde una altura h dejamos caer un cuerpo. Hallar en qué punto de su recorrido se cumple E c = 4 E p 2. Desde la parte
Problemas de Física o Bachillerato Principio de conservación de la energía mecánica. Desde una altura h dejamos caer un cuerpo. Hallar en qué punto de su recorrido se cumple E c = 4 E p 2. Desde la parte
Solución de la Tarea Número1delCursodeAnálisis Numérico.
 Solución de la Tarea Número1delCursodeAnálisis Numérico. José María Rico Martínez Departamento de Ineniería Mecánica. Universidad de Guanajuato, F. I. M. E. E. 1 Definición del Problema. Considere la banda
Solución de la Tarea Número1delCursodeAnálisis Numérico. José María Rico Martínez Departamento de Ineniería Mecánica. Universidad de Guanajuato, F. I. M. E. E. 1 Definición del Problema. Considere la banda
Ejercicios resueltos de cinemática
 Ejercicios resueltos de cinemática 1) Un cuerpo situado 50 metros por debajo del origen, se mueve verticalmente con velocidad inicial de 20 m/s, siendo la aceleración de la gravedad g = 9,8 m/s 2. a) Escribe
Ejercicios resueltos de cinemática 1) Un cuerpo situado 50 metros por debajo del origen, se mueve verticalmente con velocidad inicial de 20 m/s, siendo la aceleración de la gravedad g = 9,8 m/s 2. a) Escribe
CINEMÁTICA: MOVIMIENTO RECTILÍNEO, PROBLEMAS VARIOS
 CINEMÁTICA: MOVIMIENTO RECTILÍNEO, PROBLEMAS VARIOS Un arquero dispara una flecha que produce un fuerte ruido al chocar contra el blanco. La velocidad media de la flecha es de 150 m/s. El arquero escucha
CINEMÁTICA: MOVIMIENTO RECTILÍNEO, PROBLEMAS VARIOS Un arquero dispara una flecha que produce un fuerte ruido al chocar contra el blanco. La velocidad media de la flecha es de 150 m/s. El arquero escucha
Para revisarlos ponga cuidado en los paréntesis. No se confunda.
 Ejercicios MRUA Para revisarlos ponga cuidado en los paréntesis. No se confunda. 1.- Un cuerpo se mueve, partiendo del reposo, con una aceleración constante de 8 m/s 2. Calcular: a) la velocidad que tiene
Ejercicios MRUA Para revisarlos ponga cuidado en los paréntesis. No se confunda. 1.- Un cuerpo se mueve, partiendo del reposo, con una aceleración constante de 8 m/s 2. Calcular: a) la velocidad que tiene
Problemas de Cinemática 1 o Bachillerato
 Problemas de Cinemática 1 o Bachillerato 1. Sean los vectores a = i y b = i 5 j. Demostrar que a + b = a + b a b cos ϕ donde ϕ es el ángulo que forma el vector b con el eje X.. Una barca, que lleva una
Problemas de Cinemática 1 o Bachillerato 1. Sean los vectores a = i y b = i 5 j. Demostrar que a + b = a + b a b cos ϕ donde ϕ es el ángulo que forma el vector b con el eje X.. Una barca, que lleva una
IES Menéndez Tolosa. La Línea de la Concepción. 1 Es posible que un cuerpo se mueva sin que exista fuerza alguna sobre él?
 IES Menéndez Tolosa. La Línea de la Concepción 1 Es posible que un cuerpo se mueva sin que exista fuerza alguna sobre él? Si. Una consecuencia del principio de la inercia es que puede haber movimiento
IES Menéndez Tolosa. La Línea de la Concepción 1 Es posible que un cuerpo se mueva sin que exista fuerza alguna sobre él? Si. Una consecuencia del principio de la inercia es que puede haber movimiento
Las ecuaciones que nos dan la posición (x) de la partícula en función del tiempo son las siguientes: ( )
 DESARROLLO DE LA PARTE TEÓRICA DE LA UNIDAD DIDÁCTICA. 1. Cinemática del movimiento armónico simple. Dinámica del movimiento armónico simple 3. Energía del movimiento armónico simple 4. Aplicaciones: resorte
DESARROLLO DE LA PARTE TEÓRICA DE LA UNIDAD DIDÁCTICA. 1. Cinemática del movimiento armónico simple. Dinámica del movimiento armónico simple 3. Energía del movimiento armónico simple 4. Aplicaciones: resorte
Nombre:..Curso:.. GUIA DE TRABAJO Y POTENCIA MECANICA. Un niño traslada una caja desde el punto A al punto B recorriendo 4 m (fig.
 Nombre:..Curso:.. GUIA DE TRABAJO Y POTENCIA MECANICA Trabajo realizado por una fuerza. Un niño traslada una caja desde el punto A al punto B recorriendo 4 m (fig. N 1), fig N 1 Desde el punto de vista
Nombre:..Curso:.. GUIA DE TRABAJO Y POTENCIA MECANICA Trabajo realizado por una fuerza. Un niño traslada una caja desde el punto A al punto B recorriendo 4 m (fig. N 1), fig N 1 Desde el punto de vista
LEYES DE CONSERVACIÓN: ENERGÍA Y MOMENTO
 LEYES DE CONSERVACIÓN: ENERGÍA Y MOMENTO 1. Trabajo mecánico y energía. El trabajo, tal y como se define físicamente, es una magnitud diferente de lo que se entiende sensorialmente por trabajo. Trabajo
LEYES DE CONSERVACIÓN: ENERGÍA Y MOMENTO 1. Trabajo mecánico y energía. El trabajo, tal y como se define físicamente, es una magnitud diferente de lo que se entiende sensorialmente por trabajo. Trabajo
La masa es la magnitud física que mide la inercia de los cuerpos: N
 Pág. 1 16 Las siguientes frases, son verdaderas o falsas? a) Si el primer niño de una fila de niños que corren a la misma velocidad lanza una pelota verticalmente hacia arriba, al caer la recogerá alguno
Pág. 1 16 Las siguientes frases, son verdaderas o falsas? a) Si el primer niño de una fila de niños que corren a la misma velocidad lanza una pelota verticalmente hacia arriba, al caer la recogerá alguno
Problemas de Complementos de Matemáticas. Curso 01/02
 Problemas de Complementos de Matemáticas. Curso /2.- Resolver las E.D.O. lineales de primer orden siguientes y los problemas de condiciones x + 3x/t = 6t 2 x + 3x = 3t 2 e 3t t 4 x + 2t 3 x = tx + (tx
Problemas de Complementos de Matemáticas. Curso /2.- Resolver las E.D.O. lineales de primer orden siguientes y los problemas de condiciones x + 3x/t = 6t 2 x + 3x = 3t 2 e 3t t 4 x + 2t 3 x = tx + (tx
164 Ecuaciones diferenciales
 64 Ecuaciones diferenciales Ejercicios 3.6. Mecánica. Soluciones en la página 464. Una piedra de cae desde el reposo debido a la gravedad con resistencia despreciable del aire. a. Mediante una ecuación
64 Ecuaciones diferenciales Ejercicios 3.6. Mecánica. Soluciones en la página 464. Una piedra de cae desde el reposo debido a la gravedad con resistencia despreciable del aire. a. Mediante una ecuación
d s = 2 Experimento 3
 Experimento 3 ANÁLISIS DEL MOVIMIENTO EN UNA DIMENSIÓN Objetivos 1. Establecer la relación entre la posición y la velocidad de un cuerpo en movimiento 2. Calcular la velocidad como el cambio de posición
Experimento 3 ANÁLISIS DEL MOVIMIENTO EN UNA DIMENSIÓN Objetivos 1. Establecer la relación entre la posición y la velocidad de un cuerpo en movimiento 2. Calcular la velocidad como el cambio de posición
Mecánica Racional 20 TEMA 3: Método de Trabajo y Energía.
 INTRODUCCIÓN. Mecánica Racional 20 Este método es útil y ventajoso porque analiza las fuerzas, velocidad, masa y posición de una partícula sin necesidad de considerar las aceleraciones y además simplifica
INTRODUCCIÓN. Mecánica Racional 20 Este método es útil y ventajoso porque analiza las fuerzas, velocidad, masa y posición de una partícula sin necesidad de considerar las aceleraciones y además simplifica
Cinemática (II): algunos tipos de
 9 Cinemática (II): alunos tipos de.. 3. 4. La velocidad de un barco es de 4 nudos. Sabiendo que un nudo corresponde a una velocidad de milla náutica/h y que una milla náutica equivale a,85 km, calcula
9 Cinemática (II): alunos tipos de.. 3. 4. La velocidad de un barco es de 4 nudos. Sabiendo que un nudo corresponde a una velocidad de milla náutica/h y que una milla náutica equivale a,85 km, calcula
Recordando la experiencia
 Recordando la experiencia Lanzadera Cohete En el Taller de Cohetes de Agua cada alumno, individualmente o por parejas construisteis un cohete utilizando materiales sencillos y de bajo coste (botellas d
Recordando la experiencia Lanzadera Cohete En el Taller de Cohetes de Agua cada alumno, individualmente o por parejas construisteis un cohete utilizando materiales sencillos y de bajo coste (botellas d
CINEMÁTICA II: MRUA. 370 GUÍA DE FÍSICA Y QUÍMICA 1. Bachillerato MATERIAL FOTOCOPIABLE SANTILLANA EDUCACIÓN, S. L. PROBLEMAS RESUELTOS
 CINEMÁTICA II: MRUA PROBLEMAS RESUELTOS PROBLEMA RESUELTO Una persona lanza un objeto desde el suelo verticalmente hacia arriba con velocidad inicial de 0 m/s. Calcula: a) La altura máxima alcanzada. b)
CINEMÁTICA II: MRUA PROBLEMAS RESUELTOS PROBLEMA RESUELTO Una persona lanza un objeto desde el suelo verticalmente hacia arriba con velocidad inicial de 0 m/s. Calcula: a) La altura máxima alcanzada. b)
Energía mecánica y Caída Libre y lanzamiento vertical hacia arriba
 Soluciones Energía mecánica y Caída Libre y lanzamiento vertical hacia arriba Si no se dice otra cosa, no debe considerarse el efecto del roce con el aire. 1.- Un objeto de masa m cae libremente de cierta
Soluciones Energía mecánica y Caída Libre y lanzamiento vertical hacia arriba Si no se dice otra cosa, no debe considerarse el efecto del roce con el aire. 1.- Un objeto de masa m cae libremente de cierta
CHOQUE.(CANTIDAD DE MOVIMIENTO )
 APUNTES Materia: Tema: Curso: Física y Química Momento Lineal 4º ESO CHOQUE.(CANTIDAD DE MOVIMIENTO ) CANTIDAD DE MOVIMIENTO Si un cuerpo de masa m se está moviendo con velocidad v, la cantidad de movimiento
APUNTES Materia: Tema: Curso: Física y Química Momento Lineal 4º ESO CHOQUE.(CANTIDAD DE MOVIMIENTO ) CANTIDAD DE MOVIMIENTO Si un cuerpo de masa m se está moviendo con velocidad v, la cantidad de movimiento
GUIA DE PROBLEMAS. 3) La velocidad de un auto en función del tiempo, sobre un tramo recto de una carretera, está dada por
 Unidad : Cinemática de la partícula GUIA DE PROBLEMAS 1)-Un automóvil acelera en forma uniforme desde el reposo hasta 60 km/h en 8 s. Hallar su aceleración y desplazamiento durante ese tiempo. a = 0,59
Unidad : Cinemática de la partícula GUIA DE PROBLEMAS 1)-Un automóvil acelera en forma uniforme desde el reposo hasta 60 km/h en 8 s. Hallar su aceleración y desplazamiento durante ese tiempo. a = 0,59
OSCILACIONES ARMÓNICAS
 Tema 5 OSCILACIONES ARMÓNICAS 5.1. Introducción. 5.. Movimiento armónico simple (MAS). 5.3. Cinemática y dinámica del MAS. 5.4. Fuerza y energía en el MAS. 5.5. Péndulo simple. MAS y movimiento circular
Tema 5 OSCILACIONES ARMÓNICAS 5.1. Introducción. 5.. Movimiento armónico simple (MAS). 5.3. Cinemática y dinámica del MAS. 5.4. Fuerza y energía en el MAS. 5.5. Péndulo simple. MAS y movimiento circular
1. Hallar a qué velocidad hay que realizar un tiro parabólico para que llegue a una altura máxima de 100 m si el ángulo de tiro es de 30 o.
 Problemas de Cinemática 1 o Bachillerato Tiro parabólico y movimiento circular 1. Hallar a qué velocidad hay que realizar un tiro parabólico para que llegue a una altura máxima de 100 m si el ángulo de
Problemas de Cinemática 1 o Bachillerato Tiro parabólico y movimiento circular 1. Hallar a qué velocidad hay que realizar un tiro parabólico para que llegue a una altura máxima de 100 m si el ángulo de
EJERCICIOS PROPUESTOS
 LOS MOVIMIENTOS ACELERADOS EJERCICIOS PROPUESTOS. Cuando un motorista arranca, se sabe que posee un movimiento acelerado sin necesidad de ver la gráfica s-t ni conocer su trayectoria. Por qué? Porque al
LOS MOVIMIENTOS ACELERADOS EJERCICIOS PROPUESTOS. Cuando un motorista arranca, se sabe que posee un movimiento acelerado sin necesidad de ver la gráfica s-t ni conocer su trayectoria. Por qué? Porque al
COLEGIO HISPANO-INGLÉS SEMINARIO DE FÍSICA Y QUÍMICA SIMULACRO.
 COLEGIO HISPANO-INGLÉS SIMULACRO. SEMINARIO DE FÍSICA Y QUÍMICA 1.- Las ecuaciones de la trayectoria (componentes cartesianas en función de t de la posición) de una partícula son x=t 2 +2; y = 2t 2-1;
COLEGIO HISPANO-INGLÉS SIMULACRO. SEMINARIO DE FÍSICA Y QUÍMICA 1.- Las ecuaciones de la trayectoria (componentes cartesianas en función de t de la posición) de una partícula son x=t 2 +2; y = 2t 2-1;
Profr. Efraín Soto Apolinar. Límites
 Límites Cada rama de las matemáticas tiene conceptos que resultan centrales para el desarrollo de la misma. Nosotros empezamos el estudio del cálculo infinitesimal, que está compuesto del cálculo diferencial
Límites Cada rama de las matemáticas tiene conceptos que resultan centrales para el desarrollo de la misma. Nosotros empezamos el estudio del cálculo infinitesimal, que está compuesto del cálculo diferencial
No hay resorte que oscile cien años...
 No hay resorte que oscile cien años... María Paula Coluccio y Patricia Picardo Laboratorio I de Física para Biólogos y Geólogos Depto. de Física, FCEyN, UBA - 1999 Resumen: En el presente trabajo nos proponemos
No hay resorte que oscile cien años... María Paula Coluccio y Patricia Picardo Laboratorio I de Física para Biólogos y Geólogos Depto. de Física, FCEyN, UBA - 1999 Resumen: En el presente trabajo nos proponemos
TRABAJO Y ENERGÍA; FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS
 TRABAJO Y ENERGÍA; FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS 1. CONCEPTO DE TRABAJO: A) Trabajo de una fuerza constante Todos sabemos que cuesta trabajo tirar de un sofá pesado, levantar una pila de libros
TRABAJO Y ENERGÍA; FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS 1. CONCEPTO DE TRABAJO: A) Trabajo de una fuerza constante Todos sabemos que cuesta trabajo tirar de un sofá pesado, levantar una pila de libros
www.matyfyq.blogspot.com EJERCICIOS CINEMÁTICA 4ºESO:
 Estes exercicios foron sacados de www.matyfyq.blogspot.com EJERCICIOS CINEMÁTICA 4ºESO: 1- Define brevemente los siguientes conceptos: Posición. Trayectoria. Espacio recorrido. Desplazamiento Velocidad
Estes exercicios foron sacados de www.matyfyq.blogspot.com EJERCICIOS CINEMÁTICA 4ºESO: 1- Define brevemente los siguientes conceptos: Posición. Trayectoria. Espacio recorrido. Desplazamiento Velocidad
Parcial I Cálculo Vectorial
 Parcial I Cálculo Vectorial Febrero 8 de 1 ( Puntos) I. Responda falso o verdadero justificando matematicamente su respuesta. (i) La gráfica de la ecuación cos ϕ = 1, en coordenadas esféricas en R3, es
Parcial I Cálculo Vectorial Febrero 8 de 1 ( Puntos) I. Responda falso o verdadero justificando matematicamente su respuesta. (i) La gráfica de la ecuación cos ϕ = 1, en coordenadas esféricas en R3, es
1. Magnitudes vectoriales
 FUNDACIÓN INSTITUTO A DISTANCIA EDUARDO CABALLERO CALDERON Espacio Académico: Física Docente: Mónica Bibiana Velasco Borda mbvelascob@uqvirtual.edu.co CICLO: V INICADORES DE LOGRO VECTORES 1. Adquiere
FUNDACIÓN INSTITUTO A DISTANCIA EDUARDO CABALLERO CALDERON Espacio Académico: Física Docente: Mónica Bibiana Velasco Borda mbvelascob@uqvirtual.edu.co CICLO: V INICADORES DE LOGRO VECTORES 1. Adquiere
CAPÍTULO 10 Aplicaciones de la Derivada a Funciones Económicas
 CAPÍTULO 10 Aplicaciones de la Derivada a Funciones Económicas Introducción En la economía, la variación de alguna cantidad con respecto a otra puede ser descrita por un concepto promedio o por un concepto
CAPÍTULO 10 Aplicaciones de la Derivada a Funciones Económicas Introducción En la economía, la variación de alguna cantidad con respecto a otra puede ser descrita por un concepto promedio o por un concepto
Órbitas producidas por fuerzas centrales
 Capítulo 10 Órbitas producidas por fuerzas centrales 10.1 Introducción En un capítulo anterior hemos visto una variedad de fuerzas, varias de las cuales, como por ejemplo la elástica, la gravitatoria y
Capítulo 10 Órbitas producidas por fuerzas centrales 10.1 Introducción En un capítulo anterior hemos visto una variedad de fuerzas, varias de las cuales, como por ejemplo la elástica, la gravitatoria y
Unidad: Representación gráfica del movimiento
 Unidad: Representación gráfica del movimiento Aplicando y repasando el concepto de rapidez Esta primera actividad repasa el concepto de rapidez definido anteriormente. Posición Esta actividad introduce
Unidad: Representación gráfica del movimiento Aplicando y repasando el concepto de rapidez Esta primera actividad repasa el concepto de rapidez definido anteriormente. Posición Esta actividad introduce
Profr. Efraín Soto Apolinar. La función lineal. y = a 0 + a 1 x. y = m x + b
 La función lineal Una función polinomial de grado uno tiene la forma: y = a 0 + a 1 x El semestre pasado estudiamos la ecuación de la recta. y = m x + b En la notación de funciones polinomiales, el coeficiente
La función lineal Una función polinomial de grado uno tiene la forma: y = a 0 + a 1 x El semestre pasado estudiamos la ecuación de la recta. y = m x + b En la notación de funciones polinomiales, el coeficiente
EJEMPLOS DE CUESTIONES DE EVALUACIÓN
 EJEMPLOS DE CUESTIONES DE EVALUACIÓN 1. EL MOVIMIENTO Dirección en Internet: http://www.iesaguilarycano.com/dpto/fyq/cine4/index.htm a 1. Determine el desplazamiento total en cada uno de los casos siguientes
EJEMPLOS DE CUESTIONES DE EVALUACIÓN 1. EL MOVIMIENTO Dirección en Internet: http://www.iesaguilarycano.com/dpto/fyq/cine4/index.htm a 1. Determine el desplazamiento total en cada uno de los casos siguientes
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. Página 9 PRACTICA Sistemas lineales Comprueba si el par (, ) es solución de alguno de los siguientes sistemas: x + y 5 a) x y x y 5 x + y 8 El par (, ) es solución de un sistema si al sustituir x
Pág. Página 9 PRACTICA Sistemas lineales Comprueba si el par (, ) es solución de alguno de los siguientes sistemas: x + y 5 a) x y x y 5 x + y 8 El par (, ) es solución de un sistema si al sustituir x
[c] Qué energía mecánica posee el sistema muelle-masa? Y si la masa fuese 2 y la constante 2K?.
![[c] Qué energía mecánica posee el sistema muelle-masa? Y si la masa fuese 2 y la constante 2K?. [c] Qué energía mecánica posee el sistema muelle-masa? Y si la masa fuese 2 y la constante 2K?.](/thumbs/15/62431.jpg) Actividad 1 La figura representa un péndulo horizontal de resorte. La masa del bloque vale M y la constante elástica del resorte K. No hay rozamientos. Inicialmente el muelle está sin deformar. [a] Si
Actividad 1 La figura representa un péndulo horizontal de resorte. La masa del bloque vale M y la constante elástica del resorte K. No hay rozamientos. Inicialmente el muelle está sin deformar. [a] Si
(m 2.g - m 2.a - m 1.g - m 1.a ).R = (M.R 2 /2 ). a / R. a = ( m 2 - m 1 ).g / (m 2 + m 1 + M/2) las tensiones son distintas.
 Dos masas de 1 y 2 kg están unidas por una cuerda inextensible y sin masa que pasa por una polea sin rozamientos. La polea es izada con velocidad constante con una fuerza de 40 Nw. Calcular la tensión
Dos masas de 1 y 2 kg están unidas por una cuerda inextensible y sin masa que pasa por una polea sin rozamientos. La polea es izada con velocidad constante con una fuerza de 40 Nw. Calcular la tensión
CINEMÁTICA DEL PUNTO MATERIAL. ELEMENTOS Y MAGNITUDES DEL MOVIMIENTO
 CINEMÁTICA DEL PUNTO MATERIAL. ELEMENTOS Y MAGNITUDES DEL MOVIMIENTO Estudiar el movimiento es importante: es el fenómeno más corriente y fácil de observar en la Naturaleza. Todo el Universo está en constante
CINEMÁTICA DEL PUNTO MATERIAL. ELEMENTOS Y MAGNITUDES DEL MOVIMIENTO Estudiar el movimiento es importante: es el fenómeno más corriente y fácil de observar en la Naturaleza. Todo el Universo está en constante
Juan de la Cruz González Férez
 Curso 0: Matemáticas y sus Aplicaciones Vectores, Bases y Distancias Aplicaciones Juan de la Cruz González Férez IES Salvador Sandoval Las Torres de Cotillas (Murcia) 2012 Composición de movimientos Los
Curso 0: Matemáticas y sus Aplicaciones Vectores, Bases y Distancias Aplicaciones Juan de la Cruz González Férez IES Salvador Sandoval Las Torres de Cotillas (Murcia) 2012 Composición de movimientos Los
Movimiento en dos y tres dimensiones. Teoría. Autor:
 Movimiento en dos y tres dimensiones Teoría Autor: YeissonHerney Herrera Contenido 1. Introducción 1.1. actividad palabras claves unid 2. Vector posición 2.1. Explicación vector posición 2.2. Animación
Movimiento en dos y tres dimensiones Teoría Autor: YeissonHerney Herrera Contenido 1. Introducción 1.1. actividad palabras claves unid 2. Vector posición 2.1. Explicación vector posición 2.2. Animación
PRUEBA ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR OPCIÓN B y C, FÍSICA
 PRUEBA ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR OPCIÓN B y C, FÍSICA DATOS DEL ASPIRANTE Apellidos: CALIFICACIÓN PRUEBA Nombre: D.N.I. o Pasaporte: Fecha de nacimiento: / / Instrucciones: Lee atentamente
PRUEBA ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR OPCIÓN B y C, FÍSICA DATOS DEL ASPIRANTE Apellidos: CALIFICACIÓN PRUEBA Nombre: D.N.I. o Pasaporte: Fecha de nacimiento: / / Instrucciones: Lee atentamente
asociados a cada cuerpo de referencia, que sirven para describir el movimiento mecánico de los cuerpos respecto a esos tomados como referencia.
 CAP. 4: CINEMÁTICA DE LA PARTÍCULA. Modelo de partícula: se aplica a cuerpos muy pequeños comparados con el diámetro de la menor esfera donde cabe la trayectoria completa del cuerpo. Equivale a considerar
CAP. 4: CINEMÁTICA DE LA PARTÍCULA. Modelo de partícula: se aplica a cuerpos muy pequeños comparados con el diámetro de la menor esfera donde cabe la trayectoria completa del cuerpo. Equivale a considerar
M.R.U. v = cte. rectilíneo. curvilíneo. compos. movimiento
 RECUERDA: La cinemática, es la ciencia, parte de la física, que se encarga del estudio del movimiento de los cuerpos, tratando de definirlos, clasificarlos y dotarlos de alguna utilidad práctica. El movimiento
RECUERDA: La cinemática, es la ciencia, parte de la física, que se encarga del estudio del movimiento de los cuerpos, tratando de definirlos, clasificarlos y dotarlos de alguna utilidad práctica. El movimiento
TRABAJO Y ENERGÍA Página 1 de 13
 TRABAJO Y ENERGÍA Página 1 de 13 EJERCICIOS DE TRABAJO Y ENERGÍA RESUELTOS: Ejemplo 1: Calcular el trabajo necesario para estirar un muelle 5 cm, si la constante del muelle es 1000 N/m. La fuerza necesaria
TRABAJO Y ENERGÍA Página 1 de 13 EJERCICIOS DE TRABAJO Y ENERGÍA RESUELTOS: Ejemplo 1: Calcular el trabajo necesario para estirar un muelle 5 cm, si la constante del muelle es 1000 N/m. La fuerza necesaria
amax=aω 2 ; β=10logi/io; ω=2πf;t=1/f; κ=1/λ; τ=ln2/λ; P=1/f (m);e p= gdr; N=Noe λt ; 1/f =1/s +1/s; Fc=mv 2 /r; y(x,t)=asen(ωt±kx); W=qΔV; F=qvxB;
 E=hf;p=mv;F=dp/dt;I=Q/t;Ec=mv 2 /2; TEMA 5: VIBRACIONES Y ONDAS F=KQq/r 2 ;L=rxp;x=Asen(ωt+φo);v=λf c 2 =1/εoµo;A=πr 2 ;T 2 =4π 2 /GMr 3 ;F=ma; L=dM/dtiopasdfghjklzxcvbvv=dr/dt; M=rxF;sspmoqqqqqqqqqqqp=h/λ;
E=hf;p=mv;F=dp/dt;I=Q/t;Ec=mv 2 /2; TEMA 5: VIBRACIONES Y ONDAS F=KQq/r 2 ;L=rxp;x=Asen(ωt+φo);v=λf c 2 =1/εoµo;A=πr 2 ;T 2 =4π 2 /GMr 3 ;F=ma; L=dM/dtiopasdfghjklzxcvbvv=dr/dt; M=rxF;sspmoqqqqqqqqqqqp=h/λ;
JOSÉ PERAZA, FÍSICA 2 JOSÉ PERAZA, FÍSICA 2 JOSÉ PERAZA, FÍSICA 2 Energía Potencial eléctrica
 Energía Potencial eléctrica Si movemos la carga q2 respecto a la carga q1 Recordemos que la diferencia en la energía tenemos que: potencial U cuando una partícula se mueve entre dos puntos a y b bajo la
Energía Potencial eléctrica Si movemos la carga q2 respecto a la carga q1 Recordemos que la diferencia en la energía tenemos que: potencial U cuando una partícula se mueve entre dos puntos a y b bajo la
Electrostática: ejercicios resueltos
 Electrostática: ejercicios resueltos 1) Dos cargas de 4 y 9 microculombios se hallan situadas en los puntos (2,0) y (4,0) del eje 0X. Calcula el campo y el potencial eléctrico en el punto medio. 2) Dos
Electrostática: ejercicios resueltos 1) Dos cargas de 4 y 9 microculombios se hallan situadas en los puntos (2,0) y (4,0) del eje 0X. Calcula el campo y el potencial eléctrico en el punto medio. 2) Dos
Integrales y ejemplos de aplicación
 Integrales y ejemplos de aplicación I. PROPÓSITO DE ESTOS APUNTES Estas notas tienen como finalidad darle al lector una breve introducción a la noción de integral. De ninguna manera se pretende seguir
Integrales y ejemplos de aplicación I. PROPÓSITO DE ESTOS APUNTES Estas notas tienen como finalidad darle al lector una breve introducción a la noción de integral. De ninguna manera se pretende seguir
CAMPO ELÉCTRICO FCA 10 ANDALUCÍA
 CMO LÉCTRICO FC 0 NDLUCÍ. a) xplique la relación entre campo y potencial electrostáticos. b) Una partícula cargada se mueve espontáneamente hacia puntos en los que el potencial electrostático es mayor.
CMO LÉCTRICO FC 0 NDLUCÍ. a) xplique la relación entre campo y potencial electrostáticos. b) Una partícula cargada se mueve espontáneamente hacia puntos en los que el potencial electrostático es mayor.
ESTUDIO DEL MOVIMIENTO.
 TEMA 1. CINEMATICA. 4º E.S.O. FÍSICA Y QUÍMICA Página 1 ESTUDIO DEL MOVIMIENTO. MAGNITUD: Es todo aquello que se puede medir. Ejemplos: superficie, presión, fuerza, etc. MAGNITUDES FUNDAMENTALES: Son aquellas
TEMA 1. CINEMATICA. 4º E.S.O. FÍSICA Y QUÍMICA Página 1 ESTUDIO DEL MOVIMIENTO. MAGNITUD: Es todo aquello que se puede medir. Ejemplos: superficie, presión, fuerza, etc. MAGNITUDES FUNDAMENTALES: Son aquellas
14º Un elevador de 2000 kg de masa, sube con una aceleración de 1 m/s 2. Cuál es la tensión del cable que lo soporta? Sol: 22000 N
 Ejercicios de dinámica, fuerzas (4º de ESO/ 1º Bachillerato): 1º Calcular la masa de un cuerpo que al recibir una fuerza de 0 N adquiere una aceleración de 5 m/s. Sol: 4 kg. º Calcular la masa de un cuerpo
Ejercicios de dinámica, fuerzas (4º de ESO/ 1º Bachillerato): 1º Calcular la masa de un cuerpo que al recibir una fuerza de 0 N adquiere una aceleración de 5 m/s. Sol: 4 kg. º Calcular la masa de un cuerpo
Experimento 4 MOVIMIENTO CON ACELERACIÓN CONSTANTE. Objetivos. Teoría
 Experimento 4 MOVIMIENTO CON ACELERACIÓN CONSTANTE Objetivos 1. Medir la distancia recorrida y la velocidad de un objeto que se mueve con: a. velocidad constante y b. aceleración constante,. Establecer
Experimento 4 MOVIMIENTO CON ACELERACIÓN CONSTANTE Objetivos 1. Medir la distancia recorrida y la velocidad de un objeto que se mueve con: a. velocidad constante y b. aceleración constante,. Establecer
La derivada de y respecto a x es lo que varía y por cada unidad que varía x. Ese valor se designa por dy dx.
 Conceptos de derivada y de diferencial Roberto C. Redondo Melchor, Norberto Redondo Melchor, Félix Redondo Quintela 1 Universidad de Salamanca 18 de agosto de 2012 v1.3: 17 de septiembre de 2012 Aunque
Conceptos de derivada y de diferencial Roberto C. Redondo Melchor, Norberto Redondo Melchor, Félix Redondo Quintela 1 Universidad de Salamanca 18 de agosto de 2012 v1.3: 17 de septiembre de 2012 Aunque
MCBtec Mas información en
 MCBtec Mas información en www.mcbtec.com INTRODUCCIÓN A LA SIMULACION POR ORDENADOR Indice: Objetivo de este texto. Simulación por ordenador. Dinámica y simulación. Ejemplo disparo de un proyectil. Ejemplo
MCBtec Mas información en www.mcbtec.com INTRODUCCIÓN A LA SIMULACION POR ORDENADOR Indice: Objetivo de este texto. Simulación por ordenador. Dinámica y simulación. Ejemplo disparo de un proyectil. Ejemplo
Tema 1. Movimiento de una Partícula
 Tema 1. Movimiento de una Partícula CONTENIDOS Rapidez media, velocidad media, velocidad instantánea y velocidad constante. Velocidades relativas sobre una línea recta (paralelas y colineales) Movimiento
Tema 1. Movimiento de una Partícula CONTENIDOS Rapidez media, velocidad media, velocidad instantánea y velocidad constante. Velocidades relativas sobre una línea recta (paralelas y colineales) Movimiento
FS-2 GUÍA CURSOS ANUALES. Ciencias Plan Común. Física 2009. Descripción del movimiento I
 FS-2 Ciencias Plan Común Física 2009 Descripción del movimiento I Introducción: La presente guía tiene por objetivo proporcionarte distintas instancias didácticas relacionadas con el proceso de aprendizaje-enseñanza.
FS-2 Ciencias Plan Común Física 2009 Descripción del movimiento I Introducción: La presente guía tiene por objetivo proporcionarte distintas instancias didácticas relacionadas con el proceso de aprendizaje-enseñanza.
M.A.S. Y MOV ONDULATORIO FCA 07 ANDALUCÍA
 . La ecuación de una onda armónica que se propaga por una cuerda es: y (x, t) = 0,08 cos (6 t - 0 x) (S.I.) a) Determine el sentido de propagación de la onda, su amplitud, periodo, longitud de onda y velocidad
. La ecuación de una onda armónica que se propaga por una cuerda es: y (x, t) = 0,08 cos (6 t - 0 x) (S.I.) a) Determine el sentido de propagación de la onda, su amplitud, periodo, longitud de onda y velocidad
Capítulo 1. Mecánica
 Capítulo 1 Mecánica 1 Velocidad El vector de posición está especificado por tres componentes: r = x î + y ĵ + z k Decimos que x, y y z son las coordenadas de la partícula. La velocidad es la derivada temporal
Capítulo 1 Mecánica 1 Velocidad El vector de posición está especificado por tres componentes: r = x î + y ĵ + z k Decimos que x, y y z son las coordenadas de la partícula. La velocidad es la derivada temporal
EL MOVIMIENTO CUESTIONES Y PROBLEMAS RESUELTOS
 EL MOVIMIENTO CUESTIONES Y PROBLEMAS RESUELTOS 1 DIFICULTAD BAJA 1. Qué magnitud nos mide la rapidez con la que se producen los cambios de posición durante un movimiento? Defínela. La velocidad media.
EL MOVIMIENTO CUESTIONES Y PROBLEMAS RESUELTOS 1 DIFICULTAD BAJA 1. Qué magnitud nos mide la rapidez con la que se producen los cambios de posición durante un movimiento? Defínela. La velocidad media.
_ Antología de Física I. Unidad II Vectores. Elaboró: Ing. Víctor H. Alcalá-Octaviano
 24 Unidad II Vectores 2.1 Magnitudes escalares y vectoriales Unidad II. VECTORES Para muchas magnitudes físicas basta con indicar su valor para que estén perfectamente definidas y estas son las denominadas
24 Unidad II Vectores 2.1 Magnitudes escalares y vectoriales Unidad II. VECTORES Para muchas magnitudes físicas basta con indicar su valor para que estén perfectamente definidas y estas son las denominadas
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS DEBER # 3 TRABAJO Y ENERGÍA
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS DEBER # 3 TRABAJO Y ENERGÍA 1.- El bloque mostrado se encuentra afectado por fuerzas que le permiten desplazarse desde A hasta B.
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS DEBER # 3 TRABAJO Y ENERGÍA 1.- El bloque mostrado se encuentra afectado por fuerzas que le permiten desplazarse desde A hasta B.
FÍSICA Y QUÍMICA Solucionario CINEMÁTICA
 FÍSICA Y QUÍMICA Solucionario CINEMÁTICA 1.* Indicad qué tipo o tipos de movimiento corresponden a cada afirmación. a) MRU b) MRUA c) MCU d) Caída libre e) No hay movimiento 1.1. Una piedra lanzada desde
FÍSICA Y QUÍMICA Solucionario CINEMÁTICA 1.* Indicad qué tipo o tipos de movimiento corresponden a cada afirmación. a) MRU b) MRUA c) MCU d) Caída libre e) No hay movimiento 1.1. Una piedra lanzada desde
Capítulo 2 Energía 1
 Capítulo 2 Energía 1 Trabajo El trabajo realizado por una fuerza constante sobre una partícula que se mueve en línea recta es: W = F L = F L cos θ siendo L el vector desplazamiento y θ el ángulo entre
Capítulo 2 Energía 1 Trabajo El trabajo realizado por una fuerza constante sobre una partícula que se mueve en línea recta es: W = F L = F L cos θ siendo L el vector desplazamiento y θ el ángulo entre
EJERCICIOS SOBRE CINEMÁTICA: EL MOVIMIENTO
 EJERCICIOS SOBRE CINEMÁTICA: EL MOVIMIENTO Estrategia a seguir para resolver los ejercicios. 1. Lea detenidamente el ejercicio las veces que necesite, hasta que tenga claro en qué consiste y qué es lo
EJERCICIOS SOBRE CINEMÁTICA: EL MOVIMIENTO Estrategia a seguir para resolver los ejercicios. 1. Lea detenidamente el ejercicio las veces que necesite, hasta que tenga claro en qué consiste y qué es lo
Cinemática en una Dimensión. Posición, velocidad. Cantidades vectoriales: operación de suma y diferencia.
 Cinemática en una Dimensión. Posición, velocidad. Cantidades vectoriales: operación de suma y diferencia. Resumen Para cualquier numero que resulte de una medición es importante especificar su incertidumbre
Cinemática en una Dimensión. Posición, velocidad. Cantidades vectoriales: operación de suma y diferencia. Resumen Para cualquier numero que resulte de una medición es importante especificar su incertidumbre
ELEMENTOS DEL MOVIMIENTO
 ELEMENTOS DEL MOVIMIENTO Unidad 10 CONTENIDOS.- 1.- Introducción..- Magnitudes escalares vectoriales. 3.- Sistemas de referencia. Concepto de movimiento. 4.- Operaciones con vectores. 5.- Traectoria, posición
ELEMENTOS DEL MOVIMIENTO Unidad 10 CONTENIDOS.- 1.- Introducción..- Magnitudes escalares vectoriales. 3.- Sistemas de referencia. Concepto de movimiento. 4.- Operaciones con vectores. 5.- Traectoria, posición
PROBLEMAS DE ONDAS. EFECTO DOPPLER. Autor: José Antonio Diego Vives. Documento bajo licencia Creative Commons (BY-SA)
 PROBLEMAS DE ONDAS. EFECTO DOPPLER Autor: José Antonio Diego Vives Documento bajo licencia Creative Commons (BY-SA) Problema 1 Una sirena que emite un sonido de = 1000 Hz se mueve alejándose de un observador
PROBLEMAS DE ONDAS. EFECTO DOPPLER Autor: José Antonio Diego Vives Documento bajo licencia Creative Commons (BY-SA) Problema 1 Una sirena que emite un sonido de = 1000 Hz se mueve alejándose de un observador
35 Facultad de Ciencias Universidad de Los Andes Mérida-Venezuela. Potencial Eléctrico
 q 1 q 2 Prof. Félix Aguirre 35 Energía Electrostática Potencial Eléctrico La interacción electrostática es representada muy bien a través de la ley de Coulomb, esto es: mediante fuerzas. Existen, sin embargo,
q 1 q 2 Prof. Félix Aguirre 35 Energía Electrostática Potencial Eléctrico La interacción electrostática es representada muy bien a través de la ley de Coulomb, esto es: mediante fuerzas. Existen, sin embargo,
Unidad: Energía Cinética y Potencial
 Unidad: Energía Cinética y Potencial El teorema del Trabajo y la Energía Cinética dice que: El cambio de la Energía Cinética de un objeto que se mueve es igual al Trabajo hecho por la fuerza (neta) que
Unidad: Energía Cinética y Potencial El teorema del Trabajo y la Energía Cinética dice que: El cambio de la Energía Cinética de un objeto que se mueve es igual al Trabajo hecho por la fuerza (neta) que
1 Yoyó con cuerda despreciable 1
 1 Yoyó con cuerda despreciable 1 En este documento se describe el problema clásico de la Física elemental en el que un yoyó, modelado como un disco, cae bajo la acción de la gravedad, sujeto con una cuerda
1 Yoyó con cuerda despreciable 1 En este documento se describe el problema clásico de la Física elemental en el que un yoyó, modelado como un disco, cae bajo la acción de la gravedad, sujeto con una cuerda
Conservación de la Energía Mecánica NOMBRE: CURSO:
 NOMBRE: CURSO: La ley de conservación de la energía mecánica nos dice que la energía de un sistema aislado de influencias externas se mantiene siempre constante, lo que ocurre es una simple transformación
NOMBRE: CURSO: La ley de conservación de la energía mecánica nos dice que la energía de un sistema aislado de influencias externas se mantiene siempre constante, lo que ocurre es una simple transformación
PROBLEMAS DE DINÁMICA. 1. Calcula la fuerza que habrá que realizar para frenar, hasta detener en 10 segundos un trineo que se mueve a 50 km/h.
 PROBLEMAS DE DINÁMICA 1. Calcula la fuerza que habrá que realizar para frenar, hasta detener en 10 segundos un trineo que se mueve a 50 km/h. 2. Un vehículo de 800 kg se mueve en un tramo recto y horizontal
PROBLEMAS DE DINÁMICA 1. Calcula la fuerza que habrá que realizar para frenar, hasta detener en 10 segundos un trineo que se mueve a 50 km/h. 2. Un vehículo de 800 kg se mueve en un tramo recto y horizontal
Guía para el examen de 4ª y 6ª oportunidad de FÍsica1
 4a 4a 6a Guía para el examen de 4ª y 6ª oportunidad de FÍsica1 Capitulo 1 Introducción a la Física a) Clasificación y aplicaciones b) Sistemas de unidades Capitulo 2 Movimiento en una dimensión a) Conceptos
4a 4a 6a Guía para el examen de 4ª y 6ª oportunidad de FÍsica1 Capitulo 1 Introducción a la Física a) Clasificación y aplicaciones b) Sistemas de unidades Capitulo 2 Movimiento en una dimensión a) Conceptos
DEPARTAMENTO DE EDUCACIÓN FÍSICA CURSO 2011/2012
 ORIENTACIÓN.1ºESO Carreras de Orientación Una Carrera de Orientación consiste en recorrer en el menor tiempo posible una ruta situada en un terreno desconocido pasando por unos puntos obligados en un orden
ORIENTACIÓN.1ºESO Carreras de Orientación Una Carrera de Orientación consiste en recorrer en el menor tiempo posible una ruta situada en un terreno desconocido pasando por unos puntos obligados en un orden
Decimos que un cuerpo se mueve cuando cambia de posición respecto a un sistema de referencia que se considera fijo.
 1. EL MOVIMIENTO Decimos que un cuerpo se mueve cuando cambia de posición respecto a un sistema de referencia que se considera fijo. Por ejemplo: el coche que se mueve cambia de posición respecto a unos
1. EL MOVIMIENTO Decimos que un cuerpo se mueve cuando cambia de posición respecto a un sistema de referencia que se considera fijo. Por ejemplo: el coche que se mueve cambia de posición respecto a unos
TRABAJO. ENERGÍA. PRINCIPIO DE CONSERVACIÓN
 TRABAJO. ENERGÍA. PRINCIPIO DE CONSERVACIÓN Un coche de 50 kg (con el conductor incluido) que funciona con gasolina está situado en una carretera horizontal, arranca y acelerando uniformemente, alcanza
TRABAJO. ENERGÍA. PRINCIPIO DE CONSERVACIÓN Un coche de 50 kg (con el conductor incluido) que funciona con gasolina está situado en una carretera horizontal, arranca y acelerando uniformemente, alcanza
Leyes de movimiento. Leyes del movimiento de Newton. Primera ley de Newton o ley de la inercia. Segunda ley de Newton
 Leyes de movimiento Leyes del movimiento de Newton La mecánica, en el estudio del movimiento de los cuerpos, se divide en cinemática y dinámica. La cinemática estudia los diferentes tipos de movimiento
Leyes de movimiento Leyes del movimiento de Newton La mecánica, en el estudio del movimiento de los cuerpos, se divide en cinemática y dinámica. La cinemática estudia los diferentes tipos de movimiento
PROBLEMAS RESUELTOS TEMA: 3
 PROBLEMAS RESUELTOS TEMA: 3 1. Una partícula de 3 kg se desplaza con una velocidad de cuando se encuentra en. Esta partícula se encuentra sometida a una fuerza que varia con la posición del modo indicado
PROBLEMAS RESUELTOS TEMA: 3 1. Una partícula de 3 kg se desplaza con una velocidad de cuando se encuentra en. Esta partícula se encuentra sometida a una fuerza que varia con la posición del modo indicado
VIAJANDO EN EL TELEFÉRICO EJERCICIOS PRÁCTICOS PARA APRENDER Y DIVERTIRSE CUADERNO DEL ALUMNO
 IAJANDO EN EL TELEFÉRICO EJERCICIO PRÁCTICO PARA APRENDER Y DIERTIRE CUADERNO DEL ALUMNO DECRIPCIÓN Un viaje tranquilo y sin sobresaltos de 2,4km de longitud a través del cielo de Madrid alcanzando una
IAJANDO EN EL TELEFÉRICO EJERCICIO PRÁCTICO PARA APRENDER Y DIERTIRE CUADERNO DEL ALUMNO DECRIPCIÓN Un viaje tranquilo y sin sobresaltos de 2,4km de longitud a través del cielo de Madrid alcanzando una
2.3. ASPECTOS ENERGÉTICOS
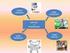 .3. ASPECTOS ENERGÉTICOS.3.1. Sobre un cuerpo actúa una fuerza representada en la gráfica de la figura. Podemos decir que el trabajo realizado por la fuerza es: a) (8/+16+16/) J b)(4+3+3) J c) (4+16+4)
.3. ASPECTOS ENERGÉTICOS.3.1. Sobre un cuerpo actúa una fuerza representada en la gráfica de la figura. Podemos decir que el trabajo realizado por la fuerza es: a) (8/+16+16/) J b)(4+3+3) J c) (4+16+4)
un coche está parado en un semáforo implica v 0 =0.
 TEMA 1 CINEMÁTICA DE LA PARTÍCULA CONSEJOS PREVIOS A LA RESOLUCIÓN DE PROBLEMAS Movimiento con aceleración constante Al abordar un problema debes fijar el origen de coordenadas y la dirección positiva.
TEMA 1 CINEMÁTICA DE LA PARTÍCULA CONSEJOS PREVIOS A LA RESOLUCIÓN DE PROBLEMAS Movimiento con aceleración constante Al abordar un problema debes fijar el origen de coordenadas y la dirección positiva.
Experimento 7 MOMENTO LINEAL. Objetivos. Teoría. Figura 1 Dos carritos sufren una colisión parcialmente inelástica
 Experimento 7 MOMENTO LINEAL Objetivos 1. Verificar el principio de conservación del momento lineal en colisiones inelásticas, y 2. Comprobar que la energía cinética no se conserva en colisiones inelásticas
Experimento 7 MOMENTO LINEAL Objetivos 1. Verificar el principio de conservación del momento lineal en colisiones inelásticas, y 2. Comprobar que la energía cinética no se conserva en colisiones inelásticas
PROBLEMAS M.A.S. Y ONDAS
 PROBLEMAS M.A.S. Y ONDAS 1) Una masa de 50 g unida a un resorte realiza, en el eje X, un M.A.S. descrito por la ecuación, expresada en unidades del SI. Establece su posición inicial y estudia el sentido
PROBLEMAS M.A.S. Y ONDAS 1) Una masa de 50 g unida a un resorte realiza, en el eje X, un M.A.S. descrito por la ecuación, expresada en unidades del SI. Establece su posición inicial y estudia el sentido
