Pruebas Maximin para la Calidad de Estabilización Robusta
|
|
|
- Ramona Naranjo Tebar
- hace 6 años
- Vistas:
Transcripción
1 8º Congreso Nacional e Mecatrónica Noviembre 6 y 7, 9. Veracruz, Veracruz. Pruebas Maximin para la Calia e Estabilización Robusta Gutiérrez Arias José Eligio Moisés, Cabrera Martínez Javier, José Fernano Reyes Cortés Faculta e Ciencias e la Electrónica, Benemérita Universia Autónoma e Puebla Av. San Clauio y Blv. 18 Sur. Col. Jarines e San Manuel, Puebla, Pue. C.P. 757, México eléfono: () jmgutierrez@ece.buap.mx / javier_cm4@ece.buap.mx, / freyes@ece.buap.mx Resumen Existen situaciones en que se esea estimar la calia e estabilización e un sistema e control, en las cuales se esconoce como funciona el sistema e icho control; pero conocemos la entraa y la salia el mismo, estas situaciones permiten consierar los sistemas e pruebas e calia e la estabilización, como lo son las pruebas maximin. Las estrategias e pruebas maximin es una nueva irección en la teoría e control óptimo y tienen su aplicación en la práctica e pruebas. Su objetivo es evaluar el esempeño e algoritmos e estabilización esconocios, así, meiante un sistema e pruebas eterminar cuan bueno es icho algoritmo e control. En el presente trabajo, se evalúa el esempeño que presenta un controlaor esconocio que se aplica a un robot móvil, utilizano para ello las pruebas maximin. Palabras clave: Pruebas maximin, inicaor e esempeño, estimación inferior, ecuación e Riccati. 1. Introucción Hacia 196 y como respuesta a las nuevas necesiaes (plantas con múltiples entraas y salias, elevaa complejia), surge la teoría moerna e control, la cual está basaa en el análisis y la síntesis en el ominio el tiempo empleano variables e estao. Los esarrollos más avanzaos están representaos por conceptos como el control óptimo, sieno éste, un tópico especial entro e la isciplina e las ecuaciones iferenciales. Con el esarrollo el principio el máximo por Pontryagin (1958) y el métoo e la programación inámica por Bellman (1957), actualmente, la teoría e control óptimo se consiera como uno e los elementos e los métoos e optimización. La iea e control puee ser expresaa como el proceso meiante el cual se ejerce una influencia sobre el comportamiento e un objeto para alcanzar un propósito previamente fijao; pero si ahora, se esea lograr tal propósito en un tiempo mínimo o con un mínimo uso e recursos e control, entonces, este es un problema e control óptimo, ya que se quiere minimizar un funcional que epene el estao el sistema y el control, e esta manera, poemos ecir que este funcional escribe la calia e estabilización. En el establecimiento e las pruebas e estabilización en sistemas inámicos, la solución e un problema el tipo maximin es consierao como el principio e las pruebas. El conocimiento o escripción e un algoritmo e estabilización no es necesario para la realización e un proceimiento e pruebas, sólo se supone el uso e una señal e entraa y salia el algoritmo.. Establecimiento e las pruebas maximin Un sistema inámico controlable está formao generalmente por cuatro partes como se observa en la fig. 1, éstas actúan e tal forma que se prouce un mecanismo e retroalimentación [1]. Fig. 1. Diagrama e un sistema inámico controlable. Asociación Mexicana e Mecatrónica A.C. 6 Instituto ecnológico e Veracruz
2 8º Congreso Nacional e Mecatrónica Noviembre 6 y 7, 9. Veracruz, Veracruz. Para el establecimiento e las pruebas maximin, consieremos las ecuaciones en esviaciones siguientes el movimiento programao: x& = Ax + Bu + Cv, x( t) X u() U = { u() KC: ui( t) υi, i= 1, K, r (1) } v() V = { v() KC: vj( t) μ j, j = 1, K, s } Done x(t) es el vector n-imensional e esviaciones e una trayectoria aa, v( ) es el vector s-imensional e perturbaciones permanentes, u( ) es el vector r-imensional e controles estabilizaores, x(t ) X es el conjunto e esviaciones iniciales, υ i y μ j son parámetros aos que escriben los recursos e control y la perturbación permanente. U y V son conjuntos aos en los cuales el constructor trabaja prácticamente. Suponemos que el sistema (1) es estabilizable y completamente controlable para cualquier v const V si el corresponiente algoritmo e estabilización u( ) U es usao. Suponemos también que la calia e la estabilización está escrita por el criterio e esempeño cuarático ao en () t1 () 1 1 t (, ) = ( + ) + ( ) ( ) L uv xgx u Nu t x t Sxt El primer sumano el funcional es una integral que epene e los valores que va tomano x(t) y u(t) a lo largo el horizonte temporal, por lo tanto, valora el comportamiento el sistema a través el tiempo. El seguno sumano valora el estao en que quea el sistema al final el intervalo e tiempo que constituye el horizonte temporal el problema. Para el establecimiento e las pruebas asumimos que conocemos el sistema inámico (1) que escribe el comportamiento e las esviaciones y el criterio (), así como los conjuntos U y W. Las matrices G, N y S son constantes y satisfacen que G, N > y S. Denotemos a w=(x(t ),v) W one W =X V, formulamos los siguientes problemas e síntesis y análisis e sistemas e control []: a) El problema e estabilización minimax. inf sup L( uw, ) (3) u() U w () W b) El problema e las pruebas maximin. sup inf L( uw, ) (4) w() W u() U El problema (4) es consierao como el soporte el proceimiento e pruebas (ver el esquema funcional e la fig. ). Fig.. Esquema Funcional e las Pruebas Maximin. En el planteamiento general e las pruebas maximin asumimos que el funcional L(u,w) alcanza su máximo y su mínimo. La caena e esigualaes (5) es muy importante [5]. L = Lu, w = maxmin Luw, ( ) ( ) ww u U min max (, ) (, ) L uw Luw % = L % (5) u U w W El proceimiento e las pruebas maximin para la calia e la estabilización robusta está constituio por tres etapas [3]: En la primera etapa, la solución el problema maximin, la estrategia óptima u (x,t), la estrategia e las pruebas w (x,u,t) (si existe) y el valor el juego inámico (4) (L es la estimación inferior es ecir la calificación excelente) son eterminaos y e la primera esiguala en (5), convenimos en tomar como parámetro e evaluación o nota excelente a la solución el problema extremal (4). La seguna etapa se lleva a cabo entro el marco e la simulación inámica, cuano generaa una contraestrategia w (x,u,t), en respuesta a la acción e salia u% (t), obtenemos la estimación e estabilización real L %. El algoritmo e estabilización es consierao para nosotros como una caja negra, ao que la forma en que se construyó es esconocia para nosotros, únicamente tenemos conocimiento e la señal e salia e icho algoritmo e estabilización (sin embargo, en algunas ocasiones se consiera que la estructura el algoritmo a evaluar Asociación Mexicana e Mecatrónica A.C. 7 Instituto ecnológico e Veracruz
3 8º Congreso Nacional e Mecatrónica Noviembre 6 y 7, 9. Veracruz, Veracruz. es lineal, u% =K(t)x, one los parámetros K(t), son esconocios para nosotros). En la tercera etapa, el resultao e la prueba L %, se compara con la estimación menor L : L k = 1 (6) L% w xut,,, u% xt, ( ( ) ( )) La relación (6) es una estimación para la calia e la estabilización, mientras más cercana a la nota excelente se encuentre la estimación mejor será el algoritmo e control que se está evaluano. 3. Pruebas maximin para un robot móvil Consieramos la clase e robots móviles autónomos que consisten e tres rueas, os activas y una pasiva, con restricciones no-holonómicas, que aparecen como consecuencia e la hipótesis e no eslizamiento []. Las velociaes el centro e las rueas son enotaas como v r y v l (ver fig.3). La posición el robot (centro el arreglo e sensores) con respecto al sistema e referencia P ξ, está aa por las siguientes relaciones: & α = ω & ξ = vcosα hsinα (7) & = vsinα + hcosα El robot es un sistema no-holonómico y las velociaes e las rueas activas eben tener la irección el eje P x (el sistema e referencia P xy, tiene situao el origen en la intersección el eje e simetría el robot y el centro el eje e las rueas activas). Figura 3: Sistema e coorenaas inercial. Para obtener las ecuaciones inámicas, se sustituyen estas restricciones por fuerzas reactivas R r r, R r l. Se tienen también os fuerzas activas F r r, F r l. Meiante los teoremas principales e la mecánica se escriben las ecuaciones en el sistema P ξ. Obtenieno las siguientes relaciones inámicas m( v& + bω ) = Fr + Fl (8) J% & ω+ mbωv = F F a ( ) Sustituyeno las fuerzas activas por torques e los motores y los voltajes que son aplicaos a los mismos M = F ρ (9) Done M es el torque el motor y el moelo más simple el motor es: M = χu σϕ& (1) El miembro erecho σϕ& es la suma e la fricción viscosa y la fuerza contraelectromotriz. Entonces para la ruea erecha χur σϕ& vr v+ ωa Fr = ; & ϕr = = (11) ρ Sustituyeno en la ecuación para caa ruea, y realizano operaciones en (11) se obtienen las ecuaciones inámicas: σ χ mv& + mbω + v = + ul) (1) a J% σ χ & ω+ mbωv+ ω = ul) Finalmente se obtienen las ecuaciones el movimiento que permiten simular la inámica e este robot: & ξ = vcosα hωsin α & = vsinα hωcosα (13) & α = ω σ χ mv& =mbω v + + ul) a ωσ χa J% & ω = mbωv + ul) Cualquier trayectoria real se puee conseguir realizano combinaciones e trayectorias rectas y semicírculos como se muestra en la fig. 4. Se observa que el robot puee realizar movimientos por líneas rectas horizontales o verticales en cualquier sentio, así como semicírculos también en ambos sentios. r l Asociación Mexicana e Mecatrónica A.C. 8 Instituto ecnológico e Veracruz
4 8º Congreso Nacional e Mecatrónica Noviembre 6 y 7, 9. Veracruz, Veracruz. rayectoria. ξ ϕ α v ω 5. Cuarante I irección reloj. 6. Cuarante I R cosϕ Rsinϕ,, ω t ω R ω ω t + R ω ω 7. Cuarante II irección reloj., ωt + R ω ω Fig. 4. ablero e posibles trayectorias programaas. La tabla 1 muestra el conjunto e trayectorias eseaas, cuano el movimiento se realiza a lo largo e un segmento e línea paralela al eje ξ o al eje. 8. Cuarante II 9. Cuarante III irección reloj. 1. Cuarante III 11. Cuarante IV irección reloj. 1. Cuarante IV R cosϕ Rsinϕ R cosϕ Rsinϕ,,,,, ω t + R ω t ω ω ω R ω ωt R ω ω ωt R ω ω ω t ω R ω rayectoria. ξ 1. Línea horizontal sentio negativo.. Línea horizontal vt sentio positivo. ξ 3. Línea vertical sentio negativo. 4. Línea vertical sentio positivo. α vt+ ξ + vt+ vt+ v ω v v v v abla 1. rayectorias programaas para las líneas horizontal y vertical. En la fig. 4 se muestra un tablero e entrenamiento one tenemos cuatro cuarantes, caa uno con una trayectoria circular la cual se puee realizar en irección a las manecillas el reloj o contraria a ella, entonces se tienen ocho posibles configuraciones como se muestra en la tabla. Utilizano las trayectorias programaas (tablas 1 y ) poemos escribir el sistema lineal en esviaciones, así el sistema lineal para la trayectoria 4 (tabla 1) es: & ξ = vα + hω & =v & α = ω (14) σ χ v& = v+ ( ul + ur) mρ mρ mbv a σ χa & ω = ω ω+ ( u r u l) J% J% ρ J% ρ abla. rayectorias programaas para las líneas circulares. De la misma forma que se obtuvo el sistema lineal (14) se pueen obtener sistemas lineales para caa una e las trayectorias mostraas en las tablas 1 y. 4. Estimación inferior e las pruebas maximin aplicaas a un robot móvil En este epígrafe resolvemos el problema extremal (4) para obtener la estimación inferior (paso 1) y establecer las pruebas maximin, para solucionar el problema interno e (4), hacemos uso e la programación inámica e Bellman. El criterio e esempeño () es minimizao, aa la inámica el proceso controlable (1), ahora efinimos la función e costo mínima t f ω ( x, t) = min ( x G() t x+ u N() t u) t+ ut () t ( 1) ( 1)} x t Sx t (15) Asumieno que las erivaas parciales e ω (x,t) existen y son acotaas, se escribe la ecuación e Hamilton-Jacobi-Bellman, one ω (x,t) ebe satisfacer la ecuación en erivaas parciales. = ω x t, t + min{ x G t x+ u N t u t ( ( ) ) () () ut () + xω ( x () t, t) A() t x+ B() t u} (16) Asociación Mexicana e Mecatrónica A.C. 9 Instituto ecnológico e Veracruz
5 8º Congreso Nacional e Mecatrónica Noviembre 6 y 7, 9. Veracruz, Veracruz. Done ω (x(t f ), t f )= x (t 1 )Sx(t 1 ). Asumimos que la solución e la ecuación (4.3) es e la forma ω (x,t)=x P(t)x, e esta manera se euce el siguiente control: 1 u = N B P t x (17) () Sustituyeno el control (17) en la ecuación (16) se obtiene: P() t = x + G+ P() t A+ A P() t t 1 P t BN B P t x (18) () () ()} P t 1 + G P() t BN B P() t + P() t A+ A P() t = t (19) Done (19) es la llamaa ecuación iferencial matricial e Riccati [4] con coniciones finales P(t 1 )=, al solucionar esta ecuación se obtiene la matriz P(t) lo que permite obtener completamente el control (17), así obtenemos la solución el problema interno e (4). Ahora para solucionar el problema externo e (4) consieramos cuatro movimientos programaos; en este caso las trayectorias y 4 e la tabla 1, así como las trayectorias 6 y 7 e la tabla como se muestra en la figura 5. e ecuaciones lineales en esviaciones, para las trayectorias mostraas en la figura 5. Variable. Valor. Descripción. v 1.5 Velocia eseaa [m/s] a.4 Distancia entre las rueas [m] b.4 Distancia el centro e masa al eje e las rueas [m] h.1 Distancia el eje e las rueas al arreglo e sensores infrarrojos [m] m 4.5 Masa el robot [Kg] ρ.8 Raio e las rueas [m] R.35 Raio e inercia el carro [m] χ.1 Fricción viscosa σ.9 Fuerza contraelectromotriz el motor. abla 3. Parámetros el robot móvil. Para la línea horizontal (sentio positivo) se tiene el siguiente sistema linealizao alreeor e esta trayectoria: & ξ = v & = 1.5α.1ω () & α = ω v& =.65v +.77( ul + u r) & ω = ω.1743 ul) Análogamente obtenemos los sistemas linealizaos con las trayectorias mostraas en la fig. 5. Meiante la programación inámica resolvemos los problemas internos para caa uno e los sistemas anteriores y obtenemos los siguientes resultaos. Fig. 5. rayectorias programaas. Como consecuencia el conjunto W se consiera un conjunto iscreto, por lo que resolvemos el problema interno 4 veces y posteriormente tomamos el máximo valor eterminano con ello la estimación inferior L. Para el esarrollo e esta parte consieramos los valores numéricos e los parámetros que intervienen en el robot móvil [5] (ver tabla 3). Sustituimos los parámetros y encontramos el sistema 1. El valor el problema interno para el sistema linealizao con la trayectoria es: El valor el problema interno para el sistema linealizao con la trayectoria 4 es: El valor el problema interno para el sistema linealizao con la trayectoria 6 es: El valor el problema interno para el sistema linealizao con la trayectoria 7 es: Por lo tanto la estimación inferior para las pruebas maximin es: L = (1) Asociación Mexicana e Mecatrónica A.C. 3 Instituto ecnológico e Veracruz
6 8º Congreso Nacional e Mecatrónica Noviembre 6 y 7, 9. Veracruz, Veracruz. 5. Evaluación e un sistema e control esconocio Ahora analizamos la calia e estabilización e un algoritmo e control (pasos y 3 el sistema e pruebas maximin) que tiene la forma lineal u% =K(t)x, one: K por: ul u% = u r k k k k k = k1 k k3 k4 k 5 k 11 ξ x = α v ω Done los parámetros e K(t) están aos 8 ( ) t ( ) ( ) + = t t t t t t k1 4 = ( ) t + ( ) t ( ) t t t t t t k = t t ( ) ( ) + ( ) t t.35581t t t 5.545t k3 = ( ) t + ( ) t t t 1.568t t 17.19t t k5 = ( ) t + ( ) t t t 3.631t t 35.8t t k = k = k = k = k = Utilizano el control u% =K(t)x eterminamos la nota real L % (paso ), para ello sustituimos el controlaor en el sistema (13) y utilizamos el ínice e esempeño ao en (), con lo cual obtenemos la estimación real: L % = 13 () La última etapa (paso 3) consiste en comparar la estimación real obtenia en () con la estimación inferior (1), para esto utilizamos la relación que nos etermina la estimación para la calia e la estabilización aa en (6) t k = *1 =.35 (3) 13 De acuero a lo anterior, poemos concluir que el algoritmo e control evaluao se ebe mejorar en su esempeño. 6. Conclusiones Este trabajo se basa principalmente en el establecimiento y análisis e las pruebas maximin para la calia e estabilización robusta y como su nombre lo ice, es una estrategia e pruebas que nos eterminarán la calia e un algoritmo e control. El uso e la programación inámica es e vital importancia, ya que con este métoo se puo obtener la estimación inferior y e esta manera tener un parámetro con quien comparar cualquier sistema e control que sea aplicao a un robot móvil como lo ejemplifica este trabajo. Referencias [1] GUIÉRREZ J. E. M. Estrategias e las Pruebas Maximin para la Calia e la Estabilización, esis e octorao, México 3, pp [] Saovnichii V. A. y otros, Maximin esting of Satellite Stabilization, Mathematical Moeling of Complex Information Processing Systems, pp [3] Alexanrov V. V. y Gutiérrez J. E. M. About the Maximin esting Strategy, Sociea Matemática Mexicana, Aportaciones Matemáticas Memoria 35, México 4, pp [4] Alexanrov V. V. y Gutiérrez J. E. M. Pruebas Maximin y Juegos Geométricos, Sociea Matemática Mexicana, Aportaciones Matemáticas Memoria 35, México 5, pp. 3-1 [5] Alexanrov V. V. y otros, Optimization an Computer-Aie esting of Stabilization Precision, Mathematical Moeling of Complex Information Processing Systems, pp Asociación Mexicana e Mecatrónica A.C. 31 Instituto ecnológico e Veracruz
Funciones de Bessel. Dr. Héctor René Vega-Carrillo
 Funciones e Bessel Dr. Héctor René Vega-Carrillo 1 2 Ínice 1. Introucción............................. 3 2. Solución e la Ecuación iferencial e Bessel........... 5 2.1. Caso n entero............................
Funciones e Bessel Dr. Héctor René Vega-Carrillo 1 2 Ínice 1. Introucción............................. 3 2. Solución e la Ecuación iferencial e Bessel........... 5 2.1. Caso n entero............................
FUNCIONES TRIGONOMÉTRICAS
 Unia os Geometría Trigonometría 8. FUNCIONES TRIGONOMÉTRICAS 8. El círculo trigonométrico o unitario En temas anteriores, las funciones trigonométricas se asociaron con razones, es ecir con cocientes e
Unia os Geometría Trigonometría 8. FUNCIONES TRIGONOMÉTRICAS 8. El círculo trigonométrico o unitario En temas anteriores, las funciones trigonométricas se asociaron con razones, es ecir con cocientes e
Unidad 1 Ecuaciones Diferenciales de Primer Orden. 1.1 Definiciones (Ecuación Diferencial, Orden, Grado, Linealidad)
 . Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) Unia Ecuaciones Diferenciales e Primer Oren. Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) En iversas áreas como son la ingeniería,
. Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) Unia Ecuaciones Diferenciales e Primer Oren. Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) En iversas áreas como son la ingeniería,
Cada grado se divide en 60 minutos (60 ) y cada minuto en 60 segundos (60 ). Así, por ejemplo, un ángulo puede medir = 38º
 Sistemas e meición e ángulos Como en toos los elementos susceptibles a meiciones, en los ángulos se han establecio iversos sistemas e meición, entre ellos los más importantes son: El sistema seagesimal
Sistemas e meición e ángulos Como en toos los elementos susceptibles a meiciones, en los ángulos se han establecio iversos sistemas e meición, entre ellos los más importantes son: El sistema seagesimal
Información importante
 Departamento e Matemática Coorinación e Matemática I (MAT01) 1 er Semestre e 010 Semana 1: Lunes 07 viernes 11 e Junio Información importante Durante esta semana se publicarán las notas el Certamen en
Departamento e Matemática Coorinación e Matemática I (MAT01) 1 er Semestre e 010 Semana 1: Lunes 07 viernes 11 e Junio Información importante Durante esta semana se publicarán las notas el Certamen en
UCLM - Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG)
 PAEG Junio 03 Propuesta B Matemáticas aplicaas a las CCSS II º Bachillerato UCLM - Pruebas e Acceso a Enseñanzas Universitarias Oiciales e Grao (PAEG) Matemáticas aplicaas a las Ciencias Sociales II Junio
PAEG Junio 03 Propuesta B Matemáticas aplicaas a las CCSS II º Bachillerato UCLM - Pruebas e Acceso a Enseñanzas Universitarias Oiciales e Grao (PAEG) Matemáticas aplicaas a las Ciencias Sociales II Junio
Información importante
 Universia Técnica Feerico Santa María Departamento e Matemática Coorinación e Matemática I (MAT021) 1 er Semestre e 2010 Semana 9: Lunes 17 viernes 21 e Mayo Información importante El control Q2A es el
Universia Técnica Feerico Santa María Departamento e Matemática Coorinación e Matemática I (MAT021) 1 er Semestre e 2010 Semana 9: Lunes 17 viernes 21 e Mayo Información importante El control Q2A es el
Seminario 12: Condensadores.
 Seminario 2: Conensaores. Fabián Anrés Torres Ruiz Departamento e Física, Universia e Concepción, Chile 30 e Mayo e 2007. Problemas. (Desarrollo) Deucción el tiempo e escarga e un conensaor 2. (Problema
Seminario 2: Conensaores. Fabián Anrés Torres Ruiz Departamento e Física, Universia e Concepción, Chile 30 e Mayo e 2007. Problemas. (Desarrollo) Deucción el tiempo e escarga e un conensaor 2. (Problema
Derivación de funciones de una variable real
 Capítulo 4 Derivación e funciones e una variable real 4.1. Derivaa e una función 4.1.1. Introucción Definición 4.1.1. Sea f : (a, b) R R y x 0 (a, b). Se ice que la función f es erivable en el punto x
Capítulo 4 Derivación e funciones e una variable real 4.1. Derivaa e una función 4.1.1. Introucción Definición 4.1.1. Sea f : (a, b) R R y x 0 (a, b). Se ice que la función f es erivable en el punto x
( ) 2. Pendiente de una Recta Tangente. Sea f una función que es continua en x. 1. Para definir la pendiente de la recta tangente ( )
 Derivaa e una Función Ínice.. Introucción.. Peniente e una recta tangente.. Derivaa e una función. 4. Derivaas laterales. 5. Derivaa e una función compuesta (Regla e la Caena). 6. Tabla e erivaas usuales.
Derivaa e una Función Ínice.. Introucción.. Peniente e una recta tangente.. Derivaa e una función. 4. Derivaas laterales. 5. Derivaa e una función compuesta (Regla e la Caena). 6. Tabla e erivaas usuales.
Regla de la cadena. Ejemplo 1. y = f (g(x)) Como las funciones son diferenciables son suaves.
 1 Regla e la caena Hasta aquí hemos erivao funciones que no son compuestas. El problema surge cuano tenemos una función que es compuesta, por ejemplo, igamos que el precio e la gasolina epene el precio
1 Regla e la caena Hasta aquí hemos erivao funciones que no son compuestas. El problema surge cuano tenemos una función que es compuesta, por ejemplo, igamos que el precio e la gasolina epene el precio
La derivada de las funciones trascendentes
 La erivaa e las funciones trascenentes Manuel Barahona, Eliseo Martínez Diciembre 205 Muchos fenómenos e la naturaleza son moelaos meiante funciones eponeciales, logarítimicas, trigonométricas y combinaciones
La erivaa e las funciones trascenentes Manuel Barahona, Eliseo Martínez Diciembre 205 Muchos fenómenos e la naturaleza son moelaos meiante funciones eponeciales, logarítimicas, trigonométricas y combinaciones
4. Mecánica en la Medicina Derivar e Integrar
 4. Mecánica en la Meicina Derivar e Integrar Teoría Dr. Willy H. Gerber Instituto e Ciencias Físicas y Matemáticas, Universia Austral, Valivia, Chile 17.04.2011 W. Gerber 4. Mecánica en la Meicina - Matemática
4. Mecánica en la Meicina Derivar e Integrar Teoría Dr. Willy H. Gerber Instituto e Ciencias Físicas y Matemáticas, Universia Austral, Valivia, Chile 17.04.2011 W. Gerber 4. Mecánica en la Meicina - Matemática
RESOLUCIÓN DE ACTIVIDADES
 RESOLUCIÓN DE ACTIVIDADES Activiaes iniciales 1. Calcula las matrices inversas e las siguientes matrices: 1 1 2-3 1 2 1 1 1 1 0 1 2 2 5 1 1 1 1 0 0 1 1 1 1 1 Las matrices buscaas son: 1/4 1/4 1/4 1/4 1
RESOLUCIÓN DE ACTIVIDADES Activiaes iniciales 1. Calcula las matrices inversas e las siguientes matrices: 1 1 2-3 1 2 1 1 1 1 0 1 2 2 5 1 1 1 1 0 0 1 1 1 1 1 Las matrices buscaas son: 1/4 1/4 1/4 1/4 1
LA DERIVADA POR FÓRMULAS
 CAPÍTULO LA DERIVADA POR FÓRMULAS. FÓRMULAS Obtener la erivaa e cualquier función por alguno e los os métoos vistos anteriormente, el e tabulaciones y el e incrementos, resulta una tarea muy engorrosa,
CAPÍTULO LA DERIVADA POR FÓRMULAS. FÓRMULAS Obtener la erivaa e cualquier función por alguno e los os métoos vistos anteriormente, el e tabulaciones y el e incrementos, resulta una tarea muy engorrosa,
ASIGNATURA: QUIMICA AGROPECUARIA (RB8002) TALLER N 6: EQUILIBRIO QUIMICO
 I. Presentación e la guía: ASIGNATURA: QUIMICA AGROPECUARIA (RB800) TALLER N 6: EQUILIBRIO QUIMICO Competencia: El alumno será capaz e escribir iferentes tipos e reacciones en equilibrio, el significao
I. Presentación e la guía: ASIGNATURA: QUIMICA AGROPECUARIA (RB800) TALLER N 6: EQUILIBRIO QUIMICO Competencia: El alumno será capaz e escribir iferentes tipos e reacciones en equilibrio, el significao
2.5 Derivación implícita
 SECCIÓN.5 Derivación implícita 4.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. E X P L O R A C I Ó N Representación gráfica
SECCIÓN.5 Derivación implícita 4.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. E X P L O R A C I Ó N Representación gráfica
[b] Aunque se puede calcular los índices de refracción, vamos a utilizar la expresión de la ley de
![[b] Aunque se puede calcular los índices de refracción, vamos a utilizar la expresión de la ley de [b] Aunque se puede calcular los índices de refracción, vamos a utilizar la expresión de la ley de](/thumbs/49/25839391.jpg) Opción A. Ejercicio [a] En qué consiste el fenómeno e la reflexión total e una ona? Qué circunstancias eben cumplirse para que ocurra? Defina el concepto e ángulo límite. ( punto) [b] Una ona sonora que
Opción A. Ejercicio [a] En qué consiste el fenómeno e la reflexión total e una ona? Qué circunstancias eben cumplirse para que ocurra? Defina el concepto e ángulo límite. ( punto) [b] Una ona sonora que
DEPARTAMENTO DE FISICA (4ºBTO)
 DEPARTAMENTO DE ISICA (4ºBTO) Electrostática y Campo Eléctrico Electrostática Introucción Cuano se frota un tejio e lana con algo e plástico, este puee levantar peazos e papel, cabellos, etc. Los griegos
DEPARTAMENTO DE ISICA (4ºBTO) Electrostática y Campo Eléctrico Electrostática Introucción Cuano se frota un tejio e lana con algo e plástico, este puee levantar peazos e papel, cabellos, etc. Los griegos
DERIVADA. Interpretación Geométrica Encontrar la pendiente de la recta tangente a una curva en un punto dado de ella.
 DERIVADA Interpretación Geométrica Objetivo: Encontrar la peniente e la recta tangente a una curva en un punto ao e ella. Para precisar correctamente la iea e tangente a una curva en un punto, se utilizará
DERIVADA Interpretación Geométrica Objetivo: Encontrar la peniente e la recta tangente a una curva en un punto ao e ella. Para precisar correctamente la iea e tangente a una curva en un punto, se utilizará
; deben llevarse las unidades de área a m 2 y distancia a m. V = 13215V = 13, 2kV
 Física II Guía e ejercicios 5 CAPACIDAD 5. Capacia 5.. Problema 5... Enunciao Las placas e un capacitor e placas paralelas están separaas por una istancia e, 8mm y caa una tiene un área e, cm. Caa placa
Física II Guía e ejercicios 5 CAPACIDAD 5. Capacia 5.. Problema 5... Enunciao Las placas e un capacitor e placas paralelas están separaas por una istancia e, 8mm y caa una tiene un área e, cm. Caa placa
TEMA 4: Transformaciones 3D
 TEMA 4: Transformaciones D Ínice. Sistemas e Coorenaas. Transformaciones Básicas. Traslación. Escalao. Rotación lana 4. Afilamiento 5. Deformaciones. Composición e Transformaciones 4. Rotación General
TEMA 4: Transformaciones D Ínice. Sistemas e Coorenaas. Transformaciones Básicas. Traslación. Escalao. Rotación lana 4. Afilamiento 5. Deformaciones. Composición e Transformaciones 4. Rotación General
RESALTO DE ONDAS (1< Fr 1 < 1,7)
 UNIVERSIDAD DE CHIE - CI 4A HIDRÁUICA RESATO DE ONDAS (< Fr
UNIVERSIDAD DE CHIE - CI 4A HIDRÁUICA RESATO DE ONDAS (< Fr
DISEÑO INTEGRADO DE PROCESOS EN EL MARCO DEL CONTROL PREDICTIVO BASADO EN MODELOS
 DISEÑO INTEGRADO DE PROCESOS EN EL MARCO DEL CONTROL PREDICTIVO BASADO EN MODELOS M. Francisco, P. Vega Dpto. Informática y Automática. E.T.S. Ingeniería Inustrial. Universia e Salamanca. Av. Fernano Ballesteros
DISEÑO INTEGRADO DE PROCESOS EN EL MARCO DEL CONTROL PREDICTIVO BASADO EN MODELOS M. Francisco, P. Vega Dpto. Informática y Automática. E.T.S. Ingeniería Inustrial. Universia e Salamanca. Av. Fernano Ballesteros
TEMA 9 Electrostática
 Bases Físicas y Químicas el Meio Ambiente TMA 9 lectrostática Cargas eléctricas ntre os cuerpos hay siempre fuerzas atractivas ebio a sus respectivas masas y pueen existir otras fuerzas entre ellos si
Bases Físicas y Químicas el Meio Ambiente TMA 9 lectrostática Cargas eléctricas ntre os cuerpos hay siempre fuerzas atractivas ebio a sus respectivas masas y pueen existir otras fuerzas entre ellos si
6. PROBLEMAS DE MARKETING
 6. PROBLEMAS DE MARKETING PROBLEMA 1 (POSICIONAMIENTO DEL PRODUCTO) Se ha realizao una encuesta sobre un grupo e consumiores e vino tinto e mesa para que, sobre una escala e 0 a 10, califiquen a las iferentes
6. PROBLEMAS DE MARKETING PROBLEMA 1 (POSICIONAMIENTO DEL PRODUCTO) Se ha realizao una encuesta sobre un grupo e consumiores e vino tinto e mesa para que, sobre una escala e 0 a 10, califiquen a las iferentes
OBTENCIÓN DE UN MODELO DINÁMICO PARA SIMULACIÓN DE UNA CALDERA DE VAPOR INDUSTRIAL
 OBTENCIÓN DE UN MODELO DINÁMICO PARA SIMULACIÓN DE UNA CALDERA DE VAPOR INDUSTRIAL Susana Pelayo Díaz Centro e Tecnología Azucarera, Universia evallaoli C/Real e Burgos. Eificio Alfonso VIII. Planta baja
OBTENCIÓN DE UN MODELO DINÁMICO PARA SIMULACIÓN DE UNA CALDERA DE VAPOR INDUSTRIAL Susana Pelayo Díaz Centro e Tecnología Azucarera, Universia evallaoli C/Real e Burgos. Eificio Alfonso VIII. Planta baja
UNIDAD IV.- CÁLCULO INTEGRAL
 UNIDAD IV.- CÁLCULO INTEGRAL En la práctica e cualquier campo científico es frecuente que se presenten prolemas relacionaos con el cálculo e áreas, algunas veces e figuras regulares y muchas otras, con
UNIDAD IV.- CÁLCULO INTEGRAL En la práctica e cualquier campo científico es frecuente que se presenten prolemas relacionaos con el cálculo e áreas, algunas veces e figuras regulares y muchas otras, con
(f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x)
![(f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x) (f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x)](/thumbs/24/2434623.jpg) Derivaa e una función en un punto: El concepto e erivaa e una función matemática se halla íntimamente relacionao con la noción e límite. Así, la erivaa se entiene como la variación que experimenta la función
Derivaa e una función en un punto: El concepto e erivaa e una función matemática se halla íntimamente relacionao con la noción e límite. Así, la erivaa se entiene como la variación que experimenta la función
PAU Campo Magnético Ejercicios resueltos
 PAU Campo Magnético jercicios resueltos 99-009 PAU CyL 99 Coeficiente e rozamiento en una arilla y trabajo rozamiento Una arilla, e masa 0 g y longitu 30 cm, escansa sobre una superficie horizontal y está
PAU Campo Magnético jercicios resueltos 99-009 PAU CyL 99 Coeficiente e rozamiento en una arilla y trabajo rozamiento Una arilla, e masa 0 g y longitu 30 cm, escansa sobre una superficie horizontal y está
Potencial eléctrico (V)
 Activia 1 [a] xplica el concepto e potencial electrostático en un punto. [b] Dibuja aproximaamente en un sistema e coorenaas el gráfico ue relaciona el potencial creao por una carga puntual positiva (eje
Activia 1 [a] xplica el concepto e potencial electrostático en un punto. [b] Dibuja aproximaamente en un sistema e coorenaas el gráfico ue relaciona el potencial creao por una carga puntual positiva (eje
P1.- La delicada vida gravitatoria del cometa 67P/Churiumov-Guerasimenko.
 P.- La elicaa via gravitatoria el cometa 67P/Churiumov-uerasimenko. El cometa 67P, escubierto en 969 por los astrónomos Klim Churiumov y Svetlana uerasimenko, se ha convertio recientemente en una estrella
P.- La elicaa via gravitatoria el cometa 67P/Churiumov-uerasimenko. El cometa 67P, escubierto en 969 por los astrónomos Klim Churiumov y Svetlana uerasimenko, se ha convertio recientemente en una estrella
3.1. DERIVADAS DE SEGUNDO ORDEN
 .. DERIVADAS DE SEGUNDO ORDEN La erivaa y ' f ' es la primera erivaa e y con respecto a, pero igualmente es posible realizar la erivaa e la erivaa, y y '' f ''. Lo que se conoce como la seguna erivaa e
.. DERIVADAS DE SEGUNDO ORDEN La erivaa y ' f ' es la primera erivaa e y con respecto a, pero igualmente es posible realizar la erivaa e la erivaa, y y '' f ''. Lo que se conoce como la seguna erivaa e
Ecuaciones Diferenciales de primer Orden
 4 Ecuaciones Diferenciales e primer Oren 1.1 1.1. Introucción Las palabras ecuaciones y iferenciales nos hacen pensar en la solución e cierto tipo e ecuación que contenga erivaas. Así como al estuiar álgebra
4 Ecuaciones Diferenciales e primer Oren 1.1 1.1. Introucción Las palabras ecuaciones y iferenciales nos hacen pensar en la solución e cierto tipo e ecuación que contenga erivaas. Así como al estuiar álgebra
Control de Nivel de Multitanques Acoplados Mediante Control Asíncrono (y Red de Comunicación)
 Control e Nivel e Multitanques Acoplaos Meiante Control Asíncrono (y Re e Comunicación) Eliceo Águila Rojas 1, J. Fermi Guerrero Castellanos 1, Josefina Castañea Camacho 1 W. Fermín Guerrero Sánchez 2
Control e Nivel e Multitanques Acoplaos Meiante Control Asíncrono (y Re e Comunicación) Eliceo Águila Rojas 1, J. Fermi Guerrero Castellanos 1, Josefina Castañea Camacho 1 W. Fermín Guerrero Sánchez 2
La capacitancia tiene la unidad del SI coulomb por volt. La unidad de capacitancia del SI es el farad (F), en honor a Michael Faraday.
 1. Qué es capacitancia? Se efine como la razón entre la magnitu e la carga e cualquiera e los conuctores y la magnitu e la iferencia e potencial entre ellos. La capacitancia siempre es una cantia positiva
1. Qué es capacitancia? Se efine como la razón entre la magnitu e la carga e cualquiera e los conuctores y la magnitu e la iferencia e potencial entre ellos. La capacitancia siempre es una cantia positiva
La regla de la constante. DEMOSTRACIÓN Sea ƒ(x) c. Entonces, por la definición de derivada mediante el proceso de límite, se deduce que.
 SECCIÓN. Reglas básicas e erivación razón e cambio 07. Reglas básicas e erivación razón e cambio Encontrar la erivaa e una función por la regla e la constante. Encontrar la erivaa e una función por la
SECCIÓN. Reglas básicas e erivación razón e cambio 07. Reglas básicas e erivación razón e cambio Encontrar la erivaa e una función por la regla e la constante. Encontrar la erivaa e una función por la
XXII OLIMPIADA NACIONAL DE FÍSICA Guadalajara, Jal de noviembre de 2011 Prueba teórica
 XXII OLIMPI NIONL E FÍSI Guaalajara, Jal. 0-4 e noviembre e 011 Prueba teórica 1. PROLEM olisión e pieras (8 puntos) Una piera esférica se eja caer ese un eificio alto e altura h (ese la calle) al tiempo
XXII OLIMPI NIONL E FÍSI Guaalajara, Jal. 0-4 e noviembre e 011 Prueba teórica 1. PROLEM olisión e pieras (8 puntos) Una piera esférica se eja caer ese un eificio alto e altura h (ese la calle) al tiempo
INTERVALOS Y SEMIRRECTAS.
 el blog de mate de aida CSI: Inecuaciones pág 1 INTERVALOS Y SEMIRRECTAS La ordenación de números permite definir algunos conjuntos de números que tienen una representación geométrica en la recta real
el blog de mate de aida CSI: Inecuaciones pág 1 INTERVALOS Y SEMIRRECTAS La ordenación de números permite definir algunos conjuntos de números que tienen una representación geométrica en la recta real
Estática de Fluidos Parte III. Vasos comunicantes. Prensa Hidráulica Manómetro
 Estática e Fluios arte III Vasos comunicantes. rensa Hiráulica Manómetro rofesor Juan anmartín - Física y Química Curso 2012/2013 Fluios Hirostática Vasos comunicantes es el nombre que recibe un conjunto
Estática e Fluios arte III Vasos comunicantes. rensa Hiráulica Manómetro rofesor Juan anmartín - Física y Química Curso 2012/2013 Fluios Hirostática Vasos comunicantes es el nombre que recibe un conjunto
Apuntes sobre la Parábola: su medición según Arquímedes y otras propiedades
 Investigación y Docencia por Néstor guilera puntes sobre la Parábola: su meición según rquímees y otras propieaes Introucción (Versión revisaa e mayo e 2001) Muchas veces habrán oío que rquímees fue el
Investigación y Docencia por Néstor guilera puntes sobre la Parábola: su meición según rquímees y otras propieaes Introucción (Versión revisaa e mayo e 2001) Muchas veces habrán oío que rquímees fue el
U(r, θ) = 1. 2.1. Conjunto completo de operadores del dipolo puntual. Si usamos el operador asociado a la componente z del momento angular
 Capítulo Dipolo puntual. Como vimos en la introucción al primer capítulo, la energía potencial que aquiere una partícula e carga eléctrica e cuano interacciona con un ipolo puntual es Ur, θ) = 4πϵ ep cos
Capítulo Dipolo puntual. Como vimos en la introucción al primer capítulo, la energía potencial que aquiere una partícula e carga eléctrica e cuano interacciona con un ipolo puntual es Ur, θ) = 4πϵ ep cos
3 DERIVADAS ALGEBRAICAS
 DERIVADAS ALGEBRAICAS DERIVADAS ALGEBRAICAS Entiénase la erivaa como la peniente e la recta tangente a la función en un punto ao, lo anterior implica que la función ebe eistir en ese punto para poer trazar
DERIVADAS ALGEBRAICAS DERIVADAS ALGEBRAICAS Entiénase la erivaa como la peniente e la recta tangente a la función en un punto ao, lo anterior implica que la función ebe eistir en ese punto para poer trazar
Derivación. (x c) que pasa por el punto fijo (c, f(c)) y el punto móvil (c + h, f(c + h)) cuando h tiende a 0.
 Derivación Definición y propieaes básicas Definición. Una función f efinia en un entorno e un punto c R es erivable en c si y sólo si el ite f c = f fc + h fc f fc c := = h h c c eiste y toma un valor
Derivación Definición y propieaes básicas Definición. Una función f efinia en un entorno e un punto c R es erivable en c si y sólo si el ite f c = f fc + h fc f fc c := = h h c c eiste y toma un valor
INSTRUCTIVO PARA TUTORÍAS
 INSTRUCTIVO PARA TUTORÍAS Las tutorías corresponen a los espacios acaémicos en los que el estuiante el Politécnico Los Alpes puee profunizar y reforzar sus conocimientos en iferentes temas e cara al eamen
INSTRUCTIVO PARA TUTORÍAS Las tutorías corresponen a los espacios acaémicos en los que el estuiante el Politécnico Los Alpes puee profunizar y reforzar sus conocimientos en iferentes temas e cara al eamen
Actividades del final de la unidad
 Activiaes el final e la unia 1. Calcula el flujo magnético a través e una espira cuaraa e 10 cm e lao situaa en un campo magnético e valor 0,2 T cuano la normal a la espira forma con la irección el campo
Activiaes el final e la unia 1. Calcula el flujo magnético a través e una espira cuaraa e 10 cm e lao situaa en un campo magnético e valor 0,2 T cuano la normal a la espira forma con la irección el campo
2.3 Reglas del producto, del cociente y derivadas de orden superior
 SECCIÓN 2.3 Reglas el proucto, el cociente y erivaas e oren superior 119 2.3 Reglas el proucto, el cociente y erivaas e oren superior Encontrar la erivaa e una función por la regla el proucto. Encontrar
SECCIÓN 2.3 Reglas el proucto, el cociente y erivaas e oren superior 119 2.3 Reglas el proucto, el cociente y erivaas e oren superior Encontrar la erivaa e una función por la regla el proucto. Encontrar
EQUILIBRIO QUÍMICO. Un sistema químico está en equilibrio heterogéneo cuando las sustancias presentes en él no están en la misma fase.
 EQUILIBRIO QUÍMICO ESTADO DE EQUILIBRIO e una reacción reversile es el estao final el sistema en el que las velociaes e reacción irecta e inversa son iguales ( NO las constantes cinéticas e velocia) y
EQUILIBRIO QUÍMICO ESTADO DE EQUILIBRIO e una reacción reversile es el estao final el sistema en el que las velociaes e reacción irecta e inversa son iguales ( NO las constantes cinéticas e velocia) y
Manual de la Práctica 2: Análisis de sistemas discretos
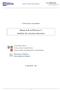 Control por computaor Manual e la Práctica : Análisis e sistemas iscretos Jorge Pomares Baeza Fracisco Anrés Canelas Herías Grupo e Innovación Eucativa en Automática 009 GITE IEA - - Introucción En la
Control por computaor Manual e la Práctica : Análisis e sistemas iscretos Jorge Pomares Baeza Fracisco Anrés Canelas Herías Grupo e Innovación Eucativa en Automática 009 GITE IEA - - Introucción En la
Teoría de la decisión
 1.- Un problema estadístico típico es reflejar la relación entre dos variables, a partir de una serie de Observaciones: Por ejemplo: * peso adulto altura / peso adulto k*altura * relación de la circunferencia
1.- Un problema estadístico típico es reflejar la relación entre dos variables, a partir de una serie de Observaciones: Por ejemplo: * peso adulto altura / peso adulto k*altura * relación de la circunferencia
APUNTES DE CONTROL PID
 APUNTES DE CONTROL PID Control 0. u/t 3 K s 3+3s +3s+ Proceso Salia T Derivaor / /Ti s Integraor Ing. Mauricio Améstegui Moreno UNIVERSIDAD MAYOR DE SAN ANDRES LA PAZ BOLIVIA ENERO DE 00 RESUMEN El controlaor
APUNTES DE CONTROL PID Control 0. u/t 3 K s 3+3s +3s+ Proceso Salia T Derivaor / /Ti s Integraor Ing. Mauricio Améstegui Moreno UNIVERSIDAD MAYOR DE SAN ANDRES LA PAZ BOLIVIA ENERO DE 00 RESUMEN El controlaor
LA CICLOIDE, UNA CURVA DE MUCHO EMPAQUE
 LA CICLOIDE, UNA CUVA DE MUCHO EMPAQUE CALOS S CHINEA LA CICLOIDE UNA CUVA DE MUCHO EMPAQUE Una breve introucción 1 Ecuaciones paramétricas La tangente y la normal en un punto 3 Longitu e un arco 4 El
LA CICLOIDE, UNA CUVA DE MUCHO EMPAQUE CALOS S CHINEA LA CICLOIDE UNA CUVA DE MUCHO EMPAQUE Una breve introucción 1 Ecuaciones paramétricas La tangente y la normal en un punto 3 Longitu e un arco 4 El
Determinación del largo de una cadena de aisladores
 eterminación el largo e una caena e aislaores Pablo Meina Coré 1. Requerimientos para una caena e aislaores El número e iscos e una caena e aislaores ebe ser tal que la caena brine un aecuao nivel e aislación
eterminación el largo e una caena e aislaores Pablo Meina Coré 1. Requerimientos para una caena e aislaores El número e iscos e una caena e aislaores ebe ser tal que la caena brine un aecuao nivel e aislación
Tema 7. Propagación por onda de superficie
 Tema 7. Propagación por ona e superficie 1 Introucción...2 1.1 Características e la propagación...2 2 Antena monopolo corto...2 2.1 Ganancia respecto a la antena isótropa y al ipolo...3 2.2 Campo raiao
Tema 7. Propagación por ona e superficie 1 Introucción...2 1.1 Características e la propagación...2 2 Antena monopolo corto...2 2.1 Ganancia respecto a la antena isótropa y al ipolo...3 2.2 Campo raiao
CONCEPTOS BÁSICOS DE CONFIABILIDAD
 CAPÍTULO II CONCEPTOS BÁSICOS DE CONFIABILIDAD El iseño e sistemas, comprene los aspectos más amplios e la organización e equipo complejo, turnos e operación, turnos e mantenimiento y e las habiliaes necesarias
CAPÍTULO II CONCEPTOS BÁSICOS DE CONFIABILIDAD El iseño e sistemas, comprene los aspectos más amplios e la organización e equipo complejo, turnos e operación, turnos e mantenimiento y e las habiliaes necesarias
Boletín audioprotésico número 35
 Boletín auioprotésico número 35 Cómo asegurar la ganancia in-situ correcta Noveaes el epartamento e Investigación auioprotésica y comunicación 9 502 1041 004 / 06-07 Introucción Normalmente, los auífonos
Boletín auioprotésico número 35 Cómo asegurar la ganancia in-situ correcta Noveaes el epartamento e Investigación auioprotésica y comunicación 9 502 1041 004 / 06-07 Introucción Normalmente, los auífonos
Z Optima X 1 + X 2 5 Z 1 -X 1 + 2X Región factible. Figura 1
 Método Gráfico El procedimiento geométrico, es únicamente adecuado para resolver problemas muy pequeños (con no más de dos variables debido al problema de dimensionalidad). Este método provee una gran
Método Gráfico El procedimiento geométrico, es únicamente adecuado para resolver problemas muy pequeños (con no más de dos variables debido al problema de dimensionalidad). Este método provee una gran
x x x x x x qv o B =m v o 2
 ísica e 2º achillerato Activia Una partícula e masa m, carga positiva q y otaa e velocia horizontal, penetra en una región el espacio one hay un campo eléctrico E y un campo magnético. Ambos campos son
ísica e 2º achillerato Activia Una partícula e masa m, carga positiva q y otaa e velocia horizontal, penetra en una región el espacio one hay un campo eléctrico E y un campo magnético. Ambos campos son
Difracción producida por un cabello Fundamento
 Difracción proucia por un cabello Funamento Cuano la luz láser se hace inciir sobre un cabello humano, la imagen e ifracción que se obtiene es similar a la que prouce una oble renija (fig.1). Existe una
Difracción proucia por un cabello Funamento Cuano la luz láser se hace inciir sobre un cabello humano, la imagen e ifracción que se obtiene es similar a la que prouce una oble renija (fig.1). Existe una
Esta expresión polinómica puede expresarse como una expresión matricial de la forma; a 11 a 12 a 1n x 1 x 2 q(x 1, x 2,, x n ) = (x 1, x 2,, x n )
 Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
MODELADO, IDENTIFICACIÓN PARAMÉTRICA Y CONTROL DEL ROBOT SCORBOT-ER 5 PLUS
 MODELADO, IDENTIFICACIÓN PARAMÉTRICA Y CONTROL DEL ROBOT SCORBOT-ER 5 PLUS Alexaner Constaín*, Karoll Torres*, Jaime Arango**, Anrés Vivas* * Departamento e Electrónica, Instrumentación y Control, Universia
MODELADO, IDENTIFICACIÓN PARAMÉTRICA Y CONTROL DEL ROBOT SCORBOT-ER 5 PLUS Alexaner Constaín*, Karoll Torres*, Jaime Arango**, Anrés Vivas* * Departamento e Electrónica, Instrumentación y Control, Universia
TEMA 1 INTRODUCCIÓN A LAS ECUACIONES DIFERENCIALES
 TEMA 1 INTRODUCCIÓN A LAS ECUACIONES DIFERENCIALES 7 INTRODUCCIÓN El propósito e este tema es introucir a los alumnos en la terminología básica e las Ecuaciones Diferenciales eaminar brevemente como se
TEMA 1 INTRODUCCIÓN A LAS ECUACIONES DIFERENCIALES 7 INTRODUCCIÓN El propósito e este tema es introucir a los alumnos en la terminología básica e las Ecuaciones Diferenciales eaminar brevemente como se
Programa de Acceso Inclusivo, Equidad y Permanencia. PAIEP, Universidad de Santiago
 Guía dinámica. En general, los problemas de dinámica se resuelven aplicando 3 pasos: 1º Dibuje un diagrama de cuerpo libre para cada cuerpo involucrado en el sistema. Es decir, identifique todas las fuerzas
Guía dinámica. En general, los problemas de dinámica se resuelven aplicando 3 pasos: 1º Dibuje un diagrama de cuerpo libre para cada cuerpo involucrado en el sistema. Es decir, identifique todas las fuerzas
F, su unidad es el Newton, las masas su unidad es el kg y la distancia, en metros, donde G es:
 Si los cuerpos que tienen masa se atraen, por qué no vemos que se atraigan os pupitres e la clase? Efectivamente, los os pupitres se atraen, e acuero con la ley e gravitación universal, pero en la misma
Si los cuerpos que tienen masa se atraen, por qué no vemos que se atraigan os pupitres e la clase? Efectivamente, los os pupitres se atraen, e acuero con la ley e gravitación universal, pero en la misma
2 o Bachillerato. Conceptos básicos
 Física 2 o Bachillerato Conceptos básicos Movimiento. Cambio de posición de un cuerpo respecto de un punto que se toma como referencia. Cinemática. Parte de la Física que estudia el movimiento de los cuerpos
Física 2 o Bachillerato Conceptos básicos Movimiento. Cambio de posición de un cuerpo respecto de un punto que se toma como referencia. Cinemática. Parte de la Física que estudia el movimiento de los cuerpos
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
IMPLEMENTACIÓN DE SENSORES VIRTUALES EN FOUNDATION FIELDBUS
 IMPLEMENACIÓN DE SENSORES VIRUALES EN FOUNDAION FIELDBUS Anrés J. Piñón Pazos Dpto. Ingeniería Inustrial, Universiae e A Coruña. E.U.P. Ferrol, Ava. 19 e Febrero, s/n, 15405 A Coruña, anrespp@cf.uc.es
IMPLEMENACIÓN DE SENSORES VIRUALES EN FOUNDAION FIELDBUS Anrés J. Piñón Pazos Dpto. Ingeniería Inustrial, Universiae e A Coruña. E.U.P. Ferrol, Ava. 19 e Febrero, s/n, 15405 A Coruña, anrespp@cf.uc.es
UN TERCER METODO EXPERIMENTAL PARA LA DETERMINACIÓN DE LA CONSTANTE DE ELASTICIDAD DE UN RESORTE
 REVISTA COLOMBIANA DE FÍSICA, VOL. 6, No. 1. 004 UN TERCER METODO EXPERIMENTAL PARA LA DETERMINACIÓN DE LA CONSTANTE DE ELASTICIDAD DE UN RESORTE Francisco Ernesto Cortés Sánchez Funación Interamericana
REVISTA COLOMBIANA DE FÍSICA, VOL. 6, No. 1. 004 UN TERCER METODO EXPERIMENTAL PARA LA DETERMINACIÓN DE LA CONSTANTE DE ELASTICIDAD DE UN RESORTE Francisco Ernesto Cortés Sánchez Funación Interamericana
1. Hallar la derivada por definición de f ( x) x x 1. Solución: para resolver la derivada aplicaremos la definición de la derivada: f '( x)
 . Hallar la erivaa por efinición e f ( ) Solución: para resolver la erivaa aplicaremos la efinición e la erivaa: f '( ) lim 0 f ( ) f ( ) f ( ) f '( ) lim 0 ara allar la erivaa meiante efinición ebemos
. Hallar la erivaa por efinición e f ( ) Solución: para resolver la erivaa aplicaremos la efinición e la erivaa: f '( ) lim 0 f ( ) f ( ) f ( ) f '( ) lim 0 ara allar la erivaa meiante efinición ebemos
APLICACIÓN DE MATRICES DE TRANSFORMACIÓN EN EL CONTROL DE POSICIÓN CINEMATICO DE UN ROBOT ARTICULADO DE TRES GRADOS DE LIBERTAD
 APIAIÓN DE MATRIE DE TRANFORMAIÓN EN E ONTRO DE POIIÓN INEMATIO DE UN ROBOT ARTIUADO DE TRE GRADO DE IBERTAD Ing. Martínez Valéz Armano (Prof. Tecnológico e Estuios uperiores e Ecatepec), M. en. ópez Amaro
APIAIÓN DE MATRIE DE TRANFORMAIÓN EN E ONTRO DE POIIÓN INEMATIO DE UN ROBOT ARTIUADO DE TRE GRADO DE IBERTAD Ing. Martínez Valéz Armano (Prof. Tecnológico e Estuios uperiores e Ecatepec), M. en. ópez Amaro
PROGRAMACIÓN LINEAL. Su empleo es frecuente en aplicaciones de la industria, la economía, la estrategia militar, etc.
 PROGRAMACIÓN LINEAL La programación lineal da respuesta a situaciones en las que se exige maximizar o minimizar funciones que se encuentran sujetas a determinadas limitaciones, que llamaremos restricciones.
PROGRAMACIÓN LINEAL La programación lineal da respuesta a situaciones en las que se exige maximizar o minimizar funciones que se encuentran sujetas a determinadas limitaciones, que llamaremos restricciones.
CONCEPTO DE CINEMÁTICA: es el estudio del movimiento sin atender a las causas que lo producen
 CINEMÁTICA CONCEPTO DE CINEMÁTICA: es el estudio del movimiento sin atender a las causas que lo producen CONCEPTO DE MOVIMIENTO: el movimiento es el cambio de posición, de un cuerpo, con el tiempo (este
CINEMÁTICA CONCEPTO DE CINEMÁTICA: es el estudio del movimiento sin atender a las causas que lo producen CONCEPTO DE MOVIMIENTO: el movimiento es el cambio de posición, de un cuerpo, con el tiempo (este
Tema I. Introducción. Ciro el Grande ( A.C.)
 1.1. La ciencia de la estadística:. El origen de la estadística:. Ciencia descriptiva. Evaluación de juegos de azar Ciro el Grande (560-530 A.C.) Si tengo 1 As y 2 reyes, que descarte es mas conveniente
1.1. La ciencia de la estadística:. El origen de la estadística:. Ciencia descriptiva. Evaluación de juegos de azar Ciro el Grande (560-530 A.C.) Si tengo 1 As y 2 reyes, que descarte es mas conveniente
EXAMEN FÍSICA 2º BACHILLERATO TEMA 2: CAMPO ELECTROMAGNÉTICO
 INSTRUCCIONES GENERALES Y VALORACIÓN La prueba consiste de dos opciones, A y B, y el alumno deberá optar por una de las opciones y resolver las tres cuestiones y los dos problemas planteados en ella, sin
INSTRUCCIONES GENERALES Y VALORACIÓN La prueba consiste de dos opciones, A y B, y el alumno deberá optar por una de las opciones y resolver las tres cuestiones y los dos problemas planteados en ella, sin
UN PROBLEMA ABIERTO DE DINÁMICA DE CUERPOS VINCULADOS POR CUERDAS Y ROZAMIENTOS BAJO EL ANÁLISIS CLÁSICO Y LA SIMULACIÓN COMPUTACIONAL
 UN PROBLEMA ABIERTO DE DINÁMICA DE CUERPOS VINCULADOS POR CUERDAS Y ROZAMIENTOS BAJO EL ANÁLISIS CLÁSICO Y LA SIMULACIÓN COMPUTACIONAL Jorge Mamprin Hugo Kofman Faculta e Ingeniería Química - Universia
UN PROBLEMA ABIERTO DE DINÁMICA DE CUERPOS VINCULADOS POR CUERDAS Y ROZAMIENTOS BAJO EL ANÁLISIS CLÁSICO Y LA SIMULACIÓN COMPUTACIONAL Jorge Mamprin Hugo Kofman Faculta e Ingeniería Química - Universia
DEFINICIONES DE HUMEDAD Y SU EQUIVALENCIA
 ENME007 DEFINICIONES DE HUMEDAD Y SU EQUIVALENCIA Enrique Martines L. Centro Nacional e Metrología División e Termometría km 45 Carretera a Los Cués El Marquez Qro. México 110500 ext. 340emartine@cenam.mx
ENME007 DEFINICIONES DE HUMEDAD Y SU EQUIVALENCIA Enrique Martines L. Centro Nacional e Metrología División e Termometría km 45 Carretera a Los Cués El Marquez Qro. México 110500 ext. 340emartine@cenam.mx
Ejercicios ejemplo clases 2.1 a 2.2 Pág 1 de 6
 Ejercicios ejemplo clases 2.1 a 2.2 Pág 1 e 6 Tema 2 HIDRÁULICA DE ACUÍFEROS 1- En una sección e un acuífero aluvial, formao por gravas y arenas limpias, se sabe que su anchura es e unos 2000 m, su espesor
Ejercicios ejemplo clases 2.1 a 2.2 Pág 1 e 6 Tema 2 HIDRÁULICA DE ACUÍFEROS 1- En una sección e un acuífero aluvial, formao por gravas y arenas limpias, se sabe que su anchura es e unos 2000 m, su espesor
FUNCIONES TRIGONOMÉTRICAS
 CAPÍTULO 6 FUNCIONES TRIGONOMÉTRICAS 6.1 FUNCIONES TRASCENDENTES (Áreas 1, y ) Las funciones trascenentes se caracterizan por tener lo que se llama argumento. Un argumento es el número o letras que lo
CAPÍTULO 6 FUNCIONES TRIGONOMÉTRICAS 6.1 FUNCIONES TRASCENDENTES (Áreas 1, y ) Las funciones trascenentes se caracterizan por tener lo que se llama argumento. Un argumento es el número o letras que lo
ALN. Repaso matrices. In. Co. Facultad de Ingeniería Universidad de la República
 ALN Repaso matrices In. Co. Facultad de Ingeniería Universidad de la República Definiciones básicas - Vectores Definiciones básicas - Vectores Construcciones Producto interno: ( x, y n i x y i i ' α Producto
ALN Repaso matrices In. Co. Facultad de Ingeniería Universidad de la República Definiciones básicas - Vectores Definiciones básicas - Vectores Construcciones Producto interno: ( x, y n i x y i i ' α Producto
TEMA 8.- NORMAS DE MATRICES Y
 Álgebra II: Tema 8. TEMA 8.- NORMAS DE MATRICES Y NúMERO DE CONDICIóN Índice. Introducción 2. Norma vectorial y norma matricial. 2 2.. Norma matricial inducida por normas vectoriales......... 4 2.2. Algunos
Álgebra II: Tema 8. TEMA 8.- NORMAS DE MATRICES Y NúMERO DE CONDICIóN Índice. Introducción 2. Norma vectorial y norma matricial. 2 2.. Norma matricial inducida por normas vectoriales......... 4 2.2. Algunos
Cálculo en varias variables
 Cálculo en varias variables Dpto. Matemática Aplicada Universidad de Málaga Resumen Límites y continuidad Funciones de varias variables Límites y continuidad en varias variables 1 Límites y continuidad
Cálculo en varias variables Dpto. Matemática Aplicada Universidad de Málaga Resumen Límites y continuidad Funciones de varias variables Límites y continuidad en varias variables 1 Límites y continuidad
LA EQUIVALENCIA DE LAS REPRESENTACIONES DE LA SOLUCIÓN PARTICULAR POR LOS MÉTODOS DE REDUCCIÓN DE ORDEN Y VARIACIÓN DE PARÁMETROS
 Faculta e Ingeniería - Universia Rafael Lanívar Boletín Electrónico No. 06 LA EQUIVALENCIA DE LAS REPRESENTACIONES DE LA SOLUCIÓN PARTICULAR POR LOS MÉTODOS DE REDUCCIÓN DE ORDEN Y VARIACIÓN DE PARÁMETS
Faculta e Ingeniería - Universia Rafael Lanívar Boletín Electrónico No. 06 LA EQUIVALENCIA DE LAS REPRESENTACIONES DE LA SOLUCIÓN PARTICULAR POR LOS MÉTODOS DE REDUCCIÓN DE ORDEN Y VARIACIÓN DE PARÁMETS
RECOMENDACIÓN 326-6. (Cuestión 59/1)
 Rc. 326-6 RECOMENDACIÓN 326-6 DETERMINACIÓN Y MEDICIÓN DE LA POTENCIA DE LOS TRANSMISORES RADIOELÉCTRICOS (Cuestión 59/) Rc. 326-6 (95-959-963-966-974-978-982-986-990) El CCIR, CONSIDERANDO a) que el artículo
Rc. 326-6 RECOMENDACIÓN 326-6 DETERMINACIÓN Y MEDICIÓN DE LA POTENCIA DE LOS TRANSMISORES RADIOELÉCTRICOS (Cuestión 59/) Rc. 326-6 (95-959-963-966-974-978-982-986-990) El CCIR, CONSIDERANDO a) que el artículo
Física para todos 1 Carlos Jiménez Huaranga MOVIMIENTO PARABÓLICO. a) Aplicamos la ecuación: ttotal. b) Para calcular la máxima altura, utilizamos la
 Física para toos 1 Carlos Jiménez Huarana MOVIMIENTO PARABÓLICO Es un movimiento compuesto por: Un movimiento orizontal rectilíneo uniforme one la componente orizontal e la velocia permanece constante
Física para toos 1 Carlos Jiménez Huarana MOVIMIENTO PARABÓLICO Es un movimiento compuesto por: Un movimiento orizontal rectilíneo uniforme one la componente orizontal e la velocia permanece constante
MOVIMIENTO PARABÓLICO
 MOIMIENTO PARABÓLICO En la naturaleza no se presentan los movimientos aislaamente, sino combinaos ó superpuestos e os o más movimientos simples. Son movimientos simples : el Movimiento Rectilíneo Uniforme
MOIMIENTO PARABÓLICO En la naturaleza no se presentan los movimientos aislaamente, sino combinaos ó superpuestos e os o más movimientos simples. Son movimientos simples : el Movimiento Rectilíneo Uniforme
UNIDAD 6.- PROGRAMACIÓN LINEAL
 UNIDAD 6.- PROGRAMACIÓN LINEAL 1. INECUACIONES LINEALES CON DOS INCÓGNITAS Una inecuación de primer grado con dos incógnitas es una inecuación que en forma reducida se puede expresar de la siguiente forma:
UNIDAD 6.- PROGRAMACIÓN LINEAL 1. INECUACIONES LINEALES CON DOS INCÓGNITAS Una inecuación de primer grado con dos incógnitas es una inecuación que en forma reducida se puede expresar de la siguiente forma:
OPCIONES. c.- Titular o Comprador de la Opción: inversionista que adquiere el derecho a comprar/vender el activo subyacente.
 arlos A. Díaz ontreras 1 OPIONES La opción es "un contrato que a erecho a su poseeor o titular (el que compró la opción), a comprar o vener un activo eterminao y a un precio eterminao, urante un perioo
arlos A. Díaz ontreras 1 OPIONES La opción es "un contrato que a erecho a su poseeor o titular (el que compró la opción), a comprar o vener un activo eterminao y a un precio eterminao, urante un perioo
Tema 2.- Formas Cuadráticas.
 Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS. Métodos multivariantes en control estadístico de la calidad
 UNIVESIDAD NACIONAL MAYO DE SAN MACOS FACULTAD DE CIENCIAS MATEMÁTICAS E.A.P. DE ESTADÍSTICA Métoos multivariantes en control estaístico e la calia Capítulo I. Gráficos e control estaístico univariaa TABAJO
UNIVESIDAD NACIONAL MAYO DE SAN MACOS FACULTAD DE CIENCIAS MATEMÁTICAS E.A.P. DE ESTADÍSTICA Métoos multivariantes en control estaístico e la calia Capítulo I. Gráficos e control estaístico univariaa TABAJO
Diseño, Implementación y Validación de un Controlador PID Autosintonizado. Design, Implementation and Validation of a Self-Tuning PID Controller
 Artículo e Investigación/Research Article Diseño, Implementación y Valiación e un Controlaor PID Autosintonizao Design, Implementation an Valiation of a Self-Tuning PID Controller Leonaro F. Lozano-Valencia
Artículo e Investigación/Research Article Diseño, Implementación y Valiación e un Controlaor PID Autosintonizao Design, Implementation an Valiation of a Self-Tuning PID Controller Leonaro F. Lozano-Valencia
PROBLEMAS DE ONDAS. Función de onda, Autor: José Antonio Diego Vives. Documento bajo licencia Creative Commons (BY-SA)
 PROBLEMAS DE ONDAS. Función de onda, energía. Autor: José Antonio Diego Vives Documento bajo licencia Creative Commons (BY-SA) Problema 1 Escribir la función de una onda armónica que avanza hacia x negativas,
PROBLEMAS DE ONDAS. Función de onda, energía. Autor: José Antonio Diego Vives Documento bajo licencia Creative Commons (BY-SA) Problema 1 Escribir la función de una onda armónica que avanza hacia x negativas,
MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II INSTRUCCIONES Y CRITERIOS GENERALES DE CALIFICACIÓN
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO DE EXAMEN CURSO 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO DE EXAMEN CURSO 2014-2015 MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES
UNIVERSIDAD POLITÉCNICA DE EL SALVADOR ESCUELA DE FORMACIÓN BÁSICA. FÍSICA II PRÁCTICA 26 PENDULO SIMPLE
 UNIVERSIDAD POLITÉCNICA DE EL SALVADOR ESCUELA DE FORMACIÓN BÁSICA. FÍSICA II PRÁCTICA 26 PENDULO SIMPLE OBJETIVOS DEL APRENDIZAJE: ESTUDIAR LAS OSCILACIONES DEL PÉNDULO Y DETERMINAR LAS SIMPLIFICACIONES
UNIVERSIDAD POLITÉCNICA DE EL SALVADOR ESCUELA DE FORMACIÓN BÁSICA. FÍSICA II PRÁCTICA 26 PENDULO SIMPLE OBJETIVOS DEL APRENDIZAJE: ESTUDIAR LAS OSCILACIONES DEL PÉNDULO Y DETERMINAR LAS SIMPLIFICACIONES
Electromagnetismo Pedagogía en Física R. Lagos. PROBLEMAS RESUELTOS
 PROBLEMAS RESUELTOS. Un capacitor e lleno e aire está compuesto e os placas paralela, caa una con un área e 7 6 [ 2 ], separaas por una istancia e,8 [mm]. Si se aplica una iferencia e potencial e 20 [V]
PROBLEMAS RESUELTOS. Un capacitor e lleno e aire está compuesto e os placas paralela, caa una con un área e 7 6 [ 2 ], separaas por una istancia e,8 [mm]. Si se aplica una iferencia e potencial e 20 [V]
En la notación C(3) se indica el valor de la cuenta para 3 kilowatts-hora: C(3) = 60 (3) = 1.253
 Eje temático: Álgebra y funciones Contenidos: Operatoria con expresiones algebraicas Nivel: 2 Medio Funciones 1. Funciones En la vida diaria encontramos situaciones en las que aparecen valores que varían
Eje temático: Álgebra y funciones Contenidos: Operatoria con expresiones algebraicas Nivel: 2 Medio Funciones 1. Funciones En la vida diaria encontramos situaciones en las que aparecen valores que varían
Reglas de derivación
 CAPÍTULO 6 Reglas e erivación OBJETIVOS PARTICULARES. Aplicar reglas básicas e erivación para calcular erivaas, e iverso oren, e funciones algebraicas.. Aplicar la regla e la caena en el cálculo e erivaas,
CAPÍTULO 6 Reglas e erivación OBJETIVOS PARTICULARES. Aplicar reglas básicas e erivación para calcular erivaas, e iverso oren, e funciones algebraicas.. Aplicar la regla e la caena en el cálculo e erivaas,
2.004 MODELISMO, DINÁMICA Y CONTROL II Primavera Soluciones del boletín de problemas 6
 2.004 MODELISMO, DINÁMICA Y CONTROL II Primavera 2003 Soluciones del boletín de problemas 6 Problema 1. Varilla deslizándose por una pared. Dado que los extremos de la varilla están forzados a permanecer
2.004 MODELISMO, DINÁMICA Y CONTROL II Primavera 2003 Soluciones del boletín de problemas 6 Problema 1. Varilla deslizándose por una pared. Dado que los extremos de la varilla están forzados a permanecer
ZONA INDUSTRIAL: Coronel Larrabure 2460 (Ruta 9 Km 562) / Tel: (0353) (Lín. Rotativas) / Fax: (0353) VILLA MARÍA
 ZONA INUSTRIAL: onel Larrabure 2460 (Ruta 9 Km 562) / Tel: (0353) 453 1694 (Lín. Rotativas) 0800 777 8300 / Fax: (0353) 453 1560 5900 VILLA MARÍA CÓROBA ARGENTINA www.bpb.com.ar bpb@bpb.com.ar 2 INICE
ZONA INUSTRIAL: onel Larrabure 2460 (Ruta 9 Km 562) / Tel: (0353) 453 1694 (Lín. Rotativas) 0800 777 8300 / Fax: (0353) 453 1560 5900 VILLA MARÍA CÓROBA ARGENTINA www.bpb.com.ar bpb@bpb.com.ar 2 INICE
REVISTA INVESTIGACION OPERACIONAL Vol. 23, No. 1, 2002
 REVISTA INVESTIGACION OPERACIONAL Vol. 23, No. 1, 2002 OPTIMIZACION DE MULTIPLES RESPUESTAS POR EL METODO DE LA FUNCION DE CONVENIENCIA PARA UN DISEÑO DE MEZCLAS Margarita Nuñez e Villavicencio Ferrer
REVISTA INVESTIGACION OPERACIONAL Vol. 23, No. 1, 2002 OPTIMIZACION DE MULTIPLES RESPUESTAS POR EL METODO DE LA FUNCION DE CONVENIENCIA PARA UN DISEÑO DE MEZCLAS Margarita Nuñez e Villavicencio Ferrer
El análisis cartesiano (René Descartes ) descubrió que las ecuaciones pueden tener una representación gráfica.
 Capítulo 4. Estudio de la línea recta El análisis cartesiano (René Descartes 1596-1650) descubrió que las ecuaciones pueden tener una representación gráfica. Para lograr esa representación gráfica es necesario
Capítulo 4. Estudio de la línea recta El análisis cartesiano (René Descartes 1596-1650) descubrió que las ecuaciones pueden tener una representación gráfica. Para lograr esa representación gráfica es necesario
