MATEMATIKA SPANYOL NYELVEN
|
|
|
- Rafael de la Cruz Vega
- hace 6 años
- Vistas:
Transcripción
1 Mtemtik spnyol nyelven középszint 061 ÉRETTSÉGI VIZSGA 007. október 5. MATEMATIKA SPANYOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM
2 Informción importnte Cuestiones formles pr l corrección del exmen: 1. El profesor tiene que corregir el exmen con un bolígrfo de diferente color l utilizdo por el lumno. El profesor indicrá los errores, los psos que fltn, etc, tl y como esté costumbrdo.. En los recudros grises de puntución, el primero indic l máxim puntución que se puede dr y el recudro de l ldo recoge los puntos que h ddo el profesor. 3. Si no hy errores en l resolución, es suficiente escribir los puntos máximos en el recudro correspondiente. 4. Si hy errores o fltn psos, indique, por fvor, los puntos correspondientes cd prte. Cuestiones de contenido: 1. En lgunos ejercicios, les hemos ofrecido l puntución correspondiente vris resoluciones. Si usted encuentr otr resolución, busque, por fvor, ls prtes equivlentes de ls resoluciones que propone l guí y reprt los puntos según dichs prtes.. Se pueden dividir los puntos que l guí recomiend pr indicr distintos psos de un prte. Pero, en culquier cso, los puntos que se den siempre serán enteros. 3. Si el desrrollo de l resolución y los resultdos finles son correctos, se puede dr l puntución máxim incluso si ls explicciones no son tn mplis como ls que precen en l guí. 4. Si en un prte de l resolución, el estudinte comete un error de cálculo o de precisión, no recibirá los puntos correspondientes est prte. Si l rrstrr este error, el resto de los psos relizdos son correctos y no cmbi el sentido del problem, entonces se punturán el resto de los psos. 5. En cso de un error de plicción teóric, dentro de un rzonmiento en l resolución (los rzonmientos distintos precen seprdos con un líne doble en l guí), no se pueden dr puntos ni siquier por los psos mtemáticmente correctos hechos trs cometer el error. Pero si en el siguiente rzonmiento, se sigue trbjndo bien, pesr del resultdo incorrecto cusdo por dicho error, se drán los puntos máximos pr ls siguientes prtes de l resolución del problem, si no h cmbido el sentido del mismo. 6. Si en l guí, lgún comentrio o un unidd de medid está entre préntesis, l solución será correct unque no se escrib. 7. Si se escriben vrios procedimientos pr resolver un ejercicio, sólo se punturá uno de ellos, el que el lumno exmindo hy indicdo como válido. 8. No se pueden dr puntos extr que excedn los puntos máximos que se pueden dr pr el ejercicio o un prte de él. 9. No se restn puntos si precen errores en lgún pso o en prtes de l resolución que el lumno no utiliz después pr resolver el ejercicio. 10. De los cinco ejercicios propuestos en l prte II. del exmen sólo se pueden puntur cutro. Probblemente el estudinte hbrá indicdo el número del ejercicio elimindo, el que no se punturá, en el cudrdo correspondiente. Si el lumno hubier resuelto este ejercicio no hbrí que corregirlo. Si no qued clro cuál es el ejercicio que el lumno exmindo no dese que se le corrij, entonces utomáticmente, según el orden en que precen los ejercicios, no se corregirá el último. írásbeli vizsg 061 / október 5.
3 I. 1. A B = {5; 7; 9} Totl: No se punturá l enumerción de los conjuntos A y B por seprdo.. C = Totl: Si determin correctmente el vlor de C 1 se puede dr. 3. A = 1, B = A > B Totl: 4. El número de bols zules: 9. El número de bols rojs: 11. csos fvorbles 11 P = = = 0,55 csos posibles 0 El resultdo finl correcto, sin especificr los psos, vle 3 puntos. Si d l respuest indicndo que l rzón de bols rojs es del 55 % y por tnto, l probbilidd buscd es 0,55, entonces tmbién recibirá 3 puntos. 5. ) fls b) verdder c) fls írásbeli vizsg / október 5.
4 6. El conjunto de los números reles positivos. Totl: Por l respuest x > 0, tmbién se signrán los puntos S n 5 = n -* 60 S 5 = 5 S = *Si no figur l fórmul, pero l plic correctmente, tmbién se drá este punto = 60 Totl: Si escribe todos los csos y lleg l resultdo finl correcto, tmbién se drán los. Si escribe l menos 30 de los números buscdos, pero no enumer todos, puede recibir. 9. π x 1 = 6 5π x = 6 Totl: Si utiliz tmbién el periodo, puede recibir sólo un punto. Si expres l solución en grdos, como máximo, se puede dr. írásbeli vizsg / október 5.
5 10. c = b; c = (3i j) ( i + 5j) c = 6i 4j + i 5j c = 7i 9j El resultdo finl correcto, sin especificr los psos, vle 3 puntos x Se x el quinto número, entonces = 7. 5 x = 5 1. El vlor mínimo de l función es 1, los vlores de l función en los extremos del intervlo ddo son 5 y 10, l imgen de l función es el intervlo [1; 10]. * * *En cso de determinr l imgen correctmente se signrán cd uno de estos puntos. Si d l imgen correct de culquier otr form, tmbién conseguirá 3 puntos. írásbeli vizsg / október 5.
6 13. ) Por ser l función (exponencil en bse 5) estrictmente monóton creciente x < 13 - x x < 5 L solución de l inecución: {1; ; 3; 4} 13. b) 0 II./A Totl: 4 puntos x * 3 x 3 = 3 Por ser l función (exponencil en bse 3) estrictmente monóton x = x 3. 4x = x 6x + 9 x 10x + 9 = 0 x 1 = 1 x = 9 El resultdo x = 1 no es solución de l ecución. L solución de l ecución en el conjunto de los * números reles es x = ) En el ul hy x mess de dibujo y el número de lumnos de l clse más numeros es y. Totl: 8 puntos x + 8 = y 3 x 7 = y x = 15 e y = 38 Comprobción En el ul hy 15 mess y el número de lumnos de l clse más numeros es 38. Totl: 6 puntos Si sólo enumer los 4 números de l solución, recibe, si hce referenci que no existen otrs soluciones, recibirá los restntes. Sin l observción referente l estrict monotoní, tmbién se drá. *Si por medio de l comprobción o por el estudio del rngo de l ecución, lleg l solución correct, recibirá l puntución complet. Si de l ecución o del sistem se deduce clrmente qué se refieren x e y, tmbién se obtendrá este punto. írásbeli vizsg / október 5.
7 14. b) El número de fechs posibles: , es decir, se pueden obtener 480 fechs en totl. 14. c) En un ño no bisiesto hy 365 fechs reles, tods ls fechs posibles pueden obtenerse con l mism probbilidd*, por lo tnto, l probbilidd de obtener un fech rel 365 es (= 0,7604 ). 480 *Si no se ñde est explicción en el rzonmiento, pero l solución es correct, tmbién recibirá los puntos. 15. ) α. β m e Por un dibujo correcto (que muestre l relción existente entre el cudrdo y el rombo). (T cudrdo = y T rombo = m ) = m 1 L ltur del rombo: m = 6,5 (cm) * 3 puntos Totl: 5 puntos *En cso de llegr l solución correct sin hcer dibujo, tmbién se drá l puntución complet. írásbeli vizsg / október 5.
8 15. b) m s enα = (donde α es el ángulo gudo) α = 30 =150 β 15. c) Si clcul l longitud de l digonl prtir de un relción bien definid de culquier de los posibles triángulos rectángulos, e por ejemplo cos15 =. 13 e = 13 cos 15 e = 5,11 (cm) Totl: 4 puntos En cso de culquier otro procedimiento correcto, (por ejemplo, plicndo el teorem del coseno), tmbién recibirá l puntución complet. írásbeli vizsg / október 5.
9 16. ) II./B Resultdos de l primer vuelt 1.ª pregunt.ª pregunt 3.ª pregunt 4.ª pregunt Respuests de Anikó correct incorrect correct incorrect Totl de respuests corrects Puntución que recibe Anikó Por cd uno de los dtos correctos se drá. Totl: 4 puntos 16. b) L column correspondiente l.ª pregunt cmbirí como: correct, 11, 9; es decir, Anikó hbrí conseguido 9 puntos en es pregunt. Con estos puntos, l puntución totl que recibirí Anikó serí de 7 puntos. Lo cul represent el 150 por ciento de l puntución originl, Es decir, Anikó hbrí umentdo un 50% su puntución totl. 16. c) Primer método: En totl Anikó puede responder ls cutro pregunts de 3 4 = 81 mners distints. Sólo en un cso tods ls respuests serán corrects, sí 1 l probbilidd buscd:. 81 Tmbién se podrí hber deducido l respuest observndo que el umento de los 9 puntos equivle l 50% de l puntución originl. Segundo método: L probbilidd de responder correctmente cd pregunt: 3 1. Totl: 3 puntos L respuest cd pregunt es independiente de ls restntes, sí l probbilidd buscd: = Totl: 3 puntos írásbeli vizsg / október 5.
10 16. d) Si x es el número de respuests corrects que surgen pr un pregunt dd, entonces 0 x son los puntos que reciben cd uno de los concursntes que responden correctmente. El totl de ls puntuciones obtenids: x(0 x). Buscmos el máximo de l función x 0x x entre los números enteros positivos menores que 0. El lugr donde l función lcnz el máximo (medinte l gráfic, o trnsformndo l expresión en otr con un binomio l cudrdo, o refiriéndose l relción existente entre ls medis ritmétic y geométric, o clculndo los vlores en todos los csos) es x = 10. En cso de que diez concursntes respondn correctmente, los concursntes obtendrán el totl de ls puntuciones myor posible. Totl: 3 puntos 7 puntos írásbeli vizsg / október 5.
11 17. ) El número de mners posibles de estblecer el orden: 5! Hy 10 mners distints de estblecer el orden en que los nietos recibn ls crts. 17. b) Culquier de los 5 nietos cuent con l mism probbilidd de recibir l crt en l últim semn. En cso de responder con el modelo, csos fvorbles 4!, csos posibles 5!, tmbién recibirá los. Así l probbilidd buscd: c) Ls longitudes de ls prtes que l buel tejió durnte determindos dís formn un progresión geométric. En l progresión geométric 1 = 8, q= 1, L sum de los n primeros términos de l progresión geométric es l longitud totl de l bufnd. n q 1 S n = 1 q 1 n 1, 1 00 = 8 0, = 1, n lg 6 n = lg1, n 9,83 L bufnd se terminó el décimo dí. Totl: 1s Si est explicción se deduce únicmente de l resolución, tmbién se drá este punto. Si este comentrio se deduce solmente del uso de ls fórmuls, tmbién recibirá los puntos. Si encuentr el resultdo de n probndo con vlores en el exponente de l potenci, entonces tmbién se drán los 3 puntos. írásbeli vizsg / október 5.
12 18. ) C φ 5 5 K A α Un buen esbozo que muestre los dtos del problem. Si φ es el ángulo del vértice, entonces ϕ 0 sen = = 0, F 0 ρ B De donde φ = 45,4 Totl: 4 puntos 18. b) m = = 48 r π m 400 π 48 V = = 3 3 V 0106,19 (cm 3 ) írásbeli vizsg / október 5.
13 18. c) El rdio de l esfer inscrit en el cono coincide con el rdio de l circunferenci inscrit en el triángulo isósceles. Los ángulos poydos en l bse son α = 67,38. ρ tg 33,69 = 0 Si est observción puede deducirse del dibujo o de los cálculos, tmbién se drán los. ρ = 13,33 (cm) El áre lterl de l esfer : A 34,01 (cm ) 18. d) L longitud del rco correspondiente l sector circulr: i = rπ, Totl: 6 puntos i = 0 π 15,66 (cm) i R T superficie lterl = = 0 π 6 T superficie lterl 367,6 (cm ) Totl: 4 puntos Si se hce el cálculo utilizndo ρ = 13,33 y sí A 3,90 (cm ), tmbién se drá este punto. Si pr este cálculo utiliz el vlor de i proximdo con dos decimles, y obtiene el resultdo 367,16 (cm ), entonces tmbién recibirá este punto. írásbeli vizsg / október 5.
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
.0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
SOLUCIONARIO Poliedros
 SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
.. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 4: Lunes 1 - Viernes 5 de Abril. Contenidos
 Coordinción de Mtemátic I (MAT01) 1 er Semestre de 013 Semn 4: Lunes 1 - Viernes 5 de Abril Complementos Contenidos Clse 1: Funciones trigonométrics. Clse : Funciones sinusoidles y ecuciones trigonométrics.
Coordinción de Mtemátic I (MAT01) 1 er Semestre de 013 Semn 4: Lunes 1 - Viernes 5 de Abril Complementos Contenidos Clse 1: Funciones trigonométrics. Clse : Funciones sinusoidles y ecuciones trigonométrics.
1 Halla las razones trigonométricas del ángulo a en cada uno de estos triángulos: a) b) c)
 Pág. 1 Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m 25 m 11,6 cm 8 m 32 m 60 m 2 Midiendo los ldos, hll ls rzones trigonométrics
Pág. 1 Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m 25 m 11,6 cm 8 m 32 m 60 m 2 Midiendo los ldos, hll ls rzones trigonométrics
DESIGUALDADES < d < En el campo de los números reales tenemos una. Un momento de reflexión muestra que una
 DESIGUALDADES 7 60 < d < 7 70 En el cmpo de los números reles tenemos un propiedd de orden que se costumbr designr con el símbolo (
DESIGUALDADES 7 60 < d < 7 70 En el cmpo de los números reles tenemos un propiedd de orden que se costumbr designr con el símbolo (
BLOQUE III Geometría
 LOQUE III Geometrí 7. Semejnz y trigonometrí 8. Resolución de triángulos rectángulos 9. Geometrí nlític 7 Semejnz y trigonometrí 1. Teorem de Thles Si un person que mide 1,70 m proyect un sombr de 3,40
LOQUE III Geometrí 7. Semejnz y trigonometrí 8. Resolución de triángulos rectángulos 9. Geometrí nlític 7 Semejnz y trigonometrí 1. Teorem de Thles Si un person que mide 1,70 m proyect un sombr de 3,40
3. El logaritmo de una potencia cuya base es igual a la base del logaritmo es igual al exponente de la potencia: Log a a m = m, ya que a m =a m
 LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
Resolución de triángulos
 8 Resolución de triángulos rectángulos. Circunferenci goniométric P I E N S A Y C A L C U L A Escribe l fórmul de l longitud de un rco de circunferenci de rdio m, y clcul, en función de π, l longitud del
8 Resolución de triángulos rectángulos. Circunferenci goniométric P I E N S A Y C A L C U L A Escribe l fórmul de l longitud de un rco de circunferenci de rdio m, y clcul, en función de π, l longitud del
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. 1 PÁGINA 70 EJERCICIOS Áres y perímetros de figurs sencills Hll el áre y el perímetro de ls figurs coloreds de los siguientes ejercicios: 1 ) b) 3 m 3 m 1,8 m 4 m 6 m ) S3 m3 m9 m b) S 6m 1,8 m 5,4
Pág. 1 PÁGINA 70 EJERCICIOS Áres y perímetros de figurs sencills Hll el áre y el perímetro de ls figurs coloreds de los siguientes ejercicios: 1 ) b) 3 m 3 m 1,8 m 4 m 6 m ) S3 m3 m9 m b) S 6m 1,8 m 5,4
Aplicaciones del cálculo integral
 Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Tema 5. Trigonometría y geometría del plano
 1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
INSTITUTO VALLADOLID PREPARATORIA Página 105 ELIPSE
 INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
1.6 Perímetros y áreas
 3 1.6 Perímetros y áres Perímetro: es l medid del contorno de un figur. Superficie (pln): es el conjunto de puntos del plno encerrdos por un figur geométric pln. Áre: es l medid de un superficie. Represente
3 1.6 Perímetros y áres Perímetro: es l medid del contorno de un figur. Superficie (pln): es el conjunto de puntos del plno encerrdos por un figur geométric pln. Áre: es l medid de un superficie. Represente
Grado en Biología Tema 3 Integración. La regla del trapecio.
 Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
REPASO DE ECUACIONES (4º ESO)
 TIPOS DE ECUACIONES.- REPASO DE ECUACIONES ( ESO) Eisten diversos tipos de ecuciones, entre ells estudiremos: Polinómics: En ells, l incógnit prece solmente en epresiones polinómics. El grdo de un ecución
TIPOS DE ECUACIONES.- REPASO DE ECUACIONES ( ESO) Eisten diversos tipos de ecuciones, entre ells estudiremos: Polinómics: En ells, l incógnit prece solmente en epresiones polinómics. El grdo de un ecución
Los números racionales:
 El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
PROBLEMAS DE OPTIMIZACIÓN
 PROBLEMAS DE OPTIMIZACIÓN Plntemiento y resolución de los problems de optimizción Se quiere construir un cj, sin tp, prtiendo de un lámin rectngulr de cm de lrg por de nch. Pr ello se recortrá un cudrdito
PROBLEMAS DE OPTIMIZACIÓN Plntemiento y resolución de los problems de optimizción Se quiere construir un cj, sin tp, prtiendo de un lámin rectngulr de cm de lrg por de nch. Pr ello se recortrá un cudrdito
FUNCIONES. Analíticamente, la correspondencia anterior se escribe del modo siguiente:
 FUNCIONES.- CONCEPTO DE FUNCIÓN Se dice que un correspondenci f definid entre dos conjuntos A B es un función (o plicción), si cd elemento del conjunto A le sign un elemento sólo uno del conjunto B. De
FUNCIONES.- CONCEPTO DE FUNCIÓN Se dice que un correspondenci f definid entre dos conjuntos A B es un función (o plicción), si cd elemento del conjunto A le sign un elemento sólo uno del conjunto B. De
Qué se puede hacer? Plan de clase (1/2) Escuela: Fecha: Profr. (a):
 Qué se puede hcer? Pln de clse (1/) Escuel: Fech: Profr. (): Curso: Mtemátics 1 secundri Eje temático: FEyM Contenido: 7..6 Justificción de ls fórmuls de perímetro y áre de polígonos regulres, con poyo
Qué se puede hcer? Pln de clse (1/) Escuel: Fech: Profr. (): Curso: Mtemátics 1 secundri Eje temático: FEyM Contenido: 7..6 Justificción de ls fórmuls de perímetro y áre de polígonos regulres, con poyo
1.- Obtener, sin calculadora, el valor de x en las siguientes expresiones: (5 ) = = = 5, por tanto 2x=-3/2 y x=-3/4 = ;
 RESOLUCIÓN DE LOS EJERCICIOS BÁSICOS DEFINICIÓN DE LOGARITMO.- Obtener, sin clculdor, el vlor de en ls siguientes epresiones: ) (/) = 7/; 7/= / =(/) =(/) -, por tnto =- b) = ; ( ) = = =, por tnto =-/ y
RESOLUCIÓN DE LOS EJERCICIOS BÁSICOS DEFINICIÓN DE LOGARITMO.- Obtener, sin clculdor, el vlor de en ls siguientes epresiones: ) (/) = 7/; 7/= / =(/) =(/) -, por tnto =- b) = ; ( ) = = =, por tnto =-/ y
7Soluciones a los ejercicios y problemas PÁGINA 161
 7Soluciones los ejercicios y problems ÁGIN 161 ág. 1 RTI Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m m 11,6 cm 8 m m 60
7Soluciones los ejercicios y problems ÁGIN 161 ág. 1 RTI Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m m 11,6 cm 8 m m 60
LA ELIPSE EJERCICIOS RESUELTOS. Colegio Sor Juana Inés de la Cruz Sección Preparatoria Matemáticas III Bloque VII Ing. Jonathan Quiroga Tinoco
 LA ELIPSE EJERCICIOS RESUELTOS Colegio Sor Jun Inés de l Cruz Sección Preprtori Mtemátics III Bloque VII Ing. Jonthn Quirog Tinoco 1. Pr encontrr l ecución de l elipse con centro en el origen, un foco
LA ELIPSE EJERCICIOS RESUELTOS Colegio Sor Jun Inés de l Cruz Sección Preprtori Mtemátics III Bloque VII Ing. Jonthn Quirog Tinoco 1. Pr encontrr l ecución de l elipse con centro en el origen, un foco
PSU Matemática NM-4 Guía 22: Congruencia de Triángulos
 Centro Educcionl Sn Crlos de Argón. Dpto. Mtemátic. Nivel: NM 4 Prof. Ximen Gllegos H. PSU Mtemátic NM-4 Guí : Congruenci de Triángulos Nombre: Curso: Fech: - Contenido: Congruenci. Aprendizje Esperdo:
Centro Educcionl Sn Crlos de Argón. Dpto. Mtemátic. Nivel: NM 4 Prof. Ximen Gllegos H. PSU Mtemátic NM-4 Guí : Congruenci de Triángulos Nombre: Curso: Fech: - Contenido: Congruenci. Aprendizje Esperdo:
DIVERSIFICACIÓN CURRICULAR
 ECUACIÓN DE PRIMER GRADO Se llmn ecuciones igulddes en ls que precen número y letrs (incógnits) relciondos medinte operciones mtemátics. Por ejemplo: - y = + Son ecuciones con un incógnit cundo prece un
ECUACIÓN DE PRIMER GRADO Se llmn ecuciones igulddes en ls que precen número y letrs (incógnits) relciondos medinte operciones mtemátics. Por ejemplo: - y = + Son ecuciones con un incógnit cundo prece un
10.- Teoremas de Adición.
 Trigonometrí 10.- Teorems de Adición. Rzones trigonométrics de los ángulos A + B y A B. Hy que tener cuiddo de no confundir l rzón trigonométric de l sum de dos ángulos, con l sum de dos rzones trigonométrics.
Trigonometrí 10.- Teorems de Adición. Rzones trigonométrics de los ángulos A + B y A B. Hy que tener cuiddo de no confundir l rzón trigonométric de l sum de dos ángulos, con l sum de dos rzones trigonométrics.
Tema 3. DETERMINANTES
 Tem. DETERMINNTES Definición de determinnte El determinnte de un mtriz cudrd es un número. Pr l mtriz, su determinnte se denot por det() o por. Pr un mtriz de orden,, se define: Ejemplo: Pr un mtriz de
Tem. DETERMINNTES Definición de determinnte El determinnte de un mtriz cudrd es un número. Pr l mtriz, su determinnte se denot por det() o por. Pr un mtriz de orden,, se define: Ejemplo: Pr un mtriz de
3. Resuelve y simplifica: 6. Resuelve y simplifica: Nombre y apellidos : Materia: MATEMATICAS (PENDIENTES) Curso: 2º ESO.
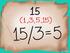 Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
UNIDAD I FUNDAMENTOS BÁSICOS
 Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
5.4. Longitud de un Arco de Curva (Rectificación)
 Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencil e Integrl 7-2 SEMANA 1: APLICACIONES DE LA INTEGRAL 5.4. Longitud de un Arco de Curv (Rectificción)
Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencil e Integrl 7-2 SEMANA 1: APLICACIONES DE LA INTEGRAL 5.4. Longitud de un Arco de Curv (Rectificción)
DETERMINANTES. Determinante es la expresión numérica de una matriz. Según el orden de la matriz el determinante se resuelve de distintas formas:
 ÁLGEBR Educgui.com DETERMINNTES Determinnte es l expresión numéric de un mtriz. Según el orden de l mtriz el determinnte se resuelve de distints forms: DETERMINNTE DE SEGUNDO ORDEN Pr poder solucionr un
ÁLGEBR Educgui.com DETERMINNTES Determinnte es l expresión numéric de un mtriz. Según el orden de l mtriz el determinnte se resuelve de distints forms: DETERMINNTE DE SEGUNDO ORDEN Pr poder solucionr un
Unidad 1: Números reales.
 Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
11. Triángulos SOLUCIONARIO 1. CONSTRUCCIÓN DE TRIÁNGULOS 2. MEDIANAS Y ALTURAS DE UN TRIÁNGULO
 SLUINRI 95 11. Triángulos 1. NSTRUIÓN DE TRIÁNULS PIENS Y LUL Justific si se pueden dibujr los siguientes triángulos conociendo los dtos: ) Tres ldos cuys longitudes son 1 cm, 2 cm y 3 cm b) Un ldo de
SLUINRI 95 11. Triángulos 1. NSTRUIÓN DE TRIÁNULS PIENS Y LUL Justific si se pueden dibujr los siguientes triángulos conociendo los dtos: ) Tres ldos cuys longitudes son 1 cm, 2 cm y 3 cm b) Un ldo de
TEMA 1. LOS NÚMEROS REALES.
 TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
O(0, 0) verifican que. Por tanto,
 Jun Antonio González Mot Proesor de Mtemátics del Colegio Jun XIII Zidín de Grnd SIMETRIA RESPECTO DEL ORIGEN. FUNCIONES IMPARES: Un unción es simétric respecto del origen O, su simétrico respecto de O
Jun Antonio González Mot Proesor de Mtemátics del Colegio Jun XIII Zidín de Grnd SIMETRIA RESPECTO DEL ORIGEN. FUNCIONES IMPARES: Un unción es simétric respecto del origen O, su simétrico respecto de O
Números Reales. Los números naturales son {1; 2; 3; }, el conjunto de todos ellos se representa por.
 Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
Optimización de funciones
 Tem 5 Optimizción de funciones 5.1. Extremos de funciones de vris vribles Definición 5.1.1. Sen f : D R n R, x 0 D y el problem de optimizción: mximizr / minimizr f(x 1, x,, x n ), (x 1, x,, x n ) D en
Tem 5 Optimizción de funciones 5.1. Extremos de funciones de vris vribles Definición 5.1.1. Sen f : D R n R, x 0 D y el problem de optimizción: mximizr / minimizr f(x 1, x,, x n ), (x 1, x,, x n ) D en
Clasifica los siguientes polígonos. a) b) c) d)
 1 FIGURS PLNS EJERIIS PR ENTRENRSE Polígonos 1.44 lsific los siguientes polígonos. ) b) c) d) ) Pentágono irregulr cóncvo. b) Heptágono regulr convexo. c) ctógono irregulr cóncvo. d) Hexágono irregulr
1 FIGURS PLNS EJERIIS PR ENTRENRSE Polígonos 1.44 lsific los siguientes polígonos. ) b) c) d) ) Pentágono irregulr cóncvo. b) Heptágono regulr convexo. c) ctógono irregulr cóncvo. d) Hexágono irregulr
Espacios vectoriales y Aplicaciones Lineales II: Núcleo e imagen. Diagonalización. Ker(f) = {x V f(x) = 0} Im(f) = {f(x) x V}.
 UNIVERSIDAD DE JAÉN ESCUELA POLITÉCNICA SUPERIOR Deprtmento de Mtemátics (Áre de Álgebr) Curso 28/9 PRÁCTICA Nº Espcios vectoriles y Aplicciones Lineles II: Núcleo e imgen. Digonlizción. NÚCLEO E IMAGEN
UNIVERSIDAD DE JAÉN ESCUELA POLITÉCNICA SUPERIOR Deprtmento de Mtemátics (Áre de Álgebr) Curso 28/9 PRÁCTICA Nº Espcios vectoriles y Aplicciones Lineles II: Núcleo e imgen. Digonlizción. NÚCLEO E IMAGEN
a Y = X donde a 1 siendo Lg el logaritmo y
 Mteri: Mtemátics de 4to ño Tem: Función logrítmic Mrco Teórico L función exponencil de l form f ( ) tiene un función invers, que llmmos función logrítmic y se escribe de l form: Un función > 0 g( ) Lg
Mteri: Mtemátics de 4to ño Tem: Función logrítmic Mrco Teórico L función exponencil de l form f ( ) tiene un función invers, que llmmos función logrítmic y se escribe de l form: Un función > 0 g( ) Lg
TEMA 3 RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES Matemáticas CCSSII 2º Bachillerato 1
 TEMA RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES Mtemátics CCSSII 2º Bchillerto 1 TEMA RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES.1 DETERMINANTES DE ORDEN 2.1.1 DEFINICIÓN: El determinnte de un mtriz
TEMA RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES Mtemátics CCSSII 2º Bchillerto 1 TEMA RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES.1 DETERMINANTES DE ORDEN 2.1.1 DEFINICIÓN: El determinnte de un mtriz
PROGRESIONES ARITMETICAS
 PROGRESIONES ARITMETICAS. Hllr l sum de los primeros cien enteros positivos múltiplos de 7. L sum de n términos de un progresión ritmétic viene dd por l expresión: + n Sn n Aplicndo pr 00 términos: + 00
PROGRESIONES ARITMETICAS. Hllr l sum de los primeros cien enteros positivos múltiplos de 7. L sum de n términos de un progresión ritmétic viene dd por l expresión: + n Sn n Aplicndo pr 00 términos: + 00
REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS
 TRIIGONOMETRÍÍA REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS Recuerd que los ángulos los medímos en grdos o en rdines. Además, los grdos podín dividirse en minutos segundos, de form similr como se distribuen
TRIIGONOMETRÍÍA REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS Recuerd que los ángulos los medímos en grdos o en rdines. Además, los grdos podín dividirse en minutos segundos, de form similr como se distribuen
1º (junio 1994) i) Estudiar, para los diferentes valores del parámetro a, la existencia de
 Sistems de ecuciones lineles SISTEMAS DE ECUACIONES LINEALES EJERCICIOS DE SELECTIVIDAD º (junio 994) i) Estudir, pr los diferentes vlores del prámetro, l eistenci de soluciones del sistem resolverlo cundo
Sistems de ecuciones lineles SISTEMAS DE ECUACIONES LINEALES EJERCICIOS DE SELECTIVIDAD º (junio 994) i) Estudir, pr los diferentes vlores del prámetro, l eistenci de soluciones del sistem resolverlo cundo
INTEGRACIÓN. CÁLCULO DE
 Cpítulo INTEGRACIÓN. CÁLCULO DE ÁREAS.. Introducción Si el problem del cálculo de l rect tngente llevó los mtemáticos del siglo XVII l desrrollo de ls técnics de l derivción, otro problem, el del cálculo
Cpítulo INTEGRACIÓN. CÁLCULO DE ÁREAS.. Introducción Si el problem del cálculo de l rect tngente llevó los mtemáticos del siglo XVII l desrrollo de ls técnics de l derivción, otro problem, el del cálculo
Repartido N 5. Limites ISCAB 3 EMT prof. Fernando Diaz
 Reprtido N 5 Limites ISCAB EMT prof. Fernndo Diz El resultdo de un límite es un vlor de y en un función cundo el vlor de se proim mucho un vlor ddo sin llegr ser igul él. Es cercrse mucho un vlor en pr
Reprtido N 5 Limites ISCAB EMT prof. Fernndo Diz El resultdo de un límite es un vlor de y en un función cundo el vlor de se proim mucho un vlor ddo sin llegr ser igul él. Es cercrse mucho un vlor en pr
TABLA DE DISTRIBUCIÓN DE FRECUENCIAS
 TABLA DE DISTRIBUCIÓN DE FRECUENCIAS L.C. y Mtro. Frncisco Jvier Cruz Ariz L.C. y Mtro. Frncisco Jvier Cruz Ariz TABLA DE DISTRIBUCIÓN DE FRECUENCIAS Un mner de simplificr los dtos es usr un tbl de frecuenci
TABLA DE DISTRIBUCIÓN DE FRECUENCIAS L.C. y Mtro. Frncisco Jvier Cruz Ariz L.C. y Mtro. Frncisco Jvier Cruz Ariz TABLA DE DISTRIBUCIÓN DE FRECUENCIAS Un mner de simplificr los dtos es usr un tbl de frecuenci
Inecuaciones con valor absoluto
 Inecuciones con vlor soluto El vlor soluto de un número rel se denot por y está definido por:, si 0 si 0 Propieddes Si y son números reles y n es un número entero, entonces: 1.. 3. n 4. n L noción de vlor
Inecuciones con vlor soluto El vlor soluto de un número rel se denot por y está definido por:, si 0 si 0 Propieddes Si y son números reles y n es un número entero, entonces: 1.. 3. n 4. n L noción de vlor
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN APLICACIONES DE LA TRIGONOMETRÍA, LEY DE SENOS Y COSENOS
 MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN APLICACIONES DE LA TRIGONOMETRÍA, LEY DE SENOS Y COSENOS Aplicciones de Trigonometrí de Triángulos Rectángulos Un triángulo tiene seis
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN APLICACIONES DE LA TRIGONOMETRÍA, LEY DE SENOS Y COSENOS Aplicciones de Trigonometrí de Triángulos Rectángulos Un triángulo tiene seis
153 ESO. La mayoría de los hombres nacen como originales y terminan como copias. Oriental
 L myorí de los omres ncen como originles y terminn como copis 15 ESO Orientl ÍNDICE: MILLA NÁUTICA PISTA DE ATLETISMO 1. FÓRMULAS FUNDAMENTALES PARA CÁLCULO DE LONGITUDES, SUPERFICIES Y VOLÚMENES. LONGITUDES
L myorí de los omres ncen como originles y terminn como copis 15 ESO Orientl ÍNDICE: MILLA NÁUTICA PISTA DE ATLETISMO 1. FÓRMULAS FUNDAMENTALES PARA CÁLCULO DE LONGITUDES, SUPERFICIES Y VOLÚMENES. LONGITUDES
MATRICES DE NÚMEROS REALES
 MTRICES. MTURITS Luis Gil Guerr.- DEFINICIÓN MTRICES DE NÚMEROS RELES Llmmos mtriz de números reles de orden m x n un conjunto ordendo de m. n números reles dispuestos en m fils y en n columns i m i m
MTRICES. MTURITS Luis Gil Guerr.- DEFINICIÓN MTRICES DE NÚMEROS RELES Llmmos mtriz de números reles de orden m x n un conjunto ordendo de m. n números reles dispuestos en m fils y en n columns i m i m
ACTIVIDADES DE APRENDIZAJE Nº 5... 112
 FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
POTENCIAS Y LOGARITMOS DE NÚMEROS REALES
 www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
6.1 Sumas de Riemann e integral definida
 Tem 6 Integrción Definid 6.1 Sums de Riemnn e integrl definid Supongmos que estmos interesdos en clculr el áre que se encuentr bjo un curv y = f(x) en un intervlo [, b] (pr simplificr, consideremos el
Tem 6 Integrción Definid 6.1 Sums de Riemnn e integrl definid Supongmos que estmos interesdos en clculr el áre que se encuentr bjo un curv y = f(x) en un intervlo [, b] (pr simplificr, consideremos el
Integral Definida. Tema 6. 6.1 Introducción. 6.2 Definición de Integral Definida
 Tem 6 Integrl Definid 6.1 Introducción En este tem estudiremos l Integrl Definid o Integrl de Riemnn, un concepto mtemático que esencilmente puede describirse como el límite de un sum cundo el número de
Tem 6 Integrl Definid 6.1 Introducción En este tem estudiremos l Integrl Definid o Integrl de Riemnn, un concepto mtemático que esencilmente puede describirse como el límite de un sum cundo el número de
Soluciones a los ejercicios
 Soluciones los ejercicios PROBLEMA : Considérese el grfo G siguiente: b f c d g h j e i ( Es G un grfo simple? Es plno? Es biprtito? Es completo? Es regulr? Es conexo? (b Hllr el número de regiones, vértices
Soluciones los ejercicios PROBLEMA : Considérese el grfo G siguiente: b f c d g h j e i ( Es G un grfo simple? Es plno? Es biprtito? Es completo? Es regulr? Es conexo? (b Hllr el número de regiones, vértices
TEMA 1. VECTORES Y MATRICES 1.3. TRAZA Y DETERMINANTE DE UNA MATRIZ
 TEM. VECTORES Y MTRICES.. TRZ Y DETERMINNTE DE UN MTRIZ . VECTORES Y MTRICES.. TRZ Y DETERMINNTE DE UN MTRIZ... Concepto de Trz.... Propieddes de l trz.... Determinnte de un mtriz.... Cálculo de determinntes
TEM. VECTORES Y MTRICES.. TRZ Y DETERMINNTE DE UN MTRIZ . VECTORES Y MTRICES.. TRZ Y DETERMINNTE DE UN MTRIZ... Concepto de Trz.... Propieddes de l trz.... Determinnte de un mtriz.... Cálculo de determinntes
Curvas en el espacio.
 Curvs en el espcio. Tod curv en el espcio R n se puede considerr como l imgen de un función vectoril r : [, b] R n, r(t) = (x 1 (t),..., x n (t)), que recibe el nombre de prmetrizción de l curv. Los puntos
Curvs en el espcio. Tod curv en el espcio R n se puede considerr como l imgen de un función vectoril r : [, b] R n, r(t) = (x 1 (t),..., x n (t)), que recibe el nombre de prmetrizción de l curv. Los puntos
( ) 4. Colegio Diocesano Sagrado Corazón de Jesús. MATEMÁTICAS I / 1º Bachillerato C y T LOGARTIMOS. log. log. log. 1 log log 3.
 Colegio Diocesno Sgrdo Corzón de Jesús MATEMÁTICAS I / º Bchillerto C y T LOGARTIMOS Logritmos El ritmo de un número, m, positivo, en bse, positiv y distint de uno, es el eponente l que hy que elevr l
Colegio Diocesno Sgrdo Corzón de Jesús MATEMÁTICAS I / º Bchillerto C y T LOGARTIMOS Logritmos El ritmo de un número, m, positivo, en bse, positiv y distint de uno, es el eponente l que hy que elevr l
LA RECTA DEL PLANO P O L I T E C N I C O 1 ECUACIÓN VECTORIAL Y ECUACIONES PARAMÉTRICAS
 L Rect del Plno Mtemátic 4º Año Cód. 44-5 P r o f. M r í d e l L u j á n M r t í n e z P r o f. J u n C r l o s B u e P r o f. M i r t R o s i t o P r o f. V e r ó n i c F i l o t t i Dpto. de Mtemátic
L Rect del Plno Mtemátic 4º Año Cód. 44-5 P r o f. M r í d e l L u j á n M r t í n e z P r o f. J u n C r l o s B u e P r o f. M i r t R o s i t o P r o f. V e r ó n i c F i l o t t i Dpto. de Mtemátic
3º.- Junio i) Producto de matrices: definición, condiciones para su realización. Si A M m n. (la matriz A tiene m filas y n columnas), B M n p
 IES EL PILES SELECTIVIDD OVIEDO DPTO. MTEMÁTICS Mtrices deterinntes Mtrices deterinntes. Ejercicios de Selectividd. º.- Junio 99. i) Define rngo de un triz. ii) Un triz de tres fils tres coluns tiene rngo
IES EL PILES SELECTIVIDD OVIEDO DPTO. MTEMÁTICS Mtrices deterinntes Mtrices deterinntes. Ejercicios de Selectividd. º.- Junio 99. i) Define rngo de un triz. ii) Un triz de tres fils tres coluns tiene rngo
En el ejercicio 3 el alumno demuestra nociones de aritmética, sobre números pares e impares, media aritmética, y nociones de lógica.
 L prueb de l XV Olimpid Mtemátic de º de ESO de Cntbri, celebrd en Universidd de Cntbri el 16 de bril de 011 const de 5 ejercicios de diferentes tems decudos los contenidos de º de ESO. Est prueb fue pensd
L prueb de l XV Olimpid Mtemátic de º de ESO de Cntbri, celebrd en Universidd de Cntbri el 16 de bril de 011 const de 5 ejercicios de diferentes tems decudos los contenidos de º de ESO. Est prueb fue pensd
Curvas en el plano y en el espacio
 Cpítulo 1 Curvs en el plno y en el espcio 1.1. Curvs prmetrizds Definición 1.1.1 (Curv prmetrizd). Un curv prmetrizd diferencible α : I R n, es un plicción de clse C, donde I R es un intervlo bierto, que
Cpítulo 1 Curvs en el plno y en el espcio 1.1. Curvs prmetrizds Definición 1.1.1 (Curv prmetrizd). Un curv prmetrizd diferencible α : I R n, es un plicción de clse C, donde I R es un intervlo bierto, que
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
N I Plegado de planos. Septiembre de 1999 EDICION: 1ª NORMA IBERDROLA
 N I 00.02.52 Septiembre de 1999 EDICION: 1ª NORMA IBERDROLA Plegdo de plnos DESCRIPTORES: Plegdo de plnos. N O R M A N I 00.02.52 Septiembre de 1999 EDICION: 1ª I B E R D R O L A Plegdo de plnos Indice
N I 00.02.52 Septiembre de 1999 EDICION: 1ª NORMA IBERDROLA Plegdo de plnos DESCRIPTORES: Plegdo de plnos. N O R M A N I 00.02.52 Septiembre de 1999 EDICION: 1ª I B E R D R O L A Plegdo de plnos Indice
PROBLEMAS RESUELTOS SUMA DE VECTORES METODO GEOMÉTRICO
 PROBLEMAS RESUELTOS SUMA DE VECTORES METODO GEOMÉTRICO 1. Los vectores mostrdos en l figur tienen l mism mgnitud (10 uniddes) El vector (+c) + (d+) - c, es de mgnitud: c ) 0 ) 0 c) 10 d) 0 e) 10 d Este
PROBLEMAS RESUELTOS SUMA DE VECTORES METODO GEOMÉTRICO 1. Los vectores mostrdos en l figur tienen l mism mgnitud (10 uniddes) El vector (+c) + (d+) - c, es de mgnitud: c ) 0 ) 0 c) 10 d) 0 e) 10 d Este
TRABAJO VACACIONES NAVIDAD 2014
 TRABAJO VACACIONES NAVIDAD 014 NOMBRE:... CURSO:. 1. Con 39 litros de gsolin el mrcdor de un coche señl 3/4 de depósito. Cuál es l cpcidd totl del depósito del coche?. Según un encuest reciente, de cd
TRABAJO VACACIONES NAVIDAD 014 NOMBRE:... CURSO:. 1. Con 39 litros de gsolin el mrcdor de un coche señl 3/4 de depósito. Cuál es l cpcidd totl del depósito del coche?. Según un encuest reciente, de cd
Determinantes y la Regla de Cramer
 Determinntes y l Regl de Crmer Mtriz Invers Not: un mtriz cudrd que no tiene invers se llm mtriz singulr. Ejemplo: Hllr l invers de A. A 4 Si l plicr el método de Guss se obtiene ceros en los elementos
Determinntes y l Regl de Crmer Mtriz Invers Not: un mtriz cudrd que no tiene invers se llm mtriz singulr. Ejemplo: Hllr l invers de A. A 4 Si l plicr el método de Guss se obtiene ceros en los elementos
TEMA 1 EL NÚMERO REAL
 Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Clase 1 El problema de la duplicación del cubo
 Clse 1 El problem de l duplicción del cubo 7 de febrero de 2012 El origen del problem de l duplicción del cubo tiene un origen mítico que se remont l siglo V.C en Atens con l muerte de su goberndor Pericles,
Clse 1 El problem de l duplicción del cubo 7 de febrero de 2012 El origen del problem de l duplicción del cubo tiene un origen mítico que se remont l siglo V.C en Atens con l muerte de su goberndor Pericles,
Respuesta: Con este resultado Anahí decide contratar a estos pintores.
 Universidd de Concepción Fcultd de Ciencis Veterinris Nivelción de Mtemátics(0) Unidd-I: Conjunto de los Números Rcionles Introducción: Al plnter l necesidd de dividir números enteros, surge un problem:
Universidd de Concepción Fcultd de Ciencis Veterinris Nivelción de Mtemátics(0) Unidd-I: Conjunto de los Números Rcionles Introducción: Al plnter l necesidd de dividir números enteros, surge un problem:
UNGS - Elementos de Matemática Práctica 7 Matriz insumo producto
 UNGS - Elementos de Mtemátic Práctic 7 Mtriz insumo producto El economist W. Leontief es el utor del modelo o l tbl de insumo producto. Est tbl refle l interrelción entre distintos sectores de l economí
UNGS - Elementos de Mtemátic Práctic 7 Mtriz insumo producto El economist W. Leontief es el utor del modelo o l tbl de insumo producto. Est tbl refle l interrelción entre distintos sectores de l economí
Tema 4. Integración de Funciones de Variable Compleja
 Tem 4. Integrción de Funciones de Vrible omplej Prof. Willim L ruz Bstids 7 de octubre de 22 Tem 4 Integrción de Funciones de Vrible omplej 4. Integrl definid Se F (t) un función de vrible rel con vlores
Tem 4. Integrción de Funciones de Vrible omplej Prof. Willim L ruz Bstids 7 de octubre de 22 Tem 4 Integrción de Funciones de Vrible omplej 4. Integrl definid Se F (t) un función de vrible rel con vlores
LÍMITES DE FUNCIONES
 LÍMITES DE FUNCIONES Se dice que un función y f() tiene límite "L" cundo l tiende "" y lo representmos por: f() L cundo pr tod sucesión de números reles que se proime "" tnto como quermos, los vlores correspondientes
LÍMITES DE FUNCIONES Se dice que un función y f() tiene límite "L" cundo l tiende "" y lo representmos por: f() L cundo pr tod sucesión de números reles que se proime "" tnto como quermos, los vlores correspondientes
Números Naturales. Los números enteros
 Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
Presentación Axiomática de los Números Reales
 Héctor Plm Vlenzuel. Dpto. de Mtemátic UdeC. 1 Prte I Presentción Axiomátic de los Números Reles 1. Axioms de los Números Reles 1.1. Axioms de Cuerpo Aceptremos l existenci de un conjunto R cuyos elementos
Héctor Plm Vlenzuel. Dpto. de Mtemátic UdeC. 1 Prte I Presentción Axiomátic de los Números Reles 1. Axioms de los Números Reles 1.1. Axioms de Cuerpo Aceptremos l existenci de un conjunto R cuyos elementos
Razones trigonométricas
 LECCIÓ CODESADA 12.1 Rzones trigonométrics En est lección Conocerás ls rzones trigonométrics seno, coseno y tngente Usrás ls rzones trigonométrics pr encontrr ls longitudes lterles desconocids en triángulos
LECCIÓ CODESADA 12.1 Rzones trigonométrics En est lección Conocerás ls rzones trigonométrics seno, coseno y tngente Usrás ls rzones trigonométrics pr encontrr ls longitudes lterles desconocids en triángulos
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I. ACTIVIDADES PARA EL VERANO.
 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I ACTIVIDADES PARA EL VERANO MATEMÁTICAS º BHCS IES EL BOHÍO EJERCICIOS Y PROBLEMAS DE APOYO ª EVALUACIÓN - Eectúe Sol -9/ - Eectúe 9 7 8 6 Sol - Eectúe 8
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I ACTIVIDADES PARA EL VERANO MATEMÁTICAS º BHCS IES EL BOHÍO EJERCICIOS Y PROBLEMAS DE APOYO ª EVALUACIÓN - Eectúe Sol -9/ - Eectúe 9 7 8 6 Sol - Eectúe 8
 1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
NÚMEROS RACIONALES. Los números racionales son todos aquellos números de la forma b
 NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números enteros y b distinto de cero. El conjunto de los números rcionles se represent por l letr Q. IGUALDAD ENTRE
NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números enteros y b distinto de cero. El conjunto de los números rcionles se represent por l letr Q. IGUALDAD ENTRE
Sistemas de ecuaciones lineales
 Sistems de ecuciones lineles º) L sum de ls tres cifrs de un número es 8, siendo l cifr de ls decens igul l medi de ls otrs dos. Si se cmbi l cifr de ls uniddes por l de ls centens, el número ument en
Sistems de ecuciones lineles º) L sum de ls tres cifrs de un número es 8, siendo l cifr de ls decens igul l medi de ls otrs dos. Si se cmbi l cifr de ls uniddes por l de ls centens, el número ument en
Resolver inecuaciones como las siguientes. Expresar la solución en forma gráfica y algebraica. Comparar las soluciones de los ejercicios e), f) y g).
 64 Tercer Año Medio Mtemátic Ministerio de Educción Actividd 3 Resuelven inecuciones y sistems de inecuciones con un incógnit; expresn ls soluciones en form gráfic y en notción de desigulddes; nlizn ls
64 Tercer Año Medio Mtemátic Ministerio de Educción Actividd 3 Resuelven inecuciones y sistems de inecuciones con un incógnit; expresn ls soluciones en form gráfic y en notción de desigulddes; nlizn ls
EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 1º E.S.O. PENDIENTES 2º PARCIAL
 Mtemátics pendientes de 1º (º prcil) 1 EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 1º E.S.O. PENDIENTES º PARCIAL Fech tope pr entregrlos: 17 de bril de 015 Exmen el 3 de bril de 015
Mtemátics pendientes de 1º (º prcil) 1 EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 1º E.S.O. PENDIENTES º PARCIAL Fech tope pr entregrlos: 17 de bril de 015 Exmen el 3 de bril de 015
Los Números Racionales
 Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
Curvas en el plano y en el espacio
 Cpítulo 1 Curvs en el plno y en el espcio 1.1. Curvs prmetrizds Definición 1.1.1 (Curv prmetrizd). Un curv prmetrizd diferencible α : I R n, es un plicción de clse C, donde I R es un intervlo bierto, que
Cpítulo 1 Curvs en el plno y en el espcio 1.1. Curvs prmetrizds Definición 1.1.1 (Curv prmetrizd). Un curv prmetrizd diferencible α : I R n, es un plicción de clse C, donde I R es un intervlo bierto, que
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 6 Curso preprtorio de l prueb de cceso l universidd pr myores de 5 ños curso 1/11 Nuri Torrdo Robles Deprtmento de Estdístic Universidd Crlos III de Mdrid
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 6 Curso preprtorio de l prueb de cceso l universidd pr myores de 5 ños curso 1/11 Nuri Torrdo Robles Deprtmento de Estdístic Universidd Crlos III de Mdrid
CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES
 FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
Estudio de funciones exponenciales y logarítmicas
 FUNCIÓN EXPONENCIAL Recomendciones l Docente: L ctividd proponer debe puntr que los lumnos puedn nlizr los siguientes spectos: 1. Cómo vrí el gráfico de l función eponencil y de qué depende su monotoní.
FUNCIÓN EXPONENCIAL Recomendciones l Docente: L ctividd proponer debe puntr que los lumnos puedn nlizr los siguientes spectos: 1. Cómo vrí el gráfico de l función eponencil y de qué depende su monotoní.
SOLUCIONARIO 1. PERÍMETROS Y ÁREAS DE LOS POLÍGONOS (I) 4. Calcula el área de un triángulo rectángulo en el que los catetos miden 22 m y 16 m
 11 elige Mtemátics, curso y tem. 13. Perímetros y áres 4. Clcul el áre de un triángulo rectángulo en el que los ctetos miden m y 16 m 1. PERÍMETROS Y ÁREAS DE LOS POLÍGONOS (I) PIENSA Y CALCULA Hll mentlmente
11 elige Mtemátics, curso y tem. 13. Perímetros y áres 4. Clcul el áre de un triángulo rectángulo en el que los ctetos miden m y 16 m 1. PERÍMETROS Y ÁREAS DE LOS POLÍGONOS (I) PIENSA Y CALCULA Hll mentlmente
P I E N S A Y C A L C U L A
 Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
CÁLCULO DIFERENCIAL E INTEGRAL EJERCICIOS PRIMERA FASE
 CÁLCULO DIFERENCIAL E INTEGRAL EJERCICIOS PRIMERA FASE CONCEPTOS CLAVE: FUNCIONES, GRAFICA DE UNA FUNCIÒN, COMPOSICIÒN DE FUNCIONES, INVERSA DE UNA FUNCIÒN, LIMITE DE UNA FUNCIÒN, LIMITES LATERALES, TEOREMAS
CÁLCULO DIFERENCIAL E INTEGRAL EJERCICIOS PRIMERA FASE CONCEPTOS CLAVE: FUNCIONES, GRAFICA DE UNA FUNCIÒN, COMPOSICIÒN DE FUNCIONES, INVERSA DE UNA FUNCIÒN, LIMITE DE UNA FUNCIÒN, LIMITES LATERALES, TEOREMAS
CURSO DE MATEMÁTICA 1. Facultad de Ciencias
 CURSO DE MATEMÁTICA 1. Fcultd de Ciencis Reprtido Teórico 1 Mrzo de 2008 1. Conceptos Básicos de Funciones Definiciones 1. Si A y B son conjuntos no vcíos, un función de A en B es un correspondenci tl
CURSO DE MATEMÁTICA 1. Fcultd de Ciencis Reprtido Teórico 1 Mrzo de 2008 1. Conceptos Básicos de Funciones Definiciones 1. Si A y B son conjuntos no vcíos, un función de A en B es un correspondenci tl
3. FUNCIONES VECTORIALES DE UNA VARIABLE REAL
 3. FUNCIONES VECTORIALES DE UNA VARIABLE REAL INDICE 3.1. Definición de función vectoril de un vrile rel, dominio y grficción.2 3.2. Límites y continuidd..3 3.3. Derivción de funciones vectoriles y sus
3. FUNCIONES VECTORIALES DE UNA VARIABLE REAL INDICE 3.1. Definición de función vectoril de un vrile rel, dominio y grficción.2 3.2. Límites y continuidd..3 3.3. Derivción de funciones vectoriles y sus
FUNCIONES ELEMENTALES
 FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() = m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() = m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
FUNCIONES TRASCENDENTALES (O NO ALGEBRAICAS ) 1-FUNCION LOGARITMO NATURAL
 FUNCIONES TRASCENDENTALES (O NO ALGEBRAICAS ) -FUNCION LOGARITMO NATURAL Definición propieddes L funcion logritmo nturl de un numero positivo se not ln su dominio es el conjunto de los números reles positivos
FUNCIONES TRASCENDENTALES (O NO ALGEBRAICAS ) -FUNCION LOGARITMO NATURAL Definición propieddes L funcion logritmo nturl de un numero positivo se not ln su dominio es el conjunto de los números reles positivos
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 NUMEROS IRRACIONALES Conocemos hst hor distintos conjuntos numéricos: - Los n nturles: (, 8,.978), representdos por l letr N - Los n enteros: ( -, -, 8, 68), representdos por l letr Z - Los n rcionles
NUMEROS IRRACIONALES Conocemos hst hor distintos conjuntos numéricos: - Los n nturles: (, 8,.978), representdos por l letr N - Los n enteros: ( -, -, 8, 68), representdos por l letr Z - Los n rcionles
Aplicaciones de la derivada (II)
 UNIVERSIDAD DEL CAUCA Fcultd de Ciencis Nturles, Ects de l Educción Deprtmento de Mtemátics CÁLCULO I Ejercicios Rects tngentes Aplicciones de l derivd (II) 1. Se l curv gráfic de l ecución ( ) =. Encuentre
UNIVERSIDAD DEL CAUCA Fcultd de Ciencis Nturles, Ects de l Educción Deprtmento de Mtemátics CÁLCULO I Ejercicios Rects tngentes Aplicciones de l derivd (II) 1. Se l curv gráfic de l ecución ( ) =. Encuentre
( )( ) 0 1,1 1, 5 2 2, 3. 1 Resuelve las siguientes inecuaciones: a) 2x + 4 > x +6 b) - x + 1 < 2x + 4 c) x + 51 > 15x + 9
 1 Resuelve ls siguientes inecuciones: x + 4 > x +6 - x + 1 < x + 4 c) x + 51 > 15x + 9 x < x > -1 c) x < 4 Resuelve ls siguientes inecuciones: x + 4 > x +6 - x + 1 > x + 4 c) 5x + 10 < 1x - 4 x > x < -
1 Resuelve ls siguientes inecuciones: x + 4 > x +6 - x + 1 < x + 4 c) x + 51 > 15x + 9 x < x > -1 c) x < 4 Resuelve ls siguientes inecuciones: x + 4 > x +6 - x + 1 > x + 4 c) 5x + 10 < 1x - 4 x > x < -
Práctico 9 - Cálculo de integrales. 1. Teorema fundamental y regla de Barrow
 Universidd de l Repúblic Cálculo Fcultd de Ingenierí - IMERL Segundo semestre 6 Práctico 9 - Cálculo de integrles. Teorem fundmentl y regl de Brrow. Utilizndo los resultdos del ejercicio 9 del práctico
Universidd de l Repúblic Cálculo Fcultd de Ingenierí - IMERL Segundo semestre 6 Práctico 9 - Cálculo de integrles. Teorem fundmentl y regl de Brrow. Utilizndo los resultdos del ejercicio 9 del práctico
