MAT 1620 Cálculo II Examen
|
|
|
- Dolores Ríos Sáez
- hace 5 años
- Vistas:
Transcripción
1 Pontificia Universidad Católica de Chile Facultad de Matemáticas Departamento de Matemática Primer Semestre de MAT 6 Cálculo II Examen. Determinar el área de la superficie generada al hacer girar la curva y x, x, alrededor del eje x. Solución. Tenemos que + ) dy dx + ) x + x+ x x entonces el área de la superficie generada al hacer girar la curva y x alrededor del eje x es ) dy S πy + dx π x+ x dx dx x π Puntaje: Total 6, puntos x+dx π 3 x+)3/ 8π ).,5 puntos por conocer la fórmula para determinar el área de la superficie.,5 puntos por calcular la derivada de y.,5 puntos por calcular la expresión y +dy/dx).,5 puntos por calcular la integral.. Considere la serie de potencias S n ) n+xn a) Demuestre quesi unaserie depotencias a n x n tiene radiode convergencia R entonces a n x n tiene radio de convergencia R. b) Calcule el radio de convergencia de S puede usar la parte a) aunque no la haya demostrado). Determine el intervalo de convergencia de la serie indicando con claridad que pasa en los extremos del intervalo. n. c) Determinar la función f asociada a la serie. Se sugiere derivar la serie, calcular su valor e integrar)
2 Solución. a) Si fx) a n x n tiene radio de convergencia R entonces fx) converge para todo x < R y diverge para todo x > R. Como fx ) a n x n entonces fx ) converge para todo x < R y diverge para x > R. Se sigue que el radio de convegencia de fx ) a n x n es R. Puntaje: a) Total, puntos b) El radio de convergencia de la serie n ) n+xn n es R lím n a n a n+ lím n Entonces, por lo mostrado en a), el radio de convergencia de la serie S es R. Note que en x y en x la serie es ) n+ n. n Por el criterio de la serie alternante, la serie es convergente. Por lo tanto, el intervalo de convergencia es I [,]. n+ n. Puntaje: b) Total, puntos punto por determinar el radio de convergencia. punto por determinar el intervalo de convergencia. c) Si fx) ) n+xn entonces su derivada es n n f x) ) n+ x n n ) n+ x n+ x x ) n x +x. Integrando con respecto a x esta última expresión x fx) +x dx ln+x )+C. n Para determinar la constante C, observe que si evaluamos la serie en x obtenemos el valor de f) y usando la expresión de arriba se tiene que f) ln) +C C. Entonces la función f asociada a la serie es fx) ln+x ). n Puntaje: c) Total, puntos punto por derivar la serie y calcular el valor de la serie.,5 puntos por integrar.,5 puntos por determinar la constante de integración.
3 3. Considere la curva que es la intersección de las superficies a) Encuentre una parametrización rt). x y +z y 3y z. b) Suponga que una partícula sigue la trayectoria definida por rt) y que en el tiempo t sale de la trayectoria por la tangente, avanzado con rapidez constante a la misma rapidez a la que avanzaba por la trayectoria rt) en t ). Dónde estará la partícula en el tiempo t? Solución. a) Tomando y t de la segunda ecuación obtenemos que z 3 y + 3 t +. Usando la ecuación de la primera superficie vemos que x + y z + t 3 t + ) t 3 8 t. Por lo tanto, una parametrización de la superficie es 7 rt) 8 + t 3 8 t,t, 3 t + ). Puntaje: a) Total 3, puntos punto por elegir una función para alguna de las variables. punto por despejar cada variable en función de la elección hecha. b) A partir de t la partícula sigue la trayectoria γt) r)+tr ) y observe que su rapidez es γ t) r ). Entonces, la partícula estará en el tiempo t en γ) r)+r ),,) +,, 3 ) Puntaje: b) Total 3, puntos 3,, 5 ).,5 puntos por determinar la trayectoria dela partícula apartir det con rapidez r ).,5 puntos por determinar el lugar en donde la particula estará en t. El lugar endondeestá lapartículaen t varíadependiendodela parametrización elegida en a)). Considere la curva r : [,π] R 3 definida por ) rt) 5 cost), sent), 3 5 cost). 3
4 a) Calcule la curvatura κt) y la torsión τt) de la curva r. b) Determine los vectores tangente t, normal n y binormal b de la curva r. Solución. a) Tenemos que r t) r t) r t) 5 sent), cost), 35 sent) ) 5 cost),sent), 35 cost) ) ) 5 sent),cost), 3 5 sent) entonces r t) para todo t [,π], es decir, la curva está arcoparametrizada. Ahora bien, r t) r t) 3 5 5),, y r t) r t)) r t). Se sigue que la curvatura y torsión de la curva son κt) r t) r t) r t) 3 τt) r t) r t)) r t) r t) r t) , 5 sent)+ 5 sent). Puntaje: a) Total 3, puntos,5 puntos por calcular correctamente la curvatura.,5 puntos por calcular correctamente la torsión. b) Como la curva rt) está arcoparametrizada obtenemos que t r t) 5 sent), cost), 35 ) sent). Sabemos que κt) para todo t [,π], se sigue en virtud de las ecuaciones de Frenet-Serret que d t κt) n n, entonces dt n r t) 5 cost),sent), 35 ) cost). Luego, el vector binormal es b t n r t) r t) 3 ) 5,,. 5 Puntaje: b) Total 3, puntos punto por calcular correctamente cada vector del triedro de Frenet.
5 Cálculo II MAT 6) Pontificia Universidad Católica de Chile Pauta del examen 6..3 Problema. Calcular el area de la superficie de revolución obtenida al girar la cicloide alrededor del eje x. xt) a t sent) ), yt) a cost) ), a >, t [, π], Solución. Sabemos por el curso que el area A pedido vale π dx ) ) dy A πyt) + dt dt dt π ) ) πa cost) cost) + sent) dt π ) 3/ πa cost) cost) dt π 3/ πa sent/) sent/) dt π 6πa senθ) 3 dθ θ t/ dθ dt/). cost) sent/) ) Ahora, la integral de senθ) 3 vale senθ) 3 dθ ) cosθ) senθ) senθ)dθ cosθ) senθ) ) dθ d cosθ) + cosθ) 3 /3 ) dθ dθ cosθ) + cosθ) 3 /3 + Const. Entonces, A 6πa cost) + cost) 3 /3 ) π 6πa /3 + /3 ) 6πa 3. Problema. a) Sea la curva en R 3 dada por las ecuaciones { x y + z 3y z. Determinar la ecuación del plano normal a la curva en el punto,, ).
6 Solución a). Pongamos primero la curva en forma paramétrica. { x y + z 3y z { z x + y z + 3y x + y + 3y x 7 8 3y Notando y t, obtenemos entonces la curva paramétrica 7 Ct) 8 3t 8 + t, t, ) + 3t, t R. Su vector tangente está dado por C t) 3t + ) 3t,,, t R. 8 + y. La curva pasa por el punto,, ) cuando t, y C ),, ) 3. Entonces, la ecuación del plano normal a la curva en el punto,, ) es ) x, y, z),, ),, 3 ) x, y, z ),, 6) x + y + 6z 9. b) Sea la curva en cordenadas polares rθ), θ [, ). + θ Determinar si la longitud total de la curva es finita o infinita. Si es finita, calcular su valor. Solución b). Como r θ) L +θ), la longitud total de la curva es rθ) + r θ) dθ + θ) + + θ) dθ t + dt t + θ dt dθ) } {{ t } lnt). t dt Pues, L, lo que significa que la longitud total de la curva es infinita. /t Problema 3. a) Sea la función f :, ), ), x + x) /3.
7 Calcular los tres primeros términos de la serie de Maclaurin de f. Solución a). Sabemos por el curso que f x) + x) /3 Maclaurin si x <. Pues, es igual a su serie de f x) f ) + f )x + f ) x + R 3 x) para x <, ) donde R 3 x) f x) f ) + f )x + f ) x es el residuo de la serie de Maclaurin. Ahora, se tiene f ), f ) 3 + x) /3 x 3 y f ) 9 + x) 5/3 x 9. Entonces, f x) + x 3 x 9 + R 3x) para x <. b) Determinar una aproximación del valor 3 )/3 con un error menor o igual a.7. Solución b). El punto a) implica que ) /3 3 f /) + / 3 /) + R 3 /) R 3/) 36 + R 3/). Pues, el valor 36 es una aproximación de 3 )/3 con un error igual a R 3 /). Ahora, tenemos que estimar el valor de R 3 /). Por eso, notamos que f x) + x) 8/3 7 para x <, 7 y entonces que R 3 x) /7 3! x 3 < para x < por la desigualdad de Taylor. En particular, R 3 /) <.7 y entonces el valor 36 aproximación de 3 )/3 con un error menor que.7. es una
8 Problema. a) Mostrar que los puntos de la curva f : [ π, π] R 3, t a + cost) ), a sent), a sent/) ), a >, pertenecen a la intersección de la esfera de radio a centrada en,, ) y el cilindro vertical con radio a y centro a,, ) en el plano xy. Solución a). La ecuaciones del cilindro y de la esfera son x a) + y a cilindro) y x + y + z a esfera). Pues, los puntos de la curva pertenecen al cilindro porque xt) a ) + yt) a + cost)) a ) + a sent) ) a cost) + a sent) a, y los puntos de la curva pertenecen a la esfera porque x + y + z a + cost) )) + a sent) ) + a sent/) ) a + cost) + cost) ) + a sent) + a sent/) a + a cost) + a cost) ) sent/) cost) ) a. b) Calcular para cada t [ π, π] la curvatura kt) de la curva f. Solución b). La curva f tiene derivadas f t) a sent), a cost), a cost/) ) f t) a cost), a sent), a sent/)/ )
9 y velocidad f t) a sent), a cost), a cost/) ) a sent) + a cost) + a cost/) Además, se tiene y f t) f t) î ĵ ˆk a sent) a cost) a cost/) a cost) a sent) a sent/)/ a + cost/). îa cost)sent/)/ ĵa cost/) cost) + ˆka sent) + ˆka cost) ĵa sent)sent/)/ + îa cost/)sent) a cost/)sent) cost)sent/)/, cost/) cost) sent)sent/)/, ) f t) f t) a cost/)sent) cost)sent/)/ ) + cost/) cost) + sent)sent/)/ ) + a cost/) + sent/) / + a 5/ + 3 cost/) / sent/) cost/) ) a cost/). Pues, kt) f t) f t) f t) cost/) a + cost/) ) 3/. De manera alternativa, si uno utiliza la relación cost/) +cost) ) /, uno puede reescribir la última fórmula como cost) kt) a 3 + cost) ). 3/
10 Pontificia Universidad Católica de Chile Facultad de Matemáticas Departamento de Matemáticas TAV MAT6 Cálculo Interrogación N Preguntas a la 8. Para obtener todo el puntaje debe tener un desarrollo impecable. Si comete un error de arrastre optará a lo mucho nota 5,. Preguntas 9 a la. Se evaluará la estrategia que se utiliza para solucionar el problema. Si la estrategia es la correcta y se plantea correctamente la parte algebraica entonces la nota comienza en 5,. Los errores de cálculo que no alteren el análisis del problema no bajarán mucho la nota en caso de no ser reiterativos.. Determine el punto de intersección de las curvas r t) t, t,3+t ) y r t) 3 t,t,t ) y el ángulo formado por sus tangentes en dicho punto. Solución. Para determinar la intersección es necesario resolver el sistema t 3 s t s ptos) 3+t s que tiene por solución t y s ptos). Luego el punto de intersección es,,). ptos) Los tangentes son r t),,t) y r s),,s) ptos) luego el producto punto de los tangentes, para t y s, es r ) r ),,),,) 6 Por lo tanto, el ángulo entre los tangentes está dada por 6,,),,) cosα) ptos) 6 6 3cosα) 3 cosα) Por lo tanto α arccos/ 3) ptos). Calcule la longitud de la curva rt) e t,e t cost),e t sint)) para t π. Solución. Si ṙt) e t,cost) sint),sint)+cost)) ptos) entonces ṙt) 3e t ptos) Por lo tanto L π 3 ṙt) dt π e t dt 3e π ) ptos)
11 3. Reparametrice respecto a la longitud de arco la curva rt) +t,3+t, 5t) medida desde el punto en que t en la dirección que t incrementa. Solución. Si ṙt),, 5) ptos) entonces st) t ṙu) du 3t ptos) Luego t s/ 3 ptos) y la reparametrización es ṙs) + s,3+ s, 5 s ) ptos). Determine el punto de la curva x t 3,y 3t,z t en que su plano normal es paralelo al plano de ecuación 6x+6y 8z. Solución. La normal al plano normal es 3t,3,t 3 ) ptos) el cual debe ser paralelo al vector 6,6, 8), lo que ocurre si t ptos). Por lo tanto, el plano normal tiene ecuación x,y,z),3,)) 3,3, ) ptos) 5. Calcule la curvatura y la torsión para la curva dada por x sinht),y cosht),z t en el punto,,). Solución. El punto,,) se obtiene para t ptos). Si rt) sinht),cosht),t) entonces ṙt) cosht), sinht), ) ṙ),, ) rt) sinht), cosht), ) r),, ) ptos) ptos) Luego, y κ ṙ) r) ṙ) 3,,),,),,) 3 τ ṙ) r)) r) ṙ) r),,),,)),,),,),,) 6. Determine los vectores T,N y B para la curva rt) Solución. El punto se obtiene para t ptos). Además Por lo tanto ptos) ptos) t, ) 3 t3,t en el punto, 3 ),. ṙt) t,t,) ṙ),,) ptos) rt),t,) r),,) ptos) T 3,,) ptos) B ṙ) r) ṙ) r) 3,,) ptos) N T B 9,,) ptos)
12 7. Determine la ecuación de una parábola que tenga curvatura igual a en el origen. Solución. Si rt) t,at +bt,) ptos) entonces κ ṙ) r) ṙ) 3,b,),a,),b,) 3,,a),b,) 3 a +b ) 3/ ptos) ptos) Si a y b ptos) se tiene la curvatura pedida. 8. Pruebe que si la torsión de una curva es cero, entonces la curva está contenida en un plano. Solución. Si la torsion es cero entonces Bt) b constante ptos) De este modo, ṙt) b ptos) para todo t. Por tanto rt) r ) b ptos) Por lo tanto la curva está sobre un plano. ptos) 9. Si r representa una curva suave, pruebe que d ds T d ds T κ κ +τ siendo κ, τ la curvatura y torsión de la curva, respectivamente. Solución. A partir de la fórmulas de Frenet-Serret se tiene entonces Por lo tanto d ds T κn ptos) d ds T κ N+κ κt+τb) d d T ds ds T κ3 T κ τb d d T ds ds T κ κ +τ ptos) ptos) ptos). Calcule la curvatura de la cicloide xt) t sint),yt) cost), con t [,π). Determine el punto en que la curvatura de esta curva es mínima. Solución. Si rt) t sint), cost),) entonces κt) 3/ cost) ptos) Luego el mínimo de la curvatura se obtiene en t π que maximiza la función gt) cost), vale decir t 3π/ 3 ptos). Por lo tanto κ3π/) 5/ ptos)
13 . Demostrar que la curva con parametrización rt) sin t),sint)cost),cost)) t < π está contenida en una esfera y que todos los planos normales a dicha curva contienen al origen. Solución. Comenzaremos que está contenida en una esfera sin t) ) +sint)cost)) +cost)) sin t)sin t)+cos t))+cos t) ptos) Por otra parte, el tangente de nuestra curva es que satisface ṙt) sint),cost), sint)) rt) ṙt) sin t),sint)cost),cost)) sint),cost), sint)) 3ptos) Por lo tanto el tangente es perpendicular al radio de la esfera, concluyendo que el plano normal pasa por el origen. ptos). Cortamos la esfera x +y +z con el plano x+y+z. Determine la curvatura y la torsión de la curva de corte. Solución. Puesto que la curvatura depende de la norma del vector Ṫ entonces la curvatura resulta invariante bajo traslación y rotación. Es claro que la curva resultante es una círcunferencia cuyo radio a se determina por d +a ptos) siendo d la distancia del plano al origen, vale decir 3 +a a 3 ptos) Ahora consideremos la curva arcoparametrizada rs) a coss/a), a sins/a), ). Luego ṙs) sins/a), coss/a), ) rs) a coss/a), sins/a),) Por lo tanto κ /a. ptos) El vector binormal está en la dirección de ṙs) rs),,/a), para todo s. Por lo tanto Ḃ, concluyendo que τ. ptos) Tiempo: 8 minutos Sin consultas
SEMANA 12: CURVAS EN EL ESPACIO. ds v(t) = d r (t) =
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 8-2 Basado en el apunte del ramo Matemáticas Aplicadas, de Felipe Álvarez, Juan Diego Dávila, Roberto Cominetti
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 8-2 Basado en el apunte del ramo Matemáticas Aplicadas, de Felipe Álvarez, Juan Diego Dávila, Roberto Cominetti
CÁLCULO III (0253) PRIMER PARCIAL (33.33%) SECCIONES 02 Y 04 27/03/09. . π
 UCV FIUCV CÁLCULO III (05) PRIMER PARCIAL (%) SECCIONES 0 Y 04 7/0/09 Una curva C está definida por y = sen(x) x 0 y = x x 0 x + (y + ) = x 0 a Parametrice la curva C en sentido horario ( puntos) b Encuentre
UCV FIUCV CÁLCULO III (05) PRIMER PARCIAL (%) SECCIONES 0 Y 04 7/0/09 Una curva C está definida por y = sen(x) x 0 y = x x 0 x + (y + ) = x 0 a Parametrice la curva C en sentido horario ( puntos) b Encuentre
Problemas resueltos del Boletín 1
 Boletines de problemas de Matemáticas II Problemas resueltos del Boletín Problema. Dada la curva r (t) = t [0, π], parametrizarla naturalmente. ( (cos t + t sen t), (sen t t cos t), t ), con En primer
Boletines de problemas de Matemáticas II Problemas resueltos del Boletín Problema. Dada la curva r (t) = t [0, π], parametrizarla naturalmente. ( (cos t + t sen t), (sen t t cos t), t ), con En primer
Soluciones de los ejercicios del segundo examen parcial
 Matemáticas II (GIC, curso 5 6 Soluciones de los ejercicios del segundo examen parcial EJERCICIO. Halla el área que encierra la curva C dada en polares por r = + sen(θ. Solución: Primero debemos hallar
Matemáticas II (GIC, curso 5 6 Soluciones de los ejercicios del segundo examen parcial EJERCICIO. Halla el área que encierra la curva C dada en polares por r = + sen(θ. Solución: Primero debemos hallar
CAMPOS VECTORIALES. Presenta: M.E.M. Enrique Arenas Sánchez. 21 de septiembre de 2016
 Presenta: M.E.M. Enrique Arenas Sánchez 21 de septiembre de 2016 Definición de Campo Escalar. Se llama campo escalar a una función que asocia a cada punto del dominio de una función un valor escalar. Ejemplo:
Presenta: M.E.M. Enrique Arenas Sánchez 21 de septiembre de 2016 Definición de Campo Escalar. Se llama campo escalar a una función que asocia a cada punto del dominio de una función un valor escalar. Ejemplo:
Certamen 2 - Mate 024 (Pauta)
 Certamen - Mate 4 (Pauta) noviembre 6, 14 1. Calcular γ x 4 + y 4 1 dx + y 3 x 4 + y 4 1 dy en cada uno de los siguientes casos: a) γ es la curva x + y = 1 4 y se recorre en sentido positivo. b) γ es la
Certamen - Mate 4 (Pauta) noviembre 6, 14 1. Calcular γ x 4 + y 4 1 dx + y 3 x 4 + y 4 1 dy en cada uno de los siguientes casos: a) γ es la curva x + y = 1 4 y se recorre en sentido positivo. b) γ es la
Universidad de Puerto Rico. Recinto Universitario de Mayagüez Departamento de Ciencias Matemáticas Examen Final Mate de mayo de 2016
 Universidad de Puerto Rico. Recinto Universitario de Mayagüez Departamento de Ciencias Matemáticas Examen Final Mate 332 5 de mayo de 26 Nombre. Sección Número de Estudiante Profesor Número de puntos disponibles:
Universidad de Puerto Rico. Recinto Universitario de Mayagüez Departamento de Ciencias Matemáticas Examen Final Mate 332 5 de mayo de 26 Nombre. Sección Número de Estudiante Profesor Número de puntos disponibles:
1 Parametrización de curvas
 Dpto. Matemática Aplicada E.T.S. Arquitectura, U.P.M. Curvas y Super cies HOJA DE PROBLEMAS: CURVAS 1 Parametrización de curvas 1. Obtener una parametrización de cada una de las siguientes cónicas: (a
Dpto. Matemática Aplicada E.T.S. Arquitectura, U.P.M. Curvas y Super cies HOJA DE PROBLEMAS: CURVAS 1 Parametrización de curvas 1. Obtener una parametrización de cada una de las siguientes cónicas: (a
Soluciones de los ejercicios del del examen final de febrero
 Matemáticas II (GIC, curso 5 6) Soluciones de los ejercicios del del examen final de febrero EJERCICIO. Determina el ángulo polar de los puntos con tangente horizontal y los puntos con tangente vertical
Matemáticas II (GIC, curso 5 6) Soluciones de los ejercicios del del examen final de febrero EJERCICIO. Determina el ángulo polar de los puntos con tangente horizontal y los puntos con tangente vertical
MATEMÁTICAS II Geometría diferencial Curso de las curvas en el espacio
 1.- a) Se denomina cicloide a la curva descrita por un punto P de una circunferencia que rueda, sin deslizar, a lo largo de una recta. Si P está inicialmente en el origen O(,) y a es el radio de la circunferencia,
1.- a) Se denomina cicloide a la curva descrita por un punto P de una circunferencia que rueda, sin deslizar, a lo largo de una recta. Si P está inicialmente en el origen O(,) y a es el radio de la circunferencia,
VELOCIDAD Y ACELERACION. RECTA TANGENTE.
 VELOCIDAD Y ACELERACION. RECTA TANGENTE. 3. Describir la trayectoria y determinar la velocidad y aceleración del movimiento descrito por las curvas siguientes: (a) r (t) = i 4t 2 j + 3t 2 k. (b) r (t)
VELOCIDAD Y ACELERACION. RECTA TANGENTE. 3. Describir la trayectoria y determinar la velocidad y aceleración del movimiento descrito por las curvas siguientes: (a) r (t) = i 4t 2 j + 3t 2 k. (b) r (t)
Análisis Matemático I (Ing. de Telecomunicación), Examen final, 26 de enero de 2010 RESPUESTAS A AMBOS MODELOS
 Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-07-4-M--00-07 CURSO: SEMESTRE: Primero CÓDIGO DEL CURSO: 07 TIPO DE EXAMEN: Eamen Final FECHA DE EXAMEN: 8
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-07-4-M--00-07 CURSO: SEMESTRE: Primero CÓDIGO DEL CURSO: 07 TIPO DE EXAMEN: Eamen Final FECHA DE EXAMEN: 8
Nombre/Código: Septiembre Parcial II
 1 Cálculo II Sección 1 Guillermo Mantilla Nombre/Código: Septiembre 11 1 Parcial II Instrucciones: Duración 7mins. Durante el examen no son permitidos libros, notas, calculadoras, celulares o en general
1 Cálculo II Sección 1 Guillermo Mantilla Nombre/Código: Septiembre 11 1 Parcial II Instrucciones: Duración 7mins. Durante el examen no son permitidos libros, notas, calculadoras, celulares o en general
y = 2x + 8x 7, y = x 4. y = 4 x, y = x + 2, x = 2, x = 3. x = 16 y, x = 6 y. y = a x, y = x, x y = a. (1 x)dx. y = 9 x, y = 0.
 . Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
. Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
Análisis II Análisis matemático II Matemática 3.
 1 Análisis II Análisis matemático II Matemática 3. 1er. cuatrimestre de 2015 Práctica 1 - urvas, integral de longitud de arco e integrales curvilíneas. urvas Ejercicio 1 1. Probar que x 1 (t) = r cos(2πt),
1 Análisis II Análisis matemático II Matemática 3. 1er. cuatrimestre de 2015 Práctica 1 - urvas, integral de longitud de arco e integrales curvilíneas. urvas Ejercicio 1 1. Probar que x 1 (t) = r cos(2πt),
CURVAS Y SUPERFICIES Hoja 1: Curvas
 CURVAS Y SUPERFICIES Hoja 1: Curvas 1. Sea σ (t) = (cos t, sen t, t) con t [0, π] y sea f(x, y, z) = x + y + z. Evaluar la integral σ fdσ. (Sol.: π 3 (3 + 4π )).. Sea σ : [0, π/] R 3 la curva σ(t) = (30
CURVAS Y SUPERFICIES Hoja 1: Curvas 1. Sea σ (t) = (cos t, sen t, t) con t [0, π] y sea f(x, y, z) = x + y + z. Evaluar la integral σ fdσ. (Sol.: π 3 (3 + 4π )).. Sea σ : [0, π/] R 3 la curva σ(t) = (30
3 Curvas alabeadas. Solución de los ejercicios propuestos.
 3 Curvas alabeadas. Solución de los ejercicios propuestos.. Se considera el conjunto C = {(x, y, z R 3 : x y + z = x 3 y + z = }. Encontrar los puntos singulares de la curva C. Solución: Llamemos f (x,
3 Curvas alabeadas. Solución de los ejercicios propuestos.. Se considera el conjunto C = {(x, y, z R 3 : x y + z = x 3 y + z = }. Encontrar los puntos singulares de la curva C. Solución: Llamemos f (x,
Análisis II Análisis matemático II Matemática 3.
 1 Análisis II Análisis matemático II Matemática 3. 1er. cuatrimestre de 2008 Práctica 1 - urvas, integral de longitud de arco e integrales curvilíneas. urvas Definición 1. Una curva R 3 es un conjunto
1 Análisis II Análisis matemático II Matemática 3. 1er. cuatrimestre de 2008 Práctica 1 - urvas, integral de longitud de arco e integrales curvilíneas. urvas Definición 1. Una curva R 3 es un conjunto
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL. 1. (5 puntos) Bosquejar la región en el primer cuadrante que está
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS RÚBRICA DE LA SEGUNDA EVALUACIÓN DE CÁLCULO DE UNA VARIABLE. (5 puntos) Bosquejar la región
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS RÚBRICA DE LA SEGUNDA EVALUACIÓN DE CÁLCULO DE UNA VARIABLE. (5 puntos) Bosquejar la región
y = x x 0, 4 π 2 π π
 UCV FIUCV CÁLCULO III (053) PRIMER PARCIAL (3333%) SECCIONES 01 Y 03 7/03/09 1 Una curva C está definida por y cos(x) x, y x x 0, x + y y,0 16 a Parametrice la curva C en sentido antihorario ( puntos)
UCV FIUCV CÁLCULO III (053) PRIMER PARCIAL (3333%) SECCIONES 01 Y 03 7/03/09 1 Una curva C está definida por y cos(x) x, y x x 0, x + y y,0 16 a Parametrice la curva C en sentido antihorario ( puntos)
Funciones Vectoriales
 Funciones Vectoriales Hermes Pantoja Carhuavilca Facultad de Ingeniería Mecánica Universidad Nacional de Ingenieria Calculo Vectorial Hermes Pantoja Carhuavilca 1 de 27 CONTENIDO Longitud de Arco Reparametrización
Funciones Vectoriales Hermes Pantoja Carhuavilca Facultad de Ingeniería Mecánica Universidad Nacional de Ingenieria Calculo Vectorial Hermes Pantoja Carhuavilca 1 de 27 CONTENIDO Longitud de Arco Reparametrización
1. INTEGRALES DEFINIDAS E IMPROPIAS
 . INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráfica de y = con el eje OX son los valores de tales que =, esto es, = y =. El
. INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráfica de y = con el eje OX son los valores de tales que =, esto es, = y =. El
Tarea 1 - Vectorial
 Tarea - Vectorial 2050. Part :. - 3.2.. Un cerro se queda en las montañas en la altura de 6 mil metros. El cerro tiene la forma del gráfico de la función z = f(x, y) = x 2 y 2. Observamos que plaquitas
Tarea - Vectorial 2050. Part :. - 3.2.. Un cerro se queda en las montañas en la altura de 6 mil metros. El cerro tiene la forma del gráfico de la función z = f(x, y) = x 2 y 2. Observamos que plaquitas
Soluciones Matemáticas II Examen Final 2º Parcial 3-Julio-07. 1) La temperatura en un punto (x, y) de una lámina metálica es T(x, y) =.
 Soluciones Matemáticas II Examen Final º Parcial 3-Julio-07 3x 1) La temperatura en un punto (x, y) de una lámina metálica es T(x, y) =. x + y a) Hallar la curva de nivel (isoterma) que pasa por el punto
Soluciones Matemáticas II Examen Final º Parcial 3-Julio-07 3x 1) La temperatura en un punto (x, y) de una lámina metálica es T(x, y) =. x + y a) Hallar la curva de nivel (isoterma) que pasa por el punto
ANALISIS II 12/2/08 COLOQUIO TEMA 1
 ANALISIS II //08 COLOQUIO TEMA Sea f : R R un campo vectorial C y C la curva parametrizada por: γ(t) = (cost, 0, sent) con t ɛ [0, π] Sabiendo que C f ds = 6 y que rot( f( ) = (z, ), calcular la integral
ANALISIS II //08 COLOQUIO TEMA Sea f : R R un campo vectorial C y C la curva parametrizada por: γ(t) = (cost, 0, sent) con t ɛ [0, π] Sabiendo que C f ds = 6 y que rot( f( ) = (z, ), calcular la integral
a n en las que n=1 s n = n + 1 Solución: a) Utilizando el criterios de D Alembert se obtiene que a n+1 n a n 3 > 1 n=1
 EJERCICIO DE FUNDAMENTO MATEMÁTICO eries. Estudia el carácter de las series (a El término general es a n en las que (b la suma parcial n-sima es a n n n+ 3 n, n,, 3,... s n n, n,, 3,... n + olución: a
EJERCICIO DE FUNDAMENTO MATEMÁTICO eries. Estudia el carácter de las series (a El término general es a n en las que (b la suma parcial n-sima es a n n n+ 3 n, n,, 3,... s n n, n,, 3,... n + olución: a
TERCER EXAMEN EJERCICIOS RESUELTOS
 MATEMÁTICAS II G. I. T. I.) TERCER EXAMEN 4 EJERCICIOS RESUELTOS EJERCICIO. ) Dibuja la región limitada por la circunferencia de ecuación r = r θ) = senθ) y la lemniscata de ecuación r = r θ) = cosθ).
MATEMÁTICAS II G. I. T. I.) TERCER EXAMEN 4 EJERCICIOS RESUELTOS EJERCICIO. ) Dibuja la región limitada por la circunferencia de ecuación r = r θ) = senθ) y la lemniscata de ecuación r = r θ) = cosθ).
Guía de Estudio para la Sección de Matemáticas del Examen de Admisión
 1 Guía de Estudio para la Sección de Matemáticas del Examen de Admisión 215-1 El material relativo al temario puede ser consultado en la amplia bibliografía que allí se menciona o en alguno de los muchísimos
1 Guía de Estudio para la Sección de Matemáticas del Examen de Admisión 215-1 El material relativo al temario puede ser consultado en la amplia bibliografía que allí se menciona o en alguno de los muchísimos
ETSI de Topografía, Geodesia y Cartografía
 Grupo A Examen de Evaluación Continua de Geometría Diferencial Curso 2011-12 El examen consta de dos partes y tiene un valor de 2/3 de la nota de Geometría Diferencial que supone el 10% de la nota total
Grupo A Examen de Evaluación Continua de Geometría Diferencial Curso 2011-12 El examen consta de dos partes y tiene un valor de 2/3 de la nota de Geometría Diferencial que supone el 10% de la nota total
Curvatura. t Rdt = Rt s = Rt t = s R. y r (s) =
 Introducción a las Funciones Vectoriales Funciones de R R n ) Curvatura En una recta, el vector unitario tangente T no cambia su dirección y por tanto T =. Si la curva no es una linea recta, la derivada
Introducción a las Funciones Vectoriales Funciones de R R n ) Curvatura En una recta, el vector unitario tangente T no cambia su dirección y por tanto T =. Si la curva no es una linea recta, la derivada
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-0---M-00-0 CURSO: Matemática Intermedia SEMESTRE: Primero CÓDIGO DEL CURSO: 0 TIPO DE EXAMEN: Eamen Final
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-0---M-00-0 CURSO: Matemática Intermedia SEMESTRE: Primero CÓDIGO DEL CURSO: 0 TIPO DE EXAMEN: Eamen Final
(x 1) + y = 1 y 1, y = (x 2) y 0,1
 CÁLCULO III (053) SECCIÓN 05 6/03/09. Una curva C está definida por y tg(x) x 0, (x ) + y y, 0. y (x ) y 0, 8 a. Parametrice la curva C en sentido antihorario. ( puntos) b. En el punto (, ) determine las
CÁLCULO III (053) SECCIÓN 05 6/03/09. Una curva C está definida por y tg(x) x 0, (x ) + y y, 0. y (x ) y 0, 8 a. Parametrice la curva C en sentido antihorario. ( puntos) b. En el punto (, ) determine las
sea a lo largo de la curva solución de la ecuación diferencial xy, = 5x
 1. Hallar κ de manera que el flujo saliente del campo f ( x, = (x + y + z, 6y a través de la frontera del cuerpo x + y + z 16 x + y κ, 0 < k < 4 f : R R un campo vectorial definido por:. Sea γ ( t ) =
1. Hallar κ de manera que el flujo saliente del campo f ( x, = (x + y + z, 6y a través de la frontera del cuerpo x + y + z 16 x + y κ, 0 < k < 4 f : R R un campo vectorial definido por:. Sea γ ( t ) =
3 Curvas alabeadas (curvas en R 3 )
 3 Curvas alabeadas (curvas en R 3 ) El estudio de curvas en el espacio es, en varios aspectos, similar al de curvas en el plano. En este capítulo consideraremos como parametrización (I, α) a un par formado
3 Curvas alabeadas (curvas en R 3 ) El estudio de curvas en el espacio es, en varios aspectos, similar al de curvas en el plano. En este capítulo consideraremos como parametrización (I, α) a un par formado
GEOMETRÍA DIFERENCIAL DE CURVAS REGULARES: NOTACIÓN Y FORMULARIO
 GEOMETRÍA DIFERENCIAL DE CURVAS REGULARES: NOTACIÓN Y FORMULARIO F. Navarrina, L. Ramírez & GMNI GMNI GRUPO DE MÉTODOS NUMÉRICOS EN INGENIERÍA Departamento de Métodos Matemáticos y de Representación Escuela
GEOMETRÍA DIFERENCIAL DE CURVAS REGULARES: NOTACIÓN Y FORMULARIO F. Navarrina, L. Ramírez & GMNI GMNI GRUPO DE MÉTODOS NUMÉRICOS EN INGENIERÍA Departamento de Métodos Matemáticos y de Representación Escuela
OCW-Universidad de Málaga, (2014). Bajo licencia. Creative Commons Attribution- NonComercial-ShareAlike 3.
 OCW-Universidad de Málaga, http://ocw.uma.es 14. Bajo licencia Creative Commons Attribution- NonComercial-ShareAlike 3. Spain Matemáticas III Relación de ejercicios Tema 3 Ejercicios Ej. 1 Reparametriza
OCW-Universidad de Málaga, http://ocw.uma.es 14. Bajo licencia Creative Commons Attribution- NonComercial-ShareAlike 3. Spain Matemáticas III Relación de ejercicios Tema 3 Ejercicios Ej. 1 Reparametriza
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-107-4-M-2-12-2017 CURSO: SEMESTRE: Vacaciones de Diciembre CÓDIGO DEL CURSO: 107 TIPO DE EXAMEN: Examen Final
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-107-4-M-2-12-2017 CURSO: SEMESTRE: Vacaciones de Diciembre CÓDIGO DEL CURSO: 107 TIPO DE EXAMEN: Examen Final
Guía Semanas 13 y RESUMEN. Universidad de Chile. Ingeniería Matemática. Triedro de vectores y factores escalares. Supongamos que r.
 1. RESUMEN Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08-1 Ingeniería Matemática Guía Semanas 13 y 14 Triedro de vectores y factores
1. RESUMEN Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08-1 Ingeniería Matemática Guía Semanas 13 y 14 Triedro de vectores y factores
MATE1207 Primer parcial - Tema B MATE-1207
 MATE7 Primer parcial - Tema B MATE-7. Si su respuesta y justificación son correctas obtendrá el máximo puntaje. Si su respuesta es incorrecta podrá obtener créditos parciales de acuerdo a su justificación.
MATE7 Primer parcial - Tema B MATE-7. Si su respuesta y justificación son correctas obtendrá el máximo puntaje. Si su respuesta es incorrecta podrá obtener créditos parciales de acuerdo a su justificación.
Tema 3: Cinemática del punto
 Tema 3: Cinemática del punto FISICA I, 1º Grado en Ingeniería Civil Escuela Técnica Superior de Ingeniería Universidad de Sevilla 1 Índice Introducción Ecuaciones de una curva Velocidad y aceleración Movimientos
Tema 3: Cinemática del punto FISICA I, 1º Grado en Ingeniería Civil Escuela Técnica Superior de Ingeniería Universidad de Sevilla 1 Índice Introducción Ecuaciones de una curva Velocidad y aceleración Movimientos
CURVAS Y SUPERFICIES, S.L. Rueda CURVAS. 1.2 Longitud de una curva. Parámetro arco.
 CURVAS. 1.2 Longitud de una curva. Parámetro arco. 1.1 Definición de curva parametrizada espacial. Representación implícita. 1.2 Longitud de una curva. Parámetro arco. 1.3 Curvatura y torsión. Triedro
CURVAS. 1.2 Longitud de una curva. Parámetro arco. 1.1 Definición de curva parametrizada espacial. Representación implícita. 1.2 Longitud de una curva. Parámetro arco. 1.3 Curvatura y torsión. Triedro
Ejercicios Resueltos de Cálculo III.
 Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
1 Estudio local de curvas
 E.T.S. Arquitectura. Curvas y Super cies.1 1 Estudio local de curvas Sea una curva C R 3 con representación paramétrica regular ~r(t), t 2 I R, de clase mayor o igual a 3 y sea s = s(t) = Z t t 0 k~r 0
E.T.S. Arquitectura. Curvas y Super cies.1 1 Estudio local de curvas Sea una curva C R 3 con representación paramétrica regular ~r(t), t 2 I R, de clase mayor o igual a 3 y sea s = s(t) = Z t t 0 k~r 0
Santiago, julio 6 del Tercera Solemne Cálculo Varias Variables. Nombre:
 Nombre: Santiago, julio 6 del 26. Tercera Solemne Cálculo Varias Variables. 1. La temperatura en un punto (x, y) sobre una placa metalica es T (x, y) 4x 2 4xy + y 2. Una hormiga camina sobre la placa alrededor
Nombre: Santiago, julio 6 del 26. Tercera Solemne Cálculo Varias Variables. 1. La temperatura en un punto (x, y) sobre una placa metalica es T (x, y) 4x 2 4xy + y 2. Una hormiga camina sobre la placa alrededor
Tema 4: Movimiento en 2D y 3D
 Tema 4: Movimiento en 2D y 3D FISICA I, 1º Grado en Ingeniería Electrónica, Robótica y Mecatrónica Departamento de Física Aplicada III Escuela Técnica Superior de Ingeniería Universidad de Sevilla Índice
Tema 4: Movimiento en 2D y 3D FISICA I, 1º Grado en Ingeniería Electrónica, Robótica y Mecatrónica Departamento de Física Aplicada III Escuela Técnica Superior de Ingeniería Universidad de Sevilla Índice
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS.
 UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS. Cálculo III, Examen Final. Semestre Primavera 1 Tiempo: 11 min. Problema 1 [1,5 puntos] La curvatura de una trayectoria
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS. Cálculo III, Examen Final. Semestre Primavera 1 Tiempo: 11 min. Problema 1 [1,5 puntos] La curvatura de una trayectoria
PONTIFICIA UNIVERSIDAD CATÓLICA DEL PERÚ ESTUDIOS GENERALES CIENCIAS. Cálculo 3 Práctica N 3 Semestre Académico
 Práctica N 3 Semestre Académico 014-1 1. a. Parametrizar la curva : b. Dadas las curvas: x 1 y z y x ; z 0. pts C 1 : Ft e t, 1, lnt 1, t 0, y 1 t C : Gr r, 9 r, ln r, r 0,. Hallar la ecuación de la recta
Práctica N 3 Semestre Académico 014-1 1. a. Parametrizar la curva : b. Dadas las curvas: x 1 y z y x ; z 0. pts C 1 : Ft e t, 1, lnt 1, t 0, y 1 t C : Gr r, 9 r, ln r, r 0,. Hallar la ecuación de la recta
Tema 4: Movimiento en 2D y 3D
 Tema 4: Movimiento en 2D y 3D FISICA I, 1º Grado en Civil Escuela Técnica Superior de Ingeniería Universidad de Sevilla Física I, GIC, Dpto. Física Aplicada III, ETSI, Universidad de Sevilla, 2017/18 1
Tema 4: Movimiento en 2D y 3D FISICA I, 1º Grado en Civil Escuela Técnica Superior de Ingeniería Universidad de Sevilla Física I, GIC, Dpto. Física Aplicada III, ETSI, Universidad de Sevilla, 2017/18 1
DEF. Una curva parametrizada diferenciable es una función vectorial diferenciable:
 Curvas DEF. Una curva parametrizada diferenciable es una función vectorial diferenciable: α : I R R 3 t α(t) = (x(t), y(t), z(t)) donde I es un intervalo (puede no ser acotado). t es el parámetro de la
Curvas DEF. Una curva parametrizada diferenciable es una función vectorial diferenciable: α : I R R 3 t α(t) = (x(t), y(t), z(t)) donde I es un intervalo (puede no ser acotado). t es el parámetro de la
3. Cinemática de la partícula: Sistemas de referencia
 3. Cinemática de la partícula: Sistemas de referencia 3.1.- Cinemática de la partícula 3.2.- Coordenadas intrínsecas y polares 3.3.- Algunos casos particulares de especial interés 3.1.- Cinemática de la
3. Cinemática de la partícula: Sistemas de referencia 3.1.- Cinemática de la partícula 3.2.- Coordenadas intrínsecas y polares 3.3.- Algunos casos particulares de especial interés 3.1.- Cinemática de la
Análisis Matemático I
 Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
CURVAS Y SUPERFICIES. RELACIÓN 1
 CURVAS Y SUPERFICIES. RELACIÓN 1 CURVAS EN EL PLANO Y EN EL ESPACIO Curso 2015-16 1. En R 2 se considera la circunferencia C de centro (0,1) y radio 1. Sea R la recta afín tangente a C en (0,2). Para cada
CURVAS Y SUPERFICIES. RELACIÓN 1 CURVAS EN EL PLANO Y EN EL ESPACIO Curso 2015-16 1. En R 2 se considera la circunferencia C de centro (0,1) y radio 1. Sea R la recta afín tangente a C en (0,2). Para cada
Pauta Auxiliar N 10 Aplicaciones de la Integral I Viernes 1 de Junio de 2012
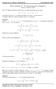 Pauta Auxiliar N Aplicaciones de la Integral I Viernes de Junio de P.- (P Examen Adicional - ) Sea A la región delimitada por las rectas y = x, y = ax, y = ax, a a) Calcule el área de A y el volumen del
Pauta Auxiliar N Aplicaciones de la Integral I Viernes de Junio de P.- (P Examen Adicional - ) Sea A la región delimitada por las rectas y = x, y = ax, y = ax, a a) Calcule el área de A y el volumen del
1.5. Integral de línea de un campo Vectorial.
 .5. Integral de línea de un campo Vectorial. Sea F ( xyz,, un campo vectorial continuo sobre R donde F representa un campo de fuerzas aplicado sobre una partícula cuya trayectoria puede ser descrita por
.5. Integral de línea de un campo Vectorial. Sea F ( xyz,, un campo vectorial continuo sobre R donde F representa un campo de fuerzas aplicado sobre una partícula cuya trayectoria puede ser descrita por
Capítulo 5. Integrales sobre curvas y superficies
 Capítulo 5. Integrales sobre curvas y superficies 5.1. Integrales de funciones escalares sobre curvas 5.2. Integrales de campos vectoriales sobre curvas 5.3. Teorema de Green 5.4. Integrales sobre superficies
Capítulo 5. Integrales sobre curvas y superficies 5.1. Integrales de funciones escalares sobre curvas 5.2. Integrales de campos vectoriales sobre curvas 5.3. Teorema de Green 5.4. Integrales sobre superficies
ETSII Febrero Análisis Matemático.
 Departamento de Análisis Matemático ETSII Febrero 2000. Análisis Matemático. Problema 1. (1 punto) Calcular los siguientes ites: e x e senx x 0 x senx x π/4 (tgx)tg2x Problema 2. (2 puntos) Considérese
Departamento de Análisis Matemático ETSII Febrero 2000. Análisis Matemático. Problema 1. (1 punto) Calcular los siguientes ites: e x e senx x 0 x senx x π/4 (tgx)tg2x Problema 2. (2 puntos) Considérese
Examen Final de Cálculo Vectorial MATE PREGUNTAS ABIERTAS TEMA A Diciembre 6 de Nombre: Código:
 UNIVERSIDAD DE LOS ANDES DEPARTAMENTO DE MATEMÁTICAS Examen Final de Cálculo Vectorial MATE 1207 PREGUNTAS ABIERTAS TEMA A Diciembre 6 de 2017 Este es un examen individual, no se permite el uso de libros,
UNIVERSIDAD DE LOS ANDES DEPARTAMENTO DE MATEMÁTICAS Examen Final de Cálculo Vectorial MATE 1207 PREGUNTAS ABIERTAS TEMA A Diciembre 6 de 2017 Este es un examen individual, no se permite el uso de libros,
Cálculo Integral Agosto 2015
 Cálculo Integral Agosto 5 Laboratorio # Antiderivadas I.- Halle las siguientes integrales indefinidas. ) (x 5 8x + 3x 3 ) ) (y 3 6y 6 5 + 8) dy 3) (y 3 + 5)(y + 3) dy 4) (t 3 + 3t + ) (t 3 + 5) dt 5) (3y
Cálculo Integral Agosto 5 Laboratorio # Antiderivadas I.- Halle las siguientes integrales indefinidas. ) (x 5 8x + 3x 3 ) ) (y 3 6y 6 5 + 8) dy 3) (y 3 + 5)(y + 3) dy 4) (t 3 + 3t + ) (t 3 + 5) dt 5) (3y
Dpto. Física y Mecánica. Cinemática del. Movimiento plano paralelo. Elvira Martínez Ramírez
 Dpto. Física y Mecánica Cinemática del sólido rígido III Movimiento plano paralelo Elvira Martínez Ramírez Distribución de las aceleraciones en el movimiento plano-paralelo. Definición y generalidades
Dpto. Física y Mecánica Cinemática del sólido rígido III Movimiento plano paralelo Elvira Martínez Ramírez Distribución de las aceleraciones en el movimiento plano-paralelo. Definición y generalidades
Geometría Diferencial. Curva
 Curva La curva en el espacio representa intuitivamente la trayectoria de un punto en movimiento. Por ejemplo, la trayectoria de un planeta en el espacio, nos sugieren la idea de curva. También la forma
Curva La curva en el espacio representa intuitivamente la trayectoria de un punto en movimiento. Por ejemplo, la trayectoria de un planeta en el espacio, nos sugieren la idea de curva. También la forma
MÉTODOS MATEMÁTICOS II
 MÉTODOS MATEMÁTICOS II (Licenciatura de Física. Curso 2007-2008) Boletín de problemas a evaluar correspondientes a los Temas I y II Fecha de entrega: Viernes, 23 de Noviembre de 2007 1. Calcula los siguientes
MÉTODOS MATEMÁTICOS II (Licenciatura de Física. Curso 2007-2008) Boletín de problemas a evaluar correspondientes a los Temas I y II Fecha de entrega: Viernes, 23 de Noviembre de 2007 1. Calcula los siguientes
INDICE 1. Desigualdades 2. Relaciones, Funciones, Graficas 3. La Línea Recta 4. Introducción al Cálculo. Límites
 INDICE 1. Desigualdades 1 1. Desigualdades 1 2. Valor absoluto 8 3. Valor absoluto y desigualdades 11 2. Relaciones, Funciones, Graficas 16 1. Conjunto. Notación de conjuntos 16 2. El plano coordenado.
INDICE 1. Desigualdades 1 1. Desigualdades 1 2. Valor absoluto 8 3. Valor absoluto y desigualdades 11 2. Relaciones, Funciones, Graficas 16 1. Conjunto. Notación de conjuntos 16 2. El plano coordenado.
Lista de Ejercicios Complementarios
 Lista de Ejercicios omplementarios Matemáticas VI (MA-3) Verano. ean α >, β > y a, b R constantes. ea la superficie que es la porción del cono de ecuación z = α x + y que resulta de su intersección con
Lista de Ejercicios omplementarios Matemáticas VI (MA-3) Verano. ean α >, β > y a, b R constantes. ea la superficie que es la porción del cono de ecuación z = α x + y que resulta de su intersección con
1 Funciones de Varias Variables
 EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 01/02
 Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.
 SEMESTRE 018-1 SERIE CURVAS EN EL PLANO POLAR 1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.. Determinar las coordenadas polares del punto C simétrico
SEMESTRE 018-1 SERIE CURVAS EN EL PLANO POLAR 1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.. Determinar las coordenadas polares del punto C simétrico
IES Fco Ayala de Granada Modelo 5 del Solución Germán-Jesús Rubio Luna. Opción A. Ejercicio 1 de la opción A del modelo 5 de 1999.
 IES Fco Ayala de Granada Modelo 5 del 999. Germán-Jesús Rubio Luna Opción A Ejercicio de la opción A del modelo 5 de 999. [ 5 puntos] Haciendo el cambio de variable t = e x, calcula Calculamos primero
IES Fco Ayala de Granada Modelo 5 del 999. Germán-Jesús Rubio Luna Opción A Ejercicio de la opción A del modelo 5 de 999. [ 5 puntos] Haciendo el cambio de variable t = e x, calcula Calculamos primero
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen de 1 de Septiembre de 2009 Primera parte
 ÁLULO Primer curso de ngeniero de Telecomunicación Examen de de Septiembre de 9 Primera parte Ejercicio. En un círculo de radio a se toma un diámetro POQ. Sobre la perpendicular al círculo en el punto
ÁLULO Primer curso de ngeniero de Telecomunicación Examen de de Septiembre de 9 Primera parte Ejercicio. En un círculo de radio a se toma un diámetro POQ. Sobre la perpendicular al círculo en el punto
Cálculo Integral Área de una superficie de revolución. Universidad Nacional de Colombia
 Cálculo Integral Área de una superficie de revolución Jeanneth Galeano Peñaloza - Claudio Rodríguez Beltrán Universidad Nacional de Colombia Segundo semestre de 2015 Área de una superficie de revolución
Cálculo Integral Área de una superficie de revolución Jeanneth Galeano Peñaloza - Claudio Rodríguez Beltrán Universidad Nacional de Colombia Segundo semestre de 2015 Área de una superficie de revolución
Cálculo de Geodésicas en Superficies de Revolución
 Cálculo de Geodésicas en Superficies de Revolución Superficies de Revolución Sea S R 3 la superficie de revolución obtenida al girar una curva regular del plano XZ que no corte al eje Z alrededor del mismo.
Cálculo de Geodésicas en Superficies de Revolución Superficies de Revolución Sea S R 3 la superficie de revolución obtenida al girar una curva regular del plano XZ que no corte al eje Z alrededor del mismo.
Áreas entre curvas. Ejercicios resueltos
 Áreas entre curvas Ejercicios resueltos Recordemos que el área encerrada por las gráficas de dos funciones f y g entre las rectas x = a y x = b es dada por Ejercicios resueltos b a f x g x dx Ejercicio
Áreas entre curvas Ejercicios resueltos Recordemos que el área encerrada por las gráficas de dos funciones f y g entre las rectas x = a y x = b es dada por Ejercicios resueltos b a f x g x dx Ejercicio
Ayudantía 23. Fuerza magnética sobre conductores, torque magnético y Ley de Ampere 31 de Mayo de 2018 Ayudante: Matías Henríquez -
 Pontificia Universidad Católica de Chile Facultad de Física FIS15 - Electricidad y Magnetismo // 1-2018 Profesor: Giuseppe De Nittis - gidenittis@uc.cl Ayudantía 2 Fuerza magnética sobre conductores, torque
Pontificia Universidad Católica de Chile Facultad de Física FIS15 - Electricidad y Magnetismo // 1-2018 Profesor: Giuseppe De Nittis - gidenittis@uc.cl Ayudantía 2 Fuerza magnética sobre conductores, torque
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO: 017 PERÍODO: PRIMER TÉRMINO MATERIA: Cálculo de una variable PROFESOR: EVALUACIÓN:
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO: 017 PERÍODO: PRIMER TÉRMINO MATERIA: Cálculo de una variable PROFESOR: EVALUACIÓN:
Integrales Múltiples.
 CAPÍTULO 8 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
CAPÍTULO 8 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
Parametrización de curvas Integrales de linea. h"p://www.sc.ehu.es/sqwpolim/metodos_matema6cos/
 Parametrización de curvas Integrales de linea h"p://www.sc.ehu.es/sqwpolim/metodos_matema6cos/ Curvas en el espacio En el espacio, una curva se define por el corte de dos superficies. La forma más general
Parametrización de curvas Integrales de linea h"p://www.sc.ehu.es/sqwpolim/metodos_matema6cos/ Curvas en el espacio En el espacio, una curva se define por el corte de dos superficies. La forma más general
Primer Parcial MA1002 Cálculo II ExMa
 Primer Parcial MA1002 Cálculo II ExMa Cualquiera de los siguientes objetivos puede ser evaluado en el primer parcial. 1. Demostrar proposiciones que se cumplen para infinidad de números naturales, aplicando
Primer Parcial MA1002 Cálculo II ExMa Cualquiera de los siguientes objetivos puede ser evaluado en el primer parcial. 1. Demostrar proposiciones que se cumplen para infinidad de números naturales, aplicando
Curvas. (cost,sent) (cos(-t),sen(-t)) (sent,cost) (cos2t,sen2t) (2cost,2sent)
 Curvas cos(t) y sen(t) son las coordenadas del punto en el circulo unitario tal que t es la longitud del arco de circulo desde el eje x hasta el punto. Para cualquier valor de t, cos 2 (t)+sen 2 (t) =
Curvas cos(t) y sen(t) son las coordenadas del punto en el circulo unitario tal que t es la longitud del arco de circulo desde el eje x hasta el punto. Para cualquier valor de t, cos 2 (t)+sen 2 (t) =
Integral definida. dx es diferencial de x, e indica cuál es la variable de la función que se integra.
 Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-07-2-M-2-00-202 CURSO: Matemática Intermedia I SEMESTRE: Segundo CÓDIGO DEL CURSO: 07 TIPO DE EXAMEN: Segundo
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-07-2-M-2-00-202 CURSO: Matemática Intermedia I SEMESTRE: Segundo CÓDIGO DEL CURSO: 07 TIPO DE EXAMEN: Segundo
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen del 14 de Septiembre de 2000 Primera parte
 ÁLULO Primer curso de Ingeniero de Telecomunicación Examen del de Septiembre de Primera parte Ejercicio. Un flan tiene forma de tronco de paraboloide de revolución, siendo r y r losradiosdesusbasesyh su
ÁLULO Primer curso de Ingeniero de Telecomunicación Examen del de Septiembre de Primera parte Ejercicio. Un flan tiene forma de tronco de paraboloide de revolución, siendo r y r losradiosdesusbasesyh su
PEP 3. Responda 4 de los siguientes 9 problemas, escogiendo al menos uno de cada sección.
 Universidad de Santiago de Chile Cálculo odrigo Vargas do semestre 1 PEP Nombre: Nota: esponda de los siguientes 9 problemas, escogiendo al menos uno de cada sección. Sección 1. 1. Use coordenadas esféricas
Universidad de Santiago de Chile Cálculo odrigo Vargas do semestre 1 PEP Nombre: Nota: esponda de los siguientes 9 problemas, escogiendo al menos uno de cada sección. Sección 1. 1. Use coordenadas esféricas
Pauta Segundo Certamen de Matemática II (MAT022) 2 do Semestre de Febrero 2012
 1. Alternativas Pauta Segundo Certamen de Matemática II (MAT0 do Semestre 011 7 de Febrero 01 Nombre: Rut: Paralelo: En las siguientes preguntas de alternativas, justifique claramente su respuesta. (10
1. Alternativas Pauta Segundo Certamen de Matemática II (MAT0 do Semestre 011 7 de Febrero 01 Nombre: Rut: Paralelo: En las siguientes preguntas de alternativas, justifique claramente su respuesta. (10
Problemas resueltos correspondientes a la selectividad de Matemáticas II de junio de 2009, Andalucía
 Problemas resueltos correspondientes a la selectividad de Matemáticas II de junio de 2009, Andalucía Pedro González Ruiz septiembre de 20. Opción A Problema. Calcular el siguiente límite ln denota logaritmo
Problemas resueltos correspondientes a la selectividad de Matemáticas II de junio de 2009, Andalucía Pedro González Ruiz septiembre de 20. Opción A Problema. Calcular el siguiente límite ln denota logaritmo
Cinemática del sólido rígido
 Cinemática del sólido rígido Teoría básica para el curso Cinemática del sólido rígido, ejercicios comentados α δ ω B B A A P r B AB A ω α O Ramírez López-Para, Pilar Loizaga Garmendia, Maider López Soto,
Cinemática del sólido rígido Teoría básica para el curso Cinemática del sólido rígido, ejercicios comentados α δ ω B B A A P r B AB A ω α O Ramírez López-Para, Pilar Loizaga Garmendia, Maider López Soto,
Funciones reales de varias variables
 PROBLEMAS DE CÁLCULO II Curso 2-22 2 Funciones reales de varias variables. Dibuja las curvas de niveles,,..., 5 y la representación gráfica de las siguientes funciones a) f(x, y) = 5 x y b) f(x, y) = x
PROBLEMAS DE CÁLCULO II Curso 2-22 2 Funciones reales de varias variables. Dibuja las curvas de niveles,,..., 5 y la representación gráfica de las siguientes funciones a) f(x, y) = 5 x y b) f(x, y) = x
Coordinación de Matemática IV Guía-Apunte de Preparación del CAR. 2 do Semestre Contenidos del Certamen
 Universidad Técnica Federico anta aría Coordinación de atemática IV Guía-Apunte de Preparación del CAR 2 do emestre 2011 Información Contenidos del Certamen Teorema de Green, Teorema de Green para Regiones
Universidad Técnica Federico anta aría Coordinación de atemática IV Guía-Apunte de Preparación del CAR 2 do emestre 2011 Información Contenidos del Certamen Teorema de Green, Teorema de Green para Regiones
Integrales Múltiples.
 CAPÍTULO 9 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
CAPÍTULO 9 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
1. Use el Teorema de Green para calcular el área de la región del. plano xy que satisface las desigualdades y x, x y, 8xy 1.
 CÁLCULO VECTORIAL (54) SEGUNO PARCIAL (%) 9//9 EPARTAMENTO E APLICAA Use el Teorema de Green para calcular el área de la región del plano xy que satisface las desigualdades y x, x y, 8xy Halle el área
CÁLCULO VECTORIAL (54) SEGUNO PARCIAL (%) 9//9 EPARTAMENTO E APLICAA Use el Teorema de Green para calcular el área de la región del plano xy que satisface las desigualdades y x, x y, 8xy Halle el área
Función Longitud de Arco
 Función Longitud de Arco Si al extremo final de la curva Lt = t f t dt e deja variable entonce el límite uperior de la a integral depende del parámetro t y e tiene que la longitud de arco de una curva
Función Longitud de Arco Si al extremo final de la curva Lt = t f t dt e deja variable entonce el límite uperior de la a integral depende del parámetro t y e tiene que la longitud de arco de una curva
Ejercicios propuestos para el cálculo de áreas
 Aplicaciones geométricas y mecánicas de la integral definida 191 Ejercicios propuestos para el cálculo de áreas 1) Calcular el área de la figura limitada por la parábola verticales = 1, = y el eje OX y
Aplicaciones geométricas y mecánicas de la integral definida 191 Ejercicios propuestos para el cálculo de áreas 1) Calcular el área de la figura limitada por la parábola verticales = 1, = y el eje OX y
Análisis Matemático I
 Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
Integrales de lı nea y de superficie
 EJERIIO DE A LULO II PARA GRADO DE INGENIERI A Elaborados por Domingo Pestana y Jose Manuel Rodrı guez, con Arturo de Pablo y Elena Romera 4 4.1 Integrales de lı nea y de superficie Integrales sobre curvas
EJERIIO DE A LULO II PARA GRADO DE INGENIERI A Elaborados por Domingo Pestana y Jose Manuel Rodrı guez, con Arturo de Pablo y Elena Romera 4 4.1 Integrales de lı nea y de superficie Integrales sobre curvas
APLICACIONES DE LA INTEGRAL DEFINIDA
 APLICACIONES DE LA INTEGRAL DEFINIDA Objetivo: El alumno analizará y comprenderá el uso y la aplicación de la integral definida en la resolución de problemas REGIONES PLANAS LIMITADAS POR DOS CURVAS Sean
APLICACIONES DE LA INTEGRAL DEFINIDA Objetivo: El alumno analizará y comprenderá el uso y la aplicación de la integral definida en la resolución de problemas REGIONES PLANAS LIMITADAS POR DOS CURVAS Sean
Análisis II Análisis matemático II Matemática 3.
 Análisis II Análisis matemático II Matemática 3. 2do. cuatrimestre de 2015 Práctica 2 - Integrales de superficie. Definición.1. Una superficie paramétrica (superficie a secas para nosotros) es un conjunto
Análisis II Análisis matemático II Matemática 3. 2do. cuatrimestre de 2015 Práctica 2 - Integrales de superficie. Definición.1. Una superficie paramétrica (superficie a secas para nosotros) es un conjunto
S O L U C I Ó N y R Ú B R I C A
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO 08 PERÍODO PRIMER TÉRMINO MATERIA Cálculo de una variable PROFESORES EVALUACIÓN SEGUNDA
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO 08 PERÍODO PRIMER TÉRMINO MATERIA Cálculo de una variable PROFESORES EVALUACIÓN SEGUNDA
Ayudantía Regla de la Cadena. Pontificia Universidad Católica de Chile Facultad de Matemáticas Departamento de Matemática
 / 010 Ayudantía 4 1. Regla de la Cadena Proposición 1 Regla de la Cadena - 1. Sea f : U R n R diferenciable y γ : I R R n una curva diferenciable contenida en U. Entonces, la función gt = f γt es derivable
/ 010 Ayudantía 4 1. Regla de la Cadena Proposición 1 Regla de la Cadena - 1. Sea f : U R n R diferenciable y γ : I R R n una curva diferenciable contenida en U. Entonces, la función gt = f γt es derivable
