INTRODUCCIÓN A PROPAGACIÓN DE ERRORES - RENÉ ZEPEDA G. - AGOSTO 2003
|
|
|
- Aurora Revuelta Torres
- hace 7 años
- Vistas:
Transcripción
1 pc /8/ - INTROD PROP ERRORES.oc - Página e 6 INTRODUCCIÓN PROPGCIÓN DE ERRORES - RENÉ ZEPED G. - GOSTO PUNTE PROVISORIO, SUJETO REVISIÓN Y CMBIOS, NO REEMPLZN NOTCIONES EN CLSES REVISIÓN DE ÁLGEBR MTRICIL El álgebra matricial reuce complicaos sistemas e ecuaciones a epresiones más sencillas y, hace más rápio los cálculos matemáticos en computaor. DEFINICIÓN DE UN MTRIZ Matriz es un conjunto e números o símbolos arreglaos e forma rectangular, por líneas y columnas. Como ejemplo, sea el siguiente sistema e ecuaciones: a + a + a b a + a + a b a + a + a b el sistema puee ser representao por: a a a b a a a b a a a { b { X B DIMENSIONES DE UN MTRIZ D ij mn 5 6 m: N o e líneas n: N o e columnas
2 pc /8/ - INTROD PROP ERRORES.oc - Página e 6 Matriz simétrica (cuaraa, mn) simétrica respecto a la iagonal principal Matriz iagonal 5 7 los elementos fuera e la iagonal principal son ceros Matriz unitaria los elementos la iagonal principal son Matriz traspuesta T se trasponen elementos e líneas por columnas Iguala. Dos matrices son iguales solo si son e misma imensión y sus elementos corresponientes también lo son. Suma e matrices + B C Multiplicación e matriz por escalar 8 6 Multiplicación e matrices N o e columnas e N o e líneas e B mn B np C mp
3 pc /8/ - INTROD PROP ERRORES.oc - Página e 6 b b a a a (a b) (a b) (a b) (a b) (a b) (a b) b b a a a (a b) (a b) (a b) (a b) (a b) (a b) b b Para granes matrices se hace en forma computacional, por ejemplo: DO I,M DO K,P C(I,K) DO J,N C(I,K) C(I,K)+(I,J)*B(J,K) SOLUCIÓN DE ECUCIONES En la solución e sistemas e ecuaciones es necesario efinir y calcular la INVERS e una matriz. Para un número real eiste uno inverso - que. - En un sistema e ecuaciones con igual número e ecuaciones e incógnitas, se tiene un sistema e oren mn, one: C X B C: matriz e los coeficientes Eiste C - tal que C C - I (matriz ientia) C - C X C - B I X C - B X C - B Coniciones. a) solo matrices cuaraas tienen inversa b) no ebe ser singular (eterminante )
4 pc /8/ - INTROD PROP ERRORES.oc - Página e 6 z y w c b a z y w c b a aw+by a+bz cw+y c+z para matrices oren () a c b a c b c b a : eterminante e Ejemplo: MRIZ DJUNT aj et er minante e ajunta e La ajunta se obtiene reemplazano caa elemento por su signo menor o cofactor y trasponieno la matriz. El elemento cofactor e a ij (-) ij multiplicao por el eterminante e la matriz restante e la eliminación e la línea i y la columna j. Ejemplo: cof a (-) (-)
5 pc /8/ - INTROD PROP ERRORES.oc - Página 5 e 6 cof a (-) (-) -6 cof a (-) (-) - cof aj T (cof ) eterminante e **+***-(**+**+**) (6++6) 88-6 aj (comprobar) Ejemplo: meición e istancia ,7m ,6m ,85m + + 5, , ,85 En notación matricial: X L
6 pc /8/ - INTROD PROP ERRORES.oc - Página 6 e L X X - L? L X
7 pc /8/ - INTROD PROP ERRORES.oc - Página 7 e 6 TEORÍ DE ERRORES En el proceso e meición e toa cantia física, factores como: limitación humana, imperfección e instrumentos e inestabilia natural, hacen que las meiciones sean afectaas e errores. Los errores pueen ser: Faltas. Debio a error grosero, proveniente e falta e cuiao o confusión. Las faltas generalmente no son clasificaas como error y ellos solo pueen removerse con cuiaoso chequeo e los atos, aislano el error grosero. Ejemplo: lectura o anotación equivocaa e las uniaes en una meición. Error sistemático. Es un error que puee ser epresao por una función matemática; afecta la meición en casi la misma magnitu y tiene una fuente específica. Ejemplo: error e ínice (e cero) en el ángulo vertical; temperatura no calibraa para una corrección; cambio e prisma en un istanciómetro. Error aleatorio o acciental: espués e removios las os clases anteriores e errores, quean errores (generalmente pequeños) e signos positivo y negativo, que pueen ser trataos e acuero a las leyes e la estaística. Ejemplo: errores e apreciación en lecturas; burbuja no centraa. Definiciones Cantia Meia: cantia observaa irectamente que contiene errores aleatorios. Valor Veraero: valor teórico o eacto (esconocio). Error: iferencia entre la cantia meia y la cantia e mayor probabilia. Valor Más Probable: valor e una cantia meia que, basaa en las observaciones, tiene la más alta probabilia. El EMP es irectamente meio e varias meiciones inepenientes por su meia aritmética. Resiuo: iferencia entre la cantia meia y el valor más probable; este es el valor que se trata en el ajuste e observaciones. Este término se usa como equivalente a error. Graos e Liberta: Es el número e meiciones en eceso, o sea, es el número observaciones menos el número e incógnitas, es el número e observaciones reunantes; hace posible el ajuste.
8 pc /8/ - INTROD PROP ERRORES.oc - Página 8 e 6 Varianza. ( ) Epresa la precisión e un grupo e observaciones; es la meia el cuarao e los errores. Error Estánar: () Raíz e la varianza; n Desviación Estánar. Similar al Error Estánar; las cantiaes y, son teóricas porque el valor veraero es ineterminao. En la práctica se usan los resiuos y una mejor estimativa e la varianza es usar resiuos: υ S n n-: graos e liberta Si n entonces S DISTRIBUCIÓN NORML yf() y probabilia y y f() representa la probabilia (por unia e intervalo e unia meia) e obtener un eterminao valor e esa meia, obviamente: p f() La ecuación e la curva e istribución normal es: ( ) y f () e π y: probabilia e ocurrencia el error entre y e: base e logaritmo natural
9 : esviación estánar pc /8/ - INTROD PROP ERRORES.oc - Página 9 e 6 Histograma: es la representación gráfica e la istribución e un grupo e meiciones o e un grupo e resiuos. Es un gráfico e barra e frecuencias. PRECISIÓN. Es el grao e consistencia, ispersión o refinamiento e un conjunto e meiciones; esta es iferente e la EXCTITUD la cual efine el acercamiento al veraero valor; comúnmente la precisión es epresaa en términos e Error Estánar o Desviación Estánar. La varianza es el cuarao el error estánar. Reemplazano: y e π Área bajo la curva: + a a y + a y + a h h e π Si a: 68% 95% - - M Interpretación: el grupo e meiciones, 68% e ellas tienen un error igual o menor que. Nivel e confianza Sigma 5%,675 68,7% 9%,69 95,5% 99%,6 99,7% 99,99%
10 pc /8/ - INTROD PROP ERRORES.oc - Página e 6 Ejemplo: Ángulos meios VMP Σ ángulos / n? Desviación Estánar S? (REVISR MTRICES) PROPGCIÓN DE ERRORES LETÓRIOS Las operaciones matemáticas con números inciertos, an resultaos también inciertos, por ese motivo es importante estimar el error resultante a partir e los errores iniciales. Consiérese el error en el cálculo el área e un terreno rectangular e laos iguales. Sean los laos iguales a 8m y con un error e m. El valor el área es e 6m. En la figura se representa la superficie en función el lao, si el error el lao es m, el error e la superficie será aproimaamente 5m (graficamente). Si se consiera que el error (o variación) e la función es suficientemente pequeño, se puee Superficie (m ) reemplazar la curva por una recta tangente a la curva. La relación entre el error el lao () y el error el área (y) es representaa por la peniente e la curva en el punto e interés, es ecir, la erivaa e la función y lao (m) y (error superficie) (error lao) y (error superficie) (error lao) 6m
11 DEDUCCIÓN DE L ECUCIÓN BÁSIC. pc /8/ - INTROD PROP ERRORES.oc - Página e 6 Sea: z y + y y, y observaciones inepenientes con errores y Y ey los errores en la eterminación e y eyi los errores en la eterminación e y El veraero valor e z será zt zt (y+ey) + (y+ey) zt y+y+ey+ey z+ey+ey ez zt z ey+ey (error e caa meición) Para i meiciones: ezi zt zi eyi+eyi Por la efinición e varianza: v n n v n Σ( eyi+eyi) eyi +eyi + eyi eyi +. eyi +eyi cero) +. ( eyi eyi tiene a Finalmente z y + y () z y + y En general para un valor calculao z en que zf(y,y, yn), la ECUCIÓN GENERL DE PROPGCIÓN DE ERRORES DE MEDICIONES INDEPENDIENTES es: z z z z y + y + yn () y y yn
12 ERROR DE L SUM pc /8/ - INTROD PROP ERRORES.oc - Página e 6 Sea: B+B+.Bn B B si los errores son iguales: n B () Bn Error Meio e la Meia (M): zi Sea: z n Sea el error e caa meición, z n z + n z + n z + n zn por tratarse e meiciones e igual precisión: n z n n n z () n El error meio e la meia se obtiene el error meio e una observación ivio por la raíz el número e observaciones. Por ejemplo, es necesario hacer observaciones para reucir el error a la mita y veces para reucirlo a,. Ejemplo: sean las meiciones e un tanque: X.m ±.5m Y.m y ±.m Z 5.m z ±.m Calcular el error el volumen.
13 v v.m v v v v v + y + z y z (.5) + ( 6.) + ( 8.) m pc /8/ - INTROD PROP ERRORES.oc - Página e 6 l meir una magnitu esta generalmente se utiliza en cálculos, por lo tanto es necesario saber como actúa el error en la magnitu final. Multiplicación: X n L (X) n (L) n L Ejemplo Sea una istancia horizontal calculaa a partir e ángulo vertical y istancia inclinaa, Di m ±.5m α º ± ; calcular el error en Dh Dh Di cos α Dh Dh Di Dh α Dh Dh Di + α Di α cos α Di sen α ( Di senα) Dh cosα (,5) + ( en raianes) Ejemplo Una esfera e raio R6.78.m; se materializa su perímetro por una cuera imaginaria; se suma m a su perímetro y se etiene el nuevo perímetro homogéneamente. Cuánto varía el raio R?
14 PESO DE LS OBSERVCIONES pc /8/ - INTROD PROP ERRORES.oc - Página e 6 Peso es la poneración relativa e valores observaos, cuano es comparao con otro valor; estima o epresa la relativa confiabilia e una observación. Meia Poneraa Sean n observaciones separaas en os conjuntos na y nb, tal que n na+nb Meia conjunto a: za Σ(za i /na) Meia conjunto b: zb Σ(zb i /nb) Hacieno na pa y nb pb (mientras mayor número e observaciones, más confiable es la observación, mayor peso) pa za + pb zb pi z z i (5) pa + pb pi Por ejemplo, una istancia es meia por os grupos. El primero logró una meia e 65,7m con meiciones, el seguno calculó 65,m con meiciones. Por lo tanto la meia poneraa ebe ser: 65,7 + 65,6 z 65,56 + EL PESO ES INVERSMENTE PROPORCIONL L VRINZ pa (6) za PESO EN L NIVELCIÓN GEOMÉTRIC Sea una línea e longitu l, con avances en istancia, la esviación estánar por caa instalación el instrumento:
15 pc /8/ - INTROD PROP ERRORES.oc - Página 5 e 6 B l C l Número e instalaciones por línea N l/ N (l /) N (l /) n N (l n /) : esviación estánar por instalación n : esviación estánar e la línea l l +l ++l n Por la ecuación (6) el peso es inversamente proporcional a la varianza y esta es respecto a la línea; el peso e una línea nivelaa es: p l pero los son toos proporcionalmente iguales p p pn l l ln Los pesos en nivelación son inversamente proporcional a sus longitues y a su vez, la longitu es proporcional al número e instalaciones, por lo tanto, los pesos son inversamente proporcional al número e instalaciones.
16 PESO EN L MEDICIÓN NGULR pc /8/ - INTROD PROP ERRORES.oc - Página 6 e 6 Sean ángulos (α, a, α) e un triángulo plano, que fueron meios n, n y n veces respectivamente por el mismo instrumento. Sea la esviación estánar e un ángulo meio, la meia e los ángulos son: α α α ; α ; α n n La varianza e la meia, aa por () es: α ; n α ; n α n ; α Nuevamente, los pesos son inversamente proporcionales a la varianza, y relativamente los pesos e los ángulos son: p p p α α α n n n n n n Los pesos e los ángulos son proporcionales al número e meiciones efectuaas (bajo las mismas coniciones). n
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE--4-M---7 CURSO: Matemática Básica SEMESTRE: Primero CÓDIGO DEL CURSO: TIPO DE EXAMEN: Eamen Final FECHA DE
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE--4-M---7 CURSO: Matemática Básica SEMESTRE: Primero CÓDIGO DEL CURSO: TIPO DE EXAMEN: Eamen Final FECHA DE
1 Conjuntos de medidas. Histogramas
 Curso 06-07 Tema.5 Análisis estaístico e errores aleatorios: Histogramas. La istribución normal. Dóne estuiar el tema.5: Capítulo 5 (ecepto apto. 5.8). J.R. Taylor, Error Analysis. Univ. Science Books,
Curso 06-07 Tema.5 Análisis estaístico e errores aleatorios: Histogramas. La istribución normal. Dóne estuiar el tema.5: Capítulo 5 (ecepto apto. 5.8). J.R. Taylor, Error Analysis. Univ. Science Books,
Cada grado se divide en 60 minutos (60 ) y cada minuto en 60 segundos (60 ). Así, por ejemplo, un ángulo puede medir = 38º
 Sistemas e meición e ángulos Como en toos los elementos susceptibles a meiciones, en los ángulos se han establecio iversos sistemas e meición, entre ellos los más importantes son: El sistema seagesimal
Sistemas e meición e ángulos Como en toos los elementos susceptibles a meiciones, en los ángulos se han establecio iversos sistemas e meición, entre ellos los más importantes son: El sistema seagesimal
RESOLUCIÓN DE ACTIVIDADES
 RESOLUCIÓN DE ACTIVIDADES Activiaes iniciales 1. Calcula las matrices inversas e las siguientes matrices: 1 1 2-3 1 2 1 1 1 1 0 1 2 2 5 1 1 1 1 0 0 1 1 1 1 1 Las matrices buscaas son: 1/4 1/4 1/4 1/4 1
RESOLUCIÓN DE ACTIVIDADES Activiaes iniciales 1. Calcula las matrices inversas e las siguientes matrices: 1 1 2-3 1 2 1 1 1 1 0 1 2 2 5 1 1 1 1 0 0 1 1 1 1 1 Las matrices buscaas son: 1/4 1/4 1/4 1/4 1
UCLM - Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG)
 PAEG Junio 03 Propuesta B Matemáticas aplicaas a las CCSS II º Bachillerato UCLM - Pruebas e Acceso a Enseñanzas Universitarias Oiciales e Grao (PAEG) Matemáticas aplicaas a las Ciencias Sociales II Junio
PAEG Junio 03 Propuesta B Matemáticas aplicaas a las CCSS II º Bachillerato UCLM - Pruebas e Acceso a Enseñanzas Universitarias Oiciales e Grao (PAEG) Matemáticas aplicaas a las Ciencias Sociales II Junio
Soluciones al examen de Estadística Aplicada a las Ciencias Sociales Junio ª Semana
 Soluciones al eamen e Estaística Aplicaa a las Ciencias Sociales Junio 009 ª Semana Ejercicio. Una agente e iguala está interesaa en conocer las iferencias salariales en España entre hombres y mujeres
Soluciones al eamen e Estaística Aplicaa a las Ciencias Sociales Junio 009 ª Semana Ejercicio. Una agente e iguala está interesaa en conocer las iferencias salariales en España entre hombres y mujeres
4.1 Antiderivadas o primitivas e integración indefinida
 48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
1. Hallar la derivada por definición de f ( x) x x 1. Solución: para resolver la derivada aplicaremos la definición de la derivada: f '( x)
 . Hallar la erivaa por efinición e f ( ) Solución: para resolver la erivaa aplicaremos la efinición e la erivaa: f '( ) lim 0 f ( ) f ( ) f ( ) f '( ) lim 0 ara allar la erivaa meiante efinición ebemos
. Hallar la erivaa por efinición e f ( ) Solución: para resolver la erivaa aplicaremos la efinición e la erivaa: f '( ) lim 0 f ( ) f ( ) f ( ) f '( ) lim 0 ara allar la erivaa meiante efinición ebemos
La capacitancia tiene la unidad del SI coulomb por volt. La unidad de capacitancia del SI es el farad (F), en honor a Michael Faraday.
 1. Qué es capacitancia? Se efine como la razón entre la magnitu e la carga e cualquiera e los conuctores y la magnitu e la iferencia e potencial entre ellos. La capacitancia siempre es una cantia positiva
1. Qué es capacitancia? Se efine como la razón entre la magnitu e la carga e cualquiera e los conuctores y la magnitu e la iferencia e potencial entre ellos. La capacitancia siempre es una cantia positiva
Seminario 12: Condensadores.
 Seminario 2: Conensaores. Fabián Anrés Torres Ruiz Departamento e Física, Universia e Concepción, Chile 30 e Mayo e 2007. Problemas. (Desarrollo) Deucción el tiempo e escarga e un conensaor 2. (Problema
Seminario 2: Conensaores. Fabián Anrés Torres Ruiz Departamento e Física, Universia e Concepción, Chile 30 e Mayo e 2007. Problemas. (Desarrollo) Deucción el tiempo e escarga e un conensaor 2. (Problema
4.1 Antiderivadas o primitivas e integración indefinida
 48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
Principio de incertidumbre de Heisenberg
 Principio e incertiumbre e Heisenberg n un átomo e irógeno, nos se pueen meir simultáneamente la cantia e movimiento mv y la posición e su electrón. a cantia e movimiento e una partícula se enomina momento,
Principio e incertiumbre e Heisenberg n un átomo e irógeno, nos se pueen meir simultáneamente la cantia e movimiento mv y la posición e su electrón. a cantia e movimiento e una partícula se enomina momento,
Cálculo matricial de pórticos biempotrados a dos aguas
 Desplazamientos y solicitaciones e una barra Cálculo matricial e pórticos biempotraos a os aguas. Hipótesis e cálculo. e verifica la ley e Hooke, lo que significa que en las estructuras los esplazamientos
Desplazamientos y solicitaciones e una barra Cálculo matricial e pórticos biempotraos a os aguas. Hipótesis e cálculo. e verifica la ley e Hooke, lo que significa que en las estructuras los esplazamientos
A y B
 TIVIDDES DE MTRIES. º HILLERTO Hallar el rango e la matriz: 7 8 7 9 8 Se observa que el menor e oren formao por la primera y tercera filas y columnas no es nulo sino igual a 8, veamos: 8 Luego rg () es
TIVIDDES DE MTRIES. º HILLERTO Hallar el rango e la matriz: 7 8 7 9 8 Se observa que el menor e oren formao por la primera y tercera filas y columnas no es nulo sino igual a 8, veamos: 8 Luego rg () es
Curso Introductorio a las Matemáticas Universitarias
 Curso Introuctorio a las Matemáticas Universitarias Tema 8: Derivación Víctor M. Almeia Lozano Jorge J. García Melián Licencia Creative Commons 2013 8. DERIVACIÓN En este tema veremos el concepto e erivaa
Curso Introuctorio a las Matemáticas Universitarias Tema 8: Derivación Víctor M. Almeia Lozano Jorge J. García Melián Licencia Creative Commons 2013 8. DERIVACIÓN En este tema veremos el concepto e erivaa
TEORÍA DE CONTROL MODELO DE ESTADO DISCRETO
 TEORÍA DE CONTROL MODELO DE ESTADO DISCRETO Moelo e estao. De la misma forma que se planteó para sistemas continuos, existe la posibilia e moelar un sistema iscreto meiante un moelo e estaos. El sistema
TEORÍA DE CONTROL MODELO DE ESTADO DISCRETO Moelo e estao. De la misma forma que se planteó para sistemas continuos, existe la posibilia e moelar un sistema iscreto meiante un moelo e estaos. El sistema
(f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x)
![(f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x) (f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x)](/thumbs/24/2434623.jpg) Derivaa e una función en un punto: El concepto e erivaa e una función matemática se halla íntimamente relacionao con la noción e límite. Así, la erivaa se entiene como la variación que experimenta la función
Derivaa e una función en un punto: El concepto e erivaa e una función matemática se halla íntimamente relacionao con la noción e límite. Así, la erivaa se entiene como la variación que experimenta la función
aletos ELECTRICIDAD POTENCIAL ELÉCTRICO
 1 4.04 01 a) El campo eléctrico asociao a la función potencial V = xy+3x 3 z+2x 2, en elpunto (1,1,2). b) El trabajo realizao para llevar una unia e carga positiva, a velocia cosntante, ese el punto (1,2,0)
1 4.04 01 a) El campo eléctrico asociao a la función potencial V = xy+3x 3 z+2x 2, en elpunto (1,1,2). b) El trabajo realizao para llevar una unia e carga positiva, a velocia cosntante, ese el punto (1,2,0)
FUNCIONES TRIGONOMÉTRICAS
 Unia os Geometría Trigonometría 8. FUNCIONES TRIGONOMÉTRICAS 8. El círculo trigonométrico o unitario En temas anteriores, las funciones trigonométricas se asociaron con razones, es ecir con cocientes e
Unia os Geometría Trigonometría 8. FUNCIONES TRIGONOMÉTRICAS 8. El círculo trigonométrico o unitario En temas anteriores, las funciones trigonométricas se asociaron con razones, es ecir con cocientes e
Unidad 1 Ecuaciones Diferenciales de Primer Orden. 1.1 Definiciones (Ecuación Diferencial, Orden, Grado, Linealidad)
 . Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) Unia Ecuaciones Diferenciales e Primer Oren. Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) En iversas áreas como son la ingeniería,
. Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) Unia Ecuaciones Diferenciales e Primer Oren. Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) En iversas áreas como son la ingeniería,
Examen Final de Precálculo (Mate 3171) Nombre 14 de diciembre de 2001
 Eamen Final e Precálculo (Mate 7) Nombre e iciembre e 00 Escriba la letra que correspone a la mejor alternativa en el espacio provisto. (os puntos caa uno) ) Si la gráfica e f es la e la erecha entonces
Eamen Final e Precálculo (Mate 7) Nombre e iciembre e 00 Escriba la letra que correspone a la mejor alternativa en el espacio provisto. (os puntos caa uno) ) Si la gráfica e f es la e la erecha entonces
CONCEPTOS BÁSICOS DE CONFIABILIDAD
 CAPÍTULO II CONCEPTOS BÁSICOS DE CONFIABILIDAD El iseño e sistemas, comprene los aspectos más amplios e la organización e equipo complejo, turnos e operación, turnos e mantenimiento y e las habiliaes necesarias
CAPÍTULO II CONCEPTOS BÁSICOS DE CONFIABILIDAD El iseño e sistemas, comprene los aspectos más amplios e la organización e equipo complejo, turnos e operación, turnos e mantenimiento y e las habiliaes necesarias
6. MODELOS KT-KD DIARIOS, CÁCERES
 6. MODELOS KT-KD DIARIOS, CÁCERES Una vez realizao el control e calia e los atos registraos en la estación e Cáceres se escartan, para el esarrollo el moelo e escomposición iaria, aquellos ías que no hayan
6. MODELOS KT-KD DIARIOS, CÁCERES Una vez realizao el control e calia e los atos registraos en la estación e Cáceres se escartan, para el esarrollo el moelo e escomposición iaria, aquellos ías que no hayan
Cálculo I. Índice Reglas Fundamentales para el Cálculo de Derivadas. Julio C. Carrillo E. * 1. Introducción 1. 2.
 3.2. Reglas Funamentales para el Cálculo e Derivaas Julio C. Carrillo E. * Ínice 1. Introucción 1 2. Reglas básicas 3 3. El Álgebra e funciones erivables 4 4. Regla e la caena 8 * Profesor Escuela e Matemáticas,
3.2. Reglas Funamentales para el Cálculo e Derivaas Julio C. Carrillo E. * Ínice 1. Introucción 1 2. Reglas básicas 3 3. El Álgebra e funciones erivables 4 4. Regla e la caena 8 * Profesor Escuela e Matemáticas,
Derivación de funciones de una variable real
 Capítulo 4 Derivación e funciones e una variable real 4.1. Derivaa e una función 4.1.1. Introucción Definición 4.1.1. Sea f : (a, b) R R y x 0 (a, b). Se ice que la función f es erivable en el punto x
Capítulo 4 Derivación e funciones e una variable real 4.1. Derivaa e una función 4.1.1. Introucción Definición 4.1.1. Sea f : (a, b) R R y x 0 (a, b). Se ice que la función f es erivable en el punto x
DERIVADAS DERIVACIÓN DE FUNCIONES
 DERIVADAS DERIVACIÓN DE FUNCIONES Introucción: Después e haber aquirio los conocimientos e los temas anteriores e funciones límites se requiere establecer un proceimiento más eficiente que nos permita
DERIVADAS DERIVACIÓN DE FUNCIONES Introucción: Después e haber aquirio los conocimientos e los temas anteriores e funciones límites se requiere establecer un proceimiento más eficiente que nos permita
LA DERIVADA UNIDAD III III.1 INCREMENTOS. y, esto es:
 Página el Colegio e Matemáticas e la ENP-UNAM La erivaa Autor: Dr. José Manuel Becerra Espinosa LA DERIVADA UNIDAD III III. INCREMENTOS Se eine como incremento e la variable al aumento o isminución que
Página el Colegio e Matemáticas e la ENP-UNAM La erivaa Autor: Dr. José Manuel Becerra Espinosa LA DERIVADA UNIDAD III III. INCREMENTOS Se eine como incremento e la variable al aumento o isminución que
f(x,y) = e x+y cos(xy)
 Universia e los Anes Departamento e Matemáticas MATE1207 Cálculo Vectorial Tarea 1 Iniviual Entregue en clase a su profesor e la MAGISTRAL la semana 6 (Lu. 3 Sep. Vi. 7 Sep.) 1. Consiere la función f efinia
Universia e los Anes Departamento e Matemáticas MATE1207 Cálculo Vectorial Tarea 1 Iniviual Entregue en clase a su profesor e la MAGISTRAL la semana 6 (Lu. 3 Sep. Vi. 7 Sep.) 1. Consiere la función f efinia
FORMULARIO V Introducción a la Física. Licenciatura en Física. f (z) = = lim = lim
 FORMULARIO V1.00 - Introucción a la Física Licenciatura en Física 1 Operaor Derivaa 1.1 De nición formal f (z 0 ) lim lim z 0!z z z 0 4z!0 f (z + 4z) 4z (1) 1. Derivaas e algunas funciones elementales
FORMULARIO V1.00 - Introucción a la Física Licenciatura en Física 1 Operaor Derivaa 1.1 De nición formal f (z 0 ) lim lim z 0!z z z 0 4z!0 f (z + 4z) 4z (1) 1. Derivaas e algunas funciones elementales
DERIVADA. Interpretación Geométrica Encontrar la pendiente de la recta tangente a una curva en un punto dado de ella.
 DERIVADA Interpretación Geométrica Objetivo: Encontrar la peniente e la recta tangente a una curva en un punto ao e ella. Para precisar correctamente la iea e tangente a una curva en un punto, se utilizará
DERIVADA Interpretación Geométrica Objetivo: Encontrar la peniente e la recta tangente a una curva en un punto ao e ella. Para precisar correctamente la iea e tangente a una curva en un punto, se utilizará
 http://www.matematicaaplicaa.co.cc jezasoft@gmail.com e MATEMÁTICA APLICADA TECNOLOGIA EN ELECTRÓNICA CÁLCULO TALLER DE DERIVADAS Manizales, 26 e Marzo e 20 Solucionar los siguientes problemas referenciaos
http://www.matematicaaplicaa.co.cc jezasoft@gmail.com e MATEMÁTICA APLICADA TECNOLOGIA EN ELECTRÓNICA CÁLCULO TALLER DE DERIVADAS Manizales, 26 e Marzo e 20 Solucionar los siguientes problemas referenciaos
UNIDAD I CÁLCULO DIFERENCIAL
 Vicerrectorao Acaémico Faculta e Ciencias Aministrativas Licenciatura en Aministración Mención Gerencia y Mercaeo Unia Curricular: Matemática I UNIDAD I CÁLCULO DIFERENCIAL Elaborao por: Ing. Ronny Altuve
Vicerrectorao Acaémico Faculta e Ciencias Aministrativas Licenciatura en Aministración Mención Gerencia y Mercaeo Unia Curricular: Matemática I UNIDAD I CÁLCULO DIFERENCIAL Elaborao por: Ing. Ronny Altuve
Funciones de Bessel. Dr. Héctor René Vega-Carrillo
 Funciones e Bessel Dr. Héctor René Vega-Carrillo 1 2 Ínice 1. Introucción............................. 3 2. Solución e la Ecuación iferencial e Bessel........... 5 2.1. Caso n entero............................
Funciones e Bessel Dr. Héctor René Vega-Carrillo 1 2 Ínice 1. Introucción............................. 3 2. Solución e la Ecuación iferencial e Bessel........... 5 2.1. Caso n entero............................
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS. S O L U C I Ó N y R Ú B R I C A
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO: 207 PERÍODO: PRIMER TÉRMINO MATERIA: Cálculo e una variable PROFESOR: EVALUACIÓN:
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO: 207 PERÍODO: PRIMER TÉRMINO MATERIA: Cálculo e una variable PROFESOR: EVALUACIÓN:
CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 MATRICES
 CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 Unidades: - Matrices (Bloque Álgebra) - Determinantes (Bloque Álgebra) - Sistemas de ecuaciones lineales (Bloque Álgebra) - Vectores (Bloque
CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 Unidades: - Matrices (Bloque Álgebra) - Determinantes (Bloque Álgebra) - Sistemas de ecuaciones lineales (Bloque Álgebra) - Vectores (Bloque
; deben llevarse las unidades de área a m 2 y distancia a m. V = 13215V = 13, 2kV
 Física II Guía e ejercicios 5 CAPACIDAD 5. Capacia 5.. Problema 5... Enunciao Las placas e un capacitor e placas paralelas están separaas por una istancia e, 8mm y caa una tiene un área e, cm. Caa placa
Física II Guía e ejercicios 5 CAPACIDAD 5. Capacia 5.. Problema 5... Enunciao Las placas e un capacitor e placas paralelas están separaas por una istancia e, 8mm y caa una tiene un área e, cm. Caa placa
Preparación para los Tutoriales Herramientas Astronómicas
 Preparación para los Tutoriales Herramientas Astronómicas Proyecto Ventana Interactiva al Universo Departamento e Ingeniería Eléctrica, Universia e Chile c Primavera 2005 Resumen En el presente tutorial
Preparación para los Tutoriales Herramientas Astronómicas Proyecto Ventana Interactiva al Universo Departamento e Ingeniería Eléctrica, Universia e Chile c Primavera 2005 Resumen En el presente tutorial
A G R. Diédrico 18. Cuerpos 5. Cubo básico A 1
 1 1 ibujar los s, e igual longitu e arista, en las cuatro posiciones siguientes: 1. poyao por la cara en el P (la posición e la izquiera).. on la iagonal vertical; se a la posición e la recta one está
1 1 ibujar los s, e igual longitu e arista, en las cuatro posiciones siguientes: 1. poyao por la cara en el P (la posición e la izquiera).. on la iagonal vertical; se a la posición e la recta one está
2.4 La regla de la cadena
 0 CAPÍTULO Derivación. La regla e la caena Encontrar la erivaa e una función compuesta por la regla e la caena. Encontrar la erivaa e una función por la regla general e la potencia. Simplificar la erivaa
0 CAPÍTULO Derivación. La regla e la caena Encontrar la erivaa e una función compuesta por la regla e la caena. Encontrar la erivaa e una función por la regla general e la potencia. Simplificar la erivaa
UNIVERSIDAD DIEGO PORTALES GUÍA N 11 CÁLCULO I. Profesor: Carlos Ruz Leiva DERIVADAS. Derivadas de orden superior. Ejemplos
 UNIVERSIDAD DIEGO PORTALES FACULTAD DE CIENCIAS DE LA INGENIERÍA INSTITUTO DE CIENCIAS BÁSICAS Profesor: Carlos Ruz Leiva GUÍA N CÁLCULO I DERIVADAS Derivaas e oren superior Ejemplos Hallar las siguientes
UNIVERSIDAD DIEGO PORTALES FACULTAD DE CIENCIAS DE LA INGENIERÍA INSTITUTO DE CIENCIAS BÁSICAS Profesor: Carlos Ruz Leiva GUÍA N CÁLCULO I DERIVADAS Derivaas e oren superior Ejemplos Hallar las siguientes
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-13-5-M-1--17 CURSO: Matemática Básica SEMESTRE: Primero CÓDIGO DEL CURSO: 13 TIPO DE EXAMEN: Primera Retrasaa
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-13-5-M-1--17 CURSO: Matemática Básica SEMESTRE: Primero CÓDIGO DEL CURSO: 13 TIPO DE EXAMEN: Primera Retrasaa
DUREZA 2 DUREZA VICKERS
 DUREZA DUREZA VICKERS OBJETIVO DE LA PRÁCTICA Familiarizarse con la meición e la ureza Vickers. Estuiar su campo e aplicación. CONSIDERACIONES TEÓRICAS GENERALES. Definición e ureza: Se entiene por ureza
DUREZA DUREZA VICKERS OBJETIVO DE LA PRÁCTICA Familiarizarse con la meición e la ureza Vickers. Estuiar su campo e aplicación. CONSIDERACIONES TEÓRICAS GENERALES. Definición e ureza: Se entiene por ureza
Información importante
 Universia Técnica Feerico Santa María Departamento e Matemática Coorinación e Matemática I (MAT021) 1 er Semestre e 2010 Semana 9: Lunes 17 viernes 21 e Mayo Información importante El control Q2A es el
Universia Técnica Feerico Santa María Departamento e Matemática Coorinación e Matemática I (MAT021) 1 er Semestre e 2010 Semana 9: Lunes 17 viernes 21 e Mayo Información importante El control Q2A es el
INTEGRAL INDEFINIDA. Una pregunta inicial para hacerse. Cuál es una función F(x), que al haber sido derivada se obtuvo f ( x) B?.
 es INTEGRAL INDEFINIDA UConcepto e antierivaau: Una pregunta inicial para hacerse. Cuál es una función F(), que al haber sio erivaa se obtuvo f ( ) =?. La repuesta es: F ( ) =. Una nueva pregunta. Es la
es INTEGRAL INDEFINIDA UConcepto e antierivaau: Una pregunta inicial para hacerse. Cuál es una función F(), que al haber sio erivaa se obtuvo f ( ) =?. La repuesta es: F ( ) =. Una nueva pregunta. Es la
Trabajo Práctico N 3
 Departamento e Geología Trabajo Práctico N 3 Técnicas geométricas auxiliares Objetivos: - Métoos gráficos para la obtención e orientaciones. Determinación gráfica el rumbo y buzamiento a partir e os atos
Departamento e Geología Trabajo Práctico N 3 Técnicas geométricas auxiliares Objetivos: - Métoos gráficos para la obtención e orientaciones. Determinación gráfica el rumbo y buzamiento a partir e os atos
EJERCICIOS Sustituyendo x 5, el nivel de producción actual, obtenemos. dc dt (0.7) 1.05
 Sustituyeno 5, el nivel e proucción actual, obtenemos 0. Repita el ejemplo 6 para la función e costo C() 5 3 C t 5 0 (0.7).05 Así que los costos e proucción se están incrementano a una tasa e.05 por año.
Sustituyeno 5, el nivel e proucción actual, obtenemos 0. Repita el ejemplo 6 para la función e costo C() 5 3 C t 5 0 (0.7).05 Así que los costos e proucción se están incrementano a una tasa e.05 por año.
mv 9, r 0,057 m 1, F F E q q v B E v B N C
 . Un electrón que se mueve a través e un tubo e rayos catóicos a 7 m/s, penetra perpenicularmente en un campo e -3 T que actúa sobre una zona e 4 cm a lo largo el tubo. Calcula: a) La esviación que ha
. Un electrón que se mueve a través e un tubo e rayos catóicos a 7 m/s, penetra perpenicularmente en un campo e -3 T que actúa sobre una zona e 4 cm a lo largo el tubo. Calcula: a) La esviación que ha
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-103-1-M--00-017 CURSO: Matemática Básica SEMESTRE: Seguno CÓDIGO DEL CURSO: 103 TIPO DE EXAMEN: Primer eamen
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-103-1-M--00-017 CURSO: Matemática Básica SEMESTRE: Seguno CÓDIGO DEL CURSO: 103 TIPO DE EXAMEN: Primer eamen
Universidad Abierta y a Distancia de México. 2 cuatrimestre. Cálculo diferencial. Unidad 3. Derivación
 Universia Abierta y a Distancia e Méico cuatrimestre Cálculo iferencial Eucación Abierta y a Distancia * Ciencias Eactas, Ingenierías y Tecnologías Ínice Presentación e la unia 3 Propósitos 3 Competencia
Universia Abierta y a Distancia e Méico cuatrimestre Cálculo iferencial Eucación Abierta y a Distancia * Ciencias Eactas, Ingenierías y Tecnologías Ínice Presentación e la unia 3 Propósitos 3 Competencia
La regla de la constante. La derivada de una función constante es 0. Es decir, si c es un número real, entonces d c 0. dx (Ver la figura 2.
 SECCIÓN. Reglas básicas e erivación razón e cambio 07. Reglas básicas e erivación razón e cambio Encontrar la erivaa e una función por la regla e la constante. Encontrar la erivaa e una función por la
SECCIÓN. Reglas básicas e erivación razón e cambio 07. Reglas básicas e erivación razón e cambio Encontrar la erivaa e una función por la regla e la constante. Encontrar la erivaa e una función por la
Lección 6. Métodos de distancias
 étoos e istancias lternativa a L para minimizar el impacto e cambios no observaos. Se pueen ver como aproximaciones rápias a L. Lección. étoos e istancias Se utilizan istancias corregias que son estimas
étoos e istancias lternativa a L para minimizar el impacto e cambios no observaos. Se pueen ver como aproximaciones rápias a L. Lección. étoos e istancias Se utilizan istancias corregias que son estimas
MEDIDA PRECISA DE PARÁMETROS
 CAPÍTULO 6 MEDIDA PRECISA DE PARÁMETROS 6.1. INTRODUCCIÓN Muchas aplicaciones e ifracción e rayos x requieren el conocimiento preciso e los parámetros e re. El proceso e meir un parámetro e re es inirecto
CAPÍTULO 6 MEDIDA PRECISA DE PARÁMETROS 6.1. INTRODUCCIÓN Muchas aplicaciones e ifracción e rayos x requieren el conocimiento preciso e los parámetros e re. El proceso e meir un parámetro e re es inirecto
Ecuación de Schrödinger
 Ecuación e Schröinger En cuanto a onas electromagnéticas, ya vimos que su comportamiento está regio por las ecuaciones e Maxwell. También hemos visto que a una partícula con masa se le puee asignar una
Ecuación e Schröinger En cuanto a onas electromagnéticas, ya vimos que su comportamiento está regio por las ecuaciones e Maxwell. También hemos visto que a una partícula con masa se le puee asignar una
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS. Métodos multivariantes en control estadístico de la calidad
 UNIVESIDAD NACIONAL MAYO DE SAN MACOS FACULTAD DE CIENCIAS MATEMÁTICAS E.A.P. DE ESTADÍSTICA Métoos multivariantes en control estaístico e la calia Capítulo I. Gráficos e control estaístico univariaa TABAJO
UNIVESIDAD NACIONAL MAYO DE SAN MACOS FACULTAD DE CIENCIAS MATEMÁTICAS E.A.P. DE ESTADÍSTICA Métoos multivariantes en control estaístico e la calia Capítulo I. Gráficos e control estaístico univariaa TABAJO
MATEMÁTICAS BÁSICAS DERIVADA INCREMENTOS x = x - x y2 = f(x2) y = y - y y = f(x )
 Faculta e Contauría Aministración. UNAM Derivaa Autor: Dr. José Manuel Becerra Espinosa MATEMÁTICAS BÁSICAS DERIVADA INCREMENTOS Se eine como incremento e la variable al aumento o isminución que eperimenta,
Faculta e Contauría Aministración. UNAM Derivaa Autor: Dr. José Manuel Becerra Espinosa MATEMÁTICAS BÁSICAS DERIVADA INCREMENTOS Se eine como incremento e la variable al aumento o isminución que eperimenta,
Pre saberes: Despeje de ecuaciones. Concepto de línea recta.
 Colegio Javier III Triestre En el 07 Activa tu fe Presentación # Tea: La recta Elaborao por: profesor Héctor Luis Fernánez Pre saberes: Despeje e ecuaciones. Concepto e línea recta. OBJETIVOS DE CLASE:.
Colegio Javier III Triestre En el 07 Activa tu fe Presentación # Tea: La recta Elaborao por: profesor Héctor Luis Fernánez Pre saberes: Despeje e ecuaciones. Concepto e línea recta. OBJETIVOS DE CLASE:.
EJERCICIOS PROPUESTOS
 Solucionario 8 Electrostática EJERCICIOS PROPUESTOS 8. Calcula la carga eléctrica e los iones Ca, F y Al 3. Es posible comunicar a un cuerpo una carga eléctrica igual a un número fraccionario e electrones?
Solucionario 8 Electrostática EJERCICIOS PROPUESTOS 8. Calcula la carga eléctrica e los iones Ca, F y Al 3. Es posible comunicar a un cuerpo una carga eléctrica igual a un número fraccionario e electrones?
Electrónica Analógica
 Electrónica Analógica Conferencia #2 Moelos y parámetros e la unión P-N. iferentes moelos el ioo. Resistencia inámica e la unión P-N. Efectos capacitivos. iempos e conmutación. Bibliografía: Microelectrónica.
Electrónica Analógica Conferencia #2 Moelos y parámetros e la unión P-N. iferentes moelos el ioo. Resistencia inámica e la unión P-N. Efectos capacitivos. iempos e conmutación. Bibliografía: Microelectrónica.
Cálculo de celosías planas de nudos articulados con el método de Ritter
 álculo e celosías planas e nuos articulaos con el métoo e Ritter pellios, Nombre Departamento entro Pérez García, gustín (aperezg@mes.upv) Guariola Víllora, rianna (aguario@mes.upv) Mecánica el Meio ontinuo
álculo e celosías planas e nuos articulaos con el métoo e Ritter pellios, Nombre Departamento entro Pérez García, gustín (aperezg@mes.upv) Guariola Víllora, rianna (aguario@mes.upv) Mecánica el Meio ontinuo
RESALTO DE ONDAS (1< Fr 1 < 1,7)
 UNIVERSIDAD DE CHIE - CI 4A HIDRÁUICA RESATO DE ONDAS (< Fr
UNIVERSIDAD DE CHIE - CI 4A HIDRÁUICA RESATO DE ONDAS (< Fr
Tema 7. Propagación por onda de superficie
 Tema 7. Propagación por ona e superficie 1 Introucción...2 1.1 Características e la propagación...2 2 Antena monopolo corto...2 2.1 Ganancia respecto a la antena isótropa y al ipolo...3 2.2 Campo raiao
Tema 7. Propagación por ona e superficie 1 Introucción...2 1.1 Características e la propagación...2 2 Antena monopolo corto...2 2.1 Ganancia respecto a la antena isótropa y al ipolo...3 2.2 Campo raiao
2.5 Derivación implícita
 SECCIÓN.5 Derivación implícita.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. EXPLORACIÓN Representación gráfica e una
SECCIÓN.5 Derivación implícita.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. EXPLORACIÓN Representación gráfica e una
mv 9, r 0,057 m 1, F F E q q v B E v B N C
 1. Un electrón que se mueve a través e un tubo e rayos catóicos a 1 7 m/s, penetra perpenicularmente en un campo e 1-3 T que actúa sobre una zona e 4 cm a lo largo el tubo. Calcula: a) La esviación que
1. Un electrón que se mueve a través e un tubo e rayos catóicos a 1 7 m/s, penetra perpenicularmente en un campo e 1-3 T que actúa sobre una zona e 4 cm a lo largo el tubo. Calcula: a) La esviación que
CAMPO MAGNÉTICO DE UNA CORRIENTE RECTILÍNEA
 Laboratorio e Física General (Electricia y Magnetismo) CAMPO MAGNÉTICO DE UNA CORRIENTE RECTILÍNEA Fecha: 02/10/2013 1. Objetivo e la práctica Estuio el campo magnético creao por una corriente eléctrica
Laboratorio e Física General (Electricia y Magnetismo) CAMPO MAGNÉTICO DE UNA CORRIENTE RECTILÍNEA Fecha: 02/10/2013 1. Objetivo e la práctica Estuio el campo magnético creao por una corriente eléctrica
Tema 8: Derivación. José M. Salazar. Noviembre de 2016
 Tema 8: Derivación. José M. Salazar Noviembre e 2016 Tema 8: Derivación. Lección 9. Derivación: teoría funamental. Lección 10. Aplicaciones e la erivación. Ínice 1 Derivaas. Principales nociones y resultaos.
Tema 8: Derivación. José M. Salazar Noviembre e 2016 Tema 8: Derivación. Lección 9. Derivación: teoría funamental. Lección 10. Aplicaciones e la erivación. Ínice 1 Derivaas. Principales nociones y resultaos.
ESTADÍSTICA PARA ADMINISTRACIÓN GRAFICAS DE CONTROL PARA LA DESVIACIÓN ESTÁNDAR DELPROCESO: GRAFICAS s
 GRAFICAS DE CONTROL PARA LA DESVIACIÓN ESTÁNDAR DELPROCESO: GRAFICAS s Desviación estánar el proceso conocia La línea central e la gráfica e control no se sitúa en la esviación estánar esignaa para el
GRAFICAS DE CONTROL PARA LA DESVIACIÓN ESTÁNDAR DELPROCESO: GRAFICAS s Desviación estánar el proceso conocia La línea central e la gráfica e control no se sitúa en la esviación estánar esignaa para el
La derivada de las funciones trascendentes
 La erivaa e las funciones trascenentes Manuel Barahona, Eliseo Martínez Diciembre 205 Muchos fenómenos e la naturaleza son moelaos meiante funciones eponeciales, logarítimicas, trigonométricas y combinaciones
La erivaa e las funciones trascenentes Manuel Barahona, Eliseo Martínez Diciembre 205 Muchos fenómenos e la naturaleza son moelaos meiante funciones eponeciales, logarítimicas, trigonométricas y combinaciones
SISTEMAS DE COORDENADAS EN EL ESPACIO
 Matemática Diseño Inustrial Coorenaas en el espacio Ing. vila Ing. Moll SISTEMS DE CRDENDS EN EL ESPCI De forma similar a la vista para el plano, se pueen efinir istintos sistemas e coorenaas. CRDENDS
Matemática Diseño Inustrial Coorenaas en el espacio Ing. vila Ing. Moll SISTEMS DE CRDENDS EN EL ESPCI De forma similar a la vista para el plano, se pueen efinir istintos sistemas e coorenaas. CRDENDS
( ) 2. Pendiente de una Recta Tangente. Sea f una función que es continua en x. 1. Para definir la pendiente de la recta tangente ( )
 Derivaa e una Función Ínice.. Introucción.. Peniente e una recta tangente.. Derivaa e una función. 4. Derivaas laterales. 5. Derivaa e una función compuesta (Regla e la Caena). 6. Tabla e erivaas usuales.
Derivaa e una Función Ínice.. Introucción.. Peniente e una recta tangente.. Derivaa e una función. 4. Derivaas laterales. 5. Derivaa e una función compuesta (Regla e la Caena). 6. Tabla e erivaas usuales.
Alcance máximo y normal en el plano horizontal
 AÑO 17 1.88 Alcance máximo y normal en el plano horizontal Maximum an normal reach in the horizontal plane a porteé maximale et normale ans le plan horizontal Autor: Instituto Nacional e Seguria e Higiene
AÑO 17 1.88 Alcance máximo y normal en el plano horizontal Maximum an normal reach in the horizontal plane a porteé maximale et normale ans le plan horizontal Autor: Instituto Nacional e Seguria e Higiene
Prueba experimental. Difracción de luz en un hilo.
 Prueba experimental. Difracción e luz en un hilo. Introucción; objetivo. El año 214 ha sio eclarao Año Internacional e la Cristalografía por las Naciones Unias, para conmemorar el centenario el escubrimiento
Prueba experimental. Difracción e luz en un hilo. Introucción; objetivo. El año 214 ha sio eclarao Año Internacional e la Cristalografía por las Naciones Unias, para conmemorar el centenario el escubrimiento
Nombre:...Curso:... CAMPO ELECTRICO
 Nombre:...Curso:... CAMPO ELECTRICO El concepto e campo es un importante meio para la escripción e algunos fenómenos físicos, un ejemplo e esto es el caso e la Tierra, ya que cualquier objeto e masa m
Nombre:...Curso:... CAMPO ELECTRICO El concepto e campo es un importante meio para la escripción e algunos fenómenos físicos, un ejemplo e esto es el caso e la Tierra, ya que cualquier objeto e masa m
PERIODO DE SEMIDESINTEGRACION RADIACTIVA
 Universia acional Autónoma e Honuras UAH-VS Experimento o. 4 PERIODO DE SEMIDESITEGRACIO RADIACTIVA OBJETIVOS Manejar un contaor Geiger-Muller como instrumento para meir raio activia. Meir la raiación
Universia acional Autónoma e Honuras UAH-VS Experimento o. 4 PERIODO DE SEMIDESITEGRACIO RADIACTIVA OBJETIVOS Manejar un contaor Geiger-Muller como instrumento para meir raio activia. Meir la raiación
Parcial de Cálculo C 0
 Parcial e Cálculo C 0 0 0 Funamentos e Matemáticas Usar los polinomios e Talor para averiguar si la función g = 7 alcanza o no un etremo local en = 0 sen ln Solución: El polinomio e Talor en = 0 e un polinomio
Parcial e Cálculo C 0 0 0 Funamentos e Matemáticas Usar los polinomios e Talor para averiguar si la función g = 7 alcanza o no un etremo local en = 0 sen ln Solución: El polinomio e Talor en = 0 e un polinomio
Derivación. (x c) que pasa por el punto fijo (c, f(c)) y el punto móvil (c + h, f(c + h)) cuando h tiende a 0.
 Derivación Definición y propieaes básicas Definición. Una función f efinia en un entorno e un punto c R es erivable en c si y sólo si el ite f c = f fc + h fc f fc c := = h h c c eiste y toma un valor
Derivación Definición y propieaes básicas Definición. Una función f efinia en un entorno e un punto c R es erivable en c si y sólo si el ite f c = f fc + h fc f fc c := = h h c c eiste y toma un valor
= 3, electrones F = K
 6 Campo eléctrico Activiaes el interior e la unia. Con frecuencia, cuano os cuerpos se frotan, auieren cargas iguales e signo opuesto. Explica ué sucee en el proceso. La fricción hace ue pasen electrones
6 Campo eléctrico Activiaes el interior e la unia. Con frecuencia, cuano os cuerpos se frotan, auieren cargas iguales e signo opuesto. Explica ué sucee en el proceso. La fricción hace ue pasen electrones
, de lo que d, como se expone en d. 62. De las gráficas dadas la que mejor corresponde con la interpretación de la ley de Coulomb:
 ELECTRICIDAD 4. Ley e Coulomb 6. Aunque la balanza e torsión fue creaa por el geólogo inglés Michell, para conocer la intensia sísmica, fue mejoraa por su paisano Cavenish, para comprobar y completar la
ELECTRICIDAD 4. Ley e Coulomb 6. Aunque la balanza e torsión fue creaa por el geólogo inglés Michell, para conocer la intensia sísmica, fue mejoraa por su paisano Cavenish, para comprobar y completar la
Derivadas de orden superior e implícitas
 CDIN06_MAAL_Implícitas Versión: Septiembre 0 Revisor: Sanra Elvia Pérez Derivaas e oren superior e implícitas por Sanra Elvia Pérez Derivación implícita Las funciones que has estuiao hasta este momento
CDIN06_MAAL_Implícitas Versión: Septiembre 0 Revisor: Sanra Elvia Pérez Derivaas e oren superior e implícitas por Sanra Elvia Pérez Derivación implícita Las funciones que has estuiao hasta este momento
Regla de la cadena. Ejemplo 1. y = f (g(x)) Como las funciones son diferenciables son suaves.
 1 Regla e la caena Hasta aquí hemos erivao funciones que no son compuestas. El problema surge cuano tenemos una función que es compuesta, por ejemplo, igamos que el precio e la gasolina epene el precio
1 Regla e la caena Hasta aquí hemos erivao funciones que no son compuestas. El problema surge cuano tenemos una función que es compuesta, por ejemplo, igamos que el precio e la gasolina epene el precio
Capacitor con dos dieléctricos en diagonal. 5 de junio de 2016
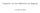 Capacitor con os ieléctricos en iagonal 5 e junio e 206 Ínice. Enunciao 2. Respuesta 3. Solución 4. Análisis e la solución 4 Física II 3 SOLUCIÓN. Enunciao Dao el capacitor e placas cuaraas paralelas e
Capacitor con os ieléctricos en iagonal 5 e junio e 206 Ínice. Enunciao 2. Respuesta 3. Solución 4. Análisis e la solución 4 Física II 3 SOLUCIÓN. Enunciao Dao el capacitor e placas cuaraas paralelas e
Diferenciales e integral indefinida
 Diferenciales e integral inefinia El estuiante: Aplicará los conceptos e iferencial e integral inefinia, meiante la solución e problemas relacionaos con las ciencias naturales, las económico-aministrativas
Diferenciales e integral inefinia El estuiante: Aplicará los conceptos e iferencial e integral inefinia, meiante la solución e problemas relacionaos con las ciencias naturales, las económico-aministrativas
d) Si tiene la siguiente función para la oferta de trabajo:
 Capítulo MERCADO DE TRABAJO, FUNCIÓN DE RODUCCIÓN Y OFERTA AGREGADA DE ARGO AZO. Sea la función e proucción: Y = A0( f 0 f ) Done las uniaes en las que se expresa la cantia e trabajaores a emplear son
Capítulo MERCADO DE TRABAJO, FUNCIÓN DE RODUCCIÓN Y OFERTA AGREGADA DE ARGO AZO. Sea la función e proucción: Y = A0( f 0 f ) Done las uniaes en las que se expresa la cantia e trabajaores a emplear son
2.5 Derivación implícita
 SECCIÓN.5 Derivación implícita 4.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. E X P L O R A C I Ó N Representación gráfica
SECCIÓN.5 Derivación implícita 4.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. E X P L O R A C I Ó N Representación gráfica
Derivadas algebraicas
 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez Derivaas algebraicas por Sanra Elvia Pérez Derivaa e una función El concepto e erivaa, base el cálculo iferencial, ha permitio
CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez Derivaas algebraicas por Sanra Elvia Pérez Derivaa e una función El concepto e erivaa, base el cálculo iferencial, ha permitio
CLASE II Estática de las construcciones II
 ntroucción a las construcciones CLASE Estática e las construcciones lustración sobre la variación e los esfuerzos e estructuras simples. Galileo Galilei, en Discorsi e Dimostrazioni Matematiche, intorno
ntroucción a las construcciones CLASE Estática e las construcciones lustración sobre la variación e los esfuerzos e estructuras simples. Galileo Galilei, en Discorsi e Dimostrazioni Matematiche, intorno
08. Un cubo de lado 0,3 m está colocado con un vértice en el origen de coordenadas, como se muestra la figura. Se encuentra en el seno de un campo
 Campo Eléctrico U 01. Dos partículas e masa 10 g se encuentran suspenias ese un mismo punto por os hilos e 30 cm e longitu. Se suministra a ambas partículas la misma carga, separánose e moo ue los hilos
Campo Eléctrico U 01. Dos partículas e masa 10 g se encuentran suspenias ese un mismo punto por os hilos e 30 cm e longitu. Se suministra a ambas partículas la misma carga, separánose e moo ue los hilos
Interferencia y difracción
 Interferencia ifracción 3 INTRODUCCIÓN TEÓRICA Los efensores e la teoría corpuscular e Newton argumentaban que si la luz era una ona, ebería manifestar fenómenos típicos e ésta. Thomas Young, en 1801,
Interferencia ifracción 3 INTRODUCCIÓN TEÓRICA Los efensores e la teoría corpuscular e Newton argumentaban que si la luz era una ona, ebería manifestar fenómenos típicos e ésta. Thomas Young, en 1801,
ELECTRICIDAD 6. Campo eléctrico 1
 LCTRICIDAD 6. Campo eléctrico 0*. n 838, Faraay, a través e los experimentos realizaos con los campos magnéticos y visualizar como se orientaba el polvillo e hierro en tales campos, sugirió una forma e
LCTRICIDAD 6. Campo eléctrico 0*. n 838, Faraay, a través e los experimentos realizaos con los campos magnéticos y visualizar como se orientaba el polvillo e hierro en tales campos, sugirió una forma e
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID. PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso )
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso 00-003) MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES:
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso 00-003) MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES:
Ejercicio Práctico 1 Enunciado
 Funamentos e Programación Grupo 5 Samuel Martín Ejercicio Práctico Enunciao Instrucciones generales El alumno eberá presentar los ejercicios planteaos en este ocumento. Aicionalmente, se han facilitao
Funamentos e Programación Grupo 5 Samuel Martín Ejercicio Práctico Enunciao Instrucciones generales El alumno eberá presentar los ejercicios planteaos en este ocumento. Aicionalmente, se han facilitao
Distancia Focal de una Lente Delgada
 Distancia Focal e una Lente Delgaa Objetivo: Análisis e iversas lentes elgaas. Equipamiento Teoría Banco Optico Lente convexa Lente concava Fuente e luz (Ampolleta) Fuente e poer para la ampolleta Pantalla
Distancia Focal e una Lente Delgaa Objetivo: Análisis e iversas lentes elgaas. Equipamiento Teoría Banco Optico Lente convexa Lente concava Fuente e luz (Ampolleta) Fuente e poer para la ampolleta Pantalla
Principio de incertidumbre
 Material iáctico ara el curso e Química Cuántica Anrés Ceillo Deartamento e Química, UAM-I Mayo e 998 Princiio e incertiumbre El estao cuántico e un sistema está escrito or la función e ona (x), y su móulo
Material iáctico ara el curso e Química Cuántica Anrés Ceillo Deartamento e Química, UAM-I Mayo e 998 Princiio e incertiumbre El estao cuántico e un sistema está escrito or la función e ona (x), y su móulo
Ecuaciones Diferenciales de primer Orden
 4 Ecuaciones Diferenciales e primer Oren 1.1 1.1. Introucción Las palabras ecuaciones y iferenciales nos hacen pensar en la solución e cierto tipo e ecuación que contenga erivaas. Así como al estuiar álgebra
4 Ecuaciones Diferenciales e primer Oren 1.1 1.1. Introucción Las palabras ecuaciones y iferenciales nos hacen pensar en la solución e cierto tipo e ecuación que contenga erivaas. Así como al estuiar álgebra
ENGRANAJES TIPOS DE ENGRANAJES
 EGRAAJES Son piezas generalmente e forma cilínrica provistas e ientes en una e sus superficies, con el fin e embonarse (conectarse) con otra pieza similar y transmitir potencia. TIPOS DE EGRAAJES RECTOS:
EGRAAJES Son piezas generalmente e forma cilínrica provistas e ientes en una e sus superficies, con el fin e embonarse (conectarse) con otra pieza similar y transmitir potencia. TIPOS DE EGRAAJES RECTOS:
Explicación de la velocidad de rotación en galaxias espirales Interpretación Lagragiana (Yul Goncalves,
 Explicación e la velocia e rotación en galaxias espirales Interpretación Lagragiana (Yul Goncalves, yulalebran9@gmail.com) A continuación se presenta una emostración e la velocia e rotación en galaxias
Explicación e la velocia e rotación en galaxias espirales Interpretación Lagragiana (Yul Goncalves, yulalebran9@gmail.com) A continuación se presenta una emostración e la velocia e rotación en galaxias
XXII OLIMPIADA NACIONAL DE FÍSICA Guadalajara, Jal de noviembre de 2011 Prueba teórica
 XXII OLIMPI NIONL E FÍSI Guaalajara, Jal. 0-4 e noviembre e 011 Prueba teórica 1. PROLEM olisión e pieras (8 puntos) Una piera esférica se eja caer ese un eificio alto e altura h (ese la calle) al tiempo
XXII OLIMPI NIONL E FÍSI Guaalajara, Jal. 0-4 e noviembre e 011 Prueba teórica 1. PROLEM olisión e pieras (8 puntos) Una piera esférica se eja caer ese un eificio alto e altura h (ese la calle) al tiempo
DOCENTE: JESÚS E. BARRIOS P.
 DOCENTE: JESÚS E. BARRIOS P. DEFINICIONES Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un texto matemático chino que proviene del año 300 A. C. a 200 A. C., Nueve capítulos
DOCENTE: JESÚS E. BARRIOS P. DEFINICIONES Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un texto matemático chino que proviene del año 300 A. C. a 200 A. C., Nueve capítulos
Soluciones Junio y Septiembre ( ) Junio 2008
 Junio 2008 1. (A1) a) A$B = b) 2 0 1 1 0 0 3 2 0 0 1 0 1 0 1 0 0 1 1 0 0 1 3 0 1 3 0 1 0 1 2 1 1 2 2 0 0 1 1 3 0 2 3 5 0 2 7 2 2 3 0 0 v 2 0 1 1 0 0 0 4 3 3 2 0 0 0 3 1 0 2 f 6 0 0 2 0 2 0 4 0 2 2 2 0
Junio 2008 1. (A1) a) A$B = b) 2 0 1 1 0 0 3 2 0 0 1 0 1 0 1 0 0 1 1 0 0 1 3 0 1 3 0 1 0 1 2 1 1 2 2 0 0 1 1 3 0 2 3 5 0 2 7 2 2 3 0 0 v 2 0 1 1 0 0 0 4 3 3 2 0 0 0 3 1 0 2 f 6 0 0 2 0 2 0 4 0 2 2 2 0
