MÉTODOS NUMÉRICOS. 1.1 Sistemas de numeración
|
|
|
- Alfredo Roldán Guzmán
- hace 7 años
- Vistas:
Transcripción
1 MÉTODOS NUMÉRICOS 1.1 Sistemas de numeración
2 Sistemas numéricos. Los números son los mismos en todos lados. Sus nombres y su simbología podrán ser diferentes, pero tienen el mismo significado. Los pueblos primitivos aprendieron a contar con los dedos, con los que no podían alcanzar cifras elevadas, pero si las suficientes para satisfacer sus necesidades. Si querían recordar algunos números, hacían incisiones en un palo o marcas en una roca.
3 Sistemas numéricos. Aún ahora, para contar algunas cosas, es útil usar rayas verticales, agrupando de cinco en cinco. Hay muchas maneras de contar: de dos en dos, porque las personas tienen dos manos, dos pies, dos ojos y dos orejas; de cinco en cinco, porque hay cinco dedos en cada mano; de diez en diez, porque son diez los dedos de las manos; de veinte en veinte, porque se tienen veinte dedos sumando los de las manos y los pies. Por eso, los números que sirven para contar se llaman naturales: x N. Cuando la gente empezó a escribir, también encontró la forma de representar los números de manera más sencilla, con símbolos.
4 Los números egipcios. Los egipcios fueron quizá los primeros que crearon una forma de escritura numérica, usando diferentes símbolos: El sistema numeral egipcio tiene como base el diez, pero no es posicional, porque no hace uso del cero; para representar un número, se repetían los ocho símbolos anotados, hasta nueve veces cada uno, con lo cual se alcanzaba un rango de representación de 1 a De izquierda a derecha, primero aparecían las unidades, luego las decenas, en seguida las centenas y así, sucesivamente. La interpretación de los números se hace leyendo de derecha a izquierda, sumando los valores de los símbolos. Ejemplo:
5 Los números romanos Los romanos usaron letras del alfabeto para construir un sistema de numeración que resultaba algo más fácil de manejar: I V X L C D M Los números romanos todavía se usan, por tradición, en relojes, para el capitulado de libros, etc., como representaciones elegantes de los números, pero ya no para fines aritméticos. Las reglas de escritura incluyen el no usar nunca tres símbolos iguales juntos, lo que implica tener que hacer restas para interpretar correctamente la representación de algunos números: IV, cinco menos uno; IX, diez menos uno; XL, cincuenta menos diez; XC, cien menos diez; CD, quinientos menos cien; y CM, mil menos cien. El sistema numeral romano usa el diez como base, es decir, que la progresión se realiza de diez en diez, de derecha a izquierda; el no uso del cero lo hace pseudo-posicional. Utiliza treinta numerales básicos para representar números en el rango de 1 a 3999:
6 Los números romanos Para las unidades: I II III IV V VI VII VIII IX Para las decenas: X XX XXX XL L LX LXX LXXX XC Para las centenas: C CC CCC CD D DC DCC DCCC CM Para las unidades de millar: M MM MMM Con objeto de aumentar el rango de escritura de los números romanos, más tarde se optó por colocar una raya sobre los numerales, para indicar que su valor se incrementa mil veces, dos rayas, para incrementarlo un millón de veces, etc.; esta regla tiene validez a partir del número IV y hasta el número MMMCMXCIX. Ejemplos: XVIII CII MCMXCVII X VIII C II M CM XC VII
7 Los números mayas El sistema numeral maya es semejante al romano, pero resulta superior por cuanto al uso del cero y porque en ningún caso es necesario restar para interpretar un número. El sistema maya usa solamente tres símbolos: Con estos símbolos se puede representar cualquier número de 0 a, para lo cual requiere del uso de veinte numerales básicos:
8 Los números mayas El sistema de numeración maya es vigesimal, es decir, que la progresión se realiza de veinte en veinte, de abajo hacia arriba, lo que le da la característica de ser posicional, donde la primera posición representa unidades, la segunda veintenas, las tercera múltiplos de cuatrocientos, la cuarta múltiplos de ocho mil, etc. Se escribe y se lee de arriba hacia abajo. Ejemplos: 4 x 400 = x 20 = x 20 = x 1 = 18 2 x 1 = 2 17 x 1 =
9 La evolución de los números. Además de contar, la gente empezó a necesitar hacer algo más con los números: medirlos, fraccionarlos, sumarlos, restarlos, multiplicarlos y dividirlos. Así nació la aritmética, la que ha evolucionado a medida que el hombre avanza y encuentra muchas cosas que calcular y también muy distintas maneras de hacerlo. Pero toda la matemática se basa en el simple acto de contar. La necesidad de utilizar números cada vez mayores trajo consigo la noción de infinito:, descubierta por los griegos a través de un elevado nivel de abstracción. Los números naturales ya no fueron suficientes; había la necesidad de fraccionarlos para dividir en partes un todo, y así nacieron los números racionales: Q = {q q = a/b}, (a, b N).
10 La evolución de los números. La aparición del cero: 0, nace de la necesidad de representar la diferencia entre dos números idénticos y constituye el elemento fundamental para la construcción de los sistemas numéricos posicionales. Con la invención del álgebra, aparecieron los números negativos como solución de ecuaciones, y con ello se pudo establecer la clasificación de los números enteros en positivos y negativos: Z + = {z > 0}; Z - = {z < 0} La necesidad de representar algunas cantidades requeridas por los desarrollos geométricos trajo consigo el advenimiento de los números irracionales: π, e, 2, etc. Q c = {u u R, u Q} La unidad y fundamento lógico del estudio de los números se alcanzó a través de la construcción del sistema de los números reales, R, que incluye a todos los mencionados anteriormente. Los números complejos, C, aparecieron de la misma manera que los negativos, al resolver ecuaciones cuyo resultado requería de la introducción de los llamados números imaginarios.
SECCIÓN SECUNDARIA SISTEMAS DE NUMERACIÓN Numeración Babilónica
 SECCIÓN SECUNDARIA SISTEMAS DE NUMERACIÓN Numeración Babilónica La civilización sumeria fue la que inventó y utilizó un sistema de numeración de base sexagesimal (la base es el 60), en donde se utiliza
SECCIÓN SECUNDARIA SISTEMAS DE NUMERACIÓN Numeración Babilónica La civilización sumeria fue la que inventó y utilizó un sistema de numeración de base sexagesimal (la base es el 60), en donde se utiliza
UNIDAD 1: SISTEMAS DE NUMERACIÓN
 UNIDAD 1: SISTEMAS DE NUMERACIÓN ÍNDICE 1.1 Nuestro sistema de numeración 1.1.1 Lectura de números naturales 1.1.2 Descomposición de números naturales 1.2 Comparación y ordenación de Nº naturales 1.3 Los
UNIDAD 1: SISTEMAS DE NUMERACIÓN ÍNDICE 1.1 Nuestro sistema de numeración 1.1.1 Lectura de números naturales 1.1.2 Descomposición de números naturales 1.2 Comparación y ordenación de Nº naturales 1.3 Los
NUMERACIÓN. Vale 5 veces
 1) Completa la siguiente tabla NUMERACIÓN En el número 1.245 8.473 4.788 6.004 5.409 El 4 vale 2) Qué número es? a) 38 UM + 58 d + 123 c = b) 15 d + 148 u + 76 c = c) 88 u + 405 d + 7 DM = 3) Indica la
1) Completa la siguiente tabla NUMERACIÓN En el número 1.245 8.473 4.788 6.004 5.409 El 4 vale 2) Qué número es? a) 38 UM + 58 d + 123 c = b) 15 d + 148 u + 76 c = c) 88 u + 405 d + 7 DM = 3) Indica la
TABLA DE CONTENIDO. Números Naturales. Series Numéricas. Valor de Posición en Números Naturales. Descomposición de los Números Naturales
 TABLA DE CONTENIDO TEMA 1 TEMA 2 TEMA 3 TEMA 4 TEMA 5 TEMA 6 TEMA 7 TEMA 8 TEMA 9 TEMA 10 TEMA 11 TEMA 12 Números Naturales Series Numéricas Valor de Posición en Números Naturales Descomposición de los
TABLA DE CONTENIDO TEMA 1 TEMA 2 TEMA 3 TEMA 4 TEMA 5 TEMA 6 TEMA 7 TEMA 8 TEMA 9 TEMA 10 TEMA 11 TEMA 12 Números Naturales Series Numéricas Valor de Posición en Números Naturales Descomposición de los
Sistema de numeración romano
 R Sistema de numeración romano Escribe con números romanos. > XXIV 8 > CCCLXXXV 8 > IVCCXXXVIII > 90 > 999 > 0 > > LV CMXCIV MMCCCLVI 0 > XC CCXL MCCLX Aplica las reglas y averigua el valor de los siguientes
R Sistema de numeración romano Escribe con números romanos. > XXIV 8 > CCCLXXXV 8 > IVCCXXXVIII > 90 > 999 > 0 > > LV CMXCIV MMCCCLVI 0 > XC CCXL MCCLX Aplica las reglas y averigua el valor de los siguientes
Un sistema de numeración es una serie de símbolos y unas normas que empleamos para expresar los números.
 MATEMÁTICAS GRADO SEXTO SISTEMA DE NUMERACIÓN DECIMAL 06/02/2017 SISTEMA DE NUMERACIÓN DECIMAL ORÍGENES Un sistema de numeración es una serie de símbolos y unas normas que empleamos para expresar los números.
MATEMÁTICAS GRADO SEXTO SISTEMA DE NUMERACIÓN DECIMAL 06/02/2017 SISTEMA DE NUMERACIÓN DECIMAL ORÍGENES Un sistema de numeración es una serie de símbolos y unas normas que empleamos para expresar los números.
Lección 1: Números naturales. Sistema de numeración decimal y orden
 Lección 1: Números naturales. Sistema de numeración decimal y orden Sistema de numeración Los números naturales son los que usamos para contar y forman un conjunto infinito, un conjunto que no se acaba.
Lección 1: Números naturales. Sistema de numeración decimal y orden Sistema de numeración Los números naturales son los que usamos para contar y forman un conjunto infinito, un conjunto que no se acaba.
Cuaderno de matemáticas 1. Numeración: Concepto y grafía del número 5.
 Cuaderno de matemáticas 1 Numeración: Concepto y grafía del número 1. Conceptos matemáticos: Formas geométricas. Nociones espacio-temporales: Dentro, fuera, en el borde. Ampliación y refuerzo: Atención
Cuaderno de matemáticas 1 Numeración: Concepto y grafía del número 1. Conceptos matemáticos: Formas geométricas. Nociones espacio-temporales: Dentro, fuera, en el borde. Ampliación y refuerzo: Atención
Tema 1. Números Naturales. Sistemas de Numeración.
 Tema 1. Números Naturales. Sistemas de Numeración. EGIPCIO MAYA CHINO BABILÓNICO ROMANA Matemáticas. Grado de Maestro en Educación Primaria. Evolución histórica de los sistemas de numeración. Un sistema
Tema 1. Números Naturales. Sistemas de Numeración. EGIPCIO MAYA CHINO BABILÓNICO ROMANA Matemáticas. Grado de Maestro en Educación Primaria. Evolución histórica de los sistemas de numeración. Un sistema
Los números y las operaciones
 Los números y las operaciones Sistema de numeración romano Escribe con números romanos. dieciséis XVI veintitrés XXIII cincuenta L cuarenta y siete XLVII sesenta y ocho LXVIII noventa y nueve XCIX ciento
Los números y las operaciones Sistema de numeración romano Escribe con números romanos. dieciséis XVI veintitrés XXIII cincuenta L cuarenta y siete XLVII sesenta y ocho LXVIII noventa y nueve XCIX ciento
SISTEMA DE ENSEÑANZA ABIERTA Y A DISTANCIA. MATEMÁTICAS I Fascículo 1 SISTEMAS DE NUMERACIÓN
 SISTEMA DE ENSEÑANZA ABIERTA Y A DISTANCIA MATEMÁTICAS I Fascículo 1 SISTEMAS DE NUMERACIÓN MATERIAL COMPLEMENTARIO PARA CONSULTA DEL ESTUDIANTE-ASESOR DE CONTENIDO Elaboró: Profesor Amado Miguel León
SISTEMA DE ENSEÑANZA ABIERTA Y A DISTANCIA MATEMÁTICAS I Fascículo 1 SISTEMAS DE NUMERACIÓN MATERIAL COMPLEMENTARIO PARA CONSULTA DEL ESTUDIANTE-ASESOR DE CONTENIDO Elaboró: Profesor Amado Miguel León
Sistema de numeración No decimal
 Sistema de numeración No decimal Cuando Ismael el mercader consiguió tener muchas vacas se sintió feliz. Pero no sabía cuántas tenía. Sabía que eran muchas más que los dedos de sus pies... Cuántas más?
Sistema de numeración No decimal Cuando Ismael el mercader consiguió tener muchas vacas se sintió feliz. Pero no sabía cuántas tenía. Sabía que eran muchas más que los dedos de sus pies... Cuántas más?
Teoría de la numeración I
 Teoría de la numeración I La ferretería Una mujer entra a una ferretería, ve un producto que le interesa y pregunta: Cuánto cuesta uno?. El vendedor responde ochenta maravedíes. Entonces ella pregunta:
Teoría de la numeración I La ferretería Una mujer entra a una ferretería, ve un producto que le interesa y pregunta: Cuánto cuesta uno?. El vendedor responde ochenta maravedíes. Entonces ella pregunta:
EXPRESIONES VARIABLES
 EXPRESIONES VARIABLES.1.1.1. Un variable es un símbolo que se usa para representar uno o más números. Es común usar letras del alfabeto como variables. El valor del variable que se usa varias veces en
EXPRESIONES VARIABLES.1.1.1. Un variable es un símbolo que se usa para representar uno o más números. Es común usar letras del alfabeto como variables. El valor del variable que se usa varias veces en
Práctica 1: Representación de números enteros
 Organización del Computador I DC - UBA Segundo Cuatrimestre 2010 Número vs Numeral Un número es un objeto matemático Un numeral es un símbolo que representa un número No posicionales Posicionales no posicionales
Organización del Computador I DC - UBA Segundo Cuatrimestre 2010 Número vs Numeral Un número es un objeto matemático Un numeral es un símbolo que representa un número No posicionales Posicionales no posicionales
Sistema de numeración Egipcio (3000 a.c.)
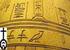 Sistemas de Numeración A lo largo de la historia de la humanidad, el ser humano ha buscado diferentes maneras de representar cantidades. Si nos remontamos hacia más de dos mil años, los pueblos de aquella
Sistemas de Numeración A lo largo de la historia de la humanidad, el ser humano ha buscado diferentes maneras de representar cantidades. Si nos remontamos hacia más de dos mil años, los pueblos de aquella
Tema 1: SISTEMAS DE NUMERACIÓN
 Tema 1: SISTEMAS DE NUMERACIÓN SISTEMAS DE NUMERACIÓN Un sistema de numeración es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos en el sistema. Necesidades
Tema 1: SISTEMAS DE NUMERACIÓN SISTEMAS DE NUMERACIÓN Un sistema de numeración es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos en el sistema. Necesidades
UNIDAD DE APRENDIZAJE III
 UNIDAD DE APRENDIZAJE III INTRODUCCIÓN Leer cuidadosamente el siguiente problema y construir un modelo matemático que dé solución a la situación. Se sabe que el perímetro de un terreno rectangular es 150
UNIDAD DE APRENDIZAJE III INTRODUCCIÓN Leer cuidadosamente el siguiente problema y construir un modelo matemático que dé solución a la situación. Se sabe que el perímetro de un terreno rectangular es 150
I.E.S Santo Domingo. Departamento Informática. Tema 1 Los Sistemas de Numeración. José Luis Mollinedo Jiménez
 I.E.S Santo Domingo Departamento Informática Tema 1 Los Sistemas de Numeración José Luis Mollinedo Jiménez El Ejido - 6 de mayo de 2012 Página:2 Índice 1. Denición 2 2. Ejemplos 2 3. Clasicación 2 3.1.
I.E.S Santo Domingo Departamento Informática Tema 1 Los Sistemas de Numeración José Luis Mollinedo Jiménez El Ejido - 6 de mayo de 2012 Página:2 Índice 1. Denición 2 2. Ejemplos 2 3. Clasicación 2 3.1.
Actividades de Cognitiva Matemáticas que recogen las diversas estrategias de cálculo metal / reflexivo
 s de suma Actividades de Cognitiva Matemáticas que recogen las diversas estrategias de cálculo metal / reflexivo Sumar utilizando los dobles de los números Sumar decenas enteras a números de dos o más
s de suma Actividades de Cognitiva Matemáticas que recogen las diversas estrategias de cálculo metal / reflexivo Sumar utilizando los dobles de los números Sumar decenas enteras a números de dos o más
Sistema De Numeración
 Sistema De Numeración Un sistema de numeración es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos. Un sistema de numeración puede representarse como donde:
Sistema De Numeración Un sistema de numeración es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos. Un sistema de numeración puede representarse como donde:
SISTEMAS NUMÉRICOS. Conocer los diferentes sistemas numéricos y su importancia en la informática y la computación
 SISTEMAS NUMÉRICOS OBJETIVO GENERAL Conocer los diferentes sistemas numéricos y su importancia en la informática y la computación OBJETIVOS ESPECÍFICOS Distinguir los sistemas de numeración Identificar
SISTEMAS NUMÉRICOS OBJETIVO GENERAL Conocer los diferentes sistemas numéricos y su importancia en la informática y la computación OBJETIVOS ESPECÍFICOS Distinguir los sistemas de numeración Identificar
MATEMÁTICAS 5. º CURSO UNIDAD 1: SISTEMAS DE NUMERACIÓN
 MATEMÁTICAS 5. º CURSO UNIDAD 1: SISTEMAS DE NUMERACIÓN OBJETIVOS Conocer los cuatro primeros órdenes de unidades y las equivalencias entre ellos. Leer, escribir y descomponer números de hasta cuatro cifras.
MATEMÁTICAS 5. º CURSO UNIDAD 1: SISTEMAS DE NUMERACIÓN OBJETIVOS Conocer los cuatro primeros órdenes de unidades y las equivalencias entre ellos. Leer, escribir y descomponer números de hasta cuatro cifras.
1. ESQUEMA - RESUMEN Página EJERCICIOS DE INICIACIÓN Página EJERCICIOS DE DESARROLLO Página EJERCICIOS DE AMPLIACIÓN Página 21
 1. ESQUEMA - RESUMEN Página 2 2. EJERCICIOS DE INICIACIÓN Página 7 3. EJERCICIOS DE DESARROLLO Página 19 4. EJERCICIOS DE AMPLIACIÓN Página 21 5. EJERCICIOS DE REFUERZO Página 22 1 1. ESQUEMA - RESUMEN
1. ESQUEMA - RESUMEN Página 2 2. EJERCICIOS DE INICIACIÓN Página 7 3. EJERCICIOS DE DESARROLLO Página 19 4. EJERCICIOS DE AMPLIACIÓN Página 21 5. EJERCICIOS DE REFUERZO Página 22 1 1. ESQUEMA - RESUMEN
LA HISTORIA DE LAS MATEMÁTICAS
 LA HISTORIA DE LAS MATEMÁTICAS ÍNDICE: 1º; LOS EGIPCIOS. 2º;LOS BABILÓNIOS. 3º;LOS ROMANOS. 4º;LOS GRIEGOS. 5º;LOS CHINOS. 6º;LOS NÚMEROS ARÁBICOS. 7º;LA EDAD MEDIA. 8º;CONCLUSIÓN. LOS EGIPCIOS: Desde
LA HISTORIA DE LAS MATEMÁTICAS ÍNDICE: 1º; LOS EGIPCIOS. 2º;LOS BABILÓNIOS. 3º;LOS ROMANOS. 4º;LOS GRIEGOS. 5º;LOS CHINOS. 6º;LOS NÚMEROS ARÁBICOS. 7º;LA EDAD MEDIA. 8º;CONCLUSIÓN. LOS EGIPCIOS: Desde
ÁREA: MATEMÁTICAS UNIDAD : 1 TEMPORALIZACIÓN: OCTUBRE 1ª QUINCENA OBJETIVOS CONTENIDOS CRITERIOS DE EVALUACIÓN
 ÁREA: MATEMÁTICAS UNIDAD : 1 TEMPORALIZACIÓN: OCTUBRE 1ª QUINCENA Conocer los nueve primeros órdenes de unidades y las equivalencias entre ellos. Leer, escribir y descomponer números de hasta nueve cifras.
ÁREA: MATEMÁTICAS UNIDAD : 1 TEMPORALIZACIÓN: OCTUBRE 1ª QUINCENA Conocer los nueve primeros órdenes de unidades y las equivalencias entre ellos. Leer, escribir y descomponer números de hasta nueve cifras.
UNIDAD DE APRENDIZAJE I
 UNIDAD DE APRENDIZAJE I Saberes procedimentales Interpreta y utiliza correctamente el lenguaje simbólico para el manejo de expresiones algebraicas. 2. Identifica operaciones básicas con expresiones algebraicas.
UNIDAD DE APRENDIZAJE I Saberes procedimentales Interpreta y utiliza correctamente el lenguaje simbólico para el manejo de expresiones algebraicas. 2. Identifica operaciones básicas con expresiones algebraicas.
CURSO PROPEDÉUTICO 2017
 CURSO PROPEDÉUTICO 2017 1 FUNDAMENTOS DE MATEMÁTICAS OBJETIVO Formar estudiantes altamente capacitados, que cuenten con competencias y conocimientos para construir y utilizar técnicas que contribuyan a
CURSO PROPEDÉUTICO 2017 1 FUNDAMENTOS DE MATEMÁTICAS OBJETIVO Formar estudiantes altamente capacitados, que cuenten con competencias y conocimientos para construir y utilizar técnicas que contribuyan a
Introducción. Desarrollo. Palabras clave. Matemáticas Unidad 1 Significado y uso de los números. Números enteros
 Matemáticas Unidad 1 Significado y uso de los números Convertir fracciones a su escritura decimal y viceversa. Definir y utilizar los números negativos. Ubicar y representar números enteros, fraccionarios
Matemáticas Unidad 1 Significado y uso de los números Convertir fracciones a su escritura decimal y viceversa. Definir y utilizar los números negativos. Ubicar y representar números enteros, fraccionarios
RESUMEN PARA EL ESTUDIO
 RESUMEN PARA EL ESTUDIO 1. Números de siete cifras U. millón CM DM UM C D U Cómo se lee 2 8 9 6 7 8 2 Cómo se descompone: 2.896.782 = 2 U. millón + 8 CM + 9 DM + 6 UM + 7 C + 8 D + 2 U Cómo se compone:
RESUMEN PARA EL ESTUDIO 1. Números de siete cifras U. millón CM DM UM C D U Cómo se lee 2 8 9 6 7 8 2 Cómo se descompone: 2.896.782 = 2 U. millón + 8 CM + 9 DM + 6 UM + 7 C + 8 D + 2 U Cómo se compone:
OBJETIVO 1 CONOCER LA ESTRUCTURA DEL SISTEMA DE NUMERACIÓN DECIMAL NOMBRE: CURSO: FECHA: Unidad de millar. Decena de millar
 OBJETIVO CONOCER LA ESTRUCTURA DEL SISTEMA DE NUMERACIÓN DECIMAL NOMBRE: CURSO: ECHA: El sistema de numeración decimal tiene dos características:. a Es decimal: 0 unidades de un orden forman unidad del
OBJETIVO CONOCER LA ESTRUCTURA DEL SISTEMA DE NUMERACIÓN DECIMAL NOMBRE: CURSO: ECHA: El sistema de numeración decimal tiene dos características:. a Es decimal: 0 unidades de un orden forman unidad del
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOMCE TEMA I : NÚMEROS NATURALES Sistema de numeración romano. Los números naturales. Números naturales como cardinales y ordinales. o Recta numérica. El sistema de numeración decimal.
MATEMÁTICAS 1º DE ESO LOMCE TEMA I : NÚMEROS NATURALES Sistema de numeración romano. Los números naturales. Números naturales como cardinales y ordinales. o Recta numérica. El sistema de numeración decimal.
CONJUNTO DE LOS NÚMEROS NATURALES
 República Bolivariana de Venezuela Ministerio de la Defensa Universidad Nacional Experimental de las Fuerzas Armadas Curso de Inducción Universitaria CIU Cátedra: Razonamiento Matemático CONJUNTO DE LOS
República Bolivariana de Venezuela Ministerio de la Defensa Universidad Nacional Experimental de las Fuerzas Armadas Curso de Inducción Universitaria CIU Cátedra: Razonamiento Matemático CONJUNTO DE LOS
GESTIÓN ACADÉMICA GUÍA DIDÁCTICA 1
 PÁGINA: 1 de 5 Nombres y Apellidos del Estudiante: Docente: Área: MATEMATICAS Grado: Cuarto Periodo: Primero GUIA 1 Duración: 25 HORAS Asignatura: MATEMATICAS ESTÁNDAR: Resuelvo y formulo problemas cuya
PÁGINA: 1 de 5 Nombres y Apellidos del Estudiante: Docente: Área: MATEMATICAS Grado: Cuarto Periodo: Primero GUIA 1 Duración: 25 HORAS Asignatura: MATEMATICAS ESTÁNDAR: Resuelvo y formulo problemas cuya
Sistemas de Numeración
 Magisterio 1er año C - Matemática 2016 IFD Comenio Canelones Sistemas de Numeración Un sistema de numeración es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos.
Magisterio 1er año C - Matemática 2016 IFD Comenio Canelones Sistemas de Numeración Un sistema de numeración es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos.
El Sistema de numeración Romano utiliza letras para escribir los números: I V X L C D M. uno cinco diez cincuenta cien quinientos mil
 BLOQUE 1. NÚMEROS Y OPERACIONES CAPÍTULO 1.2. REPRESENTACIÓN ESCRITA DE LOS NÚMEROS La necesidad de comunicación entre los seres humanos ha llevado desde antiguo a la invención y uso de signos para contar,
BLOQUE 1. NÚMEROS Y OPERACIONES CAPÍTULO 1.2. REPRESENTACIÓN ESCRITA DE LOS NÚMEROS La necesidad de comunicación entre los seres humanos ha llevado desde antiguo a la invención y uso de signos para contar,
CONTENIDOS Y CRITERIOS DE EVALUACIÓN
 CONTENIDOS Y MATEMÁTICAS 2º E. PRIMARIA PRIMERA EVALUACIÓN 1. Números n a t u ra les menores q u e 400. Nombre, grafía y 2. El sistema de numeración: descomposición de orden y de valor posicional de números
CONTENIDOS Y MATEMÁTICAS 2º E. PRIMARIA PRIMERA EVALUACIÓN 1. Números n a t u ra les menores q u e 400. Nombre, grafía y 2. El sistema de numeración: descomposición de orden y de valor posicional de números
TEMA 1 NÚMEROS NATURALES
 TEMA 1 NÚMEROS NATURALES Criterios De Evaluación de la Unidad 1 Efectuar correctamente operaciones combinadas de números naturales, aplicando correctamente las reglas de prioridad y haciendo un uso adecuado
TEMA 1 NÚMEROS NATURALES Criterios De Evaluación de la Unidad 1 Efectuar correctamente operaciones combinadas de números naturales, aplicando correctamente las reglas de prioridad y haciendo un uso adecuado
COLEGIO AUGUSTO WALTE INFORMACIÓN DE ASIGNATURA I PERÍOD DESCRIPCIÓN DE CONTENIDOS
 COLEGIO AUGUSTO WALTE INFORMACIÓN DE ASIGNATURA I PERÍOD DESCRIPCIÓN DE CONTENIDOS GRADO: 6 ASIGNATURA: Matemática PERIODO: I PROFESORA: Carina Candelario UNIDAD Nº 1 NOMBRE DE LA UNIDAD: CONOZCAMOS SISTEMAS
COLEGIO AUGUSTO WALTE INFORMACIÓN DE ASIGNATURA I PERÍOD DESCRIPCIÓN DE CONTENIDOS GRADO: 6 ASIGNATURA: Matemática PERIODO: I PROFESORA: Carina Candelario UNIDAD Nº 1 NOMBRE DE LA UNIDAD: CONOZCAMOS SISTEMAS
Clasificación de los números
 Clasificación de los números por Sandra Pérez Márquez Los números se crearon para cubrir diferentes necesidades, lo cual permite agruparlos en diferentes conjuntos que se pueden dividir en subconjuntos.
Clasificación de los números por Sandra Pérez Márquez Los números se crearon para cubrir diferentes necesidades, lo cual permite agruparlos en diferentes conjuntos que se pueden dividir en subconjuntos.
NUMEROS NATURALES. En esta unidad se da un repaso de los diferentes conjuntos de números que existen en matemáticas.
 LOS NUMEROS En esta unidad se da un repaso de los diferentes conjuntos de números que existen en matemáticas. Un conjunto es una "colección de objetos"; Así, se puede hablar de un conjunto de personas,
LOS NUMEROS En esta unidad se da un repaso de los diferentes conjuntos de números que existen en matemáticas. Un conjunto es una "colección de objetos"; Así, se puede hablar de un conjunto de personas,
Lección 1: NÚMEROS NATURALES Y ENTEROS.
 Lección 1: NÚMEROS NATURALES Y ENTEROS. 1.- LOS NÚMEROS NATURALES QUÉ ES UN NÚMERO? Un número es la expresión de la idea de cantidad. Esta idea de cantidad es algo natural, nace con nosotros de la necesidad
Lección 1: NÚMEROS NATURALES Y ENTEROS. 1.- LOS NÚMEROS NATURALES QUÉ ES UN NÚMERO? Un número es la expresión de la idea de cantidad. Esta idea de cantidad es algo natural, nace con nosotros de la necesidad
TEMA 1: NÚMEROS NATURALES
 TEMA 1: NÚMEROS NATURALES 1. NÚMEROS NATURALES Todas las civilizaciones han tenido un sistema de numeración. Estos han pasado de unos pueblos a otros y han evolucionado a lo largo del tiempo. Desde la
TEMA 1: NÚMEROS NATURALES 1. NÚMEROS NATURALES Todas las civilizaciones han tenido un sistema de numeración. Estos han pasado de unos pueblos a otros y han evolucionado a lo largo del tiempo. Desde la
FRACCION GENERATRIZ. Pasar de decimal exacto a fracción
 FRACCION GENERATRIZ Un número decimal exacto o periódico puede expresarse en forma de fracción, llamada fracción generatriz, de las formas que indicamos: Pasar de decimal exacto a fracción Si la fracción
FRACCION GENERATRIZ Un número decimal exacto o periódico puede expresarse en forma de fracción, llamada fracción generatriz, de las formas que indicamos: Pasar de decimal exacto a fracción Si la fracción
MatemáticaDiscreta&Lógica 1
 MatemáticaDiscreta&Lógica 1 Sistemas de numeración Aylen Ricca Tecnólogo en Informática San José 2014 http://www.fing.edu.uy/tecnoinf/sanjose/index.html SISTEMAS DE NUMERACIÓN.::. Introducción. Podemos
MatemáticaDiscreta&Lógica 1 Sistemas de numeración Aylen Ricca Tecnólogo en Informática San José 2014 http://www.fing.edu.uy/tecnoinf/sanjose/index.html SISTEMAS DE NUMERACIÓN.::. Introducción. Podemos
GESTIÓN ACADÉMICA GUÍA DIDÁCTICA 2
 PÁGINA: 1 de 7 Nombres y Apellidos del Estudiante: Docente: Esp. Blanca Rozo Blanco Área: Matemáticas Grado:6 Periodo: 1º GUIA 2 Duración: 5 horas Asignatura: Matemáticas ESTÁNDAR: * 1) Justifico procedimientos
PÁGINA: 1 de 7 Nombres y Apellidos del Estudiante: Docente: Esp. Blanca Rozo Blanco Área: Matemáticas Grado:6 Periodo: 1º GUIA 2 Duración: 5 horas Asignatura: Matemáticas ESTÁNDAR: * 1) Justifico procedimientos
643 = 6C + 4D + 3U 6 X X X1 Ejercicios. Escribe las posiciones que faltan de los números naturales.
 Grado Materia Bimestre Periodo de Evaluación GRADO ESCOLAR CUARTO GRADO MATERIA MATEMÁTICAS BIMESTRE/ BLOQUE PRIMER BIMESTRE PERIODO BLOQUE I CONTENIDOS 1-Notación desarrollada de números naturales y decimales
Grado Materia Bimestre Periodo de Evaluación GRADO ESCOLAR CUARTO GRADO MATERIA MATEMÁTICAS BIMESTRE/ BLOQUE PRIMER BIMESTRE PERIODO BLOQUE I CONTENIDOS 1-Notación desarrollada de números naturales y decimales
Bloque 1. Aritmética y Álgebra
 Bloque 1. Aritmética y Álgebra Los números naturales Los números naturales Los números naturales se definen como: N = { 0,1, 2, 3, 4, 5,...,64, 65, 66,...,1639,1640,1641,1642,... } El sistema de numeración
Bloque 1. Aritmética y Álgebra Los números naturales Los números naturales Los números naturales se definen como: N = { 0,1, 2, 3, 4, 5,...,64, 65, 66,...,1639,1640,1641,1642,... } El sistema de numeración
Unidad 1 Los números de todos los días
 CUENTAS ÚTILES Módulo nivel intermedio. 3ra. Edición. Primaria Unidad 1 Los números de todos los días Los números naturales son aquellos que utilizamos para contar: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,
CUENTAS ÚTILES Módulo nivel intermedio. 3ra. Edición. Primaria Unidad 1 Los números de todos los días Los números naturales son aquellos que utilizamos para contar: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,
Orden o comparación. Número 2 cifras más pequeño = Número 2 cifras más grande = Número 2 cifras más pequeño = Número 2 cifras más grande =
 Orden o comparación 1.- Con las cifras de la columna izquierda, debes encontrar el número más grande y el número más pequeño de DOS cifras que con ellas se puede obtener: 3, 8, 2, 7, 9, 6 Número 2 cifras
Orden o comparación 1.- Con las cifras de la columna izquierda, debes encontrar el número más grande y el número más pequeño de DOS cifras que con ellas se puede obtener: 3, 8, 2, 7, 9, 6 Número 2 cifras
TEMARIOS EXAMEN DE ADMISIÓN 2018 ASIGNATURA MATEMÁTICA. Emplear los números para: Identificar Contar Clasificar Sumar y restar Resolución de problemas
 TEMARIOS EXAMEN DE ADMISIÓN 2018 ASIGNATURA MATEMÁTICA 1 Básico Números y operaciones Ámbito 0 al 10 /Habilidad Emplear los números para: Identificar Contar Clasificar Sumar y restar Resolución de problemas
TEMARIOS EXAMEN DE ADMISIÓN 2018 ASIGNATURA MATEMÁTICA 1 Básico Números y operaciones Ámbito 0 al 10 /Habilidad Emplear los números para: Identificar Contar Clasificar Sumar y restar Resolución de problemas
Estándares de Contenido y Desempeño, Estándares de Ejecución y Niveles de Logro Marcado* MATEMÁTICA
 Estándares de Contenido y Desempeño, Estándares de Ejecución y Niveles de Logro Marcado* MATEMÁTICA * Se distinguen con negrita en el texto. ESTÁNDAR DE CONTENIDO Y DESEMPEÑO Nº 1 Conocer la estructura
Estándares de Contenido y Desempeño, Estándares de Ejecución y Niveles de Logro Marcado* MATEMÁTICA * Se distinguen con negrita en el texto. ESTÁNDAR DE CONTENIDO Y DESEMPEÑO Nº 1 Conocer la estructura
I Parte. Selección única. (6 puntos) Leo cada oración y marco con una (X) la respuesta correcta.
 Trimestre: I Nombre: Temas: Números hasta 99 999; Mayor que, menor que o igual que y Los números ordinales Habilidades específicas: Representar números menores que 00 000 aplicando el concepto unidad de
Trimestre: I Nombre: Temas: Números hasta 99 999; Mayor que, menor que o igual que y Los números ordinales Habilidades específicas: Representar números menores que 00 000 aplicando el concepto unidad de
Developed in Consultation with Texas Educators
 Developed in Consultation with Texas Educators Índice Carta al estudiante.......................................6 Lista de revisión para tomar exámenes......................7 Correlación de expectativas
Developed in Consultation with Texas Educators Índice Carta al estudiante.......................................6 Lista de revisión para tomar exámenes......................7 Correlación de expectativas
APUNTES DOCENTES ASIGNATURA: ANALISIS NUMERICO ASIGNATURA: ANALISIS NUMERICO UNIDADES TECNOLÓGICAS DE SANTANDER
 APUNTES DOCENTES ASIGNATURA: ANALISIS NUMERICO ASIGNATURA: ANALISIS NUMERICO PROFESOR: ESP. PEDRO ALBERTO ARIAS QUINTERO 1. ERRORES Y ARITMETICA DE PUNTO FLOTANTE 1.1. Introducción a la Computación Numérica
APUNTES DOCENTES ASIGNATURA: ANALISIS NUMERICO ASIGNATURA: ANALISIS NUMERICO PROFESOR: ESP. PEDRO ALBERTO ARIAS QUINTERO 1. ERRORES Y ARITMETICA DE PUNTO FLOTANTE 1.1. Introducción a la Computación Numérica
2 Escribe con cifras. 3 Cuál es el valor de la cifra 4 en estos números?: 4 Escribe el signo > o <, según corresponda.
 PREPARO MAT. 6º Nuestro sistema de numeración Agrupamos de diez en diez MILLONES DMM UMM 4 CM MILLARES DM UM 6 0 0 C UNIDADES D U 3 6 8 El número 4 600 368 se lee: «Cuatro millones seiscientos mil trescientos
PREPARO MAT. 6º Nuestro sistema de numeración Agrupamos de diez en diez MILLONES DMM UMM 4 CM MILLARES DM UM 6 0 0 C UNIDADES D U 3 6 8 El número 4 600 368 se lee: «Cuatro millones seiscientos mil trescientos
Lección 1:NÚMEROS NATURAIS E SISTEMAS DE NUMERACIÓN
 Lección 1:NÚMEROS NATURAIS E SISTEMAS DE NUMERACIÓN 1.1.- LOS NÚMEROS NATURALES Y LOS SISTEMAS DE NUMERACIÓN QUÉ ES UN NÚMERO? Un número es la expresión de la idea de cantidad. Esta idea de cantidad es
Lección 1:NÚMEROS NATURAIS E SISTEMAS DE NUMERACIÓN 1.1.- LOS NÚMEROS NATURALES Y LOS SISTEMAS DE NUMERACIÓN QUÉ ES UN NÚMERO? Un número es la expresión de la idea de cantidad. Esta idea de cantidad es
TEMA 1 MATEMÁTICAS 1º E.S.O.
 TEMA 1 MATEMÁTICAS 1º E.S.O. NÚMEROS NATURALES. SISTEMA DE NUMERACIÓN El conjunto de los números naturales es ilimitado y está formado por: N = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, El sistema de numeración decimal
TEMA 1 MATEMÁTICAS 1º E.S.O. NÚMEROS NATURALES. SISTEMA DE NUMERACIÓN El conjunto de los números naturales es ilimitado y está formado por: N = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, El sistema de numeración decimal
Números Reales.
 Números Reales http://www.numerosreales.com/ El conjunto de los números reales pertenece en matemáticas a la recta numérica que comprende a los números racionales y a los números irracionales. Esto quiere
Números Reales http://www.numerosreales.com/ El conjunto de los números reales pertenece en matemáticas a la recta numérica que comprende a los números racionales y a los números irracionales. Esto quiere
MULTIPLICACIÓN DE NÚMEROS NATURALES
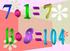 MULTIPLICACIÓN DE NÚMEROS NATURALES La solución de una adición donde los sumandos son iguales, es decir, que se repiten, se puede obtener de una forma directa y sencilla. Por ejemplo: Al calcular la cantidad
MULTIPLICACIÓN DE NÚMEROS NATURALES La solución de una adición donde los sumandos son iguales, es decir, que se repiten, se puede obtener de una forma directa y sencilla. Por ejemplo: Al calcular la cantidad
PLAN DE REFUERZO NOMBRE ESTUDIANTE: Nº
 COLEGIO BETHLEMITAS PLAN DE REFUERZO Fecha: Dia 01 Mes 04 Año 2016 META DE COMPRENSIÓN: Desarrolla comprensión acerca de la evolución histórica de los sistemas de numeración, para ubicar dentro de ellos
COLEGIO BETHLEMITAS PLAN DE REFUERZO Fecha: Dia 01 Mes 04 Año 2016 META DE COMPRENSIÓN: Desarrolla comprensión acerca de la evolución histórica de los sistemas de numeración, para ubicar dentro de ellos
CUADERNILLO DE REFUERZO DE OPTATIVA DE MATEMATICAS 1º ESO. Si la división de un número A, entre otro número B, es exacta, entonces decimos que:
 CUADERNILLO DE REFUERZO DE OPTATIVA DE MATEMATICAS 1º ESO Si la división de un número A, entre otro número B, es exacta, entonces decimos que: El número A es divisible por el número B. El número A es múltiplo
CUADERNILLO DE REFUERZO DE OPTATIVA DE MATEMATICAS 1º ESO Si la división de un número A, entre otro número B, es exacta, entonces decimos que: El número A es divisible por el número B. El número A es múltiplo
El Sistema Decimal.
 Curso: Titulo: Matemática 1 a 3 Básico Lección 3: El Sistema Decimal Unidad: Nº 2 Módulo: Desarrollo Objetivos de Aprendizaje El Sistema Decimal Se cree que la mayor parte de los sistemas de numeración
Curso: Titulo: Matemática 1 a 3 Básico Lección 3: El Sistema Decimal Unidad: Nº 2 Módulo: Desarrollo Objetivos de Aprendizaje El Sistema Decimal Se cree que la mayor parte de los sistemas de numeración
CONJUTOS NÚMERICOS NÚMEROS NATURALES
 CONJUTOS NÚMERICOS NÚMEROS NATURALES El conjunto de números naturales tiene gran importancia en la vida práctica ya que con sus elementos se pueden encontrar elementos u objetos de otros conjuntos. El
CONJUTOS NÚMERICOS NÚMEROS NATURALES El conjunto de números naturales tiene gran importancia en la vida práctica ya que con sus elementos se pueden encontrar elementos u objetos de otros conjuntos. El
EDUCACIÓN PRIMARIA TERCER CICLO Luis Pereda erein
 EDUCACIÓN PRIMARIA TERCER CICLO Luis Pereda erein Para trabajar la matemática durante este curso, además de este libro y del CD interactivo del Taller sobre Resolución de Problemas, se te facilitará una
EDUCACIÓN PRIMARIA TERCER CICLO Luis Pereda erein Para trabajar la matemática durante este curso, además de este libro y del CD interactivo del Taller sobre Resolución de Problemas, se te facilitará una
Expresión C. numérico Factor literal 9abc 9 abc
 GUÍA DE REFUERZO DE ÁLGEBRA Un término algebraico es el producto de una o más variables (llamado factor literal) y una constante literal o numérica (llamada coeficiente). Ejemplos: 3xy ; 45 ; m Signo -
GUÍA DE REFUERZO DE ÁLGEBRA Un término algebraico es el producto de una o más variables (llamado factor literal) y una constante literal o numérica (llamada coeficiente). Ejemplos: 3xy ; 45 ; m Signo -
Cantidades imaginarias - numeros complejos
 Cantidades imaginarias - numeros complejos Las operaciones directas (Suma, multiplicación y potenciación) no crearon problema de cálculo, por ser siempre realizables. En cambio las operaciones inversas
Cantidades imaginarias - numeros complejos Las operaciones directas (Suma, multiplicación y potenciación) no crearon problema de cálculo, por ser siempre realizables. En cambio las operaciones inversas
Matemáticas aliadas a las salud
 Matemáticas aliadas a las salud MATE 3035 Tema: Repaso de números cardinales Copyright 2014, 2009 by Pearson Education, Inc. All Rights Reserved Cuando escribimos 12 = 6 x 2 decimos que 6 x 2 corresponde
Matemáticas aliadas a las salud MATE 3035 Tema: Repaso de números cardinales Copyright 2014, 2009 by Pearson Education, Inc. All Rights Reserved Cuando escribimos 12 = 6 x 2 decimos que 6 x 2 corresponde
Por ejemplo: el número se tiene que separar por una coma cada tres números contando de derecha a izquierda, entonces queda 678,345.
 LEYENDO LOS NÚMEROS 13 Pone en práctica la lectura y escritura de los números. El maestro recuerda a sus alumnos que para leer una cifra se habrá de separar por una coma; explica de qué forma se pone y
LEYENDO LOS NÚMEROS 13 Pone en práctica la lectura y escritura de los números. El maestro recuerda a sus alumnos que para leer una cifra se habrá de separar por una coma; explica de qué forma se pone y
*Número natural, el que sirve para designar la cantidad de. *El cero, a veces, se excluye del conjunto de los números
 *Número natural, el que sirve para designar la cantidad de elementos que tiene un cierto conjunto, y se llama cardinal de dicho conjunto. *Los números naturales son infinitos. El conjunto de todos ellos
*Número natural, el que sirve para designar la cantidad de elementos que tiene un cierto conjunto, y se llama cardinal de dicho conjunto. *Los números naturales son infinitos. El conjunto de todos ellos
GESTIÓN ACADÉMICA PLAN DE ASIGNATURA GUÍA DIDÁCTICA 1
 PÁGINA: 1 de 9 Nombres y Apellidos del Estudiante: Docente: Área: MATEMATICAS Grado: Cuarto Periodo: Primero GUIA 1 Duración: 25 HORAS Asignatura: MATEMATICAS ESTÁNDAR: Resuelvo y formulo problemas cuya
PÁGINA: 1 de 9 Nombres y Apellidos del Estudiante: Docente: Área: MATEMATICAS Grado: Cuarto Periodo: Primero GUIA 1 Duración: 25 HORAS Asignatura: MATEMATICAS ESTÁNDAR: Resuelvo y formulo problemas cuya
Capítulo 5. Operaciones Básicas División
 Capítulo Operaciones Básicas División División Tercer Nivel de Abstracción Concepto de división La división es la operación inversa de la multiplicación. En la multiplicación agrupamos o sumamos los cuadritos
Capítulo Operaciones Básicas División División Tercer Nivel de Abstracción Concepto de división La división es la operación inversa de la multiplicación. En la multiplicación agrupamos o sumamos los cuadritos
Matemáticas 2º E.S.P.A. Pág.1 C.E.P.A. Plus Ultra. Logroño
 ALGEBRA 1. LETRAS EN VEZ DE NÚMEROS En muchas tareas de las matemáticas es preciso trabajar con números de valor desconocido o indeterminado. En esos casos, los números se representan por letras y se operan
ALGEBRA 1. LETRAS EN VEZ DE NÚMEROS En muchas tareas de las matemáticas es preciso trabajar con números de valor desconocido o indeterminado. En esos casos, los números se representan por letras y se operan
Universidad de Puerto Rico en Arecibo Departamento de Matemáticas Expresiones Algebraicas y Polinomios
 Universidad de Puerto Rico en Arecibo Departamento de Matemáticas Expresiones Algebraicas y Polinomios Prof. Glorymill Santiago Labrador Adaptado por: Prof. Anneliesse Sánchez, Prof. Caroline Rodríguez
Universidad de Puerto Rico en Arecibo Departamento de Matemáticas Expresiones Algebraicas y Polinomios Prof. Glorymill Santiago Labrador Adaptado por: Prof. Anneliesse Sánchez, Prof. Caroline Rodríguez
CONTENIDOS EXÁMEN DE ADMISIÓN MATEMÁTICA SEGUNDO BÁSICO 2017
 SEGUNDO BÁSICO 2017 DEPARTAMENTO ÁMBITO NUMÉRICO 0-50 - Escritura al dictado - Antecesor y sucesor - Orden (menor a mayor y viceversa) - Patrones de conteo ascendente (2 en 2, 5 en 5, 10 en 10) - Comparación
SEGUNDO BÁSICO 2017 DEPARTAMENTO ÁMBITO NUMÉRICO 0-50 - Escritura al dictado - Antecesor y sucesor - Orden (menor a mayor y viceversa) - Patrones de conteo ascendente (2 en 2, 5 en 5, 10 en 10) - Comparación
SISTEMA DE NUMERACIÓN DECIMAL
 SISTEMA DE NUMERACIÓN DECIMAL Se llama decimal o de base diez porque se utilizan diez símbolos para representar todos los números. Los diez símbolos, cifras son: 0, 1, 2,3, 4, 5, 6, 7, 8, 9 La relación
SISTEMA DE NUMERACIÓN DECIMAL Se llama decimal o de base diez porque se utilizan diez símbolos para representar todos los números. Los diez símbolos, cifras son: 0, 1, 2,3, 4, 5, 6, 7, 8, 9 La relación
CONJUNTO DE LOS NÚMEROS NATURALES
 CONJUNTO DE LOS NÚMEROS NATURALES 1.- DEFINICIÓN DEL CONJUNTO DE LOS NÚMEROS NATURALES (Conjunto N): Un número natural es cualquier número que se puede usar para contar los elementos de un conjunto finito.
CONJUNTO DE LOS NÚMEROS NATURALES 1.- DEFINICIÓN DEL CONJUNTO DE LOS NÚMEROS NATURALES (Conjunto N): Un número natural es cualquier número que se puede usar para contar los elementos de un conjunto finito.
Conectados con el pasado, proyectados hacia el futuro Plan Anual de Matemática II Año PAI VII Grado
 Actualizado en febrero del 2013 Conectados con el pasado, proyectados hacia el futuro Plan Anual de Matemática II Año PAI VII Grado CONTENIDOS OBJETIVOS ESPECÍFICOS HABILIDADES CRITERIOS DE EVALUACIÓN
Actualizado en febrero del 2013 Conectados con el pasado, proyectados hacia el futuro Plan Anual de Matemática II Año PAI VII Grado CONTENIDOS OBJETIVOS ESPECÍFICOS HABILIDADES CRITERIOS DE EVALUACIÓN
Material Educativo. Matemática. 6to grado. Matemática/jljf
 1 Material Educativo Matemática 6to grado Carrizal, septiembre 2016 2 República Bolivariana de Venezuela Ministerio del Poder Popular para la Educación Unidad Educativa Dr. José María Vargas Municipio
1 Material Educativo Matemática 6to grado Carrizal, septiembre 2016 2 República Bolivariana de Venezuela Ministerio del Poder Popular para la Educación Unidad Educativa Dr. José María Vargas Municipio
PROGRAMACIÓN DE AULA MATEMÁTICAS 5.º CURSO
 PROGRAMACIÓN DE AULA MATEMÁTICAS 5.º CURSO Página 1 UNIDAD 1: SISTEMAS DE NUMERACIÓN CEIP El Parque Conocer los nueve primeros órdenes de unidades y las equivalencias entre ellos. Leer, escribir y descomponer
PROGRAMACIÓN DE AULA MATEMÁTICAS 5.º CURSO Página 1 UNIDAD 1: SISTEMAS DE NUMERACIÓN CEIP El Parque Conocer los nueve primeros órdenes de unidades y las equivalencias entre ellos. Leer, escribir y descomponer
FICHAS DE TRABAJO REFUERZO
 FICHAS DE TRABAJO REFUERZO DEPARTAMENTO DE MATEMATICAS CONTENIDO 1. Números naturales a. Leer y escribir números naturales b. Orden de cifras c. Descomposición polinómica d. Operaciones combinadas e. Potencias
FICHAS DE TRABAJO REFUERZO DEPARTAMENTO DE MATEMATICAS CONTENIDO 1. Números naturales a. Leer y escribir números naturales b. Orden de cifras c. Descomposición polinómica d. Operaciones combinadas e. Potencias
CCT 15EES1420H, TURNO: VESPERTINO
 Escuela Secundaria Oficial 0765 Vladimir Ilich Ulianov Lenin CCT 15EES1420H, TURNO: VESPERTINO Guía para presentar examen extraordinario Materia: Matemáticas I Grado: Primero TEMA: Aritmética. INSTRUCCIONES:
Escuela Secundaria Oficial 0765 Vladimir Ilich Ulianov Lenin CCT 15EES1420H, TURNO: VESPERTINO Guía para presentar examen extraordinario Materia: Matemáticas I Grado: Primero TEMA: Aritmética. INSTRUCCIONES:
Bloque 1. Aritmética y Álgebra
 Bloque 1. Aritmética y Álgebra 3. Los números racionales 1. Los números racionales o fraccionarios Fracción es una o varias partes iguales en que dividimos la unidad. Las fracciones representan siempre
Bloque 1. Aritmética y Álgebra 3. Los números racionales 1. Los números racionales o fraccionarios Fracción es una o varias partes iguales en que dividimos la unidad. Las fracciones representan siempre
GLOSARIO GENERAL DE TÉRMINOS
 GLOSARIO GENERAL DE TÉRMINOS Binomio al cuadrado: es una expresión agrupada en dos términos y elevada al cuadrado. Se resuelve con la siguiente regla, un binomio al cuadrado es igual al cuadrado del primer
GLOSARIO GENERAL DE TÉRMINOS Binomio al cuadrado: es una expresión agrupada en dos términos y elevada al cuadrado. Se resuelve con la siguiente regla, un binomio al cuadrado es igual al cuadrado del primer
UNIDAD I CLASES DE NUMEROS
 UNIDAD I CLASES DE NUMEROS LOS NÚMEROS ARÁBIGOS Los números arábigos, tal y como los usamos ahora, son 1, 2, 3, 4, 5, 6, 7, 8, 9 y el importantísimo 0. Se trata de un sistema de tipo decimal cuyas cifras
UNIDAD I CLASES DE NUMEROS LOS NÚMEROS ARÁBIGOS Los números arábigos, tal y como los usamos ahora, son 1, 2, 3, 4, 5, 6, 7, 8, 9 y el importantísimo 0. Se trata de un sistema de tipo decimal cuyas cifras
Tema 1: Números naturales. Sistemas de numeración
 Tema 1: Números naturales. Sistemas de numeración SELECCIÓN DE EJERCICIOS RESUELTOS 1. Utiliza nuestro sistema de numeración oral para expresar el número, 754.120.004.002000.000.000 Utiliza nuestro sistema
Tema 1: Números naturales. Sistemas de numeración SELECCIÓN DE EJERCICIOS RESUELTOS 1. Utiliza nuestro sistema de numeración oral para expresar el número, 754.120.004.002000.000.000 Utiliza nuestro sistema
VERÓNICA GRIMALDI HÉCTOR PONCE
 Matemática CLAUDIA BROITMAN VERÓNICA GRIMALDI HÉCTOR PONCE Índice Capítulo I el sistema de numeración... 7 Escribir, leer y comparar números naturales... 8 Relaciones entre sistema de numeración y operaciones...
Matemática CLAUDIA BROITMAN VERÓNICA GRIMALDI HÉCTOR PONCE Índice Capítulo I el sistema de numeración... 7 Escribir, leer y comparar números naturales... 8 Relaciones entre sistema de numeración y operaciones...
NOTACIÓN MATEMÁTICA INTRODUCCION:
 INTRODUCCION: NOTACIÓN MATEMÁTICA La matemática tiene, como la mayoría de las ciencias y otras disciplinas del saber, un lenguaje particular, específico, el cual simplifica, en algunos casos, la comunicación,
INTRODUCCION: NOTACIÓN MATEMÁTICA La matemática tiene, como la mayoría de las ciencias y otras disciplinas del saber, un lenguaje particular, específico, el cual simplifica, en algunos casos, la comunicación,
00-A-1/24. Nombre: 2, 3, 4, 5, 6,... Si queremos saber la cantidad de bombones que hay en esta caja, los contamos: 1, naturales
 00-A-1/24 Si queremos saber la cantidad de bombones que hay en esta caja, los contamos: 1, 2, 3, 4, 5, 6,... Estos números se llaman naturales El sistema de numeración que usamos normalmente se llama cambiando
00-A-1/24 Si queremos saber la cantidad de bombones que hay en esta caja, los contamos: 1, 2, 3, 4, 5, 6,... Estos números se llaman naturales El sistema de numeración que usamos normalmente se llama cambiando
Resumen anual de Matemática 1ª Convocatoria: jueves 24 de noviembre, 2016 Octavo nivel 2ª Convocatoria: miércoles 1 de febrero, 2017 broyi.jimdo.
 Resumen anual de Matemática 1ª Convocatoria: jueves 4 de noviembre, 016 Octavo nivel ª Convocatoria: miércoles 1 de febrero, 017 broyi.jimdo.com Contenidos Los números... Objetivo 1... El conjunto de los
Resumen anual de Matemática 1ª Convocatoria: jueves 4 de noviembre, 016 Octavo nivel ª Convocatoria: miércoles 1 de febrero, 017 broyi.jimdo.com Contenidos Los números... Objetivo 1... El conjunto de los
Simple Solutions Mathematics Nivel 2. Nivel 2. Páginas de Ayuda y Quién sabe?
 Nivel 2 y Quién sabe? 147 Vocabulario Operaciones aritméticas Addition (suma) Cuando combinas números, sumas. El signo + significa sumar. La respuesta para un ejercicio de adición se llama suma. Ejemplo:
Nivel 2 y Quién sabe? 147 Vocabulario Operaciones aritméticas Addition (suma) Cuando combinas números, sumas. El signo + significa sumar. La respuesta para un ejercicio de adición se llama suma. Ejemplo:
Herramientas del Algebra
 8 GIMNASIO PARAISO ANTARES PERIODO: I FECHA: DIAGNOSTICO TALLER QUIZ: BIMESTRAL APOYO PEDAGOGICO PRUEBA DE SUPERACION DOCENTE:JOSE A. URQUIJO Herramientas del Algebra AREA/ASIGNATURA: MATEMÁTICAS ESTUDIANTE:
8 GIMNASIO PARAISO ANTARES PERIODO: I FECHA: DIAGNOSTICO TALLER QUIZ: BIMESTRAL APOYO PEDAGOGICO PRUEBA DE SUPERACION DOCENTE:JOSE A. URQUIJO Herramientas del Algebra AREA/ASIGNATURA: MATEMÁTICAS ESTUDIANTE:
Un sistema de numeración está compuesto por el conjunto de símbolos y reglas que se utilizan para representar cantidades.
 Repaso Sistemas Numéricos Un sistema de numeración está compuesto por el conjunto de símbolos y reglas que se utilizan para representar cantidades. A la cantidad de símbolos, que componen dicho conjunto,
Repaso Sistemas Numéricos Un sistema de numeración está compuesto por el conjunto de símbolos y reglas que se utilizan para representar cantidades. A la cantidad de símbolos, que componen dicho conjunto,
FUNDAMENTOS DE MATEMÁTICAS
 FUNDAMENTOS DE MATEMÁTICAS Dr. Miguel Angel Morales Cabrera E-mail: miguelmorales.uv@gmail.com CONTENIDO 1. Introducción al álgebra 2. Exponentes y radicales 3. Operaciones con Polinomios (Suma, Resta,
FUNDAMENTOS DE MATEMÁTICAS Dr. Miguel Angel Morales Cabrera E-mail: miguelmorales.uv@gmail.com CONTENIDO 1. Introducción al álgebra 2. Exponentes y radicales 3. Operaciones con Polinomios (Suma, Resta,
ECUACIONES EN N (NÚMEROS NATURALES)
 ECUACIONES EN N (NÚMEROS NATURALES) Una ecuación es una igualdad en la que aparecen constantes y variables ligadas mediante operaciones, la cual se satisface para determinados valores de las variables
ECUACIONES EN N (NÚMEROS NATURALES) Una ecuación es una igualdad en la que aparecen constantes y variables ligadas mediante operaciones, la cual se satisface para determinados valores de las variables
Tema 4. Los números reales.
 Tema 4. Los números reales. Números irracionales. En el tema anterior, has visto que los números racionales pueden escribirse en forma decimal, produciendo siempre un decimal exacto o periódico. También
Tema 4. Los números reales. Números irracionales. En el tema anterior, has visto que los números racionales pueden escribirse en forma decimal, produciendo siempre un decimal exacto o periódico. También
Comprende e interpreta valores posicionales de los números.
 ENTEROS Y DECIMALES 09 Comprende e interpreta valores posicionales de los números. El maestro recuerda el orden de posición menor al entero (1, 0.1, 0.01, etc); resuelven ejercicios sobre el uso del punto
ENTEROS Y DECIMALES 09 Comprende e interpreta valores posicionales de los números. El maestro recuerda el orden de posición menor al entero (1, 0.1, 0.01, etc); resuelven ejercicios sobre el uso del punto
open green road Guía Matemática NOTACIÓN ALGEBRAICA profesor: Nicolás Melgarejo .cl
 Guía Matemática NOTACIÓN ALGEBRAICA profesor: Nicolás Melgarejo.cl 1. De la aritmética al álgebra El concepto de los números aparece por primera vez en los pueblos primitivos entre el 25.000 y 5.000 antes
Guía Matemática NOTACIÓN ALGEBRAICA profesor: Nicolás Melgarejo.cl 1. De la aritmética al álgebra El concepto de los números aparece por primera vez en los pueblos primitivos entre el 25.000 y 5.000 antes
CAPÍTULO 4: VARIABLES Y RAZONES
 Capítulo 4: Variables y razones CAPÍTULO 4: VARIABLES Y RAZONES Fecha: 33 2014 CPM Educational Program. All rights reserved. Core Connections en español, Curso 2 Fecha: Caja de herramientas 2014 CPM Educational
Capítulo 4: Variables y razones CAPÍTULO 4: VARIABLES Y RAZONES Fecha: 33 2014 CPM Educational Program. All rights reserved. Core Connections en español, Curso 2 Fecha: Caja de herramientas 2014 CPM Educational
