FUNCIONES EXPONENCIALES Y LOGARÍTMICAS
|
|
|
- José María Ramos Herrero
- hace 7 años
- Vistas:
Transcripción
1 CAPÍTULO 7 FUNCIONES EXPONENCIALES Y LOGARÍTMICAS 7. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS Una fnción eponencial es aqella en la qe la variable está en el eponente. Ejemplos e fnciones eponenciales son y y 4 5 y 8 + y 0 - Antes e entrar e lleno en el estio e las fnciones logarítmicas conviene repasar el concepto e logaritmo, ya qe es frecente qe los estiantes llegen a este momento sin recorar qé son los logaritmos o, en el caso más etremo, sin haberlos estiao nnca rante s carrera estiantil. En Matemáticas toa operación o too proceso tiene s inverso, s camino e retorno al pnto inicial. Por ejemplo, si a 4 se le sma se llega al 7; el retorno el 7 al 4 es restar. El retorno e la mltiplicación es la ivisión, etc. De manera qe si se tienen las sigientes potencias: ) 8 ) 9 07
2 Fnciones eponenciales y logarítmicas ) ) ) etc. si se pregnta Cál es el inverso (el camino e retorno) e caa na e ellas? por inercia el estiante respone conforme a la sigiente tabla: Potencia 8 Inverso lo cal es cierto. Sin embargo, obsérvese qe en caa potencia (primera colmna) se tienen os cantiaes, la base y el eponente, y en la tabla anterior el retorno se hizo hacia la base. No poría haber sio el retorno hacia el eponente? Dicho e otra forma: Cómo hacer para regresar al eponente, en vez e a la base? Allí es one aparece el concepto e logaritmo. Cano se tiene la potenciación a k c one a, k y c son calqier número (son tres cantiaes las qe intervienen: la base, el eponente y el resltao), a partir el resltao c eisten os posibiliaes e regreso, no hacia la 08
3 Fnciones eponenciales y logarítmicas base y otro hacia el eponente. Para regresar a la base se emplea la raíz k-ésima e c; para regresar al eponente se emplea el logaritmo base a e c. En ambos casos la operación raíz o la operación logaritmo se le aplica al resltao c e la potenciación; aemás, se ebe hacer intervenir a la tercera cantia, en el primer caso para señalar el ínice el raical, en el segno caso para señalar la base. Volvieno al ejemplo e la tabla anterior, eisten os caminos e retorno, no hacia la base y otro hacia el eponente. Cano es a la base, se emplea la raíz k-ésima, cano es al eponente se emplea el logaritmo base a: Potencia Regreso a la base Regreso al eponente 8 8 log log log log log De manera qe la efinición e logaritmo es: En el iioma Español, para enotar los números orinales se emplea la terminación ésimo. Así, el orinal e 0 es vigésimo; el e 70 es septagésimo; el e 00 es bicentésimo; el e 700 es septingentésimo, el e 84 es octingentésimo trigésimo carto, etc. Cano se habla en términos genéricos sele emplearse la letra k o la letra n para referirse a calqier número. De tal manera qe el orinal e n número genérico k es k-ésimo; el orinal e n número genérico n es n-ésimo. Es na grave incorrección ecir veinteavo en vez e vigésimo, o setentavo en vez e septagésimo. 09
4 Fnciones eponenciales y logarítmicas El logaritmo e n número n es el eponente al qe ebe elevarse la base para obtener icho número n. Como los logaritmos peen ser base e calqier número, habría n número infinito e iferentes logaritmos, por lo qe en algún momento los matemáticos acoraron emplear solamente os tipos e logaritmos: a) los logaritmos base iez (por tratarse e n sistema ecimal), llamaos logaritmos vlgares o logaritmos ecimales, representaos simplemente por el símbolo log sin especificar la base, qe se sobreentiene qe es 0. b) los logaritmos natrales, representaos por el símbolo ln y cya base es el número irracional.78888,. De manera semejante a como con π se representa el nú- mero e veces qe el iámetro cabe en s propia circnferencia (.46), la base e los logaritmos natrales se simboliza con la letra e, o sea qe e Para obtener el valor e e con la calclaora ebe oprimirse la tecla e qe en casi toos los moelos se localiza como segna fnción el logaritmo natral, y espés teclear el número. Con eso realmente se está ingresano e qe es e. Este número sale el límite lim 0 ( + ) / el cal, por no ser tema e este crso, no se va a etallar más. 0
5 Fnciones eponenciales y logarítmicas 7. PROPIEDADES DE LOS LOGARITMOS Los logaritmos, no importa cál sea s base, toos tienen las sigientes tres propieaes: ª: log A + log B log AB ª: log A log B log A log B ª: A log B log B A De éstas, la tercera será my útil para resolver algnas erivaas e logaritmos, como se eponrá en algnos e los ejemplos venieros. 7. FÓRMULAS (5) ln (6) e e La erivaa el logaritmo natral e, ( es el argmento) es na fracción: en el nmeraor, la erivaa el argmento; en el enominaor, el argmento tal cal. Ejemplo : Hallar la erivaa e y ln 9. Solción: En este caso, el argmento es 9, es ecir 9. Aplicano la fórmla (5):
6 Fnciones eponenciales y logarítmicas Ejemplo : Derivar y ln (7 + ). Solción: En este ejemplo, el argmento es 7 +, es ecir qe 7 +. Así qe aplicano la fórmla (5): 7 + ( 7 + ) 7 7 +
7 Fnciones eponenciales y logarítmicas Ejemplo : Obtener la erivaa e y ln ( - + 7). Solción: El argmento es - + 7, esto es qe Utilizano la fórmla (5): + ( + 7) Ejemplo 4: Calclar la erivaa e y ln Solción: El argmento el logaritmo es, por lo qe empleano la fórmla (5):
8 Fnciones eponenciales y logarítmicas Por la ley e la herrara: Otra forma: Como y ln es lo mismo qe y ln, se pee aplicar la tercera propiea e los logaritmos, página, qe leía e erecha a izqiera se tiene qe y (- ) ln, es ecir qe la fnción a erivar es y - ln. qe es el mismo resltao obtenio antes. 4
9 Fnciones eponenciales y logarítmicas Ejemplo 5: Hallar la erivaa e y ln Solción: El argmento es, e moo qe empleano la fórmla (5): ( ) / ( ) ( ) / ( ) ( ) Aplicano la ley e la herrara: ( ) 5
10 Fnciones eponenciales y logarítmicas Otra forma: Como y ln es lo mismo qe y ln, aplicano la ª propiea e los lo- / ( ) garitmos, página, leía e erecha a izqiera se tiene qe y ln, por lo qe: qe es el mismo resltao obtenio antes. Ejemplo 6: Calclar la erivaa e y ln 5 Solción: El argmento es. Empleano la fórmla (5): 5 6
11 Fnciones eponenciales y logarítmicas 5 5 ( 5 ) / ( ) ( ) / ( ) ( ) 5 0 ( ) 4 / 5 5 Por la ley e la herrara: ( ) / 7
12 Fnciones eponenciales y logarítmicas ( ) 4/ ( ) / Recorano qe para simplificar cano se tiene la misma base se restan los eponentes: 0 ( ) ( 5 ) 0 ( ) / 5 0 ( ) Simplificano nevamente: Ejemplo 7: Derivar y e. Solción: Empleano la fórmla (6), one : 8
13 Fnciones eponenciales y logarítmicas e e e Ejemplo 8: Obtener la erivaa e y e 5 - Solción: Aplicano la fórmla (6), one 5 - : e ( 5 ) 5 e 5 5 Ejemplo 9: Hallar la erivaa e y e Solción: Por la fórmla (6), en one : e 9
14 Fnciones eponenciales y logarítmicas e / e e Orenano conforme a las reglas e escritra matemática: e Ejemplo 0: Hallar la erivaa e y e 6 Solción: Como se trata e n procto, ebe emplearse la fórmla (7) e la página 77: ( v) v + v en one y v e e + e v v 0
15 Fnciones eponenciales y logarítmicas Para la primera erivaa peniente se emplea la fórmla (6) e e 6 ( ) e ( ) e 6 + e 6 6 Orenano conforme a las reglas e escritra matemática: 6 e e Ejemplo : Calclar la erivaa e y e ln Solción: Como se trata e n procto, ebe emplearse la fórmla e v: e ln + ln e v v Para la primera erivaa peniente se tiliza la fórmla (5) el logaritmo natral y para la segna erivaa peniente la fórmla (6) e e :
16 Fnciones eponenciales y logarítmicas e ln e + e + ln e Finalmente, orenano conforme a las reglas e escritra matemática: e + e ln Ejemplo : Derivar y sene Solción: La fnción es e la forma sen ; one el argmento es e. Por lo tanto, empleano la fórmla (9) e la página 9 se tiene qe sen e cos e e cos e e cos e e ( ) Finalmente, orenano conforme a las reglas e escritra matemática:
17 Fnciones eponenciales y logarítmicas e cos e Ejemplo : Hallar la erivaa e y ln sec Solción: La fnción tiene la forma e ln, one el argmento es sec, por lo tanto ebe tilizarse la fórmla (5) e la página : ln sec sec sec La erivaa peniente tiene la forma e sec, one el argmento e la secante es, por lo qe ahora ebe emplearse la fórmla () e la página 9: tan sec sec tan sec sec tan sec sec [ ] tan
18 Fnciones eponenciales y logarítmicas Ejemplos avanzaos: y ln Ejemplo 4: Obtener la erivaa e ( ) ( ) ( ) 4 Solción: Como ln 6 5 ln 6 5, la fnción tiene la forma e n, e manera qe empleano la fórmla (6) e la página 69: 4 ( ) 4 4 ln 6 5 ln( 6 5 ) n n - ( ) ( 6 5) ln ( 6 5) La erivaa peniente es e la forma n, por lo qe ebe emplearse nevamente la fórmla (6) e la página 69: ( ) ( ) ln ( 6 5) ( 6 5) ( ) ( ) ( 6 5) ln ( 6 5) 4
19 Fnciones eponenciales y logarítmicas Finalmente simplificano, mltiplicano 4 6 y orenano conforme a las reglas e escritra matemática, se llega a ( ) ( 6 5) ln ( 6 5) ( 6 5) ln Ejemplo 5: Derivar y ln( sen 5) Solción: El argmento el logaritmo natral es sen 5, por lo tanto sen 5. Utilizano la fórmla el logaritmo natral: sen 5 sen 5 La erivaa peniente sen 5 es n procto, o sea e la forma v, e manera qe aplicano la fórmla el procto se obtiene v v sen 5 + sen 5 sen 5 5
20 Fnciones eponenciales y logarítmicas Ahora, la primera erivaa peniente es e la forma sen : cos5 5 sen5 + sen 5 5 cos 5 + sen 5 sen 5 Ejemplo 6: Hallar la erivaa e y ln Solción: La fnción a erivar se pee escribir como y ln, qe toma la forma e n, one ln y n -. Utilizano entonces icha fórmla se llega a qe: ln ln n n - La erivaa peniente es e la forma ln, con : 6
21 Fnciones eponenciales y logarítmicas ln ln ln ( )( ) ln ln otra forma: Por las propieaes e los logaritmos, la fnción original se pee escribir como y ln ln ( ln ) y ( ln ) (El eponente el argmento pasa como coeficiente el logaritmo). 7
22 Fnciones eponenciales y logarítmicas La cal tiene la forma e n, con - ln y n -. ( ln ) ( ln ) n n - ( ln ) ( ln ) ln ( ) Nevamente, por las propieaes e los logaritmos, pasano el coeficiente el logaritmo como eponente el argmento: ( ) ln ln 8
23 Fnciones eponenciales y logarítmicas EJERCICIO Obtener la erivaa e las sigientes fnciones: y ln 6 ) ) ) 4) y ln ( + 7) y ln( ) y ln 8 5) y ln 8 6) 5 y ln 7 6 7) y ln 8) 7 ( ) 5 y ln 7 6 9) y ln 0) 4 y e ) y e ) y e / 7 ) 4) y 5e 6 5) 6) y y e 7 e / y e 5 8 7) y ( 5 ) ln( 5 ) 8) y ln Avanzaos: 5 9) y ln 9 0) y ln( 5 ) y senln( 7 6) 5 ) y tane ) y cosln( 6 ) ) y csce 6 4) 9
24 Fnciones eponenciales y logarítmicas 5) y cot4ln5 6) y ln 8 ( 8 9) ( ) 7) y ln 7 8) y 4 9 e ( ) ) y ln 5 0) y 5 4 ln y ln 5 ( 7) 6 ) y lncot ) y e y sen ) 4) e 6 0
LOGARITMOS página 147
 LOGARITMOS página 147 página 148 INSTITUTO VALLADOLID PREPARATORIA 8 LOGARITMOS 8.1 CONCEPTOS Y DEFINICIONES Una función exponencial es aquella en la que la variable está en el exponente. Ejemplos de funciones
LOGARITMOS página 147 página 148 INSTITUTO VALLADOLID PREPARATORIA 8 LOGARITMOS 8.1 CONCEPTOS Y DEFINICIONES Una función exponencial es aquella en la que la variable está en el exponente. Ejemplos de funciones
CALCULO DIFERENCIAL Escuela Colombiana de Ingeniería 5.1. DERIVADA DE LA FUNCIÓN EXPONENCIAL ( ) f ( x) = a Enunciado. x h x. x h.
 Escela Colombiana e Ingeniería.. DERIVADA DE LA FUNCIÓN EXPONENCIAL Aplicano la efinición e la erivaa se tiene: f a Ennciao. + f + f a a f ' Lim Lim Aplicano la efinición e la erivaa. 0 0 a a a a ( a f
Escela Colombiana e Ingeniería.. DERIVADA DE LA FUNCIÓN EXPONENCIAL Aplicano la efinición e la erivaa se tiene: f a Ennciao. + f + f a a f ' Lim Lim Aplicano la efinición e la erivaa. 0 0 a a a a ( a f
Derivadas de funciones trigonométricas
 MB0004_MAAL3_Trigonométricas Derivaas e fnciones trigonométricas por Oliverio Ramírez Debio a s comportamiento, no toos los fenómenos físicos peen estiarse y representarse e la misma manera. Algnos fenómenos
MB0004_MAAL3_Trigonométricas Derivaas e fnciones trigonométricas por Oliverio Ramírez Debio a s comportamiento, no toos los fenómenos físicos peen estiarse y representarse e la misma manera. Algnos fenómenos
FUNCIONES TRIGONOMÉTRICAS
 CAPÍTULO 6 FUNCIONES TRIGONOMÉTRICAS 6.1 FUNCIONES TRASCENDENTES (Áreas 1, y ) Las funciones trascenentes se caracterizan por tener lo que se llama argumento. Un argumento es el número o letras que lo
CAPÍTULO 6 FUNCIONES TRIGONOMÉTRICAS 6.1 FUNCIONES TRASCENDENTES (Áreas 1, y ) Las funciones trascenentes se caracterizan por tener lo que se llama argumento. Un argumento es el número o letras que lo
LA DERIVADA POR FÓRMULAS
 CAPÍTULO LA DERIVADA POR FÓRMULAS. FÓRMULAS Obtener la erivaa e cualquier función por alguno e los os métoos vistos anteriormente, el e tabulaciones y el e incrementos, resulta una tarea muy engorrosa,
CAPÍTULO LA DERIVADA POR FÓRMULAS. FÓRMULAS Obtener la erivaa e cualquier función por alguno e los os métoos vistos anteriormente, el e tabulaciones y el e incrementos, resulta una tarea muy engorrosa,
2. Considere un duopolio de Cournot repetido dos veces (se juega dos veces). El juego de etapa puede ser representado por el siguiente árbol:
 Teoría e Jegos Segno parcial. //. Consiere la sigiente versión el jego el ltimátm. Hay 3 moneas. J pee ofrecer qearse con o con. J acepta o rechaza. Si rechaza, los os jgaores obtienen. Sponga qe los jgaores
Teoría e Jegos Segno parcial. //. Consiere la sigiente versión el jego el ltimátm. Hay 3 moneas. J pee ofrecer qearse con o con. J acepta o rechaza. Si rechaza, los os jgaores obtienen. Sponga qe los jgaores
INTEGRAL INDEFINIDA. Una pregunta inicial para hacerse. Cuál es una función F(x), que al haber sido derivada se obtuvo f ( x) B?.
 es INTEGRAL INDEFINIDA UConcepto e antierivaau: Una pregunta inicial para hacerse. Cuál es una función F(), que al haber sio erivaa se obtuvo f ( ) =?. La repuesta es: F ( ) =. Una nueva pregunta. Es la
es INTEGRAL INDEFINIDA UConcepto e antierivaau: Una pregunta inicial para hacerse. Cuál es una función F(), que al haber sio erivaa se obtuvo f ( ) =?. La repuesta es: F ( ) =. Una nueva pregunta. Es la
1. Hallar la derivada por definición de f ( x) x x 1. Solución: para resolver la derivada aplicaremos la definición de la derivada: f '( x)
 . Hallar la erivaa por efinición e f ( ) Solución: para resolver la erivaa aplicaremos la efinición e la erivaa: f '( ) lim 0 f ( ) f ( ) f ( ) f '( ) lim 0 ara allar la erivaa meiante efinición ebemos
. Hallar la erivaa por efinición e f ( ) Solución: para resolver la erivaa aplicaremos la efinición e la erivaa: f '( ) lim 0 f ( ) f ( ) f ( ) f '( ) lim 0 ara allar la erivaa meiante efinición ebemos
AUTOVALORES DE OPERADORES DIFERENCIALES. Los problemas de autovalores tienen su origen en el álgebra de matrices.
 AUTOVALORES DE OPERADORES DIFERENCIALES Los problemas e atovalores tienen s origen en el álgebra e matrices. En el caso el álgebra se parte e na matriz A y esencialmente se trata e bscar atovalores y los
AUTOVALORES DE OPERADORES DIFERENCIALES Los problemas e atovalores tienen s origen en el álgebra e matrices. En el caso el álgebra se parte e na matriz A y esencialmente se trata e bscar atovalores y los
Regla de la cadena. Ejemplo 1. y = f (g(x)) Como las funciones son diferenciables son suaves.
 1 Regla e la caena Hasta aquí hemos erivao funciones que no son compuestas. El problema surge cuano tenemos una función que es compuesta, por ejemplo, igamos que el precio e la gasolina epene el precio
1 Regla e la caena Hasta aquí hemos erivao funciones que no son compuestas. El problema surge cuano tenemos una función que es compuesta, por ejemplo, igamos que el precio e la gasolina epene el precio
FÓRMULAS DE DERIVACIÓN
 SESIÓN Nº 1 Derivaas e Funciones Trigonométricas, Eponenciales y Logarítmicas Ahora correspone revisar las fórmulas principales e erivación y algunos ejemplos e aplicación. FÓRMULAS DE DERIVACIÓN 1) (
SESIÓN Nº 1 Derivaas e Funciones Trigonométricas, Eponenciales y Logarítmicas Ahora correspone revisar las fórmulas principales e erivación y algunos ejemplos e aplicación. FÓRMULAS DE DERIVACIÓN 1) (
LA DERIVADA UNIDAD III III.1 INCREMENTOS. y, esto es:
 Página el Colegio e Matemáticas e la ENP-UNAM La erivaa Autor: Dr. José Manuel Becerra Espinosa LA DERIVADA UNIDAD III III. INCREMENTOS Se eine como incremento e la variable al aumento o isminución que
Página el Colegio e Matemáticas e la ENP-UNAM La erivaa Autor: Dr. José Manuel Becerra Espinosa LA DERIVADA UNIDAD III III. INCREMENTOS Se eine como incremento e la variable al aumento o isminución que
Facultad de Ciencias Sociales, Universidad de la República, Uruguay Teoría de Juegos 2012
 Segno parcial. 1. (1 pnto) Sponga qe el precio qe enfrentan os opolistas qe se comportan a lo Stackelberg es: + =12 y los costos qe enfrenta caa na e las empresas es: =4 con i=1,2. Sponga qe caa empresa
Segno parcial. 1. (1 pnto) Sponga qe el precio qe enfrentan os opolistas qe se comportan a lo Stackelberg es: + =12 y los costos qe enfrenta caa na e las empresas es: =4 con i=1,2. Sponga qe caa empresa
Derivación de funciones trascendentes.
 57 Derivación e funciones trascenentes. Como en el caso e las funciones algebraicas eisten teoremas para erivar las funciones trascenentes como se muestra a continuación: Teoremas e erivación: Sean u y
57 Derivación e funciones trascenentes. Como en el caso e las funciones algebraicas eisten teoremas para erivar las funciones trascenentes como se muestra a continuación: Teoremas e erivación: Sean u y
FUNCIONES IMPLÍCITAS. y= e tanx cos x. ln x. y= x x CAPÍTULO 10. 10.1 FUNCIONES IMPLÍCITAS (Áreas 1, 2 y 3)
 CAPÍTULO 10 FUNCIONES IMPLÍCITAS 10.1 FUNCIONES IMPLÍCITAS (Áreas 1, 3) En el curso e Precálculo el 4º semestre se vieron iferentes clasificaciones e las funciones, entre ellas las funciones eplícitas
CAPÍTULO 10 FUNCIONES IMPLÍCITAS 10.1 FUNCIONES IMPLÍCITAS (Áreas 1, 3) En el curso e Precálculo el 4º semestre se vieron iferentes clasificaciones e las funciones, entre ellas las funciones eplícitas
DERIVADA. Interpretación Geométrica Encontrar la pendiente de la recta tangente a una curva en un punto dado de ella.
 DERIVADA Interpretación Geométrica Objetivo: Encontrar la peniente e la recta tangente a una curva en un punto ao e ella. Para precisar correctamente la iea e tangente a una curva en un punto, se utilizará
DERIVADA Interpretación Geométrica Objetivo: Encontrar la peniente e la recta tangente a una curva en un punto ao e ella. Para precisar correctamente la iea e tangente a una curva en un punto, se utilizará
4.1 Antiderivadas o primitivas e integración indefinida
 48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
Cálculo I Derivadas de Funciones Trascendentes. Julio C. Carrillo E. * 1. Introducción Derivadas de funciones trigonométricas inversas 7
 3.3. Derivaas e Funciones Trascenentes Julio C. Carrillo E. * Ínice. Introucción 2. Derivaas e funciones trigonométricas 3. Derivaas e funciones trigonométricas inversas 7 4. Derivaas e la función exponencial
3.3. Derivaas e Funciones Trascenentes Julio C. Carrillo E. * Ínice. Introucción 2. Derivaas e funciones trigonométricas 3. Derivaas e funciones trigonométricas inversas 7 4. Derivaas e la función exponencial
DERIVADAS (1) (para los próximos días)
 DERIVADAS (1) (para los próimos días) Derivada de una constante K K F ( ) 0 LA DERIVADA DE UNA CONSTANTE es cero. Ejercicio nº 1) Ejercicio nº 2) Ejercicio nº 3) Ejercicio nº 4) Ejercicio nº 5) Ejercicio
DERIVADAS (1) (para los próimos días) Derivada de una constante K K F ( ) 0 LA DERIVADA DE UNA CONSTANTE es cero. Ejercicio nº 1) Ejercicio nº 2) Ejercicio nº 3) Ejercicio nº 4) Ejercicio nº 5) Ejercicio
2.4 La regla de la cadena
 0 CAPÍTULO Derivación. La regla e la caena Encontrar la erivaa e una función compuesta por la regla e la caena. Encontrar la erivaa e una función por la regla general e la potencia. Simplificar la erivaa
0 CAPÍTULO Derivación. La regla e la caena Encontrar la erivaa e una función compuesta por la regla e la caena. Encontrar la erivaa e una función por la regla general e la potencia. Simplificar la erivaa
MATEMÁTICAS BÁSICAS DERIVADA INCREMENTOS x = x - x y2 = f(x2) y = y - y y = f(x )
 Faculta e Contauría Aministración. UNAM Derivaa Autor: Dr. José Manuel Becerra Espinosa MATEMÁTICAS BÁSICAS DERIVADA INCREMENTOS Se eine como incremento e la variable al aumento o isminución que eperimenta,
Faculta e Contauría Aministración. UNAM Derivaa Autor: Dr. José Manuel Becerra Espinosa MATEMÁTICAS BÁSICAS DERIVADA INCREMENTOS Se eine como incremento e la variable al aumento o isminución que eperimenta,
DERIVADAS (1) Derivada de una constante. LA DERIVADA DE UNA CONSTANTE es cero. Derivada de una función potencial: Forma simple.
 DERIVADAS (1) Derivada de una constante f ( ) K K F ( ) 0 LA DERIVADA DE UNA CONSTANTE es cero. nº 1) nº ) nº 3) nº 4) nº 5) nº 6) Derivada de una función potencial: Forma simple r f ( ) r f ( ) r. r 1
DERIVADAS (1) Derivada de una constante f ( ) K K F ( ) 0 LA DERIVADA DE UNA CONSTANTE es cero. nº 1) nº ) nº 3) nº 4) nº 5) nº 6) Derivada de una función potencial: Forma simple r f ( ) r f ( ) r. r 1
ADVERTENCIA: una respuesta sin fundamentación o explicación podrá ser calificada como insuficiente.
 Segno parcial. Es na preba con materiales a la vista ADVERTENCIA: na respesta sin fnamentación o explicación porá ser calificaa como insficiente. Ejercicio 1 Un gobierno fija la tasa e imposición al capital
Segno parcial. Es na preba con materiales a la vista ADVERTENCIA: na respesta sin fnamentación o explicación porá ser calificaa como insficiente. Ejercicio 1 Un gobierno fija la tasa e imposición al capital
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE--4-M---7 CURSO: Matemática Básica SEMESTRE: Primero CÓDIGO DEL CURSO: TIPO DE EXAMEN: Eamen Final FECHA DE
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE--4-M---7 CURSO: Matemática Básica SEMESTRE: Primero CÓDIGO DEL CURSO: TIPO DE EXAMEN: Eamen Final FECHA DE
4.1 Antiderivadas o primitivas e integración indefinida
 48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
Prof. Enrique Mateus Nieves PhD In Advanced Mathematics. El Cálculo Integral
 Prof. Enriqe Mates Nieves El Cálclo Integral El cálclo integral, encarao en el cálclo infinitesimal, es na rama e las matemáticas avanzaas. Se tiliza principalmente para el cálclo e áreas y volúmenes e
Prof. Enriqe Mates Nieves El Cálclo Integral El cálclo integral, encarao en el cálclo infinitesimal, es na rama e las matemáticas avanzaas. Se tiliza principalmente para el cálclo e áreas y volúmenes e
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 A-09 - Incorporado a la Enseñanza Oficial COLEGIO SAN PATRICIO - 0 - Prof. Celia R. Sánchez MATEMÁTICA - TRABAJO PRÁCTICO Nº 8 AÑO FUNCIÓN EXPONENCIAL Y LOGARÍTMICA - ECUACIONES POTENCIACIÓN: Ejercicio
A-09 - Incorporado a la Enseñanza Oficial COLEGIO SAN PATRICIO - 0 - Prof. Celia R. Sánchez MATEMÁTICA - TRABAJO PRÁCTICO Nº 8 AÑO FUNCIÓN EXPONENCIAL Y LOGARÍTMICA - ECUACIONES POTENCIACIÓN: Ejercicio
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-103-1-M--00-017 CURSO: Matemática Básica SEMESTRE: Seguno CÓDIGO DEL CURSO: 103 TIPO DE EXAMEN: Primer eamen
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-103-1-M--00-017 CURSO: Matemática Básica SEMESTRE: Seguno CÓDIGO DEL CURSO: 103 TIPO DE EXAMEN: Primer eamen
DERIVADA DE LA FUNCIÓN EXPONENCIAL DE CUALQUIER BASE Y DE LA FUNCIÓN LOGARÍTMO NATURAL
 DERIVADA DE LA FUNCIÓN EXPONENCIAL DE CUALQUIER BASE Y DE LA FUNCIÓN LOGARÍTMO NATURAL Sgerencias para qien imparte el crso: Se deberá concebir a la Matemática como na actividad social y cltral, en la
DERIVADA DE LA FUNCIÓN EXPONENCIAL DE CUALQUIER BASE Y DE LA FUNCIÓN LOGARÍTMO NATURAL Sgerencias para qien imparte el crso: Se deberá concebir a la Matemática como na actividad social y cltral, en la
Macar lo que corresponda: Reglamentado Libre. Nombre C.I.
 Teoría e jegos Examen e iciembre e 06 Macar lo qe correspona: eglamentao Libre Nombre C.I. NOTA: Es na preba con materiales a la vista ADVETENCIA: na respesta sin fnamentación o explicación porá ser calificaa
Teoría e jegos Examen e iciembre e 06 Macar lo qe correspona: eglamentao Libre Nombre C.I. NOTA: Es na preba con materiales a la vista ADVETENCIA: na respesta sin fnamentación o explicación porá ser calificaa
INTEGRACIÓN POR PARTES EN FORMA TABULAR José A. Rangel M. 1
 1. Introdcción INTEGRACIÓN POR PARTES EN FORMA TABULAR José A. Rangel M. 1 Es conocida la dificltad qe encentra el estdiante al aplicar la fórmla de integración por partes: = v vd. Tal dificltad comienza
1. Introdcción INTEGRACIÓN POR PARTES EN FORMA TABULAR José A. Rangel M. 1 Es conocida la dificltad qe encentra el estdiante al aplicar la fórmla de integración por partes: = v vd. Tal dificltad comienza
2.5 Derivación implícita
 SECCIÓN.5 Derivación implícita 4.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. E X P L O R A C I Ó N Representación gráfica
SECCIÓN.5 Derivación implícita 4.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. E X P L O R A C I Ó N Representación gráfica
Fórmulas de Derivación. Fórmulas de Integración
 Integrl Inefini A l operción e clclr l ntieriv (primitiv) e n fnción se le llm integrción se enot con el símbolo qe es l inicil e l plbr sm. Si F( es n fnción primitiv e f( se epres: f ( F( C si sólo si
Integrl Inefini A l operción e clclr l ntieriv (primitiv) e n fnción se le llm integrción se enot con el símbolo qe es l inicil e l plbr sm. Si F( es n fnción primitiv e f( se epres: f ( F( C si sólo si
Apuntes de Cálculo Diferencial para la asesoría en el área de matemáticas
 Universidad Atónoma del Estado de Méico Plantel Ignacio Ramírez Calzada Academia de Matemáticas Núcleo de formación: Matemáticas Apntes de Cálclo Diferencial para la asesoría en el área de matemáticas
Universidad Atónoma del Estado de Méico Plantel Ignacio Ramírez Calzada Academia de Matemáticas Núcleo de formación: Matemáticas Apntes de Cálclo Diferencial para la asesoría en el área de matemáticas
Matemáticas CCSS LÍMITES DE FUNCIONES 1. INTRODUCCIÓN BÁSICA: A) LÍMITES SOBRE GRÁFICAS. Ejercicio nº 1.- Ejercicio nº 2.
 LÍMITES DE FUNCIONES. INTRODUCCIÓN BÁSICA: A) LÍMITES SOBRE GRÁFICAS Ejercicio nº.- Ejercicio nº.- Página B) LÍMITES APOYÁNDONOS EN LAS GRÁFICAS B.) FUNCIONES POLINÓMICAS De grado : a ) 3 + b ) 3 + c )
LÍMITES DE FUNCIONES. INTRODUCCIÓN BÁSICA: A) LÍMITES SOBRE GRÁFICAS Ejercicio nº.- Ejercicio nº.- Página B) LÍMITES APOYÁNDONOS EN LAS GRÁFICAS B.) FUNCIONES POLINÓMICAS De grado : a ) 3 + b ) 3 + c )
Derivadas algebraicas:
 49 Derivaas algebraicas: El métoo e los cuatro pasos para hallar la erivaa e una función es en la mayoría e los casos laborioso y complicao, por lo que se han esarrollao teoremas e erivación que nos permiten
49 Derivaas algebraicas: El métoo e los cuatro pasos para hallar la erivaa e una función es en la mayoría e los casos laborioso y complicao, por lo que se han esarrollao teoremas e erivación que nos permiten
Tema 8: Derivación. José M. Salazar. Noviembre de 2016
 Tema 8: Derivación. José M. Salazar Noviembre e 2016 Tema 8: Derivación. Lección 9. Derivación: teoría funamental. Lección 10. Aplicaciones e la erivación. Ínice 1 Derivaas. Principales nociones y resultaos.
Tema 8: Derivación. José M. Salazar Noviembre e 2016 Tema 8: Derivación. Lección 9. Derivación: teoría funamental. Lección 10. Aplicaciones e la erivación. Ínice 1 Derivaas. Principales nociones y resultaos.
1.2 TÉCNICAS DE LA DERIVACIÓN.
 . TÉCNICAS DE LA DERIVACIÓN... DERIVACIÓN DE FUNCIONES ALGEBRAICAS Generalmente la derivación se lleva acabo aplicando fórmlas obtenidas mediante la regla general de la derivación y qe calclaremos a continación,
. TÉCNICAS DE LA DERIVACIÓN... DERIVACIÓN DE FUNCIONES ALGEBRAICAS Generalmente la derivación se lleva acabo aplicando fórmlas obtenidas mediante la regla general de la derivación y qe calclaremos a continación,
Universidad Abierta y a Distancia de México. 2 cuatrimestre. Cálculo diferencial. Unidad 3. Derivación
 Universia Abierta y a Distancia e Méico cuatrimestre Cálculo iferencial Eucación Abierta y a Distancia * Ciencias Eactas, Ingenierías y Tecnologías Ínice Presentación e la unia 3 Propósitos 3 Competencia
Universia Abierta y a Distancia e Méico cuatrimestre Cálculo iferencial Eucación Abierta y a Distancia * Ciencias Eactas, Ingenierías y Tecnologías Ínice Presentación e la unia 3 Propósitos 3 Competencia
DERIVADAS DE LAS FUNCIONES ELEMENTALES
 Universia Metropolitana Dpto. e Matemáticas Para Ingeniería Cálculo I (FBMI0) Proesora Aia Montezuma Revisión: Proesora Ana María Roríguez Semestre 08-09A DERIVADAS DE LAS FUNCIONES ELEMENTALES DERIVADAS
Universia Metropolitana Dpto. e Matemáticas Para Ingeniería Cálculo I (FBMI0) Proesora Aia Montezuma Revisión: Proesora Ana María Roríguez Semestre 08-09A DERIVADAS DE LAS FUNCIONES ELEMENTALES DERIVADAS
REVISIÓN DE ANÁLISIS MATEMÁTICO CONCEPTOS Y EJEMPLOS
 E.T. Nº 7 - Brig. Gral. Apnte teórico TEORÍA DE LOS IRUITOS II REVISIÓN DE ANÁLISIS MATEMÁTIO ONEPTOS Y EJEMPLOS INDIE Página FUNIONES LÍMITES DERIVADAS oncepto definición Derivadas de las fnciones algeraicas
E.T. Nº 7 - Brig. Gral. Apnte teórico TEORÍA DE LOS IRUITOS II REVISIÓN DE ANÁLISIS MATEMÁTIO ONEPTOS Y EJEMPLOS INDIE Página FUNIONES LÍMITES DERIVADAS oncepto definición Derivadas de las fnciones algeraicas
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS. S O L U C I Ó N y R Ú B R I C A
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO: 207 PERÍODO: PRIMER TÉRMINO MATERIA: Cálculo e una variable PROFESOR: EVALUACIÓN:
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO: 207 PERÍODO: PRIMER TÉRMINO MATERIA: Cálculo e una variable PROFESOR: EVALUACIÓN:
ADVERTENCIA: una respuesta sin fundamentación o explicación podrá ser calificada como insuficiente.
 Faclta e Ciencias Sociales, Universia e la República, Urgay Teoría e Jegos 24 Segno parcial. Es na preba con materiales a la vista ADVERTENCIA: na respesta sin fnamentación o explicación porá ser calificaa
Faclta e Ciencias Sociales, Universia e la República, Urgay Teoría e Jegos 24 Segno parcial. Es na preba con materiales a la vista ADVERTENCIA: na respesta sin fnamentación o explicación porá ser calificaa
( ) 2. Pendiente de una Recta Tangente. Sea f una función que es continua en x. 1. Para definir la pendiente de la recta tangente ( )
 Derivaa e una Función Ínice.. Introucción.. Peniente e una recta tangente.. Derivaa e una función. 4. Derivaas laterales. 5. Derivaa e una función compuesta (Regla e la Caena). 6. Tabla e erivaas usuales.
Derivaa e una Función Ínice.. Introucción.. Peniente e una recta tangente.. Derivaa e una función. 4. Derivaas laterales. 5. Derivaa e una función compuesta (Regla e la Caena). 6. Tabla e erivaas usuales.
Semana 14-Derivadas I[1/29] Derivada. 7 de junio de Derivada
![Semana 14-Derivadas I[1/29] Derivada. 7 de junio de Derivada Semana 14-Derivadas I[1/29] Derivada. 7 de junio de Derivada](/thumbs/71/65048770.jpg) Semana 14-s I[1/9] 7 e junio e 007 s Introucción Semana 14-s I[/9] Introucción P f Q Consieremos el gráfico e una función f con ominio R. Sea P = (x 0, y 0 ) un punto el gráfico e f y sea Q = (x 1, y 1
Semana 14-s I[1/9] 7 e junio e 007 s Introucción Semana 14-s I[/9] Introucción P f Q Consieremos el gráfico e una función f con ominio R. Sea P = (x 0, y 0 ) un punto el gráfico e f y sea Q = (x 1, y 1
RELACIÓN DE EJERCICIOS LÍMITES Y ASÍNTOTAS
 RELACIÓN DE EJERCICIOS LÍMITES Y ASÍNTOTAS. Calcla los sigientes límites: sen() (a) cos() sen() (b) cos(). Calcla los sigientes límites a) e b) a) e e sen() e. Calcla los sigientes límites: tg() sen()
RELACIÓN DE EJERCICIOS LÍMITES Y ASÍNTOTAS. Calcla los sigientes límites: sen() (a) cos() sen() (b) cos(). Calcla los sigientes límites a) e b) a) e e sen() e. Calcla los sigientes límites: tg() sen()
Derivación. (x c) que pasa por el punto fijo (c, f(c)) y el punto móvil (c + h, f(c + h)) cuando h tiende a 0.
 Derivación Definición y propieaes básicas Definición. Una función f efinia en un entorno e un punto c R es erivable en c si y sólo si el ite f c = f fc + h fc f fc c := = h h c c eiste y toma un valor
Derivación Definición y propieaes básicas Definición. Una función f efinia en un entorno e un punto c R es erivable en c si y sólo si el ite f c = f fc + h fc f fc c := = h h c c eiste y toma un valor
Cálculo I. Índice Reglas Fundamentales para el Cálculo de Derivadas. Julio C. Carrillo E. * 1. Introducción 1. 2.
 3.2. Reglas Funamentales para el Cálculo e Derivaas Julio C. Carrillo E. * Ínice 1. Introucción 1 2. Reglas básicas 3 3. El Álgebra e funciones erivables 4 4. Regla e la caena 8 * Profesor Escuela e Matemáticas,
3.2. Reglas Funamentales para el Cálculo e Derivaas Julio C. Carrillo E. * Ínice 1. Introucción 1 2. Reglas básicas 3 3. El Álgebra e funciones erivables 4 4. Regla e la caena 8 * Profesor Escuela e Matemáticas,
 http://www.matematicaaplicaa.co.cc jezasoft@gmail.com e MATEMÁTICA APLICADA TECNOLOGIA EN ELECTRÓNICA CÁLCULO TALLER DE DERIVADAS Manizales, 26 e Marzo e 20 Solucionar los siguientes problemas referenciaos
http://www.matematicaaplicaa.co.cc jezasoft@gmail.com e MATEMÁTICA APLICADA TECNOLOGIA EN ELECTRÓNICA CÁLCULO TALLER DE DERIVADAS Manizales, 26 e Marzo e 20 Solucionar los siguientes problemas referenciaos
UCLM - Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG)
 PAEG Junio 03 Propuesta B Matemáticas aplicaas a las CCSS II º Bachillerato UCLM - Pruebas e Acceso a Enseñanzas Universitarias Oiciales e Grao (PAEG) Matemáticas aplicaas a las Ciencias Sociales II Junio
PAEG Junio 03 Propuesta B Matemáticas aplicaas a las CCSS II º Bachillerato UCLM - Pruebas e Acceso a Enseñanzas Universitarias Oiciales e Grao (PAEG) Matemáticas aplicaas a las Ciencias Sociales II Junio
UNIDAD 1 Ecuaciones Diferenciales de Primer Orden
 UNIDAD UNIDAD Ecaciones Diferenciales de Primer Orden Definición Clasificación de las Ecaciones Diferenciales Una ecación diferencial es aqélla qe contiene las derivadas o diferenciales de na o más variables
UNIDAD UNIDAD Ecaciones Diferenciales de Primer Orden Definición Clasificación de las Ecaciones Diferenciales Una ecación diferencial es aqélla qe contiene las derivadas o diferenciales de na o más variables
LA DERIVADA DE UNA CONSTANTE
 DERIVADAS ( Derivada de una constante K K R F ( 0 LA DERIVADA DE UNA CONSTANTE es cero. nº nº nº nº 4 nº 5 nº 6 Derivada de una función potencial: Forma simple r r R r. r LA DERIVADA DE UNA FUNCIÓN POTENCIAL
DERIVADAS ( Derivada de una constante K K R F ( 0 LA DERIVADA DE UNA CONSTANTE es cero. nº nº nº nº 4 nº 5 nº 6 Derivada de una función potencial: Forma simple r r R r. r LA DERIVADA DE UNA FUNCIÓN POTENCIAL
La derivada de las funciones trascendentes
 La erivaa e las funciones trascenentes Manuel Barahona, Eliseo Martínez Diciembre 205 Muchos fenómenos e la naturaleza son moelaos meiante funciones eponeciales, logarítimicas, trigonométricas y combinaciones
La erivaa e las funciones trascenentes Manuel Barahona, Eliseo Martínez Diciembre 205 Muchos fenómenos e la naturaleza son moelaos meiante funciones eponeciales, logarítimicas, trigonométricas y combinaciones
1. PRIMITIVA DE UNA FUNCIÓN 2. PROPIEDADES DE LA INTEGRAL INDEFINIDA 3. INTEGRALES INMEDIATAS Ejemplos de integrales inmediatas tipo potencia
 Cálculo de primitivas MATEMÁTICAS II. PRIMITIVA DE UNA FUNCIÓN. PROPIEDADES DE LA INTEGRAL INDEFINIDA. INTEGRALES INMEDIATAS.. Ejemplos de integrales inmediatas tipo potencia.. Ejemplos de integrales inmediatas
Cálculo de primitivas MATEMÁTICAS II. PRIMITIVA DE UNA FUNCIÓN. PROPIEDADES DE LA INTEGRAL INDEFINIDA. INTEGRALES INMEDIATAS.. Ejemplos de integrales inmediatas tipo potencia.. Ejemplos de integrales inmediatas
UNIVERSIDAD DE CONCEPCION DEPARTAMENTO DE MATEMATICA Prof. Jorge Ruiz Castillo. 1.1 Repaso de propiedades de funciones inversas
 Funciones Inversas UNIVERSIDAD DE CONCEPCION DEPARTAMENTO DE MATEMATICA Prof Jorge Ruiz Castillo Repaso e propieaes e funciones inversas Sea f : A B una función biectiva sea f : B A su función inversa
Funciones Inversas UNIVERSIDAD DE CONCEPCION DEPARTAMENTO DE MATEMATICA Prof Jorge Ruiz Castillo Repaso e propieaes e funciones inversas Sea f : A B una función biectiva sea f : B A su función inversa
DERIVADAS (1) LA DERIVADA DE UNA CONSTANTE es cero. Derivada de una función potencial: Forma simple
 DERIVADAS Derivada de una constante K K F 0 LA DERIVADA DE UNA CONSTANTE es cero. nº nº nº nº nº 5 nº Derivada de una unción potencial Forma simple r r r. r LA DERIVADA DE UNA FUNCIÓN POTENCIAL es igual
DERIVADAS Derivada de una constante K K F 0 LA DERIVADA DE UNA CONSTANTE es cero. nº nº nº nº nº 5 nº Derivada de una unción potencial Forma simple r r r. r LA DERIVADA DE UNA FUNCIÓN POTENCIAL es igual
Examen Final de Precálculo (Mate 3171) Nombre 14 de diciembre de 2001
 Eamen Final e Precálculo (Mate 7) Nombre e iciembre e 00 Escriba la letra que correspone a la mejor alternativa en el espacio provisto. (os puntos caa uno) ) Si la gráfica e f es la e la erecha entonces
Eamen Final e Precálculo (Mate 7) Nombre e iciembre e 00 Escriba la letra que correspone a la mejor alternativa en el espacio provisto. (os puntos caa uno) ) Si la gráfica e f es la e la erecha entonces
Universidad Antonio Nariño Matemáticas Especiales Guía N 3: Funciones elementales complejas: exponencial, logaritmo, trigonométricas e hiperbólicas
 Universia Antonio Nariño Matemáticas Especiales Guía N 3: Funciones elementales complejas: exponencial, logaritmo, trigonométricas e hiperbólicas Grupo e Matemáticas Especiales Resumen Se presenta la efinición
Universia Antonio Nariño Matemáticas Especiales Guía N 3: Funciones elementales complejas: exponencial, logaritmo, trigonométricas e hiperbólicas Grupo e Matemáticas Especiales Resumen Se presenta la efinición
Ejercicios resueltos de cálculo integral. 13 de marzo del 2016
 Ejercicios reseltos de cálclo integral Ciro Fabián Bermúez Márqez 3 de marzo del 06 Para todas esas personas qe sienten n profndo afecto por las matemáticas, me gstaría contarles na anécdota. En algna
Ejercicios reseltos de cálclo integral Ciro Fabián Bermúez Márqez 3 de marzo del 06 Para todas esas personas qe sienten n profndo afecto por las matemáticas, me gstaría contarles na anécdota. En algna
1. Función exponencial y funciones definidas mediante la exponencial
 TEMA 3 FUNCIONES COMPLEJAS ELEMENTALES 1. Función exponencial funciones efinias meiante la exponencial 1.1 La función exponencial 1. Funciones trigonométricas 1.3 Funciones hiperbólicas. Función logaritmo
TEMA 3 FUNCIONES COMPLEJAS ELEMENTALES 1. Función exponencial funciones efinias meiante la exponencial 1.1 La función exponencial 1. Funciones trigonométricas 1.3 Funciones hiperbólicas. Función logaritmo
DERIVACIÓN. mtan. y x x. lim lim y ' f '( x) CAPÍTULO IV
 75 CAPÍTULO IV DERIVACIÓN. LA DERIVADA COMO PENDIENTE DE UNA CURVA La peniente e una curva en un punto ao, es iual a la peniente e la recta tanente a la curva en icho punto. Δ Q, Δ Q Q P, La peniente e
75 CAPÍTULO IV DERIVACIÓN. LA DERIVADA COMO PENDIENTE DE UNA CURVA La peniente e una curva en un punto ao, es iual a la peniente e la recta tanente a la curva en icho punto. Δ Q, Δ Q Q P, La peniente e
2.3 Reglas del producto, del cociente y derivadas de orden superior
 SECCIÓN 2.3 Reglas el proucto, el cociente y erivaas e oren superior 119 2.3 Reglas el proucto, el cociente y erivaas e oren superior Encontrar la erivaa e una función por la regla el proucto. Encontrar
SECCIÓN 2.3 Reglas el proucto, el cociente y erivaas e oren superior 119 2.3 Reglas el proucto, el cociente y erivaas e oren superior Encontrar la erivaa e una función por la regla el proucto. Encontrar
2.5 Derivación implícita
 SECCIÓN.5 Derivación implícita.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. EXPLORACIÓN Representación gráfica e una
SECCIÓN.5 Derivación implícita.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. EXPLORACIÓN Representación gráfica e una
Criterio de la segunda derivada para funciones de dos variables por Sergio Roberto Arzamendi Pérez
 Criterio de la segnda derivada para fnciones de dos variables por Sergio Roberto Arzamendi Pérez Sea la fnción f de dos variables definida por f (, ) contina de primera segnda derivadas continas en s dominio,
Criterio de la segnda derivada para fnciones de dos variables por Sergio Roberto Arzamendi Pérez Sea la fnción f de dos variables definida por f (, ) contina de primera segnda derivadas continas en s dominio,
Derivadas algebraicas
 CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez Derivaas algebraicas por Sanra Elvia Pérez Derivaa e una función El concepto e erivaa, base el cálculo iferencial, ha permitio
CDIN0_M1AAL1_Algebraicas Versión: Septiembre 01 Revisor: Sanra Elvia Pérez Derivaas algebraicas por Sanra Elvia Pérez Derivaa e una función El concepto e erivaa, base el cálculo iferencial, ha permitio
1 Composición de funciones
 Composición de fnciones La composición de fnciones o la fnción de fnción es na operación qe aparece natralmente en varias sitaciones. En esta nota, presentaremos (sin demostración) algnos de los resltados
Composición de fnciones La composición de fnciones o la fnción de fnción es na operación qe aparece natralmente en varias sitaciones. En esta nota, presentaremos (sin demostración) algnos de los resltados
Resolviendo la Ecuación de Schrodinger en 1-D
 Resolvieno la Ecación e Schoinge en -D D. Hécto René VEGA-ARRILLO so e Física Moena Unia Acaémica e Ingenieía Eléctica Univesia Atónoma e Zacatecas Docmento: FM/Notas/RES/070309 Domingo/-Mazo/009 ontenio
Resolvieno la Ecación e Schoinge en -D D. Hécto René VEGA-ARRILLO so e Física Moena Unia Acaémica e Ingenieía Eléctica Univesia Atónoma e Zacatecas Docmento: FM/Notas/RES/070309 Domingo/-Mazo/009 ontenio
Apellidos: Nombre: Curso: 2º Grupo: Día: CURSO
 EXAMEN DE MATEMATICAS II º ENSAYO (FUNCIONES) Apellidos: Nombre: Crso: º Grpo: Día: CURSO 056 Instrcciones: a) Dración: HORA y 30 MINUTOS. b) Debes elegir entre realizar únicamente los catro ejercicios
EXAMEN DE MATEMATICAS II º ENSAYO (FUNCIONES) Apellidos: Nombre: Crso: º Grpo: Día: CURSO 056 Instrcciones: a) Dración: HORA y 30 MINUTOS. b) Debes elegir entre realizar únicamente los catro ejercicios
DERIVADAS (1) LA DERIVADA DE UNA CONSTANTE es cero. Sol: Sol: Sol: Sol: Derivada de una función potencial: Forma simple
 DERIVADAS ( Derivada de una constante K K R F ( 0 LA DERIVADA DE UNA CONSTANTE es cero. nº nº nº nº 4 nº 5 nº 6 Derivada de una función potencial: Forma simple r r R r. r LA DERIVADA DE UNA FUNCIÓN POTENCIAL
DERIVADAS ( Derivada de una constante K K R F ( 0 LA DERIVADA DE UNA CONSTANTE es cero. nº nº nº nº 4 nº 5 nº 6 Derivada de una función potencial: Forma simple r r R r. r LA DERIVADA DE UNA FUNCIÓN POTENCIAL
Regla de la cadena. Regla de la cadena y. son diferenciables, entonces: w w u w v y u y v y. y g. donde F, w w u w v x u x v x
 Regla de la cadena Una de las reglas qe en el cálclo de na variable reslta my útil es la regla de la cadena. Dicho grosso modo, esta regla sirve para derivar na composición de fnciones, esto es, na fnción
Regla de la cadena Una de las reglas qe en el cálclo de na variable reslta my útil es la regla de la cadena. Dicho grosso modo, esta regla sirve para derivar na composición de fnciones, esto es, na fnción
Tutorial MT-a2. Matemática Tutorial Nivel Avanzado. Función exponencial y logarítmica II
 467890467890 M ate m ática Tutorial MT-a Matemática 006 Tutorial Nivel Avanzado Función eponencial y logarítmica II Matemática 006 Tutorial Función eponencial y logarítmica Marco Teórico. Función eponencial..
467890467890 M ate m ática Tutorial MT-a Matemática 006 Tutorial Nivel Avanzado Función eponencial y logarítmica II Matemática 006 Tutorial Función eponencial y logarítmica Marco Teórico. Función eponencial..
Información importante
 Universia Técnica Feerico Santa María Departamento e Matemática Coorinación e Matemática I (MAT021) 1 er Semestre e 2010 Semana 9: Lunes 17 viernes 21 e Mayo Información importante El control Q2A es el
Universia Técnica Feerico Santa María Departamento e Matemática Coorinación e Matemática I (MAT021) 1 er Semestre e 2010 Semana 9: Lunes 17 viernes 21 e Mayo Información importante El control Q2A es el
Regla de la cadena. f (x) 1 x 3. d dx x3 1 x 3. (3x 2 ) 3 x. f(x) 3 d dx ln x 3. 1 x. para x70, d dx ln x 1. para x60, d dx ln( x) 1x.
 74 CAPÍTULO 3 La erivaa EJEMPLO 4 Diferencie f ()=ln 3. Regla e la caena Solución Debio a que 3 ebe ser positiva, se entiene que 70. Así, por (3), con u= 3, tenemos Solución alterna: Por iii) e las lees
74 CAPÍTULO 3 La erivaa EJEMPLO 4 Diferencie f ()=ln 3. Regla e la caena Solución Debio a que 3 ebe ser positiva, se entiene que 70. Así, por (3), con u= 3, tenemos Solución alterna: Por iii) e las lees
REACTIVOS DE LA UNIDAD 4 FUNCIONES EXPONENCIALES Y LOGARITMICAS. Resuelve cada una de las preguntas siguiente y elige la respuesta correcta
 REACTIVOS DE LA UNIDAD 4 FUNCIONES EXPONENCIALES Y LOGARITMICAS Resuelve cada una de las preguntas siguiente y elige la respuesta correcta 1.-El punto común a todas las funciones eponenciales de la forma
REACTIVOS DE LA UNIDAD 4 FUNCIONES EXPONENCIALES Y LOGARITMICAS Resuelve cada una de las preguntas siguiente y elige la respuesta correcta 1.-El punto común a todas las funciones eponenciales de la forma
() 25 de mayo de / 9
 DEFINICION. Una función es iferenciable en a si f (a) existe, y iremos que es iferenciable en un intervalo abierto si es iferenciable en caa uno e los puntos el intervalo. NOTA. Para las funciones que
DEFINICION. Una función es iferenciable en a si f (a) existe, y iremos que es iferenciable en un intervalo abierto si es iferenciable en caa uno e los puntos el intervalo. NOTA. Para las funciones que
INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. en un intervalo al siguiente cociente:
 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES Crecimiento de una Función en un Intervalo Tasa de Variación Media (T.V.M.) Se llama tasa de variación media (T.V.M.) de una función y f() en un intervalo
INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES Crecimiento de una Función en un Intervalo Tasa de Variación Media (T.V.M.) Se llama tasa de variación media (T.V.M.) de una función y f() en un intervalo
Parcial de Cálculo C 0
 Parcial e Cálculo C 0 0 0 Funamentos e Matemáticas Usar los polinomios e Talor para averiguar si la función g = 7 alcanza o no un etremo local en = 0 sen ln Solución: El polinomio e Talor en = 0 e un polinomio
Parcial e Cálculo C 0 0 0 Funamentos e Matemáticas Usar los polinomios e Talor para averiguar si la función g = 7 alcanza o no un etremo local en = 0 sen ln Solución: El polinomio e Talor en = 0 e un polinomio
Logaritmo Natural. x I t dt = ln(x) = ln(x) > 0 para x (1, ) Observación 5. El primer teorema fundamental del Cálculo implica que
 Logaritmo Natural Si n ya sabemos que x t n t = n+ xn+ + C, con C una constante. Definición. La regla e corresponencia ln(x) = x t t = x I efine una función con ominio D ln = (0, ). A esta función se le
Logaritmo Natural Si n ya sabemos que x t n t = n+ xn+ + C, con C una constante. Definición. La regla e corresponencia ln(x) = x t t = x I efine una función con ominio D ln = (0, ). A esta función se le
1. Idea intuitiva del concepto de derivada de una función en un punto.
 Tema : Derivadas. Idea intitiva del concepto de derivada de na fnción en n pnto. Comencemos pensando en na fnción f () t, donde t represente el tiempo y f la evolción de na cantidad calqiera a lo largo
Tema : Derivadas. Idea intitiva del concepto de derivada de na fnción en n pnto. Comencemos pensando en na fnción f () t, donde t represente el tiempo y f la evolción de na cantidad calqiera a lo largo
Concurso Nacional de Matemáticas Pierre Fermat Problemas
 Concrso Nacional de Matemáticas Pierre Fermat 014 Examen para Nivel Secndaria Etapa Eliminatoria Instrcciones: No tilizar cellar (éste deberá de estar apagado), ipod, notebook, calcladora ó calqier otro
Concrso Nacional de Matemáticas Pierre Fermat 014 Examen para Nivel Secndaria Etapa Eliminatoria Instrcciones: No tilizar cellar (éste deberá de estar apagado), ipod, notebook, calcladora ó calqier otro
5.2 La función logaritmo natural: integración
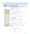 CAPÍTULO 5 Funciones logarítmica, eponencial otras funciones trascenentes 5. La función logaritmo natural: integración Usar la regla e logaritmo e integración para integrar una función racional. Integrar
CAPÍTULO 5 Funciones logarítmica, eponencial otras funciones trascenentes 5. La función logaritmo natural: integración Usar la regla e logaritmo e integración para integrar una función racional. Integrar
1. Grafique la familia de curvas que representa la solución general de la ecuación diferencial: y ' + y = 0
 Elaborao por: Jhonn Choquehuanca Lizarraga Ecuaciones Diferenciales e Primer oren Aplicaciones. Grafique la familia e curvas que representa la solución general e la ecuación iferencial: ' + = 0 Solución:
Elaborao por: Jhonn Choquehuanca Lizarraga Ecuaciones Diferenciales e Primer oren Aplicaciones. Grafique la familia e curvas que representa la solución general e la ecuación iferencial: ' + = 0 Solución:
Fórmulas generales III FÓRMULA DE LA POTENCIA
 III FÓRMULA DE LA POTENCIA Las fórmlas vistas en el capítlo anterior feron my específicas para integrales de x elevada a calqier potencia; sin embargo, no siempre, o más bien, pocas veces lo qe está elevado
III FÓRMULA DE LA POTENCIA Las fórmlas vistas en el capítlo anterior feron my específicas para integrales de x elevada a calqier potencia; sin embargo, no siempre, o más bien, pocas veces lo qe está elevado
ECUACIONES NO POLINÓMICAS CON UNA INCÓGNITA
 Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones ECUACIONES NO POLINÓMICAS CON UNA INCÓGNITA Una ecuación no polinómica es, en general, más difícil de resolver que una
Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones ECUACIONES NO POLINÓMICAS CON UNA INCÓGNITA Una ecuación no polinómica es, en general, más difícil de resolver que una
Se define la derivada de una función f(x) en un punto "a" como el resultado, del siguiente límite:
 TEMA: DERIVADAS. Derivada de una función en un punto Se define la derivada de una función f() en un punto "a" como el resultado, del siguiente límite: f ( a + ) f ( a) f '( a) lim Si el límite eiste es
TEMA: DERIVADAS. Derivada de una función en un punto Se define la derivada de una función f() en un punto "a" como el resultado, del siguiente límite: f ( a + ) f ( a) f '( a) lim Si el límite eiste es
La regla de la constante. La derivada de una función constante es 0. Es decir, si c es un número real, entonces d c 0. dx (Ver la figura 2.
 SECCIÓN. Reglas básicas e erivación razón e cambio 07. Reglas básicas e erivación razón e cambio Encontrar la erivaa e una función por la regla e la constante. Encontrar la erivaa e una función por la
SECCIÓN. Reglas básicas e erivación razón e cambio 07. Reglas básicas e erivación razón e cambio Encontrar la erivaa e una función por la regla e la constante. Encontrar la erivaa e una función por la
UNIDAD I CÁLCULO DIFERENCIAL
 Vicerrectorao Acaémico Faculta e Ciencias Aministrativas Licenciatura en Aministración Mención Gerencia y Mercaeo Unia Curricular: Matemática I UNIDAD I CÁLCULO DIFERENCIAL Elaborao por: Ing. Ronny Altuve
Vicerrectorao Acaémico Faculta e Ciencias Aministrativas Licenciatura en Aministración Mención Gerencia y Mercaeo Unia Curricular: Matemática I UNIDAD I CÁLCULO DIFERENCIAL Elaborao por: Ing. Ronny Altuve
Decimos que f es derivable en dicho punto si existe y es finito: Lím. En tal
 UNIDAD : DERIVADAS Y APLICACIONES.- DERIVADA DE UNA FUNCIÓN EN UN PUNTO. Definición : Sea f una función definida en un a, b Dom f. Se llama tasa de intervalo [ ] variación media de f en dicho intervalo
UNIDAD : DERIVADAS Y APLICACIONES.- DERIVADA DE UNA FUNCIÓN EN UN PUNTO. Definición : Sea f una función definida en un a, b Dom f. Se llama tasa de intervalo [ ] variación media de f en dicho intervalo
3.1 Definiciones previas
 ÍNDICE 3.1 Definiciones previas............................... 1 3.2 Operaciones con funciones........................... 8 3.3 Límite e una función en un punto...................... 15 3.3.1 Operaciones
ÍNDICE 3.1 Definiciones previas............................... 1 3.2 Operaciones con funciones........................... 8 3.3 Límite e una función en un punto...................... 15 3.3.1 Operaciones
Solución: Utiliza la definición anterior, también llamada la "clave".
 Materia: Matemáticas de 4to año Tema: Definición de Logaritmo Definición de logaritmo Marco Teórico Probablemente puedes adivinar que en y en. Pero, cuánto es si? Hasta ahora, no hemos tenido una relación
Materia: Matemáticas de 4to año Tema: Definición de Logaritmo Definición de logaritmo Marco Teórico Probablemente puedes adivinar que en y en. Pero, cuánto es si? Hasta ahora, no hemos tenido una relación
Tema 5: Ecuaciones diferenciales de primer orden homogéneas
 Tema 5: Ecaciones diferenciales de primer orden homogéneas 5.1 Primer método de solción En la e.d. homogénea d (1) f (, ) d donde, de acerdo con lo visto en (.), f(t, t) f(, ), se sstite () v s correspondiente
Tema 5: Ecaciones diferenciales de primer orden homogéneas 5.1 Primer método de solción En la e.d. homogénea d (1) f (, ) d donde, de acerdo con lo visto en (.), f(t, t) f(, ), se sstite () v s correspondiente
3 DERIVADAS ALGEBRAICAS
 DERIVADAS ALGEBRAICAS DERIVADAS ALGEBRAICAS Entiénase la erivaa como la peniente e la recta tangente a la función en un punto ao, lo anterior implica que la función ebe eistir en ese punto para poer trazar
DERIVADAS ALGEBRAICAS DERIVADAS ALGEBRAICAS Entiénase la erivaa como la peniente e la recta tangente a la función en un punto ao, lo anterior implica que la función ebe eistir en ese punto para poer trazar
LA CICLOIDE, UNA CURVA DE MUCHO EMPAQUE
 LA CICLOIDE, UNA CUVA DE MUCHO EMPAQUE CALOS S CHINEA LA CICLOIDE UNA CUVA DE MUCHO EMPAQUE Una breve introucción 1 Ecuaciones paramétricas La tangente y la normal en un punto 3 Longitu e un arco 4 El
LA CICLOIDE, UNA CUVA DE MUCHO EMPAQUE CALOS S CHINEA LA CICLOIDE UNA CUVA DE MUCHO EMPAQUE Una breve introucción 1 Ecuaciones paramétricas La tangente y la normal en un punto 3 Longitu e un arco 4 El
UNIVERSIDAD DIEGO PORTALES GUÍA N 11 CÁLCULO I. Profesor: Carlos Ruz Leiva DERIVADAS. Derivadas de orden superior. Ejemplos
 UNIVERSIDAD DIEGO PORTALES FACULTAD DE CIENCIAS DE LA INGENIERÍA INSTITUTO DE CIENCIAS BÁSICAS Profesor: Carlos Ruz Leiva GUÍA N CÁLCULO I DERIVADAS Derivaas e oren superior Ejemplos Hallar las siguientes
UNIVERSIDAD DIEGO PORTALES FACULTAD DE CIENCIAS DE LA INGENIERÍA INSTITUTO DE CIENCIAS BÁSICAS Profesor: Carlos Ruz Leiva GUÍA N CÁLCULO I DERIVADAS Derivaas e oren superior Ejemplos Hallar las siguientes
Curso Introductorio a las Matemáticas Universitarias
 Curso Introuctorio a las Matemáticas Universitarias Tema 8: Derivación Víctor M. Almeia Lozano Jorge J. García Melián Licencia Creative Commons 2013 8. DERIVACIÓN En este tema veremos el concepto e erivaa
Curso Introuctorio a las Matemáticas Universitarias Tema 8: Derivación Víctor M. Almeia Lozano Jorge J. García Melián Licencia Creative Commons 2013 8. DERIVACIÓN En este tema veremos el concepto e erivaa
CLAVES DE CORRECCIÓN GUÍA DE EJERCITACIÓN FACTORES Y PRODUCTOS PREGUNTA ALTERNATIVA Nivel
 Estimado alumno: Aquí encontrarás las claves de corrección, las habilidades y los procedimientos de resolución asociados a cada pregunta, no obstante, para reforzar tu aprendizaje es fundamental que asistas
Estimado alumno: Aquí encontrarás las claves de corrección, las habilidades y los procedimientos de resolución asociados a cada pregunta, no obstante, para reforzar tu aprendizaje es fundamental que asistas
INSTRUCTIVO PARA TUTORÍAS
 INSTRUCTIVO PARA TUTORÍAS Las tutorías corresponen a los espacios acaémicos en los que el estuiante el Politécnico Los Alpes puee profunizar y reforzar sus conocimientos en iferentes temas e cara al eamen
INSTRUCTIVO PARA TUTORÍAS Las tutorías corresponen a los espacios acaémicos en los que el estuiante el Politécnico Los Alpes puee profunizar y reforzar sus conocimientos en iferentes temas e cara al eamen
