Modulador de polarización mediante placas de vidrio plano paralelas
|
|
|
- José Manuel Valdéz Cortés
- hace 7 años
- Vistas:
Transcripción
1 NINVI ncunro Invsgacón n I, 4 5 Marzo, NINVI UAZ 004 ncunro Invsgacón n Ingnría lécrca Zacacas, Zac, Marzo 4 5, 004 Moulaor polarzacón man placas vro plano parallas M Monoa, G Paz, D Malacara-Hrnánz J García, Cnro Invsgacons n Ópca, A C, Lón, Go, CP 3750 TL: +(477)77307, 97, corro-: monoa@ com Rsumn Frcunmn nos nconramos n nusros arrglos prmnals qu la nraccón la luz con algún lmno ópco mofca la polarzacón qu corrgrla u obnr la saa mplca complcacons n l arrglo Prsnamos un análss órco-prmnal l uso placas vro para cambar la polarzacón lípca aprománola a una polarzacón crcular n un análss con marcs vcors Jons usamos un lmno al, al qu llamamos moulaor ransmancas (MT), con frns ransmancas n És lmno convr la polarzacón lípca n crcular cuano l j maor la lps conc con uno los os js l moulaor, smpr cuano la rlacón nr la ransmanca maor mnor sa la acuaa Los rsulaos prmnals son conssns con la oría Absrac I s frqunl foun ha polarzaon changs as a consqunc of nracon bwn lgh an h varous opcal lmns passs hrough To corrc hs s no alwas as bu w show a vr smpl mho o corrc crcular polarzaon ha has chang slghl no llpc polarzaon Th basc a s o moula h ransmancs of h lcrc fl n boh major an mnor as of h llps of polarzaon I s on b mans of glass plas a non normal ncnc prmnal rsuls ar roughl conssn Palabras clav Polarzacón, polarmría I INTRODUCCIÓN ORMALMNT, lo qu s hac al planar jcuar una mcón nrfromérca s raar Nqu la polarzacón s consrv snclla manjar Sn mbargo, ao qu la polarzacón s un aspco funamnal n la nauralza lcromagnéca la luz, no smpr s posbl var alguna complcacón Aunqu la maoría los cors ponca lumnosa son rlavamn nsnsbls a la polarzacón, la nraccón con los lmnos ópcos camba la polarzacón n maor o mnor grao, lo qu a fnal cunas alra la srbucón ponca n l prsn rabajo, comnzamos por una scrpcón los funamnos órcos para nusra propusa mofcar l sao polarzacón lípca a práccamn crcular man un moulaor ransmancas Lugo prsnamos una prmra solucón prmnal con una sola nrfas Y fnalmn, prsnamos una solucón usano las os nrfass una placa vro, con lo qu omamos n cuna la posbl nrfrnca nr múlpls hacs Las posbls aplcacons son múlpls Por jmplo, un rabajo rlaconao con l prsn, ao qu s consra l cambo la polarzacón al pasar por una placa vro, s l Schchnr [] Él propon un méoo para la rconsruccón mágns roraas por l paso la luz a ravés una vnana vro nclnaa parcalmn rflcora Para llo calcula
2 NINVI ncunro Invsgacón n I, 4 5 Marzo, prmramn la rflcanca a ravés las os suprfcs la vnana, la cual supon hcha un maral homogéno, no absorbn no conucor La luz ncn s supon ncohrn no polarzaa l méoo s ravo busca la magnu la corrlacón cruzaa nr os mágns propusas como solucón la magn arás la vnana la magn parcalmn rfljaa n la vnana n gnral, sn muchas oras manras mofcar conrolar l sao polarzacón la luz Por jmplo, s pu proucr un rraso fas varabl usano l compnsaor Soll o una mofcacón l compnsaor Babn, l moulaor fco Faraa [], las clas Krr [3], Pockls [4], placas raraoras, c Zhuang [5] propon un méoo para corrgr cualqur sao polarzacón manra qu obngamos l sao polarzacón sao sn mporar cual sa és l méoo s basa n l uso rs clas crsal líquo La brrfrngnca prouca n las clas man un campo lécrco s moulaa para movr l sao polarzacón n la sfra Poncaré n l prsn rabajo, la a funamnal s qu s nmos luz lípcamn polarzaa, pomos hacrla crcularmn polarzaa nroucno una placa vro convnnmn ornaa moo qu la ransmanca sa frn n l j maor rspco al j mnor la lps polarzacón La mosracón s hcho s snclla cuano nmos una sola nrfas l problma s complca cuano consramos luz monocromáca cohrn spacal mporalmn aravsano una placa plana paralla lgaa n s caso, l haz prncpal los ransmos spués múlpls rflons, s bn sumar omano n cuna las fass caa uno l fco s una srbucón la nnsa alraa por la nrfrnca s s un fnómno usao n l pasao para mr ángulos man l cono franjas (o fraccons franjas) nrfrnca proucas por la rflón luz lásr rfljaa n ambas caras una placa vro l méoo s báscamn l nrfrómro splazamno laral Mur varano l ángulo ncnca Conform gra la placa vro las franjas nrfrnca van pasano por la panalla obsrvacón on s pu calcular l cambo n l ángulo ncnca [6] n s sno, oro rabajo rlaconao con l prsn s l Azzam [7] [8], n l qu propon una plícula un maral spcífco para caa longu ona manra al qu l ínc rfraccón l grosor la plícula ngan cra rlacón fja rspco al ínc rfraccón l susrao, l mo n l cual s splaza hasa llgar a la plícula l ángulo ncnca Para las concons qu él sablc, la polarzacón l haz ncn s ransma rfljaa sn alracón, aunqu la razón nr ransmanca rflcanca s % úncamn para cro ángulo ncnca n su sgun rabajo hac una mofcacón n la qu nclu un rrazo ma ona n l haz rfljao n un vsor haz Prsna un análss órco prmnal para un vsor haz a 45 n l nfrarrojo lo aplca a un nrfrómro Mchlson l aspco sobrsaln n sos rabajos, por su rlacón con l prsn, s qu ambos usan vnanas ransparns qu pun sr usaas como vsors haz n ambos casos, l ángulo ncnca s mann fjo o al mnos mu crcano a un ángulo al sño s cr, no s oma n cuna las varacons n la ransmanca qu porían ocurrr a conscunca varar l ángulo ncnca con un spsor consan la plícula II FUNDAMNTOS TORICOS La polarzacón una ona T (Transvrsal lécrca), monocromáca unform s pu
3 NINVI ncunro Invsgacón n I, 4 5 Marzo, rprsnar n un ssma coornao rcho,, z como l la Fg n lla vmos la rprsnacón un campo lécrco (z, ) splazános a lo largo l j z, sobr la normal a sa págna n rccón al lcor sa s una gnralzacón qu nclu la polarzacón lnal la crcular como casos parculars l campo lécrco (z, ) gra n l plano, scrbno una lps con js maor mnor sobr los js rspcvamn s nuvo ssma coornao, cuo j z s colnal con z, sá grao un ángulo α n l plano l campo lécrco (z, ) n cra poscón z n un mpo nrá una magnu qu rá l orgn a la prfra la lps con un ángulo β Too so pu sr rprsnao man la c () a (z,) β α b Fgura lps polarzacón [ cos( ω kz + )] + [ cos( ω kz + )] ( z, ) = ˆ ˆ, () on l campo lécrco (z, ) s scompon n os onas: una con amplu, n la rccón l vcor unaro ˆ ora, con amplu, n la rccón l vcor unaro ŷ Ambas osclan cosnoalmn, con una frcunca angular ω, con un númro ona k=π/λ, on λ s la longu ona una fas ncal rspcvamn sa rprsnacón prm nfcar oas las varabls ncsaras para rprsnar un haz luz unform con polarzacón lípca ncluno los casos parculars polarzacón lnal crcular Pro la noacón Jons nos prm rprsnar la msma ona una manra mucho más compaca manjabl Para consgurlo s b usar la rprsnacón fasoral una osclacón armónca aplcaa a caa uno los érmnos la c () runrlos n una rprsnacón marcal n al rprsnacón, la c () qua como una marz por lmnos l lmno (,) connrá la componn n mnras qu l lmno (,) connrá la componn n la c () l vcor n al rprsnacón concsa quará como j = j () La rprsnacón fasoral raslaa l vcor a un spaco absraco on las magnus fass son rprsnacons polars n campos compljos sa rprsnacón obc oas las rglas l cálculo fasoral pro no rprsnan vcors n l spaco físco Para rgrsar a la rprsnacón físca la c () bmos mulplcar la c () por ˆ{j(ω-kz)}, omar la par
4 NINVI ncunro Invsgacón n I, 4 5 Marzo, ral l rsulao nfcar las componns vbrano n n man los vcors unaros ˆ ŷ III CORRCCIÓN D LA POLARIZACIÓN LÍPTICA n l caso qu a ngamos luz lípcamn polarzaa, por jmplo = 0 lgramn frn a los 90 n la cuacón (), pomos convrrla n crcularmn polarzaa man l moulaor ransmancas qu s rprsna por ' 0 T ' =, (3) 0 ' fno n l plano, on s la ransmanca corrsponn a la componn la luz polarzaa vajano n l plano z, s la ransmanca corrsponn a la componn la luz polarzaa vajano n l plano z Cuano un haz luz polarzaa, como l rprsnao por la c (), nc sobr un objo como l rprsnao por la c (3) l vcor l campo lécrco rsulan s calcula man la sgun cuacón marcal: o cos( α) sn( α) sn( α) ' cos( α) 0 0 cos( α) ' sn( α) sn( α) cos( α) j = j, (4) on,, son los valors l campo lécrco ncn Lno la c (4) rcha a zqura pomos vr qu l vcor Jons l campo lécrco ncn s ransporao l ssma coornaas (, ) al (, ) para por calcular l fco l objo rprsnao por la c (3) n l plano (, ) fnalmn una ransformacón nvrsa l plano (, ) al (, ) Usano la c (4) vmos qu s posbl mofcar la lpca man un objo como l la c (3) Por jmplo, para llvar la lpca, prsaa como l cocn =a/b, =089 a =, cuano la lps n ángulo α=934 s ncsaro nr un MT con =089 = con l msmo ángulo α Como vmos, n s caso s convnn usar la msma varabl α para prsar l ángulo l j maor la lps rspco al j para rprsnar l gro coornaas n la c (4) pro, como vrmos más alan, no smpr s así n s caso, s ncsaro qu ambos ángulos san éncos para por hacr la corrccón qu proponmos IV MT CON UNA SOLA INTRFAS D VIDRIO Una solucón sría consrur l MT man una sola nrfas vro nclnaa rspco a la rccón propagacón la ona lumnosa Cuano un haz luz nc sobr la nrfas con un ángulo θ rspco a su normal, l haz s ransmrá con un ángulo θ acuro con la l Snll n sn( θ ) = n sn( θ ), (5) on n s l ínc rfraccón l mo on vaja l haz ncn n s l ínc
5 NINVI ncunro Invsgacón n I, 4 5 Marzo, rfraccón l mo n on s ransm Por oro lao, n las cuacons Frsnl vmos qu un haz luz qu aravsa una nrfas nr os mos lécrcos s rflja o ransm con alracons fas amplu l campo lécrco qu pn θ, n n Las cuacons Frsnl para las ransmancas l campo lécrco la luz polarzaa n l plano ncnca orogonal a és, son rspcvamn: p n cos( θ ) =, (6) n cos( θ ) + n cos( θ ) s n cos( θ ) = (7) n cos( θ ) + n cos( θ ) La sgun gráfca (vr Fgura ), musra las varacons p s vrsus l ángulo ncnca θ para una nrfas ar-vro l ínc rfraccón l ar s omó como n = l ínc rfraccón l vro como n =5 s p Fgura Cofcns ransmsón n amplu para una nrfas ar-vro (n = n =5) Connuano con l msmo jmplo la pasaa sccón nconramos qu, para corrgr la msma lpca man la nrfas ar-vro la Fg, bmos ponr cha nrfas con un ángulo ncnca θ =64 sobr l plano z, para nr = s =0535 = p =060 V SOLUCIÓN CON UNA PLACA PLANO-PARALLA D VIDRIO Cuano usamos una placa vro plano-paralla para consrur l moulaor ransmancas l problma s complca un poco n la Fg 3 vmos las varabls qu nrvnn n l problma La placa vro ínc rfraccón n nmrsa n ar n a =, con un spsor, sá nclnaa un ángulo θ rspco a la rccón propagacón l haz luz ncn Como la placa s almn plana paralla, l ángulo rfraccón θ s ambén l ángulo ncnca n la
6 NINVI ncunro Invsgacón n I, 4 5 Marzo, sguna cara por lo ano θ 3 = θ S l haz luz s sufcnmn cohrn spacal mporalmn, l campo lécrco m frns punos n l frn ona, qu suponmos almn plano, conrburá a ravés múlpls rflons al haz qu sal n l puno P 0 θ θ θ P θ 3 = θ m 0 m r m j m m (m ) n a = n n a = Fgura 3 Conrbucón múlpls punos n un frn ona al campo qu sal n l puno P una placa vro La sumaora los campos lécrcos consra cofcns ransmsón rflón n amplu los raros fas Así, s l cofcn ransmsón n amplu n la nrfas ar-vro, s l cofcn ransmsón n amplu n la nrfas vro-ar, r s l cofcn rflón nrna n amplu = + F, l rrazo fas bo al camno ópco aconal más l cambo fas bo a la rflón nrna F Para calcular la sumaora bmos rcorar qu ésa b fcuars ano para la componn l campo lécrco parallo al plano ncnca como orogonal a él Los cofcns ransmsón a furon fnos n las cs (6) (7) Los rflón son los sguns: r r p s n cos( θ ) n cos( θ ) =, (8) n cos( θ ) + n cos( θ ) n cos( θ) n cos( θ ) = (9) n cos( θ ) + n cos( θ ) Caa uno los cofcns b sr calculao para la nrfas corrsponn, ar-vro o vro-ar, usano un apósrof para los úlmos l rrazo fas bo al camno ópco aconal rcorro por l rao (m+) rspco l rao m sá ao por: = k n cos( θ ) (0) La fas nrouca por las rflons nrnas la pomos rmnar por las cuacons Frsnl D la Fg 3 vmos qu l rao (m+) sufr os rflons nrnas más qu l rao m,
7 NINVI ncunro Invsgacón n I, 4 5 Marzo, por lo qu l cambo oal fas para la polarzacón paralla s: π 0 < θ < θ p F p =, () 0 θ p < θ < π on θ p s l ángulo polarzacón n rflón rna Aunqu los cambos fas ocurrn n rflón nrna, por convnnca, hmos fno cho cambo fas n funcón l ángulo ncnca rno so s posbl porqu, conocno la gomría l problma, l ángulo ncnca rno la l Snll, vmos qu l ángulo polarzacón n ncnca rna θ p ocurr smulánamn con l ángulo polarzacón n ncnca nrna Por oro lao, l cambo fas por las rflons nrnas para l campo lécrco orogonal al plano ncnca s F s = 0 0 < θ < π () Fnalmn, suponr una srbucón unform nfna l haz ncn nos prm llgar a una forma compaca la sumaora l campo lécrco qu sal n l puno P la fgura, quano ~ = j, (3) on s la ransmanca oal l MT sá aa por = r' cos ' + r' 4, (4) s un cambo fas nrouco por l MT sá ao como r' sn = an r' cos (5) Como n l caso una sola nrfas, la ransmanca oal varía conform los cofcns ransmsón rflón varían con l ángulo ncnca θ Pro amás, l cos( ), n l nomnaor, prouc una osclacón n amplu conform θ s ncrmna La Fg 4 a) musra la ransmanca oal para las componns la polarzacón s p D la c (0), pomos vr qu la frcunca la osclacón pn l grosor la placa, l númro ona k l ínc rfraccón n s moulaa n frcunca por la no lnala l cos(θ ) La frcunca máma ocurr apromaamn a 48 la mínma cuano θ s crcana a 0 o 90 concno con lo rporao n la rfrnca 7 La Fg 4 b) musra algunos alls la osclacón No qu ha sucsvos ángulos para los cuals l MT s complamn ransparn, n oras palabras, la ransmanca oal ano para la componn s como p smulánamn s lvan a uno No obsan, nr os mámos smpr s un mínmo para la ransmanca para ambas componns sos mínmos nn una rlacón s mn / p mn, qu crc conform l ángulo ncnca θ s ncrmna so lo pomos vr grafcao n la Fg 4 a) n una prmra apromacón, s sufcn localzar la rlacón más apropaa s mn / p mn para lvar la lpca
8 NINVI ncunro Invsgacón n I, 4 5 Marzo, a un valor crcano a uno Dbmos omar n cuna qu l MT nrouc un cambo fas prsao n la c (5) Un all sa fas lo pomos vr n la Fg 4 c) Como pomos vr, la fas pasa por cro acamn cuano s proucn los mínmos las ransmancas n la Fg 4 b) so hac posbl la prmra apromacón sñalaa s p p s s - p s mn / p mn s / p p s θ θ θ a) b) c) Fg 4 a) Transmancas oals (normalzaas) vs ángulo ncnca (n graos), b) alls c) cambo oal fas nrouco por l MT (n raans) vs ángulo ncnca (n graos) Para consgur una lpca maor bmos soluconar la sgun cuacón paramérca o' o' o' o' = = ' ( α') ( θ ) ( α') ( θ ) = 0 [ ( α') + ( θ )] [ ( α') + ( θ )] = 90 ' ' ' ' ' ' ', (6) on = p, = s, = p, = s s calculan man las cuacons (4) (5), α s l ángulo nr cuano s úlmo no s colnal con l j maor la lps Djarmos la lral α úncamn para l ángulo subno nr l j l j maor la lps polarzacón,, s calculan man la c (4), pro subsuno α con α Como vrmos, sn múlpls solucons para la c (6) Para mosrar l méoo rommos l problma planao ans: un haz lásr, λ=638nm, qu prsna una lpca =089 b sr corrgo para obnr una lpca 095 (valor sablco por l lím la rsolucón l polarímro usao n la mosracón prmnal, un molo Thor Labs PA40) Usamos un MT qu conss n un cubrobjos con n= 539 =47 mcras Para vsualzar mjor los rsulaos sablcmos α=0 Para nconrar las solucons órcas al problma smplmn calculamos la lpca como funcón α θ alror la prmra apromacón La nsa los cálculos s sablc con aua la Fg 4 s mjora hasa obnr los rsulaos grafcaos n lína connua n la Fg 5 n sa gráfca ambén pomos vr los rsulaos prmnals, qu concn apromaamn con los calculaos órcamn A parr cro ángulo, n l qu s ncunra la prmra apromacón, pomos nconrar más solucons conform ncrmnamos θ pro s b compnsar la fas nrouca por l MT para cumplr con la c (6) so hac qu s ncunrn solucons ano para α > α como para α < α D los rsulaos, pomos conclur qu no s ncsan rmaamn bunas placas plano parallas para l MT La únca concón
9 NINVI ncunro Invsgacón n I, 4 5 Marzo, s qu l MT nga un spsor sufcnmn pquño para por sprcar los fcos su propa mprfccón así como las abrracons fala unforma n l frn ona Bajo sas concons, l MT funcona apropaamn los rsulaos prmnals son prcbls prmnal aa Thorcal aa Fg 5 Solucons prmnals vs solucons órcas para llvar la lpca s =089 a = 095 VI CONCLUSIONS l sao polarzacón un haz luz pu sr moulao man un moulaor ransmancas (MT) como l scro aquí Bajo cras concons, un haz lípcamn polarzao pu sr hcho crcularmn polarzao l MT mosrao conss una smpl placa cubrobjos aravsaa oblcuamn n l haz lásr D on pomos conclur qu no s ncsan rmaamn bunas placas plano parallas para l MT La únca concón s qu l MT nga un spsor sufcnmn pquño para por sprcar los fcos su propa mprfccón, las abrracons l frn ona la fala unforma Bajo sas concons, l MT funcona apropaamn los rsulaos prmnals s pun prcr RFRNCIAS [] Y Y Schchnr, J Shamr an N Kra, Vson hrough smrflcng ma: polarzaon analss, Op L, 4, 6, , (999) [] X Ma an C Lang, ffc of anrflcon coang on h prformanc of Faraa roaors, Appl Op, 33, 9, , (994) [3] D C Huchngs an J M Arnol, Mofcaon of h lnar an nonlnar polarzaon namcs n smconucors owng o h Krr magno-opc ffc, J Op Soc Am B, 7, 0, , (000) [4] D Mlam, Brwsr-angl Pockls cll sgn, Appl Op,, 3, , (973) [5] Zhuang Z, S-W Suh, an J S Pal, Polarzaon conrollr usng nmac lqu crsals, Op L, 4, 0, 694-, 696, (999) [6] Malacara D an O Harrs, Inrfromrc Masurmn of Angls, Appl Op, 9, 7, , (970) [7] Azzam R M A, Smulanous rflcon an rfracon of lgh whou chang of polarzaon b a sngl-lar-coa lcrc surfac, Op L, 0, 3, 07-09, (985) [8] Azzam R M A, Thn-flm bam splr ha rflcs lgh as a half-wav rarr an ransms whou chang of polarzaon: applcaon o a Mchlson nrfromr, J Op Soc Am A, 3,, , (986)
8. CONTROL ÓPTIMO PARA SISTEMAS DE TIEMPO DISCRETO.
 8. CONTROL ÓPTIMO PARA SISTEMAS DE TIEMPO DISCRETO. La oría conrol ópmo lnal mpo scro s nrsan por su aplcacón n l conrol por compuaor. 8. DESCRIPCION EN VARIABLES DE ESTADO A vcs nrsa obsrvar un ssma n
8. CONTROL ÓPTIMO PARA SISTEMAS DE TIEMPO DISCRETO. La oría conrol ópmo lnal mpo scro s nrsan por su aplcacón n l conrol por compuaor. 8. DESCRIPCION EN VARIABLES DE ESTADO A vcs nrsa obsrvar un ssma n
CAPITULO 2º FUNCIONES DE VECTORES Y MATRICES_02. Ing. Diego Alejandro Patiño G. M.Sc, Ph.D.
 CAPITULO º FUNCIONES DE VECTORES Y MATRICES_ Ing. Dgo Aljandro Paño G. M.Sc, Ph.D. Funcons d Marcs Torma: Sa f( una funcón arbrara dl scalar y sa A una marz con polnomo caracrísco: S dfn g( un polnomo
CAPITULO º FUNCIONES DE VECTORES Y MATRICES_ Ing. Dgo Aljandro Paño G. M.Sc, Ph.D. Funcons d Marcs Torma: Sa f( una funcón arbrara dl scalar y sa A una marz con polnomo caracrísco: S dfn g( un polnomo
Control inversores trifásicos
 Conrol nvror rfáco Tranformaa Conrol nvror rfáco Tranformaa αβ Spac cor Moulaon SPWM Conrolaor baao n SPWM E rfrnca roaoro Tranformaa Park Inrpracón l conrolaor PI obr roaoro Obncón la ranformaa αβ a b
Conrol nvror rfáco Tranformaa Conrol nvror rfáco Tranformaa αβ Spac cor Moulaon SPWM Conrolaor baao n SPWM E rfrnca roaoro Tranformaa Park Inrpracón l conrolaor PI obr roaoro Obncón la ranformaa αβ a b
Teoría cuántica de Schroedinger
 Caíulo 5 Toría cuánca Schrongr Dfcncas la oría Bohr. La oría Bohr roujo una lcacón lausbl l áoo H, ro no uo lcar o Las frncas nr las nnsas las línas scrals o La ullca algunas línas o La foracón agrgaos
Caíulo 5 Toría cuánca Schrongr Dfcncas la oría Bohr. La oría Bohr roujo una lcacón lausbl l áoo H, ro no uo lcar o Las frncas nr las nnsas las línas scrals o La ullca algunas línas o La foracón agrgaos
José Angel Arias Cruz Julián Ramírez Ramírez Elizabeth Pérez Corona
 Lásrs Pulso Ulracoro Aosgundos José Angl Aras Cru Julán Ramír Ramír Elabh Pér Corona Anono d Jsús Olvars Robls Pulso Ulracoro A dfrnca d lo qu ocurr n l funconamno usual d un lásr dond s n una onda connua
Lásrs Pulso Ulracoro Aosgundos José Angl Aras Cru Julán Ramír Ramír Elabh Pér Corona Anono d Jsús Olvars Robls Pulso Ulracoro A dfrnca d lo qu ocurr n l funconamno usual d un lásr dond s n una onda connua
UNIDAD Nº 7 RESPUESTA DE COMPONENTES PASIVOS A LA CORRIENTE CONTINUA
 UNIDAD Nº 7 SPUSTA D OMPONNTS PASIOS A A OINT ONTINUA Sñal cuadrada Una onda cuadrada smérca IDA adqur nsanánamn ( n mpo cro ) la máxma amplud, prmanc duran un mpo n dcho valor y lugo ca nsanánamn a su
UNIDAD Nº 7 SPUSTA D OMPONNTS PASIOS A A OINT ONTINUA Sñal cuadrada Una onda cuadrada smérca IDA adqur nsanánamn ( n mpo cro ) la máxma amplud, prmanc duran un mpo n dcho valor y lugo ca nsanánamn a su
3. Determinación de la fuente y la respuesta en el dominio de la
 3. Drmnacón d la fun y la rspusa n l dmn d la frcunca. Para ulzar l algrm d MDFDT, pdms mar ds pcns. La prmra, ncalzar l camp cn valrs 0, pr jmpl l cas d la cavdad d la sccón..5 bn clcar una fun qu nrduzca
3. Drmnacón d la fun y la rspusa n l dmn d la frcunca. Para ulzar l algrm d MDFDT, pdms mar ds pcns. La prmra, ncalzar l camp cn valrs 0, pr jmpl l cas d la cavdad d la sccón..5 bn clcar una fun qu nrduzca
LA SOSTENIBILIDAD DE LA DEUDA PÚBLICA EN UNA ECONOMÍA ABIERTA Waldo Mendoza Bellido Pedro Herrera Catalán Febrero, 2004
 23 LA SOSTIILIDAD D LA DUDA PÚLICA UA COOMÍA AIRTA Walo Mnoza llo Pro Hrrra Caalán Frro, 24 DOCUMTO D TRAAJO 23 hp://www.pucp.u.p/conoma/pf/ddd23.pf LA SOSTIILIDAD D LA DUDA PÚLICA UA COOMÍA AIRTA Walo
23 LA SOSTIILIDAD D LA DUDA PÚLICA UA COOMÍA AIRTA Walo Mnoza llo Pro Hrrra Caalán Frro, 24 DOCUMTO D TRAAJO 23 hp://www.pucp.u.p/conoma/pf/ddd23.pf LA SOSTIILIDAD D LA DUDA PÚLICA UA COOMÍA AIRTA Walo
El comportamiento ideal del CN sirve como estándar, contra el cual se compara el comportamiento de cuerpos reales
 Propas raatvas curpos opa El comportamnto al l CN srv como stánar contra l cual s compara l comportamnto curpos rals El comportamnto ral s xprsa por una sr propas fnas n rlacón al CN En gnral las propas
Propas raatvas curpos opa El comportamnto al l CN srv como stánar contra l cual s compara l comportamnto curpos rals El comportamnto ral s xprsa por una sr propas fnas n rlacón al CN En gnral las propas
CLAMP EUGLICÉMICO HIPERINSULINÉMICO
 Mrcds Lomar CLAMP EUGLCÉMCO HPERNULNÉMCO El dsarrollo d sa écnca prm onr una sr d parámros rlvans para los modlos mamácos d homosass dl ssma glucosa-nsulna. Prmra par 2h d ayuno. 2 Onr musra d sangr asal
Mrcds Lomar CLAMP EUGLCÉMCO HPERNULNÉMCO El dsarrollo d sa écnca prm onr una sr d parámros rlvans para los modlos mamácos d homosass dl ssma glucosa-nsulna. Prmra par 2h d ayuno. 2 Onr musra d sangr asal
LA ECUACIÓN DE GOMPERTZ COMO MODELO DE CRECIMIENTO
 LA ECUACIÓN DE GOMPERTZ COMO MODELO DE CRECIMIENTO Ana María Islas Cors Insuo Polécnco Naconal, ESIT amslas@pn.mx Gabrl Gullén Bunda Insuo Polécnco Naconal, ESIME-Azcapozalco ggulln@pn.mx Yolanda Monoya
LA ECUACIÓN DE GOMPERTZ COMO MODELO DE CRECIMIENTO Ana María Islas Cors Insuo Polécnco Naconal, ESIT amslas@pn.mx Gabrl Gullén Bunda Insuo Polécnco Naconal, ESIME-Azcapozalco ggulln@pn.mx Yolanda Monoya
MATEMÁTICAS II 2011 OPCIÓN A
 MTEMÁTICS II OPCIÓN Ejrcicio : Una vnana normanda consis n un rcángulo coronado con un smicírculo. D nr odas las vnanas normandas d prímro m, halla las dimnsions dl marco d la d ára máima. Solución: El
MTEMÁTICS II OPCIÓN Ejrcicio : Una vnana normanda consis n un rcángulo coronado con un smicírculo. D nr odas las vnanas normandas d prímro m, halla las dimnsions dl marco d la d ára máima. Solución: El
Circuitos no senoidales
 Crcuos no snodals A6 Objos Famlarzars con los componns d la xpansón d la sr d Fourr para cualqur funcón snodal o no snodal. Enndr cómo la aparnca y la cura n l j d mpo d una forma d onda pudn dnfcar qué
Crcuos no snodals A6 Objos Famlarzars con los componns d la xpansón d la sr d Fourr para cualqur funcón snodal o no snodal. Enndr cómo la aparnca y la cura n l j d mpo d una forma d onda pudn dnfcar qué
Tema 10: RÉGIMEN TRANSITORIO
 Tma : ÉGMEN TANSTOO. OBJETVOS. NTODUÓN. UTOS NEAES DE PME ODEN.. DESAGA DE EEMENTOS AGADOS SOBE UNA ESSTENA. ESPUESTA DE UN UTO A ENTADA EO..3 ESPUESTA DE EEMENTOS A ESTADO NA EO EXTADOS PO FUENTES..3.
Tma : ÉGMEN TANSTOO. OBJETVOS. NTODUÓN. UTOS NEAES DE PME ODEN.. DESAGA DE EEMENTOS AGADOS SOBE UNA ESSTENA. ESPUESTA DE UN UTO A ENTADA EO..3 ESPUESTA DE EEMENTOS A ESTADO NA EO EXTADOS PO FUENTES..3.
Cualquier transformador puede diseñarse haciendo uso de tres ecuaciones generales.
 7. Transformaors Cállo ransformaors S s onsrano n oro qvaln. Calqr ransformaor p sñars hano so rs aons nrals. Prmra aón. Dfnón nsa fljo manéo (nón ampo manéo). B A Sna aón. y Ampèr. l I 7. Transformaors
7. Transformaors Cállo ransformaors S s onsrano n oro qvaln. Calqr ransformaor p sñars hano so rs aons nrals. Prmra aón. Dfnón nsa fljo manéo (nón ampo manéo). B A Sna aón. y Ampèr. l I 7. Transformaors
DISEÑO DE EQUIPOS DE TRANSFERENCIA DE CALOR
 DISEÑO DE EQUIPOS DE TRNSFERENCI DE CLOR Intrcambaors obl tubo Los ntrcambaors obl tubo son muy populars, sncllos construr y fácls ntnr. Son muy comuns spcalmnt cuano la furza mpulsora s gran y l ára transfrnca
DISEÑO DE EQUIPOS DE TRNSFERENCI DE CLOR Intrcambaors obl tubo Los ntrcambaors obl tubo son muy populars, sncllos construr y fácls ntnr. Son muy comuns spcalmnt cuano la furza mpulsora s gran y l ára transfrnca
Se estudiarán las soluciones de algunas redes dinámicas básicas sin excitaciones y con excitaciones constantes y sinusoidales.
 apíulo 7 REDES DINÁMIAS Rds qu conngan condnsadors nducors s dnomnan dnámcas. Su comporamno quda dscro por cuacons dfrncals. S sudarán las solucons d algunas rds dnámcas báscas sn xcacons y con xcacons
apíulo 7 REDES DINÁMIAS Rds qu conngan condnsadors nducors s dnomnan dnámcas. Su comporamno quda dscro por cuacons dfrncals. S sudarán las solucons d algunas rds dnámcas báscas sn xcacons y con xcacons
( )exp( ) 2. La transformada de Fourier
 xp F d π La ransormada d Fourr F xp d D la Sr d Fourr a la ransormada d Fourr La sr d Fourr nos prm obnr una rprsnacón n l domno d la rcunca d uncons pródcas. Es posbl xndr d alguna manra las srs d Fourr
xp F d π La ransormada d Fourr F xp d D la Sr d Fourr a la ransormada d Fourr La sr d Fourr nos prm obnr una rprsnacón n l domno d la rcunca d uncons pródcas. Es posbl xndr d alguna manra las srs d Fourr
Ayu. Ignacio Trujillo Silva (alias nao) Integrales Impropias
 Mamáicas II Ingrals Impropias Mamáicas II IMPORTANTE: Es ipo d ingrals s llaman ipo P (EN ESTE CASO TIPO ALFA) Mamáicas II Mamáicas II Ejmplo 7.5. (Problma 5.f) Dcida si la siguin ingral convrg d ln( )
Mamáicas II Ingrals Impropias Mamáicas II IMPORTANTE: Es ipo d ingrals s llaman ipo P (EN ESTE CASO TIPO ALFA) Mamáicas II Mamáicas II Ejmplo 7.5. (Problma 5.f) Dcida si la siguin ingral convrg d ln( )
Capitulo III. III 2. Métodos analíticos de análisis cinemático. Universidad de Cantabria Departamento de Ing. Estructural y Mecánica
 Unvsa Cantaba Dpatamnto Ing. Estuctual y Mcánca Captulo III III. Métoos analít análss cnmátco 1 Cnmátca y Dnámca Máqunas. III. Métoos analít análss cnmátco. Unvsa Cantaba Dpatamnto Ing. Estuctual y Mcánca
Unvsa Cantaba Dpatamnto Ing. Estuctual y Mcánca Captulo III III. Métoos analít análss cnmátco 1 Cnmátca y Dnámca Máqunas. III. Métoos analít análss cnmátco. Unvsa Cantaba Dpatamnto Ing. Estuctual y Mcánca
Tema 4. Ondas de Señal: Onda Alterna Senoidal E 0 es la amplitud ω es la pulsación ω t + φ es el ángulo de fase φ es el ángulo de fase inicial
 Ondas d sñal ma 4 f f Ondas d Sñal: Onda lrna Snodal f sn ( + φ) s la amplud s la pulsacón + φ s l ángulo d fas φ s l ángulo d fas ncal f < f >. d scalón mplud Ondas d Sñal: Ondas d xcacón y Rspusa f f
Ondas d sñal ma 4 f f Ondas d Sñal: Onda lrna Snodal f sn ( + φ) s la amplud s la pulsacón + φ s l ángulo d fas φ s l ángulo d fas ncal f < f >. d scalón mplud Ondas d Sñal: Ondas d xcacón y Rspusa f f
Sistemas de Ecuaciones Diferenciales
 ismas d Ecuacions Difrncials Un sisma d dos cuacions difrncials d primr ordn s pud rprsnar n forma gnral como g g, x,, x, Dond x, son las variabls dpndins s la variabl indpndin dl sisma. i cada una d las
ismas d Ecuacions Difrncials Un sisma d dos cuacions difrncials d primr ordn s pud rprsnar n forma gnral como g g, x,, x, Dond x, son las variabls dpndins s la variabl indpndin dl sisma. i cada una d las
Las Expectativas CAPÍTULO 7. Profesor: Carlos R. Pitta. Macroeconomía General. Universidad Austral de Chile Escuela de Ingeniería Comercial
 Univrsidad Ausral d Chil Escula d Ingniría Comrcial Macroconomía Gnral CAPÍTULO 7 Las Expcaivas Profsor: Carlos R. Pia Macroconomía Gnral, Prof. Carlos R. Pia, Univrsidad Ausral d Chil. Capíulo 7: Las
Univrsidad Ausral d Chil Escula d Ingniría Comrcial Macroconomía Gnral CAPÍTULO 7 Las Expcaivas Profsor: Carlos R. Pia Macroconomía Gnral, Prof. Carlos R. Pia, Univrsidad Ausral d Chil. Capíulo 7: Las
( t ) ( ) exp( ) 2. La transformada de Fourier
 xp F d La ransormada d Fourr F xp d D la Sr d Fourr a la ransormada d Fourr La sr d Fourr nos prm obnr una rprsnacón n l domno d la rcunca d uncons pródcas. Es posbl xndr d alguna manra las srs d Fourr
xp F d La ransormada d Fourr F xp d D la Sr d Fourr a la ransormada d Fourr La sr d Fourr nos prm obnr una rprsnacón n l domno d la rcunca d uncons pródcas. Es posbl xndr d alguna manra las srs d Fourr
Desintegración radiactiva
 Daramno Física Fac. Cincias Exacas - UNLP Dsingración raiaciva El núclo y sus raiacions Página 1 (DF Facor caimino DF DF = x (- = x {(- ln2/t 1/2 } Una amolla connino 99m Tc (T 1/2 = 6h sá roulaa 75 kbq/ml
Daramno Física Fac. Cincias Exacas - UNLP Dsingración raiaciva El núclo y sus raiacions Página 1 (DF Facor caimino DF DF = x (- = x {(- ln2/t 1/2 } Una amolla connino 99m Tc (T 1/2 = 6h sá roulaa 75 kbq/ml
Un forward sobre commodities como el oro sufre una pequeña variación ya que se incluye la tasa de interés del oro (lease rate) con la variable l
 El Forward U corao fuuro o a plazo, s odo aqul cuya lqudacó o slm dfr hasa ua fcha posror spulada l msmo, s dcr s dos pas acurda hacr la rasaccó hasa u prodo fuuro dígas por jmplo 6 mss, so s u corao forward.
El Forward U corao fuuro o a plazo, s odo aqul cuya lqudacó o slm dfr hasa ua fcha posror spulada l msmo, s dcr s dos pas acurda hacr la rasaccó hasa u prodo fuuro dígas por jmplo 6 mss, so s u corao forward.
PAQUETE DE ONDAS. Un paquete construido por N ondas de la forma (1) se puede poner como
 PAQUT D ONDAS - onsrucción un paqu Pomos finir un paqu onas como una suprposición onas armónicas qu viajan n la misma ircción, con ifrns valors k, ω, ampliu y fas. La n-ésima ona armónica viajano n ircción
PAQUT D ONDAS - onsrucción un paqu Pomos finir un paqu onas como una suprposición onas armónicas qu viajan n la misma ircción, con ifrns valors k, ω, ampliu y fas. La n-ésima ona armónica viajano n ircción
UNIDAD 4 Modelos Probabilísticos Variable Continua TEORÍA. Mg.Ing. Susana Vanlesberg Profesor Titular
 Unvrsdad Naconal dl Loral Faculad d Ingnría Cncas Hídrcas ESTADÍSTICA Ingnrías: Rcursos Hídrcos-Ambnal-Agrmnsura TEORÍA Mg.Ing. Susana Vanlsbrg Profsor Tular UNIDAD 4 Modlos Probablíscos Varabl Connua
Unvrsdad Naconal dl Loral Faculad d Ingnría Cncas Hídrcas ESTADÍSTICA Ingnrías: Rcursos Hídrcos-Ambnal-Agrmnsura TEORÍA Mg.Ing. Susana Vanlsbrg Profsor Tular UNIDAD 4 Modlos Probablíscos Varabl Connua
Tema 2. Corriente alterna. Joaquín Vaquero López, 2013 Ingeniería Eléctrica
 Tma. orrn alrna Joaquín aquro óz, 03 ngnría Elécrca 0 Sñals varabls con l mo. Ondas snodals Índc 0 égmn snodal rmann 03 rcuos d r ordn. 04 onca acva y racva. Facor d onca 05 susa n frcunca ngnría Elécrca
Tma. orrn alrna Joaquín aquro óz, 03 ngnría Elécrca 0 Sñals varabls con l mo. Ondas snodals Índc 0 égmn snodal rmann 03 rcuos d r ordn. 04 onca acva y racva. Facor d onca 05 susa n frcunca ngnría Elécrca
INFLUENCIA DE LA FUERZA DE INFECCIÓN Y LA TRANSMISIÓN VERTICAL EN LA MALARIA: MODELADO MATEMÁTICO
 sa Facula Cncas Báscas 9-699 ompag: p://rsasunmlaruco/nxpp/rfcb ol 3 7-8 p://xoorg/8359/rfcb98 FLUCA D LA FUZA D FCCÓ Y LA TAMÓ TCAL LA MALAA: MODLADO MATMÁTCO FLUC OF FCTO FOC AD TCAL TAMO MALAA: MATMATCAL
sa Facula Cncas Báscas 9-699 ompag: p://rsasunmlaruco/nxpp/rfcb ol 3 7-8 p://xoorg/8359/rfcb98 FLUCA D LA FUZA D FCCÓ Y LA TAMÓ TCAL LA MALAA: MODLADO MATMÁTCO FLUC OF FCTO FOC AD TCAL TAMO MALAA: MATMATCAL
Administración de inventarios. Ejercicio práctico.
 Admnstracón d nvntaros. Ejrcco práctco. La Cía. GOMA REDONDA S.A. llva n nvntaro un crto tpo d numátcos, con las sgunts caractrístcas: Vntas promdo anuals: 5000 numátcos Costo d ordnar: $ 40/ ordn Costo
Admnstracón d nvntaros. Ejrcco práctco. La Cía. GOMA REDONDA S.A. llva n nvntaro un crto tpo d numátcos, con las sgunts caractrístcas: Vntas promdo anuals: 5000 numátcos Costo d ordnar: $ 40/ ordn Costo
= 6 ; -s -4 s = 6 ; s= - 1,2 m. La imagen es real, invertida respecto del objeto y de mayor tamaño.
 F F a) La lnt s convrgnt l objto stá situado ants dl foco objto: β = = = 4 ; = 4 s ; s + = 6 ; -s -4 s = 6 ; s= -, m s, 4,8 ; ; = = = s f 4,8. f, 4,8 f f =0,96 m. La imagn s ral, invrtida rspcto dl objto
F F a) La lnt s convrgnt l objto stá situado ants dl foco objto: β = = = 4 ; = 4 s ; s + = 6 ; -s -4 s = 6 ; s= -, m s, 4,8 ; ; = = = s f 4,8. f, 4,8 f f =0,96 m. La imagn s ral, invrtida rspcto dl objto
Análisis de Señales. Descripción matemática de señales
 Análisis d Sñals Dscripción mamáica d sñals Sñals Las sñals son funcions d variabls indpndins, poradoras d información Sñals lécricas:nsions y corrins n un circuio Sñals acúsicas: audio Sñals d vido: variación
Análisis d Sñals Dscripción mamáica d sñals Sñals Las sñals son funcions d variabls indpndins, poradoras d información Sñals lécricas:nsions y corrins n un circuio Sñals acúsicas: audio Sñals d vido: variación
Tema 3. Corriente alterna. Ingeniería Eléctrica y Electrónica
 Tma 3. orrn alrna ngnría Elécrca y Elcrónca Índc 0 Sñals varabls con l mo. Ondas snodals 0 égmn snodal rmann 03 rcuos d r ordn. susa n frcunca 04 onca acva y racva. Facor d onca ngnría Elécrca y Elcrónca
Tma 3. orrn alrna ngnría Elécrca y Elcrónca Índc 0 Sñals varabls con l mo. Ondas snodals 0 égmn snodal rmann 03 rcuos d r ordn. susa n frcunca 04 onca acva y racva. Facor d onca ngnría Elécrca y Elcrónca
Resumen TEMA 6: Momentos de inercia
 EMA 6: Momntos d nrca Mcánca Rsumn EMA 6: Momntos d nrca. Dfncons Sstma matral d puntos matrals d masa m, =, 2,...,. a) Momnto d nrca rspcto d un plano π md (d = dstanca d la masa m al plano π) π =Σ 2
EMA 6: Momntos d nrca Mcánca Rsumn EMA 6: Momntos d nrca. Dfncons Sstma matral d puntos matrals d masa m, =, 2,...,. a) Momnto d nrca rspcto d un plano π md (d = dstanca d la masa m al plano π) π =Σ 2
Reguladores de compensación
 Rgulaors compnsación Dfinimos la salia saa para l sistma m D N La función transfrncia gnraliaa pos un rtaro ao por m. n n n q q q q A a a a b b b b G 0 0 Conicions: 0 q b, timpo murto la planta, G tin
Rgulaors compnsación Dfinimos la salia saa para l sistma m D N La función transfrncia gnraliaa pos un rtaro ao por m. n n n q q q q A a a a b b b b G 0 0 Conicions: 0 q b, timpo murto la planta, G tin
AGRUPACIONES DE ANTENAS
 AGRUPACIONES DE ANTENAS - Antenas planas. Manuel Serra Pérez AGRUPACIONES PLANAS Agrupacones retculares rectangulares. Los elementos raantes se colocan en los nuos e una re rectangular unforme La separacón
AGRUPACIONES DE ANTENAS - Antenas planas. Manuel Serra Pérez AGRUPACIONES PLANAS Agrupacones retculares rectangulares. Los elementos raantes se colocan en los nuos e una re rectangular unforme La separacón
Límites finitos cuando x: ˆ
 . Límits latrals its al infinito 7 FIGURA.3 3 3 La gráfica d = >. (b) La cuación () no s aplica a la fracción original. Ncsitamos un n l dnominador, no un 5. Para obtnrlo multiplicamos por >5 l numrador
. Límits latrals its al infinito 7 FIGURA.3 3 3 La gráfica d = >. (b) La cuación () no s aplica a la fracción original. Ncsitamos un n l dnominador, no un 5. Para obtnrlo multiplicamos por >5 l numrador
Curso 2006/07. Tema 8: Retardos en el comportamiento económico y dinamicidad de los modelos. Dinámica y predicción
 Economría II Tma 8: Rardos n l comporamino conómico y dinamicidad d los modlos. Dinámica y prdicción 1. Moivos d dinamicidad n las rlacions 2. El mcanismo d corrcción dl rror y l quilibrio a largo plazo
Economría II Tma 8: Rardos n l comporamino conómico y dinamicidad d los modlos. Dinámica y prdicción 1. Moivos d dinamicidad n las rlacions 2. El mcanismo d corrcción dl rror y l quilibrio a largo plazo
Universidad de Puerto Rico Recinto Universitario de Mayagüez Departamento de Ciencias Matemáticas
 Univrsidad d Puro Rico Rcino Univrsiario d Maagüz Dparamno d incias Mamáicas Eamn II - Ma álculo II d marzo d 9 Nombr Númro d sudian Scción Profsor Db mosrar odo su rabajo. Rsulva odos los problmas, scriba
Univrsidad d Puro Rico Rcino Univrsiario d Maagüz Dparamno d incias Mamáicas Eamn II - Ma álculo II d marzo d 9 Nombr Númro d sudian Scción Profsor Db mosrar odo su rabajo. Rsulva odos los problmas, scriba
1) Resolver las siguientes ecuaciones:
 Rsolvr las sunts uaons: a j k l,, Rsolvr las sunts nuaons: a RECONOCIMIENTO DE ECUACIONES LINEALES Una uaón s lnal s n lla no a proutos varals, las varals sólo uran lvaas a la prmra potna, no a varals
Rsolvr las sunts uaons: a j k l,, Rsolvr las sunts nuaons: a RECONOCIMIENTO DE ECUACIONES LINEALES Una uaón s lnal s n lla no a proutos varals, las varals sólo uran lvaas a la prmra potna, no a varals
Grupo de Ingeniería Gráfica Escuela Técnica Superior de Ingenieros Industriales Universidad Politécnica de Madrid 12 DE JUNIO DE 2002
 Grupo e Ingenería Gráfca Escuela Técnca Superor e Ingeneros Inustrales Unversa Poltécnca e Mar EXAMEN DE DIBUJO INDUSTRIAL II Y TÉCNICAS DE REPRESENTACIÓN NOTAS : DE JUNIO DE 00 º Caa ejercco ebe ser entregao
Grupo e Ingenería Gráfca Escuela Técnca Superor e Ingeneros Inustrales Unversa Poltécnca e Mar EXAMEN DE DIBUJO INDUSTRIAL II Y TÉCNICAS DE REPRESENTACIÓN NOTAS : DE JUNIO DE 00 º Caa ejercco ebe ser entregao
MATEMÁTICAS FINANCIERAS
 MATEMÁTICAS FINANCIERAS TEMA: INTERÉS COMPUESTO CONTINUO. Inrés Compuso Coninuo 2. Mono Compuso a Capialización Coninua 3. Equivalncia nr Tasas d Inrés Compuso Discro y Coninuo 4. Equivalncia nr Tasa d
MATEMÁTICAS FINANCIERAS TEMA: INTERÉS COMPUESTO CONTINUO. Inrés Compuso Coninuo 2. Mono Compuso a Capialización Coninua 3. Equivalncia nr Tasas d Inrés Compuso Discro y Coninuo 4. Equivalncia nr Tasa d
Apéndice A ANÁLISIS TENSORIAL
 Apéndc A ANÁLISIS TENSORIAL El análss tnsoral s cntra n l studo d nts abstractos llamados tnsors, cuyas propdads son ndpndnts d los sstmas d rfrnca mplados para dtrmnarlos. Un tnsor stá rprsntado n un
Apéndc A ANÁLISIS TENSORIAL El análss tnsoral s cntra n l studo d nts abstractos llamados tnsors, cuyas propdads son ndpndnts d los sstmas d rfrnca mplados para dtrmnarlos. Un tnsor stá rprsntado n un
H 2 = 3,6 kn + 3,6 kn = 7,2 kn
 Trabajo Pracco Nº 8: Torsón n Ejs Ejrcco 1: Una coluna d sccón crcular acúa coo soor d un carl sodo a cargas horzonals (vno). A los fns d dl dnsonano sas cargas las suonos alcadas n ars guals n las cuaro
Trabajo Pracco Nº 8: Torsón n Ejs Ejrcco 1: Una coluna d sccón crcular acúa coo soor d un carl sodo a cargas horzonals (vno). A los fns d dl dnsonano sas cargas las suonos alcadas n ars guals n las cuaro
PROBLEMAS RESUELTOS DE INTERACCIÓN MAGNÉTICA
 PROLEMAS RESUELTOS DE INTERACCIÓN MAGNÉTICA PROEMAS DEL CURSO Una carga q = 2 C y 0,01 g masa, ncalmnt n rposo n un punto A, s aclraa por un campo léctrco horzontal orntao haca la zqura. Al llgar al punto,
PROLEMAS RESUELTOS DE INTERACCIÓN MAGNÉTICA PROEMAS DEL CURSO Una carga q = 2 C y 0,01 g masa, ncalmnt n rposo n un punto A, s aclraa por un campo léctrco horzontal orntao haca la zqura. Al llgar al punto,
LAS ECUACIONES DEL CAMPO ELECTROMAGNETICO
 LS CUCIONS DL CMPO LCTROMGNTICO Calos S CIN 999 LS CUCIONS DL CMPO LCTROMGNTICO Dfnón: l ampo lomagnéo: S pu fn po l valo l nso máno y po l valo la nsa aón n vaío s po l valo χ al qu l nvalo s s χ y po
LS CUCIONS DL CMPO LCTROMGNTICO Calos S CIN 999 LS CUCIONS DL CMPO LCTROMGNTICO Dfnón: l ampo lomagnéo: S pu fn po l valo l nso máno y po l valo la nsa aón n vaío s po l valo χ al qu l nvalo s s χ y po
Cinemática (parte II)
 Cnmác p II Z Dnccón n con spco l mpo α omulcón Lnn R 3 Dbuos Lono Dnc 3 R 3 3 α α 3 α X R Z Dnccón n con spco l mpo M M M omulcón Euln α α Dnccón n con spco l mpo Z α omulcón Euln Dnccón n con spco l mpo
Cnmác p II Z Dnccón n con spco l mpo α omulcón Lnn R 3 Dbuos Lono Dnc 3 R 3 3 α α 3 α X R Z Dnccón n con spco l mpo M M M omulcón Euln α α Dnccón n con spco l mpo Z α omulcón Euln Dnccón n con spco l mpo
Tema 1. Repaso de Teoría de Circuitos
 Tma. paso d Toría d rcuos Joaquín aquro ópz Elcrónca, 7 Joaquín aquro ópz paso d Toría d rcuos: índc. oncpos prlmars. oncpo d crcuo, lmnos d un crcuo. ys fundamnals d los crcuos lécrcos: ys d Krchhoff.3
Tma. paso d Toría d rcuos Joaquín aquro ópz Elcrónca, 7 Joaquín aquro ópz paso d Toría d rcuos: índc. oncpos prlmars. oncpo d crcuo, lmnos d un crcuo. ys fundamnals d los crcuos lécrcos: ys d Krchhoff.3
1 IES Carlos Bousoño
 1 2 3 5 6 7 MIS DEL PP MRCELLO CREDO G.P. Palsrna 8 9 10 11 12 13 L L NN LLL LLL NN OO OO OO OO OO OO 1 PRQSUXWZY[ PRQSUXWZY[\[ ]_^UXWZY `asdcf_[ `a Sdcf_[g[ hh QYgYXWdY ML ML )! #"%$')( *+',-(./$0213(
1 2 3 5 6 7 MIS DEL PP MRCELLO CREDO G.P. Palsrna 8 9 10 11 12 13 L L NN LLL LLL NN OO OO OO OO OO OO 1 PRQSUXWZY[ PRQSUXWZY[\[ ]_^UXWZY `asdcf_[ `a Sdcf_[g[ hh QYgYXWdY ML ML )! #"%$')( *+',-(./$0213(
1. Introducción, n, concepto y clasificación
 Tema 5: Números índces. Inroduccón, n, concepo y clasfcacón 2. Números índces smples. Defncón y propedades 3. Números índces complejos Números índces complejos sn ponderar Números índces complejos ponderados
Tema 5: Números índces. Inroduccón, n, concepo y clasfcacón 2. Números índces smples. Defncón y propedades 3. Números índces complejos Números índces complejos sn ponderar Números índces complejos ponderados
Semana 12: Tema 9 Movimiento Rotacional
 Semana : Tema 9 Movmeno Roaconal 9. Velocdad y Aceleracón angular 9. Roacón con aceleracón angular consane 9.3 Energía cnéca roaconal 9.4 Cálculo de momeno de nerca y el eorema de los ejes paralelos Capíulo
Semana : Tema 9 Movmeno Roaconal 9. Velocdad y Aceleracón angular 9. Roacón con aceleracón angular consane 9.3 Energía cnéca roaconal 9.4 Cálculo de momeno de nerca y el eorema de los ejes paralelos Capíulo
UNIVERSIDAD POLITÉCNICA. TEMA: Modelo Cinemático. E.U.I.T. Industrial FECHA: Titulación: Grado en Ingeniería Electrónica y Automática
 7//5 IGNTUR: Robótca UNIVERIDD POLITÉNI DE MDRID TEM: Moelo nemátco E.U.I.T. Inustral Ttulacón: Grao en Ingenería Electrónca y utomátca Área: Ingenería e stemas y utomátca Departamento e Electrónca utomátca
7//5 IGNTUR: Robótca UNIVERIDD POLITÉNI DE MDRID TEM: Moelo nemátco E.U.I.T. Inustral Ttulacón: Grao en Ingenería Electrónca y utomátca Área: Ingenería e stemas y utomátca Departamento e Electrónca utomátca
4.1 Procedimientos de inferencia para la distribución exponencial
 4 Ifrca paramétrca 4 Procdmtos d frca para la dstrbucó xpocal La dstrbucó xpocal fu la prmra dstrbucó para modlar tmpos d falla y para lla s ha dsarrollado métodos stadístcos d mara xtsva a T ua va xpocal
4 Ifrca paramétrca 4 Procdmtos d frca para la dstrbucó xpocal La dstrbucó xpocal fu la prmra dstrbucó para modlar tmpos d falla y para lla s ha dsarrollado métodos stadístcos d mara xtsva a T ua va xpocal
Sistemas Suavemente Variantes
 Sismas Suavmn Varians Adriana Lópz, Alfrdo Rsrpo Laboraorio d Sñals, Dparamno d Elécrica y Elcrónica, Univrsidad d Los Ands, adriana_lopz5@homail.com, arsrp@uniands.du.co, Bogoa. Rsumn Normalmn, los sismas
Sismas Suavmn Varians Adriana Lópz, Alfrdo Rsrpo Laboraorio d Sñals, Dparamno d Elécrica y Elcrónica, Univrsidad d Los Ands, adriana_lopz5@homail.com, arsrp@uniands.du.co, Bogoa. Rsumn Normalmn, los sismas
BLOQUE A. IES Mediterráneo de Málaga Solución Junio 2011 Juan Carlos Alonso Gianonatti
 IES Mdirráno d Málg Solución Junio Jun Crlos lonso Ginoni BLOQUE CUESTIÓN..- Dmusr sin uilir l rgl d Srrus sin dsrrollr dircmn por un il /o column qu.indiqu n cd pso qu propidd (o propidds) d los drminns
IES Mdirráno d Málg Solución Junio Jun Crlos lonso Ginoni BLOQUE CUESTIÓN..- Dmusr sin uilir l rgl d Srrus sin dsrrollr dircmn por un il /o column qu.indiqu n cd pso qu propidd (o propidds) d los drminns
Corriente Alterna y la Potencia Activa & Reactiva
 Corrn Alrna y la Ponca Aca & aca Fundanos Maácos La nsón s una onda lcroagnéca snusodal d frcunca n [rad/s], con f con f n [Hz]. ( n( ω Al so po, la corrn abén srá una sñal snusodal d frcunca, con un ángulo
Corrn Alrna y la Ponca Aca & aca Fundanos Maácos La nsón s una onda lcroagnéca snusodal d frcunca n [rad/s], con f con f n [Hz]. ( n( ω Al so po, la corrn abén srá una sñal snusodal d frcunca, con un ángulo
Taller 4 cálculo Un rectángulo se inscribe en un semicírculo de radio 4 Cuál es el área máxima que puede tener y cuáles son sus dimensiones?
 Tallr cálculo 1 Profsor Jaim Andrés Jaramillo Gonzálz. jaimaj@concpocompuadors.com. www.jaimaj.concpocompuadors.com UdA 017-1 Problmas d Opimización Rfrncia sudiar jrcicios scción.8 dl o d Zill 1. A un
Tallr cálculo 1 Profsor Jaim Andrés Jaramillo Gonzálz. jaimaj@concpocompuadors.com. www.jaimaj.concpocompuadors.com UdA 017-1 Problmas d Opimización Rfrncia sudiar jrcicios scción.8 dl o d Zill 1. A un
Análisis. b) Calcular razonadamente b y c para que sea derivable y calcular su función derivada.
 MATEMÁTICAS º BACHILLERATO B 6-3- Análisis OPCIÓN A.- Dada la función + b + c f = Ln( + ) > a) Calcular sus asínoas b) Calcular razonadamn b y c para qu sa drivabl y calcular su función drivada. a) El
MATEMÁTICAS º BACHILLERATO B 6-3- Análisis OPCIÓN A.- Dada la función + b + c f = Ln( + ) > a) Calcular sus asínoas b) Calcular razonadamn b y c para qu sa drivabl y calcular su función drivada. a) El
Ingeniería de las reacciones químicas
 Ingnría d las raccons químcas Ingnría d las raccons químcas. Un componnt dfund a través d un tubo, con ntrada por uno solo d sus xtrmos. Dntro dl tubo hay un componnt j. El componnt, raccona sgún k 0,5
Ingnría d las raccons químcas Ingnría d las raccons químcas. Un componnt dfund a través d un tubo, con ntrada por uno solo d sus xtrmos. Dntro dl tubo hay un componnt j. El componnt, raccona sgún k 0,5
Apertura de M. de bienes y financieros
 Aprura d M. d bns y fnancros Aprura d los mrcados d bns y fnancros 5. Inroduccón 5.2 Balanza d pagos 5.3 l mrcado d dvsas: l po d cambo nomnal 5.4 l po d cambo ral 5.5 La pardad no cubra d nrss 5.. Inroduccón
Aprura d M. d bns y fnancros Aprura d los mrcados d bns y fnancros 5. Inroduccón 5.2 Balanza d pagos 5.3 l mrcado d dvsas: l po d cambo nomnal 5.4 l po d cambo ral 5.5 La pardad no cubra d nrss 5.. Inroduccón
9 Momentos y funciones generatrices de Momentos
 9 omos y fucos grarcs d omos Edgar Acua ESA 400 Edgar Acua 9. omos Sa ua varabl alaora s df su smo momo co rspco al org como μ E[ ], smpr qu l caso dscro y qu p < f d < l caso couo. Obvam, μμ..tamb, s
9 omos y fucos grarcs d omos Edgar Acua ESA 400 Edgar Acua 9. omos Sa ua varabl alaora s df su smo momo co rspco al org como μ E[ ], smpr qu l caso dscro y qu p < f d < l caso couo. Obvam, μμ..tamb, s
5.1 La función logaritmo natural: derivación
 CAPÍTULO Funcions logarímica, ponncial oras funcions rascnns. La función logarimo naural: rivación Dsarrollar usar propias la función logarimo naural. Comprnr la finición l númro. Drivar funcions qu involucran
CAPÍTULO Funcions logarímica, ponncial oras funcions rascnns. La función logarimo naural: rivación Dsarrollar usar propias la función logarimo naural. Comprnr la finición l númro. Drivar funcions qu involucran
LOCALIZACIÓN DE UN SERVICIO NO DESEADO EN REDES USANDO EL CRITERIO ANTI-CENT-DIAN
 27 Congro Naconal d Eadíca Invgacón Oprava Llda, 8-11 d abrl d 2003 LOCALIZACIÓN DE UN SERVICIO NO DESEADO EN REDES USANDO EL CRITERIO ANTI-CENT-DIAN M. Colbrook, J.M. Guérrz, J. Scla Dparamno d Eadíca,
27 Congro Naconal d Eadíca Invgacón Oprava Llda, 8-11 d abrl d 2003 LOCALIZACIÓN DE UN SERVICIO NO DESEADO EN REDES USANDO EL CRITERIO ANTI-CENT-DIAN M. Colbrook, J.M. Guérrz, J. Scla Dparamno d Eadíca,
GIG - ETSII - UPM A(5:1) E.T.S.I.I.M. - DIBUJO INDUSTRIAL II /DIBUJO INDUSTRIAL 3:4. Válvula de bola. febrero SIS. REP. Escala: FIRMA SERIE Nº:
 E.T.S.I.I.M. - DIBUJO INDUSTRIAL II /DIBUJO INDUSTRIAL A febrero 006 3 A(5:) SIS. REP. Escala: FIRMA SERIE Nº: 3:4 Válvula e bola Realzao: Nombre: DNI Apellos: GIG - ETSII - UPM Examen e febrero -- 006
E.T.S.I.I.M. - DIBUJO INDUSTRIAL II /DIBUJO INDUSTRIAL A febrero 006 3 A(5:) SIS. REP. Escala: FIRMA SERIE Nº: 3:4 Válvula e bola Realzao: Nombre: DNI Apellos: GIG - ETSII - UPM Examen e febrero -- 006
CAPÍTULO 2. Ecuación paraxial de Helmholtz.
 CAPÍTLO Ecuacón paraal d Hlmholt. S dscut la posbldad d vsualar mdant un procsador óptco [1] a las solucons d la cuacón paraal d Hlmholt. Para llo s rala una comparacón d los rsultados obtndos consdrando
CAPÍTLO Ecuacón paraal d Hlmholt. S dscut la posbldad d vsualar mdant un procsador óptco [1] a las solucons d la cuacón paraal d Hlmholt. Para llo s rala una comparacón d los rsultados obtndos consdrando
TEORÍA. PREGUNTA 1 (1 p). La ecuación del movimiento de un péndulo simple está dada por θ = A cos
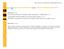 FÍIC PLICD. EXMEN FINL ORDINRIO JUNIO 16 TEORÍ PREGUNT 1 (1 p). La ecuacón el movmento e un pénulo smple está aa por θ = cos, seno = 5º. (a) Qué ángulo formará este pénulo con la vertcal cuano el tempo
FÍIC PLICD. EXMEN FINL ORDINRIO JUNIO 16 TEORÍ PREGUNT 1 (1 p). La ecuacón el movmento e un pénulo smple está aa por θ = cos, seno = 5º. (a) Qué ángulo formará este pénulo con la vertcal cuano el tempo
GENERADORES DE BARRIDO DE TENSIÓN
 GENERADORES DE BARRDO DE TENSÓN RUTO DE BARRDO TRANSSTORZADO ON ORRENTE ONSTANTE El funconamnto d t crcuto dfn como, la carga un condnador lnalmnt a partr d una funt d corrnt contant. Excpto para valor
GENERADORES DE BARRDO DE TENSÓN RUTO DE BARRDO TRANSSTORZADO ON ORRENTE ONSTANTE El funconamnto d t crcuto dfn como, la carga un condnador lnalmnt a partr d una funt d corrnt contant. Excpto para valor
Universidad Simón Bolívar Departamento de Procesos y Sistemas. Guía de Ejercicios de Sistemas de Control Avanzados PS-4313
 Unvrdad Smón Bolívar Dparamno d Proco y Sma Guía d Ejrcco d Sma d Conrol Avanzado PS-433 Pro. Alxandr Hoyo hp://pro.ub.v/ahoyo ahoyo@ub.v ÍNDICE Pág. Tranormada d Laplac 3 Tranormada Invra d Laplac y Rolucón
Unvrdad Smón Bolívar Dparamno d Proco y Sma Guía d Ejrcco d Sma d Conrol Avanzado PS-433 Pro. Alxandr Hoyo hp://pro.ub.v/ahoyo ahoyo@ub.v ÍNDICE Pág. Tranormada d Laplac 3 Tranormada Invra d Laplac y Rolucón
Capítulo 3 Metodología.
 Capíulo 3 Meodología. 3.1. Represenacón paramérca de la relacón enre el ngreso per cápa de los hogares y las caraceríscas soco-demográfcas de sus membros. La meodología ulzada en ese rabajo se basa en
Capíulo 3 Meodología. 3.1. Represenacón paramérca de la relacón enre el ngreso per cápa de los hogares y las caraceríscas soco-demográfcas de sus membros. La meodología ulzada en ese rabajo se basa en
División 5. Ejemplo de síntesis de un mecanismo articulado de barras
 Vrsón 0 CAITUL MECANISMS vsón 5 Ejmplo d síntss d un mcansmo artculado d barras UTN-F Cátdra: Elmntos d Máqunas. rofsor: r. Ing. Marclo Tulo ovan Vrsón 0. sumn En sta dvsón s dscrbrá l uso d la mtodología
Vrsón 0 CAITUL MECANISMS vsón 5 Ejmplo d síntss d un mcansmo artculado d barras UTN-F Cátdra: Elmntos d Máqunas. rofsor: r. Ing. Marclo Tulo ovan Vrsón 0. sumn En sta dvsón s dscrbrá l uso d la mtodología
- 2,5% de cargas verticales
 Drminación d la slz d las pards Espsor d las pards 11 cm (sin conar rvoqus) Eslz gomérica = λ g 27 Dond: Con: c λg = = disancia lir nr apoyos orizonals d la pard (nrpisos, ord suprior d la fundación) =
Drminación d la slz d las pards Espsor d las pards 11 cm (sin conar rvoqus) Eslz gomérica = λ g 27 Dond: Con: c λg = = disancia lir nr apoyos orizonals d la pard (nrpisos, ord suprior d la fundación) =
Cinemática del movimiento rotacional
 Cnemátca del movmento rotaconal Poscón angular, θ Para un movmento crcular, la dstanca (longtud del arco) s, el rado r, y el ángulo están relaconados por: 180 s r > 0 para rotacón en el sentdo anthoraro
Cnemátca del movmento rotaconal Poscón angular, θ Para un movmento crcular, la dstanca (longtud del arco) s, el rado r, y el ángulo están relaconados por: 180 s r > 0 para rotacón en el sentdo anthoraro
Análisis de Fourier en TC. Teorema de Fourier Serie de Fourier Transformada de Fourier Fórmulas de análisis y síntesis Respuesta en f de sistemas LTI
 Análisis d Fourir n C orma d Fourir Sri d Fourir ransformada d Fourir Fórmulas d análisis y sínsis Rspusa n f d sismas LI Modología Dominio d Frcuncia -Sñals lmnals a parir d las cuals s pud consruir por
Análisis d Fourir n C orma d Fourir Sri d Fourir ransformada d Fourir Fórmulas d análisis y sínsis Rspusa n f d sismas LI Modología Dominio d Frcuncia -Sñals lmnals a parir d las cuals s pud consruir por
Ciencia Ergo Sum ISSN: Universidad Autónoma del Estado de México México
 Cnca rgo Sum ISSN: 45-69 cnca.rgosum@yahoo.com.mx Unvrsa Autónoma l stao Méxco Méxco Gutérrz, César Onas no lnals n l plasma Cnca rgo Sum, vol. 8, núm., novmbr, Unvrsa Autónoma l stao Méxco Toluca, Méxco
Cnca rgo Sum ISSN: 45-69 cnca.rgosum@yahoo.com.mx Unvrsa Autónoma l stao Méxco Méxco Gutérrz, César Onas no lnals n l plasma Cnca rgo Sum, vol. 8, núm., novmbr, Unvrsa Autónoma l stao Méxco Toluca, Méxco
Tema 3. LA COMPETENCIA PERFECTA PROBLEMA RESUELTO
 Mcroconomía AE Tma 3. LA COMPETENCIA PERFECTA PROBLEMA REUELTO uponga qu cada una d las 144 mprsas qu forman una ndustra prfctamnt compttva tnn una curva d costs totals a corto plazo déntca qu vn dada
Mcroconomía AE Tma 3. LA COMPETENCIA PERFECTA PROBLEMA REUELTO uponga qu cada una d las 144 mprsas qu forman una ndustra prfctamnt compttva tnn una curva d costs totals a corto plazo déntca qu vn dada
ejercicios NkT NkT NkT q de dt NkT q d dt dq dt NkT q N q NkT
 jrccos E.- uál s la nrgía raconal molar d la molécula d odo a las dos tmpraturas antrors?. Haz srvr las nrgías raconals xprmntals. ln Q, ( ) ln! 5 v,, v 5 v ln c v d ln d d d d d 5 v v 5 v v d d 5 v v
jrccos E.- uál s la nrgía raconal molar d la molécula d odo a las dos tmpraturas antrors?. Haz srvr las nrgías raconals xprmntals. ln Q, ( ) ln! 5 v,, v 5 v ln c v d ln d d d d d 5 v v 5 v v d d 5 v v
Se plantea para el sistema térmico un circuito eléctrico equivalente en donde Tc es la temperatura del calefactor y Th es la temperatura del líquido.
 La figura musra n forma squmáica un sisma d calnamino d líquidos conocido como pava lécrica. Un rsisor d masa dsprciabl calfacciona una placa málica cuya capacidad érmica la suponmos concnrada n C1 y su
La figura musra n forma squmáica un sisma d calnamino d líquidos conocido como pava lécrica. Un rsisor d masa dsprciabl calfacciona una placa málica cuya capacidad érmica la suponmos concnrada n C1 y su
Factor de devanado en máquinas rotativas de C.A.
 Factor vanao n máqunas rotatvas C.A. Ramón Gullrmo Borrás Formoso Lcncao n Marna Cvl (Máqunas Navals) Ingnro Técnco Inustral (Elctrca). Ejrcó profsonalmnt como Ofcal Máqunas n vrsos buqus la M.M. y n Ingnría
Factor vanao n máqunas rotatvas C.A. Ramón Gullrmo Borrás Formoso Lcncao n Marna Cvl (Máqunas Navals) Ingnro Técnco Inustral (Elctrca). Ejrcó profsonalmnt como Ofcal Máqunas n vrsos buqus la M.M. y n Ingnría
OPCIÓN A. a) Estudiar si A y B tienen inversa y calcularla cuando sea posible (1 punto)
 San Blas, 4, ntrplanta. 983 30 70 54 OPCIÓN A 4 E.- San A = 3 y B = a) Estudiar si A y B tinn invrsa y calcularla cuando sa posibl ( punto) 0 b) Dtrminar X tal qu AX = B I sindo I = 0 (.5 puntos) a) Una
San Blas, 4, ntrplanta. 983 30 70 54 OPCIÓN A 4 E.- San A = 3 y B = a) Estudiar si A y B tinn invrsa y calcularla cuando sa posibl ( punto) 0 b) Dtrminar X tal qu AX = B I sindo I = 0 (.5 puntos) a) Una
Por otro lado, las raíces características de la nueva ecuación son: Entonces la solución tendrá la forma: t
 Ejriio rsuo Suponga a siguin uaión irnia primr orn qu rprsna omporamino un iruio RC omo a igura. ' ( ) x( ) Don RC, x() s a nsión apiaa () s a nsión n apaior. Enunr a rspusa oa sisma si a nraa s un saón
Ejriio rsuo Suponga a siguin uaión irnia primr orn qu rprsna omporamino un iruio RC omo a igura. ' ( ) x( ) Don RC, x() s a nsión apiaa () s a nsión n apaior. Enunr a rspusa oa sisma si a nraa s un saón
Capítulo 6. Navier Stokes ALE
 Capílo 6 Navr Soks ALE 6.- Inrodccón En los capílos anrors hmos do avanzando n la programacón y valdacón d n códgo n dsnos nvls hasa llgar a sa apa nal n dond complarmos l msmo agrgándol los érmnos dsvos,
Capílo 6 Navr Soks ALE 6.- Inrodccón En los capílos anrors hmos do avanzando n la programacón y valdacón d n códgo n dsnos nvls hasa llgar a sa apa nal n dond complarmos l msmo agrgándol los érmnos dsvos,
Cálculo Estocástico Variación Cuadrática para Martingalas Continuas y Acotadas
 1 Cálculo Esocásco Varacón Cuadráca para Marngalas Connuas y Acoadas Gullermo Garro Defncón Varacón fna. Un proceso X es de varacón fna o acoada s sus rayecoras son de varacón fna, c.s. Es decr, s exse
1 Cálculo Esocásco Varacón Cuadráca para Marngalas Connuas y Acoadas Gullermo Garro Defncón Varacón fna. Un proceso X es de varacón fna o acoada s sus rayecoras son de varacón fna, c.s. Es decr, s exse
Soluciones del capítulo 11 Teoría de control
 Solucions dl capíulo Toría d conrol Hécor Lomlí y Bariz Rumbos d marzo d a x = y u = S raa d un máximo b x = + y u = S raa d un mínimo c x = 5 + y u = 5 S raa d un mínimo d x = 4 + y u = + S raa d un máximo
Solucions dl capíulo Toría d conrol Hécor Lomlí y Bariz Rumbos d marzo d a x = y u = S raa d un máximo b x = + y u = S raa d un mínimo c x = 5 + y u = 5 S raa d un mínimo d x = 4 + y u = + S raa d un máximo
3.-AMORTIZACIÓN DE PRÉSTAMOS
 .-MORTZÓ DE PRÉSTMOS..- Un prson solc un présmo. pr morzrlo n ños mn nuls consns pospgbls y un po nrés fcvo nul l 8%. Trnscurros ños y hbno bono l nul l rcr ño, curn uor y cror pr morzr l u pnn ls sguns
.-MORTZÓ DE PRÉSTMOS..- Un prson solc un présmo. pr morzrlo n ños mn nuls consns pospgbls y un po nrés fcvo nul l 8%. Trnscurros ños y hbno bono l nul l rcr ño, curn uor y cror pr morzr l u pnn ls sguns
SOLUCIONARIO. UNIDAD 13: Introducción a las derivadas ACTIVIDADES-PÁG Las soluciones aparecen en la tabla.
 UNIA : Introducción a las drivadas ACTIVIAES-PÁG. 0. Las solucions aparcn n la tabla. [0, ] [, 6] a) f () = b) f () = + c) f () = 9 d) f () = 7, 6 8, 67. El valor d los límits s: f ( h) f () a) lím 6 h
UNIA : Introducción a las drivadas ACTIVIAES-PÁG. 0. Las solucions aparcn n la tabla. [0, ] [, 6] a) f () = b) f () = + c) f () = 9 d) f () = 7, 6 8, 67. El valor d los límits s: f ( h) f () a) lím 6 h
Capitulo IV. Síntesis dimensional de mecanismos
 Captulo IV Síntss dmnsonal d mcansmos Capítulo IV Síntss dmnsonal d mcansmos IV. Síntss dmnsonal d mcansmos. Gnracón d funcons. IV. Gnracón d trayctoras.. Introduccón a la síntss d gnracón d trayctoras..
Captulo IV Síntss dmnsonal d mcansmos Capítulo IV Síntss dmnsonal d mcansmos IV. Síntss dmnsonal d mcansmos. Gnracón d funcons. IV. Gnracón d trayctoras.. Introduccón a la síntss d gnracón d trayctoras..
Optimización multicriterial del diseño del cuerpo de los cilindros oleohidráulicos.
 Ingnría Mcánca, 1 (003 55-60 55 Opmzacón mulcrral dl dsño dl curpo d los clndros olohdráulcos. V. G. Gómz Rodríguz, R. Goyzolo Espnosa, J. J. Cabllo Eras. Unvrsdad d Cnfugos. Carrra a Rodas km. Cnfugos.Cuba.
Ingnría Mcánca, 1 (003 55-60 55 Opmzacón mulcrral dl dsño dl curpo d los clndros olohdráulcos. V. G. Gómz Rodríguz, R. Goyzolo Espnosa, J. J. Cabllo Eras. Unvrsdad d Cnfugos. Carrra a Rodas km. Cnfugos.Cuba.
MÉTODO DIRECTO DE LA RIGIDEZ. MÉTODO MATRICIAL
 El méodo dirco d la rigidz. Méodo maricial MÉTODO DIRECTO DE LA RIGIDEZ. MÉTODO MATRICIAL 1. SISTEMAS DE REERENCIA La sismaización dl méodo cuyos fundamnos s han prsnado anriormn rquir dl paso d unas caracrísicas
El méodo dirco d la rigidz. Méodo maricial MÉTODO DIRECTO DE LA RIGIDEZ. MÉTODO MATRICIAL 1. SISTEMAS DE REERENCIA La sismaización dl méodo cuyos fundamnos s han prsnado anriormn rquir dl paso d unas caracrísicas
2. Interacción radiación-materia
 Tpos d cagas:. Inaccón adacón-maa Cagas lbs: no sán nlazadas dno d un áomo. S suponn punuals. Basa con spcfca su caga, masa y aycoa. m F Cagas lgadas: son ssmas d caga con sucua nna: áomos, moléculas,
Tpos d cagas:. Inaccón adacón-maa Cagas lbs: no sán nlazadas dno d un áomo. S suponn punuals. Basa con spcfca su caga, masa y aycoa. m F Cagas lgadas: son ssmas d caga con sucua nna: áomos, moléculas,
Universo de Einstein. k=1 curvatura positiva k=0 universo plano k=-1 curvatura negativa
 3 ( & % 8 ( % E & #! * G) & # ' $ 3 ' $ Para l caso rlativista, la cuación s, l Univrso. Notar qu k lgimos las unias Univrso Einstin La nrgía n l campo grava Nwton s, 3 ( & % 8 ( % kc " c & #! * G) & #!
3 ( & % 8 ( % E & #! * G) & # ' $ 3 ' $ Para l caso rlativista, la cuación s, l Univrso. Notar qu k lgimos las unias Univrso Einstin La nrgía n l campo grava Nwton s, 3 ( & % 8 ( % kc " c & #! * G) & #!
TEMA 4: CANALES DIGITALES EN BANDA BASE CON RUIDO
 PROBLEMA EMA 4: CANALES DIGIALES EN BANDA BASE CON RUIDO Se desea realzar una ransmsón bnara de símbolos equprobables, para ello se recurre a una codfcacón NRZ de po AMI y cuyas señales se ndcan a connuacón:
PROBLEMA EMA 4: CANALES DIGIALES EN BANDA BASE CON RUIDO Se desea realzar una ransmsón bnara de símbolos equprobables, para ello se recurre a una codfcacón NRZ de po AMI y cuyas señales se ndcan a connuacón:
TEMA 9: DETERMINANTES
 más º llo. Ál Lnl TE : DETERNNTES. DETERNNTE DE UN TRZ UDRD. PROPEDDES DE LOS DETERNNTES. ENOR OPLEENTRO Y DJUNTO DE UN ELEENTO DE UN TRZ UDRD. DESRROLLO DE UN DETERNNTE POR LOS ELEENTOS DE UN LÍNE. ENORES
más º llo. Ál Lnl TE : DETERNNTES. DETERNNTE DE UN TRZ UDRD. PROPEDDES DE LOS DETERNNTES. ENOR OPLEENTRO Y DJUNTO DE UN ELEENTO DE UN TRZ UDRD. DESRROLLO DE UN DETERNNTE POR LOS ELEENTOS DE UN LÍNE. ENORES
() t ( )exp( ) 2. La transformada de Fourier
 1 x d La ransormada d ourr x d La ransormada d ourr Sa una uncón localmn ngrabl cuya ngral valor absoluo sa acoada n R. S dn su ransormada d ourr como: 1 d Esas xrsons nos rmn calcular la xrsón domno d
1 x d La ransormada d ourr x d La ransormada d ourr Sa una uncón localmn ngrabl cuya ngral valor absoluo sa acoada n R. S dn su ransormada d ourr como: 1 d Esas xrsons nos rmn calcular la xrsón domno d
LUGAR DE LAS RAÍCES. Lugar de las raíces.
 Unversdad Carlos III de Madrd Señales y Sstemas LUGAR DE LAS RAÍCES Lugar de las raíces. 1. Introduccón. Crteros del módulo y argumento. 2. Gráfcas del lugar de las raíces. 3. Reglas para construr el lugar
Unversdad Carlos III de Madrd Señales y Sstemas LUGAR DE LAS RAÍCES Lugar de las raíces. 1. Introduccón. Crteros del módulo y argumento. 2. Gráfcas del lugar de las raíces. 3. Reglas para construr el lugar
CAPÍTULO 1 RÉGIMEN TRANSITORIO EN CIRCUITOS DE PRIMER Y SEGUNDO ORDEN 1.1 INTRODUCCIÓN
 APÍTUO ÉGIMEN TANSITOIO EN IUITOS DE PIME Y SEGUNDO ODEN. INTODUIÓN Todo cambo d sado n un crcuo lécrco(s dcr n un ncnddo, aagado, accdn, c.) sgnfca un cambo n la candad d la nrgía dl ssma ya sa s mcánco,
APÍTUO ÉGIMEN TANSITOIO EN IUITOS DE PIME Y SEGUNDO ODEN. INTODUIÓN Todo cambo d sado n un crcuo lécrco(s dcr n un ncnddo, aagado, accdn, c.) sgnfca un cambo n la candad d la nrgía dl ssma ya sa s mcánco,
ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE TELECOMUNICACIÓN UNIVERSIDAD POLITÉCNICA DE VALENCIA
 SCULA ÉCNCA SUPROR D NGNROS D LCOMUNCACÓN UNRSDAD POLÉCNCA D ALNCA ANNAS 7-no-3 PROBLMA Una antna conocia po los aioaficionaos como W8JK, consta n su configuación más simpl os ipolos mu póimos longitu
SCULA ÉCNCA SUPROR D NGNROS D LCOMUNCACÓN UNRSDAD POLÉCNCA D ALNCA ANNAS 7-no-3 PROBLMA Una antna conocia po los aioaficionaos como W8JK, consta n su configuación más simpl os ipolos mu póimos longitu
