Mecánica de Sistemas y Fenómenos Ondulatorios. Primer Parcial, 24 setiembre de Problema 1 (15 puntos)
|
|
|
- Víctor Franco Méndez
- hace 7 años
- Vistas:
Transcripción
1 nstituto de Física - Facultad de ngeniería 009 Mecánica de Sistemas y Fenómenos Ondulatorios mportante: Primer Parcial, 4 setiembre de 009 El estudiante deberá hacer un esfuerzo para comunicar claramente su razonamiento. Las respuestas correctas que no incluyan una denición, un esquema o una explicación, serán consideradas como incompletas. Del mismo modo, deje por escrito sus comentarios en relación a la interpretación física de los resultados matemáticos que obtiene. PONER EL NOMBRE EN TODAS LAS HOJAS. Se recuerda que la prueba es individual. Problema 1 (15 puntos) Un disco de masa M y Radio R puede girar enroscado en una barra horizontal. La rosca es tal, que cuando el disco gira un ángulo θ (relativo a la barra), su centro de masa avanza una distancia igual a L θ donde L es una contante dada. Un resorte de constante elástica k y longitud natural nula, conecta al disco con la pared; dicho resorte se conecta al disco por medio de una guía, de modo que el resorte permanece siempre en la misma posición paralela a la barra y sin girar. En torno al disco se enrolla una cuerda de la que pende una masa m. Sobre el sistema actúa un par viscoso b θ, proporcional a la velocidad angular relativa a la barra. La barra es forzada a girar con un ángulo α(t) dado. Se puede suponer: La cuerda que sostiene la masa m permanece siempre vertical. El movimiento de la masa es tal, que la cuerda se mantiene tensa en todo momento. La barra es de radio depreciable comparado con el radio del disco. (a) (b) (c) (d) Conocido α(t), hallar la ecuación de movimiento del sistema (ecuación en la coordenada θ). Suponiendo que se impone una oscilación para la barra, α(t) = A cos (ωt), indicar como será el movimiento θ(t) del sistema en régimen. Calcular la frecuencia de resonancia en amplitud, y gracar la amplitud de las oscilaciones en función de la frecuencia ω impuesta. Señale claramente las características más importantes de la gráca. Calcular la potencia media disipada por el par viscoso. 1
2 nstituto de Física - Facultad de ngeniería 009 Problema (15 puntos) Un aro de masa M y radio R puede girar en su propio plano alrededor de uno de sus puntos (punto O). Una cuenta de masa m se encuentra sujeta al aro y puede moverse por él (sin rozamiento). (a) (b) Determinar el lagrangeano del sistema. Suponiendo que solo pueden haber oscilaciones de pequeña amplitud, determine las ecuaciones de movimiento del sistema. (c) Calcule las frecuencias normales en el caso M = m. (d) (e) ndique condiciones iniciales del sistema para que oscile con una única frecuencia. i) Si la posición de la cuenta está relacionada con la parte real de la solución compleja, ¾cómo se relaciona la velocidad con la parte imaginaria? ii) Calcular las leyes horarias del aro y la cuenta si ambos parten de la posición de equilibrio siendo la velocidad inicial de la cuenta v 0 y la velocidad inicial del aro nula. Figura 1: Pregunta 1 (5 puntos) Se considera una barra de masa m y de longitud L, articulada en el punto O jo. Un disco de radio R se apoya en el piso y se mantiene en el plano vertical del dibujo. Sobre el disco actúa una fuerza de magnitud constante F. La barra se apoya en el disco, formando con el piso un ángulo θ. Determine el valor de la fuerza F para que la posición de equilibrio del sistema se de para θ = π/3. Pregunta (5 puntos) Una partícula de masa m se encuentra connada a moverse sobre la supercie de un paraboloide de revolución, como se muestra en la gura. Dicho paraboloide está determinado por la ecuación z = α(x + y ). La partícula se encuentra además bajo la acción del peso, que actúa como se muestra en la gura. denticar las magnitudes físicas que se conservan a lo largo del movimiento de la partícula.
3 nstituto de Física - Facultad de ngeniería 009 Problema 1 Solución Considerando x, θ, α y z como se muestra en la Figura, y observando los vínculos existentes, obtenemos: x = L θ (1) z = (θ + α)r () ω disco = α + θ (3) Figura : (a) Utilizando como coordenada generalizada θ, podemos escribir el lagrangeano del sistema, como: L = M [ ] L θ + 1 MR [ ( α + θ) ] + m [ ( α + θ) R + θ L ] [ ] 1 k(θl) + (θ + α)rmg L = 1 θ [M ) (L + R [ 1 k(θl) + (θ + α)rmg ] + m(l + R ) ] ( + α [R θ m + M )] + 1 ( [R α m + M )] Aplicando las ecuaciones de Lagrange, teniendo en cuenta que Q NC θ = b θ y deniendo ( ) = M L + R + m(l + R ) obtenemos la ecuación de movimiento entorno a la posición de equilibrio: ( θ + R m + M ) α + kl θ = b θ (4) θ + b θ + kl θ = R ( ) m + M α (5) (b) La ecuación de movimiento, corresponde a la de un oscilador forzado, con fricción; es decir, es de la forma: ( ) θ + ζω 0 θ + ω 0 θ = R m + M ω0 = kl α Donde (6) ζω 0 = b La solución θ(t) en régimen, es de la forma θ(t) = Re[εe jωt ] donde ε es una constante compleja. Sustituyendo en la ecuación 6 obtenemos: ( ) ε = AR m + M ω (ω0 ω ) + jζω 0 ω ( θ(t) = AR m + M ) ω ( ( )) ζω0 ω cos ωt Arctg (ω 0 ω ) + (ζω 0 ω) ω0 ω 3
4 nstituto de Física - Facultad de ngeniería 009 (c) De la parte anterior, conocemos la amplitud de oscilación en función de la frecuencia. ( ) ε(ω) = AR m + M ω (7) (ω 0 ω ) + (ζω 0 ω) Dividiendo numerador y denominador por ω, se puede observar que el máximo se da donde se minimiza ( ) ω ( ) f(ε) = 0 ω 1 ζω0 + ω Buscamos entonces soluciones a f (ω) = 0: f (ω) = ( ) ω 0 ω 1 + ζ = 0 ω res = ω 0 1 ζ que ζ < 1 0, 7 ωres kl = ( ) que b < kl 1 b kl Cabe señalar las siguientes propiedades: El fenómeno de resonancia existe si el amortiguamiento es débil. La frecuencia de resonancia tiende a ω 0 si el par viscoso tiende a cero. La amplitud en la resonancia, tiende a cuando se elimina la viscosidad. Figura 3: Amplitud en función de ω (d) La potencia media disipada por el par viscoso se puede calcular como a : P b = bω P b = 1 T T 0 ( AR m + M b θ dt = bω ε ) ω (ω0 ω ) + (ζω 0 ω) a recordar que 1 T cos (ωt)dt = 1 T 0 4
5 nstituto de Física - Facultad de ngeniería 009 Problema Eligiendo coordenadas absolutas (θ, ϕ), como se indica en la Figura 4, la velocidad del centro del anillo es v C = R θê θ y la velocidad de la masa m es v m = R θê θ + R ϕê ϕ. Por lo tanto la energía cinética del sistema, teniendo en cuanta que ê θ. ê ϕ = cos(ϕ θ): Figura 4: (a) T = MR θ + MR θ + mr ( θ + ϕ + θ ϕ cos(ϕ θ)) (8) La energía potencial gravitatoria es U = MgR cos(θ) mgr(cos(θ) + cos(ϕ)) (9) Por lo tanto el Lagrangeano del sistema es: L = MR θ + mr ( θ + ϕ + θ ϕ cos(ϕ θ)) + MgR cos(θ) + mgr(cos(ϕ) + cos(θ)) (10) Las ecuaciones de movimiento son: (M + m)r θ + mr ( ϕ cos(ϕ θ) ϕ sin(ϕ θ)) + (m + M)gR sin(θ) = 0 (11) mr ϕ + mr ( θ cos(ϕ θ) + θ sin(ϕ θ)) + mgr sin(ϕ) = 0 (1) (b) En torno al punto jo (θ = 0, ϕ = 0), estudiamos las pequeñas oscilaciones del sistema. Se linealizan las ecuaciones de movimiento en torno a ese punto: (M + m)r θ + mr ϕ + (m + M)gRθ = 0 (13) mr ( ϕ + θ) + mgrϕ = 0 (14) (c) Para determinar los modos normales probamos soluciones complejas para determinar las diferentes frecuencias normales, recordando que la parte real determina las leyes horarias de las coordenadas. Supongamos que ϕ(t) = Ae iωt y θ(t) = Be iωt. Sustituyendo m = M, y dividiendo por mr ambas ecuaciones se obtiene: 3Bω + Aω Bω o = 0 (15) Aω + Bω Aω o = 0 (16) donde se denió ω o = g R. Para obtener soluciones no triviales, se impone la condición sobre el determinante del sistema que debe ser nulo. Por lo tanto: (ω o ω )(ω o 3ω ) ω 4 = 0 = ω 4 5ω ω o + ω 4 o = 0 (17) Por lo tanto, las frecuencias normales son ω 1 = ω o y ω = ω o. 5
6 nstituto de Física - Facultad de ngeniería 009 (d) La relacionan entre las distintas amplitudes en los dos modos se determina a partir de las ecuaciones de movimiento. Para la frecuencia ω 1 tenemos que Aωo + Bωo Aωo = 0, por lo que B = A. Por lo tanto, si inicialmente el sistema está en reposo y (θ(0) = φ o,ϕ(0) = φ o ), el sistema oscilará en el modo con frecuencia ω 1. Para la otra frecuencia ω, se tiene que Aω o + Bω o Aωo = 0, de forma que A = B. Nuevamente si el sistema parte del reposo, con condiciones iniciales en posición ( θ(0) = φ o,ϕ(0) = φ o ), el sistema oscilar únicamente con frecuencia ω. (e) i) Supongamos que θ(t) = Ae iωt = A e i(ωt+δ), de forma que tomando parte real θ(t) = Re[ θ(t)] = A cos(ωt + δ). La velocidad es θ(t) = A ω sin(ωt + δ). Recordando que m[ θ(t)] = A sin(ωt + δ), es claro que θ(t) = ωm[ θ(t)] ii) ncorporando las fases y las relaciones entre las amplitudes encontradas en la parte (d) se obtiene que la solución general es de la forma: θ(t) = A cos(ω t + δ ) + B cos(ω 1 t + δ 1 ) (18) ϕ(t) = A cos(ω t + δ ) B cos(ω 1 t + δ 1 ) (19) Las condiciones iniciales son (θ(0), ϕ(0), θ(0), ϕ(0)) = (0, 0, 0, ϕ o ), donde ϕ o = vo R. por lo tanto el sistema de ecuaciones se reduce a: A cos(δ ) + B cos(δ 1 ) = 0 (0) A cos(δ ) B cos(δ 1 ) = 0 (1) Aω sin(δ ) + Bω 1 sin(δ 1 ) = 0 () Aω sin(δ ) + Bω 1 sin(δ 1 ) = ϕ o (3) Restando la primera y segunda ecuación se obtiene que B cos(δ 1 ) = 0. Sustituyendo en cualquiera de las dos también se obtiene que A cos(δ ) = 0. Sumando la tercera y la cuarta ecuación se obtiene que 3Bω 1 sin(δ 1 ) = ϕ o, por lo tanto Aω sin(δ ) = Bω 1 sin δ 1. Resumiendo, las condiciones iniciales determinan las siguientes ecuaciones: B cos(δ 1 ) = 0 (4) A cos(δ ) = 0 (5) 3Bω 1 sin(δ 1 ) = ϕ o (6) Aω sin(δ ) = Bω 1 sin δ 1 (7) Para encontrar soluciones compatibles, se obtien de la primera y segunda δ 1 = δ = π. De la tercera y cuarta ecuación se determina que A = ϕo 3ω y B = ϕo 3ω. Recordando que 1 cos(φ + π ) = sin(φ), las leyes horarias son: θ(t) = ϕ o 3 ϕ(t) = ϕ o 3 ( 1 sin(ω t) 1 ) sin(ω 1 t) ω ω 1 ( 1 sin(ω t) + ) sin(ω 1 t) ω ω 1 (8) (9) Pregunta 1 Las únicas fuerzas activas que realizan un trabajo virtual son el peso de la barra y la fuerza F. El desplazamiento virtual del centro de la barra G es δ r G = L δθê θ. El desplazamiento del centro del disco C es δ r C = δx i. El vínculo de apoyo de la barra sobre el disco determina la relación entre las coordenadas x y θ. La recta que une el centro del disco y la articulación es la bisectriz del ángulo θ. 6
7 nstituto de Física - Facultad de ngeniería 009 Por lo tanto, tan(θ/) = R R x, despejando x, x = tan(θ/) ; de esta forma, Operando obtenemos que, El desplazamiento virtual del centro del disco es: δx = x θ δθ x θ = R sin (θ/) δx = R sin (θ/) δθ Utilizando el principio de los trabajos virtuales se obtiene que: δw T = 0 = mgĵ δ r G + ( F )î δ r C Utilizando las relaciones anteriores se obtiene:. δw T = 0 = mg L cos(θ)δθ + F R sin (θ/) δθ Por lo tanto, para un desplazamiento arbitrario de θ se obtiene: Evaluando en θ = π/3: F = Lmg cos(θ)sin (θ/) R F = Lmg 8R Pregunta Dada la geometría del problema, es conveniente utilizar coordenadas cilíndricas para describir el movimiento de la partícula. Utilizando la convención usual, la posición de la partícula puede escribirse como: r = rê r + zˆk (30) En estos términos, el vínculo que impone el hecho de que la partícula deba moverse sobre la supercie del paraboloide queda: z = αr (31) Se obtiene entonces la velocidad de la partícula en términos de las coordenadas θ y r: r = ṙê r + r θê θ + αrṙˆk (3) 7
8 nstituto de Física - Facultad de ngeniería 009 Debido a que la única fuerza que trabaja es el peso, el sistema es conservativo por lo que la energía mecánica se conserva a lo largo de las trayectorias: El lagrangeano del sistema queda: E = m [ṙ + r θ + α 4r ṙ ] + mgαr = constante (33) L = m [ṙ + r θ + α 4r ṙ ] mgαr (34) Vemos que el lagrangeano no depende de θ, entonces, aplicando las ecuaciones de Lagrange: L θ = mr θ = constante (35) que coincide con la componente según z del momento angular de la partícula con respecto al origen. 8
Física y Química 1º Bachillerato LOMCE. Bloque 3: Trabajo y Energía. Trabajo y Energía
 Física y Química 1º Bachillerato LOMCE Bloque 3: Trabajo y Energía Trabajo y Energía 1 El Trabajo Mecánico El trabajo mecánico, realizado por una fuerza que actúa sobre un cuerpo que experimenta un desplazamiento,
Física y Química 1º Bachillerato LOMCE Bloque 3: Trabajo y Energía Trabajo y Energía 1 El Trabajo Mecánico El trabajo mecánico, realizado por una fuerza que actúa sobre un cuerpo que experimenta un desplazamiento,
Práctico 2: Mecánica lagrangeana
 Mecánica Anaĺıtica Curso 2016 Práctico 2: Mecánica lagrangeana 1. La polea y la cuerda de la figura son ideales y los bloques deslizan sin roce. Obtenga las aceleraciones de los bloques a partir de las
Mecánica Anaĺıtica Curso 2016 Práctico 2: Mecánica lagrangeana 1. La polea y la cuerda de la figura son ideales y los bloques deslizan sin roce. Obtenga las aceleraciones de los bloques a partir de las
ECUACION DINÁMICA DE ROTACIÓN PURA DE UN CUERPO RIGIDO ALREDEDOR DE UN EJE ω
 ECUACION DINÁMICA DE ROTACIÓN PURA DE UN CUERPO RIGIDO ALREDEDOR DE UN EJE ω Suponiendo un cuerpo rígido que gira con velocidad angular ω alrededor del eje Z que permanece fijo al cuerpo. dl = ( dm R 2
ECUACION DINÁMICA DE ROTACIÓN PURA DE UN CUERPO RIGIDO ALREDEDOR DE UN EJE ω Suponiendo un cuerpo rígido que gira con velocidad angular ω alrededor del eje Z que permanece fijo al cuerpo. dl = ( dm R 2
Examen de Física-1, 1 Ingeniería Química Examen final. Septiembre de 2014 Problemas (Dos puntos por problema).
 Examen de Física-1, 1 Ingeniería Química Examen final. Septiembre de 014 Problemas (Dos puntos por problema). Problema 1 (Primer parcial): Un cuerpo de masa 10 g se desliza bajando por un plano inclinado
Examen de Física-1, 1 Ingeniería Química Examen final. Septiembre de 014 Problemas (Dos puntos por problema). Problema 1 (Primer parcial): Un cuerpo de masa 10 g se desliza bajando por un plano inclinado
Problemas. Laboratorio. Física moderna 09/11/07 DEPARTAMENTO DE FÍSICA E QUÍMICA. Nombre:
 Física moderna 9/11/7 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: 1. Un muelle de constante k =, 1 3 N/m está apoyado en una superficie horizontal sin rozamiento. A 1, m hay un bucle vertical de
Física moderna 9/11/7 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: 1. Un muelle de constante k =, 1 3 N/m está apoyado en una superficie horizontal sin rozamiento. A 1, m hay un bucle vertical de
TALLER DE OSCILACIONES Y ONDAS
 TALLER DE OSCILACIONES Y ONDAS Departamento De Fı sica y Geologı a, Universidad De Pamplona DOCENTE: Fı sico Amando Delgado. TEMAS: Todos los desarrollados el primer corte. 1. Determinar la frecuencia
TALLER DE OSCILACIONES Y ONDAS Departamento De Fı sica y Geologı a, Universidad De Pamplona DOCENTE: Fı sico Amando Delgado. TEMAS: Todos los desarrollados el primer corte. 1. Determinar la frecuencia
Momento angular de una partícula. Momento angular de un sólido rígido
 Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
INDICE. Introducción 1. Movimiento vibratorio armónico simple (MVAS) 1. Velocidad en el MVAS 2. Aceleración en el MVAS 2. Dinámica del MVAS 3
 INDICE Introducción 1 Movimiento vibratorio armónico simple (MVAS) 1 Velocidad en el MVAS Aceleración en el MVAS Dinámica del MVAS 3 Aplicación al péndulo simple 4 Energía cinética en el MVAS 6 Energía
INDICE Introducción 1 Movimiento vibratorio armónico simple (MVAS) 1 Velocidad en el MVAS Aceleración en el MVAS Dinámica del MVAS 3 Aplicación al péndulo simple 4 Energía cinética en el MVAS 6 Energía
Movimiento armónico simple.
 1 Movimiento armónico simple. 1.1. Concepto de movimiento armónico simple: Su ecuación. Supongamos un muelle que cuelga verticalmente, y de cuyo extremo libre pende una masa m. Si tiramos de la masa y
1 Movimiento armónico simple. 1.1. Concepto de movimiento armónico simple: Su ecuación. Supongamos un muelle que cuelga verticalmente, y de cuyo extremo libre pende una masa m. Si tiramos de la masa y
Capítulo 10. Rotación de un Cuerpo Rígido
 Capítulo 10 Rotación de un Cuerpo Rígido Contenido Velocidad angular y aceleración angular Cinemática rotacional Relaciones angulares y lineales Energía rotacional Cálculo de los momentos de inercia Teorema
Capítulo 10 Rotación de un Cuerpo Rígido Contenido Velocidad angular y aceleración angular Cinemática rotacional Relaciones angulares y lineales Energía rotacional Cálculo de los momentos de inercia Teorema
Programa de Doctorado en Física Pontificia Universidad Católica de Valparaíso Universidad Técnica Federico Santa María
 1 Mecánica Clásica - II Semestre 2014 Programa de Doctorado en Física Pontificia Universidad Católica de Valparaíso Universidad Técnica Federico Santa María Problema 1. Una barra rígida (de altura despreciable)
1 Mecánica Clásica - II Semestre 2014 Programa de Doctorado en Física Pontificia Universidad Católica de Valparaíso Universidad Técnica Federico Santa María Problema 1. Una barra rígida (de altura despreciable)
Mecánica de Sistemas y Fenómenos Ondulatorios Práctico 4
 Práctico 4 Ejercicio 1 Considere el sistema de la figura, formado por masas puntuales m unidas entre sí por resortes de constante K y longitud natural a. lamemos y n al desplazamiento de la n-ésima masa
Práctico 4 Ejercicio 1 Considere el sistema de la figura, formado por masas puntuales m unidas entre sí por resortes de constante K y longitud natural a. lamemos y n al desplazamiento de la n-ésima masa
OSCILACIONES ACOPLADAS
 OSCILACIONES ACOPLADAS I. Objetivos: Analizar el movimiento conjunto de dos osciladores armónicos similares (péndulos de varilla), con frecuencia natural f 0, acoplados por medio de un péndulo bifilar.
OSCILACIONES ACOPLADAS I. Objetivos: Analizar el movimiento conjunto de dos osciladores armónicos similares (péndulos de varilla), con frecuencia natural f 0, acoplados por medio de un péndulo bifilar.
Ejemplos de los capítulos I, II, III y IV
 1. Considere el péndulo compuesto mostrado a continuación. Dicho péndulo consiste de una barra esbelta de longitud L, masa m, pivotada en el punto O. Utilizando el desplazamiento angular de la barra θ
1. Considere el péndulo compuesto mostrado a continuación. Dicho péndulo consiste de una barra esbelta de longitud L, masa m, pivotada en el punto O. Utilizando el desplazamiento angular de la barra θ
Física I F-123 PF1.7 Año 2017
 Práctica 6: Sólido Rígido 1. Determinar en cada caso el momento de inercia del sistema respecto de los ejes indicados. Utilizar cuando sea conveniente el teorema de Steiner. 2. Un disco de masa m = 50
Práctica 6: Sólido Rígido 1. Determinar en cada caso el momento de inercia del sistema respecto de los ejes indicados. Utilizar cuando sea conveniente el teorema de Steiner. 2. Un disco de masa m = 50
Unidad 12: Oscilaciones
 Apoyo para la preparación de los estudios de Ingeniería y Arquitectura Física (Preparación a la Universidad) Unidad 12: Oscilaciones Movimiento armónico simple: x(t), v(t) y a(t) 10,0 x(t) a(t) 8,0 6,0
Apoyo para la preparación de los estudios de Ingeniería y Arquitectura Física (Preparación a la Universidad) Unidad 12: Oscilaciones Movimiento armónico simple: x(t), v(t) y a(t) 10,0 x(t) a(t) 8,0 6,0
MOVIMIENTO ARMÓNICO SIMPLE
 MOVIMIENTO ARMÓNICO SIMPLE Estudio del movimiento armónico simple. Desde el punto de vista dinámico, es el movimiento de una partícula que se mueve sobre una recta, sometida a la acción de una fuerza atractiva
MOVIMIENTO ARMÓNICO SIMPLE Estudio del movimiento armónico simple. Desde el punto de vista dinámico, es el movimiento de una partícula que se mueve sobre una recta, sometida a la acción de una fuerza atractiva
Movimiento Oscilatorio
 Movimiento Oscilatorio 1. Introducción.. El Movimiento Armónico Simple. a) Estudio cinemático. b) Estudio dinámico. c) Estudio energético. 3. Péndulos. a) Péndulo simple. b) Péndulo físico. 4. Oscilaciones
Movimiento Oscilatorio 1. Introducción.. El Movimiento Armónico Simple. a) Estudio cinemático. b) Estudio dinámico. c) Estudio energético. 3. Péndulos. a) Péndulo simple. b) Péndulo físico. 4. Oscilaciones
II. Vibración libre de un sistema de un grado de libertad
 Objetivos: 1. Definir que es vibración libre. 2. Recordar el método de diagrama de cuerpo libre para deducir las ecuaciones de movimiento. 3. Introducir el método de conservación de energía para deducir
Objetivos: 1. Definir que es vibración libre. 2. Recordar el método de diagrama de cuerpo libre para deducir las ecuaciones de movimiento. 3. Introducir el método de conservación de energía para deducir
PRUEBA ESPECÍFICA PRUEBA 2016
 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES PRUEBA ESPECÍFICA PRUEBA 2016 PRUEBA SOLUCIONARIO PROBAK 25 URTETIK Contesta 4 de los 5 ejercicios propuestos (Cada pregunta tiene un valor de 2,5 puntos, de los
PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES PRUEBA ESPECÍFICA PRUEBA 2016 PRUEBA SOLUCIONARIO PROBAK 25 URTETIK Contesta 4 de los 5 ejercicios propuestos (Cada pregunta tiene un valor de 2,5 puntos, de los
Mecánica Clásica - 2do. cuatrimestre de 2011 Guía 7: Ecuaciones de Hamilton, transformaciones canónicas. Hamilton Jacobi.
 Mecánica Clásica - 2do. cuatrimestre de 20 Guía 7: Ecuaciones de Hamilton, transformaciones canónicas. Hamilton Jacobi.. Escriba el hamiltoniano, las ecuaciones de Hamilton y construya los diagramas de
Mecánica Clásica - 2do. cuatrimestre de 20 Guía 7: Ecuaciones de Hamilton, transformaciones canónicas. Hamilton Jacobi.. Escriba el hamiltoniano, las ecuaciones de Hamilton y construya los diagramas de
NOTA CALI/ORDEN/PRES ORTOGRAFÍA PUNTUACIÓN EXPRESIÓN NOTA FINAL
 1. Conteste razonadamente a las siguientes preguntas: a) Puede asociarse una energía potencial a una fuerza de rozamiento? b) Qué tiene más sentido físico, la energía potencial en un punto o la variación
1. Conteste razonadamente a las siguientes preguntas: a) Puede asociarse una energía potencial a una fuerza de rozamiento? b) Qué tiene más sentido físico, la energía potencial en un punto o la variación
MOVIMIENTO ARMÓNICO SIMPLE
 MOVIMIENTO ARMÓNICO SIMPLE Junio 2016. Pregunta 2A.- Un bloque de 2 kg de masa, que descansa sobre una superficie horizontal, está unido a un extremo de un muelle de masa despreciable y constante elástica
MOVIMIENTO ARMÓNICO SIMPLE Junio 2016. Pregunta 2A.- Un bloque de 2 kg de masa, que descansa sobre una superficie horizontal, está unido a un extremo de un muelle de masa despreciable y constante elástica
( ) 2 = 0,3125 kg m 2.
 Examen de Física-1, 1 Ingeniería Química Examen final Enero de 2014 Problemas (Dos puntos por problema) Problema 1: Un bloque de masa m 1 2 kg y un bloque de masa m 2 6 kg están conectados por una cuerda
Examen de Física-1, 1 Ingeniería Química Examen final Enero de 2014 Problemas (Dos puntos por problema) Problema 1: Un bloque de masa m 1 2 kg y un bloque de masa m 2 6 kg están conectados por una cuerda
ACADEMIA CENTRO DE APOYO AL ESTUDIO MOVIMIENTO VIBRATORIO.
 MOVIMIENTO VIBRATORIO. Movimiento vibratorio armónico simple 1. Explica como varía la energía mecánica de un oscilador lineal si: a) Se duplica la amplitud. b) Se duplica la frecuencia. c) Se duplica la
MOVIMIENTO VIBRATORIO. Movimiento vibratorio armónico simple 1. Explica como varía la energía mecánica de un oscilador lineal si: a) Se duplica la amplitud. b) Se duplica la frecuencia. c) Se duplica la
Dinámica en dos o tres dimensiones
 7.0.2. Dinámica en dos o tres dimensiones Ejercicio 7.27 Un cuerpo de masa 8kg, describe una trayectoria cuyas ecuaciones paramétrica son: x =2+5t 2t 2 m e y = t 2 m.determinela fuerza aplicada sobre el
7.0.2. Dinámica en dos o tres dimensiones Ejercicio 7.27 Un cuerpo de masa 8kg, describe una trayectoria cuyas ecuaciones paramétrica son: x =2+5t 2t 2 m e y = t 2 m.determinela fuerza aplicada sobre el
10 cm longitud 30 m. Calcular: (a) la velocidad en el pie del plano inclinado si
 Las pesas de la figura ruedan sin deslizar y sin 6 cm rozamiento por un plano inclinado 30 y de 10 cm longitud 30 m. Calcular: (a) la velocidad en el pie del plano inclinado si 100 cm las pesas parten
Las pesas de la figura ruedan sin deslizar y sin 6 cm rozamiento por un plano inclinado 30 y de 10 cm longitud 30 m. Calcular: (a) la velocidad en el pie del plano inclinado si 100 cm las pesas parten
TEMA 9. MOVIMIENTO ARMÓNICO SIMPLE
 TEMA 9. MOVIMIENTO ARMÓNICO SIMPLE Un movimiento periódico es aquel que describe una partícula cuando las variables posición, velocidad y aceleración de su movimiento toman los mismos valores después de
TEMA 9. MOVIMIENTO ARMÓNICO SIMPLE Un movimiento periódico es aquel que describe una partícula cuando las variables posición, velocidad y aceleración de su movimiento toman los mismos valores después de
Oscilaciones amortiguadas.
 PROBLEMAS DE OSCILACIONES. Oscilaciones amortiguadas. Autor: José Antonio Diego Vives Documento bajo licencia Creative Commons 3.0, BY-SA (Atribución-CompartirIgual) Problema 1 Un oscilador armónico amortiguado,
PROBLEMAS DE OSCILACIONES. Oscilaciones amortiguadas. Autor: José Antonio Diego Vives Documento bajo licencia Creative Commons 3.0, BY-SA (Atribución-CompartirIgual) Problema 1 Un oscilador armónico amortiguado,
1. Introducción: Movimiento Circular Uniforme
 FI1A2 - SISTEMAS NEWTONIANOS GUIA TEORICA Departamento de Física Unidad 5A: Oscilaciones Facultad de Ciencias Físicas y Matemáticas Profs: H. Arellano, D. Mardones, N. Mujica Universidad de Chile Semestre
FI1A2 - SISTEMAS NEWTONIANOS GUIA TEORICA Departamento de Física Unidad 5A: Oscilaciones Facultad de Ciencias Físicas y Matemáticas Profs: H. Arellano, D. Mardones, N. Mujica Universidad de Chile Semestre
Oscilaciones. José Manuel Alcaraz Pelegrina. Curso
 José Manuel Alcaraz Pelegrina Curso 007-008 1. Introducción En el presente capítulo vamos a estudiar el movimiento en torno a una posición de equilibrio estable, concretamente estudiaremos las oscilaciones
José Manuel Alcaraz Pelegrina Curso 007-008 1. Introducción En el presente capítulo vamos a estudiar el movimiento en torno a una posición de equilibrio estable, concretamente estudiaremos las oscilaciones
Movimiento Armónico Simple (M.A.S.)
 Anexo: Movimiento Armónico Simple (M.A.S.) 1.- Oscilaciones armónicas Los movimientos periódicos que se producen siempre sobre la misma trayectoria los vamos a denominar movimientos oscilatorios o vibratorios.
Anexo: Movimiento Armónico Simple (M.A.S.) 1.- Oscilaciones armónicas Los movimientos periódicos que se producen siempre sobre la misma trayectoria los vamos a denominar movimientos oscilatorios o vibratorios.
Tema 1: Oscilaciones
 1/42 Fátima Masot Conde Ing. Industrial 2006/07 2/42 Índice: 1.. Características. Representación Matemática. 2. Energía del M.A.S. 3. Algunos Sistemas Oscilantes. Péndulo Simple. Péndulo Físico. Masa+Muelle
1/42 Fátima Masot Conde Ing. Industrial 2006/07 2/42 Índice: 1.. Características. Representación Matemática. 2. Energía del M.A.S. 3. Algunos Sistemas Oscilantes. Péndulo Simple. Péndulo Físico. Masa+Muelle
Dinámica del Sólido Rígido
 Dinámica del Sólido Rígido El presente documento de clase sobre dinámica del solido rígido está basado en los contenidos volcados en la excelente página web del curso de Física I del Prof. Javier Junquera
Dinámica del Sólido Rígido El presente documento de clase sobre dinámica del solido rígido está basado en los contenidos volcados en la excelente página web del curso de Física I del Prof. Javier Junquera
Módulo 1: Mecánica Energía
 Módulo 1: Mecánica Energía Por qué ayuda la energía? El movimiento, en general, es difícil de calcular Y si usamos fuerzas, aceleración, etc. se complica porque son todo vectores (tienen módulo y dirección)
Módulo 1: Mecánica Energía Por qué ayuda la energía? El movimiento, en general, es difícil de calcular Y si usamos fuerzas, aceleración, etc. se complica porque son todo vectores (tienen módulo y dirección)
Departamento de Física Aplicada III Escuela Técnica Superior de Ingeniería
 Departamento de Física Aplicada III Escuela Técnica Superior de Ingeniería Grado en Ingeniería Aeroespacial Física I Segunda prueba de control, Enero 2016. Curso 2015/16 Nombre: DNI: Este test se recogerá
Departamento de Física Aplicada III Escuela Técnica Superior de Ingeniería Grado en Ingeniería Aeroespacial Física I Segunda prueba de control, Enero 2016. Curso 2015/16 Nombre: DNI: Este test se recogerá
1 Movimiento Oscilatorio
 1 Movimiento Oscilatorio 1.1 El Resorte Ley de Hooke: F = kx k: constante del resorte, se mide en N/m. 1.2 Movimiento Oscilatorio La solución de la ecuación de movimiento: ma = kx 1 es: x(t) = A cos(!t
1 Movimiento Oscilatorio 1.1 El Resorte Ley de Hooke: F = kx k: constante del resorte, se mide en N/m. 1.2 Movimiento Oscilatorio La solución de la ecuación de movimiento: ma = kx 1 es: x(t) = A cos(!t
TEMA 5.- Vibraciones y ondas
 TEMA 5.- Vibraciones y ondas CUESTIONES 41.- a) En un movimiento armónico simple, cuánto vale la elongación en el instante en el que la velocidad es la mitad de su valor máximo? Exprese el resultado en
TEMA 5.- Vibraciones y ondas CUESTIONES 41.- a) En un movimiento armónico simple, cuánto vale la elongación en el instante en el que la velocidad es la mitad de su valor máximo? Exprese el resultado en
Problemas de M.A.S. La partícula se encuentra en el extremo opuesto al que estaba al iniciar el movimiento.
 Problemas de M.A.S. 1.- Una partícula animada de m.a.s. inicia el movimiento en el extremo positivo de su trayectoria y tarda 0'5 s en llegar al centro de la misma. La distancia entre ambas posiciones
Problemas de M.A.S. 1.- Una partícula animada de m.a.s. inicia el movimiento en el extremo positivo de su trayectoria y tarda 0'5 s en llegar al centro de la misma. La distancia entre ambas posiciones
TEMA 0. FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS
 TEMA 0. FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS 1. Trabajo mecánico. 2. Teorema de la energía cinética. 3. Fuerzas conservativas y energía potencial. 4. Conservación de la energía mecánica. 5. Consejos
TEMA 0. FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS 1. Trabajo mecánico. 2. Teorema de la energía cinética. 3. Fuerzas conservativas y energía potencial. 4. Conservación de la energía mecánica. 5. Consejos
Movimiento Armónico Simple
 Movimiento Armónico Simple Ejercicio 1 Una partícula vibra con una frecuencia de 30Hz y una amplitud de 5,0 cm. Calcula la velocidad máxima y la aceleración máxima con que se mueve. En primer lugar atenderemos
Movimiento Armónico Simple Ejercicio 1 Una partícula vibra con una frecuencia de 30Hz y una amplitud de 5,0 cm. Calcula la velocidad máxima y la aceleración máxima con que se mueve. En primer lugar atenderemos
Ejercicios Física PAU Comunidad de Madrid Enunciados Revisado 25 noviembre 2014
 2015-Modelo A. Pregunta 2.- Un bloque de masa m = 0,2 kg está unido al extremo libre de un muelle horizontal de constante elástica k = 2 N m -1 que se encuentra fijo a una pared. Si en el instante inicial
2015-Modelo A. Pregunta 2.- Un bloque de masa m = 0,2 kg está unido al extremo libre de un muelle horizontal de constante elástica k = 2 N m -1 que se encuentra fijo a una pared. Si en el instante inicial
FISICA 2º BACHILLERATO
 A) Definiciones Se llama movimiento periódico a aquel en que la posición, la velocidad y la aceleración del móvil se repiten a intervalos regulares de tiempo. Se llama movimiento oscilatorio o vibratorio
A) Definiciones Se llama movimiento periódico a aquel en que la posición, la velocidad y la aceleración del móvil se repiten a intervalos regulares de tiempo. Se llama movimiento oscilatorio o vibratorio
(Lógico si la amplitud disminuyó a la mitad en 2.4 minutos tardará otros 2.4 minutos en reducirse de nuevo a la mitad)
 M.A.S. AMORTIGUADO Un bloque suspendido de un muelle se pone a oscilar con una amplitud inicial de 120 mm. Después de 2.4 minutos la amplitud ha disminuido hasta 60 mm. a) Cuándo será la amplitud de 30
M.A.S. AMORTIGUADO Un bloque suspendido de un muelle se pone a oscilar con una amplitud inicial de 120 mm. Después de 2.4 minutos la amplitud ha disminuido hasta 60 mm. a) Cuándo será la amplitud de 30
es e valor máximo de la fem
 U Tópicos apítulo de : Electricidad orriente Alterna y Magnetismo J. Pozo, J. Pozo, A. A. eón eón y.m. y.m. horbadjian. APÍTUO OENTE ATENA (A.. ntroducción Para generar corriente alterna, se puede considerar
U Tópicos apítulo de : Electricidad orriente Alterna y Magnetismo J. Pozo, J. Pozo, A. A. eón eón y.m. y.m. horbadjian. APÍTUO OENTE ATENA (A.. ntroducción Para generar corriente alterna, se puede considerar
Ejercicios Física PAU Comunidad de Madrid Enunciados Revisado 18 septiembre 2012.
 2013-Modelo A. Pregunta 2.- Un objeto está unido a un muelle horizontal de constante elástica 2 10 4 Nm -1. Despreciando el rozamiento: a) Qué masa ha de tener el objeto si se desea que oscile con una
2013-Modelo A. Pregunta 2.- Un objeto está unido a un muelle horizontal de constante elástica 2 10 4 Nm -1. Despreciando el rozamiento: a) Qué masa ha de tener el objeto si se desea que oscile con una
Ayudantía 4. Ignacio Reyes Dinámica, Trabajo y Energía
 P. Universidad Católica de Chile Facultad de Física Estática y Dinámica Profesor Rafael Benguria Ayudantía 4 Ignacio Reyes (iareyes@uc.cl). Prob. 2/I--200 Dinámica, Trabajo y Energía Una partícula de masa
P. Universidad Católica de Chile Facultad de Física Estática y Dinámica Profesor Rafael Benguria Ayudantía 4 Ignacio Reyes (iareyes@uc.cl). Prob. 2/I--200 Dinámica, Trabajo y Energía Una partícula de masa
Índice. Leyes de Newton Interacción Gravitatoria Reacción en Apoyos Leyes del Rozamiento. Ejemplos. Leyes de la Dinámica en SRNI.
 Índice Leyes de Newton Interacción Gravitatoria Reacción en Apoyos Leyes del Rozamiento Ejemplos Leyes de la Dinámica en SRNI Ejemplos Teorema de la Cantidad de Movimiento. Conservación. Teorema del Momento
Índice Leyes de Newton Interacción Gravitatoria Reacción en Apoyos Leyes del Rozamiento Ejemplos Leyes de la Dinámica en SRNI Ejemplos Teorema de la Cantidad de Movimiento. Conservación. Teorema del Momento
Problemas de Física I
 Problemas de Física I DINÁMICA DEL SÓLIDO RÍGIDO (1 er Q.:prob impares, 2 ndo Q.:prob pares) 1. (T) Dos partículas de masas m 1 y m 2 están unidas por una varilla de longitud r y masa despreciable. Demostrar
Problemas de Física I DINÁMICA DEL SÓLIDO RÍGIDO (1 er Q.:prob impares, 2 ndo Q.:prob pares) 1. (T) Dos partículas de masas m 1 y m 2 están unidas por una varilla de longitud r y masa despreciable. Demostrar
TRABAJO Y ENERGIA EN ROTACIÓN. Consideremos un cuerpo que gira alrededor de un eje tal como se muestra en la figura. La energía cinética de un
 TRABAJO Y ENERGIA EN ROTACIÓN. Consideremos un cuerpo que gira alrededor de un eje tal como se muestra en la figura. La energía cinética de un elemento de masa dm que gira a una distancia r del eje de
TRABAJO Y ENERGIA EN ROTACIÓN. Consideremos un cuerpo que gira alrededor de un eje tal como se muestra en la figura. La energía cinética de un elemento de masa dm que gira a una distancia r del eje de
MOVIMIENTO OSCILATORIO O VIBRATORIO
 MOVIMIENTO OSCILATORIO O VIBRATORIO 1. Movimiento armónico simple (MAS). 2. Ecuaciones del MAS. 3. Dinámica del MAS. 4. Energía del MAS. 5. El oscilador armónico. 6. El péndulo simple. Física 2º bachillerato
MOVIMIENTO OSCILATORIO O VIBRATORIO 1. Movimiento armónico simple (MAS). 2. Ecuaciones del MAS. 3. Dinámica del MAS. 4. Energía del MAS. 5. El oscilador armónico. 6. El péndulo simple. Física 2º bachillerato
La última igualdad se deduce del hecho que los vectores d r/dt = v y p son paralelos. Usando (8.2) en (8.1) se obtiene
 Capítulo 8 Momento angular 8.1. Momento angular de una partícula Consideremos una partícula de masa m y cuya posición (respecto a algún sistema de referencia inercial) viene dada por el vector r. Sea F
Capítulo 8 Momento angular 8.1. Momento angular de una partícula Consideremos una partícula de masa m y cuya posición (respecto a algún sistema de referencia inercial) viene dada por el vector r. Sea F
27 de octubre de 2010
 Pontificia Universidad Católica de Chile Facultad de Física FIZ 11 Mecánica Clásica Profesor: Andrés Jordán Ayudantes: Eduardo Bañados T. eebanado@uc.cl Ariel Norambuena ainoramb@uc.cl Torque, Momento
Pontificia Universidad Católica de Chile Facultad de Física FIZ 11 Mecánica Clásica Profesor: Andrés Jordán Ayudantes: Eduardo Bañados T. eebanado@uc.cl Ariel Norambuena ainoramb@uc.cl Torque, Momento
Problema # 2. Problema # 1
 En la Figura aparece Daniel Bernoulli (1700-1782). Es el autor de la ecuación que lleva su nombre y que representa la conservación de la energía en un fluido. Fue uno de los matemáticos más destacados
En la Figura aparece Daniel Bernoulli (1700-1782). Es el autor de la ecuación que lleva su nombre y que representa la conservación de la energía en un fluido. Fue uno de los matemáticos más destacados
Física 2º Bach. Ondas 16/11/10
 Física º Bach. Ondas 16/11/10 DEPARTAMENTO DE FÍSICA E QUÍMICA Nombre: Puntuación máxima: Problemas 6 puntos (1 cada apartado). Cuestiones 4 puntos (1 cada apartado o cuestión, teórica o práctica) No se
Física º Bach. Ondas 16/11/10 DEPARTAMENTO DE FÍSICA E QUÍMICA Nombre: Puntuación máxima: Problemas 6 puntos (1 cada apartado). Cuestiones 4 puntos (1 cada apartado o cuestión, teórica o práctica) No se
CÁTEDRA DE FÍSICA I OSCILACIONES - PROBLEMAS RESUELTOS
 CÁTEDRA DE FÍSICA I Ing. Civil, Ing. Electromecánica, Ing. Eléctrica, Ing. Mecánica OSCILACIONES - PROBLEMAS RESUELTOS PROBLEMA Nº 1 Un cuerpo oscila con movimiento armónico simple a lo largo del eje x.
CÁTEDRA DE FÍSICA I Ing. Civil, Ing. Electromecánica, Ing. Eléctrica, Ing. Mecánica OSCILACIONES - PROBLEMAS RESUELTOS PROBLEMA Nº 1 Un cuerpo oscila con movimiento armónico simple a lo largo del eje x.
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA TERCERA EVALUACIÓN DE FÍSICA A SEPTIEMBRE 17 DE 2014 SOLUCIÓN Pregunta 1 (8 puntos) P y R señalan
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA TERCERA EVALUACIÓN DE FÍSICA A SEPTIEMBRE 17 DE 2014 SOLUCIÓN Pregunta 1 (8 puntos) P y R señalan
PÉNDULO BALÍSTICO FÍSICO
 PÉNDULO BALÍSTICO FÍSICO 1.- OBJETIVO Determinar la velocidad del proyectil que incide sobre el péndulo y la pérdida de energía cinética en el choque.- DESCRIPCIÓN DEL EQUIPO Lanzador Soporte del péndulo
PÉNDULO BALÍSTICO FÍSICO 1.- OBJETIVO Determinar la velocidad del proyectil que incide sobre el péndulo y la pérdida de energía cinética en el choque.- DESCRIPCIÓN DEL EQUIPO Lanzador Soporte del péndulo
Slide 1 / 47. Movimiento Armónico Simple Problemas de Práctica
 Slide 1 / 47 Movimiento Armónico Simple Problemas de Práctica Slide 2 / 47 Preguntas de Multiopcion Slide 3 / 47 1 Un bloque con una masa M está unida a un resorte con un constante k. El bloque se somete
Slide 1 / 47 Movimiento Armónico Simple Problemas de Práctica Slide 2 / 47 Preguntas de Multiopcion Slide 3 / 47 1 Un bloque con una masa M está unida a un resorte con un constante k. El bloque se somete
P2.- El escape de áncora
 P.- El escape de áncora. Como es bien sabido desde hace tiempo, las oscilaciones de un péndulo son isócronas, por lo que son idóneas como referencia para la medida del tiempo en los relojes. Sin embargo,
P.- El escape de áncora. Como es bien sabido desde hace tiempo, las oscilaciones de un péndulo son isócronas, por lo que son idóneas como referencia para la medida del tiempo en los relojes. Sin embargo,
LISTA DE SÍMBOLOS. Capítulo 2 EJEMPLOS Y TEORIA DE LAS VIBRACIONES PARAMÉTRICAS 2.1 Introducción T - Periodo Ω - Frecuencia a- parámetro b- parámetro
 LISTA DE SÍMBOLOS Capítulo 2 EJEMPLOS Y TEORIA DE LAS VIBRACIONES PARAMÉTRICAS 2.1 Introducción T - Periodo Ω - Frecuencia a- parámetro b- parámetro 2.1.1 Rigidez Flexiva que Difiere en dos Ejes x- Desplazamiento
LISTA DE SÍMBOLOS Capítulo 2 EJEMPLOS Y TEORIA DE LAS VIBRACIONES PARAMÉTRICAS 2.1 Introducción T - Periodo Ω - Frecuencia a- parámetro b- parámetro 2.1.1 Rigidez Flexiva que Difiere en dos Ejes x- Desplazamiento
X. Fundamentos de Vibración
 Objetivos: 1. Indicar la importancia del estudio de la vibración. 2. Discutir algunos conceptos básicos de la vibración: qué es la vibración?, cuáles son las partes elementales de un sistema vibratorio?,
Objetivos: 1. Indicar la importancia del estudio de la vibración. 2. Discutir algunos conceptos básicos de la vibración: qué es la vibración?, cuáles son las partes elementales de un sistema vibratorio?,
Movimiento armónico simple Modelo A. Pregunta 2.- Un bloque de masa m = 0,2 kg está unido al extremo libre de un muelle horizontal de
 Movimiento armónico simple 1.- 2015-Modelo A. Pregunta 2.- Un bloque de masa m = 0,2 kg está unido al extremo libre de un muelle horizontal de constante elástica k = 2 N m -1 que se encuentra fijo a una
Movimiento armónico simple 1.- 2015-Modelo A. Pregunta 2.- Un bloque de masa m = 0,2 kg está unido al extremo libre de un muelle horizontal de constante elástica k = 2 N m -1 que se encuentra fijo a una
ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA AERONÁUTICA Y DEL ESPACIO FÍSICA I
 ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA AERONÁUTICA Y DEL ESPACIO FÍSICA I PROBLEMAS RESUELTOS José Carlos JIMÉNEZ SÁEZ Santiago RAMÍREZ DE LA PISCINA MILLÁN.- DINÁMICA DE SISTEMAS DE PARTÍCULAS Dinámica
ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA AERONÁUTICA Y DEL ESPACIO FÍSICA I PROBLEMAS RESUELTOS José Carlos JIMÉNEZ SÁEZ Santiago RAMÍREZ DE LA PISCINA MILLÁN.- DINÁMICA DE SISTEMAS DE PARTÍCULAS Dinámica
2 o Bachillerato. Conceptos básicos
 Física 2 o Bachillerato Conceptos básicos Movimiento. Cambio de posición de un cuerpo respecto de un punto que se toma como referencia. Cinemática. Parte de la Física que estudia el movimiento de los cuerpos
Física 2 o Bachillerato Conceptos básicos Movimiento. Cambio de posición de un cuerpo respecto de un punto que se toma como referencia. Cinemática. Parte de la Física que estudia el movimiento de los cuerpos
Tema 8 Trabajo potencia y energía
 1. Trabajo Tema 8 Trabajo potencia y energía En física, decimos que hay trabajo cuando una fuerza provoca un desplazamiento En la naturaleza se produce transferencia de energía entre unos sistemas y otros.
1. Trabajo Tema 8 Trabajo potencia y energía En física, decimos que hay trabajo cuando una fuerza provoca un desplazamiento En la naturaleza se produce transferencia de energía entre unos sistemas y otros.
Módulo 1: Mecánica Sólido rígido. Rotación (II)
 Módulo 1: Mecánica Sólido rígido. Rotación (II) 1 Segunda ley de Newton en la rotación Se puede hacer girar un disco por ejemplo aplicando un par de fuerzas. Pero es necesario tener en cuenta el punto
Módulo 1: Mecánica Sólido rígido. Rotación (II) 1 Segunda ley de Newton en la rotación Se puede hacer girar un disco por ejemplo aplicando un par de fuerzas. Pero es necesario tener en cuenta el punto
2DA PRÁCTICA CALIFICADA
 2DA PRÁCTICA CALIFICADA DINÁMICA (IC 244) ALUMNOS : CARITAS BARRIENTOS, Ronald ROBLES ROCHA, Hamilton TORRES PÉREZ, Walter A. TORO VELARDE, William DOCENTE : Ing. CASTRO PÉREZ, Cristian CINÉTICA DE UNA
2DA PRÁCTICA CALIFICADA DINÁMICA (IC 244) ALUMNOS : CARITAS BARRIENTOS, Ronald ROBLES ROCHA, Hamilton TORRES PÉREZ, Walter A. TORO VELARDE, William DOCENTE : Ing. CASTRO PÉREZ, Cristian CINÉTICA DE UNA
EXAMEN FÍSICA 2º BACHILLERATO TEMA 3: ONDAS
 INSTRUCCIONES GENERALES Y VALORACIÓN La prueba consiste de dos opciones, A y B, y el alumno deberá optar por una de las opciones y resolver las tres cuestiones y los dos problemas planteados en ella, sin
INSTRUCCIONES GENERALES Y VALORACIÓN La prueba consiste de dos opciones, A y B, y el alumno deberá optar por una de las opciones y resolver las tres cuestiones y los dos problemas planteados en ella, sin
Tema 2. Dinámica básica de la partícula aislada y de los sistemas de partículas
 Mecánica teórica Tema 2. Dinámica básica de la partícula aislada y de los sistemas de partículas Tema 2B Universidad de Sevilla - Facultad de Física cotrino@us.es 22 de septiembre de 2016 Tema 2B (Grupo
Mecánica teórica Tema 2. Dinámica básica de la partícula aislada y de los sistemas de partículas Tema 2B Universidad de Sevilla - Facultad de Física cotrino@us.es 22 de septiembre de 2016 Tema 2B (Grupo
UNIVERSIDAD POLITÉCNICA DE EL SALVADOR ESCUELA DE FORMACIÓN BÁSICA. FÍSICA II PRÁCTICA 26 PENDULO SIMPLE
 UNIVERSIDAD POLITÉCNICA DE EL SALVADOR ESCUELA DE FORMACIÓN BÁSICA. FÍSICA II PRÁCTICA 26 PENDULO SIMPLE OBJETIVOS DEL APRENDIZAJE: ESTUDIAR LAS OSCILACIONES DEL PÉNDULO Y DETERMINAR LAS SIMPLIFICACIONES
UNIVERSIDAD POLITÉCNICA DE EL SALVADOR ESCUELA DE FORMACIÓN BÁSICA. FÍSICA II PRÁCTICA 26 PENDULO SIMPLE OBJETIVOS DEL APRENDIZAJE: ESTUDIAR LAS OSCILACIONES DEL PÉNDULO Y DETERMINAR LAS SIMPLIFICACIONES
Péndulo de torsión y momentos de inercia
 Prácticas de Física Péndulo de torsión y momentos de inercia 1 Objetivos Curso 2009/10 Determinar la constante de un muelle espiral Determinar el momento de inercia de varios sólidos rígidos Comprobar
Prácticas de Física Péndulo de torsión y momentos de inercia 1 Objetivos Curso 2009/10 Determinar la constante de un muelle espiral Determinar el momento de inercia de varios sólidos rígidos Comprobar
Cinemática del movimiento armónico simple
 PROBLEMAS DE OSCILACIONES. Cinemática del movimiento armónico simple Autor: José Antonio Diego Vives Documento bajo licencia CC Attribution-Share Alike 3.0 (BY-SA) Problema 1 Un pequeño objeto de masa
PROBLEMAS DE OSCILACIONES. Cinemática del movimiento armónico simple Autor: José Antonio Diego Vives Documento bajo licencia CC Attribution-Share Alike 3.0 (BY-SA) Problema 1 Un pequeño objeto de masa
UNIDAD 9: TRABAJO Y ENERGÍA MECÁNICA 1. Trabajo mecánico
 UNIDAD 9: TRABAJO Y ENERGÍA MECÁNICA 1. Trabajo mecánico a) Indica en los siguientes casos si se realiza o no trabajo mecánico: Un cuerpo en caída libre (fuerza de gravedad Un cuerpo apoyado en una meda
UNIDAD 9: TRABAJO Y ENERGÍA MECÁNICA 1. Trabajo mecánico a) Indica en los siguientes casos si se realiza o no trabajo mecánico: Un cuerpo en caída libre (fuerza de gravedad Un cuerpo apoyado en una meda
Física P.A.U. GRAVITACIÓN 1 GRAVITACIÓN
 Física P.A.U. GRAVITACIÓN 1 GRAVITACIÓN PROBLEMAS SATÉLITES 1. El período de rotación de la Tierra alrededor del Sol es un año y el radio de la órbita es 1,5 10 11 m. Si Júpiter tiene un período de aproximadamente
Física P.A.U. GRAVITACIÓN 1 GRAVITACIÓN PROBLEMAS SATÉLITES 1. El período de rotación de la Tierra alrededor del Sol es un año y el radio de la órbita es 1,5 10 11 m. Si Júpiter tiene un período de aproximadamente
 Universidad Rey Juan Carlos. Prueba de acceso para mayores de 25 años. Física obligatoria. Año 2010. Opción A. Ejercicio 1. a) Defina el vector velocidad y el vector aceleración de un movimiento y escribe
Universidad Rey Juan Carlos. Prueba de acceso para mayores de 25 años. Física obligatoria. Año 2010. Opción A. Ejercicio 1. a) Defina el vector velocidad y el vector aceleración de un movimiento y escribe
Problemas Movimiento Armónico Simple
 Problemas Movimiento Armónico Simple 1. Una partícula describe un M.A.S de pulsación w=π rad/s. En un instante dado se activa el cronómetro. En ese momento la elongación que tiene un sentido de recorrido
Problemas Movimiento Armónico Simple 1. Una partícula describe un M.A.S de pulsación w=π rad/s. En un instante dado se activa el cronómetro. En ese momento la elongación que tiene un sentido de recorrido
Guia N 6 - Primer cuatrimestre de 2007 Sólidos rígidos planos. Energía potencial y mecánica.
 æ Mecánica CLásica Guia N 6 - Primer cuatrimestre de 2007 Sólidos rígidos planos. Energía potencial y mecánica. Problema 1: Dos barras delgadas uniformes de longitudes iguales, l=0.5 m, una de 4 kg y la
æ Mecánica CLásica Guia N 6 - Primer cuatrimestre de 2007 Sólidos rígidos planos. Energía potencial y mecánica. Problema 1: Dos barras delgadas uniformes de longitudes iguales, l=0.5 m, una de 4 kg y la
TEMA 1 Parte I Vibraciones libres y amortiguadas
 TEMA 1 Parte I Vibraciones libres y aortiguadas 1.1. Introducción: grados de libertad y agnitudes características VIBRACIÓN MECÁNICA: Oscilación repetida en torno a una posición de equilibrio - Vibraciones
TEMA 1 Parte I Vibraciones libres y aortiguadas 1.1. Introducción: grados de libertad y agnitudes características VIBRACIÓN MECÁNICA: Oscilación repetida en torno a una posición de equilibrio - Vibraciones
1. Oscilador Armónico simple
 1. Oscilador Armónico simple La ecuación de un oscilador armónico simple es una Ecuación Diferencial Ordinaria (EDO) lineal y tiene la forma: ÿ = ω 2 0 y (1) y(0) = y 0 ;ẏ(0) = v 0 (2) Donde y es la posición
1. Oscilador Armónico simple La ecuación de un oscilador armónico simple es una Ecuación Diferencial Ordinaria (EDO) lineal y tiene la forma: ÿ = ω 2 0 y (1) y(0) = y 0 ;ẏ(0) = v 0 (2) Donde y es la posición
Tema 1 Movimiento Armónico Simple
 Tema Movimiento Armónico Simple. Conceptos de movimiento oscilatorio: el movimiento armónico simple (MAS).. Ecuación general del MAS..3 Cinemática del MAS..4 Dinámica del MAS..5 Energía del MAS..6 Aplicación
Tema Movimiento Armónico Simple. Conceptos de movimiento oscilatorio: el movimiento armónico simple (MAS).. Ecuación general del MAS..3 Cinemática del MAS..4 Dinámica del MAS..5 Energía del MAS..6 Aplicación
Soluciones a los problemas de los temas 7 y 8 no resueltos en clase
 Asignatura Física General. Licenciatura en Química. Grupo B Soluciones a los problemas de los temas 7 y 8 no resueltos en clase 2. Teniendo en cuenta que el momento de la fuerza aplicada con respecto al
Asignatura Física General. Licenciatura en Química. Grupo B Soluciones a los problemas de los temas 7 y 8 no resueltos en clase 2. Teniendo en cuenta que el momento de la fuerza aplicada con respecto al
Aceleración n de la gravedad Péndulo simple
 Aceleración n de la gravedad Péndulo simple Experiencia de Laboratorio, Física F experimental I, 2007 A. Biera, G. Huck y P. Palermo Tandil - Octubre de 2007 1 Aceleración n de la gravedad - Péndulo simple
Aceleración n de la gravedad Péndulo simple Experiencia de Laboratorio, Física F experimental I, 2007 A. Biera, G. Huck y P. Palermo Tandil - Octubre de 2007 1 Aceleración n de la gravedad - Péndulo simple
Opción B ANDALUCÍA CONVOCATORIA JUNIO GM T m s (3R T ) 2 Despejando la velocidad orbital: m s v 0 (3R T ) F g F c
 Física 1 Física SOLUCIÓN DE LA PRUEBA DE ACCESO AUTOR: Tomás Caballero Rodríguez Opción A a) I 1 B B 1 F 1, F, 1 Vemos que la lente divergente desvía los rayos paralelos al eje óptico y que los rayos que
Física 1 Física SOLUCIÓN DE LA PRUEBA DE ACCESO AUTOR: Tomás Caballero Rodríguez Opción A a) I 1 B B 1 F 1, F, 1 Vemos que la lente divergente desvía los rayos paralelos al eje óptico y que los rayos que
Ejercicio nº 1 Deducir la ecuación del movimiento asociado a la gráfica. Ejercicio nº 2 Deducir la ecuación del movimiento asociado a la gráfica.
 1(9) Ejercicio nº 1 Deducir la ecuación del movimiento asociado a la gráfica. X(m) 4 2 4 6 8 t(s) -4 Ejercicio nº 2 Deducir la ecuación del movimiento asociado a la gráfica. X(m) 3 1 2 3 t(s) -3 Ejercicio
1(9) Ejercicio nº 1 Deducir la ecuación del movimiento asociado a la gráfica. X(m) 4 2 4 6 8 t(s) -4 Ejercicio nº 2 Deducir la ecuación del movimiento asociado a la gráfica. X(m) 3 1 2 3 t(s) -3 Ejercicio
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA PRIMERA EVALUACIÓN DE FÍSICA A DICIEMBRE 10 DE 2014 SOLUCIÓN TEMA 1 (8 puntos) Una persona corre
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA PRIMERA EVALUACIÓN DE FÍSICA A DICIEMBRE 10 DE 2014 SOLUCIÓN TEMA 1 (8 puntos) Una persona corre
Estática y Dinámica Analítica
 Estática y Dinámica Analítica p. 1/25 Estática y Dinámica Analítica Mecánica II Temas 6 y 7 Manuel Ruiz Delgado Escuela Técnica Superior de Ingenieros Aeronáuticos Universidad Politécnica de Madrid Mecánica
Estática y Dinámica Analítica p. 1/25 Estática y Dinámica Analítica Mecánica II Temas 6 y 7 Manuel Ruiz Delgado Escuela Técnica Superior de Ingenieros Aeronáuticos Universidad Politécnica de Madrid Mecánica
Actividades del final de la unidad
 Actividades del final de la unidad. Un cuerpo baja por un plano inclinado y sube, a continuación, por otro con igual inclinación, alcanzando en ambos la misma altura al deslizar sin rozamiento. Este movimiento,
Actividades del final de la unidad. Un cuerpo baja por un plano inclinado y sube, a continuación, por otro con igual inclinación, alcanzando en ambos la misma altura al deslizar sin rozamiento. Este movimiento,
MOVIMIENTO ARMÓNICO PREGUNTAS
 MOVIMIENTO ARMÓNICO PREGUNTAS 1. Qué ocurre con la energía mecánica del movimiento armónico amortiguado? 2. Marcar lo correspondiente: la energía de un sistema masa resorte es proporcional a : i. la amplitud
MOVIMIENTO ARMÓNICO PREGUNTAS 1. Qué ocurre con la energía mecánica del movimiento armónico amortiguado? 2. Marcar lo correspondiente: la energía de un sistema masa resorte es proporcional a : i. la amplitud
VI. Sistemas de dos grados de libertad
 Objetivos: 1. Describir que es un sistema de dos grados de.. Deducir las ecuaciones diferenciales de movimiento para un sistema de dos grados de masa-resorte-amortiguador, con amortiguamiento viscoso y
Objetivos: 1. Describir que es un sistema de dos grados de.. Deducir las ecuaciones diferenciales de movimiento para un sistema de dos grados de masa-resorte-amortiguador, con amortiguamiento viscoso y
TEMA 6 Movimiento oscilatorio
 TEMA 6 Movimiento oscilatorio 1.- Movimiento armónico simple (M.A.S.).- Oscilaciones amortiguadas 3.- Oscilaciones forzadas. Resonancia 1.- Movimiento armónico simple 1.1.- Estudio dinámico del M.A.S.
TEMA 6 Movimiento oscilatorio 1.- Movimiento armónico simple (M.A.S.).- Oscilaciones amortiguadas 3.- Oscilaciones forzadas. Resonancia 1.- Movimiento armónico simple 1.1.- Estudio dinámico del M.A.S.
Problemas de Movimiento vibratorio. MAS 2º de bachillerato. Física
 Problemas de Movimiento vibratorio. MAS º de bachillerato. Física 1. Un muelle se deforma 10 cm cuando se cuelga de él una masa de kg. Se separa otros 10 cm de la posición de equilibrio y se deja en libertad.
Problemas de Movimiento vibratorio. MAS º de bachillerato. Física 1. Un muelle se deforma 10 cm cuando se cuelga de él una masa de kg. Se separa otros 10 cm de la posición de equilibrio y se deja en libertad.
K m = 20,0[N m 1 ] =6,32 rad/s 0,500[kg] 0,050 = 0,050 sen (ω 0+ φ 0 ) φ 0 = arc sen 1 = π / 2. x = 0,050 sen (6,32 t + 1,57) [m]
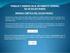
![K m = 20,0[N m 1 ] =6,32 rad/s 0,500[kg] 0,050 = 0,050 sen (ω 0+ φ 0 ) φ 0 = arc sen 1 = π / 2. x = 0,050 sen (6,32 t + 1,57) [m] K m = 20,0[N m 1 ] =6,32 rad/s 0,500[kg] 0,050 = 0,050 sen (ω 0+ φ 0 ) φ 0 = arc sen 1 = π / 2. x = 0,050 sen (6,32 t + 1,57) [m]](/thumbs/70/61977155.jpg) Física º Bach. Examen de Setiembre de 005 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: [1½ PUNTOS / UNO] X 1. El cuerpo de la figura tiene masa m = 500 g, está apoyado sobre una superficie horizontal
Física º Bach. Examen de Setiembre de 005 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: [1½ PUNTOS / UNO] X 1. El cuerpo de la figura tiene masa m = 500 g, está apoyado sobre una superficie horizontal
Fuerza de roce. Multiplicación de vectores. Impulso Momentum Torque Trabajo Potencia
 Multiplicación de vectores Fuerza de roce Impulso Momentum Torque Trabajo Potencia Disipación de energía y roce. Coeficientes de roce estático y dinámico. Magnitud y dirección de la fuerza de roce en cada
Multiplicación de vectores Fuerza de roce Impulso Momentum Torque Trabajo Potencia Disipación de energía y roce. Coeficientes de roce estático y dinámico. Magnitud y dirección de la fuerza de roce en cada
2005 septiembre original 1º ejercicio Dinámica
 2005 septiembre original 1º ejercicio Dinámica Sea un plano inclinado, de longitud L, que forma un ángulo + /2 con la horizontal. Este plano, en su cota más baja enlaza con un plano horizontal, de longitud
2005 septiembre original 1º ejercicio Dinámica Sea un plano inclinado, de longitud L, que forma un ángulo + /2 con la horizontal. Este plano, en su cota más baja enlaza con un plano horizontal, de longitud
Sólido Rígido. Momento de Inercia 17/11/2013
 Sólido ígido Un sólido rígido es un sistema formado por muchas partículas que tiene como característica que la posición relativa de todas ellas permanece constante durante el movimiento. A B El movimiento
Sólido ígido Un sólido rígido es un sistema formado por muchas partículas que tiene como característica que la posición relativa de todas ellas permanece constante durante el movimiento. A B El movimiento
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA SEGUNDA EVALUACIÓN DE FÍSICA A FEBRERO 18 DE 2015 SOLUCIÓN Analice las siguientes preguntas
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE FÍSICA SEGUNDA EVALUACIÓN DE FÍSICA A FEBRERO 18 DE 2015 SOLUCIÓN Analice las siguientes preguntas
Fundamentos de espectroscopia: Vibraciones
 Fundamentos de espectroscopia: Vibraciones Jesús Hernández Trujillo Facultad de Química, UNAM Agosto de 2017 Vibraciones/JHT 1 / 28 Oscilador armónico Movimiento oscilatorio: Una partícula describe un
Fundamentos de espectroscopia: Vibraciones Jesús Hernández Trujillo Facultad de Química, UNAM Agosto de 2017 Vibraciones/JHT 1 / 28 Oscilador armónico Movimiento oscilatorio: Una partícula describe un
Prof. Jorge Rojo Carrascosa CINEMÁTICA
 CINEMÁTICA La cinemática estudia el movimiento de los cuerpos sin tener en cuenta las causas que los producen. Por tanto, tan sólo se ocupa de los aspectos externos como son el desplazamiento, el espacio
CINEMÁTICA La cinemática estudia el movimiento de los cuerpos sin tener en cuenta las causas que los producen. Por tanto, tan sólo se ocupa de los aspectos externos como son el desplazamiento, el espacio
Solucionario de las actividades propuestas en el libro del alumno
 Solucionario de las actividades propuestas en el libro del alumno 4.. MOVIMIENOS PERIÓDICOS Página 75. Conocido el período de rotación de la Luna en torno a la ierra y sabiendo que la Luna no emite luz
Solucionario de las actividades propuestas en el libro del alumno 4.. MOVIMIENOS PERIÓDICOS Página 75. Conocido el período de rotación de la Luna en torno a la ierra y sabiendo que la Luna no emite luz
