En ciencias e ingeniería (experimentales) es imprescindible realizar mediciones, que consisten en obtener
|
|
|
- José Ramón Víctor Carmona Rojas
- hace 7 años
- Vistas:
Transcripción
1 ERRORES DE MEDICION Y SU PROPAGACION En ciencias e ingeniería (experimentales) es imprescindible realizar mediciones, que consisten en obtener la magnitud fisica de algun atributo de objetos ( proceso, fenomeno, sustancia, etc). Ejemplos de algunos atributos son; longitud, masa, temperatura, sonsistencia. Para determinar el valor de una magnitud fisica se emplea un instrumento de medicion y un metodo de medicion. Asi tambien se requiere definir una unidad de medicion. [practica: definir el patron de medicion de longitud, masa, tiempo] El termino error es sinonimo como incertidumbre experimental. Existen limitaciones instrumentales, fisicas y humanas que causan una desviacion del valor verdadero de las cantidades que se desean medir. Estas desviaciones son denominadas incertidumbres experimentales o errores en la medicion. El valor verdadero es aquel que obtendriamos si no existiesen errores en las mediciones, sin embargo esto es imposible. Se puede mejorar el procedimiento de medicion pero jamas se puede eliminar el error, por lo que jamas podemos esperar el valor verdadero. Entre las varias limitaciones de medicion se tienen: la precision y exactitud de los instrumentos de medicion la interaccion del metodo de medicion con el mesurando la definicion del objeto a medir la influencia del observador que realiza la medicion. En la presentacion y analisis de los reusltados de medicion se requiere expresar el grado de error o el limite probabilistico de la incertidumbre. El estudiante debe ser capaz de cuantificar el error asociado a las mediciones y analizar como se afectan los resultados (esto es propagacion de error). El error se puede concebir como la dispersion de las diferentes mediciones de un valor central. TIPOS DE ERRORES
2 Los errores experimentales son de dos tipos: determinados (sistematicos) e indeterminados. Los errores determinados o sistematicos. Sistematico, significa que cuando se realizan mediciones repetidas, el error tiene la misma magnitud y el mismo signo algebraico, Determinado, significa que pueden ser reconocidos e identificados, por lo tanto la magnitud y el signo son determinables. Ejemplos: un instrumento o escala no calibrada, una persona que no distingue colores correctos, el uso de un valor no correcto de una constante (o unidades no adecuadas). Los errores indeterminados estan siempre presentes en las mediciones experimentales. En estos no existe la manera de determinar el signo ni la magnitud del error en mediciones repetidas. Los errores indeterminados resultan, en el proceso de medicion, en la obtencion de diferentes valores cuando se efectuan mediciones repetidas (asumiendo que todas las condiciones permanecen constantes). Las causas en los errores indeterminados son diversas; error del operador o sesgo, condiciones experimentales fluctuantes, variabilidad inherente en los instrumentos de medicion, etc. El efecto que tienen los errores indeterminados en los resultados se puede minimizar al efectuar mediciones repetidas y despues calcular el promedio. El promedio se considera una mejor representacion del valor verdadero que una sola medicion, ya que los errores de signo positivo y los de signo negativo tienden a compensarse en el calculo de la media. Los errores determinados pueden ser mas importantes que los indeterminados por tres razones; no existe metodo seguro para descubrirlos e identificarlos al analizar los datos experimentales, sus efectos no pueden ser reducidos al promediar mediciones repetidas, los errores determinados tienen la misma magnitud y signo para cada medicion en un conjunto de mediciones repetidas, por lo que no tienden a cancelarse los errores negativos y los positivos. EXPRESION DEL ERROR
3 Se ha mencionado que el error en la medicion esta asociado al concepto de incertidumbre. Se desea expresar el grado de error en las mediciones o el limite probabilistico de la incertidumbre. Conceptualmente se concibe el error como la dispersion de las diferentes mediciones de un valor central. Esto se expresa como: x ± x = (x x) < x < (x + x) Ej; 24.2 ±.8 = (24.2.8) < 24.2 < ( ) El error se puede expresar como: error absoluto є = x error relativo є x = x/x eror porcentual є x % = є x * 100 PRECISION Y EXACTITUD La presicion de un instrumento o metodo de medicion esta asociado a la sensibilidad o menor variacion de la magnitud que se puede detectar con dicho instrumento o metodo. La exactitud es una medida de la cercania de nuestro resultado con respecto al valor verdadero. Una medicion con un error indeterminado relativamente pequeno se diece que tiene una alta precision. Una medicion con un error pequeno indeterminado y determinado se dice que tiene una alta exactitud. La precision no implica necesariamente exactitud. Una medicion precisa puede ser inexacta si tiene un error determinado. COMPARACION DE CANTIDADES
4 Desviacion: Cuando se efectua un conjunto de mediciones repetidas de una cantidad fisica es util expresar la diferencia de cada medicion con respecto al promedio del conjunto. Esto se llama la desviacion de cada medicion de la media. La desviacion, en general, es la diferencia entre cada dato de un valor representativo del conjunto de datos (puede ser mediana, moda u otro). Las desviaciones se pueden expresar en valores realtivos o absolutos. Diferencia: Existen situaciones que requieren comparar mediciones o resultados que se estima tienen la misma confiabilidad, se puede expresar la diferencia en valores absolutos o relativos. Ejemplo; comparar dos mediciones independientes una misma cantidad, o comporar los resultados experimentales con los de otra persona o por otro procedimiento. El expresar la diferencia no implica el analizar y juzgar sobre la cofiabilidad de uno u otro. Discrepancia Experimental: Cuando se compara una medicion (resultado) con otra que se considera mas confiable, a su diferencia se le llama la discrepancia experimental. Esta puede expresarse en valores absolutos o relativos (porcentuales). Se acostumbra expresar el porcentaje al dividir la discrepancia entre la cantidad mas confiable (mult. Por 100). Si la diferencia es muy pequena no importa (practicamente) que cantidad de las dos se coloca en el denominador. PROCEDIMIENTO ESTADISTICO Para la expresion del error, primero se obtiene un valor de tendencia central, para nuestros fines sera el promedio de un conjunto de mediciones repetidas. Para la dispersion (el eror) se calculara la desviacion estandar ( en ocaciones se emplea el promedio de las desviaciones). Los pasos a seguir son: Se encuentra le media (promedio)
5 Se encuentra la desviacion de cada observacion de la media Se suman los cuadrados de cada desviacion Se divide por el numero de datos menos uno (n 1). Este resultado se denomina la varianza Se saca la raiz cuadrada de la varianza. Este resultado se denomina la desviacion estandar, el cual es el error asociado a un conjunto de mediciones. Las formulas para lo anterior se expresa a continuacion; El promedio es la suma de las observaciones dividida por el numero de mediciones. El promedio de las desviaciones se expresa en valor absoluto La varianza es la suma de los cuadrados de las desviaciones de cada observacion sobre la media. A esta suma se divide por numero de observaciones menos uno La varianza tiene las dimensiones cuadraticas de las observaciones, por lo que es practica comun sacar la raiz cuadrada de la varianza y se obtiene la desviacion estandar. Finalmente toda observacion experimental se expresa con el valor de la tendencia central, el promedio y el intervalo de confianza o error estandar (desviacion estandar). Si consideramos que las desviaciones se distribuyen como una funcion de probabilidad de tipo normal (campana de Gauss) entonces se puede decir que el valor de cada medicion (x) se encuentra dentro del intervalo con una probabilidad de po = Si expresamos el resultado con dos veces la desviacion estandar, entonces tenemos que el valor de x se encuentra en el intervalo con po =.93 PROPAGACION DE ERRORES
6 Supongamos que se miden dos dimensiones con sus respectivos errores (x ± x), (y ± y) y con las mismas unidades, pero se desea encontrar una tercera cantidad que es el resultado de operaciones aritemeticas de las dos primeras mediciones (x, y). Lo cual puede ser: z = x + y z = x y z = x*y z = x/y Por lo tanto se propaga para el resultado (z) a partir de los errores asociados a cada dimension original (x, y). Finalmente se expresa el resultado respectivo con un error propagado. Z ± z Para encontrar el error propagado z se emplean diversas formulas, dependiendo de la operacion aritmetica empleada en el calculo de z. Los valores de x y y corresponden a la desviacion estandar respectiva. Formulas de propagacion de errores: Caso suma y resta Z = x + y z = { ( x) 2 + ( y) 2 } 1/2 Z = x y z = { ( x) 2 + ( y) 2 } 1/2 Caso multiplicacion y division
7 Z = x * y ( z /Zz) = { ( x/x) 2 + ( y/y) 2 } 1/2 Z = x/y ( z/z) = { ( x/x) 2 + ( y/y) 2 } 1/2 Ejemplos:
3 ANALISIS DESCRIPTIVO DE LOS DATOS
 3 ANALISIS DESCRIPTIVO DE LOS DATOS 3.1 La tabulación de los datos 3.1.1 Tabla de distribución de frecuencias. 3.1.2 El histograma. 3.2 Medidas de tendencia central 3.2.1 La media. 3.2.2 La mediana. 3.2.3
3 ANALISIS DESCRIPTIVO DE LOS DATOS 3.1 La tabulación de los datos 3.1.1 Tabla de distribución de frecuencias. 3.1.2 El histograma. 3.2 Medidas de tendencia central 3.2.1 La media. 3.2.2 La mediana. 3.2.3
LABORATORIO No. 0. Cálculo de errores en las mediciones. 0.1 Introducción
 LABORATORIO No. 0 Cálculo de errores en las mediciones 0.1 Introducción Es bien sabido que la especificación de una magnitud físicamente medible requiere cuando menos de dos elementos: Un número y una
LABORATORIO No. 0 Cálculo de errores en las mediciones 0.1 Introducción Es bien sabido que la especificación de una magnitud físicamente medible requiere cuando menos de dos elementos: Un número y una
Mediciones II. Todas las mediciones tienen asociada una incertidumbre que puede deberse a los siguientes factores:
 Mediciones II Objetivos El alumno determinará la incertidumbre de las mediciones. El alumno determinará las incertidumbres a partir de los instrumentos de medición. El alumno determinará las incertidumbres
Mediciones II Objetivos El alumno determinará la incertidumbre de las mediciones. El alumno determinará las incertidumbres a partir de los instrumentos de medición. El alumno determinará las incertidumbres
CALCULO DE INCERTIDUMBRE DE LAS MEDICIONES DE ENSAYOS
 Gestor de Calidad Página: 1 de 5 1. Propósito Establecer una guía para el cálculo de la incertidumbre asociada a las mediciones de los ensayos que se realizan en el. Este procedimiento ha sido preparado
Gestor de Calidad Página: 1 de 5 1. Propósito Establecer una guía para el cálculo de la incertidumbre asociada a las mediciones de los ensayos que se realizan en el. Este procedimiento ha sido preparado
Distribución Gaussiana o normal
 FLUCTUACIONES ESTADÍSTICAS Los postulados fundamentales de la teoría estadística de errores establecen que, dado un conjunto de medidas, todas efectuadas en idénticas condiciones, suficientemente grande
FLUCTUACIONES ESTADÍSTICAS Los postulados fundamentales de la teoría estadística de errores establecen que, dado un conjunto de medidas, todas efectuadas en idénticas condiciones, suficientemente grande
MEDICIÓN Y PROPAGACIÓN DE ERRORES. Comprender el proceso de medición y expresar correctamente el resultado de una medida realizada.
 LABORATORIO Nº 1 MEDICIÓN Y PROPAGACIÓN DE ERRORES I. LOGROS Comprender el proceso de medición y expresar correctamente el resultado de una medida realizada. Aprender a calcular el error propagado e incertidumbre
LABORATORIO Nº 1 MEDICIÓN Y PROPAGACIÓN DE ERRORES I. LOGROS Comprender el proceso de medición y expresar correctamente el resultado de una medida realizada. Aprender a calcular el error propagado e incertidumbre
INTRODUCCIÓN AL CÁLCULO DE INCERTIDUMBRES DE ENSAYO
 INTRODUCCIÓN AL CÁLCULO DE INCERTIDUMBRES DE ENSAYO 1. Introducción 2. Error e incertidumbre 3. Exactitud y precisión de medida 4. Tipos de medidas 5. Incertidumbre típica o de medida 6. Incertidumbre
INTRODUCCIÓN AL CÁLCULO DE INCERTIDUMBRES DE ENSAYO 1. Introducción 2. Error e incertidumbre 3. Exactitud y precisión de medida 4. Tipos de medidas 5. Incertidumbre típica o de medida 6. Incertidumbre
Error en las mediciones
 Error en las mediciones TEORIA DE ERROR-GRAFICOS Y APLICACIÓN Representar en un gráfico los datos obtenidos experimentalmente (encontrar relación funcional) Conocer, comprender y analizar algunos elementos
Error en las mediciones TEORIA DE ERROR-GRAFICOS Y APLICACIÓN Representar en un gráfico los datos obtenidos experimentalmente (encontrar relación funcional) Conocer, comprender y analizar algunos elementos
Teoría de errores. 4 Otro de estos ejemplos pueden ser el de la medición de la densidad de un compuesto sólido o la velocidad de la luz.
 1. Preliminar Cuando se realizan mediciones siempre estamos sujetos a los errores, puesto que ninguna medida es perfecta. Es por ello, que nunca se podrá saber con certeza cual es la medida real de ningún
1. Preliminar Cuando se realizan mediciones siempre estamos sujetos a los errores, puesto que ninguna medida es perfecta. Es por ello, que nunca se podrá saber con certeza cual es la medida real de ningún
Introducción a la Teoría de Errores
 Introducción a la Teoría de Errores March 21, 2012 Al medir experimentalmente una magnitud física (masa, tiempo, velocidad...) en un sistema físico, el valor obtenido de la medida no es el valor exacto.
Introducción a la Teoría de Errores March 21, 2012 Al medir experimentalmente una magnitud física (masa, tiempo, velocidad...) en un sistema físico, el valor obtenido de la medida no es el valor exacto.
2.4. Medidas de variabilidad o dispersión
 2.4. MEDIDAS DE VARIABILIDAD O DISPERSIÓN 55 Q 3 = l i 1 + 3 n/4 N i 1 37, 5 35 a i = 7 + 5 = 9, 5 n i 5 2.4. Medidas de variabilidad o dispersión Los estadísticos de tendencia central o posición nos indican
2.4. MEDIDAS DE VARIABILIDAD O DISPERSIÓN 55 Q 3 = l i 1 + 3 n/4 N i 1 37, 5 35 a i = 7 + 5 = 9, 5 n i 5 2.4. Medidas de variabilidad o dispersión Los estadísticos de tendencia central o posición nos indican
Práctica de Laboratorio. Tema: Contraste de Instrumentos.
 Universidad Nacional de Mar del Plata. Práctica de Laboratorio Tema: Contraste de Instrumentos. Cátedra: Medidas léctricas I 3º año de la carrera de Ingeniería léctrica. Área Medidas léctricas UNMDP. Prof.
Universidad Nacional de Mar del Plata. Práctica de Laboratorio Tema: Contraste de Instrumentos. Cátedra: Medidas léctricas I 3º año de la carrera de Ingeniería léctrica. Área Medidas léctricas UNMDP. Prof.
Introducción al tratamiento de datos
 Introducción al tratamiento de datos MEDICIÓN? MEDICIÓN Conjunto de operaciones cuyo objetivo es determinar el valor de una magnitud o cantidad. Ej. Medir el tamaño de un objeto con una regla. MEDIR? MEDIR
Introducción al tratamiento de datos MEDICIÓN? MEDICIÓN Conjunto de operaciones cuyo objetivo es determinar el valor de una magnitud o cantidad. Ej. Medir el tamaño de un objeto con una regla. MEDIR? MEDIR
Práctica No 1. Análisis estadísticos de los datos termodinámicos
 Práctica No 1 Análisis estadísticos de los datos termodinámicos 1. Objetivo general: Aplicación correcta de las herramientas estadísticas en el manejo de propiedades, tales como: presión, temperatura y
Práctica No 1 Análisis estadísticos de los datos termodinámicos 1. Objetivo general: Aplicación correcta de las herramientas estadísticas en el manejo de propiedades, tales como: presión, temperatura y
INCERTIDUMBRE DE LA MEDIDA
 INCERTIDUMBRE DE LA MEDIDA 22 de septiembre de 2017 1. Resultado de la mediciòn 2. Definiciones 3. Por qué se debe estimar la incertidumbre 3. Modelo matemático 4. Valor mejor estimado 5. Dos métodos de
INCERTIDUMBRE DE LA MEDIDA 22 de septiembre de 2017 1. Resultado de la mediciòn 2. Definiciones 3. Por qué se debe estimar la incertidumbre 3. Modelo matemático 4. Valor mejor estimado 5. Dos métodos de
ERRORES. Identificar las causas de errores en las medidas. Expresar matemáticamente el error de una medida cm cm cm 4 12.
 ERRORES OBJETIVOS Identificar las causas de errores en las medidas.. lasificar los errores según sus causas. Expresar matemáticamente el error de una medida. Determinar el error del resultado de una operación
ERRORES OBJETIVOS Identificar las causas de errores en las medidas.. lasificar los errores según sus causas. Expresar matemáticamente el error de una medida. Determinar el error del resultado de una operación
Algunas nociones básicas sobre Estadística
 Escuela de Formación Básica - Física 1 Laboratorio - 10 Semestre 2010 Comisiones 15 Y 16 (Docentes: Carmen Tachino - Graciela Salum) ntroducción Algunas nociones básicas sobre Estadística Como se ha explicado
Escuela de Formación Básica - Física 1 Laboratorio - 10 Semestre 2010 Comisiones 15 Y 16 (Docentes: Carmen Tachino - Graciela Salum) ntroducción Algunas nociones básicas sobre Estadística Como se ha explicado
DESCRIPCIÓN DE DATOS. Medidas Numéricas
 DESCRIPCIÓN DE DATOS Medidas Numéricas MEDIDAS DE TENDENCIA CENTRAL O POSICIÓN MEDIA ARITMÉTICA O PROMEDIO Media poblacional Cualquier característica medible de una población recibe el nombre de parámetro
DESCRIPCIÓN DE DATOS Medidas Numéricas MEDIDAS DE TENDENCIA CENTRAL O POSICIÓN MEDIA ARITMÉTICA O PROMEDIO Media poblacional Cualquier característica medible de una población recibe el nombre de parámetro
Teoría de errores -Hitogramas
 FÍSICA I Teoría de errores -Hitogramas Autores: Pablo Iván ikel - e-mail: pinikel@hotmail.com Ma. Florencia Kronberg - e-mail:sil_simba@hotmail.com Silvina Poncelas - e-mail:flo_kron@hotmail.com Introducción:
FÍSICA I Teoría de errores -Hitogramas Autores: Pablo Iván ikel - e-mail: pinikel@hotmail.com Ma. Florencia Kronberg - e-mail:sil_simba@hotmail.com Silvina Poncelas - e-mail:flo_kron@hotmail.com Introducción:
ESTADÍSTICA. Población Individuo Muestra Muestreo Valor Dato Variable Cualitativa ordinal nominal. continua
 ESTADÍSTICA Población Individuo Muestra Muestreo Valor Dato Variable Cualitativa ordinal nominal Cuantitativa discreta continua DISTRIBUCIÓN DE FRECUENCIAS Frecuencia absoluta: fi Frecuencia relativa:
ESTADÍSTICA Población Individuo Muestra Muestreo Valor Dato Variable Cualitativa ordinal nominal Cuantitativa discreta continua DISTRIBUCIÓN DE FRECUENCIAS Frecuencia absoluta: fi Frecuencia relativa:
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO
 UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO CENTRO UNIVERSITARIO UAEM ZUMPANGO LICENCIATURA EN TURISMO UNIDAD DE APRENDIZAJE: ESTADISTICA TEMA 1.5 : ESTADISTICA DESCRIPTIVA M. EN C. LUIS ENRIQUE KU MOO FECHA:
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO CENTRO UNIVERSITARIO UAEM ZUMPANGO LICENCIATURA EN TURISMO UNIDAD DE APRENDIZAJE: ESTADISTICA TEMA 1.5 : ESTADISTICA DESCRIPTIVA M. EN C. LUIS ENRIQUE KU MOO FECHA:
INSTITUTO NACIONAL DE ESTADÍSTICAS (INE) 29 de Abril de 2016
 ANEXO ESTADÍSTICO 1 : COEFICIENTES DE VARIACIÓN Y ERROR ASOCIADO AL ESTIMADOR ENCUESTA NACIONAL DE EMPLEO (ENE) INSTITUTO NACIONAL DE ESTADÍSTICAS (INE) 9 de Abril de 016 1 Este anexo estadístico es una
ANEXO ESTADÍSTICO 1 : COEFICIENTES DE VARIACIÓN Y ERROR ASOCIADO AL ESTIMADOR ENCUESTA NACIONAL DE EMPLEO (ENE) INSTITUTO NACIONAL DE ESTADÍSTICAS (INE) 9 de Abril de 016 1 Este anexo estadístico es una
VALOR MEDIO Y DESVIACION ESTANDAR DE UNA SERIE DE MEDIDAS. x 1, x 2, x 3,..., x N. La media aritmética de las N medidas (valor medio o promedio) será:
 VALOR MEDIO Y DESVIACION ESTANDAR DE UNA SERIE DE MEDIDAS Si medimos N veces la magnitud de interés obtendremos los N datos eperimentales: 1, 2, 3,..., N La media aritmética de las N medidas (valor medio
VALOR MEDIO Y DESVIACION ESTANDAR DE UNA SERIE DE MEDIDAS Si medimos N veces la magnitud de interés obtendremos los N datos eperimentales: 1, 2, 3,..., N La media aritmética de las N medidas (valor medio
1.2 Medidas de variación: Rango, desviación estándar y coeficiente de variación
 1.2 Medidas de variación: Rango, desviación estándar y coeficiente de variación Medidas de Variación Amplitud Coeficiente variación Desviación estándar Rango Valor Z Varianza de Diferencia entre los valores
1.2 Medidas de variación: Rango, desviación estándar y coeficiente de variación Medidas de Variación Amplitud Coeficiente variación Desviación estándar Rango Valor Z Varianza de Diferencia entre los valores
Estadística ESTADÍSTICA
 ESTADÍSTICA La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones. Un estudio estadístico consta
ESTADÍSTICA La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones. Un estudio estadístico consta
Metrología e incertidumbre
 1. Introducción Metrología e incertidumbre Universidad Nacional de Colombia Bogotá D.C., Colombia Angie C. Guevara, Daniela A. Casallas, Juan D. Urrea Facultad de ciencias Departamento de física La postura
1. Introducción Metrología e incertidumbre Universidad Nacional de Colombia Bogotá D.C., Colombia Angie C. Guevara, Daniela A. Casallas, Juan D. Urrea Facultad de ciencias Departamento de física La postura
Sistemas de Medición. Unidad I: Conceptos básicos de mediciones
 Unidad I: Conceptos básicos de mediciones Presentado por: Ing. Alvaro Antonio Gaitán Encargado de Cátedra FEC-UNI 20 de abr de 2015 Ing. Electrónica Objetivos de la Unidad I Describir un proceso de medición
Unidad I: Conceptos básicos de mediciones Presentado por: Ing. Alvaro Antonio Gaitán Encargado de Cátedra FEC-UNI 20 de abr de 2015 Ing. Electrónica Objetivos de la Unidad I Describir un proceso de medición
Estadística Inferencial. Estadística Descriptiva
 INTRODUCCIÓN Estadística: Ciencia que trata sobre la teoría y aplicación de métodos para coleccionar, representar, resumir y analizar datos, así como realizar inferencias a partir de ellos. Recogida y
INTRODUCCIÓN Estadística: Ciencia que trata sobre la teoría y aplicación de métodos para coleccionar, representar, resumir y analizar datos, así como realizar inferencias a partir de ellos. Recogida y
Estadística Aplicada
 Estadística Aplicada Universidad Maimónides 2016 Clase 2. Medidas de Tendencia Central y Dispersión Pedro Elosegui Medidas de Descripción del Conjunto de Datos -Estadísticas sumarias que permiten describir
Estadística Aplicada Universidad Maimónides 2016 Clase 2. Medidas de Tendencia Central y Dispersión Pedro Elosegui Medidas de Descripción del Conjunto de Datos -Estadísticas sumarias que permiten describir
Probabilidad y Estadística, EIC 311
 Probabilidad y Estadística, EIC 311 Medida de resumen 1er Semestre 2016 1 / 105 , mediana y moda para datos no Una medida muy útil es la media aritmética de la muestra = Promedio. 2 / 105 , mediana y moda
Probabilidad y Estadística, EIC 311 Medida de resumen 1er Semestre 2016 1 / 105 , mediana y moda para datos no Una medida muy útil es la media aritmética de la muestra = Promedio. 2 / 105 , mediana y moda
Medidas de dispersión
 Medidas de dispersión Las medidas de dispersión nos informan sobre cuánto se alejan del centro los valores de la distribución. Las medidas de dispersión son: Rango o recorrido El rango es la diferencia
Medidas de dispersión Las medidas de dispersión nos informan sobre cuánto se alejan del centro los valores de la distribución. Las medidas de dispersión son: Rango o recorrido El rango es la diferencia
Fundamentos de Estadística y Simulación Básica
 Fundamentos de Estadística y Simulación Básica TEMA 2 Estadística Descriptiva Clasificación de Variables Escalas de Medición Gráficos Tabla de frecuencias Medidas de Tendencia Central Medidas de Dispersión
Fundamentos de Estadística y Simulación Básica TEMA 2 Estadística Descriptiva Clasificación de Variables Escalas de Medición Gráficos Tabla de frecuencias Medidas de Tendencia Central Medidas de Dispersión
UNIVERSO QUE QUEREMOS ESTUDIAR
 EXPERIMENTACION UNIVERSO QUE QUEREMOS ESTUDIAR QUEREMOS saber: Cómo funciona? Cómo evolucionará en el tiempo? EXPERIMENTACION SISTEMA Porción representativa del universo de estudio Obtenemos información
EXPERIMENTACION UNIVERSO QUE QUEREMOS ESTUDIAR QUEREMOS saber: Cómo funciona? Cómo evolucionará en el tiempo? EXPERIMENTACION SISTEMA Porción representativa del universo de estudio Obtenemos información
UNIVERSIDAD DE PUERTO RICO EN HUMACAO DEPARTAMENTO DE QUÍMICA (www.uprh.edu/~quimgen) Revisado: 16/agosto/ 2007
 UNIVERSIDAD DE PUERTO RICO EN HUMACAO DEPARTAMENTO DE QUÍMICA (www.uprh.edu/~quimgen) Revisado: 16/agosto/ 2007 QUIM 3003-3004 MEDIDAS: TRATAMIENTO DE LOS DATOS EXPERIMENTALES I. INTRODUCCIÓN La mayor
UNIVERSIDAD DE PUERTO RICO EN HUMACAO DEPARTAMENTO DE QUÍMICA (www.uprh.edu/~quimgen) Revisado: 16/agosto/ 2007 QUIM 3003-3004 MEDIDAS: TRATAMIENTO DE LOS DATOS EXPERIMENTALES I. INTRODUCCIÓN La mayor
Mediciones Eléctricas
 UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERIA ELECTRICA Y ELECTRONICA Mediciones Eléctricas Ing. Roberto Solís Farfán CIP 84663 1 TEORIA DE ERRORES Cuando se mide una cantidad, ya directa, ya
UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERIA ELECTRICA Y ELECTRONICA Mediciones Eléctricas Ing. Roberto Solís Farfán CIP 84663 1 TEORIA DE ERRORES Cuando se mide una cantidad, ya directa, ya
FISICA I Escuela Politécnica de Ingeniería de Minas y Energía TEORÍA DE ERRORES
 TEORÍA DE ERRORES Se pretende en este capítulo dar una explicación de la Teoría de Errores, lo más somera posible y fundamentalmente práctica, que pueda servir al alumno cuando efectúe sus trabajos en
TEORÍA DE ERRORES Se pretende en este capítulo dar una explicación de la Teoría de Errores, lo más somera posible y fundamentalmente práctica, que pueda servir al alumno cuando efectúe sus trabajos en
Medidas de variabilidad (dispersión)
 Medidas de posición Las medidas de posición nos facilitan información sobre la serie de datos que estamos analizando. Estas medidas permiten conocer diversas características de esta serie de datos. Las
Medidas de posición Las medidas de posición nos facilitan información sobre la serie de datos que estamos analizando. Estas medidas permiten conocer diversas características de esta serie de datos. Las
IMADIL /10/2014
 TEMA 3: Características estadísticas fundamentales (Segunda parte: Dispersión y forma) Ignacio Martín y José Luis Padilla IMADIL 2014-2015 2 POSICIÓN DISPERSIÓN ESTADÍSTICOS SIMETRÍA APUNTAMIENTO 3. ESTADÍSTICOS
TEMA 3: Características estadísticas fundamentales (Segunda parte: Dispersión y forma) Ignacio Martín y José Luis Padilla IMADIL 2014-2015 2 POSICIÓN DISPERSIÓN ESTADÍSTICOS SIMETRÍA APUNTAMIENTO 3. ESTADÍSTICOS
Tema 1: Estadística descriptiva. Probabilidad y Estadística (Ing. Informática). Tema 1: Estadística descriptiva 1
 Tema 1: Estadística descriptiva Probabilidad y Estadística (Ing. Informática). Tema 1: Estadística descriptiva 1 Introducción Objetivo: estudiar una característica o variable en una población. Ejemplos:
Tema 1: Estadística descriptiva Probabilidad y Estadística (Ing. Informática). Tema 1: Estadística descriptiva 1 Introducción Objetivo: estudiar una característica o variable en una población. Ejemplos:
MEDIDAS DE TENDENCIA CENTRAL
 Medidas de Tendencia Central y de Dispersión Ciclo 2017 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE CIENCIAS MÉDICAS FASE I, PRIMER ANO U.D. ESTADISTICA Documento elaborado por: MEDIDAS DE TENDENCIA
Medidas de Tendencia Central y de Dispersión Ciclo 2017 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE CIENCIAS MÉDICAS FASE I, PRIMER ANO U.D. ESTADISTICA Documento elaborado por: MEDIDAS DE TENDENCIA
PRINCIPIOS DE PSICOMETRIA. Universidad Intercontinental Facultad de Psicología Área de la Salud
 PRINCIPIOS DE PSICOMETRIA Universidad Intercontinental Facultad de Psicología Área de la Salud PRINCIPIOS DE PSICOMETRIA MEDICION La medición de habilidades cognitivas Prueba: muestra de una conducta particular.
PRINCIPIOS DE PSICOMETRIA Universidad Intercontinental Facultad de Psicología Área de la Salud PRINCIPIOS DE PSICOMETRIA MEDICION La medición de habilidades cognitivas Prueba: muestra de una conducta particular.
INTRODUCCIÓN AL USO DE PAQUETES COMPUTACIONALES
 INTRODUCCIÓN AL USO DE PAQUETES COMPUTACIONALES TEMAS MEDIDAS DE TENDENCIA CENTRAL MEDIDAS DE DISPERSION MATRICES DEFINICIONES POBLACION: conjunto de elementos de referencia sobre el que se realizan las
INTRODUCCIÓN AL USO DE PAQUETES COMPUTACIONALES TEMAS MEDIDAS DE TENDENCIA CENTRAL MEDIDAS DE DISPERSION MATRICES DEFINICIONES POBLACION: conjunto de elementos de referencia sobre el que se realizan las
RENTABILIDAD Y RIESGO
 RENTABILIDAD Y RIESGO 1. MEDICIONES 1. SITUACIÓN La rentabilidad que tienen que entregar las inversiones, no solo involucran el beneficio natural que debe otorgar al capital por su utilización, sino la
RENTABILIDAD Y RIESGO 1. MEDICIONES 1. SITUACIÓN La rentabilidad que tienen que entregar las inversiones, no solo involucran el beneficio natural que debe otorgar al capital por su utilización, sino la
UNIDAD I. ESTADISTICA
 MEDIDAS DE ESTADÍSTICA DESCRIPTIVA (Tomado de: http://www.universidadabierta.edu.mx/serest/map/metodos%20cuantitativos/py e/tema_12.htm) UNIDAD I. ESTADISTICA 1.2 Medidas Descriptivas MEDIDAS DESCRIPTIVAS
MEDIDAS DE ESTADÍSTICA DESCRIPTIVA (Tomado de: http://www.universidadabierta.edu.mx/serest/map/metodos%20cuantitativos/py e/tema_12.htm) UNIDAD I. ESTADISTICA 1.2 Medidas Descriptivas MEDIDAS DESCRIPTIVAS
Estadística Inga Patricia Juárez, 2017 MEDIDAS DE TENDENCIA CENTRAL
 MEDIDAS DE TENDENCIA CENTRAL Las medidas de tendencia central nos proporcionan la descripción significativa de un conjunto de observaciones. Como su nombre lo indica, son datos de una variable que tienden
MEDIDAS DE TENDENCIA CENTRAL Las medidas de tendencia central nos proporcionan la descripción significativa de un conjunto de observaciones. Como su nombre lo indica, son datos de una variable que tienden
Dr. Richard Mercado Rivera 18 de agosto de 2012 Matemática Elemental
 Universidad de Puerto Rico Recinto de Aguadilla Programa CeCiMat Elemental Definición de conceptos fundamentales de la Estadística y la Probabilidad y su aportación al mundo moderno Dr. Richard Mercado
Universidad de Puerto Rico Recinto de Aguadilla Programa CeCiMat Elemental Definición de conceptos fundamentales de la Estadística y la Probabilidad y su aportación al mundo moderno Dr. Richard Mercado
CÁLCULO DE INCERTIDUMBRE EN LAS MEDICIONES
 OBJETIVOS CÁLCULO DE INCERTIDUMBRE EN LAS MEDICIONES Reportar correctamente resultados, a partir del procesamiento de datos obtenidos a través de mediciones directas. INTRODUCCION En el capítulo de medición
OBJETIVOS CÁLCULO DE INCERTIDUMBRE EN LAS MEDICIONES Reportar correctamente resultados, a partir del procesamiento de datos obtenidos a través de mediciones directas. INTRODUCCION En el capítulo de medición
Medidas de Tendencia Central.
 Medidas de Tendencia Central www.jmontenegro.wordpress.com MEDIDAS DE RESUMEN MDR MEDIDAS DE TENDENCIA CENTRAL MEDIA MEDIANA MODA CUARTILES,ETC. MEDIDAS DE DISPERSIÓN RANGO DESVÍO EST. VARIANZA COEFIC.
Medidas de Tendencia Central www.jmontenegro.wordpress.com MEDIDAS DE RESUMEN MDR MEDIDAS DE TENDENCIA CENTRAL MEDIA MEDIANA MODA CUARTILES,ETC. MEDIDAS DE DISPERSIÓN RANGO DESVÍO EST. VARIANZA COEFIC.
Introducción al estudio de las mediciones
 y fluidos 1.0 Medición Una medición es el resultado de una operación humana de observación mediante la cual se compara una magnitud con un patrón de referencia. Por ejemplo, al medir el diámetro de una
y fluidos 1.0 Medición Una medición es el resultado de una operación humana de observación mediante la cual se compara una magnitud con un patrón de referencia. Por ejemplo, al medir el diámetro de una
CLASE 2 INTRODUCCION A LA ESTADISTICA
 CLASE 2 INTRODUCCION A LA ESTADISTICA Medidas descriptivas Medidas de Centralización o Tendencia Central Nos dan un centro de la distribución de frecuencias, es un valor que se puede tomar como representativo
CLASE 2 INTRODUCCION A LA ESTADISTICA Medidas descriptivas Medidas de Centralización o Tendencia Central Nos dan un centro de la distribución de frecuencias, es un valor que se puede tomar como representativo
Estadísticas aplicadas a la. Javier Toro, Ph.D. Psicólogo Clínico
 Estadísticas aplicadas a la psicología Javier Toro, Ph.D. Psicólogo Clínico MEDIDAS DE TENDENCIA CENTRAL Las medidas de tendencia central son aquellas que identifican el punto en la distribución respecto
Estadísticas aplicadas a la psicología Javier Toro, Ph.D. Psicólogo Clínico MEDIDAS DE TENDENCIA CENTRAL Las medidas de tendencia central son aquellas que identifican el punto en la distribución respecto
Medidas de centralización
 1 1. Medidas de centralización Medidas de centralización Hemos visto cómo el estudio del conjunto de los datos mediante la estadística permite realizar representaciones gráficas, que informan sobre ese
1 1. Medidas de centralización Medidas de centralización Hemos visto cómo el estudio del conjunto de los datos mediante la estadística permite realizar representaciones gráficas, que informan sobre ese
Mediciones experimentales
 Mediciones experimentales Extraído de Análisis de Datos e Incertidumbres en Física Experimental ; S. Pérez, C. Schurrer y G. Stutz; Famaf - UNC La importancia del experimento en la ciencia: La física,
Mediciones experimentales Extraído de Análisis de Datos e Incertidumbres en Física Experimental ; S. Pérez, C. Schurrer y G. Stutz; Famaf - UNC La importancia del experimento en la ciencia: La física,
Cifras significativas e incertidumbre en las mediciones
 Unidades de medición Cifras significativas e incertidumbre en las mediciones Todas las mediciones constan de una unidad que nos indica lo que fue medido y un número que indica cuántas de esas unidades
Unidades de medición Cifras significativas e incertidumbre en las mediciones Todas las mediciones constan de una unidad que nos indica lo que fue medido y un número que indica cuántas de esas unidades
Tema 04: Medición y error
 Tema 04: Medición y error Solicitado: Ejercicios 01: Análisis estadístico M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom 1 Contenido Definiciones
Tema 04: Medición y error Solicitado: Ejercicios 01: Análisis estadístico M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom 1 Contenido Definiciones
1. Estadística. 2. Seleccionar el número de clases k, para agrupar los datos. Como sugerencia para elegir el k
 1. Estadística Definición: La estadística es un ciencia inductiva que permite inferir características cualitativas y cuantitativas de un conjunto mediante los datos contenidos en un subconjunto del mismo.
1. Estadística Definición: La estadística es un ciencia inductiva que permite inferir características cualitativas y cuantitativas de un conjunto mediante los datos contenidos en un subconjunto del mismo.
ESTADÍSTICA BASICA EN CONTROL DE CALIDAD
 ESTADÍSTICA BASICA EN CONTROL DE CALIDAD El control estadístico de la calidad, aplica la teoría del muestreo estadístico, al estudio de las características de calidad. Pretende determinar la variabilidad,
ESTADÍSTICA BASICA EN CONTROL DE CALIDAD El control estadístico de la calidad, aplica la teoría del muestreo estadístico, al estudio de las características de calidad. Pretende determinar la variabilidad,
CONCEPTOS DE ERROR Y TOLERANCIA
 UNIVERSIDAD AUTÓNOMA CHAPINGO DEPARTAMENTO DE IRRIGACIÓN Cap 1. Introducción (Definiciones y conceptos básicos) CONCEPTOS DE ERROR Y TOLERANCIA Profesor: M. C. Fco. Raúl Hernández Saucedo 1 Conceptos de
UNIVERSIDAD AUTÓNOMA CHAPINGO DEPARTAMENTO DE IRRIGACIÓN Cap 1. Introducción (Definiciones y conceptos básicos) CONCEPTOS DE ERROR Y TOLERANCIA Profesor: M. C. Fco. Raúl Hernández Saucedo 1 Conceptos de
Estadísticas Elemental Tema 3: Describir, Explorar, y Comparar Data
 Estadísticas Elemental Tema 3: Describir, Explorar, y Comparar Data (parte 2) Medidas de dispersión 3.1-1 Medidas de dispersión La variación entre los valores de un conjunto de datos se conoce como dispersión
Estadísticas Elemental Tema 3: Describir, Explorar, y Comparar Data (parte 2) Medidas de dispersión 3.1-1 Medidas de dispersión La variación entre los valores de un conjunto de datos se conoce como dispersión
ANÁLISIS CUANTITATIVO POR WDFRX
 ANÁLISIS CUANTITATIVO POR WDFRX El análisis cuantitativo se obtiene mediante la medida de las intensidades de las energías emitidas por la muestra. Siendo la intensidad de la emisión (número de fotones)
ANÁLISIS CUANTITATIVO POR WDFRX El análisis cuantitativo se obtiene mediante la medida de las intensidades de las energías emitidas por la muestra. Siendo la intensidad de la emisión (número de fotones)
ELECTRICIDAD Y MAGNETISMO TRABAJO PRÁCTICO Nº 11 "INSTRUMENTAL Y MEDICIONES ELECTRICAS"
 ELECTRICIDAD Y MAGNETISMO TRABAJO PRÁCTICO Nº 11 "INSTRUMENTAL Y MEDICIONES ELECTRICAS" CONTENIDOS Conceptos básicos de mediciones eléctricas. Tipos de instrumentos de medición. Descripción y Uso de los
ELECTRICIDAD Y MAGNETISMO TRABAJO PRÁCTICO Nº 11 "INSTRUMENTAL Y MEDICIONES ELECTRICAS" CONTENIDOS Conceptos básicos de mediciones eléctricas. Tipos de instrumentos de medición. Descripción y Uso de los
ESTADISTICA DESCRIPTIVA. Mediante la presentación ordenada de los datos observados en tablas y gráficos estadísticos.
 ESTADISTICA DESCRIPTIVA 1. DEFINICION La estadística es una ciencia que facilita la toma de decisiones: Mediante la presentación ordenada de los datos observados en tablas y gráficos estadísticos. Reduciendo
ESTADISTICA DESCRIPTIVA 1. DEFINICION La estadística es una ciencia que facilita la toma de decisiones: Mediante la presentación ordenada de los datos observados en tablas y gráficos estadísticos. Reduciendo
Teoría de la decisión
 1.- Un problema estadístico típico es reflejar la relación entre dos variables, a partir de una serie de Observaciones: Por ejemplo: * peso adulto altura / peso adulto k*altura * relación de la circunferencia
1.- Un problema estadístico típico es reflejar la relación entre dos variables, a partir de una serie de Observaciones: Por ejemplo: * peso adulto altura / peso adulto k*altura * relación de la circunferencia
Criterios de evaluación. Tema 1. Matemáticas. 6º Primaria
 Criterios de evaluación. Tema 1. Matemáticas. 6º Primaria Leer, escribir y descomponer números de hasta nueve cifras Aproximar números naturales a distintos órdenes. Comparar y ordenar números de hasta
Criterios de evaluación. Tema 1. Matemáticas. 6º Primaria Leer, escribir y descomponer números de hasta nueve cifras Aproximar números naturales a distintos órdenes. Comparar y ordenar números de hasta
MEDICIÓN OBJETIVOS. Fundamentos Teóricos. Medición. Cifras Significativas
 OBJETIVOS MEDICIÓN Declarar lo que es una medición, error de una medición, diferenciar precisión de exactitud. Reportar correctamente una medición, con las cifras significativas correspondientes utilizando,
OBJETIVOS MEDICIÓN Declarar lo que es una medición, error de una medición, diferenciar precisión de exactitud. Reportar correctamente una medición, con las cifras significativas correspondientes utilizando,
Medidas de tendencia central
 Medidas de tendencia central Medidas de tendencia central Medidas de Posición: son aquellos valores numéricos que nos permiten o bien dar alguna medida de tendencia central, dividiendo el recorrido de
Medidas de tendencia central Medidas de tendencia central Medidas de Posición: son aquellos valores numéricos que nos permiten o bien dar alguna medida de tendencia central, dividiendo el recorrido de
UNIVERSIDAD LIBRE - SECCIONAL BARRANQUILLA DEPARTAMENTO DE CIENCIAS BASICAS PROGRAMA: MICROBIOLOGÍA Y/O BACTERIOLOGÍA LABORATORIO DE BIOFISICA
 UNIVERSIDAD LIBRE - SECCIONAL BARRANQUILLA DEPARTAMENTO DE CIENCIAS BASICAS PROGRAMA: MICROBIOLOGÍA Y/O BACTERIOLOGÍA LABORATORIO DE BIOFISICA ERRORES EN LAS MEDICIONES. EXPERIENCIA No. 1 Competencias
UNIVERSIDAD LIBRE - SECCIONAL BARRANQUILLA DEPARTAMENTO DE CIENCIAS BASICAS PROGRAMA: MICROBIOLOGÍA Y/O BACTERIOLOGÍA LABORATORIO DE BIOFISICA ERRORES EN LAS MEDICIONES. EXPERIENCIA No. 1 Competencias
UNIVERSIDAD AUTONOMA DEL ESTADO DE MEXICO ESCUELA PREPARATORIA TEXCOCO
 UNIVERSIDAD AUTONOMA DEL ESTADO DE MEXICO ESCUELA PREPARATORIA TEXCOCO MEDIDAS DE TENDENCIA CENTRAL Y DE DISPERSIÓN PARA DATOS NO AGRUPADOS MATERIAL DIDACTICO SOLO VISION ASIGNATURA QUE CORRESPONDE: ESTADISTICA
UNIVERSIDAD AUTONOMA DEL ESTADO DE MEXICO ESCUELA PREPARATORIA TEXCOCO MEDIDAS DE TENDENCIA CENTRAL Y DE DISPERSIÓN PARA DATOS NO AGRUPADOS MATERIAL DIDACTICO SOLO VISION ASIGNATURA QUE CORRESPONDE: ESTADISTICA
UNIDAD 7 Medidas de dispersión
 UNIDAD 7 Medidas de dispersión UNIDAD 7 MEDIDAS DE DISPERSIÓN Al calcular un promedio, por ejemplo la media aritmética no sabemos su representatividad para ese conjunto de datos. La información suministrada
UNIDAD 7 Medidas de dispersión UNIDAD 7 MEDIDAS DE DISPERSIÓN Al calcular un promedio, por ejemplo la media aritmética no sabemos su representatividad para ese conjunto de datos. La información suministrada
ENRIC RUIZ MORILLAS ESTADÍSTICA APLICADA A EXPERIMENTOS Y MEDICIONES
 ENRIC RUIZ MORILLAS ESTADÍSTICA APLICADA A EXPERIMENTOS Y MEDICIONES Índice 1. Experimento y medición...1 2. Frecuencia y probabilidad...3 3. Características teóricas de las variables aleatorias...25 4.
ENRIC RUIZ MORILLAS ESTADÍSTICA APLICADA A EXPERIMENTOS Y MEDICIONES Índice 1. Experimento y medición...1 2. Frecuencia y probabilidad...3 3. Características teóricas de las variables aleatorias...25 4.
CAPITULO 1 MEDICIONES E INCERTIDUMBRES
 CAPITULO 1 MEDICIONES E INCERTIDUMBRES 1.1) Importancia de la Medición La medición ha jugado un papel esencial en la actividad del hombre a lo largo de la historia. El corte de un bloque de piedra para
CAPITULO 1 MEDICIONES E INCERTIDUMBRES 1.1) Importancia de la Medición La medición ha jugado un papel esencial en la actividad del hombre a lo largo de la historia. El corte de un bloque de piedra para
2. EL DISEÑO UNIFACTORIAL (COMPARACION DE TRATAMIENTOS)
 2. EL DISEÑO UNIFACTORIAL (COMPARACION DE TRATAMIENTOS) La idea principal en este capitulo es el inicio a planear los diseño experimentales y su correspondiente análisis estadístico. En este caso iniciaremos
2. EL DISEÑO UNIFACTORIAL (COMPARACION DE TRATAMIENTOS) La idea principal en este capitulo es el inicio a planear los diseño experimentales y su correspondiente análisis estadístico. En este caso iniciaremos
ESTADÍSTICA DESCRIPTIVA
 ESTADÍSTICA DESCRIPTIVA Medidas de tendencia central y de dispersión Giorgina Piani Zuleika Ferre 1. Tendencia Central Son un conjunto de medidas estadísticas que determinan un único valor que define el
ESTADÍSTICA DESCRIPTIVA Medidas de tendencia central y de dispersión Giorgina Piani Zuleika Ferre 1. Tendencia Central Son un conjunto de medidas estadísticas que determinan un único valor que define el
M edidas de dispersión P rof. S. V élez
 M edidas de dispersión P rof. S. V élez Introducción Las medidas de tendencia central permiten describir una distribución por medio de sus valores típicos. Sin embargo estas medidas son sólo parte de la
M edidas de dispersión P rof. S. V élez Introducción Las medidas de tendencia central permiten describir una distribución por medio de sus valores típicos. Sin embargo estas medidas son sólo parte de la
Fase 2. Estudio de mercado: ESTADÍSTICA
 1. CONCEPTO DE ESTADÍSTICA. ESTADÍSTICA DESCRIPTIVA 2. 3. TABLA DE FRECUENCIAS 4. REPRESENTACIONES GRÁFICAS 5. TIPOS DE MEDIDAS: A. MEDIDAS DE POSICIÓN B. MEDIDAS DE DISPERSIÓN C. MEDIDAS DE FORMA 1 1.
1. CONCEPTO DE ESTADÍSTICA. ESTADÍSTICA DESCRIPTIVA 2. 3. TABLA DE FRECUENCIAS 4. REPRESENTACIONES GRÁFICAS 5. TIPOS DE MEDIDAS: A. MEDIDAS DE POSICIÓN B. MEDIDAS DE DISPERSIÓN C. MEDIDAS DE FORMA 1 1.
ESTADÍSTICA. Rincón del Maestro:
 ESTADÍSTICA Definición de Estadística La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones. Conceptos
ESTADÍSTICA Definición de Estadística La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones. Conceptos
INTRODUCCIÓN A LA TEORÍA DE ERRORES Y A LAS TÉCNICAS DEL LABORATORIO DE FÍSICA
 1 INTRODUCCIÓN A LA TEORÍA DE ERRORES Y A LAS TÉCNICAS DEL LABORATORIO DE FÍSICA La medida y la medición como proceso de cuantificar nuestra experiencia, son tan habituales en nuestra vida que apenas nos
1 INTRODUCCIÓN A LA TEORÍA DE ERRORES Y A LAS TÉCNICAS DEL LABORATORIO DE FÍSICA La medida y la medición como proceso de cuantificar nuestra experiencia, son tan habituales en nuestra vida que apenas nos
Estadística descriptiva VARIABLES CUANTITATIVAS
 Estadística descriptiva VARIABLES CUANTITATIVAS DESCRIPTIVA Medidas de tendencia central Media Mediana Moda Medidas de dispersión Rango Varianza Desviación estándar Coeficiente de variación Cuantiles (
Estadística descriptiva VARIABLES CUANTITATIVAS DESCRIPTIVA Medidas de tendencia central Media Mediana Moda Medidas de dispersión Rango Varianza Desviación estándar Coeficiente de variación Cuantiles (
ESTADISTICA Y PROBABILIDAD ESTADÍSTICA
 ESTADÍSTICA La estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comprobaciones y sacar conclusiones. Un estudio estadístico consta
ESTADÍSTICA La estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comprobaciones y sacar conclusiones. Un estudio estadístico consta
MEDIDAS DE TENDENCIA CENTRAL
 MEDIDAS DE TENDENCIA CENTRAL Al describir grupos de observaciones, con frecuencia es conveniente resumir la información con un solo número. Este número que, para tal fin, suele situarse hacia el centro
MEDIDAS DE TENDENCIA CENTRAL Al describir grupos de observaciones, con frecuencia es conveniente resumir la información con un solo número. Este número que, para tal fin, suele situarse hacia el centro
DATOS: 1. DIÁMETRO D (diámetro nominal del cilindro 15 mm): a) Instrumento utilizado: micrómetro de rango 0-25 mm y apreciación 0.01 mm.
 METROLOGIA E INGENIERIA DE CALIDAD 1 EJERCICIO 1 (Modelo resuelto) Se desea determinar el volumen del cilindro hueco de la figura y su correspondiente incertidumbre expandida para un intervalos de confianza
METROLOGIA E INGENIERIA DE CALIDAD 1 EJERCICIO 1 (Modelo resuelto) Se desea determinar el volumen del cilindro hueco de la figura y su correspondiente incertidumbre expandida para un intervalos de confianza
ANEXO 1. CONCEPTOS BÁSICOS. Este anexo contiene información que complementa el entendimiento de la tesis presentada.
 ANEXO 1. CONCEPTOS BÁSICOS Este anexo contiene información que complementa el entendimiento de la tesis presentada. Aquí se exponen técnicas de cálculo que son utilizados en los procedimientos de los modelos
ANEXO 1. CONCEPTOS BÁSICOS Este anexo contiene información que complementa el entendimiento de la tesis presentada. Aquí se exponen técnicas de cálculo que son utilizados en los procedimientos de los modelos
Parte I. Medidas directas. Uso e interpretación de instrumentos
 Parte I. Medidas directas. Uso e interpretación de instrumentos Desarrollo experimental Material y equipo 3 Instrumentos diferentes para medir longitud (también puede ser otra dimensión) 5 Objetos diferentes
Parte I. Medidas directas. Uso e interpretación de instrumentos Desarrollo experimental Material y equipo 3 Instrumentos diferentes para medir longitud (también puede ser otra dimensión) 5 Objetos diferentes
Herramientas estadísticas aplicadas a la validación de métodos analíticos.
 Herramientas estadísticas aplicadas a la validación de métodos analíticos. Analítica Experimental III P. en F. Romero Martínez Marisol Revisión: Dra. Silvia Citlalli Gama González Analítica Experimental
Herramientas estadísticas aplicadas a la validación de métodos analíticos. Analítica Experimental III P. en F. Romero Martínez Marisol Revisión: Dra. Silvia Citlalli Gama González Analítica Experimental
Técnicas de Muestreo Métodos
 Muestreo aleatorio: Técnicas de Muestreo Métodos a) unidad muestral elemental: a.1) muestreo aleatorio simple a.2) muestreo (seudo)aleatorio sistemático a.3) muestreo aleatorio estratificado b) unidad
Muestreo aleatorio: Técnicas de Muestreo Métodos a) unidad muestral elemental: a.1) muestreo aleatorio simple a.2) muestreo (seudo)aleatorio sistemático a.3) muestreo aleatorio estratificado b) unidad
ESTADÍSTICA. A su vez, las variables pueden ser :
 ESTADÍSTICA La ESTADÍSTICA es una rama de las Matemáticas que recoge, ordena, analiza e interpreta datos relativos a un conjunto de personas o cosas ( POBLACIÓN ). La población es FINITA cuando lo es el
ESTADÍSTICA La ESTADÍSTICA es una rama de las Matemáticas que recoge, ordena, analiza e interpreta datos relativos a un conjunto de personas o cosas ( POBLACIÓN ). La población es FINITA cuando lo es el
MANUAL DE PRÁCTICAS DE LABORATORIO
 INSTITUTO TECNOLÓGICO SUPERIOR DE LIBRES MANUAL DE PRÁCTICAS DE LABORATORIO CIENCIAS BASICAS ASIGNATURA: Fundamentos de Física CLAVE: ALC- 1010 ELABORÓ M.C. Martha Irene Bello Ramírez Libres, Puebla FORMATO
INSTITUTO TECNOLÓGICO SUPERIOR DE LIBRES MANUAL DE PRÁCTICAS DE LABORATORIO CIENCIAS BASICAS ASIGNATURA: Fundamentos de Física CLAVE: ALC- 1010 ELABORÓ M.C. Martha Irene Bello Ramírez Libres, Puebla FORMATO
PROBABILIDAD. Unidad I Ordenamiento de la Información
 1 PROBABILIDAD Unidad I Ordenamiento de la Información 2 Captura de datos muestrales Conceptos básicos de la estadística 3 Población (o universo): Totalidad de elementos o cosas bajo consideración Muestra:
1 PROBABILIDAD Unidad I Ordenamiento de la Información 2 Captura de datos muestrales Conceptos básicos de la estadística 3 Población (o universo): Totalidad de elementos o cosas bajo consideración Muestra:
+ f 2. + f 3. p i. =h i 100. F i. = f i. H i. = h i. P i. = p i
 OCIOES de ESTADÍSTICA En las tablas estadísticas se pueden tabular, entre otros, los siguientes aspectos: La frecuencia absoluta ( f i ), es decir, el número de veces que aparece un determinado valor en
OCIOES de ESTADÍSTICA En las tablas estadísticas se pueden tabular, entre otros, los siguientes aspectos: La frecuencia absoluta ( f i ), es decir, el número de veces que aparece un determinado valor en
PREFIJOS MEDIDAS CIFRAS SIGNIFICATIVAS. Prefijo Símbolo Factor de multiplicación
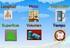 PREFIJOS MEDIDS CIFRS SIGNIFICTIVS 1- Prefijo de múltiplos y submúltiplos: Prefijo Símbolo Factor de multiplicación Tera T x10 12 Giga G x10 9 Mega M x10 6 Kilo K x10 3 Hecto h x10 2 Deca da x10 2 deci
PREFIJOS MEDIDS CIFRS SIGNIFICTIVS 1- Prefijo de múltiplos y submúltiplos: Prefijo Símbolo Factor de multiplicación Tera T x10 12 Giga G x10 9 Mega M x10 6 Kilo K x10 3 Hecto h x10 2 Deca da x10 2 deci
MEDIDAS DE TENDENCIA CENTRAL
 UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS (Universidad del Perú, DECANA DE AMERICA) MEDIDAS DE TENDENCIA CENTRAL 20/05/2008 Ing. SEMS 2.1 INTRODUCCIÓN En el capítulo anterior estudiamos de qué manera los
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS (Universidad del Perú, DECANA DE AMERICA) MEDIDAS DE TENDENCIA CENTRAL 20/05/2008 Ing. SEMS 2.1 INTRODUCCIÓN En el capítulo anterior estudiamos de qué manera los
EXPERIMENTO 2 (DOS SESIONES)
 1 EXPERIMENTO 2 TRATAMIENTO ESTADÍSTICO DE DATOS EXPERIMENTALES Y APLICACIÓN DEL MÉTODO GENERAL PARA EL CÁLCULO DE INCERTIDUMBRE DE MEDICIÓN (MEDIDAS DIRECTAS) (DOS SESIONES) 1. OBJETIVOS Realizar de manera
1 EXPERIMENTO 2 TRATAMIENTO ESTADÍSTICO DE DATOS EXPERIMENTALES Y APLICACIÓN DEL MÉTODO GENERAL PARA EL CÁLCULO DE INCERTIDUMBRE DE MEDICIÓN (MEDIDAS DIRECTAS) (DOS SESIONES) 1. OBJETIVOS Realizar de manera
Medidas descriptivas I. Medidas de tendencia central A. La moda
 Medidas descriptivas I. Medidas de tendencia central A. La moda Preparado por: Roberto O. Rivera Rodríguez Coaching de matemática Escuela Eduardo Neuman Gandía 1 Introducción En muchas ocasiones el conjunto
Medidas descriptivas I. Medidas de tendencia central A. La moda Preparado por: Roberto O. Rivera Rodríguez Coaching de matemática Escuela Eduardo Neuman Gandía 1 Introducción En muchas ocasiones el conjunto
Incertidumbre, Validación y Trazabilidad en el Laboratorio de Análisis Clínicos. Cómo cumplir con requisitos de la ISO 15189
 Incertidumbre, Validación y Trazabilidad en el Laboratorio de Análisis Clínicos Cómo cumplir con requisitos de la ISO 15189 Calidad en mediciones químicas Validación de métodos Estoy midiendo lo que intentaba
Incertidumbre, Validación y Trazabilidad en el Laboratorio de Análisis Clínicos Cómo cumplir con requisitos de la ISO 15189 Calidad en mediciones químicas Validación de métodos Estoy midiendo lo que intentaba
COLEGIO INTERNACIONAL SEK ALBORÁN. Middle Years Programme [PROGRAMA DE AÑOS INTERMEDIOS] CURSO ACADÉMICO
![COLEGIO INTERNACIONAL SEK ALBORÁN. Middle Years Programme [PROGRAMA DE AÑOS INTERMEDIOS] CURSO ACADÉMICO COLEGIO INTERNACIONAL SEK ALBORÁN. Middle Years Programme [PROGRAMA DE AÑOS INTERMEDIOS] CURSO ACADÉMICO](/thumbs/70/62467656.jpg) COLEGIO INTERNACIONAL SEK ALBORÁN Departamento de MATEMÁTICAS Middle Years Programme [PROGRAMA DE AÑOS INTERMEDIOS] CURSO ACADÉMICO 2012-2013 2º ESO Apuntes de estadística y probabilidad 3. ESTADÍSTICA.
COLEGIO INTERNACIONAL SEK ALBORÁN Departamento de MATEMÁTICAS Middle Years Programme [PROGRAMA DE AÑOS INTERMEDIOS] CURSO ACADÉMICO 2012-2013 2º ESO Apuntes de estadística y probabilidad 3. ESTADÍSTICA.
Errores e Incertidumbre. Presentación PowerPoint de Ana Lynch, Profesora de Física Unidad Educativa Monte Tabor Nazaret
 Errores e Incertidumbre Presentación PowerPoint de Ana Lynch, Profesora de Física Unidad Educativa Monte Tabor Nazaret Notación Científica 0 1 2 (1,45 ± 0,05) cm Objetivos: Después de completar este tema,
Errores e Incertidumbre Presentación PowerPoint de Ana Lynch, Profesora de Física Unidad Educativa Monte Tabor Nazaret Notación Científica 0 1 2 (1,45 ± 0,05) cm Objetivos: Después de completar este tema,
Estadística Descriptiva
 Estadística Descriptiva 1 Sesión No. 12 Nombre: Medidas de dispersión Contextualización En la sesión anterior se explicaron los temas relacionados con la desviación estándar, la cual es una medida para
Estadística Descriptiva 1 Sesión No. 12 Nombre: Medidas de dispersión Contextualización En la sesión anterior se explicaron los temas relacionados con la desviación estándar, la cual es una medida para
TERMINOLOGÍA ANALÍTICA - PROCESO ANALÍTICO - TÉCNICA ANALÍTICA - MÉTODO ANALÍTICO - PROCEDIMIENTO ANALÍTICO - PROTOCOLO ANALÍTICO
 TERMINOLOGÍA ANALÍTICA - PROCESO ANALÍTICO - TÉCNICA ANALÍTICA - MÉTODO ANALÍTICO - PROCEDIMIENTO ANALÍTICO - PROTOCOLO ANALÍTICO PROCESO ANALÍTICO Conjunto de operaciones analíticas intercaladas que se
TERMINOLOGÍA ANALÍTICA - PROCESO ANALÍTICO - TÉCNICA ANALÍTICA - MÉTODO ANALÍTICO - PROCEDIMIENTO ANALÍTICO - PROTOCOLO ANALÍTICO PROCESO ANALÍTICO Conjunto de operaciones analíticas intercaladas que se
Diagnóstico. Dirección de Cómputo para la Docencia. UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO Dirección General de Servicios de Cómputo Académico
 TALLER DE APLICACIONES ESTADÍSTICAS CON EXCEL Diagnóstico Elaborado por Mónica Patricia Ballesteros Chávez 1. Es una expresión en Excel que puede incluir operadores, referencias a celdas, valores, funciones
TALLER DE APLICACIONES ESTADÍSTICAS CON EXCEL Diagnóstico Elaborado por Mónica Patricia Ballesteros Chávez 1. Es una expresión en Excel que puede incluir operadores, referencias a celdas, valores, funciones
TEMA 14 ESTADÍSTICA. Cuantitativa: si puede medirse y expresarse con números (es una variable), por ejemplo la talla de calzado.
 Objetivos / Criterios de evaluación TEMA 14 ESTADÍSTICA O.15.1 Conocer el significado y saber calcular los parámetros de centralización y dispersión O.15.2 Interpretar y utilizar los parámetros de dispersión.
Objetivos / Criterios de evaluación TEMA 14 ESTADÍSTICA O.15.1 Conocer el significado y saber calcular los parámetros de centralización y dispersión O.15.2 Interpretar y utilizar los parámetros de dispersión.
