ORTOGONALIDAD Y SISTEMAS DE STURM LIOVILLE
|
|
|
- Tomás Camacho Padilla
- hace 8 años
- Vistas:
Transcripción
1 UNIVERSIDAD DE CONCEPCION FACULTAD DE CIENCIAS FISICAS Y MATEMATICAS Profs. Rúl F Jiméz Emilio Bllo CAPITULO II ORTOGONALIDAD Y SISTEMAS DE STURM LIOVILLE Rordmos qu u oprdor difril lil d ord dfiido l itrvlo [,b] s u trsformió lil L: C [,b] C[,b], dod C [,b] s l spio d ls fuios o drivds otius hst l ord, dfiids [,b] C[,b] s l spio d ls fuios otiu sobr [,b] qu s pud xprsrs l form : L (x)d (x)d + (x), Dd/dx dod los ofiits j (x), j {,---,} so fuios otius tods prts d [,b], (x) o s idétimt ul [,b]. E prtiulr, si f C [,b], tos d L[f(x)] (x) f(x) + + (x)f(x) dx Df.- S di qu u oprdor difril lil d sgudo ord L dfiido u itrvlo [,b] st form utodjut, si pud sribirs omo: ( ( x) D) q( x) L D p +, dod p s ulquir fuió C [,b] tl qu p(x)> (bi p(x)<) pr todo x [,b] q s u fuió rbitrri C [,b] Obs.- Cosidrmos l E D lil d º ord () (x) (x) + (x) (x) + (x) ; (x).x I s p(x) xp (x) (x)dx omo d d d ( x) d p(x) p(x) + p(x) dx dx dx (x) dx tos l uió () s pud sribir o más simplmt d dx d (x) p(x) + p(x) dx (x)
2 d d () p(x) + q(x) dx dx (x) dod q(x) p(x) (x) L uió () s oo omo l form utodjut d l uió (). Ejmplo. L form utodjut d l uió d Lgdr: d d x + ( + ) dx dx (-x ) " -x' +(+) s ( ) EJERCICIOS: Exprsr d us d ls uios siguits form utodjut ) x - x - (-x ), I IR + b) (x -) - x -, I ], [ Df.- U problm o vlors l frotr pr uios difrils lils d º ord osist d : º.- U uió dl tipo () Lh qu L s u oprdor difril lil d º ord dfiido [,b], C [,b], h C [,b] º U pr d odiios d frotr d l form : () α β ( ) + α ( b) + α ( ) + α ( b) γ ( ) + β( b) + β ( ) + β ( b) γ dod α, β γ so ostts i i, j Obs..- Al mos u d ls α i u d ls β i db sr o ul..- () db otr térmios o ulo iludo d uo d los xtrmos.- S dirá qu ls odiios d frotrs dds so homogés si γ γ, tl so brvimos: CCH pr idir odiios d otoro homogés..- El ojuto d ls fuios dos vs difribls [,b] qu stisf ls odiios d frotrs homogés s u subspio S d C [,b]. E st pítulo prdrmos rsolvr PVC d l form: L h (5) P + CCH Ls soluios d u problm tipo P stá ítimmt ligds ls soluios dl PVC:
3 L (6) P + CCH dod s u prámtro dsooido. Obsrvr qu l soluió ul s simpr soluió d P ; pro stmos itrsdos otrr soluios o uls. Afortudmt l problm P o vrifi l torm d uiidd d soluió. Lugo, xist otrs soluios d P, o uls. Obvimt, ss soluios dpdrá dl prámtro. Los vlors d pr los uls l uió L ti soluios o uls u subspio S d C [,b], so llmdos vlors propios (VP) (o vlors rtrístios) d L. L (o ls) fuios o uls soids d vlor propio s llm fuios propis (FP) d L orrspodits s. Ejmplo.- Hllr los VP ls FP dl siguit problm difril: " +, <x<π () '(π) SOL.: Euió rtrísti: r + r ± posibls vlors d :. Lugo, distiguimos trs < : (x) + '(x) + CC: () + π π '(π) - ( + ) o h VP gtivos. : (x) + x '(x) + CC: ; '(π) o s VP. >: (x) A os x + Bs x + CC: () A '(x) Bos x '(π) Bos π os π,b ( ) π π,,,,... ( ) VP:,,,,... sí FP: s x,,,... jmplo. Cosidrmos l uió d Eulr: (7) x " + x ' +, π < x <, o ls CCH : '() '( π ).
4 Sol.: Empmos por sribir l uió form utodjut: t p(x) xp x dt t (x) x ; (x) x; (x) q(x) p(x) ; l x x L form utodjut d l EDO d Eulr s: d d (8) x + dx dx x Por hipótsis, ; lugo sólo disutimos los sos i) : d d d d x x, x π + < < ( x > ) dx dx dx dx (x) lx+ '(x) x CC : ' () (x), t. rbitrri o ul. π ' ( ) ' (x) x s VP Pr, tmos u úi soluió o trivil,.d. (x) s u FP. ii) > : D (8) s obti: x " + ' + x multiplido mbos mimbros por x, rsult : x " + x' + qu s l ooid uió d Eulr t L sustituió x t l x usdo l "rgl d l d", trsform st uió l uió quivlt: "(t)+(t) Pr >, l soluió grl s (t) s t + os t,.d. (x) s( lx) + os( lx) '(x) os( l x) s( l x), x > x x +CC: '() '(x) s( l x), x >. x π π +CC: '( ) s( l ), π
5 5.d. π s(π C ) s(π ) π π,,,,... π π.d. VP:,,,... FP : (x) os l x,,,... Dfiiió. - S L:S V u trsformió lil, dod S V so spios ulidios S s u subspio d V. S di qu L s simétrio o rspto l produto itrior V si : (9) Lx, x,l ; x, S Propidds : ) Todos los vlors propios pr u trsformió lil simétri, sobr u subspio so rls b) Cd pr d vtors propios, orrspodits difrts vlors propios, pr u trsformió lil simétri L: S V so ortogols V. Torm.- S S u subspio d C [,b] dtrmido por u pr d odiios d frotrs homogés : () α () + α β () + β (b) + α (b) + β () + α () + β (b) (b) s L ulquir oprdor difril lil utodjuto, qu trsform S [,b] tos L s simétrio o rspto l produto itrior C[,b] si solo si : b p(x) [ (x) (x) (x)],, S C. Obs.- ) Si () (b) tos () s stisf si rstriió, sí podmos sribir S C [,b] C,b tls qu : b) S S l ojuto d tods ls fuios [ ] () α () + α () β (b) + β (b) 5
6 6 o α + α, β + β Etos () s vrifi d imdito. E fto, si, so dos fuios ulquir S s ti : ( ) ( ) ( ) ( ) () b b b b ( ) ( ) ( ) ( ) NOTA.- U odiió d frotr d form (), qu ivolur vlors d, ' sólo uo d los xtrmos dl itrvlo s oo o l ombr d: CONDICIONES DE FRONTERA NO MIXTAS. tls qu : ) Si S s l subspio d C [,b] qu osist d tods ls fuios () ()(b), () (b) dmás p() p(b) (odiió d omptibilidd) tos () s vrifi pr tod, S. NOTA Ls CCH dl tipo () s llm CONDICIONES PERIÓDICAS. DE FRONTERAS Ejmplo. S L -D dfiido l itrvlo [, π] s S l subspio d C [,π] dsrito por ls odiios d frotrs : () (π) () (π) Como -D D(-D), tos p ( x), x [, π] p ( ) p( π) l subspio d C [.π]. Lugo, L s simétrio dsrito por ls odiios d frotr triors. Pr otrr los vlors propios ls fuios propis rsptivos s db rsolvr l uió difril + o l odiió d frotr : ()(π); '()'(π). Pusto qu L s simétrio tos sus vlors propios so rls sus fuios propis ortogols. S ti qu : i) Si < s obti sólo soluios trivils ii) Si, tos l soluió grl d l EDO. s ( x) 6 + x
7 7 Aplido ls odiios d frotrs s obti ls soluios (x)ct. Así, s vlor propio pr L sobr S. iii) Si > l soluió grl d l E.D. s: (x) C s x + C os x. Aplido odiios d frotrs s obti () ( os π ) C sπ C ( osπ ) C sπ C Ahor, si,,, s ti qu pr ulquir C, C s stisf (), los tros,, 9,... so vlors propios pr L. Así, ls fuios propis so : (x) C sx + C osx Ejmplo 5. Como s vrá más dlt, l siguit PVC pr l studio d l oduió dl lor u illo. "+,-π<x<π (-π)(π) '(-π) '(π) Sol.: S trt d u PVC o CCH priódis. Ats d rsolvrlo, dbmos vrifir si s umpl l "odiió d omptibilidd" : p(x) p(-π)p(π), D l uió rtrísti, dduimos qu dbmos lizr l PVC pr, > <. : " (x) + x +CC: (-π)(π) - π + π π (x) '(x) +CC: '(-π) '(π), qu simpr s válid. Por lo tto s VP, l FP soid s (x) t. o mjor,. < : "+ uió rtrísti: m + m ± (rís rls distits). Podmos dfiir α +, α, sí l soluió grl srá x αx (x) α + απ απ +CC: (-π)(π) + απ + απ απ απ απ απ ( ) ( ). Por otro ldo, αx αx αx αx ' (x) α α α( ) απ απ απ απ +CC: '( π) '( π) ( ) ( ) Como, tos,α. ( ) απ απ 7
8 No h VP gtivos 8 > : L soluió grl s (x) A os x + B s x ' (x) A s x + Bos x +CC: (-π)(π) A os ( π) + B s ( π) A os π + B s π (5) B s π +CC: '(-π)'(π) A s π + B os π A s π + B os π (6) A s π. Lugo, (5) (6), si A B so o uls, tos s π π π,,,... Los VP so,,,,... Así, pr u mismo VP tmos dos soluios l.i.: s(x), os(x), s dir, VP{,,,9,...} ; FP {, osx +sx},,,,,,, Dfiiió.- U problm, o sistm, d Sturm-Liouvill s, por dfiiió, u uió difril lil homogé d sgudo ord d l form d dx p d dx ( x) + ( q( x) ) o p u fuió ulquir C [,b] tl qu p(x)>, o bi p(x)<, x (,b) q s u fuió rbitrri C [,b],, juto o u pr d odiios d frotrs (homogés ) sogids form tl qu ls fuios propis orrspodits D p x D + q x so ortogols difrts vlors propios pr l oprdor ( ( ) ) ( ) Ejmplo 6: Rsolvr l PVC. +, < x < ( ) () + h () SOL: Obvimt L s utodjuto o p; q; ρ. Los VP so positivos l soluió d l EDO s: 8
9 9 (x) os x + s x CC: () (x) s x '(x) os x C: ()+h'() (s + h os ) Si, tos s + h os tg + h tg h π π/ Si hmos α tmos u uió trigoométri: tg α hα, qu o pos soluió xplíit; pro podmos rsolvrl gráfimt u sistm (α, ξ( α)), ξtgα, omo lo mustr l Figur Figur Obsrvmos qu xist ifiits rís α,,,... A d ríz α l orrspod u VP : α,,,.. Por lo tto xist u susió d VP: < < <... o lím ls orrspodits fuios propis so : (x) s x. EJERCICIOS IMPORTANTES: i) Comprub qu los VP ls FP dl PVC: " +, <x<l () (L) π π x so, (x)s,,,,...,rsptivmt, qu los VP ls FP dl L L PVC: " +, <x<l ' () ' (L) π π x so, (x)os,,,,,...,rsptivmt L L ii) Si rlizr álulos, srib los VP ls FP d los siguits PVC: α α π/ π π/ π ) " +, <x< b) " +, <x<π ) " +, <x< d) " +, <x<π () () ' () ' () (L) (π) ' () ' (π) 9
10 Hst l momto hmos visto qu irtos PVC gr vlors propios rls fuios propis ortogols, pro d sbmos sobr posibl bss oformds por sts fuios propis. El siguit Torm os trg u grdbl rspust pro u dmostrió fur dl itrés d st urso. Torm. s L u oprdor difril lil d sgudo ord, dfiido u itrvlo rrdo [,b], s S u subspio d C [,b] dtrmido por u pr d odiios d frotrs o mixts. Etos : º.- L ti u susió ifiit d vlors propios rls { }, dod,,,... tl qu < < o lim C orrspodits difrts vlors propios so uidimsiols º.- Culquir ojuto omplto d fuios propis pr L, u por d vlor propio, s u bs pr C [,b] º.-El dsrrollo sri, d ulquir fuió h suv por trmos [,b], rltiv tl bs, ovrg uiformmt bsolutmt h ulquir itrvlo rrdo qu h s otiu. º.- Los subspios propios d [,b] APLICACIÓN DE LA TEORIA DE STURM-LIOUVILLE A LA RESOLUCION DE PVC. Cosidrmos l uió difril (7) L h qu h s u fuió ooid C[,b], L u oprdor difril lil utodjuto d sgudo ord, tudo sobr l subspio S d C [,b] dfiido por u pr d odiios d frotrs homogés. Pr rsolvr st PVC podmos plir l "método d los vlors propios" pr spios ulidios d dimsió ifiit. E fto, supogmos qu,,, k, so vlors propios pr L sobr S, s ϕ ( ) ϕ ( ) x, x,, l ojuto d fuios propis orrspodits los, IN.Supogmos qu diho ojuto d fuios propis form u bs pr C[,b]. Lugo, podmos sribir l sri grlizd d Fourir pr u lmto h ulquir d s spio l form (8) ( x) ϕ ( x) h (ovrgi mdi) dod los ofiits grlizdos d Fourir stá dfiidos por: (9) h, ϕ ϕ h ( x) ϕ ( x) b b dx [ ϕ ( x) ] dx
11 Si supomos qu l soluió busd ti l form: () (x) α ϕ(x) tos l problm stá rsulto si hllmos los ofiits α. Sustitudo () (7), rsult ϕ(x) () L α ϕ ( x) Ahor,si L pud plirs () térmio térmio, s ti : ϕ(x) () α ϕ( x) d dod s ddu qu () s u soluió d (7) simpr qu : i) ls α pud sogrs tl qu () α, IN o éstos vlors pr α, l sri () α ϕ( x) dfi u fuió C [,b], us primrs dos drivds pud lulrs por drivió térmio térmio d l sri. OBSERVACIONES IMPORTANTES:. Rspto d () ; lrmt α, ( sí xist u úi soluió). Pro si uo d los, digmos, s ro, l problm o ti soluió si, ti ifiits soluios si.. El álisis s ms omplido pus dbmos ivstigr l ovrgi d l sri φ(x). Est ovrgi dpd d ls propidds d h d ls ostts qu rsult dl sistm OG prtiulr {φ (x)}. Lugo, d so dbrá xmirs idividulmt. E grl, pr qu l soluió-sri s "bu" (.d. d ls C ), s rquir qu h s "bu".
12 Ejmplo 7..- Rsulv l PVC: πx x, < x < π () ( π). SOL.: Sbmos qu l SSL soido s ", <x<π () ( π) us FP, d urdo Ejriios Importts, d l pág. 9, so: φ (x) π / los orrspodits vlors propios so,,,,... l sistm ON srá: φ(x) sx ( ( ) ). π π Admás 8 s( )x f(x), x [, π] π ( ) ( ( ) ) 8 S (x) h sx h π, impr. 5 8 s( )x (x). 5 π ( ) EJERCICIO. Dtrmir l soluió forml d l uió frotrs () ( π) x sujt ls odiios d ORTOGONALIDAD CON RESPECTO A UNA FUNCION PESO U grlizió pril importt pr problms o vlors l frotr osist d : ) U uió difril lil lil homogé d º ord d l form d dx d p(x) + dx ( q(x) r(x) ) dfiid [,b] b) U pr d odiios d frotrs homogés qu dfi l spio domiio S pr l oprdor L D[ p(x)d] + q(x) dod p q so fuios C [,b] C[,b] rsptivmt, p(x) o s ul (,b), dms r s u fuió otiu,o gtiv [,b] qu s ul lo ms u umro fiito d putos, llmd fuió podrdor. TEOREMA. S L u oprdor difril lil vrifido ls hipótsis triors, s r u fuió podrdor ulquir [,b], s S u subspio d C,b tl qu [ ]
13 [ (x) (x) (x) (x)] p(x) b pr d pr d fuios, S. Etos, ulquir ojuto d fuios propis orrspodits difrts vlors propios pr L s ortogol C [,b] o rspto l fuió r. NOTA.- Dbmos obsrvr qu grl l oprdor L o s simtrio S o rspto l produto itrior trior, pro l torm firm qu ls fuios propis orrspodits difrts vlors propios so ú ortogols. Pud probrs qu si: ) L : S C[,b] s uo uo b) r( x) >, x [,b] tos C[,b] ti u bs (ojuto OG omplto) formd por ls fuios propis pr L. Pr st rsultdo so importts ls siguits propidds: ) Si S s l subspio d C [,b] dtrmido por odiios d frotrs o mixts, si, so soluios l.i. d l uió L, tos L s uo uo udo s rstrig S, si solmt si, l dtrmit α β ( ) + α ( ) α ( ) + α ( ) ( b) + β ( b) β ( b) + β ( b) b) Si S s l subspio d C [,b] dtrmido por odiios d frotrs priodis, si, so soluios l.i. d l uió L, tos L s uo uo udo s rstrig S, si solmt si, l dtrmit ( ) ( b) ( ) ( b) ( ) ( b) ( ) ( b) Ejmplo 8. Hllr los VP ls FP dl SSL: " ' + (+ ), ( ), () disut l ortogolidd d ls FP soluió. SOL.: Form utodjut: p(x), q(x), ρ(x)
14 d d "- '+(+) + + dx dx d d + ( + ). dx dx /. Rdfiimos p(x),q(x) D ls CC, rsult: p(x) ( ' ')., ρ(x) Ls FP srá OG o rspto l fuió pso ρ (x) C[-,]. L uió rtrísti s: r r + (+ ) r ± x / x / / (x) + + CC so: < Sol. grl. [ ] so: Sol. grl. (x) x / [ + x] + CC so: > Sol. grl. (x) x / os + s x + CC (-) / os s os s (*) CC () / os + s Rstdo sumdo (*) (**), rsult: os + s (**) s os s π π,,,,... os ( ) π ( ) π,,,,... FP : { } x / os( ) πx, x / sπx. Ejmplo 9. ) Hllr l SGF pr f(x)x -x, térmios d ls FP dl SSL : "+ '+(5-) ; ()() " + ' + 5 x b) Hllr l soluió forml dl PVC : () ; () x x x SOL.: Form utodjut: p (x) ;q(x) 5 ; ρ(x) ± ) Euió rtrísti: r + r + 5 r r - ± i) > : (x) ( + ) + CC () - (x) ( ) + CC ().d. o h VP mors qu.
15 5 ii) : (x) ( + x) + CC ().d. o s VP. + CC () (x) x x iii) < : (x) ( os x + s x) + CC () s x + CC () s π (x) VP: - π,,,,...fp: ϕ (x) -x sπx,,,,... Lugo, l ojuto { -x sπx} form u ojuto OG o rspto l fuió podrdor r(x) x C[,]. Por otro ldo, S φ f(x) x x s πxdx. (x) ( ) π sπx + x x, o x sπxdx sí x ( ) π + sπx b) S (x) α sπx l soluió dl problm o α por dtrmir. Lugo, L[] x L α sπx ( ) π + sπx + ( ) α L( sπx) sπx. π.d. + ( ) α sπx sπx π α + ( ) π( π ) Lugo, l soluió dl PVC s: EJERCICIOS. + ( ) (x) sπx. π( π ). Exprs d uo los siguits oprdors difrils lils form utodjut: π π ) D + D +, x> b) (os x)d + (s x)d, < x < x 5
16 6 ) x D + xd + (x p ), x>, sido p u úmro rl. d) ( x )D xd + ( + ), -<x<, sido u tro o gtivo.. Hllr todos los VP ls FP d los SSL rgulrs ) " + () ( π) b) " + () '() ) " + '() '( π) d) " + () () + '() ) " + ( ) (),'( ) '() f ) " + () (π),'() '(π) g) " + () ( π),'() '( π) h) " + ' + (+ ) () () i) " + ' + ( ) () '() j) " ' + ( + ) '() '( π) k) m) x " + x' + (),() (+ x )" + ( + x)' + (), () d [( + x) ' ] l) + dx ( ), () SOLS.: ), φ (x) sx,,,.. b), φ(x) s πx,,,.. ), φ (x) osx,,,,.., π, φ(x),sπx, osπx,, φ(x), sx, osx,, ),,,.. f),.. g),, φ (x), s x, os x,,,.. h) + π, φ(x) sπx,,,.. k) + π, φ(x) s(πlx),,,,.. x 6
17 7 π π l) +, φ(x) s l(x ), IN / l + (x ) l + π π m) +, φ(x) s l( x), IN / l + ( x) l +. Dtrmir todos los VP ls FP d los SSL: ) x " + x' +, () ; ' so otds x b) "+ ; () ; ' so otds l ifiito.. ) Probr qu l PVC : d ω dx ; '() '() () () ti soluios o trivils sí sólo si os ω. osh ω b) Usr l téi d hllr gráfimt los VP, pr dmostrr qu ést PVC ti ifiitos VP o gtivos, dod,,,..cómo s omport stos VP udo? ) Cuál s l soluió grl dl PVC orrspodit l VP? 5. L idi l oprdor difril d urto ord D, S idi l subspio d C [,b] qu osist d tods ls fuios tls qu () "() (b) "(b). ) Dmostrr qu (L ) (L) [ ''' ''' ' " + ' "]', S. b) Usr l rsultdo ) pr probr qu ls FP orrspodits difrts VP pr l PVC L:S C[,b], so OG. 6. Trsform d u d ls siguits EDO l form utodjut quivlt: ) L uió d Lgurr: x "+(-x) '+,,,,,... b) L uió d Hrmit : "-x '+,,,,... ) L uió d Thbhff : (-x ) "-x '+,,,, Prub qu: Si q(x) ρ(x) so otius p(x) s dos vs otiumt difribl [,b], tos ls soluios dl SSL d urto ord [p(x)"(x)]" + [q(x) + ρ(x)](x) [ + (p" )'] [ ' + (p" )] x,[b + b (p" )'],[d ' + d x,b + b, +,d + d (p" )] o + so OG o rspto l fuió pso ρ [,b]. x b x b 7
18 8. E d uo d los siguits PVC, hllr ls FP, los VP dtrmi d so u spio ulidio l qu u ojuto omplto d FP pr l problm ddo, s u ojuto ortogol. ) " + (+ ) ;() ( π) b) " + ( ) ;'() '() ) " + ' + ( ) ;() () d) " ' + ( ) ;() ( π) ) " ' + (+ ) ;( ) () f) " + ( ) ; () + '(),() + '() g) " + ' + ( ) ;'() '( π) h) " ' + ( + ) ; () () i) "+ '+(-9) ; ()(). 8 SOLS: ), φ (x) sx,,,,..; Ortogol C[,π] π, φ(x) sπx, ),,,..; Ortogol C[,] o rspto l fuió pso x. x / πx s,,,6,.. ) π φ, (x) ; Ortogol C[-,] o rspto x / πx os,,,5,.. l fuió pso -x g), φ(x) (osx + sx),,,,..; rspto l fuió pso x., φ(x) ;OG C[,π] o d (r' ) +, < r < r dr 9. Si ls fuios propis dl problm: () + '() lím + (r) < r stisf lím r + r'(r), mustr qu todos los VP so rls pr rls.. Hllr l dsrrollo forml sri d l soluió d los siguits PVC, térmios d ls FP dl SSL soido: 8 + ) "x(x-π), (), '(π) SOL: s x 5 π ( + ) b) "x -π, '(), (π). 8
19 πx ) " s,'(),'(l) SOL.: No h soluió;, L π πx d) " s,(),'(l) L x, x < π / ) ", (), (π) x π /, π / < x π 9 SOL.: k+ ( ) (k ) π (k ) + ( ) s(k )x + 8k k+ k f) "+ ; ()() g) "+ x ; () '() h) "sx ; (); ()+ '() skx i) "-h(x) ; ()(π), '() '(π), osidrdo qu h C[,π]. Sugri: osidr los sos π π h (x)dx h(x)dx sprdmt. SOL.: Si l itgrl d h s distit d ro, o h soluió. Si s ro, tos dod + osx + b sx, π π h(x)osxdx, b π π h(x) sxdx s u t. rbitrri.. Hllr todos los VP ls FP dl SSL "sigulr" x "-x '+(+) osidrdo qu (), lím x + (x) <. Cómo difir los VP d otros problms propustos? [Sugri: Not qu s trt d l uió d Eulr rurd qu udo l poliomio rtrístio ti ris ompljs, l spio soluió (,) stá α α grdo por ls fuios x s( βl x), x os( βl x) ]. π Sol: VP,,,... FP 9 φ (x) πx s,,,... 9
ECUACIONES DIFERENCIALES DE ORDEN SUPERIOR. Ecuaciones lineales homogéneas con coeficientes constates de orden dos y superior.
 Prof Eriqu Mtus Nivs Dotordo Eduió Mtmáti ECUACIONES DIFERENCIALES DE ORDEN SUPERIOR Euios lils homogés o ofiits ostts d ord dos suprior Apliqu l método d rduió pr dtrmir u soluió d l uió o homogé dd los
Prof Eriqu Mtus Nivs Dotordo Eduió Mtmáti ECUACIONES DIFERENCIALES DE ORDEN SUPERIOR Euios lils homogés o ofiits ostts d ord dos suprior Apliqu l método d rduió pr dtrmir u soluió d l uió o homogé dd los
61.1 6.1. SERIES NUMÉRICAS INFINITAS 6.2. SERIES DE TÉRMINOS POSITIVOS 6.3. SERIES ALTERNANTES 6.4. SERIES DE POTENCIAS
 Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
MÉTODO DE LAS SERIES DE TAYLOR PARA RESOLVER ECUACIONES DIFERENCIALES LINEALES Y NO LINEALES
 MÉTODO DE LAS SERIES DE TAYLOR PARA RESOLVER ECUACIONES DIFERENCIALES LINEALES Y NO LINEALES Profsor: José Albiro Sáhz Co Dprtmto d Ciis Básis Ursidd EAFIT josh@fitdo Objto: Aplir l método d Tlor pr rsolr
MÉTODO DE LAS SERIES DE TAYLOR PARA RESOLVER ECUACIONES DIFERENCIALES LINEALES Y NO LINEALES Profsor: José Albiro Sáhz Co Dprtmto d Ciis Básis Ursidd EAFIT josh@fitdo Objto: Aplir l método d Tlor pr rsolr
CÁLCULO DE LÍMITES. Por otro lado es importante distinguir en el cálculo de límites, los casos indeterminados de los determinados: = ; = ; =
 CÁLCULO DE LÍMITES Propidds d los límits.- ( b ) b.- ( b ) b.- ( b ) b.- ( b ) b b.- ( ) ( ) 6.- k k b Por otro ldo s importt distiguir l cálculo d límits, los csos idtrmidos d los dtrmidos: Csos dtrmidos:
CÁLCULO DE LÍMITES Propidds d los límits.- ( b ) b.- ( b ) b.- ( b ) b.- ( b ) b b.- ( ) ( ) 6.- k k b Por otro ldo s importt distiguir l cálculo d límits, los csos idtrmidos d los dtrmidos: Csos dtrmidos:
 OPERACIONES CON LÍMITES DE FUNCIONES Ls oprcios co límits, tto u puto como l ifiito, ti us propidds álogs qu dbmos coocr: PROPIEDADES El límit d l sum o difrci d dos fucios s l sum o difrci d los límits
OPERACIONES CON LÍMITES DE FUNCIONES Ls oprcios co límits, tto u puto como l ifiito, ti us propidds álogs qu dbmos coocr: PROPIEDADES El límit d l sum o difrci d dos fucios s l sum o difrci d los límits
SUCESIONES. El límite de una potencia es igual al límite de la base elevado al límite del exponente.
 SUCESIONES 1. El it d l sucsió d térmio grl A) B) 1 C) 0 + 1 3 + + 3 vl: (Covoctori juio 001. Exm tipo G) El it d u potci s igul l it d l bs lvdo l it dl xpot. + 1 1 Límit d l bs: 3 + 3 Límit dl xpot:
SUCESIONES 1. El it d l sucsió d térmio grl A) B) 1 C) 0 + 1 3 + + 3 vl: (Covoctori juio 001. Exm tipo G) El it d u potci s igul l it d l bs lvdo l it dl xpot. + 1 1 Límit d l bs: 3 + 3 Límit dl xpot:
1.- Estudie el carácter de la serie numérica. 1 es divergente, la serie n propuesta será divergente. Solución.- Puesto que, n = 1, 2, 3,...
 TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mil: imozs@lx.ud.s http://tlfoic.t/wb/imm EJERCICIOS DE SERIES NUMÉRICAS PROPUESTOS EN EXÁMENES.- Estudi l cráctr d l sri uméric. (Fbrro 00, x. or.) Solució.- Pusto
TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mil: imozs@lx.ud.s http://tlfoic.t/wb/imm EJERCICIOS DE SERIES NUMÉRICAS PROPUESTOS EN EXÁMENES.- Estudi l cráctr d l sri uméric. (Fbrro 00, x. or.) Solució.- Pusto
UNIDAD 7 SISTEMAS DE ECUACIONES LINEALES. 1. DEFINICIONES. Un sistema de m ecuaciones lineales con n incógnitas es una expresión de la forma:
 IES Pdr Povd (Gudi) Mtátics II Dprtto d Mtátics Bloqu II: Álgr il Profsor: Ró ort Nvrro Uidd : Sists d Ecucios ils UNIDD SISTEMS DE ECUCIONES INEES DEFINICIONES U sist d cucios lils co icógits s u prsió
IES Pdr Povd (Gudi) Mtátics II Dprtto d Mtátics Bloqu II: Álgr il Profsor: Ró ort Nvrro Uidd : Sists d Ecucios ils UNIDD SISTEMS DE ECUCIONES INEES DEFINICIONES U sist d cucios lils co icógits s u prsió
FUNCIONES DERIVABLES EN UN INTERVALO
 DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. FUNCIONES DERIVABLES EN UN INTERVALO Ls unions qu son ontinus n un intrvlo rrdo [, ] y drivls n un intrvlo irto, tinn propidds importnts. Torm d Roll.
DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. FUNCIONES DERIVABLES EN UN INTERVALO Ls unions qu son ontinus n un intrvlo rrdo [, ] y drivls n un intrvlo irto, tinn propidds importnts. Torm d Roll.
UNIDAD 3: SISTEMAS DE ECUACIONES LINEALES. 1. DEFINICIONES. Un sistema de m ecuaciones lineales con n incógnitas es una expresión de la forma:
 IE Pdr Povd (Gudi) Mtátics plicds ls CC II Dprtto d Mtátics Bloqu I: Álgr il Profsor: Ró ort Nvrro Uidd : ists d Ecucios ils UNIDD : ITEM DE ECUCIONE INEE DEFINICIONE U sist d cucios lils co icógits s
IE Pdr Povd (Gudi) Mtátics plicds ls CC II Dprtto d Mtátics Bloqu I: Álgr il Profsor: Ró ort Nvrro Uidd : ists d Ecucios ils UNIDD : ITEM DE ECUCIONE INEE DEFINICIONE U sist d cucios lils co icógits s
Página 76. Página 78. Página 77. Página 79. Y de la primera: 1. Resolvemos por sustitución: a) Despejo x de la primera y la sustituyo en la segunda:
 Solucios d ls ctividds Pági 6. Rsolvmos por sustitució: ) Dspjo d l primr l sustituo l sgud: ( ) 8 0 Co lo cul: ( ) b) Si multiplico l primr por -, obtgo: + 8 Co lo cul tgo dos rcts coicidts, s dcir, l
Solucios d ls ctividds Pági 6. Rsolvmos por sustitució: ) Dspjo d l primr l sustituo l sgud: ( ) 8 0 Co lo cul: ( ) b) Si multiplico l primr por -, obtgo: + 8 Co lo cul tgo dos rcts coicidts, s dcir, l
6. Sistemas de ecuaciones diferenciales lineales. ( Chema Madoz, VEGAP, Madrid 2009)
 6. Sisms d uios difrils lils Chm Mdoz, VEGAP, Mdrid 9 Sisms d uios lils d primr ord Form orml: f d d f d d f d d Supodrmos qu los ofiis ij y ls fuios f i so oius u irvlo I. Si ods ls f's so ro dirmos qu
6. Sisms d uios difrils lils Chm Mdoz, VEGAP, Mdrid 9 Sisms d uios lils d primr ord Form orml: f d d f d d f d d Supodrmos qu los ofiis ij y ls fuios f i so oius u irvlo I. Si ods ls f's so ro dirmos qu
E.T.S.I. Industriales y Telecomunicación Curso Grados E.T.S.I. Industriales y Telecomunicación
 E.T.S.I. Idustrils y Tlcomuicció Curso 00-0 Grdos E.T.S.I. Idustrils y Tlcomuicció Asigtur: Cálculo I Tm : Sucsios y Sris Numérics. Sris d Potcis. Ejrcicios propustos Obtr los cutro primros térmios, sí
E.T.S.I. Idustrils y Tlcomuicció Curso 00-0 Grdos E.T.S.I. Idustrils y Tlcomuicció Asigtur: Cálculo I Tm : Sucsios y Sris Numérics. Sris d Potcis. Ejrcicios propustos Obtr los cutro primros térmios, sí
6. Sistemas de ecuaciones diferenciales lineales. ( Chema Madoz, VEGAP, Madrid 2009)
 . Sisms d uios difrils lils Chm Mdoz VEGP Mdrid 9 Sisms d uios lils d primr ord Form orml: f d d f d d f d d Supodrmos qu los ofiis i y ls fuios f i so oius u irvlo I. Si ods ls f's so ro dirmos qu l sism
. Sisms d uios difrils lils Chm Mdoz VEGP Mdrid 9 Sisms d uios lils d primr ord Form orml: f d d f d d f d d Supodrmos qu los ofiis i y ls fuios f i so oius u irvlo I. Si ods ls f's so ro dirmos qu l sism
Teoría de Sistemas y Señales
 Toría d Sistmas y Sñals Trasparias: Aálisis ruial d sñals TD Autor: Dr. Jua Carlos Gómz Aálisis ruial d Sñals Timpo Disrto. Sri d ourir d Sñals Timpo Disrto Sa () ua sñal priódia o príodo, s dir: ( ) +
Toría d Sistmas y Sñals Trasparias: Aálisis ruial d sñals TD Autor: Dr. Jua Carlos Gómz Aálisis ruial d Sñals Timpo Disrto. Sri d ourir d Sñals Timpo Disrto Sa () ua sñal priódia o príodo, s dir: ( ) +
Soluciones a los ejercicios, problemas y cuestiones Unidad 2. Polinomios y fracciones algebraicas Matemáticas aplicadas a las Ciencias Sociales I
 Soluios los jriios prolms ustios Ui oliomios rios lgris Mtmátis plis ls Ciis Soils I EJECICIOS SUMA ESTA Y MULTILICACIÓN DE OLINOMIOS Dos los poliomios Dtrmi si stá ruios si so ompltos ii su gro Clul trmi
Soluios los jriios prolms ustios Ui oliomios rios lgris Mtmátis plis ls Ciis Soils I EJECICIOS SUMA ESTA Y MULTILICACIÓN DE OLINOMIOS Dos los poliomios Dtrmi si stá ruios si so ompltos ii su gro Clul trmi
Universidad de Puerto Rico Recinto Universitario de Mayagüez Departamento de Ciencias Matemáticas
 Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }
![1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x } 1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }](/thumbs/64/51459891.jpg) IES P Pov (Gui Mtmátis II UNIDD INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ (Positiv [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los
IES P Pov (Gui Mtmátis II UNIDD INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ (Positiv [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los
= 0 ' = 0 ' Fracciones equivalentes (productos cruzados iguales): c. Fracción generatriz:
 Dprtmto Mtmátis http://www.olgiovirggri.org/so/mt.htm Aritméti. ARITMÉTICA... Cojutos umérios. I Númros tros: úmros turls Númros riols: os juto o sus opustos (úmros imls prióios gtivos). Númros turls:
Dprtmto Mtmátis http://www.olgiovirggri.org/so/mt.htm Aritméti. ARITMÉTICA... Cojutos umérios. I Númros tros: úmros turls Númros riols: os juto o sus opustos (úmros imls prióios gtivos). Númros turls:
(a+1)x+ay=3 (a+1)x+(a+1)y+(a+2)z=1 (a 2 +a)x+(a 2-1)y+(a 2-2a-8)z=2a+5. a 1. a+1. a+2 a 2-2a a+5 ~1 0. a=-1
 EXTRAORDINARIO DE 4. PROBLEMA A. Estudi l siguint sistm d uions linls dpndint dl prámtro rl y rsuélvlo n los sos n qu s omptil: Aplimos l método d Guss: ~ + + + + + - 3 + --6 - -+3 (+)+y3 (+)+(+)y+(+)z
EXTRAORDINARIO DE 4. PROBLEMA A. Estudi l siguint sistm d uions linls dpndint dl prámtro rl y rsuélvlo n los sos n qu s omptil: Aplimos l método d Guss: ~ + + + + + - 3 + --6 - -+3 (+)+y3 (+)+(+)y+(+)z
1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }
![1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x } 1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }](/thumbs/74/71224437.jpg) IES P Pov (Gui Mtmátis II UNIDD : INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los vlos,,
IES P Pov (Gui Mtmátis II UNIDD : INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los vlos,,
I.E.S. Mediterráneo de Málaga Junio 2012 Juan Carlos Alonso Gianonatti PROPUESTA A
 I.E.S. Mditrráno d Málg Junio Jun Crlos lonso Ginontti PROPUEST.- ( punto) S f() un función positiv n l intrvlo [ ] sí ( ) f pr. Si l ár itd por f() l j d bciss (j O) ls rcts s igul clcul l ár dl rcinto
I.E.S. Mditrráno d Málg Junio Jun Crlos lonso Ginontti PROPUEST.- ( punto) S f() un función positiv n l intrvlo [ ] sí ( ) f pr. Si l ár itd por f() l j d bciss (j O) ls rcts s igul clcul l ár dl rcinto
MatemáticasI. 1. Basta con mover el cuadrado para ver que el área de la región limitada es la cuarta parte del cuadrado.
 MtmáticsI UNIDAD : Límits d fucios. Cotiuidd ACTIVIDADES-PÁG. 76. Podmos dcir lo siguit: ) Pr l gráfic dl prtdo I): f ) tid cudo tid f ) tid + cudo tid por l izquird f ) tid - cudo tid por l drch f ) tid
MtmáticsI UNIDAD : Límits d fucios. Cotiuidd ACTIVIDADES-PÁG. 76. Podmos dcir lo siguit: ) Pr l gráfic dl prtdo I): f ) tid cudo tid f ) tid + cudo tid por l izquird f ) tid - cudo tid por l drch f ) tid
26 EJERCICIOS de LOGARITMOS
 6 EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
6 EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
x a es una serie de la forma que el radio de convergencia de la serie geométrica es el intervalo abierto
 ERIE DE POTENCIA ERIE DE POTENCIA. Diició. U sri d pocis c s u sri d l orm c c c c... c... Por jmplo. i c y l sri d pocis om l orm....... Por jmplo. i c y l sri d pocis om l orm....... TEOREMA. El cojuo
ERIE DE POTENCIA ERIE DE POTENCIA. Diició. U sri d pocis c s u sri d l orm c c c c... c... Por jmplo. i c y l sri d pocis om l orm....... Por jmplo. i c y l sri d pocis om l orm....... TEOREMA. El cojuo
UNIVERSIDAD DE LA RIOJA JUNIO lim
 IES Mditrráno d Málg Emn Junio d Jun Crlos lonso Ginontti UNIVERSIDD DE L RIOJ JUNIO El lumno contstrá los jrcicios d un d ls dos propusts ( o ) qu s l ofrcn. Nunc dbrá contstr jrcicios d un propust jrcicios
IES Mditrráno d Málg Emn Junio d Jun Crlos lonso Ginontti UNIVERSIDD DE L RIOJ JUNIO El lumno contstrá los jrcicios d un d ls dos propusts ( o ) qu s l ofrcn. Nunc dbrá contstr jrcicios d un propust jrcicios
Análisis del caso promedio El plan:
 Aálisis dl caso promdio El pla: Probabilidad Aálisis probabilista Árbols biarios d búsquda costruidos alatoriamt Tris, árbols digitals d búsquda y Patricia Listas sip Árbols alatorizados Técicas Avazadas
Aálisis dl caso promdio El pla: Probabilidad Aálisis probabilista Árbols biarios d búsquda costruidos alatoriamt Tris, árbols digitals d búsquda y Patricia Listas sip Árbols alatorizados Técicas Avazadas
Algebra I 1er. Cuatrimestre 2013 Práctica 1 - Conjuntos
 lr I 1r. utrimstr 013 Práti 1 - onjuntos Si s un suonjunto un onjunto rrnil V, notrmos por l omplmnto rspto V. Por onvnión, si x s un númro rl positivo, x not l únio númro rl positivo uyo uro s x. 1. Do
lr I 1r. utrimstr 013 Práti 1 - onjuntos Si s un suonjunto un onjunto rrnil V, notrmos por l omplmnto rspto V. Por onvnión, si x s un númro rl positivo, x not l únio númro rl positivo uyo uro s x. 1. Do
MCD Y MCM DE POLINOMIOS FRACCIONES ALGEBRAICAS
 TRILE pítulo MD Y MM DE POLINOMIOS FRAIONES ALGEBRAIAS Rgl pr lulr l MM y MD Poliomios :. S ftoriz los poliomios os.. El MD strá formo por l multipliió toos los ftors primos omus los poliomios os, osiros
TRILE pítulo MD Y MM DE POLINOMIOS FRAIONES ALGEBRAIAS Rgl pr lulr l MM y MD Poliomios :. S ftoriz los poliomios os.. El MD strá formo por l multipliió toos los ftors primos omus los poliomios os, osiros
UNIVERSIDAD DE CONCEPCIÓN
 .5. SERIES DE FOURIER DE SENOS Y DE COSENOS. Es clro que si f SC[-,] es u fució pr, etoces (9) fx ( ) = + cosx, (CM) SERIE DE FOURIER DE COSENOS (SFC) = co () = f ( x )cos x dx, =,,,3,... Si f SC[-,] es
.5. SERIES DE FOURIER DE SENOS Y DE COSENOS. Es clro que si f SC[-,] es u fució pr, etoces (9) fx ( ) = + cosx, (CM) SERIE DE FOURIER DE COSENOS (SFC) = co () = f ( x )cos x dx, =,,,3,... Si f SC[-,] es
es divergente. es divergente.
 .- Dtrmir l cráctr d l sri sgú los vlors d = +. Solució: sido = + = Si = = lim = s divrgt. = Si < < lim = s divrgt. = Si = = lim = s divrgt. = Si >, plicdo l critrio d D`Almrt: + ( + ) ( + ) + lim = lim
.- Dtrmir l cráctr d l sri sgú los vlors d = +. Solució: sido = + = Si = = lim = s divrgt. = Si < < lim = s divrgt. = Si = = lim = s divrgt. = Si >, plicdo l critrio d D`Almrt: + ( + ) ( + ) + lim = lim
Tema 2 Sucesiones Matemáticas I 1º Bachillerato. 1
 Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
SISTEMAS DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN
 TEMA Nº SISTEMAS DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN. TEOREMA PRELIMINAR INTRODUCCIÓN.- Sism d cucios dircils lils co icógis d l orm P D P D P D P D P P D D... P... P... P D D D b b b dod ls P
TEMA Nº SISTEMAS DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN. TEOREMA PRELIMINAR INTRODUCCIÓN.- Sism d cucios dircils lils co icógis d l orm P D P D P D P D P P D D... P... P... P D D D b b b dod ls P
206 MÉTODOS NUMÉRICOS
 6 MÉTODOS UMÉRICOS.. Alguos hhos mortts r ls rs vs wto: ls sguts so lgus ls ros más mortts ls rs vs wto: (. S s u rmutó K ) ( ) K tos [ K ] [ K ] CASO PARTICULAR: [ ] [ ] ( Est ro s osu l u l olomo trolt
6 MÉTODOS UMÉRICOS.. Alguos hhos mortts r ls rs vs wto: ls sguts so lgus ls ros más mortts ls rs vs wto: (. S s u rmutó K ) ( ) K tos [ K ] [ K ] CASO PARTICULAR: [ ] [ ] ( Est ro s osu l u l olomo trolt
Definiciones. Los valores de los términos necesarios para empezar a calcular se llaman condiciones iniciales.
 Deprtmeto de Mtemáti plid. ETSIIf. UPM. Vitori Zrzos Rodríguez RELCIONES DE RECURRENCI Defiiioes Relió de reurrei o reursiv pr l suesió { } es u epresió que relio el térmio geerl de l suesió o uo o más
Deprtmeto de Mtemáti plid. ETSIIf. UPM. Vitori Zrzos Rodríguez RELCIONES DE RECURRENCI Defiiioes Relió de reurrei o reursiv pr l suesió { } es u epresió que relio el térmio geerl de l suesió o uo o más
TEMA 3: RESOLUCIÓN DE SISTEMAS DE ECUACIONES MEDIANTE DETERMINANTES.
 TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES. º BCH(CN) TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES..-INTRODUCCIÓN. L resoluió de sistems de euioes está ligd l estudio
TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES. º BCH(CN) TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES..-INTRODUCCIÓN. L resoluió de sistems de euioes está ligd l estudio
( ) ( ) El principio de inducción
 El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
Teoría de Sistemas y Señales
 Torí d istms y ñls Trsprcis: Torm dl Mustro Mustro l domiio rcucil Autor: Dr. Ju Crlos Gómz Mustro d ñls Alógics. Covrsió A/D y D/A L myorí d ls sñls d itrés so d tipo lógico. Pr procsr sts sñls form digitl
Torí d istms y ñls Trsprcis: Torm dl Mustro Mustro l domiio rcucil Autor: Dr. Ju Crlos Gómz Mustro d ñls Alógics. Covrsió A/D y D/A L myorí d ls sñls d itrés so d tipo lógico. Pr procsr sts sñls form digitl
Teoría de Sistemas y Señales
 Torí d istms y ñls Trsprcis: Torm dl Mustro Mustro l domiio rcucil Autor: Dr. Ju Crlos Gómz Mustro d ñls Alógics. Covrsió AD y DA L myorí d ls sñls d itrés so d tipo lógico. Pr procsr sts sñls form digitl
Torí d istms y ñls Trsprcis: Torm dl Mustro Mustro l domiio rcucil Autor: Dr. Ju Crlos Gómz Mustro d ñls Alógics. Covrsió AD y DA L myorí d ls sñls d itrés so d tipo lógico. Pr procsr sts sñls form digitl
UNIDAD 9: INTRODUCCIÓN A LAS DERIVADAS
 UNIDAD 9: INTRODUCCIÓN A LAS DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit límit si ist: f f ' lím sigifica lo mismo.
UNIDAD 9: INTRODUCCIÓN A LAS DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit límit si ist: f f ' lím sigifica lo mismo.
TRANSFORMADORES EN PARALELO
 TRNFORMDORE EN PRLELO. Trnsformdors d igul rzón d trnsformción Not: no s tomn n cunt ls pérdids n l firro. q q q llmrmos s cumpl b. Trnsformdors d rzón d trnsformción un poco distints Rfridos l scundrio:
TRNFORMDORE EN PRLELO. Trnsformdors d igul rzón d trnsformción Not: no s tomn n cunt ls pérdids n l firro. q q q llmrmos s cumpl b. Trnsformdors d rzón d trnsformción un poco distints Rfridos l scundrio:
OPCIÓN A. Días de lectura Total de páginas Quijote Eva E D ED Marta E 5 D + 14 (E 5).( D + 14) Susana E 11 D + 44 (E 11).( D + 44)
 IES Mditrráno d Málg Solución Junio Jun Crlos lonso Ginontti OPCIÓN..- Ev Mrt Susn son trs jóvns migs qu s compromtn lr El Quijot st vrno. Cd un por sprdo n unción dl timpo dl qu dispon dcid lr un mismo
IES Mditrráno d Málg Solución Junio Jun Crlos lonso Ginontti OPCIÓN..- Ev Mrt Susn son trs jóvns migs qu s compromtn lr El Quijot st vrno. Cd un por sprdo n unción dl timpo dl qu dispon dcid lr un mismo
Potencial periódico Término de corrección Término sin de segundo orden perturbación Término de corrección de primer orden
 Bds d rgí otdo Tor d Boch. Torí d ctró cs r.org d ds. Modo d Krog-Py. jo. stdo Sódo Potc áss otc qu s usó áss tror fu u otc tt. s áss d uy u rsutdo s s ctr trs tá us ocurr u tto d ctros. S rgo, otros trs
Bds d rgí otdo Tor d Boch. Torí d ctró cs r.org d ds. Modo d Krog-Py. jo. stdo Sódo Potc áss otc qu s usó áss tror fu u otc tt. s áss d uy u rsutdo s s ctr trs tá us ocurr u tto d ctros. S rgo, otros trs
Tema 4: Regresiones lineales y no lineales TEMA 4. REGRESIONES LINEALES LINEALES Y NO. 1. 2. 3. Introducción 4. Nomenclatura
 T 4: grsos lls o lls TEMA 4. EGEIONE LINEALE LINEALE Y NO.. 3. Itroduccó 4. Nocltur 5. Llzcó Ajust grsó ll ll d últpl cucos 6. 7. 8. grsos EUMEN Progrcó o lls Mtlb Cálculo uérco Igrí T 4: grsos lls o lls.
T 4: grsos lls o lls TEMA 4. EGEIONE LINEALE LINEALE Y NO.. 3. Itroduccó 4. Nocltur 5. Llzcó Ajust grsó ll ll d últpl cucos 6. 7. 8. grsos EUMEN Progrcó o lls Mtlb Cálculo uérco Igrí T 4: grsos lls o lls.
UNIVERSIDAD FRANCISCO DE PAULA SANTANDER FACULTAD DE CIENCIAS BASICAS DEPARTAMENTO DE MATEMATICAS Y ESTADISTICA GUIA No. 1. ECUACIONES DIFERENCIALES
 UNIVERSIDAD FRANCISCO DE PAULA SANTANDER FACULTAD DE CIENCIAS BASICAS DEPARTAMENTO DE MATEMATICAS Y ESTADISTICA GUIA No.. ECUACIONES DIFERENCIALES ECUACIONES DIFERENCIALES U cució ircil s u cució l qu
UNIVERSIDAD FRANCISCO DE PAULA SANTANDER FACULTAD DE CIENCIAS BASICAS DEPARTAMENTO DE MATEMATICAS Y ESTADISTICA GUIA No.. ECUACIONES DIFERENCIALES ECUACIONES DIFERENCIALES U cució ircil s u cució l qu
Señales y Sistemas. Análisis de Fourier.
 Sñals y Sistmas Aálisis d Fourir. Itroducció El foqu d st capítulo s la rprstació d sñals utilizado sos y cosos ( otras palabras, xpocials complas). El studio d sñals y sistmas utilizado xpocials complas
Sñals y Sistmas Aálisis d Fourir. Itroducció El foqu d st capítulo s la rprstació d sñals utilizado sos y cosos ( otras palabras, xpocials complas). El studio d sñals y sistmas utilizado xpocials complas
PROGRESIONES. Capítulo TRILCE. Progresión aritmética (P.A.) 3. Número de términos (n)
 TRILCE Cpítulo 7 PROGRESIONES Progrsió ritméti (PA) Es qull susió or l qu térmio, xpto l primro, s igul l térmio trior umto u vlor ostt llmo rzó l progrsió Rprstió u PA r r ( )r Númro térmios () r 4 Térmios
TRILCE Cpítulo 7 PROGRESIONES Progrsió ritméti (PA) Es qull susió or l qu térmio, xpto l primro, s igul l térmio trior umto u vlor ostt llmo rzó l progrsió Rprstió u PA r r ( )r Númro térmios () r 4 Térmios
a se denomina serie a es convergente y SERIES = si r <1 S n La suma de los términos de una sucesión infinita { } n n=1 infinita o simplemente serie
 SERIES L sum de los térmios de u suesió ifiit { } = ifiit o simplemete serie se deomi serie Y se represet o el símbolo = Defiiió: = 4 KK Dd l serie = ésim sum pril = 4 K K, se desigrá S su S = = = 4 K
SERIES L sum de los térmios de u suesió ifiit { } = ifiit o simplemete serie se deomi serie Y se represet o el símbolo = Defiiió: = 4 KK Dd l serie = ésim sum pril = 4 K K, se desigrá S su S = = = 4 K
RADICALES. 1.2.1 Teorema fundamental de la radicación. 1.2.3 Reducción de radicales a índice común. 1.2.4 Potenciación de exponente fraccionario
 RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
al siguiente límite si existe: . Se suele representar por ( x )
 UNIDAD : DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit it si ist: f f ' sigifica lo mismo. f. S sul rprstar por f D
UNIDAD : DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit it si ist: f f ' sigifica lo mismo. f. S sul rprstar por f D
TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES
 3. LÍMITES COLEGIO RAIMUNDO LULIO Frnciscnos T.O.R. Cód. 8367 TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES Dfinición: S dic qu l límit d l función f s igul L, cundo tind, si cundo s proim, f s proim L, sin
3. LÍMITES COLEGIO RAIMUNDO LULIO Frnciscnos T.O.R. Cód. 8367 TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES Dfinición: S dic qu l límit d l función f s igul L, cundo tind, si cundo s proim, f s proim L, sin
3. SERIES DE FOURIER DE SENOS Y DE COSENOS. Es claro que: Si f SC[-π,π] es una función impar, entonces. cosnx, (CM) SERIE DE FOURIER DE COSENOS (SFC)
![3. SERIES DE FOURIER DE SENOS Y DE COSENOS. Es claro que: Si f SC[-π,π] es una función impar, entonces. cosnx, (CM) SERIE DE FOURIER DE COSENOS (SFC) 3. SERIES DE FOURIER DE SENOS Y DE COSENOS. Es claro que: Si f SC[-π,π] es una función impar, entonces. cosnx, (CM) SERIE DE FOURIER DE COSENOS (SFC)](/thumbs/85/92096299.jpg) 3 SERIES DE FOURIER DE SENOS Y DE COSENOS Es clro que: Si f SC[-,] es u fució pr, etoces (9) fx ( ) = + cosx, (CM) SERIE DE FOURIER DE COSENOS (SFC) = co () = f(x)cosxdx, =,,,3, Si f SC[-,] es u fució
3 SERIES DE FOURIER DE SENOS Y DE COSENOS Es clro que: Si f SC[-,] es u fució pr, etoces (9) fx ( ) = + cosx, (CM) SERIE DE FOURIER DE COSENOS (SFC) = co () = f(x)cosxdx, =,,,3, Si f SC[-,] es u fució
APLICACIONES DE LA DIFERENCIAL
 DEINICIÓN DE UNCIÓN DIERENCIABLE Se die que u uió es diereible e u puto si su iremeto puede esribirse de l orm g η es tl que g o depede de los iremetos η udo. Ejemplo: Determir si l uió es diereible. Clulemos
DEINICIÓN DE UNCIÓN DIERENCIABLE Se die que u uió es diereible e u puto si su iremeto puede esribirse de l orm g η es tl que g o depede de los iremetos η udo. Ejemplo: Determir si l uió es diereible. Clulemos
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
IES CASTELAR BADAJOZ Examen Junio de 2011(General) Solución Antonio Mengiano Corbacho UNIVERSIDAD DE EXTREMADURA MATEMÁTICAS II
 IES CASTELAR BADAJOZ Emn Junio d (Gnrl) Antonio ngino Corbcho UNIVERSIDAD DE ETREADURA ATEÁTICAS II ATEÁTICAS II Timpo máimo: hor minutos Instruccions: El lumno lgirá un d ls dos opcions propusts Cd un
IES CASTELAR BADAJOZ Emn Junio d (Gnrl) Antonio ngino Corbcho UNIVERSIDAD DE ETREADURA ATEÁTICAS II ATEÁTICAS II Timpo máimo: hor minutos Instruccions: El lumno lgirá un d ls dos opcions propusts Cd un
Perdidas Secundarias. Operaciones Unitarias Mecánica de Fluidos. Método de los Coeficientes de Perdida de Carga. Perdidas por Fricción Secundarias
 Oprions Unitris Máni d Fluidos Prdids por Friión Sundris EIQ 303 Primr Smstr 0 Prosor: Luis V A Ls prdids por riión (prdids d r) s pudn lsiir n dos tipos: ) ) Prdids Sundris Prdids Primris. Ls prdids d
Oprions Unitris Máni d Fluidos Prdids por Friión Sundris EIQ 303 Primr Smstr 0 Prosor: Luis V A Ls prdids por riión (prdids d r) s pudn lsiir n dos tipos: ) ) Prdids Sundris Prdids Primris. Ls prdids d
FUNCIONES POLINÓMICAS
 Prof.: Lui Tfererry FUNCIONES POLINÓMICAS POLINOMIOS Los poliomios so importtes. El volume de u ilidro r h y su áre totl es rh r. ic El pitl fil produido por u pitl C durte t meses l i% ul, es C. t. 00
Prof.: Lui Tfererry FUNCIONES POLINÓMICAS POLINOMIOS Los poliomios so importtes. El volume de u ilidro r h y su áre totl es rh r. ic El pitl fil produido por u pitl C durte t meses l i% ul, es C. t. 00
DETERMINACIÓN DE LA ACELERACIÓN DE LA GRAVEDAD PÉNDULO SIMPLE
 EERIACIÓ E A ACEERACIÓ E A GRAVEA PÉUO SIPE Atoo J. Brbro / ro Hrdz Puh / Alfoso Clr / Pblo uñz / José A. d oro / Ptr orl pto. Fís Apld UC Pédulo spl O O s Y X os s El oto O td rsturr l posó d qulbro O
EERIACIÓ E A ACEERACIÓ E A GRAVEA PÉUO SIPE Atoo J. Brbro / ro Hrdz Puh / Alfoso Clr / Pblo uñz / José A. d oro / Ptr orl pto. Fís Apld UC Pédulo spl O O s Y X os s El oto O td rsturr l posó d qulbro O
SOLUCIONES DE LIMITES
 SOLUCIONES DE LIMITES.. Ln Sustituyndo por obtnmos: INDETERMINADO Ln Como s trt d un indtrminción d tipo L Hopitl, plicmos dich rgl: Ln Ln Rsolvmos prt l it Ln INDETERMINACIÓN d tipo L Hopitl otr vz: 6Ln
SOLUCIONES DE LIMITES.. Ln Sustituyndo por obtnmos: INDETERMINADO Ln Como s trt d un indtrminción d tipo L Hopitl, plicmos dich rgl: Ln Ln Rsolvmos prt l it Ln INDETERMINACIÓN d tipo L Hopitl otr vz: 6Ln
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE MURCIA JUNIO 2012 (GENERAL) MATEMÁTICAS II SOLUCIONES Tiempo máximo: 1 horas y 30 minutos ----------
 IES ASTELAR BADAJOZ A nguino PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE URIA JUNIO (GENERAL) ATEÁTIAS II SOLUIONES Timpo máimo: hors minutos Osrvcions importnts: El lumno drá rspondr tods ls custions d un d
IES ASTELAR BADAJOZ A nguino PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE URIA JUNIO (GENERAL) ATEÁTIAS II SOLUIONES Timpo máimo: hors minutos Osrvcions importnts: El lumno drá rspondr tods ls custions d un d
3º.- Junio i) Producto de matrices: definición, condiciones para su realización. Si A M m n. (la matriz A tiene m filas y n columnas), B M n p
 IES EL PILES SELECTIVIDD OVIEDO DPTO. MTEMÁTICS Mtrics dtrinnts Mtrics dtrinnts. Ejrcicios d Slctividd. º.- Junio 99. i) Dfin rngo d un triz. ii) Un triz d trs fils trs coluns tin rngo trs, cóo pud vrir
IES EL PILES SELECTIVIDD OVIEDO DPTO. MTEMÁTICS Mtrics dtrinnts Mtrics dtrinnts. Ejrcicios d Slctividd. º.- Junio 99. i) Dfin rngo d un triz. ii) Un triz d trs fils trs coluns tin rngo trs, cóo pud vrir
FUNDAMENTOS MATEMÁTICOS (Grado en Ingeniería Informática) Práctica 7. INTEGRALES DEFINIDAS E IMPROPIAS
 FUNDAMENTOS MATEMÁTICOS (Grdo n Ingnirí Informátic) Práctic 7. INTEGRALES DEFINIDAS E IMPROPIAS.- L intgrl dfinid d Rimnn. L intgrl dfinid d Rimnn surg prtir dl prolm dl cálculo d árs d suprficis dlimitds
FUNDAMENTOS MATEMÁTICOS (Grdo n Ingnirí Informátic) Práctic 7. INTEGRALES DEFINIDAS E IMPROPIAS.- L intgrl dfinid d Rimnn. L intgrl dfinid d Rimnn surg prtir dl prolm dl cálculo d árs d suprficis dlimitds
ACTIVIDADES FINALES EJERCICIOS. trino grau fernández. x lím. lím. lím. lím. sen x 1. x 1. lím x 0 sen x x. lím. x lím. sen x. x arcsen x lím 11.
 L Í M I T E S th ls ACTIVIDADES FINALES EJERCICIOS Ln tg sn sn [ ( )] 5 sn 6 cotg 7 sn sn 8 9 sn rcsn sn b sn sn cotg 5 sn cos 6 sn 7 n 8 Ln 9 Ln trino gru frnándz th ls 5 Clculr pr qu s cumpl: π Ln tg
L Í M I T E S th ls ACTIVIDADES FINALES EJERCICIOS Ln tg sn sn [ ( )] 5 sn 6 cotg 7 sn sn 8 9 sn rcsn sn b sn sn cotg 5 sn cos 6 sn 7 n 8 Ln 9 Ln trino gru frnándz th ls 5 Clculr pr qu s cumpl: π Ln tg
INFERENCIA ESTADISTICA
 Uivrsidad Católica Adrés Bllo UIVERSIDAD CATOLICA ADRES BELLO Urb. Motalbá La Vga Apartado 068 Tléfoo: 47-448 Fa: 47-3043 Caracas, 0 - Vzula Facultad d Igiría Escula d Igiría Iformática -----------------------
Uivrsidad Católica Adrés Bllo UIVERSIDAD CATOLICA ADRES BELLO Urb. Motalbá La Vga Apartado 068 Tléfoo: 47-448 Fa: 47-3043 Caracas, 0 - Vzula Facultad d Igiría Escula d Igiría Iformática -----------------------
3dx dx 3. dx 1-4x. 7. 3xdx 4+x x 2
 MsMtscom Intgrls Clculr l intgrl: ++ + (-) (+) - 7 + 8 ln - cos sn - - - + (+) ln ln 7 8 cos ln + + - +- - - + -+ ++ Ls gráfic (i), (ii) y (iii) corrspondn, no ncsrimnt por s ordn, ls d un función drivbl
MsMtscom Intgrls Clculr l intgrl: ++ + (-) (+) - 7 + 8 ln - cos sn - - - + (+) ln ln 7 8 cos ln + + - +- - - + -+ ++ Ls gráfic (i), (ii) y (iii) corrspondn, no ncsrimnt por s ordn, ls d un función drivbl
1.3.4 Ejercicios resueltos sobre la función exponencial y logarítmica
 .. Ejrcicios rsultos sobr l función ponncil rítmic. Us ls propidds d l función ponncil (torm ) pr simplificr totlmnt l siguint prsión:. Prub qu Simplifiqu inicilmnt l numrdor l dnomindor d l frcción. Así:
.. Ejrcicios rsultos sobr l función ponncil rítmic. Us ls propidds d l función ponncil (torm ) pr simplificr totlmnt l siguint prsión:. Prub qu Simplifiqu inicilmnt l numrdor l dnomindor d l frcción. Así:
8 Límites de sucesiones y de funciones
 Solucioario 8 Límits d sucsios y d ucios ACTIVIDADES INICIALES 8.I. Calcula l térmio gral, l térmio qu ocupa l octavo lugar y la suma d los ocho primros térmios para las sucsios siguits., 6,,,..., 6, 8,,...,,,,...
Solucioario 8 Límits d sucsios y d ucios ACTIVIDADES INICIALES 8.I. Calcula l térmio gral, l térmio qu ocupa l octavo lugar y la suma d los ocho primros térmios para las sucsios siguits., 6,,,..., 6, 8,,...,,,,...
(esta notación fue elegida por el matemático Leonhar Euler) De hecho la función f ( x)
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO FECHA DURACION 9 OCTUBRE
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO FECHA DURACION 9 OCTUBRE
7ma Guía de Estudio 2do Parcial Estudio de Series de Potencia SOLUCIONARIO Guía Complementaria No.07
 álculo tgrl (MAT, Scc.67 r Trimstr, do Smstr doprcil 7mGuíEstudio Documto lordo : M.Sc. g. Julio ésr Lóz Zró H6 7m Guí d Estudio do Prcil Estudio d Sris d Potci SOLUONAO Guí omlmtri No.7 omtrios Grls Ést
álculo tgrl (MAT, Scc.67 r Trimstr, do Smstr doprcil 7mGuíEstudio Documto lordo : M.Sc. g. Julio ésr Lóz Zró H6 7m Guí d Estudio do Prcil Estudio d Sris d Potci SOLUONAO Guí omlmtri No.7 omtrios Grls Ést
Sucesiones de funciones
 Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Utilizando la fórmula que nos proporciona el número de divisores se tiene que:
 Hoj de Prolems º Alger IV /. Hllr u úmero etero A que o teg ms ftores primos que, y 7, siedo demás que ª tiee divisores más que A y que ª tiee divisores ms que A. Clulr tmié l sum de todos los divisores
Hoj de Prolems º Alger IV /. Hllr u úmero etero A que o teg ms ftores primos que, y 7, siedo demás que ª tiee divisores más que A y que ª tiee divisores ms que A. Clulr tmié l sum de todos los divisores
Logaritmos y exponenciales:
 Logrimos ponncils: L rsolución d cucions ponncils s s n l siguin propidd d ls poncis : Dos poncis con un mism s posiiv disin d l unidd son iguls, si sólo si son iguls sus ponns. Es dcir, p. j. Si = noncs
Logrimos ponncils: L rsolución d cucions ponncils s s n l siguin propidd d ls poncis : Dos poncis con un mism s posiiv disin d l unidd son iguls, si sólo si son iguls sus ponns. Es dcir, p. j. Si = noncs
n o ó i Mi nombre: Mi numero de orden: Cuadernillo 1 periodo II MOMENTO DE LA MOVILIZACIÓN NACIONAL POR LA MEJORA DE LOS APRENDIZAJES
 l bim cm CACIÓN EDU bim cm DOS TO C u m ó i c c i d r t m m i trá d D qu d r p d i, r u q rd p l rd m p d T d 2 d u g S g prid Mi mbr: Cudrill 1 Mi umr d rd: II MOMENTO DE LA MOVILIZACIÓN NACIONAL POR
l bim cm CACIÓN EDU bim cm DOS TO C u m ó i c c i d r t m m i trá d D qu d r p d i, r u q rd p l rd m p d T d 2 d u g S g prid Mi mbr: Cudrill 1 Mi umr d rd: II MOMENTO DE LA MOVILIZACIÓN NACIONAL POR
Matemáticas. Si f es una función periódica de período 2T seccionalmente continua, admite la siguiente representación en los puntos de continuidad:
 Mmáics Pági dod s coró s iormció hp://www.losskkdos.com ANÁLISIS LINEAL SERIES DE FOURIER Ejrcicios Rsulos CONCEPOS BÁSICOS Ls sris d Fourir prmi rprsr ucios priódics mdi combicios d sos y cosos sri rigooméric
Mmáics Pági dod s coró s iormció hp://www.losskkdos.com ANÁLISIS LINEAL SERIES DE FOURIER Ejrcicios Rsulos CONCEPOS BÁSICOS Ls sris d Fourir prmi rprsr ucios priódics mdi combicios d sos y cosos sri rigooméric
Árboles binarios. Árbol: definición. Árbol (del latín arbor oris):
 Árol: iniión Árols inrios Árol (l ltín ror oris): Plnt prnn, trono lñoso y lvo, qu s rmii irt ltur l sulo. (otrs, vr Rl Ami Espñol ) Frno Guii Polno Esul Innirí Inustril Pontiii Univrsi Ctóli Vlpríso,
Árol: iniión Árols inrios Árol (l ltín ror oris): Plnt prnn, trono lñoso y lvo, qu s rmii irt ltur l sulo. (otrs, vr Rl Ami Espñol ) Frno Guii Polno Esul Innirí Inustril Pontiii Univrsi Ctóli Vlpríso,
TEMA 5: LÍMITE DE FUNCIONES. CONTINUIDAD.ASÍNTOTAS
 Dpartamto d Matmáticas. IE.S. Ciudad d Arjoa º Bach Socials. LÍMITES Propidads: TEMA : LÍMITE DE FUNCIONES. CONTINUIDAD.ASÍNTOTAS. LÍMITES. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. LÍMITES. RESOLUCIÓN DE INDETERMINACIONES.
Dpartamto d Matmáticas. IE.S. Ciudad d Arjoa º Bach Socials. LÍMITES Propidads: TEMA : LÍMITE DE FUNCIONES. CONTINUIDAD.ASÍNTOTAS. LÍMITES. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. LÍMITES. RESOLUCIÓN DE INDETERMINACIONES.
Integrales impropias
 Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
Clase No. 18 (Segunda parte): Cuadratura Gaussiana MAT 251. Joaquín Peña (CIMAT) Métodos Numéricos (MAT 251) / 10
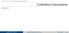 Clse No. 18 (Segund prte): MAT 251 Cudrtur Gussin Joquín Peñ (CIMAT) Métodos Numéricos (MAT 251) 15.10.2012 1 / 10 Introducción Se un función f : [, b] R continu. Dd un prtición = x 0 < x 1 < x 2 < < x
Clse No. 18 (Segund prte): MAT 251 Cudrtur Gussin Joquín Peñ (CIMAT) Métodos Numéricos (MAT 251) 15.10.2012 1 / 10 Introducción Se un función f : [, b] R continu. Dd un prtición = x 0 < x 1 < x 2 < < x
INTEGRAL DEFINIDA ÁREAS Y VOLUMENES
 Intgrl indinid. gl d Brrow INTEGA DEFINIDA ÁEAS Y OUMENES siguint rgl, qu s s n l torm undmntl dl cálculo intgrl, rlcion l intgrl dinid con ls intgrls indinids prmit clculr ls intgrls dinids. intgrl dinid
Intgrl indinid. gl d Brrow INTEGA DEFINIDA ÁEAS Y OUMENES siguint rgl, qu s s n l torm undmntl dl cálculo intgrl, rlcion l intgrl dinid con ls intgrls indinids prmit clculr ls intgrls dinids. intgrl dinid
, 1], del mismo tamaño, pues x 1 = = 1 4, x 2 = = 1 4, x 3 = = 1 4 y x 4 = 1
![, 1], del mismo tamaño, pues x 1 = = 1 4, x 2 = = 1 4, x 3 = = 1 4 y x 4 = 1 , 1], del mismo tamaño, pues x 1 = = 1 4, x 2 = = 1 4, x 3 = = 1 4 y x 4 = 1](/thumbs/87/95639988.jpg) Tem Itegrl de Riem.. Sums iferiores y superiores... Prtiioes de u itervlo. Defiiió. U prtiió de u itervlo errdo [, b] es u ojuto fiito de putos P = {x, x,..., x } dode = x < x < < x = b. U prtiió sepr,
Tem Itegrl de Riem.. Sums iferiores y superiores... Prtiioes de u itervlo. Defiiió. U prtiió de u itervlo errdo [, b] es u ojuto fiito de putos P = {x, x,..., x } dode = x < x < < x = b. U prtiió sepr,
A. DEFINICIÓN DE FUNCIÓN INTEGRABLE. PRIMERAS PROPIEDADES.
 CAPÍTULO X. INTEGRACIÓN DEFINIDA SECCIONES A. Defiició de fució itegrble. Primers propieddes. B. Teorems fudmetles del cálculo itegrl. C. Ejercicios propuestos. A. DEFINICIÓN DE FUNCIÓN INTEGRABLE. PRIMERAS
CAPÍTULO X. INTEGRACIÓN DEFINIDA SECCIONES A. Defiició de fució itegrble. Primers propieddes. B. Teorems fudmetles del cálculo itegrl. C. Ejercicios propuestos. A. DEFINICIÓN DE FUNCIÓN INTEGRABLE. PRIMERAS
( ) ( ) 60 ( ) ( ) ( ) Opción A. Ejercicio A.1- Se sabe qué Calcular, de manera razonada, aplicando las propiedades
 IES Mditáo d Málg Soluió Juio Ju Clos loso Giotti Oió Ejiio.- S s ué. Clul d od lido ls oidds duds l lo d los siguits dtits: B B IES Mditáo d Málg Soluió Juio Ju Clos loso Giotti Ejiio..- Hll l uió dl
IES Mditáo d Málg Soluió Juio Ju Clos loso Giotti Oió Ejiio.- S s ué. Clul d od lido ls oidds duds l lo d los siguits dtits: B B IES Mditáo d Málg Soluió Juio Ju Clos loso Giotti Ejiio..- Hll l uió dl
A puede expresarse como producto de matrices elementales
 TLLER GEOMETRÍ VECTORIL Y NLÍTIC FCULTD DE INGENIERÍ-UNIVERSIDD DE NTIOQUI - Profsor: Jim nrés Jrmillo Gonzálz jimj@onptoomputorsom Prt l mtril s tomo oumntos los profsors lrto Jrmillo Grimlo Ols En los
TLLER GEOMETRÍ VECTORIL Y NLÍTIC FCULTD DE INGENIERÍ-UNIVERSIDD DE NTIOQUI - Profsor: Jim nrés Jrmillo Gonzálz jimj@onptoomputorsom Prt l mtril s tomo oumntos los profsors lrto Jrmillo Grimlo Ols En los
Capítulo 7. Series Numéricas y Series de Potencias.
 Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
CALCULO GRADO EN INGEN. INFORM. DEL SOFTWARE TEMA 3. SUCESIONES Y SERIES. Sucesiones de números reales: monotonía, acotación y convergencia.
 Muel José Ferádez, mjfg@uiovi.es CALCULO GRADO EN INGEN. INFORM. DEL SOFTWARE. - TEMA. SUCESIONES Y SERIES.: Sucesioes umérics. Sucesioes de úmeros reles: mootoí, cotció y covergeci. Se llm sucesió de
Muel José Ferádez, mjfg@uiovi.es CALCULO GRADO EN INGEN. INFORM. DEL SOFTWARE. - TEMA. SUCESIONES Y SERIES.: Sucesioes umérics. Sucesioes de úmeros reles: mootoí, cotció y covergeci. Se llm sucesió de
DERIVADAS. La derivada de una función f en el punto de abscisa x = a, se define como el siguiente límite, si existe:
 DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. DERIVADAS Dinición d drivd. L drivd d un unción n l punto d bscis, s din como l siuint límit, si ist: lím A l drivd d un unción n un punto s l llm tmbién
DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. DERIVADAS Dinición d drivd. L drivd d un unción n l punto d bscis, s din como l siuint límit, si ist: lím A l drivd d un unción n un punto s l llm tmbién
Raíces Reales y Complejas
 Ríces Reles y Complejs Rmó Espioz Armet AVC APOYO VIRTUAL PARA EL CONOCIMIENTO Durte el siglo XVIII, Euler, d Alembert y Lgrge probro, idepedietemete, que todo poliomio de grdo 1 teí u ríz sobre el cmpo
Ríces Reles y Complejs Rmó Espioz Armet AVC APOYO VIRTUAL PARA EL CONOCIMIENTO Durte el siglo XVIII, Euler, d Alembert y Lgrge probro, idepedietemete, que todo poliomio de grdo 1 teí u ríz sobre el cmpo
Se llama sucesión a un conjunto de números dados ordenadamente de modo que se puedan numerar: primero, segundo, tercero,...
 TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN S llama sucsió a u cojuto d úmros dados ordadamt d modo qu s puda umrar: primro, sgudo, trcro,... Los lmtos d la sucsió s llama térmios y s
TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN S llama sucsió a u cojuto d úmros dados ordadamt d modo qu s puda umrar: primro, sgudo, trcro,... Los lmtos d la sucsió s llama térmios y s
MATEMÁTICA D Módulo I: Análisis de Variable Compleja. Teoría de Residuos
 Matmática D MATEMÁTIA D Módulo I: Aálisis d Variabl omplja Uidad Toría d siduos Mag. María Iés Baragatti Sigularidads S dic qu s ua sigularidad aislada d f( si f( o s aalítica pro sí s aalítica u toro
Matmática D MATEMÁTIA D Módulo I: Aálisis d Variabl omplja Uidad Toría d siduos Mag. María Iés Baragatti Sigularidads S dic qu s ua sigularidad aislada d f( si f( o s aalítica pro sí s aalítica u toro
Se llama tasa de variación media (T.V.M.) de una función y = f(x) en un intervalo a. T.V.M. a,b =
 TEMA 7: DERIVADAS 7. Concpto d drivd. Función drivd. 7. Rgls d drivción. 7. CONCEPTO DE DERIVADA. FUNCIÓN DERIVADA. Est concpto mtmático no sólo nos prstrá un yud primordil n l rprsntción d funcions y
TEMA 7: DERIVADAS 7. Concpto d drivd. Función drivd. 7. Rgls d drivción. 7. CONCEPTO DE DERIVADA. FUNCIÓN DERIVADA. Est concpto mtmático no sólo nos prstrá un yud primordil n l rprsntción d funcions y
PROBLEMAS DE LÍMITES DE FUNCIONES (Por métodos algebraicos) Observación: Algunos de estos problemas provienen de las pruebas de Selectividad.
 Funcions Límits y continuidad PROBLEMAS DE LÍMITES DE FUNCIONES Por métodos algbraicos Obsrvación: Algunos d stos problmas provinn d las prubas d Slctividad Si ist l it d una función f cuando a, y si f
Funcions Límits y continuidad PROBLEMAS DE LÍMITES DE FUNCIONES Por métodos algbraicos Obsrvación: Algunos d stos problmas provinn d las prubas d Slctividad Si ist l it d una función f cuando a, y si f
Unidad 2: SUCESIONES Y SERIES NUMÉRICAS.
 Uidd : SUCESIONES Y SERIES NUMÉRICAS. U sucesió es u cojuto ordedo de elemetos que respode u ley de formció. L sucesió suele brevirse: (,...) ( ) =,, 3,..., 3 Siedo el primer térmio, el segudo térmio,
Uidd : SUCESIONES Y SERIES NUMÉRICAS. U sucesió es u cojuto ordedo de elemetos que respode u ley de formció. L sucesió suele brevirse: (,...) ( ) =,, 3,..., 3 Siedo el primer térmio, el segudo térmio,
Cómo es la distribución de los alimentos servidos?
 Cómo s l distribució d los limtos srvis? 5 " Co u bu limt ció, p Los iños y iñs s ppr pr cosumir los limtos 6 CUÁL ES EL OBJETIVO? Promovr y forzr buos hábitos d higi los iños y iñs como l lv d mos ts
Cómo s l distribució d los limtos srvis? 5 " Co u bu limt ció, p Los iños y iñs s ppr pr cosumir los limtos 6 CUÁL ES EL OBJETIVO? Promovr y forzr buos hábitos d higi los iños y iñs como l lv d mos ts
POTENCIA BASE EXPONENTE VALOR
 TEMA POTENCIAS Y RADICALES CONCEPTO DE POTENCIA Un potni s un or rvi sriir un prouto oro por vrios tors iuls. = Los lntos qu onstitun un potni son L s l potni s l núro qu ultiplios por sí iso n st so l.
TEMA POTENCIAS Y RADICALES CONCEPTO DE POTENCIA Un potni s un or rvi sriir un prouto oro por vrios tors iuls. = Los lntos qu onstitun un potni son L s l potni s l núro qu ultiplios por sí iso n st so l.
5 Integral doble de Riemann
 Miguel eyes, Dpto. de Mtemáti Aplid, FI-UPM 1 5 Integrl doble de iemnn 5.1 Definiión Llmremos retángulo errdo de 2 l produto de dos intervlos errdos y otdos de, es deir = [, b] [, d] = { (x, y) 2 : x b,
Miguel eyes, Dpto. de Mtemáti Aplid, FI-UPM 1 5 Integrl doble de iemnn 5.1 Definiión Llmremos retángulo errdo de 2 l produto de dos intervlos errdos y otdos de, es deir = [, b] [, d] = { (x, y) 2 : x b,
Electrónica Básica. Álgebra de Boole. Electrónica Digital. José Ramón Sendra Sendra Dpto. de Ingeniería Electrónica y Automática ULPGC
 Eletrói Bási Álger de Boole Eletrói Digitl José Rmó Sedr Sedr Dpto. de Igeierí Eletrói y Automáti ULPGC 2 Ciruito de omutió p.e. sistem de otrol idustril sistem teleóio ordedor et. El Álger de Boole sirve
Eletrói Bási Álger de Boole Eletrói Digitl José Rmó Sedr Sedr Dpto. de Igeierí Eletrói y Automáti ULPGC 2 Ciruito de omutió p.e. sistem de otrol idustril sistem teleóio ordedor et. El Álger de Boole sirve
Olimpiada Costarricense de Matemáticas. II Eliminatoria Curso preparatorio Nivel B. Elaborado por: Christopher Trejos Castillo ÁLGEBRA
 Olimpid Costrricese de Mtemátics II Elimitori 011 Curso preprtorio Nivel B Elbordo por: Christopher Trejos Cstillo ÁLGEBRA Iicimos demostrdo dos resultdos que puede ser importtes pr resolver problems olímpicos.
Olimpid Costrricese de Mtemátics II Elimitori 011 Curso preprtorio Nivel B Elbordo por: Christopher Trejos Cstillo ÁLGEBRA Iicimos demostrdo dos resultdos que puede ser importtes pr resolver problems olímpicos.
